CryoPROS: Correcting misalignment caused by preferred orientation using AI-generated auxiliary particles

Abstract

The preferred orientation phenomenon is a common issue in cryo-EM, posing a persistent challenge to conventional reconstruction methods. In this study, we introduce cryoPROS, a computational framework designed to correct misalignment caused by preferred orientation through co-refining the raw and auxiliary particles. These auxiliary particles, generated using a self-supervised deep generative model, enhance the alignment accuracy of particles in datasets affected by preferred orientation. CryoPROS achieved near-atomic resolution with the untilted HA-trimer dataset and successfully resolved high-resolution structures from three experimental datasets, including P001-Y, Na_X, and hormone-sensitive lipase dimer, all affected by preferred orientation issues. Extensive experiments validate the robustness of cryoPROS and its minimal risk of introducing model bias. These findings suggest that in many cases thought to suffer from preferred orientation, addressing misalignment issues can lead to significant improvements in the density map.

Introduction

Recent advancements in cryogenic electron microscopy (cryo-EM) hardware and image processing software have ushered in a transformative era in structure determination, establishing it as the predominant method in structural biology. Despite these advances, a significant challenge that continues to impede structural analysis is the issue of preferred orientation^{1,2,3,4,5,6,7}. Ideally, biological macromolecules of interest should exhibit uniformly random orientations within the vitreous amorphous ice. However, it is commonly observed that samples tend to adopt a specific, preferred orientation due to interactions at the air-water or the support-water interface^8,9. Using conventional computational methods to analyze preferred orientation data often results in significant artifacts in density maps^10,11.

Numerous attempts have been made to address the preferred orientation in cryo-EM, focusing mainly on grid preparation and data collection. Techniques such as using detergents^12,13,14,15, ice thickening¹⁶, shortening the spot-to-plunge time¹⁷, and biomolecule modifications¹⁸ have shown promise with specific proteins but often require time-consuming and costly condition screening. Replacing the grid and foil, as well as introducing graphene supports, has been explored to equalize particle pose distribution^19,20, but their success is case-dependent or only partially effective. Tilt collection strategy⁴ offers an alternative by bypassing sample preparation challenges, but it introduces drawbacks such as reduced image acquisition efficiency, increased beam-induced movement, elevated noise levels due to the longer path electrons must travel, and the need for precise defocus gradient estimation⁸. Although per-particle CTF and motion refinements have been proposed to mitigate resolution drops from tilt collection^21,22, these methods involve complex parameter adjustments and can be unstable, particularly for small proteins, which are more likely to suffer from preferred orientation than larger ones. Despite these efforts, tilt collection remains one of the most effective solutions. On the other hand, the computational aspect remains underexplored, particularly concerning whether advanced algorithms can be developed to reconstruct high-resolution density maps from previously unsolved preferred orientation datasets.

When a dataset exhibits a preferred orientation problem, particles from non-preferred views are typically present, but in much lower quantities compared to those from preferred views. Achieving isotropic reconstruction depends heavily on the number of particles captured from these non-preferred orientations. If the number is too small, for instance, below the theoretical threshold predicted by Rosenthal and Henderson²³, reconstructing a high-resolution map becomes impossible without incorporating additional data or prior knowledge. However, since the number of particles required in each direction increases exponentially with resolution²³, if a small degree of anisotropy is acceptable, even a limited number of particles from non-preferred orientations may suffice. As a result, in many datasets with preferred orientation, the particles may still be sufficient to recover a satisfactory density map, provided that they are utilized effectively. In such cases, we found that misalignment becomes the primary computational bottleneck during the refinement process, particularly affecting the axial resolution. While adopting a high-quality initial reference model in conventional methods often helps alleviate misalignment, we observed that this approach is usually insufficient and frequently fails to achieve satisfactory results in many challenging preferred orientation datasets. This suggests a need for new computational tools to address misalignment issues in these datasets.

In this work, we introduce cryoPROS (PReferred Orientation dataset Solver), a computational framework designed to address the misalignment issues caused by preferred orientation in cryo-EM. This framework integrates raw and auxiliary particles through a co-refinement process. By leveraging the expressive power of deep neural networks and employing a conditional generative model, these auxiliary particles are generated in a self-supervised manner^24,25. The combined dataset, which includes both raw and auxiliary particles, results in a more balanced pose distribution. This significantly improves the alignment accuracy of raw particles when using conventional pose estimation software. To the best of our knowledge, this methodology of enhancing raw particles with auxiliary particles has not yet been applied to cryo-EM analysis. Additionally, the inherently low signal-to-noise ratio (SNR) in cryo-EM presents a challenge for data synthesis. CryoPROS addresses this by utilizing a hierarchical variational autoencoder (VAE) model within its generative module, enabling the synthesis of auxiliary particles without the need for training samples. We demonstrate that cryoPROS can achieve near-atomic resolution of the HA-trimer solely through the utilization of untilted data⁴, exhibiting performance on par with cutting-edge outcomes derived from the per-particle refinement of tilt-collected datasets. Such per-particle refinement encompasses various techniques, including per-particle polishing²⁶, contrast transfer function (CTF) refinement^21,27, and 3D classification. We also find that cryoPROS can be adapted for membrane proteins by filtering micelle effects using our ReconDisMis algorithm for initializing the reference model. Our results with four unpublished datasets—Na_X, hormone-sensitive lipase dimer (HSL-dimer), P001-Y, P002-M—demonstrate cryoPROS’s ability to recover high-resolution structures from preferentially orientated datasets. Finally, through comprehensive analysis and testing, we validate cryoPROS’s low model bias, affirming its reliability as a valuable tool in cryo-EM. By integrating auxiliary particles with raw data through co-refinement, this approach addresses the misalignment caused by preferred orientation, providing the cryo-EM community with new strategies to tackle datasets with preferred orientation issues.

Results

Misalignment: a key challenge for processing preferred orientation datasets

In many preferred orientation datasets, particles from non-preferred views are not entirely absent but are significantly fewer in number compared to those from preferred views. This highly imbalanced pose distribution poses challenges for conventional 2D or 3D classification methods, which often rely on K-means clustering and assume equal-sized clusters^{28,29,30,31,32,33}. As a result, signals from particles in non-preferred views are frequently overshadowed by those from dominant preferred views. A similar principle applies during the refinement process, leading to misalignments and the introduction or amplification of artifacts in subsequent reconstruction.

Meanwhile, if a slight degree of anisotropic resolution is acceptable, the required number of particles from non-preferred views can be reduced exponentially²³. Although the number of particles from non-preferred views is small for many unsolved preferred orientation datasets, this indicates that additional data may not be necessary, and that misalignment is likely the primary challenge in the reconstruction process (see “Discussion” for more details).

We evaluated the impact of misalignment during refinement using two synthesized preferred orientation datasets: Uni-HA-Syn and PO-HA-Syn (see Table 1 and Methods). Both datasets contain 130,000 noisy particles. The Uni-HA-Syn dataset has a uniform directional distribution, while the PO-HA-Syn dataset is biased toward orientations near the Z-axis (Fig. 1a). The distribution of the PO-HA-Syn dataset mirrors that of the untilted HA-trimer (EMPIAR-10096), ensuring an accurate replication of the true pose distribution of the HA-trimer. The reconstruction-only density maps for both datasets are shown in Fig. 1b, demonstrating similar quantitative performance (Supplementary Table 1) with a model-to-map resolution of 2.62 Å. However, the post-refinement density map of the PO-HA-Syn dataset, with pose re-estimated by CryoSPARC, shows significant deterioration, with the model-to-map resolution dropping to 23.95 Å (Fig. 1b, bottom). This degradation is attributable to misalignment during the refinement process. Specifically, CryoSPARC’s autorefine module misassigned 35,706 out of 82,709 particles (approximately 43.1%), with many particles originally in the preferred (top) view incorrectly reassigned to a non-preferred (side) view, thereby severely compromising the reconstruction resolution (Fig. 1c, left).

Fig. 1: Misalignment on structural determination in preferential oriented datasets.

a Pose distribution of Uni-HA-Syn (left) and PO-HA-Syn (right) datasets. b Comparison of density maps for the Uni-HA-Syn reconstruction (top), PO-HA-Syn reconstruction (middle), and PO-HA-Syn auto refinement (bottom). Density map quality metrics for each density map are shown to the right. The global half-maps FSC is plotted as a solid blue line, and the map-to-model FSC is shown as a dotted purple line. The green shaded area (bounded by dotted green lines) indicates the spread of directional resolution values, defined as the mean ±1 standard deviation (SD). The light coral region represents the histogram of directional FSCs. c Particle misalignments in PO-HA-Syn auto refinement. d Visualization of reprojection error between auto refinement estimates and ground-truth orientations for selected particles.

A conventional method for mitigating the misalignment issue is to apply an isotropic reference model during the initial round of optimization. However, in subsequent refinement rounds, reference models are reconstructed from particles with orientation bias and incorrect poses, resulting in increasingly deteriorated maps. In our experiments, we refined the PO-HA-Syn-Re100 to PO-HA-Syn-Re00 and PO-HA-Syn-NM10 to PO-HA-Syn-NM45 datasets using isotropic homologous proteins as reference models (Supplementary Fig. 4 and Supplementary Fig. 5). The results showed poor reconstruction quality, which deteriorated significantly as the number of non-preferred particles decreased. This indicates that using an isotropic reference model alone is insufficient to correct misalignment. The evidence presented above strongly motivated us to design a new computational tool to address misalignment during the refinement process.

The cryoPROS method: correcting misalignment caused by preferred orientation

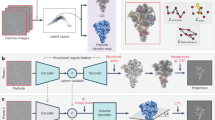
To correct the misalignment caused by the high imbalance of poses in preferred orientation datasets, cryoPROS synthesizes auxiliary particles to enhance the balance of the combined datasets using a deep generative model trained in a self-supervised manner. CryoPROS consists of two main modules: the generative module and the co-refinement module (Fig. 2). This novel integration of auxiliary and raw particles through a co-refinement process not only increases the ratio of detectable particles from non-preferred views but also addresses the preferred orientation issues by improving pose estimation accuracy.

Fig. 2: The workflow of cryoPROS.

The cryoPROS protocol includes two components: generative module and co-refinement module. Using imaging parameters $\Theta$, the generative module trains three networks: the encoding network $q({z|}\Theta,)$, the prior network $p({z|}\Theta )$, and the decoding network $p({x|z},\Theta )$. After training, this module can generate auxiliary particles through $p({z|}\Theta )$ and $p({x|z},\Theta )$, indicated by a blue arrow. Additionally, the optional ReconDisMic algorithm can be employed to generate micelles in studies involving membrane proteins. The co-refinement module employs cryo-EM single-particle analysis software for global co-refinement with both raw and auxiliary particles, estimating the pose parameters for the raw particles. Optionally, these pose parameters can be further refined through a local refinement step. Co-classification can also be adopted with existing single-particle analysis software. The refined pose parameters are then utilized to reconstruct a volume for subsequent iterations.

The generative module, a variant of our previous work on unpaired and semi-paired data learning^24,25, aims to synthesize auxiliary particles using a conditional model. This model takes raw particles and imaging parameters—including CTF, pose parameters, and a low-resolution 3D reference model—as inputs. The module comprises three components: (1) conditional encoding of the raw particles into latent features, (2) a conditional prior model with embedded imaging parameters, and (3) a decoder mapping latent features to synthesized particles. The deep networks within this module are based on a hierarchical structure (Supplementary Fig. 1), which significantly enhances the expressive power to model the complex data distribution in cryo-EM. Utilizing a conditional VAE framework, the network is trained in a self-supervised manner. This training process involves minimizing two loss terms: the particle reconstruction loss between raw and synthesized particles, derived from the latent features of the raw particles, and the Kullback-Leibler (KL) divergence between the conditional encoding feature of raw particles and the embedding feature of imaging parameters (see Methods). After training, the network can synthesize auxiliary particles with evenly distributed orientations (Supplementary Figs. 13, 14). These particles, produced by the generative module, yield density maps that meet expectations, regardless of whether the training particles had uniform or preferred orientations (Supplementary Fig. 2). Furthermore, the generative model is highly adept at managing datasets with preferentially oriented particles during training, making it ideal for generating auxiliary particles (Supplementary Fig. 3).

The co-refinement module combines raw particles with auxiliary particles generated by the generative module and utilizes cryo-EM image processing software (such as Relion, CryoSPARC, or cisTEM³⁴) to perform ab initio reconstruction with re-estimating poses. It is important to note that the generated auxiliary particles are used solely to assist in estimating the poses of the raw particles, not for the final reconstruction of the density map. Moreover, after co-refinement, it is optional to discard some raw particles from the preferred view to increase the balance of raw particles from different views. This approach allows for local refinement of the selected raw particles, followed by an optional post-processing step using tools such as EMReady³⁵, which can reduce anisotropy and further improve the quality of the final reconstructed density map.

Challenges arise when target proteins are embedded in detergent micelles or lipid nanodiscs. In such cases, it becomes crucial to reconstruct the relevant micellar environment for the low-pass filtered homologous protein, which is used as the initial reference model. Therefore, we propose the ReconDisMic algorithm (see Methods), an additional feature in the generative module of cryoPROS, tailored for reconstructing micellar information in membrane proteins.

Validation with several preferential oriented datasets

We systematically evaluated the performance of cryoPROS using a simulated dataset (PO-HA-Syn), a manually curated dataset (PO-TRPA1) with selected top views and a limited number of side views from TRPA1 datasets, a widely recognized benchmark dataset for preferred orientation (HA-trimer, EMPIAR-10096), and four unpublished datasets exhibiting preferred orientation (Na_X, HSL-dimer, P001-Y, and P002-M). See Table 1 for a complete overview. For the membrane protein datasets P001-Y and Na_X, we incorporated the ReconDisMic algorithm.

Table 1 Sources and metadata of the nine datasets employed in the study

For evaluating the reconstructed 3D density maps, we applied consistent metrics across all datasets, including model-to-map FSC, model-to-map resolution (defined as the resolution at the 0.5 cut-off on the model-to-map FSC curve), gold-standard half-maps FSC, half-maps resolution (defined as the resolution at the 0.143 cut-off on the half-map FSC curve), and Q-scores. Half-maps resolutions and FSC curves were included for completeness, despite the known limitations of this method in accurately estimating resolution when preferred orientation issues are present.

PO-HA-Syn: correcting misalignment caused by preferred orientation

We employed cryoPROS on the PO-HA-Syn dataset by applying a 10 Å low-pass filter to a homologous protein (PDB ID: 2RFU), which has 17% sequence identity with the target protein. This filtered protein served as the initial reference model for training the generative module in the first iteration of cryoPROS. The results demonstrated substantial improvements in the density map, particularly in effectively restoring the missing density along the Z-axis. A model-to-map resolution of 2.62 Å was achieved by cryoPROS (Fig. 3c, violet), as determined by comparing the density map with the HA-trimer atomic model (PDB ID: 3WHE). This represents a significant improvement compared to the model-to-map resolution of 23.95 Å obtained from conventional auto-refinement (Fig. 3c, yellow), with additional metrics provided in Supplementary Table 1.

Fig. 3: Correcting misalignment with cryoPROS on PO-HA-Syn and PO-TRPA1 datasets.

a Histograms showing the mean square differences between ground truth projections and estimated reprojections from cryoPROS and conventional autorefine for the PO-HA-Syn dataset. b Pose distributions for TRPA1 and PO-TRPA1 datasets. c Comparison of reconstructed density maps and FSCs between conventional autorefine (top) and cryoPROS (bottom) for the PO-HA-Syn dataset. d Comparison of density maps obtained by reconstruction only (top), autorefine (middle), and cryoPROS (bottom) for the PO-TRPA1 dataset. Density maps in panel (c, d) are overlaid on backgrounds derived from their ground truth atomic models (in magenta). Density map quality metrics for each density map are shown to the right. The global half-maps FSC is plotted as a solid blue line, and the map-to-model FSC is shown as a dotted purple line. The green shaded area (bounded by dotted green lines) indicates the spread of directional resolution values, defined as the mean ±1 standard deviation (SD). The light coral region represents the histogram of directional FSCs.

We further compared the pose assignment accuracy between cryoPROS and conventional auto-refinement by computing the mean square difference (MSE) between the noise-free ground truth projection and the projection derived from the orientation estimated by CryoSPARC’s auto-refine (Fig. 3a). Reduced MSEs of residuals from cryoPROS were observed, indicating overall higher orientation accuracy. Using residuals greater than 13 as the threshold for significant orientation errors, cryoPROS decreased the rate of severe misalignments from 14.85% to 1.27%. These results demonstrate the effectiveness of cryoPROS in correcting misalignment issues.

Moreover, during our investigation of the PO-HA-Syn dataset, we systematically manipulated the non-preferred view proportion from 100% to 0%, resulting in datasets named PO-HA-Syn-Re100 to PO-HA-Syn-Re00. Similarly, we varied the missing cone range from ±10° to ±45° creating datasets labeled PO-HA-Syn-MW10 to PO-HA-Syn-MW45. On these datasets, we evaluated the performance of cryoPROS and compared it with conventional refinement methods. For density maps obtained using either cryoPROS or conventional refinement, EMReady post-processing was applied prior to model-to-map resolution assessment and other quality metrics.

CryoPROS achieved model-to-map resolutions ranging from 2.62 Å at PO-HA-Syn-Re100 to 3.69 Å at PO-HA-Syn-Re00 (Supplementary Fig. 4). Notably, even with side views reduced to 25% of their original amount, the method yielded a resolution of 2.89 Å. Removal of all side views maintained a resolution of 3.69 Å, acceptable for model building. Similarly, experiments on PO-HA-Syn-MW10 to PO-HA-Syn-MW45 corroborate these trends (Supplementary Fig. 5), with a 2.87 Å result at ±20° missing cone data, nearing Nyquist resolution (2.62 Å). In contrast, conventional refinement methods, whether relying on ab initio volume or homologous proteins (Supplementary Fig. 4 and Supplementary Fig. 5), exhibit inferior performance in these datasets. This finding underscores the adaptability of cryoPROS in addressing challenges associated with severe preferred orientation, if deep learning methods are adopted to alleviate anisotropy after correcting misalignment caused by preferred orientation with cryoPROS.

PO-TRPA1: restoring missing density

We evaluated the effectiveness of cryoPROS in restoring missing density due to misalignment using the manually curated dataset with preferred orientation, designated as PO-TRPA1. From the raw particle images deposited in EMPIAR-10024³⁶ (containing 43,585 particles and referred to as the TRPA1 dataset), we selected only top views and a limited number of side views. This selection process resulted in a subset with preferential orientation, denoted as PO-TRPA1, which comprised 14,436 particles (Fig. 3b). Given that the TRPA1 dataset suffered only from slightly preferred orientation, we presumed accurate particle poses. Utilizing these poses, we performed reconstruction-only of PO-TRPA1 dataset. Although the resolution slightly decreased due to the reduced particle count, the map remained holistic (Fig. 3d, gray).

In contrast, conventional auto-refinement applied to the PO-TRPA1 dataset resulted in an unsatisfactory density map (Fig. 3d, yellow). This map exhibited significant density loss along the preferred view Additionally, its quantitative indicators, such as Q-scores and FSC-based resolutions, were considerably lower than those achieved by the reconstruction-only method (Supplementary Table 2). These findings underscore the impact of misalignment caused by preferred orientation on the quality of reconstructions.

Next, we employed cryoPROS to mitigate the preferred orientation issue in the PO-TRPA1 dataset. Since there were no available deposited structures of homologous proteins, we utilized AlphaFold2³⁷ to predict the structure of the rat-derived TRPA1 protein (UniProt ID: F1LRH9). This predicted structure was subjected to a 10 Å low-pass filter and then used as the initial volume for the generative module of cryoPROS in its first iteration. The sequence identity between the predicted model and the target model was 77%. After two iterations, cryoPROS produced a more accurate and complete density map of TRPA1 (Fig. 3d, violet), achieving a model-to-map resolution of 8.10 Å. CryoPROS’s output aligned with the results from the reconstruction-only method (7.44 Å), indicating its robustness against density loss due to misalignment caused by preferred orientation (additional metrics in Supplementary Table 2).

HA-trimer: achieving near-atomic resolution structure using untilted dataset

We employed cryoPROS to process untilted data exhibiting preferential orientation sourced from the EMPIAR repository (EMPIAR-10096) and conducted an extensive comparison with results derived from data obtained through the tilt-collection technique. The tilted data were also sourced from the EMPIAR repository (EMPIAR-10097⁴). As tilt-collection⁴ remains one of the most effective solutions to preferred orientation, this dataset (HA-trimer) is widely recognized as the benchmark for preferred orientation. For the first iteration of cryoPROS, we selected a homologous protein (PDB ID: 6IDD) with a sequence identity of 47% to the target protein for 10 Å low-pass filtering as the reference model for generative module training. CryoPROS generated auxiliary particles with uniform poses in each iteration (see pose distribution in Fig. 4b, middle). Subsequently, the refinement module yielded complete and high-resolution results (Fig. 4b, cyan, model-to-map resolution of 3.72 Å). Subsequently, we chose a subset comprising 31,146 particles with a more balanced pose distribution (see pose distribution in Fig. 4b, right), and subjected this subset to local refinement. This process noticeably corrected anisotropic issues and resulted in quality enhancement (Fig. 4b, magenta, model-to-map resolution of 3.49 Å). Visually, the density map exhibited substantial improvement compared to the automatic refinement of untilted data, outperforming the automatic refinement of data collected at a tilt of $4{0}^{\circ }$ (Fig. 4a, pink, model-to-map resolution of 4.72 Å) and being comparable to the state-of-the-art results on tilted data (EMD-0152, Fig. 4a, violet, model-to-map resolution of 3.41 Å). However, obtaining this density map from the tilt-collection strategy required multiple rounds of 3D classification along with complex subsequent refinements at the per-particle level, including multi-round of per-particle defocus refinement, 3D classification and Bayesian polishing²¹. These results validate the efficacy of cryoPROS in enhancing the density map to near-atomic resolution by correcting misalignment in the dataset with preferred orientation, which was previously thought to be untackleable for obtaining a decent density map. Significantly, this achievement was attained without necessitating additional data collection or the intricate per-particle CTF or motion refinement, typically employed to mitigate the inherent limitations of the tilt-collection strategy.

Fig. 4: CryoPROS enables near-atomic resolution recovery from an untilted dataset of highly preferentially oriented HA trimer.

a Pose distribution and reconstructed density maps of the tilt-collected dataset, showing autorefinement (left) and state-of-the-art results (right). b Pose distribution and reconstructed density maps of the untilted dataset, comparing autorefinement (left), cryoPROS (middle), and cryoPROS with local refinement (right). Density maps in (a, b) are overlaid on backgrounds derived from their ground truth atomic models (in gray). c Close-up views of selected regions from the density maps, highlighting the $\alpha$-helix (top) and $\beta$-sheet (bottom). d Selected regions in gray mesh style, with the embedded atomic model colored by average Q-score.sc and Q-score.bb values, respectively.

Specific sites were selected in the known atomic model (PDB ID: 3WHE) for density comparison. The results illustrated that the density map generated by cryoPROS was well-preserved, delineating distinct regions with $\alpha$-helical pitch, $\beta$-strand separation, and prominent side chains (Fig. 4c). We utilized Q-score.bb (backbone) and Q-score.sc (side chain) to color the atomic model, revealing high scores for both the main chain and side chain in the results produced by cryoPROS (Fig. 4d). Moreover, in most cases, cryoPROS surpassed the results obtained from tilt-collection autorefinement, nearly reaching the performance of the state-of-the-art processing of the tilted dataset. Additional metrics can be found in Supplementary Fig. 6 and Supplementary Table 3. Additionally, we conducted a test of cryoPROS on the untilted dataset P002-M, which produced results comparable to those obtained from the wet lab using tilted datasets (Supplementary Fig. 15).

P001-Y, Na_X and HSL-dimer: application to unpublished experimental datasets

CryoPROS is a versatile method designed to address preferred orientation issues in cryo-EM data, while also being capable of tackling other structural challenges. In this study, we showcase its broad applicability using real datasets, including two membrane proteins (P001-Y and Na_X) and a hormone-sensitive triglyceride lipase dimer (HSL-dimer).

We first examined two membrane proteins, P001-Y and Na_X (a sodium channel). Membrane proteins are vital for physiological processes and drug development. However, the combination of preferred orientation issues and micelle effects complicates pose estimation and makes resolving high-resolution structures more challenging. To address these challenges, we devoloped micelle reconstruction algorithm ReconDisMic and integrated it into cryoPROS to mimic the micelle effects in the initial reference model (see Methods). In this study, we introduce P001-Y, referred to by a symbol for confidentiality reasons, and Na_X, a sodium channel. The datasets for these proteins consist of 247,267 and 210,924 particles, respectively (see pose distribution in Fig. 5a, left and middle). We processed these datasets using cryoPROS. Initially, a 10 Å low-pass filtered density map derived from the Nav1.6 atomic model (PDB ID: 8FHD, with 56% sequence identity) was used as the initial reference model. A similar approach was used for P001-Y. Subsequent iterations of cryoPROS yielded improved maps (Fig. 5b,c).

Fig. 5: CryoPROS enables structure determination for three preferentially oriented experimental datasets.

a Pose distributions for the three experimental datasets: P001-Y (left), Na_X (middle), and HSL-dimer (right), showing the proportion of particles in preferred and non-preferred orientations. b Comparison of density maps from conventional refinement (cyan) and cryoPROS (violet) for the P001-Y dataset. c Comparison of density maps from conventional refinement (cyan) and cryoPROS (pink) for the Na_X dataset. d Density maps of HSL-dimer from conventional refinement (cyan) and cryoPROS (magenta), with enlarged views highlighting conformational differences at the central interface (pink box) and prominent $\alpha$-helix features (blue box). Close-up views of selected regions from HSL-dimer density maps, comparing conventional refinement (left) and cryoPROS (right), are shown with embedded atomic models colored by Q-score.

CryoPROS showed a significant effect on P001-Y (Fig. 5b, cryoPROS resulting map in violet vs. conventional refinement in cyan), particularly in trans-membrane domain. Though the atomic model is undisclosed due to ongoing research, visible improvements were apparent. For Na_X, cryoPROS significantly outperformed conventional refinement (Fig. 5b, cryoPROS resulting map in pink vs. conventional refinement in cyan), enhancing clarity in central trans-membrane domain and achieving a resolution of 4.32 Å. Additional metrics are compared in Supplementary Fig. 7. Together with the ReconDisMic algorithm, cryoPROS demonstrates its capability to process datasets with preferred orientations from membrane proteins.

In addition to its role in membrane protein analysis, cryoPROS can be combined with cryoDRGN to resolve high-resolution structures of new conformations, enhancing structural interpretation, as demonstrated with the HSL-dimer, a key enzyme in lipolysis. This dataset, comprising 231,878 particles, exhibited pronounced preferred orientation (see pose distribution in Fig. 5a, right). Initial conventional refinement with C2 symmetry produced a density map (Fig. 5d, cyan) with a model-to-map resolution of 8.39 Å. The map suffered from distorted side views and chain breakages, particularly at the dimer interface. To overcome these issues, we applied cryoPROS using an initial model predicted by AlphaFold2 and combined it with cryoDRGN for additional density analysis. We successfully refined the map, achieving an improved side view with clearer spiral stratification (Fig. 5d, magenta), which aided subsequent model building. The final density map resolution was 3.97 Å (model-to-map resolution), with the newly resolved density providing insights into dimer formation.

These findings highlight cryoPROS’s wide applicability in addressing complex datasets, not only for membrane protein analysis but also for resolving additional density when used in combination with cryoDRGN, further expanding its utility in structural biology research.

Risk analysis of model bias in cryoPROS

We assess model bias in cryoPROS, crucially important because it depends on a reference model to train the generative module in its initial iteration. This thorough evaluation ensures cryoPROS has a negligible risk of model bias. This assessment is divided into three parts. First, we demonstrate that the noise in the auxiliary particles, a key feature of the conditional VAE in cryoPROS’s generative module, exhibits significantly less, often negligible, model bias compared to naive additive Gaussian noise. Secondly, we introduce the attributes of cryoPROS auxiliary particles, enabling reconstruction without overfitting. Finally, we validate that cryoPROS does not suffer from model bias through a series of experiments using the experimental HA-trimer dataset.

Minimized model bias in auxiliary particles noise compared to Gaussian noise

A distinctive feature of cryoPROS’s generative module is that the noise in the auxiliary particles is generated through a self-supervised neural network, rather than by adding Gaussian noise to the projections of the reference model. The auxiliary particles generated by cryoPROS more closely resemble raw particles compared to those produced by adding Gaussian noise, exhibiting smaller KL divergence and closer SNR to raw particles (Fig. 6a). Here, SNR is defined using the same method as that employed in Topaz-Denoise³⁸. Additionally, a visual comparison of the low-frequency power spectra from Gaussian noise, real noise, and noise learned by cryoPROS shows that the latter closely emulates the characteristics of real noise found in raw particles (Fig. 6d).

Fig. 6: Model bias risk analysis of cryoPROS.

a Evaluation of similarity between raw particles and generated noisy particles (including Gaussian-noisy and cryoPROS-generated noisy particles) using KL divergence and SNR. b Model-to-map resolution of “phantom” density maps from the “Einstein from noise” experiment, with autorefinement performed on Gaussian and cryoPROS noise stacks using varying degrees of lowpass-filtered density maps (ribosome, PDB ID: 6PCQ) as references. c Comparison of average densities from the “Einstein from noise” experiment. d Comparison of Gaussian, real, and cryoPROS-generated noise, with power spectral density plots and an enlarged view of low frequencies (red box). e Slice comparison of “phantom” density maps from the “Einstein from noise” experiment, showing results from Gaussian and cryoPROS-generated noise with different levels of lowpass-filtered homologous proteins. f Structure refinement results using different homologous proteins: cryoPROS-6IDD and cryoPROS-2RFU. 6IDD (light green atomic model, light purple density) and 2RFU (dark green atomic model, pink density) are shown on the left and right, with cryoPROS-6IDD (dark blue), tilt-collected (red), and cryoPROS-2RFU (cyan) densities in the middle. Structure-refined models are below. Similarity was assessed using RMSD and TM-score. g Atomic model alignment for cryoPROS-6IDD and cryoPROS-2RFU, focusing on selected regions, with colors matching panel (f). h Template bias assessment using cisTEM’s measure_template_bias script, with 6IDD as the baseline.

Besides failing to mimic the noise distribution of raw particles, Gaussian noise is unsuitable for generating auxiliary particles by adding it to volume projections due to its susceptibility to model bias. This issue arises because it does not accurately replicate real noise. We conducted a comparative analysis between this approach and cryoPROS using the HA-trimer dataset. Our findings indicate that results obtained from Gaussian noise closely resemble the utilized homologous protein, underscoring its model bias risk (Supplementary Table 4). In addition to causing model bias, Gaussian-noisy particles with uniform orientation are unable to mitigate the bias in orientation estimation within the Na_X dataset (Supplementary Table 4).

To further analyze the differences in model bias between Gaussian noise and the conditional VAE in cryoPROS, we conducted the “Einstein-from-noise” experiment (see Methods). This revealed that noise from the conditional VAE in cryoPROS’s generative module exhibits minimal overfitting in density maps. In contrast, Gaussian noise tends to produce phantom density (resulting from pure noise overfitting), a problem known as the “Einstein-from-noise” effect³⁹. It’s noteworthy that when using a 7 Å low-pass filtered density map (or lower) as a reference, cryoPROS-generated noise was refined to an ultra-low resolution density map, which indicates that the cryoPROS-generated noise can avoid overfitting and not introduce “phantom density” during the refinement process. In contrast, Gaussian noise necessitates more extensive low-pass filtering, typically ranging from 10 Å to 15 Å, to achieve a similar effect (Fig. 6b). When using the same resolution (meaning the same low-pass filtering) density map as a refinement reference, the quality of phantom density refined with cryoPROS-generated noise is about two orders of magnitude lower than with Gaussian noise (Fig. 6c), as shown in the central slice of the density map (Fig. 6e). In summary, these results validate the importance of using a generative module in cryoPROS to fit the complex noise distribution in raw particles, which is also helpful in reducing the model bias.

Attributes of auxiliary particles enable reconstruction without overfitting

CryoPROS utilizes several strategies to mitigate overfitting risks in cryoEM data processing. It applies low-pass filtering to the reference model during the first iteration—a standard practice in cryoEM—to focus on relevant low-frequency information. Additionally, cryoPROS uses the external reference model only in the first iteration, ensuring its influence diminishes in subsequent iterations to prevent dependency on initial assumptions and enhance adaptability.

Following training, cryoPROS can generate particles with uniformly distributed orientations. It has been demonstrated that the generated auxiliary particles closely resemble those from experimental datasets after averaging 2D classifications (Supplementary Fig. 14). Furthermore, the reconstructed map of generated particles reflects the input volume, when lowering the resolution of the input volume (Supplementary Fig. 2) or decreasing the number of particles from non-preferred views (Supplementary Fig. 12). These findings validate the reconstruction capabilities and low risk of overfitting associated with auxiliary particles generated by deep neural networks, thus confirming the minimal model bias of cryoPROS when combining auxiliary particles with raw particles for subsequent co-refinement stages.

Moreover, cryoPROS’s inability to generate valid signals when irrelevant proteins are applied as initial volume (Supplementary Fig. 16) underscores its principle to data generation, distinguishing it from mere noise addition. This ensures that the model avoids producing false signals, thus avoiding spurious reconstructions.

Validating cryoPROS model bias with HA-trimer dataset experiments

The risk of model bias in cryoPROS when using the HA-trimer dataset is negligible, as demonstrated by the following four sets of experiments (see Methods).

Firstly, we demonstrated that the results obtained through cryoPROS closely resemble the ground-truth atomic model and exhibit significant differences from the external volume used as the reference model in the initial iteration of cryoPROS (Fig. 6f, g). CryoPROS-6IDD, which utilizes a 10 Å low-pass filtered homologous structure (PDB-6IDD) as the initial reference model closely aligns with the ground-truth atomic model and diverges significantly from the atomic model 6IDD. This alignment is assessed by the model-to-map resolution, Q-score of the density map, as well as RMSD and TMscore after structure refinement of the atomic model. Similar results were observed across other datasets (Supplementary Fig. 10). Additionally, cryoPROS did not introduce unique features of the homologous protein (e.g., the glycosylation in Supplementary Fig. 9c-i), while successfully recovering features unique to the target protein that are absent in the homologous protein (e.g., the loop in Supplementary Fig. 9c-i, the glycosylation in Supplementary Fig. 9c-ii). Additionally, we capitalized on the HA-trimer data and reprocessed it using the another homologous protein 2RFU (17% sequence identity with target model) as initial reference model, following the previously described computational approach. The calculated resolution is 4.04 Å, positioning the result in proximity to the target protein while diverging significantly from the homologous protein (Fig. 6f, g). Similar to the observations made using 6IDD as the initial reference model, cryoPROS restored unique features of the target protein (e.g., the $\alpha$-helix in Supplementary Fig. 9d-i, and the glycosylation in Supplementary Fig. 9d-ii) while successfully preventing features unique to the homologous protein from appearing in the density map (e.g., the loop in Supplementary Fig. 9d-ii).

Secondly, we used the cisTEM script measure_template_bias to assess template bias, revealing minimal bias from various initial reference models (Fig. 6h).

Thirdly, we performed subsequent local refinement using raw particles only (utilizing a 4 Å low-pass filter cryoPROS result map as reference), with a maximum search range of 20° in rotation and 20 Å in shift. The resolution of the locally refined results shows minimal alteration (Supplementary Fig. 9a). This demonstrates the stability of cryoPROS-corrected pose, indicating cryoPROS faithfully reflects the genuine information rather than inducing fake signals by overfitting from noise.

Fourthly, frequency-based correlation analysis among homologous proteins, the target protein, and cryoPROS results shows that the correlation between the target and homologous proteins falls below 0.5 at 8.59 Å, while the correlation between the initial volume and the cryoPROS density map drops below 0.5 at 20.96 Å (Supplementary Fig. 9b, pink and bright blue curves, respectively). This demonstrates that cryoPROS results share lower frequency information with the homologous protein, which served as the reference model in the first iteration, than with the target protein. This indicates that no undesired information is transferred from the homologous protein.

Discussion

This work presents cryoPROS, a systematic solution to address the misalignment issue caused by preferred orientation in cryo-EM. We leverage the expressive power of deep neural networks to generate auxiliary particles that enhance pose balance in the combined dataset, in contrast to the raw datasets. This enhancement is key to improving alignment accuracy and achieving high-resolution reconstruction with untilted raw particles. Besides the case of HA-trimer, we compare the results of cryoPROS using untilted data with those obtained from the wet labs using the tilt-collection strategy in a protein P002-M (Supplementary Fig. 15), which shows that cryoPROS can achieve comparable or even superior results. This advantage is notable because collecting tilted datasets is time-consuming, and processing them increases computational complexity due to their sensitivity to parameter estimation and the requirement for per-particle refinement. Finally, we design a series of experiments to validate the reliability of cryoPROS by confirming its low risk of model bias. We emphasize that cryoPROS fundamentally differs from VAE related methods in cryo-EM, such as cryoDRGN and 3DFlex⁴⁰. CryoDRGN primarily uses particle representations to analyze heterogeneity in latent space while simultaneously inferring volumes. In contrast, 3DFlex focuses on optimizing the deformation field of a canonical 3D map, enhancing reconstruction and determining motion in the flexible domain. Unlike these methods, cryoPROS leverages the generative capabilities of the conditional VAE model to synthesize auxiliary particles. This task is particularly challenging due to the extremely low signal-to-noise ratio of raw particles and their complex noise distribution. To effectively address this, cryoPROS employs a hierarchical structure within the VAE model to fit the complex conditional likelihood (Supplementary Fig. 1).

Misalignment is the primary issue for preferred orientation datasets when the number of particles from non-preferred views is small. SNR is a critical factor, and the number of particles in non-preferred views, denoted as N, significantly affects the directional resolution. Preferred orientation datasets can be categorized into three cases:

• If $N$ is less than the theoretical limit given by Rosenthal and Henderson²³, we refer to this as “missing data”, and additional data or information is needed; otherwise, obtaining a satisfactory reconstruction is impossible. According to the theoretical predictions in²³, which account for contrast loss due to the B-factor, the required number of particles has an exponential relationship with resolution. Thus, if a slight degree of anisotropic reconstruction is acceptable, the required number of particles decreases exponentially.

• If $N$ is larger than a certain threshold, conventional computational methods, including initialization by homologous protein, can correct the misalignment issue.

• If $N$ is larger than the theoretical limit but smaller than the threshold given in (b), this is the main focus of our work. In this case, a new method is needed to address the misalignment issue and achieve satisfactory reconstruction.

In this work, we found that several important unsolved preferred orientation datasets falls into the last case. We conducted a series of experiments comparing results obtained using homologous protein initialization and cryoPROS in both simulated and experimental datasets. Specifically, we performed two experiments: one by varying the retention rate of non-preferred orientation particles (Supplementary Fig. 4) and another by adjusting the missing cone range (Supplementary Fig. 5). The results showed that while using homologous proteins improved the density maps, the outcomes were still significantly below those achieved by our method (cryoPROS). Additional results related to the experimental datasets can be found in Supplementary Table 2, Supplementary Table 3, Supplementary Fig. 7d, and Supplementary Fig. 8d.

Synthesizing particles using a conditional deep generative neural network. A critical component of cryoPROS is its generative module, designed to synthesize auxiliary particles that assist in pose determination of raw particles. The complex noise distribution in particles and the unknown density maps present significant challenges for particle synthesis, motivating the design of a self-supervised hierarchical VAE model (Fig. 2, Supplementary Fig. 1), which has been validated for its exceptional generative capabilities in image synthesis^41,42 and degradation modeling^24,25. This is the first attempt in cryo-EM analysis to synthesize particles with deep learning, which opens exciting avenues for future research. Further advancements could involve developing or incorporating cutting-edge tools in deep learning, such as diffusion-based generative modeling and transformers.

Board applications in co-particle processing module. The combined dataset, which includes both raw and auxiliary particles, significantly alleviates the imbalance issue present in the original raw dataset. This improvement not only addresses the misalignment issue but also facilitates subsequent data analysis procedures and tools. Notably, directly applying conventional local refinement to the untilted HA-trimer dataset yields poorer results. Conversely, when applied to the combined dataset, this technique significantly enhances the reconstruction (Fig. 4b). In the future, we will explore additional applications of the combined datasets using existing cryoEM data analysis tools and investigate the potential for extension to cryo-ET.

Validating the reliability of cryoPROS. Besides the implicit regularization in deep neural networks, which may introduce overfitting risks to the auxiliary particles, the initial low-resolution volume can also bring the risk of model bias. Our experiments demonstrate that additive Gaussian noise can lead to “Einstein from noise” issues. In contrast, the noise generated by cryoPROS does not suffer from this problem, yielding more reliable results (Fig. 6b, c, e). In addition, we conducted a series of tests by varying the initial template models and parameters contained in low-pass filters (Supplementary Fig. 9e, f). These results validate the low risk of model bias in cryoPROS.

Moreover, to evaluate the application boundaries of cryoPROS, we tested its performance by varying the retention rate of non-preferred views ranging from -45 to 45 degrees (Supplementary Fig. 4). We found that cryoPROS can achieve comparable results if the non-preferred view has missing data ranging from -20 to 20 degrees (Supplementary Fig. 5), though missing data issue is not the main contributor to the preferred orientation artifacts in experimental cases.

Opportunities in collaboration with tilt-collection strategy. It is noted that the tilt-collection technique is an effective experimental method for solving the preferred orientation issue by collecting particles from different views, which also helps reduce the imbalance of pose distribution (Fig. 4a). Rather than being competitors, cryoPROS and the tilt technique can complement each other. For example, using tilted data may yield a better initial volume; moreover, developing new methods for integrating tilted, untilted, and synthesized datasets could help reduce the complexity inherent in tilt techniques. We firmly believe that the joint advancement of experimental methods and computational algorithms has the potential to address more challenging problems, opening new avenues in cryo-EM analysis.

It is important to acknowledge that although combining simulated and experimental data can provide new opportunities in cryo-EM, it also poses challenges in developing a systematic approach to validate the results from a computational perspective, beyond experimental validation. This aspect deserves further study in the future.

Methods

The generative module

The generative module of cryoPROS aims to produce auxiliary particles with specified CTF parameters, pose parameters, and a reference model. To achieve this, we have developed a conditional generative model that simulates the physical imaging process, which can be expressed as:

$$x=C\left({{{\psi }}}\right)P\left({{{\phi }}}\right){\bf{V}}_{{\rm{model}}}+n,$$

where ${{\boldsymbol{x}}}$ represents the particle, ${{C}}$ is the CTF operator dependent on parameter $\psi$, $P$ represents the projection operator with the pose parameter $\phi$, ${{{\bf{V}}}}_{{\rm{model}}}$ denotes the reference model, and ${{\boldsymbol{n}}}$ represents the noise. Specifically, we utilize a deep generative model known as conditional VAE as our particle generator. Defining $\Theta=\left\{\psi,\phi,{{{\bf{V}}}}_{{\rm{model}}}\right\}$ to be the set of imaging parameters, the conditional VAE model learns a generative model that maximizes the conditional log-likelihood $\log p\left({{\boldsymbol{x}}}|\Theta \right)$. In practice, using cryo-EM SPA software such as Relion, CryoSPARC, or cisTEM, we derive the initial estimates of pose parameters $\{{\phi }_{i}\}_{{i}={1}}^{N}$ and CTF parameters $\{{\psi }_{i}\}_{{i}={1}}^{N}$ from a set of collected raw particles $\{{{\bf{x}}}_{i}\}_{{i}={1}}^{N}$. We start with a low-resolution density map as the reference model, which is subsequently updated with the output from the co-refinement module.

Since $p\left({{\boldsymbol{x}}},|\Theta \right)$ is difficult to optimize directly, the conditional VAE model involves maximizing a lower bound of $\log p\left({{\boldsymbol{x}}}|\Theta \right)$, known as the conditional Evidence Lower BOund (cELBO). The negative cELBO is given by

$$-{{\mathbb{E}}}_{q({{\bf{z}}}|{{\bf{x}}},\Theta )}\log p\left({{\bf{x}}}|{{\bf{z}}},\Theta \right)+{{\rm{KL}}}\left(q\left({{\bf{z}}}|{{\bf{x}}},\Theta \right)\,{{||}\,p}\left({{\bf{z}}}|\Theta \right)\right),$$

(1)

forming the loss function to train our model. Here, ${{\bf{z}}}$ is the latent variable of this conditional VAE model, $q\left({{\bf{z}}}|{{\bf{x}}},\Theta \right)$ is the conditional encoding model, $p\left({{\bf{z}}}|\Theta \right)$ is the conditional prior model, and $p\left({{\bf{x}}}|{{\bf{z}}},\Theta \right)$ is the decoding model. As illustrated in Fig.2, $q\left({{\bf{z}}}|{{\bf{x}}},\Theta \right)$ represents the encoding of the raw particles ${{\bf{z}}}$ and imaging parameters $\Theta$. Furthermore, $p\left({{\bf{z}}}|\Theta \right)$ is the embedding of imaging parameter features $\Theta$, and $p\left({{\bf{x}}}|{{\bf{z}}},\Theta \right)$ is the decoder for the latent features ${{\bf{z}}}$ and imaging parameters $\Theta$. All these models are parameterized by deep neural networks (Supplementary Fig. 1). After the training stage, inputting an imaging parameter $\Theta$, the conditional VAE model samples the latent variable ${{\bf{z}}}$ through the prior model $p\left({{\bf{z}}}|\Theta \right)$, and subsequently, ${{\bf{z}}}$ is transformed into a synthetic particle through the generative model $p\left({{\bf{x}}} | {{\bf{z}}},\Theta \right)$. Furthermore, a hierarchical structure^41,42 is used to enhance the representation capability. In particular, we assume the latent variable has $L$ stochastic layers: ${{\bf{z}}}=({{{\bf{z}}}}^{1},\ldots,{{{\bf{z}}}}^{L})$, and a top-down structure⁴³ is adopted for the inference and generation process in the conditional VAE model.

Hierarchical structure of the conditional VAE model

Let ${{\bf{z}}}=\left({{{\bf{z}}}}^{1},\ldots,{{{\bf{z}}}}^{L}\right)$, the conditional prior model $p\left({{\bf{z}}}|\Theta \right)$ has the decomposition:

$$p\left({{\bf{z}}}|\Theta \right)=p\left({{{\bf{z}}}}^{L}|\Theta \right){\prod }_{l=1}^{L-1}p({{{\bf{z}}}}^{l}{|{{\bf{z}}}}^{ > l},\Theta )$$

(2)

where ${{{\bf{z}}}}^{ > l}=\left({{{\bf{z}}}}^{l+1},\ldots,{{{\bf{z}}}}^{L}\right)$. Similarly, the decomposition of conditional encoding model $q\left({{\bf{z}}}|{{\bf{x}}},\Theta \right)$ is

$$q\left({{\bf{z}}}|{{\bf{x}}},\Theta \right)=q\left({{{\bf{z}}}}^{{{\boldsymbol{L}}}}|{{\bf{x}}},\Theta \right){\prod }_{l=1}^{L-1}q\left({{{\bf{z}}}}^{l}|{{{\bf{z}}}}^{ > l},{{\bf{x}}},\Theta \right).$$

(3)

Then, the cELBO in (1) can be expressed as:

$${{\rm{cELBO}}}= {{\mathbb{E}}}_{q\left({{\bf{z}}}|{{\bf{x}}},\Theta \right)}\log p\left({{\bf{z}}}|{{\bf{x}}},\Theta \right)-{\rm{KL}}\left(q\left({{{\bf{z}}}}^{L}|{{\bf{x}}},\Theta \right)\parallel p\left({{{\bf{z}}}}^{L}|\Theta \right)\right)\\ -\mathop{\sum }\limits_{l=1}^{L-1}{{\mathbb{E}}}_{q\left({{{\bf{z}}}}^{ > {{\boldsymbol{l}}}} |\,{{\bf{x}}},\,\Theta \right)}{\rm{KL}}\left(q\left({{{\bf{z}}}}^{l}|{{{\bf{z}}}}^{ > l},{{\bf{x}}},\Theta \right)\parallel p\left({{{\bf{z}}}}^{l}|{{{\bf{z}}}}^{ > l},\Theta \right)\right).$$

(4)

Regarding the conditional encoding model $q\left({{\bf{z}}},|{{\bf{x}}},\Theta \right)$, we assume:

$$q\left({{{\bf{z}}}}^{l}|{{{\bf{z}}}}^{ > l},{{\bf{x}}},\Theta \right)={{\mathscr{N}}}\left({\mu }_{q}^{l}\left({{{\bf{a}}}}^{l},{{{\bf{b}}}}^{l},{h}_{\theta }^{l}\left({{\bf{v}}}\right),{e}_{\theta }^{l}\left(\phi \right)\right),{\sigma }_{q}^{l}\left({{{\bf{a}}}}^{l}{,{{\bf{b}}}}^{l},{h}_{\theta }^{l}\left({{\bf{v}}}\right),{e}_{\theta }^{l}\left(\phi \right)\right)\right),$$

(5)

where $l=1,2,\ldots,L$. Hence, $q\left({{{\bf{z}}}}^{l}|{{{\bf{z}}}}^{ > l},{{\bf{x}}},\Theta \right)$ represents a Gaussian distribution with the mean and variance determined by the outputs of two networks, ${\mu }_{q}^{l}$ and ${\sigma }_{q}^{l}$, respectively. Furthermore, ${\mu }_{q}^{l}$ and ${\sigma }_{q}^{l}$ each accept four inputs, ${{{\bf{a}}}}^{l}$ and ${{{\bf{b}}}}^{l}$, which denotes the encoding and decoding features in the $l$-th layer, respectively. ${h}_{\theta }^{l}\left({{\bf{v}}}\right)$ and ${e}_{\theta }^{l}\left(\phi \right)$ represent the embedding of the imaging parameter $\Theta$. Here, ${{\bf{v}}}={{\bf{C}}}\left(\psi \right)P\left(\phi \right){{{\bf{V}}}}_{{\rm{model}}}$ denotes the projection of the reference model, which is embedded into the latent space through a CNN denoted as ${h}_{\theta }\left({{\bf{v}}}\right)$. The volume pose parameter $\phi$ includes both orientation and translation parameters. We adopt quaternions to represent orientation and a two-dimensional vector to represent translation; thus, $\phi$ is a vector in ${{\mathbb{R}}}^{6}$. Subsequently, we employ a network composed of a multi-layer perceptron (MLP) and CNN to embed $\phi$ into the latent space, denoted as ${e}_{\theta }(\phi )$ (Supplementary Fig. 1). The encoding features ${\left\{{{{\bf{a}}}}^{l}\right\}}_{l=1}^{L}$ are recursively obtained as follows:

$${{{\bf{a}}}}^{1}={f}_{\theta }^{1}({{\bf{x}}}),{{{\bf{a}}}}^{l}={f}_{\theta }^{l}\left({{{\bf{a}}}}^{l-1}\right),l=2,\ldots,L,$$

(6)

where ${f}_{\theta }^{l}$ represents the convolutional block in the $l$-th encoding layer. The decoding features ${{{\bf{b}}}}^{l}$ are obtained through the recursion:

$${{{\bf{b}}}}^{l}={g}_{\theta }^{l+1}\left({{{\bf{z}}}}^{l+1},{{{\bf{b}}}}^{l+1}\right),l=1,\ldots,L-1,$$

(7)

where ${{{\bf{z}}}}^{l+1}$ is sampled from $q\left({{{\bf{z}}}}^{l+1}|{{{\bf{z}}}}^{ > l+1},{{\bf{x}}},\Theta \right)$, ${{{\bf{b}}}}^{L}$ is a constant vector that is set as a learnable parameter, and ${g}_{\theta }^{l}$ is the convolutional block in $l$-th decoding layer. Additionally, for the conditional prior model $p({{\bf{z}}}|\Theta )$, we assume the following form:

$$p\left({{{\bf{z}}}}^{l}|{{{\bf{z}}}}^{ > l},\Theta \right)={{\mathscr{N}}}\left({\mu }_{p}^{l}\left({{{\bf{b}}}}^{l},{h}_{\theta }^{l}\left({{\bf{v}}}\right),{e}_{\theta }^{l}\left(\phi \right)\right),{\sigma }_{p}^{l}\left({{{\bf{b}}}}^{l},{h}_{\theta }^{l}\left({{\bf{v}}}\right),{e}_{\theta }^{l}\left(\phi \right)\right)\right),l=1,2,\ldots,L,$$

(8)

and the decoding model $p\left({{\bf{x}}} | {{\bf{z}}},\Theta \right)$ is assumed to be ${{\mathscr{N}}}({g}_{\theta }^{1}\left({{{\bf{z}}}}^{1},{{{\bf{b}}}}^{1}\right),{{\bf{I}}})$. We adopt the Residual Dense Block (RDB)⁴⁴ as our convolutional block for ${f}_{\theta }^{l}$ and ${g}_{\theta }^{l}$, and the architecture is shown in Supplementary Fig. 1. The loss function for the conditional VAE aims to minimize the $-{{\rm{cELBO}}}$, and with the given parametrization, the loss function is:

$${{\rm{Loss}}}\left({{\bf{x}}},\Theta \right)={{\mathbb{E}}}_{q({{{\bf{z}}}}^{1}|{{\bf{x}}},\Theta )}{||}{{g}_{\theta }^{1}\left({{{\bf{z}}}}^{1},{{{\bf{b}}}}^{1}\right)-{{\bf{x}}}{||}}_{2}^{2}+\mathop{\sum }\limits_{l=1}^{L}{{\rm{KL}}}\left({{\mathscr{N}}}({\mu }_{q}^{l},{\sigma }_{q}^{l}){||}\mathscr{N}({\mu }_{p}^{l},{\sigma }_{p}^{l})\right).$$

(9)

The KL divergence for two Gaussian distributions has an analytical form, which is:

$${{\rm{KL}}}\left(({\mu }_{q},{\sigma }_{q}){||}({\mu }_{p},{\sigma }_{p})\right)= \frac{1}{2}\left(\log (|{\sigma }_{p}|/|{\sigma }_{q}|)-K\right.\\ \left.+{{\rm{Tr}}}({\sigma }_{p}^{-1}{\sigma }_{q})+{({\mu }_{q}-{\mu }_{p})}^{T}{\sigma }_{p}^{-1}({\mu }_{q}-{\mu }_{p})\right),$$

(10)

where $K$ denotes the dimension of the latent variable ${{\bf{z}}}$.

The conditional VAE model in the generative module undergoes training for 20,000 iterations using the Adam optimizer⁴⁵. We set the learning rate to $1\times 1{0}^{-4}$ and the batch size to 8. The model architecture includes 15 hierarchical layers. To mitigate the issue of posterior collapse, we employ the KL annealing method⁴⁶, implementing a linear annealing scheme during the first 10,000 iterations.

The co-refinement module

The co-refinement module is designed to correct misalignment caused by the preferred orientation issue and enhance the quality of the reconstructed density map by utilizing auxiliary particles generated by the generative module. This is achieved through a two-step process. First, refinement is performed on the combined dataset of raw and auxiliary particles. In this study, refinement is conducted using CryoSPARC, although other cryo-EM SPA software can also be applied. Subsequently, the auxiliary particles are discarded, and reconstruction-only is performed exclusively with the raw particles, utilizing the poses estimated during the first step.

Standard workflow of cryoPROS

Data Preparation

Curate a dataset of particle images for the target protein. Using cryo-EM SPA software like Relion, CryoSPARC, or cisTEM, obtain the initial estimates of pose parameters $\{{\phi }_{i}\}_{i=1}^{N}$ and CTF parameters $\{{\psi }_{i}\}_{i=1}^{N}$ from the collected raw particles $\{{{{\bf{x}}}}_{i}\}_{i=1}^{N}$.

Initialization

Apply a low-pass filter, typically at 10 Å. The resulting filtered volume is then used as the initial reference model for training the generative module in the first iteration of cryoPROS. Ensuring consistent low-frequency characteristics between the initial reference model and the target protein is crucial for enhancing the initial training of the generative model. Various methodologies can be employed to obtain this initial reference model, such as using the atomic model of a homologous protein, structures predicted by AlphaFold2³⁷, or automatic model-building tools like Model-Angelo⁴⁷.

CryoPROS iterations

Perform multiple iterative rounds of the generative and co-refinement modules. During co-refinement, use appropriate pose estimation software such as CryoSPARC or RELION, with the reference model, low-pass filtered to 30 Å, as the initial reference model. Tailor this iterative process to the specific requirements of the protein dataset.

Optional post-processing

Utilize EMReady or other post-processing tools to further optimize the results obtained from the final round of cryoPROS iterations.

Optional local refinement

Select a subset of raw particles with a balanced pose distribution and perform a local search on cryoPROS-corrected pose parameters. The density map obtained in step 4 can serve as the initial reference for local refinement.

General settings for cryoPROS in this study

The network weights of the conditional VAE in the generative module were initialized randomly, with the process spanning two iterations. In the first iteration, the initial reference model was generated using a low-frequency similarity model, such as a low-pass filter applied to homologous proteins or models obtained from AlphaFold2. In the second iteration, EMReady³⁵ was used to postprocess the results, helping to restore anisotropy in the reconstructed density map caused by uneven orientation distributions. CryoSPARC, a widely used cryo-EM orientation estimation software, was employed to estimate the pose of particles in the co-refinement module of cryoPROS.

ReconDisMic: reconstruction of disordered detergent micelles or lipids nanodiscs

When the target protein is embedded in detergent micelles or lipid nanodiscs, cyroPROS adds a procedure to reconstruct the micelles ${{{\bf{V}}}}_{{{\bf{M}}}}$. This procedure is combined with the low-pass filtered homologous protein ${{{\bf{V}}}}_{{{\rm{homo}}}}$, which constructs the initial reference model ${{{\bf{V}}}}_{{{\rm{model}}}}$.

To accomplish this, we first constrain the homologous protein through a volume mask ${{\bf{M}}}$, which can be determined through a thresholding process:

$${{\bf{M}}}\left[i,j,k\right]=\left\{\begin{array}{l}1,\hfill {{{\bf{V}}}}_{{{\rm{homo}}}}\left[i,j,k\right] \geq T \hfill \\ 0,\hfill {{{\bf{V}}}}_{{{\rm{homo}}}}\left[i,j,k\right]{{\boldsymbol{ < }}}T\end{array}\right.,i,j,k=1,\ldots,M,$$

where $T$ is the threshold value, and $M$ denotes the of voxels in each axis. Subsequently, we set the value of the homologous protein ${{{\bf{V}}}}_{{{\rm{homo}}}}$ within the mask and proceed to reconstruct the regions outside the mask by solving the following optimization problem:

$$\begin{array}{c}{\min}_{{\bf{V}}_{\bf{M}}} \end{array}\mathop{\sum }\limits_{i=1}^{N}{{\rm{||}}}{{{{C}}}\left({\psi_i}\right)P\left({\phi }_{i}\right)\left({{\bf{M}}}\odot {{{\bf{V}}}}_{{{\rm{homo}}}}{{\boldsymbol{+}}}\left(1-{{\bf{M}}}\right)\odot {{{\bf{V}}}}_{{{\bf{M}}}}\right)-{{{\bf{x}}}}_{i}{{\rm{||}}}}_{2}^{2},$$

where $\odot$ denotes the element-wise multiplication. The optimization problem stated above can be efficiently resolved using the stochastic gradient descent method, and the initial reference model ${{{\bf{V}}}}_{{{\rm{model}}}}$ for the generative module is obtained through ${{{\bf{V}}}}_{{{\rm{model}}}}={{\bf{M}}}\odot {{{\bf{V}}}}_{{{\rm{homo}}}}{{\boldsymbol{+}}}\left(1-{{\bf{M}}}\right)\odot {{{\bf{V}}}}_{{{\bf{M}}}}$.

Simulated dataset generation

To quantitatively analyze cryoPROS performance amid orientation imbalances, we created two datasets: Uni-HA-Syn and PO-HA-Syn. Additionally, to explore the boundaries of cryoPROS, we generated datasets ranging from PO-HA-Syn-Re100 to PO-HA-Syn-Re00 and PO-HA-Syn-MW10 to PO-HA-Syn-MW45.

Uni-HA-Syn and PO-HA-Syn

Utilizing the atomic model (PDB ID: 6WXB), we employed the Relion’s relion_project module to generate datasets. CTF modulation, based on experimental dataset (EMPIAR-10096) parameters, and additive Gaussian noise (with zero mean and a standard deviation of 60) were applied to the datasets, followed by normalization of the particle images. Both the Uni-HA-Syn and PO-HA-Syn datasets contain 130,000 particles, each with an average SNR of –15.63 dB. The Uni-HA-Syn dataset features uniformly distributed orientations, whereas the PO-HA-Syn dataset shows a preference for orientations near the Z-axis, with 82,909 particles positioned within 36 of alignment. The distribution of the PO-HA-Syn dataset is identical to the cryoPROS-corrected pose distribution of the untilted HA-trimer (EMPIAR-10096), thereby ensuring that it accurately replicates the pose distribution of the HA-trimer experimental dataset.

Pose imbalance variation and missing data: PO-HA-Syn-Re100 to PO-HA-Syn-Re00 and PO-HA-Syn-MW10 to PO-HA-Syn-MW45

To probe pose imbalance effects, we generated PO-HA-Syn-Re100 to PO-HA-Syn-Re00 datasets, gradually removing particles within specific angle ranges near the equator. PO-HA-Syn-MW10 to PO-HA-Syn-MW45 simulate missing data by progressively limiting views along the preferred orientation axis, facilitating a comprehensive evaluation of cryoPROS under varied pose imbalances.

Computation of KL divergence and SNR

To demonstrate the superiority of cryoPROS-generated noisy particles over those generated by the Gaussian noise substitution method, we compute the KL divergence between the generated and real particles and the particle SNR. Let $\{{{{\bf{x}}}}_{i}^{g}\}_{i=1}^{N}$ and $\{{{{\bf{x}}}}_{i}^{r}\}_{i=1}^{N}$ represent the sets of generated and real particles, respectively, with $N$ denoting the number of particles. To compute the KL divergence, we first convert the particle images to probability histograms, denoting the number of bins as $B$, and for a particle image ${{\bf{x}}}$, its probability histogram ${{{\bf{p}}}{\mathbb\,{\in }}\,{\mathbb{R}}}^{B}$. Let the probability histograms for $\{{{{\bf{x}}}}_{i}^{g}\}_{i=1}^{N}$ and $\{{{{\bf{x}}}}_{i}^{r}\}_{i=1}^{N}$ be represented as $\{{{{\bf{p}}}}_{i}^{g}\}_{i=1}^{N}$ and $\{{{{\bf{p}}}}_{i}^{r}\}_{i=1}^{N}$, respectively. Then, the average KL divergence for all particles is defined as:

$${\rm{KL}}\left({\left\{{{{\bf{x}}}}_{i}^{g}\right\}}_{i=1}^{N}{{\rm{||}}}{\left\{{{{\bf{x}}}}_{i}^{r}\right\}}_{i=1}^{N}\right)=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\,\mathop{\sum }\limits_{j=1}^{B}{{{\boldsymbol{p}}}}_{{ij}}^{g}\log \frac{{{{\boldsymbol{p}}}}_{{ij}}^{g}}{{{{\boldsymbol{p}}}}_{{ij}}^{r}}$$

(11)

where ${{{\bf{p}}}}_{{ij}}^{g}$ and ${{{\bf{p}}}}_{{ij}}^{r}$ denotes the $j$-th component of ${{{\bf{p}}}}_{i}^{g}$ and ${{{\bf{p}}}}_{i}^{r}$, respectively. In practice, since the pixel values within a particle image remain unbounded, we first clip the pixel values within the range of $\left[-4,\,4\right]$, and the number of bins $B$ is set to 1024.

We estimate the SNR of noisy particles using the method proposed in³⁸. First, we randomly sample $N$ noisy particles, denoted as $\{{{{\bf{x}}}}_{i}\}_{i=1}^{N}$. Subsequently, we randomly sample $N$ background particles from the original micrographs, denoted as $\{{{{\bf{x}}}}_{i}^{b}\}_{i=1}^{N}$, which contain only pure noise. Denote the mean and variance for each background particle ${{{\bf{x}}}}_{i}^{b}$ as ${\mu }_{i}^{b}$ and ${{{\bf{v}}}}_{i}^{b}$, respectively. Then, we normalize the noise in ${{{\bf{x}}}}_{i}$ and convert it to ${\hat{{{\bf{x}}}}}_{i}$ through: ${\hat{{{\bf{x}}}}}_{i}={{{\bf{x}}}}_{i}-{\mu }_{i}^{b}$. Denote the mean and variance for ${\hat{{{\bf{x}}}}}_{i}$ as ${\mu }_{i}$ and ${{{\bf{v}}}}_{i}$, the average SNR (dB) for the noisy particles is then defined as:

$${{\rm{SNR}}}=\frac{10}{N}\mathop{\sum }\limits_{i=1}^{N}{\log }_{10}\left({{{\bf{v}}}}_{i}\right)-{\log }_{10}\left({{{\bf{v}}}}_{i}^{b}\right).$$

In practice, we set the value of $N$ to 10.

“Einstein from noise” 3D refinement experiment

The phenomenon of “Einstein from noise” has gained considerable attention in the field. It describes a scenario where averaging a large number of white noise images onto a reference image can easily lead to overfitting, thereby generating false densities, which we refer to as “phantom” densities. In order to thoroughly investigate the risk of cryoPROS-learned noise producing such phantom densities, we devised the following experiments and employed a Gaussian white noise group for comparison:

We compared the auto-refinement results obtained from pure Gaussian noise stacks with those from cryoPROS-learned noise stacks. Utilizing low-pass filtered density maps with various cutoff frequencies as references (e.g., ribosome, PDB ID: 6PCQ) for noise refinement, the resulting 3D density primarily represents a misleading signal derived from noise. We employed two metrics to evaluate the degree of overfitting: the resolution of the phantom density map and the quality of the density. Higher resolution and better quality indicate that the false signal is more high-frequency and solid, suggesting a greater risk of noise overfitting to false signal in actual computations.

Validation cryoPROS result

Experiment 1: structure refinement experiment to measure distances between cryoPROS results, ground truth, and initial reference models to assess model bias

Following the standard cryoPROS procedure, we analyzed HA-trimer data using two different homologous proteins, 2RFU and 6IDD, as reference models in the first iteration of cryoPROS, resulting in cryoPROS-2RFU and cryoPROS-6IDD, respectively. We compared these structures to the state-of-the-art result (serving as ground truth) and their respective homologous proteins. To quantify distances, we introduced an atomic model of HA trimer (PDB ID: 3WHE) and using the “real space refinement” module in Phenix software refined it to fit three density maps: cryoPROS-2RFU, cryoPROS-6IDD, and the state-of-the-art result. The refined structures will be designated as 3WHE-cryoPROS-2RFU, 3WHE-cryoPROS-6IDD, and 3WHE-state-of-the-art, respectively. Subsequently, we used TMscore and RMSD to evaluate the differences between the models (Fig. 6f), with detailed visualizations provided in Fig. 6g.

Experiment 2: measurement of model bias

We assessed potential template bias in cryoPROS using the cisTEM script measure_template_bias. The baseline template, homologous protein 6IDD, was compared against alternative initial reference models, including 6IDD-omitted, 5XL8, and 2RFU. The script was executed for each cryoPROS result that differs from the initial reference model to evaluate template bias. Specifically, the 6IDD-omitted model, from which all side chains have been removed resulting in an atomic retention rate of 50.91%, was examined (Fig. 6h).

Experiment 3: follow-up local refinement experiments on cryoPROS

On the HA-trimer data, we conducted local refinement experiments on the outcomes from cryoPROS-2RFU and cryoPROS-6IDD. These experiments involved utilizing varying ranges for rotation and shift searches (Supplementary Fig. 9a).

Experiment 4: homologousModel-to-map FSC

To assess the frequency-based correlation between homologous proteins, the target protein, and cryoPROS results, we computed model-to-map FSC curves between the homologous atomic model and the density maps (including target protein and those obtained via cryoPROS). Specifically, we focused on the homologous protein 6IDD as a representative example. The correlation between the density map generated by cryoPROS and the homologous protein was compared with that of the target protein in each frequency band. A threshold correlation value of 0.5, corresponding to 8.59 Å, was established. This threshold delineated the common characteristic frequency band shared by both proteins (below 8.59 Å) and the unique characteristic frequency band of the homologous protein (above 8.59 Å). The correlation of the cryoPROS result was analyzed to determine its position relative to the threshold. A correlation below 0.5 at 20.96 Å, within the low-frequency band, suggested successful avoidance of incorporating specific local details from homologous proteins by cryoPROS. This setup enabled us to evaluate cryoPROS’s ability to preserve low-frequency features while avoiding the inclusion of high-frequency local details from homologous proteins. The results were shown in Supplementary Fig. 9b.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.