Introduction

Over the past decades, interdisciplinary efforts in nanoscience and condensed matter physics have cultivated the promising field of spintronics, leveraging spin-orbit coupling (SOC)1. Research has focused on developing efficient methods to convert charge to spin via SOC, promising ultrafast and energy-efficient magnetic memory2 and logic devices3. Conventional methods involve manipulating the magnetization in ferromagnets (FMs) by injecting electron spins, transferring their angular momentum to magnetization through spin-orbit torques (SOTs)4,5, enabled by the spin Hall effect (SHE)5,6 and/or interfacial SOC phenomena4,7. However, this method often suffers from excessive Joule heating8,9 and inevitable spin loss due to interfacial scattering10,11, highlighting the need for more efficient spin transfer mechanisms.

To mitigate these issues, researchers have focused on minimizing spin dissipation and enhancing spin transport efficiency12,13. Efforts include developing innovative materials14,15 refining interfacial engineering to reduce spin scattering10,11, and exploring magnonic spin currents16,17,18,19 for efficient spin injection, moving beyond conventional electron-mediated methods. These endeavors aim to achieve high spin transport efficiency with minimal loss, based on the common belief that dissipation hinders efficient magnetization control. Despite these advancements, dissipation remains an inherent process that cannot be entirely eliminated.

Given these challenges, the discovery of intrinsic spin currents (ISC) within FMs presents a promising new avenue20,21,22,23. When combined with asymmetric spin absorption, these ISCs can generate SOTs without additional spin sources20,21,22. This has prompted numerous experiments to validate their practical impact21,24,25. However, isolating the effect of the ISC from other effects, such as interfacial SOC, has proven to be a formidable challenge, often yielding ambiguous results26,27. Moreover, in controlled settings, mostly utilizing asymmetric interfacial SOC, the observed impact of the ISC has been subtle, not in line with theoretical predictions20 and leading to their significance being underestimated26,28.

In this context, we propose that magnonic spin dissipation can decisively tackle the fundamental challenges and provide a transformative method for creating highly efficient spintronic devices. Contrary to the convention that minimizing dissipative losses in spin transport is essential for high-efficiency SOTs, our findings reveal that enhancing magnonic dissipation significantly boosts SOT efficiency, enabling robust magnetization switching. This paradigm shift not only overcomes the fundamental challenge of accessing the impact of the ISC unambiguously but also unveils the untapped potential of using the magnonic spin dissipation as an alternative, yet efficient, method for controlling magnetization.

Results

Fundamental mechanism of SOTs driven by magnonic spin dissipation

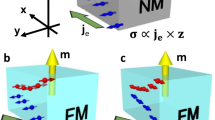
Our approach employs a heterostructure composed of an FM metal and an antiferromagnetic insulator (AFI). Unlike conventional methods relying on external spin injection from heavy metals (HMs) into FMs (Fig. 1a), we leverage an ISC, arising from the SHE within a ferromagnetic metal20,21. When a charge current passes through a ferromagnetic metal sandwiched between two insulating layers, the net spin angular momentum (SAM) within the FM is the sum of two incoming SAM with opposite spin polarizations, arising from the ISC reflected at each interface. Typically, these contributions cancel each other out due to symmetry in electron-mediated spin transport, leading to negligible net SAM within the FM. Previous studies have attempted to break this symmetry in spin transport by employing an extra metallic layer21 or through interfacial SOC21,26,28. However, these methods disrupt the symmetry breaking in charge transport as well, effectively acting as spin current generators and thereby complicating the analysis of the desired effects.

Fig. 1: SAM transfer in HM/FM/Insulator and AFI/FM metal/Insulator.
figure 1

a Schematic illustration of the spin transfer mechanism in conventional HM/FM/Insulator. When a charge current (\({{{I}}}_{{{C}}}\)) is applied along the x-axis in the HM layer, SHE generated a spin current carrying SAM (\({J}_{\tt{in}}\)) into the adjacent FM layer. The net SAM (\({J}_{{S}}^{\tt{net}}\)) in the FM layer is then equivalent to the incoming \({J}_{\tt{in}}\), resulting in a specific amount of spin torques exerted on the magnetization (M) due to the transverse spin component. b Schematic illustration of spin transfer through magnonic spin dissipation in AFI/FM/Insulator. The charge current \({I}_{C}\) flowing in a ferromagnetic metal generates ISC via the SHE within the FM layer. The SAM flowing toward the normal insulator is entirely reflected at their interface (\({J}_{\tt{out}}\)). Conversely, the SAM with the opposite sign moving toward the AFI is partially transferred to the AFI layer, being converted into magnons, with the remaining SAM reflected back to the FM at the FM/AFI interface (\({J}_{\tt{ref}{{1}}}\)). The magnons reflected at the outer boundary of the AFI layer carry the SAM back to the FM (\({J}_{\tt{{ref}}{{2}}}\)). The net SAM \({J}_{{{S}}}^{\tt{{net}}}\) in the FM layer then is given by the total sum of three incoming SAM, \(-{J}_{\tt{{out}}}+{J}_{\tt{{ref}}{{1}}}+{J}_{\tt{{ref}}{{2}}}\). In the absence of magnon dissipation, \(-{J}_{\tt{{out}}}+{J}_{\tt{{ref}}{{1}}}+{J}_{\tt{{ref}}{{2}}}\) becomes zero. However, in the presence of non-zero magnon dissipation, it results in the non-zero spin transfer to M.

Full size image

To tackle the challenge, we introduce an AFI, serving as a generic spin sink through magnon dissipation, to selectively break the symmetry in spin transport while maintaining the symmetry in charge transport (see Fig. 1b). This symmetry breaking in spin transport results in a non-zero net SAM, generating SOTs especially when the SAM is oriented transverse to the magnetization. In this mechanism, the SOTs depend on two key factors: efficient transmission of SAM from the FM to the AFI, with minimal reflection at their boundary, and effective internal dissipation of the magnonic spin current within the AFI. The first factor hinges on the spin-to-magnon conversion efficiency at the FM/AFI interface, characterizing how effectively it converts electron spins into magnons. The second factor, magnonic spin dissipation, directly correlates with the magnetic damping of the AFI, reducing the SAM reflection back to the FM.

Proof-of-concept experiments of SOTs driven by magnonic spin dissipation

To demonstrate our concept, we fabricated two types of AFI/FM/SiOx trilayer structures: NiO/Ni/SiOx and Cr2O3/Ni/SiOx, where NiO and Cr2O3 were selected as representative antiferromagnetic insulators with easy-plane and easy-axis anisotropy29,30, respectively. The AFI thin films were grown epitaxially on single-crystalline substrates (MgO or Al2O3) using pulsed laser deposition (PLD) or reactive sputtering, followed by in-situ magnetron sputtering to deposit polycrystalline Ni and SiOx layers (see “Methods”). This process yields high-quality crystallinity in AFI layers, as confirmed by X-ray diffraction and transmission electron microscopy in Supplementary Information (SI) S1. Importantly, our structure design excludes potential SOTs from external sources, such as spin/orbital Hall effects from non-magnetic layers5,31,32,33,34,35,36, as charge currents flow exclusively within the metallic FM. In addition, we exclude interfacial SOC effects6, which could also generate spin currents and act as another spin dissipation channel, as elaborated later.

The SOTs in AFI/Ni/SiOx were characterized by azimuthal-angle-dependent harmonic measurements8 (Fig. 2a), whereby the first- (\({R}_{{xy}}^{{1} \omega }\)) and second-harmonic (\({R}_{{xy}}^{{2} \omega }\)) Hall signals were measured simultaneously while rotating the azimuthal angle (ϕH) of the in-plane magnetic field (Hext) (see Methods and Supplementary Information S2). Figure 2b presents SOT fields corresponding to damping-like (HDL) and field-like (HFL) components for both NiO/Ni/SiOx and Cr2O3/Ni/SiOx.

Fig. 2: SOTs in AFI/FM/Insulator.
figure 2

a Schematic illustration of the harmonic Hall voltage measurement, where IAC is a.c. charge current, ϕH is an azimuthal angle of the external magnetic field (Hext) applied in the x-y plane with respect to the applied current direction. b The field-like (HFL) and damping-like (HDL) components of SOTs vs. the charge current density (JAC), as measured in four different materials stacks: NiO(1.5)/Ni(3)/SiOx(2), V2O3(3)/Cr2O3(80)/Ni(3)/SiOx(2), SiOx(Subs.)/Ni(3)/SiOx(2), and MgO(Subs.)/Ni(3)/SiOx(2). The numbers and “Subs.” in the parentheses denote the thickness in nanometers and the substrate, respectively. The two controls samples, MgO(Subs.)/Ni(3)/SiOx(2) and SiOx(Subs.)/Ni(3)/SiOx(2), have nominally asymmetric and symmetric interfaces, respectively. The solid lines represent the linear fitting curves.

Full size image

A key observation is that the presence of an AFI layer —regardless of whether it is NiO or Cr2O3—leads to a significantly larger slope in the current dependence of the damping- and field-like effective fields compared to the control samples, indicating larger effective spin Hall angles. In contrast, our control samples with both symmetric and asymmetric interfaces incorporating normal insulators instead of the AFIs exhibit negligible slopes due to the suppression of both charge and magnon transport. This highlights the crucial role of AFIs in generating SOTs, while suggesting minimal contribution from interfacial SOC effects in our system.

The extracted HDL and HFL values for NiO/Ni/SiOx are (− 0.38 ± 0.02) × 10-11 mT m2/A and (0.19 ± 0.02) × 10−11 mT m2/A, respectively. For Cr2O3/Ni/SiOx, the corresponding values are (− 1.81 ± 0.21) × 10−11 mT m2/A and (0.29 ± 0.09) × 10−11 mT m2/A. We evaluated the effective spin Hall angles using \({{\theta }}_{S}^{{{\rm{DL}}}({{\rm{FL}}})}=\frac{2e{M}_{{{\rm{S}}}}{t}_{{{\rm{FM}}}}}{\hslash }\frac{{H}_{{{\rm{DL}}}({{\rm{FL}}})}}{{J}_{C}}\), where MS and tFM denote the saturation magnetization and the thickness of the FM layer, respectively. This yields values of − 0.018 ± 0.001 (0.008 ± 0.001) for NiO and − 0.082 ± 0.009 (0.013 ± 0.004) for Cr2O3. Notably, these values are comparable to or even larger than those measured in non-magnetic metals (NMs) with strong spin/orbital Hall effects such as Pt, Ti, Cr, etc.5,31,32,33,34,35,36.

As a remark, we note that the control samples of AFI/FM/normal insulator, with CoFeB or Py as the FM, exhibit a spin Hall angle of the same order of magnitude as Ni (see Supplementary Information S2). This finding aligns well with previous theoretical predictions for ISC20 and suggests that the observed SOTs originate from the antiferromagnet, regardless of the FM used.

SOTs reliant on the relative alignment between spin polarization and Néel axis

While our proof-of-concept experiments demonstrate a clear correlation between the presence of the AFI and the observed SOTs, directly identifying magnon-mediated spin transport within the AFI as the underlying mechanism is essential to fully corroborate the proposed magnon dissipation-driven SOTs. This necessitates a detailed understanding of the interfacial spin transfer process—where spin accumulation induced by the ISC in the FM is converted into magnonic spin currents in the AFI—and the subsequent propagation and dissipation of these magnons, which ultimately govern the resulting SOTs.

The spin transport properties of AFIs are fundamentally governed by their magnetic anisotropy, which dictates the nature of the intrinsic magnon modes available for spin transport. In easy-axis AFIs, the Néel vector aligns along a specific crystallographic axis, allowing for two circularly polarized magnon eigenmodes29, each carrying spin angular momentum in opposite directions along the Néel axis. In easy-plane AFIs, by contrast, the anisotropy allows for two linearly polarized magnon eigenmodes within the plane29. Although these individual modes carry no net spin angular momentum, their superposition allows for spin transport along the Néel axis, with rapid dephasing between the modes (see Supplementary Information S3), resulting in much shorter magnon diffusion length than in the easy-axis anisotropy case37,38.

Despite these differences, both easy-axis and easy-plane AFIs share a key feature: magnon-mediated spin transport is intrinsically linked to their Néel orientation (see Supplementary Information S3). This directional dependence arises because the Néel vector defines the internal magnetic order of the antiferromagnet, thereby setting the preferred axis for spin transport. Consequently, both the efficiency and angular dependence of spin transport directly reflect the relative orientation between the injected spins into the AFI and the Néel axis. This Néel axis dependence serves as a distinctive experimental signature for identifying the magnonic origin of the observed SOTs.

To experimentally confirm this, we have systematically examined how the SOTs vary with the relative orientations between the magneto-crystalline easy axis n of AFIs —closely related to the Néel axis— and the spin polarization μ induced by the ISC in the FM. This was achieved by using single-crystalline substrates with different orientations and fabricating devices along various in-plane directions, effectively altering the current flow direction (I) and, consequently, the orientation of μ accumulated at the FM/AFI interface relative to the crystallographic axes of the AFI (Fig. 3a).

Fig. 3: Correlation between SOTs and the relative alignment between the spin polarization and the magneto-crystalline easy axis of AFIs.
figure 3

a Schematics of Hall bar devices patterned on a single crystalline substrate (MgO or Al2O3). The devices are patterned in different directions relative to the substrate’s crystallographic orientations, which affect the direction of current flow I and, consequently, the orientation of spin polarization μ of ISC in FM relative to the magneto-crystalline easy axis n of AFIs. The μ of the ISC in the FM is transverse to the I. b Effective spin Hall angles vs. charge current direction, as obtained from devices patterned on NiO(1.5)/Ni(3)/SiOx thin films grown on MgO substrates with different crystallographic orientations: (001), (110), and (111). The numbers in the parentheses denote the thickness in nanometers. \(\bar{{{\bf{S}}}\,}\) in the graphs represents the summed values of the component of all preferred \(\hat{{{\bf{n}}}}\) along \(\hat{{{\boldsymbol{\mu }}}}\), as obtained from \(\mathop{\sum }_{i=1}^{N}\left|\widehat{{{\boldsymbol{\mu }}}}\cdot {\widehat{{{\bf{n}}}}}_{i}\right|\). c Effective spin Hall angles vs. charge current direction, as obtained from devices patterned on V2O3(3)/Cr2O3(20)/Ni(3)/SiOx thin films grown on two sapphire substrates with different crystallographic orientations: c-plane (0001) and m-plane (\(10\bar{1}0\)). For the devices on the c-plane sapphire substrate, the μ of the ISC is always transverse to the n, irrespective of the device’s pattern orientation. In contrast, for devices on the m-plane sapphire substrate, the μ can be either transverse or parallel to the n, depending on the device’s pattern orientation.

Full size image

Figure 3b and c present the effective spin Hall angle θSDL(FL) as a function of the charge current direction, measured from two sets of samples. Figure 3b shows the results for NiO/Ni/SiOx trilayers grown on MgO substrates with (001), (110), and (111) orientations, while Fig. 3c displays data for Cr2O3/Ni/SiOx trilayers grown on Al2O3 substrates with different crystallographic orientations: c-plane (0001) and m-plane (\(10\bar{1}0\)). In both cases, θSDL(FL) varies significantly with the substrate orientation. More notably, devices patterned in different in-plane directions on the same substrate exhibit a large difference in θSDL(FL) —up to a threefold variation — despite having consistent interfacial conditions.

To gain further insight into these experimental results, we estimated the preferred n and its relationship to μ. For NiO, the Néel vector can, in principle, adopt 12 equivalent orientations at equilibrium. However, epitaxial strain at the interface lifts this degeneracy, making only a subset of these orientations energetically favorable, as reported in previous studies39,40. Based on this, we identified the most likely configurations of n for NiO grown on each MgO substrate (see Supplementary Information S4) and calculated their projection along μ by using \(\bar{{{\bf{S}}}}=\mathop{\sum }_{i=1}^{N}\left|\widehat{{{\boldsymbol{\mu }}}}\cdot {\widehat{{{\bf{n}}}}}_{i}\right|\), where \(\bar{{{\bf{S}}}}\) quantifies the effective alignment between μ and all possible n.

This analysis reveals a clear trend: across all substrate orientations, θSDL increases with larger \(\bar{{{\bf{S}}}}\) values when comparing devices fabricated on the same substrates with different pattern orientations. This strongly suggests that the spin-to-magnon conversion efficiency is enhanced when n and μ are closely aligned. A similar, and even clearer, correlation between θSDL and the relative orientation of n and μ is observed in Cr2O3, an easy-axis AFI with a relatively simple and well-ordered magnetic domain structure attributed to its well-defined magnetic easy axis along the c-axis. For devices on the c-plane sapphire substrate, where μ is always transverse to n, θSDL remains nearly constant across all pattern orientations. In contrast, for devices on the m-plane substrate, where μ can be either transverse or parallel to n, θSDL varies significantly, showing the largest values when μ is parallel to n. This consistent behavior across both easy-plane and easy-axis AFIs strongly supports our theoretical prediction (see Supplementary Information S3) that the longitudinal spin component along the Néel axis predominantly governs the generation of the observed SOTs37,41, further highlighting their magnonic origin. We note, however, that the field-like component —often attributed to interfacial spin precession and thus more sensitive to the interface than the damping-like counterpart42— does not perfectly follow the same angular dependence. This suggests that additional interfacial processes may be contributing to its behavior, calling for further investigation.

It is also important to consider possible interfacial effects that could influence our results. While the interfacial coupling between the FM and AFI may modify the detailed magnetic structure of the AFI near the interface40, the Néel orientations in our samples are expected to be predominantly aligned along the magneto-crystalline easy axes. This is further supported by our control experiment on AFI/Cu/Ni/SiOx, where a thin Cu layer reduces interfacial coupling, yet the same angular dependence is observed (see Supplementary Information S4).

We remark that, although our analyses provide reasonable estimations of preferred Néel orientations, precise quantitative determination of the Néel axes remains challenging. In addition, variations in film quality across different substrates complicate direct comparisons of SOTs between different substrates. Nonetheless, we emphasize that our results —a significant variation in SOTs depending on the current direction under the same interface— effectively rule out interfacial SOC as a major source of spin dissipation. Moreover, the strong correlation between SOTs and the alignment of μ with the magneto-crystalline easy axes provides compelling evidence that the observed SOTs originate from magnon-mediated spin transport within the AFI.

Finally, we highlight that the observed SOTs are not resulting from the spin currents generated by external sources but indeed from the ISCs within the FMs. This is evidenced by the non-monotonic dependence of θSDL(FL) on the FM thickness (tFM), in contrast to the monotonic 1/tFM dependence in FM/NM bilayers32,35,43 (see Supplementary Information S6). This unique trend provides conclusive evidence that our SOTs result from the ISC in the FM, implying that the role of interfacial SOC as a spin source is also negligible in our systems28,44.

Correlation between the SOTs and magnonic dissipation

Building on our verification of the magnonic nature of the SOTs, we now aim to establish whether magnonic spin dissipation indeed serves as the primary driving mechanism. Unlike conventional systems where spin currents are externally injected into the AFI via magnons, our proposed mechanism predicts a distinct dependence of the SOTs on the thickness of the AFI (tAFI). In conventional NM/AFI/FM systems, the SAM delivered to the FM via magnons from the NM decreases with increasing the tAFI, eventually vanishing due to dissipative losses over longer distances. In contrast, within the dissipation-driven framework, a thicker AFI leads to enhanced magnonic spin dissipation inside the AFI, which in turn increases the net SAM in the FM, thereby enhancing the SOTs. Importantly, this mechanism predicts that the SOTs remain non-zero even for sufficiently thick AFIs, where magnons fully dissipate. These distinctive features can compellingly demonstrate that magnonic spin dissipation is the primary driving mechanism behind the observed SOTs, offering strong validation for our hypothesis.

Figure 4a illustrates the dependence of θSDL(FL) on the thickness of NiO (tNiO). Our results reveal a non-monotonic thickness dependence, peaking at tNiO ~ 1.5 nm to 2.0 nm, followed by a gradual decrease at larger tNiO. This non-monotonic thickness dependence is consistent with previous results45,46 on conventional magnon-mediated spin injection in NM/NiO/FM structures, where the spin transmission through NiO reaches a maximum at a characteristic thickness and subsequently decreases as tNiO increases further. This trend can be attributed to two key factors. First, NiO’s magnetic susceptibility exhibits a strong thickness dependence within a few nanometers45,46, as demonstrated in the previous studies and also supported by our temperature-dependent measurements of θSDL(FL) in Supplementary Information S5, leading to significant variations in spin-to-magnon conversion efficiency as a function of tNiO. In addition, within this thickness range, magnon dissipation in NiO is already nearly complete, as the rapid magnon decay inherent to NiO causes the total SAM dissipated within the AFI to saturate (see Supplementary Information S4). Consequently, the expected increase in SOTs with increasing tAFI is no longer observed beyond this characteristic thickness. Nonetheless, our experiments clearly demonstrate a key feature predicted by the dissipation-driven mechanism: SOTs do not vanish even for relatively thick NiO layers, maintaining finite values at larger tNiO. Given that the interfacial SOC—which could otherwise contribute to a similar effect— is negligible in our system, these non-zero, saturated SOTs strongly indicate that magnonic spin dissipation plays a central role in generating the observed SOTs.

Fig. 4: AFI-thickness dependent SOTs.
figure 4

a Dependence of effective spin Hall angles on NiO thickness (tNiO) for NiO(tNiO)/Ni(3)/SiOx(2) films, as measured at room temperature. The numbers in parentheses are in nanometers. The top and bottom panels correspond to field-like (θSFL) and damping-like (θSDL) components, respectively. b Dependence of effective spin Hall angles on Cr2O3 thickness \({t}_{{{{\rm{Cr}}}}_{2}{{{\rm{O}}}}_{3}}\) for V2O3(3)/Cr2O3\({t}_{{{{\rm{Cr}}}}_{2}{{{\rm{O}}}}_{3}}\)/Ni(3)/SiOx(2) films on m-plane sapphire \(({10}\bar{1}{0})\) substrates, as measured at room temperature. The solid lines represent the fitting curves obtained from Eq. (1) in Methods (see Supplementary Information S7 for more details).

Full size image

To further verify this mechanism, we also present the tAFI dependence of θSDL(FL) for the easy-axis Cr2O3, which offers a better platform for this purpose due to its longer magnon decay lengths41,47 and relatively stable spin-to-magnon conversion efficiency at thicker AFI. Figure 4b presents the θSDL(FL) measured at room temperature across varying Cr2O3 thicknesses (\({t}_{{{{\rm{Cr}}}}_{2}{{{\rm{O}}}}_{3}}\)). Notably, the θSDL(FL) increases with \({{t}}_{{{{\rm{Cr}}}}_{2}{{{\rm{O}}}}_{3}}\) — a trend that diverges from conventional systems, yet aligns well with our prediction. Given that the blocking temperature of Cr2O3 remains nearly constant for the observed thickness range (see Supplementary Information S5), the unconventional thickness dependence is attributed to magnonic spin dissipation rather than variations in spin-to-magnon conversion efficiency, as seen in NiO. Moreover, the observed trend further suggests that SOTs remain non-zero and saturate in thicker Cr2O3 layers once magnons are fully dissipated. These experimental observations of distinct behaviors compellingly demonstrate that the observed SOTs are indeed driven by magnonic spin dissipation, highlighting the critical role of magnonic spin dissipation in generating intrinsic SOTs.

Further support for this dissipation-driven mechanism comes from control experiments where we used the spin pumping process to deliberately tune the magnetic damping of the AFI (see Supplementary Information S8). By strategically placing a Pt with strong SOC on the surface of the AFI opposite the FM, we can effectively alter the magnetic damping48 while preserving the FM/AFI interface and spin-to-magnon conversion efficiency. Remarkably, these experiments reveal a significant enhancement of SOTs when the Pt was introduced on top of the AFI. This observation provides additional compelling evidence that the observed SOTs originate from magnonic spin dissipation.

Magnetization switching by the magnon-dissipation-driven SOTs

Lastly, we present an experimental demonstration of magnetization switching by magnonic spin dissipation, highlighting its applicability. To monitor the switching of the in-plane magnetization through currents, we measure the unidirectional spin Hall magnetoresistance (USMR)49 that displays a marked difference in longitudinal resistance depending on the polarity of the magnetization (see details in Methods and Supplementary Information S9). In order to ensure that the magnetization lies along the y-axis at remanence, our device is fabricated in a rectangular form as depicted in Fig. 5a. By measuring the second-harmonic component of the longitudinal resistance \({R}_{{xx}}^{{2} \omega }\), as a function of Hext, under a.c. charge currents (IAC) with a current density of JAC = 1.3 × 1011 A/m2 (Fig. 5b), we observe a distinct resistance difference of ~2 mΩ between ±My, confirming the feasibility of measuring the in-plane magnetization switching by an electrical approach. Given this result, we demonstrate current-driven magnetization switching enabled by magnon dissipation. By varying the amplitude of the current pulse and measuring \({R}_{{xx}}^{{2} \omega }\) as a function of the pulse current density JP, we observe a sign reversal of \({R}_{{xx}}^{{2} \omega }\) at the critical current density of JP = ± 6 × 1011 A/m2, indicating the deterministic magnetization switching depending on the polarity of the current, as illustrated in Fig. 5c. To corroborate the switching mechanism, we perform a series of experiments utilizing a complex sequence of current pulses (Fig. 5d). Starting with magnetization saturated along the +y direction, we apply the sequence of current pulses with JP = ± 8.3 × 1011 A/m2, leading to noticeable reversals in the polarity of the magnetization. The reproducible and deterministic switching, dependent on the current polarity, provides compelling evidence that the magnetization switching for in-plane magnetized ferromagnetic materials cannot be attributed to the current-induced Oersted field or a Joule heating effect. Importantly, our multilayer is comprised of a single ferromagnetic metal, which prevents any significant net Oersted field effect within the materials. Consequently, our findings are concluded to provide definitive evidence that the magnon-dissipation-driven SOTs govern the switching mechanism.

Fig. 5: Magnetization switching by magnon-dissipation-driven SOTs.
figure 5

a Schematic illustration of USMR measurement (top) and an optical microscope image of the device under test (bottom). The charge current pulse (IP) is applied along the x-axis, subsequently longitudinal voltage Vxx is measured using a harmonics measurement technique under an IAC. b Second-harmonic longitudinal resistance \(({R}_{xx}^{{{2}}{{\omega }}})\) as a function of the external field (Hext) applied along the y-axis under the charge current density JAC = 1.3 × 1011 A/m2. c \({R}_{xx}^{{2}{{\omega }}}\) as a function of the pulse current density (JP). Colored arrows represent the direction of current sweep. d Deterministic magnetization switching by a complex sequence of current pulses. The top and bottom panels display the sequence of the current pulses applied into the device and the corresponding \({R}_{xx}^{{2}{{\omega }}}\) measured after each pulse, respectively.

Full size image

Discussions

As a remark, we would like to stress that the magnonic spin dissipation offers an extra degree of freedom in designing materials for enhanced SOTs, even in combination with the conventional FM/HM system. We explicitly demonstrate this possibility with a Ni/Pt structure assembly integrated with a NiO layer. Interestingly, the effective spin Hall angle of the NiO/Ni/Pt structure significantly enhances that of Ni/Pt (see Supplementary Information S10). This not only highlights the crucial roles of magnon dissipation but also underlines its substantial potential in engineering energy-efficient spintronic devices.

Our study brings attention to the substantial role of spin dissipation for magnetization manipulation in FM metals. It is important to also note that this effect is not limited to the FM/AFI system, but can play a significant role in general FM/HM systems, where the SOC in the HM serves as a spin dissipation channel. Nonetheless, comprehensive examination and quantification of this effect has been challenging due to the intricate interplay of multiple phenomena, and thus has been overlooked in earlier studies. Our results emphasize its importance by providing a quantitative assessment exclusively associated with the ISC within an FM (see Supplementary Information S10). Furthermore, the discovery of substantial SOTs via spin dissipation carries the important message that extra care should be taken when experimentally determining the effective spin Hall angle in magnetic multilayers and interpreting non-trivial SOC phenomena solely in terms of interfacial50,51 or orbital effects33,34. The innovative perspective, where dissipation can be beneficial to achieve efficient spin torques, provides a guideline for designing a new class of low-power spintronic devices, and expands our understanding of intricate spin transport phenomena in magnetic multilayers.

Methods

Sample fabrications

For the growth of magnetic trilayers, we employed a custom-built hybrid deposition system that combines PLD and DC/RF magnetron sputtering techniques. We deposited a series of NiO/FM/SiOx/Ta samples on MgO substrates with different crystallographic orientations (001), (110), and (111). The epitaxial NiO thin films were grown using PLD at a temperature of 500 °C and under an oxygen pressure of 1.0 × 10−6 Torr. Prior to the NiO growth, we carried out a pre-annealing process on MgO substrates to reform the substrate surface, converting it from the hydroxide composition back to its pristine state. For this, the substrate was heated to 700 °C and exposed to an oxygen pressure of 1.0 × 10−6 Torr for 30 min. After depositing the NiO, the film was cooled down to near room temperature and then in-situ transferred to the sputtering chamber. In addition to the easy-plane NiO thin films, we also grew a series of Cr2O3/FM/SiOx/Ta samples to explore the SOTs in easy-axis AFIs. The epitaxial Cr2O3 thin films were grown using reactive sputtering of a Cr target, at a temperature of 200 °C, under a pressure of 2 mTorr and with a mixture of O2/(Ar + O2) = 0.167. To minimize the lattice mismatch between Cr2O3 and Al2O3, a 3 nm-thick V2O3 film was deposited prior to the Cr2O3 thin film onto the Al2O3 substrate using PLD at 500 °C and under an oxygen atmosphere of 10−6 Torr. After the deposition of AFI thin films, the Ni (Py), SiOx, and Ta layers were sequentially deposited onto the film at a working pressure of 2 mTorr. For the control samples of substrates/FM/SiOx(2)/Ta(2), we used oxidized Si substrates or MgO substrates. We utilized photolithography and an Ar ion-milling process to pattern the films into devices with Hall-bar and rectangular structures for the SOTs and switching experiments, respectively. The width of the Hall-bar pattern is 10 μm, and the lateral dimension of the rectangular structure is 40 × 30 μm2.

Electrical measurements

For the characterization of the SOTs, the azimuthal-angle (ϕH)-dependent harmonic Hall measurement was conducted using a home-built electrical measurement system and a physical property measurement system (Quantum Design-PPMS). An a.c. charge current with a frequency of 427.3 Hz and amplitudes of 3-20 mA (corresponding to a current density of ~ 1 × 1011 Am−2) was applied using a Keithley 6221 A current source. Simultaneous collection of the first- and second-harmonic Hall voltages was achieved using two lock-in amplifiers. Prior to the harmonic measurement, we subjected all samples to a demagnetization process by applying a damped-oscillating AC magnetic field at temperatures above their blocking temperatures. This procedure effectively neutralizes the exchange bias effect, allowing us to simplify our analysis. The measurement was performed under an external magnetic field ranging from 0.3 T to 2 T while rotating the device in the x-y plane with the azimuthal angle (ϕH) varying from − π to + π. For the magnetization switching experiments, we measured the second-harmonic longitudinal voltage \({V}_{{xx}}^{{2} \omega }\) at an a.c. charge current with an amplitude of 16 mA and a frequency of 1117.3 Hz to determine the magnetization direction. We applied current pulses with a width of 10 μs and ranging from − 100 mA to 100 mA. A sequence of pulsing and measuring \({V}_{{xx}}^{{2} \omega }\) was carried out to track the change in magnetization. Error bars shown in the figures represent either (i) one standard deviation (SD) of repeated measurements or (ii) fitting uncertainty derived from nonlinear least squares analysis.

Fitting procedure

For fitting the tAFI dependence in Fig. 4, we use (see Supplementary Information S7)

$${\tau }_{{{\rm{DL}}}}+i{\tau }_{{{\rm{FL}}}}=\frac{\widetilde{A}}{\widetilde{B}+{\lambda }_{{{\rm{AFI}}}}\coth \frac{{t}_{{{\rm{AFI}}}}}{{\lambda }_{{{\rm{AFI}}}}}},$$
(1)

where \({\tau }_{{{\rm{DL}}}/{{\rm{FL}}}}\) is the damping-like/field-like component of the SOT and \(\widetilde{A}\) and \(\widetilde{B}\) are complex fitting parameters. For NiO, according to ref. 18, λAFI is an increasing function of the thickness for NiO. Therefore, we adopt a phenomenological model \({\lambda }_{{{\rm{AFI}}}}={\lambda }_{0}+{\lambda }_{1}{\left(1-{e}^{-{t}_{{{\rm{AFI}}}}/{\lambda }_{2}}\right)}^{2}\) and treat λ0,1,2 as fitting parameters52,53 (see Supplementary Information S7). On the other hand, λAFI is treated as a single fitting parameter for the Cr2O3 case. We fit the thickness dependence of the complex numbers \({\tau }_{{{\rm{DL}}}}+i{\tau }_{{{\rm{FL}}}}\) to the right-hand side of Eq. (1) to find the fitting parameters which minimize the squared sum of the modulus of the complex residuals. Since fitting with five parameters (complex \(\widetilde{A}\),\(\,\widetilde{B}\) and positive λ0,1,2) for NiO easily result in converging them to an incorrect local minimum, we carry out four-parameter fittings with fixed values of λ1 which is chosen to minimize the squared sum of the magnitude of the residuals (see Supplementary Information S7 for the detailed procedure).