Uncovering causal gene-tissue pairs and variants through a multivariate TWAS controlling for infinitesimal effects

Abstract

Transcriptome-wide association studies (TWAS) are commonly used to prioritize causal genes underlying associations found in genome-wide association studies (GWAS) and have been extended to identify causal genes through multivariate TWAS methods. However, recent studies have shown that widespread infinitesimal effects due to polygenicity can impair the performance of these methods. In this report, we introduce a multivariate TWAS method named tissue-gene pairs, direct causal variants, and infinitesimal effects selector (TGVIS) to identify tissue-specific causal genes and direct causal variants while accounting for infinitesimal effects. In simulations, TGVIS maintains an accurate prioritization of causal gene-tissue pairs and variants and demonstrates comparable or superior power to existing approaches, regardless of the presence of infinitesimal effects. In the real data analysis of GWAS summary data of 45 cardiometabolic traits and expression/splicing quantitative trait loci from 31 tissues, TGVIS is able to improve causal gene prioritization and identifies novel genes that were missed by conventional TWAS.

Introduction

Over the past two decades, genome-wide association studies (GWAS) have identified thousands of genetic variants associated with complex traits^1,2,3. However, most GWAS signals are detected in non-coding regions and have been shown to have complex regulatory landscapes across different tissues and cell types⁴, making it challenging to pinpoint causal variants and genes driving these GWAS signals. Joint GWAS and expression quantitative trait loci (eQTL) data analysis methods, such as colocalization⁵, transcriptome-wide association studies (TWAS)⁶, and cis-Mendelian randomization (cis-MR)^7,8, have been developed to prioritize causal genes at GWAS loci⁹. Colocalization simultaneously examines the expression of a gene and a trait to determine whether they share common causal genetic variants at a locus⁵. Both TWAS and cis-MR assume a causal diagram where eQTLs regulate tissue-specific gene expression that subsequently affects a trait, and they identify these tissue-specific causal genes by testing the significance of the causal effect estimates^6,7,8. Furthermore, these methods have been extended to a broader range of molecular phenotypes, such as splicing events¹⁰ and protein abundance¹¹, with regulatory QTLs being splicing QTLs (sQTLs) and protein QTLs (pQTLs), which we call xQTLs in general.

Nevertheless, colocalization, TWAS, and cis-MR are all univariable methods that statistically measure the marginal correlations of genetic effect sizes between a trait and a tissue-specific expression of a gene. Non-causal gene-tissue pairs may be falsely detected by these univariable methods due to the cis-gene-tissue co-regulations with causal gene-tissue pairs^9,12,13. The underlying mechanism may come in the following respects: the tissue-specific eQTLs of a causal gene are in linkage disequilibrium (LD) with (1) the eQTLs of nearby non-causal genes¹⁴ and (2) the eQTLs of causal genes expressed in non-causal tissues¹⁵. In addition, some variants can influence a trait independently of causal gene-tissue pairs, which are frequently denoted as direct causal variants¹⁴ and horizontal pleiotropy¹⁶. The non-causal gene-tissue pairs may be incorrectly detected when their eQTLs are in LD with direct causal variants.

Multivariate TWAS methods, such as causal TWAS (cTWAS)¹⁴, gene-based integrative fine-mapping through conditional TWAS (GIFT)¹⁷, and tissue-gene fine-mapping (TGFM)¹⁵, have been proposed to address these issues. Specifically, cTWAS is a Bayesian multivariate TWAS method, which identifies causal genes and direct causal variants among multiple candidates using the sum of single effects (SuSiE)^14,18 by examining tissues separately. TGFM extends cTWAS to allow multiple tissues to be analyzed simultaneously and can identify the trait-relevant tissues beyond the causal variants and genes. Furthermore, GIFT is a frequentist multivariate TWAS method, which explicitly models both expression correlation and LD of eQTLs across multiple genes through a likelihood framework.

However, Cui et al. ¹⁹ recently reported that current Bayesian fine-mapping methods, including SuSiE^18,20 and FINEMAP²¹, have a high replication failure rate (RFR) in practice. Cui et al. ¹⁹ discovered that the widespread infinitesimal effects are the sources of the high RFR, and accounting for the infinitesimal effects can reduce the RFR and improve statistical power. In general, the infinitesimal effect model is equivalent to a polygenic architecture in which all genetic variants contribute to phenotypic variation, each with small effects²². Cui et al.¹⁹ extended this model to a cis-region, which assumes that a subset of variants has relatively large effect sizes besides the infinitesimal effects. Notably, the impact of infinitesimal effects is not limited to fine-mapping, as it has been observed to inflate the test statistics in standard TWAS²³ and traditional linkage studies²⁴. Thus, due to the lack of modeling infinitesimal effects, it is expected that cTWAS and TGFM can be vulnerable to spurious prioritization and reduced statistical power.

We present the tissue-gene pair, direct causal variants, and infinitesimal effect selector (TGVIS), a multivariate TWAS method to identify causal gene-tissue pairs and direct causal variants while incorporating infinitesimal effects. TGVIS employs SuSiE^14,18 for fine-mapping causal gene-tissue pairs and direct causal variants, and uses restricted maximum likelihood (REML)²⁵ to estimate the infinitesimal effects. In addition, we introduce the Pratt index²⁶ to rank the importance for improving the prioritization of causal genes and variants. We applied TGVIS to identify causal cis-gene-tissue pairs and direct causal variants for 45 cardiometabolic traits using GWAS datasets with the largest sample sizes to date^{3,27,28,29,30,31,32,33,34,35}, by incorporating the eQTL and sQTL summary statistics from 28 tissues from genotype-tissue expression (GTEx)¹³, and the eQTL summary statistics of kidney tubulointerstitial³⁶, kidney glomerular³⁶, and pancreatic islets³⁷ tissues. We summarized the causal gene-tissue pairs and direct causal variants, highlighted the pleiotropic effects at the gene-tissue level, and demonstrated the different functional activity³⁸ of eQTLs/sQTLs mediated through gene-tissues and the direct causal variants. Moreover, we mapped the trait-relevant major tissues and demonstrated the enrichments of genes identified by TGVIS in terms of colocalization⁵, on the silver standard of lipid genes¹⁴, FDA-approved drug-target genes³⁹, and genes detected through pQTL summary data¹¹. Our study reveals a broader picture of gene and tissue co-regulations, which can provide novel biological insights into complex traits.

Results

Overview of TGVIS

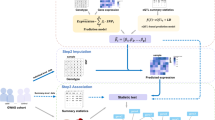
Figure 1A illustrates the causal diagram assumed in this report. Specifically, we hypothesize that a set of xQTLs influences the products of genes (e.g., expressions and splicing events) at a locus. Gene co-regulation^9,13, i.e., the correlation of xQTL effects among multiple gene products, can emerge due to shared xQTLs or being in LD among them. Meanwhile, tissue co-regulation^12,40,41, defined as the correlation of gene expression across multiple tissues, can arise because of the same mechanism. In the gene and tissue co-regulation network, certain gene-tissue pairs directly influence a trait without mediation by other gene-tissue pairs, which are referred to as causal gene-tissue pairs. In addition, some genetic variants may directly influence the trait, which we consider as direct causal variants. Besides these direct causal variants, which have relatively large effects, we assume there are polygenic or infinitesimal effects that can be modeled through a normal distribution with mean zero and small variance¹⁹. In addition to the biological basis of polygenic trait architecture, there are non-biological factors that can produce similar effects to infinitesimal models. These include population structure, errors in estimating the LD matrix, imputation errors in GWAS effect sizes, and the possibility that a true causal variant was either not genotyped or was removed during LD clumping (Methods).

Fig. 1: Overview of TGVIS.

A A hypothetical causal diagram illustrating the relationships between variants (including xQTLs, direct causal variants, and non-causal variants), tissue-specific gene expressions, and an outcome in a cis-region, where the arrows indicate the flow of causal effects in the causal diagram. Variants may be in LD, with only a subset having cis-regulatory effects. Gene expressions or splicing events are tissue-specific and form a complex co-regulation network. Only molecular phenotypes directly connected to the outcome are considered causal. B Locus-zoom plot of the LDL-C GWAS in the PCSK9 locus. The bottom panel displays the coding regions of genes located within this locus, including PCSK9, UPS24, BSND, etc. P values were calculated by ${\chi }^{2}$-test with 1 degree of freedom. C Workflow of TGVIS, consisting of three main steps. (I) Input, including GWAS summary data, eQTL summary data from multiple tissues, and LD matrix. (II) Preprocessing, including eQTL selection and pre-screening. We applied S-Predixcan to pre-screen some noise pairs, aiming to reduce the dimension of the multivariable TWAS model to a reasonable scale. (III) Estimation, where TGVIS first selects the causal gene-tissue pairs and direct causal variants via SuSiE and then estimates the infinitesimal effect via REML. (IV) Output, including the causal effect estimate, direct causal effect estimate, and infinitesimal effect estimates. We output plots demonstrating the causal gene-tissue pairs, direct causal variants and predicted infinitesimal effects: (1) the Pratt indices and other statistics such as PIPs, estimates, SEs of causal gene-tissue pairs in the 95% credible sets, (2) the Pratt indices of the direct causal variants in the 95% credible sets, and (3) the best linear unbiased predictors of infinitesimal effects. The non-zero variance in output III in this figure suggests the non-zero contribution of infinitesimal effects. The figure was created in BioRender. Yang, Y. (2025) https://BioRender.com/tpngnr4.

The curse of dimensionality poses a substantial challenge in the multivariate TWAS model. Figure 1B illustrates this challenge by an example of the association evidence with low-density lipoprotein cholesterol (LDL-C)¹ at the PCSK9 locus, where dozens of coding genes and long non-coding ribonucleic acids (lncRNAs) are located, along with multiple potential direct causal variants. Conventional statistical methods cannot precisely identify causal gene-tissue pairs and variants because there are many correlated candidates that frequently range from hundreds to thousands¹⁸. The proposed TGVIS overcomes the curse of dimensionality. Figure 1C describes the workflow of TGVIS, where the inputs are the GWAS summary statistics of a trait, xQTL summary statistics of gene-tissue pairs, and a reference LD matrix of the variants at the locus. TGVIS is a two-stage method. In the first stage, TGVIS employs SuSiE to identify a small set of xQTLs that best predict the genetic effects of gene-tissue pairs. These xQTLs are treated as informative variants instead of biologically causal variants. In the second stage, TGVIS utilizes a profile-likelihood approach to estimate the causal effects of gene-tissue pairs and directly causal variant effects with SuSiE^18,20, and model the infinitesimal effects via REML²⁵. This profile-likelihood iterates until all estimates are converge. The details are described in the “Methods” and the Supplementary Materials.

In practice, another challenge arises when selecting a causal gene-tissue pair based solely on its posterior inclusion probability (PIP) because many gene-tissue pairs share the same sets of xQTLs at a locus, making them statistically indistinguishable. SuSiE groups these pairs into a credible set during fine-mapping and introduces a single effect to describe the contributions of the variables in the same credible set. Therefore, all inferences should be made based on the single effects defined by SuSiE’s credible sets. In TGVIS, we introduce the Pratt index^42,43 as a metric parallel to PIP, to quantify the contribution of a credible set of gene-tissue pairs and direct causal variants. While PIP measures the significance of variables from a Bayesian viewpoint, the Pratt index quantifies their predictive importance. In the application, we calculated the cumulative Pratt index of variables in a 95% credible set (CS-Pratt) and filtered out the credible sets with low CS-Pratt values (Methods and Supplementary Materials). We observed that this procedure improved the precision of causal gene and variant identification.

Simulation

We compared the TGVIS with 4 multivariate MR and TWAS methods: cisIVW⁴⁴, Grant2022⁴⁵, cTWAS¹⁴, and TGFM¹⁵. We applied the following criteria for determining the causality: the 95% credible set for TGVIS, TGFM, and cTWAS; P < 0.05 for cisIVW; and selection by lasso in the Grant2022. We did not consider univariable methods because of their high type-I error rates when the goal is to identify causal genes, given that xQTL effect sizes for multiple genes are often correlated¹⁴. Detailed information on the settings and more simulation results beyond the specific case presented below can be found in Methods and Supplementary Materials.

We first assessed the accuracy of causal effect estimation for gene-tissue pairs. When infinitesimal effects were absent, TGVIS showed a mean square error (MSE) for causal effect estimates similar to that of cTWAS, and TGFM, while both cisIVW and Grant2022 exhibited substantially larger MSE (as shown in the left two panels in Fig. 2A). However, when infinitesimal effects were present, TGVIS demonstrated a visibly lower MSE compared to the other methods, with cTWAS and TGFM showing ~32% higher MSE than TGVIS (as shown in the right two panels in Fig. 2A). These results indicate that TGVIS generally outperforms its competitors by accounting for infinitesimal effects.

Fig. 2: Simulation results comparing the performances of TGVIS, TGFM, cTWAS, Grant2022, and cisIVW with xQTL sample size = 200 and replications = 500.

A The MSE of causal effect estimates under no pleiotropy, in the presence of direct causal variants, infinitesimal effects, and both. B The true negative rate of identifying all 98 non-causal gene-tissue pairs under different scenarios i.e., no pleiotropy, in the presence of direct causal variants, infinitesimal effects, and both. This is equivalent to that if a method incorrectly identifies any non-causal pairs as causal, it will not be counted as a true negative event. C Bar plots display the true positive rates of identifying all 2 causal gene-tissue pairs under different scenarios. D The averaged number of identified direct causal variants by the different methods. The number of true causal variants were set to 0, 2, 0, and 2 for no-pleiotropy, direct-causal-variant, infinitesimal-effects, and direct-causal-variant and infinitesimal-effects, respectively. E The averaged correlation of the true and estimated direct causal effects across simulations. F The averaged correlation of the true and predicted infinitesimal effects across simulations.

We then compared the true negative rate (TNR) and true positive rate (TPR) of these five methods. A true negative is defined as a method that correctly identifies all 98 non-causal gene-tissue pairs. Similarly, a true positive is defined as a method that correctly identifies the 2 causal gene-tissue pairs. Across all the scenarios (Fig. 2B), TGVIS achieved the highest TNR, with an average of 0.614, followed by TGFM and cTWAS, with average TNRs of 0.513 and 0.499, respectively. CisIVW and Grant2022 performed worst, with average TNR of 0.064 and 0.013, respectively, indicating that these two methods are prone to identifying a substantial number of false-positive gene-tissue pairs. On the other hand, TGVIS exhibited a similar TPR (average TPR = 0.667) as TGFM, cTWAS, and cisIVW (average TPRs of 0.649, 0.667, and 0.661, respectively), while Grant2022 had the highest TPR (average TPR = 0.831) (Fig. 2C), which is not surprising given that Grant2022 also has lowest TNR.

We further assessed the performance in detecting direct causal variants. In scenarios where no direct causal variants were present, among the 400 variants, the TGVIS identified fewer direct causal variants, with an average number of 0.92, compared to 2.39 for TGFM and 2.38 for cTWAS (Fig. 2D). Due to the LD among the 400 variants, we estimated that they correspond to ~77 independent variants (number of eigenvalues > 1). Under the null hypothesis of no direct causal variants, we would expect to detect at most 4 false-positive variants. Thus, all three methods are relatively conservative when no direct causal variants are present. When there were two direct causal variants present, TGVIS identified an average of 2.86 direct causal variants, compared to 3.58 for both cTWAS and TGFM. The averaged correlations between the estimated and true direct causal effects across simulations were high for all three methods (Fig. 2E). However, predicting infinitesimal effects remains challenging, as evidenced by an average correlation of 0.663 between the predicted and true infinitesimal effects in TGVIS (Fig. 2F). Additionally, direct causal effect estimates were consistent in terms of mean square error (MSE), whereas the variance of infinitesimal effects was inflated due to absorbing estimation errors from direct causal effects and gene-tissue pair effects carrying genetic information (Supplementary Materials).

Searching for potentially causal gene-tissue pairs and variants for 45 cardiometabolic traits

We systematically analyzed 45 cardiometabolic traits and eQTL/sQTL summary statistics (Supplementary Data 1–2) to identify potential causal gene-tissue pairs and direct causal variants. For the TVGIS, we considered whether a gene-tissue pair or direct causal variant was causal if (1) it was within a 95% credible set and (2) had a CS-Pratt >  0.15. The criteria of CS-Pratt >0.15 was established based on empirical evidence by summarizing the CS-Pratt scores from the all the loci and traits we analyzed (Methods). For TGFM, we followed the authors’ recommendation of considering individual PIP > 0.5 as indicative of causality. We did not compare with cTWAS because it analyzes tissues separately¹⁴.

TGVIS and TGFM identified a median of 119.5 and 227.5 causal gene-tissue pairs, and 42 and 183 causal variants per trait (Fig. 3A and Supplementary Data 3–6), respectively. Additionally, TGVIS detected a median of 0.313 causal gene-tissue pairs and 0.115 direct causal variants per locus, while TGFM identified a median of 0.469 causal gene-tissue pairs and 0.466 direct causal variants per locus (Fig. 3C). Overall, TGVIS reduced the number of causal gene-tissue pairs by a median of 55.7% and the number of direct causal variants by 24.5% per trait compared to TGFM. Along with our simulations showing that TGVIS and TGFM have comparable power, with TGVIS exhibiting a lower false positive rate, our real data results are likely to support the improved resolution of TGVIS over TGFM; see, e.g., the four examples shown in Fig. 7.

Fig. 3: Summary of the identification of causal gene-tissue pairs and direct causal variants.

A, B The number and proportion of causal and likely novel causal gene-tissue pairs identified by TGVIS and TGFM, respectively. Likely novel gene-tissue pairs are defined as those do not present in the list of significant gene-tissue pairs identified by univariable S-PrediXcan (P < 0.05/20000). The proportion refers to the average number of causal and likely novel causal gene-tissue pairs per locus. C The number and proportion of direct causal variants identified by TGVIS and TGFM. D The distribution of the number of traits affected by causal gene-tissue pairs. E, F The distributions of scores for FathmmXF and Encode H3K9me3Sum annotations. Raincloud plots illustrate four classes: direct causal variants and xQTLs of causal gene-tissue pairs identified by TGVIS and TGFM. Pairwise Wilcoxon signed-rank test P values (two-side) are displayed at the top, while medians of annotation scores are shown at the bottom. The median was shown as a black bar. The lower and upper hinges corresponded to the 25th and 75th percentiles. The “sample sizes” in the test are the numbers of variants, which are 1256, 4787, 9552, 19057 for TGVIS (direct causal variant), TGVIS (xQTL of gene-tissue pairs), TGFM (direct causal variant), TGFM (xQTL of gene-tissue pairs), respectively. Source data are provided as a Source Data file. The figure was created in BioRender. Yang, Y. (2025) https://BioRender.com/b65f9a0.

We expected that general causal gene-tissue pairs detected by TGVIS and TGFM would likely be included among those identified by univariable TWAS methods such as S-PrediXcan⁴⁶. Surprisingly, among the causal pairs identified by TGVIS, a median of 34.3% were undetected by S-PrediXcan, and this proportion was 60.1% for TGFM (Fig. 3A and Supplementary Data 22). For example, TGVIS identified SCN2A-Nerve_Tibial as a novel causal gene-tissue pair for 17 traits (Supplementary Fig. 37) but was missed by S-PrediXcan. In fact, among the 17 traits, S-PrediXcan only identified SCN2A-Nerve_Tibial for type 2 diabetes. Our findings suggest SCN2A may regulate a wide range of metabolic traits. These results indicate that TGVIS not only fine-maps causal genes but also uncovers novel genes by modeling multiple tissue-gene pairs simultaneously.

We investigated how many traits can be influenced by a causal gene-tissue pair, reflecting the pleiotropic effect at the gene-tissue level. Among the causal gene-tissue pairs falling in credible sets of sizes ≤ 2, 22.4% identified by TGVIS and 16.7% by TGFM exhibit pleiotropic effect (Fig. 3D and Supplementary Data 7–8), indicating that many of these causal genes contribute to shared biological mechanisms across multiple traits.

We further examined whether the direct causal variants and xQTLs mediated by causal gene-tissue pairs differ in functionality using functional annotations³⁸ (Methods). Significant differences were observed between these two types of variants identified by either TGVIS or TGFM across multiple annotations (Supplementary Data 11). As shown in Fig. 3E, F, the direct causal variants generally have higher FathmmXF and h3k9me3 scores than the xQTLs mediated by causal gene-tissue pairs (Wilcoxon signed-rank test, P < 2.2E-16), suggesting distinct biological mechanisms for many of these variants.

We observed that multiple eGenes and sGenes often shared the same set of variants as their xQTL, highlighting the importance of making inferences based on credible sets rather than individual variables. Most credible sets consisted of 2 to 4 gene-tissue pairs (60.5%), although some credible sets included more than 10 (11.5%) for TGVIS (Fig. 4A and Supplementary Data 12). In comparison, TGFM resulted in predominantly featured single gene-tissue pairs (56.0%) and 2 to 4 pairs (41.7%) per credible set (Supplementary Fig. 18 and Supplementary Data 12). On the other hand, most of the credible sets only had one xQTL (66.6%), followed by two xQTLs (12.6%) for TGVIS (Fig. 4B and Supplementary Data 13). As for TGFM, these percentages were 26.9% for one xQTL and 24.4% for two xQTLs (Supplementary Fig. 20 and Supplementary Data 13). These differences arise because TGFM resampled all xQTLs in the 95% credible sets, typically incorporating more variants, whereas TGVIS applied a stricter criterion for selecting xQTLs (Methods, Supplementary Fig. 18–19).

Fig. 4: Genetic architecture inferred from the identification of causal gene-tissue pairs and direct causal variants.

A The ratio of identified causal gene-tissue pairs per credible set by TVGIS. Different gene-tissue pairs may share the same set of xQTLs, and end in the same credible set. B The ratio of the number of causal eQTLs over the number of sQTLs per causal gene-tissue pair, indicating the distribution of eQTLs and sQTLs contributing to the gene-tissue pairs. C The distribution of eGene and sGene in credible sets identified by TGVIS and TGFM. When a credible set contains multiple gene-tissue pairs, we calculate the proportion of eGenes and sGenes. D The distribution of Pratt Index estimates for different traits, with a comparison between TGVIS and TGFM. In the boxplot, each point represents the Pratt Index of various molecular phenotypes within a single locus. The median was shown as a black bar. The lower and upper hinges corresponded to the 25th and 75th percentiles. Source data are provided as a Source Data file. The figure was created in BioRender. Yang, Y. (2025) https://BioRender.com/ch89ux4.

We investigated the proportions of identified causal eGenes and sGenes for the 45 cardiometabolic traits (Methods). TGVIS showed eGenes and sGenes proportions of 58.1% and 41.9%, respectively, while TGFM resulted in 63.5% for eGenes and 36.5% for sGenes (Fig. 4C and Supplementary Fig. 21). These results align with the proportions observed in the GTEx Consortium (63% cis-eQTL vs. 37% cis-sQTL)¹³, with TGFM’s proportions being slightly closer. A potential explanation is that TGVIS’ eGenes and sGenes were more likely enriched for causal genes specific to cardiometabolic traits, leading to a slight difference, though this difference is not substantial.

We calculated the Pratt index of gene-tissue pairs, direct causal variants, and infinitesimal effects based on their additive property (Fig. 4D and Supplementary Data 15), which helps measure the contributions of these three potentially correlated components (Methods). For TGVIS, the median of the Pratt index was 0.161, 0.059, and 0.182 for gene-tissue pairs, direct causal variants, and infinitesimal effects, respectively, with a median sum of the Pratt index of 0.403. In comparison, for TGFM, the median of the Pratt index was 0.145 for gene-tissue pairs and 0.114 for direct causal variants, with a median sum of the Pratt index of 0.262. These results support the existence of widespread infinitesimal effects.

Major relevant tissue map of cardiometabolic traits

We searched for the major relevant tissues by counting their numbers to the causal gene-tissue pairs in credible sets identified by TGVIS and TGFM (Methods). We ranked the top relevant tissues according to their contributions and clustered similar traits and tissues based on the similarity of the identified causal gene-tissue pairs (Fig. 5A, B and Supplementary Figs. 22 and 23). Overall, we observed similar major relevant tissues and clustering patterns using both methods, although there were some notable differences. TGVIS tended to cluster similar traits more closely together than TGFM. For instance, TGVIS grouped all blood pressure traits into close clusters, placing them near coronary artery disease (CAD), whereas TGFM positioned systolic and diastolic blood pressures (SBP and DBP) farther from pulse pressure (PP) and CAD. Similarly, serum lipid traits were clustered together by TGVIS, but not by TGFM. On the other hand, arterial tissues consistently emerged as the major tissue for blood pressure traits and CAD, while heart tissues were the major tissue for the QRS complex, atrial fibrillation, QT interval, and JT interval. Fibroblasts were highlighted as an important tissue for many traits, aligning with recent findings about their role in tissue integrity and chronic inflammation, alongside other tissues such as adipose tissue and liver⁴⁷.

Fig. 5: Distribution of major tissues for cardiometabolic traits.

A Heatmaps display the major tissues associated with each trait, identified by TGVIS. B Heatmaps display the major tissues associated with each trait, identified by TGFM. The major gene-tissue pairs are cataloged based on stringent criteria (CS-Pratt > 0.15 for TGVIS and PIP > 0.5 for TGFM), and the proportions of major tissues derived from significant gene-tissue pairs for each trait are quantified. Hierarchical clustering is applied to arrange the heatmaps, utilizing the Ward2 method and Euclidean distance. C Major tissues of lipid traits identified by TGVIS and TGFM. This panel shows bar plots detailing the number of causal gene-tissue pairs for various lipid traits, including HDL-C, LDL-C, TC, triglycerides, APOA1, and APOB, as identified by both TGVIS (top) and TGFM (bottom). Source data are provided as a Source Data file. The figure was created in BioRender. Yang, Y. (2025) https://BioRender.com/1s8s2iy.

It is possible that the major tissue rank may be affected by the number of background genes expressed in tissue and the eQTL sample size, although most of the tissue data in this study was from the GTEx data, with the sample size being generally comparable for different tissues. We first examined the correlation between the number of background genes expressed and the count of causal genes relevant to a tissue across the traits, and the median correlation is −0.16 (SE = 0.1410), suggesting that background expressed genes do not affect the rank of a tissue. We next calculated the correlation between the eQTL sample size and the count of causal genes relevant to a tissue. We observed the median correlation of 0.6214 (SE = 0.1178), which is not entirely surprising. We then regressed the count of causal genes on the sample size and calculated the corresponding residuals. The residuals were highly correlated with the count of causal genes (median rank correlation = 0.7443, SE = 0.1382), suggesting the tissue rank cannot be fully explained by eQTL sample size. Thus, our major tissue map may be partially affected by the eQTL sample size, warranting future replication using large eQTL data.

We considered several lipid traits, including LDL-C, HDL-C, TC, triglyceride, apolipoprotein A1 (APOA1), and apolipoprotein B (APOB), as examples to illustrate the proportional counts of each tissue identified in the credible sets. For HDL-C and triglycerides, the most relevant tissue was subcutaneous adipose (Fig. 5C). In contrast, liver tissue was consistently the most relevant tissue for LDL-C, APOB, and TC, despite the small sample size for the liver tissue gene expression data¹³. For APOA1, the two most relevant tissues were the liver and subcutaneous adipose tissue. Supplementary Figs. 24–32 display the plots of major tissues for the rest of the traits. Overall, TGVIS and TGFM produced consistently the most relevant tissues.

Evaluation of the identified gene-tissue pairs

To evaluate the accuracy of the prioritization of causal gene-tissue pairs, we first compared the colocalization evidence of the causal credible sets identified by TGVIS and TGFM through Coloc-SuSiE⁵. Since a credible set could include multiple tissue-gene pairs, we defined a colocalization of a credible set in two criteria: (1) the credible set contained at least one gene-tissue pair that is colocalized with the trait; (2) more than 50% of the gene-tissue pairs in the credible set were colocalized with the trait (Methods). TGVIS had much higher proportions of colocalized credible sets (the median proportions across traits were 93.1% and 77.8% for the two criteria, respectively) than TGFM (the median proportions across traits were both 40.9% for two criteria) (Fig. 6A and Supplementary Data 16–17), suggesting a substantial number of causal tissue-gene pairs identified by TGFM do not have colocalization evidence.

Fig. 6: Evaluation of identified gene-tissue pairs.

A The colocalized proportions of causal credible sets (under two criteria) yielded by TGVIS and TGFM, respectively. B The numbers and proportions of causal cis-genes in the list of FDA-approved drug-target genes provided by Trajanoska et al., identified by TGVIS (left) and TGFM (right), respectively. C The number of significant pGenes in univariable MR analysis and the ratio of significant pGene in univariable MR analysis divided by significant eGenes/sGenes in eQTL/sQTL analysis. Source data are provided as a Source Data file. The figure was created in BioRender. Yang, Y. (2025) https://BioRender.com/ouhjfzd.

We next followed the previous analysis strategy¹⁴ to assess the causal genes for LDL-C identified by TGVIS and TGFM. Precision was evaluated using the 69 known lipid-related genes as the silver standard positive gene set, and nearby genes within a 1MB-radius region as the negative set, as studied by Zhao et al. ¹⁴. We disregarded the tissue part of the identified causal gene-tissue pairs and then calculated how many causal genes were within the lists of sliver and nearby genes. TGVIS demonstrated a precision of 60.0% (9 out of 15), outperforming TGFM, which had a precision of 37.5% (10 out of 28) (Supplementary Data 18 and Supplementary Fig. 33).

It is reasonable to assume that causal genes are more likely to be druggable targets. We utilized the published list of 6,690 FDA/EMA-approved non-cancer drugs (Supplementary Data 1 provided by Trajanoska et al. ³⁹) to calculate the enrichment of the identified causal genes in the drug list (Fig. 6B and Supplementary Data 19–20). Although the number of causal genes identified by TGVIS in the drug-targeted gene list was only 74.3% of that identified by TGFM, the enrichment identified by TGVIS was 1.43 times more than that by TGFM (P = 1.56E-3).

We hypothesized that causal genes detected through eQTLs/sQTLs may be more likely to demonstrate association evidence in protein data. To test this, we conducted univariable MR analysis of protein abundances (pGenes) in blood tissue for genes identified by TGVIS and TGFM, using both trans- and cis-pQTLs as instrument variables (Fig. 6C and Supplementary Data 21). On average, 18.1% of pGenes identified by TGVIS showed significant causal evidence, compared to 13.7% of pGenes for TGFM (P = 3.1E-3). However, this proportion is lower than the estimated true positive association rate of 27.8% between predicted cis-regulated gene expression and plasma protein abundances⁴⁸. The discrepancy may arise from the fact that pGenes are influenced by widespread trans-pQTLs¹¹, whereas predicted gene expression is predominantly contributed by cis-eQTLs, and their trans-regulated effects are much more difficult to detect. This result suggests that eGenes/sGenes and pGenes may represent distinct biological processes related to complex traits⁴⁸.

Fine-mapping of causal gene-tissue pairs and variants in GWAS loci

We exemplified four loci associated with LDL-C, CAD, and BMI. The first locus contains the PCSK9 gene for LDL-C (Fig. 7A). TGVIS identified three 95% credible sets, including PCSK9-Whole_Blood and two direct causal variants rs11591147 and rs11206517 (Fig. 7B). After applying the threshold of CS-Pratt > 0.15, PCSK9-Whole_Blood (CS-Pratt = 0.17) and rs11591147 (CS-Pratt = 0.492) remained. In contrast, TGFM identified nine gene-tissue pairs and direct causal variants with PIPs > 0.5 (Fig. 7C), including the MROH7-Esophageal_Mucosa, which has no clear connection to the biology of LDL-C. Applying the CS-Pratt threshold, PCSK9-Whole_Blood (CS-Pratt = 0.204) and rs11591147 (CS-Pratt = 0.524) remained consistent with the results yielded by TGVIS. This example demonstrates how TGVIS reduces false positives by modeling infinitesimal effects and applies the Pratt Index as an additional criterion.

Fig. 7: Locus-zoom plots comparing the results of TGVIS and TGFM.

A PCSK9 locus-zoom plot for LDL-C GWAS. B PCSK9 locus results for TGVIS. C PCSK9 locus results for TGFM. D HMGCR locus-zoom plot for LDL-C GWAS. E HMGCR locus results for TGVIS. F HMGCR locus results for TGFM. G PHACTR1 locus-zoom plot for CAD GWAS. H PHACTR1 locus results for TGVIS. I PHACTR1 locus results for TGFM. J FTO locus-zoom plot for BMI GWAS. K FTO locus results for TGVIS. L FTO locus results for TGFM. In each panel of fine-mapping results, the upper portion displays individual PIPs of identified gene-tissue pairs and direct variants, while the lower portion shows Pratt indices of identified credible sets. For TGVIS, causality is determined by (1) the variables are in a 95% credible set and (2) the Pratt index of this credible set is larger than 0.15. For TGFM, the causality is determined by (1) the individual PIP is larger than 0.5. The red diamond in a locus-zoom plot indicates the most significant SNP at the locus. PIPs were calculated by SuSiE. Source data are provided as a Source Data file. The figure was created in BioRender. Yang, Y. (2025) https://BioRender.com/jrzcdig.

The second locus contains the HMGCR gene causal⁴⁹ to LDL-C (Fig. 7D). TGVIS identified five 95% credible sets (Fig. 7E). The first credible set (the darkest green) includes 9 gene-tissue pairs, such as HMGCR-Muscle_Skeletal and five of its sGenes in esophagus mucosa, nerve tibial, fibroblasts, and adipose visceral, all sharing the same xQTL rs2112653. When we applied the threshold of individual PIP > 0.5, none of the pairs in this credible set were selected, although they were all in a 95% credible set. However, this set had the highest CS-Pratt of 0.322 among the five 95% credible sets. Conversely, TGFM identified POLK-Lung (CS-Pratt = 0.684) but missed the crucial HMGCR gene (Fig. 7F). This is likely a false discovery, as HMGCR inhibitor is a key component of statins, which works by inhibiting HMG-CoA reductase and thus reduces LDL-C in the blood⁴⁹.

In the third example, we focused on the PHACTR1 locus related to CAD (Fig. 7G). Both TGVIS and TGFM identified a major credible set at this locus, including PHACTR1-Artery_Coronary and PHACTR1-Artery_Aorta, with CS-Pratt values of 0.632 and 0.612, respectively (Fig. 7H, I). In TGVIS, the individual PIPs of them were both 0.5, and the cumulative PIP for this credible set was 1. In contrast, TGFM resampled both the eQTL effect estimates and the individual PIPs (Methods), resulting in a higher individual PIP and individual Pratt index for PHACTR1-Artery_Aorta (PIP = 0.597, Pratt = 0.472) than PHACTR1-Artery_Coronary (PIP = 0.222, Pratt = 0.053). However, as noted by Strober et al. ¹⁵, this resampling process tends to favor gene-tissue pairs with larger sample sizes, which may explain the exclusion of PHACTR1-Artery_Coronary. TGVIS adheres to the original interpretation of SuSiE that the variables within a credible set cannot be distinguished from the available data.

The final exemplary locus is the FTO locus associated with BMI (Fig. 7J). TGVIS identified only two direct causal variants, rs7206790 and rs3751813, and did not find any gene-tissue pairs at this locus (Fig. 6K). In contrast, TGFM identified four gene-tissue pairs: FTO_Kidney_Glomerulus, FTO_Thyroid, FTO_Artery Tibial, and IRX3-Adipose_Subcutaneous, and five direct causal variants (Fig. 7L). However, the associations between obesity and the expression of the FTO gene in the kidney glomerulus, thyroid, and tibial artery are not well-established in the literature. After applying the Pratt index threshold, only two direct causal variants, rs7206790 and rs3751813, remained, which is consistent with the result from the TGVIS. When we reduced the locus radius from 1MB to 500KB and re-ran the analysis, both TGVIS and TGFM identified the sGene of FTO-Pancreas as causal, with CS-Pratt values of 0.345 and 0.407, respectively (Supplementary Fig. 35). The sQTLs of this FTO sGene are rs7206790 and rs11642841, which have been reported by Xu et al.⁵⁰. This example suggests that when applying multivariate TWAS methods, the size of a cis-region can be sensitive and needs to be calibrated.

Discussion

In this report, we developed TGVIS to identify causal gene-tissue pairs and direct causal variants in loci identified through GWAS by integrating xQTL summary statistics. Compared to cTWAS¹⁴ and TGFM¹⁵, TGVIS not only analyzes multiple tissue-specific xQTL summary data simultaneously to pinpoint causal gene-tissue pairs and direct causal variants, but also models the widespread presence of infinitesimal effects underlying polygenic traits to reduce false discovery rates in detecting causal molecular phenotypes¹⁹. In addition, TGVIS quantifies the importance of a causal variable by the Pratt index, which has been well established in statistics^42,43 and has recently been applied to estimate the gene-by-environment contribution²⁶. Through simulations, we demonstrated that under the presence of infinitesimal effects, TGVIS has lower MSE and higher TPR and TNR compared to both cTWAS and TGFM (Fig. 2). In real data analysis, TGVIS outperformed TGFM in the following four aspects: (1) identifying more interpretable major trait-relevant tissues (Fig. 5); (2) resulting in a higher proportion of colocalized causal credible sets (93.1% vs 40.9%, Fig. 6A); (3) achieving notably higher precision in the “silver standard” sets of lipids (60.0% vs 37.5%, Supplementary Data 15); and (4) demonstrating significantly greater enrichment evidence based on druggable genes (1.43 times, Fig. 6B) and causal proteins (1.31 times, Fig. 6C). We also observed that the default PIP > 0.5 for TGFM may be a little liberal but a threshold of PIP > 0.9 may be too conservative, and incorporating Pratt index > 0.15 will lead to much consistent causal gene-tissue pairs and variants with TGVIS (Supplementary Materials).

Our analysis of 45 cardiometabolic traits provides several key insights. First, we identified a median of 34.3% causal gene-tissue pairs that were missed in univariable TWAS analysis, suggesting that TGVIS is able to identify novel genes besides fine-mapping the genes detected by conventional TWAS (Fig. 3A), representing a significant advance in TWAS. Second, we observed that infinitesimal effects can make a substantial contribution to local genetic variation of traits besides the gene-tissue pairs and direct variant (Fig. 4D), which is consistent with recent studies^19,24,51. Beyond underlying biological mechanisms such as the polygenicity of human complex traits, the emergence of infinitesimal effects may also be attributed to non-biological factors, particularly population structure, estimation errors in the LD matrix, xQTL effect sizes, and trait GWAS imputation (Methods). Both empirical observations and theoretical investigation underscore the importance of including infinitesimal effects in future genetic research and methodological development. Third, our study indicates that a significant proportion of causal gene-tissue pairs (22.4%) exhibit pleiotropic effects at the gene-tissue level, suggesting shared biological mechanisms across multiple traits (Fig. 3D and Supplementary Data 7–8). Fourth, our findings suggest that for most traits, only a limited number of relevant major tissues are involved (Fig. 4A), implying that concentrating multi-omics data analyses on these relevant major tissues can be more powerful and efficient, as well as it can make the findings more biologically interpretable. For example, when the analysis is focused on the four major blood-pressure-relevant tissues, i.e., adrenal gland, artery, heart, and kidney, it leads to the identification of more causal gene-tissue pairs, with an increased Pratt index for blood pressure traits (Yang, Y. et al. Personal communication 2025). Fifth, our results indicate that only 18.1% of causal genes from eQTL/sQTL analyses also show causal evidence in univariable MR using pQTL summary data (Fig. 6C), suggesting that gene expressions and protein abundance represent distinct biological processes in complex traits⁴⁸. Finally, we identified an average of 0.304 causal gene-tissue pairs per locus and failed to identify any causal gene-tissue pairs in many GWAS loci (Fig. 3A), which is consistent with the recent study showing that the GWAS and eQTL studies are systematically biased toward different types of variants⁴. Interestingly, the eQTLs/sQTLs of causal gene-tissue pairs and direct causal variants have substantially different functional annotations (Fig. 3E, F and Supplementary Data 11), warranting further investigation.

Our study has some limitations. First, due to the data and computational constraints, we only analyzed genes using cis-eQTL/sQTL summary statistics, limiting our ability to distinguish between genes that share cis-eQTLs/sQTLs, which may lead to false discoveries. This issue could potentially be addressed by incorporating trans-eQTLs/sQTLs, although this would require much larger sample sizes. In addition, we observed that a credible set often contains 2-4 gene-tissue pairs (Fig. 3C), likely due to the small sample size in the GTEx data, which results in only 1 or 2 eQTL/sQTL for most gene-tissue pairs (Fig. 4B). In other words, while TGVIS was able to narrow down to a range of causal gene-tissue pairs, it could not always pinpoint the exact causal pair(s) in some loci. Incorporating external information, such as colocalization evidence with TGVIS, may aid in distinguishing these pairs⁵². Second, our eQTL/sQTL analysis relies on bulk tissue expression data, which may limit our ability to identify cell-type-specific causal genes⁵³. For example, recent studies increasingly suggest that FTO may not be the causal gene for BMI; instead, experimental evidence indicates that IRX3 and IRX5 are the causal genes⁵⁴. However, the causality of IRX3 and IRX5 was observed in experiments using preadipocytes, rather than bulk subcutaneous adipose tissue, which may explain why TGVIS failed to identify these genes (Supplementary Fig. 36). Third, we used the Pratt index²⁶ to rank the importance of variables, but it has inherent statistical limitations²⁶. In simulations, the Pratt index slightly underestimates the true contribution, although this underestimation becomes negligible as the sample size increases (Supplementary Figs. 1–8). In real data analysis, we used an empirical cutoff learned by K-means (CS-Pratt = 0.15) to extract important causal variables, which gives us higher precision but may have potentially hindered the discovery of causal gene-tissue pairs with small to moderate causal effects. Fourth, the window size of cis-region can have an impact on the result, and the current TGVIS only applies the convention method of ±1 Mb from the transcription start site (TSS). Applying automatically selecting the window sizes may improve statistical power and accuracy to identify causal genes and warrants for additional investigation⁵⁵. Last, as suggested in previous studies¹⁵, the inference of causality based on statistical methods comes with a caveat, assuming no model misspecification and no potential causal elements are missing from the model.

In summary, our developed TGVIS and accompany software pipeline provide a valuable tool in fine-mapping and interpreting GWAS findings.

Methods

Multivariable TWAS model

The causal diagram shown in Fig. 1A can be described by the following multivariate TWAS model:

$${y}_{i}={\sum }_{j=1}^{J}{\sum }_{t=1}^{T}{X}_{{ijt}}{\theta }_{{jt}}+{{{{\bf{G}}}}}_{i}^{{{\top }}}\left({{{\boldsymbol{\gamma }}}}+{{{\boldsymbol{\upsilon }}}}\right)+{\varepsilon }_{i},$$

(1)

where ${y}_{i}$ is a trait; ${X}_{{ijt}}$ is the levels (e.g., expressions and splicing events) of the ${j}^{{{\mbox{th}}}}$ gene and ${t}^{{{\mbox{th}}}}$ tissue pair; ${{{{\bf{G}}}}}_{i}={\left({G}_{i1},\ldots,{G}_{{iM}}\right)}^{{{\!\!\top }}}$ is an $(M\times 1)$ vector of genetic variants in the cis-region; ${{{\boldsymbol{\theta }}}}={\left({\theta }_{11},\ldots,{\theta }_{{JT}}\right)}^{{{\!\!\top }}}$ is an $(\,{JT}\times 1)$ vector of causal effects with ${\theta }_{{jt}}$ being the causal effect of the $\left(j,t\right)$ th tissue-gene pair; ${{{\boldsymbol{\gamma }}}}={\left({\gamma }_{1},\ldots,{\gamma }_{M}\right)}^{{{\top }}}$ is an $(M\times 1)$ vector of direct causal effects; ${{{\boldsymbol{\upsilon }}}}={\left({\upsilon }_{1},\ldots,{\upsilon }_{M}\right)}^{{{\top }}}$ is an $(M\times 1)$ vector of infinitesimal effects; and ${\epsilon }_{i}$ is the random error. Let ${{{{\boldsymbol{\beta }}}}}_{{jt}}={({\beta }_{{jt}1},\ldots,{\beta }_{{jtM}})}^{{{\top }}}$ is an $(M\times 1)$ vector of the cis-eQTL effects of ${JT}$ tissue-gene pairs. Then we have

$${X}_{{ijt}}={{{{\boldsymbol{\beta }}}}}_{{jt}}^{{{\top }}}{{{{\bf{G}}}}}_{i}+{\epsilon }_{{ijt}},$$

(2)

where ${\epsilon }_{{ijt}}$ is the noise of the $j{t}^{{{\mbox{th}}}}$ gene-tissue pair. The reduced form of (1) is then given by:

$${y}_{i}={{{{\bf{G}}}}}_{i}^{{{\top }}}\left({\sum }_{j=1}^{J}{\sum }_{t=1}^{T}{{{{\boldsymbol{\beta }}}}}_{{jt}}{\theta }_{{jt}}+{{{\boldsymbol{\gamma }}}}+{{{\boldsymbol{\upsilon }}}}\right)+{\epsilon }_{i},$$

(3)

where mathematically ${\epsilon }_{i}={\varepsilon }_{i}+{\sum }_{j=1}^{J}{\sum }_{t=1}^{T}{\epsilon }_{{ijt}}{\theta }_{{jt}}$.

An alternative version of (1) based on summarized statistics⁵⁶ is:

$$\hat{{{{\bf{a}}}}}{{{\mathscr{\sim }}}}{{{\mathcal{N}}}}\left({{{\bf{R}}}}\left({\sum }_{j=1}^{J}{\sum }_{i=1}^{T}{{{{\boldsymbol{\beta }}}}}_{{jt}}{\theta }_{{jt}}+{{{\boldsymbol{\gamma }}}}+{{{\boldsymbol{\upsilon }}}}\right),{\sigma }_{\alpha }^{2}{{{\bf{R}}}}\right),$$

(4)

where $\hat{{{{\bf{a}}}}}={\left({\hat{a}}_{1},\ldots,{\hat{a}}_{M}\right)}^{{{\!\!\top }}}$ represents the GWAS effects of the outcome, ${{{\bf{R}}}}$ is an $\left(M\times M\right)$ LD matrix of the $M$ variants, and ${\sigma }_{\alpha }^{2}$ is the variance of this model. The eQTL effect vector ${{{{\boldsymbol{\beta }}}}}_{{jt}}$ follows the model based on summarized statistics below:

$${\hat{{{{\bf{b}}}}}}_{{jt}}{{{\mathscr{\sim }}}}{{{\mathcal{N}}}}\left({{{\bf{R}}}}{{{{\boldsymbol{\beta }}}}}_{{jt}},{\sigma }_{{\beta }_{{jt}}}^{2}{{{\bf{R}}}}\right)$$

(5)

where ${\hat{{{{\bf{b}}}}}}_{{jt}}={({\hat{b}}_{{jt}1},\ldots,{\hat{b}}_{{jtM}})}^{{{\top }}}$ represents the marginal cis-eQTL effect estimates for the $j{t}^{{{\mbox{th}}}}$ tissue-gene pair, and ${\sigma }_{{\beta }_{{jt}}}^{2}$ denotes the variance of this model.

To resolve this curse of dimensionality, we utilized the three sparsity conditions that are commonly assumed in current fine-mapping methods^18,21: (SP1) one or small number of variants causally contribute to tissue or cell-type specific gene expression¹³; (SP2) one or small number of gene-tissue pairs causally contribute to the trait^14,15; (SP3) one or small number of direct causal variants exist with relatively large effect sizes^14,15. In terms of statistical model: SP1 corresponds to ${{{{\boldsymbol{\beta }}}}}_{{jt}}$ being sparse for all $j$ ${{\mbox{and}}}$ $t$; SP2 corresponds to ${{{\boldsymbol{\theta }}}}$ being sparse; SP3 corresponds to ${{{\boldsymbol{\gamma }}}}$ being sparse. In addition, we incorporated that variants can have infinitesimal effects: ${{{\boldsymbol{\upsilon }}}}$ is normally distributed with a mean 0 and a small, unknown variance¹⁹. To our best knowledge, infinitesimal effects have not been modeled in current multivariate TWAS methods.

Estimation of cis-regulatory effect

TGVIS first applies SuSiE²⁰ to estimate the non-zero eQTL effect for each gene-tissue pair, based on the fine-mapping model (Eq. 5). Specifically, we set $L=3$ for each pair and determined the non-zero ${cis}$-regulatory effects based on two criteria: (1) if they are within any 95% credible set and their PIPs exceeds 0.25, and (2) if their individual PIPs are >0.5. The rationale behind this approach is that SuSiE’s 95% credible set can sometimes include too many weakly correlated variants (even after removing highly correlated ones using LD clumping), leading to low PIPs for each variant. Therefore, we used a moderate threshold to filter out credible sets with too many variants. Additionally, due to the low power of detection, the maximum PIP of credible sets might fall below 0.95, so we retained variants with individual PIPs >0.5. Since a locus often contains over 10,000 gene-tissue pairs (mostly sGenes), dynamically selecting using BIC would be computationally burdensome. Additionally, with GTEx sample sizes under 200, only 1–2 gene-tissue pairs can be identified for most gene-tissue pairs. Therefore, we choose to fix $L=3$.

Infinitesimal effects may also influence the prediction of gene expression. We did not consider this issue in xQTL selection, because the variance of estimation errors of GWAS effect sizes is much larger than the variance of the infinitesimal effects when the sample size is small.

Joint modeling of causal tissue-gene pairs, direct causal variants, and infinitesimal effects using profile likelihood

TGVIS estimates ${{{\boldsymbol{\theta }}}}$, ${{{\boldsymbol{\gamma }}}}$, and ${{{\boldsymbol{\upsilon }}}}$ using a profile likelihood approach. Given the estimate ${{{{\boldsymbol{\upsilon }}}}}^{\left(s\right)}$ from the sth iteration, we considered the following fine-mapping model:

$$\hat{{{{\bf{a}}}}}-{{{\bf{R}}}}{{{{\boldsymbol{\upsilon }}}}}^{\left(s\right)}{{{\mathscr{\sim }}}}{{{\mathcal{N}}}}\left({{{\bf{R}}}}{{{\boldsymbol{\gamma }}}}{{{\boldsymbol{+}}}}{{{\bf{R}}}}\hat{{{{\bf{B}}}}}{{{\boldsymbol{\theta }}}},{\sigma }_{\alpha }^{2}{{{\bf{R}}}}\right),$$

(6)

where $\hat{{{{\bf{B}}}}}=({\hat{{{{\boldsymbol{\beta }}}}}}_{11},\ldots,{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}},\ldots,{\hat{{{{\boldsymbol{\beta }}}}}}_{{JT}})$ is an $M\times {JT}$ matrix consisting of estimated ${cis}$-regulatory effects. To update ${{{\boldsymbol{\gamma }}}}$ and ${{{\boldsymbol{\theta }}}}$ simultaneously, we applied the same scheme as cTWAS and TGFM, using the function susie_rss($\cdot$). The input z-score vector is computed as:

$$z={\left(\frac{{\hat{{{{\boldsymbol{\beta }}}}}}_{11}^{{{\top }}}(\hat{{{{\bf{a}}}}}-{{{\bf{R}}}}{{{{\boldsymbol{\upsilon }}}}}^{\left({{s}}\right)})}{\sqrt{{\hat{{{{\boldsymbol{\beta }}}}}}_{11}^{{{\top }}}{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{11}}},\cdots,\frac{{\hat{{{{\boldsymbol{\beta }}}}}}_{{{JT}}}^{{{\top }}}\left(\hat{{{{\bf{a}}}}}-{{{\bf{R}}}}{{{{\boldsymbol{\upsilon }}}}}^{\left({{s}}\right)}\right)}{\sqrt{{\hat{{{{\boldsymbol{\beta }}}}}}_{{{JT}}}^{{{\top }}}{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{{JT}}}}},{\hat{a}}_{1}-{{{{\bf{r}}}}}_{1}^{{{\top }}}{{{{\boldsymbol{\upsilon }}}}}^{\left({{s}}\right)},\cdots,{\hat{a}}_{M}-{{{{\bf{r}}}}}_{M}^{{{\top }}}{{{{\boldsymbol{\upsilon }}}}}^{\left({{s}}\right)}\right)}^{{{\top }}},$$

(7)

and the other elements of input correlation matrix are computed as:

$${{\mbox{cor}}}\left({{{{{\bf{G}}}}}_{{{{\bf{i}}}}}\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}},{{{{\bf{G}}}}}_{{{{\bf{i}}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{j}^{{\prime} }{t}^{{\prime} }}\right)=\frac{{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}^{{{\top }}}{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{j}^{{\prime} }{t}^{{\prime} }}}{\sqrt{{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}^{{{\top }}}{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}}\sqrt{{\hat{{{{\boldsymbol{\beta }}}}}}_{{j}^{{\prime} }{t}^{{\prime} }}^{{{\top }}}{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{j}^{{\prime} }{t}^{{\prime} }}}},\\ {{\mbox{cor}}}\left({{{{{\bf{G}}}}}_{{{{\bf{i}}}}}\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}},{{{{\bf{G}}}}}_{{{{\bf{i}}}}}\right)=\frac{{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}}{\sqrt{{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}^{\top }{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}}},{{\mbox{cor}}}\left({{{{\bf{G}}}}}_{{{{\bf{i}}}}}\right)={{{\bf{R}}}}$$

(8)

The outputs are denoted as ${{{{\boldsymbol{\gamma }}}}}^{\left({{s}}+1\right)}$ and ${{{{\boldsymbol{\theta }}}}}^{\left({{{\boldsymbol{s}}}}+1\right)}$.

Next, we consider the following model:

$$\hat{{{{\bf{a}}}}}-{{{{\boldsymbol{\eta }}}}}^{\left(s+1\right)}|{{{\boldsymbol{\upsilon }}}}{{{\mathscr{\sim }}}}{{{\mathcal{N}}}}\left({{{\bf{R}}}}{{{\boldsymbol{\upsilon }}}},{\sigma }_{\alpha }^{2}{{{\bf{R}}}}\right),{{{\boldsymbol{\upsilon }}}}{{{\mathscr{\sim }}}}{{{\mathcal{N}}}}\left(0,{\sigma }_{\upsilon }^{2}{{{\bf{I}}}}\right),$$

(9)

where ${{{{\boldsymbol{\eta }}}}}^{\left(s+1\right)}={{{\bf{R}}}}(\hat{{{{\bf{B}}}}}{{{{\boldsymbol{\theta }}}}}^{\left(s+1\right)}+{{{{\boldsymbol{\gamma }}}}}^{\left(s+1\right)}).$ The penalized quasi-likelihood (PQL) of ${{{\boldsymbol{\upsilon }}}}$ is

$${{{{\boldsymbol{\upsilon }}}}}^{\left(s+1\right)}={{\arg }}{\min }_{{{{\boldsymbol{\upsilon }}}}}\left\{{\left(\hat{{{{\bf{a}}}}}-{{{{\boldsymbol{\eta }}}}}^{\left(s+1\right)}-{{{\bf{R}}}}{{{\boldsymbol{\upsilon }}}}\right)}^{{{\top }}}{{{{\bf{R}}}}}^{-1}\left(\hat{{{{\bf{a}}}}}-{{{{\boldsymbol{\eta }}}}}^{\left(s+1\right)}-{{{\bf{R}}}}{{{\boldsymbol{\upsilon }}}}\right)+\frac{{\sigma }_{\alpha }^{\left(s\right)2}}{{\sigma }_{\upsilon }^{\left(s\right)2}}\parallel {{{\boldsymbol{\upsilon }}}}{\parallel }_{2}^{2}\right\},$$

(10)

which results in

$${{{{\boldsymbol{\upsilon }}}}}^{\left(s+1\right)}={\left({{{\bf{R}}}}+\frac{{\sigma }_{\alpha }^{\left(s\right)2}}{{\sigma }_{\upsilon }^{\left(s\right)2}}{{{\bf{I}}}}\right)}^{-1}\left(\hat{{{{\bf{a}}}}}-{{{{\boldsymbol{\eta }}}}}^{\left(s+1\right)}\right),$$

(11)

where ${\sigma }_{\alpha }^{\left(s\right)2}$ is the current variance estimate. The variance ${\sigma }_{\upsilon }^{\left(s\right)2}$ is updated by REML:

$${\sigma }_{\upsilon }^{\left(s+1\right)2}={{\arg }}{\min }_{{\sigma }_{\upsilon }^{2}}\left\{\frac{\parallel {{{{\boldsymbol{\upsilon }}}}}^{\left(s+1\right)}{\parallel }_{2}^{2}}{{\sigma }_{\upsilon }^{2}}+M\log \left({\sigma }_{\upsilon }^{2}\right)+{\log\det}\left(\frac{1}{{\sigma }_{\alpha }^{\left(s\right)2}}{{{\bf{R}}}}+\frac{1}{{\sigma }_{\upsilon }^{\left(s\right)2}}{{{\bf{I}}}}\right)\right\},$$

(12)

which simplifies to

$${\sigma }_{\upsilon }^{\left(s+1\right)2}=\frac{1}{M}\parallel {{{{\boldsymbol{\upsilon }}}}}^{\left(s+1\right)}{\parallel }_{2}^{2}+\frac{1}{M}{\mbox{tr}}\left({\left({{{\bf{R}}}}+\frac{{\sigma }_{\alpha }^{\left(s\right)2}}{{\sigma }_{\upsilon }^{\left(s\right)2}}{{{\bf{I}}}}\right)}^{-1}\right),$$

(13)

where $M$ is the number of variants. We replace ${\sigma }_{\upsilon }^{2}$ in the last term by its current estimate ${\sigma }_{\upsilon }^{\left(s\right)2}$ to obtain a closed-form expression. Note that in Eq. (13), $\frac{{\sigma }_{\alpha }^{\left(s\right)2}}{{\sigma }_{\upsilon }^{\left(s\right)2}}$ is usually replaced by $\frac{1}{{\sigma }_{\upsilon }^{\left(s\right)2}}$ to avoid non-identifiability issues²⁵.

When the profile likelihood converges, TGVIS estimates ${\sigma }_{\alpha }^{2}$ as follows:

$${\sigma }_{\alpha }^{\left(s+1\right)2}=\frac{1}{M}{\left(\hat{{{{\bf{a}}}}}-{{{\bf{R}}}}\left(\hat{{{{\bf{B}}}}}{{{{\boldsymbol{\theta }}}}}^{\left(s+1\right)}+{{{{\boldsymbol{\gamma }}}}}^{\left(s+1\right)}+{{{{\boldsymbol{\upsilon }}}}}^{\left(s+1\right)}\right)\right)}^{{{\top }}}\\ {{{{\bf{R}}}}}^{-1}\left(\hat{{{{\bf{a}}}}}-{{{\bf{R}}}}\left(\hat{{{{\bf{B}}}}}{{{{\boldsymbol{\theta }}}}}^{\left(s+1\right)}+{{{{\boldsymbol{\gamma }}}}}^{\left(s+1\right)}+{{{{\boldsymbol{\upsilon }}}}}^{\left(s+1\right)}\right)\right)$$

(14)

In the software of TGVIS, we applies the convergence criterion: the convergence tolerance is smaller than a threshold (e.g., max(${||}{{{{\boldsymbol{\theta }}}}}^{\left({{{\boldsymbol{s}}}}+1\right)}-{{{{\boldsymbol{\theta }}}}}^{\left({{{\boldsymbol{s}}}}\right)}|{|}_{2},{||}{{{{\boldsymbol{\gamma }}}}}^{\left(s+1\right)}-{{{{\boldsymbol{\gamma }}}}}^{\left(s\right)}|{|}_{2}$) < 0.001), and the number of iterations is larger than 50 (e.g., $s > 50$).

Bayesian information criterion for summary data

Based on Eq. (3), we define the BIC for summary data:

$${\mbox{BIC}}=\log \left({\sigma }_{\alpha }^{2}\right)+\frac{\log M}{M}{\mbox{df}},$$

(15)

where $M$ is the number of IVs and ${\mbox{df}}$ is the degree of freedom of the model⁵⁷. In practice, ${\sigma }_{\alpha }^{2}$ is replaced by its empirical estimate ${\hat{\sigma }}_{\alpha }^{2}$, and ${\mbox{df}}$ is the sum of non-zero causal effect estimates and non-zero direct causal variant estimates. Our default setting assumes $L$ can be 2,3,4,5,6,7, or 8 and uses BIC to select the optimal $L$ among them. We found that when considering the infinitesimal effect, it tends to capture variants with very small effects that SuSiE does not identify, making it rare for $L$ to exceed 8 in practice.

Pratt index

We use the Pratt index to assess the contribution of a gene-tissue pair. For a general linear model: ${y}_{i}={\sum }_{j=1}^{p}{X}_{j}{\beta }_{j}+{\epsilon }_{i}$, the Pratt index of ${x}_{{ij}}$ is defined as ${V}_{j}={\beta }_{j}\times {b}_{j},$ where ${b}_{j}={{\mathrm{cov}}}(y,{X}_{j})$. This definition assumes standardization where ${\mbox{E}}\left(y\right)={\mbox{E}}({X}_{j})=0$ and ${{\mathrm{var}}}\left(y\right)={{\mathrm{var}}}({X}_{j})=1$, $1\le j\le p$. The Pratt index measures the contribution of a variable in a linear model because ${R}^{2}={\sum }_{j=1}^{p}{V}_{j}$ where ${R}^{2}={{\mathrm{var}}}({\sum }_{j=1}^{p}{X}_{j}{\beta }_{j})/{{\mathrm{var}}}(y)$. In practice, the Pratt index can be estimated by ${\hat{V}}_{j}={\hat{\beta }}_{j}\times {\hat{b}}_{j}$, where ${\hat{b}}_{j}$ is the sample correlation between ${X}_{j}$ and $y$.

The proportion of variance explained (PVE) is defined as ${PV}{E}_{j}={\beta }_{j}^{2}$, assuming that all variables are standardized. The Pratt index has two key advantages over PVE: (1) Pratt indices are additive across variables, and (2) the sum of Pratt indices is the total trait variance explained by covariates. In contrast, PVE lacks these advantages.

Pratt index serves as an additional important matric for evaluating a gene or causal variant besides PIP. While the PIP reflects the statistical significance of a variable from a Bayesian perspective, the Pratt index quantifies its predictive contribution to the outcome when multiple predictors are correlated. PIP behaves similarly to a frequentist p-value and is influenced by sample size, in contrast that Pratt index is less affected by sample size.

Pratt index in TGVIS

We show how to yield the Pratt index ${V}_{{jt}}$ in practice. We first estimate the marginal correlation:

$${\widetilde{\delta }}_{{jt}}={{\widehat{{\mbox{cor}}}}}\left({\widehat{{{{\boldsymbol{\beta }}}}}}_{{jt}},\widehat{{{{\bf{a}}}}}\right)=\frac{{\widehat{{{{\boldsymbol{\beta }}}}}}_{{jt}}^{{{\top }}}\widehat{{{{\bf{a}}}}}}{\sqrt{{\widehat{{{{\boldsymbol{\beta }}}}}}_{{jt}}^{{{\top }}}{{{\bf{R}}}}{\widehat{{{{\boldsymbol{\beta }}}}}}_{{jt}}}\sqrt{{\widehat{{{{\bf{a}}}}}}^{{{\top }}}{{{{\bf{R}}}}}^{-1}\widehat{{{{\bf{a}}}}}}}.$$

(16)

As for the causal effect estimate ${\hat{\theta }}_{{jt}}$, we apply the transformation

$${\widetilde{\theta }}_{{jt}}={\hat{\theta }}_{{jt}}\frac{\sqrt{{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}^{{{\top }}}{{{\bf{R}}}}{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}}}{\sqrt{{\hat{{{{\bf{a}}}}}}^{{{\top }}}{{{{\bf{R}}}}}^{-1}\hat{{{{\bf{a}}}}}}},$$

(17)

since the Pratt index requires the covariates and trait are all standardized. Thus, the Pratt index of the $\left(j,t\right)$ th gene-tissue pair is

$${\hat{V}}_{{jt}}={\widetilde{\theta }}_{{jt}}\times {\widetilde{\delta }}_{{jt}}={\hat{\theta }}_{{jt}}\frac{{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}^{{{\top }}}\hat{{{{\bf{a}}}}}}{{\hat{{{{\bf{a}}}}}}^{{{\top }}}{{{{\bf{R}}}}}^{-1}\hat{{{{\bf{a}}}}}}.$$

(18)

Since Pratt indices are additive, the Pratt index of a credible set is simply calculated as

$${\hat{V}}_{c{s}_{l}}={\sum }_{j\in {{{\boldsymbol{c}}}}{{{{\boldsymbol{s}}}}}_{{{{\boldsymbol{l}}}}}}{\hat{V}}_{j}.$$

(19)

Note that the Pratt index is only comparable within the same locus, as it represents the ratio of the variance explained by the variable to the total variance of the trait.

It is worth comparing the gene-tissue pair, direct causal variant, and infinitesimal effect contributions at a locus. To simplify the estimation, we consider the linear predictors of all gene-tissue pairs and pleiotropy:

$${\widetilde{{{{\boldsymbol{\eta }}}}}}_{\theta }={{{{\bf{R}}}}}^{\frac{1}{2}}\hat{{{{\bf{B}}}}}\hat{{{{\boldsymbol{\theta }}}}},{\widetilde{{{{\boldsymbol{\eta }}}}}}_{\gamma }={{{{\bf{R}}}}}^{\frac{1}{2}}\hat{{{{\boldsymbol{\gamma }}}}},{\widetilde{{{{\boldsymbol{\eta }}}}}}_{\upsilon }={{{{\bf{R}}}}}^{\frac{1}{2}}\hat{{{{\boldsymbol{\upsilon }}}}}.$$

(20)

and $\widetilde{{{{\bf{a}}}}}={{{{\bf{R}}}}}^{-\frac{1}{2}}\hat{{{{\bf{a}}}}}$, where ${{{{\bf{R}}}}}^{-\frac{1}{2}}$ is specified to remove the correlations of $\hat{{{{\bf{B}}}}}$ and $\hat{{{{\bf{a}}}}}$. Then, the Pratt indices for the gene-tissue pairs, direct causal variants, and infinitesimal effects are

$${\hat{V}}_{\theta }=\frac{{\widetilde{{{{\boldsymbol{\eta }}}}}}_{\theta }^{{{\top }}}\widetilde{{{{\bf{a}}}}}}{\parallel \widetilde{{{{\bf{a}}}}}{\parallel }_{2}^{2}},{\hat{V}}_{\gamma }=\frac{{\widetilde{{{{\boldsymbol{\eta }}}}}}_{\gamma }^{{{\top }}}\widetilde{{{{\bf{a}}}}}}{\parallel \widetilde{{{{\bf{a}}}}}{\parallel }_{2}^{2}},{\hat{V}}_{\upsilon }=\frac{{\widetilde{{{{\boldsymbol{\eta }}}}}}_{\upsilon }^{{{\top }}}\widetilde{{{{\bf{a}}}}}}{\parallel \widetilde{{{{\bf{a}}}}}{\parallel }_{2}^{2}}.$$

(21)

Threshold of Pratt index

We used empirical data to determine the threshold for Pratt index to enhance the precision of causal selection. Specifically, we employed K-means clustering with clusters to group the CS-Pratt indices of all gene-tissue pairs and direct variants identified by TGVIS within the 95% credible sets. We hypothesize that one cluster contains credible sets with smaller CS-Pratt values, which are more likely to include falsely causal variables. Interestingly, regardless of whether we focus on gene-tissue pairs, direct causal variants, or both, the minimum value in the cluster with the larger centroid consistently remains at 0.15 (Supplementary Fig. 34). Consequently, we set the threshold at CS-Pratt = 0.15 to prioritize the gene-tissue pairs and direct causal variants identified by TGVIS, considering variables with CS-Pratt > 0.15 to have a higher likelihood of being true causal.

Potential reasons leading to infinitesimal effects

Here we list four possible reasons that can lead to an infinitesimal effect. First, it has been gradually understood that even within the same ethnic group, such as the European population, different subgroups may have different genetic architectures, leading to different LD structures. Therefore, it is natural to suspect that the LD structures of populations in the GTEx consortium and those in traits GWAS differ, which results in

$${\mbox{E}}\left(\hat{{{{\boldsymbol{\alpha }}}}}\right)={{{{\bf{R}}}}}_{{\mbox{Meta}}}\left({{{\bf{B}}}}{{{\boldsymbol{\theta }}}}+{{{\boldsymbol{\gamma }}}}\right),{\mbox{E}}\left({\hat{{{{\bf{b}}}}}}_{{jt}}\right)={{{{\bf{R}}}}}_{{\mbox{GTEx}}}{{{{\boldsymbol{\beta }}}}}_{{jt}}.$$

(22)

When we try to estimate ${{{{\boldsymbol{\beta }}}}}_{{jt}}$ using ${{{{\bf{R}}}}}_{{\mbox{Meta}}}$, then ${\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}$ is biased to ${{{{\boldsymbol{\beta }}}}}_{{jt}}$, which generates infinitesimal effect ${{{\boldsymbol{\upsilon }}}}={\sum}_{{jt}}({{{{\boldsymbol{\beta }}}}}_{{jt}}-{\hat{{{{\boldsymbol{\beta }}}}}}_{{jt}}){\theta }_{{jt}}$. It should be noted that the small sample size in the GTEx consortium can also cause biased eQTL effect estimates, resulting in the appearance of infinitesimal effects. There are other possible sources which may lead to infinitesimal effects, such as (2) the estimation errors of LD matrix, (3) the imputation errors of outcome GWAS effect sizes, and (4) a true causal variant is either not genotyped or is filtered out during the LD clumping, which are shown in Supplementary Materials. It should be noted that all four sources are not biologically relevant, although we can model them through the infinitesimal effect model.

Score test of variance of infinitesimal effects

In implementation, dynamically determining whether to consider the infinitesimal effect is a clever empirical measure. Therefore, we apply the score test of the variance of the random effect in the linear mixed model to test whether the variance of the infinitesimal effect is zero. Specifically, we consider the following hypothesis testing problem:

$${{\mbox{H}}}_{0}:{\sigma }_{\upsilon }^{2}=0,v.s.{{\mbox{H}}}_{1}:{\sigma }_{\upsilon }^{2} > 0.$$

(23)

The testing statistics of this hypothesis test is constructed according to Zhang and Lin⁵⁸. Let ${{{\bf{A}}}}=({{{\bf{R}}}}{\hat{{{{\bf{B}}}}}}_{{{{{\mathscr{M}}}}}_{\theta }},{{{{\bf{R}}}}}_{{{{{\mathscr{M}}}}}_{\gamma }})$ and ${{{\boldsymbol{\vartheta }}}}={({{{{\boldsymbol{\theta }}}}}_{{{{{\mathscr{M}}}}}_{\theta }}^{{{\top }}},{{{{\boldsymbol{\gamma }}}}}_{{{{{\mathscr{M}}}}}_{\gamma }}^{{{\top }}})}^{{{\top }}},{\mbox{where }} \, {{\mathscr{M}}}_{\theta}\,{\mbox{ and }}\,{{\mathscr{M}}}_{\gamma}$ refer to the index sets of non-zero elements in ${\boldsymbol{\theta }}$ and ${{\boldsymbol{\gamma }}}$, respectively. When ${\sigma }_{\upsilon }^{2}=0$ and ${\sigma }_{\upsilon }^{2} > 0$, the covariance matrix of $\hat{{{{\boldsymbol{\alpha }}}}}-{{{\bf{A}}}}{{{\boldsymbol{\vartheta }}}}$ are

$${{\mathrm{cov}}}\left(\hat{{{{\boldsymbol{\alpha }}}}}-{{{\bf{A}}}}{{{\boldsymbol{\vartheta }}}}\right)={\sigma }_{\alpha }^{2}{{{\bf{R}}}},{{\mathrm{cov}}}\left(\hat{{{{\boldsymbol{\alpha }}}}}-{{{\bf{A}}}}{{{\boldsymbol{\vartheta }}}}\right)={\sigma }_{\alpha }^{2}{{{\bf{R}}}}+{\sigma }_{\upsilon }^{2}{{{{\bf{R}}}}}^{2},$$

(24)

respectively. Similar to estimating ${\sigma }_{\upsilon }$, we replace ${\sigma }_{\alpha }^{2}$ by 1 to avoid non-identifiability. The score described in Zhang and Lin⁵⁸ defined the following three statistics:

$$u=\frac{1}{2}\parallel \hat{{{{\boldsymbol{\alpha }}}}}-{{{\bf{A}}}}{{{\boldsymbol{\vartheta }}}}{\parallel }_{2}^{2},e=\frac{1}{2}{\mbox{tr}}\left({{{\bf{P}}}}{{{{\bf{R}}}}}^{2}\right),h=\frac{1}{2}{\mbox{tr}}\left({{{\bf{P}}}}{{{{\bf{R}}}}}^{2}{{{\bf{P}}}}{{{{\bf{R}}}}}^{2}\right),$$

(25)

where ${{{\bf{P}}}}={{{{\bf{R}}}}}^{-1}-{{{{\bf{R}}}}}^{-1}{{{\bf{A}}}}{({{{{\bf{A}}}}}^{{{\top }}}{{{{\bf{R}}}}}^{-1}{{{\bf{A}}}})}^{-1}{{{{\bf{A}}}}}^{{{\top }}}{{{{\bf{R}}}}}^{-1}$. Under the null hypothesis, $u\sim \kappa {\chi }_{v}^{2}$ where $\kappa=h/\left(2e\right)$ and $v=2{e}^{2}/h$. If the null hypothesis is accepted, we enforce ${{{{\boldsymbol{\upsilon }}}}}^{\left(s+1\right)}=0$.

In addition to true biological polygenicity, the infinitesimal component may also absorb residual genetic signals not adequately modeled due to estimation errors. For this reason, we do not claim the score test is to test whether there is a biological polygenicity. Instead, the purpose of modeling infinitesimal effects, similar to the rationale proposed by Cui et al. ¹⁹, is to improve the precision of identifying both gene—tissue pairs and direct causal variants.

cTWAS and TGFM programs

For cTWAS, since its software is designed to be user-friendly to practical projects, it involves complex settings that are not ideal for simulations, such as requiring a reference panel in BED format and a.db file of eQTL fine-mapping data. Therefore, we directly utilize the principles of cTWAS to develop an R function that employs SuSiE for the first-stage selection of ${cis}$-regulatory effects and the second-stage selection of causal and horizontally pleiotropic effects. Therefore, we did not consider the first step of cTWAS to estimate two universal prior parameters using the EM algorithm across all loci in the genome. Instead, we restrict cTWAS simulations to a single locus. In addition, we applied the following settings for cTWAS, TGFM, and TGVIS: for the prior weight $\pi$ in SuSiE, we applied $\pi={p}^{-1}$ for gene-tissue pairs and $\pi={M}^{-1}$ for variants, where $p$ represents the number of gene-tissue pairs and $M$ the number of variants.

At the time of writing this paper, the TGFM software has not yet been released, and hence, we also developed the TGFM software on our side. TGFM’s two-stage resampling scheme can make it significantly slower than cTWAS and TGVIS, even with a modest number of resampling iterations (e.g., 100) in each stage. To improve computational efficiency, we applied a slightly different resampling scheme compared with the original TGFM. Specifically, we first resampled the eQTL effects from the posterior for $25$ times, calculated their mean as ${\hat{\beta }}_{{jt}}^{{t}_{i}}$, and used these means to estimate ${\hat{{{{\boldsymbol{\theta }}}}}}^{{t}_{i}}$ and ${\hat{{{{\boldsymbol{\gamma }}}}}}^{{t}_{i}}$. This procedure was repeated $100$ times, recording the estimates and PIP for each iteration. We then compute the mean of ${t}_{1}\times {t}_{2}$ resampled eQTL effects, ${\hat{\beta }}_{{jt}}^{{t}_{i}},$ and estimate the empirical ${\hat{{{{\boldsymbol{\theta }}}}}}^{TGFM}$ and ${\hat{{{{\boldsymbol{\gamma }}}}}}^{TGFM}$. The PIPs of ${\hat{{{{\boldsymbol{\theta }}}}}}^{TGFM}$ and ${\hat{{{{\boldsymbol{\gamma }}}}}}^{TGFM}$ were taken as the empirical PIPs given by SuSiE in each resampling iteration. Finally, we recorded the credible sets of variables from the final step and calculated the PIPs and Pratt indices of credible sets by summing the individual PIPs and Pratt indices of variables within each credible set.

Another key difference between TGVIS and methods such as cTWAS and TGFM is that the latter require in-sample LD matrices, which are often unavailable for many GWAS datasets. In contrast, TGVIS uses LD matrices estimated from an external reference panel.

Simulation settings

We simulated 20 genes across 5 tissues, resulting in $p=$ 100 gene-tissue pairs. Correlations were simulated both within and between genes across tissues. The first and last gene-tissue pairs were designated as causal, with effect sizes of ${\theta }_{1}=1$ and ${\theta }_{100}=-1$, respectively. The total number of variants was $M=$ 400, with only 1,2,3, or 4 of them being eQTLs with non-zero effects for each gene-tissue pair, while the remaining variants were associated with the trait due to LD. We set 4 different sample sizes for the eQTL data (${n}_{{eQTL}}$ = 100, 200, 400, 800) and a fixed trait GWAS sample size ${n}_{{trait}}=$ 0.5M. Infinitesimal effect were generated from a normal distribution, and gene-tissue pairs, direct causal variants, and infinitesimal effects together were set to explain the trait heritability. For example, when only gene-tissue pairs and infinitesimal effects are present, they each explain 50% of the local heritability for the outcome. When all three are present, each explains 33% of the local heritability for the outcome. The detailed settings, along with corresponding R codes, are provided in Section 2 of the Supplementary Materials.

GWAS summary data

We conducted a meta-analysis on a subset of the 45 metabolic and cardiovascular traits. The publicly available data for these traits are listed in Supplementary Data 1, while the MVP GWAS summary statistics can be accessed through dbGAP under accession number phs001672.v7.p1. For the pleiotropy traits of SBP and DBP, we applied the approach developed in Zhu et al. ³² using the most recent GWAS summary statistics of SBP and DBP. To perform the meta-analysis, we used METAL⁵⁹. We performed the meta-analysis on the Z-scores, weighting by the sample sizes of the meta-analysis datasets. For binary trait, we always used the effective sample size ${n}_{eff}$. We used CHR:BP (in GRCH37) as the identifier.

EQTL summary data

We utilized bulk eQTL and sQTL summary statistics from 28 tissues provided by GTEx¹³ (with sample size N ranging from 113 (Lymphocytes) to 588 (Muscle Skeletal)), as well as additional eQTL summary statistics from tubulointerstitial³⁶ (N = 311), kidney glomerular³⁶ (N = 240), and islet³⁷ (N = 420) tissues (Supplementary Data 2).

Linkage disequilibrium reference panel

Our study used variants from the UKBB project conducted by Neale’s lab, which initially includes 13 million SNPs. We selected ~9.3 million SNPs with a minor allele frequency >0.01 for our analysis. We also identified the top 9620 unrelated individuals from ~500,000 individuals in the UKBB (Field ID: 22828), consisting of 5205 females and 4475 males. Data from these 9.3 million SNPs were extracted for these individuals to construct our LD reference panel.

Clumping and thresholding

We restricted the studied regions to those within 1MB of the genome-wide significant loci for these traits. These loci were identified using the clumping and thresholding (C + T) method in PLINK⁶⁰: --clump-kb 1000, --clump-p1 5E-8, --clump-p2 5E-8, and --clump-r2 0.01.

We recommend using C + T to filter out variants in high LD, which prevents the inclusion of numerous highly correlated or redundant variants in the analysis, which can unnecessarily complicate the model and result in multiple credible sets consisting of these variants. We evaluated the minimum P-value of each variant across gene-tissue pairs in eQTL/sQTL data. In PLINK, we applied the C + T with the following parameters: --clump-kb 1000, --clump-p1 1E-5, --clump-p2 1E-5, and --clump-r2 0.5. Given that the true causal variant for a trait might not be included in the eQTL/sQTL variants, we combined these variants from outcome GWAS satisfying P < 5E-8 and r² < 0.5.

Note that this preprocessing step removes SNPs in moderate to high LD by clumping (r² < 0.5), as the goal of the first stage is to build an accurate prediction of exposures. Our analyses show that using variant sets clumped at different LD thresholds yields comparable prediction accuracy, and also suggest that both LD clumping and biological infinitesimal effects contribute to the detection of infinitesimal effects (Supplementary Materials).

Removing gene-tissue pairs based on significance in S-Predixcan

We used the minimum P-value from S-Predixcan and a modifier accounting for direct causal variants (Supplementary Materials) to exclude eGenes/sGene with P > 0.05. These weak filters will eliminate redundant gene-tissue pairs, thereby reducing the model’s dimensionality. Since our goal is fine-mapping the causal gene-tissue pairs and identifying direct causal variants on the GWAS loci with significant signals, it will not induce a winner’s curse.

Searching causal gene-tissue pairs missed by univariable TWAS

We compared the causal gene-tissue pairs identified by TGVIS and TGFM with the significant gene-tissue pairs identified by S-PrediXcan. We considered genes with P < 0.05/20,000 as significant gene-tissue pairs in tissue specific S-PrediXcan analysis. We did not adjust for number of tissues. We then searched the gene-tissue pairs identified by TGVIS or TGFM but missed by S-PrediXcan.

Obtaining annotation scores from FAVOR and performing differential annotation tests

We combined the direct causal variants and xQTLs of causal gene-tissue pairs identified by TGVIS or TGFM across all 45 traits into two separate files and uploaded them to the FAVOR online platform³⁸ to obtain annotation scores for these variants. We performed Wilcoxon signed-rank test with both “less” and “greater” as alternative hypotheses for determining the direction of shift location and calculated corresponding P values. We used the R package FDREstimation to convert the P values to FDR Q-values using the Benjamini–Yekutieli (BY) procedure. Annotations with Q-values < 0.05 were considered to have significantly different scores.

Mapping major trait relevant tissues

For TGVIS, a 95% credible set often includes multiple gene-tissue pairs. In such cases, we calculated the proportion of each tissue appearing among these pairs, allowing the number of tissues in a causal credible set of gene-tissue pairs to be fractional. For TGFM, we first removed the gene-tissue pairs with PIPs < 0.5, and then applied the same procedure to map the dominant tissues.

Enrichment of identified causal genes in lipids silver gene list and druggable gene database

We applied the following strategy to map silver genes. First, we checked each credible set to see if any genes are part of the silver gene list; if so, we counted 1. If no silver gene was present, we then checked if any genes in the credible set were among the nearby genes; if so, we also counted 1. In other words, each credible set of gene-tissue pairs was counted only once. For TGFM, we first removed the gene-tissue pairs with PIPs <0.5, and then applied the same procedure as TGVIS to count the silver and nearby genes. Similar to the mapping procedure for silver genes, we examined each credible set identified as causal to see if it contained any druggable genes. If a druggable gene is present, we count it once.

We used the following statistics to compare the enrichments of TGVIS and TGFM. For example, regarding TGVIS and a given trait, we consider three metrics: the number of causal genes identified by TGVIS, the overlap between genes identified by TGVIS and those in the drug-target list, and the ratio of these two metrics (referred to as Ratio hereafter). To compare whether TGVIS or TGFM had a higher enrichment across traits, we performed a paired t-test using two vectors of Ratio.

Colocalization of credible sets

We use colocalization to evaluate the causal credible sets identified by TGFM and TGVIS. Within each region, we select variants from the outcome GWAS with P-values less than 5E-5 and ${r}^{2}$ < 0.81 for colocalization analysis. We perform fine-mapping on both the outcome and the gene-tissue pairs within credible sets using SuSiE, then calculate the posterior probability for hypothesis ${H}_{4}$, i.e., both traits are associated and share the same single causal variant, between each outcome and exposure pair using Coloc-SuSiE. We use a posterior probability of ${H}_{4}$ > 0.5 as the threshold to determine colocalization evidence between gene-tissue pairs and the outcome; notably, as long as at least one variant meets this criterion, it suffices.

Mendelian randomization using pQTL summary data

We performed both univariable and multivariable MR using pQTLs of protein abundance as IVs to evaluate the identified causal tissue-gene pairs. Because to the lack of tissue-specific protein data, we focused on a subset of pGenes identified in blood tissues provided by Sun et al. ¹¹. We selected independent, genome-wide significant pQTLs for each protein as IVs. The selection method for independent IVs was C + T (--clump-kb 1000 --clump-p1 5e-8 --clump-p2 5e-8 --clump-r2 0.01 using PLINK), with LD reference panels consisting of the 9680 individuals and 9.3 M variants from UKBB. We applied five univariable MR methods: MRMedian⁶¹, IMRP⁶², MRCML⁶³, MRCUE⁶⁴, and MRBEE⁶⁵. Both MRCUE and MRBEE account for sample overlap, with sample overlap correlations estimated using insignificant variants. We used the R package FDREstimation to convert the P-values obtained by these methods to FDR Q-values, using “BY” as the adjustment method. A pGene was considered significant if it was identified as such by at least four methods. We also conducted an analysis comparing the enrichments of TGVIS and TGFM, where the three corresponding metrics are: the overlap between causal genes identified by TGVIS or TGFM and the pGenes reported in Sun et al. ¹¹, the number of significant pGenes identified in univariable MR analysis, and the ratio of these two metrics.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.