Nonlocal electrical detection of reciprocal orbital Edelstein effect

Abstract

The orbital Edelstein effect and orbital Hall effect, where a charge current induces a nonequilibrium orbital angular momentum, offer a promising method for efficiently manipulating nanomagnets using light elements. Despite extensive research, understanding the Onsager’s reciprocity of orbital transport remains elusive. In this study, we experimentally demonstrate the Onsager’s reciprocity of orbital transport in an orbital Edelstein system by utilizing nonlocal measurements. This method enables the precise identification of the chemical potential generated by orbital accumulation, avoiding the limitations associated with local measurements. We observe that the direct and inverse orbital-charge conversion processes produce identical electric voltages, confirming Onsager’s reciprocity in orbital transport. Additionally, we find that the orbital decay length, approximately 100 nm at room temperature, is independent of the Cu thickness and decreases with decreasing temperature, revealing a distinct contrast to the spin transport behavior. Our findings provide valuable insights into both the reciprocity of the charge-orbital interconversion and the nonlocal correlation of orbital degree of freedom, laying the ground for orbitronics devices with long-range interconnections.

Introduction

Research on the dynamics and transport of different electronic degrees of freedom has driven advancements in physics, material science, and device engineering. Spin angular momenta (SAM) and their conversion, transport, and interaction with magnetization have been extensively studied in spintronics over the past decades. The spintronics community has utilized charge-to-spin conversion mechanisms, such as the well-known spin Hall effect^1,2 and spin Edelstein effect^3,4, to generate nonequilibrium accumulation. Recently, the emerging field of orbitronics, which focuses on orbital angular momenta (OAM)^5,6,7,8, offers a complementary direction to the traditional reliance on SAM. Similar to charge-to-spin conversion, charge-to-orbital conversion occurs through the orbital Hall effect (OHE)^5,6,7,9,10 and orbital Edelstein effect (OEE)^11,12,13,14. Nonequilibrium OAM can be electrically induced in various light element systems with negligible spin-orbit coupling (SOC), such as Cr^15,16,17, Ti^5,18, Mn^16,19, Al₂O₃/Ru interface²⁰, oxides/Cu interface^21,22, and naturally oxidized Cu^{23,24,25,26,27}, as revealed by optical⁵, terahertz emission⁹, torque^{11,17,20,21,22,28}, magnetoresistance^16,24,29 and magnon³⁰ measurements, demonstrating the high efficiency of orbital torque and the broad selection of orbital source materials. However, these studies relied on local measurements, where the regions for OAM generation, distribution, and conversion overlap, potentially involving processes unrelated to OAM. This overlap could complicate the precise quantification of the interconversion between nonequilibrium OAM and charge current.

Nonlocal transport measurements^{1,31,32,33,34,35,36,37,38,39,40} offer a promising approach to investigating various quantum transport phenomena, ranging from diffusive spin transport in metal^{1,31,32,33,34,35,36,37} to unconventional spin conversion in moiré superlattices^41,42 as well as the quantum spin Hall³⁸ and quantum anomalous Hall effects^39,40. In nonlocal transport devices, charge transport and nonequilibrium OAM can be spatially separated, enabling direct and isolated observation of the OAM distribution. Additionally, the nonlocal transport geometry naturally facilitates the measurement of both the direct (DOEE) and inverse (IOEE) orbital Edelstein effect within a single device, allowing verification of Onsager’s reciprocal relation—a principle of fundamental importance in the study of quantum transport.

In this study, we present measurements of the lateral OAM distribution and the reciprocity of the orbital Edelstein effect using nonlocal transport devices comprising Al₂O₃, Cu, and ferromagnets (FMs). The nonequilibrium OAM can reach ~100 nm along a lateral direction. This decay length remains unaffected by the Cu thickness, suggesting the OAM distribution in the lateral direction differs from that in the vertical direction, which aligns with the formation of interfacial orbital Rashba states between Cu and oxides. The lateral decay length decreases with lower temperature, distinct from spin diffusion behavior. Crucially, all the experimental results comply with Onsager’s reciprocal relations. Our work offers significant insights into the nonlocal correlation behaviors of nonequilibrium OAM and expands the design possibilities for orbitronics devices.

Results and discussion

Measurement of orbital accumulation in a nonlocal transport device structure

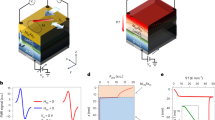
We investigated the OAM distribution using a nonlocal lateral transport structure^{1,31,32,33,34,35,36,37} (Fig. 1a, b), where the nonlocal resistance signals arise from DOEE and IOEE. In our samples, an oxidized Cu layer (denoted by CuO_x hereafter) <3 nm thick (Supplementary Section 1) forms between the Al₂O₃ and Cu layers due to natural oxidation (method). In the direct measurement configuration (Fig. 1a), a charge current I_c is applied to the Al₂O₃/CuO_x/Cu nanowire oriented along the y axis in Fig. 1a (denoted by Cu_y nanowire hereafter). This current induces nonequilibrium OAM (L) polarized in the x-direction according to the OEE Hamiltonian, ${H}_{{{{\rm{OEE}}}}}={\alpha }_{{{{\rm{OEE}}}}}\left({{{\bf{L}}}}\times {{{\bf{k}}}}\right)\cdot \hat{{{{\bf{z}}}}}$, where ${\alpha }_{{{{\rm{OEE}}}}}$ is the orbital Rashba coefficient, k is the wavevector, and $\hat{{{{\bf{z}}}}}$ is the unit vector along the z axis. If a nonlocal orbital response occurs at the Cu/FM junction, it can be converted into spins through the SOC of the FM, generating an output voltage V across the Cu/FM junction. We chose FM as the orbital converter instead of heavy metal so that we can separate the nonequilibrium OAM-induced signal from the bypass current-induced offset by varying the magnetization direction Φ. The nonlocal signal as a function of the separation distance d reflects the lateral distribution of the nonequilibrium OAM.

Fig. 1: Schematic illustration of nonlocal transport measurements and verification of orbital response through ferromagnetic materials dependence experiments.

a Nonlocal measurement configuration to observe DOEE (direct measurement). The nonequilibrium OAM (L) is generated by the charge current I_c at the CuO_x/Cu interface through DOEE. The orbital accumulation then converts into SAM (S) via SOC in FMs and induces a nonlocal response V. b Nonlocal measurement configuration to observe IOEE (inverse measurement). A charge current brings nonequilibrium OAM from the FMs. The orbital accumulation then converts to charge current at the CuO_x/Cu interface through IOEE. In nonlocal measurement (a, b), the orbital generator and detector are sufficiently isolated in space with a separation distance d (center-to-center distance), allowing the measurement of nonlocal orbital response. c, d Typical results of direct (c, R_DOEE) and inverse (d, R_IOEE) nonlocal orbital Edelstein resistance R, which is defined as $R\equiv V/{I}_{{{{\rm{c}}}}}$. The results are observed in sample A with separation distance d = 140 nm, Cu thickness t_Cu = 40 nm and FM = Co₂₅Fe₇₅ (Methods) while the external magnetic field B_ext swept along the hard axis of FM (Φ = 0°) from −1.25 T to 1.25 T. All the signals are globally offset to position their center at R = 0 Ω. The double-headed arrows in c, d indicate the definition of 2ΔR_DOEE and 2ΔR_IOEE, where 2ΔR_DOEE = − 2ΔR_IOEE ≈ 0.22 mΩ. e, f FM dependence results of 2ΔR_DOEE (e) and 2ΔR_IOEE (f). The solid curves represent the fitting of the data to Eq. (1), implying a long-range decay length of orbital accumulation λ_o of ~100 nm regardless of the selection of FMs. The dotted curves are guiding lines showing the value R = 0 Ω. The error bars indicate the standard deviation of R after the magnetization is saturated. All the results are measured at room temperature. All the results are in solid agreement with Onsager’s reciprocal relations.

In the inverse measurement configuration, the processes are reversed according to Onsager’s reciprocal relations (Fig. 1b). A charge current I_c is injected into the Al₂O₃/CuO_x/Cu nanowire, which is oriented along the x axis in Fig. 1b (denoted by Cu_x nanowire hereafter) from the FM magnetized along the x axis. This generates a nonequilibrium x-polarized OAM in the Cu_x nanowire via the SOC of the FM, which is converted to a charge current through IOEE, resulting in the voltage signal V_IOEE. Spin current is also generated in this process; however, the negligible SOC in Cu³³ should only lead to a tiny contribution to the voltage signal, as will be demonstrated below.

We first demonstrate both direct and inverse measurements to validate the feasibility of measuring nonequilibrium OAM using a nonlocal configuration. Fig. 1c, d illustrate the typical direct (R_DOEE) and inverse (R_IOEE) orbital Edelstein resistance as a function of the magnetic field along the x axis, observed in sample A (separation distance d = 140 nm, Cu thickness t_Cu = 40 nm and FM = Co₂₅Fe₇₅). The nonlocal orbital Edelstein resistance is defined as $R\equiv V/{I}_{{{{\rm{c}}}}}$, where R refers to both R_DOEE and R_IOEE, V is the measured voltage signal, and I_c is the applied current. Both R_DOEE and R_IOEE exhibit a linear response to the external magnetic field B_ext within the range of −0.5 T to +0.5 T, saturating once the magnitude of B_ext exceeds the saturation field B_sat (given by the anisotropic magnetoresistance curve, see Supplementary Section 2) of magnetization. Taking the difference of R_DOEE and R_IOEE at +B_ext and –B_ext, we obtained a 2ΔR_DOEE = 0.22 mΩ and 2ΔR_IOEE = − 0.22 mΩ. The absolute value of the signal is two orders of magnitude larger than the artifact coming from the stray field-induced Hall effect in Cu, estimated via the COMSOL simulation (Supplementary Section 3).

As a typical way to provide evidence for nonequilibrium OAM^{18,20,21,43,44}, we conducted FM dependence experiments using Co₂₅Fe₇₅, Co₅₀Fe_50, and Ni₈₁Fe_19, as shown in Fig. 1e, f, where 2ΔR is the overall change in nonlocal resistance. |2ΔR(Co₂₅Fe₇₅)| is larger than |2ΔR(Co₅₀Fe₅₀)|, and |2ΔR(Ni₈₁Fe₁₉)| is at least one order of magnitude smaller than them. A different measurement focusing on the local responses⁴⁵ also confirms the FM dependence (measurement configurations and results are detailed in Supplementary Section 4), where the orbital response is measured by FM nanowires right below the orbital generation part. Consistent with previous studies^{18,20,21,43,44}, the FM-dependent results identify the characteristic of orbital responses. We attribute the strong FM dependence to the spin-orbit correlation ${\left\langle {{{\bf{L}}}}{{{\cdot }}}{{{\bf{S}}}}\right\rangle }^{{{{\rm{FM}}}}}$ within FMs^43,44,46. ${\left\langle {{{\bf{L}}}}{{{\cdot }}}{{{\bf{S}}}}\right\rangle }^{{{{\rm{FM}}}}}$ near the Fermi level in FMs varies significantly with slight changes in FM composition, leading to ${\left\langle {{{\bf{L}}}}{{{\cdot }}}{{{\bf{S}}}}\right\rangle }^{{{{\rm{C}}}}{{{{\rm{o}}}}}_{25}{{{\rm{F}}}}{{{{\rm{e}}}}}_{75}}\, > \,{\left\langle {{{\bf{L}}}}{{{\cdot }}}{{{\bf{S}}}}\right\rangle }^{{{{\rm{C}}}}{{{{\rm{o}}}}}_{50}{{{\rm{F}}}}{{{{\rm{e}}}}}_{50}} > \,{\left\langle {{{\bf{L}}}}{{{\cdot }}}{{{\bf{S}}}}\right\rangle }^{{{{\rm{N}}}}{{{{\rm{i}}}}}_{81}{{{\rm{F}}}}{{{{\rm{e}}}}}_{19}}$⁴³. As the stray fields of the Co₂₅Fe₇₅ and the Ni₈₁Fe₁₉ are in the same order, the large difference between |2ΔR(Co₂₅Fe₇₅)| and |2ΔR(Ni₈₁Fe₁₉)| also excludes the stray field-induced artifacts in the nonlocal resistance. The spin-induced nonlocal resistance also cannot strongly depend on the FM type (see Supplementary Section 5, where Co₂₅Fe₇₅ and Ni₈₁Fe₁₉ show comparable nonlocal spin valve signals), suggesting that the observed ΔR is dominated by OAM.

Next, we analyzed the nonlocal resistance as a function of the separation distance d. The nonlocal resistance decreases exponentially with increasing d (Fig. 1f), indicating that the OAM accumulation decays as the detection point moves farther from the charge current source. A significant signal persists up to d ~ 350 nm, corresponding to an exponential decay length of approximately 100 nm. At the same time, a trivial current bypass effect can generate a nonlocal response, as previously reported^47,48; both COMSOL simulations and analytical modeling estimate a decay length of approximately 47 nm (Supplementary Section 6). This is substantially shorter than the experimentally observed value of ~100 nm, thereby excluding the current bypass effect as the sole origin of the observed nonlocal response. Accounting for both OAM decay and bypass effects, we applied the following equation to evaluate the lateral decay length of orbital accumulation distribution (Supplementary Section 6):

$$2\Delta R=\frac{A}{\frac{1}{{\lambda }_{{{{\rm{o}}}}}}-\frac{\pi }{{W}_{x}}}\left[\exp \left(-\frac{\pi d}{{W}_{x}}\right)-\exp \left(-\frac{d}{{\lambda }_{{{{\rm{o}}}}}}\right)\right],$$

(1)

where A is the fitting parameter for local processes, including the vertical OAM decay, charge-to-orbital and orbital-to-spin conversion, λ_o is the lateral decay length of orbital accumulation, and W_x is the width of the Cu nanowire. As shown in Fig. 1e, f, fitting the data for Co₂₅Fe₇₅ (circles) and Co₅₀Fe₅₀ (diamonds) to Eq. (1) yields λ_o ~ 100 nm, regardless of the FM selection, suggesting that the nonlocal correlation is determined by the processes in the Al₂O₃/CuO_x/Cu nanowire and unaffected by the Cu/FM junctions.

Measuring nonequilibrium OAM using the nonlocal lateral transport structure demonstrates the feasibility of detecting OAM through the chemical potential, allowing the measurement of pure orbital accumulation. Onsager’s reciprocal relations are then validated in the experiments: the relationship 2ΔR_DOEE = − 2ΔR_IOEE holds across all the measurements. This highlights that the OAM degree of freedom is an active and essential factor in electronic transport, a consideration that has been overlooked in previous research.

Angular dependence

We then performed an angular dependence experiment on sample A to clarify the orientation of OAM. As the angle Φ of B_ext to the x axis varied in-plane from 0° to 180°, R_DOEE (Fig. 2a) and R_IOEE (Fig. 2b) evolved accordingly. Notably, 2ΔR_DOEE (Fig. 2c) and 2ΔR_IOEE (Fig. 2d) show a strong correlation with the corresponding cosine curves $f\left(\it\varPhi \right)={f}_{1}\cos \it\varPhi$, where f₁ represents the value of 2ΔR_DOEE or 2ΔR_IOEE at 90°. Analogous to the angle dependence in spin measurements³¹, this strongly suggests that we are detecting OAM projected along the magnetization direction. This trend further implies that the measured OAM is polarized along the x-direction, consistent with OEE, perpendicular to the applied charge current^12,49. Minor deviations from the cosine curve, where the data points vertically shift towards 2ΔR = 0 Ω, can be attributed to the magnetic anisotropy of the FM nanowire (Supplementary Section 7).

Fig. 2: Angle dependence experiments.

a, b R_DOEE (a) and R_IOEE (b) for sample A observed with magnetic field B_ext at various angle Φ. c, d 2ΔR_DOEE and 2ΔR_IOEE as a function of Φ. The insets show the measurement configuration and the definition of angle Φ. The results are measured at room temperature. The solid curves in c, d are guiding lines employing a cosine function $f\left(\it\varPhi \right)={f}_{1}\cos \it\varPhi$. The angle-dependent 2ΔR_DOEE and 2ΔR_IOEE well match the cosine function, indicating that x-polarized OAM is measured. The error bars in c, d indicate the standard deviation of R after the magnetization is saturated. All the results ascertain Onsager’s reciprocal relations.

Cu thickness dependence

To reveal both the lateral and vertical distributions of the OAM in the Al₂O₃/CuO_x/Cu nanowire system (Fig. 3a), we investigated the Cu thickness (t_Cu) dependence of the nonlocal signals, as summarized in Fig. 3b, c. Fitting 2ΔR_DOEE (Fig. 3b) and |2ΔR_IOEE| (Fig. 3c) to Eq. (1), we observed that increasing t_Cu causes only a slight change in λ_o (Fig. 3d) but a significant reduction in A (Fig. 3e). Considering that the thickness (t_CuO) of the oxidized Cu regions (CuO_x) remains the same in all the samples due to the identical atmospheric exposure times, almost no dependence of λ_o on the Cu thickness suggests that oxidized Cu supports the lateral nonlocal orbital response. Conversely, the thickness of unoxidized Cu depends on t_Cu. We thus assumed A contains the information on the vertical orbital distribution as $A={A}_{{{{\rm{Cu}}}}}^{{\prime} }\exp \left(-{t}_{{{{\rm{Cu}}}}}/{\lambda }_{{{{\rm{o}}}}}^{z}\right)$ where ${A}_{{{{\rm{Cu}}}}}^{{\prime} }$ is a thickness-independent fitting parameter, and ${\lambda }_{{{{\rm{o}}}}}^{z}$ is the vertical decay length of OAM. The fitting (Fig. 3e) yields ${\lambda }_{{{{\rm{o}}}}}^{z}\approx 25\,{{{\rm{nm}}}}$. The Cu thickness dependence in the local configuration shows consistent results (Supplementary Section 8).

Fig. 3: Cu thickness dependence experiments.

a Schematic illustration of lateral and vertical OAM distribution and the role of oxidized and unoxidized Cu. The top Cu layer is oxidized and homogenous (CuO_x region), assisting the long-range orbital response; the bottom Cu layer remains unoxidized (Cu region), exhibiting a short vertical decay length of orbital accumulation. In a nonlocal configuration, orbital accumulation distributes laterally and vertically. b, c Cu thickness dependence results of 2ΔR_DOEE (b) and 2ΔR_IOEE (c). The results are measured at room temperature with FM = Co₂₅Fe₇₅. The solid curves represent the fitting of the data to Eq. (1). The error bars in b, c indicate the standard deviation of R after the magnetization is saturated. d λ_o at various Cu thicknesses estimated from fitting, whose values are almost constant. The dotted line marks the value of λ_o = 100 nm. e Fitting result of parameter A. The solid curves show the exponential fitting for A. The vertical decay length of orbital accumulation (${\lambda }_{{{{\rm{o}}}}}^{z}$ ~ 25 nm) is much smaller than the lateral one (λ_o ~ 100 nm), suggesting a distinction between lateral and vertical distribution of OAM. Error bars in d, e represent 95% confidence intervals from fitting results. All the results agree with Onsager’s reciprocal relations.

The distinction between λ_o and ${\lambda }_{{{{\rm{o}}}}}^{z}$ suggests different physical mechanisms governing the lateral and vertical OAM distribution in the oxide/Cu systems^21,22. Previous studies on the vertical distribution of OAM^21,22,24 have highlighted the crucial role of oxidation. In oxidized Cu, the 3 d electron shell is not fully occupied; orbital states allow electrons to host OAM. Such OAM can barely penetrate the unoxidized Cu region where the 3 d electron shell is nearly fully occupied⁵⁰, leading to a short decay length. Meanwhile, the continuously oxidized Cu region with a specific thickness t_CuO provides a uniform electronic band structure across the x-y plane, supporting orbital accumulation associated with the large λ_o.

Temperature dependence

We next performed temperature-dependent experiments to gain deeper insight into the nonlocal orbital response. Fig. 4a shows R_DOEE at 300 K (black squares) and 50 K (green circles) in sample A. The R_DOEE signal is sizable at 300 K but vanishes at 50 K, demonstrating that the nonlocal orbital response diminishes at low temperatures. To disentangle the local and nonlocal contributions during the temperature evolution, we also performed temperature-dependent measurements in the local configuration⁴⁵, where the orbital response is probed by FM nanowires located below the orbital generation region, as shown in Fig. 4b. At 300 K (black squares), the local ${R}_{{{{\rm{DO}}}}{{{\rm{EE}}}}}^{(0)}$ signal is also larger than that at 50 K (green circles), although half of the signal remains at 50 K. These behaviors are in sharp contrast with the spin transport in a nonlocal spin valve (NLSV) structure^31,32,33,34, characterized by R_NLSV (Fig. 4c), where the signal at 50 K is larger (green circles) than that at 300 K (black squares).

Fig. 4: Temperature dependence experiments.

a–c Typical signals for R_DOEE (a), ${R}_{{{{\rm{DOEE}}}}}^{(0)}$ (b), and R_NLSV (c) at 300 K (black squares) and 50 K (green circles). R_DOEE and ${R}_{{{{\rm{DOEE}}}}}^{(0)}$ signals decrease with lower temperatures, while R_NLSV signals increase as the temperature decreases. The double-headed arrows in b, c indicate the definition of $2\Delta {R}_{{{{\rm{DOEE}}}}}^{(0)}$ and 2ΔR_NLSV. The insets in a–c represent the measurement configuration, respectively. a–c t_Cu = 40 nm and FM = Co₂₅Fe₇₅. d Temperature dependence results of $2{\Delta R}_{{{{\rm{DOEE}}}}}^{(0)}$ (open diamond markers with green color, left y axis) and 2ΔR_DOEE (circle and triangle markers filled with other colors, right y axis). The error bars indicate the standard deviation of R in the plateau. The results are measured in samples with t_Cu = 40 nm and FM = Co₂₅Fe₇₅. All the $2{\Delta R}_{{{{\rm{DOEE}}}}}^{(0)}$ and 2ΔR_DOEE decrease with lowering temperature. e Summarized temperature dependence results of 2ΔR_NLSV with Co₂₅Fe₇₅ (open blue squares) and Ni₈₁Fe₁₉ (open red circles). The error bars indicate the standard deviation of R_NLSV in the plateau. 2ΔR_NLSV increases with lowering temperature. The spacing distance between two FM nanowires is d_NLSV = 400 nm for both Ni₈₁Fe₁₉ and Co₂₅Fe₇₅ samples (Methods). The opposite temperature dependence on the behaviors of DOEE (d) and NLSV (e) implies distinct physics between orbital accumulation and spin accumulation.

Fig. 4d summarizes the temperature dependence of the local $2{\Delta R}_{{{{\rm{DO}}}}{{{\rm{EE}}}}}^{(0)}$ (green circles) and the nonlocal 2ΔR_DOEE at different distances d (other different colors). The corresponding raw data are presented in Supplementary Section 9 (Figs. S12 and S13). The signal decreases at low temperatures in both local and nonlocal measurements. At 50 K, while the nonlocal signals drop to nearly zero, the local signals still retain a finite value, indicating that the local signal decreases more slowly than the nonlocal signal. The same temperature dependence is observed in the inverse measurement (Fig. S14), and no signal is observed at any temperature in the nonlocal orbital device with FM = Ni₈₁Fe₁₉ (Fig. S15). Meanwhile, the nonlocal spin signal 2ΔR_NLSV increases with decreasing temperature (Fig.4e) and is present in both devices with FM = Co₂₅Fe₇₅ and Ni₈₁Fe₁₉, clearly indicating the different physics involved in the observed nonlocal orbital and spin signals (also see Supplementary Section 10).

To isolate the contribution of the nonlocal process in the temperature dependence of 2ΔR_DOEE, we assume that the local process parameter A for the nonlocal signal 2ΔR_DOEE in Eq. (1) has the same temperature dependence as the local signal $2{\Delta R}_{{{{\rm{DO}}}}{{{\rm{EE}}}}}^{(0)}$. This leads to the relationship $A(T)/A(300{{{\rm{K}}}})\,={\Delta R}_{{{{\rm{DO}}}}{{{\rm{EE}}}}}^{\left(0\right)}(T)/{\Delta R}_{{{{\rm{DO}}}}{{{\rm{EE}}}}}^{\left(0\right)}(300\,{{{\rm{K}}}})$, allowing us to calculate the A(T) values at different temperatures using $A(300{{{\rm{K}}}})$ (Fig. 1e, f) and the temperature dependence of the local signal. We then fitted the distance d dependence of 2ΔR_DOEE (Fig. 5a) and |2ΔR_IOEE| (Fig. S16) at each temperature using Eq. (1) and A(T) given above so that λ_o becomes the only fitting parameter as summarized in Fig. 5b. Interestingly, λ_o decreases as temperature drops, which contrasts with the typical behavior of spin transport in metals, where diffusion length is longer at lower temperatures³². The temperature-dependent λ_o also contrasts with the bypass effect, which remains unchanged at different temperatures^47,48 (Supplementary Section 11). This suggests that different physical mechanisms mediate the nonlocality of OAM. Calculations have shown that the orbital diffusion length in centrosymmetric systems is often below 10 nm⁵¹. Therefore, the nonlocality may not be linked to a diffusive orbital current. Still, rather due to the eigenstates in the Rashba band, which host OAM by themselves, the Rashba effect locks the nonequilibrium OAM locally to the diffusive linear momentum^52,53 of the electrons. We propose a possible picture for the temperature dependence as shown in Fig. 5c. At low temperatures, the limited hopping between the localized states in the oxidized Cu cannot support orbital Rashba bands. The itinerant electrons have wavefunctions constrained within the unoxidized Cu layer without carrying OAM. The OAM propagation is more likely to occur in the high-temperature region, where free carriers can be excited due to the thermal broadening of localized states, and a conductive channel is formed at the oxidized Cu layer (Supplementary Section 12). As a result, the itinerant electrons have wavefunctions extending into the oxidized Cu layer, creating hybridized states with OAM. Thus, continuous orbital Rashba bands are formed on the whole Al₂O₃/CuO_x/Cu nanowire, and long-range orbital propagation is allowed.

Fig. 5: Analysis on temperature-dependent orbital transport.

a Fitting of the temperature-dependent 2ΔR_DOEE data with Eq. (1). Here, t_Cu = 40 nm and FM = Co₂₅Fe₇₅. The solid curves represent the fitting results. The error bars indicate the standard deviation of R after the magnetization is saturated. b Fitting result of λ_o for 2ΔR_DOEE (blue squares) and 2ΔR_IOEE (red squares) as functions of temperature. The error bars indicate the 95% confidence intervals from fitting results. All the results obey Onsager’s reciprocal relations. c Schematic of the proposed mechanism for the temperature-dependent orbital propagation. At low temperatures (upper panel), hopping between the localized states in the oxidized Cu (CuO_x layer) is limited, so the itinerant electrons (green arrow) are confined to the unoxidized Cu layer without carrying OAM (L = 0). Thus, continuous orbital Rashba bands are not forming. At high temperature (lower panel), the localized states are thermally broadened, establishing the conductive channel in the CuO_x layer. The electron wavefunctions are extended into the CuO_x layer, creating hybridized states with OAM (L ≠ 0), which form the continuous orbital Rashba bands and allow the long-range orbital propagation.

In summary, our study investigates the lateral distribution of nonequilibrium OAM and the reversible OEE by utilizing nonlocal response in an orbital Edelstein system composed of Al₂O₃, Cu, and ferromagnetic materials. The nonlocal response is observed ~100 nm away from the injected electric current at room temperature, with its orbital nature confirmed by FM dependence and the polarization direction verified through angular dependence. The decay length λ_o of orbital accumulation is unaffected by Cu thickness, suggesting that the oxidized Cu region assists the long-range nonlocal orbital response. In contrast to the spin diffusion length, λ_o decreases with decreasing temperature, indicating that mechanisms other than diffusive orbital current mediate OAM transport. Importantly, in all the experiments, the orbital and charge accumulation induced by DOEE and IOEE are observed in the same devices and are mathematically equivalent, consistent with Onsager’s reciprocal relations. Our work provides clear insights into the intrinsic reciprocal relationship of orbital effects. It reveals a long-range lateral correlation of OAM accumulation, paving the way for inter-connectable orbitronics devices capable of operating over long distances.

Methods

Sample fabrication

All devices were microfabricated on SiO₂/Si substrates using electron-beam lithography with polymethyl-methacrylate resist, followed by development, deposition, and lift-off processes. The FM nanowires were electron-beam evaporated on SiO₂/Si substrates. The Cu nanowires were deposited across the FM nanowires using a Joule heating evaporator. Before Cu deposition, the FM surface was carefully Ar-ion milled to obtain a transparent interface between the FM and Cu. The samples were exposed to the atmosphere at room temperature for 10 minutes prior to Al₂O₃ deposition to achieve a naturally oxidized Cu layer. The Al₂O₃ capping layers to prevent Cu from further oxidation were only deposited on the Cu nanowires by electron-beam deposition. All fabrication processes were performed at room temperature, with a base pressure of deposition lower than 5.0 × 10^–8 Torr and a pressure during deposition lower than 1.0 × 10^–7 Torr.

Unless otherwise specified, all the samples are fabricated in an identical and carefully designed geometry. In all the samples, the FM nanowires were composed of Co₂₅Fe₇₅, Co₅₀Fe₅₀, or Ni₈₁Fe₁₉, with a thickness of 20 nm (t_FM) and a width of 100 nm (w_FM). All Cu nanowires are 40 nm thick (t_Cu), with additional values of 30 nm and 50 nm used in the Cu thickness dependence experiment. The thickness of the Al₂O₃ capping layer is 15 nm for all the samples.

In nonlocal orbital transport devices (shown in Figs. 1a, b, and 4a), the cross-shaped Cu nanowires were fabricated where the Cu nanowires lying on the y axis (Cu_y, parallel to FM nanowire) are 100 nm wide. The one lying on the x axis (Cu_x, perpendicular to FM nanowire) is 150 nm wide. The center-to-center separation distance, d, between Cu_y and FM, varies from 140 to 350 nm.

In local orbital transport devices (Fig. 4b), the FM nanowires are aligned collinearly with a 50 nm spacing gap. The 200 nm wide straight Cu nanowires are deposited perpendicular to the FM pair to bridge the gap.

In nonlocal spin valve devices (Fig. 4c), two parallel FM nanowires are separated by a fixed center-to-center spacing d_NLSV = 400 nm (for both Ni₈₁Fe₁₉ and Co₂₅Fe₇₅ samples). The Cu nanowires bridging the FM pairs are 150 nm in width.

Electrical measurements

All the electric transport measurements were carried out in a He flow cryostat using the lock-in measurement technique. Electrical contacts to devices were made with wire bonding with Al wires. The applied alternating currents were calibrated to 500 μA for all measurements. An in-plane external magnetic field, B_ext, was applied during all measurements. In nonlocal orbital transport measurements, B_ext was aligned along the hard axis of the FM nanowire. In angle-dependent measurements, the B_ext was rotated from the x axis by the angle Φ (0°~180°). In nonlocal spin valve and local orbital transport measurements, B_ext was applied along the easy axis of the FM nanowires.