Chirality-transferred epitaxy of circular polarization-sensitive ReS₂ monolayer single crystals

Abstract

The epitaxial growth of semiconducting two-dimensional (2D) materials is vital to achieve wafer-scale single-crystalline films for beyond-silicon electronics. However, gaining full control over both in-plane and out-of-plane orientations (i.e., lateral crystal alignments and chirality) is particularly challenging when growing low-symmetry 2D single crystals. Here, using triclinic ReS₂ semiconductor monolayers as a model system, we demonstrate the chirality-controlled epitaxial growth of unidirectional, anisotropic single crystals on an insulating chiral surface via the synergy of terraces, steps, and kinks, yielding >97.5% chirality selectivity and >99% in-plane orientation consistency. The products display an anisotropic ratio of 1.9 in photodetection (comparable to exfoliated samples) and high distinguishability of circularly polarized light. Theoretical calculations combined with a set of microscopy and spectroscopy methods show that terrace facets determine the epitaxial growth direction, while steps and kinks break the degeneracy of ReS₂ in the lateral orientation and chirality. This approach is also applicable to the chiral epitaxy of other low-symmetry 2D single crystals, like monoclinic MoO₂. Our method extends the range of control over 2D material growth, enabling chirality transfer from the substrate to the crystal, and promotes the large-area synthesis of chirality-selected, single-crystal 2D materials.

Introduction

The epitaxial growth of two-dimensional (2D) materials is a promising route to wafer-scale, single-crystalline, atomically thin films, showing great potential in integrated electronic and optoelectronic devices beyond silicon^1,2,3,4. Substrate engineering plays a crucial role in realizing this goal. For monolayer growth, methods like introducing step edges^5,6,7,8,9, defects^10,11, and interfacial reconstructed layers^12,13, as well as selecting appropriate substrate surface symmetry^14,15,16, have been utilized to prepare graphene, hexagonal boron nitride, 2H-MoSe₂, and 2H-WSe₂. For multilayers, techniques like bevel-edge epitaxy¹⁷, interfacial epitaxy¹⁸, and remote epitaxy¹⁹ have been applied to control interfacial stacking order and thickness for rhombohedral boron nitride, 2H-MoS₂, and 2H-WS₂. However, most of these 2D materials are high-symmetry crystals (e.g., graphene: C_6v; h-BN: C_3v, 2H-MoS₂, −MoS₂, −WS₂, and −WSe₂: D_3h), while low-symmetry ones such as triclinic ReX₂ (X = S, Se) and monoclinic 1T′-MTe₂ (M = Mo, W) receive limited attention in epitaxial 2D fabrication studies. These low-symmetry 2D layers require more stringent control of the lattice orientation than the high-symmetry crystals even for monolayers due to the following reasons.

Firstly, low-symmetry crystal structures lead to abundant in-plane anisotropic properties, which can only be effectively manifested at the macroscopic scale when the 2D material adopts a single lateral lattice orientation across a wide range. The presence of different orientated domains results in grain boundaries (GBs) that degrade carrier mobility and spatially averages out the anisotropic properties of low-symmetry crystals, ultimately impacting mechanical, electronic, and optical applications. Efforts have been devoted to the in-plane orientation-controlled epitaxial growth via substrate engineering^{20,21,22,23,24}. Take ReS₂ $\left({{{\rm{P}}}}\bar{1}\right)$ as an example, which is a typical low-symmetry semiconducting 2D material possessing only an inversion center as the symmetric element, monolayer single-crystalline ReS₂ domains with unidirectionally aligned b-axis (orientation of Re4 chains) were grown on Au(101) due to strong interfacial coupling and low-symmetry of the substrate surface (C_2v)²³. More recently, continuous 2D ReS₂ films with a consistent b-axis orientation were achieved on Au(111) by introducing step edges along $\left[01\bar{1}\right]$ to decrease the surface symmetry to C_s (having a mirror plane)²⁴. However, these approaches suffer from high substrate cost (noble metal), limited crystal quality, non-uniform thickness, and, more importantly, the inability to control the out-of-plane lattice orientation of monolayers, which will result in the achievement of racemic mixture rather than a single structure (discussed in the next paragraph).

The necessity to control orientations of low-symmetry 2D crystals comes from an even more important reason, i.e., monolayers with opposite vertical lattice directions have different chirality in two dimensions when they are confined to a plane, meaning that they cannot be interconverted by any rotation about the axis perpendicular to the substrate. This is illustrated by monolayer ReS₂ in Fig. 1a. R-ReS₂ and S-ReS₂ are enantiomers, despite having the same in-plane b-axis orientation (Re4 chain direction marked in red), and they display exotic physical properties like chiral Raman scattering^25,26. In other words, when monolayer ReS₂, which is achiral in three dimensions, binds to a substrate, its original inversion center disappears, thus generating a chiral ReS₂/substrate interface in space. This phenomenon introduces an additional degree of freedom for structural control of low-symmetry 2D crystals, expanding the possibility for performance tuning but also increasing the difficulty of material fabrication. Currently, the construction of chiral 2D structures predominantly focuses on twisted-stacked 2D crystals via sequential mechanical transfer and screw dislocation-triggered growth^27,28,29,30, layered 2D crystals intercalated by chiral molecules³¹, and chiral perovskites via direct synthesis^32,33, among which diversified chirality-dependent exotic properties like spin selectivity, magnetic phases, and photoelectric responses were discovered^33,34,35. Yet chirality-selected growth of low-symmetry monolayer single crystals by complete control over both in-plane and out-of-plane lattice orientations is blank and urgently needed.

Fig. 1: Terrace-step-kink strategy of substrate design.

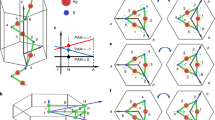
a Schematic illustrating chirality of monolayer ReS₂ on the substrate, where R and S refer to rectus and sinister in Latin, respectively, representing two types of enantiomers. The structural differences between R- and S-ReS₂ on the substrate surface are marked by red symbols. b–d Schematics showing the substrate surface reconstruction from MgO(11l) to terrace facets (001) with bunched steps along $\left[\bar{1}10\right]$ (b) and reconstruction from chiral surface R-(12l)/S-(21l) to terrace facets (001) with bunched steps along $\left[\bar{1}10\right]$ and kinks along $\left[\bar{1}00\right]$/[010] (c and d). e–g Scheme of the designed terrace-step-kink strategy, which gradually increases the structural selectivity of the as-grown ReS₂ on the MgO substrate by sequentially introducing specific terraces, steps, and kinks to the reconstructed substrate surfaces to reduce their structural symmetry, thus eliminating energy degeneracy of monolayer ReS₂ single crystals with different orientations and chirality. Blue and red blocks represent ReS₂ domains in different chirality. The gray lines represent microstructures on the reconstructed substrate surfaces with the zoomed-in inset highlighting steps and kinks. h Binding energies (E_b) calculated using density functional theory (DFT) for ReS₂ single-crystalline domains with different rotation angles (θ) on MgO(001), θ represents the angle between the b-axis ([010]) of ReS₂ and MgO$\left[\bar{1}10\right]$. i Formation energies (E_f) of three grain boundaries with different inter-grain twist angles (insets). j Binding energies (E_b) of monolayer single-crystalline ReS₂ domains oriented perpendicularly on reconstructed MgO(11l) composed of terrace(001) and step$\left[\bar{1}10\right]$. The red lines in the top panel of the insets represent step$\left[\bar{1}10\right]$ on the reconstructed MgO surface, while the blue rhombuses represent Re4 chains of monolayer ReS₂. k Binding energies (E_b) of R- and S-ReS₂ monolayer single crystals with the same b-axis orientation on the chiral reconstructed MgO(12l)^R surface. The red curves (top panels in the insets) represent the “step + kink” configuration on MgO.

Herein, we demonstrate the chemical vapor deposition (CVD) growth of chirality-selected unidirectionally aligned monolayer ReS₂ single crystals on a cost-effective and industry-compatible insulating substrate via a terrace-step-kink strategy. The acquisition of the target material is decomposed into three steps with correspondingly developed substrate engineering methods (Fig. 1e–g). Step 1: Realizing the single-crystallinity of each ReS₂ domain, fulfilled by choosing the substrate terrace facet with an appropriate rotation symmetry, which can prohibit ReS₂ from generating thermodynamically favorable GBs during the epitaxial growth (Fig. 1e). Step 2: Realizing the in-plane unidirectional alignment of every single-crystalline domain, reached by introducing specific steps on the terrace (Fig. 1f), thus breaking the binding energy degeneracy of differently oriented ReS₂ domains. Step 3: Realizing the chirality selectivity of unidirectionally aligned single crystals. A chiral substrate surface was constructed by further introducing selected kinks to the “terrace + step” microstructures (Fig. 1g) so that a chirality transfer mechanism functions, which enables breaking both interfacial configuration and energy degeneracy of monolayer single-crystalline ReS₂ enantiomers (definitions of steps and kinks are included in Supplementary Fig. 1).

Results

Terrace-step-kink strategy of substrate design

Considering crystal structure, physical properties, and material costs, MgO, a binary cubic system with high chemical and thermal stability, was selected as the substrate. Its insulating characteristic also facilitates better compatibility of the 2D semiconducting materials grown on it with the current integrated circuit technology. Firstly, we performed DFT calculations to verify the theoretical feasibility of the above substrate design strategy. The key to achieving single-crystalline ReS₂ domains (Step 1) is to prevent Re4 chains from deflecting during growth and forming GBs. Previous literature has demonstrated that, distinct from 2D materials like MoS₂ and WS₂ which can spontaneously grow into triangular/hexagonal single crystals under most conditions, Re4 chains in ReS₂ are prone to deflect integer multiples of ∼ 60° during domain growth, thereby generating a series of highly coherent GBs with low formation energies and leading to polycrystalline products^36,37,38. Therefore, we chose MgO(001) with C_4v as the substrate terrace facet rather than α-Al₂O₃(0001) (C_3v) and mica(0001) (C_6v) in order to prohibit ReS₂ from generating thermodynamically advantageous GBs when epitaxially grown on the single-crystalline substrate. Theoretical calculations exhibit that monolayer ReS₂ single crystals have two optimal epitaxial growth orientations orthogonal to each other on MgO(001), whose intersectional angles (θ) between the b-axis of ReS₂ and MgO$\left[\bar{1}10\right]$ is 0° and 90°, respectively. The suboptimal epitaxial orientation is θ = 45° (Fig. 1h and Supplementary Fig. 2). On the premise of ensuring a superior epitaxial growth orientation on the substrate, monolayer ReS₂ can only construct GBs with inter-grain angles of 45° and 90°, whose calculated formation energies are significantly larger than those highly coherent GBs commonly observed in previous work³⁸ (e.g., the GB with an inter-grain angle of 120°, Fig. 1i). It indicates thermodynamic prohibition to form GBs for epitaxially grown ReS₂ single layers on MgO(001) with C_4v symmetry.

To achieve unidirectional alignment of single-crystalline domains (Step 2), we introduced steps along the crystallographic orientation of $\left[\bar{1}10\right]$ (named step$\left[\bar{1}10\right]$) on the terrace(001) of MgO. Such surface microstructures, in principle, can be obtained by spontaneous reconstruction of the vicinal MgO(001), referred to as MgO(11l) ($l$≫$1$), after annealing (Fig. 1b). It is noteworthy that the step orientation was deliberately designed to be parallel with and perpendicular to the b-axis orientations of two orthogonally oriented ReS₂ single crystals epitaxially grown on the terrace(001). This design can maximize the interfacial structural disparity of two oriented ReS₂ single crystals on the substrate and break energy degeneracy remarkably. DFT calculations show a prominently lower interfacial binding energy when the b-axis direction of ReS₂ is parallel with step$\left[\bar{1}10\right]$ on MgO than when they are perpendicular (Fig. 1j), implying that introducing step$\left[\bar{1}10\right]$ can thermodynamically drive uniform orientation of monolayer ReS₂ single crystals. It is worth noting that since the reconstructed MgO(11l) still has mirror symmetry (C_s), the structures of ReS₂ enantiomers on the substrate surface mirror each other (Supplementary Fig. 3), displaying the same manner of interfacial atomic alignment and thus degenerated binding energies. Therefore, chirality selectivity is incapable of being realized solely by the “terrace(001) + step$\left[\bar{1}10\right]$” substrate design.

Finally, we introduced kinks along lattice directions of $\left[\bar{1}00\right]$ and [010] (named kink$\left[\bar{1}00\right]$ and kink[010]) on the MgO surface involving terrace(001) and step$\left[\bar{1}10\right]$. Such design eliminates the mirror symmetry of the substrate, thus constructing chiral surfaces which may realize chirality-selective growth (Step 3, Fig. 1c, d and Supplementary Fig. 4). The chiral surfaces can commonly be obtained by thermal treatment of MgO(12l) and MgO(21l) ($l$≫$2$) because unstable high-index facets are inclined to reconstruct to thermodynamically favorable low-index counterparts. By definition, (12l) and (21l) can be assigned to rectus (R) and sinister (S) configurations, which are termed (12l)^R and (12l)^S ($l\gg 2$), respectively (Supplementary Fig. 5). It is noteworthy that the construction of chiral surfaces only requires (hkl) to satisfy h ≠ k ≠ l and h × k × l ≠ 0 geometrically. Here, we designed chiral surfaces of (12l)^R and (12l)^S ($l\gg 2$) for the following reasons: (i) Selection of high-index planes with $l\gg 2$ ensures a sufficiently large area of each terrace layer and a low height of every step/kink after surface reconstruction, which facilitate monolayer nucleation and rapid domain expansion across steps/kinks. (ii) Reconstructed surfaces of (12l)^R and (12l)^S have a similar density of step$\left[\bar{1}10\right]$ to that of the reconstructed (11l) designed in Step 2. Moreover, the length of the newly introduced kink$\left[\bar{1}10\right]$/kink[010] is 1/√2 ≈ 70% of the step$\left[\bar{1}10\right]$ length. Such design allows the substrate to effectively control both the in-plane alignment and chirality of ReS₂ single crystals. DFT calculations display that the binding energy of R-ReS₂ on MgO(12l)^R is lower than that of S-ReS₂ on MgO(12l)^R (Fig. 1k), suggesting chirality transfer from the substrate surface to the as-grown monolayer products.

Growth of chirality-selected, unidirectional ReS₂ single crystals

Experimentally, the chiral substrate (e.g., (12l)^S) was achieved by custom-designing MgO(001) with a cutting angle of ～1° towards [210] (Supplementary Figs. 6 and 7). The surface was reconstructed into terraces(001) with a bunch of parallelly aligned steps along $\left[\bar{1}20\right]$ (Supplementary Fig. 8) after annealing in oxygen. These steps are, in principle, composed of step$\left[\bar{1}10\right]$ and kink[010] at the nanometer scale (Fig. 1d). Figure 2a shows spindle-shaped ReS₂ crystals with a length of 15–20 µm grown on MgO(12l)^S by hydrogen-free atmospheric-pressure CVD. They were unidirectionally aligned along MgO$\left[\bar{1}10\right]$ and can merge together with atomically stitched interfaces (Supplementary Fig. 9). The angle-dependent Raman intensities of the vibrational mode at 212 cm⁻¹ were measured in the parallel polarization configuration for different crystals and various locations in the same crystal of the as-grown ReS₂ (inset of Fig. 2a and Supplementary Fig. 10). They exhibited almost overlapped double-lobed patterns with the maximized intensity corresponding to an angle of 353° ± 4° (0° in the polar plot corresponded to the major axis direction of the spindle-like domain), indicating that the as-prepared products have consistent crystallographic orientation within and between crystals and the major axis direction of the spindle-shaped crystals corresponds to the b-axis orientation of ReS₂. The second harmonic generation (SHG) spectra and mapping further verified single-crystallinity without GBs of ReS₂ grown on MgO(12l)^S because no obvious signal was detected, which was in stark contrast to the strong SHG intensity observed in polycrystalline ReS₂ prepared on α-Al₂O₃(0001) (Supplementary Figs. 11 and 12). Annular dark-field scanning transmission electron microscopy (ADF-STEM) showed well-organized Re4 chains with neither detectable lattice deformation nor atom missing, demonstrating monolayer thickness of the 2D products with superior crystal quality at the atomic scale (Fig. 2b). Selected area electron diffraction (SAED) captured at different domains displayed only one set of quasi-hexagonal patterns aligning in the same orientation without high-order diffraction spots splitting (Fig. 2c), manifesting consistent lattice orientation of disparate domains (Supplementary Fig. 13).

Fig. 2: Growth and characterization of chirality-selected, unidirectional, single-crystalline monolayer ReS₂.

a Scanning electron microscopy (SEM) image of unidirectionally aligned spindle-like ReS₂ domains grown on MgO(12l)^S. The inset shows the angle-resolved Raman intensities of the vibrational mode of ReS₂ at 212 cm⁻¹ captured at three different locations in one domain. Scale bar: 20 µm. b Annular dark-field scanning transmission electron microscopy (ADF-STEM) image of monolayer ReS₂. The Re4 chains are represented by white rhombuses with crystallographic directions a [100] and b [010] labeled. Scale bar: 2 nm. c Selected area electron diffraction (SAED) patterns obtained at four different domains. The yellow hexagons mark the innermost diffraction spots, while the insets are the zoomed-in views of the red- and blue-boxed high-index diffraction spots. Scale bar: 2 nm⁻¹. d Circularly polarized Raman (CPR) spectra of as-grown ReS₂ in (a) (bottom) and the difference between the Raman intensities excited by right-handed (RCP) and left-handed (LCP) circularly polarized light (top). The wavelength of the polarized light is 532 nm. e Histogram showing the circular intensity difference (CID) distribution of Raman modes III (153 cm⁻¹), V (212 cm⁻¹), and VI (235 cm⁻¹) captured from ≈50 ReS₂ domains located at different regions on MgO(12l)^S. f Atomic force microscopy (AFM) image displaying a ReS₂ domain (left to the white dashed line) grown on bare MgO(12l)^S (right to the white dashed line). The reconstructed steps along MgO$\left[\bar{1}20\right]$ (which are composed of step$\left[\bar{1}10\right]$ and kink[010] at the atomic scale) are marked by the red arrow, while the b-axis of ReS₂ is labeled by the white arrow. Scale bar: 200 nm. g, Zoomed-in atomically resolved AFM image of the ReS₂ domain in (f). The Re rhombic lattice along the b-axis is marked by white lines. Scale bar: 2 nm. h Cross-sectional ADF-STEM image of the ReS₂/MgO interface viewed along MgO$\left[\bar{1}10\right]$. Scale bar: 1 nm. i Schematic illustrating the epitaxial relationship of monolayer ReS₂ on reconstructed MgO(12l)^S. The orange and white spheres represent the first and second layers of O atoms of the MgO surface, respectively.

We then applied CPR spectroscopy to determine the 2D chirality of ReS₂ on MgO(12l)^S. Remarkable differences in relative intensities were observed in CPR spectra of as-grown domains under RCP and LCP due to phase differences among multiple phonon-mediated electron scattering pathways²⁵ (Fig. 2d). The CID values, defined as (I_RCP–I_LCP) / (I_RCP + I_LCP), for vibrational mode III (151 cm⁻¹), V (212 cm⁻¹), and VI (235 cm⁻¹) were measured to be 0.124, 0.523, and −0.214, respectively, agreeing well with those for S-ReS₂. We characterized CPR spectra from 50 randomly selected ReS₂ domains grown at various positions on MgO(12l)^S. The statistical results demonstrated that the CID feature exhibited in Fig. 2d was universal, implying S chiral configuration enrichment of our sample (Fig. 2e).

Atomic force microscopy (AFM) and cross-sectional ADF-STEM were employed to unveil the epitaxial relationship between ReS₂ and MgO(12l)^S. The b-axis direction of monolayer ReS₂ was found to deflect ∼ 18.5° from parallelly aligned edges along $\left[\bar{1}20\right]$ on reconstructed MgO(12l)^S in the AFM image (Fig. 2f, g and Supplementary Fig. 14), proving again that the major axis (b-axis) of the spindle-shaped ReS₂ crystals is parallel to MgO$\left[\bar{1}10\right]$ rather than MgO$\left[\bar{1}20\right]$. The cross-sectional ADF-STEM image displayed the atomic arrangement of monolayer S-ReS₂ on MgO along MgO$\left[\bar{1}10\right]$ (Fig. 2h). The lattice spacing of ReS₂ in the lateral direction was measured as 5.60 Å, well matching with ${a}_{{{{{\rm{ReS}}}}}_{2}}\times \sin {\alpha }_{{{{{\rm{ReS}}}}}_{2}}=5.61\,{{{\text{\AA }}}}\,\left(\right.{a}_{{{{{\rm{ReS}}}}}_{2}}=6.58\,{{{\text{\AA}}}},{\alpha }_{{{{{\rm{ReS}}}}}_{2}}=121.5^\circ$ representing the angle between a-axis and b-axis of ReS₂), which corresponds to the lattice spacing of ReS₂ perpendicular to its b-axis direction. The lattice spacing of MgO was measured as 2.98 Å, consistent with ${\sqrt{2}a}_{{{{\rm{MgO}}}}}/2=2.98\,{{{\text{\AA }}}}\,({a}_{{{{\rm{MgO}}}}}=4.21\,{{{\text{\AA }}}})$. These results directly confirmed that the (001) lattice plane of ReS₂ is parallel to the (001) terrace facet of MgO and the b-axis of ReS₂ is parallel to the $\left[\bar{1}10\right]$ lattice direction of MgO, which can be expressed as [010]ReS₂₍₀₀₁₎// $\left[\bar{1}10\right]$MgO₍₀₀₁₎ (Fig. 2i). In addition, the atomic step on the reconstructed substrate showed a height of ∼2.14 Å corresponding to half the lattice constant of MgO (a_MgO/2 = 2.16 Å), and ReS₂ was observed to grow across steps (Supplementary Fig. 15). The distance between ReS₂ and the MgO step edge (2.75 Å) is close to the van der Waals gap between ReS₂ and the MgO terrace (3.10 Å), suggesting van der Waals coupling at the ReS₂/MgO step edge interface. These characteristics indicate that the terrace facets of MgO determine the epitaxial orientation of monolayer ReS₂, while the steps/kinks are used to break the energy degeneracy of ReS₂ with different lattice directions to achieve full structural control. The terrace-step-kink strategy can also be extended to the chirality-selective growth of other unidirectional low-symmetry 2D single crystals, such as monoclinic MoO₂ (Supplementary Fig. 16).

Structural selectivity improvement by substrate engineering

To achieve an in-depth comprehension of how terraces, steps, and kinks on MgO control the structure of monolayer ReS₂ and validate the theoretical calculations in Fig. 1, we compared the growth results of ReS₂ on MgO(001), MgO(11l), and chiral surfaces of MgO(12l)^R and MgO(12l)^S, respectively. On the flat MgO(001) without steps and kinks (Fig. 3a), the contrast under a polarized optical microscope and the angle-resolved Raman intensity mapping at 212 cm⁻¹ displayed homogeneous brightness in each crystal (inset of Fig. 3e and Supplementary Figs. 17 and 18), indicating the achievement of single-crystalline ReS₂ domains on MgO(001) with C_4v symmetry. However, two epitaxial growth orientations of ReS₂ crystals along [110] and $\left[\bar{1}10\right]$ of MgO, respectively, were observed, which were evidenced by the optical microscopy (OM) image and the sharp intensity disparity between two orthogonally oriented ReS₂ crystals in the angle-resolved Raman mapping (Fig. 3e). Moreover, twelve spots which can be assigned to two sets of quasi-hexagonal patterns perpendicular to each other were obtained when conducting low-energy electron diffraction (LEED) on the as-grown ReS₂ (Fig. 3f), further demonstrating the incapability of realizing unidirectional alignment of ReS₂ single crystals on MgO(001).

Fig. 3: Step-by-step structural selectivity improvement of as-grown ReS₂ by substrate engineering.

a–d AFM images showing bare MgO(001) (a), and monolayer ReS₂ grown on reconstructed MgO(11l) (b), MgO(12l)^R (c), and MgO(12l)^S (d), respectively. Regions to the left of the white dashed lines in (b–d) are monolayer ReS₂-covered MgO surfaces with steps along $\left[\bar{1}10\right],\left[\bar{2}10\right]$, and $\left[\bar{1}20\right]$ marked by white, blue, and red arrows, respectively. Areas to the right of the white lines are bare substrates. The atomic models corresponding to each surface are displayed below the AFM images. Large spheres in different shades of orange represent O atoms in different layers of the MgO substrate, while small gray spheres represent Mg atoms. Scale bars: 200 nm. Insets in (b–d) are the nanometer-scale AFM images showing the reconstructed steps and kinks on the corresponding substrates after annealing. The white and yellow dashed lines mark the steps and kinks, respectively. Scale bar: 30 nm. e Optical image showing ReS₂ domains grown on MgO(001) with two preferred orientations of 0° and 90°. Scale bar: 50 µm. The inset is an angle-resolved Raman intensity mapping of mode V for ReS₂ domains grown on MgO(001). Scale bar: 5 μm. f Low-energy electron diffraction (LEED) patterns of ReS₂ grown on MgO(001). g In-plane orientation histograms of ReS₂ domains grown on MgO(001) and MgO(11l), respectively. 100 domains were counted on each substrate. h Linearly polarized Raman spectra of R-ReS₂ and S-ReS₂ for a laser wavelength of 532 nm. Inset is an optical image showing that the b-axis of ReS₂ (black arrow) is rotated 120° with respect to the polarization direction of the incident laser (green arrow) during characterization. Scale bar: 5 μm. i, j Polarization dependence of the intensities of Raman modes III (red) and V (blue) at 151 cm⁻¹ and 212 cm⁻¹ for R-ReS₂ (i) and S-ReS₂ (j), respectively. The b-axis of ReS₂ is marked by the black arrow. k, l Statistical distributions of the normalized intensity of Raman mode III (I_III/I_V) for ReS₂ domains grown on MgO(12l)^R and MgO(12l)^S (insets), respectively. The measurement condition was the same as that in (h). Each substrate counted ≈ 200 domains.

We then cut MgO(001) towards [110] with an angle of ～1° to achieve MgO(11l). The substrate surface was reconstructed to straight, low-index atomic steps arranged parallel to $\left[\bar{1}10\right]$ after annealing (Fig. 3b). OM and angle-resolved polarization Raman spectroscopy showed that the introduction of step$\left[\bar{1}10\right]$ on MgO(001) led to unidirectional alignment of spindle-shaped ReS₂ single crystals with an orientation selectivity of >99% (red columns in Fig. 3g and Supplementary Fig. 19). In contrast, on MgO(001), the ratio of ReS₂ domains aligning along [110] and $\left[\bar{1}10\right]$ was 49:51 (blue columns in Fig. 3g), demonstrating the decisive role of step $\left[\bar{1}10\right]$ in breaking the symmetry of the orthogonal orientations of ReS₂ single crystals. Next, we applied a method to rapidly identify the chiral configuration of the 2D products by comparing the Raman peak intensity between the chirality-sensitive mode III (151 cm⁻¹) and chirality-insensitive mode V (212 cm⁻¹), which was measured by setting an angle (φ = 120°) between the linear polarization direction of the incident laser and the b-axis of ReS₂ (Fig. 3h, details discussed in the next paragraph and Supplementary Fig. 20). The statistics captured from 100 showed that the quantity ratio of S- and R-ReS₂ was 43:57 (Supplementary Fig. 21), implying that solely introducing step$\left[\bar{1}10\right]$ on terrace(001) cannot reach chirality selectivity of monolayer ReS₂.

Finally, the chiral surfaces of MgO(12l)^R and MgO(12l)^S were applied to prepare monolayer ReS₂. Well-organized step edges along $\left[\bar{2}10\right]$ and $\left[\bar{1}20\right]$ were displayed on the reconstructed chiral surfaces after annealing (top panels in Fig. 3c, d), which exhibited jagged edges composed of low-index step$\left[\bar{1}10\right]$ and kink$\left[\bar{1}00\right]$ /kink[010] at the nanometer scale (bottom panels in Fig. 3c, d). Since Fig. 2 has included comprehensive characterization of the single-crystallinity, orientation consistency, and epitaxial relationship of monolayer ReS₂ on MgO(12l)^S and utilized CID to demonstrate the single chirality of the 2D products qualitatively, here we focused on the quantitative analysis of the chirality selectivity of monolayer ReS₂ crystals grown on R and S chiral MgO surfaces from the statistics perspective. The prerequisite to realizing this goal is to find a fast, accurate, and non-destructive approach for chiral structure identification. It is worth noting that the CPR method used in Fig. 2d has several limitations, including the requirement of frequent optical path switching (each test point needs to switch the optical path once in order to achieve RCP and LCP light), low characterization efficiency, and difficulty in maintaining the test position precisely unchanged before and after optical path switching. Therefore, the CPR method is not suitable for statistical chirality characterization of a quantity of 2D crystals. We utilized the approach mentioned in Fig. 3h and used the peak intensity ratio between Raman mode III and V (I_III/I_V), denoted as the normalized intensity of mode III, to determine the 2D chiral configuration of ReS₂ on MgO. This strategy needs no optical path switching and can identify the chirality of each test point by only one spectrum. Figure 3i, j showed the angle-resolved Raman intensities of mode III and mode V under parallel configuration corresponding to one R-ReS₂ domain and one S-ReS₂ domain grown on MgO(12l)^R and MgO(12l)^S, respectively. It displayed that the double-lobed pattern of mode V (blue) did not change with the variation of the product chirality, manifesting that Raman mode V of ReS₂ is insensitive to the product’s chirality. On the contrary, the patterns of mode III (red) corresponding to R- and S-ReS₂ were mirror symmetric, indicating that the intensity of mode III had a significant dependence on the product’s chirality. We measured I_III/I_V under φ = 120° to determine ReS₂ chirality, which is due to the following reasons: (i) Selecting the normalized rather than the absolute intensity of Raman mode III as chirality criterion can avoid the influence of experimental variables unrelated to ReS₂ chiral configurations, such as tiny fluctuation of incident laser power and subtle variation of laser focusing degree on different samples. (ii) When φ = 120°, the I_III/I_V corresponding to S- and R-ReS₂ reach the maximum and secondary maximum values in their polar plots, respectively (Supplementary Fig. 22), implying that the change rates of I_III/I_V with φ are minimum at these two points. Therefore, selecting φ = 120° helps improve the robustness of the measured I_III/I_V even when the true φ values in the experiments slightly deviated from 120°. The normalized mode III intensities of R- and S-ReS₂ were measured to be 2.2 ± 0.6 and 6.3 ± 1.8, respectively. Polarization-resolved Raman mapping further shows homogeneous I_III/I_V distributions within and across crystals, confirming single-crystallinity and uniform chirality (Supplementary Fig. 23). Statistics of I_III/I_V corresponding to ∼200 ReS₂ crystals grown on MgO(12l)^R and MgO(12l)^S, showed that R-ReS₂ accounted for 97.5% of the total domains on MgO(12l)^R (Fig. 3k), and S-ReS₂ accounted for 98.7% on MgO(12l)^S (Fig. 3l). Apart from the control of chirality, the nucleation density of monolayer ReS₂ single crystals can also be modulated by adjusting the density of step edges and kinks on the chiral MgO substrate (Supplementary Figs. 24–26).

Device performance of chiral ReS₂ single crystals

We transferred the as-grown ReS₂ on a SiO₂/Si substrate to fabricate a back-gated field effect transistor (FET) with Cr/Au utilized as the contact electrode to achieve matched work function at the interface (Supplementary Fig. 27). The I_ds-V_ds curve displays linear characteristics, indicating a low-resistance ohmic contact between ReS₂ and the electrode (Supplementary Fig. 28). The transfer curve in Fig. 4a manifests a typical n-type semiconducting behavior. We calculated the carrier mobility ($\mu=\frac{d{I}_{{{{\rm{ds}}}}}}{d{V}_{{{{\rm{g}}}}}}\cdot \frac{L}{W}\cdot \frac{1}{{C}_{{{{\rm{i}}}}}\cdot {V}_{{{{\rm{d}}}}{{{\rm{s}}}}}}$, where L and W represent the length and width of the FET device, and C_i = 12.1 nF cm⁻² is the measured capacitance per unit area for 285 nm SiO₂ layer), yielding μ = 3.35 cm²V⁻¹ s⁻¹ for the single-crystalline ReS₂ grown on MgO(12l)^R at room temperature, which is among the highest reported for CVD-grown ReS₂ and is 30 times higher than that of polycrystalline ReS₂ prepared on α-Al₂O₃(0001) (0.11 cm²V⁻¹ s⁻¹). The transconductance (${g}_{m}=\frac{{{dI}}_{{ds}}}{{{{\rm{d}}}}{V}_{g}}$) extracted from the linearly region of the transfer curve is 0.35 μA/V, comparable to those of mechanically exfoliated ReS₂^39,40.

Fig. 4: Electrical and photoelectric properties of chiral monolayer ReS₂ single crystals.

a I_ds-V_g curves of single-crystalline and polycrystalline monolayer ReS₂-based field effect transistor (FET) devices. Here, I_ds denotes the drain-source current, and V_g is the gate voltage. The channel length/width ratios (L/W) are 2.57 and 2.49 for the single- and poly-crystalline devices, respectively. Inset is the linear polarization-dependent photocurrent of the single-crystalline device under 532 nm laser illumination. b Carrier mobility vs. anisotropic ratio in photodetection of various 2D low-symmetry materials to compare our ReS₂ device performance with the other state-of-the-art devices (Supplementary Table 1). c Statistical distributions of full width at half maximum (FWHM) and intensities corresponding to Raman mode I and V for ReS₂ single crystals grown on chiral MgO and polycrystals grown on α-Al₂O₃. Each substrate counted 30 domains. d CPR spectra for R- and S-ReS₂ transferred onto the MgO(001), α-Al₂O₃(0001), and SiO₂/Si substrate, respectively. e CID values for R- and S-ReS₂ on MgO(001), α-Al₂O₃(0001), and SiO₂/Si. Each substrate counted 20 domains. Error bars are standard deviations. f, g I_ds-V_ds curves of R- and S-ReS₂-based photodetectors under 532 nm circularly polarized light (CPL) illumination. Error bars represent the standard deviation from several measurements. h Comparison of the asymmetrical factor for photocurrent between our monolayer chiral single-crystalline ReS₂-based photodetector for CPL detection and the other state-of-the-art low-symmetry 2D material-based devices (Supplementary Table 2).

Monolayer ReS₂ can produce anisotropic photoresponse in the visible band due to its low lattice symmetry and direct bandgap of 1.43 eV⁴¹ (Supplementary Fig. 29). Under 532 nm laser illumination, the responsivity of the single-crystalline ReS₂ device ($R=\frac{{I}_{{{{\rm{ph}}}}}}{P},{{{\mbox{where }}}}\,{I}_{{{{\rm{ph}}}}}$ is the photocurrent and P is the light power) was 113.76 A W⁻¹ at zero gate voltage (V_g = 0) and a low bias voltage (V_ds = 0.1 V), whose performance is in the first echelon among the CVD-prepared 2D anisotropic materials under similar measurement conditions. More importantly, the photocurrent of the ReS₂ device showed prominent dependence on the linear polarization direction of the incident light under the bias voltage ranging from 0 to 2 V (Supplementary Fig. 30), yielding a superior anisotropic ratio of 1.9 when V_ds = 1.7 V (inset of Fig. 4a). The photocurrent reached maximum when the laser polarization direction was parallel to the b-axis of ReS₂. Both the optical anisotropic ratio and the carrier mobility of our single-crystalline ReS₂-fabricated device are among the highest values reported for CVD-grown ReS₂ to date and are comparable to those of many mechanically exfoliated anisotropic 2D materials with larger thickness (Fig. 4b).

We further verified the crystal quality by the in-plane (mode I at 131 cm⁻¹) and out-of-plane (mode V at 212 cm⁻¹) Raman vibrational modes to unclose the excellence reason of our sample in some electrical and photoelectric performances. Statistics show that single-crystalline ReS₂ grown on MgO(12l)^R exhibits remarkably narrower distributions of full width at half maximum (FWHM) and more uniform Raman peak intensities for both mode I and V compared with the polycrystalline counterparts prepared on α-Al₂O₃(0001) (Fig. 4c). The FWHM and peak intensity variances of the single-crystalline samples are only ～30% and ～20% of those of the polycrystalline specimens (Supplementary Fig. 31), indicating high and homogeneous crystal quality.

Next, we investigated the 2D chiral structure-related physical properties and device performances of as-grown ReS₂. We transferred monolayer R-and S-ReS₂ grown on MgO(12l)^R and MgO(12l)^S to three achiral substrate surfaces with different chemical compositions and structures, which are MgO(001), α-Al₂O₃(0001) and the amorphous SiO₂/Si. The ReS₂ enantiomers displayed obvious helicity-dependent Raman intensities on all three substrates, and the R- and S-ReS₂ showed opposite chiral Raman responses, indicating that the 2D chirality of monolayer ReS₂ is predominantly determined by its out-of-plane orientation and is independent of whether the substrate surface is chiral or not (Fig. 4d, e). These results validate a universal and robust strategy to construct 2D chiral interfaces on diversified substrates using atomically thin low-symmetry materials. The CID values of R-ReS₂ on the three substrates excited by LCP are higher than those by RCP for mode III (153 cm⁻¹) and V (212 cm⁻¹), while mode IV (162 cm⁻¹) and VI (235 cm⁻¹) display opposite chiral Raman responses. S-ReS₂ behaved the opposite. In addition, the CID values for the same Raman mode of ReS₂ on different substrates vary slightly, which may stem from different electron-photon and electron-phonon interactions in ReS₂ due to disparate charge transfer between ReS₂ and the substrate and the intrinsic optical property disparity of various substrates^25,42,43.

The CPL detection ability of our chiral monolayer ReS₂ was then studied by fabricating a photodetector directly on the MgO substrate in order to eliminate the negative impact on the device performance from the contamination introduced in the transfer procedure. The R-ReS₂ device displayed a larger photocurrent under 532 nm RCP illumination than under the LCP illumination, while the S-ReS₂ device behaved the opposite, demonstrating prominent CPL distinguishability (Fig. 4f, g). We quantified the distinguishability of CPL detection by an asymmetrical factor for photocurrent (${g}_{{{{\rm{Iph}}}}}=\frac{2({I}_{{{{\rm{LCP}}}}}-{I}_{{{{\rm{RCP}}}}})}{{I}_{{LCP}}+{I}_{{{{\rm{RCP}}}}}}$, where I_LCP and I_RCP are the photocurrent under LCP and RCL irradiation) and yielded ${g}_{{{{\rm{Iph}}}}}$ of −0.31 and 0.20 for R-ReS₂ and S-ReS₂, respectively, which are comparable to those chiral perovskites and metal oxides with larger thickness (Fig. 4h and Supplementary Table 2).

Discussion

We demonstrate a terrace-step-kink strategy for the direct growth of single-chirality, unidirectional, semiconducting, anisotropic monolayer ReS₂ single crystals on the custom-designed chiral surface of insulating MgO, yielding >99% in-plane orientation consistency and >97.5% chirality selectivity. Our combined experimental and theoretical results show that terrace facets determine the epitaxial direction of ReS₂ while steps and kinks break the configuration and energy degeneracy of ReS₂ in the lateral orientation and chirality. The as-grown products can be facilely transferred to various substrates and robustly construct chiral interfaces. The high quality of monolayer ReS₂ is further evidenced by the large carrier mobility, superior anisotropic ratio in photoresponse (1.9) comparable to mechanically exfoliated samples, and high distinguishability of CPL comparable to those typical chiral materials with larger thickness. The terrace-step-kink strategy is applicable to the chiral epitaxy of other low-symmetry 2D single crystals, like monoclinic MoO₂. This work extends the range of control over 2D material growth to chirality, demonstrating full manipulation of both in-plane and out-of-plane lattice orientations of 2D crystals via the synergy of terraces, steps, and kinks on the substrate and enabling chirality transfer from the substrate to the 2D materials. Our findings offer the opportunity to produce wafer-scale, chirality-selective, single-crystalline ReS₂ membranes and have the potential to be generalized to other low-symmetry 2D crystals.

Methods

Annealing of MgO substrate

Single-side polished MgO substrates were purchased from Hefei Ruijing Photoelectric Technology Co. To reconstruct terraces, steps, and kinks on the surface, the MgO substrates were annealed in an oxygen atmosphere at 1050 °C for approximately 2 h.

Growth and transfer of ReS₂ domains

A 0.0025 mol/L aqueous solution of NaReO₄ was prepared by dissolving NaReO₄ in deionized water. Single-side polished c-plane sapphire were treated with oxygen plasma to create a hydrophilic surface. The prepared salt solution was spin-coated onto the plasma-treated sapphire surface at 5000 rpm for 30 s, which was then used to provide precursor vapor to the target substrate for ReS₂ growth. The growth process was carried out in a 1-inch diameter atmospheric pressure CVD system. During growth, sulfur powder was placed in an Al₂O₃ crucible and positioned at the center of the low-temperature zone, with the temperature set to 140–180 °C. The MgO substrate or other substrates were placed face-to-face on the sapphire substrate spin-coated by NaReO₄ solution to form a spatially confined reaction microchamber, which was positioned at the center of the high-temperature zone (820–880 °C). For the growth of monolayer ReS₂ domains, 50 sccm of high-purity Ar was used as a carrier gas, and growth was conducted for 10–20 min (Supplementary Fig. 32).

The transfer of ReS₂ domains was conducted using a polymer-assisted method. A thin film of poly (methyl methacrylate) (PMMA) was spin-coated onto the ReS₂/substrate surface. The sample was then floated on a 2 mol/L potassium hydroxide (KOH) solution, allowing the PMMA/ReS₂ film to gently detach from the substrate. The detached film was rinsed in deionized water three times to remove residual etchants. The PMMA/ReS₂ film was subsequently transferred onto a TEM grid or other substrates, naturally dried in air, and baked on a hotplate at 180 °C for 15 min. To remove the PMMA, the sample was immersed in acetone for 8 h.

Characterization

• (i). Optical characterization. Optical images were captured using an Olympus BX53M microscope. Raman spectra were acquired using a Renishaw Qontor confocal Raman spectrometer with a 532 nm excitation laser. The laser was focused, and scattered light was collected through either a 100× or 50× Leica objective lens. A grating of 1800 lines/mm was used for spectral acquisition. All linearly polarized Raman measurements were conducted in a parallel polarization configuration, where the analyzer was aligned parallel to the incident polarization direction. The CPR spectra were obtained by inserting a quarter-wave plate into the light path. SHG measurements were carried out using a microspectral scanning system (MStarter 100) with a 1064 nm laser.

• (ii). Top-view STEM characterization. ADF-STEM imaging in Fig. 2b was performed at room temperature using an aberration-corrected Titan Cubed Themis G2 300 microscope. The STEM was operated under an accelerating voltage of 300 kV, with a condenser lens aperture of 50 mm, a convergence semi-angle of 21.3 mrad, and a collection angle of 39–200 mrad. The dwell time for a single frame was set to 2 µs per pixel, with a pixel size of 0.012 nm px⁻¹ and a beam current of 30 pA. Image processing was conducted using ImageJ software. A Gaussian blur filter (≈ 2 pixels) was applied to high-magnification ADF-STEM images for smoothing. To enhance visualization, false color LUT was applied to some grayscale ADF-STEM images. Atomic models were constructed using the Accelrys Discovery Studio Visualizer and VESTA⁴⁴ software.

• (iii). Cross-sectional STEM characterization. A dual-beam focused ion beam (FIB) system (Thermo Scientific Scios 2) was employed for sample preparation. Initially, a 200-nm carbon protective layer was deposited using e-beam deposition within the FIB system. The sample was then tilted perpendicular to the ion beam, after which a tungsten strap layer (2 μm) was deposited to shield the region of interest during the milling process. A Ga+ ion beam was utilized to thin and purge the sample to a final thickness of 50 nm for subsequent analysis. For in-plane STEM investigations, the prepared samples were transferred onto TEM grids via a wet-transfer method, and the experiments were conducted using a JEOL GrandARM300F at an accelerating voltage of 300 kV. In STEM imaging, the electron beam was focused to <0.1 nm, using a semi-convergence angle of approximately 24 mrad and a 30 μm condenser lens aperture.

• (iv). SEM and AFM characterization. SEM images were obtained using Regulus 8100 system at 3 kV, 10 μA. AFM measurements were performed by an Asylum Cypher S system. Oxford (AC200TS) Al(100)-coated silicon cantilevers were used. The resonance frequency was ∼150 kHz. The spring constant was ∼9 N m^–1 and the tip curvature radius was ∼7 nm.

• (v). XRD, SAED, and LEED characterization. XRD measurements were conducted using multipurpose X-ray diffractometer (SmaterLab SE) with a copper target. SAED patterns were obtained using transmission electron microscopy (JEOL F200). LEED (OCI, LEED 450) were performed under an ultrahigh vacuum at room temperature.

• (vi). Device fabrications and measurements. The ReS₂ domains grown on MgO and α-Al₂O₃ substrates were transferred onto SiO₂/Si (285 nm) substrates for the fabrication of FETs (Fig. 4a), while photodetectors (Fig. 4f, g) were fabricated directly on the chiral MgO substrates. Both FETs and photodetectors were constructed using a photolithographic pattern transfer technique. Electrodes (10 nm Cr/40 nm Au) were deposited on the substrate through standard photolithography, followed by thermal evaporation and a lift-off process. The prepared electrodes were then transferred onto the target sample using the aligned dry-transfer method. Electronic and optoelectronic measurements were performed on a probe station using a semiconductor device analyzer (Keithley 2612B). A linearly polarized beam (532 nm) with a defined polarization direction was focused onto the device through a 50× objective, with its intensity calibrated using a standard optical power meter (Thorlabs PM100D). CPL was generated using a quarter-wave plate (KungXuan K0.A225.532). All measurements were conducted in the air at room temperature.

DFT calculations

DFT calculations were performed using the plane-wave method implemented in the Vienna Ab initio Simulation Package^45,46. The projected augmented wave pseudo-potentials⁴⁷, the Perdew-Burke-Ernzerh exchange-correlation functional were adopted in all the calculations⁴⁸. The energy cutoff was set as 400 eV for the plane-wave basis set for the sake of high accuracy. A vacuum layer of 20 Å was used to avoid the interference of the adjacent periodic images. For supercells featuring distinct geometries or sizes, Monkhorst–Pack k-point sampling was implemented with a grid spacing of ~ 0.03 Å⁻¹ along each reciprocal lattice vector within the Brillouin zone. The energy and force convergence criteria were set to 10⁻⁴ eV and 0.01 eV/Å, respectively.

We constructed the ReS₂-MgO(001) heterojunction with orientations varying by intervals of 15°(Supplementary Fig. 33 and Supplementary Table 3). The 0° orientation corresponds to the configuration where the b-axis of ReS₂ is aligned parallel to the MgO[110] direction. The binding energies were calculated as

$${E}_{b}=\left({E}_{{{{{\rm{ReS}}}}}_{2}-{{{\rm{MgO}}}}(001)}-{E}_{{{{{\rm{ReS}}}}}_{2}}-{E}_{{{{\rm{MgO}}}}(001)}\right)/S$$

(1)

where the ${E}_{{{{{\rm{ReS}}}}}_{2}-{{{\rm{MgO}}}}(001)},{E}_{{{{{\rm{ReS}}}}}_{2}},{E}_{{{{\rm{MgO}}}}(001)}$ represent the total energy of ReS₂ on MgO(001) substrate and the energy of isolated ReS₂ and MgO(001) substrate, respectively. S indicates the contacting area between ReS₂ and MgO(001) substrate. Then, we compared the grain boundary formation energies of 90° and 45° GBs using the following formula:

$${E}_{f}={E}_{{tot}}-{xE}({{{\mathrm{Re}}}{{{\rm{S}}}}}_{2})$$

(2)

where ${E}_{{tot}}$ is the total energy of the ReS₂ with GBs, $E({{{\mathrm{Re}}}{{{\rm{S}}}}}_{2})$ is the energy of ReS₂ per unit (each unit here has one Re and two S atoms), x is the total number of Re atoms (number of units) in the structure of ReS₂ with GBs.

Next, we built a ReS₂-MgO(11l) heterojunction featuring step $\left[\bar{1}10\right]$ (Supplementary Fig. 34 and Supplementary Table 4). We compared the binding energies between two orientations where the b-axis in ReS₂ aligns parallel or perpendicular to the step $\left[\bar{1}10\right]$. The binding energies were calculated as

$${E}_{b}=\left({E}_{{{{{\rm{ReS}}}}}_{2}-{{{\rm{MgO}}}}\left(11l\right)}-{E}_{{{{{\rm{ReS}}}}}_{2}}-{E}_{{{{\rm{MgO}}}}\left(11l\right)}\right)/2L$$

(3)

where ${E}_{{{{{\rm{ReS}}}}}_{2}-{{{\rm{MgO}}}}\left(11l\right)},{E}_{{{{{\rm{ReS}}}}}_{2}},{{{\mbox{and }}}}\,{E}_{{{{\rm{MgO}}}}\left(11l\right)}$ represent the total energy of ReS₂ on the MgO(11l) substrate, the energy of isolated ReS₂, and the energy of the MgO(11l) substrate, respectively. L indicates the length along the step $\left[\bar{1}10\right]$.

Finally, we constructed ReS₂-chiral MgO heterojunction, introducing both step $\left[\bar{1}10\right]$ and kink $\left[\bar{1}00\right]$, (Supplementary Fig. 35 and Supplementary Table 5). We compared the binding energies of ReS₂ with different chirality on the chiral MgO surface, using the formula:

$${E}_{b}=\left({E}_{{{{{\rm{ReS}}}}}_{2}-{{{\rm{chiral\; MgO}}}}}-{E}_{{{{{\rm{ReS}}}}}_{2}}-{E}_{{{{\rm{chiral\; MgO}}}}}\right)/S$$

(4)

where the ${E}_{{{{{\rm{ReS}}}}}_{2}-{{{\rm{chiral\; MgO}}}}},{E}_{{{{{\rm{ReS}}}}}_{2}},{E}_{{{{\rm{chiral\; MgO}}}}}$ represent the total energy of ReS₂ on chiral MgO substrate, the energy of isolated ReS₂ and the energy of chiral MgO substrate, respectively. S denotes the contact area between ReS₂ and chiral MgO substrate.