Introduction

Inorganic nanomaterials with intrinsic chirality can be designed to manipulate optical, physical, and chemical properties for widespread applications including sensing, catalysis, biomedicine, and photonics1,2. Particularly, chiral plasmonic nanomaterials exhibit remarkable chiral light-matter interactions and fascinating geometry-dependent chiroptical properties3,4,5, thus becoming promising candidates for various applications such as chiral sensing6,7,8, asymmetric catalysis9,10, biomedicine11,12, and chiroptics13,14. While notable success has been achieved in the synthesis of chiral plasmonic nanoparticles with strong chiroptical effects3,15 as well as their self-assembly for tunable optical activity16,17,18, the self-assembly of achiral nanoparticles into chiral superstructures holds immense promise for inexpensive and scalable production of chiral plasmonic nanomaterials with a broad range of chiral designs and controllable chiroptical properties2,19,20,21,22. In this regard, a variety of strategies including additive-induced, template-directed, and physical field-mediated approaches have been explored for achieving precise control over the chiral nanostructures23. However, it remains challenging to develop facile and efficient strategies to realize the chiral self-assembly of achiral plasmonic nanoparticles into chiral assemblies with high optical asymmetry.

Since the geometric features of nanoparticles play a crucial role in determining their self-assembly behaviors as well as the properties of the hierarchical assemblies, the controlled assembly of anisotropic nanoparticles into organized superstructures is attracting increasing interest24,25,26. It is noteworthy that novel superlattices exhibiting planar chirality, which are not intrinsically chiral in three dimensions, have been fabricated through self-assembly of achiral polyhedral nanoparticles such as gold tetrahedra27,28 and bipyramids29. However, it is difficult to achieve a single handedness in the absence of chiral templates and inducers. Considering that either end-to-end or side-by-side aligned nanorods can be conferred geometric chirality when the twist angle falls between 0° and 90°, a variety of homochiral assemblies of gold nanorods (GNRs) have been obtained with the assistance of chiral templates and additives in solution. For example, twisted GNR dimers with tunable spatial configurations were fabricated using DNA origami templates30,31, and helical GNR chains with enhanced optical asymmetry were prepared using amyloid fibrils as chiral templates32,33. An optical asymmetry factor (g-factor) as high as 0.12 was achieved for the chain-like chiroplasmonic assemblies but the increase of the g-factor was limited by maintaining the long-range order33. Interestingly, natural proteins including serum albumin have been used as chiral additives or destabilizers to induce chiral side-by-side self-assembly of GNRs with twisted structures34,35,36, and a g-factor up to 0.03 was realized37. Nevertheless, the optical asymmetry achieved so far for the chiral plasmonic nanomaterials obtained by self-assembly of achiral nanoparticles without templates is still relatively weak22.

Adopting concave nanoparticles as the nanoscale building blocks may be beneficial for efficient chiral self-assembly considering the steric constraints38,39 and interlocking tendency40,41,42,43 offered by the concavity. Notably, gold nanodumbbells (GNDs) consisting of two expanded tips connected by a central shaft were self-assembled into stacked assemblies with varied twist angles38,44; however, the overall assemblies were uncovered to be a racemic mixture of individual nanostructures exhibiting both chiroptical signals45.

Herein, bovine serum albumin (BSA) is utilized as a chiral additive to induce the chiral self-assembly of GNDs into helically stacked, side-by-side assemblies (SSAs) exhibiting strong chiroptical activity with g-factor up to 0.23, which is considerably higher than those reported for the chiral superstructures self-assembled from achiral nanoparticles. The structure-optical activity relationships are explored experimentally and theoretically, revealing that the concavity of the GNDs greatly enhances the chirality and stability of the assemblies in comparison to their GNR counterparts. Additionally, the obtained chiral assemblies exhibit application potential in inducing circular polarization luminescence (CPL) of achiral fluorescent species. This work may open a new avenue toward chiral plasmonic superstructures with high chiroptical activity.

Results

BSA-induced chiral self-assembly GNDs

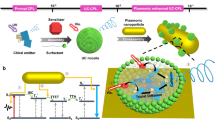
The biomolecule BSA was employed as a chiral additive to induce the twisted side-by-side self-assembly of cetyltrimethylammonium bromide (CTAB)-stabilized GNDs in solution to form chiral assemblies (Fig. 1a). After the chiral BSA molecules were introduced, the negatively charged biomolecules were adsorbed on the surface of the positively charged GNDs and a significant decrease in the electrostatic repulsion occurred, leading to the side-by-side assembly of the GNDs. Meanwhile, due to the concave shape and interlocking tendency of the GNDs, twisted SSAs showing a staggered interlocking arrangement with a chiral characteristic were formed so as to maximize van der Waals (vdW) attractions44. The chiral surface charge distributions of the tertiary structures of serum albumin37,46 and the related chiral charge distributions on the lateral surface of the BSA-modified GNDs could result in homochiral SSAs of GNDs. Particularly, among possible SSAs with different configurations, such as the left-handed (L), parallel (P), and right-handed (R) arrangements, the right-handed twisted SSAs including stacked dimers and helical oligomers were preferentially formed (Fig. 1b).

Fig. 1: Schematics of chiral self-assembly of GNDs.
figure 1

a BSA-induced self-assembly of CTAB-stabilized GNDs. b Preferred formation of right-handed GND dimers and oligomers among GND assemblies with different side-by-side arrangements.

Full size image

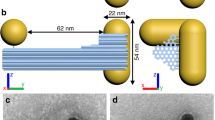
Uniform GNDs were prepared by controlled overgrowth of the initial GNRs with a length of ~ 80 nm and a diameter of ~ 11 nm (Supplementary Fig. 1). By adjusting the HAuCl4 concentration during the overgrowth, the morphology of the GNDs could be readily regulated, as shown by the representative transmission electron microscopy (TEM) and scanning electron microscopy (SEM) images (Supplementary Figs. 2 and 3). Here, the GNDs were approximately modeled as cylindrical rods with two spheroidal tips, and three structural parameters were defined, namely, the particle length (L), tip width (D), and rod diameter (d) (Supplementary Fig. 4). It was observed that the L, D, and d values were gradually increased with increasing the HAuCl4 concentration. Particularly, GNDs with L ~ 94 nm, D ~ 24 nm, and d ~ 17 nm were obtained at a HAuCl4 concentration of 300 μM, which were used as the typical anisotropic building blocks for the subsequent self-assembly experiments. The UV-vis-NIR absorption spectra of the dispersions of the GNDs in water exhibited two absorption bands at shorter and longer wavelengths, which can be assigned to the transverse and longitudinal bands of the localized surface plasmon resonance (LSPR), respectively (Supplementary Fig. 5). An increase in the HAuCl4 concentration resulted in a notable reduction in the aspect ratio (L/D), leading to a significant blue shift in the longitudinal mode. The simulated extinction spectra of the GNDs with varied structural parameters are basically consistent with experimental results (Supplementary Fig. 6). When the dispersions of GNDs were dropped onto a silicon wafer, evaporation-induced self-assembly resulted in three-dimensional stacked assemblies with varied interlocking alignments (Supplementary Fig. 7), indicating their tendency to form interlocking assembly structures.

The chiral self-assembly of the GNDs was achieved by adding a GND dispersion to a solution of BSA in phosphate buffer solution (PBS) at room temperature. The absorption and CD spectra of the GNDs and their assemblies formed under the induction of BSA were measured and the corresponding g-factor spectra were calculated. Figure 2a shows a significant blue shift of the longitudinal plasmon band accompanied by a significant decrease in the absorbance as well as a small red shift in the transverse plasmon resonance, indicating the occurrence of side-by-side assembly of the GNDs while the BSA does not exhibit noticeable absorption within the tested wavelength range. For the preservation of the native assembly configurations, the SSAs of the GNDs in solution were stabilized by silica coating, which has been frequently used for the characterization of the native configurations of nanoparticle assemblies formed in solution47. It can be seen that minor red shift occurred in both the transverse and longitudinal plasmon resonances after the silica coating, which could be attributed to the change in the refractive index of the environment surrounding the SSAs.

Fig. 2: Optical and morphological characterizations of chiral GND assemblies.
figure 2

a Absorption, b CD, and c g-factor spectra of BSA solution, GNDs, and GND assemblies before and after silica coating. SEM images of GND assemblies d before and e, f after silica coating. Inset in d show a TEM image of a GND assembly. Red and blue circles in e indicate the R-type and L-type stacking, respectively. Red and blue colors in f highlight the R-type and L-type stacked assemblies, respectively. g Single-axis TEM tilt-series images of a right-handed GND tetramer with a silica shell (upper) and the geometric models (lower). Red arrows in g indicate the R-type junctions. The self-assembly process was conducted at room temperature (~ 23 °C) for ~ 1.5 h at a BSA concentration of 158 nM. Source data are provided as a Source Data file.

Full size image

While the BSA solution and the original GND dispersion exhibited no CD signals in the wavelength range of 400–850 nm, the SSAs of GNDs showed a strong CD signal (Fig. 2b) with a g-factor as high as 0.23 (Fig. 2c), indicating successful chiral transfer and amplification from the chiral BSA molecules during assembly. It is noteworthy that the achieved g-factor is significantly higher than the values reported to date for nanoparticle assemblies in solution22,33. Particularly, a comparison with the representative 3D chiral assemblies of achiral plasmonic nanoparticles induced by chiral molecules or templates, such as amino acids, serum albumins, DNAs, and amyloid fibrils, suggests that the current chiral GND assemblies exhibit the highest g-factor, which is typically one or two orders of magnitude higher than those of the serum albumin and DNA-based assemblies (Supplementary Table 1). Since the strong circular dichroism of the SSAs imparts them with optical rotation dispersion properties48, a visible disparity in brightness and color was observed between the dispersions of the chiral SSAs and achiral GNDs under orthogonal polarization conditions (Supplementary Fig. 8). After the silica coating, the SSAs of the GNDs still had a strong chiroptical activity despite somewhat lowered chiral signals (Fig. 2b, c), indicating that their chiral structure was essentially preserved. During the continuous silica coating process, both the absorption and CD spectra of the SSAs showed only little change although a notable change in the spectra occurred when the reagents for the silica coating (e.g., TEOS and CTAB) were introduced to the solution (Supplementary Fig. 9). It indicated that the gradual thickening of the silica layer after adding the coating agents had negligible impact on the assembly structure.

SEM and TEM images of the GND assemblies obtained by directly drying a droplet of the dispersion on the substrates (e.g., silicon substrate and copper grid) revealed the presence of a large amount of side-by-side assemblies (Fig. 2d). However, it is infeasible to determine the real spatial alignments of the GNDs constituting the SSAs from the dried samples due to the drying effects. As such, in situ liquid-phase TEM imaging with a cone-shaped quartz nanopipette as the liquid cell49 was performed to characterize the structure of the SSAs in solution (Supplementary Fig. 10), which demonstrated the twisted side-by-side alignments of the GNDs in the assemblies (Supplementary Fig. 11). The tilt-series images revealed the presence of a right-handed stacked GND trimer; however, identifying the chirality of the assemblies remained challenging as the liquid layer should be kept thin (up to a few hundred nanometers) for electrons to transmit in the liquid-phase TEM experiment, which was additionally influenced by the motion induced blurring due to the particle translational diffusion. The thin liquid layer created confinements for the GNDs and their assemblies, and the wall effects impacted the structure of the assemblies. It may be noted that the observed GND assemblies were much larger than those shown in Fig. 2, which could be ascribed to the inherent limitations associated with the current liquid-phase TEM imaging technique, such as the longer time required for the preparation of the assembled samples as well as the progressive accumulation of the GNDs near the tip region due to slow liquid volatilization. Considering the inevitable limitations of the liquid-phase TEM experiments, cryo-TEM experiments were further conducted to reveal the natural state of the SSAs (Supplementary Fig. 12), which suggested that the SSA size or the number of GNDs in an SSA (n) was comparable to those shown in Fig. 2. While the cryo-TEM characterization can avoid excessive particle aggregation arising from sample preparation, slight particle displacement may still occur during the drying process and hence it remains challenging to identify the real spatial alignments of the GNDs.

In this regard, the silica coating offered a feasible method to stabilize the GND assemblies in solution and preserve the spatial alignments of the GNDs after drying on substrates for SEM and TEM characterizations. SEM images of the silica-coated assemblies suggested that the GND assemblies mainly consisted of side-by-side stacked oligomers and the right-handed (R-type) stacking was the predominant stacking mode although the left-handed (L-type) stacked assemblies were observed occasionally (Fig. 2e, f). Single-axis TEM images of a typical tetramer at various tilt angles together with the related geometric models demonstrated that all adjacent GNDs were aligned in the R-type arrangement and the assembly exhibited a right-handed nanohelix (Fig. 2g). The twist angle (θ) between two stacked GNDs can be measured through careful SEM observations of the silica-coated GND dimers. According to the statistical analysis on the obtained SEM images (Supplementary Fig. 13), the twist angle was estimated to be 38.3 ± 5.6°. Hence, it can be inferred that the BSA induced the formation of the chiral GND assemblies with a preferred right-handed helical structure, leading to the strong chiroptical activity.

As the chiral additive to induce chiral self-assembly, the BSA played a key role in determining the assembly behaviors of the GNDs as well as the optical properties of the resultant GND assemblies. When the self-assembly process was conducted for 2 h at a thermostated temperature of 25 °C, an increase of the BSA concentration from 98 nM to 248 nM resulted in a blue shift and weakening of the longitudinal plasmon band as well as a slight red shift of the transverse plasmon band (Fig. 3a), indicating an increase in assembly degree. On the other hand, the CD signals of the GND assemblies were first increased with increasing the BSA concentration to 129 nM and then decreased with further increasing the BSA concentration (Fig. 3b). As a result, the g-factor reached a maximum at a BSA concentration of 158 nM (Fig. 3c), indicating that the addition of BSA was essential to the chiral self-assembly of the GNDs but excess BSA could be detrimental to the regular homochiral assembly toward high chiroptical activity.

Fig. 3: Effects of the BSA concentration and assembly time on the assembly behaviors of GNDs.
figure 3

a, d Absorption, b, e CD, and c, f g-factor spectra of GND assemblies obtained a–c with an assembly time of ~ 2 h at different BSA concentrations and d–f with different assembly times at a BSA concentration of 158 nM. Distributions of g the numbers of GNDs per oligomers and h the junction configurations in the assemblies at varied assembly times ([BSA] = 158 nM). i SEM images of silica coated SSAs with different GND numbers per oligomer. Red and blue arrows indicate the R-type and L-type junctions, respectively. The self-assembly process was conducted at 25 °C. Source data are provided as a Source Data file.

Full size image

The measurements of the zeta potentials of the CTAB-stabilized GNDs and the assemblies of GNDs induced by different concentrations of BSA suggested that a considerable decrease in the zeta potential occurred upon the addition of BSA, namely, from ~ 30 mV to less than 16 mV (Supplementary Fig. 14). While the adsorption of the BSA on the surface of the CTAB-stabilized GNDs brought about the decrease in the electrostatic repulsion and the side-by-side stacking of the GNDs, the chiral surface charge distributions of the adsorbed BSA would lead to the homochiral twisting of the stacked GNDs37,46. However, if excess BSA was adsorbed, the conformation and local surface charge distributions of the adsorbed BSA might change in an opposite direction36, leading to a decrease in the overall chirality. Furthermore, it may be noted that besides electrostatic interactions between BSA and GNDs, the adsorption of BSA may occur via van der Waals attractions, hydrogen bonding, hydrophobic and covalent Au-S chemisorption50,51. Therefore, significantly excess BSA could bridge the separated GNDs and bring about severe aggregation of the GNDs, thus lowering the chirality. Particularly, both the dynamic light scattering (DLS) and SEM characterizations of the GND assemblies obtained at a high BSA concentration of 375 nM confirmed severe aggregation (Supplementary Figs. 15 and 16). Moreover, by adjusting the concentration of CTAB in the solution for the self-assembly of GNDs, the surface charge of the GNDs could be regulated (Supplementary Fig. 17), which in turn affected the structure and optical properties of the SSAs (Supplementary Fig. 18). It was found that a maximum chirality was obtained at a moderate CTAB concentration of 0.3 mM, which was hence adopted as the optimized condition for the BSA-induced chiral self-assembly of the GNDs. In short, when the electrostatic repulsion was decreased in the presence of BSA, the vdW attractions would lead to the twisting of a parallel GND dimer, and the interactions among the adsorbed BSA molecules with appropriate conformations would induce the R-type stacking, leading to the preferential formation of the R-type assemblies (Fig. 1).

Moreover, we examined the assembly kinetics and identified the critical role of the assembly time in the chiral self-assembly of GNDs. Figure 3d–f shows the temporal variation of the optical properties of the GND assemblies formed in the presence of 158 nM BSA. With prolonging assembly time, the longitudinal plasmon band gradually blue-shifted with the intensity weakened, indicating an increase in the amount of assembled GNDs (Fig. 3d). The CD intensity initially increased and then slowly decreased with time (Fig. 3e) and the g-factor reached the maximum at around 2 h (Fig. 3f). To understand the weakening of the chirality with time, we employed silica coating to stabilize the configurations of the GND SSAs at different assembly times, and quantified the number of the GNDs within each SSA and the junction configurations of adjacent GNDs in the assemblies, which included the L, R, and P arrangements, and an achiral end-to-end cross connection (C). Statistical analyses of the SEM images indicated that the number of GNDs per aggregate was gradually increased during the assembly process (Fig. 3g and Supplementary Fig. 19). It was worth noting that there was little change in the overall chirality of the junctions during the assembly process (Fig. 3h). In particular, the R junction was always the dominant configuration, and its proportion (73.9%) was significantly larger than that for the L junction (12.2%) in the SSAs assembled for 2 h. As shown in Fig. 3i, for tetramers or shorter oligomers, their chiral structures can be unambiguously identified. After further assembly, although the chiral preference of the junctions remained unchanged, the increase in the chain length of the SSAs led to a twisting of the helical chain and hence impairment of the helical structure and chiral features. Therefore, an appropriate assembly time or extent was essential to obtaining chiral GND assemblies with high chiroptical activity.

It is noteworthy that as the GNDs were achiral, the chirality of their assemblies would be largely dependent on the chiral characteristics of the chiral molecules adsorbed on the GNDs. Therefore, two other chiral proteins, namely, human serum albumin (HSA) and transferrin (Tf), which were previously used for the chiral self-assembly of GNRs36, were employed as chiral molecules to induce the chiral self-assembly of the current GNDs. When HSA was present, the CD spectra of the GND assemblies exhibited a negative peak, similar to that observed in the assemblies induced by BSA, and a somewhat lower g-factor of 0.13 was achieved (Supplementary Fig. 20). Remarkably, when Tf was used as the chiral inducer, the CD spectra of GND assemblies exhibited a pronounced positive peak within the LSPR region (Supplementary Fig. 21), indicating the formation of a predominantly left-handed structure with a g-factor of 0.038. The relatively smaller g-factor could be attributed to the limited aggregation size and the lower proportion of left-handed assemblies (Supplementary Fig. 22). It is expected that enhanced chiroptical activity could be achieved under optimized assembly conditions. Although both serum albumin and transferrin belong to globular proteins, they have considerable difference in conformation; for example, Tf contains α-helical and β-sheet structures, whereas serum albumins contain primarily α-helical secondary structure36, which could contribute to the different handedness of the GND assemblies. However, it remains a challenging task to fully elucidate the exact mechanism underlying the formation of specific handedness under the induction of certain chiral molecules.

Numerical simulations of chiroptical properties

The obtained experimental results suggested that the strong chiroptical activity of the GND assemblies was closely related to the chiral arrangements of the GNDs in the SSAs. To reveal the relationship between the configurational structure and optical properties of the chiral GND assemblies, we performed the electromagnetic simulations of the optical properties using the finite element method (FEM). Figure 4a shows the structural model of an R-type GND dimer in the SSAs employed in the simulation, which can be described by the parameter twist angle (θ) in addition to the structural parameters L, D, and d for an individual GND. Note that the minimum θ value for a dimer of the GNDs with fixed structural parameters can be achieved when the two GNDs adopt the close-contact configuration (i.e., both the end tips and central rods are contacted). Furthermore, the number of GNDs in an SSA is defined as the chain length (n) and the GND dimer has an n value of 2. Figure 4b, c illustrates the simulated extinction and CD spectra of the R-type GND dimers with a close-contact configuration (θ = 32°) in three orthogonal orientations (x, y, and z) relative to the incident light, as well as their average values. The average results can approximately represent the overall spectra of the assemblies in the dispersion solution52. The simulated average CD spectra exhibited a strong negative peak at ~ 750 nm within the LSPR region, in good agreement with the key features observed in experimental results shown in Fig. 2b. Notably, the chiroptical activity primarily originated from the x-direction contribution, as evidenced by the strongest CD intensity observed when the assembly axis was perpendicular to the incident light. When the wave vector k was parallel to the y direction, the negative CD peak at ~ 690 nm contributed to the negative shoulder in the average CD spectrum. These simulation results demonstrated that the chiroptical activity originated from the twisted side-by-side arrangement of the GNDs. Furthermore, the effects of silica coating on the chiroptical activity of the assemblies were examined by comparison of the simulated absorption and CD spectra of the GND dimers before and after silica coating (Supplementary Fig. 23). It was shown that upon coating a 5 nm silica layer, both the absorption and CD peaks exhibited a redshift, accompanied by a slight reduction in CD intensity, in fairly good agreement with the experimental observations (Fig. 2a, b). These results suggested that the silica coating could not considerably change the packing structure of the GND dimers and its influence on the CD spectra could be primarily ascribed to the variation in refractive index.

Fig. 4: Simulated optical properties of right-handed GND assemblies.
figure 4

a Schematic illustration of the structural parameters of a GND dimer (n = 2). Simulated b extinction and c CD spectra of GND dimers with different k-vector directions (L = 108 nm, D = 30 nm, d = 21 nm, θ = 32°). Simulated d extinction, e CD, and f g-factor spectra of helical GND oligomers with different n values (L = 108 nm, D = 30 nm, d = 21 nm, θ = 32°). Simulated CD spectra of stacked GND dimers with different g θ values (L = 94 nm, D = 23.5 nm, d = 17.4 nm), h L values (D = 23.5 nm, d = 17.4 nm, θ = 35°), and i D values (L = 100 nm, d = 17 nm, θ = 35°). Source data are provided as a Source Data file.

Full size image

Considering that the obtained GND assemblies mostly consisted of the GND oligomers (n ≥ 2), the simulations of the extinction, CD, and g-factor spectra of the R-type helical GND oligomers with varied n values (n = 2–6) were performed (Fig. 4d–f). Due to the strong plasmon resonance coupling between GNDs, all the simulated extinction spectra exhibited two LSPR peaks and they gradually blue-shifted with increasing the chain length (Fig. 4d), which is consistent with simulated results for the GNR systems53. The presence of multiple chiral centers in the oligomers containing more than two GNDs could potentially enhance the CD signal if they were enantiomerically pure54. The simulations demonstrated that an increase in n resulted in an increase in the CD intensity (Fig. 4e). Notably, the g-factor was increased from 0.09 for the GND dimers to 0.54 for the GND hexamers (Fig. 4f), which was significantly higher than the experimental values. If the n value was further increased, the increase in the g-factor was considerably slowed down; specifically, the g-factor was increased from 0.57 to 0.63 with increasing n from 7 to 9 (Supplementary Fig. 24). Since the obtained GND assemblies in the experiments usually consisted of a mixture of oligomers with different chain lengths, the measured spectra may represent a weighted average of the simulation results for various n values.

Simulations of the optical properties of the R-type GND dimers with varied configurations suggested that the chiroptical properties of the SSAs were considerably affected by the twist angle (θ) of each GND dimer as well as the structural parameters of individual GNDs. For example, when the θ value was increased, the CD signal was gradually increased from 35° to 60°, and then decreased until it disappeared at 90° where the dimer adopted a symmetrical structure, which was accompanied by a blue shift in the main positive peak and a red shift in the main negative peak (Fig. 4g). The g-factor was gradually decreased with increasing the θ value until complete disappearance of the chiroptical activity at 90° (Supplementary Fig. 25). When the GND length (L) was increased from 80 to 120 nm, the CD peaks gradually red-shifted with the intensity gradually increased (Fig. 4h). As the tip width (D) was increased from 17 to 30 nm, the CD peaks also gradually red-shifted with the intensity gradually increased (Fig. 4i). Notably, a 1.4-fold increase in the intensity of the key negative peak was observed, which could be attributed to the stronger coupling of plasmon resonance modes from the enlarged tips. In order to reveal the origins of the high g-factor of the GND assembly, we conducted simulations comparing the optical properties between the GNR and GND dimers. The simulated CD spectra indicated that the GND dimer showed the same dip-peak signature but with increased amplitude and its CD peak was red-shifted, matching the shift in the extinction maximum (Supplementary Fig. 26). The simulated near-field enhancement distribution maps showed a significant electric field enhancement between the coupled GNDs, compared to the coupled GNRs (Supplementary Fig. 27), confirming that the enlarged tips of GNDs lead to more efficient optical coupling55. In addition, the additional peaks in the CD spectra are likely attributed to the Rabi splitting arising from strong plasmonic resonance coupling between GNDs53. Since the experimentally measured spectra correspond to the high-energy mode that has a strongly dipolar character, the additional peaks in the simulated spectra could not be experimentally observed. These results indicated the advantage of the dumbbell-shaped nanoparticles in obtaining high chiroptical activity compared with their rod-shaped counterparts.

Considering that the GND assemblies obtained in the experiments were actually a mixture of oligomers with different chain lengths, a direct comparison of the optical properties between the simulated and experimental results is difficult to make. However, our preliminary experimental results showed that the chiroptical properties of the GND assemblies were largely dependent on the structural parameters of the GNDs, which can be modulated within a certain range by changing the HAuCl4 concentration in the growth solution (Supplementary Figs. 3 and 4). Particularly, as the HAuCl4 concentration was increased from 74 to 600 μM, there was a gradual blue shift in the longitudinal plasmon band as well as the negative CD and g-factor peaks (Supplementary Fig. 28). At a moderate HAuCl4 concentration (300 μM), the g-factor of the assemblies reached the maximum, indicating that appropriate structural parameters are important for obtaining the GND assemblies with high chiroptical activity.

Stability and CPL of chiral GND assemblies

The stability of chiral assemblies of nanoparticles is an important factor in determining their performance in applications. A comparative study of the chiroptical activity and stability at varied assembly temperatures was conducted for assembly systems of the concave GNDs and the normal GNRs. At 40 °C, the CD intensity of the GND assemblies reached its maximum quickly (less than 6 min after the assembly was induced with BSA) and then gradually decreased with minor blue shift of the peak (Fig. 5a). Similarly, there was only minor variation in the CD peak position at assembly temperatures ranging from 30 °C to 60 °C (Supplementary Fig. 29). For simplicity, the variation of the CD value and g-factor with time was measured at the wavelengths corresponding to the approximate peak positions of the g-factor curves for the GND and GNR assemblies (i.e., 730 nm and 650 nm), respectively. Basically, there was no significant decrease in the chiroptical activity after 6 min of assembly (Fig. 5b, c and Supplementary Fig. 30).

Fig. 5: Comparison of the assembly behaviors of GNDs and GNRs.
figure 5

Time evolutions of a CD spectra at 40 °C, and b CD intensity and c g-factor at 730 nm at different temperatures for GND assemblies. Time evolutions of d CD spectra at 40 °C, and e CD intensity and f g-factor at 650 nm at different temperatures for GNR assemblies. Source data are provided as a Source Data file.

Full size image

In contrast, the CD peak of the GNR assemblies blue shifted significantly with time at 40 °C (Fig. 5d), and the CD intensities were much lower than those for the GND assemblies at the same assembly time. Theoretical simulations of the CD spectra of the helical oligomers of both GNDs and GNRs with different n values at typical twisting angles showed that the negative CD peak for both the GNR and GND assemblies exhibited a blue shift with increasing the n value, and the blue shift tended to be more pronounced with increasing the θ value (Supplementary Fig. 31). In particular, the GNR assemblies with smaller θ values exhibited much more pronounced blue shift compared with the GND assemblies with larger θ values. Therefore, the blue shift in the CD spectra of both GND and GNR assemblies with the assembly time could be ascribed to the gradual increase in the n value, and the more pronounced blue shift observed for the GNR assemblies could be attributed to their much smaller twisting angles.

Notably, when the temperature was above 50 °C, there was an inversion in the sign of the CD signals (Fig. 5e and Supplementary Fig. 32). Similar temperature-induced inversion of chiroptical responses in cysteine-induced SSAs of GNRs was previously reported56, which was ascribed to the conformation change of the ligand layer. The measurements of the CD spectra of a BSA solution at different temperatures suggested that the protein underwent conformational alterations at elevated temperatures; particularly, the BSA experienced a gradual decrease of CD magnitude with increasing the temperature from 30 °C to 60 °C (Supplementary Fig. 33), indicating a conformational change and partial loss of its primarily α-helical secondary structure57. Therefore, the inversion of the chiroptical responses could be attributed to the temperature-triggered conformation change of the adsorbed BSA. It is noteworthy that such a temperature-induced inversion did not occur in the GND assembly systems, indicating that the concavity of the GNDs could endow the chiral assemblies with enhanced stability. Furthermore, compared with the GND assemblies, the chiroptical activity of the GNR assemblies was considerably weaker at all tested temperatures (Fig. 5f and Supplementary Fig. 34), confirming the concavity-enhanced formation of chiral nanoparticle assemblies. In addition, the relative change in the g-factor of the assemblies at 60 min compared to that at 6 min was quantified (Supplementary Fig. 35), which clearly showed that the g-factor of the GND assemblies exhibited the most significant change at 30°C whereas the g-factor of the GNR assemblies changed most significantly at high temperatures. Particularly, the g-factor and the handedness of the GND assemblies were kept stable at 50° and 60°, whereas considerable changes in the g-factor occurred for the GNR assemblies accompanied by a notable chiral inversion, indicating the superior capability of the GND assemblies in maintaining the g-factor.

As discussed before, the van der Waals attractions would lead to the twisting of a parallel GND dimer, and the interactions between the adsorbed BSA molecules would induce the R-type stacking, resulting in the formation of stable, homochiral assemblies with the R-type configuration. In contrast, the twisting of a parallel GNR dimer corresponds to a decrease in the van der Waals attractions, leading to a much weaker tendency to form a chiral, twisted dimer even though the interactions between the adsorbed BSA molecules are favorable for the R-type stacking. Furthermore, the end protrusions of GNDs restrict their free rotation in their chiral assemblies, leading to a stable chiral structure in solution, whereas the convex surface of the GNRs is beneficial for free rotation, leading to easier chiral structure conversion. These results highlighted the superiority of concave nanoparticles as building blocks in forming homochiral assemblies. It is noteworthy that although there have been numerous studies on the self-assembly of chiral plasmonic structures using various chiral inducers including BSA, the current work highlights the superiority of GNDs with a concave geometry in the self-assembly into stable, homochiral assemblies with strong chiroptical activity. Thus, it may provide a practical approach based on the rational morphological design of nanoscale building blocks toward chiroplasmonic nanomaterials with high optical asymmetry.

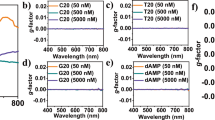
The GND assemblies, characterized by strong CD signals, were investigated as potential hosts for achiral fluorescent species to generate CPL. Figure 6a illustrates a schematic diagram of the CPL emission from achiral fluorescent species using a designed two-cell CPL system with the chiral GND assemblies. Upon excitation with incident light, specific fluorophores emit achiral light, which is selectively absorbed by the chiral GND assemblies in another sample cell, leading to the CPL with a chirality opposite to that of the absorbed light. Particularly, a CPL system was constructed using CdTe quantum dots (QDs) as the fluorescent species and the GND assemblies as the chiral species. It may be noted that if the incident light passed through the assemblies first, only minimal CPL could be detected; in contrast, strong CPL could be detected when light passed through QDs first (Supplementary Fig. 36), confirming that the generation of CPL was caused by the “filtering effect” of the chiral species58,59. Furthermore, if a single-cell CPL system was adopted instead of the two-cell CPL system, a decrease in CPL intensity was observed upon mixing the GND assemblies and the QDs, which could be attributed to the influence of the QDs on the state of the GND assemblies. Notably, the CPL could be captured through a near-infrared filter and a circular polarization filter (CPF). The intensity of the CPL varied after passing through different circular polarization filters, indicating a strong chiral emission (Fig. 6b). When the fluorescent species were changed, the CPL spectra range could be modulated with the peak position consistent with the wavelength of the emitted light (Fig. 6c, d). It is worth noting that, larger CPL values were observed at longer wavelengths, resulting in a luminescent dissymmetric g-factor (glum) value up to 0.12 obtained for the CdTe QD system (Supplementary Fig. 37). Accordingly, it is expected that this CPL system holds promise for constructing novel near-infrared optical anti-counterfeiting devices.

Fig. 6: CPL properties of designed two-cell CPL systems with chiral GND assemblies.
figure 6

a Schematic illustration of chiral GND assemblies as hosts for generating CPL from achiral fluorophores. b NIR photographs of the transmission through the CPL systems containing CdTe QDs with L-CPF and R-CPF when illuminated with unpolarized UV light. c CPL and d DC spectra of GND assemblies in the CPL systems containing different fluorescent species. Source data are provided as a Source Data file.

Full size image

Discussion

We have demonstrated the realization of BSA-induced chiral self-assembly of achiral dumbbell-shaped gold nanoparticles into helically stacked, side-by-side assemblies showing strong chiroptical activity. It was revealed that while the van der Waals attractions led to the twisted stacking and interlocking of GNDs, the interactions among the adsorbed BSA molecules induced the right-handed stacking, leading to stable homochiral assemblies. As a result, the obtained chiral GND assemblies exhibited high g-factors up to 0.23, which is the highest among the chiral plasmonic structures formed by self-assembly of achiral nanoparticles. Experimental and simulation results suggested that the chiroptical properties of the assemblies were considerably influenced by the geometric features of the nanoparticle units as well as the spatial configurations of the nanoparticle assemblies. In addition, induced intense CPL from achiral luminophores was achieved through utilizing the chiral GND assemblies as nanopolarizers. Notably, left-handed twisted GND assemblies were obtained when the transferrin was employed as the chiral inducer, demonstrating the potential of this assembly strategy in controlling the handedness of chiral nanoparticle assemblies. The concavity-enhanced self-assembly strategy shows great potential in preparing chiral plasmonic structures with strong chiroptical activity as well as adjustable handedness through judiciously selecting chiral inducers. Taken together, this work highlights the unique opportunities offered by the geometric concavity for chiral self-assembly of anisotropic nanoparticles, and provides a practical and facile approach to construct chiroplasmonic nanomaterials with attractive applications such as chiral sensing, anti-counterfeiting, bioimaging, and chiroptics.

Methods

Materials

Cetyltrimethylammonium bromide (CTAB, 99%), and cetyltrimethylammonium chloride (CTAC, 25 wt.% in water) were purchased from Sigma-Aldrich. L-ascorbic acid (AA, 99%) was obtained from TCI. Tetrachloroauric (III) tetrahydrate (HAuCl4·4H2O) and silver nitrate (AgNO3) were purchased from Sinopharm Chemical Reagent and Beijing Beihua, respectively. Sodium borohydride (NaBH4, 98%) and tetraethyl orthosilicate (TEOS, 99.99%) were obtained from Aladdin Reagent. Hydroquinone (HQ, 99%) was purchased from Macklin and phosphate buffer solution (PBS, 0.01 M) was obtained from Gibco. Hydrochloric acid and sodium hydroxide were purchased from Xilong Scientific and Beijing Tongguang, respectively. Bovine serum albumin (BSA, 98%) and transferrin (Tf, 98%) were obtained from Mreda. Human serum albumin (HSA, 98%) was obtained from Adamas. Aqueous dispersion of CdTe quantum dots (QDs with a fluorescence maximum at ~ 815 nm and a half-peak width of ~ 100 nm, 5 μM) was purchased from Beida Jubang and Chlorins e6 (Ce6, 98%) was purchased from Frontier Scientific. Fluorescein isothiocyanate (FITC, 95%) and Rhodamine B (RhB, 95%) were purchased from Aladdin Reagent. All chemicals were used as received. All aqueous solutions were prepared using deionized water (18.2 MΩ cm−1).

Synthesis of GNRs

GNRs were prepared by a modified seed-mediated growth method60. The seed solution was prepared by adding an aqueous HAuCl4 solution (0.25 mL, 10 mM) into a CTAB solution (10 mL, 0.1 M) in a glass vessel. A freshly prepared NaBH4 solution (0.6 mL, 0.01 M dissolved in 0.01 M NaOH) was then injected into the mixture under rapid stirring. The seed solution was aged at 30 °C for 1 h before use. For the preparation of the growth solution, a CTAB solution (120 mL, 0.1 M) was mixed with AgNO3 (4.8 mL, 0.01 M) and HAuCl4 (6 mL, 0.01 M). The mixture was kept undisturbed for 15 min at 30 °C, and aqueous HQ solution (6 mL, 0.1 M) was then added. Under vigorous stirring, 1.92 mL of seed solution was added and the mixture was aged at 30 °C overnight. The resultant GNRs were purified by centrifugation at 10,278 × g (namely, 10,000 rpm), and redispersed in 1 mM CTAB solution for further overgrowth.

Synthesis of GNDs by overgrowth of GNRs

Uniform GNDs were synthesized by controlled overgrowth of the prepared GNRs in the presence of CTAC. Typically, 10 mL of 0.1 M CTAC was mixed with HAuCl4 (0.3 mL, 0.01 M) and HCl (0.2 mL, 1 M), then stored for 10 min at 30 °C. Next, an AA solution (150 μL, 0.1 M) was added, and the solution was vigorously stirred for 30 s. Finally, 0.48 mL of the 10-fold concentrated GNR seed solution was added under stirring, and left undisturbed for the growth of GNDs for 2 h at 30 °C. The resultant GNDs were centrifuged three times (8325 × g, 10 min), and redispersed in 0.3 mM CTAB solution, resulting in a GND dispersion for the following assembly. For the adjustment of the structural parameters of the GNDs, the concentrations of HAuCl4 and AA in the growth solutions were changed with a fixed molar ratio (i.e., [AA]/[Au] = 5).

BSA-induced chiral self-assembly of GNDs

The chiral self-assembly of the GNDs was induced by adding 1 mL of GND dispersion to 1 mL of a freshly-prepared solution of BSA in 1.0 mM phosphate buffer solution (pH ~ 7.4). The BSA concentration in the assembly solution was adjusted in the range of 98 μM to 248 μM with a typical concentration of 158 nM. The assembly process was conducted at varied temperatures (typically, room temperature) for different time periods (typically, 2 h).

Silica coating of GND assemblies

The silica coating of the GND assemblies was achieved through base-catalyzed hydrolysis of TEOS following the reported method47 with certain modification. Briefly, 1 mL dispersion of GND assemblies was mixed with 1 mL of CTAB (1 mM), followed by the addition of 10 μL of NaOH (0.1 M). Next, a TEOS solution in ethanol (100 μL, 2.5 vol%) was introduced under vigorous stirring, and the mixture was left undisturbed at 45 °C for over 10 h in a thermostatic water bath. The resulting product was centrifuged (8325 × g, 10 min) and redispersed in ethanol.

Electron microscopy

SEM images were taken on a Hitachi S-4800 microscope at an operation voltage of 5 kV. TEM imaging was performed on a FEI Tecnai F20 microscope at an operation voltage of 200 kV on carbon-coated TEM grids. In situ liquid-phase TEM experiments were performed as previously reported49. Briefly, a dispersion of GND assemblies was injected into a quartz capillary with a nanosized conical tip from the wide-open end to allow the assemblies to diffuse to the nano-tip. The tip (0.5–1 mm long) was cut and sealed with vacuum grease at the wide-open end, and subsequently loaded onto a carbon-coated TEM grid to fabricate a nanopipette liquid cell. Liquid-phase TEM images were collected with an FEI Tecnai F20 microscope with a Gatan OneviewIS camera operated at 200 kV. Cryo-TEM images were taken on a FEI Titan Krios TEM operated at 300 kV.

Extinction and CD spectroscopy

After assembly for 90 min, the dispersion solution of GND assemblies was divided into two parts for extinction and CD measurements, respectively. Three mm path length quartz cuvettes were used for both measurements. CD spectra were recorded with a JASCO J-815 circular dichroism spectrometer with a bandwidth of 1.00 nm and a scan rate of 100 nm/min. Extinction spectra were measured on a Hitachi U-4100 UV-vis-NIR spectrometer with a data interval of 2 nm. When changing the incubation temperature, the GND and BSA dispersions were thermostated at the test temperature for 30 min. The Kuhn’s dissymmetry factor (g-factor) was calculated from the measured extinction (A) and CD (θ) values using the following equation:

$$g-{{\mathrm{factor}}}=\frac{\theta \left({{\mathrm{mdeg}}}\right)}{32,980\times A}$$
(1)

DLS and zeta potential measurements

Dynamic light scattering (DLS) and zeta potential measurements were performed using a 90Plus Zeta (Brookhaven). The mixtures of GNDs and BSA were incubated for 30 min at room temperature before DLS measurement. Bubbles were removed from the sample cell prior to conducting the zeta potential measurement, and the measurement were repeated for three times. In these measurements, the dispersion solution of GND assemblies was not diluted.

CPL spectroscopy

Circularly polarized luminescence (CPL) was measured by a JASCO CPL-200 spectrometer. The CPL spectra were collected using a 1 cm path length quartz cuvette with a scan rate of 200 nm/min and a slit width of 3000 μm, and the DC values were monitored to about 0.5 V. For the two-cell design system, the dispersion/solution containing fluorescent agents (e.g., CdTe QDs, FITC, and RhB) and the dispersion of GND assemblies were added in two quartz cells, respectively. For the two-cell design system, the two cells were placed side by side in the sample cell of the CPL spectrophotometer. For the single-cell design system, the dispersion in the aforementioned two cells were mixed and added into a single cell. Experimentally, the luminescence dissymmetry factor (glum) was calculated from the measured ellipticity (θ) and fluorescence intensity (DC) values using the following equation:

$${g}_{{{\mathrm{lum}}}}=\frac{\theta \left({{\mathrm{mdeg}}}\right)\times {{\mathrm{ln}}}10}{32,980 \times {{\rm{DC}}}\left({{{\rm{V}}}}\right)}$$
(2)

Polarized photography

The samples were illuminated by an unpolarized blue LED (465 nm) and the transmitted light was captured by a conventional digital camera (Nikon D80) with an infrared transmitting filter (IR720). The dispersions of QDs and GND assemblies were added in two quartz cells, and the quartz cuvette containing QDs was positioned close to the excitation light source, while the quartz cuvette containing GND assemblies was placed near the camera. Left- or right-handed circular polarization filters (L/R-CPFs) were placed before the camera for the comparison of the LCP and RCP components in the transmitted light.

Electromagnetic simulations

Electromagnetic simulations of extinction, CD, g-factor spectra of GNDs and GND assemblies were performed with COMSOL Multiphysics using the finite element method (FEM). The GNDs were modeled as spherically capped cylinders, and the detailed geometric parameters were based on the corresponding SEM and TEM images. The simulation domain was encapsulated by the perfectly matched layers (PML). The refractive index for Au was obtained from the Johnson and Christy61, and the surrounding medium was water with a refractive index of 1.33.

The GNDs were illuminated by circularly polarized light, which consisted of two planar polarized waves with the same k-vector but with a phase difference of 90°. Here, the average over 3 orthogonal incident directions were used to account for the random orientation of the GNDs in a water medium. The extinction spectra were recorded as the sum of extinction (εmolar) under left/right-handed CPL. The conversion between σext (extinction cross section, units of m−2) and εmolar (units of M−1 cm−1) was described by

$${\varepsilon }_{{{{\rm{molar}}}}}=\frac{{{{{N}}}}_{{{{\rm{A}}}}}\times {\sigma }_{{{{\rm{ext}}}}}}{0.2303}$$
(3)

where NA is Avogadro’s number. The CD spectra were calculated as the difference between the extinction spectra under left/right-handed CPL. The g-factor spectra were calculated as the ratio of CD spectra to extinction spectra.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.