Introduction

The free energy minimization principle for equilibrium systems states that all interactions between constituents must obey action-reaction symmetry. However, this constraint is no longer present once the system is driven out of equilibrium1,2. Such non-reciprocal interactions are in fact ubiquitous in Nature: the brain is composed of inhibitory and excitatory neurons that interact in an asymmetric manner3,4,5,6; the predator chases the prey and the prey runs away because of their asymmetry in the interaction; colloids immersed in a chemically/optically active media exhibit non-reciprocal forces that give rise to chase-and-run dynamics7,8,9,10. Recent studies revealed that non-reciprocal interactions fundamentally affect the collective properties of many-body systems11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26. A prominent example is the emergence of non-reciprocal phase transitions15,16,17,18,19,20,21,22,23,24,25,27,28, where a time-dependent phase exhibiting a collective and persistent chase-and-run motion of macroscopic quantities arises. Its critical point is characterized by the coalescence of a collective mode to the Nambu-Goldstone mode15,17,20,21,22,23,25 – rather than mere degeneracy as in the conventional cases – which is strictly forbidden in equilibrium.

Non-reciprocal interactions are not restricted to the classical systems mentioned above. Quantum systems may also exhibit non-reciprocity28,29,30 by carefully tailoring dissipation microscopically31,32. Indeed, such non-reciprocity has been implemented in synthetic quantum systems such as cold atoms33, optomechanics34, and circuit QED35. However, these schemes require fine control of dissipation and gauge flux at a single-site/plaquette level, imposing a challenge to realize non-reciprocal interactions in solid-state systems.

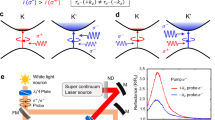
In this work, we propose a novel dissipation-engineering scheme to realize non-reciprocal interactions in solid-state systems with light (Fig. 1(a),(b)). Specifically, we show that the Ruderman-Kittel-Kasuya-Yosida (RKKY)36,37,38 interaction between localized spins in a magnetic metal can be made non-reciprocal by irradiating the sample at a frequency that opens a decay channel from the doubly occupied state of a selected subset of spins, while leaving the rest off-resonant. The optical drive continuously removes these activated spins from the system—a loss that is compensated by the conduction band. Crucially, we point out that this process is most efficient when the activated spins reside in the energetically favored configuration, thereby generating a torque that pushes them away from the ground-state configuration. Since the inactive spins experience no such torque (Fig. 1b), the resulting exchange becomes intrinsically non-reciprocal: spin A attempts to align with spin B, but spin B attempts to anti-align with spin A, leading to a chase-and-run dynamics. We estimate the injection power needed for their emergence is within reach of the current techniques. Applying this scheme to a layered ferromagnet, we find that the light-induced interlayer non-reciprocal interaction triggers a non-reciprocal phase transition15 to a time-dependent chiral phase in which the magnetization of the two layers perpetually chase and flee one another (Fig. 1c). The origin of the non-reciprocity of our proposal is the imbalance in the amount of energy injected into each spin, conceptually akin to those arising in soft active matter8,9,10,39, yet distinct from earlier quantum schemes that use engineered gauge fluxes to control interference effects31,32.

Fig. 1: Light control of magnetic interactions and magnetism via dissipation.
figure 1

a In the absence of light, the interaction between the local spins (thick blue arrow) is reciprocal. The spins are driven towards the equilibrium configuration [alignment in the ferromagnetic case illustrated here] through a magnetic friction called the Gilbert damping (green arrows). b When the light is tuned to a frequency hν that selectively activates the red spin [in the way illustrated in Fig. 3], the light-induced torque (pink arrows) acts on the activated spin. As a result, the two spins effectively interact non-reciprocally, where the active (inactive) spin tries to anti-align (align) with the opponent’s spin. c Phase diagram of a layered ferromagnet under light injection, determined by our meanfield description (Eq. (8)). Here, the two ferromagnetic layers (A and B) are separated by a non-magnetic metal and the laser is injected to introduce active dissipation to the B layer at rate γB, making the interlayer magnetic interactions non-reciprocal. When the light is off (γB = 0), the magnetization of the two layers aligns for ferromagnetic interlayer interaction jAB(=jBA) > 0 (blue region). As the light-induced dissipation is turned on γB > 0, the system exhibits a phase transition to an antialigned configuration (red) at γB ≃ αB∣gB∣ and a non-reciprocal phase transition to a time-dependent chiral phase [where the two magnetizations exhibit many-body chase-and-runaway dynamics](cyan). [See text and Fig. 5 for further details.] We set the intralayer interaction and Gilbert damping of the layer A (B) as jAA = 10meV(jBB = 5meV) and αA = 0.1(αB = 2 × 10−3), respectively. The sd coupling strength for B is gB = − 10meV, the filling n = 1, and the temperature is kBT = 9meV. The dashed lines are the phase boundary at a lower temperature kBT = 5meV.

Full size image

We expect our scheme to be applicable to a wide class of quantum materials such as Mott insulating phases in strongly correlated electrons40,41, multi-band superconductivity42,43, and optical phonon-mediated superconductivity that arises e.g., in SrTiO344,45. This broad applicability is anticipated because our proposal does not rely on any properties specific to magnetic metals: as long as the interaction is mediated via a virtual high-energy state, our scheme should equally work.

Results

The dissipation engineering scheme

To illustrate our idea of creating non-reciprocal interactions in solid-state platforms, we first briefly review how such non-reciprocal interactions arise in soft active systems, which inspired this work. Consider a metal colloidal system under light irradiation as a paradigmatic example9,10 (Fig. 2). When light reaches metal colloid B, part of it is absorbed while the rest is reflected. The reflected light then reaches metal colloid A, exerting an optical force FAB on it. Conversely, a similar optical force FBA is generated when the light incident on colloid A is partially absorbed and partially reflected toward colloid B. Crucially, in this situation, Newton’s third law is not necessarily satisfied (FAB ≠ − FBA). This can be seen clearly by considering the extreme case where one colloid, say A, is a perfect absorber, leading to FBA = 0 while FAB ≠ 0. This has been verified experimentally, where the “chase-and-runaway” dynamics of the colloids are observed9,10.

Fig. 2: Example of non-reciprocal interaction arising in soft active systems.
figure 2

Here, two metal colloids are immersed under light irradiation. The light that reaches the metal colloid A(B) is partly absorbed, and the rest is reflected. The reflected light reaches the metal colloid B(A), giving rise to an optical force FBA(AB). When the absorption/reflection properties of the two colloids are different, the optical forces need not obey Newton’s third law FAB ≠ − FBA.

Full size image

Fundamentally, the interaction is non-reciprocal because (a) the energy conservation law is violated for the degrees of freedom of interest, and (b) a mediating field facilitates the interaction. Condition (a) indicates that there is an external energy source that is continuously injected into the relevant system, and condition (b) enables the system to transform the absorbed energy into mechanical force, such that a net force is exerted on the center of mass of the two colloids only during the interaction process – an effect that is the very hallmark of non-reciprocal interactions. Notably, many of the known examples of non-reciprocal interactions in soft active systems are induced by such a mediating field: phoretic active matter8,46 (where two colloids interact via the hydrodynamic interaction arising from the coupling to a chemically reactive medium), living matter39,47 (the self-propulsion or rotation of the agents affects the surrounding environments that affect the hydrodynamic interactions between the agents), and quorum sensing48,49 (where cells interact by detecting and reacting to the released chemicals) all satisfy the above conditions (a) and (b).

In this paper, we propose to implement a solid-state analog of the above scenario to realize non-reciprocal interactions between electrons in a solid-state platform. The electrons in solid-state systems often interact by exchanging bosonic excitations, such as phonons, spin waves, and density waves, etc. Our idea is to inject light that induces dissipation during this interaction process, satisfying the two conditions (a) and (b) mentioned above and hence, gives rise to non-reciprocal interaction.

In this paper, for concreteness, we consider magnetic metals50 (Fig. 3). These materials are composed of localized spins (responsible for magnetic properties) and conduction electrons that are free to move (responsible for metallic properties), which couple through the spin-exchange coupling called the sd coupling51,52 (Fig. 3a). The sd coupling arises through the exchange of electrons, where the conduction electrons tunnel to the localized orbital to virtually excite the localized electron to a double-occupied state (see the “speech bubble” in Fig. 3a). Even in the case where the localized spins do not directly interact with each other, they may interact indirectly through this sd coupling using the conduction electrons as the mediating field, giving rise to magnetic interactions known as the RKKY interactions36,37,38.

Fig. 3: Dissipation engineering RKKY interactions in magnetic metals.
figure 3

a Schematic description of magnetic metals. It is composed of localized spins (thick blue arrows) and conduction electrons (yellow spheres with arrows attached). The conduction electrons form a Fermi sea up to the Fermi energy εF. The localized electrons are modeled as a spin degenerate localized orbital of bare energy εd with an on-site Coulomb interaction U. The two types of electrons couple through a spin exchange coupling called the sd coupling. Here, the sd spin exchange coupling arises through the second-order process where the conduction electron tunnels into the localized orbital to virtually excite to a double-occupied state and back, which involves spin-flip (the bottom panel). Using the conduction electrons as a medium, a magnetic interaction between the localized spins arises (the so-called RKKY interaction). [Note: there is another process where the localized electron first tunnels to the conduction band and back.] As these perturbative processes lower the energy, the ground state configuration is the state that activates these processes the most. b Our dissipation-engineering scheme is to inject light at a frequency hν resonant with the double-occupied state and a higher-level state (say, an unoccupied higher-level f-orbital state) at the energy εf,B that quickly dissipates with rate Γf,B. Since the decay occurs only when the localized-conduction electron exchange process activates (which lowers the energy), this process selectively destroys the energetically favored states, giving rise to a light-induced torque (pink arrow in Fig. 1b) that applies opposite to Gilbert damping (green arrows in Fig. 1(a),(b)). When this decay is turned on only to spin B but not A, the light-induced torque is applied only to B spins and hence a non-reciprocal interaction emerges. The lost electron is immediately resupplied from the surrounding environment.

Full size image

We propose to dissipation engineer the RKKY interaction by injecting light that has its energy hν tuned to selectively turn on the tunneling from the double-occupied state to a higher-energy state that quickly dissipates (Fig. 3b). This introduces a finite lifetime to the virtual state, directly affecting the properties of the sd coupling and hence the RKKY interaction. The lost electron is immediately resupplied from the conduction electrons so that localized electrons are always singly occupied.

We show below from explicit microscopic calculations that this light-induced dissipation gives rise to a torque (pink arrows in Fig. 1b), which interestingly applies in the direction opposite to the energetically favored configuration. This light-induced torque competes with the magnetic friction called the Gilbert damping53,54 (green arrows) that relaxes the system to the ground state. When we choose the frequency of the light hν in a way that it only resonates with a portion of the spins (red spins in Fig. 1b), this light-induced torque only applies to those activated spins, giving rise to non-reciprocal interactions.

Why does our dissipation scheme give rise to torque that applies in the opposite direction from the Gilbert damping? This can be understood from the general picture we provide below. Our light-injection scheme only dissipates the virtual state of the second-order process illustrated in Fig. 3(b). Hence, the decay channel is turned on only when this process is activated; the configuration that activates the process more is the one that is likely to decay faster. Note crucially that these second-order processes always lower the energy in equilibrium because, according to the second-order perturbation theory, the energy change due to this process is given by ΔE = ∑m∣vi,m∣2/(Ei − Em) < 0, where Ei(m) is the energy of the initial (intermediate) state of the unperturbed system and vi,m is the matrix element between these states. (Note that Ei < Em.) For example, the sd exchange coupling is antiferromagnetic because the above process can only be activated when conduction and localized spins are antialigned due to the Pauli-blocking effect. Similarly, the sign of RKKY interactions is determined by which configuration the perturbative processes activate the most frequently. Therefore, the energetically favorable state is the state that experiences the strongest decay. This results in dissipative interaction in the direction opposite from the friction towards the ground state arising due to the coupling with the surrounding environment, such as the substrate, bulk phonons, etc. We remark that similar physics was discussed in Refs. 55,56 in the context of cold atomic systems, where they also dissipation-engineered sign-reversal of (reciprocal) interactions, but see also Methods for their crucial differences arising from the absence of the surrounding environment.

Since the above scenario does not rely on features specific to magnetic systems, we expect our scheme to be equally relevant to a wide class of quantum materials40,41,42,43,44,45.

Quantum master equation

Our goal from here on is to develop a formalism that allows us to describe the effective spin dynamics of the open quantum system with dissipation induced by continuous light injection. In this work, we consider magnetic metals modeled by the Anderson impurity model50,57 (Fig. 3a), described by the Hamiltonian \({\hat{H}}_{{{{\rm{A}}}}}={\hat{H}}_{0}+{\hat{H}}_{cd}\),

$${\hat{H}}_{0}={\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}=\uparrow,\downarrow }{\varepsilon }_{{{{\boldsymbol{k}}}}}{\hat{c}}_{{{{\boldsymbol{k}}}}{{{\boldsymbol{\sigma }}}}}^{{{\dagger}} }{\hat{c}}_{{{{\boldsymbol{k}}}}{{{\boldsymbol{\sigma }}}}}+{\sum}_{a}\left[{\sum}_{\sigma=\uparrow,\downarrow }{\varepsilon }_{d,a}{\hat{d}}_{\sigma,a}^{{{\dagger}} }{\hat{d}}_{\sigma,a}+{U}_{a}{\hat{d}}_{\uparrow,a}^{{{\dagger}} }{\hat{d}}_{\uparrow,a}{\hat{d}}_{\downarrow,a}^{{{\dagger}} }{\hat{d}}_{\downarrow,a}\right],$$
(1)
$${\hat{H}}_{cd}={\sum}_{a,\sigma }\left[{v}_{a}{\hat{d}}_{\sigma,a}^{{{\dagger}} }{\hat{c}}_{{{{{\boldsymbol{R}}}}}_{a}{{{\boldsymbol{\sigma }}}}}+{{{\rm{h.c.}}}}\right].$$
(2)

Here, conduction electrons are modeled as free electrons, where \({\hat{c}}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}\) is the fermionic annihilation operator of the conduction electrons with spin σ = ↑, ↓ and momentum k and \({\hat{c}}_{{{{\boldsymbol{r}}}},{{{\boldsymbol{\sigma }}}}}={\sum }_{{{{\boldsymbol{k}}}}}{e}^{i{{{\boldsymbol{k}}}}\cdot {{{\boldsymbol{r}}}}}{\hat{c}}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}\) is its Fourier transform. εk is the kinetic energy. The conduction electrons are assumed to be large enough to be always in thermal equilibrium, where its distribution is given by the Fermi distribution function \(f({\varepsilon }_{{{{\boldsymbol{k}}}}})={[{e}^{({\varepsilon }_{{{{\boldsymbol{k}}}}}-{\varepsilon }_{{{{\rm{F}}}}})/({k}_{{{{\rm{B}}}}}T)}+1]}^{-1}\) (εF is the Fermi energy and kB is the Boltzmann constant) at low temperature kBT ≪ εF. The localized electron at site a is modeled as a spin-degenerate localized orbital of bare energy εd,a; if both spin states are occupied, the configuration is penalized by an on-site Coulomb energy Ua. va is the conduction-localized electron mixing (c-d mixing), and Ra is the position of the localized electron. The energy level of localized electrons εd,a sits below the Fermi energy εF, but the double-occupied state εd,a + Ua is above it. As a result, the localized electrons are singly occupied in the steady state. Below, we consider systems with strong enough Coulomb repulsion Ua ≫ va that justifies the perturbative treatment of the c-d mixing va (See Supplemental Information (SI) Sec. III.C for a more precise condition).

As mentioned previously, we introduce a decay channel to localized electrons in the double-occupied state by injecting a laser that couples this state to a higher-energy state that quickly relaxes (see Fig. 3b). This dissipative process can be safely regarded as a Markov process as long as the higher-energy state decays fast enough compared to its re-population rate, which is true in the range of interest (see Methods for details). Such Markovian open quantum systems are generally described by the Gorini-Kossakowski-Sudarshan-Lindblad (GKSL) master equation58,59 (also called the Lindblad master equation; see e.g., Ref. 60 and SI Sec. I for a brief review), given by (where \(\hat{\rho }\) is the reduced system density operator),

$${\partial }_{t}\hat{\rho }=-i[{\hat{H}}_{{{{\rm{A}}}}},\hat{\rho }]+{\sum}_{a,\sigma }{\kappa }_{a}{{{\mathcal{D}}}}\left[{\hat{d}}_{\sigma,a}{\hat{P}}_{\uparrow \downarrow }^{a}\right]\hat{\rho },$$
(3)

for our system. The dissipator \({{{\mathcal{D}}}}[\hat{L}]\hat{\rho }=\hat{L}\hat{\rho }{\hat{L}}^{{{\dagger}} }-\frac{1}{2}\{{\hat{L}}^{{{\dagger}} }\hat{L},\hat{\rho }\}\) makes the time evolution non-unitary. Here, \({\hat{P}}_{\uparrow \downarrow }^{a}\) is a projection operator onto the double-occupied state at site a, turning on a decay channel at the rate κa only when site a is double-occupied. We note that Eq. (3) can be derived from a microscopic model that treats the time-dependent laser drive and a higher unoccupied level explicitly, as done in SI Sec. V.

We wish to derive the localized spin dynamics in the presence of light-induced dissipation κa > 0. In the equilibrium limit κa → 0, a standard procedure to analyze the Anderson impurity model (Eq. (1) and (2)) is to map the localized electrons in the fermionic picture to localized spins, which is performed by projecting out the virtual excited states that have fast oscillations50,52. This incorporates the second-order process in terms of va illustrated in Fig. 3a). Here, we perform the same procedure in spirit but employ it to the GKSL master equation (3)61,62,63,64,65,66, see Methods and SI Sec. I-III for details. It yields,

$${\partial }_{t}\hat{\rho }=-i[{\hat{H}}_{{{{\rm{sd}}}}},\hat{\rho }]+{\sum}_{a}\left[{\gamma }_{a}{{{\mathcal{D}}}}\left[{\sum}_{\sigma }{\hat{d}}_{\sigma,a}^{{{\dagger}} }{\hat{c}}_{{{{{\boldsymbol{R}}}}}_{a},{{{\boldsymbol{\sigma }}}}}{\hat{P}}_{{{{\rm{s}}}}}^{a}\right]+{\sum}_{\sigma }{\kappa }_{a}{{{\mathcal{D}}}}\left[{\hat{d}}_{\sigma,a}{\hat{P}}_{\uparrow \downarrow }^{a}\right]\right]\hat{\rho }.$$
(4)

The first term on the right-hand side describes the coherent dynamics that have an identical form to those found in equilibrium and the second and the third are the light-induced dissipative terms. The sd Hamiltonian51\({\hat{H}}_{{{{\rm{sd}}}}}=-(1/2){\sum }_{a}{g}_{a}{\hat{P}}_{{{{\rm{s}}}}}^{a}[\hat{{{{\boldsymbol{\tau }}}}}({{{{\boldsymbol{R}}}}}_{a})\cdot {\hat{{{{\boldsymbol{S}}}}}}_{a}]{\hat{P}}_{{{{\rm{s}}}}}^{a}\) describes the spin exchange coupling between the conduction and localized spins, where \({\hat{P}}_{{{{\rm{s}}}}}^{a}\) is the projection operator to singly-occupied localized electron states at site a. Here, \({({\hat{{{{\boldsymbol{S}}}}}}_{a})}_{i}={\sum }_{\sigma,{\sigma }^{{\prime} }}{\hat{d}}_{\sigma,a}^{{{\dagger}} }{({\sigma }_{i})}_{\sigma {\sigma }^{{\prime} }}{\hat{d}}_{{\sigma }^{{\prime} },a}\) is the localized spins, σ = (σ1, σ2, σ3) are the Pauli matrices, \(\hat{{{{\boldsymbol{\tau }}}}}({{{{\boldsymbol{R}}}}}_{a})={\sum }_{\sigma,{\sigma }^{{\prime} }}({\hat{c}}_{{{{{\boldsymbol{R}}}}}_{a},{{{{\boldsymbol{\sigma }}}}}^{{\prime} }}^{{{\dagger}} }{{{{\boldsymbol{\sigma }}}}}_{{\sigma }^{{\prime} },\sigma }{\hat{c}}_{{{{{\boldsymbol{R}}}}}_{a},{{{\boldsymbol{\sigma }}}}})\) is the conduction spin at position Ra, and \({g}_{a}\simeq -| {v}_{a}{| }^{2}[{({\varepsilon }_{d,a}+{U}_{a}-{\varepsilon }_{{{{\rm{F}}}}})}^{-1}+{({\varepsilon }_{{{{\rm{F}}}}}-{\varepsilon }_{d,a})}^{-1}] < 0\) (where κa ≪ Ua is assumed) is the sd coupling strength that is antiferromagnetic. (Note that εd,a < εF < εd,a + Ua.) As usual, we have assumed that only the excitations near the Fermi surface are responsible. We have also ignored the impurity potential of conduction electrons, as they play a minor role.

The second term is the emergent correlated dissipation with the rate \({\gamma }_{a}\simeq {\kappa }_{a}| {v}_{a}{| }^{2}/{({\varepsilon }_{d,a}+{U}_{a}-{\varepsilon }_{{{{\rm{F}}}}})}^{2}\) that arises from the interplay between the strong correlation effect and the light-induced decay. (See also Methods.) This term induces dissipative tunneling of electrons from the conduction band to the localized orbital when the electron a is singly occupied. The third term describes the decay of electrons from the double-occupied state at a much faster rate than the correlated tunneling (κa ≫ γa), driving the system immediately back to the singly occupied state.

The emergent correlated dissipation (the second term in Eq. (4)) already captures the underlying mechanism of the dissipation-induced sign-reversal of interactions described in the previous section. This can be seen from the localized spin dynamics that are derived from the master equation (4),

$${\dot{{{{\boldsymbol{S}}}}}}_{a}={g}_{a}\langle {\hat{{{{\boldsymbol{S}}}}}}_{a}\times \hat{{{{\boldsymbol{\tau }}}}}({{{{\boldsymbol{R}}}}}_{a})\rangle -{\gamma }_{a}n{{{{\boldsymbol{S}}}}}_{a}+{\gamma }_{a}{{{\boldsymbol{\tau }}}}({{{{\boldsymbol{R}}}}}_{a}),$$
(5)

where \(\langle \hat{O}\rangle={{{\rm{tr}}}}[\hat{\rho }\hat{O}]\) represents the expectation value, \({{{{\boldsymbol{S}}}}}_{a}=\langle {\hat{{{{\boldsymbol{S}}}}}}_{a}\rangle, {{{\boldsymbol{\tau }}}}({{{{\boldsymbol{R}}}}}_{a})=\langle \hat{{{{\boldsymbol{\tau }}}}}({{{{\boldsymbol{R}}}}}_{a})\rangle\), and n is the filling of the conduction electron. The first and second terms describe the coherent dynamics arising from sd interaction and the light-induced decay of the dipole moment of the localized spin, respectively. Here, the latter arises since the localized electrons that carry the spins are continuously lost and resupplied, which makes the (statistically averaged) spin dipole decay. The third term is the emergent dissipative torque, which drives the localized spin toward alignment with the conduction spins. This is the opposite of what is expected from energetics, where the sd coupling is antiferromagnetic ga < 0. We note that it was crucial for this light-induced dissipator in Eq. (4) to have the form \({{{\mathcal{D}}}}[{\sum }_{\sigma }{\hat{o}}_{\sigma }]\) instead of \({\sum }_{\sigma }{{{\mathcal{D}}}}[{\hat{o}}_{\sigma }]\) for the dissipative torque to appear, generating quantum entanglement between localized and conduction electrons that is important for non-reciprocal interactions to emerge; see SI Sec. III.C for details.

Landau-Lifshitz-Gilbert equation with light-induced interactions

The remaining task to obtain the effective interaction between the localized spins36,37,38 (i.e., the dissipation-engineered RKKY interaction) is to integrate out the conduction electron degrees of freedom that we regard as a (non-Markovian) bath. We perform this by mapping the master equation (4) to a Keldysh action67 that allows us to utilize field-theoretic approaches, taking into account non-adiabatic effects from the Fermi statistics of the conduction electrons. Once the Keldysh action is obtained, we integrate out the conduction electrons’ degrees of freedom within the second-order perturbation in terms of sd coupling ga and light-induced correlated decay rate γa under the gradient approximation (i.e., Markov approximation plus a first-order non-Markovian correction). We extract the localized spin dynamics in the saddle-point approximation from the obtained reduced Keldysh action consisting only of localized electrons’ degrees of freedom. We detail the procedure in Methods and SI Sec. IV.

The obtained semiclassical localized spin dynamics are

$${\dot{{{{\boldsymbol{S}}}}}}_{a}={\sum}_{b(\ne a)}{J}_{ab}{{{{\boldsymbol{S}}}}}_{a}\times {{{{\boldsymbol{S}}}}}_{b}-{\alpha }_{a}{{{{\boldsymbol{S}}}}}_{a}\times {\dot{{{{\boldsymbol{S}}}}}}_{a}-{\gamma }_{a}n{{{{\boldsymbol{S}}}}}_{a}-{\sum}_{b(\ne a)}{\Omega }_{ab}{{{{\boldsymbol{S}}}}}_{b},$$
(6)

which is one of the main results of this work. We emphasize that all terms, including the Gilbert damping term, are obtained microscopically. Here, for simplicity, we have assumed that we are at low temperature (kBT/εF ≪ 1) and omitted the non-local non-Markovian (Gilbert-damping-like) terms68,69,70 arising from the dissipative part of the spin wave propagator.

The first two terms on the right-hand side reproduce the conventional the Landau-Lifshitz-Gilbert form53,54, while the last two terms are terms generated through our controlled dissipation. The first term gives rise to the coherent precession motion around the effective magnetic field Beff = ∑b(≠a)Jab(Rab)Sb, where Jab(= Jba) is the RKKY interaction strength given by Jab(Rab) = − 9π[(gagb)/εF]n2F(2kFRab) in the case of parabolic dispersion εk = ℏ2k2/(2m) in three spatial dimensions, where m is the conduction electron mass, \({k}_{{{{\rm{F}}}}}=\sqrt{2m{\varepsilon }_{{{{\rm{F}}}}}}/\hslash\) is the Fermi momentum, Rab = ∣Ra − Rb∣ is the inter-spin distance, \(F(x)=[-x\cos x+\sin x]/{x}^{4}\), and ℏ is the Dirac constant. The second term, obtained as the first-order correction to the Markov approximation70, is the Gilbert damping term describing the spins’ magnetic friction53,54. This drives the system toward the ground state configuration when combined with the first term (green arrows in Fig. 1). Here, αa is the Gilbert damping rate, which, in the parabolic dispersion case, reads \({\alpha }_{a}=(9{\pi }^{2}/2){n}^{2}{({g}_{a}/{\varepsilon }_{{{{\rm{F}}}}})}^{2}\). The relaxation rate for such a process is \({\gamma }_{{{{\rm{Gil}}}}}^{ab} \sim {\alpha }_{a}| {J}_{ab}|\).

The light-induced dissipative interactions Ωab(Rab) = (γa/∣ga∣)Jab(Rab) ≃ (κa/Ua)Jab(Rab)[≠Ωba] compete with this equilibration dynamics (pink arrows in Fig. 1b). In addition to the unavoidable decay with rate γa of the dipole moment described by the third term, our light induces effective interactions that cannot be written as the derivative of the energy function. (We briefly note that we have ignored the contribution from self-dissipative interaction Ωaa, which merely renormalizes the decay rate γa.) This dissipative interaction drives the system towards a configuration opposite to the ground state configuration. When κa ≳ αaUa, this light-induced contribution (Ωab = κa/Ua ⋅ Jab) exceeds the Gilbert damping (\({\gamma }_{{{{\rm{Gil}}}}}^{ab} \sim {\alpha }_{a}\,{J}_{ab}\)), causing the effective interaction to change its sign. When this sign flip occurs to one of the spins but not the other, non-reciprocal interactions with effective opposite signs emerge, resulting in chase-and-runaway dynamics (the situation illustrated in Fig. 1b).

In Methods, we estimate the pumping power P required to achieve this regime as

$$P\, \gtrsim\, {\alpha }_{a}\frac{2\pi {U}_{a}\nu {m}_{0}{\epsilon }_{0}c}{{e}^{2}}{\Gamma }_{f,a}$$
(7)

using a Lorentz oscillator model, where e is the electron charge, m0 is the electron mass, ϵ0 is the vaccuum dielectric constant, and c is the speed of light. Setting the typical values Ua ~1 eV, αa ~10−2, Γf,a ~10 meV, hν ~1 eV, the required pump power is P ≳ 108W/cm2. Not only is this pump power achievable, e.g., with Raman lasers with pulse duration of O(10ns)71 or even with a steady-state resource72, but the heating effect should be minimal for magnetic metals. For instance, in Ref. 73, it was reported that the sample (GdFeCo) did not demagnetize until the pump power exceeded P ~1010W/cm2 for the pulsed experiment, and in Ref. 72, the ferromagnetic of the sample (NiFe) retained at least up to P ~ 108W/cm2 (3.5 mW power on a 580 nm diameter spot). For convenience for the readers, we have summarized the typical energy scales in Fig. 4.

Fig. 4: Typical energy scales in different physical pictures.
figure 4

The energy scales in (left panel) localized electrons immersed in conduction electrons picture described by Eq. (3), (middle panel) localized spins immersed in conduction electrons picture described by Eq. (4), and (right panel) in the interacting localized spin picture (where the conduction electrons are integrated out) described by Eq. (6). These pictures map from one to the other via the projection method (SI Sec. III) and Keldysh theory (SI Sec. IV). Each panel lists the energy scales in the coherent (Hamiltonian) and dissipative dynamics. The equilibration occurs at the timescale set by the energy scale in the Hamiltonian multiplied by the Gilbert damping rate αa. This competes with the light-induced dissipation and the sign reversal of interaction occurs when the latter exceeds the former.

Full size image

Non-reciprocal phase transitions

So far, we have shown from microscopic calculations that one can generate non-reciprocal interactions with light. An intriguing question is how such non-reciprocal interaction affects the collective properties of many-body systems. In this work, at the outset, we consider a simple setup illustrated in Fig. 5a), where light is exposed to two layers of ferromagnets (that we label A and B) that sandwich a non-magnetic metal. The light is tuned to activate only layer B spins. In the absence of light, this is a type of MRAM device. The itinerant electrons in the non-magnetic metal layer mediate the interlayer RKKY interaction74,75,76,77. The light injection induces additional torque to the B layer, applying oppositely from conventional RKKY interaction, giving rise to non-reciprocal interlayer interaction (Fig. 5a).

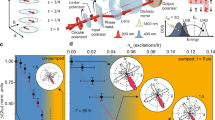
Fig. 5: Non-reciprocal phase transitions in light-activated layered ferromagnets.
figure 5

a Layered ferromagnet composed of A and B layers separated by a non-magnetic metal exposed of light injection that activates the B layer. The interlayer RKKY interaction is mediated by the itinerant electrons in the non-magnetic metal layer, which is modified by light. In particular, the magnetization in the A layer aligns with the rate αAjAB for ferromagnetic interlayer interactions jAB > 0, while the B layer may align or antialign with layer A depending on the sign of the modified effective interaction αBjAB − ΩAB. φA(B) is the orientation direction of the magnetization mA(B) of A(B)-layer ferromagnet. b–d Different phases arising in this system. b Aligned phase (Δφ = φA − φB = 0) realized in the equilibrium limit γB = 0. c Antialigned phase (Δφ = π) at γB/(αB∣gB∣) = 1.1. d Chiral phase (Δφ ≠ 0, π) at γB/(αB∣gB∣) = 1.5. (e) The orientation angle difference Δφ and (f) the magnitude of the magnetization ∣mA,B∣ as a function of γB. We set jAB = 5 meV, kBT = 9 meV, and the other parameters are the same as those used in Fig. 1c). The simulations were run from random initial conditions and have been checked that there is essentially no initial condition dependence on the final state.

Full size image

We wish to predict the magnetization dynamics of this system. Unfortunately, deriving the governing equation of the collective magnetization dynamics from a microscopic model is a highly non-trivial task that requires a beyond-saddle-point approximation we employed above (where a longitudinal relaxation is not incorporated)78. Although deriving such a coarse-grained description from microscopics is an important challenge, here, we take a phenomenological approach below.

We make the following observations: (a) In the absence of light, the magnetism ma=A,B should converge to the known equilibrium value. (b) Since the relaxation towards this state occurs through the Gilbert damping, their relaxation time for the a-layer is expected to be \({\tau }_{{{{\rm{Gil}}}}}^{a}=O({[{\alpha }_{a}{\sum }_{b}\,{j}_{ab}]}^{-1})\), where jab(= jba) is the interaction strength Jab multiplied by the number of spins a given spin couples to. (c) When light is injected into the B layer, the light-induced torque ΩBA and a decay with the rate γB is introduced to B layer magnetization mB. This brings us to propose the following phenomenological meanfield description:

$${\dot{{{{\boldsymbol{m}}}}}}_{{{{\rm{A}}}}}={\alpha }_{{{{\rm{A}}}}}\left[-{k}_{{{{\rm{B}}}}}T{{{{\boldsymbol{m}}}}}_{{{{\rm{A}}}}}+\left[1-\frac{{\left({{{{\boldsymbol{h}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{A}}}}}\right)}^{2}}{3{({k}_{{{{\rm{B}}}}}T)}^{2}}\right]{{{{\boldsymbol{h}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{A}}}}}\right],$$
(8a)
$${\dot{{{{\boldsymbol{m}}}}}}_{{{{\rm{B}}}}}={\alpha }_{{{{\rm{B}}}}}\left[-{k}_{{{{\rm{B}}}}}T{{{{\boldsymbol{m}}}}}_{{{{\rm{B}}}}}+\left[1-\frac{{\left({{{{\boldsymbol{h}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{B}}}}}\right)}^{2}}{3{({k}_{{{{\rm{B}}}}}T)}^{2}}\right]{{{{\boldsymbol{h}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{B}}}}}\right] -{\gamma }_{{{{\rm{B}}}}}n{{{{\boldsymbol{m}}}}}_{{{{\rm{B}}}}}-{\Omega }_{{{{\rm{BA}}}}}{{{{\boldsymbol{m}}}}}_{{{{\rm{A}}}}},$$
(8b)

where \({{{{\boldsymbol{h}}}}}_{{{{\rm{eff}}}}}^{a}={\sum }_{b={{{\rm{A,B}}}}}\,{j}_{ab}{{{{\boldsymbol{m}}}}}_{b}\) is the effective field applied to ma and ΩBA = (γB/∣gB∣)jAB is the light-induced torque. For simplicity, we have assumed that the system is close enough to the disordered-ordered transition point such that the Ginzburg-Landau expansion is justified and the anisotropy is strong enough that z-component of the magnetization vanishes \({m}_{a}^{z}=0\). In the absence of light γB = 0, the steady state \({\dot{{{{\boldsymbol{m}}}}}}_{a}=0\) reproduces the known result from the Weiss theory. This is of the general form introduced in Ref. 15.

Figure 1c shows the phase diagram obtained by simulating Eq. (8). In the absence of the light injection γB = 0, unsurprisingly, the magnetization orientation of the two layers aligns Δφ = φA − φB = 0 (Fig. 5b), where the orientation of the magnetism is defined by \({{{{\boldsymbol{m}}}}}_{a}=| {{{{\boldsymbol{m}}}}}_{a}| (\cos {\varphi }_{a},\sin {\varphi }_{a})\). As one increases the laser power that increases γB, the light-induced torque ΩBA weakens the ferromagnetic interaction, until it swaps the sign at ΩBA ≳ αBjAB or γB ≳ αB∣gB∣ (see Fig. 5(e)). This causes a transition from aligned Δφ = 0 to antialigned configuration Δφ = π (blue thin line in Figs. 1c and 5c). Remarkably, the B layer completely demagnetizes at the transition point ∣mB∣ = 0, while the A layer is still ferromagnetic mA ≠ 0 (Fig. 5f) even though the interlayer coupling is still present.

As γB is further increased, the system exhibits a non-reciprocal phase transition15,26 to a time-dependent chiral phase (see Fig. 1c) exhibiting a many-body chase-and-runaway motion (Fig. 5d). The parity spontaneously breaks in this chiral phase, where the relative orientation angle converges to a state Δφ = (≠ 0, π) that is not invariant under the parity operation Δφ → − Δφ. This cannot be understood from the Landau theory15, where the critical point is characterized by the coalescence of the collective modes to the Nambu-Goldstone mode17,20.

One can estimate the necessary condition for the emergence of the chiral phase as (See SI Sec. VI for the derivation),

$$\frac{{\alpha }_{{{{\rm{B}}}}}}{{\alpha }_{{{{\rm{A}}}}}}\frac{{g}_{{{{\rm{B}}}}}^{2}}{{j}_{{{{\rm{AB}}}}}^{2}{n}^{2}}\, \lesssim\, 1$$
(9)

where we have assumed a small Gilbert damping rate of the B layer spins αBjBB ≪ αAjAA and αB ≪ γB/∣gB∣. Plugging in the values used in Figs. 1(c) and 5(b)-(f), we find the required interlayer RKKY interaction strength to be jAB ≳ 1 meV, in agreement with our numerics. Since the electrons in the non-magnetic metal layer mediate the RKKY interaction, we estimate the interlayer RKKY interaction strength as jAB ~gAgBρspacer, where ρspacer is the density of states of the electrons in the non-magnetic spacer layer at the Fermi level. The condition for the chiral phase is then derived as

$$\frac{{\alpha }_{{{{\rm{B}}}}}}{{\alpha }_{{{{\rm{A}}}}}}\frac{1}{{g}_{{{{\rm{A}}}}}^{2}{\rho }_{{{{\rm{spacer}}}}}^{2}{n}^{2}}\,\lesssim \,1.$$
(10)

This implies that the larger the density of states of the spacer is, the more likely the chiral phase is achievable. For instance, taking typical values gA = 0.1 eV, αA = 0.1, n = 1, and αB = 0.001, we expect the chiral phase may emerge by choosing the spacer material with ρspacer ≳ 1 eV−1. (See SI Sec. VI for more details, including phase diagrams with different parameters).

Interestingly, there are regions where this symmetry-broken phase expands when increasing the temperature, which is opposite from what is conventionally expected (see the dashed lines in Fig. 1c) that show the phase boundary at a lower temperature). This is a signature of order-by-disorder phenomena discussed in Ref. 26, where a direct analogy between the geometrically frustrated systems and non-reciprocal matter was drawn.

Discussion

In summary, we have proposed a scheme to dissipation-engineer non-reciprocal interactions with light. We showed microscopically that the light injection to magnetic metals that introduces decay of a virtually excited state induces non-reciprocal interaction between localized spins. Applying this method to layered ferromagnets, we showed that a non-reciprocal phase transition to a time-dependent chiral phase emerges15,26. The pump intensity required to achieve this is estimated to be within reach of the current experimental techniques.

The effect of non-reciprocal interactions on the collective properties of many-body systems is currently under heavy investigation in many different disciplines of science, ranging from active matter8,9,10,15,46,47,48,49,79,80,81,82,83, levitated particles84,85,86, photonics7, robotics87, living matter39,88,89,90, open quantum systems27,28,29,30,31,91, ecology92,93,94,95,96,97, and neuroscience3,4,5,6, to sociology98. Particularly, recent works showed that non-reciprocal phase transitions exhibit unconventional critical phenomena associated with anomalously giant fluctuations17, fluctuation-induced first-order transition20, and diverging entropy production21,22,23, due to the unique feature that the criticality is driven by the coalescence of the modes to the Nambu-Goldstone mode. Furthermore, non-reciprocal interactions have been shown to give rise to emergent features such as odd elasticity11,12 (anti-symmetric part of the static elastic modulus tensor), long-ranged order in two spatial dimensions13,14 (in an apparent violation of the Hohenberg-Mermin-Wagner theorem), and phenomena analogous to those occurring in geometrically frustrated systems26. Our dissipation-engineering scheme may allow exploring these non-reciprocal physics in solid-state platforms.

Methods

Outline of the derivation of Eq. (4) and Eq. (6)

We provide here a brief outline of the derivation of Eq. (4) and Eq. (6) in the main text. The full detail is provided in the SI Sec. III and IV, respectively.

Derivation of Eq. 4

Our starting point to derive Eq. (4) is the quantum master equation (3), which, for convenience, we write it as

$${\partial }_{t}\hat{\rho }={{{\mathcal{L}}}}\hat{\rho },$$
(11)

where we have expressed the right-hand side of Eq. (3) using a superoperator (an operator that acts on a matrix) called the Lindbladian \({{{\mathcal{L}}}}\). We split the Lindbladian into two contributions \({{{\mathcal{L}}}}={{{{\mathcal{L}}}}}_{0}+{{{{\mathcal{L}}}}}_{1}\):

$${{{{\mathcal{L}}}}}_{1}\rho=-i[{\hat{H}}_{cd},\hat{\rho }]$$
(12)

is the contribution from the c-d mixing \({\hat{H}}_{cd}={\sum }_{a,\sigma }[{v}_{a}{\hat{d}}_{\sigma,a}^{{{\dagger}} }{\hat{c}}_{{{{{\boldsymbol{R}}}}}_{a}{{{\boldsymbol{\sigma }}}}}+{{{\rm{h.c.}}}}]={\sum }_{a}{\sum }_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}[{v}_{a}{e}^{i{{{\boldsymbol{k}}}}\cdot {{{{\boldsymbol{R}}}}}_{a}}{\hat{d}}_{\sigma,a}^{{{\dagger}} }{\hat{c}}_{{{{\boldsymbol{k}}}}{{{\boldsymbol{\sigma }}}}}+{{{\rm{h.c.}}}}]\) that we treat as a perturbation. The rest \({{{{\mathcal{L}}}}}_{0}={{{{\mathcal{L}}}}}_{c0}+{\sum }_{a}{{{{\mathcal{L}}}}}_{d0,a}\) is the non-perturbative part, given by,

$${{{{\mathcal{L}}}}}_{c0}\hat{\rho }=-i\left[{\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}{\varepsilon }_{{{{\boldsymbol{k}}}}}{\hat{c}}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{{{\dagger}} }{\hat{c}}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}},\hat{\rho }\right],$$
(13)
$${{{{\mathcal{L}}}}}_{d0,a}\hat{\rho }= -i\left[\left({\sum}_{\sigma }{\varepsilon }_{d,a}{\hat{d}}_{\sigma,a}^{{{\dagger}} }{\hat{d}}_{\sigma,a}+{U}_{a}{\hat{d}}_{\uparrow,a}^{{{\dagger}} }{\hat{d}}_{\uparrow,a}{\hat{d}}_{\downarrow,a}^{{{\dagger}} }{\hat{d}}_{\downarrow,a}\right),\hat{\rho }\right]\\ +{\sum}_{\sigma }{\kappa }_{a}{{{\mathcal{D}}}}[{\hat{d}}_{\sigma,a}{\hat{P}}_{\uparrow \downarrow }^{a}]\hat{\rho }.$$
(14)

In the following, we take advantage of the property that our system has a separation of timescales by dividing the double Hilbert space (where the density operator \(\hat{\rho }\) lives in) into slow and fast degrees of freedom. By perturbatively projecting out the latter52, we obtain an effective low-energy description. Specifically, we first divide the right (left) eigenstates \({\hat{r}}_{n}^{(0)}\) (\({\hat{l}}_{n}^{(0)}\)) with the eigenvalue \({\lambda }_{n}^{(0)}\) of the non-perturbative Lindbladian, defined as \({{{{\mathcal{L}}}}}_{0}{\hat{r}}_{n}^{(0)}={\lambda }_{n}^{(0)}{\hat{r}}_{n}^{(0)}\) (\({\hat{l}}_{n}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{0}={\hat{l}}_{n}^{(0){{\dagger}} }{\lambda }_{n}^{(0)}\)), to slow (\(n\in {\mathfrak{s}}\)) and fast (\(n\in {\mathfrak{f}}\)) degrees of freedom (\(| {\lambda }_{n\in {\mathfrak{s}}}^{(0)}| \ll | | {\lambda }_{n\in {\mathfrak{f}}}^{(0)}|\)). The perturbative Lindbladian \({{{{\mathcal{L}}}}}_{1}\) couples the slow and fast modes. Then, as derived in SI Sec. I.A.2, we perturbatively project out the fast degrees of freedom to yield the effective low-energy Lindbladian,

$${({{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}})}_{{n}_{l},{n}_{r}} \equiv \left({\hat{l}}_{{n}_{l}}^{(0)},{{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}}{\hat{r}}_{{n}_{r}}^{(0)}\right)={{{\rm{tr}}}}\left[{\hat{l}}_{{n}_{l}}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}}{\hat{r}}_{{n}_{r}}^{(0)}\right] \\ ={{{\rm{tr}}}}\left[{\hat{l}}_{{n}_{l}}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{0}{\hat{r}}_{{n}_{r}}^{(0)}\right]+{{{\rm{tr}}}}\left[{\hat{l}}_{{n}_{l}}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{1}{\hat{r}}_{{n}_{r}}^{(0)}\right]\\ \;\;-{\sum}_{m\in {\mathfrak{f}}}\frac{{{{\rm{tr}}}}\left[{\hat{l}}_{{n}_{l}}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{1}{\hat{r}}_{m}^{(0)}\right]{{{\rm{tr}}}}\left[{\hat{l}}_{m}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{1}{\hat{r}}_{{n}_{r}}^{(0)}\right]}{{\lambda }_{m}^{(0)}}+O({({{{{\mathcal{L}}}}}_{1})}^{3}).$$
(15)

Here, \((\hat{A},\hat{B})={{{\rm{tr}}}}[{\hat{A}}^{{{\dagger}} }\hat{B}]\) is the Hilbert-Schmidt inner product and \({\hat{r}}_{{n}_{r}}^{(0)}\) (\({\hat{l}}_{{n}_{l}}^{(0)}\)) is the right (left) eigenstates that form the basis of the slow degrees of freedom (\({n}_{r},{n}_{l}\in {\mathfrak{s}}\)). The first, second, and third terms on the rightmost side are the zeroth, first, and second-order contributions in terms of \({{{{\mathcal{L}}}}}_{1}\), respectively. In the third term, the sum is taken over the fast degrees of freedom. Note how the third term has a similar form to the familiar second-order Rayleigh-Schrödinger perturbation theory, which is given by the matrix element \({{{\rm{tr}}}}[{\hat{l}}_{{n}_{l}}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{1}{\hat{r}}_{m}^{(0)}]{{{\rm{tr}}}}[{\hat{l}}_{m}^{(0){{\dagger}} }{{{{\mathcal{L}}}}}_{1}{\hat{r}}_{{n}_{r}}^{(0)}]\) divided by the eigenvalue of the intermediate state \({\lambda }_{m}^{(0)}\). Equation (15) is consistent with the so-called Lindblad perturbation theory63,64,65.

In our problem, first note that the localized and conduction electrons are decoupled in the non-perturbative Lindbladian \({{{{\mathcal{L}}}}}_{0}={{{{\mathcal{L}}}}}_{c0}+{\sum }_{a}{{{{\mathcal{L}}}}}_{d0,a}\) and therefore the right eigenstate is expressed as a direct product \({\hat{r}}_{{n}_{r}}^{(0)}=({\prod }_{a}{\hat{r}}_{a,{n}_{r}}^{d(0)})\otimes {\hat{r}}_{{n}_{r}}^{c(0)}\) of the right eigenstates of \({{{{\mathcal{L}}}}}_{d0,a}\) and \({{{{\mathcal{L}}}}}_{c0}\) described by \({\hat{r}}_{a,{n}_{r}}^{d(0)}\) and \({\hat{r}}_{{n}_{r}}^{c(0)}\), respectively. For the conduction electrons, we will always be considering low-temperature states that have their conduction electrons in their ground state that forms a Fermi sea \({\hat{r}}_{{n}_{r}}^{c(0)}=| F\left.\right\rangle \left\langle \right.F|\), where \(| F\left.\right\rangle={\prod }_{{\varepsilon }_{{{{\boldsymbol{k}}}}} < {\varepsilon }_{{{{\rm{F}}}}}}{\prod }_{\sigma=\uparrow,\downarrow }{\hat{c}}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{{{\dagger}} }| 0\left.\right\rangle\). For the localized electrons, we regard the eigenstates with singly occupied state as slow degrees of freedom, i.e., \(\{{|\!\! \uparrow \!\!\left.\right\rangle }_{a}{\left\langle \right.\!\!\uparrow \!\!| }_{a},{|\!\! \uparrow \!\!\left.\right\rangle }_{a}{\left\langle \right.\!\!\downarrow \!\!| }_{a},{|\!\! \downarrow \!\!\left.\right\rangle }_{a}{\left\langle \right.\!\!\uparrow \!\!| }_{a},{|\!\! \downarrow \!\!\left.\right\rangle }_{a}{\left\langle \right.\!\!\downarrow \!\!| }_{a},\}\) where \({| \sigma \left.\right\rangle }_{a}={\hat{d}}_{\sigma,a}^{{{\dagger}} }{| \varnothing \left.\right\rangle }_{a}\) is a singly occupied state and \({| \varnothing \left.\right\rangle }_{a}\) is a vacant state. We also regard eigenstates that are diagonal in the Fock basis as slow modes for the localized electrons (which includes states like \({|\!\! \uparrow \!\!\downarrow \!\!\left.\right\rangle }_{a}{\left\langle \right.\!\!\uparrow \downarrow \!\!| }_{a}\), where \({|\!\! \uparrow \!\!\downarrow \!\!\left.\right\rangle }_{a}\) is a double-occupied state) as they do not involve fast coherent dynamics. The rest, such as \({|\!\! \uparrow \!\!\downarrow \!\!\left.\right\rangle }_{a}{\left\langle \right.\!\!\uparrow \!\!| }_{a}\) and \({| \varnothing \left.\right\rangle }_{a}{\left\langle \right.\downarrow | }_{a}\), are fast degrees of freedom.

Among these slow degrees of freedom, we are mainly interested in the states where the localized electron is singly occupied, i.e., \({\hat{r}}_{{n}_{r}}^{(0)}={\prod }_{a}{| {\sigma }_{a}\left.\right\rangle }_{a}{\left\langle \right.{\sigma }_{a}^{{\prime} }| }_{a}\otimes | F\left.\right\rangle \left\langle \right.F|\) (\({\sigma }_{a},{\sigma }_{a}^{{\prime} }=\!\! \uparrow \!\!,\!\downarrow\)). In this case, note that the c-d mixing \({{{{\mathcal{L}}}}}_{1}\) transfers the state into a state where (a) the localized electron is double-occupied and a hole is excited in the conduction band [the process illustrated in Fig. 3] or (b) the localized electron is vacant and a particle is excited in the conduction band. Since these processes excite the system to a fast mode, the first-order contribution (the second term in the rightmost side of Eq. (15)) is absent and the leading term is second-order. The second-order contribution (the third term in Eq. (15)) arises from the processes where the intermediate state involves states with eigenvalues \({\lambda }_{{{{\rm{(a)}}}}\pm }^{(0)}=\pm i({\varepsilon }_{{{{\boldsymbol{k}}}}}-{\varepsilon }_{d,a}-{U}_{a})-{\kappa }_{a}/2\) from the process (a) and \({\lambda }_{{{{\rm{(b)}}}}\pm }^{(0)}=\pm i({\varepsilon }_{d,a}-{\varepsilon }_{{{{\boldsymbol{k}}}}})\) from the process (b). The real part of the process (a) \({{{\rm{Re}}}}{\lambda }_{{{{\rm{(a)}}}}\pm }=-{\kappa }_{a}/2\) reflects the light-induced decay that turns on in the double-occupied state. Assuming further that only excitation near the Fermi surface contributes εk ≈ εF, this yields, as detailed in SI Sec. III,

$${{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{sd}}}}}\left({\hat{P}}_{{{{\rm{s}}}}}^{a}\hat{\rho }{\hat{P}}_{{{{\rm{s}}}}}^{a}\right)=-i[{\hat{H}}_{{{{\rm{sd}}}}},\hat{\rho }]+{\sum}_{a}{\gamma }_{a}{{{\mathcal{D}}}}\left[{\sum}_{\sigma }{\hat{d}}_{\sigma,a}^{{{\dagger}} }{\hat{c}}_{{{{{\boldsymbol{R}}}}}_{a},{{{\boldsymbol{\sigma }}}}}{\hat{P}}_{{{{\rm{s}}}}}^{a}\right]\hat{\rho }.$$
(16)

Here, the sd coupling

$${g}_{a}=-| {v}_{a}{| }^{2}\left[\frac{{\varepsilon }_{d,a}+{U}_{a}-{\varepsilon }_{{{{\rm{F}}}}}}{{({\varepsilon }_{d,a}+{U}_{a}-{\varepsilon }_{{{{\rm{F}}}}})}^{2}+\frac{{\kappa }_{a}^{2}}{4}}+\frac{1}{{\varepsilon }_{{{{\rm{F}}}}}-{\varepsilon }_{d,a}}\right]$$
(17)

in the sd Hamiltonian \({\hat{H}}_{{{{\rm{sd}}}}}=-(1/2){\sum }_{a}{g}_{a}{\hat{P}}_{{{{\rm{s}}}}}^{a}[\hat{{{{\boldsymbol{\tau }}}}}({{{{\boldsymbol{R}}}}}_{a})\cdot {\hat{{{{\boldsymbol{S}}}}}}_{a}]{\hat{P}}_{{{{\rm{s}}}}}^{a}\) and the correlated dissipation

$${\gamma }_{a}=\frac{| {v}_{a}{| }^{2}{\kappa }_{a}}{{({\varepsilon }_{d,a}+{U}_{a}-{\varepsilon }_{{{{\rm{F}}}}})}^{2}+\frac{{\kappa }_{a}^{2}}{4}},$$
(18)

are given by the imaginary and real part, respectively, of \(| {v}_{a}{| }^{2}[{\lambda }_{{{{\rm{(a)}}}}+}^{-1}+{\lambda }_{{{{\rm{(b)}}}}+}^{-1}]\) that arise from the two processes (a) and (b). The expression valid at regimes κa ≪ εF, εd,a, Ua is reported in the main text.

The correlated dissipation (the second term in Eq. (16)) adds an electron to the localized orbital such that the state transfers to a double-occupied state. This is quickly returned to a singly-occupied state via the light-induced decay with rate κa, which can readily be seen from the effective Lindbladian applied to \({\hat{r}}_{{n}_{r}}^{(0)}={|\!\! \uparrow \!\!\downarrow \!\!\left.\right\rangle }_{a}{\left\langle \right.\!\!\uparrow \downarrow \!\!| }_{a}\otimes | F\left.\right\rangle \left\langle \right.F|\) as,

$${{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{sd}}}}}\left({\hat{P}}_{\uparrow \downarrow }^{a}\hat{\rho }{\hat{P}}_{\uparrow \downarrow }^{a}\right)={\sum}_{a,\sigma }{\kappa }_{a}{{{\mathcal{D}}}}[{\hat{d}}_{\sigma,a}{\hat{P}}_{\uparrow \downarrow }^{a}]\hat{\rho },$$
(19)

where we have ignored the contribution to the coherent dynamics since we are not interested in the details of the double-occupied state. When applied to a vacant state \({\hat{r}}_{{n}_{r}}^{(0)}={\prod }_{a}{| \varnothing \left.\right\rangle }_{a}{\left\langle \right.\varnothing | }_{a}\otimes | F\left.\right\rangle \left\langle \right.F|\), we find \({{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{sd}}}}}({\hat{P}}_{\varnothing }^{a}\hat{\rho }{\hat{P}}_{\varnothing }^{a})=0\) (\({\hat{P}}_{\varnothing }^{a}\) is a projection operator to a vacant state), where again, we have ignored the contribution to the coherent dynamics. Summing up these results gives the desired Eq. (4) in the main text.

Derivation of Eq. 6

We next integrate out the conduction electron degrees of freedom to derive the RKKY interactions between the localized spins modified by light. As emphasized in the main text, it is crucial to consider the non-adiabatic (non-Markovian) effect arising from the Fermi distribution function of the conduction electrons. A useful approach to take such effect into account is to analyze a generating function called the Keldysh partition function, defined as67,99,100 (See SI Sec. I for a brief review.),

$$Z\equiv {{{\rm{tr}}}}[\hat{\rho }({t}_{f})]={{{\rm{tr}}}}\left[{e}^{{{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{sd}}}}}({t}_{f}-{t}_{0})}\hat{\rho }({t}_{0})\right],$$
(20)

for the master equation (4). We expand the time evolution operator \({e}^{{{{{\mathcal{L}}}}}_{{{{\rm{eff}}}}}({t}_{f}-{t}_{0})}\) in terms of fermionic coherent states into a product of infinitesimally short time intervals, similarly to the path integral formalism in quantum mechanics. Unlike in quantum mechanics (that deals with wave functions \(| \psi \left.\right\rangle\)) that involves one Grassmann field ψ(t) per degree of freedom, however, as we are dealing with the dynamics of the density matrix \(\hat{\rho }\) that lives in the double Hilbert space, each degree of freedom is assigned with two fields ψ+(t) and ψ−(t) that loosely describes the time evolution of the ket and bra space, respectively. For our system (Eq. (4)), the Keldysh partition function is given by,

$$Z=\int\,{{{\mathcal{D}}}}({d}_{+},{\bar{d}}_{+},{d}_{-},{\bar{d}}_{-}){{{\mathcal{D}}}}({c}_{+},{\bar{c}}_{+},{c}_{-},{\bar{c}}_{-}){e}^{iS}$$
(21)

where \(S[{d}_{+},{\bar{d}}_{+},{d}_{-},{\bar{d}}_{-},{c}_{+},{\bar{c}}_{+},{c}_{-},{\bar{c}}_{-}]={S}_{d}^{0}[d,\bar{d}]+{S}_{c}^{0}[c,\bar{c}]+{S}_{{{{\rm{sd}}}}}^{{{{\rm{coh}}}}}[c,\bar{c},d,\bar{d}]+{S}_{{{{\rm{sd}}}}}^{{{{\rm{dis}}}}}[c,\bar{c},d,\bar{d}]\) is the so-called Keldysh action, given by

$${S}_{d}^{0}[d,\bar{d}]=\int\,dt{\sum}_{s=\pm }{\sum}_{a,\sigma }s{\bar{d}}_{\sigma,a}^{s}(t)i{\partial }_{t}{d}_{\sigma,a}^{s}(t)$$
(22)
$${S}_{c}^{0}[c,\bar{c}]=\int\,dt{\sum}_{s=\pm }{\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}s\times \left[{\bar{c}}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{s}(t)i{\partial }_{t}{c}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{s}(t)-{\varepsilon }_{{{{\boldsymbol{k}}}}}{\bar{c}}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{s}(t){c}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{s}(t)\right],$$
(23)
$${S}_{{{{\rm{sd}}}}}^{{{{\rm{coh}}}}}[c,\bar{c},d,\bar{d}]= -\int\,dt{\sum}_{s=\pm }s{\sum}_{a}{\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}}}(-{g}_{a}){e}^{i{{{\boldsymbol{q}}}}\cdot {{{{\boldsymbol{R}}}}}_{a}}\\ \times {\sum}_{\sigma,{\sigma }^{{\prime} }}{\bar{d}}_{\sigma,a}^{s}(t){\bar{c}}_{{{{\boldsymbol{k}}}}+{{{\boldsymbol{q}}}},{\sigma }^{{\prime} }}^{s}(t){c}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{s}(t){d}_{{\sigma }^{{\prime} },a}^{s}(t),$$
(24)
$${S}_{{{{\rm{sd}}}}}^{{{{\rm{dis}}}}}[c,\bar{c},d,\bar{d}]= -i\int\,dt{\sum}_{a}{\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}}}{\gamma }_{a}{e}^{i{{{\boldsymbol{q}}}}\cdot {{{{\boldsymbol{R}}}}}_{a}}\\ \times {\sum}_{\sigma,{\sigma }^{{\prime} }}\left[{\bar{c}}_{{{{\boldsymbol{k}}}}+{{{\boldsymbol{q}}}},{\sigma }^{{\prime} }}^{-}(t){d}_{{\sigma }^{{\prime} },a}^{-}(t){\bar{d}}_{\sigma,a}^{+}(t){c}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{+}(t)\right.\\ -\frac{1}{2}{\bar{c}}_{{{{\boldsymbol{k}}}}+{{{\boldsymbol{q}}}},{\sigma }^{{\prime} }}^{+}({t}_{+\delta }){d}_{{\sigma }^{{\prime} },a}^{+}({t}_{+\delta }){\bar{d}}_{\sigma,a}^{+}({t}_{-\delta }){c}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{+}({t}_{-\delta })\\ -\left.\frac{1}{2}{\bar{c}}_{{{{\boldsymbol{k}}}}+{{{\boldsymbol{q}}}},{\sigma }^{{\prime} }}^{-}({t}_{-\delta }){d}_{{\sigma }^{{\prime} },a}^{-}({t}_{-\delta }){\bar{d}}_{\sigma,a}^{-}({t}_{+\delta }){c}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{-}({t}_{+\delta })\right],$$
(25)

Here, \({c}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{\sigma }}}}}^{\pm }\) and \({d}_{\sigma,a}^{\pm }\) are the Grassmann variables of conduction and localized electrons, respectively, and t±δ = t ± 0+.

Since the Keldysh action S is quadratic in terms of \((c,\bar{c})\), one can analytically integrate out the conduction electron degrees of freedom to obtain the effective action \({S}_{{{{\rm{eff}}}}}[d,\bar{d}]\) defined as \(Z\equiv \int\,{{{\mathcal{D}}}}(d,\bar{d}){e}^{i{S}_{{{{\rm{eff}}}}}[d,\bar{d}]}\). As detailed in SI Sec IV, the effective action within the second-order perturbation in terms of ga and γa (with several additional assumptions detailed in SI Sec. IV) reads \({S}_{{{{\rm{eff}}}}}[d,\bar{d}]={S}_{d}^{0}[d,\bar{d}]+{S}_{\gamma }[d,\bar{d}]+{S}_{M}[d,\bar{d}]\), where

$${S}_{\gamma }[d,\bar{d}]= i\int\,dt{\sum}_{a,\sigma }{\gamma }_{a}n\left[{d}_{\sigma,a}^{-}(t){\bar{d}}_{\sigma,a}^{+}(t)\right.\\ -\left.\frac{1}{2}{d}_{\sigma,a}^{+}({t}_{+\delta }){\bar{d}}_{\sigma,a}^{+}({t}_{-\delta })-\frac{1}{2}{d}_{\sigma,a}^{-}({t}_{-\delta }){\bar{d}}_{\sigma,a}^{-}({t}_{+\delta })\right],$$
(26)

is the first-order contribution and \({S}_{M}[d,\bar{d}]={S}_{{{{\rm{RKKY}}}}}^{{{{\rm{coh}}}}}[d,\bar{d}]+{S}_{{{{\rm{Gilbert}}}}}[d,\bar{d}]+{S}_{{{{\rm{RKKY}}}}}^{{{{\rm{neq}}}}}[d,\bar{d}]\) is the second-order contribution, with

$${S}_{{{{\rm{RKKY}}}}}^{{{{\rm{coh}}}}}[d,\bar{d}]=\int\,dt{\sum}_{a,b}\frac{{J}_{a,b}({{{{\boldsymbol{R}}}}}_{a,b})}{2}{\sum}_{j=0}^{3}{\sum}_{s=\pm }s{\hat{m}}_{a,j}^{s,s}{\hat{m}}_{b,j}^{s,s},$$
(27)
$${S}_{{{{\rm{Gilbert}}}}}[d,\bar{d}]=-{\sum}_{a}\frac{{\alpha }_{a}}{4}\int dt{\sum }_{j=0}^{3}{\hat{m}}_{a,j}^{+,+}(t){\partial }_{t}{\hat{m}}_{a,j}^{-,-}(t),$$
(28)
$${S}_{{{{\rm{RKKY}}}}}^{{{{\rm{neq}}}}}[d,\bar{d}]= i\int dt{\sum}_{a,b}\frac{{\Omega }_{a,b}({{{{\boldsymbol{R}}}}}_{a,b})}{2}\times {\sum }_{j=0}^{3}\left[{\hat{m}}_{a,j}^{+,+}{\hat{m}}_{b,j}^{+,+}+{\hat{m}}_{a,j}^{-,-}{\hat{m}}_{b,j}^{-,-}\right.\\ -\left.{\hat{m}}_{a,j}^{+,-}{\hat{m}}_{b,j}^{+,+}-{\hat{m}}_{a,j}^{-,-}{\hat{m}}_{b,j}^{+,-}\right].$$
(29)

Here, \({\hat{m}}_{a,j}^{{l}_{1},{l}_{2}}[d,\bar{d}]={\sum }_{\mu,\nu=\!\! \uparrow \!\!,\downarrow }{\bar{d}}_{\mu,a}^{{l}_{1}}{\hat{\sigma }}_{j}^{\mu \nu }{d}_{\nu,a}^{{l}_{2}}\,({l}_{1},{l}_{2}=+ ,-)\) is a localized spin written in terms of Grassmann variables, and

$${J}_{a,b}({{{{\boldsymbol{R}}}}}_{a,b})=-\frac{| {g}_{a}| | {g}_{b}| }{2}{\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}}}\cos ({{{\boldsymbol{q}}}}\cdot {{{{\boldsymbol{R}}}}}_{a,b})\frac{{f}_{+}-{f}_{-}}{{\varepsilon }_{+}-{\varepsilon }_{-}},$$
(30)
$${\Omega }_{a,b}({{{{\boldsymbol{R}}}}}_{a,b})=-\frac{{\gamma }_{a}| {g}_{b}| }{2}{\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}}}\cos ({{{\boldsymbol{q}}}}\cdot {{{{\boldsymbol{R}}}}}_{a,b})\frac{{f}_{+}-{f}_{-}}{{\varepsilon }_{+}-{\varepsilon }_{-}},$$
(31)
$${\alpha }_{a}=-4\pi {g}_{a}^{2}{\sum}_{{{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}}}\frac{{f}_{+}-{f}_{-}}{{\varepsilon }_{+}-{\varepsilon }_{-}}\delta ({\varepsilon }_{+}-{\varepsilon }_{-}),$$
(32)

with ε± = εk±q/2 and f± = f(εk±q/2). Ja,b(Ra,b) is identical to the well-known form of the RKKY interaction strength50. In calculating SM, we have employed a gradient approximation, i.e., a Markovian approximation (\({S}_{{{{\rm{RKKY}}}}}^{{{{\rm{coh}}}}}\) and \({S}_{{{{\rm{RKKY}}}}}^{{{{\rm{neq}}}}}\)) plus the first-order correction to it (SGilbert).

The physical meaning of each term becomes clear by deriving the equation of motion of the spins. To do this, we introduce a set of auxiliary fields m and Lagrange multipliers λ as

$$Z =\int\,{{{\mathcal{D}}}}[m]{e}^{i{S}_{M}[m]} \times \int\,{{{\mathcal{D}}}}[\lambda ]\int\,{{{\mathcal{D}}}}[d,\bar{d}]{e}^{i{S}_{d}^{0}[d,\bar{d}]+i{S}_{\gamma }[d,\bar{d}]}{e}^{i{S}_{\lambda }[\lambda,m,\hat{m}[d,\bar{d}]]}\\ \equiv \int\,{{{\mathcal{D}}}}[m]\int\,{{{\mathcal{D}}}}[\lambda ]{e}^{i{S}_{M}[m]}{e}^{i{S}_{B}^{\lambda }[\lambda,m]}$$
(33)

with

$${S}_{\lambda }[\lambda,m,\hat{m}[d,\bar{d}]]= \int\,dt{\sum}_{a}{\sum}_{{l}_{1},{l}_{2}=q,c}{\sum }_{j=0}^{3}{\lambda }_{a,j}^{{l}_{1},{l}_{2}}(t)\\ \times \left[{m}_{a,j}^{{l}_{1},{l}_{2}}(t)-{\hat{m}}_{a,j}^{{l}_{1},{l}_{2}}[d(t),\bar{d(t)}]\right].$$
(34)

As detailed in SI Sec. IV.C, taking the saddle-point approximation of Eq. (33) as \(\frac{\delta {S}_{M}^{{{{\rm{eff}}}}}[\lambda,m]}{\delta {\lambda }_{a,j}^{{l}_{1},{l}_{2}}}=\frac{\delta {S}_{M}^{{{{\rm{eff}}}}}[\lambda,m]}{\delta {m}_{a,j}^{{l}_{1},{l}_{2}}}=0\) (where \({S}_{M}^{{{{\rm{eff}}}}}[\lambda,m]={S}_{M}[m]+{S}_{B}^{\lambda }[\lambda,m]\)) gives

$${\partial }_{t}{{{{\boldsymbol{S}}}}}_{a}= -{\gamma }_{a}n{{{{\boldsymbol{S}}}}}_{a}-{\sum}_{b(\ne a)}{\Omega }_{a,b}({{{{\boldsymbol{R}}}}}_{a,b}){{{{\boldsymbol{S}}}}}_{b}(t)\\ -\left[{\sum}_{a}\,{J}_{a,b}({{{{\boldsymbol{R}}}}}_{a,b}){{{{\boldsymbol{S}}}}}_{b}(t)-{\alpha }_{a}{\dot{{{{\boldsymbol{S}}}}}}_{a}(t)\right]\times {{{{\boldsymbol{S}}}}}_{a}(t),$$
(35)

where \({S}_{a,j}={m}_{a,j}^{++ }(t)={m}_{a,j}^{--}(t)=\langle {\sum }_{\sigma,{\sigma }^{{\prime} }=\!\! \uparrow \!\!,\downarrow }{\hat{d}}_{\sigma,a}^{{{\dagger}} }(t){\sigma }_{j}^{\sigma,{\sigma }^{{\prime} }}{\hat{d}}_{a,{\sigma }^{{\prime} }}(t)\rangle\) and \({m}_{a,j}^{+-}(t)={m}_{a,j}^{-+}(t)=0\), which is the desired Eq. (6) in the main text. The first, second, third, and fourth terms on the right-hand side arise from \({S}_{\gamma },{S}_{{{{\rm{RKKY}}}}}^{{{{\rm{neq}}}}},{S}_{{{{\rm{RKKY}}}}}^{{{{\rm{coh}}}}}\), and SGilbert, respectively.

Estimation of the required power

Below, we estimate the required laser power P to realize the sign-inversion of the interactions, which occurs when the decay rate of the double-occupied state κa exceeds αaUa (see main text and Fig. 4). Our scheme considers the situation where the double-occupied (at energy εd,a + Ua) and higher-level states (at energy εf,a) are coupled through the injected laser. We assume that the higher-level state is localized and dissipates with the rate Γf,a, so one can model it with a Lorentz oscillator model101.

When a laser with the pump power P is injected into the material, the dissipation causes the energy loss of the laser intensity if the system is in a double-occupied state. The lost energy density per unit time and volume W is given by

$$W=\frac{1}{2}{\epsilon }_{0}\omega {\chi }^{{\prime\prime} }(\omega )| E{| }^{2}=\frac{\omega {\chi }^{{\prime\prime} }(\omega )}{c}P,$$
(36)

where ω = 2πν is the laser frequency. Here, we have expressed the pump power \(P=\frac{1}{2}c{\epsilon }_{0}| E{| }^{2}\) in terms of speed of light c, vacuum dielectric constant ϵ0, and electric field E. The absorption susceptibility χ″(ω) is computed according to the Lorentz oscillator model as

$${\chi }^{{\prime\prime} }(\omega )=\frac{n{e}^{2}}{{\epsilon }_{0}{m}_{0}}\frac{\omega {\Gamma }_{f,a}}{{({\omega }_{0}^{2}-{\omega }^{2})}^{2}+{\omega }^{2}{\Gamma }_{f,a}^{2}}\simeq \frac{n{e}^{2}}{{\epsilon }_{0}{m}_{0}}\frac{1}{{\omega }_{0}{\Gamma }_{f,a}}.$$
(37)

Here, ω0 is the resonant frequency (which, in our case, corresponds to ℏω0 = εf,a − (εd,a + Ua)), n is the number of electrons per unit volume, and m0 is the electron mass. In the second equality, we have set the laser frequency to be on resonance hν = ℏω = ℏω0.

The decay rate of the double-occupied state κa per electron is estimated as

$${\kappa }_{a}=\frac{W}{n\cdot {\omega }_{0}}.$$
(38)

This needs to be larger than αaUa to achieve the regime for showing laser-induced switching of interactions. This condition is given by,

$${\kappa }_{a}=\frac{{\chi }^{{\prime\prime} }({\omega }_{0})P}{n\cdot c}\, \gtrsim\, {\alpha }_{a}{U}_{a}.$$
(39)

This yields the condition,

$$P\, \gtrsim\, \frac{{\alpha }_{a}{U}_{a}n\cdot c}{{\chi }^{{\prime\prime} }({\omega }_{0})}={\alpha }_{a}\frac{{U}_{a}{\omega }_{0}{m}_{0}c{\epsilon }_{0}}{{e}^{2}}{\Gamma }_{f,a},$$
(40)

shown in Eq. (7).

Justification of Markov approximation

For the Markov approximation to be valid, the relaxation rate of the bath must be much faster than the timescale of the system dynamics. We argue here that this is likely to be justified in the range of interest at realistic parameters for magnetic metals.

In our setup, the double-occupied state couples to the higher-level state with the decay rate Γf,a via a laser injection tuned to be resonant with the two states. The higher-level state can be regarded as our “external bath” in the context of open quantum systems. As explained above, this process gives rise to the decay rate κa once the site a is double occupied (see Fig. 6a). Note crucially that, as illustrated in Fig. 6b, this is different from the rate at which the relevant system pumps an electron to this high-energy state because the relevant system transfers into a double-occupied state only once in a while when the conduction electron tunnels to the localized orbital. For example, when the c-d mixing is absent va = 0, there would be no electron transfer from the relevant system to the higher-energy state. The relevant transfer rate of a localized electron from the relevant system to the higher-energy state is estimated to be \({\gamma }_{a}\simeq {\kappa }_{a}| {v}_{a}{| }^{2}/{U}_{a}^{2}\), which we have derived in Eq. (4).

Fig. 6: Light-injection induced dissipation and their energy scales.
figure 6

a The double-occupied (at the energy εd,a + Ua) and the higher energy states (at the energy εf,a) are coupled by the injection of a resonant laser hν = εf,a − (εd,a + Ua). The higher-energy state dissipates with the rate Γf,a. The localized electrons are typically in a single-occupied state but may virtually excite once in a while to a double-occupied state via the c-d mixing va. Note that no electrons decay in the absence of c-d mixing va = 0 because they are always in the single-occupied state. b Localized spin picture obtained after projecting out the double-occupied states (see Eq. (5)). In this picture, one finds that the effective transfer rate from the localized electron to the higher-energy state is given by \({\gamma }_{a}\approx {\kappa }_{a}| {v}_{a}{| }^{2}/{U}_{a}^{2}\). We require γa ≪ Γf,a to justify the Markov approximation.

Full size image

For the Markov approximation to be valid, the dissipation rate of this higher energy state (i.e., the “external bath”) Γf,a must be much faster than the supply rate to this state γa ≪ Γf,a. This is because when the higher-level state is occupied, the Pauli blocking effect would suppress the decay. A slow relaxation of the occupancy of the state would lead to a non-Markovian effect.

It should be relatively easy to satisfy this Markov condition at the regime of interest. We are interested in the regime where we see the sign-reversal of the RKKY interactions, which happens when the dissipation rate exceeds κa ≳ αaUa or γa ≳ αa∣ga∣ (see the discussion above Eq. (7)). In the case αa = 10−2 and ∣ga∣ = 10 meV, this sets the condition, γa ≳ 0.1 meV. This required dissipation rate is less than the typical value of linewidth Γf,a, satisfying the justification condition for the Markov approximation, γa ≪ Γf,a.

Putting the conditions together,

$${\alpha }_{a}{U}_{a}\frac{| {v}_{a}{| }^{2}}{{U}_{a}^{2}}\lesssim \frac{P{e}^{2}}{{\epsilon }_{0}{m}_{0}c}\frac{1}{{\omega }_{0}{\Gamma }_{f,a}}\frac{| {v}_{a}{| }^{2}}{{U}_{a}^{2}}={\gamma }_{a}\, \ll\, {\Gamma }_{f,a}.$$
(41)

This shows that the required pump power P to achieve sign inversion becomes less by choosing the higher-energy state that has a longer lifetime (i.e., smaller Γf,a) as shown in Eq. (7) but small Γf,a makes it more difficult to satisfy the Markovian condition γa ≪ Γf,a. We remark that a smaller c-d mixing ∣va∣/Ua helps satisfy the Markovian condition γa ≪ Γf,a without modifying the condition for the sign inversion, which physically makes sense because small va makes the double-occupied state rarer and hence rarer for the electrons to escape from the relevant system.

Comparison to cold atom experiments

It is interesting to compare our proposal relevant to solid-state systems to the recent cold atom experiment of dissipative Fermi Hubbard model55,56, where they demonstrated a dynamic sign reversal of interactions. In their experiment, similar to our situation, they introduced a controlled decay channel that is activated only when the sites are double occupied, causing both atoms to decay whenever they are on the same site. They demonstrated that this engineered dissipation decreases the anti-ferromagnetic correlation (present in the ground state) and increases the ferromagnetic correlation, again analogous to our sign reversal of effective interactions. We briefly note, however, that the possibility of implementing non-reciprocal interactions was not explored in their work.

In contrast to our solid-state case, where the coupling to the environment is unavoidable, their cold atomic systems are almost perfectly isolated from the environment other than the decay to the vacuum they purposely introduced. This fundamental difference critically impacts the resulting dynamics. First, in our proposal, the surrounding environment (i.e., the conduction band) immediately compensates for the lost electrons such that localized orbitals are always singly occupied, while their atomic system only has a loss channel. As a result, their dissipation stops activating when the atoms stop colliding, resulting in a strong initial state dependence on the final configuration. This is in stark contrast to ours, where no initial-state dependence is present and even exhibits persistent time-dependent to a collective chase and runaway phase due to non-reciprocal interaction. Second, the Gilbert damping (present in our system) is absent in the cold atomic systems, as there is no environment where the atoms can dissipate their spin angular momentum. The competition between the friction (that drives the system toward equilibrium) and the light-induced dissipative interaction is hence a unique feature of our proposal for solid-state systems.