Introduction

Flow-weighted (FW) networks, often represented by directed and weighted edges whose weights represent the amount of flow between nodes1,2, are ubiquitous in many domains, including passenger movement in transportation, information dissemination in society, and capital circulation in the economy. However, these networks are vulnerable to node or link failures, where even small damage can cause cascading failures and catastrophic collapses, attracting significant attention in the past decades. Early approaches focused largely on structural resilience3,4,5, also known as network robustness6,7—the system’s ability to retain large-scale connectivity in the face of attacks. It is usually characterized by analyzing how the size of the giant component (G) changes as nodes or edges are randomly removed using percolation theory to determine the minimum structural requirements a network must meet to support its functionality8,9,10,11,12,13,14,15. However, resilience is not purely a structural problem16,17,18 (Fig. 1a–d). Consider transportation networks, which can become gridlocked in a natural disaster even if the underlying roads and railways are unscathed. To truly address the dynamical resilience of FW networks, we must consider the flow dynamic models and cascading failures due to flow reallocation (Fig. 1e–g), ultimately resulting in a large-scale collapse of network connectivity.

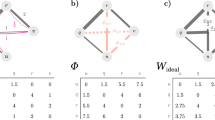
Fig. 1: A general resilience analysis framework of high-order interactions of the FW network.
figure 1

a In Scenario 1, under an intact network topology, this flow allocation scheme causes slight congestion, resulting in a declined flow delivery function. b Scenario 2 maintains the same network structure as Scenario 1 but adopts a different flow allocation scheme, and no congestion is observed. c After one edge is damaged in Scenario 1, although the network remains connected, capacity limitations under this flow allocation scheme lead to severe congestion, which significantly degrades the flow delivery function. d Scenario 2 experiences more severe damage, resulting in a disconnected network, yet no congestion occurs. This indicates a disparity between the structural resilience and dynamical resilience of the FW network. e–g During disturbances, the FW network experiences flow redistribution and disturbance propagation, ultimately leading to cascading failures. h Initial state of the FW network before hypergraph construction. i Small-scale cascading failures occur after certain nodes in the network are disturbed. j Coupled effects emerge from small-scale cascading failures. k The network is divided into several distinct clusters. l The emergence of the Black Swan node results in global-scale failures. m Matrix representation of the hypergraph. n Black swan node in the hypergraph causes network-wide impact. o Protecting the Black Swan node from failure, the hypergraph remains connected. p The removal of a key hyperedge leads to a percolation transition in the hypergraph. q The distribution of hypergraph cardinality. r Percolation transition process on the hypergraph. s Forms of hyper-motifs existing in the network post-percolation transition. Hyper-motifs composed of more hyperedges can be represented by hyper-motifs formed by pairwise combinations. Therefore, this study only considers hyper-motifs formed by pairwise combinations.

Full size image

Growing evidence reveals that the cascading failure caused by perturbing a node depends not only on that node’s properties but also on the network topology, flow dynamics, and external disturbances19,20,21. Although we consider FW networks including only pairwise interactions (Fig. 1h), disrupting a single node can trigger failures of multiple nodes. All the affected nodes can be viewed as collectively forming a higher-order interaction, with the event acting as a hyperedge that connects them beyond simple pairwise relationships (Fig. 1i). As the number of perturbed nodes increases, some trigger minor cascades, while others unleash large-scale failures, creating a complex and heterogeneous hypergraph (Fig. 1j–l). Recent substantial evidence indicates that higher-order interactions provide an effective framework for decoding the intricacies of network dynamics22,23,24,25,26,27, prompting us to develop a hypergraph-based framework for the resilience analysis of FW networks28.

To address these challenges, we develop a framework for analyzing the dynamical resilience in FW networks through high-order interactions. Specifically, we map perturbed pairwise interacting FW networks as hypergraphs through Coupled Map Lattices-based (CML-based) cascading dynamics, where hyperedges serve as a tool to encode the dynamic cascades. When disturbances are sufficiently large, the failure of a single node can lead to network-wide impacts; we refer to such nodes as Black Swan nodes, which can be identified using a threshold-based clustering method29 (see the “Methods” section for details). Subsequently, we observed a percolation transition in the hypergraph and objectively evaluated dynamical resilience through hyper-motifs (Fig. 1m–s). These findings demonstrate the effectiveness of our framework and have significant implications for enhancing the resilience of real-world FW networks.

Results

FW network dynamic propagation models

Flow propagation phenomena exhibit distinct characteristics across different real-world FW networks. For instance, the trophic lengths of food web networks are constrained by energy transfer efficiency, while transportation networks experience congestion propagation due to vehicle flow dynamics. To characterize these diverse propagation mechanisms in FW networks, researchers have developed various dynamical models, including the Motter-Lai model for overload failures in infrastructure networks and the SIR model for epidemic spreading30,31. Recently, CML models have been extensively employed to describe flow propagation dynamics in FW networks across multiple domains32,33,34,35,36, such as the non-linear dynamics and bifurcation phenomena in biological neural networks37,38, spatiotemporal system recognition in computational neural networks39, and cascading failures in transportation systems40. To capture the cascading dynamics in FW networks, we extend the existing model as shown in Eq. (1).

$$\begin{array}{rcl}{x}_{i}(t)=\left|\begin{array}{c}(1-{\mu }_{1}-{\mu }_{2})\varphi ({x}_{i}(t-1))+{\mu }_{1}{\sum}_{{{\rm{\forall }}}j\in N,j\ne i}\frac{{f}_{ij}\varphi ({x}_{j}(t-1))}{{S}_{i}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}}+\\ {\mu }_{2}{\sum}_{{{\forall }}j\in N,j\ne i}\frac{{f}_{ji}\varphi ({x}_{j}(t-1))}{{S}_{i}^{{{\rm{i}}}{{\rm{n}}}}}\end{array}\right|+R\end{array}$$
(1)

where \(\varphi \left(x\right)\) represents a chaotic logistic mapping function, signifying the evolution of the node’s state at the previous time34; \({x}_{i}(t)\) denotes the status of node i at moment t; μ1 and \(\mu\)2 are the coupling coefficients of each term in the model, representing the degree to which the current node state is influenced by that component. The first part of the model represents the inheritance of the current node state from the previous timestep node state, the second part represents the impact of the outgoing flow, and the third part represents the impact of the incoming flow. If μ1 = 0.2, and μ2 = 0.3, it implies that the current node state inherits 50% from the previous timestep node state, with 20% influenced by the surrounding outgoing flow, and 30% influenced by the surrounding incoming flow. In all experiments presented in this study, unless otherwise specified, we set \({\mu }_{1}={\mu }_{2}=0.4\); \({S}_{i}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}\) and \({S}_{i}^{{{\rm{i}}}{{\rm{n}}}}\) respectively represent the sum of the outflow and inflow at node \(i\); \(N\) is the set of all nodes in the network; \(R\) represents a given perturbation factor for the node, which typically ranges within the interval \(R=(0,\,+\infty ]\), and a larger value signifies a stronger disturbance. The calculation methods for the various parts of the model are shown in Eqs. (2)–(4).

$${S}_{i}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}=\sum\limits_{{{\rm{\forall }}}j\in N,j\ne i}{f}_{ij}$$
(2)
$${S}_{i}^{{{\rm{i}}}{{\rm{n}}}}=\sum\limits_{{{\rm{\forall }}}j\in N,j\ne i}{f}_{ji}$$
(3)
$$\varphi \left(x\right)=4x(1-x)$$
(4)

The chaotic logistic mapping function ensures the stable inheritance of the node state (\({x}_{i}\left(t\right)\in (0,\,1]\), \(\varphi \left(x\right)\in (0,\,1]\)). When the node state value \({x}_{i}(t) > 1\), the node is considered failed, and \({x}_{i}(t)\) is set to 0. The initial state of each node, \({x}_{i}(0)\), is represented by the ratio of the node’s current flow to the maximum flow among nodes in the network, as shown in Eq. (5).

$${x}_{i}(0)=\frac{{S}_{i}^{{{\rm{i}}}{{\rm{n}}}}+{S}_{i}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}}{max\{{S}_{i}^{{{\rm{i}}}{{\rm{n}}}}+{S}_{i}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}\}}$$
(5)

During the CML simulation process, if a node in the FW network fails, the flow passing through this node needs to be redistributed. We assume that after the node fails, the flow of this node is allocated to the nearest K nodes, with each node being allocated a flow size proportional to its own flow share. For the failed node, since its own flow is 0, there will be no allocation to this failed node during the flow distribution. This can be specifically expressed using Eqs. (6) and (7).

$${f}_{{ki}}={S}_{k}^{{{\rm{in}}}}\frac{{S}_{i}^{{{\rm{in}}}}}{\displaystyle {\sum }_{i=1}^{K}{S}_{i}^{{{\rm{in}}}}}$$
(6)
$${f}_{ik}={S}_{k}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}\frac{{S}_{i}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}}{\displaystyle {\sum }_{i=1}^{K}{S}_{i}^{{{\rm{o}}}{{\rm{u}}}{{\rm{t}}}}}$$
(7)

where \({f}_{{ki}}\) represents the inflow allocated to node \(i\), and \({f}_{{ik}}\) represents the outflow allocated to node \(i\). In fact, the flow allocation to neighboring nodes from a failed node is subject to a degree constraint such that \(K\le {k}_{i}\), \(i\in N\), implying that for a given network, the set of possible \(K\) values is \(\left\{1,\,2,\,...,\max \left\{{k}_{i}\right\}\right\}\). Throughout all experiments presented in this paper, unless otherwise specified, we set \(K=7\). The detailed steps for cascading failure simulation based on the CML model and hypergraph construction can be found in the Methods section.

Topological analysis of real FW networks

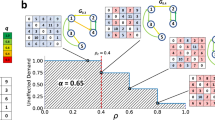
Before assessing the resilience of FW networks, we first examine the fundamental topological characteristics across six real-world FW networks from distinct domains (as shown in Supplementary Table 1 in the Supplementary Information, SI), namely the European email social network, the United States congressional voting network, the economic trade network, the Chinese transportation network, the United States wet food web network, and the United States dry food web network (referred to as Nets 1–6 in subsequent discussions). Subsequently, we compared the hyperedge cardinality distributions when mapping FW networks to hypergraphs under Motter–Lai-based cascading dynamics, SIR dynamics (the details of these two models are provided in the Methods), and CML-based cascading dynamics41,42, as shown in Fig. 2a. Here, \(C\) denotes the hyperedge cardinality, and \({p}_{C}\) represents the occurrence probability of hyperedges with size \(C\). It can be observed that all six FW networks exhibit outliers (red squares) under the three dynamical models. The sizes of these outliers approach the network scale, indicating that the cascading failures caused by these outliers would lead to systemic collapse. We refer to these outliers as Black Swan nodes. To identify Black Swan nodes in networks, we adopt cardinality as a node feature and apply threshold-based K-means clustering to classify nodes into two sets (\(P\) and \(\bar{P}\)). The implementation involves two steps: (1) Determine whether hyperedges exceeding the given threshold size \(T\left|N\right|\) exist in the network, where \(T\in \left[{\mathrm{0,1}}\right]\). If none are found, no Black Swan nodes exist, and \(P=N,\bar{P}=\varnothing\). If such hyperedges exist, (2) Initialize cluster centers using the minimum and maximum hyperedge sizes, then apply K-means to identify Black Swan nodes. \(\bar{P}\) is the set of Black Swan nodes and \(P=N-\bar{P}\) (refer to the “Methods” section for the details of Black Swan nodes detection approach). The fitting results of nodes in \(P\) (blue dots) exhibit characteristics of a power-law distribution but display distinct slopes under different models. And the distribution demonstrates Lévy features when nodes in \(P\) and \(\bar{P}\) are treated as a whole43 (for a detailed analysis of different parameters of the CML model, please refer to Supplementary Figs. 2–9). Such Black Swan events not only appear in the cascade failures of complex networks, but also in human hunting and gathering behaviors44, economic growth fluctuations45, and animal movement processes46. Therefore, a thorough analysis of the characteristics of these nodes is crucial for understanding FW network resilience.

Fig. 2: Cardinality distribution and Black Swan nodes.
figure 2

a The probability distribution of the cardinality in real-world network hypergraphs based on different dynamic models. The green solid line signifies the fitting condition after the exclusion of outliers, resulting in a considerably improved fit for the local data. Consequently, it can be posited that the local data conforms to a power-law distribution, yet when accounting for outliers, the global data adheres to a Lévy distribution. Different networks exhibit varying degrees of resilience to perturbations due to their inherent characteristics, and they demonstrate similar properties under varying disturbances. b Hyperedge cardinality distributions for three types of network models under varying parameters. In both random and scale-free networks, the number of connections increases with the gradual rise in parameters, leading to an increased probability of the emergence of Black Swan nodes. This is attributed to disturbances and flow being able to propagate through an increasing number of pathways, thereby exerting a larger impact within the system. Since the average degree of small-world networks does not change with parameter increases, the probability of Black Swan nodes arising in these networks does not exhibit significant variation.

Full size image

The cardinality distribution in synthetic networks also demonstrates similar properties, as shown in Fig. 2b, where \({\varepsilon }_{{{\rm{r}}}}\) represents the probability of connection between two nodes in a random network model, \({\varepsilon }_{{{\rm{s}}}{{\rm{f}}}}\) represents the number of connections between new and existing nodes in a scale-free network model, and \({\varepsilon }_{{{\rm{s}}}{{\rm{w}}}}\) represents the probability of rewiring long-range connections in a small-world network (see Supplementary Figs. 10–13 for more results on synthetic networks). These conclusions indicate that whether in real-world FW networks or synthetic networks, there inevitably exist some high-influence nodes that, once disrupted, have a significant impact47,48. If such nodes could be reasonably protected, it would significantly enhance the network’s resilience.

Percolation transition in FW network

We compared the differences in percolation transition processes under four distinct percolation rules. These rules are predicated on the principles of maximum flow, maximum degree, minimum flow, and minimum degree, respectively, and map onto four varied real-world scenarios. In reality, nodes that boast a higher flow or a greater degree are frequently deemed more critical and are thus more vulnerable to targeted attacks; conversely, nodes with a lower flow or a reduced degree often receive less attention and are more prone to spontaneous failures, especially when protective measures fall short. Fig. 3 illustrates the percolation process for various networks under the percolation rules predicated on maximal flow. It is observable that on these real-world FW networks, a distinct percolation transition phenomenon emerges. In the other three rule-based scenarios (see Supplementary Figs. 14–18), however, the network displayed no evident signs of percolation transition, indicating that flow plays a decisive role in the network properties within the FW network.

Fig. 3: The process of network percolation under maximum flow rule in the real-world FW network.
figure 3

Diverse networks demonstrate distinct phase transition points, with a delayed percolation transition indicating a diminished resilience of the network at that juncture. Near the critical percolation threshold \({q}_{{{\rm{c}}}}\), the size of the giant component G drops sharply, and the size of the second giant component SG reaches its peak. a–d FW networks formed by human activities in various fields. e, f FW networks formed by species predation relationships in nature.

Full size image

We analyze the impact of varying parameter values on the critical percolation threshold of the original network, as well as on networks that have been reinforced by four other resilience enhancement strategies (as shown in Supplementary Figs. 19–27). To be specific, the resilience enhancement strategy based on the CML simulation model (CML-based strategy) entails prioritizing the fortification of Black Swan nodes. The flow-based resilience enhancement strategy (flow-based strategy) involves prioritizing the reinforcement of nodes with higher flow, the degree-based resilience enhancement strategy (degree-based strategy) emphasizes the strengthening of nodes with greater degree, and the random-based resilience enhancement strategy (random-based strategy) serves as a benchmark model against which other enhanced strategies are compared. We simulate a random-based strategy on all networks 100 times and then average the results to ensure statistical robustness in our findings. In our study, we enhance the resilience of 10% of nodes across all networks, operating under the assumption that these reinforced nodes do not succumb to cascading failures subsequent to perturbations.

We compared the variations of critical percolation thresholds under no enhancement strategy and four enhancement strategies, as shown in Fig. 4b, d, f, h, j, l. In Nets 1–4, flow-based strategy and degree-based strategy performed comparably, slightly underperforming the CML-based strategy; however, in Nets 5 and 6, the CML-based strategy and flow-based strategy exhibited similar performance, outperforming the degree-based strategy. The dynamical resilience of networks under the Random-based strategy remained the lowest among the four enhancement strategies, only marginally higher than that of networks without enhancement.

Fig. 4: Comparison and analysis of the effects of different enhancement strategies.
figure 4

a, c, e, g, i, k Joint distributions of node flow and degree for Nets 1–6, and the Black Swan nodes are emphasized with triangles outlined in black. b, d, f, h, j, l The critical percolation thresholds under four scenarios for Nets 1–6. “O” represents the origin network without any enhancement strategy, “C” denotes the CML-based strategy, “F” signifies the flow-based strategy, “D” corresponds to the degree-based strategy, and “Rd” represents the random-based strategy. a, c, e, g Nets 1–4 exhibit analogous characteristics in their joint flow-degree distributions. i, k Nets 5 and 6 also manifest comparable joint flow-degree distribution characteristics. b, d, f, h Within Nets 1–4, the flow-based strategy and degree-based strategy show parallel performance. j and l In Nets 5 and 6, the performance of the CML-based strategy aligns closely with that of the flow-based strategy.

Full size image

The efficacy of the four methods for enhancing resilience varies across different networks, attributable to the intrinsic characteristics of each network49. For instance, Nets 1–4 are not naturally occurring but artificially constructed. Within these networks, nodes with higher degrees tend to handle more substantial flow; hence, the performance of the degree-based strategy exhibits similarities to the flow-based strategy. Nets 5 and 6 represent naturally formed food web networks, where producers (plants) inherently possess the highest carbon content. As one ascends the trophic levels, higher-order consumers exhibit lower carbon content. Under these circumstances, producer nodes may not exhibit high degrees but sustain significant flow; therefore, the CML-based strategy demonstrates results comparable to the flow-based strategy and significantly outperforms the degree-based strategy.

In summary, since network cascading failures represent a dynamic process, the CML-based strategy is adept at identifying pivotal nodes when faced with various disturbances, whereas the key nodes identified by the other three methods contribute only to enhancing network resilience.

Various stable hyper-motifs in FW network

Motifs and hyper-motifs serve as fundamental meso-scale structures in network composition, playing a critical role in understanding network dynamics and resilience50,51,52. After the percolation transition occurs in the network, the Black Swan nodes are reasonably protected, greatly enhancing the network's resilience. However, small-scale, interdependent cascading failure processes persist within the network. These interrelated cascading failure processes, which remain difficult to eliminate even after resilience enhancement, can be well-represented by stable hyper-motifs. The nodes covered by these patterns could still cause localized impacts on the network if attacked. In basic graphs, hyper-motifs are often defined as combinations of different motifs, categorized into directed and undirected types52,53. However, there are still differing views on the definition of hyper-motifs in hypergraphs. For example, Lee et al.54 suggest that hyper-motifs are used to describe the connectivity patterns of three connected hyperedges, whereas Lotito et al.55 define hyper-motifs as subgraphs involving a given number of nodes, which can be connected through higher-order interactions of arbitrary order. Therefore, providing a rigorous definition of hyper-motifs in the context of hypergraphs is critical56. In this study, we define a certain class of hyper-motifs \(\Pi (u,v)\) in hypergraphs as all patterns that include \(u\) hyperedges, each containing a maximum of \(v\) nodes. It is evident that there exists \(\Pi \left(u,v\right)\in \Pi (u,v+1)\) and \(\Pi \left(u,v\right)\cap \Pi \left(u+1,v\right)=\varnothing\). Fig. 5a illustrates all hyper-motifs contained in \(\Pi ({\mathrm{2,4}})\).

Fig. 5: Employing hyper-motifs to analyze the local resilience of the FW network.
figure 5

Owing to the heterogeneous scales of networks, a direct comparison of the frequency of hyper-motifs across distinct networks is devoid of significance. This stems from the observation that, purely in terms of quantity, networks of a larger scale tend to present an increased count of hyper-motifs. Consequently, we undertake a comparative analysis post-normalization of the hyper-motif occurrences across networks of varying scales, for which the specific methodology is delineated in the “Methods” section. a All kinds of hyper-motifs in \(\Pi ({\mathrm{2,4}})\). b The normalized occurrence frequency of hyper-motifs. c A higher value indicates poorer local resilience, whereas networks characterized by high substitutability tend to demonstrate greater local resilience.

Full size image

We quantified the normalized counts of all \(\Pi ({\mathrm{2,4}})\) hyper-motifs throughout the percolation process in the six real-world networks, as shown in Fig. 5b. During the dry season, the ecological interactions between Florida’s taxa become more locally fragile, and the interspecies impacts are more pronounced, leading to a more diverse exhibition of stable hyper-motifs in Net 6. In contrast, during the wet season, when both flora and fauna thrive and food sources are more abundant, the resilience of each taxon is markedly superior to that of the dry season, resulting in a reduction in both the diversity and quantity of stable hyper-motifs. Therefore, Nets 5 and 6 show the starkest contrast. These findings indicate that distinct stable hyper-motifs signify variations in the local vulnerability of FW networks to disturbances, and different networks tend to develop various hyper-motif structures.

However, a network’s global resilience can differ significantly from its local resilience57. For instance, in a regional power grid, large-scale outages may be rare due to strong global resilience; however, localized perturbations can still trigger local cascading failures. To evaluate local resilience, we employed stable hyper-motifs, as depicted in Fig. 5c (for details on the metric calculation, refer to Supplementary Eq. (3) and Supplementary Fig. 28). Here, \({R}_{l}\) denotes the network’s local resilience, referring to the resilience of the network as represented by the residual structure. Our results align closely with empirical observations. For example, while Nets 5 and 6 appear comparable in global resilience, a local analysis reveals that the food web during the dry season is significantly more vulnerable than during the rainy season. Similarly, in Nets 1 and 2, social or voting relationships exhibit strong substitutability and diversity, contributing to stronger local resilience, like Net 3. In contrast, Net 4, representing human mobility patterns58, exhibit a high degree of spatiotemporal correlation, resulting in severe congestion on certain routes. As a result, Net 4 is more vulnerable to local cascading failures, negatively impacting its local resilience.

Discussion

This study begins with pairwise-interacting FW networks, disregarding complex features of real-world FW networks59. such as diverse efficiency among various species in food web networks, and maps six real-world FW networks to hypergraphs via CML-based cascading dynamics. We first analyzed the hypergraphs’ cardinality distributions. The results demonstrate that the cardinality distributions generally follow Lévy distributions, but transition to power-law distributions when Black Swan nodes are excluded. Existing research predominantly focuses on power-law distributions or scale-free properties in networks, with limited analysis of Black Swan nodes. In reality, these Black Swan nodes critically determine the dynamical resilience of FW networks60. Subsequently, we compared critical percolation thresholds for Nets 1–6 without enhancement versus four enhancement strategies using percolation theory. The CML-based strategy effectively identifies critical nodes in networks, thereby enhancing the dynamical resilience of FW networks. Following percolation transitions, the cascading failures exhibit discrete characteristics. By quantifying hyper-motif occurrence levels, we achieved deeper insights into FW networks’ cascading dynamics, ultimately enabling comprehensive analysis of dynamical resilience61.

For future research, we believe that our work can be expanded to analyze the dynamic properties of evolving FW networks over time, exploring the formation rules of community phenomena in the early stages of FW evolution, summarizing the formation rules of high-order interactions in the FW network, building a multidimensional resilience assessment framework for FW networks, investigating the nonlinear phenomena within other types of networks62,63,64,65,66, thereby providing theoretical foundation for the design and resilience enhancement of FW networks existing in various fields in the real world67,68,69,70.

Methods

Data processing

We have selected six representative FW networks from the real world. Each network includes data on the node set, along with detailed information on the direction and size of each flow. For Nets 1–3, 5 and 6, which lack tangible distance metrics, we define the distance between nodes through a generalized distance, as presented in Eq. (8).

$${d}_{{ij}}=1-\frac{{f}_{{ij}}}{\mathop{\max }_{i,j\in N,i\ne j}\{\,{f}_{{ij}}\}}$$
(8)

where \({d}_{{ij}}\) represents the distance between node \(i\) and \(j\), \({f}_{{ij}}\) represents the flow between node \(i\) and \(j\), and \(N\) is the set of nodes. The rationale behind defining the generalized distance in this manner is that flow typically favors traversing shorter paths, thus edges with substantial flow have correspondingly shorter distances. The application of this generalized distance is extremely versatile, able to depict flow networks in the real world that do not have actual distances, such as economic trade networks, Internet networks, shopping networks, etc. For Net 4, we employ the distances between nodes as they exist in the real world.

Given that the flow from a node to itself does not interact with other nodes in practical scenarios, we set \({f}_{{ii}}=0,\,\forall i\in N\). Meanwhile, in terms of the generalized distance between nodes, to prevent a portion of the flow from being allocated to the node itself, we set \({d}_{{ii}}=1,\forall i\in N\). Ultimately, we obtain the processed flow matrix and distance matrix as shown below.

$${{\rm{F}}}{{\rm{l}}}{{\rm{o}}}{{\rm{w}}}\,{{\rm{m}}}{{\rm{a}}}{{\rm{t}}}{{\rm{r}}}{{\rm{i}}}{{\rm{x}}}:\,{{{\bf{M}}}}_{{{\bf{F}}}}={({f}_{ij})}_{n\times n},{f}_{ii}=0,{{\rm{\forall }}}i,j\in N$$
$${{\rm{Distance}}}\,{{\rm{matrix}}}:{{{\bf{M}}}}_{{{\bf{D}}}}={({d}_{{ij}})}_{n\times n},{d}_{{ii}}=1,{{\rm{\forall }}}i,j\in N$$

Hypergraph construct method

This section elaborates on the specific methods and steps required to construct the hypergraph based on the given FW network. The robustness validation of the algorithm is detailed in Supplementary Figs. 29–31, and the detailed steps are as shown in Table 1.

Table 1 Hypergraph construction algorithm pseudo-code
Full size table

Hypergraph percolation model

In the proposed hypergraph percolation model within this study, each hyperedge represents the simulation result corresponding to a specific node’s cascading failure after it has suffered a disturbance. This implies that subjecting a node within the network to a certain degree of perturbation, based on the CML model, will result in the propagation of disturbances that lead to cascading faults, furthering the spread of perturbations and flow. This establishes complex interactions between nodes, ultimately causing an area of cascading degradation. We regard these complex interactions as higher-order interactions, which are represented by hyperedges. Upon the disruption of a certain vertex in the hypergraph in accordance with various percolation rules, the corresponding hyperedge in the network is correspondingly removed. In practice, this can be construed as fortifying the resilience of the vertex in the FW network, such that its destruction would not trigger cascading failures affecting other nodes, thereby ensuring the functionality of the network. Hence, for a given threshold \(q\), when the state of the node \({w}_{i}\) is greater than \(q\), high-order interactions are present and the hyperedge is retained; otherwise, the hyperedge is removed, as shown in Eq. (9).

$${h}_{i}=\left\{\begin{array}{cc}{h}_{i},& {w}_{i} > q\\ \left[0,\,\ldots,0\right],& {w}_{i}\le q\end{array}\right.$$
(9)

Herein, \({h}_{i}\) denotes the ith row in the hypergraph matrix, and \({w}_{i}\) signifies the state of the ith node (see Supplementary Fig. 1 for details). Consequently, for a specified \(q\), a hypergraph delineating the influence of cascading failures can be constructed.

In the study, we adopted four different percolation rules, namely, those based on maximal flow, maximal degree, minimal flow, and minimal degree. The differences among these four percolation rules mainly lie in the sequence of node disruption: priority is given to disrupting nodes with the highest flow, nodes with the highest degree, nodes with the lowest flow, and nodes with the lowest degree, respectively. The formula for calculating the node status is shown in Eq. (10), where \({\sigma }_{i}\) represents node \(i\) state quantity, such as flow or degree.

$${w}_{i}=\frac{1-\frac{{\sigma }_{i}}{\max \{{\sigma }_{i}\}}}{\max \left\{1-\frac{{\sigma }_{i}}{\max \{{\sigma }_{i}\}}\right\}}$$
(10)

Black Swan nodes identification

The essential distinction between Black Swan nodes and ordinary nodes lies in the differing number of nodes affected by cascading failures they induce; while the failure of an ordinary node can lead to localized, small-scale cascading faults, the failure of a Black Swan node can trigger widespread cascading faults throughout the network. Thus, the primary criterion for differentiating the two is the extent of the cascading failures caused by perturbations \(R\) to the nodes, denoted as \({{{\rm{C}}}{{\rm{F}}}}_{i}^{R}\), where \(i\in N\).

In any given FW network \({G}_{{{\rm{F}}}{{\rm{W}}}}=(N,E)\), under perturbation \(R\), there exists a set of cascade failure ranges \(\{{{{\rm{C}}}{{\rm{F}}}}_{1}^{R},{{{\rm{C}}}{{\rm{F}}}}_{2}^{R},\ldots,{{{\rm{C}}}{{\rm{F}}}}_{|N|}^{R}\}\) for different nodes. To identify Black Swan nodes in networks, we adopt cardinality as a node feature and apply threshold-based K-means clustering to classify nodes into two sets (\(P\) and \(\bar{P}\)). The implementation involves two steps: (1) Determine whether hyperedges exceeding the given threshold size \(\left|N\right|T\) exist in the network, where \(T\in \left[{\mathrm{0,1}}\right]\) (see Supplementary Fig. 8 for the sensitivity analysis results of \(T\)). If none are found, no Black Swan nodes exist, and \(P=N,\bar{P}=\varnothing\). If such hyperedges exist, (2) Initialize cluster centers using the minimum and maximum hyperedge sizes, then apply K-means to identify Black Swan nodes. \(\bar{P}\) is the set of Black Swan nodes and \(P=N-\bar{P}\).

Stable hyper-motifs normalization

In the process of percolation, upon the occurrence of a phase transition, the network collapses into several smaller components. At this juncture, the internal connectivity of these components relies on short-range hyperedges, which effectively represent localized cascading failures. This means that after a subset of nodes in the network has been appropriately reinforced, extensive failure events within the network are effectively thwarted. However, there still exist stable, interdependent cascading failure processes within the network. Consequently, to denote the persistent interdependencies and interactions of cascading faults post phase transition within the network, we employ the term hyper-motifs. These hyper-motifs are referred to as stable hyper-motifs.

The normalization of hyper-motifs refers to the process of adjusting the counts of hyper-motifs found across networks of various scales, thereby enabling a comparative analysis across different systems. We normalize the stable hyper-motifs in each network using Eq. (11). In this context, \(H\) denotes the set of hyperedges, the term \({\pi }_{i}\) signifies the frequency of occurrence for the type \(i\) of hyper-motif, while \({l}_{i}\) indicates the level of presence for the type \(i\) of hyper-motif.

$${l}_{i}={\pi }_{i}/\left(\begin{array}{c}{|H|}\\ u\end{array}\right)$$
(11)

Motter–Lai model

In the Motter–Lai model, nodes are categorized into two states: operational and failed. Each node is characterized by the flow passing through it and its inherent capacity. During the simulation, if a node fails, the flow that it was carrying is transferred to its neighboring nodes, which may consequently undergo abnormal states (when the flow exceeds their capacity, the capacity is \(\alpha\) times of the initial flow), potentially triggering a cascade of failures. The simulation is considered complete when no new failures occur, and the extent of a node’s failure that leads to subsequent node failures is regarded as the cascade failure range.

SIR model

In the SIR model, we categorize nodes into three distinct states: susceptible (S), infectious (I), and recovered (R). These states undergo unidirectional transitions only. When susceptible individuals come into contact with infectious ones, there is a certain probability, \({\theta }_{1}\), that they will become infectious. Likewise, infectious individuals have a probability, \({\theta }_{2}\), of transitioning to the recovered state.

In the simulation process, the network topology is initially intact, and all nodes are in the susceptible state, denoted as S. A single node is then selected to transition to the infected state, I, marking the initiation of the iterative process. During each iteration, all susceptible nodes connected to an infected node transition to the infected state with a probability of \({\theta }_{1}\), while infected nodes have a probability of \({\theta }_{2}\) to recover. The simulation is set to run for 100 iterations and is repeated 10 times. The extent of the infection caused by the initial node, which includes nodes in the states I and R, is considered the scope of the cascading failure.