Abstract
The ‘abundant-centre’ hypothesis posits that a species’ abundance is highest at its range centre and declines towards its range edge. Recently, the hypothesis has been much debated, with supporting empirical evidence remaining limited. Here, we test the hypothesis on 3660 species using 5,703,589 abundance observations. We summarise species-level patterns and test the effects of dispersal-related species traits and phylogeny on abundance–distance relationships. Support for the hypothesis is dependent on taxonomic group, with abundant-centre patterns being more pronounced for plants but non-significant when summarised across all animals. Dispersal capability does not explain abundance–distance relationships in animals but likely explains abundance patterns in non-woody plants. Phylogeny improves models of abundance–distance patterns for plants but not for animals. Despite this, controlling for phylogeny yields non-significant group-level results for plants, suggesting that only certain, phylogenetically clustered plant groups may conform to abundant-centre patterns. Overall, we demonstrate that abundant-centre patterns are not a general ecological phenomenon; they tend to not apply to animals but can manifest in certain plant groups, depending on dispersal capabilities and evolutionary histories. Leveraging species’ traits that account for dispersal improves models of abundant-centre patterns across geographic space.
Similar content being viewed by others
Introduction
Understanding patterns of biodiversity and the processes that drive them across varying spatial, temporal and taxonomic scales is a shared goal within macroecological and biogeographical research1,2,3. Such information is essential to improving our understanding of species’ responses to environmental change, with applications to invasive species management4,5 and conservation planning6,7.
A common approach to studying macroecological processes and patterns is to develop and test ecogeographical “rules” or “hypotheses”. As outlined by Baiser et al8., over the last decade, the study of ecogeographical rules has seen a resurgence due to increased data availability, methodological advancements and the need for applied research efforts, for example in invasive species management5,9,10 and environmental change research11,12. Historically, many ecogeographical rules were developed to describe scaling relationships in species’ diversity13, body mass14, range size15, and geographical distributions of populations16, such as the ‘abundant-centre’ hypothesis.
The abundant-centre hypothesis derives from early ideas proposed by Grinnell16, who likened the distribution and dispersal of animal populations to those of gas molecules occupying a vacuum17,18. The abundant-centre hypothesis posits that species’ abundances are highest in their range centres and decline towards their range edges17,18,19,20,21,22,23,24. The hypothesis assumes that 1) a species’ geographic range is a representation of its environmental or ecological niche25 and 2) that environmental conditions are more optimal near the centre of a species’ range and less optimal towards the range edges18,26. Since its inception, the abundant-centre hypothesis has been debated by macroecologists and biogeographers alike23,27,28,29,30. It has been tested within many taxonomic groups including birds30,31,32, vascular plants33,34,35, reef fishes22,36,37, mammals38,39,40,41, and coastal invertebrates21,42,43,44,45,46. It has also been tested across taxonomic groups17,23,47. Previous studies have employed an array of methodological approaches, such as focusing on centrality23,48 as opposed to marginality17,49.
Initially, the abundant-centre hypothesis has been tested across species’ geographic space19,21,22,44. Support for the hypothesis remains scarce and recent research has shifted focus towards exploring abundance distributions across species’ environmental or ecological niche space29,30,39,41,48,50,51. Specifically, Dallas et al.23 tested the abundant-centre hypothesis across the geographical and the ecological niche spaces of 1400 species of North American birds, mammals, freshwater fishes and trees, concluding no consistent relationships between abundance and distance from range centre (hereafter ‘abundance–distance relationships’) in either case. Relatedly, Sporbert et al.35 tested multiple macroecological rules, including the abundant-centre hypothesis, on 517 species of European vascular plants, suggesting that mixed support for abundant-centre patterns are likely driven by various environmental factors. It is often assumed that species’ abundance is positively correlated with environmental suitability (an assumption of niche modelling), but this is far from always being the case52. To date, inconclusive empirical support for the abundant-centre hypothesis has been repeatedly found across geographic and ecological niche space17,23,35,47. It also remains unclear why abundant-centre patterns are rarely dominant (although others have concluded support45,53). Explanations may include differences in the methods used17, interpretation of results or taxonomic groups studied, e.g., species that possess certain life histories such as juvenile planktonic life stages46.
A major assumption of the hypothesis is that it assumes a species is in equilibrium with its environment, and that environmental conditions influencing abundance change gradually and monotonically from the range centre towards the range edge—as implied by Grinnell16. Similarly, it also assumes that conspecific populations are equally adapted to their environments, with recent research using species distribution models challenging this notion, instead finding that species demonstrate local adaptation across their ranges54. The hypothesis also assumes that optimal environments occur in the centre of a species’ range and that the environment is strongly spatially autocorrelated. Accounting for these broad assumptions when testing the hypothesis, we would expect to find that species with higher dispersal capabilities, such as birds, larger-bodied mammals (e.g., large-bodied ungulates vs. small mammals) and plants with faster life cycles (e.g., non-woody vs. woody plants), may tend to follow abundant-centre patterns. These species may be better at tracking changing environments55,56, maintaining higher abundances in their range centres where environmental conditions are assumed to be most favourable57. Given this, the underlying assumptions of equilibrial population dynamics across a species’ geographic range assumes that population fluctuations are trivial, and that the species is not actively expanding its range.
Since the foundational work of Martínez-Meyer et al.,48 exploration of abundant-centre patterns has shifted towards ecological niche space. However, no clear consensus has been reached within the scientific community as to which type of “space” is most appropriate to test this highly debated hypothesis, as the evidence supporting either perspective remains unconvincing. Calculating abundance–distance relationships in ecological niche space requires high-resolution data, to accurately capture the niche of the species at the micro-scale, which are often unavailable for most macroecological studies. Furthermore, the same environmental space would be required across all taxonomic groups, using the same environmental predictors, which may be more meaningful for some species than others. As such, fundamental research opportunities remain outstanding in geographic space, which can be explored with available large-scale species distribution data. One of many potential research avenues relates to linking species’ ecological characteristics (species traits), as proxies for dispersal capabilities58, to sampled abundance estimates.
Notably, multi-species analyses could be biased due to phylogenetic non-independence between taxa59,60. Lack of consideration and quantification of species’ evolutionary relatedness limits our understanding of global abundance–distance relationships, resulting in calls for more robust studies incorporating appropriate comparative phylogenetic techniques61. To date, other than Dallas et al.23, who explored the effects of body size and phylogenetic relatedness on support for the abundant-centre hypothesis, and Rivadeneira et al.21, who linked evolutionary history and traits to porcelain crab (Porcellanidae spp.) abundance distributions, there have been no examinations of the effects of species’ traits or phylogeny on support for the hypothesis across large taxonomic and spatial scales.
In this study, we use a trait-based and comparative phylogenetic approach to test the abundant-centre hypothesis across five major taxonomic groups: birds, mammals, freshwater fishes, reef fishes and plants. Given that previous research has suggested that support for the hypothesis may be scale-dependent17,23, and abundance patterns might be closely related to species’ dispersal capabilities17,58,62, we also explore the effects of spatial scale and body size.
Based on previous research on animal distributions, we may expect to find differences between taxonomic groups, aligning with abundant-centre patterns, due to variation in dispersal capabilities between taxa63. Specifically, larger-bodied animals may be expected to conform more to such patterns as they are better able to track changing environments64 (Table S1). Furthermore, omnivorous diets are known to affect dispersal capability, and thus we expect to find a dietary effect on abundance–distance relationships64. Dispersal capability in plants is also known to correlate with height, and to a lesser degree with seed mass65, with taller species and those with smaller seeds being able to disperse further66. Therefore, we expect to find height and seed mass effects on plant abundance–distance relationships (Table S1). In line with r/K-selection theory, species towards the faster end of the fast-slow life-history continuum (i.e., r-selected species) may be better able to track changing environments due to their rapid population fluctuations, relative to K-selected species67,68. Similarly, based on previous research we expect to find effects of functional group69, life span, and life form70, on plant abundance–distance relationships (Table S1). Faster-growing species (e.g., grasses and herbs), and shorter-lived species (e.g., annuals and biennials), should be more likely to conform to abundant-centre patterns relative to their longer-lived and slower-growing congeners (e.g., trees). In addition, if abundant-edge distributions accurately represent invasion fronts—benefiting invasive species when dispersing71—then we may expect invasive species to not conform to abundant-centre patterns (Table S1). Dispersal capability is an important process that moderates a species’ range size72; therefore, we expect that species with larger ranges are better adapters to the wider environment and will conform to abundant-centre patterns. Concurrently, terrestrial species distributed at higher latitudes tend to have larger ranges73, and abundant-centre patterns may be more detectable at higher latitudes (Table S1). Finally, if abundant-centre patterns manifest themselves in species groups that possess similar dispersal capabilities through trait combinations, then we may expect to find abundant-centres nested within phylogenetically clustered taxa. To test this, we expect to find strong phylogenetic signals for abundant-centre conforming taxa but not for those that do not conform to the expected pattern.
Here, we use field observations of abundance to explore the effects of dispersal capability on species’ abundance patterns using traits as proxies. We examine differences in conformity to abundant-centre patterns between taxonomic groups and test for the effects of spatial scale by compiling the following data for animals: 1) taxonomic group (categorical), 2) body size (cm; g), 3) invasive status (binary), 4) feeding guild (categorical), 6) extent (km), 7) grain (km2) and 8) focus (km2); and for plants: 1) functional group (categorical), 2) mean plant height (m), 3) invasive status (binary), 4) life span (categorical), 5) life form (categorical), 6) seed mass (mg), 7) extent (km), 8) grain (km2) and 9) focus (km2). To explore spatial patterns within global abundance–distance relationships, we also compiled geographic data for species-level range sizes (km2) and calculated absolute latitudes (°) from range centroids.
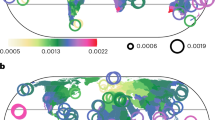
We compute abundance–distance correlation coefficients (transformed to Fisher’s Z values) which quantify the relationships between species’ abundance and distance to range centroids from 14 published studies covering 3060 animal and 600 plant species. Collectively, we analyse 3,698,959 and 2,004,630 abundance observations for animals and plants, respectively (Table 1; Fig. 1a). The animal dataset includes 1683 bird species, 1,131 reef fish species, 202 mammal species and 44 freshwater fish species (Fig. 1a-d; Fig. 1f). The plant dataset comprises 386 herb species, 120 trees, 65 grasses and 29 shrubs (Fig. 1e). On average, there were 1209 ± 1944 ( ± SD) animal abundance observations (range: 5–11,948), and 3341 ± 5182 (range: 5–67,486) plant abundance observations (Table 1). Using separate weighted linear effects models to summarise the compiled correlation coefficients from abundance–distance relationships into grand mean and subgroup average Fisher’s Z values, we test for the effects of dispersal-related traits and range size variables on conformity to abundant-centre patterns (Table S2). To account for differences in Fisher’s Z precision, we weighted each transformed correlation coefficient by the natural logarithm of the number of abundance observations.
a all taxonomic groups combined, b birds, c freshwater fishes, d mammals, e plants and f reef fishes. Data for 3060 animal and 600 plant species were subsequently used for statistical analyses. Maps represent the number of species with abundance data per 2.5° grid cell (for display purposes only), reprojected into the Robinson projection. Values range from dark purple (low number of species) to light yellow (high number species), with breaks obtained using a square-root transformation. Data underlying this figure are provided in Dryad at https://doi.org/10.5061/dryad.zgmsbccj2.
Our results suggest that plants with better dispersal capabilities tend to conform to abundant-centre patterns. For animals, support for abundant-centre patterns is negligible across all taxonomic groups. Accounting for species’ evolutionary histories improves models of abundance–distance relationships in geographic space but only for plants. Phylogenetically clustered taxa, such as non-woody plants, tend to conform to abundant-centre patterns. Evolutionary history did not explain abundance–distance relationships in animals, and thus evidence for abundant-centre patterns in animals remains weak.
Results
Abundance–distance relationships are relatively rare across taxonomic groups
Overall, global abundance–distance relationships differed between the animal and the plant data sets. Animals showed no clear abundant-centre patterns (Fig. 2a–d; Fig. 3a; grand mean of Fisher’s Z = 0.006 ± 0.004 (SE), t = 1.447, df = 3059, p = 0.148), with 47% (n = 1430; ntotal = 3060) of animal species showing negative correlations between abundance and distance from the range centroid (indicative of an abundant-centre pattern) (Table 2). Of these negative correlations, 43% (n = 620 of 1430) were statistically significant, i.e., p < 0.05. Reef fishes and mammals generally did not conform to abundant-centre patterns, with 33% (n = 370 of 1131) and 50% (n = 101 of 202) of species within these groups having negative abundance–distance correlations, respectively (Fig. 2c, d; Table 2). Birds and freshwater fishes showed some support for abundant-centre patterns. However, these between-group differences were marginal, with 56% (n = 936 of 1683) and 52% (n = 23 of 44) of species showing negative abundance–distance correlations, respectively (Fig. 2a, b; Table 2).
Abundance–distance relationships were calculated using Spearman’s Rank Correlation Coefficients (rs) visualised for animal taxonomic group (birds, freshwater fishes, mammals and reef fishes) and plant functional group (grasses, herbs, shrubs and trees). An ‘abundant-centre’ distribution would be expected to feature predominantly negative rs values (illustrated in top-left panel). a Kernel density distribution of abundance–distance relationships for 1683 bird species, b Kernel density distribution of abundance–distance relationships for 44 freshwater fish species, c Kernel density distribution of abundance–distance relationships for 202 mammal species, d Kernel density distribution of abundance–distance relationships for 1131 reef fish species, e Kernel density distribution of abundance–distance relationships for 65 grass species, f Kernel density distribution of abundance–distance relationships for 386 herb species, g Kernel density distribution of abundance–distance relationships for 29 shrub species, and h) Kernel density distribution of abundance–distance relationships for 120 tree species. Source data are provided as a Source Data file.
a Effects of species traits and geographical variables for 3060 animal species, and b effects of species traits and geographical variables for 600 plant species. Negative Fisher’s Z scores (left of dotted line) indicate an ‘abundant-centre’ distribution effect. Group-level Z values were derived from marginal mean estimates for categorical predictors (animals: Taxonomic group, Invasiveness and Feeding guild; plants: Functional group, Invasive and Life Form) and from regression relationships for continuous predictors (animals: log10 Body size (cm; g), Absolute latitude (°) and log10 Range size (km2); plants: log10 Mean plant height (m), Absolute latitude (°), log10 Range size (km2) and log10 Seed mass (mg), each scaled to unit variance) (see Table S4 for interaction model outputs). Error bars represent approximated 95% confidence intervals. Source data are provided as a Source Data file.
Plants generally showed some consistency with the abundant-centre hypothesis (Fig. 2e–h; Fig. 3b; grand mean of Fisher’s Z = −0.08 ± 0.005 (SE), t = −15.7, p < 0.001), with 75% (n = 446 of 600) of plant species having negative correlations between abundance and distance from the range centroid (Table 2). Of these negative correlations, 75% (n = 332 of 446) were statistically significant. Grasses, herbs and shrubs tended to follow abundant-centre patterns with 82% (n = 53 of 65), 84% (n = 332 of 386) and 62% (n = 18 of 29) of species possessing negative abundance-distance correlations, respectively (Fig. 2e-g; Table 2). Trees were the only plant subgroup inconsistent with abundant-centre patterns, with only 44% (n = 53 of 120) of species showing negative abundance-distance correlations (Fig. 2h; Table 2).
Accounting for species traits and range size can improve models of abundant-centre patterns across geographic space
We used a stepwise model selection approach to test the significance of different predictor variables for the distribution of Fishers Z scores for animal (i.e., taxonomic group, invasive status, body mass, feeding guild, absolute latitude and log10 range size) and plant species (i.e., functional group, invasive status, life form, absolute latitude, and log10 seed mass). For animals, the most parsimonious model included the taxonomic group and log10 transformed range size with predicted negative abundance–distance relationships for birds, positive relationships for mammals and reef fishes, and a positive effect of log10 range size on abundance–distance relationships (Fig. 3a; Table S3).
For plants, the most parsimonious model included the functional group, invasive status, absolute latitude and log10 transformed seed mass. This model predicted negative abundance–distance relationships for grasses and herbs, more negative relationships for invasive versus non-invasive plants and a negative effect of log10 seed mass and absolute latitude on abundance–distance relationships (Fig. 3b; Table S3).
Repeating this stepwise variable selection approach for the different taxonomic groups yielded different sets of significant predictors. For birds and freshwater fishes, feeding guild was the only significant predictor indicating that herbivorous species showed more negative abundance-distance relationships than carnivores or omnivores (Table S4). For reef fishes, there was a significant negative effect of absolute latitude on abundance–distance relationships (Table S4). However, there were no significant predictors of abundance–distance relationships for mammals (Table S4). Within plant taxa, grasses and herbs showed more negative relationships at higher latitudes, whereas a higher number of negative relationships were found for invasive shrubs relative to non-invasive species, and for those with larger seed mass (Table S4). For trees, none of the predictors were significantly related to the observed differences in abundance–distance relationships (Table S4).
Interactions between species traits and geographic variables
Separately within the animal and the plant data sets, we explored whether linear models could be improved by incorporating bivariate interactions between predictor variables. For each data set, we calculated all fixed effect combinations and bivariate interaction terms and selected the most important interactions based on the Akaike Information Criterion (AIC) (Burnham & Anderson 2002). For animals, there were important interaction effects between taxonomic group and feeding guild (group × feeding guild: F1,6 = 3.875, p < 0.001), body size (group × body size: F1,3 = 4.251, p = 0.005) and latitude (group × latitude: F1,3 = 12.111, p < 0.0001) (Fig. 4a–c; Table S5). These interactions indicated that omnivorous mammals and reef fishes more closely approached the expected abundance–distance pattern (while being non-significant compared to herbivorous or carnivorous species which had significantly positive relationships) (Fig. 4a; Table S5). Larger-bodied mammals were more likely to conform to abundant-centre patterns (Fig. 4b), as were mammals and freshwater fishes from higher latitudes (Fig. 4c; Table S5). For plants, there was a significant interaction effect between functional group and seed mass (functional group × seed mass: F1,3 = 6.483, p < 0.001) (Fig. 5a; Table S5), with shrubs that have larger seeds tending to support abundant-centre patterns, whereas invasive species with larger seed mass tended not to conform with this pattern (Fig. 5b; Table S5).
Negative Fisher’s Z scores (left of dotted line) indicate an ‘abundant-centre’ distribution effect, derived from a linear model weighted by the number of abundance observations per species. Interactions modelled as marginal joint effects (Table S5) for a Group × Feeding guild, b Group × log10 Body size (cm; g), c Group × Absolute latitude (°) and d) log10 Body size (cm; g) × Absolute latitude (°). a Error bars represent 95% confidence intervals. Source data are provided as a Source Data file.
Negative effects (left of dotted line) indicate an ‘abundant-centre’ distribution effect, derived from a linear model weighted by the number of abundance observations per species. Interactions modelled as marginal joint effects (Table S5) for a Functional group × log10 Seed mass (mg) and b Invasive status × log10 Seed mass (mg). Source data are provided as a Source Data file.
Phylogenetic signals in abundance–distance relationships
Accounting for phylogenetic relatedness did not improve the model fit for the animal data set (Table 3). Conversely, for plants, incorporating the phylogenetic correction matrix with the observed value of Pagel’s λ (~0.2) significantly improved the model fit and removed the significance of the estimated grand mean effect (Fisher’s Z = −0.04, t = −0.98, p = 0.33). Similarly, our model residuals (tested separately for the bird, fish, mammal, and plant data sets) were mostly independent of species phylogenetic relatedness – again, except for the calculation of the grand mean effect in the plant data set (Table 3).
Discussion
Across what is, to our knowledge, the most extensive global dataset on animal and plant species abundances to have been used for testing the abundant centre hypothesis, we observed that global abundance–distance relationships followed taxon-specific patterns, often including both positive and negative values. Our findings bring some clarity to previous research which yielded little to no support for the abundant-centre hypothesis17,23,34,36,46,53,74. However, in contrast to these studies, we observed that some plant groups appeared to follow abundant-centre patterns, whereas animals did not show any strong tendency toward such patterns. Inclusion of dispersal-related species traits and evolutionary histories improved some of our models of abundance–distance relationships. We expected to find conformity to abundant-centre patterns in species with higher dispersal capabilities. We found that dispersal capability does not explain abundance–distance relationships in animals but likely explains such patterns in non-woody plants, which may be better at tracking changing environments due to shorter generation times and higher dispersal abilities. Our findings suggest that plant species less limited by dispersal constraints are more likely to follow abundant-centre patterns in geographic space. Inclusion of phylogenetic relatedness in abundance–distance relationships returned a phylogenetic signal for certain taxonomic groups, indicating that abundance-distance relationships are not a general phenomenon but are restricted to phylogenetically clustered taxa.
Underlying assumptions may explain why global abundance–distance relationships remain relatively rare
Fundamental assumptions of the abundant-centre hypothesis are that a species is in equilibrium with its environment and that environmental conditions influencing abundance change gradually and monotonically from the range centre towards the range edge. Violation of these assumptions may explain why global abundance–distance relationships were relatively rare across most taxonomic groups. It may be even more challenging to detect abundant-centre patterns in species with fine-scale habitat selection, where changes in structural heterogeneity, orography, aspect, soil type, microclimate and availability of cover structures influence a species’ abundance throughout time and space.
A recent study found general support for abundant-centre patterns in birds57, despite other studies suggesting that these patterns are rarely detected in this group17,23. We failed to detect a strong pattern in our bird data. Wing morphology has been shown to be an important predictor of dispersal distance in birds75,76. To account for this, we conducted a supplementary analysis exploring the effects of the Hand-Wing Index (HWI) on global abundance–distance relationships for 1,683 bird species (see Supplementary Methods). We extracted HWI values from the AVONET database77 and found no significant HWI effect on modelled bird abundance–distance relationships (F1,1681 = 0.0004, p = 0.986, R2 = < 0.001; Table S9). This suggests that dispersal capability in birds does not explain abundance–distance relationships across geographic space.
As predicted, invasive animals did not show support for abundant-centre patterns; however, they also did not show significantly positive abundance–distance relationships, which might be expected of invasion fronts78. Unlike other studies23,35, our test of the abundant-centre hypothesis was global in its approach. Prior to this study, the largest existing test of the hypothesis found weak support for abundant-centre patterns in geographic and ecological niche space23. The authors also attempted to explain variation in abundance–distance relationships by exploring the effects of body size, range size and climatic niche area23. We decided not to use the range size variable calculated by Dallas et al.,23 who interpreted minimum convex polygons (MCPs) around sampling points as proxies for a species’ range, and instead sourced most of our range size estimates from published IUCN expert range maps79. Only where expert range maps were unavailable, we used MCPs for some terrestrial species with small ranges, i.e., understudied species. It must be noted that MCPs have a coarse outer edge at low sampling intensities and are therefore sensitive to outliers80, and sampling efforts only cover most of a species’ range in exceptional circumstances (such as thorough field surveys of endemic species on small islands81). Furthermore, Dallas et al.23 used eBird data to test range-wide abundant-centre patterns in North American birds, which may introduce challenges associated with sampling procedures when calculating abundance–distance relationships57. To ensure that our approach was as comprehensive as possible, we also included the largest data set on birds from Dallas et al.23; however, we are aware that caution must be used when interpreting the results because of the known issues with the use of presence-only data. Traits included in Dallas et al.23—body size, range size and climatic niche area — explained very little variation within their models (birds: R2 = 3%; trees = R2 = 3%, mammals: R2 = 4% and freshwater fishes: R2 = 2%), whereas our most parsimonious trait interactions models explained 5% of model heterogeneity for animals and 16% for plants. An explanation for this may simply lie in the number of dispersal-related traits used to test the hypothesis or the choice of methods used (more robust analytical techniques, which may be more appropriate when testing broad-scale relationships between species abundances and their environments17,50,52.
The use of species traits to explore global abundance–distance relationships enabled strong signals to be detected within a comparatively large data set. Compared to animals, our trait-based method appeared to work better when explaining support for abundant-centre patterns in plants, suggesting that other processes that remain untested here may contribute to the unexplained heterogeneity in observed abundance–distance patterns. Biotic and abiotic processes may include, but are not limited to, interspecific interactions82, spatiotemporal patterns in resource availability83, climate and environmental suitability84, geodiversity85, and pressures from human activities86. Failure to account for phylogeny in ecological regression models may violate independence assumptions87, although previous evidence suggests that phylogeny has no broad effect on modelled abundance–distance relationships at the species level23. Here, we demonstrate that incorporating species’ evolutionary histories in models of abundance–distance relationships can improve model robustness and generalizability. However, this effect appears to depend strongly on the taxonomic group studied, and was only significant in plant species for which common traits through shared ancestries might jointly influence the strength of the abundance–distance relationships. Pagel’s λ assumes that traits follow a Brownian motion model of evolution88 which is likely a broad oversimplification (but may also explain some of the observed patterns in our dataset). Furthermore, it should be note that the metric used to calculate phylogenetic signal in our data set will likely influence the results obtained89.
Our focus on species’ dispersal capabilities responds to recent research58 which found dispersal to be an important process driving abundance–distance patterns within simulated environments. Other research has found that species that are better dispersers tend not to conform to abundant-centre patterns46. However, Ntuli et al.46 tested the abundant-centre hypothesis on intertidal species with planktonic life stages, and direct comparisons with our findings may not yield ecologically meaningful conclusions. In the context of the taxonomic groups included in our analysis, our use of dispersal-related species traits suggests that dispersal capabilities should be accounted for when testing macroecological hypotheses such as the abundant-centre hypothesis.
Similar to other tests of the abundant-centre hypothesis, our sampling approach involves caveats. One limitation relates to the underlying abundance database used, which inherently vary in different sampling protocols, time periods studied, study sites and taxonomic focus. We explored the effects of underlying databases within each study on abundance–distance relationships for animals and plants as part of our supplementary analyses (see Supplementary Methods). There were significant effects of the underlying database in both animal (F1,3051 = 14.364, p < 0.0001) and plant (F1,598 = 66.302, p < 0.0001) data sets, contributing 3% and 10% of variation within our animal and plant abundance–distance relationships, respectively (Table S6; Table S7). These signals may simply be an artifact of the species included within each data set, as duplicated species data between studies were removed prior to analysis and abundance data from the study with the higher number of observations was retained. In addition to this, most species’ geographical ranges are likely to have been under-sampled, and abundance estimates are mostly not derived from the full extents of their ranges.
Our test of the hypothesis assumes that conspecific populations are equally adapted to the environment. However, there is local adaptation across some species’ ranges54, which we were unable to account for using our approach. Species that have undergone historical range contractions, either naturally or from human activities, may become ecologically marginalised90, which may introduce error into our assessments of abundance–distance relationships. We attempted to account for this by exploring how abundance–distance relationships manifest in species that have undergone historical range contractions. Using historical range data from the PHYLACINE database91 (version 1.2), we found no significant effect of historical range contractions on global abundance–distance relationships in 202 mammal species (F1,200 = 1.242, p = 0.266, R2 = 0.001; Table S10). Despite not finding a significant effect of historical range contractions on abundance–distance relationships, it is important to consider that our study investigates natural processes using data from a human-modified world. Future research should leverage available historical range data across multiple taxonomic groups and explore, in detail, the effects of natural and human historical range dynamics on abundance–distance relationships.
Sampling efforts are likely to be influenced by differences in data quantity and quality between taxa. For example, bird abundance data are more readily available from open-source repositories (such as eBird – ebird.org) than abundance data for most other taxa. We attempted to account for this by weighting the linear models by the natural logarithm of species sample size, such that better-sampled species were assigned larger weights in our analyses than less-sampled species. Even though we employed a global approach to testing the abundant-centre hypothesis, our study is still bound by the geographical constraints of the studies included within our data set. This is demonstrated by the geographical biases within our data set (see Fig. 1), which may influence our findings. There were notable taxonomic gaps within our data set, and a skew towards more commonly sampled groups. During our literature searches, we were unable to obtain any abundance estimates for reptiles, amphibians, marine mammals, pelagic fishes, corals, fungi and most invertebrate groups.
Despite these limitations, we were able to calculate abundance–distance relationships for 4036 species, with 3,660 used in our analyses. Due to the volume of species data included in this study, we were unable to control for spatiotemporal differences between migratory and non-migratory species abundances, which have been shown to influence support for the abundant-centre hypothesis30. However, previous research has suggested otherwise23,47. Our supplementary analyses on a data set of 1,683 bird species suggest that migratory strategy has no effect on global abundance–distance relationships (F1,1680 = 0.526, p = 0.591, R2 = < 0.001; Table S8); this aspect warrants further attention by future studies. We focused on testing the hypothesis by a measure of centrality as opposed to marginality. Depending on the shape of a species’ geographic range, such measures can differ largely as occurrences far from the range centroid can also be far from the range edge17. All of the studies included in our analyses specifically tested the abundant-centre hypothesis in some form. Relatedly, preference towards the publication of studies that find positive support for abundant-centre patterns over those that do not may be apparent, which should be taken into consideration when interpreting our findings. Finally, we searched for studies published in English, French and Spanish, but did not obtain any relevant search results in languages other than English, which is a limitation of our results. We suspect this is due to the search terms being optimised for literature published in English.
Our study indicates that accounting for dispersal-related traits and phylogeny improves models of abundant-centre patterns across geographic space. Future tests of the abundant-centre hypothesis should aim to (i) include data for under-represented taxonomic groups, such as reptiles, amphibians and fungi, to enhance our overall understanding of broad-scale patterns of species’ abundances, and (ii) compare relationships between abundant-centre patterns and habitats at the micro-scales. Finally, we recommend that future tests of the abundant-centre hypothesis attempt to examine other processes, such as interspecific interactions and impacts of human activities, which may underlie abundance–distance relationships and account for additional unexplained heterogeneity in our data set.
Methods
Literature searches
We conducted a systematic literature search on 23rd July 2021 by querying the ISI Web of Science database (apps.webofknowledge.com) with the following search string for an initial broad search: “(abundan* OR abundance-cent* OR abundant niche-cent* OR niche cent* OR abundant-centre hypothesis) AND (range OR geographic range OR range size OR range edge OR species distribution)” using the TITLE field. We retained all studies that 1) comprised peer-reviewed primary studies, 2) presented globally extensive abundance point observations across all taxonomic groups, 3) were published between 1990 and 2020, 4) included extractable data relating to observed/estimated abundance counts and 5) were published in English, French or Spanish language.
Examination of the returned studies (N = 818) revealed that some key literature was missing from our results. Therefore, we used the studies returned from our initial search as reference sources for additional key search terms to derive an optimised search string using the litsearchr R package92. Search terms were extracted from unique study titles, abstracts and tagged keywords (e.g., terms such as ‘range edge’, ‘abundance’ and ‘species range’). We built a keyword co-occurrence network and quantitatively assessed potential search terms using a 60% cumulative cut-off point92. Resulting search terms (N = 326) were grouped into either 1) the ‘species group’, 2) ‘geographic group’ or 3) ‘both groups’ depending on whether the term referred to a species concept or geographic concept. Grouping refers to the string of search terms either side of the Boolean operator ‘AND’. We manually removed irrelevant search terms (N = 268; e.g., ‘field sites’, ‘habitat patch’ and ‘statistically significant’) and retained the most relevant search terms (N = 58) which formed our optimised search string (Table S11). To verify whether our resulting search string was fully optimised, we cross-referenced four key articles that we expected to be included in the optimised search results23,34,38,44—all of which were included. We queried the Web of Science database using our optimised search string and obtained 531 studies. After screening of titles and abstracts, we retained 23 studies for data extraction.
We supplemented our Web of Science literature search with the studies included within the foundational synthesis by Sagarin & Gaines19. We then conducted a snowball search of the literature that cited Sagarin & Gaines19 up until 31st December 2020. This resulted in a combined literature database of 1109 studies. Due to non-conformity to our selection criteria, we excluded 1000 studies after screening titles and abstracts and an additional 95 studies after screening of full texts, leaving us with 14 studies that were suitable for data extraction.
Data extraction and processing
From each study, and for each species, we extracted raw abundance values and distance from the species’ geographic range centroids (in km). Corresponding authors were contacted via email correspondence if data were not publicly available. Where data were not publicly available and the corresponding author was unable to provide the data, we extracted abundance and distance data from appropriate figures within the published articles using the web-based tool WebPlotDigitizer (version 4.5)93. If abundance data were available but distance values were not, global range maps were obtained in shapefile formats for each species and range centroids were calculated. We obtained global range shapefiles for terrestrial mammals from the IUCN Red List79 and for birds from the BirdLife Data Zone (version 2020.1)94, thus accounting for the entire ranges for migratory and non-migratory species. IUCN range maps have been criticized due to oversimplification of species’ ranges derived from sampling bias95 but represent the most comprehensive spatial data set available for our study species. If global polygon range maps for particularly under-sampled taxonomic groups were unavailable, e.g., invertebrates and some plant species (N spp. = 8), we downloaded species occurrence point data from the Global Biodiversity Information Facility (https://www.gbif.org). Occurrence data were then cleaned using the CoordinateCleaner package96 and manual checks were performed to remove any remaining outliers97. We calculated minimum convex hulls for terrestrial species, in an attempt to not overestimate their global range sizes by accounting for unsuitable terrestrial environments, which we interpreted as proxies for global species ranges and calculated range centroids using QGIS (version 3.14.16)98. Then, we calculated the geodesic distances on a sphere (km) between the sampling sites with associated abundance values to obtain the distance to the species’ range centroid, using the WGS84 co-ordinate reference system. Abundance and distance values were log10-transformed prior to statistical analyses to account for scaling inconsistencies. Species with unresolved species level taxonomies (N = 106) as well as species with fewer than five observations were omitted from the analysis. We calculated Spearman Rank Correlation Coefficients (rs) between log10(abundance) and log10(distance) values (Fig. 2). Negative rs values are consistent with an ‘abundant-centre’ distribution (Fig. 2).
Spatial scale effects on abundance–distance relationships
We used three measurements to attempt to explore the effect of scale on ‘abundant-centre’ patterns: 1) we calculated the study extent (km), i.e., the spatial extent at which the study was conducted, encompassing the total study area between sampling locations in the data. This was measured using both latitudinal and longitudinal measurements. Initially, we used four categorical levels: ‘Local’ ≤ 250 km, ‘Landscape’ > 251–500 km, ‘Regional’ > 501–1500 km and ‘Continental’ > 1501 km. 2) We calculated the grain (km2), i.e., the spatial scale at which data were collected, which is important because the area of the base unit defines the spatial scale of the study99, and variation in grain may be reflected in population abundance estimates100. Grain was extracted from each study by taking the base unit area for each sampling technique, e.g., sampling units measured in km2. 3) We calculated study focus (km2), defined as the spatial scale at which data were analysed. Often, abundance estimates from individual sampling sites are averaged across larger sampling areas, e.g. a protected area sampled using a number of line transects and multiple sampling points along each transect, with abundance values averaged across all the sampling points to produce an estimate for each transect. In most cases, grain and focus were the same for a given study, e.g. when abundance data were recorded in the form of points within a species’ geographic range. Grain and focus values were log10 transformed due to the large variation in the range of these values. We then plotted the distribution of the log10-transformed values on separate histograms and visualised the natural breaks in the data. Using these we binned both grain and focus into two new categorical levels: ‘small’ and ‘large’ (−10 to −3 and −3 to 3 on log10 scale, respectively). We decided to drop extent from our analyses due to uneven sample sizes: data for only three groups (birds, mammals and plants) global 2717 species vs. local 146 species. We also dropped focus from our analyses because the natural break categorical bins were identical to those for grain. Grain was subsequently omitted from the statistical analyses due to its strong correlation with animal species group and plant functional group variables and thus could not be included within the same models due to colinearity.
Compilation of dispersal-related species traits and geographic variables
We compiled six dispersal-related species traits for animal and eight traits for plant species to examine their effects on abundance–distance relationships (Table 1; Table S2). Traits were selected based on the morphological and/or ecological characteristics of the study species and included: for animals 1) taxonomic group (categorical), 2) body size (continuous), 3) invasive status (binary 1,0) and 4) feeding guild (categorical); and for plants: 1) functional group (categorical), 2) mean plant height (m), 3) seed mass (mg), 4) invasive status (binary 1,0), 5) life span (categorical) and 6) life form (categorical) (see Table 1 for an overview and Table S3 for justifications for the inclusion of each species trait/geographic variable). To explore spatial patterns within global abundance–distance relationships, we also compiled geographic data for species-level range sizes (km2) and absolute latitudes (°).
To examine the effects of body size, we compiled body mass (g) data for mammals and birds, and snout-vent lengths (SVL; cm) for freshwater and reef fishes to produce the trait variable ‘body size’. For plants, we used mean plant height (m) as a proxy for body size. Mean plant height was used instead of maximum plant height as these were the only data available for our selected species, and notable effects of plant height on species abundance patterns would be reflected in either measurement. Where plant height and seed mass data were unavailable, we supplemented our data with gap-filled measurements101,102 which were estimated using Bayesian Hierarchical Probabilistic Matrix Factorization103. Trait data for plant functional groups were sourced from the BiolFlor database104 and the corresponding levels ‘dwarf shrub’ (N = 11 species) and ‘subshrub’ (N = 4 species) were merged into the level ‘shrub’ to produce four distinct categorical levels: ‘grasses’, ‘herbs’, ‘shrubs’ and ‘trees’. Plant life-form data followed the classification of Raunkiær105 but due to small sample sizes for ‘chamaephytes’ (woody plants with perennating buds borne close to the soil surface), we merged these with the ‘phanerophytes’ (woody perennial plants with buds at a distance from the surface, such as trees and shrubs). Invasive status was assessed using a binary approach (1 = invasive and 0 = non-invasive) according to the Invasive Species Specialist Group’s Global Invasive Species Database (http://www.iucngisd.org/gisd/). For both animal and plant species, absolute latitude (°) was calculated as the absolute value of the range centroid. The following species traits/geographic variables were log10-transformed prior to analysis: body size (cm; g), mean plant height (m), seed mass (mg) and range size (km2) to account for right-skew within the data. We tested for, but did not find, collinearity between continuous explanatory variables using a correlation threshold value ≥ 0.70 in the hmisc106 package with visualisations created in the pheatmap package107 (Fig. S1).
Statistics and reproducibility
All data analyses were performed R (version 4.0.5)108. No statistical method was used to predetermine sample size. Due to small sample sizes (N = 9 species), invertebrate abundance data were excluded from the statistical analyses. Coefficients from Spearman’s rank correlation between species’ abundances and range-centre distances were transformed to Fisher’s Z scores (to achieve approximate normality), using the package metafor109. We analysed the animal and plant data separately because of different sets of trait combinations and the different sampling methods (e.g., abundances estimated from line transects for animals vs. vegetation plot-based cover estimates for plants). In all analyses, the influence of each Fisher’s Z score was weighted by the natural logarithm of the sample size (to down-weight the influence of sparsely sampled species).
Grand mean effects and linear modelling
We calculated the grand mean Fisher’s Z scores of abundance–distance relationships as weighted averages of Fisher’s Z values (using weighted intercept-only models), which we determined to be significant if the approximated 95% confidence intervals of the estimated intercept did not include zero.
To explore the effects of dispersal-related species traits and geographic variables on abundance–distance relationships, we expanded the weighted intercept-only models by including the species traits and geographic variables as fixed effects (hereafter ‘predictors’). We determined the significance of these predictors using a stepwise model selection approach in which we started with a full model and (stepwise) removed non-significant predictors (based on F-tests on the explained variation between nested models) until we reached the most parsimonious models that included only statistically significant predictors. From these most parsimonious models, we calculated the marginal effects of each significant predictor using the ggeffects package110.
Interactions between predictor variables
To explore any potential interaction effects between the suggested predictors, we applied a multimodel inference approach111. Separately for animal and plant data, we constructed all weighted linear effects models for any combination and two-way interactions between all tested predictors, accumulating 40,069 models for the animal dataset and 1450 models for the plant dataset. All competing models were ranked by the AIC111, which favours the models that explain the highest amount of variation with the smallest number of fixed and interaction effects (using the dredge function of the MuMIn package112). From the emerging set of best models (those with a ∆AIC of <2 from the best model), we extracted all included fixed effects and interaction terms into two interaction models (separately for animal and plant data) from which we calculated the marginal interactions effects again with the ggeffects package.
Testing for phylogenetic signals in abundance–distance relationships
To test for phylogenetic signal in our models and model residuals, we assembled phylogenies for a data subset consisting of 1645 birds (on 1547 nodes), 1151 freshwater and reef fishes (on 1031 nodes), and 201 mammals (on 184 nodes) from the Open Tree of Life (OTL)113,114,115 using the rotl R package116. The plant phylogeny was obtained from the phylogenetic backbone of sPlot (version 3.0)101,117 which is also based on the OTL with additional resolution and included 589 species on 552 nodes.
Separately for birds, fishes, mammals, and plant data, we compared the AIC values between three generalized least square models (estimated with maximum likelihood) that included a phylogenetic correlation matrix118 with three different values of Pagel’s λ, a robust index of phylogenetic signal in continuous traits119. A λ value of zero indicates no phylogenetic signal, whereas a value of one indicates full branch length separation, i.e. full phylogenetic signal. In addition to this, we used a further λ value calculated from the distribution of Fisher’s Z values to reflect the observed phylogenetic evolution with the phylosig function from the phytools package120. In addition to the model comparison, we tested whether the residuals from our linear models were significantly predicted by species’ phylogenetic relatedness. For this, we re-calculated the intercept-only model, the most parsimonious model (with fixed effects), and the interaction model (with important fixed and interaction terms) for the birds, fishes, mammals, and plant data set and tested the significance of the phylogenetic signal using Pagel’s λ again using the phylosig function from the phytools package. See supplement.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The abundance–distance correlation coefficients, trait, and range data generated in this study have been deposited in the Dryad database [https://doi.org/10.5061/dryad.zgmsbccj2]. Original abundance data sources are outlined in Table S6 in the supplementary information. Source data are provided with this paper.
Code availability
R code associated with this article is has been deposited in the Dryad database [https://doi.org/10.5061/dryad.zgmsbccj2].
References
Beck, J. et al. What’s on the horizon for macroecology? Ecography 35, 673–683 (2012).
Shade, A. et al. Macroecology to unite all life, large and small. TREE 33, 731–744 (2018).
McGill, B. The what, how and why of doing macroecology. Glob. Ecol. Biogeogr. 28, 6–17 (2018).
Hui, C., Richardson, D. M., Robertson, M. P., Wilson, J. R. U. & Yates, C. J. Macroecology meets invasion ecology: linking the native distributions of Australian acacias to invasiveness. Divers. Distrib. 17, 872–883 (2011).
Hansen, G. J. A. et al. Commonly rare and rarely common: comparing population abundance of invasive and nature aquatic species. PLoS ONE 8, e77415 (2013).
Pearce, J. & Ferrier, S. The practical value of modelling relative abundance of species for regional conservation planning: a case study. Biol. Conserv. 98, 33–43 (2001).
Santini, L. et al. The interface between macroecology and conservation: existing links and untapped opportunities. Front. Biogeogr. 13.4, e53025 (2021).
Baiser, B. et al. Ecogeographical rules and the macroeocology of food webs. Glob. Ecol. Biogeogr. 28, 1204–1218 (2019).
Lomolino, M. V., Sad, D. F., Riddle, B. R. & Brown, J. H. The island rule and research agenda for studying ecogeographical patterns. J. Biogeogr. 33, 1503–1510 (2006).
Mathys, B. A. & Lockwood, J. L. Rapid evolution of great kiskadees on Bermuda: an assessment of the island rule to predict the direction of contemporary evolution in exotic vertebrates. J. Biogeogr. 36, 2204–2211 (2009).
Millien, V. et al. Ecotypic variation in the context of global climate change: revisiting the rules. Ecol. Lett. 9, 853–869 (2006).
Ehrlén, J. & Morris, W. F. Predicting changes in the distribution and abundance of species under environmental change. Ecol. Lett. 18, 303–314 (2015).
Pianka, E. R. Latitudinal gradients in species diversity: a review of concepts. Am. Nat. 100, 33–46 (1966).
Bergmann, K. G. L. C. Über die Verhältnisse der wärmeokönomie der Thiere zu ihrer Grösse. Göttinger Stud. 3, 595–708 (1847).
Stevens, G. C. The latitudinal gradient in geographical range: how so many species coexist in the tropics. Am. Nat. 133, 240–256 (1989).
Grinnell, J. The role of the “accidental. Auk 39, 373–380 (1922).
Santini, L., Pironon, S., Maiorano, L. & Thuiller, W. Addressing common pitfalls does not provide more support to geographical and ecological abundant-centre hypotheses. Ecography 42, 696–705 (2018a).
Pironon, S. et al. Geographic variation in genetic and demographic performance: new insights from an old biogeographic paradigm. Biol. Rev. 92, 1877–1909 (2016).
Sagarin, R. D. & Gaines, S. D. The ‘abundant centre’ distribution: to what extent is it a biogeographical rule? Ecol. Lett. 5, 137–147 (2002a).
McGill, B. & Collins, C. A unified theory for macroecology based on spatial patterns of abundance. Evol. Ecol. Res. 5, 469–492 (2003).
Rivadeneira, M. M. et al. Testing the abundant-centre hypothesis using intertidal porcelain crabs along the Chilean coast: linking abundance and life-history variation. J. Biogeogr. 37, 486–498 (2010).
Shalom, H. Y. et al. A closer examination of the ‘abundant centre’ hypothesis for reef fishes. J. Biogeogr. 47, 2194–2209 (2020).
Dallas, T., Decker, R. R. & Hastings, A. Species are not most abundant in the centre of their geographic range or climatic niche. Ecol. Lett. 20, 1526–1533 (2017).
Dallas, T., Santini, L., Decker, R. R. & Hastings, A. Weighing the evidence for the abundant-center hypothesis. Biodiv. Inf. 15, 81–91 (2020a).
Hutchinson, G. E. Cold Spring Harbor Symposium on Quantitative Biology. In Concluding Remarks. 415–427 (Cold Spring Harbor Laboratory Press, Long Island, 1957).
Brown, J. H. On the relationship between abundance and distribution of species. Am. Nat. 124, 255–279 (1984).
Dallas, T. & Santini, L. The influence of stochasticity, landscape structure and species traits on abundant-centre relationships. Ecography 43, 1341–1351 (2020b).
Soberón, J., Townsend Peterson, A. & Osorio-Olvera, L. A comment on “species are not most abundant in the centre of their geographic range or climatic niche. Rethinking Ecol. 3, 13–18 (2018).
Osorio-Olvera, L., Soberón, J. & Falconi, M. On population abundance and niche structure. Ecography 42, 1415–1425 (2019).
Osorio-Olvera, L., Yáñez-Arenas, C., Martínez-Meyer, E. & Townsend Peterson, A. Relationships between population densities and niche-centroid distances in North American birds. Ecol. Lett. 23, 555–564 (2020).
Freeman, B. G. & Beehler, B. M. Limited support for the “abundant centre” hypothesis in birds along a tropical elevational gradient: implications for the fate of lowland tropical species in a warmer future. J. Biogeogr. 45, 1884–1895 (2018).
Burner, R. C., Styring, A. R., Rahman, M. A. & Sheldon, F. H. Occupancy patterns and upper range limits of lowland Bornean birds along an elevation gradient. J. Biogeogr. 46, 2583–2596 (2019).
Pérez-Collazos, E., Sanchez-Gómez, P., Jiménez, J. F. & Catalán, P. The phygeographical history of the Iberian steppe plant Ferula loscosii (Apiaceae): a test of the abundant-centre hypothesis. Mol. Ecol. 18, 848–861 (2009).
Dixon, A., Herlihy, C. R. & Busch, J. W. Demographic and population-genetic test provide mixed support for the abundant centre hypothesis in the endemic plant Leavenworthia stylosa. Mol. Ecol. 22, 1777–1791 (2013).
Sporbert, M. et al. Testing macroecological abundance patterns: the relationship between local abundance and range size, range position and climatic suitability among European vascular plants. J. Biogeogr. 47, 2210–2222 (2020).
Tuya, F., Wernberg, T. & Thomsen, M. S. Testing the ‘abundant centre’ hypothesis on endemic reef fishes in south-western Australia. Mar. Ecol. Prog. Ser. 372, 225–230 (2008).
Waldock, C., Stuart-Smith, R. D., Edgar, G. J., Bird, T. J. & Bates, A. E. The shape of abundance distributions across temperature gradients in reef fishes. Ecol. Lett. 22, 685–696 (2019).
Virgós, E. et al. Body size clines in the European badger and the abundant centre hypothesis. J. Biogeogr. 38, 1546–1556 (2011).
Martínez-Gutiérrez, P. G., Martínez-Meyer, E., Palomares, F. & Fernández, N. Niche centrality and human influence predict rangewide variation in population abundance of a widespread mammal: the collared peccary (Pecari tajacu). Divers. Distrib. 24, 103–115 (2017).
Wen, Z. et al. Varying support for abundance-centre and congeneric-competition hypotheses along elevation transects of mammals. J. Biogeogr. 48, 616–627 (2020).
Chaiyes, A. et al. An assessment of the niche centroid hypothesis: Pteropus lylei (Chiroptera). Ecosphere 11, e03134 (2020).
Sagarin, R. D. & Gaines, S. D. Geographical abundance distributions of coastal invertebrates: using one-dimensional ranges to test biogeographic hypotheses. J. Biogeogr. 29, 985–997 (2002b).
Tam, J. C. & Scrosati, R. A. Mussel and dogwhelk distribution along the north-west Atlantic coast: testing predications derived from the abundant-centre model. J. Biogeogr. 38, 1536–1545 (2011).
Baldanzi, S., McQuaid, C. D., Cannicci, S. & Porri, F. Environmental domains and range-limiting mechanisms: testing the abundant centre hypothesis using southern African sandhoppers. PLoS ONE 8, e54598 (2013).
Scrosati, R. A. & Freeman, M. J. Density of intertidal barnacles along their full elevational range of distribution conforms to the abundant-centre hypothesis. PeerJ 7, e6719 (2019).
Ntuli, N. N. et al. Rejection of the genetic implications of the “abundant centre hypothesis” in marine mussels. Sci. Rep. 10, 604 (2020).
Chevalier, M., Broennimann, O. & Guisan, A. Using a robust multi-settings inference framework on published datasets still reveals limited support for the abundant centre hypothesis: more testing needed on other datasets. Glob. Ecol. Biogeogr. 30, 2211–2228 (2021).
Martínez-Meyer, E., Días-Porras, D., Townsend Peterson, A. & Yáñez-Arenas, C. Ecological niche structure and rangewide abundance patterns of species. Biol. Lett. 9, 20120637 (2013).
Blackburn, T. M., Gaston, K. J., Quinn, R. M. & Gregory, R. D. Do local abundances of British birds change with proximity to range edge? J. Biogeogr. 26, 493–505 (1999).
VanDerWal, K., Shoo, L. P., Johnson, C. N. & Williams, S. E. Abundance and the environmental niche: environmental suitability estimated from niche models predicts the upper limit of local abundance. Am. Nat. 174, 283–291 (2009).
Yáñez-Arenas, C. et al. The abundant niche-centroid hypothesis: key points about unfilled niches and the potential use of supraspecific modeling units. Biodiv. Inf. 15, 92–102 (2020).
Weber, M. M., Stevens, R. D., Diniz-Filho, J. A. F. & Grelle, C. E. V. Is there a correlation between abundance and environmental suitability derived from ecological niche modelling? A meta-analysis. Ecography 40, 817–828 (2017).
Hidas, E. Z., Ayre, D. J. & Minchinton, T. E. Patterns of demography for rocky shore, intertidal invertebrates approaching their geographical range limits: tests of the abundant-centre hypothesis in south-eastern Australia. Mar. Freshw. Res. 61, 1243–1251 (2010).
Chen, Q. et al. Incorporating local adaptation into species distribution modeling of Paeonia mairei, an endemic plant to China. Front. Plant Sci. 10, 1717 (2020).
Kokko, H. & López-Sepulcre, A. From individual dispersal to species ranges: perspectives for a changing world. Science 313, 789–791 (2006).
Thompson, P. L. & Gonzalez, A. Dispersal governs the reorganization of ecological networks under environmental change. Nat. Ecol. Evol. 1, 0162 (2017).
Fristoe, T. S., Vilela, B., Brown, J. H. & Botero, C. A. Abundant-core thinking clarifies exceptions to the abundant-center distribution pattern. Ecography 2, e06365 (2022).
Feng, X. & Qiao, H. Accounting for dispersal using simulated data improves understanding of species abundance patterns. Glob. Ecol. Biogeogr. 31, 200–214 (2022).
Gaston, K. J., Chown, S. L. & Evans, K. L. Ecogeographical rules: elements of a synthesis. J. Biogeogr. 35, 483–500 (2007).
Chamberlain, S. A. et al. Does phylogeny matter? Assessing the impact of phylogenetic information in ecological meta-analysis. Ecol. Lett. 15, 627–636 (2012).
Martins, E. P. & Hansen, T. F. Phylogenies and the comparative method: a general approach to incorporating phylogenetic information into the analysis of interspecific data. Am. Nat. 149, 646–667 (1997).
Dallas, T. A. & Santini, L. The influence of stochasticity, landscape structure and species traits on abundant-centre relationships. Ecography 43, 1341–1351 (2020).
Bohonak, A. J. Dispersal, gene flow, and population structure. Q. Rev. Biol. 74, 1 (1999).
Stevens, V. M. et al. A comparative analysis of dispersal syndromes in terrestrial and semi-terrestrial animals. Ecol. Lett. 17, 1039–1052 (2014).
Venable, D. L. & Brown, J. S. The selective interactions of dispersal, dormancy and seed size as adaptations for reducing risk in variable environments. Am. Nat. 131, 360–384 (1988).
Thomson, F. J., Moles, A. T., Auld, T. D. & Kingsford, R. T. Seed dispersal distance is more strongly correlated with plant height than with seed mass. J. Ecol. 99, 1299–1307 (2011).
Pianka, E. R. On r- and K-Selection. Am. Nat. 104, 940 (1970).
Albaladejo-Robles, G., Böhm, M. & Newbold, T. Species life-history strategies affect population responses to temperature and land-cover changes. Glob. Change Biol. 29, 97–109 (2022).
Aslan, C. et al. Employing plant functional groups to advance seed dispersal ecology and conservation. AoBP 11, plz006 (2019).
Beckman, N. G., Bullock, J. M. & Salguero-Gómez, R. High dispersal ability is related to fast life-history strategies. J. Ecol. 106, 1349–1362 (2018).
Arim, M., Abades, S. R., Neill, P. E., Lima, M. & Marquet, P. A. Spread dynamics of invasive species. PNAS 103, 374–378 (2005).
Lester, S. E., Ruttenberg, B. I., Gaines, S. D. & Kinlan, B. P. The relationship between dispersal ability and geographic range size. Ecol. Lett. 10, 745–758 (2007).
Ruggiero, A. & Werenkraut, V. One-dimensional analyses of Rapoport’s rule reviewed through meta-analysis. Glob. Ecol. Biogeogr. 16, 401–414 (2007).
Samis, K. E. & Eckert, C. G. Testing the abundant center model using range-wide demographic surveys of two coastal dune plants. Ecol 88, 1747–1758 (2007).
Sheard, C. et al. Ecological drivers of global gradients in avian dispersal inferred from wing morphology. Nat. Commun. 11, 2463 (2020).
Weeks, B. C. et al. Morphological adaptations linked to flight efficiency and aerial lifestyle determine natal dispersal distance in birds. Funct. Ecol. 36, 1681–1689 (2022).
Tobias, J. A. et al. AVONET: morphological, ecological and geographical data for all birds. Ecol. Lett. 25, 581–597 (2022).
Giometto, A., Rinaldo, A., Carrara, F. & Altermatt, F. Emerging predictable features of replicated biological invasion fronts. PNAS 111, 297–301 (2013).
IUCN. The IUCN Red List of Threatened Species. 2022-1. https://www.iucnredlist.org (2022).
Burgman, M. A. & Fox, J. C. Bias in species range estimates from minimum convex polygons: implications for conservation and options for improved planning. Anim. Conserv. 6, 19–28 (2003).
Phiri, E. E., McGeoch, M. A. & Chown, S. L. The abundance structure of Azorella selago Hook. f. on sub-Antarctic Marion Island: testing the peak and tail hypothesis. Polar Biol. 38, 1881–1890 (2015).
Goldberg, D. E. & Barton, A. M. Patterns and consequences of interspecific competition in natural communities: a review of field experiments in plants. Am. Nat. 139, 771–801 (1992).
Liu, Y. et al. Soil resource availability is much more important than soil resource heterogeneity in determining the species diversity and abundance of karst plant communities. Ecol. Evol. 11, 16680–16692 (2021).
Maitra, A., Pandit, R., Mungee, M. & Athreya, R. Testing a theoretical framework for the environment-species abundance paradigm: a new approach to the abundant centre hypothesis. bioRxiv https://doi.org/10.1101/2022.01.03.474819 (2022).
Bailey, J. J., Boyd, D. S. & Field, R. Models of upland species’ distributions are improved by accounting for geodiversity. Landsc. Ecol. 33, 2071–2087 (2018).
Lepczyk, C. A. et al. Human impacts on regional avian diversity and abundance. Conserv. Biol. 22, 405–416 (2008).
Cinar, O., Nakagawa, S. & Viechtbauer, W. Phylogenetic multilevel meta-analysis: a simulation study on the importance of modelling the phylogeny. Methods Ecol. Evol. 13, 383–395 (2022).
Revell, L. J., Harmon, L. J. & Collar, D. C. Phylogenetic signal, evolutionary process, and rate. Syst. Biol. 57, 591–601 (2008).
Münkemüller, T. et al. How to measure and test phylogenetic signal. Methods Ecol. Evol. 3, 743–756 (2012).
Britnell, J. A., Zhu, Y., Kerley, G. I. H. & Shultz, S. Ecological marginalization is widespread and increases extinction risk in mammals. PNAS 120, e2205315120 (2023).
Faurby, S. et al. PHYLACINE 1.2: the phylogenetic atlas of mammal macroecology. Ecol 99, 2626–2626 (2018).
Grames, E. M., Stillman, A. N., Tingley, M. W. & Elphick, C. S. An automated approach to identifying search terms for systematic reviews using keyword co-occurrence networks. Methods Ecol. Evol. 10, 1645–1654 (2019).
Rohatgi, A. Webplotdigitizer: 4.5 https://automeris.io/WebPlotDigitizer (2021).
BirdLife International and Handbook of the Birds of the World. Bird species distribution maps of the world. Version 2020.1. Available at http://datazone.birdlife.org/species/requestdis (2020).
Herkt, K. M. B., Skidmore, A. K. & Fahr, J. Macroecological conclusions based on IUCN expert maps: a call for caution. Glob. Ecol. Biogeogr. 26, 930–941 (2017).
Zizka, A. et al. CoordinateCleaner: standardized cleaning of occurrence records from biological collection databases. Methods Ecol. Evol. 10, 744–751 (2019).
Panter, C. T. et al. To clean or not to clean: cleaning open-source data improves extinction risk assessments for threatened plant species. Conserv. Sci. Pract. 2, e311 (2020).
QGIS.org. QGIS Geographic Information System. QGIS Association. http://www.qgis.org (2022).
Field, R. et al. Spatial species-richness gradients across scales: a meta-analysis. J. Biogeogr. 36, 132–147 (2009).
Caten, C. T., Holian, L. & Dallas, T. Weak but consistent abundance–occupancy relationships across taxa, space and time. Glob. Ecol. Biogeogr. 31, 968–977 (2022).
Bruelheide, H. et al. Global trait-environment relationships of plant communities. Nat. Ecol. Evol. 2, 1906–1917 (2018).
Kattge, J. et al. TRY plant trait database – enhanced coverage and open access. Glob. Change Biol. 26, 119–188 (2020).
Schrodt, F. et al. BHPMF – a hierarchical Bayesian approach to gap-filling and trait prediction for macroecology and functional biogeography. Glob. Ecol. Biogeogr. 24, 1510–1521 (2015).
Kühn, I., Durka, W. & Klotz, S. Biolflor—a new plant-trait database as a tool for plant invasion ecology. Divers. Distrib. 10, 363–365 (2004).
Raunkiær, C. The life forms of plants and statistical plant geography, being the collected papers of C. Raunkiær. (Clarendon Press, 1934).
Harrell Jr, F. Hmisc: Harrell Miscellaneous. R package version 4.7.0, https://CRAN.R-project.org/prackage=Hmisc (2022).
Kolde, R. pheatmap: Pretty Heatmaps. R package version 1.0.12, https://CRAN.R-project.org/package=pheatmap (2019).
R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/ (2021).
Viechtbauer, W. Conducting meta-analyses in R with the metafor package. J. Stat. Softw. 36, 1–48 (2010).
Lüdecke & Danial ggeffects: tidy data frames of marginal effects from regression models. J. Open Softw. 26, 772 (2018).
Burnham, K. P. & Anderson, D. R. Model Selection and Multimodel Inference: A Practical Information-theoretic Approach. 2. (Springer, 2002).
Barton, K. MuMIn: Multi-model Inference. R package version 1.43.17 https://cran.r-project.org/package=MuMIn (2020).
Redelings, B. D. & Holder, M. T. A supertree pipeline for summarizing phylogenetic and taxonomic information for millions of species. PeerJ 5, e3058 (2017).
Open Tree et al. Open tree of life synthetic tree version 14.9. https://doi.org/10.5281/zenodo.3937741 (2023a).
Open Tree et al. Open tree of life taxonomy version 3.6. https://doi.org/10.5281/zenodo.3937750 (2023b).
François, M., Brown, J. W. & Winter, D. J. rotl: an R package to interact with the open tree of life data. Methods Ecol. Evol. 7, 1476–1481 (2017).
Hähn, G. J. A. et al. Global decoupling of functional and phylogenetic diversity in plant communities. Nat. Ecol. Evol. 9, 237–248 (2024).
Westoby, M., Yates, L., Holland, B. & Halliwell, B. Phylogenetically conservative trait correlation: quantification and interpretation. J. Ecol. 111, 2105–2117 (2023).
Pagel, M. Inferring the historical patterns of biological evolution. Nature 401, 877–884 (1999).
Revell, L. J. Phytools 2.0: an updated R ecosystem for phylogenetic comparative methods (and other things). PeerJ 12, e16505 (2024).
Feldman, R. E., Anderson, M. G., Howerter, D. W. & Murray, D. L. Where does environmental stochasticity most influence population dynamics? An assessment along a regional core-periphery gradient for prairie breeding ducks. Glob. Ecol. Biogeogr. 24, 896–904 (2015).
McMinn, R. L., Russell, F. L. & Beck, J. B. Demographic structure and genetic variability throughout the distribution of platte thistle (Cirsium canescens Asteraceae). J. Biogeogr. 44, 375–385 (2016).
Baer, K. C. & Maron, J. L. Declining demographic performance and dispersal limitation influence the geographic distribution of the perennials forb Astragalus utahensis (Fabaceae). J. Ecol. 107, 1250–1262 (2019).
Gao, W.-Q. et al. Population structure and regeneration dynamics of Quercus variabilis along latitudinal and longitudinal gradients. Ecosphere 8, e01737 (2017).
Acknowledgements
The authors would like to thank the following for their assistance with data collation and analyses, thought-provoking discussions and ideas: Jonathan Belmaker, Itai Granot, Luca Santini, Marten Winter, Erik Welk, Reinhard Klenke, Annegreet Veeken and Tom Reader. This project is generously supported by a NERC-funded ENVISION Doctoral Training Partnership PhD Studentship titled “Abundance within species’ ranges: understanding species’ responses to environmental change” (NE/S007423/1 2436183) (C.T.P., S. P. B., H.B., R.F. & F.S.).
Author information
Authors and Affiliations
Contributions
C.T.P., S.P.B., H.B., R.F. and F.S. conceptualised the study, C.T.P. & M.S. curated the original dataset, C.T.P., O.B., H.B., S.K., G.J. A.H., R.F. and F.S. developed the methodology, C.T.P., S.P.B., H.B., S.K., M.S., R.F. and F. S. conducted validation of the methodology and results, C.T.P., O.B., H.B., G.J.A.H and S.K. performed the formal analysis, C.T.P., O.B., S.K. and G.J.A.H. contributed to the visualisation, C.T.P. wrote the original draft, C.T.P., S.P.B., O.B., H.B., S.K., G.J.A.H., R.F., and F.S. contributed to writing review and editing, C.T.P. administered the project, H.B., S.P.B., R.F. and F.S. contributed to resource gathering and funding acquisition, H.B., S.P.B., R.F. and F.S. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Panter, C.T., Kambach, S., Bachman, S.P. et al. Plants with higher dispersal capabilities follow ‘abundant-centre’ distributions but such patterns remain rare in animals. Nat Commun 16, 8205 (2025). https://doi.org/10.1038/s41467-025-63566-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-63566-0