Introduction

Sea ice mediates air–sea heat and gas exchange1,2,3, and thus, accurately predicting sea ice thickness and extent is necessary to improve weather forecasts and future climate projections4,5. However, sea ice and ocean properties vary across a wide range of space and time scales, which are not fully captured by Earth System Models (ESMs) used for sea ice prediction6,7,8. For example, ESMs do not resolve small-scale leads or transient sea ice growth and loss processes associated with mesoscale and submesoscale eddies9,10. Yet, models that resolve submesoscale flows, \({\mathcal{O}}\)(1–10 km), have larger vertical velocities11,12, that impact the upper-ocean heat budget at basin scales13. Still, the extent to which submesocale processes affect larger-scale ocean variability in the seasonal ice zone (SIZ) remains poorly understood due to the difficulty of collecting observations underneath sea ice14.

Submesoscale flows are energized by a variety of instabilities, including mixed-layer baroclinic instability that converts potential energy stored in lateral buoyancy gradients into eddy kinetic energy15,16. The SIZ is particularly susceptible to baroclinic instability due to the presence of strong lateral density gradients associated with sea ice growth and melt9,17,18. Indeed, satellite images of sea ice concentration (SIC) reflect the presence of submesoscale eddies, fronts, and filaments. Thus, past studies have investigated sea ice-ocean interactions at the submesoscale, typically using in situ data from targeted glider campaigns19,20,21, or idealized models that isolate fundamental aspects of the dynamics9,10,17,22,23. These approaches have provided insight into the physics governing marginal ice zones. However, upscaling the impact of these dynamics on larger-scale processes is challenging since observational campaigns target energetic regions, while high-resolution numerical simulations are confined to small regional domains or short time periods.

A complete understanding of submesoscale sea ice-ocean interactions is further limited by the seasonal bias in fine-scale observations from the high-latitude Southern Ocean, which are weighted toward summer when the region is more accessible by ship14. This is an obstacle since sea ice properties have a strong seasonality24; additionally, observations from the subtropics suggest that submesoscale turbulence also undergoes a seasonal cycle25. Specifically, deeper winter mixed-layers provide more potential energy for submesoscale instabilities to develop, which leads to larger vertical buoyancy fluxes26. However, it is unclear whether this same seasonality applies to ice-covered regions, where increased sea ice cover in winter may suppress submesoscale activity through surface damping and a reduction in mixed-layer depths27. The SIZ presents a distinct environment due to the numerous feedbacks that link sea ice and upper-ocean variability28,29,30, which may produce more complex and regionally dependent submesoscale behavior compared to the ice-free ocean.

Here, we leverage measurements collected by instrumented marine mammals to conduct a comprehensive survey of spatiotemporal variability in submesoscale dynamics across the Southern Ocean seasonal ice zone. We show that the region can be separated into three distinct regimes based on the magnitude and sign of the mean vertical heat transport induced by mixed-layer eddies. These dynamical regimes align geographically with the i) off-shelf portion of the SIZ, as well as ii) “dense" and iii) “warm" continental shelves31. In dense shelf regions, like the Weddell and Ross seas, the mean submesoscale vertical heat flux is positive (upward) and variations in this flux are controlled by mixed-layer depth (MLD) fluctuations. Whereas in warm shelf regions, such as the Amundsen and Bellingshausen seas, the mean heat flux is negative (downward) and controlled by variations in the lateral buoyancy gradient (M2). Finally, in the off-shelf sector of the seasonal ice zone, the mean heat flux is weak and its variability is governed by a combination of MLD and M2. These differences suggest that the contribution of submesoscale fluxes to the upper-ocean heat budget varies considerably at regional scales.

Results

Submesoscale buoyancy and heat flux estimation

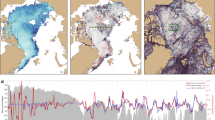
Submesoscale processes evolve rapidly, which necessitates high-resolution sampling in both space and time, making them difficult to observe. This is particularly true in the seasonally sea ice-covered Southern Ocean, where harsh conditions and limited accessibility create logistical constraints. Furthermore, quantifying regional variations in submesoscale dynamics requires resolving both small and large scales, which poses additional challenges. In recent years, hydrographic data from seal-borne sensors have been used to investigate submesoscale vertical energy fluxes32,33,34. Thus far, these studies remain confined to regional subsets of the full dataset from the Marine Mammals Exploring the Oceans Pole to Pole (MEOP) program35. The MEOP dataset includes 233,610 year-round Conductivity-Temperature-Depth (CTD) profiles from south of the climatological maximum winter sea ice edge (Fig. 1). This is the only observational dataset with both multi-year, circumpolar coverage and high-frequency ( < 1 day) sampling (Fig. 1c, d). Here, we use the along-trajectory density gradients from the MEOP measurements to estimate the vertical buoyancy and heat fluxes associated with mixed-layer baroclinic instabilities (Methods)34,36.

Fig. 1: Instrumented seal data distribution and associated sea ice state.
figure 1

a Map showing all available seal-borne Conductivity-Temperature-Depth data from the Southern Ocean. Profiles south of the climatological maximum winter sea ice edge (red) are colored by the collocated satellite sea ice concentration. A dashed red line marks the continental shelf break (1000 m isobath). b Number of profiles in the whole dataset, aggregated over 2° × 5° latitude-longitude boxes. Boxes north of maximum winter ice edge are partially transparent to emphasize the data within the seasonal ice zone. Histograms of the (c) distance and (d) time between consecutive dives along a seal track, for data in the seasonal ice zone only. In both panels, a solid and dotted line mark the mean and 90th percentile, respectively. e Number of profiles by month, for data in the seasonal ice zone only.

Full size image

To illustrate some aspects of the methodology, consider an example seal trajectory from the West Antarctic Peninsula region (Fig. 2). Density variations along this trajectory (Fig. 2c) occur over a range of scales, which relate to the seal’s movement into the Bellingshausen Sea (Fig. 2a) as well as seasonal and sub-seasonal fluctuations in winds and sea ice concentration (Fig. 2b). Disentangling spatial and temporal variability is not straightforward. To isolate the impact of submesoscale dynamics from the full signal, we employ a commonly used parameterization for mixed-layer eddies37. In this framework, the transport induced by baroclinic instability is cast as an overturning streamfunction that depends on M2 and the MLD (Methods). To estimate this streamfunction from the MEOP data, we follow the approach of previous studies34,36, and assume that the density difference between consecutive dives (10.2 km separation distance on average) is primarily representative of a lateral gradient, rather than a temporal one. This allows us to calculate M2, which together with MLD, determines the available potential energy for baroclinic instability. It is also possible to express a vertical buoyancy flux associated with mixed-layer eddies (QMLE) and a vertical heat flux (QVHF) in terms of this streamfunction (Methods).

Fig. 2: Individual seal trajectory and along-trajectory properties.
figure 2

a Map of example seal trajectory colored by satellite sea ice concentration collocated with the profile time and location, underlying contours mark bathymetry, and a cyan line denotes the climatological maximum winter sea ice edge. b Time series of reanalysis wind stress magnitude (green) and satellite sea ice concentration (gray), and (c) vertical section of potential density (shading) and mixed-layer depth (orange) along the seal trajectory shown in (a).

Full size image

For the representative seal track, M2 and MLD vary at high frequencies, \({\mathcal{O}}\)(hour-days), whether in open water or underneath sea ice (Fig. 3a). Variations in either quantity can drive episodic changes in QMLE (Fig. 3b), which has a quadratic dependence on both M2 and MLD (Methods). QMLE is always a restratifying flux, since its formulation is based on the assumption that mixed-layer eddies slump isopycnals. Because the seasonal ice zone is salt-stratified, however, the vertical heat flux, QVHF, can be either positive or negative, depending on the orientation of the horizontal temperature gradient across the front. A positive heat flux (upward) occurs when the buoyant side of the front is warmer, while a negative flux (downward) arises when the buoyant side of the front is colder. Within the SIZ, upper-ocean temperatures are fixed near the freezing point in winter, which leads to weak lateral temperature gradients. Consequently, QVHF is around an order of magnitude smaller than QMLE, when both are expressed in units of W m−2 (Fig. 3b).

Fig. 3: Along-trajectory submesoscale flux estimation.
figure 3

a Mixed-layer depth (MLD; orange) and lateral buoyancy gradient (M2; blue) calculated for the example seal whose trajectory is shown in Fig. 2, gray shading marks the collocated satellite sea ice concentration. The thicker orange and blue lines denote the MLD and M2 after applying the Gaussian smoothing described in the Methods section. Vertical (b) heat flux (red) and buoyancy flux (black) induced by mixed-layer baroclinic instabilities, gray shading marks the collocated satellite sea ice concentration as in (a).

Full size image

Peaks in QMLE and QVHF may reflect stronger lateral gradients or deeper mixed-layers. For example, high submesoscale flux magnitudes are inferred in late March before sea ice formation (Fig. 3), when the mixed-layer was relatively shallow. This corresponds to the portion of the trajectory when the seal approached the coastline and crossed the Antarctic Coastal Current38, where meltwater input amplifies M2. The second sequence of elevated QMLE and QVHF are observed in late July, when SIC was high and the mixed-layer was deeper (Fig. 3), which coincided with the seal traversing the continental slope and the Antarctic Slope Current39. In both cases, the largest submesoscale fluxes were associated with persistent frontal features and strong background flows. That said, smaller peaks of QMLE in early May and June co-occur with large changes in SIC—presumably due to generation of lateral buoyancy gradients by sea ice melt and growth processes. There were no peaks in QVHF during these rapid SIC changes, suggesting that the buoyancy fluxes were salinity-driven. However, interpreting the along-trajectory seal data is complicated by the confounding effects of spatial and temporal variability associated with the seal’s movement through different environmental conditions. Given that a single seal can transit between different shelf regimes and the open ocean within a few months, examining the entire dataset is necessary to disentangle regional and seasonal patterns.

Distribution and drivers of dynamical regimes

While previous studies have applied similar methods to estimate submesoscale fluxes from MEOP data33,34,36, we extend this analysis to all available observations from the Southern Ocean seasonal ice zone, which demonstrates substantial regionality in both M2 and MLD. Mixed-layers are deepest in dense shelf water formation regions, such as the Weddell and Ross seas31,40, and near the maximum winter sea ice edge (Fig. 4a). In contrast, M2 is enhanced along the ice shelf margin and continental slope, particularly in West Antarctica (Fig. 4b). The mean QMLE distribution (Fig. 4c), in turn, is set by the interplay between the patterns in M2 and MLD. QMLE and QVHF are elevated on the continental shelf (Fig. 4c, d), where a large percentage of profiles have a balanced Richardson number (Rib) less than 1 (Supplementary Fig. 1), which indicates that the water column is favorable to submesoscale instabilities41. To determine the drivers of this heightened submesoscale activity on the shelf, we decompose QMLE anomalies, relative to the local space-time mean, into contributions from changes in M2 and MLD (Methods).

Fig. 4: Regional patterns of submesoscale vertical buoyancy and heat transport.
figure 4

Mean (a) mixed-layer depth, (b) lateral buoyancy gradient, (c) equivalent buoyancy flux (QMLE) and (d) heat flux (QVHF) associated with mixed-layer eddies. Averages calculated from all seal data (2004–2024) in 2° × 5° latitude-longitude boxes.

Full size image

In general, MLD exerts a stronger control over QMLE in dense shelf regions (Fig. 5d), where the MLD seasonal cycle amplitude is large due to convective mixing events in winter42,43. In these locations, around 75% of QMLE anomalies are associated primarily with a MLD anomaly, which, in turn, reflect the MLD seasonal cycle (Fig. 5d). Thus, submesoscale fluxes peak in winter when mixed-layers are deepest (Supplementary Fig. 2)—as in the temperate oceans26. Additionally, QVHF is positive, on average, indicating an upward heat flux (i.e., submesoscale eddies warm the surface ocean). On the other hand, areas where QMLE anomalies are controlled by M2—including the Amundsen and Bellingshausen seas—exhibit a spatially averaged negative (downward) QVHF. This means that fronts are usually oriented with cold water on the buoyant side of the front. Furthermore, submesoscale fluxes peak in spring and fall (Supplementary Data Fig. 2), when the production of surface lateral buoyancy gradients is maximized due to sea ice melt and formation20,21. Therefore, distinguishing regions based on the relative importance of M2 and MLD anomalies to the overall QMLE variability is necessary to understand the seasonality and drivers of submesoscale vertical fluxes.

Fig. 5: Physical drivers of submesoscale flux variability.
figure 5

Probability density functions of the (a) logarithm of lateral buoyancy gradient (M2), (b) mixed-layer depth (MLD), and (c) logarithm of balanced Richardson number (Rib). For all panels, profiles are sorted by the collocated sea ice concentration (SIC)—no ice, SIC = 0 (red), marginal ice zone (MIZ), 0 < SIC < 0.8 (black), and full ice cover, SIC > 0.8 (blue). d The percent of profiles, in each 2° × 5° box, where a submesoscale buoyancy flux anomaly is primarily associated with a MLD anomaly (see “Methods”).

Full size image

Typically, M2 anomalies dominate QMLE variations in places with greater M2 variance (Supplementary Fig. 3), which correspond to locations where the time-mean M2 is elevated, such as the continental slope and margins (Fig. 4b). Additionally, sea ice processes are thought to generate lateral buoyancy gradients that can energize submesoscale motions9,17. Indeed, MEOP data indicate enhanced M2 for marginal ice zone (MIZ) conditions (0 < SIC < 0.8), based on collocated satellite sea ice concentration (Fig. 5a). However, sea ice meltwater fronts are also accompanied by stronger vertical stratification21, and thus increased M2 in the MIZ does not necessarily lead to stronger submesoscale turbulence (Fig. 5c). In fact, the mean M2, QMLE, and QVHF are weak throughout much of the off-shelf area of the seasonal ice zone (Fig. 4). This could be due to sampling bias, since meltwater fronts dissipate quickly21, although observations are roughly evenly distributed across different sea ice conditions (Supplementary Fig. 4). Therefore, persistent frontal features linked to coastal and slope currents seem to more efficiently energize submesoscales compared to sea ice meltwater fronts.

Contribution of submesoscale fluxes to the heat budget

The magnitude of QMLE and QVHF increases poleward (Fig. 4), which suggests that submesoscale fluxes are most important on the continental shelf. There, deep mixed-layers and frontal boundary currents energize the upper ocean, and air–sea fluxes are weak due to higher sea ice concentrations, which limit solar radiation penetration to the surface ocean44. QVHF also exhibits notable zonal structure, particularly on the shelf. In dense shelf water forming regions, including the southern Weddell Sea43, Ross Sea45, and Prydz Bay46, QVHF is positive, on average. In these locations, deep convection occurs in winter due to wind-driven sea ice transport and subsequent heat loss in coastal polynyas47. Therefore, the positive QVHF, which opposes the intense surface heat loss, may be important in setting Dense Shelf Water (DSW) formation rates, and, through the export of DSW down the continental slope, contribute to Southern Ocean overturning48,49. Submesoscale heat fluxes are also likely key to springtime restratification in coastal polynyas50, which impacts phytoplankton bloom initiation and biogeochemical cycling51.

In warm shelf regions, such as the Amundsen and Bellingshausen seas, QVHF is negative, on average. In other words, cold water is typically on the buoyant side of the front, presumably because lateral buoyancy gradients are driven by the input of cold, fresh water from ice shelf melt—as opposed to dense shelf regions, which have much lower meltwater content. Indeed, the location of the strongest downward submesoscale heat fluxes coincides with areas previously identified as having significant meltwater content52,53,54. The link between meltwater fronts and downward heat fluxes is also consistent with the shallower depth of the maximum lateral buoyancy gradient in the Bellingshausen as compared to the Weddell (Supplementary Fig. 5). The negative values of QVHF in warm shelf regions suggest that submesoscale heat fluxes may promote sea ice formation by cooling the surface ocean. This behavior is different from dense shelf regions, where QVHF transfers heat upwards. Finally, in East Antarctica, except for Prydz Bay, the mean QVHF is near-zero, despite QMLE values similar to those in the rest of continental shelf (Fig. 4c). This aligns with the “fresh" shelf regime, where vertical and horizontal temperature gradients are weak due to limited onshore heat transport31. Thus, differences in hydrographic properties over the Antarctic continental shelf also imprint on the submesoscale vertical fluxes and their role in the mixed-layer heat budget.

Directly quantifying the submesoscale contribution to the upper-ocean heat budget is difficult from observations. However, we can compare the mean values of QVHF and QMLE to other terms in the budget using a data-assimilating state estimate55,56. For example, the ocean surface heat and freshwater fluxes in the Biogeochemical Southern Ocean State Estimate (B-SOSE; Supplementary Fig. 6) are similar in magnitude to those estimated from the MEOP data on the continental shelf. For example, in the Bellingshausen Sea (70-100°W), the mean seal-derived QVHF is −4.2 ± 2.3 W m−2, while the 2013-2023 mean surface ocean heat flux in B-SOSE is −10.9  ± 3.8 W m−2. The restratification rates associated with mixed-layer baroclinic instabilities37, \({\mathcal{O}}(1{0}^{-7}-1{0}^{-6}\,{{\rm{m}}}^{2}\,{{\rm{s}}}^{-3})\), are also comparable in magnitude to the destratification associated with surface cooling from air-sea exchange15. In the off-shelf SIZ, on the other hand, the mean QVHF is less than 1 W m−2, which is an order of magnitude smaller than the surface fluxes in B-SOSE over the same region (Supplementary Fig. 6). This negligible mean QVHF is due to the weak lateral temperature gradients across large swaths of the Southern Ocean seasonal ice zone. In other words, the salinity-driven stratification at high latitudes permits strong submesoscale buoyancy fluxes without requiring large heat fluxes. Therefore, the nature of submesoscale heat transport in the seasonal ice zone is different compared to other parts of the global ocean.

Given that submesoscale processes are episodic, the limited data coverage in certain regions may miss strong events. For instance, large data gaps exist in the Weddell and Ross sectors, as well as the East Antarctic continental shelf (Fig. 1b). There is also a seasonal bias to the entire dataset caused by the timing of seal tagging and molting (Fig. 1e). Thus, regional-scale flux magnitudes are not well constrained. This is compounded by the uncertainties associated with the individual flux estimates. First, based on the measurement accuracy, there is an uncertainty of 22% and 28% relative to the flux magnitude for QVHF and QMLE, respectively (Methods). There is also uncertainty in applying the parameterization to along-trajectory observations, since the parameterization assumes an idealized crossing perpendicular to the front. Averaging over all possible angles leads to a root-mean-square error of the buoyancy gradient amplitude by a factor of \(1/\sqrt{2}\)25. This, in turn, causes a 50% reduction in the flux magnitude. In other words, our QMLE and QVHF are likely underestimates. Nevertheless, the regional-scale patterns are robust since the random uncertainty associated with the measurement accuracy is smaller than the systematic uncertainty due to the seal sampling behavior. More extensive high-resolution measurements, particularly in data-sparse regions, would help to refine these submesoscale flux estimates and allow us to examine a wider range of scales than the time-mean patterns identified in this study.

It is also worth noting that the flux estimates presented here only reflect mixed-layer baroclinic instabilities. These are a good proxy for other submesoscale processes including elevated frontal subduction57. Still, submesoscale motions may be energized by other instabilities16—including symmetric instability58 and inertial instability59— which are difficult to constrain from seal-derived data but deserve further consideration to form a more comprehensive view of submesoscale dynamics in the seasonal ice zone. Wind-front interactions also need additional investigation. Surface winds have been shown to alter the magnitude of lateral buoyancy gradients20, acting to intensify or weaken the front depending on the relative wind direction60. Furthermore, cross-frontal wind-driven flows, and the associated Ekman buoyancy fluxes, may be important to the seasonal mixed-layer variability and heat budget21,61,62. For the data considered here, the strongest submesoscale heat fluxes occurred under a wide range of wind conditions (Supplementary Fig. 7), and the wind stress distribution during these strong events is indistinguishable from that of the full dataset (Supplementary Fig. 7c). Given the regionality in mixed-layer eddies described here, future work should assess how wind-front interactions may differ across different hydrographic regimes.

Discussion

The Southern Ocean seasonal ice zone is a dynamic region with a critical role in Earth’s energy budget and the global overturning circulation14,49,63. Sparse observations suggest that the SIZ is highly energetic due to the production of lateral buoyancy gradients by sea ice processes20,21,54,64. However, generalizing the insights from regional process studies requires constraining large-scale patterns in submesoscale dynamics. Toward this end, we used hydrographic data from seal-borne sensors to construct a circumpolar, observation-based estimate of submesoscale vertical buoyancy and heat fluxes across the Southern Ocean seasonal ice zone. These fluxes depend on M2 and MLD, which exhibit substantial spatial variability within the SIZ. Consequently, submesoscale vertical fluxes are also spatially variable, and can be divided into three regimes (Fig. 6) that align with: i) the off-shelf SIZ, as well as ii) dense and iii) warm continental shelves.

Fig. 6: Mean submesoscale dynamical regime distribution.
figure 6

Schematic summarizing the three dynamical regimes, which are identified based on the mean submesoscale heat flux (QVHF) distribution. Namely, regions where the time-mean submesoscale vertical heat flux is positive (red), negative (blue), and negligible (yellow), which corresponds to the relative control of mixed-layer depth (MLD) versus lateral buoyancy gradient (M2) variations.

Full size image

These regimes exhibit distinct vertical heat transport characteristics, including magnitude, sign, and leading driver. In dense shelf regions, where winter mixed-layers reach hundreds of meters deep, submesoscale fluxes are controlled by MLD variations. QVHF is positive (upward) and supports springtime restratification in coastal polynyas47,50,51. By contrast, in warm shelf regions where ice shelf meltwater input is strong52,53,54, there is generally cold water on the buoyant side of the front. As a result, QVHF is negative (downward) and its variability is determined primarily by M2 anomalies. On the other hand, QVHF is weak in East Antarctica and across much of the off-shelf sector of the seasonal ice zone. Although sea ice melt generates lateral buoyancy gradients throughout the SIZ, enhanced stratification associated with sea ice meltwater fronts acts to suppress the vertical extent of submesoscale motions21. Furthermore, the strength of the eddy-induced overturning streamfunction is not necessarily proportional to the tracer flux; weak lateral temperature gradients across much of the seasonal ice zone lead to small submesoscale heat fluxes in many regions. However, other tracers that exhibit stronger upper-ocean gradients, such as nutrients and dissolved inorganic carbon, may experience significant vertical transport from submesoscale processes65,66.

Regional variations in submesoscale vertical heat transport must be considered in order to determine the rectified effect of small-scale processes on the upper-ocean heat budget and sea ice evolution. For example, seasonal and interannual fluctuations in sea surface temperature and sea ice concentration may be more sensitive to submesoscale flows in certain locations, such as boundary currents and coastal polynyas. Continued examination of these spatial patterns is necessary to understand the mechanisms driving sea ice variability across a range of time scales, which may feed back onto long-term trends in ice area and extent. However, quantifying large-scale differences in fine-scale variability under sea ice is challenging from observations due to the low spatiotemporal resolution of most oceanographic datasets with circumpolar coverage. Therefore, despite the assumptions inherent in estimating QMLE and QVHF from the MEOP data (Methods), this study represents a key first step toward characterizing regionality of submesoscale vertical fluxes within the Southern Ocean seasonal ice zone. This, in turn, can inform the upscaling of observational results from regional process studies, and serve as a baseline for submesoscale-resolving model simulations.

Methods

This study uses in situ data from the Marine Mammals Exploring the Oceans Pole to Pole (MEOP) program35. We analyze the quality-controlled temperature and salinity data from the March 8, 2024 version of the MEOP-CTD dataset. Sampling is uneven in the vertical, designed to maximize variance explained when linearly interpolated32. The resolution ranges from 2–10 m in the top 100 m of the water column, and 10–150 m below that. Following the standard protocol for the interpolated fields provided in the delayed-mode MEOP dataset, all profiles are linearly interpolated onto a regular vertical grid with 1 m resolution from the surface down to 1000 m or the dive depth. For each profile, potential density referenced to the surface (σθ) and buoyancy frequency (N2) are calculated using the Gibbs-Seawater (GSW) Oceanographic Toolbox67. Mixed-layer depth (MLD) is defined using a Δσθ = 0.03 kg m−3 density threshold68. The MLD is then used to compute mixed-layer averages of various properties. For example, mixed-layer buoyancy is given by

$$b=g\left(1-\frac{\rho }{{\rho }_{0}}\right),$$
(1)

where g is gravitational acceleration, ρ is the potential density referenced to the surface and averaged over the mixed-layer, and ρ0 is a reference density (1027 kg m−3). For each seal trajectory, the mixed-layer buoyancy is linearly interpolated onto an along-trajectory horizontal grid with 500 m resolution36; then a Gaussian smoothing window of 5 km is applied to account for the ± 5 km uncertainty in the geolocating ability of the seal-borne CTD sensor69, although others have suggested that the position uncertainty may be larger than this70. Nevertheless, from the horizontally smoothed buoyancy, we then calculate the along-trajectory buoyancy gradient in the mixed-layer and take this to be M2. Note that in reality, the along-trajectory gradients reflects both spatial and temporal variability. Also, seals are unlikely to sample fronts perpendicularly, so the magnitude of the density gradient is likely underestimated71. Still, a previous study found, by subsampling a high-resolution model along several seal tracks, that calculating M2 from the MEOP data is a reasonable first-order estimate36.

We also compute the balanced Richardson number (Rib), which is a non-dimensional parameter that, when less than or equal to 1, indicates that the water column is susceptible to the development of submesoscale instabilities34,41. It is defined as

$$R{i}_{b}=\frac{{N}^{2}{f}^{2}}{{M}^{4}},$$
(2)

where f is the Coriolis parameter, and the buoyancy frequency (N2) and lateral buoyancy gradient (M2) are given by

$${N}^{2}=\frac{\partial b}{\partial z},\,{M}^{2}={\nabla }_{h}b.$$
(3)

In practice, in order to compute Rib from the MEOP data, we calculate N2 in the center of the mixed-layer using the GSW Toolbox67 and take M2 to be the along-trajectory mixed-layer buoyancy gradient. Here, and in the rest of the analysis, we mask out M2 for consecutive profiles that are separated by more than 15 km, although the results are not sensitive to this threshold. While 15 km is larger than the local Rossby radius of deformation, the fronts need not be at the deformation radius since Equation (4) below assumes that submesoscale baroclinic instabilities are energized by larger-scale lateral gradients (e.g., from mesoscale structures). To estimate submesoscale vertical fluxes, we utilize a parameterization for the overturning induced by mixed-layer baroclinic instabilities37, which is expressed as an two-dimensional overturning streamfunction with units m2 s−1:

$$\Psi={C}_{E}\frac{{M}^{2}{H}^{2}}{| \, f | }\mu (z)\Lambda,$$
(4)

where CE is an empirical coefficient taken to be 0.0634,37, M2 is the lateral buoyancy gradient, H is the mixed-layer depth, f is the Coriolis parameter, and μ is a vertical structure function that ranges from 0 (at the surface and mixed-layer depth) to 1. We take μ to be 1 to represent that maximum value in the water column, which may be at the center of the mixed-layer or closer to the mixed-layer base72. Λ is a sea ice concentration dependent scaling factor that accounts for the damping of eddies by sea ice cover. Following Shrestha & Manucharyan (2022), this takes the form of a step function,

$$\Lambda=\left\{\begin{array}{ll}1\quad &{\rm{SIC}}\le 0.7\\ 0.26\quad &{\rm{SIC}} > 0.7\end{array}\right.$$
(5)

Although the overturning streamfunction decays to 0 at the mixed-layer base by definition, subsequent work has shown that the vertical decay scale of a tracer anomaly due to mixed-layer baroclinic instability depends on N73. In regions, such as the Southern Ocean, with weak vertical stratification, the extent of baroclinic instability may penetrate well below the mixed layer74. Using this streamfunction, and following methods similar to those in Biddle & Swart (2020), we calculate an equivalent buoyancy flux associated with mixed-layer eddies, expressed as an energy flux with units W m−2. This is a standard application of the parameterization34,75,76,77, which is based on the notion that baroclinic instabilities restratify the mixed layer by flattening isopycnals. Although these submesoscale eddies move denser water downward and lighter water upward along isopycnals (i.e., adiabatically), the net effect is similar to that of a vertical buoyancy flux in that it stabilizes the mixed layer. So, while the mechanism being invoked is adiabatic, the restratification can be associated with an “equivalent” buoyancy flux,

$${Q}_{MLE}=\frac{{c}_{p}\rho }{\alpha g}\Psi {M}^{2},$$
(6)

where cp is the specific heat capacity, ρ is the mixed-layer density, α is the thermal expansion coefficient, and g is gravitational acceleration. cp and g are constants, and all other parameters are calculated from the MEOP data using the GSW package67. QMLE is positive-definite since it depends on the square of the lateral buoyancy gradient. In other words, the effect of mixed-layer eddies is always to restratify. Note that the actual vertical heat flux is not always positive, if stratification is not temperature-driven.

In the high-latitude Southern Ocean, where salinity controls the stratification, it is possible to have cold water on the buoyant side of the front, which is advected upward by the submesoscale overturning. The vertical heat flux induced by mixed-layer eddies, QVHF, is calculated as

$${Q}_{VHF}={c}_{p}\rho \Psi {\theta }_{x},$$
(7)

following Spungin et al. (2025), where the parameters are identical to Equation (6) except for θx, which is the along-trajectory gradient in mixed-layer potential temperature. Importantly, QVHF can be either positive or negative. A positive (upward) flux occurs when the along-trajectory mixed-layer buoyancy and temperature gradients have the same sign, i.e., when warm water is on the buoyant side of the front. Conversely, a negative (downward) flux arises when colder water sits on the buoyant side of the front.

There are several different sources of uncertainty in the calculation of QMLE and QVHF. First, the data itself goes through the standard quality control procedure, which includes salinity adjustments using a pressure-dependent linear correction derived by comparison to shipboard CTD profiles78,79, a thermal cell correction for both temperature and salinity32,80, and a density inversion removal algorithm81. Following these adjustments, the individual profiles have an accuracy of   ± 0.04 °C for temperature and   ± 0.03 g/kg for salinity32. Based on this measurement accuracy, we can generate possible realizations of the input temperature and salinity, and propagate this through the submesoscale flux calculation, using a Monte Carlo simulation with 5000 iterations. This indicates an uncertainty of 22% and 28% relative to the flux magnitude for QVHF and QMLE, respectively. There is also uncertainty in applying the parameterization to along-trajectory observations, since the parameterization is based on a perpendicular front crossing. Averaging over all possible angles leads to a root-mean-square error of the buoyancy gradient amplitude by a factor of \(1/\sqrt{2}\); since QMLE depends on the buoyancy gradient squared, this means that the submesoscale flux will be underestimated by a factor of 2 due to the uncertainty associated with frontal orientation, assuming the seals sample submesoscale fronts at a randomly distributed angle25.

QMLE, as calculated from Equation (6), varies primarily as a function of M2 and H. In order to isolate the impact of each property, we apply a Reynold’s decomposition to separate QMLE into mean and fluctuating components:

$$\overline{{Q}_{MLE}}+{Q}_{MLE}^{{\prime} }=K\left(\overline{{M}^{4}}+{({M}^{4})}^{{\prime} }\right)\left(\overline{{H}^{2}}+{({H}^{2})}^{{\prime} }\right)=K\left[ \, \overline{{M}^{4}}\,\overline{{H}^{2}}+\overline{{M}^{4}}\,{({H}^{2})}^{{\prime} }+\right.\\ \left. {({M}^{4})}^{{\prime} }\,\overline{{H}^{2}}+{({M}^{4})}^{{\prime} }\,{({H}^{2})}^{{\prime} }\right],$$
(8)

where K is equal to \(\frac{{C}_{E}{c}_{p}\rho \mu }{f\alpha g}\), which is assumed to be approximately constant. Note that we have separated M4 and H2 into mean and fluctuating components rather than M2 and H, which would result in more cross-terms. These cross-terms can be sizable because fluctuations in M2 can be large relative to the mean. By following Equation (8), the linear terms in the decomposition dominate the variance. Although, note that M4 and H2 are being treated as new derived variables with their own mean and fluctuation structure. This is still relevant to our goal of attributing QMLE anomalies to mixed-layer depth versus lateral buoyancy gradient variations. If we consider an instantaneous flux anomaly, the anomaly-mean terms (\(\overline{{M}^{4}}\,{({H}^{2})}^{{\prime} }\) and \({({M \, }^{4})}^{{\prime} }\,\overline{{H}^{2}}\)) allow us to partition the variance in H 2 ⋅ M 4 to variance in H2 and M 4, respectively.

In Fig. 5, we take \(\overline{{Q}_{MLE}}\) to be the mean value in 2° × 5° latitude-longitude boxes, and \({Q}_{MLE}^{{\prime} }\) to be the anomaly from the local box average. This same, relatively coarse, 2° × 5° grid is used in Figs. 4 and 6, and was selected so that most boxes have  > 100 profiles (Fig. 1b) and at least 6 unique months (Supplementary Fig. 8). In other words, to minimize sampling alias such that the box averages reflect regional-scale patterns. However, we primarily interpret these patterns qualitatively, so results are not sensitive to the precise horizontal grid. It should be noted that \({Q}_{MLE}^{{\prime} }\), which is defined relative to the local space-time mean, reflects processes occurring at different scales. For example, MLD anomalies primarily represent seasonality, whereas M2 anomalies express fluctuations from hours to days. Although the high-frequency M 2 changes themselves may vary seasonally due to seasonal-scale transitions in sea ice state. Nevertheless, we can still consider the terms of \({Q}_{MLE}^{{\prime} }\) from the Reynold’s decomposition in order to determine the dominant driver of QMLE variability in different locations. Namely, we regress the observed QMLE anomaly onto the \(\overline{{M}^{4}}\,{({H}^{2})}^{{\prime} }\) and \({({M}^{4})}^{{\prime} }\,\overline{{H}^{2}}\) terms. Comparing the relative magnitude of the correlation coefficients allows us to associate a given QMLE anomaly with either a MLD anomaly or M2 anomaly. Figure 5d shows the percentage of profiles within each latitude-longitude box where a QMLE anomaly is associated primarily with a MLD anomaly (i.e., correlation with the \(\overline{{M}^{4}}\,{({H}^{2})}^{{\prime} }\) term is higher).

In addition to the MEOP dataset, we also utilize daily passive microwave sea ice concentration from the NOAA/NSIDC Climate Data Record, Version 3 with 25 km resolution82, and daily averages of wind stress magnitude (∣τ∣) from the 0.25° resolution ERA5 reanalysis83. Supplementary Fig. 6 shows the mean ocean surface heat and freshwater fluxes from the Biogeochemical Southern Ocean State Estimate (B-SOSE)56. B-SOSE is a data-assimilating state estimate that constrains a general circulation model with satellite and in situ observations. Here, we use Iteration 155, which has 1/6° horizontal resolution and runs from 2013 to 2023. The freshwater flux was converted to units of W m−2 by assuming a latent heat of vaporization of 2.5 × 106 J kg−1.