Introduction

Predicting the properties of crystals is a problem with many useful applications, such as understanding the behavior and functionality of crystalline solids1,2. Additionally, the ability to predict crystal properties would greatly accelerate the discovery and development of new crystals by identifying candidate materials warranting experimental study3,4,5,6,7,8,9.

Similar to proteins10,11,12,13,14,15,16, crystals are often represented as graphs that model the interactions between nearest neighbors; atoms in atomic crystals and molecules in molecular crystals7,8,9,17,18. For either case, crystal lattice sites are represented as nodes and the bonds (e.g., ionic or covalent or van der Waals) between them are represented as edges. Graph neural networks (GNNs) are then typically used to learn the contextual representation of each node and edge within the crystal graph to predict its properties. CGCNN18, a main baseline for GNN-based crystal property predictors uses a convolutional neural network (CNN) on top of node embeddings from a crystal graph to learn the interactions between atoms in the crystal and predict crystal properties. Although CGCNN outperformed classical methods19,20,21, it does not incorporate the many symmetries that crystals abide by. Several follow-up works tried to alleviate this limitation. One of those follow-up works is MEGNet7, a neural network architecture that incorporates crystal periodicity and only relies on GNNs to represent crystals. MEGNet outperforms CGCNN on various tasks; however, it still fails to account for critical information such as bond angles. ALIGNN8 was proposed to explicitly incorporate bond angles in addition to the other information accounted for by MEGNet and achieves state-of-the-art results compared to previous GNN approaches. Despite all these advances, GNNs still face several challenges when it comes to predicting crystal properties: They fail to efficiently encode the periodicity inherent to any crystal which results from the repetitive arrangement of unit cells within a lattice, a representation distinct from standard molecular graphs22. Furthermore, it is very complex to incorporate into GNNs, critical atomic and molecular information such as bond angles8 and crystal symmetry information such as space groups23. Finally, graphs may lack expressiveness, which is useful in conveying complex and nuanced crystal information that is critical for accurate crystal property prediction.

The aforementioned challenges are due to the complexities of crystal graph representation. We aim to mitigate these challenges by modeling the crystal structure from its text description as opposed to its graph representation. Textual data contain rich information and are very expressive (see Table 1); additionally, incorporating critical/desired information in text is generally more straightforward compared to graphs.

Table 1 Visualizing the difference between the information in the GNNs input versus LLMs input for NaCl and AcBrO
Full size table

Crystal representations can for instance be learned by pre-training large language models (LLMs) on a large body of scientific literature which contains diverse chemical and structural information about crystal design principles and fundamental properties24,25,26,27. Then, one can fine-tune these pre-trained LLMs on labeled data to solve specific tasks such as crystal property prediction28,29, crystal recommendation and ranking29, and synthesis action retrieval30. However, these methods also face the challenges of limited pre-training and downstream data, limited computational resources, a lack of efficient strategies to use the available resources, and they all rely on an LLM that needs to be further pre-trained on millions of materials science articles.

In this work, we demonstrate effective strategies for the use of LLMs for the accurate prediction of crystal properties from their text descriptions. Existing approaches for fine-tuning LLMs for prediction tasks often either rely on both the encoder and the decoder or leverage encoder-only large models that tend to have as many parameters as encoder-decoder models. In this paper, we make the simple choice to use a pretrained encoder-decoder model, here T531, entirely discard its decoder and fine-tune its encoder for regression and classification tasks. This has many desiderata: it allows us to cut the network size in half and importantly enables us to fine-tune on longer sequences and therefore account for longer-term dependencies in the crystal descriptions. With this simple yet effective choice, our approach outperforms not only large encoder-only models such as MatBERT, but also state-of-the-art GNN-based crystal property predictors such as ALIGNN. In addition, our approach does not rely on indomain pre-trained LLMs and has significantly fewer parameters. Furthermore, we perform extensive and carefully designed experiments, comparing performance against the strongest GNN-based approaches to shed light on the benefits of using text and highlight the shortcomings of current GNN-based models for crystals. Finally, we release to the public the curated dataset we used as a benchmark, called TextEdge, to accelerate natural language processing (NLP) for materials science research.

Results

LLM-Prop framework

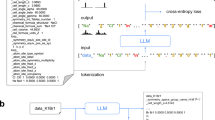
Our LLM-Prop framework (Fig. 1a) is composed of a carefully fine-tuned encoder part of small version of T5 model (Fig. 1b)31 on text descriptions of crystal structures to learn crystal representations that are used to predict the physical and electronic properties of any crystal material.

Fig. 1: The general LLM-Prop framework.
figure 1

a depicts how LLM-Prop works compared to GNNs-based models. On the left most of the figure, we show how we get the description from the crystal structure using Robocrystallographer. The middle part shows the comparison between our approach (text-based) and baselines (structure-based). The yellow colored information is related to Sodium (Na), green colored information is related to Chlorine (Cl), and blue colored information is related to additional information that text data provide such as space groups and bond distances. On the right most part of the figure, we then show our proposed LLM-Prop architecture (see 2.1 for more details). b details the T5 encoder architecture used in LLM-Prop, which is a stack of six layers of Transformer encoders47.

Full size image

T531 is an encoder-decoder Transformer-based architecture which was the first unified language model that converts all text-based language problems into a text-to-text problem to perform both generative and predictive tasks. This framework is important for adapting and fine-tuning T5 on many tasks, and enables efficient multitask fine-tuning. Raffel et al31. carefully compared different architectures, pretraining objectives, unlabeled datasets, transfer approaches, and more on dozens of natural language tasks and then combined the best-performing approaches in each comparison to pre-train T5. For instance, while MatBERT, a BERT-based model, was pre-trained using a masked language model (MLM) objective32, T5 uses a spanmasking objective33 as it was shown to outperform MLM objective in terms of predictive power and speed. These considerations motivate our choice to use T5 as our main pre-trained model.

Transforming each task to text-to-text format requires T5 to use its decoder part to generate the output. While the decoder is necessary for generative and many downstream tasks, it adds unnecessary memory, time complexity, and work overhead when adapted for predictive tasks. Furthermore, Raffel et al.31 argued that the text-to-text format does not work well on regression tasks where the model is asked to generate the actual numerical value as the target instead of predicting the entire probability distribution. Raffel et al.31 resorted to only predicting the range to which a given value belonged instead of performing full regression with T5.

How can we leverage T5 for highly accurate performance on predictive tasks, especially regression tasks? We propose LLM-Prop as an approach. LLM-Prop leverages T5 by directly adding a linear layer on top of its encoder for regression tasks. This linear layer can be composed with a sigmoid or softmax activation for classification tasks. Relying only on the T5 encoder reduces the total number of parameters by half which allows us to train on longer sequences and therefore incorporate more crystal information to improve predictive performance. LLM-Prop framework as shown in Fig. 1 starts by preprocessing the crystal descriptions, tokenizing them, feeding the tokenized input to T5 encoder which is then followed by a prediction layer.

For the input preprocessing step we did the following: (1) We removed stopwords from the text descriptions as this preprocessing step has been shown to improve performance on predictive tasks34,35. We processed all publicly available English stopwords and excluded them from the crystal text descriptions, except for digits and certain signs that may carry important information for crystal representation such as bond distances and angles. (2) We Replaced bond distance with a [NUM] token and bond angle with an [ANG] token. Several works have shown that LLMs struggle to resolve contextual numerical information required for general common-sense reasoning36,37,38,39. For example, Zhang et al.37. replaced numbers in the training data with their scientific notation using the [EXP] token (i.e., 314.1 with 3141[EXP]2) to train a new BERT model which outperforms the original BERT on tasks that require numerical reasoning skills such as question answering. In our case, numbers not only add reasoning complexity but also increase the input sequence tokens since they are generally tokenized on a digit basis. We replace all bond distances and bond angles in the crystal text descriptions along with their units with [NUM] and [ANG] tokens, respectively. Those tokens are then added to the vocabulary as new tokens (i.e., we replace 3.03 A˚ with [NUM] and 120 degrees or 120° with [ANG]). While we are aware that this might also limit LLM-Prop to learn from the information related to bond distances and angles between atoms and molecules in the crystal structure, our results show that compressing the description as described—representing bond distances and angles with the same two special tokens described above—enables LLM-Prop to see more context in the text and achieve better performance. (3) We removed bond distances and bond angles. To further investigate the importance of having bond lengths and bond angles versus removing them entirely to more compress the input description, we also train LLM-Prop on the descriptions where bond lengths and bond angles are retained and when they are removed to see the effect this information have on LLMs in general when predicting crystal properties. (4) We prepended a [CLS] token to the input. Delvin et al.32 showed that prepending a [CLS] token to every input, updating the embedding of that token together with the input tokens, and then using it for prediction improves predictive performance on downstream tasks. We used this same preprocessing step on LLM-Prop, adding a [CLS] token in front of every input and also in the vocabulary, and then learning its representation jointly with the rest of the model. We used the embedding of the [CLS] token as the input to the linear layer for prediction.

Finally, to perform label scaling for regression tasks, we train LLM-Prop on normalized targets using different label normalization techniques: z-score normalization, min-max normalization and log normalization. Then we denormalize the outputs to calculate the prediction errors on the actual values. Suppose that we have N crystals X1,…, XN and their corresponding properties Y1,…, YN as a training set. Here Xi denotes the text description of the ith crystal. Denote by µ and σ the mean and standard deviation over all targets in the training set, respectively. Denote by Ymin and Ymax the minimum and the maximum target value in the training data, respectively. The three normalization techniques we explored normalize a given target value Yi as follows:

$${\hat{Y}}_{i}\left({\rm{z}}-{\rm{score}}\right)=\frac{{Y}_{i}-\mu }{\sigma },$$
(1)
$${\hat{Y}}_{i}\left(\min -\max \right)=\frac{{Y}_{i}-{Y}_{min }}{{Y}_{max }-{Y}_{min }},$$
(2)
$${\rm{and}}{\hat{Y}}_{i}(\log -{\rm{norm}})=\log {Y}_{i}+1.$$
(3)

Data collection and analysis

We collected the dataset used in this work from the Materials Project database40 using the Materials Project free API as of November 1, 2022. We focus on six crystal properties that include both regression and classification tasks and are diverse enough to evaluate the capabilities of any property predictor. We collect the data of band gap, formation energy per atom (FEPA), energy above hull (Ehull), crystal volume, energy per atom (EPA), and an indicator of whether the band gap is direct or indirect (Is-gap-direct). These properties have not yet been explored in other text-based methods and are usually also challenging to predict even for GNN-based methods. The data originally contained 145,825 crystals structure-description pairs which we randomly split into 125,825 samples for the training set, 10,000 samples for the validation set and 10,000 samples for the test set. However, when parsing the CIF files to build the graphs that are used to fine-tune GNN’s baselines, some structure files failed to be incorporated, ending up with 125, 098 training samples, 9, 945 validation samples, and 9, 888 samples for the test set that make up the final dataset to contain 144, 931 total samples, so that both LLMs and GNNs are trained on the same amount of data for a fair comparison. For each crystal, we collect its ID, structural information, structure text description, and the aforementioned six properties. We generated the crystal text descriptions using Robocrystallographer41, a tool that generates a deterministic human readable text description of a structure given its CIF file.

The whole dataset contains approximately 157 million tokens or words of crystal text descriptions in total and each description has approximately 1467.3 subword tokens (small chunks of words that LLMs can easily understand) on average. Figure 2 shows a summary of what tokens/words are most frequent in the crystal text descriptions. For instance, in Fig. 2b), we can see that O2− occurs approximately 17,500 times while Mg occurs approximately 5000 times in TextEdge.

Fig. 2: Visualization of the most frequent tokens in TextEdge.
figure 2

a The wordcloud of top 200 most frequent tokens in TextEdge. b The frequency statistics of the top 50 most frequent tokens in TextEdge.

Full size image

Crystal property prediction results

LLM-Prop vs GNN-based models. We first compare LLM-Prop with the GNN baselines when LLM-Prop is configured to input structural information directly, similar to GNN models. This is in the form of CIF files or JSON files with condensed structural features generated by Robocrystallographer given CIF files as input (see Table 3). We find that LLM-Prop outperforms all GNN-based baselines on volume prediction and it outperforms the best-performing baseline (DeeperGATGNN) on the test set by approximately 67%. For other tasks, LLM-prop gives competitive performance, for instance where it is the second best after ALIGNN for predicting band gap and the third best after ALIGNN and CGCNN when predicting FEPA and after MEGNet and ALIGNN when predicting EPA. Based on our assumption that LLMs understand natural language better compared to other input modalities, we compare the LLM-Prop performance when it takes in crystal structure description as input (see Table 2 and Fig. 3) and observe its performance get improves on several tasks. For instance, it achieves the best performance when predicting band gap with approximately 8% improvement compared to the best baseline (ALIGNN) and when classifying whether a crystal has a direct or indirect band gap with approximately 3% improvement over the best baseline (CGCNN). The possible reason for the overall improvement of LLM-Prop over GNN-based models when predicting certain properties might be the relative ease and ability to access some important information that is sensitive to these properties, e.g., space group information (see Table 1 and Table 5). However, further thorough evaluations should be conducted to confirm which information in the crystal descriptions contribute most to the performance of LLM-Prop on each property. Overall, this insight encourages: (1) the development of text-based methods for crystal property prediction and the creation of high-quality text datasets needed for crystalline solids and (2) the development of new graph-based architectures that can incorporate more information, such as space group and Wyckoff sites. Unfortunately, LLM-Prop is not able to yield better performance when we do zero-shot predictions since T5 was not explicitly trained on in-domain data. However, the fine-tuned LLM-Prop (LLM-Prop-transfer) on band gap exhibits strong transfer learning ability compared to other models when transferred to volume prediction and vice versa (see Table 4).

Table 2 Performance comparison on test set between LLM-Prop and a text/description-based baseline (MatBERT)
Full size table
Fig. 3: Performance comparison of LLM-Prop with baselines on test set across different input modalities.
figure 3

“Robo.” means that the input is a condensed structure in a JSON format generated by Robocrystallographer, “CIF” denotes that the input is a CIF file, and “Descr.” represents having input as crystal descriptions. For description-based models we only show the best performing input preprocessing strategy (refer to Table 2 for more details). From (a–f) represents the performance visualization when predicting Band gap, FEPA, EPA, Volume, Ehull, and Is-gap-direct, respectively.

Full size image

LLM-Prop vs MatBERT. To allow for a fair comparison, we trained MatBERT with the same input modalities and preprocessing strategies as LLM-Prop. In Table 3 and Fig. 4, we compare results when both models are trained on structure information directly. LLM-Prop outperforms MatBERT by a large margin on all properties except on classifying whether a crystal band gap is direct or indirect. When MatBERT is trained on crystal description, the results in Table 2 and Fig. 5 show that LLM-Prop outperforms MatBERT on both regression and classification tasks by a large margin despite having 3× fewer parameters. In addition, although MatBERT was pre-trained on in-domain data and is larger, LLM-Prop shows stronger transfer learning ability when transferring between models fine-tuned on volume and band gap (see Table 4). The MatBERT results show that naively fine-tuning pre-trained LLMs (even though they have been pre-trained on domain specific data) is insufficient for accurate crystal property prediction and additional strategies such as those we introduce in this paper are needed to achieve a better performance.

Table 3 Performance comparison on test set when the input is a structure
Full size table
Fig. 4: Performance visualization of LLM-Prop and MatBERT on validation set when the input is a structure.
figure 4

(a–f) Represent the performance visualization when predicting Band gap, FEPA, EPA, Volume, Ehull, and Is-gap-direct, respectively.

Full size image
Fig. 5: Performance visualization of LLM-Prop on validation set with different input modalities (description and structure).
figure 5

(a–f) Represent the performance visualization when predicting Band gap, FEPA, EPA, Volume, Ehull, and Is-gap-direct, respectively.

Full size image
Table 4 Transfer learning performance comparison
Full size table

For classic machine learning (ML) methods, despite conducting an extensive grid search to optimize hyperparameters for each model (see Section 3), the overall performance of XGBoost and RF remained the lowest among the methods tested (Table 3). This outcome highlights that Robocrystallographer features require more sophisticated models to be effective in predicting material properties. We believe this insight underscores the importance of exploring how available tools and advanced methods can be leveraged to further advance the field of materials science.

Which input processing technique results in better text-based performance? To respond to this question, in Fig. 6, we show the results of LLM-Prop when different input processing strategies are applied to the input crystal description. We considered three possible strategies; “w/ [NUM]&[ANG]” where we replace bond lengths and bond angles with [NUM] and [ANG] tokens, respectively, “w/ Numbers” where we retain both bond lengths and angles, and “w/o Numbers” which denotes where we remove both bond lengths and bond angles from the crystal description without replacing them with any special tokens. Surprisingly, the results show that removing the numerical information completely often results in better performance. We explain the possible reasons behind these surprising results as follows. While intuitively, bond angles and distances are critical to understand a crystal structure, unfortunately, current LLMs treat numerical information as normal tokens (words). They are not able to understand the quantitative meaning that numerical values convey. Also tokenizing numerical values often increases the input sequence length (for instance tokenizing 3.12 results in four tokens: “3”,“.”,“1”,“2”) which limits the ability of the model to consume as much important information as it should. Thus, to get a comparable performance when including numerical information, we had to increase the number of input tokens to 2000 tokens from 888 tokens (and reduced the original batch size from 64 to 16 for the model to fit in our GPUs) to ensure that LLM-Prop is able to consume as much context as possible, but which also makes the training slow.

Fig. 6: Performance visualization of different input preprocessing strategies on validation set when LLM-Prop is trained on crystal descriptions.
figure 6

(a–f) Represent the performance visualization when predicting Band gap, FEPA, EPA, Volume, Ehull, and Is-gap-direct, respectively.

Full size image

Which input modality contributes more to the performance of the LLM-based models for property prediction? In Figs. 7 and 3, we see that, overall, both MatBERT and LLM-Prop benefit from having the input as a crystal description compared to when it is a structure-like input. We assume that there are several reasons for this: 1) LLMs tend to easily learn from the inputs that are more likely to look like a natural language such as descriptions where having a sequence of tokens is more meaningful compared to non-natural ones like CIF files (see Table 1). 2) CIF files contain many numerical values that make the input longer after tokenization so the model is trained on only a small portion of the input. It has also proven in previous studies that LLMs struggle to understand numerical information where it often treats them as normal tokens yet do not benefit from the quantitative meaning that numerical values convey36,37,38,39,42. Future work should consider investigating different techniques that can be used to leverage CIF files as a direct input to LLMs to improve performance on predicting the properties of crystalline materials.

Fig. 7: Performance visualization of LLM-Prop on validation set with different input modalities (description and structure).
figure 7

(a–f) Represent the performance visualization when predicting Band gap, FEPA, EPA, Volume, Ehull, and Is-gap-direct, respectively.

Full size image

How much data does LLM-Prop need to achieve SOTA results? We fine-tune LLM-Prop with randomly sampled data from the training set with the data size ranging from 5k to 90k and compare its performance with the baselines and the LLM-Prop model trained on the full data. The results in Fig. 8 show that LLM-Prop can achieve SOTA results on predicting band gap and volume with just about 90k training data points (log1090k ≈ 4.95 on the figure) corresponding to 35k fewer data points compared to what baselines are trained on. Surprisingly, for volume prediction, LLM-Prop can outperform all GNN-based baselines with just 30k training data points (log1030k ≈ 4.48 on the figure) corresponding to about 95k fewer data points than what GNN-based baselines are trained on. These results highlight the efficiency and capabilities of LLM-Prop on predicting the properties of crystalline solids compared to the baselines.

Fig. 8: Training data size needed by LLM-Prop to achieve state-of-the-art (SOTA) results when predicting band gap, volume, and is-gap-direct.
figure 8

a–c The results for band gap, volume, and Is-gap-direct, respectively. For instance, LLM-Prop achieves SOTA results on predicting band gap and volume with just about 90k training data (log1090k ≈ 4.95 on the figure) that corresponds to 35k fewer data than what baselines are trained on. We used log of the training data size on the x-axis for clarity. The performance of each model is calculated on validation set.

Full size image

Ablation studies

How does each LLM-Prop design choice improve its performance? Table 5 shows how each technique we use to make LLM-Prop a capable property predictor contributes to its performance. We first naively fine-tune a T5 encoder with its original tokenizer and without preprocessing the input (LLM-Prop-baseline) and then add to it each strategy separately. We also compare the performance of each strategy to when all strategies are combined together to make LLM-Prop (LLM-Prop+all). Overall, LLM-Prop+all provides the best results except on volume prediction where it shows comparable performance with the LLM-Prop+[CLS] version. Among all strategies, adding the [CLS] token for pooling seems to give the best improvement on all property prediction tasks. Replacing bond distances with the [NUM] token tends to slightly harm the performance, especially on volume prediction, compared to replacing bond angles with [ANG]. Label scaling significantly improves performance on both band gap and volume prediction while removing stopwords slightly improves the performance on band gap and volume prediction, but slightly harms the performance on predicting whether the band gap is direct or indirect. The modified tokenizer slightly improves the performance of LLM-Prop on band gap prediction but harms the performance on predicting other properties.

Table 5 The contribution of each preprocessing strategy on LLM-Prop performance
Full size table

How does LLM-Prop perform with respect to the label scaling strategy? We also analyze how each label scaling technique impacts performance on regression tasks. The results in Fig. 9a) show that when predicting band gap the performance difference among label normalization strategies is not significant while for volume prediction, z-score normalization (z norm) significantly outperforms other normalization schemes. How does LLM-Prop perform with respect to the number of input tokens? Fig. 9b) shows the performance of LLM-Prop as a function of the input sequence length. The results show that there is a clear correlation between performance and input sequence length. Accounting for longer sequences tends to improve performance. Therefore, by default, LLM-Prop is set to process up to 888 input tokens which is the maximum length that could be processed by the NVIDIA RTX A6000 GPUs that we used for training. And, as the results show, we believe that accounting for longer input sequence length will yield even better performance on crystal property prediction.

Fig. 9: LLM-Prop ablation performance.
figure 9

From (a–c) per input sequence length. From (d, e) per label scaling strategy. For the band gap and volume, the lower the better. While for the Is-gap-direct, the higher the better. The performance of each model is calculated on validation set.

Full size image

To further understand the origin of LLM-Prop’s superior performance on certain properties, we compared its bandgap prediction performance against the baselines for different material categories. As shown in Fig. 10, we analyzed the performance for metallic (row (b)) versus non-metallic (row (c)) crystals and stable (row (d)) versus unstable (row (e)) materials, reporting the performance gain or loss of the baselines relative to LLM-Prop. The results indicate that LLM-Prop significantly outperforms the baselines in predicting the bandgap of stable and metallic materials, compared to its performance on unstable and non-metallic materials, which may partly explain its overall superior performance (top panel or row (a)).

Fig. 10: Parity plots for band gap prediction.
figure 10

The figure is organized as follows: row (a) displays results for all crystals, row (b) for metallic crystals, row (c) for non-metallic materials, row (d) for stable materials, and row (e) for unstable materials. Each column corresponds to a model applied across all material types. Percentages in parentheses indicate baselines’ performance changes relative to LLM-Prop, with red showing losses and green showing gains.

Full size image

Discussion

We introduced LLM-Prop, a carefully fine-tuned network derived from T5 for crystal property prediction. We showed, through an extensive set of experiments, that LLM-Prop achieves superior performance in predicting the properties of crystalline solids, outperforming the current state-of-the-art and ubiquitously used GNN-based architectures such as ALIGNN by a large margin on certain tasks. Our results highlight the great potential that text-based methods have in materials science and we release a benchmark text data, TextEdge, composed of text descriptions of crystals and their properties to encourage research in this nascent area.

Our experimental results also highlight that a carefully fine-tuned non-domain-specific pre-trained language model on crystal text descriptions can outperform a naively fine-tuned domain-specific one that is 3x bigger in size. This challenges the current common practice in AI for science consisting of pre-training domain-specific models, which is costly. We believe that the data, results, and insights we bring in this work could help to significantly advance the NLP for materials science which is still in its early stage due to many challenges that we have discussed and addressed in this work.

We acknowledge the limited investigation into the origin of the LLM-Prop’s performance improvement over GNNs. We highlighted that LLM-Prop benefits from explicitly encoded expert information extracted by the Robocrystallographer and its strong capability in extracting useful information. We additionally provided the preliminary insights in Table 5, as well as Figs. 8, 9, and 10. However, distinguishing whether the performance boost arises from the explicit inclusion of additional structured information or the different data representations/modalities remains a compelling research direction that is yet to be further explored in our future work.

Methods

We compare LLM-Prop with seven baselines: two classic ML models—XGBoost43 and Random Forest (RF)44, four GNN-based models—CGCNN18, MEGNet7, ALIGNN8, and DeeperGATGNN45, and one text-based model, MatBERT25. The GNN-based methods are also trained and evaluated on the same benchmark dataset using the same splits to ensure a fair comparison. Note that we do not include the results reported in the original articles since the dataset used was collected from an old version of the Materials Project, the 2018 version, and only contains about 70k crystals. We train all models using NVIDIA RTX A6000 GPUs. We next describe how we set up the experiments for all the baselines and for LLM-Prop. To further evaluate the stability of each method, we run each model on the test set five times and report the averaged MAE.

Baselines

For classic ML models, we train XGBoost and RF using the ML features generated by Robocrystallographer to evaluate whether these features alone can provide accurate predictions without relying on the text descriptions it generates. We conduct an extensive grid search to optimize three key hyperparameters for each model. For RF, the hyperparameters include the number of estimators (50, 100, 150), maximum depth (None, 5, 10), and maximum number of features (None, 0.3, 0.7). For XGBoost, they include the number of estimators (100, 1000, 2000), maximum depth (0, 3, 6), and learning rate (0.1, 0.01, 0.001). This results in 27 combinations per model, and we report the best performance achieved.

For CGCNN, we directly use the publicly available code to implement CGCNN. We train and evaluate it on TextEdge with different hyperpameter settings where we found the following combination of settings to give the best performance; hidden dimensions of 128, batch size of 256, three CGCNN message passing layers, learning rate of 1e-2, radius cutoff of 8.0, setting the nearest neighbors to 12, and training it from scratch for 1000 epochs.

For MEGNet, we train it from scratch and evaluate it on our benchmark dataset by implementing the training pipeline following the article and the implementation details released by the authors. We train MEGNET with different training configurations that give better performance depending on the task. For volume prediction we set the number of epochs to 250 while for other tasks the number of epochs was set to 1000 epochs. On all tasks we found the following hyperparameter settings to give better performance; a radius cutoff of 4.0, the gaussian width of 0.5, the number of bond features set to 100, the learning rate of 1e-3, and the batch size of 128. Unfortunately, for MEGNet, we could not find the implementation details on classification tasks, thus we only compared against it on regression tasks.

For ALIGNN, we follow the original implementation details of ALIGNN released in the paper using the publicly available code from the authors to train and evaluate it on our benchmark dataset. For the hyperparameter settings we found the combination of 1e-3 learning rate, 64 batch size, and 500 epochs to perform better on all six tasks.

For DeeperGATGNN, we implement the traning pipeline following the the publicly available code from Omee et al.45. We select the best combination of settings for the number of graph convolutional layers which were set to {15, 20, 25} and the number of epochs which were set to {500, 1000} and we found the combination of 20 layers and 500 epochs to perform the best. On all tasks, we train DeeperGATGNN with the maximum learning rate of 5e−3 that reduce on plateau with the learning rate scheduler of patience set to 10 and the minimun learning rate of 1e−5. The batch size was set to 100.

For MatBERT, we fine-tune it on our benchmark dataset using its original tokenizer. We initially preprocessed the input text descriptions of MatBERT as described in 2.1. However, these preprocessing steps led to worse performance for MatBERT. The possible reason might be that since MatBERT can process only 512 tokens as input, the compressed information in 512 tokens that the preprocessing step gives, does not provide enough context for MatBERT. We therefore fine-tuned MatBERT with a batch size of 64 crystal descriptions, a learning rate of 5e−5, and a dropout rate of 0.5 for 200 epochs using the Adam optimizer with a onecycle learning rate scheduler46 for all the experiments.

LLM-Prop

For LLM-Prop, we directly fine-tune the encoder only part of the original T5-small encoder-decoder model (with about 60 millions parameters) on our benchmark dataset without further pre-training it on domain-specific data. Fine-tuning the encoder part only reduces the T5-small size about half which makes the LLM-Prop to have 37 millions of parameters after adding the prediction layer. We first train the original T5 tokenizer on the benchmark data with a vocabulary size of 32k, then preprocess the data as described in 2.1. For regression tasks, we fine-tune LLM-Prop on normalized property values and denormalize the predicted values to calculate the error on the original values. Unless otherwise mentioned, we use z-score normalization when fine-tuning both LLM-Prop and MatBERT. Unless otherwise mentioned, we fine-tune LLM-Prop on either 2,000 input tokens using a batch size of 16, or 888 input tokens using a batch size of 64. Surprisingly, we found that setting input tokens to 2,000 results in better performance for regression tasks while for classification tasks 888 input tokens perform the best. We train with the learning rate of 1e−3, and a dropout rate of 0.2 using the Adam optimizer with a one-cycle learning rate scheduler. For predicting the Ehull, FEPA, EPA, and when the input is a structure, we found that setting the number of epochs to 300 result in a better performance while for other properties reducing the number of epochs to 200 does not hurt the performance. Therefore we use 200 epochs for other properties to speed up the training. For all models, we save the checkpoint of each epoch and evaluate on the test set with the checkpoint that gives the best performance on the validation set. Training LLM-Prop takes about 40 min per epoch and the inference takes about one minute to predict the properties of 10,000 materials on one NVIDIA RTX A6000 GPU.

For regression tasks, we train both MatBERT and LLM-Prop with the mean absolute error (MAE) loss and evaluate them in terms of MAE error while the GNN-based models are trained with root mean square error (RMSE) loss and evaluated with the MAE error. For classification, we train them with binary cross entropy (BCE) loss and evaluate with the area under the ROC curve (AUC).