An early giant planet instability recorded in asteroidal meteorites

Abstract

Giant planet migration appears widespread among planetary systems in our Galaxy. However, the timescales of this process, which reflect the underlying dynamical mechanisms, are not well constrained, even within the Solar System. As planetary migration scatters smaller bodies onto intersecting orbits, it would have resulted in an epoch of enhanced bombardment in the Solar System’s asteroid belt. Here, to accurately and precisely quantify the timescales of migration, we interrogate thermochronologic data from asteroidal meteorites, which record the thermal imprint of energetic collisions. We present a database of ⁴⁰K–⁴⁰Ar system ages from chondrite meteorites and evaluate it with an asteroid-scale thermal code coupled to a Markov chain Monte Carlo inversion. Simulations require bombardment to reproduce the observed age distribution and identify a bombardment event beginning $11.{3}_{-6.6}^{+9.5}\, {\mathrm{Myr}}$ after the Sun formed (50% credible interval). Our results associate a giant planet instability in our Solar System with the dissipation of the gaseous protoplanetary disk.

Main

Planetary migrations seem to be commonplace in our Galaxy. The proximity of ‘hot Jupiters’ to their host stars results from inward migration from more distant planetary birth radii¹. Planets in the TRAPPIST-1 system also probably migrated inwards from larger radii where they inherited their volatile inventories². Distributions of both exoplanet eccentricity and orbital spacing in multi-planet systems are most readily explained by histories of dynamical instability and orbital reorganization (for example, refs. ^3,4).

Several lines of evidence indicate that the Solar System’s giant planets underwent at least one episode of migration. The admixture of material from the inner and outer Solar System among main belt asteroids⁵ and asteroidal meteorites⁶ requires dynamical mixing of protoplanetary reservoirs. The orbital architecture of giant planets^7,8 and the Kuiper Belt⁹ as well as the low masses of Mars and the asteroid belt^10,11,12 could not have formed in situ and require a history of dynamical excitation. Consequently, giant planet migration (GPM) established the long-term (>4 billion years) physical and chemical structure of the Solar System^{5,6,7,8,9,10,11,12} and perhaps promoted terrestrial habitability by supplying volatile-rich material from the outer Solar System to the early Earth^13,14,15. As a corollary, we expect migrations to similarly imprint these characteristics in exoplanetary systems¹⁵.

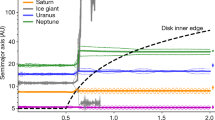
While dynamical models of GPM vary widely in their assumptions and details, the overarching mechanisms that drive GPM fall into one of two categories (Fig. 1): dynamical instability triggered by interplanetary gravitational interactions^7,8,9,11,16 or inward migration triggered by tidal interactions with a surrounding gaseous disk, also known as ‘type II’ migration^17,18. As these two processes require the absence or presence, respectively, of a gaseous protoplanetary disk and gaseous disks are transient features¹⁹, constraining the timescale of migration may help resolve its underlying stimulus (Fig. 1). We examine the Solar System as a natural laboratory to test the timescales of GPM and identify the mechanism that best describes Solar System history and chronology.

Fig. 1: Timescales of GPM stimuli.

Left: inward (type II) migration of a proto-Jupiter and proto-Saturn within gaps in the gaseous protoplanetary disk (in brown, white arrows indicate motion). The Solar System’s gaseous disk dissipated ≤5 Myr_ss (ref. ³⁶). Right: a giant planet instability (giant planets on high-eccentricity orbits) in the presence of an outer planetesimal disk. Such an instability might be caused by dissipation of the gaseous disk, a giant planet orbital configuration that is inherently unstable without the presence of the gaseous disk, or interactions with an outer planetesimal disk. Gas dissipation occurs between 3 Myr_ss and 5 Myr_ss (black box), destabilization of a self-unstable system occurs ≤10 Myr after gas dissipation (~5–15 Myr_ss), and planetesimal disk-triggered instability occurs within 100 Myr of gas dissipation¹⁶. An LHB scenario occurs >400 Myr_ss, beyond the scale of the timeline. Note that each scenario corresponds to a distinct timeframe in Solar System history, and the resultant dynamical excitation scatters inner Solar System bodies (black dots). Myr_ss reflects million years after Solar System formation, assigned to the age of the oldest CAIs.

A dynamical instability was first proposed as an explanation for the hypothesized Late Heavy Bombardment (LHB; described below)²⁰ and the orbital architecture of the outer Solar System^7,8,9. In these original giant planet instability (hereafter ‘instability’) models, interactions between the giant planets and an outer planetesimal disk caused secular migration of Jupiter and Saturn into a 1:2 mean motion orbital resonance. This excited the planets’ orbits and caused a Solar System-scale instability⁸: a period of chaotic and intersecting planetary orbits. More recent simulations have revealed a variety of plausible instability stimuli^16,21.

A gas-driven migration model was originally proposed to explain the low mass of Mars and the admixture of bodies from the inner and outer Solar System in the asteroid belt¹⁰. In this model, the proto-Jovian and proto-Saturnian cores formed embedded in a gaseous protoplanetary disk. As they reached sufficiently large masses, they carved out gaps in the disk and migrated inwards due to associated torques, following the pattern of type II planet migration^17,18. Jupiter began migrating before Saturn, until the latter began a faster migration. When the cores reached a 2:3 mean motion resonance, their migration reversed outwards—a so-called Grand Tack—until the disk eventually dissipated and froze their orbital positions.

In all GPM scenarios, migrating planets scatter smaller bodies onto dynamically excited and intersecting orbits, resulting in a surge of collisions^10,11,12,20. Conversely, acute collisional episodes require dynamical excitation, and we are not aware of a hypothesis other than GPM that so reliably accomplishes widespread collisions. Thus, bombardment events seem to be a reliable proxy for GPM. We posit that the epoch of enhanced collisions resulting from GPM is a diagnostic event that may be recorded in planetary records^10,20, and its timescales, if precisely constrained, could be used to identify the causal dynamical processes (Fig. 1).

We reconstruct the timescales of reheating during GPM-triggered bombardment by evaluating the thermochronologic records of asteroidal meteorites. Thermochronologic mineral systems record the timescales of thermal processes through the temperature-dependent retention of radiogenic isotopes in mineral lattices. As asteroids cool to sufficiently low temperatures, these minerals retain radiogenic daughter isotopes and record a ‘cooling age’. The energy released by collisional impacts are well-established sources of heat in (proto)planetary systems and are recorded in their thermochronologic records (for example, refs. ^22,23).

This study integrates early Solar System chronologies from a variety of sources, including cosmochronologic data and physics-based simulations, which rely on fundamentally different timescales. Several cosmochronologies (for example, ⁴⁰K–⁴⁰Ar ages) are derived from radioisotopic measurements that record time relative to the present. Following the conventions of isotope geo- and cosmochemistry, we report these ages in annum (a), meaning ‘years before the present’. However, physics-based simulations record time after reference events. To connect cosmochemical records with astrophysical processes, a solar time-zero is canonically anchored to Ca–Al-rich inclusions (CAIs), the Solar System’s oldest macroscopic solids, which condensed from a solar composition gas²⁴ heated by the infant Sun as it entered its pre-main-sequence phase²⁵. We report astronomically referenced time in terms of years after CAIs (yr_ss), such that 0 Myr_ss ≡ 4,567.3 Ma (ref. ²⁶), although our results are insensitive to the chosen datum (Methods).

Previous work on the Solar System’s GPM history has relied on a combination of thermochronologic data and the modern Solar System architecture. The LHB was first hypothesized as a period of enhanced lunar bombardment at ~4 Ga, based on the absence of >4 Ga thermochronologic cooling ages in Apollo mission return samples and an apparent paucity of >4 Ga craters on the lunar surface^23,27. Subsequent studies revealed that neither of these lunar records actually required an ~4 Ga lunar bombardment^28,29 and could be explained instead by a monotonic decline in bombardment flux since the epoch of planetary assembly. More recently, dynamical constraints on instability triggers¹⁶, the survival of binary asteroids³⁰ and meteorite thermochronology³¹ have constrained the timescales of GPM to the Solar System’s first 100 Myr.

A variety of models for ‘early’ (<100 Myr_ss) GPM fall within different timeframes (Fig. 1). While each model varies in its physical details and relies on its own suite of assumptions, the fundamental stimuli for GPM rely on the presence, absence or dissipation of the gaseous protoplanetary disk. The Grand Tack model requires the presence of a gaseous protoplanetary disk¹⁰. Observations of solar-mass stars limit gas disks to the first 10 Myr of stellar lifetimes^19,32,33, with a typical lifetime of <5 Myr_ss derived from observations³⁴, dynamical models³⁵ and cosmochemical constraints³⁶. In contrast, instability models require the dissipation of the gaseous disk during or before the GPM event. In the earliest scenario, instability occurs during gas dissipation, due to asymmetric torques on giant planets from the inner edge of the outward-migrating gas disk²¹. After gas dissipation, simulations seeded with plausible planet formation/evolution histories³⁷ reveal that an early giant planet instability can occur by canonical planet–planetesimal disk interactions or by a self-triggered instability resulting from unstable orbital architectures established while embedded in the gas disk¹⁶. The self-triggered instabilities occur rapidly, within 10 Myr after gas dissipation (~15 Myr_ss), whereas self-stable systems interacting with a planetesimal disk typically experienced instabilities >30 Myr after gas dissipation. In summary, plausible GPM stimuli occur at ≲5 Myr_ss (gas-disk stimulus or gas dissipation), 5–15 Myr_ss (unstable orbital architectures) or >15 Myr_ss (planetesimal-disk interactions) (Fig. 1).

This study aims to resolve the timescale of GPM and concomitant inner Solar System bombardment through its imprint on the thermochronologic record of asteroidal meteorites. We focus on the ⁴⁰K–⁴⁰Ar system, which is susceptible to resetting at relatively low temperatures (for example, ref. ²²), and therefore well suited to capturing the relatively subtle thermal signals of impact heating^38,39. We exclude other thermochronometers to focus our study on lower-temperature perturbations and limit the dimensionality of our statistical inversion (Methods). Moreover, we follow the logic of ref. ²⁹ that protracted, bombardment-warmed planetary histories systematically young ⁴⁰K–⁴⁰Ar system ages. Although previous evaluation of meteorite thermochronology has constrained dynamical instability to within the first ~100 Myr_ss (ref. ³¹), establishing more precise constraints has been challenging because these timescales overlap with those of radiogenic heating and subsequent cooling of the meteorite parent planetesimals. To deconvolve these endogenic thermal histories of asteroidal meteorite parent bodies from exogenic bombardment reheating histories, we use a Bayesian statistical approach.

We compiled a database of cooling ages from the thermochronologic ⁴⁰K–⁴⁰Ar system for chondrite meteorites with provenance in the inner Solar System⁶: the ordinary chondrites (OCs), comprising the H, L and LL types; the enstatite chondrites (ECs), comprising the EH and EL types; and the Rumuruti-type chondrites (RCs). These groups come from undifferentiated planetesimals with well-characterized thermal histories largely explained by simple conductive cooling histories⁴⁰, which are relatively straightforward to model (Methods). The various parent bodies corresponding to these meteorites probably experienced similar thermal histories, and our Bayesian statistical approach allows us to rigorously account for uncertainties stemming from modest differences among parent-body histories (Methods). While previous work has explored the chronologies of highly shocked and impact-melted chondrites⁴¹, we consider all chondritic ⁴⁰K–⁴⁰Ar system ages, as shock effects and shock heating are heterogeneously distributed^39,42 and seemingly unshocked meteorites may still record heating from impacts. This approach allows us to use a database that spans Solar System history, with a high density of ages throughout the timescales of potential GPM (Figs. 1 and 2).

Fig. 2: Distributions of ⁴⁰K–⁴⁰Ar system ages, measured by the K–Ar and ⁴⁰Ar–³⁹Ar methods.

Time is reported as both age (Ma, lower x axis) and time after Solar System formation (Myr_ss, upper x axis). Histograms reflect the summed distributions of ages from each dataset. K–Ar age density has a broad, shallow maximum at ~4,200 Ma, that gradually decays to low probability densities with minor local maxima extending to the present day. ⁴⁰Ar–³⁹Ar age density monotonically decreases from a sharp peak (>2× the height of the K–Ar peak) shortly after the age of the Solar System (dashed line), with minor local peaks between ~4,200 Ma and 3,600 Ma. By 3,500 Ma, the distribution converges on near-nil probability density until an approximately symmetric local maximum within the last 2,000 Ma. As these <2,000 Ma ages (shaded) are not associated with GPM (see text), we exclude them from our analyses. If we recalculate the ⁴⁰Ar–³⁹Ar age distribution with lower precision (σ = 6%) to mimic the K–Ar system, the early peak is more broad and shallow but the maximum remains >4,300 Ma.

To resolve the respective contributions of endogenic and exogenic heating on the chondritic ⁴⁰K–⁴⁰Ar record, we explore the parameter space describing this two-component thermal history with a Markov chain Monte Carlo (MCMC) algorithm (Methods). This model is constrained by two sets of priors: our database of ⁴⁰K–⁴⁰Ar system ages (Fig. 2) and published constraints on the thermochronologic model parameters (Table 1). Through its exploration of the parameter space, the algorithm produces Markov chains whose stationary distributions yield Bayesian posterior estimates of each parameter in the simulation. To constrain the timescales of GPM and dynamical excitation, the simulated thermochronologic histories include exponentially decaying bombardment fluxes, which may mimic either collisional pulses resulting from GPM or a more secular decline in collisions as the Solar System ages (Extended Data Fig. 1). In the following sections, we report and discuss the results of these simulations and their implications for the GPM history of the Solar System.

Table 1 Parameters in the asteroid thermochronologic code and prior distributions used in the Bayesian inversion

Results

Database of ⁴⁰K–⁴⁰Ar system ages

Figure 2 shows the distribution of ⁴⁰K–⁴⁰Ar system ages in our database (n = 203), which includes measurements by the ⁴⁰Ar–³⁹Ar and K–Ar techniques (Methods). ⁴⁰Ar–³⁹Ar ages follow a bimodal distribution. The maximum of its probability density is slightly younger than the solar age and declines monotonically to minimal density by ~3 Ga, followed by a secondary peak of ages at ≲1 Ga. The distinct bimodality of ⁴⁰Ar–³⁹Ar ages results from the technique’s higher analytical resolution and capability for identifying and excluding disturbed K-bearing domains from age calculations (for example, ref. ⁴³; see Methods for a more comprehensive explanation of the two methods). In contrast, the peak K–Ar age density is >300 Ma younger than the ⁴⁰Ar–³⁹Ar peak and has a broad noisy tail that extends to the present day, which reflects the propensity of K–Ar ages for partial resetting by low-temperature Ar loss (Methods). Even when ⁴⁰Ar–³⁹Ar ages are resampled at the lower precision of K–Ar ages (on average σ = 6%), it produces a broader and shallower density profile, but its maximum is still older and more pronounced than the maximum of the K–Ar age distribution (Fig. 2). As K–Ar ages are systematically younger due to partial resetting, we include only ⁴⁰Ar–³⁹Ar ages in our analyses and interpretations.

The recent peak in ⁴⁰Ar–³⁹Ar cooling ages at 500 Ma comprises only the OC groups, represented predominantly by the L chondrites (Extended Data Fig. 2). This is consistent with the ~460 Ma disruption of an L chondrite parent body inferred by previous studies^22,44. As the ⁴⁰K–⁴⁰Ar system is resilient to resetting during atmospheric entry^45,46, we are confident that these <2 Ga cooling ages reflect collisional heating events rather than modern resetting. Thus, we interpret the ~500 Ma secondary peak of ⁴⁰Ar–³⁹Ar cooling ages as a relatively recent collisional event—or events—that comminuted asteroids and left meteoroid rubble piles on near-resonant orbits, which were later perturbed onto Earth-crossing trajectories⁴⁷. The apparently coordinated ~500 Ma reheating of OCs implies a relationship in their excavation and delivery to Earth. We suggest that this coordination may reflect either an orbital relationship among discreet H, L and LL parent bodies or a shared provenance of these stones from an L-dominant OC rubble pile parent body. As these young impact-heating ages occur on timescales substantially post-dating any plausible GPM processes (Fig. 1), we exclude all <2 Ga ⁴⁰Ar–³⁹Ar ages from our analyses. Table 2 reports population statistics of the >2 Ga ⁴⁰Ar–³⁹Ar ages that we use as priors in our Bayesian inversion calculations.

Table 2 Population statistics of >2,000 Ma ⁴⁰Ar–³⁹Ar dates (n = 97), used as priors in this study

We interpret the ancient peak and decline in ⁴⁰Ar–³⁹Ar cooling ages to reflect endogenic thermal histories overlain by exogenic reheating. We associate the exogenic reheating with impacts related to secular collisional history and/or early bombardment(s)³¹. An LHB predicts an enhancement in bombardment ≤4 Ga, which would appear as a distinct peak in cooling ages at its onset, but the predominantly monotonic decline from 4.5–3.0 Ga contradicts such a history. Minor local maxima in the distribution around 4 Ga may reflect a subtle LHB signal (Fig. 2), which we rigorously test (and reject) with the Bayesian inversion we apply herein.

Thermochronologic evidence for a bombardment history

Thermochronologic simulations of an unperturbed, radiogenically heated body produce a monotonic decline of cooling ages following an initial peak (Extended Data Fig. 1). To test whether or not these features of the >2 Ga ⁴⁰Ar–³⁹Ar age distribution require reheating by impacts, we run MCMC inversions with and without any bombardment histories. We concurrently use two sets of priors: the distribution of measured >2 Ga ⁴⁰Ar–³⁹Ar ages and constraints on the thermochronologic model parameters (Table 1). Simulations that are inconsistent with the prior information (that is, too many/few bombardments) yield posteriors in poor agreement (hereafter ‘tension’) with those priors, whereas scenarios that are consistent with prior information converge on posterior distributions that are largely concordant with priors.

Figure 3 compares the prior distribution (measured) with the posterior (simulated) distributions of ⁴⁰Ar–³⁹Ar ages from simulations with 0–3 bombardment episodes. Simulations without impact reheating (Fig. 3a) yield posterior distributions of ⁴⁰Ar–³⁹Ar ages that fail to reproduce the brief early peak of ages, the shape of the monotonic decline and the near-nil density of ages between 3.5 Ga and 2 Ga. The posterior distributions of several model parameters are in stark tension with their priors (Extended Data Fig. 3 and Extended Data Table 1). In contrast, each of the simulated asteroid thermal histories that incorporate impact reheating (Fig. 3b–d) yield posterior distributions that are concordant with the prior distributions of ⁴⁰Ar–³⁹Ar ages and model parameters. These observations are quantitatively supported by the corresponding log-likelihoods (ℓ), such that a no-impact history corresponds to a mean ℓ = −1,016 ± 2(1σ), whereas bombardment histories yielded similar ℓ > −1,000. We conclude that the meteorite record requires one or more >2 Ga bombardment events to explain the chondritic ⁴⁰Ar–³⁹Ar age distribution.

Fig. 3: Comparison of prior and posterior ⁴⁰Ar–³⁹Ar age distributions for different bombardment histories.

Time is reported as both age (Ma, lower x axes) and time after Solar System formation (Myr_ss, upper x axes). The dashed lines demarcate 0 Myr_ss. The purple heatmaps show the relative density of posterior (modelled) age distributions (darker colour indicates higher density), overlain by the prior distribution of measured ages in black (as in Fig. 2). a, A no-impact scenario yields a relatively poor agreement between measured and simulated thermochronologic ages, corresponding to a mean log-likelihood (ℓ) of −1,016 ± 2(1σ). b–d, Scenarios with impact fluxes yield posterior distributions that are concordant with the prior, corresponding to ℓ = −992 ± 2 for a single impact flux scenario (b) and ℓ = −989 ± 3 for scenarios with 2 or 3 impact fluxes (c,d). To mimic the contribution of uncertainties in the prior distribution, each posterior age distribution (n = 10⁶) is recalculated by randomly resampling 100 draws with the mean uncertainty of the measured ⁴⁰Ar–³⁹Ar dates (σ ≈ 1%) and calculating a histogram (as in Fig. 2) from the resampled ages.

Impact flux parameters and their characteristics

We simulate episodes of enhanced collisions and bombardment in the asteroid belt with exponentially decaying fluxes characterized by an onset date (t_o), initial impactor flux (F_o) and e-folding timescale (τ). We simulate impact reheating non-physically (Methods), so the values of F_o are proportional to an impact flux rate and reflect the degree of thermochronologic resetting but ought not be interpreted as quantitative estimates of asteroid belt impact flux. Our model framework accommodates up to three-bombardment events, which we denote with α, β and γ. To limit multimodality in the posterior distributions of multi-bombardment simulations, we require the onset dates of these bombardments to occur sequentially (t_oα < t_oβ < t_oγ). In addition, in simulations with >1 bombardment, we assign the first bombardment (α) as a primordial bombardment (t_o = 0 Myr_ss) to reduce dimensionality. We envision this primordial flux as the long-term (billion-year scale) background rate of inner Solar System collisions (as in refs. ^48,49,50), distinct from punctuated and transient GPM-triggered bombardment. For this reason, we require that the τ of the primordial flux exceeds those of the post-accretion bombardments meant to simulate the dynamical consequences of GPM.

In all simulations, we find that F_o and τ are closely related. Within any given bombardment event, F_o decreases with increasing τ (Fig. 4 and Extended Data Figs. 4–6). This inverse scaling of F_o and τ indicates that a longer bombardment duration can compensate for a relatively low initial flux while, conversely, rapid recovery can compensate for a high initial flux. Among bombardment events, each bombardment event falls into one of two categories with respect to F_o and τ: intense and brief bombardments (hereafter, intense/brief) are characterized by F_o > 100 Myr⁻¹ and τ ≪ 100 Myr (for example, Fig. 4a), whereas mild and protracted bombardments (hereafter mild/protracted) are characterized by F_o ≪ 100 Myr⁻¹ and τ > 100 Myr (for example, Fig. 4b). In addition, t_o scales inversely with F_o, such that more intense bombardment events occur earlier in Solar System history. Notably, parameters from separate bombardment events never appear correlated, indicating that they are independent with respect to each other. These patterns are consistent among all simulations that include bombardment events.

Fig. 4: Posterior distributions of simulated bombardment history parameters.

a,b, Corner plot diagrams. The diagonals depict one-dimensional histograms of each parameter, and off-diagonals depict the two-dimensional distributions of each parameter pair, with heatmaps of distribution density within 2σ of the means (darker cells reflect higher density). Black lines trace the median values of each parameter. a, A ‘post-accretion’ flux, for which the Bayesian inversion explores its onset time t_o (Myr_ss = Myr after CAIs), initial impact flux F_o (Myr⁻¹) and e-folding time τ (Myr). F_o tends to decrease as τ and t_o increase. b, A ‘primordial’ flux where the inversion explores values of F_o and τ, but t_o (not shown) is anchored to 0 Myr_ss. F_o and τ show a pronounced inverse relationship. Notably, the median values of F_o and τ for the post-accretion flux (a) are 1,000× and <0.1× the primordial flux, respectively (b). Summary statistics are tabulated in Extended Data Table 2. c, Comparison of the posterior distribution of bombardment onset date (t_o in a) with the timescales of potential GPM stimuli, as in Fig. 1. Dark bars demarcate the 95% and 50% CIs. The lower 26% of the distribution overlaps the timescales of gas-disk-driven migration, the uppermost 38% overlaps the timescales of planetesimal disk-triggered instabilities, and 45% of the distribution interior—including the median (11.3 Myr_ss, vertical line) and mean (15.0 Myr_ss)—overlaps the timescales of gas dissipation and self-triggered instabilities. The hypothesized LHB timescale lies beyond the domain. Distributions reflect 10⁶ Markov chain steps.

Number, timescale and intensity of bombardment events

A single-bombardment scenario converges on posterior impact flux parameter distributions that reflect a mild/protracted bombardment (Extended Data Fig. 4), such as that expected for the background rate of inner Solar System collisions. The persistence of the mild/protracted impact flux over the intense/brief flux emphasizes the critical importance of secular collisions to explain the thermochronologic histories of chondrites as well as the inner Solar System impact record^49,50.

Numerous lines of independent evidence indicate that there was an episode of GPM in Solar System history that would have driven extensive small-body migration through the region of the asteroid belt^{5,8,9,11,12,20,51} and thereby precipitated a punctuated episode of asteroid collisions. Therefore, the abovementioned single-bombardment scenario is insufficient to meet the requisite dynamical history of the Solar System, and at least one more impact flux is required. In support of this conclusion, the posterior distributions of several model parameters are in greater tension with their priors for single-bombardment simulations than those with two- and three-bombardment histories (Extended Data Figs. 7 and 8).

Figure 4 reports the posterior distributions of bombardment parameters for simulations characterized by two bombardments: a primordial bombardment anchored to the solar age (0 Myr_ss) and a post-accretion bombardment with an onset date (t_o) that varies along with all other parameters in Table 1. The post-accretion bombardment (Fig. 4a) is intense/brief with a median onset date of $11.{3}_{-6.6}^{+9.5}\,{\mathrm{Myr}}_{\mathrm{{ss}}}$ (50% credible interval, hereafter CI; ${+15.0 \atop -8.6}\,{\mathrm{Myr}}_{\mathrm{{ss}}}$ at 68% CI, ${+44.4 \atop -11.0}\,{\mathrm{Myr}}_{\mathrm{{ss}}}$ at 95% CI) and mean of 15 ± 14 Myr_ss (1σ). We favour the median as an estimate of central tendency, as the distribution is skewed. In contrast, the primordial flux (Fig. 4b) is mild/protracted. These results are consistent with a Solar System history characterized by a slowly decaying background rate of infrequent collisions punctuated by an early (<100 Myr_ss) episode of dynamical excitation and intense bombardment^31,49. Moreover, this intense and transient collisional episode satisfies theoretical predictions of GPM-associated bombardment in the inner Solar System^10,12,20.

We also explore the effect of incorporating a third impact flux γ (also post-accretion) and find that three-bombardment events reproduce the ⁴⁰Ar–³⁹Ar age distribution as well as two-bombardment events (Fig. 3). In this scenario, the α (primordial) and β (post-accretion) impact fluxes are nearly identical to the respective fluxes of the two-bombardment simulation shown in Fig. 4 (Extended Data Fig. 6). The posterior of the γ flux is bimodally distributed with respect to t_o and τ. One mode mimics the β bombardment with a local maximum at t_o ≈ 10 Myr_ss and τ ≈ 10 Myr. The other mode is extremely late in the simulation time domain with t_o > 1,000 Myr_ss—perhaps capturing one of the minor maxima between 3.5 Ga and 2 Ga—and has an extremely brief lifetime of τ ≈ 0.01 Myr (that is, the flux becomes negligible within a single 1 Myr timestep). Thus, the third flux either mimics the β event or is suppressed by an extremely short τ. As a third flux neither adds new information nor has any discernible effect on the simulated age distribution (Fig. 4), we conclude that it is unnecessary and do not consider it further.

In our multi-bombardment simulations, the α bombardment t_o is always primordial (t_o = 0 Myr_ss). If we instead simulate two post-accretion impact fluxes (β, γ) with no primordial bombardment requirement (Extended Data Fig. 5 and Supplementary Fig. 1), we get a similar result to the one-primordial/one-post-accretion two-bombardment scenario in Fig. 4. The posterior distributions of β-flux parameters are indistinguishable between these scenarios, and the distributions of F_o and τ for the γ/α fluxes are very similar. Curiously, in scenarios with only post-accretion bombardments, the t_o of the mild/protracted fluxes have median values between 100 Myr_ss and 140 Myr_ss, rather than a more ‘primordial’ value near 0 Myr_ss. In the case of the two-bombardment distribution, the late onset date partly reflects the model requirement that t_oβ < t_oγ. As there is no such restriction in the case of the one-bombardment distribution, the inversion probably favours the later onset because it produces the long, shallow tail of cooling ages to 3.5 Ga without also placing a larger, long-lasting impact flux overlapping with the timeframe of maximum age density at ~4,500 Ma (Fig. 2). Nonetheless, whether the mild bombardment is primordial or post-accretion does not discernibly affect the characteristics of intense bombardment or the concordance between the observed and simulated ⁴⁰Ar–³⁹Ar age distributions (ℓ = −990 ± 3 for two post-accretion bombardments). Thus, our assumption of a primordial α bombardment is valid for the purposes of this study, and we favour this approach as it is more consistent with the mild/protracted impact flux representing a secular process.

Comparison with non-bombardment parameters

For all bombardment scenarios, posterior distributions of environmental, cosmochemical, asteroidal and material parameters are overall concordant with their prior constraints (Extended Data Fig. 8, Extended Data Table 2, and Supplementary Figs. 1 and 2). Our models’ ability to satisfy both these independent constraints as well as the chondritic ⁴⁰Ar–³⁹Ar record supports their overall veracity. We briefly consider three minor discrepancies between the priors and posteriors. First, accretion time (t_a) tends towards slightly later values, probably reflecting a bias towards the later accretion timescales for the parent bodies of OCs⁵², which comprise >70% of the ⁴⁰Ar–³⁹Ar database. Second, the disk midplane temperature (T_m) tends towards lower values than the observation-constrained prior⁵³ but remains consistently within chondritic constraints of <503 K (ref. ⁵⁴). As the relatively warm gaseous disk dissipated early on in the asteroids’ thermal histories, the tendency towards lower temperature may reflect the unimodal model compensating for this bimodal temperature history, although insulation from surface regolith layers probably reduced the effect of the temperature drop. Third, effective Ar closure temperatures (T_c) trend very slightly towards higher values compared with the expected distribution constrained from Ar degassing data (Table 1), suggesting that effective cooling rates were slightly faster than those assumed in previous studies (for example, ref. ⁴³).

Discussion

As a two-bombardment history is necessary and sufficient to explain the chondrite thermochronologic record in the context of post-accretion dynamical instability (‘Results’), we select the scenario shown in Figs. 3c and 4 (two bombardments: one primordial, one post-accretion) as our preferred model to interpret the timescales of GPM. The posterior e-folding timescales of the mild/protracted primordial fluxes modelled here (~380 Myr) are consistent with those of the long-term ‘tails’ predicted for the inner Solar System cratering record (for example, 200–400 Myr)⁵⁰ due to the gradual dynamical ‘leaking’ of asteroids on Mars-crossing orbits onto planet-crossing trajectories⁴⁸. As this primordial impact flux reflects a secular rate of collisions over Solar System history, we conclude that it is not related to GPM. In contrast, the intense/brief impact flux is consistent with a violent yet transient bombardment event. Although our parameterization uses arbitrary units, the median F_o of this bombardment heats ~50% of the simulated asteroid volume at the onset of bombardment. Although the upper constraints on F_o are poorly constrained by our model and may not be representative of the body’s deeper interior (see extended discussion in Methods), the large values underscore the severity of this event, especially for shallower portions of early chondritic bodies. In addition, this bombardment dissipates on a timescale similar to the most intense and short-lived component of impact flux models for the inner Solar System⁴⁹, which are comparable to the timescales predicted for dynamical cooling after GPM^10,20. This concordance motivates our first of two key conclusions: the thermochronologic record of the asteroid belt records a single GPM event. The second key conclusion regards its timing. Figure 4c compares the posterior distribution of the GPM-induced bombardment onset with the timescales of potential stimuli, as described above and in Fig. 1. The timescales of GPM pre-date canonical LHB timescales by hundreds of millions of years (Figs. 1 and 4). As bombardment of the terrestrial planets by asteroids or comets requires scattering within or through the asteroid belt, we expect that at least one of the (approximately) six parent bodies represented in our database would record these collisions. Our findings firmly refute any intense bombardment occurring ≫100 Myr_ss, consistent with other recent work^{16,28,29,30,31,55}.

We do not resolve a unique timeframe for <100 Myr_ss GPM, as all 4 timescales fall within the traditional 95% CI. However, only the lower 26% of the distribution overlaps timeframes during which the gaseous disk could have played a causal role in GPM (<5 Myr_ss; Fig. 4). Observations of protoplanetary disks for solar-type stars show that disk lifetimes are consistently <10 Myr, with few disks surviving >6 Ma and most dissipated within ≲3 Ma (refs. ^19,32,33). Dynamical models corroborate these observations and predict mean disk lifetimes of 3.7 Ma (refs. ^34,35). This is consistent with meteoritical evidence for gas-disk dissipation beyond Jupiter’s current orbit (~5 AU) by 3.5–5 Myr_ss (ref. ³⁶). Thus, we approximate the plausible timescales of gas dissipation to 3–5 Myr_ss. As a Grand Tack-style migration must be shortly followed by gas dissipation to halt the outwards migration of Jupiter and Saturn, we assign a generous lower limit for gas-embedded GPM onset at 1 Myr_ss (Fig. 4c). This 1–5 Myr_ss timeframe for a Grand Tack-style migration overlaps with only 20% of the posterior distribution of onset times, and even this is an upper limit due to potential insensitivity of the Bayesian inversion at very early timescales (see extended discussions in Methods). We conclude that a Grand Tack-style migration was unlikely.

The remaining upper 75% of the distribution overlaps timescales post-dating dissipation of the gaseous disk (Fig. 4c). The 50% CI of the distribution (4.75–20.76 Myr_ss), including the mean (15.0 Myr_ss) and median (11.3 Myr_ss), overlaps the timescales of instability resulting from self-unstable orbital architectures left behind after dissipation of the gaseous disk. This interval is consistent with Pd–Ag cooling ages of iron meteorites ranging from ~7.8 Myr_ss to 12.8 Myr_ss that reflect widespread energetic asteroid collisions in this timeframe⁵⁶. The upper 38% of the posterior overlaps the timescales of GPM caused by interaction with an outer planetesimal disk¹⁶. Collectively, >75% of the distribution overlaps timescales associated with dynamical instability of giant planets (>3–5 Myr_ss) rather than a type II -style migration embedded in a gaseous disk (≤5 Myr_ss). This motivates our second key conclusion that GPM in our Solar System was probably a result of a dynamical instability occurring shortly after the dissipation of the gaseous disk. Although the results are non-unique at the canonical 95% CI, the most probable mechanistic stimulus of instability was an unstable giant planet orbital configuration, potentially exacerbated by interaction with a massive outer disk of planetesimals¹⁶. Whether the systems were destabilized by asymmetric torques of a receding disk²¹, inherently unstable orbital configurations without the support of a gaseous disk¹⁶, interactions with an outer planetesimal disk^8,12,16, or any combination of these processes, gas dissipation was a critical process in triggering or predisposing the system to GPM.

Our results provide a cosmochronological constraint on the timescales of GPM in our Solar System, constrained with quantitative precision by a broad subset of the meteorite record (n = 97). We expect that our results will be refined as future efforts expand meteorite thermochronometry, provide greater astronomical context for this data (for example, asteroid sample return missions) and improve thermal models to simulate more physical scenarios. In particular, improved ⁴⁰K–⁴⁰Ar decay constant calibration at early solar timescales and more nuanced understanding of bulk chondritic Ar release patterns will pave the way for substantially improving the quality of our database of ages and inversion results (Methods). We recognize that the model is a simplification of meteorite thermal histories. Its greatest limitation is its relative insensitivity to impact heating before thermochronologic closure (see Methods for comprehensive treatments of all assumptions and limitations). Although over-early (<1 Myr_ss) bombardment scenarios are already incompatible with plausible Solar System GPM chronologies (Fig. 4), we expect that simulations incorporating more nuanced impact processes and numerically solved thermal histories may solidify and refine our present findings. Yet, despite its simplicity, the model effectively replicates the broad ⁴⁰Ar–³⁹Ar thermochronologic record of chondrites and corroborates extant constraints on chondritic planetesimals (Table 1), both of which support its overall veracity for early Solar System chronology.

GPMs appear to be a quotidian feature of planetary systems^3,4. Our findings further solidify the growing evidence that this process is characteristically constrained to the earliest stages of a planetary system’s history. We encourage future dynamical studies to focus on this epoch of planetary evolution, as it probably plays an outsized role on the long-term physical and chemical structure of exoplanetary systems, as it did in the Solar System. Similarly, our results motivate observational emphases on young (<20 Myr) exoplanetary systems (for example, refs. ^57,58) that might host planetary architectures on the verge of or recovering from instability and migration.

Methods

Database of ⁴⁰K–⁴⁰Ar system ages

To evaluate the thermal histories of undifferentiated bodies in the Solar System, we compiled a database of ⁴⁰K–⁴⁰Ar system cooling ages for chondrites with inner Solar System provenance (OCs, ECs and RCs). ⁴⁰K undergoes branching decay to ⁴⁰Ar and ⁴⁰Ca with a half-life of ~1.25 Gyr. The ⁴⁰K–⁴⁰Ar decay system is a thermochronometer due to the temperature-dependent diffusivity of gaseous Ar through mineral crystal lattices. The nominal closure temperature of plagioclase (the most K-rich mineral found in chondrites) to Ar diffusion is approximately 500 K for cooling rates spanning 1–1,000 K Myr⁻¹ (refs. ^43,59).

Dates in the ⁴⁰K–⁴⁰Ar system have been measured by one of two techniques: the K–Ar and ⁴⁰Ar–³⁹Ar methods. The K–Ar method entails first degassing Ar and measuring its isotopic composition to obtain the total abundance of ⁴⁰Ar, and then measuring the K abundance of the degassed sample and correcting for a known or assumed ⁴⁰K/K to obtain the absolute abundance of ⁴⁰K, and finally calculating a date from the ratio ⁴⁰Ar/⁴⁰K. While the earliest ⁴⁰K–⁴⁰Ar system ages were measured by this method, K–Ar ages are inaccurate and misleading if the system was previously heated and partially degassed, which results in ages that fall between the primary cooling age and the age of reheating. To circumvent this issue, the ⁴⁰Ar–³⁹Ar method entails irradiating a sample with fast neutrons to convert ³⁹K to ³⁹Ar and then degassing the sample and measuring the isotopes of Ar. As ⁴⁰K/³⁹K only varies substantively due to time-dependent ⁴⁰K decay, ³⁹K (and therefore irradiated ³⁹Ar) is a reliable proxy for ⁴⁰K for a given moment in geologic time. A standard of known age is irradiated alongside the unknown sample and its measured ⁴⁰Ar/³⁹Ar is used to correct for the incomplete conversion of ³⁹K to ³⁹Ar. Thus, paired measurements of ⁴⁰Ar/³⁹Ar for a sample of unknown age and a standard may be used to calculate the unknown sample’s ⁴⁰Ar/⁴⁰K and age. By sequentially degassing samples at a range of temperatures with the ⁴⁰Ar–³⁹Ar method, phases that experienced partial loss of Ar at lower temperatures can be identified and excluded from the final age calculation.

We compiled a database of both K–Ar and ⁴⁰Ar–³⁹Ar cooling ages from the published literature, using several previous compilations as a starting point^22,31,60. In most cases, we followed the recommended ages reported by the publishing authors, typically plateau or ‘reduced plateau’ ages in the case of the ⁴⁰Ar–³⁹Ar method. If there were two clear ⁴⁰Ar–³⁹Ar plateaus, we incorporated the older, as this study focuses on the early cooling history of asteroids and the younger cooling ages (typically <1 Ga) typically reflect collisions that ejected meteoroids from larger parent bodies towards Earth-crossing orbits⁶¹. However, the uncertainties of dates were not always reported or calculated from rigorously propagated uncertainties. We do not include ages that are reported as only minimum and maximum ages, as quantified uncertainties are necessary for our Bayesian approach. Where dates were given without uncertainty or calculated from an assumed K abundance, we assumed a cautiously large uncertainty of 2σ = 10%. In cases where multiple ages were reported and there was not a clearly more contemporary or less disrupted age (n = 13), we calculated the mean of the reported ages by the Monte Carlo method.

Using common constants and re-calibrating ⁴⁰K–⁴⁰Ar ages

For quantitative comparison, all the ages in our database must be calculated relative to a common set of decay constants and ⁴⁰K/K. The branching decays of ⁴⁰K to ⁴⁰Ar by electron capture and ⁴⁰Ca by β⁻-emission are respectively described by the decay constants λ_e and λ_β (the summed decay constant is denoted λ). However, the values of these constants used to calculate ⁴⁰K–⁴⁰Ar ages have changed over the history of the system’s geochronometric use. The decay constants of ref. ⁶² (hereafter, SJ77) have been used almost ubiquitously by the meteoritics community since its publication, despite publication of more recently revised ⁴⁰K decay constants^63,64. This is in part due to uncertainty regarding the accuracy of ⁴⁰K decay constants on early Solar System timescales (the decay constants of refs. ^63,64 were calibrated to <3 Ga standards) and debate over the appropriate approach to recalibration for timescales ≥4 Ga (refs. ^64,65). However, a recently reported ⁴⁰Ar–³⁹Ar age calculated with the SJ77 decay constants for a ureilitic clast (MS-MU-011) of the Almahata Sitta meteorite agrees with its corresponding Pb–Pb age nearly within 1σ (ref. ⁶⁶). As this fast-quenched system probably cooled through effective Pb and Ar closure almost simultaneously⁶⁶, the SJ77 decay constant seems more accurate on early Solar System timescales than previously argued. In addition, the ubiquitous use of SJ77 combined with inconsistent reporting of co-irradiated standard information across much of the literature inhibits accurate recalibration. Thus, we conclude that the SJ77 decay constants are the best option available at this time for calculating ⁴⁰K–⁴⁰Ar system ages of meteorites, and note that errors stemming from using the different decay constants (<22 Ma) are well within the 1σ uncertainties of most ages in our database. Nonetheless, we explore the effects of using alternative calibration schemes below.

To ensure that all ⁴⁰K–⁴⁰Ar ages used in this study are calculated relative to a set of common decay constants and ⁴⁰K/K ratio (K), we recalculate all ⁴⁰Ar–³⁹Ar and K–Ar ages published before 1977 with the values of SJ77. Given the two different methods employed and non-standardized reporting of methods, these recalculations required one of three scenarios, each of which we employed using a Monte Carlo method to propagate all reported uncertainties.

The first and most straightforward scenario entails recalculating K–Ar ages. To do this, we rearrange the ⁴⁰K–⁴⁰Ar age equation to calculate the measured ⁴⁰Ar/⁴⁰K ratio from the reported age, correct for the updated K ratio, and recalculate the age:

$$t=\frac{1}{\lambda }\left(\ln\left[\frac{\lambda }{{\lambda }_{{\mathrm{e}}}}\,\frac{K^{\prime} }{K}\,\frac{\lambda_{{\mathrm{e}}} ^{\prime} }{\lambda ^{\prime} }\,({{\mathrm{e}}}^{t^{\prime} \lambda ^{\prime} }-1)\right]+1\right)$$

(1)

where the prime symbol indicates the reported age and its corresponding decay and K constants, which were consistently (within rounding error) the values used by ref. ⁶⁷.

In the case of the ⁴⁰Ar–³⁹Ar method, dates are calculated relative to a co-irradiated standard of known age by the equation:

$$t= \frac{1}{\lambda} \ln\left[1 + J{\frac{{40\atop}{\mathrm{Ar}}}{{39\atop}{\mathrm{Ar}}}} \right]$$

(2)

where J is calculated from the standard’s age, t_s, and its measured ⁴⁰Ar/³⁹Ar ratio:

$$J=\frac{{40\atop}{\mathrm{Ar}}}{{39\atop}{\mathrm{Ar}}}({\mathrm{e}}^{\lambda t_{\mathrm{s}}} -1)$$

(3)

Thus, an ⁴⁰Ar–³⁹Ar age may be recalculated simply by correcting the J term:

$$t=\frac{1}{\lambda }\,\ln\left[1+{k}_{J}\,({{\mathrm{e}}}^{\lambda ^{\prime} t^{\prime} }-1)\right]$$

(4)

where k_J is the ratio of the recalculated and original J factors (J/J′). So, the second and third scenarios depend on how the standards used to calculate the J term are calibrated and how methods were reported in each corresponding study.

The second scenario entails cases where t_s was calculated with a chronometric system other than the ⁴⁰K–⁴⁰Ar system. As t_s is constrained independent of the ⁴⁰K decay constants used, k_J is simply calculated by

$${k}_{J}=\frac{{{\mathrm{e}}}^{\lambda {t}_{{\mathrm{s}}}}-1}{{{\mathrm{e}}}^{\lambda ^{\prime} {t}_{{\mathrm{s}}}}-1}$$

(5)

The third scenario entails cases where t_s was calibrated by the K–Ar method, as was typical of ⁴⁰Ar–³⁹Ar dates measured early in the history of this technique. In these situations, we recalculated t_s from the previously used t′ with equation (1), and calculated k_J through a slightly modified version of equation (5) (note the t′):

$${k}_{J}=\frac{{{\mathrm{e}}}^{\lambda {t}_{{\mathrm{s}}}}-1}{{{\mathrm{e}}}^{\lambda ^{\prime} t_{{\mathrm{s}}}^{\prime} }-1}$$

(6)

Unfortunately, not all studies report the standard or its corresponding t_s. In these ambiguous cases, we calculated a distribution of k_J values by the Monte Carlo method using equation (5), where t′ is uniformly distributed over the interval [0, 3) Ga, which generously encompasses the full range of standards commonly used for the ⁴⁰Ar–³⁹Ar method. This approach results in a range of values for k_j over the interval 1.04 < k_j < 1.10, which results in a minor increase in the uncertainty of the recalculated age. For example, for an age of 4,500 ± 20 Ma, the uncertainty increases to ~30 Ma. As most ⁴⁰Ar–³⁹Ar dates measured before 1977 have much larger analytical uncertainties than this (typically >1%), the effect was minor.

The complete database and these calculations are available in the ImpactChron.jl package at https://github.com/grahamedwards/ImpactChron.jl/tree/main/data. Supplementary Table 1 is a human-readable table of the ⁴⁰Ar–³⁹Ar ages used in this study.

Software and code

We invert ⁴⁰K–⁴⁰Ar system ages for asteroid formation and bombardment histories using an asteroid-scale thermochronologic simulation coupled to an MCMC inversion, written in the Julia language⁶⁸ and contained in the package ImpactChron.jl (https://github.com/grahamedwards/ImpactChron.jl). We explain this code in detail in the following sections. We prepared figures and diagrams with Makie.jl⁶⁹, Pairplots.jl (https://github.com/sefffal/PairPlots.jl) and Inkscape vector graphics editor.

Thermochronologic model

We simulate the thermal history of a probabilistic asteroid characterized by the thermal histories of the inner Solar System chondrites—OCs, ECs and RCs. This assumption is reasonable given the similarities in the inferred parent-body histories of OCs and ECs^70,71,72,73 as well as the observation that intergroup variability of material properties is typically less than intragroup variability for these chondrite groups^{74,75,76,77,78,79}. Although the parent-body history of the RCs is less well constrained, they represent only a minor portion (n = 2) of the ⁴⁰Ar–³⁹Ar age database (n = 136). We exclude carbonaceous chondrites, which have lower-temperature aqueous alteration histories, and achondrites, which underwent partial to complete differentiation, as including these samples would require simulating the thermal histories of several distinct parent bodies (and accompanying parameters) that are poorly constrained compared with the OC, EC and RC parent bodies. Hence, we exclude these groups to prevent an expansion of dimensionality that might leave our inversion (see below) underconstrained, for a relatively minor increase in sample size from the comparatively rare carbonaceous chondrite and achondrite meteorite groups.

For computational efficiency, we separately model (1) radiogenic heating and conductive cooling through thermochronologic closure for a body unperturbed by impacts, and (2) impact reheating and resetting of ⁴⁰Ar–³⁹Ar ages. To model the unperturbed thermal histories that would result from radiogenic heating and conductive cooling in the absence of any bombardment, we use an analytical solution to the heat equation for a spherical body with an exponentially decaying heat source^80,81. The parameterization assumes constant bulk density (ρ), specific heat capacity C_p, thermal conductivity k, ambient temperature T_m (that is, the Solar System midplane temperature at 2.5 AU) and body radius R (Table 1). Heat production is a function of the time of accretion t_a relative to the Solar System age t_ss, the initial ²⁶Al/²⁷Al of the Solar System ²⁶Al_o and chondritic Al abundance [Al] (Table 1). We calculate the time–temperature histories of unperturbed cooling in equally spaced concentric shells of the body, and identify the cooling age of each shell as the first timestep with a temperature below the Ar closure temperature (Extended Data Fig. 1a,b). We calculate the volumetric proportion of each shell to produce a distribution of the volumetric abundance of these cooling ages (Extended Data Fig. 1c, black curve).

To account for sampling biases in our database, we consider both (1) the delivery and preservation of asteroidal material to Earth, and (2) the non-random sampling of meteorites for isotopic analyses. We assume that meteoroid sampling and delivery to Earth is pseudorandom and therefore meteorite collections approximately reflect the proportions of proto-asteroidal parent-body material. In contrast, the selection of meteorites for isotopic analysis and thermochronology are biased and non-random. For instance, researchers have specifically sought out highly shocked L chondrites to test the hypothesis of a roughly 500 Ma disruption event²², which we partly account for by excluding ages <2,000 Ma. To more thoroughly account for human-induced bias, we weight our simulated abundances of asteroidal material relative to representation in the ⁴⁰K–⁴⁰Ar database.

While we cannot comprehensively control for heterogeneous sampling of asteroidal parent bodies, delivery of meteoroids to Earth and selection of meteorites for study, we account for heterogeneous representation of parent-body material in our database by weighting our results by petrologic type, as petrologic type is predominantly controlled by a meteorite’s provenance within its parent body (for example, ref. ⁴⁰). For each shell, we assign a petrologic type based on its peak temperature (T_type in °C): T₃ ≤ 600 < T₄ ≤ 700 < T₅ ≤ 800 < T₆, following the recommendations of ref. ⁸² for the maximum temperatures of types 3 and 4 and a minimum type 6 temperature derived from extensive measurements of type 6 OCs⁸³. As type 7 and impact-melted chondrites reflect exogenous heating events that are not directly related to provenance within a parent body⁷⁰, we do not incorporate these classifications into our weighting calculations. We weight the calculated volumetric abundances of each volumetric shell in our simulation so that the relative abundances of each assigned petrologic type (the sum of the volumetric abundances of all shells of that type) equals the relative abundance of that petrologic type in the ⁴⁰Ar–³⁹Ar age database (Extended Data Fig. 1c).

We test the accuracy of the primary endogenic thermal model by running an inversion (described below) on a no-bombardment scenario, constrained by a curated database of ⁴⁰Ar–³⁹Ar ages from H chondrites that are interpreted to have experienced minimally perturbed cooling histories⁸⁴. The overall agreement between the posterior distributions and predicted H parent-body properties validates our radiogenic heating and conductive cooling model (Supplementary Fig. 3).

We then superimpose a bombardment reheating history over the primary cooling history by simulating impacts that reheat a fixed fractional volume of each shell within the body. To simplify our model and underlying code, we assume that impacts only deposit energy and neither excavate nor implant material beyond the original body volume, in line with the probabilistic nature of our model asteroid.

Although the distribution of impact heating in asteroidal bodies is heterogeneous and complex^38,39, both the H and LL chondrites record evidence for impacts while the body was still cooling from radiogenic heating^70,85, and H chondrites directly record the presence of nearly kilometre-scale melt sheets⁸⁶ that would have promoted heat transfer into parent-body interiors. Indeed, suprasolidus type 7 and impact-melt chondrites are by-products of impact heating in early asteroid planetesimals and are observed in every chondrite family evaluated in this study (Table 2). On the basis of this reasoning, we conclude that collisions in the early Solar System were capable of depositing substantial amounts of thermal energy into chondritic planetesimal interiors.

ImpactChron.jl accommodates three different geometries for the zone reheated by an impact: a cone, a parabololoid or a hemisphere. As the shape, depth and radius of the reheating zone beneath an impact site would vary drastically with impactor size and trajectory, we do not assume a single finite morphology for reheating. Instead, we simulate a more probabilistic reheating scenario that heats a cone extending to the centre of the body, allowing for reheating of interior zones that might be exposed by larger collisions. We assign the outermost radius of the cone to cover 1% of the asteroid’s circumference to limit geometric error stemming from our simplified assumption of disk-shaped reheating volumes (which do not account for curvature) for each shell. We justify this assumption in a later section.

We model the bombardment history of the model asteroid with one or more fluxes of impactors that reheat fractions of the body as described above. Each bombardment event is modelled by an exponentially decaying flux defined by an initial impact flux F_o (impacts per Myr), e-folding timescale τ (Myr) and bombardment onset date t_o (Myr_ss). The bombardment flux for any given date t in Myr_ss is

$$F=\left\{\begin{array}{ll}{F}_{{\mathrm{o}}} \exp\left(-\frac{t-{t}_{{\mathrm{o}}}}{\tau }\right),\quad &\,\text{if}\,t\ge {t}_{{\mathrm{o}}}\\ 0,\quad &\,\text{if}\,t < {t}_{{\mathrm{o}}}\end{array}\right.$$

(7)

This formulation results in fractional impacts (Extended Data Fig. 1d), which we accept given the approximate nature of our modelled volumes of impact reheating. At each timestep in the model, we sum all fluxes F to calculate the total number of ‘impacts’ (n_t = ∑FΔt, where the model timestep is Δt = 1 Myr) and scale the volumetric proportion of each shell reheated per impact (${v}_{{t}}^{\,z}$) by n_t.

We assume complete resetting of the ⁴⁰K–⁴⁰Ar system within the reheated zone and instantaneous cooling through Ar closure. While we consider this assumption sufficient for the relatively low-temperature ⁴⁰K–⁴⁰Ar system, this does not afford us the ability to simultaneously model the different temperature-dependent behaviour of multiple thermochronometers; hence we only consider the ⁴⁰K–⁴⁰Ar system. For each shell in the body at each timestep, we reset equal proportions (scaled by ${n}_{{t}} {v}_{{t}}^{z}$) of the cooling age(s) recorded within that shell to the timestep age. Thus, for the first timestep of an impact flux (t₁), ${n}_{{t}1} {v}_{{t}1}^{z}$ of the primary cooling age (t_o) is reset to the age of that timestep (t₁). For the second timestep of that impact flux (t₂), $\frac{1}{2}{n}_{{t}2} {v}_{{t}2}^{\,z}$ of t_o and t₁ are set to an age of t₂. And so on. When iterated over each timestep of the simulation, this produces a matrix of fractional volumes for each modelled shell of the asteroid, with rows and columns corresponding to time/age and radial depth in the parent body. By summing the volumetric proportions corresponding to each timestep, we get a distribution of cooling ages for the model asteroid (Extended Data Fig. 1c).

Bayesian inversion

To reconstruct the planetary history that accounts for the observed distribution of ⁴⁰K–⁴⁰Ar system ages, we use an MCMC method that uses this distribution of measured ages as a prior. The thermochronologic model described above returns a distribution of cooling ages that correspond to the chosen suite of parameters describing the environmental, chemical, physical and material properties of a model asteroid as well as its bombardment history (Table 1). To explore this parameter space and estimate posterior distributions for each parameter, we use a modification of the Metropolis algorithm⁸⁷, based on the underlying statistical architecture of ref. ⁸⁸.

In addition to the prior distribution of measured ⁴⁰K–⁴⁰Ar system ages, we incorporate a comprehensive set of ‘parameter priors’, compiled from published data, to constrain all the parameters describing the environmental, cosmochemical, material and asteroidal properties of the simulation (Table 1). We parameterized each prior as a log-normal distribution based on either the shape of its distribution (the histogram is approximately log-normal) or the fact that the property must be >0 by definition (for example, temperatures in kelvin). Using a log-normal distribution ensures that the MCMC cannot jump to physically impossible negative values for such properties. For each prior, we compiled a variety of measurements or estimates of the parameter, which included discrete values, normal distributions and uniform distributions for data reported as ranges. We then calculated the natural-logarithm-space μ and σ of each distribution from 10⁶ random samples of the compiled data. The two exceptions to this approach are the very precise solar age (assigned to the oldest CAIs), which we treat as a constant in our model, and the initial ²⁶Al/²⁷Al of the protoplanetary disk, which was reported as a normal distribution (Table 1).

As the bombardment history of the asteroid belt is poorly constrained, we do not have prior distributions for the initial impactor flux, e-folding time or onset of each bombardment episode. We assume uniform distributions that span the entire simulation timescale (${\mathcal{U}}[2,000,4,567.3]\,{\mathrm{Ma}}$) for the bombardment onset and e-folding time (Table 1). As the volume of impact reheating is simulated non-physically, setting a maximum on the number of impacts need only accommodate an upper-limit reheating scenario and prevent numerical instability at extreme values. As our parameterization of the reheating zone would completely reheat the full volume of the sphere with ~4,000 impacts, we set an arbitrary upper bound of 10⁴ Myr⁻¹ (Table 1).

The model accommodates up to three-bombardment events (α, β, γ), each described by its own t_o, F_o and τ (Table 1). In simulations with multiple bombardment histories, we assign α as a primordial flux anchored to the solar age (t_o = 0 Myr_ss), and the MCMC algorithm explores the value(s) of t_o for the other flux(es) (β, γ) within the time domain. We impart two rules on these fluxes to ensure reproducible model behaviour. (1) To avoid unnecessary bimodal distributions, we require each flux to occur in chronological order (t_oα < t_oβ < t_oγ), which prevents the Markov chains from ‘swapping’ parameter spaces. (2) We also require that all post-accretion fluxes (β, γ) have a shorter e-folding timescale than the primordial flux, framing bombardment events as transient episodes of enhanced asteroidal collisions that recover more quickly than the background rate of intersecting orbits. Any steps that violate either of these rules are rejected.

Thus, for a given model result—a distribution of simulated ⁴⁰Ar–³⁹Ar ages—we calculate the log-likelihood (ℓ) that the collection of measured ages (with corresponding, normally distributed uncertainties) were drawn from the simulated distribution. We add to this ℓ the log-likelihoods that each simulated parameter was drawn from its corresponding prior distribution. For each step of the Markov chain, we randomly perturb one parameter at a time to explore the full parameter space and accept proposals for any given step i with a probability of min{ℓ_i − ℓ_i−1, 1}. After each accepted step, we scale the step size of the most recently perturbed variable by a constant tuned for an acceptance rate of ~50%. After an extended burn-in/warm-up period (8 × 10⁵ steps), we record 10⁶ subsequent steps of the Markov chain as the stationary distribution.

Evaluating and testing assumptions

In this section, we consider some of the assumptions made to simplify our model and construct the ⁴⁰K–⁴⁰Ar age database.

Decay constants

Above, we justify our decision to calibrate our database of ⁴⁰K–⁴⁰Ar ages with the SJ77 decay constants. Some studies have suggested that these constants underestimate early Solar System ages (relative to the absolute U–Pb thermochronometric system) by ≥30 Ma (refs. ^65,84). However, more recent work on a rapidly quenched system indicates that SJ77-calculated ⁴⁰Ar–³⁹Ar ages underestimate absolute Pb–Pb ages by ≲10 Ma (ref. ⁶⁶). Here we explore how two alternative age calibrations affect the results from inversions of our preferred model (two bombardments—one primordial, one post-accretion). First, we test the effects of linearly shifting all ⁴⁰Ar–³⁹Ar ages in our database 10 Ma earlier in Solar System history (Supplementary Fig. 4). Second, we test the effects of using the more contemporary decay constants calibrated from high-precision geochronology of <3 Ga terrestrial standards^63,64 (Supplementary Fig. 5).

In both cases, the inversion converges on posteriors with median bombardment onset dates >12 Myr_ss (Supplementary Figs. 4 and 5), that is, younger than the median onset date yielded from the SJ77-calibrated database. This is initially surprising, as both alternative age calibrations yield systematically older ages than those calculated with the SJ77 constants. However, we emphasize that the MCMC does not fit individual ages, but rather a distribution of ages. Shifting the entire distribution to earlier timescales (whether linearly or nonlinearly) establishes a new shape of distribution that is modelled by a complex, nonlinear endogenic/exogenic thermal model. Thus, a shift in ages will not necessarily yield a proportional shift in the bombardment onset date. In conclusion, while debate among appropriate decay constants and age calibrations for the ⁴⁰Ar–³⁹Ar system add some uncertainty to our conclusions, the effects do not challenge our primary conclusion that GPM probably post-dated dissipation of the gaseous protoplanetary disk.

Ar closure temperature

As Ar loss from mineral crystal lattices is a diffusive process, effective Ar closure temperature is dependent on many variables, including mineralogy, grain size and cooling rate. As a result, empirically derived Ar closure temperatures for chondrites range broadly (300–800 K) due to variability of these properties among samples. Moreover, the concept of closure temperature itself is a fictitious (albeit useful) simplification of the concurrent processes of radiogenic production and temperature-dependent diffusive loss of atoms within a thermochronometric mineral system⁸⁹. In highly constrained mineral systems, fully modelling the production–diffusion process can simulate accurate thermochronologic histories^70,71. However, in the case of bulk chondrite Ar isotope measurements with few to no mineralogic constraints (the typical case for the ages used in this study), such complete diffusion parameterization is infeasible. To circumvent this heterogeneity and complexity, we instead treat chondrite Ar closure temperatures as distributions rather than absolute values and explore this parameter with the MCMC algorithm, allowing the Bayesian posterior to accommodate its inherent variability. We assert that exploring an effective Ar closure temperature as a free parameter in our Bayesian inversion allows us to capture the heterogeneity and complexity of Ar production–diffusion in chondritic mineral systems without the computational overhead and parametric uncertainty of explicitly simulating Ar diffusion.

Geometry of impact heating

We assume a non-physical geometry—a cone extending to the planetesimal centre—to simulate impact reheating. This assumption allows us to consider impact reheating in a more agnostic, probabilistic fashion by resetting all depths and petrologic types in equal proportions. This should in part capture the thermal effects of impact reheating of material from the asteroid interior exposed by large, more catastrophic disruptions. Although we assume that the parent body was not catastrophically disrupted during the timescales of primary cooling (see below), the delivery of type 6 chondrites to Earth requires eventual excavation of deeper material. Nonetheless, the consequences of full-radius reheating are relatively minor for the deepest portions of our model asteroids. As planetary centres cool slowest, they are still hot (that is, above the Ar closure temperature) and insensitive to thermochronologic resetting during early reheating events. For instance, median conditions from our preferred model (τ ≈ 20 Ma) result in negligibly low fluxes (<1‰ of F_o) after 150 Myr, about half the time it takes for the asteroid centre to cool below Ar closure after accretion (>300 Myr). Correspondingly, our model ignores reheating events before thermochronologic closure (discussed further below).

To test whether our selected parameterization is consistent with more physical approaches, we compare the results of reheating a parabolic region of fixed depth corresponding to impactors of 15 km and 1 km diameters in a 2-bombardment scenario (1 primordial, as in our preferred case; Fig. 4). We approximate the relative dimensions of simulated reheating (per impactor) from the results of previous impact-heating work³⁸. The results show that reheating to ≫1 km depths is necessary: a smaller impactor (1 km diameter) yields posterior parameter distributions that mimic a no-impact scenario (Supplementary Fig. 6 and Extended Data Fig. 3). For sufficient heating depths, posterior bombardment histories are similar between the partial- and full-radius impact-heating parameterizations: the posterior distributions of bombardment parameters for a ≥15 km impactor diameter (results for a 20 km impactor, not shown, are nearly identical) are similar to those produced by the full-radius reheating approach (compare Extended Data Fig. 8 with Supplementary Fig. 7, and Fig. 4 with Supplementary Fig. 8). Thus, as long as sufficiently deep (types 5 and 6) material is reheated by our simulated impact fluxes, the posteriors are largely unchanged.

Two-stage thermal model

As described above, we use a two-stage thermal model: we first model the unperturbed cooling history of a model asteroid with an analytical solution and then superimpose a secondary impact-reheating history over the primary cooling history. While using this analytical solution vastly reduces computation time, it has a few drawbacks. First, it requires constant material parameters (for example, density, thermal conductivity), although these are known to vary as a function of temperature⁷⁷ and shock histories⁷⁹. In addition, we assume instantaneous accretion of the planetesimal to a fixed radius. In each case, our use of the MCMC algorithm allows much (if not all) of the error stemming from these assumptions to be captured within the variation of the posterior estimates for each parameter.

Our use of the two-stage model requires the assumption that the OC, RC and EC parent planetesimals were not catastrophically disrupted before body-wide cooling below Ar closure temperatures. This assumption that planetesimals did not experience early disruptions is supported by several lines of evidence: thermochronologic evidence for the survival of OCs to ≥60–90 Myr_ss (refs. ^70,71) and observational/dynamical evidence for the long-term preservation of large asteroidal bodies⁹⁰ (diameters >120 km, compare with diameters of ~300 km from Table 1). Using the median values of the posterior estimates of our preferred model (Fig. 4 and Extended Data Fig. 8), the planetesimal centre cools through Ar closure after ~300 Myr, but 50% (by volume) of the same body cools through Ar closure within the first 100 Myr_ss. We conclude that parent bodies of the chondrites examined in this study were probably not catastrophically disrupted within the most important timescales of the model and that any samples from the deep interior that were prematurely quenched by disruption reflect a relatively minor volume of material. Nonetheless, this is a notable assumption in our model that future studies could ameliorate by employing more physical thermal histories.

Finally, the two-stage thermal model structure ignores all impact events before the primary cooling age of any given shell. The logic behind our assumption is simple: if the shell had not already cooled through closure, the addition of energy by an impact would not reset a not-yet closed thermochronologic system. Instead, this energy might prolong a cooling history, which is accounted for (at least partly) by subsequent impacts in the flux following the primary closure time of the corresponding shell. The drawback of this approach is that there is little statistical sensitivity to simulated impact scenarios that begin early in time with very large fluxes, before widespread closure of the parent body. However, this drawback reflects an inherent limitation of thermochronology: persistent high temperatures (either sustained or reheated) erase previous thermal information. Thus, similar to nature, our model effectively ignores early, short-lived bombardment events. As the primary cooling ages of the outermost shells of our model asteroids are typically ≥5 Myr_ss, bombardment onsets before this timestep are not well constrained. Thus, we suspect that the exaggerated early tail of bombardment onset dates near 0 Myr_ss in Fig. 4 may be an artefact of this insensitivity.

Age of the Solar System

The architecture of our code requires a fixed solar time-zero (t_ss =0 Myr_ss), and we use the earliest-formed CAIs as our datum. In our simulations, we use the widely applied datum of 4,567.3 Ma, calculated from n = 4 CAI samples²⁶. However, another study precisely estimates the earliest episode of CAI formation at 4,568.2 Ma (ref. ⁹¹), and recent cosmochronological models estimate an absolute age of 4,568.7 Ma for the oldest CAIs⁹². While any of these ages are defensible as a solar datum, the results of our simulations are insensitive to variability in Solar System age. Using our inversion with an upper bound estimate for the age of CAIs (t_ss = 4,568.7 Ma) yields posterior distributions (Supplementary Fig. 9) that appear indistinguishable from those corresponding to t_ss = 4,567.3 Ma (Fig. 4). The median and mean bombardment onset ages for the older-datum scenario are shifted later (relative to the younger datum scenario) by 0.7 Myr_ss and 0.9 Myr_ss, respectively, consistent with the earlier solar datum.