Main

The ocean currently removes about a quarter of the annual anthropogenic CO2 emissions from the atmosphere1,2,3. However, how further global warming4 and the increasing occurrence of anomalously high sea surface temperatures (SSTs)5,6,7 might affect the functioning of this sink remains unclear. Given that most parts of the ocean experienced record-high SSTs in 20238,9,10, this particular year provides a unique opportunity to study this impact. Without global warming, this anomalous state of the surface ocean would have been virtually impossible11. Even accounting for the linear trend in SSTs over the past 34 years, the annual mean anomaly of +0.21 ± 0.02 °C was the largest observed between 50° S and 65° N (Fig. 1a). In addition to global warming, a strong El Niño was an important contributor to this unprecedented SST anomaly8,10,12. The spatial pattern of the SST anomalies represented in many parts the typical response to this phenomenon (Fig. 1c), but unusually high temperatures in the North Atlantic Ocean made 2023 distinct13,14.

Fig. 1: Diagnosis of the record-high SSTs in 2023 and their impact on sea-to-air CO2 fluxes.
figure 1

a,b, Time series of mean SSTs (a) and FCO2 (b) over the region between 50° S and 65° N based on the ensemble mean of four fCO2 products (Extended Data Table 1). Annual (black lines) and monthly mean (grey lines) values are shown. Annual mean anomalies relative to the linear long-term trend from 1990 to 2022, representing the baseline of our analysis, are shaded in red and blue (the meaning of the shading is indicated in the respective panel). Error bars indicate the standard deviation of the annual anomalies across the four fCO2 products (the annual anomalies for each fCO2 product are shown individually in Supplementary Fig. 1). EN indicates years with a strong El Niño. In b, the green bar for 2023 indicates the FCO2 range expected from the linear relationship between global mean FCO2 and SST anomalies between 1990 and 2022 (see ‘Expected FCO2 anomaly in 2023’ in Methods). c,d, Maps of the SST (c) and FCO2 (d) anomalies for 2023 relative to the extrapolated long-term trend. Stippling indicates regions where the ensemble standard deviation is higher than the absolute anomaly.

Full size image

It is well established that warming reduces the solubility of CO2 in seawater, favouring increased outgassing of CO2 to the atmosphere15. Under isochemical conditions, that is, when the dissolved inorganic carbon (DIC) concentration and alkalinity (TA) remain constant, each 1 °C rise in temperature increases the fugacity of CO2 (fCO2) by ~4% (ref. 16). Thus, in the absence of any compensating mechanism, the 2023 SST anomaly of +0.2 °C would have raised fCO2 by 4 µatm. Such an increase in the oceanic fCO2 would largely eliminate the mean sea–air fCO2 gradient (ΔfCO2) over the non-polar global ocean17 and cause the uptake of CO2 from the atmosphere to cease.

However, non-thermal processes, such as changes in ocean circulation, mixing and biogeochemical processes, can compensate for the SST-driven (thermal) effects by modifying the DIC and TA concentrations18. Thermal and non-thermal drivers are often in a delicate balance, which is well documented for the seasonal cycle of surface ocean fCO2 (refs. 16,19,20). In some cases, non-thermal processes even overcompensate the direct temperature effect. This was observed during previous El Niño years, when the oceanic uptake of CO2 became unusually strong (Fig. 1a) despite anomalously high global SSTs. This strengthening during El Niño results from the reduced outgassing of CO2 in the eastern equatorial Pacific Ocean of roughly −0.1 to −0.2 PgC yr−1 due to reduced upwelling of cold and CO2-rich waters21. Note that here we report sea-to-air CO2 fluxes: an (anomalous) oceanic CO2 uptake is negative and outgassing is positive. In contrast, fCO2 in the subtropics tends to be thermally controlled, so that exceptionally warm SSTs are associated with enhanced outgassing of CO2 (refs. 22,23,24). Hence, the overall response of the ocean carbon sink to unusual warming depends sensitively on the regional distribution of the SST anomalies and the outcome of the ‘tug of war’ between the thermal and non-thermal drivers of the surface ocean carbon cycle.

To quantify the impact of 2023’s record-high SSTs on the oceanic uptake of CO2, we employed four observation-based fCO2 products25,26,27,28,29. These products are machine learning-based statistical models that were first trained on in situ fCO2 observations and then used to produce gap-filled maps of the evolution of surface ocean fCO2 based on remotely sensed predictor variables. Our main results were obtained with fCO2 products trained on version 2024 of the Surface Ocean CO2 Atlas (SOCAT) providing observations through December 202330. From the mapped fCO2 fields, we computed the sea-to-air CO2 flux (FCO2) as the product of ΔfCO2, the wind-dependent gas transfer velocity (kw) and the solubility of CO2 in seawater (K0; see Methods). In addition, we provide in Supplementary Figs. 14 and 15 the originally submitted near-real-time (NRT) estimates obtained from the same four fCO2 products trained on observations available only through 2022, but still used to predict surface ocean fCO2 through the end of 2023. These NRT estimates were initially validated through a prediction skill assessment based on truncated training data and comparisons with individual fCO2 observations from 2023 (Supplementary Information)30,31,32,33 and overall agree well with the updated estimates. Furthermore, we employed hindcast simulations from two global ocean biogeochemical models (GOBMs)29,34,35, physically forced with reanalysis data36, to explore how physical and biogeochemical anomalies in the ocean interior shape the surface anomalies.

We focused primarily on the low and middle latitudes between ~50° S and ~65° N, referred to as the global non-polar ocean. This region covers >90% of the global non-sea-ice-covered ocean surface. The Arctic and polar and subpolar biomes of the Southern Ocean are excluded from the discussion because data sparsity leads to higher uncertainties in the flux anomaly estimates, as evidenced by the substantially larger spread across the four fCO2 products. However, we still report the anomalies and associated uncertainties for these high-latitude regions (Table 1 and Extended Data Figs. 3 and 4).

Table 1 Annual mean FCO2 and SSTs in 2023 together with the respective anomalies relative to a linear trend baseline
Full size table

Impact of record-high SSTs on the oceanic CO2 uptake

The four observation-based fCO2 products infer for 2023 an anomalous weakening of the ocean carbon sink by +0.17 ± 0.12 PgC yr−1 integrated over the global non-polar analysis region (Fig. 1b,d and Table 1). This flux anomaly corresponds to a roughly 10% reduction in CO2 uptake relative to a baseline estimate that accounts for the linear trend from 1990 through 2022 (Fig. 1b and Methods), reflecting the expected increase in the uptake of CO2 due to rising atmospheric CO2 (ref. 2). The magnitude of the decline in ocean carbon uptake in 2023 is not unprecedented over the past 34 years, but it is unusual in a year with record-high SSTs exceeding +0.2 °C (Fig. 2a). In fact, a decline in the ocean carbon sink has not occurred before in years with an annual mean SST anomaly in excess of +0.1 °C. Based on the (largely El Niño-driven) relationship between annual mean anomalies in SSTs and oceanic CO2 uptake over the global non-polar ocean (Fig. 2a), an anomalously strong uptake of −0.11 ± 0.04 PgC yr−1 could have been expected in 2023 (Figs. 1b and 2a). Compared with this expectation, the actual CO2 uptake was 0.27 ± 0.13 PgC yr−1 weaker. Thus, something was different in 2023 compared with in previous exceptionally warm years.

Fig. 2: Relationship between annual mean SST and FCO2 anomalies from 1990 to 2023.
figure 2

a–d, All SST and FCO2 anomalies were determined relative to a linear long-term trend and are shown for the global non-polar ocean (a), NA-SPSS (b), NA-STPS (c) and PEQU-E (d). Symbols and error bars represent the mean and standard deviation across the ensemble of four observation-based fCO2 products, respectively. The El Niño years 1997, 2015 and 2023 are highlighted by warm colours. The grey lines and ribbons indicate linear regressions and 68% confidence intervals, respectively, across all annual mean anomalies from 1990 to 2022. A biome map and correlation plots for other biomes are presented in Extended Data Figs. 2 and 3, respectively.

Full size image

The exceptional reduction in uptake in 2023 was not caused by the eastern equatorial Pacific (PEQU-E) biome. In fact, this biome actually experienced reduced outgassing of CO2 by −0.09 ± 0.06 PgC yr−1, that is, an anomalous uptake, which is consistent with the expectation based on the 2023 SST anomaly (Fig. 2d) and matches the response to previous El Niño events21,37,38. Slightly reinforced by reduced CO2 outgassing from the tropical Atlantic and Indian oceans (Fig. 1d), the flux anomalies integrated over the global tropics amounted to −0.11 ± 0.05 PgC yr−1 (Table 1), which closely matches the expected uptake anomaly for the global ocean (Fig. 1b).

Hence, the decline in the uptake of CO2 must have occurred entirely in the extratropical ocean. Here, widespread positive SST anomalies, especially in the Northern Hemisphere (Fig. 1c), triggered an anomalous outgassing of CO2 (Table 1) that was stronger than in previous years, especially those affected by El Niño (Supplementary Fig. 7).

Among the extratropical regions, the North Atlantic experienced the highest, most persistent and extensive SST anomalies in 2023. In particular, the North Atlantic subtropical permanently stratified (NA-STPS) biome (see the biome map in Extended Data Fig. 2) faced an unprecedented annual mean SST anomaly of +0.50 ± 0.05 °C, which caused a substantial decline in the CO2 uptake by +0.04 ± 0.01 PgC yr−1 (Table 1). This response fits the historic relationship between CO2 flux and SST anomalies very well (Fig. 2c), although the SST anomaly exceeds the previous record over the past 34 years by more than 50%. The North Atlantic subpolar seasonally stratified (NA-SPSS) and subtropical seasonally stratified (NA-STSS) biomes experienced even stronger CO2 flux density anomalies. They exceed those in the NA-STPS (Table 1) and are stronger than expected from the annual mean SST anomalies (Extended Data Fig. 1). However, the integrated CO2 flux anomalies in the two seasonally stratified biomes are lower than in the STPS biome due to their smaller surface area. In total, the North Atlantic contributed a flux anomaly of +0.10 ± 0.03 PgC yr−1.

In 2023, the CO2 uptake also weakened in all biomes of the North Pacific (Table 1). The strongest anomalous outgassing per surface area occurred in the two smaller biomes of the North Pacific (NP-STSS and NP-SPSS), but all biomes jointly contributed +0.10 ± 0.07 PgC yr−1 to the weakening of the global ocean carbon sink (Fig. 1d and Table 1). These flux anomalies were substantially stronger than expected from past responses to SST anomalies alone (Extended Data Fig. 1).

The STPS biomes of the Southern Hemisphere revealed overall weak CO2 flux anomalies in 2023. Even though all three basins showed a positive SST anomaly, only the Indian Ocean STPS biome showed anomalous outgassing (Table 1). Considering also the STSS biome of the Southern Ocean, the Southern Hemisphere extratropics contributed in total +0.08 ± 0.11 PgC yr−1 to the global flux anomaly.

In the above analysis, we formally quantified the uncertainty of our estimates as the standard deviation across the four observation-based fCO2 products. At the regional scale, we have high confidence in our estimates for the tropical and subtropical biomes of the Northern Hemisphere, given that the fCO2 products agree in sign and magnitude (Table 1 and Extended Data Fig. 4). Due to the larger spread in the subpolar biomes of the Northern and Southern hemispheres, we assign only medium confidence to these estimates. Estimates for the non-polar global ocean (Table 1 and Extended Data Fig. 4) range from a very minor strengthening of the sink (OceanSODA) to a strong weakening by +0.27 PgC yr−1 (SOM-FFN). As the fCO2 products agree (mostly) in sign but not in magnitude, we assign a medium confidence to our estimate for the non-polar global ocean (+0.17 ± 0.12 PgC yr−1). However, when compared against the expectation of an anomalous strengthening of the sink (−0.11 ± 0.04 PgC yr−1) instead of the zero flux anomaly at the baseline (Fig. 1b), the consistency of estimates is higher. Hence, we have high confidence in our conclusion that the ocean carbon sink in 2023 was indeed weaker (+0.27 ± 0.13 PgC yr−1) than expected based on the long-term trend and the global annual mean SST anomaly. The overall confidence in our estimates is further supported by an almost identical mean estimate of the global non-polar CO2 flux anomaly based on the NRT version of our fCO2 products (+0.16 ± 0.28 PgC yr−1), as well as highly consistent spatial patterns in the flux anomalies (Supplementary Fig. 14), except for the STSS biome in the South Atlantic.

Driver attribution and seasonality of CO2 flux anomalies

The annual mean CO2 flux anomaly over the non-polar global ocean in 2023 was primarily (>95%) driven by anomalies in ΔfCO2 (Fig. 3a and Extended Data Fig. 5). The ΔfCO2 anomaly triggered positive CO2 flux anomalies (that is, a weaker sink) in all regions that experienced a positive SST anomaly, except in PEQU-E (Figs. 1c and 3a). Anomalies in wind speed further modulated the annual mean CO2 flux at regional scales (Fig. 3b), for example, in PEQU-E or the North Pacific off Japan (NP-STSS), but they had a small net impact on globally integrated fluxes (Extended Data Fig. 5). The modulation of ΔfCO2-driven flux anomalies through wind anomalies (that is, the cross term ΔfCO2 × kwK0) was negligible (Fig. 3c and Extended Data Fig. 5) and will not be discussed further.

Fig. 3: Attribution of 2023 annual mean CO2 flux anomalies and oceanic fCO2 decomposition.
figure 3

a–c, Attribution of CO2 flux anomalies to their primary drivers, that is, the CO2 fugacity gradient between ocean and atmosphere (ΔfCO2) (a), the product of the gas transfer velocity and the solubility of CO2 (kwK0), which is primarily controlled by wind speed (b), and the cross product of both drivers (ΔfCO2 ⨯ kwK0) (c). d–f, Decomposition of the total oceanic fCO2 anomalies (f) into thermal (d) and non-thermal (e) components. Stippling indicates regions where the ensemble standard deviation is higher than the absolute ensemble mean.

Full size image

To quantify the causes of the 2023 anomalies in ΔfCO2, we further decomposed the main contributor, the oceanic fCO2 anomaly, into thermal and non-thermal components (see Methods). The regions with the strongest SST anomalies revealed, by definition, the largest thermal component of the fCO2 anomaly, that is, PEQU-E, the subpolar North Pacific and subtropical North Atlantic (Fig. 3d). These regions also experienced the strongest non-thermal component (Fig. 3e). Hence, the resulting total fCO2 anomaly remained comparably small at regional scales (Fig. 3f) and was slightly positive (+0.3 ± 0.9 µatm) when averaged over the global non-polar ocean weighted by the surface area and kwK0 (Extended Data Fig. 6).

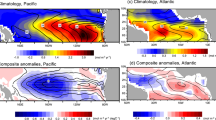
To delve further into the attribution of the 2023 CO2 flux anomalies, we compared their seasonal evolution and drivers for three characteristic biomes with robust anomaly estimates, namely, PEQU-E, NA-STPS and NA-SPSS. For this attribution analysis, we further corroborated the observation-based surface anomalies with simulations from two GOBMs that permit us to connect the processes at the surface with those occurring at depth (see Methods). The GOBM simulations showed a similar seasonal evolution of the SST and CO2 flux anomalies in 2023 as our observation-based estimates (Fig. 4 and Extended Data Fig. 7) and are therefore considered reliable tools to interpret the underlying physical and biogeochemical processes.

Fig. 4: Modelled and observation-based seasonal evolution of surface and interior ocean properties for three key biomes.
figure 4

a,b, Monthly mean surface anomalies of the CO2 flux density (a) and SST (b) in the NA-SPSS (left), NA-STPS (middle) and PEQU-E (right) biomes. The red and grey lines represent the fCO2 product ensemble mean for 2023 and individual years 1990–2022, respectively; the orange lines represent the GOBM ensemble mean for 2023. In a, the triangles indicate the direction of the prevailing absolute CO2 flux into (downwards) or out of (upwards) the ocean. c,d, Model simulations of the vertical mean monthly anomalies of sDIC − sTA (c) and temperature (d) in the NA-SPSS (left), NA-STPS (middle) and PEQU-E (right) biomes. In c, sDIC anomalies are adjusted for the sTA anomaly to capture the sDIC anomaly that is directly linked to fCO2 anomalies. The sDIC − sTA anomalies are presented as changes since January 2023 to remove legacy anomalies from 2022 and to allow direct comparison with the instantaneous surface flux anomalies. The black lines indicate the mean mixed layer depth. All vertical anomalies represent the mean of the two GOBMs.

Full size image

The seasonal evolution in 2023 of SST anomalies in PEQU-E resembles that of previous El Niño events. A positive SST anomaly of around 2 °C established gradually over the first half of 2023 and remained stable thereafter (Fig. 4b, right). This SST evolution was mirrored by a reduction in the outgassing of CO2 (that is, a growing sink) by up to 0.8 mol m−2 yr−1 in the fCO2 products and 0.2 mol m−2 yr−1 in the GOBMs. The reduced outgassing was primarily a consequence of negative ΔfCO2 anomalies, but was reinforced by anomalously low wind speeds. The negative ΔfCO2 anomalies in PEQU-E resulted from reduced upwelling of remineralized DIC. To quantify this well-known non-thermal driver, we used GOBM simulations and subtracted the salinity-normalized TA (sTA) anomaly from the salinity-normalized DIC (sDIC) anomaly. We then converted the anomalous decline in sDIC − sTA (−25 µmol kg−1; Fig. 4c, right) into an equivalent fCO2 reduction of about 50 µatm (see Methods). This DIC-driven fCO2 reduction is already partly compensated by the reduced outgassing of CO2 over the course of 2023, but it still remains substantially stronger than the SST-driven increase in fCO2 of ~30 µatm at the end of the year. Hence, the non-thermal component clearly won the ‘tug of war’ in PEQU-E.

In NA-STPS, the monthly SST anomalies peaked in the summer at around +1 °C and remained well above the range of past anomalies for the remainder of 2023. In contrast to PEQU-E, the resulting CO2 flux anomaly in NA-STPS was positive, that is, the CO2 uptake in winter weakened and the outgassing in summer became stronger. This anomalous outgassing was found in both the fCO2 products and GOBMs. This can be attributed to thermally driven ΔfCO2 anomalies (Fig. 4a, centre and Extended Data Figs. 5 and 6) and was slightly enhanced by weak winds that further reduced the CO2 uptake from January to April (Extended Data Fig. 7). The mixed layer depth simulated by the GOBMs was anomalously shallow in 2023, suggesting increased stratification and reduced mixing of remineralized DIC into the surface layer (Extended Data Fig. 8). However, the simulated surface sDIC − sTA anomaly of −3 µmol kg−1 in NA-STPS was much weaker than in PEQU-E. This anomaly was established primarily in the summer, when the surface CO2 flux anomalies were also strongest (Fig. 4a, centre). Integrated over the summertime mixed layer depth of ~50 m, the sDIC − sTA inventory decreased by roughly 0.15 mol m−2 over the course of 2023 (Fig. 4c, centre), which is almost identical to the cumulative CO2 flux anomaly. This suggests that the surface CO2 flux anomaly was the primary driver of the inventory anomaly in the surface mixed layer. Hence, the reduced mixing of DIC into the surface layer due to the increased stratification was either negligibly small or nearly balanced by a reduced primary production of organic matter (Extended Data Fig. 8). Overall, the thermal driver won the ‘tug of war’ and determined the CO2 flux anomalies during the onset of the SST anomaly in NA-STPS.

In NA-SPSS, the monthly peak SST anomalies were about as high as in NA-STPS, but more confined to the summer months and less exceptional compared with the variability in previous decades (Fig. 4a, left). Similarly, the model- and observation-based CO2 flux anomalies were less exceptional compared with previous years (Fig. 2), albeit more intense than in NA-STPS (Fig. 4a, left). In contrast to NA-STPS, wind anomalies played a more important role in regulating the 2023 CO2 fluxes in NA-SPSS (Extended Data Figs. 5 and 7). Strong winds until May favoured the natural CO2 sink, whereas weak winds throughout the rest of 2023 reduced the natural sink and thereby reinforced the anomalous outgassing triggered by positive ΔfCO2 anomalies. The interpretation of the GOBM simulations in the NA-SPSS biome is rather complex. The simulated increase in the summertime temperature was confined to a very shallow surface layer (10–20 m). This increase in temperature in the GOBMs is very similar to those seen in the fCO2 products and hence induced a similar thermal fCO2 anomaly. However, it triggered a higher ΔfCO2 anomaly because the compensating non-thermal fCO2 anomaly simulated with the GOBMs is weaker than that diagnosed by the fCO2 products (Extended Data Fig. 7). This difference can probably be attributed to an underestimation of the non-thermal fCO2 component by the GOBMs20 in the NA-SPSS biome, as previously documented for the seasonal cycle20.

Discussion

We have demonstrated that widespread record-high SSTs led to a reduction in the ocean carbon sink in 2023 compared with a linearly increasing baseline estimate. This reduction was unexpected considering the strengthening of the sink during previous unusually warm years, all characterized by El Niño conditions. To confirm this finding, we derived a first alternative estimate of the expected sink strength that is based on the actual spatial distribution of the SST anomalies in 2023 and the regional response of the air–sea CO2 fluxes in previous decades (−0.10 ± 0.02 PgC yr−1; Extended Data Fig. 1a,b), and a second alternative estimate that predicts the sink strength with a multiple linear regression model that considers as predictor variables the concentration and growth rate of atmospheric CO2 and an El Niño index based on the SST anomalies in the equatorial Pacific (−0.21 ± 0.07 PgC yr−1; Extended Data Fig. 1c). All three alternatives agree in that the ocean carbon sink should have strengthened in 2023. The reason for the unexpected decline of the ocean carbon sink is the overcompensation of an anticipated anomalous CO2 uptake in the tropics by an increase in CO2 outgassing from the non-polar extratropics (Fig. 5b). Among these regions, the anomalous CO2 outgassing in the subtropical North Atlantic, driven by unusually strong and persistent SST anomalies (Fig. 5a), stands out as a strong and robust feature.

Fig. 5: Annual mean anomalies in FCO2 and the corresponding SST anomalies for 2023.
figure 5

a, Bivariate map of FCO2 and SST anomalies. b, Zonal mean SST anomalies and zonally integrated FCO2 anomalies, adapting the colour scale from a to highlight latitudes with anomalously high (pink) or low (grey) SSTs and a weak (turquoise) or strong (grey) CO2 uptake. All estimates are based on the ensemble mean of four fCO2 products.

Full size image

Interestingly, the depletion of DIC in the NA-STPS biome by the end of 2023, reflected by the sDIC − sTA anomaly of −3 µmol kg−1 (Fig. 4b, centre), had an effect on surface ocean fCO2 (~5 µatm) that was similar in magnitude but opposite in direction to that caused by the SST anomaly (+0.5 °C). This suggests that, by the end of the year, the DIC depletion fully compensated the thermal driver. The resulting decline in the anomalous outgassing towards winter is evident in our GOBM simulations, but less so in the observation-based fCO2 products (Fig. 4a, centre). In contrast to the near balance of the thermal and non-thermal drivers in the NA-STPS biome, the non-thermal DIC anomaly remained dominant in PEQU-E by the end of 2023. Here, the integrated anomaly of sDIC − sTA over the top 100 m had reached −2 mol m−2, far exceeding the CO2 flux anomaly of about −0.1 mol m−2 that occurred cumulatively over the course of the year (Fig. 4, right).

Using the anomalous state of the ocean by the end of 2023 to forecast the proceeding CO2 flux anomalies, the expectation is that the anomalous outgassing in NA-STPS might have ceased, despite the continued elevated SSTs, provided that the DIC depletion remained during the first half of 2024. However, mixing during the boreal wintertime of 2023–2024 might have replenished the surface DIC pool. Hence, we expect a neutral to a reduced sink strength in NA-STPS in the first half of 2024. In PEQU-E, the remaining negative DIC anomaly favours continued reduced outgassing, provided that these water masses stay in contact with the atmosphere. However, as SST anomalies in PEQU-E decreased during the first half of 2024, CO2 outgassing in this biome most probably returned to normal levels and we expect a rather neutral sink strength in PEQU-E in the first half of 2024. If indeed the reduced outgassing in the tropics faded out while the extratropics remained anomalously warm, the global ocean carbon sink might have continued to be in weak in early 2024.

Whether these projected CO2 flux anomalies materialized in 2024 remains to be confirmed, ultimately through fCO2 observations. A more immediate opportunity to quantify the oceanic CO2 uptake in 2024 emerges from the possibility to predict the observation-based fCO2 products25,26,27,28 that were trained on in situ fCO2 observations through December 202330 for 1 year beyond the training data using the observed predictor fields already available for 2024. In fact, this study was originally conducted with such NRT predictions for 2023, and the similarity of the ensemble mean FCO2 anomalies, as well as a thorough prediction skill assessment based on truncated training data (Supplementary Figs. 8–13), indicate that this approach is suitable for quantifying CO2 flux anomalies with low latency.

The limitation of thermally induced CO2 outgassing by DIC depletion that we observed for the 2023 warming event is crucial when considering the long-term response of the ocean carbon sink to global warming. Between 2000 and 2019, warming weakened the oceanic uptake of CO2 (ref. 39), but the impact was much weaker than expected from decreased solubility alone (that is, the thermal driver). This is because the temperature-induced outgassing of CO2 and the reduced upwelling of DIC (both non-thermal drivers) caused a negative feedback that compensated the initial perturbation. While these negative feedbacks have been demonstrated for historic warming SST extremes22,23,24 and historic trends in the ocean carbon sink, it remains unclear whether these stabilizing mechanisms of the ocean carbon sink will remain effective under future extreme SST events, which are expected to become more frequent, intense and longer lasting5, or progressing global warming. Deviations from the negative feedbacks observed in the past could, for example, occur if longer-lasting SST extremes cause stronger limitations of CO2 outgassing due to DIC depletion or if the efficiency of the biological carbon pump becomes more strongly affected. To keep track of changes in the ocean carbon sink, the continued, revived and extended observation of the ocean through high-quality fCO2 measurements remains indispensable and it needs to be accompanied by an improved understanding of the fCO2 mapping skill at seasonal to interannual timescales and across ocean biomes40,41.

Methods

Data sources

This study relied on four fCO2 products and two global ocean biogeochemical models, for which technical details are provided in Extended Data Tables 1 and 2, respectively. These data sources constitute a subset of those used in the Global Carbon Budget1,29 (except for the fCO2-Residual product) and the second iteration of the Regional Carbon Cycle Assessment and Processes project (RECCAP2)42,43. The observation-based SST fields used as predictor variables in the fCO2 products were also used for our analysis of SST trends and anomalies. The GOBM simulations used in this study are equivalent to those considered as ‘simulation A’ in RECCAP2, that is, they are forced with (1) reanalysis data to represent the observed climate variability over the hindcast period and (2) historic atmospheric CO2 observations to represent anthropogenic emissions.

Biome definition

To average or integrate surface ocean properties regionally, we used ocean biomes originally defined by Fay and McKinley44 and slightly modified for use in the RECCAP2 project43,45,46,47. We used a single, time-invariant definition of the biome boundaries (Extended Data Fig. 2a) to obtain estimates that are directly comparable across data products, across seasons and to numerous previous studies.

Anomaly determination against moving baseline

All anomalies determined in this study are expressed relative to a moving baseline to remove long-term trends driven by the growth in atmospheric CO2 or global warming. The moving baseline for any variable of interest was determined by fitting a linear regression model to the historic observations from 1990 through 2022 as a function of the calendar year. The baseline estimate for a given year, including 2023, was then obtained as the predicted value of this linear regression model. The underlying data are either annual or monthly mean values. The data for 2023 were excluded from the regression to achieve a baseline estimate that is unbiased from the actual anomaly in 2023. For the atmospheric and surface ocean fCO2, the linear regression model was replaced by a quadratic fit to better approximate the actual evolution of their growth rates over time. Finally, anomalies were calculated by subtracting the predicted baseline value from the observed value.

Expected FCO2 anomaly in 2023

To determine the expected FCO2 anomaly in 2023 for the global non-polar ocean, we fitted linear regression models of the integrated annual mean FCO2 anomaly as a function of the annual mean SST anomaly to the hindcast estimates of our four fCO2 products from 1990 through 2022. The intercepts (in PgC yr−1) and slopes (in PgC yr−1 °C−1) of these four regression models were determined to be −7.3 × 10−15 PgC yr−1 and −0.55 PgC yr−1 °C−1 (CMEMS), 2.1 × 10−15 PgC yr−1 and −0.79 PgC yr−1 °C−1 (fCO2-Residual), −5.7 × 10−15 PgC yr−1 and −0.40 PgC yr−1 °C−1 (OceanSODAv2), and −3.4 × 10−15 PgC yr−1 and −0.30 PgC yr−1 °C−1 (SOM-FFN), respectively.

Based on these regression models, the expected FCO2 anomaly in 2023 was calculated for each fCO2 product from the SST anomaly in 2023. The 2023 SST anomalies (in °C) and the derived expected FCO2 anomalies (in PgC yr−1) are 0.19 °C and −0.10 PgC yr−1 (CMEMS), 0.2 °C and −0.16 PgC yr−1 (fCO2-Residual), 0.22 °C and −0.09 PgC yr−1 (OceanSODAv2), and 0.23 °C and −0.07 PgC yr−1 (SOM-FFN), respectively. The mean and standard deviation of this expected FCO2 anomaly are −0.11 ± 0.04 PgC yr−1 (Fig. 1b).

In addition to the approach outlined above, we investigated two alternative methods to constrain the expected flux anomaly. First, we used the actual spatial distribution of the SST anomalies in 2023 (Fig. 1c) and multiplied those by the slope of a linear regression between air–sea CO2 flux anomalies and SST anomalies from 1990 through 2022 to obtain a spatially resolved map of expected flux anomalies in 2023 (Extended Data Fig. 1a,b). The globally integrated expected flux anomaly for 2023 from this approach (−0.10 ± 0.02 PgC yr−1) is almost identical to that obtained from our standard approach, that is, the regression of global annual mean SST and integrated flux anomalies (−0.11 ± 0.04 PgC yr−1). Second, we fitted a multiple linear regression model that considers the concentration and growth rate of atmospheric CO2, as well as SST anomalies in the equatorial Pacific as an indicator of the El Niño and Southern Oscillation (ENSO) state, as predictor variables for the annual mean ocean carbon sink from 1990 through 2022. This model was used to predict the expected carbon sink over time, providing an expected value of −0.21 ± 0.07 PgC yr−1 for 2023. The unexpected component of the global non-polar ocean carbon sink, which is the difference between the expected and the observed value, is very similar when using this multiple linear regression model or the linear baseline approach together with the expected CO2 flux anomaly based on the global mean SST anomaly (Extended Data Fig. 1c). As for our standard approach, these alternative methods were applied to each fCO2 product individually and the results are reported as the mean and standard deviation across products.

Computation and attribution of flux anomalies

The CO2 flux (FCO2) across the air–sea interface is calculated as the product of the fugacity difference between ocean and atmosphere (ΔfCO2), the gas transfer velocity (kw) and the solubility of CO2 in seawater (K0) and is scaled with the fractional ice coverage (fice) according to:

$$F{{\rm{CO}}}_{2}=\Delta f{{\rm{CO}}}_{2}\times ({k}_{{\rm{w}}}{K}_{0})\times (1-{f}_{{\rm{ice}}})$$
(1)

To attribute flux anomalies to the underlying anomalies in the drivers, we applied a classical Reynolds decomposition. For this purpose, we considered the product kwK0 as a single term that is largely temperature independent because the temperature dependence in kw and K0 tend to cancel out. While the exact degree of this cancellation depends on the chosen parameterization of kw and K0, widely used formulations15,48 suggest a gradual increase in kw of 120% and a decrease in K0 of 50% on a temperature increase from 0 to 30 °C. In contrast, the corresponding kwK0 changes by less than 10% over the same temperature range. As a consequence, kwK0 depends primarily on the prevailing wind speed. Furthermore, we neglected the modulation of FCO2 by the fractional ice coverage as this study focused on ice-free ocean. To derive the Reynolds decomposition, in general, the individual components in equation (1) can be described as:

$$F{{\rm{CO}}}_{2}=F{{\rm{CO}}}_{2,{\rm{baseline}}}+{\prime} F{{\rm{CO}}}_{2}$$
(2)
$$\Delta f{{\rm{CO}}}_{2}=\Delta f{{\rm{CO}}}_{2,{\rm{baseline}}}+{\prime} \Delta f{{\rm{CO}}}_{2}$$
(3)
$$({k}_{{\rm{w}}}{K}_{0})={({k}_{{\rm{w}}}{K}_{0})}_{{\rm{baseline}}}+{\prime} ({k}_{{\rm{w}}}{K}_{0})$$
(4)

where prime symbols (′) and ‘baseline’ denote anomalies and detrended baseline estimates, respectively.

Inserting equations (3) and (4) into equation (1) and expanding the product leads to:

$$\begin{array}{l}F{{\rm{CO}}}_{2}=\Delta f{{\rm{CO}}}_{2,{\rm{baseline}}}\times {({k}_{{\rm{w}}}{K}_{0})}_{{\rm{baseline}}}+{\prime} \Delta f{{\rm{CO}}}_{2}\times {\left({k}_{{\rm{w}}}{K}_{0}\right)}_{{\rm{baseline}}}\\\qquad\quad+\Delta f{{\rm{CO}}}_{2,{\rm{baseline}}}\times {\prime} ({k}_{{\rm{w}}}{K}_{0})+{\prime} \Delta f{{\rm{CO}}}_{2}\times {\prime} ({k}_{{\rm{w}}}{K}_{0})\end{array}$$
(5)

The first term in equation (5), that is, the product ΔfCO2,baseline × (kwK0)baseline, represents the baseline flux FCO2,baseline in equation (2), whereas the three other terms describe the flux anomaly ′FCO2. Hence, we can decompose the observed flux anomaly into its components according to:

$${\prime} F{{\rm{CO}}}_{2}={\prime} \Delta f{{\rm{CO}}}_{2}\times {({k}_{{\rm{w}}}{K}_{0})}_{{\rm{baseline}}}+\Delta f{{\rm{CO}}}_{2,{\rm{baseline}}}\times {\prime} ({k}_{{\rm{w}}}{K}_{0})+{\prime} \Delta f{{\rm{CO}}}_{2}\times {\prime} ({k}_{{\rm{w}}}{K}_{0})$$
(6)

We initially computed the flux anomaly contributions according to equation (6) using the original grid of our estimates (monthly, 1° × 1°) and then averaged the components in space and time (for example, to compute biome annual means).

Thermal and non-thermal decomposition of fCO2 anomalies

To assess the mechanistic drivers causing the 2023 anomalies in ΔfCO2, we decomposed the main contributor to this anomaly, that is, the surface ocean fCO2 anomaly, into a thermal and non-thermal component based on the SST anomalies. We performed this decomposition initially on the original grid of our estimates (monthly, 1° × 1°) and then averaged the components in space and time (for example, to compute biome annual means).

Specifically, we determined in a first step the thermally driven fCO2 anomaly (′fCO2,thermal) according to equation (7):

$${\prime} f{{\rm{CO}}}_{2,{\rm{thermal}}}=f{{\rm{CO}}}_{2,{\rm{baseline}}}\times \exp ({\gamma }_{{\rm{T}}}\times {\prime} {\rm{SST}})-f{{\rm{CO}}}_{2,{\rm{baseline}}}$$
(7)

where fCO2,baseline is the monthly baseline value of fCO2, γT is the temperature sensitivity of fCO2 (0.0423 K−1)16 and ′SST is the monthly anomaly in SST determined against a linear regression baseline fitted to the monthly SST data from 1990 through 2022. Note that fCO2,baseline inherits a seasonal cycle and is expressed in absolute values that are similar to the observed fCO2 values. In contrast, ′SST represents only the deviation of the observed SST from the expected baseline value, that is, it is a numerically small value of positive or negative sign and does not follow a classical seasonal cycle. As a consequence, the variable ′fCO2,thermal computed according to equation (7) is also a numerically small value of positive or negative sign and does not follow a typical seasonal pattern. In this regard, our thermal anomaly component ′fCO2,thermal differs from the widely used thermal component of fCO2 that is defined as fCO2,thermal = fCO2,mean × exp[γT × (SSTobs − SSTmean)], where fCO2,mean and SSTmean are the regional annual mean values of the surface ocean CO2 fugacity and SST, respectively, and SSTobs is the actual observed monthly SST. In this classical decomposition of absolute fCO2 values (instead of anomalies), SSTobs − SSTmean and hence also fCO2,thermal follow a classical seasonal cycle and the value of fCO2,thermal has the same order of magnitude as fCO2 itself. fCO2,thermal can be considered as the seasonal cycle of fCO2 driven solely by the seasonal cycle in SST.

Based on ′fCO2,thermal and the directly determined total fCO2 anomaly (′fCO2), we calculated the non-thermally driven fCO2 anomaly (′fCO2,non-thermal) according to:

$${\prime} f{{\rm{CO}}}_{2,{\rm{non}}-{\rm{thermal}}}={\prime} f{{\rm{CO}}}_{2}-{\prime} f{{\rm{CO}}}_{2,{\rm{thermal}}}$$
(8)

While our definition of ′fCO2,non-thermal according to equation (8) resembles the definition of the fCO2 residual in previous studies25,28, it differs in that it does not inherit a classical seasonal cycle. Similarly, our anomaly component ′fCO2,non-thermal differs from the widely used19,49 non-thermal component of fCO2 that is defined as fCO2,non-thermal = fCO2,obs × exp[γT × (SSTmean – SSTobs)], with fCO2,obs being the observed monthly surface ocean CO2 fugacity, and describes the fCO2 seasonality that would occur if the SST remained at the annual mean, but all other processes followed their natural seasonal cycle.

Conversion from DIC to fCO2 anomalies

To convert DIC anomalies into fCO2 anomalies, it is important to consider TA anomalies that occur simultaneously because the fraction of the DIC anomaly that is caused by the TA anomaly has no effect on fCO2. The conversion can formally be derived by considering the sensitivity of fCO2 to changes in either DIC (γDIC) or TA (γTA) (ref. 50):

$$\gamma _{{\rm{DIC}}}=(\Delta f{{\rm{CO}}}_{2,{\rm{DIC}}}/f{{\rm{CO}}}_{2})/\Delta {\rm{DIC}}$$
(9)

and

$$\gamma _{{\rm{TA}}}=(\Delta f{{\rm{CO}}}_{2,{\rm{TA}}}/f{{\rm{CO}}}_{2})/\Delta {\rm{TA}},$$
(10)

where ΔDIC and ΔTA denote changes in DIC and TA, respectively, ΔfCO2,DIC and ΔfCO2,TA denote changes in fCO2 exclusively due to ΔDIC and ΔTA, respectively, and fCO2 denotes the surface ocean CO2 fugacity in absolute terms. Given that the total change in fCO2 is the sum of the change driven by TA and DIC:

$$\Delta f{{\rm{CO}}}_{2}=\Delta f{{\rm{CO}}}_{2,{\rm{DIC}}}+\Delta f{{\rm{CO}}}_{2,{\rm{TA}}}$$
(11)

the two sensitivities γDIC and γTA can be inserted into equation (11) to derive the expression:

$$\Delta f{{\rm{CO}}}_{2}={\gamma }_{{\rm{DIC}}}\times f{{\rm{CO}}}_{2}\times \Delta {\rm{DIC}}+{\gamma }_{{\rm{TA}}}\times f{{\rm{CO}}}_{2}\times \Delta {\rm{TA}}$$
(12)

We computed ΔfCO2 according to equation (12) using the output of our model simulations for fCO2, ΔDIC and ΔTA and computing γDIC and γTA from the model temperature.

To support the mechanistic interpretation of equation (12), the approximation γDIC ≈ −γTA can be introduced. This approximation is valid, given that the global surface ocean γDIC and γTA are of very similar magnitude but opposite sign50. Inserting the approximation into equation (12) leads to the expression:

$$\Delta f{{\rm{CO}}}_{2}={\gamma }_{{\rm{DIC}}}\times f{{\rm{CO}}}_{2}\times (\Delta {\rm{DIC}}-\Delta {\rm{TA}})$$
(13)

The term ΔDIC − ΔTA can be interpreted as the effective change in DIC that is not compensated for by a change in TA. Intuitively, a positive DIC anomaly that is not fully balanced by a TA anomaly would lead to a positive fCO2 anomaly.

Interestingly, the approximation for carbonate ion concentration [\({\rm{C}}{{\rm{O}}}_{3}^{2-}\)] ≈ TA − DIC can also be introduced18. Hence, the change in fCO2 can also be expressed as:

$$\Delta f{{\rm{CO}}}_{2}=-{\gamma }_{{\rm{DIC}}}\,(\;f{{\rm{CO}}}_{2}/{\rm{DIC}})\Delta [{\rm{C}}{{\rm{O}}}_{3}^{2-}]$$
(14)

While equations (13) and (14) were not used to compute ΔfCO2, they are useful to illustrate that a negative anomaly in fCO2 is in essence equivalent to a positive anomaly in carbonate ion concentration. Hence, Fig. 4c could be redrawn with an inverted colour scale and show [\({\rm{C}}{{\rm{O}}}_{3}^{2-}\)] instead of DIC − TA.