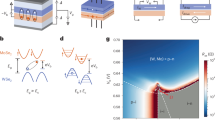
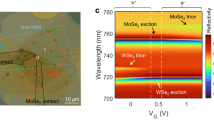
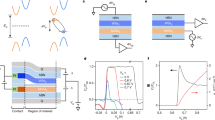
Abstract
Excitonic insulators represent a unique quantum phase of matter that enables the study of exotic quantum bosonic states. Strongly coupled electron–hole bilayers, which host stable dipolar exciton fluids with an exciton density that can be adjusted electrostatically, offer an ideal platform to investigate correlated excitonic insulators. On the basis of electron–hole bilayers made of MoSe2/hexagonal boron nitride/WSe2 heterostructures, here we study the behaviour of excitonic insulators in a perpendicular magnetic field. We report the observation of excitonic quantum oscillations in both Coulomb drag signals and electrical resistance at low to medium magnetic fields. Under a strong magnetic field, we identify multiple quantum phase transitions between the excitonic insulator phase and the bilayer quantum Hall insulator phase. These findings underscore the interplay between the electron–hole interactions and Landau-level quantization, and enable further exploration of quantum phenomena in composite bosonic insulators.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data that support the findings of this study are available from the corresponding author upon request.
References
Zeng, Y. & MacDonald, A. H. Electrically controlled two-dimensional electron-hole fluids. Phys. Rev. B 102, 085154 (2020).
Wu, F.-C., Xue, F. & MacDonald, A. H. Theory of two-dimensional spatially indirect equilibrium exciton condensates. Phys. Rev. B 92, 165121 (2015).
Qi, R. et al. Thermodynamic behavior of correlated electron-hole fluids in van der Waals heterostructures. Nat. Commun. 14, 8264 (2023).
Ma, L. et al. Strongly correlated excitonic insulator in atomic double layers. Nature 598, 585–589 (2021).
De Palo, S., Rapisarda, F. & Senatore, G. Excitonic condensation in a symmetric electron-hole bilayer. Phys. Rev. Lett. 88, 206401 (2002).
Fogler, M. M., Butov, L. V. & Novoselov, K. S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 5, 4555 (2014).
Liu, X., Watanabe, K., Taniguchi, T., Halperin, B. I. & Kim, P. Quantum Hall drag of exciton condensate in graphene. Nat. Phys. 13, 746–750 (2017).
Eisenstein, J. P. & MacDonald, A. H. Bose–Einstein condensation of excitons in bilayer electron systems. Nature 432, 691–694 (2004).
Zhu, X., Littlewood, P. B., Hybertsen, M. S. & Rice, T. M. Exciton condensate in semiconductor quantum well structures. Phys. Rev. Lett. 74, 1633–1636 (1995).
Maezono, R., López Ríos, P., Ogawa, T. & Needs, R. J. Excitons and biexcitons in symmetric electron-hole bilayers. Phys. Rev. Lett. 110, 216407 (2013).
Dai, D. D. & Fu, L. Strong-coupling phases of trions and excitons in electron-hole bilayers at commensurate densities. Phys. Rev. Lett. 132, 196202 (2024).
Qi, R. et al. Electrically controlled interlayer trion fluid in electron-hole bilayers. Preprint at https://arxiv.org/abs/2312.03251 (2023).
Nguyen, P. X. et al. A degenerate trion liquid in atomic double layers. Preprint at https://arxiv.org/abs/2312.12571 (2023).
Nguyen, P. X. et al. Perfect Coulomb drag in a dipolar excitonic insulator. Science 388, 274–278 (2025).
Qi, R. et al. Perfect Coulomb drag and exciton transport in an excitonic insulator. Science 388, 278–283 (2025).
Liu, X. et al. Crossover between strongly coupled and weakly coupled exciton superfluids. Science 375, 205–209 (2022).
Eisenstein, J. P. Exciton condensation in bilayer quantum Hall systems. Annu. Rev. Condens. Matter Phys. 5, 159–181 (2014).
Li, J. I. A., Taniguchi, T., Watanabe, K., Hone, J. & Dean, C. R. Excitonic superfluid phase in double bilayer graphene. Nat. Phys. 13, 751–755 (2017).
Croxall, A. F. et al. Anomalous Coulomb drag in electron-hole bilayers. Phys. Rev. Lett. 101, 246801 (2008).
Du, L. et al. Evidence for a topological excitonic insulator in InAs/GaSb bilayers. Nat. Commun. 8, 1971 (2017).
Wang, R., Sedrakyan, T. A., Wang, B., Du, L. & Du, R.-R. Excitonic topological order in imbalanced electron–hole bilayers. Nature 619, 57–62 (2023).
Han, Z., Li, T., Zhang, L., Sullivan, G. & Du, R.-R. Anomalous conductance oscillations in the hybridization gap of InAs/GaSb quantum wells. Phys. Rev. Lett. 123, 126803 (2019).
Xiao, D., Liu, C.-X., Samarth, N. & Hu, L.-H. Anomalous quantum oscillations of interacting electron-hole gases in inverted type-II InAs/GaSb quantum wells. Phys. Rev. Lett. 122, 186802 (2019).
Shao, Y. & Dai, X. Quantum oscillations in an excitonic insulating electron-hole bilayer. Phys. Rev. B 109, 155107 (2024).
Zou, B., Zeng, Y., MacDonald, A. H. & Strashko, A. Electrical control of two-dimensional electron-hole fluids in the quantum Hall regime. Phys. Rev. B 109, 085416 (2024).
Li, L., Sun, K., Kurdak, C. & Allen, J. W. Emergent mystery in the Kondo insulator samarium hexaboride. Nat. Rev. Phys. 2, 463–479 (2020).
Pirie, H. et al. Visualizing the atomic-scale origin of metallic behavior in Kondo insulators. Science 379, 1214–1218 (2023).
Shen, H. & Fu, L. Quantum oscillation from in-gap states and a non-Hermitian Landau level problem. Phys. Rev. Lett. 121, 026403 (2018).
Zhang, L., Song, X.-Y. & Wang, F. Quantum oscillation in narrow-gap topological insulators. Phys. Rev. Lett. 116, 046404 (2016).
Knolle, J. & Cooper, N. R. Quantum oscillations without a Fermi surface and the anomalous de Haas-van Alphen effect. Phys. Rev. Lett. 115, 146401 (2015).
Knolle, J. & Cooper, N. R. Excitons in topological Kondo insulators: theory of thermodynamic and transport anomalies in SmB6. Phys. Rev. Lett. 118, 096604 (2017).
Erten, O., Chang, P.-Y., Coleman, P. & Tsvelik, A. M. Skyrme insulators: insulators at the brink of superconductivity. Phys. Rev. Lett. 119, 057603 (2017).
Lee, P. A. Quantum oscillations in the activated conductivity in excitonic insulators: possible application to monolayer WTe2. Phys. Rev. B 103, L041101 (2021).
He, W.-Y. & Lee, P. A. Quantum oscillation of thermally activated conductivity in a monolayer WTe2-like excitonic insulator. Phys. Rev. B 104, L041110 (2021).
Chowdhury, D., Sodemann, I. & Senthil, T. Mixed-valence insulators with neutral Fermi surfaces. Nat. Commun. 9, 1766 (2018).
Sodemann, I., Chowdhury, D. & Senthil, T. Quantum oscillations in insulators with neutral Fermi surfaces. Phys. Rev. B 97, 045152 (2018).
Li, G. et al. Two-dimensional Fermi surfaces in Kondo insulator SmB6. Science 346, 1208–1212 (2014).
Tan, B. S. et al. Unconventional Fermi surface in an insulating state. Science 349, 287–290 (2015).
Wang, P. et al. Landau quantization and highly mobile fermions in an insulator. Nature 589, 225–229 (2021).
Xiang, Z. et al. Quantum oscillations of electrical resistivity in an insulator. Science 362, 65–69 (2018).
Rikken, G. L. J. A. et al. Two-terminal resistance of quantum Hall devices. Phys. Rev. B 37, 6181–6186 (1988).
Moon, K. et al. Spontaneous interlayer coherence in double-layer quantum Hall systems: charged vortices and Kosterlitz-Thouless phase transitions. Phys. Rev. B 51, 5138–5170 (1995).
Jungwirth, T., Shukla, S. P., Smrčka, L., Shayegan, M. & MacDonald, A. H. Magnetic anisotropy in quantum Hall ferromagnets. Phys. Rev. Lett. 81, 2328–2331 (1998).
Shi, Q. et al. Odd- and even-denominator fractional quantum Hall states in monolayer WSe2. Nat. Nanotechnol. 15, 569–573 (2020).
Larentis, S. et al. Large effective mass and interaction-enhanced Zeeman splitting of K-valley electrons in MoSe2. Phys. Rev. B 97, 201407 (2018).
Fenton, E. W. Excitonic insulator in a magnetic field. Phys. Rev. 170, 816–821 (1968).
Shoenberg D. Magnetic Oscillations in Metals (Cambridge Univ. Press, 2009).
Zhu, J., Li, T., Young, A. F., Shan, J. & Mak, K. F. Quantum oscillations in two-dimensional insulators induced by graphite gates. Phys. Rev. Lett. 127, 247702 (2021).
Zou, B. & MacDonald, A. H. Vortex lattice states of bilayer electron-hole fluids in quantizing magnetic fields. Preprint at https://arxiv.org/abs/2411.08810 (2024).
Li, H. et al. Electrode-free anodic oxidation nanolithography of low-dimensional materials. Nano Lett. 18, 8011–8015 (2018).
Acknowledgements
This work was primarily funded by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under contract no. DE-AC02-05-CH11231 within the van der Waals heterostructure program KCFW16 (device fabrication and transport measurements). Optical characterization was supported by the AFOSR award no. FA9550-23-1-0246. K.W. and T.T. acknowledge support from the Japan Society for the Promotion of Science (KAKENHI grant nos. 21H05233 and 23H02052) and World Premier International Research Center Initiative, Ministry of Education, Culture, Sports, Science and Technology, Japan. R.Q. acknowledges support from Kavli ENSI graduate student fellowship. A.H.M. and B.Z. were supported by the US Department of Energy, Office of Science, Basic Energy Sciences under award DE-SC0021984: ‘Controlling Quantum Exciton Coherence and Interactions via Trapping Environments (ExCITE)’.
Author information
Authors and Affiliations
Contributions
F.W. and R.Q. conceived the research. Q.L., R.Q. and J.N. fabricated the devices with help from Z.C. and S.C. R.Q. performed the optical measurements. R.Q. and Z.Z. performed the transport measurements with help from H.K., J.X. and C.S. R.Q., Z.Z. and F.W. analysed the data with inputs from M.F.C., B.Z. and A.H.M. K.W. and T.T. grew the hBN crystals. All authors discussed the results and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Materials thanks Denis Golež and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Main results from a second device (D2).
a, An optical microscopy image of device D2 (WSe2/six-layer hBN/MoSe2 heterostructure) with flakes outlined. In this device, the MoSe2 contacts in the second reservoir region are mechanically broken, preventing us from performing the Coulomb drag measurements. b, c, Measured Rh at B = 0 T (b) and 12 T (c). The results are consistent with the data from device D1 shown in the main text. d, Fan diagram of Rh along the CNL. Due to a smaller interlayer distance compared to device D1, the exciton binding energy is larger, requiring a larger magnetic field to induce QOs and EI-QHI phase transitions. e, Rh along the CNL at B = 12 T as a function of VB and T.
Extended Data Fig. 2 Main results from a third device (D3).
a, An optical microscopy image of device D3 (WSe2/five-layer hBN/MoSe2 heterostructure). In this device, the TG is patterned to split the WSe2 contacts into four regions, enabling independent measurement of longitudinal and Hall resistances in the hole layer. b, c, Four-terminal longitudinal resistance Rxx (b) and Hall resistance Rxy (c) of the WSe2 layer, measured at B = 12 T. The longitudinal resistance vanishes periodically at integer hole filling, which is interrupted by the EI states near CNL. The Hall resistance shows quantized plateaus, consistent with typical QH states. d, A vertical linecut of Rxy at constant VG = 0.4 V (blue dashed line in c), confirming precise quantization of the Hall resistance.
Extended Data Fig. 3 Drive and drag currents.
a-b, Drive and drag currents at B = 0 with 5 mV drive voltage applied across the MoSe2 layer. c-d, Drive and drag currents at B = 12 T.
Extended Data Fig. 4 Determination of Pt-WSe2 contact resistance.
a, Schematic circuit diagram for two different Rh measurement configurations. b, Comparison of the obtained resistances as a function of VB along the CNL, measured at B = 0. Their difference (yellow line) corresponds to the total Pt-WSe2 contact resistance on the two sides. Nearly no VB dependence is observed, with an average value of 2.2 kΩ. c, Magnetic field dependence of the Pt-WSe2 contact resistance, showing a slight increase at high fields.
Extended Data Fig. 5 Optical measurement of charge compressibility and charge gap.
a, Charge compressibility of the e-h bilayer, defined as the numerical derivative of net charge density ne−nh with respect to gate voltage VG, measured at B = 0. In the EI phase, the charge compressibility is zero despite finite carrier density (Fig. 1c-d). b, Charge compressibility measured at B = 12 T. c, Charge gap size as a function of VB at B = 12 T. The horizontal line marks the cyclotron energy of electrons/holes using an effective mass of 0.5m0.
Extended Data Fig. 6 Comparison of pair densities derived from QO frequency and from optical spectroscopy.
Solid line, pair density determined using optical spectroscopy (B = 12 T). Open circles, pair density obtained from the QO period.
Extended Data Fig. 7 Carrier densities in graphite gates modeled by a capacitor model.
a-d, The hole density nh in the WSe2 layer (a), the electron density ne in the MoSe2 layer (b), the electron density in the graphite top gate nt (c), and the hole density in the graphite bottom gate nb (d), as functions of VG and VB. The densities are calculated based on a simple capacitor model that accounts for the geometric capacitances and the type-II band gap (1.5 eV, assumed to be symmetric with respect to the graphite Fermi level). Parameters used in the model: hBN out-of-plane dielectric constant 3.5, top and bottom hBN thicknesses 7 nm, interlayer distance 2.7 nm, antisymmetric gating VBG−VTG = 7 V. e-f, Calculated densities in the TMD layers (e) and the graphite gates (f) as a function of VB along the net charge neutrality. Solid lines trace integer LL fillings in the magnetic field. The densities in the gates are always about 10 times higher than that in the TMD layers, and depend on VB very weakly. Therefore, QOs in the gates would happen at a dramatically higher frequency along the B axis and cannot explain the experimental data.
Extended Data Fig. 8 Temperature dependence of QOs (device D3).
a, Temperature dependence of WSe2 Rxx when only holes are present, keeping MoSe2 layer intrinsic. The oscillation amplitude smoothly decreases with increasing temperature, consistent with typical metallic systems in the QH regime. b, Oscillatory part of longitudinal resistance ΔRxx as a function of temperature, at hole density nh = 1.9 × 1012 cm−2 (black arrow in a). It can be described well by the LK formula (right axis). c, Temperature dependence of Rxx along the CNL. d, ΔRxx as a function of temperature, at electron and hole density ne = nh = 1.9 × 1012 cm−2 (black arrow in c). For T > 2 K, the temperature dependence can be well captured by the LK formula. In the EI phase below 2 K, the resistance oscillation deviates significantly from the LK formula, which is dominated by thermally activated unpaired charge.
Extended Data Fig. 9 Circuit diagram for the transport measurements.
a, Circuit diagram for two-terminal Rh measurement. b, Circuit diagram for the closed-circuit Coulomb drag measurement.
Extended Data Fig. 10 Interlayer tunneling current.
a, Interlayer tunneling current as a function of VG and VB at B = 0. The tunneling current is barely above the picoampere noise level. b, A linecut of tunneling current along net charge neutrality ne = nh as a function of VB. The experimental data (open circles) is fitted to a linear line to estimate the interlayer tunneling resistance, giving a lower bound of 40 GΩ.
Supplementary information
Source Data Fig. 1
Source data for Fig. 1.
Source Data Fig. 2
Source data for Fig. 2.
Source Data Fig. 3
Source data for Fig. 3.
Source Data Fig. 4
Source data for Fig. 4.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Qi, R., Li, Q., Zhang, Z. et al. Competition between excitonic insulators and quantum Hall states in correlated electron–hole bilayers. Nat. Mater. (2025). https://doi.org/10.1038/s41563-025-02316-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41563-025-02316-5