Precision spectroscopy of the hyperfine components of the 1S–2S transition in antihydrogen

Abstract

The antimatter equivalent of atomic hydrogen—antihydrogen—is an outstanding testbed for precision studies of matter–antimatter symmetry. Here we report on the simultaneous observation of both accessible hyperfine components of the 1S–2S transition in trapped antihydrogen. We determine the 2S hyperfine splitting in antihydrogen and—by comparing our results with those obtained in hydrogen—constrain the charge–parity–time-reversal symmetry-violating coefficients in the standard model extension framework. Our experimental protocol allows the characterization of the relevant spectral lines in 1 day, representing a 70-fold improvement in the data-taking rate. We show that the spectroscopy is applicable to laser-cooled antihydrogen with important implications for future tests of fundamental symmetries.

Main

More than nine decades after Dirac’s theory foreshadowed the discovery of the positron¹, the fate of antimatter in the Early Universe or the reason for its apparent absence today is still unknown. Antihydrogen remains the only anti-atom that has been synthesized and studied in the laboratory, and it offers a unique opportunity for elegant tests of matter–antimatter symmetry. In recent years, the techniques necessary to trap and spectroscopically probe antihydrogen have been demonstrated at CERN^{2,3,4,5,6,7,8}. Today, more than 1,000 antihydrogen atoms can be accumulated in a few hours for study in the magnetic gradient trap of the ALPHA apparatus. The recent advent of ballistic studies of antihydrogen under the effect of Earth’s gravity enables tests of the weak equivalence principle⁹. The frequency of the 1S–2S transition in antihydrogen, which has a natural linewidth of 1.3 Hz in hydrogen, has been determined for the d–d hyperfine component (Fig. 1c) with a precision of two parts per trillion⁶. The c–c hyperfine component of the 1S–2S manifold offers a theoretical gain of up to 20,000 in sensitivity in models that allow charge–parity–time-reversal symmetry (CPT) violation¹⁰ compared with the d–d component. In hydrogen, the resonant frequency of the d–d component has been measured¹¹ together with the b–b component with an extremely high precision of a few parts in 10¹⁵. However, to date, there have been no published, precise direct measurements on the c–c component in either hydrogen or antihydrogen, to the best of our knowledge. In the absence of hypothetical violations of CPT or Lorentz symmetry, the shifts in the resonant frequencies of all the hyperfine components due to a magnetic field are well known to follow the Breit–Rabi formula, and at zero field, the b–b, c–c and d–d component frequencies coincide exactly. In this scenario, together with the well-known magnetic-field behaviour, the frequency of the c–c component in hydrogen can be estimated with the same precision as the centroid¹¹. However, in the standard model extension (SME), the components can experience different shifts¹² due to hypothetical symmetry violations in a manner that may also depend on B. Here we show that the resonance frequency of the c–c component in antihydrogen can be determined with the same precision as the d–d component. From a single uncooled sample of trapped antihydrogen containing 1,673 ± 49 atoms, accumulated¹³ over an 11.5 h period, we simultaneously extract the measured resonant frequencies from both hyperfine transitions available in our experiment, yielding a measurement of the d–d component, too. In combination with our previous measurement of the 1S hyperfine splitting⁵, the resonant frequencies yield the 2S hyperfine splitting. By comparing frequency measurements in hydrogen and antihydrogen, CPT-violating couplings in the SME framework can be constrained. Here we provide a constraint on the coupling ${\mathring{a}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{a}}}_{2,{\rm{p}}}^{{\rm{NR}}}$ in the electron and proton sectors of the SME. The current result was made possible by advances in the accumulation of antihydrogen atoms¹³ and a dedicated protocol for 1S–2S spectroscopy, allowing us to characterize a complete spectral lineshape in a single day. Taken together with the recently demonstrated laser cooling of antihydrogen¹⁴, our results represent a paradigm shift in the ability to study these transitions, promising rapid progress towards matter-like precision in antimatter spectroscopy. We present in detail how the spectroscopic signal arises and discuss systematic effects relevant both to this study and to spectroscopy with laser-cooled antihydrogen.

Fig. 1: The ALPHA-2 experiment, magnetic-field profile and level diagram of antihydrogen.

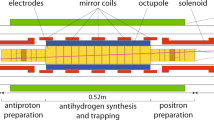
a, The ALPHA-2 central apparatus (adapted from another work¹⁴). The Penning–Malmberg trap electrodes with the superconducting octupole and mirror magnet coils, which form the magnetic minimum trap, are shown to scale. The solenoids at either end boost the field in the preparation traps to 3 T for a more efficient cyclotron cooling of leptons. For this work, they are actively stabilized and kept on continuously, which increases our efficiency in antihydrogen accumulation and reduces magnetic-field drifts during spectroscopy. A cryogenic optical cavity serves to both build up the 243 nm laser light needed to drive the 1S–2S transitions and to provide the counterpropagating photons that cancel the first-order Doppler shift. Blocking potentials applied to the brown-shaded electrodes prevent antiprotons, created by ionizing antihydrogen, from escaping axially. Pulsed laser light at 121.6 nm for laser cooling is produced in a Kr/Ar third-harmonic generation (THG) gas cell immediately outside the ultrahigh-vacuum chamber. The light enters the chamber via a MgF₂ window and travels straight through the atom trap to be detected on the far side using a photomultiplier tube (PMT). The cylindrical silicon vertex detector (SVD) for annihilations (shown in green) surrounds the trapping apparatus. b, Profile of magnetic (B) field on the trap axis. The five mirror coils combine to make the field on axis uniform within ±1.5 Gauss in the centremost 6 cm of the trap (shaded). c, Hydrogen energy levels. Level diagram showing relevant states (S states in black and P states in blue) in the manifolds of the first two principal quantum numbers, n = 1 and n = 2, at B = 0 T and B = 1 T (not to scale). States 1S_a and 1S_b are untrappable and transitions from these states are, therefore, not accessible in our experiment. The pink arrows indicate the optical transitions driven from the trappable states. The two-photon transitions are 1S_d–2S_d and 1S_c–2S_c. The purple arrow identifies the single-photon cooling transition of 1S_d–2P_a.

Antihydrogen must be synthesized before it can be trapped and studied. The techniques for doing so have been described elsewhere¹³. In brief, a cold plasma of about 3 million positrons is mixed with around 100,000 antiprotons in a Penning–Malmberg trap to create antihydrogen. In a single such mixing cycle, an estimated average of 50,000 antihydrogen atoms are created, about 20 of which remain confined in the superconducting magnetic trap. The trap, formed by an octupole winding in the radial direction and five coaxial mirror coils that combine to tailor the axial well (Fig. 1a,b), has a well depth of about 50 µeV (corresponding to a maximum speed of about 90 ms⁻¹). Crucially, antihydrogen atoms produced in many such mixing cycles, each requiring about 4 min to complete, can be accumulated, reaching—in several hours—the populations of trapped atoms that we subject to laser spectroscopy in this work.

In three experimental runs, we accumulated three separate samples of antihydrogen atoms. Each sample had roughly equal populations in trappable 1S_c and 1S_d states. We then subjected each sample to Doppler-free, two-photon spectroscopy of the two available hyperfine 1S–2S lines (Fig. 1c), either with or without a preceding laser-cooling¹⁴ step. The spectroscopy consists of multiple short (1 s or 2 s) exposures of 243 nm light (Methods) at predefined, discrete frequencies, resulting in two-photon excitation to a trappable hyperfine 2S state. As in our previous work^4,6, the spectroscopy is based on the resonant loss of anti-atoms. The resonantly excited anti-atoms are ejected from the trap either due to third-photon ionization or because of decay to an untrappable state via spin flips, and their subsequent annihilation is detected (Methods). Short exposures and a small number of frequencies are essential to avoid the distortion of the recorded lineshape arising from the excessive depletion of the trapped sample during single exposures. For each sample of antihydrogen, we chose a set of nine frequency detunings around the expected line centre. We then cycled through them and assigned annihilations to the relevant frequency (Methods), first in ascending order and then in descending order, constituting one ‘double sweep’ over a spectral line. In runs 1 and 2, we alternated targeting each component with every double sweep, resulting in an essentially simultaneous recording of both lineshapes from a single sample of antihydrogen, whereas in run 3, only the d–d transition was probed. Each transition was probed with a total of 200 s laser exposure per frequency detuning, leading to an overall exposure of 1,800 s. In runs 2 and 3, laser cooling was applied before 1S–2S spectroscopy. The d–d component data from runs 1 and 3 have been discussed previously¹⁴ without extracting the resonant frequency, which is reported here for atoms that were not laser cooled. The experimental parameters are listed in Table 1.

Table 1 Experimental parameters for the three runs

Laser cooling is achieved by driving the closed transition from the ground state to the maximally polarized 2P_a state with pulsed, 121.6 nm light¹⁴ (Methods). The cooling transition has two hyperfine components (not distinguished in Fig. 1c) sufficiently far apart in frequency that only one of them can be efficiently used for cooling with one laser. For these runs, the cooling laser frequency was detuned to –220 MHz from the calculated resonance (Methods) to selectively cool the atoms in the 1S_d state only. To maximize the atom interaction with the cooling laser, we use the ‘stack and cool procedure’¹⁴. The atoms are irradiated from the beginning of the antihydrogen accumulation phase, which lasts between 9 and 12 h (Table 1). We continue applying the cooling laser for another 6 h after accumulation ends, before turning it off and starting the 1S–2S spectroscopy.

Figure 2 shows the 1S–2S spectra obtained from runs 1 and 2. In the cooled sample (run 2), the d–d transition linewidth (full-width at half-maximum) narrows substantially compared with the uncooled sample (run 1), whereas the c–c transition remains unchanged. This is expected since the cooling laser is much further detuned from resonance with atoms in the 1S_c state (about –890 MHz), which suppresses the interaction. The observed narrowing in the cooled population stems mainly from a reduction in the transit-time broadening, which is proportional to the speed of the atoms perpendicular to the laser beam and dominates the spectral width in our trapped samples.

Fig. 2: Antihydrogen spectra.

Measured spectra recorded in run 1 (hollow circles) and run 2 (hollow squares) showing both d–d and c–c transitions (note the discontinuous x axis). The frequency-independent background has been subtracted, and both spectra in each run have been normalized to the fitted height of the c–c line in that run. Therefore, the relative heights of the d–d and c–c lines within a run are conserved. The solid lines show the fits using the lineshape function guided by simulation (Methods). The fit shown with a dashed line (run 2, d–d) is not well constrained due to the sparse sampling in the peak region. The peak of this fit extends beyond the displayed vertical range and reaches a maximum value of 3.5 on this scale. The plotted uncertainties are one-standard-deviation counting errors.

To determine the resonance frequencies of both c–c and d–d transitions, we fit each of the uncooled spectra (both transitions in run 1 and the c–c spectrum in run 2) with fixed shape functions determined from detailed simulations of the experiment using known hydrogen physics (Methods and Extended Data Fig. 1). The only parameters to be fit to the data are the amplitude of each line, a constant background parameter and a frequency offset of each line from its respective simulated hydrogen line. From the fits, we extract the transition frequencies at our measured central magnetic field, and list them in Table 2. With recent improvements in our magnetometry through the technique of electron cyclotron resonance¹⁵, we determine the central magnetic field in our trap during the spectroscopy phase to within about seven parts per million (Methods). The result for the d–d transition frequency is in good agreement with the corresponding frequency in ordinary hydrogen adjusted to our magnetic field, and with our previous result, which was obtained from many separate samples⁶. The agreement with our previous result adds confidence that our conclusions are independent of protocol. Both c–c spectra yield good agreement with frequencies based on the hydrogen centroid adjusted to the magnetic fields in our experiment, and the offsets from hydrogen are also in mutual agreement. In Table 3, we detail the error budgets for each of the extracted transition frequencies. The combined uncertainty of the d–d transition frequency of 5.8 kHz is comparable with the 5.4 kHz uncertainty in our previous result, which was based on 10 weeks of data taking. The current measurement, by contrast, required only 1 day.

Table 2 Fit results for 1S–2S spectra

Table 3 Summary of statistical and systematic uncertainties

Assuming that the magnetic-field dependence of the S states in antihydrogen is the same as in ordinary hydrogen, we can combine the present c–c and d–d frequency measurements with the previously measured 1S hyperfine splitting in antihydrogen⁵, to extract the hyperfine splitting of the 2S state (Methods). For this analysis, we use the spectra from run 1, where both transitions are measured at the same magnetic field. The resulting 2S hyperfine splitting is 177.6(0.5) MHz, in good agreement with the more precisely measured hydrogen value of 177.55683887(85) MHz (ref. ¹⁶). The contribution to uncertainty in the antihydrogen 2S hyperfine splitting from the measurement of c–c and d–d lines presented here is only about 0.018 MHz. Thus, the uncertainty is dominated by the uncertainty in the 1S hyperfine splitting, which can be markedly improved with further work.

The narrower lineshape of the d–d component in run 2 (Fig. 2) is consistent with only cooling 1S_d-state atoms as expected, since the cooling laser is not resonant with transitions from the 1S_c state. Under this premise, the unchanged lineshape for the c–c transition qualitatively adds confidence that the narrowing is due to laser cooling. However, the frequency detunings of the 243 nm laser were chosen too sparsely to capture the resonant feature in full. For run 3, we adapted the frequency detunings to the narrower width and limited the spectroscopy to the d–d line. The resulting data were previously presented as additional evidence of laser cooling of antihydrogen¹⁴. Here we provide further details relevant to the analysis of both cooled and uncooled samples. If the trapped sample is cooled, the spectroscopy laser causes a faster depletion of the trapped population (Methods), which is evident in the time evolution of annihilation data during laser exposures (Fig. 3). In run 2, where both transitions are simultaneously probed after laser cooling was applied, probing the d–d transition causes substantially faster depletion than that observed for the c–c transition. This is expected since laser cooling acts nearly exclusively on the atoms in the 1S_d state, whereas other factors that affect the depletion rate such as spectroscopy laser power and background gas annihilation are equal. The depletion rate is sufficiently fast for the cooled population that we expect a significant distortion of the recorded lineshapes originating from those atoms. This possible distortion together with the modelling uncertainty arising from the energy distribution¹³ prevent us from using the spectra arising from the coldest samples for extracting transition frequencies. For future measurements, the effect from depletion can be practically avoided by reducing the power of the spectroscopy laser, thereby simultaneously reducing other systematic effects related to the laser power. It will also be beneficial to lower the background magnetic field of the atom trap, both to reduce systematic effects from the high field and to eventually extrapolate the measured transition frequencies to their zero-field values.

Fig. 3: Annihilation rates.

Temporal evolution of the annihilation rates during each of the laser exposures, normalized to the fitted rate during the first bin, with the fits drawn as solid or dot–dashed lines. The bin width corresponds to a full double sweep over the spectral line for runs 1 and 2. For run 3, the same bin width is achieved with two double sweeps, since the exposures are half as long. It can be seen that the depletion rate for the laser-cooled d–d transition in runs 2 and 3 (filled square symbols) is much higher than the uncooled transitions. The inset shows the d–d component spectra of runs 1 and 3 (ref. ¹⁴), which are included for self-consistency. The fits and data are normalized so that the fits have a peak value of 1. The plotted uncertainties represent one-standard-deviation counting errors.

In a local quantum field theory, the CPT theorem^17,18,19,20 states that Lorentz invariance implies invariance under CPT transformations. In turn, CPT invariance implies that the spectra of antihydrogen and hydrogen are identical. The extremely high precision afforded by atomic spectroscopy makes a direct comparison of the antihydrogen spectrum with hydrogen—a compelling test of Lorentz and CPT symmetries.

A natural theoretical framework to analyse potential violations of Lorentz and CPT symmetries is the SME, introduced elsewhere¹² and extensively developed since. This may be viewed as an effective field theory, in which the effect of unknown high-energy physics is described at low energies by adding Lorentz and CPT non-invariant operators to the standard model Lagrangian, with couplings corresponding to the dimension and tensor character of the operators. In this framework, higher-dimensional operators are expected to be suppressed by powers of the ratio of momenta characteristic of the low-energy experiment to the high-energy scale of new physics. Here we analyse our results in terms of the minimal SME (that is, restricting to operators with dimensions ≤4), augmented by the dimension-five operator ${a}_{\mu \nu \lambda }^{\left(5\right)}\bar{\psi }{\gamma }^{\mu }{\partial }^{\nu }{\partial }^{\lambda }\psi$, which gives the leading spin-independent CPT-odd contribution to the 1S–2S transitions. Couplings of this type also, in principle, provide a mechanism for leptogenesis in the Early Universe, with CPT violation allowing lepton asymmetry to be generated in thermal equilibrium^21,22.

The SME has two important advantages for our work. First, it provides a standard parameterization of Lorentz and CPT violations, allowing the results of different experimental searches to be expressed in terms of bounds on a common set of relevant couplings. These are conventionally referred to a standard Sun-centred frame, with components labelled T, X, Y and Z (refs. ^23,24,25). We note that in this frame, the Z axis is parallel with the Earth’s axis of rotation (Supplementary Information). In the laboratory frame, the axis with index 3 is defined as aligned with the magnetic field. Second, the SME explicitly shows how Lorentz and CPT violations may arise in different ways in different experiments, for example, appearing in some transitions in the antihydrogen/hydrogen spectrum but not others, thereby motivating a comprehensive programme of antihydrogen spectroscopy. We stress, however, that CPT violation could still arise in ways that are not captured by the SME, and the direct comparison of the antihydrogen spectrum with hydrogen remains a strong model-independent test.

A direct comparison of our measured antihydrogen 1S–2S transition frequencies with hydrogen is complicated in the SME analysis because our experiment cannot yet trap hydrogen. This is due to additional technical challenges such as formation at low energy and detection of small samples of hydrogen, which—unlike antihydrogen—does not produce an annihilation signal. We, therefore, rely on comparison with hydrogen data taken in experiments^11,26,27,28 in a different laboratory at different times and with different magnetic fields. Since, by definition, the SME couplings are not Lorentz scalars, comparisons of antihydrogen and hydrogen in different reference frames requires the consideration of Lorentz boosts due to the Earth’s rotation and orbital motion around the Sun. These would produce sidereal and annual variations in the transition frequencies (though suppressed by factors of O(10^–6) and O(10^–4), which are the ratios of the respective velocities to the speed of light). Rotations, however, only affect the spin-dependent SME couplings. In particular, the SME framework clearly shows how a difference in the spectra of antihydrogen and hydrogen taken in different frames (for example, different laboratories) would not necessarily be a signal of CPT violation but could instead be due to a Lorentz violation in a CPT-symmetric theory. This emphasizes the importance of explicitly testing Lorentz symmetry through searches for sidereal and annual variations in the transition frequencies.

The different magnetic fields are accommodated by using the Breit–Rabi formula²⁹ to adjust the measured frequencies to compensate for the Paschen–Back effects on the appropriate hyperfine states (Methods). However, the published hydrogen measurements^11,26,27,28 are optimized to determine the 1S–2S centroid frequency with the highest possible precision, and the results are quoted for combinations of transitions, specifically 1S_d–2S_d and 1S_b–2S_b at zero or small magnetic field, which are insensitive to the spin-dependent SME couplings. This means that we cannot isolate the CPT-odd spin-dependent couplings by comparing our antihydrogen results with currently published hydrogen data, although this is possible for the spin-independent couplings, particularly the ${a}_{\mu \nu \lambda }^{\left(5\right)}$ tensor coupling.

Comparing our 1S_d–2S_d transition frequency with the 1S–2S hydrogen centroid frequency¹¹ determines the CPT-odd, dimension-five isotropic couplings as ${\mathring{a}}_{2,w}^{{\rm{NR}}}={a}_{{{\rm{TTT}}},w}^{(5)}$ + ${a}_{{{\rm{TKK}}},w}^{(5)}$, where the suffix w = e and p specifies the positron and antiproton, respectively. For this important SME coupling (Methods), we find ${\mathring{a}}_{2,{\rm{e}}}^{{\rm{NR}}}+{\mathring{a}}_{2,{\rm{p}}}^{{\rm{NR}}}$ = (0.4 ± 1.2) × 10^–9 GeV^–1.

The result is derived under the assumption (justified a posteriori) that the spin-dependent couplings ${\widetilde{g}}_{{{\rm{DZ}}}}$ and ${\widetilde{d}}_{\rm{Z}}$ contributing to the 1S_d–2S_d transition are relatively small. Including the CPT-odd ${\widetilde{g}}_{\rm{DZ}}$ (but neglecting the CPT-even ${\widetilde{d}}_{\rm{Z}}$ for which astrophysical bounds constrain ${|\widetilde{d}}_{\rm{Z}}|$ < 10^–19 GeV (ref. ²³)), our 1S_d–2S_d comparison imposes the bounds ${|\widetilde{g}}_{{\rm{DZ}},{\rm{e}}}|$ < 2.0 × 10^–15 GeV and ${|\widetilde{g}}_{{\rm{DZ}},{\rm{p}}}|$ < 6.6 × 10^–9 GeV. These are already within two orders of magnitude of the corresponding results of ${|\widetilde{b}^{\prime} }_{{\rm{Z}},{\rm{e}}}|$ < 1.7 × 10^–17 GeV and ${|\widetilde{b}^{\prime} }_{{\rm{Z}},{\rm{p}}}|$ < 1.2 × 10^–10 GeV inferred from high-precision Penning trap experiments on antiprotons^30,31,32. Note that restricted to the minimal SME, ${\widetilde{b}^{\prime} }_{Z}\equiv -{\widetilde{g}}_{\rm{DZ}}$. Further improvements towards hydrogen precision put these bounds within reach of antihydrogen spectroscopy.

A special feature of the 1S_c–2S_c transition in the SME is the occurrence¹⁰, due to the magnetic-field-dependent mixing of the spin states, of a contribution to the transition frequency at O(1) in the fine-structure constant, unlike the 1S_d–2S_d transition, which is O(α²). The difference in the 1S_c–2S_c and 1S_d–2S_d transition frequencies depends only on the spin-dependent couplings. In addition to giving bounds on ${\widetilde{g}}_{\rm{DZ}}$ and ${\widetilde{d}}_{\rm{Z}}$ as above, our result determines the dimension-three coupling ${\widetilde{b}}_{\rm{Z}}^{* }$, which appears at O(1). In laboratory coordinates, we find ${\widetilde{b}}_{3,{\rm{e}}}^{* }-{\widetilde{b}}_{3,{\rm{p}}}^{* }$ = (–1.2 ± 3.0) × 10^–17 GeV. This bound could be improved by lowering the magnetic field, which would lift the O(10^–3) suppression arising from the field-dependent mixing-angle prefactor in the 1S_c–2S_c transition frequency. Maximum sensitivity occurs at a central magnetic field of approximately 10 mT, which is experimentally accessible but requires further magnetometry development before precision measurements become feasible. This particular coupling is, however, extremely constrained by existing Penning trap experiments^33,34,35,36, with the SME data tables quoting $|{\widetilde{b}}_{{\rm{Z}},{\rm{e}}}^{* }|$ ≤ 7 × 10^–24 GeV and $|{\widetilde{b}}_{{\rm{Z}},{\rm{p}}}^{* }|$ ≤ 1.5 × 10^–24 GeV.

This work demonstrates that it is now, in principle, possible to interrogate trapped antihydrogen atoms with lower velocities than those in the sample of hydrogen used in the current best measurements for matter¹¹. The ability, demonstrated here, to characterize a spectral line in antihydrogen in a single day will also allow an unprecedented understanding and control of systematic effects in our measurements, as well as the opportunity to search for annual or even daily variations. In combination with ballistic studies under gravity, the ALPHA experiment will allow addressing fundamental symmetry from a holistic perspective, with the tantalizing prospect of distinguishing between the origin of putative effects that would render antimatter different from matter. For example, should antihydrogen behave differently from hydrogen in a future free-fall test with high precision, it can also be investigated if a redshift occurs in the 1S–2S spectrum. The current precision is already sufficient to investigate annual variations in the gravitational potential of the Sun^22,37. Rapid excitation to the 2S state in a large sample of trapped antihydrogen as demonstrated here also opens the door to probing transitions from the 2S state to other excited states. This would—in combination with the 1S–2S results—allow for a measurement of the antiproton charge radius. Our analysis shows that to extract spin-dependent coefficients in the SME framework from the hydrogen–antihydrogen system, a measurement on the c–c component in a magnetic field (even if small) is needed for hydrogen. Our analysis illustrates that, ideally, CPT tests within the SME framework with hydrogen and antihydrogen should be carried out in the same reference frame.

Methods

Laser cooling

Linearly polarized, narrow-linewidth 121.6 nm pulses at 10 Hz repetition rate are generated from the third-harmonic generation of 365 nm pulses in a Kr/Ar high-pressure gas mixture. The 365 nm pulses are produced by frequency doubling 730 nm light from a titanium/sapphire-based pulsed amplifier in a beta barium borate crystal. Up to 8 nJ of 121.6 nm light in a roughly 15-ns-long pulse is detected right after the gas cell, and up to 2.3 nJ is transported into the trap containing the antihydrogen atoms. The frequency detuning from the calculated 1S_d–2P_a line centre of –220 MHz was kept constant. More details about the laser system and the cooling process can be found elsewhere¹⁴.

Annihilation event identification and background suppression

Hit positions of charged secondary products of antiproton annihilation are recorded by a three-layer silicon vertex detector surrounding the trap region³⁸ (Fig. 1). Tracks and track vertices are reconstructed from these hits and associated with their contemporary laser frequency during the spectroscopy phase. Annihilations are distinguished from cosmic ray background events with machine learning. Using the selection variables described in another work⁷, a boosted decision tree classifier was trained using the Toolkit for Multivariate Analysis³⁹ on annihilation events, and 1,018,981 background events from the time period in and around data taking. The machine learning classifier was optimized for an expected signal-to-background ratio, based on the known background rates (measured with no antiprotons present) and estimates of the trapped-atom populations. Thus, the optimization is blind to the real data sample.

243 nm laser system

The laser system has been described in detail previously^4,6, but to briefly summarize, 100 mW of 243 nm light is generated by frequency doubling a 972 nm master laser twice. The master laser is locked to an ultrastable reference cavity, which reduces the short-term (1 s) linewidth to 1 Hz. The linewidth of the master oscillator is continuously monitored by measuring the beat note against an identical system. A frequency comb, referenced to a Symmetricom Cs4000 caesium frequency standard and cross-referenced against a K+K Messtechnik GPS-disciplined quartz oscillator, provides an accuracy of 250 Hz (1 kHz at 243 nm) over a gated averaging period of 1,000 s, which is the turnover point of the Allan deviation of the stabilized laser frequency as observed with the frequency comb. The 243 nm light travels along a stabilized 7 m path to the enhancement cavity, which builds up more than 1 W of circulating power. A Thorlabs PDA25K2 photodiode is used to monitor the laser power exiting the cavity.

The laser control system allows the precise execution of many short sequential exposures of the trapped atoms. For each exposure, the controller verifies that the laser linewidth is below 10 Hz before actuating a shutter to allow the trapped atoms to be irradiated for a set amount of time. The control system sends a set of markers to the data acquisition system so that annihilation events during the exposure time can be distinguished. The timing jitter from the shutter opening and closing and the enhancement cavity locking is small compared with the exposure times of 1–2 s (around 1%). Changing between frequency detunings around one transition requires <1 s, whereas ramping the laser frequency between the c–c and d–d transitions requires around 10 s.

The frequency detunings shown in Fig. 2 differ from the nominal detunings listed in Table 1 due to a nonlinear drift in the reference cavity that was not corrected by the laser frequency control system. The reported frequency detunings are based on the reference cavity frequency measured with the frequency comb during the relevant laser exposures.

Simulations of laser interactions with trapped atoms

The simulations are mostly the same as in previous reports^4,6. The atoms follow classical trajectories in the trap with the position-dependent force calculated from the magnetic dipole moment and the spatial dependence of the magnetic field. The magnetic field is calculated on a spatial grid from a Biot–Savart approximation of the octupole and mirror coils and interpolated to the position of the simulated atom. The main departure from our previous work is in the initial conditions of the simulated atoms. The atoms are launched in a high Rydberg state from a spatial region estimated to be that of the positron plasma. The lifetime and magnetic moment of the excited state are from known atomic properties. After reaching the ground state, we simulate laser cooling using a stochastic treatment of Doppler cooling. During each Lyman-α laser pulse, we compute the probability for photon absorption using the laser intensity and detuning at the position of the atom. The detuning is position dependent due to the position dependence of the magnetic-field strength. If a photon is absorbed, the atom is given a momentum kick of h/λ in the laser propagation direction. A photon is then emitted in a random direction given by the transition matrix elements and the atom is given a momentum kick opposite to the photon emission direction. The atoms that survive the cooling process are then used as the initial conditions for the simulation of the 1S–2S transition. The simulation of the 1S–2S transition mimics the method used in the experiment including the laser intensity, waist and angle and how the frequency of the laser is changed in steps (see the main text). The 1S–2S transition probability is calculated using an optical Bloch equation for each time the atom passes near the 243 nm beam and includes the detuning from the magnetic field and the a.c. Stark shift. By solving the optical Bloch equation, the transition broadening is automatically included. If the atom is excited, there is a probability that it will decay back to a trapped 1S state; in this case, the simulation continues. There are two main processes that lead to a loss of atoms and hence the detection of the transition to the 2S state: spin flip during decay to an untrappable 1S state or ionization by the 243 nm laser. The evolution of the 2S state is followed using time-dependent rate equations that govern each process. The time and position of the spin flip or ionization event is recorded.

Comparison of simulated and measured spectra

To extract the transition frequencies from the recorded spectra, we build a fit function with a fixed shape, based on our simulations of the experiment with hydrogen physics. This function is used to fit the data and search for a difference in the centre frequency. In our previous work, an independent sample of antihydrogen atoms was exposed at each laser frequency⁶, and we meticulously ensured that the samples contained a similar number of atoms to avoid systematic shifts in the line centre. This method inherently causes a broadening of the line, stemming from the unequal depletion of the samples exposed at different laser frequencies. This depletion broadening causes the linewidth to grow with laser power, but is essentially absent from our reported technique, since the rapid cycling through frequencies on the same sample ensures that the population of remaining atoms—integrated over the exposure time—is nearly identical for all the applied laser frequencies. The choice of how rapidly to cycle through frequencies for this measurement was based on simulations of the experiment and practical limitations in the laser control system. Due to the elimination of depletion broadening, compared with our previous work, our current data are much less sensitive to the laser power, which mainly affects the shape only through the a.c. Stark shift. Removing one of the broadening mechanisms also changes the expected lineshape, bringing it closer to the theoretical result for transit-time-dominated thermal atoms in a box, which is a double-exponential shape⁴⁰. Some discrepancy with this theoretical shape remains since the velocity distribution of our trapped atoms is not thermal (with no laser cooling, our trapped distribution is consistent with a high-temperature thermal distribution, truncated at the trap depth of about 0.5 K (ref. ⁴¹)). Furthermore, because we have a finite a.c. Stark shift, the cusp of the double exponential is somewhat smoothed out. In addition, the atoms can interact with the laser at a range of magnetic fields that are higher than in the trap centre. This causes an asymmetric shape with an extended blue tail. To accommodate this, we fit the simulated lineshapes with an asymmetric double-exponential shape, allowing the exponential decay factors on either side of the peak to vary independently. At some point on the extended blue tail, also determined by the fit, we smoothly transition the exponential into a power function, which better accommodates the tail. To smooth out the infinitely sharp peak of the double exponential, we take the convolution of the double exponential with a Gaussian function, which approximates the simulated lineshapes well, and adding only one fit parameter (Gaussian width, σ) describing the length over which the peak is smoothed and retaining the double-exponential shape in the σ→0 limit. An example fit to a simulated spectrum is shown in Extended Data Fig. 1. The fit to the simulation is used to fix the shape of the above lineshape function, thereby defining the fixed shape function used to fit the data and determine the transition frequencies. The shape parameters that are fixed by the simulation are as follows: one exponential decay factor for each side of the peak, σ and the transition point on the blue tail at which the exponential is substituted for a power function.

Our frequency analysis depends, to some extent, on having correctly modelled the magnetic trap, trapping and excitation dynamics, as well as all other physics that goes into the simulations. The size of the simulation-dependent correction is roughly 7 kHz (at 121.6 nm) for our experimental parameters, and the systematic error we associate with making this correction is 2.5 kHz (Table 3, the ‘modelling errors’ row). An independent analysis was also performed, in which the background values were determined from the counts during the periods with no laser light in the trap and using independent fitting codes. The results and uncertainties were consistent with those presented in Table 2.

Time evolution of annihilations during the laser scan

The rate at which antihydrogen atoms are removed from the magnetic trap by the spectroscopy laser depends—among other factors—on the laser power and the velocity distribution of the trapped anti-atoms. The decrease in velocity from laser cooling leads to an increase in the depletion rate both through an increase in the density of atoms overlapping with the laser and through the decrease in transit-time broadening, amplifying the on-resonance rate. In the two cases in which laser cooling has been applied, the depletion is substantially faster. A depletion-reducing effect occurs for the cooled atoms because the nine frequency detunings overlap less with the narrower line, reducing the time in which transitions can be efficiently driven. However, the effect is evidently less important.

The accelerated depletion observed in our cooled samples causes additional distortion in the lineshape, which—although included in our simulations of the experiment—adds uncertainty to the determination of transition frequencies. Without the possibility to conduct additional systematic measurements to validate our modelling of this effect, we decided to exclude these spectra from our frequency results, before unblinding ourselves to any of the fitted transition frequencies. For future measurements, the depletion rate can be reduced simply by shortening the length of the exposures to the spectroscopy laser at 243 nm or by reducing the power of that laser.

Association of annihilations to resonant excitation frequency

The coincidence of annihilation events with 1S–2S laser exposure at a given frequency detuning has been tested by examining the periods when the laser is shuttered during frequency changes, where a sharp drop in the annihilation rate is observed when the laser shutter closes. The cumulative event count resulting from a total of 32 exposures at frequency detunings of –12.5, 0, 12.5 and 25 kHz in the time window when the shutter is actuated is shown in Supplementary Fig. 1. We observe 97 annihilations during the cumulative 32 s that the shutter is open, whereas there are no annihilations in the cumulative 44.8 s that immediately follow when the shutter is closed. Thus, the rate in the dark period is reduced to less than 0.4% (the 1σ limit from the fit) of the shutter-open rate, and the drop occurs over a period of less than around 20 ms, which is commensurate with the shutter-closing time. It is further noted that the 243 nm laser control system monitors that the shutter has closed and waits a further 40 ms thereafter before changing the frequency detuning. This firmly establishes the association between the observed annihilation event counts and the excitation frequency.

A recent study using small electron plasmas has identified weak transverse electric fields, probably originating from patch potentials in the Penning–Malmberg trap⁴², rendering the potential confinement of the ionized antihydrogen (antiproton) in the inhomogeneous trapping fields unlikely.

Systematic uncertainties

The frequency reference and modelling errors are discussed in the sections above. We describe the remaining entries in Table 3 in order of appearance below.

Magnetic field

The magnetic field is determined by electron cyclotron resonance magnetometry, which has been described in detail elsewhere¹⁵. Briefly, a small target electron plasma (about 120,000 electrons of 0.1 mm radius) is extracted from a reservoir and moved axially along the Penning trap by carefully adjusting the axial electrostatic trap potential for a magnetic-field measurement in the desired location. The target plasma is then illuminated with microwave radiation of a frequency corresponding to the cyclotron resonance, which is fixed by the local magnetic-field magnitude. The resonance condition is determined by measuring plasma heating as a function of microwave frequency. The measured magnetic-field variations along the axis, which are below ±10^–4 T in the flat-field region (about ±30 mm axially around the centre; Fig. 1b), are consistent with a numerical calculation using a model of the combined magnetic field of the octupole and mirror magnets based on the spatially accurate knowledge of the conductor layout and the main uniform solenoidal magnetic field. The magnetic-field model is used in all the simulations of antihydrogen trajectories and interactions, with the 243 nm laser in this work yielding the central 1S–2S frequencies and takes the measured currents in the conductors of the trap magnets as the input. The propagation of the laser beam in the magnetic field is known from geometry and included in the simulations. The simulations produce a prediction of the 1S–2S signal as a function of detuning, which agrees in shape with the measured data of uncooled antihydrogen. This agreement gives further confidence that the field model is accurate at the level of precision required to extract the centre frequency of the c–c and d–d components. The 1S–2S transition is relatively insensitive to magnetic fields, with an illustrative example at 1 T of 19 kHz mT^–1 and 1 kHz mT^–1 for the c–c and d–d transitions, respectively. For illustrative purposes, equation (1) for c–c and the corresponding expression from ref. ⁶ for d–d yield a total shift from B = 0 of 605.2 kHz and 604.9 MHz for the respective components in run 1. The contribution from the uncertainty of the magnetic field is given in Table 3. The diamagnetic correction term, which yields the largest magnetic shift, is programmed with about 2 ppm accuracy in the simulations, corresponding to shifts in the c–c and d–d components of 20 Hz and 3 Hz, respectively, over the entire trap depth of ~1 T. As described in the ‘Comparison of simulated and measured spectra’ section, we assign a modelling uncertainty in the central frequency of 2.5 kHz, which includes effects from having correctly modelled the trap. Thus, the main remaining uncertainty in the magnetic field relevant to extracting the central frequency of the 1S–2S transition components arises from the knowledge of the central magnetic field, which is subject to a drift due to the slowly decaying persistent current in the external solenoid. The magnetic field at the trap centre is measured both before and after every run to track the drift (roughly 80 μT per day). The electron cyclotron resonance magnetometry yields a precision of 7 ppm, and the corresponding frequency error is calculated using the formulae in ref. ²⁹. The magnetic field at the trap centre from the combined octupole, mirrors and external solenoid in the simulations is matched to the measured magnetic field independently of any measured antihydrogen spectra. The location of the centre is constrained by geometry and is insensitive to laser alignment at the level of precision required in this work (see below).

Mean laser power

Sensitivity to the mean laser cavity power is obtained from the difference in peak fits to simulations determining the shape parameters (see the ‘Comparison of simulated and measured spectra’ section above) for each power and peak fits to data with the corresponding shape parameters fixed. This method mimics the way in which the data analysis is performed but uses at least two orders of magnitude more statistics than the experimental data. The resulting sensitivities are 4.13 kHz W^–1, 4.76 kHz W^–1 and 5.05 kHz W^–1, respectively, on the frequency of transitions in run 1 (d–d), run 1 (c–c) and run 2 (c–c). An uncertainty of ±350 mW is assigned to the cavity power, consistent with the photodiode measurement of the power exiting the cavity as well as the simulated power matching the 1S excitation rate.

Motional d.c. Stark shift and frequency choice

The motional d.c. Stark shift is calculated from elsewhere²⁹. The frequency choice systematically reflects a dependence on the positions of the samples relative to the lineshape and becomes large when the sampling is sparse. It is calculated from the multioffset simulations (Extended Data Fig. 1).

We find no correlations between frequency detuning (in order of exposures in the experiment) and laser power. Uncertainties arising from cavity misalignment with respect to the magnetic trap have been investigated by fitting to simulated resonance features (as described above), but with the laser path rotated around the centre of the apparatus from the nominal axis (both angular and azimuthal rotations were investigated). We conclude that any sensitivity to path angle is firmly within the statistical noise in our measurement.

Comparison of spectral widths

For the comparison of spectral widths, we use the same functional shape as described above, but in this case, we need to fit all the parameters of the functions rather than fixing the shape before fitting the data. The fit to nine data points in a recorded spectrum has only a few degrees of freedom. Therefore, to compare with simulations, we fit the simulated spectra with the same number of data points. For the errors on the fitted widths, we evaluate two main error sources: a statistical error, which is evaluated through variation studies on the recorded spectra themselves, and a systematic error originating from the selection of probed frequencies, which we evaluate from the spread of many simulated spectra differing in this choice of probed frequencies.

Calculation of the 2S hyperfine splitting

For high magnetic fields, the separation between the two hyperfine components of the 1S–2S transition probed here tends towards half the difference in hyperfine splitting between the 1S and 2S states: f_c–c – f_d–d ≈ 1/2(HFS1S – HFS2S), where HFS1S and HFS2S denote the hyperfine splittings of the 1S and 2S states, respectively. At our finite field of roughly B = 1 T, we correct this expression by assuming the same magnetic-field dependence as in our calculation of the hydrogen frequencies. The expression for the field-adjusted frequency of hydrogen (H), ${f}_{{\text{d-d}}}^{\,{\rm{H}},{\rm{ADJ}}}$, is given elsewhere⁶. For the c–c transition, we have

$$\begin{array}{c}{f}_{{\text{c-c}}}^{\,{\rm{H}},{\rm{ADJ}}}\left(B\right)={f}_{1{\rm{S}}2{\rm{S}}}^{\,{\rm{H}}}+{f}_{{\text{c-c}}}^{\,{\rm{H}},{\rm{HFS}}}(B)\\ \begin{array}{c}={f}_{1{\rm{S}}2{\rm{S}}}^{\,{\rm{H}}}+\frac{1}{4}\left({\rm{HFS}}1{\rm{S}}-{\rm{HFS}}2{\rm{S}}\right)+{\left(\frac{{m}_{{\rm{e}}}}{\mu }\right)}^{3}\frac{13{e}^{2}{a}_{0}^{2}}{4{m}_{{\rm{e}}}h}{B}^{2}\\ +\frac{1}{2}\sqrt{4\frac{{B}^{2}}{{h}^{2}}{\left({\mu }_{{\rm{e}}}\left(2{\rm{S}}\right)+{\mu }_{{\rm{p}}}\left(2{\rm{S}}\right)\right)}^{2}+{\rm{HFS}}2{{\rm{S}}}^{2}}\\ -\frac{1}{2}\sqrt{4\frac{{B}^{2}}{{h}^{2}}{\left({\mu }_{{\rm{e}}}\left(1{\rm{S}}\right)+{\mu }_{{\rm{p}}}\left(1{\rm{S}}\right)\right)}^{2}+{\rm{HFS}}1{{\rm{S}}}^{2}},\end{array}\end{array}$$

(1)

where ${f}_{1{\rm{S}}2{\rm{S}}}^{\,{\rm{H}}}$ is the centroid-to-centroid frequency; h is Planck’s constant; m_e and µ are the electron mass and reduced electron mass, respectively; e is the elementary charge; a₀ is the Bohr radius; and µ_e and µ_p are the magnitudes of the magnetic moments of the positron and antiproton, respectively, which depend on the quantum state 1S or 2S, as described elsewhere⁶. We then expand the frequency difference in terms of the hyperfine splitting divided by magnetic energy and write the expression for the measured frequency difference in antihydrogen $(\bar{{\rm{H}}})$, noting that the diamagnetic term proportional to B² cancels perfectly.

$$\begin{array}{c}{f}_{{\text{c-c}}}^{\bar{\,{\rm{H}}}}-{f}_{{\text{d-d}}}^{\bar{\,{\rm{H}}}}=\frac{1}{2}\left(\text{HFS}1\text{S}-\text{HFS}2\text{S}\right)+\frac{2B}{h}\left({{\mu }_{{\rm{p}}}\left(2{\rm{S}}\right)-\mu }_{{\rm{p}}}\left(1{\rm{S}}\right)\right)\\ +\frac{{\text{HFS}2\text{S}}^{2}}{8\frac{B}{h}\left({\mu }_{{\rm{e}}}\left(2{\rm{S}}\right)+{\mu }_{{\rm{p}}}\left(2{\rm{S}}\right)\right)}-\frac{{\text{HFS}1\text{S}}^{2}}{8\frac{B}{h}\left({\mu }_{{\rm{e}}}\left(1{\rm{S}}\right)+{\mu }_{{\rm{p}}}\left(1{\rm{S}}\right)\right)}\\ -\frac{{\text{HFS}2\text{S}}^{4}}{128{\left(\frac{B}{h}\left({\mu }_{{\rm{e}}}\left(2{\rm{S}}\right)+{\mu }_{{\rm{p}}}\left(2{\rm{S}}\right)\right)\right)}^{3}}+\frac{{\text{HFS}1\text{S}}^{4}}{128{\left(\frac{B}{h}\left({\mu }_{{\rm{e}}}\left(1{\rm{S}}\right)+{\mu }_{{\rm{p}}}\left(1{\rm{S}}\right)\right)\right)}^{3}}+\ldots \end{array}$$

(2)

To extract HFS2S with the relevant precision, we include terms up to HFS2S⁶, where the last included term contributes roughly 10 Hz—a negligible contribution compared with the measurement error on ${f}_{{\text{c-c}}}^{\bar{\,{\rm{H}}}}-{f}_{{\text{d-d}}}^{\bar{\,{\rm{H}}}}$. We then find the roots of the resulting polynomial in HFS2S. For our result here, we use the transition frequencies measured in run 1, where both transitions are probed at the same field.

Constraining coefficients in the SME

The contributions to the 1S_d–2S_d and 1S_c–2S_c transition energies in antihydrogen from the SME couplings are^{10,23,43,44,45} (Supplementary Information)

$$\begin{array}{l}\Delta {E}_{2{{\rm{S}}}_{{\rm{d}}}\longleftrightarrow 1{{\rm{S}}}_{{\rm{d}}}}^{\bar{{\rm{H}}}}=\displaystyle\frac{1}{4}\frac{{\alpha }^{2}{\mu }^{2}}{{m}_{{\rm{e}}}^{2}}\left[3{m}_{{\rm{e}}}^{2}\left({{\mathring{c}}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{c}}}_{2,{\rm{p}}}^{{\rm{NR}}}+{{\mathring{a}}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{a}}}_{2,{\rm{p}}}^{{\rm{NR}}}\right)\right.\\\qquad\qquad\qquad\left.-\,\left({\widetilde{g}}_{{\rm{D}}3,{\rm{e}}}+\epsilon {\widetilde{g}}_{{\rm{D}}3,{\rm{p}}}+{\widetilde{d}}_{3,{\rm{e}}}+\epsilon {\widetilde{d}}_{3,{\rm{p}}}\right)\right]\end{array}$$

(3)

and

$$\begin{array}{l}{E}_{2{{\rm{S}}}_{{\rm{c}}}\longleftrightarrow 1{{\rm{S}}}_{{\rm{c}}}}^{\bar{{\rm{H}}}}=(\cos 2{\theta }_{2}-\cos 2{\theta }_{1})\left({\widetilde{b}}_{3,{\rm{e}}}^{* }-{\widetilde{b}}_{3,{\rm{p}}}^{* }\right)\\\qquad\qquad\quad+\,\frac{1}{4}\frac{{\alpha }^{2}{\mu }^{2}}{{m}_{{\rm{e}}}^{2}}\left[3{m}_{{\rm{e}}}^{2}\left({{\mathring{c}}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{c}}}_{2,{\rm{p}}}^{{\rm{NR}}}+{{\mathring{a}}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{a}}}_{2,{\rm{p}}}^{{\rm{NR}}}\right)\right.\\\qquad\qquad\quad\left.+\,\frac{1}{3}(\cos 2{\theta }_{2}-4\cos 2{\theta }_{1})\left({\widetilde{g}}_{{\rm{D}}3,{\rm{e}}}-\epsilon {\widetilde{g}}_{{\rm{D}}3,{\rm{p}}}+{\widetilde{d}}_{3,{\rm{e}}}-\epsilon {\widetilde{d}}_{3,{\rm{p}}}\right)\right],\end{array}$$

(4)

where $\epsilon ={m}_{{\rm{e}}}^{2}/{m}_{{\rm{p}}}^{2}$ and µ = m_em_p/(m_e + m_p). The magnetic-field-dependent factors, determined by the hyperfine Zeeman mixing angle defining the |c〉 states, are numerically (cos2θ₂ – cos2θ₁) = 0.0012 and $\frac{1}{3}(\cos 2{\theta }_{2}-4\cos 2{\theta }_{1})=-0.9984$ at the ALPHA magnetic field of B ≃ 1.0326 T. For hydrogen, existing measurements of the 1S–2S centroid frequency are insensitive to the spin-dependent SME couplings, leaving

$$\Delta {E}_{1{\rm{S}}2{\rm{S}}}^{{\rm{H}}}=\frac{3}{4}{\alpha }^{2}{\mu }^{2}\left({{\mathring{c}}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{c}}}_{2,{\rm{p}}}^{{\rm{NR}}}-{{\mathring{a}}}_{2,{\rm{e}}}^{{\rm{NR}}}-{{\mathring{a}}}_{2,{\rm{p}}}^{{\rm{NR}}}\right),$$

(5)

To extract bounds on the SME couplings from equations (3) and (5), we first need to adjust the measured transition frequencies by the hyperfine Zeeman energies described above, which are self-consistently calculated with the antihydrogen contribution identical to that of hydrogen. This identifies

$$\begin{array}{l}\Delta {E}_{2{{\rm{S}}}_{{\rm{c}}}\longleftrightarrow 1{{\rm{S}}}_{{\rm{c}}}}^{\bar{{\rm{H}}}}-\Delta {E}_{2{{\rm{S}}}_{{\rm{d}}}\longleftrightarrow 1{{\rm{S}}}_{{\rm{d}}}}^{\bar{{\rm{H}}}}={f}_{{\text{c-c}}}^{\bar{\,{\rm{H}}}}-{f}_{{\text{d-d}}}^{\bar{\,{\rm{H}}}}-\left({f}_{{\text{c-c}}}^{\bar{\,{\rm{H}}},{\rm{HFS}}}\left(B\right)-{f}_{{\text{d-d}}}^{\bar{\,{\rm{H}}},{\rm{HFS}}}\left(B\right)\right)\\=-3.5\pm 8.6\,{\rm{kHz}}.\end{array}$$

(6)

The measured antihydrogen 1S_c–2S_c and 1S_d–2S_d frequencies, ${f}_{{\text{c-c}}}^{\bar{\,{\rm{H}}}}$ and ${f}_{{\text{d-d}}}^{\bar{\,{\rm{H}}}}$, respectively, are taken from run 1, which commenced at 11:58 (local time) on 14 July 2018 (Tables 2 and 3). Errors are added in quadrature. Initially keeping only the term of O(1) in the fine-structure constant, which is accessible only from the c–c transition here, gives the bound (converted to units of gigaelectronvolts): ${\widetilde{b}}_{3,{\rm{e}}}^{* }-{\widetilde{b}}_{3,{\rm{p}}}^{* }$ = (–1.2 ± 3.0) × 10^–17 GeV.

Since existing bounds on the ${\widetilde{b}}_{Z}$ and ${\widetilde{b}}_{Z}^{* }$ couplings are considerably more stringent²³, we can also use equation (6) to infer values for the remaining spin-dependent couplings by neglecting the O(1) term. This gives ${\widetilde{g}}_{D3,{\rm{e}}}+{\widetilde{d}}_{3,{\rm{e}}}$ = (–0.7 ± 1.7) × 10^–12 GeV and ${\widetilde{g}}_{D3,{\rm{p}}}+{\widetilde{d}}_{3,{\rm{p}}}$ = (–1.8 ± 4.5) × 10^–9 GeV, the former being substantially weakened by the near cancellation of the mixing-angle factor. The relation between SME couplings expressed in the local laboratory frame and in the standard Sun-centred frame^23,25 is given in the Supplementary Information. The bounds on the spin-dependent couplings quoted in the main text assume that our results are typical of an average over a sidereal day, for which ${\widetilde{b}}_{3}=0.35{\widetilde{b}}_{Z}$ using parameters specifying the orientation of the ALPHA experiment at CERN.

Comparing the antihydrogen 1S_d–2S_d measurement with the hydrogen centroid frequency gives

$$\Delta {E}_{2{{\rm{S}}}_{{\rm{d}}}\longleftrightarrow 1{{\rm{S}}}_{{\rm{d}}}}^{\bar{{\rm{H}}}}-\Delta {E}_{1{\rm{S}}2{\rm{S}}}^{{\rm{H}}}={f}_{{\text{d-d}}}^{\bar{\,{\rm{H}}}}-{f}_{{\text{d-d}}}^{\,{\rm{H}},{\rm{ADJ}}}=2.2\pm 5.8\,{\rm{kHz}},$$

(7)

where ${f}_{{\text{d-d}}}^{\bar{\,{\rm{H}}},{\rm{ADJ}}}={f}_{1{\rm{S}}2{\rm{S}}}^{\,{\rm{H}}}+{f}_{1{\rm{S}}2{\rm{S}}}^{\,{\rm{H}},{\rm{HFS}}}(B)$ is defined as that in equation (1). This value is found by combining our measured 1S_d–2S_d frequency with the average of the hydrogen data¹¹ from July 1999, which coincides with the orbital location in the Sun-centred system that our measurement was conducted in. With the assumption that sidereal and annual variations arising from Lorentz boosts are relatively small (Supplementary Information), this can be used to isolate the CPT-odd spin-independent couplings ${{\mathring{a}}}_{2}^{{\rm{NR}}}$. This gives ${{\mathring{a}}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{a}}}_{2,{\rm{p}}}^{{\rm{NR}}}$ = (–0.4 ± 1.2) × 10^–9 GeV^–1.

Alternatively, applying the bound purely to the ${\widetilde{g}}_{{\rm{D}}3,{\rm{p}}}$ and ${\widetilde{d}}_{3,{\rm{p}}}$ couplings in equation (3) for the electron and proton separately would give the values ${\widetilde{g}}_{{\rm{D}}3,{\rm{e}}}+{\widetilde{d}}_{3,{\rm{e}}}$ = (–0.7 ± 1.8) × 10^–15 GeV and ${\widetilde{g}}_{{\rm{D}}3,{\rm{p}}}+{\widetilde{d}}_{3,{\rm{p}}}$ = (–2.3 ± 6.1) × 10^–9 GeV for the spin-dependent couplings. Recalling that in the minimal SME ${\widetilde{g}}_{{DZ}}=-{\widetilde{b}^{\prime} }_{Z}$, these can be compared with the bounds²³ $\left|{\widetilde{b}}_{Z,{\rm{e}}}^{{\prime} }\right|$ < 1.7 × 10^–17 GeV and $\left|{\widetilde{b}}_{Z,{\rm{p}}}^{{\prime} }\right|$ < 1.2 × 10^–10 GeV from Penning trap experiments by ATRAP^30,31 and BASE³², together with the astrophysics bound of $\left|{\widetilde{d}}_{Z,{\rm{e}}}^{{\prime} }\right|$ < 10^–19 GeV (ref. ⁴⁶). These currently stronger bounds a posteriori justify the neglect of the spin-dependent SME couplings in extracting the value for ${{\mathring{a}}}_{2,{\rm{e}}}^{{\rm{NR}}}+{{\mathring{a}}}_{2,{\rm{p}}}^{{\rm{NR}}}$.