Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Topological interactions drive the first fate decision in the Drosophila embryo

Nature Physics volume 21, pages 632–643 (2025)Cite this article

Subjects

Abstract

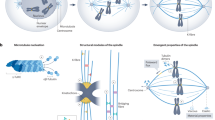
During embryogenesis, the first cell fate decision—whether the cell participates in development of the embryo or not—is often linked to the positioning of the nucleus. The cell cycle oscillator and associated cytoskeletal dynamics contribute to the control of nuclear positioning. However, the mechanisms that ensure that the correct number of nuclei move to their appropriate place remain poorly understood. Here we show that the orientation of the mitotic spindle controls the first fate decision, embryonic or yolk cell fate, in Drosophila embryos using light sheet microscopy experiments. Combining computational methods inspired by integral geometry, manipulation of cell cycle genes, and investigation of the relationship between geometry and topology, we show that spindle orientation is controlled by topological interactions with neighbouring nuclei and not by internuclear distance. Leveraging the physics of space-filling systems, we develop a theory for topological dependency in microtubule structures. Our work shows how the topological interplay of microtubule mechanics can ensure robust control of nuclear density and determine cell fate.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Symmetry breaking in nuclear positioning underlies embryo–yolk fate choice.
Fig. 2: Spindle orientation drives nuclear positioning.
Fig. 3: Geometry and mechanics of cortical migration via local force balance.
Fig. 4: Theoretical model predicts aster–aster alignment interactions are scale independent and topological.
Fig. 5: Cell cycle manipulations confirm scale-independent and robust aster–aster alignment.
Fig. 6: Local and geometric control of topology and spindle orientation.

Similar content being viewed by others

Data availability

All image data are available upon reasonable request to S.D.T. Source data are provided with this paper.

Code availability

Codes are available upon reasonable request to S.D.T.

References

  1. Sneyd, J., Theraulaz, G., Bonabeau, E., Deneubourg, J.-L. & Franks, N. R. Self-organization in Biological Systems (Princeton Univ. Press, 2001).

  2. Gerhart, J. & Kirschner, M. Cells, Embryos and Evolution (Wiley, 1997).

  3. Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).

    Article  ADS  Google Scholar 

  4. Cavagna, A. & Giardina, I. Bird flocks as condensed matter. Annu. Rev. Condens. Matter Phys. 5, 183–207 (2014).

    Article  ADS  Google Scholar 

  5. Ballerini, M. et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl Acad. Sci. USA 105, 1232–1237 (2008).

    Article  ADS  Google Scholar 

  6. Almonacid, M., Terret, M.-E. & Verlhac, M.-H. Nuclear positioning as an integrator of cell fate. Curr. Opin. Cell Biol. 56, 122–129 (2019).

    Article  Google Scholar 

  7. Gundersen, G. G. & Worman, H. J. Nuclear positioning. Cell 152, 1376–1389 (2013).

    Article  Google Scholar 

  8. Lim, H. Y. G. & Plachta, N. Cytoskeletal control of early mammalian development. Nat. Rev. Mol. Cell Biol. 22, 548–562 (2021).

    Article  Google Scholar 

  9. Cockburn, K. et al. Making the blastocyst: lessons from the mouse. J. Clin. Invest. 120, 995–1003 (2010).

    Article  Google Scholar 

  10. Lv, Z., De-Carvalho, J., Telley, I. A. & Großhans, J. Cytoskeletal mechanics and dynamics in the Drosophila syncytial embryo. J. Cell Sci. 134, jcs246496 (2021).

    Article  Google Scholar 

  11. Deshpande, O. & Telley, I. A. Nuclear positioning during development: pushing, pulling and flowing. Sem. Cell Dev. Biol. 120, 10–21 (2021).

    Article  Google Scholar 

  12. Deneke, V. E. et al. Self-organized nuclear positioning synchronizes the cell cycle in Drosophila embryos. Cell 177, 925–941 (2019).

    Article  Google Scholar 

  13. Donoughe, S., Hoffmann, J., Nakamura, T., Rycroft, C. H. & Extavour, C. G. Nuclear speed and cycle length co-vary with local density during syncytial blastoderm formation in a cricket. Nat. Commun. 13, 3889 (2022).

    Article  ADS  Google Scholar 

  14. Brantley, S. E. & Di Talia, S. Cell cycle control during early embryogenesis. Development 148, dev193128 (2021).

    Article  Google Scholar 

  15. Howard, J., Grill, S. W. & Bois, J. S. Turing’s next steps: the mechanochemical basis of morphogenesis. Nat. Rev. Mol. Cell Biol. 12, 392–398 (2011).

    Article  Google Scholar 

  16. Collinet, C. & Lecuit, T. Programmed and self-organized flow of information during morphogenesis. Nat. Rev. Mol. Cell Biol. 22, 245–265 (2021).

    Article  Google Scholar 

  17. Farrell, J. A. & O’Farrell, P. H. From egg to gastrula: how the cell cycle is remodeled during the Drosophila mid-blastula transition. Annu. Rev. Genet. 48, 269–294 (2014).

    Article  Google Scholar 

  18. Royou, A., Sullivan, W. & Karess, R. Cortical recruitment of nonmuscle myosin II in early syncytial Drosophila embryos: its role in nuclear axial expansion and its regulation by Cdc2 activity. J. Cell Biol. 158, 127–137 (2002).

    Article  Google Scholar 

  19. von Dassow, G. & Schubiger, G. How an actin network might cause fountain streaming and nuclear migration in the syncytial Drosophila embryo. J. Cell Biol. 127, 1637–1653 (1994).

    Google Scholar 

  20. López, C. H. et al. Two-fluid dynamics and micron-thin boundary layers shape cytoplasmic flows in early Drosophila embryos. Proc. Natl Acad. Sci. USA 120, e2302879120 (2023).

    Article  Google Scholar 

  21. Baker, J., Theurkauf, W. E. & Schubiger, G. Dynamic changes in microtubule configuration correlate with nuclear migration in the preblastoderm Drosophila embryo. J. Cell Biol. 122, 113–121 (1993).

    Article  Google Scholar 

  22. Foe, V. E. & Alberts, B. M. Studies of nuclear and cytoplasmic behaviour during the five mitotic cycles that precede gastrulation in drosophila embryogenesis. J. Cell Sci. 61, 31–70 (1983).

    Article  Google Scholar 

  23. Deshpande, O., De-Carvalho, J., Vieira, D. V. & Telley, I. A. Astral microtubule cross-linking safeguards uniform nuclear distribution in the drosophila syncytium. J. Cell Biol. 221, e202007209 (2021).

    Article  Google Scholar 

  24. Riparbelli, M. G. & Callaini, G. Assembly of yolk spindles in the early drosophila embryo. Mech. Dev. 120, 441–454 (2003).

    Article  Google Scholar 

  25. Hayden, L. et al. Cullin-5 mutants reveal collective sensing of the nucleocytoplasmic ratio in Drosophila embryogenesis. Curr. Biol. 32, 2084–2092 (2022).

    Article  Google Scholar 

  26. Lu, X., Li, J. M., Elemento, O., Tavazoie, S. & Wieschaus, E. F. Coupling of zygotic transcription to mitotic control at the Drosophila mid-blastula transition. Development 136, 2101–2110 (2009).

    Article  Google Scholar 

  27. Erickson, J. W. & Cline, T. W. A bZIP protein, sisterless-a, collaborates with bHLH transcription factors early in Drosophila development to determine sex. Genes Dev. 7, 1688–1702 (1993).

    Article  Google Scholar 

  28. Walker, J. J., Lee, K. K., Desai, R. N. & Erickson, J. W. The Drosophila melanogaster sex determination gene sisA is required in yolk nuclei for midgut formation. Genetics 155, 191–202 (2000).

    Article  Google Scholar 

  29. Tingvall, T. Ö., Roos, E. & Engström, Y. The GATA factor serpent is required for the onset of the humoral immune response in Drosophila embryos. Proc. Natl Acad. Sci. USA 98, 3884–3888 (2001).

    Article  ADS  Google Scholar 

  30. Ono, H. et al. Spook and Spookier code for stage-specific components of the ecdysone biosynthetic pathway in Diptera. Dev. Biol. 298, 555–570 (2006).

    Article  Google Scholar 

  31. de Carvalho, J., Tlili, S., Saunders, T. E. & Telley, I. A. The positioning mechanics of microtubule asters in Drosophila embryo explants. eLife 12, RP90541 (2023).

    Article  Google Scholar 

  32. Raff, J. W. & Glover, D. M. Centrosomes, and not nuclei, initiate pole cell formation in Drosophila embryos. Cell 57, 611–619 (1989).

    Article  Google Scholar 

  33. Freeman, M., Nüsslein-Volhard, C. & Glover, D. M. The dissociation of nuclear and centrosomal division in gnu, a mutation causing giant nuclei in drosophila. Cell 46, 457–468 (1986).

    Article  Google Scholar 

  34. Stiffler, L. A., Ji, J.-Y., Trautmann, S., Trusty, C. & Schubiger, G. Cyclin a and b functions in the early Drosophila embryo. Development 126, 5505–5513 (1999).

    Article  Google Scholar 

  35. Krzic, U., Gunther, S., Saunders, T. E., Streichan, S. J. & Hufnagel, L. Multiview light-sheet microscope for rapid in toto imaging. Nat. Methods 9, 730–733 (2012).

    Article  Google Scholar 

  36. Telley, I. A., Gáspár, I., Ephrussi, A. & Surrey, T. Aster migration determines the length scale of nuclear separation in the Drosophila syncytial embryo. J. Cell Biol. 197, 887–895 (2012).

    Article  Google Scholar 

  37. Albright, A. R., Stadler, M. R. & Eisen, M. B. Single-nucleus RNA-sequencing in pre-cellularization Drosophila melanogaster embryos. PLoS ONE 17, e0270471 (2022).

    Article  Google Scholar 

  38. Field, C. M., Pelletier, J. F. & Mitchison, T. J. Disassembly of actin and keratin networks by aurora b kinase at the midplane of cleaving Xenopus laevis eggs. Curr. Biol. 29, 1999–2008 (2019).

    Article  Google Scholar 

  39. Mooney, P. et al. Tau-based fluorescent protein fusions to visualize microtubules. Cytoskeleton 74, 221–232 (2017).

    Article  Google Scholar 

  40. Buttrick, G. J. et al. Akt regulates centrosome migration and spindle orientation in the early Drosophila melanogaster embryo. J. Cell Biol. 180, 537–548 (2008).

    Article  Google Scholar 

  41. Sullivan, W. & Theurkauf, W. E. The cytoskeleton and morphogenesis of the early Drosophila embryo. Curr. Opin. Cell Biol. 7, 18–22 (1995).

    Article  Google Scholar 

  42. Dalton, B. A., Oriola, D., Decker, F., Jülicher, F. & Brugués, J. A gelation transition enables the self-organization of bipolar metaphase spindles. Nat. Phys. 18, 323–331 (2022).

    Article  Google Scholar 

  43. Wühr, M., Tan, E. S., Parker, S. K., Detrich, H. W. & Mitchison, T. J. A model for cleavage plane determination in early amphibian and fish embryos. Curr. Biol. 20, 2040–2045 (2010).

    Article  Google Scholar 

  44. Théry, M., Jiménez-Dalmaroni, A., Racine, V., Bornens, M. & Jülicher, F. Experimental and theoretical study of mitotic spindle orientation. Nature 447, 493–496 (2007).

    Article  ADS  Google Scholar 

  45. Subramanian, R. & Kapoor, T. M. Building complexity: insights into self-organized assembly of microtubule-based architectures. Dev. Cell 23, 874–885 (2012).

    Article  Google Scholar 

  46. De-Carvalho, J., Tlili, S., Hufnagel, L., Saunders, T. E. & Telley, I. A. Aster repulsion drives short-ranged ordering in the Drosophila syncytial blastoderm. Development 149, dev199997 (2022).

    Article  Google Scholar 

  47. Chaté, H., Ginelli, F., Grégoire, G., Peruani, F. & Raynaud, F. Modeling collective motion: variations on the vicsek model. Eur. Phys. J. B 64, 451–456 (2008).

    Article  ADS  Google Scholar 

  48. De Magistris, G. & Marenduzzo, D. An introduction to the physics of active matter. Physica A 418, 65–77 (2015).

    Article  ADS  Google Scholar 

  49. Mahault, B. et al. Self-propelled particles with velocity reversals and ferromagnetic alignment: active matter class with second-order transition to quasi-long-range polar order. Phys. Rev. Lett. 120, 258002 (2018).

    Article  ADS  Google Scholar 

  50. Winters, L. et al. Pivoting of microtubules driven by minus-end-directed motors leads to spindle assembly. BMC Biol. 17, 42 (2019).

    Article  Google Scholar 

  51. Strogatz, S. H. Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering (CRC Press, 2024).

  52. Kepler, J. Ad Vitellionem Paralipomena, quibus astronomiae pars optica traditur (Claude de Marne & heir Jean Aubry, Frankfurt, 1604).

  53. Jain, A. et al. Regionalized tissue fluidization is required for epithelial gap closure during insect gastrulation. Nat. Commun. 11, 5604 (2020).

    Article  ADS  Google Scholar 

  54. Santaló, L. A. Integral Geometry and Geometric Probability (Cambridge Univ. Press, 2004).

  55. MacPherson, R. D. & Srolovitz, D. J. The von Neumann relation generalized to coarsening of three-dimensional microstructures. Nature 446, 1053–1055 (2007).

    Article  ADS  Google Scholar 

  56. Descartes, R. Oeuvres de Descartes (Charpentier, 1857).

  57. Von Neumann, J. in Metal Interfaces (ed. Herring, C.) 108–110 (American Society for Metals, 1952).

  58. Verde, F., Labbé, J.-C., Dorée, M. & Karsenti, E. Regulation of microtubule dynamics by cdc2 protein kinase in cell-free extracts of Xenopus eggs. Nature 343, 233–238 (1990).

    Article  ADS  Google Scholar 

  59. Crest, J., Oxnard, N., Ji, J.-Y. & Schubiger, G. Onset of the DNA replication checkpoint in the early Drosophila embryo. Genetics 175, 567–584 (2007).

    Article  Google Scholar 

  60. Ji, J.-Y., Crest, J. & Schubiger, G. Genetic interactions between Cdk1-CyclinB and the separase complex in Drosophila. Development 132, 1875–1884 (2005).

    Article  Google Scholar 

  61. Ji, J.-Y., Haghnia, M., Trusty, C., Goldstein, L. S. B. & Schubiger, G. A genetic screen for suppressors and enhancers of the Drosophila Cdk1-Cyclin B identifies maternal factors that regulate microtubule and microfilament stability. Genetics 162, 1179–1195 (2002).

    Article  Google Scholar 

  62. Berger, M. & Senechal, L. J. Geometry Revealed: A Jacob’s Ladder to Modern Higher Geometry Vol. 1232 (Springer, 2010).

  63. Halperin, B. I. & Nelson, D. R. Theory of two-dimensional melting. Phys. Rev. Lett. 41, 121–124 (1978).

    Article  ADS  MathSciNet  Google Scholar 

  64. Irvine, W. T. M., Vitelli, V. & Chaikin, P. M. Pleats in crystals on curved surfaces. Nature 468, 947–951 (2010).

    Article  ADS  Google Scholar 

  65. Waddington, C. H. Canalization of development and the inheritance of acquired characters. Nature 150, 563–565 (1942).

    Article  ADS  Google Scholar 

  66. Ishihara, K. et al. Topological morphogenesis of neuroepithelial organoids. Nat. Phys. 19, 177–183 (2023).

    Google Scholar 

  67. Diaz-Cuadros, M., Pourquié, O. & El-Sherif, E. Patterning with clocks and genetic cascades: segmentation and regionalization of vertebrate versus insect body plans. PLoS Genet. 17, e1009812 (2021).

    Article  Google Scholar 

  68. Church, S. H., Donoughe, S., De Medeiros, B. A. S. & Extavour, C. G. Insect egg size and shape evolve with ecology but not developmental rate. Nature 571, 58–62 (2019).

    Article  ADS  Google Scholar 

  69. Maître, J. L. et al. Asymmetric division of contractile domains couples cell positioning and fate specification. Nature 536, 344–348 (2016).

    Article  ADS  Google Scholar 

  70. Mitchison, T. J. & Field, C. M. Self-organization of cellular units. Annu. Rev. Cell Dev. Biol. 37, 23–41 (2021).

    Article  Google Scholar 

  71. Cheng, X. & Ferrell Jr, J. E. Spontaneous emergence of cell-like organization in Xenopus egg extracts. Science 366, 631–637 (2019).

    Article  ADS  Google Scholar 

  72. Rinaldin, M. et al. Robust cytoplasmic partitioning by solving an intrinsic cytoskeletal instability. Preprint at bioRxiv https://doi.org/10.1101/2024.03.12.584684 (2024).

  73. Kawaguchi, K., Kageyama, R. & Sano, M. Topological defects control collective dynamics in neural progenitor cell cultures. Nature 545, 327–331 (2017).

    Article  ADS  Google Scholar 

  74. Copenhagen, K., Alert, R., Wingreen, N. S. & Shaevitz, J. W. Topological defects promote layer formation in Myxococcus xanthus colonies. Nat. Phys. 17, 211–215 (2021).

    Article  Google Scholar 

  75. Katsani, K. R., Karess, R. E., Dostatni, N. & Doye, V. In vivo dynamics of Drosophila nuclear envelope components. Mol. Biol. Cell 19, 3652–3666 (2008).

    Article  Google Scholar 

  76. Streichan, S. J., Lefebvre, M. F., Noll, N., Wieschaus, E. F. & Shraiman, B. I. Global morphogenetic flow is accurately predicted by the spatial distribution of myosin motors. eLife 7, e27454 (2018).

    Article  Google Scholar 

  77. Preibisch, S., Saalfeld, S., Schindelin, J. & Tomancak, P. Software for bead-based registration of selective plane illumination microscopy data. Nat. Methods 7, 418–419 (2010).

    Article  Google Scholar 

Download references

Acknowledgements

We acknowledge S. Gunther and L. Hufnagel for discussion and for sharing their original observations of cortical migration. We thank the Bloomington Drosophila Stock Center and the Kyoto Drosophila Stock Center for providing stocks. We thank the Drosophila Genomics Resource Center and J. Gatlin for constructs. We thank C. Field and T. Mitchison for discussions. N.P.M. acknowledges support from NICHD award number K99HD110675. This work was supported by NIH R35-GM153490; R01-GM136763; R01-GM122936 to S.D.T.

Author information

Author notes

  1. These authors contributed equally: Woonyung Hur, Arghyadip Mukherjee.

Authors and Affiliations

  1. Department of Cell Biology, Duke University School of Medicine, Durham, NC, USA

    Woonyung Hur, Luke Hayden, Ziqi Lu, Anna Chao & Stefano Di Talia

  2. Laboratoire de physique de l’Ecole Normale Superieure, CNRS, PSL Research University, Sorbonne Universite, Paris, France

    Arghyadip Mukherjee & Massimo Vergassola

  3. Kavli Institute for Theoretical Physics, University of California, Santa Barbara, Santa Barbara, CA, USA

    Noah P. Mitchell & Sebastian J. Streichan

  4. Department of Physics, University of California, Santa Barbara, Santa Barbara, CA, USA

    Noah P. Mitchell & Sebastian J. Streichan

  5. Department of Physics, University of California, San Diego, La Jolla, CA, USA

    Massimo Vergassola

Authors
  1. Woonyung Hur
    View author publications

    Search author on:PubMed Google Scholar

  2. Arghyadip Mukherjee
    View author publications

    Search author on:PubMed Google Scholar

  3. Luke Hayden
    View author publications

    Search author on:PubMed Google Scholar

  4. Ziqi Lu
    View author publications

    Search author on:PubMed Google Scholar

  5. Anna Chao
    View author publications

    Search author on:PubMed Google Scholar

  6. Noah P. Mitchell
    View author publications

    Search author on:PubMed Google Scholar

  7. Sebastian J. Streichan
    View author publications

    Search author on:PubMed Google Scholar

  8. Massimo Vergassola
    View author publications

    Search author on:PubMed Google Scholar

  9. Stefano Di Talia
    View author publications

    Search author on:PubMed Google Scholar

Contributions

Conceptualization: W.H., A.M., S.J.S., M.V. and S.D.T. Methodology: W.H., A.M. and S.J.S. Software: W.H., A.M. and S.J.S. Validation: W.H. and A.M. Data processing and preparation: W.H. Formal analysis: A.M. Investigation: W.H., A.M., L.H., Z.L., A.C. and N.P.M. Resources: W.H., A.M. and A.C. Data curation: W.H., A.M. and Z.L. Writing—original draft: W.H., A.M. and S.D.T. Writing—review and editing: all authors. Visualization: W.H., A.M. and Z.L. Supervision: S.J.S., M.V. and S.D.T. Project administration: S.J.S., M.V. and S.D.T. Funding acquisition: A.M., M.V. and S.D.T.

Corresponding authors

Correspondence to Arghyadip Mukherjee, Massimo Vergassola or Stefano Di Talia.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Ruth Lehmann, Timothy Saunders, Ivo Telley and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

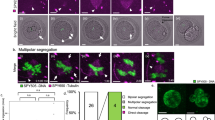
Extended Data Fig. 1 Symmetry breaking in nuclear positioning underlies embryo-yolk fate choice.

A, Lineage tracing of segmented and tracked nuclei are shown along their relative position in the anterior posterior axis from cycle 8 to cycle 11. Different colours indicate each unique lineage trace that is, same colour means it originated from the same nucleus. A=anterior, P=posterior. B, A schematic depiction of a nucleus with respect to the embryo cortex is shown. The nuclear velocity \(\overrightarrow{v_{i}}\), the unit orientation vector \(\hat{u_{c}}\) pointing to the closest plane in the cortex is marked. The dashed line connects to the approximated closest plane indicated. C-D, Frequency distributions of movement direction of the nuclei during cycle 8 and cycle 9 is shown. The movement direction is defined as the dot product of unit nuclear velocity and orientation vector. E, Nuclear speed towards the embryo cortex is shown as a function of time. Black lines=outer shell nuclei, red lines=nuclei in bulk (yolk), vertical dashed line=chromosome separation event. F, Enrichment score for the top 25 expressed genes in the yolk nuclei (with respect to the rest of the nuclei) are shown in rank order. Genes sisA, serp and spo are highlighted.

Source data

Extended Data Fig. 2 Orientational dynamics and its effect on nuclear trajectories.

A, Frequency distribution of tilt angle ψ is shown for an embryo during cycle 10 when they have already reached the embryo cortex. Vertical dashed line indicates 45 degrees in angle. B, Temporal traces of tilt angle ψ is shown from mid-interphase to onset of metaphase during cycle 8. Different colours indicate each unique trace of the spindle. C, The average change in tilt angle Δψ is shown for cycles 7,8 and 9. Shaded region marks the standard deviation. D, The probability distribution function of tilt angles is shown for cycle 8 and cycle 9. E, Left- The probability distribution function of tilt angles is shown for a randomized reference state. To derive the distribution one can assume a neamtic object inside a sphere oriented randomly and measure the latitude. Right- Comparison of the random distribution of angles is shown with cycle 8 and cycle 9. Measured Kullback-Leibler divergence between the random state and data from cycle 8 and cycle 9 is ~ 0.08 while between data from the two cycles is <0.01. F, Individual (grey) and average (red dots with errorbars representing 95% confidence interval of the mean) trajectories are shown for nuclei that show >45 degree with respect to the cortex at the onset of nuclear division. A clear bifurcation is indicated just after 2 min timepoint. G, Individual (gray) and average (blue dots with errorbars representing 95% confidence interval of the mean) trajectories are shown for nuclei that show <45 degree with respect to the cortex at the onset of nuclear division. A collective migration is found in the trajectories. H, A two dimensional count density map is shown for tilt angle ψ and location along the normalized anterior posterior (AP) axis for pooled 8 wild type (WT) embryos during cycle 9. Colorbar indicates the bin counts. I, Probability density function of tilt angle ψ is plotted for spindles belonging to binned locations along the AP axis with 5 equally sized bins (every 20% along the AP axis). Color indicates location along the normalized AP axis (see colorbar).

Source data

Extended Data Fig. 3 Dynamics of nuclear shell expansion.

A, A hemispherical view of the nuclear shell/boundary is shown during cycle 7-10 for wildtype (WT) and cul-5 mutants. Inflation and differences in morphology is noted. B, Average nuclear speed towards the embryo cortex is plotted for wildtype and cul-5 mutants (for different embryos), during the transition from cycle 7 to cycle 8 (left) and from cycle 8 to cycle 9 (right). Vertical dashed line=chromosome separation. C, Distance of the nuclei from the cortex is shown as a function of time for a cul-5 mutant embryo. Temporal traces (dots) and average trajectories are shown for different anterior-posterior regions (color coded shown as in the inset image). c=cycle. D, Lineage tracing of segmented and tracked nuclei are shown along their relative position in the anterior posterior axis from cycle 7 to cycle 10 for a cul-5 mutant embryo. Note that the axial spread is smaller than a WT embryo (Extended Data Fig. 1A). Different colors indicate each unique lineage trace that is, same color means it originated from the same nucleus. A=anterior, P=posterior. E, Nuclei shell area A(t) from cycle 7 to cycle 10 (A(t)–A0, with A0 = 1.2*104 μm2 for WT and A0 = 0 for cul-5 mutant) is plotted against predicted shell area from the pushing model based on nuclei number N(t) on the shell as a0N(t), where a0 = 700μm2 is the extracted domain area. Colorbar indicates time with respect to end of cycle 10. y= x line indicates the excellent agreement of the prediction while the flat dashed line indicates the saturation as the nuclear shell reaches the cortex at cycle 10.

Source data

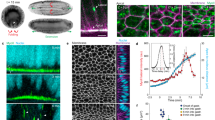
Extended Data Fig. 4 Morphometric analysis of the nuclear shell.

A, An example of a mesh reconstruction is shown for a nuclear point cloud data from a wildtype embryo during cycle 9. B, Dual/Voronoi mesh is shown for the reconstructed mesh. Facecolor indicates isoperimetric quotient (Perimeter/√Area), a measure of shape for astral domains. C, Probability density is shown for isoperimetric quotient for an example embryo (same as Extended Data Fig. 4B), with numerically associated regular polygons/circle to emphasize an intuition of the shape. D, Correlation coefficient is calculated between tilt ψ and negative strain ϵ < 0 (see Fig. 3a) after randomization. A probability distribution is plotted for the correlation coefficients upon randomization. Standard deviation of the randomization σr is shown in orange. The correlation of the experimental data is found to be ~ 2σr. E, Binscatter plots for experimental data (left) of tilt angle ψ and strain ϵ and a randomized sample of the experimental data (right) is shown. A and \(\overline{A}\) indicate domain area and its’ average. F, Scatter plots are shown for tilt angle ψ vs rescaled distance with the closest neighbour (right) and the average distance to the three closesr neighbours (left). No significant correlation is found. Pearson correlation is reported in the legend. Pooled data over n=8 WT cycle 9 embryos.

Source data

Extended Data Fig. 5 Scaling of microtubule density.

A, Rescaled microtubule radial intensity profile is shows for wild type (WT) and mutants (legend) in a log-log plot. The tail can be well-captured by a power law with exponent of − 2.1, shown by a dashed line. Measurements are performed on intensity profiles of tau-mCherry around the centrosome as in Fig. 2b. Different conditions are annotated in the fig. B, Rescaling factor/maxmimal microtubule intensity at the centrosome is plotted across genetic backgrounds for comparison (see inset). CycB 1x and CycB 6x show clear differences.

Source data

Extended Data Table 1 Resources used in the study
Full size table

Supplementary information

Supplementary Information

Supplementary Note.

Reporting Summary

Supplementary Video 1

Time-lapse imaging with maximum intensity projection of an exemplary Drosophila embryo from cycle 7 to cycle 10 is shown with mRFP-Nup107 (red). Scale bar, 100 μm.

Supplementary Video 2

Tracing of three-dimensional segmented nuclei (marked in variety of colours) is shown during cycle 7 to cycle 10. As the video progresses, expansion of the nuclear shell can be seen. Scale bar, 100 μm.

Supplementary Video 3

Segmented spindles are rendered and visualized in three dimensions. Spindles with tilt angle <45° are marked in gold, while spindles with tilt angle ≥45° are marked in red.

Supplementary Video 4

A typical simulation of expansion is shown where the system starts with 20 particles that divide/double and relaxes the forces by pushing on each other. This leads to inflation as well increase in eccentricity. After relaxation, the number is again doubled and the process is repeated until interaction with the boundary.

Supplementary Video 5

Tracking of nuclei are shown, colour-coded for initial tilt angle with respect to the embryo cortex. Perpendicular nuclei >45° are marked in red and parallel ones in yellow. Side and polar views are shown, which reveal a significant number of red daughter nuclei moving inwards while most yellow nuclei move towards the cortex.

Source data

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hur, W., Mukherjee, A., Hayden, L. et al. Topological interactions drive the first fate decision in the Drosophila embryo. Nat. Phys. 21, 632–643 (2025). https://doi.org/10.1038/s41567-025-02796-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02796-x

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing