Main

It is long established that planets form out of protoplanetary disks of gas and dust5, but there have been limited attempts so far to directly measure primordial stellar obliquities. The largest effort6 investigated the orientations of only seven single Sun-like stars. However, the resulting obliquity constraints were broad, preventing robust conclusions about the underlying obliquity distribution. Also, nine other stars in their sample had stellar companions that could affect the inferred stellar obliquities in those systems. Other studies7,8,9 have attempted to provide insights into the origin of spin–orbit obliquity by measuring stellar orientations with respect to debris disks—second-generation disks of dust around stars with intermediate ages (approximately 10–500 Myr). These works found general agreement with alignment, although the combined sample amounts to only 21 single Sun-like stars.

Directly measuring primordial obliquities for a sufficiently large sample of young stars is the natural next step, which has only recently become possible with the sensitivity and angular resolution of the Atacama Large Millimeter/submillimeter Array (ALMA) to measure disk inclinations coupled with nearly all-sky precision light curves from space-based facilities such as the Transiting Exoplanet Survey Satellite (TESS) and K2 to determine stellar inclinations. Here we carry out a statistical investigation into the primordial stellar obliquity of single young stars with respect to their outer protoplanetary disks to form a more complete picture of the initial angular momentum architecture of protoplanetary systems. Our approach compares the inclination of the stellar spin axis with disk inclination measurements from resolved millimetre observations sensitive to the dust in the outer disk (≥10 au) to obtain a measurement of the minimum star–disk obliquity for a sample of 49 systems.

Sample description

Our sample consists of T Tauri stars with spatially resolved protoplanetary disks and well-characterized disk inclinations (idisk), stellar radii (R*), projected rotation velocities (vsini*) and rotation periods (Prot). Stellar inclinations are determined by merging projected rotational velocities with stellar radii and rotation periods. With our adopted measurements of R*, vsini* and Prot, we determine the stellar inclination (i*) following a Bayesian probabilistic framework10, which properly accounts for the correlation between vsini* and the equatorial rotation velocity (veq, in which veq = 2πR*/Prot). In particular, we use the analytical expression for the posterior distribution of i* (ref. 11) (see Methods). We also compile spectral types, masses (M*) and effective temperatures (Teff) to more broadly assess potential trends in the resulting obliquity distribution. In selecting our sample, we reject stars with spectral types earlier than F6 to avoid pulsating variables12 with periodic brightness signatures that are difficult to distinguish from rotation13. Most of our sample consists of stars with spectral types between K0 and M5 with masses spanning approximately 0.5–1.5 M⊙. Last, we focus our investigation on gravitationally isolated systems and exclude those with known binary companions, which can induce torques on protoplanetary disks and erase initial conditions14.

The true star–disk obliquity (Ψ) is the angle between the star’s rotational angular momentum vector and the angular momentum vector of the disk. For this work, this angle cannot be determined in full because the spatial orientation of the star’s rotational axis (the polar position angle) and spin direction (clockwise or anticlockwise) are unknown. Similarly, spatially resolved kinematic measurements of the disk and information about its orientation (the longitude of ascending versus descending nodes)—which is needed to identify whether its angular momentum vector is angled towards or away from Earth—are not always available. We therefore report the absolute difference between the sky-projected inclination of the star and disk (Δi), which corresponds to a lower limit on the true obliquity angle, Ψ.

Stellar obliquities in planet-forming systems

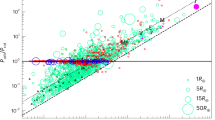
Most systems in the sample show a tendency for low minimum obliquities, but there is also a spread in Δi out to about 60° (Fig. 1). We found no statistically significant correlation in Δi with spectral type, M*, Teff, R*, Prot, vsini* or i*. The average Δi of the sample is 17°. It is apparent that a notable portion of stars are misaligned with respect to their protoplanetary disks, at least at the characteristic spatial scales sampled by ALMA observations of tens to hundreds of au. We classify a star as misaligned if the maximum a posteriori (MAP) value of its Δi probability distribution is at least two times the lower (‘–’) Δi uncertainty, corresponding to a departure from 0° at 95.4% confidence. In the sample, we find a misalignment fraction of 16/49, corresponding to a primordial misalignment rate of \({33}_{-6}^{+7} \% \). The remaining 33/49 systems show no significant evidence of misalignment (see Supplementary Discussion).

Fig. 1: Minimum stellar obliquity, Δi, as a function of spectral type.
figure 1

a, Point colours represent the misalignment status of each system (n = 49). Dark-purple circles are misaligned at the >2σ level and light-blue circles show no evidence of misalignment. The yellow star represents the location of the pre-main sequence Sun (which would have corresponded to a spectral type of approximately K9 at an age of about 5 Myr) assuming that the origin of its current obliquity is primordial. Error bars are shown at 1σ confidence. b, Reconstructed distributions of Δi. The light-green area shows the Gaussian KDE of the distribution of Δi. The HBM results for the Rayleigh distribution generated with a log-uniform prior (labelled as ‘log-U Pr’) are represented by the dotted dark-blue line and the same model fit with a truncated Gaussian prior (‘TG Pr’) is shown by the solid light-blue line. The Gaussian distribution model fits produced with a log-uniform prior and truncated Gaussian prior are plotted as the purple dashed and solid lines, respectively. The truncated Gaussian model fit generated with a uniform prior (‘U Pr’) is shown in dark teal. c, Best-fit HBM results using a beta distribution for the minimum obliquities of a sample of 25 hot (‘H’) and 22 warm (‘W’) Jupiter systems28 also determined using a similar Δi methodology, shown here for comparison. Here, ‘log-N Pr’ represents model fits produced with a log-normal prior.

Source Data

Full size image

Next, we assess the behaviour of the distribution of Δi at a population level with two approaches. Our first approach is the computation of a fixed-width Gaussian kernel density estimate (KDE) of Δi to characterize the overall shape of the distribution. The KDE is a non-parametric model constructed from individual Δi probability distributions in the sample. The resulting KDE shows a broad spread in minimum stellar obliquity, peaking between 0° and 15° and tapering off beyond 60°. We also model the underlying distribution of Δi using a hierarchical Bayesian modelling (HBM) approach. HBM is a method to reconstruct the population-level behaviour of a sample by constraining the hyperparameters of a parametric model based on constraints for many individual objects. This method is well suited to model the underlying distribution in Δi given the marked variation among individual probability distributions of Δi across the sample. Here we explore three population-level models to represent the underlying distribution in Δi: a Rayleigh distribution, a Gaussian distribution and a truncated Gaussian distribution. The Rayleigh and Gaussian best-fit models of the underlying distribution of Δi yield similar results. The best-fit truncated Gaussian model shows more concentrated power towards lower obliquities. Together, the model fits of the Δi distribution indicate that it is broad with a characteristic peak value between about 10° and 25°.

The primary source of potential systematics in this study arises from the possible overestimation of stellar rotation periods and underestimation of stellar radii. In particular, unknown systematic errors in estimates of Prot or R* could bias the parameter inferences of i*, which, in turn, could propagate to the resulting distribution of Δi. To assess whether any unanticipated biases in Prot or R* could affect the conclusions from this study, we conduct a series of tests in which i* is computed with amended values of R* and Prot that represent multiplicative corrections to the fiducial values. A total of 25 individual tests were performed for all combinations of −30%, −15%, 0%, +15% and +30% offsets applied to each of the nominal values of R* and Prot, resulting in a new distribution of Δi for each permutation. The results of each test are shown in Figs. 2 and 3. What we learn from these tests is that, even if there are notable deviations from the nominal values of R* and Prot, the effect on i* yields a broad distribution in Δi, in which the misalignment fraction remains substantial. From this test, we also find that the misalignment probability (Fig. 3) is higher in grid cells with large Prot and low R*, which both act to increase i*. This enhancement in misalignment probability is probably the result of the increasing frequency of equator-on stars for certain combinations of Prot and R*, which also seem to show a greater number of non-physical veq; so, although misaligned obliquities in these cells seem more probable, they are not likely to be realistic. The conclusion from this work nevertheless remains: most young stars are consistent with being aligned with their planet-forming disks, and modest misalignment in primordial stellar obliquity is also common.

Fig. 2: The results of 25 independent tests to investigate the effect that potential biases in Prot and R* could have on the computation of i*.
figure 2

a–y, Each cell represents an individual test in which Δi is determined using larger or smaller values of Prot and/or R* compared with the nominal adopted values. Cells show Δi as a function of spectral type, with data points shaded with respect to i*. The nominal results of our analysis are shown in the centre of the grid, identified by a shaded background. Grid cells to the right of centre show outcomes for incrementally greater rotation periods and grid cells to the left of centre show outcomes for incrementally decreased rotation. Nominal stellar radii were increased for cells above the centre row and were decreased for cells in the bottom two rows. In several cases, the combination of test values of Prot and R* produced equatorial velocities that were less than vsini* by more than 2σ and are therefore not physically viable. The non-physical results are indicated by the faded points and are excluded from further analysis. Error bars are shown at 1σ confidence.

Source Data

Full size image
Fig. 3: The resulting Δi distributions corresponding to the grid cells in Fig. 2.
figure 3

a–y, Each cell contains the KDE representation of the distribution of Δi in the corresponding cell in Fig. 2. The misalignment probability (Pmis) of each Δi distribution is shown in its respective cell.

Source Data

Full size image

Causes and consequences of misalignment

This sample consists of single stars that reside in low-density environments15, so stellar fly-bys that could torque the outer disk are unlikely to induce misalignment. The isolated nature of the stars in our sample means that it represents a population of effectively pristine systems16. More likely scenarios from which misalignment could have occurred in these systems include chaotic processes during cloud core collapse17,18, as well as late-stage gas accretion onto young disks from the surrounding envelope through large-scale streamers, which may impart further angular momentum onto the outer disk, inducing misalignment in the outer region19,20. Such streamers have primarily been detected feeding Class I systems21, although several recent discoveries demonstrate that this process can occur as late as the Class II evolutionary stage22,23.

The scale of obliquity misalignments observed here can be generated by several possible scenarios. For example, hydrodynamic simulations of cloud core collapse indicate that obliquity angles reach about 40° on average, but can be as high as 80° as a result of turbulence in the formation environment17. Giant planets on moderately inclined orbits can tilt the inner disk, usually by a few degrees24. However, sufficiently massive planets can disconnect the inner and outer disks and, in some cases, broken inner–outer disks can induce considerable obliquity misalignments spanning approximately 20°–150° by torquing the host star and reorienting its spin axis25. Although the timescale for star–disk torquing agrees with stellar ages in our sample (a few Myr), there does not seem to be a trend in morphological characteristics in the disk sample with respect to misalignment. Late accretion infall also has the potential to affect the orientation of outer protoplanetary disks with misalignment angles up to about 80° (ref. 26).

A consequence of misalignment is that planets on wide orbits could form with very inclined orbits17. If these disks maintain the same inclinations at smaller separations of 1–10 au, at which most giant planets form27, then the outer disk orientations may offer clues about primordial alignment of gas giants. In this context, it is noteworthy that the distribution in star–outer disk Δi seems generally similar to the distributions of stellar spin–orbit obliquities observed in transiting hot and warm Jupiters around Sun-like stars (Fig. 1). Although most of these systems seem to be aligned28,29, a notable fraction of obliquity misalignments could therefore be primordial in nature. In this work, the absolute difference between the stellar and disk inclinations represents the lower limit of the true obliquity angle, Ψ (ref. 30). It is therefore possible that some systems could have extreme star–disk misalignments much higher than the projected Δi value and may be connected to hot Jupiters with polar or retrograde orbits31. Without complete knowledge of the spin–orbit angular momentum geometry of the star and disk, the prevalence of primordial retrograde disks cannot be addressed with Δi alone (although the latter configurations are expected to be unlikely outcomes of single-star formation32). Also, primordial obliquity has the potential to explain the misalignments of some coplanar multiplanet systems (such as Kepler-30 (ref. 28)), which do not have a known outer planetary or stellar companion that could be responsible for exciting the inclination of the inner system.

The Solar System has a slight but unambiguous misalignment of about 6° relative to the Sun’s spin axis33,34. This feature is even more appreciable when considering the flatness of the Solar System; the mutual inclinations of the gas and ice giants is 0.3° on spatial scales extending out to 30 au and this flatness continues out to the dynamically cold Kuiper belt at nearly twice this distance. The primordial stellar obliquity distribution found in this work may provide context for the Sun’s obliquity. If the current solar obliquity reflects its primordial obliquity, we can more precisely place it in context with the star–disk systems in this sample by estimating its spectral type at a comparably young age (about 5 Myr). On the basis of evolutionary models35, a 1 M⊙ star at 5 Myr has an effective temperature of about 3,800 K. Comparing this effective temperature with the spectral type calibration appropriate for pre-main sequence stars36, we estimate the pre-main sequence solar spectral type to be approximately K9. Placed into context, the Sun’s obliquity in its pre-main sequence phase is in agreement with most of the sample, which shows a preference for minimum obliquities within about 10° (the typical precision of Δi). Considering the relatively common occurrence of more severe misalignments in protoplanetary disk systems, the slight (yet precise) misalignment angle of the Sun is not at all unusual. Although the origin of the solar obliquity is still a topic of debate37,38,39, these results may indicate that a slightly inclined planet-forming disk is a natural explanation for the observed solar misalignment without the need to invoke post-formation torques.

Considering inner–outer disk misalignment

Several recent studies have investigated the relative alignment of the inner and outer regions of protoplanetary disks. For instance, inner disk misalignment has been inferred from the existence of ‘dipper’ stars (a common class of young variable stars that undergo strong dips in brightness) that host a protoplanetary disk. A population-level analysis of the outer disk inclinations among dipper stars40 found that the dipping phenomenon is probably unrelated to the outer disk, suggesting further that inner–outer disk misalignments may be common. Supporting evidence of inner–outer disk misalignments has also emerged in observations of shadows cast onto outer disks as a result of an inclined inner disk that blocks light from the central star41. Furthermore, scattered-light observations of inner dust disks at sub-au separations have shown direct evidence of inner–outer disk misalignment. Recent observations with VLTI/GRAVITY identified 6 out of 11 systems with substantial inner–outer disk misalignment42. A handful of systems in our sample have shown evidence of inner–outer disk misalignment in the form of dips, shadowing or scattered-light imaging; however, the sample size of systems with complete stellar, inner disk and outer disk inclination measurements is limited and prevents a more extensive analysis of this broader angular momentum architecture (see Supplementary Discussion).

The ‘primordial versus post-formation’ question

Direct imaging of exoplanets is sensitive to separations spanning tens to hundreds of au (ref. 43) and, recently, minimum obliquities of this population have been explored by comparing the stellar inclination to planetary orbital planes traced out with patient orbit monitoring11,44. This emerging population consists of 11 planets across six systems44,45,46,47,48,49, which show a trend towards alignment with the central star. As more planets are discovered at wide separations with direct imaging across a broad range of ages, a direct comparison can be made between the primordial and long-period planet obliquity distributions to determine the role of dynamics in exciting orbital inclinations over time.

The fundamental differences across space and time between the protoplanetary disk sample and planet samples complicate the question of whether the primordial obliquities of Sun-like stars are the primary basis for the obliquity distribution of mature short-period giant planets. This gap in parameter space, the possibility of inner–outer disk misalignments and uncertainty about the dynamical evolutionary pathways following the epoch of planet formation prevent firm conclusions on this topic. However, this gulf in age and orbital distance can soon be addressed with the Gaia astrometric survey’s fourth data release, which is expected to yield thousands of 3D Keplerian orbit fits of cold Jupiters—including their inclinations—at orbital distances up to about 7 au (ref. 50).

Methods

Protoplanetary disk inclinations

We assemble a catalogue of resolved protoplanetary disks by first referencing the list of resolved disks in the Catalog of Circumstellar Disks (https://www.circumstellardisks.org/), which identifies 227 disks around pre-main sequence stars as of its last update on 13 August 2021. We supplement these with entries from another recent compilation of ALMA-detected disks51, as well as resolved disks from individual studies compiled from the recent literature. This amounted to a sample of 690 unique systems. For this study, we isolate our sample to systems with well-determined inclinations (\({{\sigma }}_{{{i}}_{\text{disk}}}\) < 10°) derived from resolved submillimetre observations from ALMA (\({{\sigma }}_{{{i}}_{\text{disk}}}\) = 2.6°, on average). Our adopted measurements of idisk therefore describe the orientation of dust in the outer disk at characteristic spatial scales of tens to hundreds of au. After filtering out disks that do not meet the uncertainty threshold, we are left with 172 systems. We then remove known binaries and stars with spectral types earlier than F6, yielding a sample of 94. Most stars belong to well-studied star-forming regions, primarily the Taurus-Auriga complex, the Lupus complex, and ρ Ophiuchi, with ages ranging from about 1 to 3 Myr (refs. 52,53,54,55,56). For many disks, several independent inclination measurements have been made. For our analysis, we adopt the measurement of idisk with the highest reported precision. We note that some disk inclinations are reported with asymmetric uncertainties. In these cases, we adopt the mean of the upper and lower limits.

Stellar properties

For each object in the initial sample of 94 single, low-mass, protoplanetary-disk-bearing stars, we compile vsini*, Prot and R* measurements available in the literature. Rotation periods are either adopted from previous measurements or are newly determined using light curves from TESS or K2. After selecting for stars that satisfy the requirement that vsini*, Prot and R* have been reliably measured (detailed below), we arrive at a final sample of 49 systems. A minimum uncertainty of 5% is imposed on all adopted stellar parameters if the reported values are smaller than this. Adopted values of Teff, M*, vsini*, Prot and R* are given in Extended Data Table 1.

Projected rotation velocities

For each object in the sample, we compile published independent measurements of the stellar vsini* that were obtained with high-resolution spectra and adopt the weighted mean. Because our measurements are drawn from a diverse array of sources, our adopted vsini* could be subject to systematic effects related to data acquisition, processing and uncertainty estimation. To account for this, we impose a 5% lower limit on the precision of vsini* to mitigate the possibility of a single measurement unfairly weighting the mean. Also, if an object has two or more measurements with no reported uncertainties, we combine them into a single average value and adopt the standard deviation as an estimate of the uncertainty. If only one vsini* is reported without an uncertainty, it is excluded.

Rotation periods

We compiled stellar rotation periods in the literature drawn from independent datasets and adopt the weighted mean and uncertainty. To supplement these, we uniformly analyse TESS57,58 and K2 (ref. 59) light curves for targets in our compilation of resolved disks, avoiding the duplication of Prot measurements from previous analyses of the same TESS and K2 datasets we consider here60,61,62,63,64,65,66,67. We add new rotation periods for 43 objects.

We use the Python package Lightkurve68 to download the TESS 2-min and K2 30-min cadence Pre-search Data Conditioning Simple Aperture Photometry (PDCSAP) light curves69,70,71,72 and, for seven objects, we analyse the TESS light curves reduced with the MIT Quick-Look Pipeline57. For K2 light curves in which instrumental systematics seem to be present in the PDCSAP data, we assess the K2 light curves reduced with either the EPIC Variability Extraction and Removal for Exoplanet Science Targets73 pipeline (one object) or the K2 Systematics Correction74 pipeline (two objects). Because of the potential for crowding in the field, we visually inspect each full-frame image to verify that there is no visibly apparent contamination from nearby stars.

We prepare the data products from each TESS sector or K2 campaign by removing any ‘NaNs’ from the data series and dividing the light curve by the median flux. Some objects were observed over several sectors or campaigns. If an object was observed over two or more consecutive TESS sectors, we stitch the data together to form one light curve. We do not merge light curves that are separated by one or more sectors because the spot evolution that occurs during long gaps in time may cause the rotation signature to no longer be coherent over the duration of the time series, making it difficult to properly assess the periodogram75 and the phase curve. Next, we remove features unrelated to rotational variability from the data (that is, flares and other photometric outliers) by applying a high-pass Savitzky–Golay filter76 and selecting only the points in the original dataset that fall within three standard deviations of the flattened time series. After detrending the data, we compute generalized Lomb–Scargle periodograms77 of the prepared light curves with a sampling resolution of 0.01 days over a search window from 0.2 days to one-third of the total length of time in the light curve. We identify the stellar rotation period as that which corresponds to the maximum signal in the periodogram. The uncertainty on Prot is estimated as the half-width of the peak profile in the power spectrum. If one object has more than one TESS or K2 light curve, each light curve is analysed separately and we adopt the weighted mean of the individual results.

Doppler imaging of young stars demonstrates that spots can exist at high and intermediate latitudes rather than at the equator78,79,80,81,82,83,84,85,86. This can affect the measured rotation periods if the young stars in our sample experience differential rotation. Periodic signals detected in the light curves may not actually trace the equatorial rotation period used to compute the stellar inclination angle, which would bias the results towards higher values of i*. We account for the effect of possible differential rotation of spots at unknown latitudes by inflating the uncertainties of the rotation periods with an error term σshear that represents half the maximum difference in rotation between the pole and the equator11. This term relates the star’s absolute shear, ΔΩ (a metric to quantify differential rotation), and the equatorial rotation period, Pmax, determined from the light curve:

$${\sigma }_{{\rm{shear}}}\approx \frac{1}{2}\left({P}_{\max }-{\left(\frac{\Delta \varOmega }{2{\rm{\pi }}}+\frac{1}{{P}_{\max }}\right)}^{-1}\right).$$
(1)

We assume a Sun-like shear of ΔΩ = 0.07 rad day−1 and add σshear in quadrature to the Prot uncertainties from the periodogram analysis in our sample. Given that the exact spot distributions are unknown, we do not apply any explicit corrections to the measured period value.

Stellar radii

We adopt R* estimates from the TESS Input Catalog87 (TIC). Although the overall distribution of the TIC radii in our sample does not differ substantially from the weighted mean values of other radii found in the literature (Extended Data Fig. 1), adopting radii from the TIC ensures consistency across the sample. TIC radius estimates are determined by means of the Stefan–Boltzmann relation based on Gaia-determined distances, extinction-corrected G-band magnitudes and G-band bolometric corrections88. Moreover, the accuracy of R* in the TIC is well characterized; stellar radii in the catalogue are found to be typically within 7% of the values measured for the same stars with asteroseismology89. We therefore inflate the uncertainties on R* from the TIC by adding a 7% error term in quadrature with the nominal uncertainty11. For most stars in the sample, there is no uncertainty reported with the TIC radius. For these objects, we assume a conservative uncertainty of 16%, which corresponds to the 95% quantile of the entire TIC radius uncertainty distribution. To this, we then add an extra 7% systematic error in quadrature.

The stellar radius and rotation period should always yield an equatorial rotation velocity (veq, in which veq = 2πR*/Prot) that is greater than or equal to vsini*. Most of the sample follows this to within 2σ, with the exception of nine stars (2MASS J04202555+2700355, 2MASS J04360131+1726120, AA Tau, DoAr 25, FT Tau, IQ Tau, Sz 73, T Cha and WSB 52). This disagreement could be the result of potentially overestimated rotation periods, overestimated vsini* or underestimated radii. The average Prot and vsini* of this subset (Prot = 5.0 ± 2.7 days and vsini* = 18.7 ± 9.3 km s−1) compared with non-discrepant systems (Prot = 4.8 ± 2.0 days and vsini* = 16.6 ± 11.3 km s−1) do not indicate that an overestimation of either parameter is the cause of the disagreement. However, the TIC radii of the stars in this subset are, on average, 36% lower than the mean of all non-TIC radii compiled for these same stars, whereas the rest of the objects in the sample that do not yield discrepant veq and vsini* values are, on average, only 3% lower than the mean of their non-TIC counterparts. Some TIC radii may therefore be underestimated, leading to the disagreement in viable values of veq.

For the discrepant stars, we adopt radii from alternative sources, most of which originate from a separate catalogue of radius estimates90 using spectra from the APOGEE91, GALAH92 and RAVE93 surveys, validated with CHARA interferometry94, Hubble Space Telescope flux standards95 and asteroseismology96, which we refer to as the Y23 catalogue. The Y23 catalogue has a characteristic accuracy within 5% of asteroseismology measurements96. We thus add a conservative 5% systematic error term in quadrature to the uncertainties quoted in the Y23 catalogue. Four stars do not have a radius estimate from Y23 (2MASS J04202555+2700355, Sz 73, V1094 Sco and WSB 52), so we adopt the mean of the literature radii and estimate a conservative uncertainty equal to two times the standard deviation. After these adjustments to radii, the sample veq and vsini* are consistent to within 2σ (Extended Data Fig. 2), the only exception being WSB 52, which is discrepant at the 2.4σ level. Five systems did not have reported TIC radii (2MASS J04334465+2615005, CIDA-7, Elias 2-24, MHO 6 and WSB 63), so for these systems, we also adopt the radius estimate from the Y23 catalogue, adding a 5% systematic error term in quadrature to the quoted uncertainties. All compiled values of Teff, M*, vsini*, Prot and R* from the literature are provided in the Supplementary Methods.

Stellar inclination

With our adopted measurements of R*, vsini* and Prot, we determine the stellar inclination i* following a Bayesian probabilistic framework10, which properly accounts for the correlation between vsini* and veq. In particular, we use the analytical expression for the posterior distribution of i* (ref. 11), which assumes an isotropic prior on i* and considers uniform priors on vsini*, R* and Prot (with a moderately precise measurement uncertainty of Prot < 20%):

$$P({i}_{\ast }|{P}_{{\rm{r}}{\rm{o}}{\rm{t}}},{R}_{\ast },v\sin {i}_{\ast })\propto \sin {i}_{\ast }\times \frac{{{\rm{e}}}^{-\frac{{\left(v\sin {i}_{\ast }-\frac{2{\rm{\pi }}{R}_{\ast }}{{P}_{{\rm{r}}{\rm{o}}{\rm{t}}}}\sin {i}_{\ast }\right)}^{2}}{2\left({{\sigma }}_{v\sin {i}_{\ast }}^{2}+{{\sigma }}_{{v}_{{\rm{e}}{\rm{q}}}}^{2}{\sin }^{2}{i}_{\ast }\right)}}}{\sqrt{{{\sigma }}_{v\sin {i}_{\ast }}^{2}\,+\,{{\sigma }}_{{v}_{{\rm{e}}{\rm{q}}}}^{2}{\sin }^{2}{i}_{\ast }}},$$
(2)

in which

$${\sigma }_{{v}_{{\rm{eq}}}}=\frac{2{\rm{\pi }}{R}_{* }}{{P}_{{\rm{rot}}}}\sqrt{{\left(\frac{{\sigma }_{{R}_{* }}}{{R}_{* }}\right)}^{2}+{\left(\frac{{\sigma }_{{P}_{{\rm{rot}}}}}{{P}_{{\rm{rot}}}}\right)}^{2}},$$
(3)

and \({\sigma }_{{P}_{{\rm{rot}}}}\), \({\sigma }_{v\sin {i}_{* }}\) and \({\sigma }_{{R}_{* }}\) are the uncertainties on the rotation period, projected rotational velocity and stellar radius, respectively. We note that the reported vsini* measurements for four objects in our sample (2MASS J16083070-3828268, GW Lup, Sz 114 and Sz 130) are upper limits. For these cases, we use the analytical expression

$$P({i}_{* }| {P}_{{\rm{rot}}},{R}_{* },v\sin {i}_{* })\propto {\sin i}_{* }\times \left({\rm{erf}}\left(\frac{l-\frac{2{\rm{\pi }}{R}_{* }}{{P}_{{\rm{rot}}}}\sin {i}_{* }}{\sqrt{2}{\sigma }_{{v}_{{\rm{eq}}}}\sin {i}_{* }}\right)+{\rm{erf}}\left(\frac{\sqrt{2}{\rm{\pi }}{R}_{* }}{{\sigma }_{{v}_{{\rm{eq}}}}{P}_{{\rm{rot}}}}\right)\right),$$
(4)

in which l is the upper limit of vsini*. The i* posterior distributions are shown in the Supplementary Methods. For each star, we report the i* MAP value and 68% highest density interval in Extended Data Table 2.

Star–disk minimum obliquity, Δi

To determine Δi for each object, we randomly draw 106 samples from the posterior distribution of i* and the probability distribution of idisk and compute the absolute difference between each sampled pair. Our adopted value of Δi is the distribution mode and our reported uncertainty range is the 68% highest density interval. Resulting Δi values and confidence ranges are provided in Extended Data Table 2 and Δi probability distributions are shown in the Supplementary Methods. Extended Data Fig. 3 shows Δi plotted as a function of system properties such as spectral type, M*, Teff, R*, Prot, vsini*, idisk and i*. We compute the Pearson correlation coefficient, r, between Δi and each system property to test for correlated dependencies and identify no strong relationship with any parameter. Correlation coefficients in this test range from −0.04 to 0.37. These tests further yield high P-values, suggesting that any correlation indicated in the resulting r-values is statistically indistinguishable from the null hypothesis of no correlation. Correlation coefficients are shown in Extended Data Fig. 3. We note that the correlation coefficient for Δi with respect to i* seems to be moderately correlated, with r = 0.37 and P = 0.01. However, these results do not take into account the uncertainties of the individual data points. When we repeat this test 100 times drawing Δi randomly from the individual probability distributions, the average Pearson r correlation coefficient is equal to 0.01, with an average P-value of 0.48. The moderate but notable correlation in i* versus Δi that is initially apparent does not hold when taking into account the uncertainties in Δi. Repeating this procedure for all other system parameters yields similar results. We therefore identify no notable correlation in Δi with respect to spectral type, M*, Teff, R*, Prot, vsini*, idisk or i*.

Because potential trends in Δi may not present only as a linear relationship, we conduct a second test to identify possible clustering of minimum obliquities at higher or lower values within subpopulations of dependent variables. Specifically, we separate the sample into two subgroups equal in size consisting of smaller or larger stellar parameters. We then determine the mean and standard deviation of each subgroup and compute the significance of the difference of the means. For every system parameter, the two subpopulations are consistent at a <1σ level. We therefore find no evidence that Δi clusters at low or high values for either subpopulation of sample parameters (Extended Data Fig. 3).

KDE of the Δi distribution

The KDE of the population-level Δi distribution is computed for 500 samples drawn from each individual Δi probability distribution in the sample (resulting in a total of 21,500 samples). We choose a kernel broadening parameter of 5.3°, which is the average deviation from the mean of the 68% confidence interval limits for each Δi distribution. Next, we use the uncertainties of idisk, vsini*, Prot and R* to generate a family of KDE reconstructions of the Δi distribution. For every object, we randomly sample 500 new values for each parameter, drawn from a normal distribution that reflects the adopted value and uncertainty of the parameter. From the samples, we generate 500 new Δi probability distributions for each object, which are then used to generate new KDEs following the same method to compute the nominal KDE. The diversity of the resulting family of KDE reconstructions is shown in Extended Data Fig. 4.

HBM of Δi

We estimate the underlying distribution of Δi with HBM using the open-source Python software ePop! (ref. 97). Although the package was originally developed to model eccentricities, it can be generalized by mapping observations that span different ranges to a single domain from 0 to 1. ePop! uses an importance sampling methodology98 and offers several choices for underlying parametric models, which have previously been used to characterize stellar obliquity distributions28. In the context of HBM, the model parameters are hyperparameters with posterior distributions determined with the affine-invariant Markov chain Monte Carlo (MCMC) sampler emcee99. Here we explore three population-level models to represent the underlying distribution in Δi. We choose these models because they are flexible and consist of just one or two free parameters, easing the interpretation of the results. The first underlying model we test is the Rayleigh distribution, \({\mathcal{R}}(\Delta i|\nu )\), given by

$${\mathcal{R}}(\Delta i|\nu )=\frac{\Delta i}{{\nu }^{2}}{{\rm{e}}}^{-\frac{\Delta {i}^{2}}{2{\nu }^{2}}}.$$
(5)

The second is a Gaussian distribution, \({\mathcal{N}}(\Delta i| \mu ,\sigma )\),

$${\mathcal{N}}(\Delta i| \mu ,\sigma )=\frac{1}{\sigma \sqrt{2{\rm{\pi }}}}{{\rm{e}}}^{-\frac{1}{2}{\left(\frac{\Delta i-\mu }{\sigma }\right)}^{2}},$$
(6)

and the third is a truncated Gaussian, \({\mathcal{T}}\,(\Delta i|\mu ,\sigma ,a,b)\),

$$\begin{array}{cc}{\mathcal{T}}\,(\Delta i|\mu ,{\sigma },a,b)=\frac{1}{{\sigma }}\frac{\frac{1}{\sqrt{2{\rm{\pi }}}}{{\rm{e}}}^{-\frac{1}{2}{\left(\frac{\Delta i-\mu }{{\sigma }}\right)}^{2}}}{\varPhi \left(\frac{b-\mu }{{\sigma }}\right)-\varPhi \left(\frac{a-\mu }{{\sigma }}\right)}, & a\le \Delta i\le b,\end{array}$$
(7)

where Φ is the cumulative density function of the standard normal distribution. We convert each object’s distribution in Δi (originally ranging from 0° to 90°) to a new, normalized variable Δi′ = Δi/90°, spanning the interval [a = 0, b = 1] to satisfy the generalized domain space in ePop!. The resulting posterior is then readily remapped to the original scale. Two hyperpriors are tested on the Rayleigh and Gaussian distributions to evaluate the degree to which our choice of priors affects the posteriors. We choose hyperpriors that have demonstrated the ability to produce families of distributions with sufficiently diverse morphologies to yield the most robust results56. Our first hyperprior is a truncated Gaussian with μ′ = 0.69, σ′ = 1.0:

$$p(\Delta i| {\mu }^{{\prime} },{\sigma }^{{\prime} })=\frac{1}{{\sigma }^{{\prime} }}\frac{\frac{1}{\sqrt{2{\rm{\pi }}}}{{\rm{e}}}^{-\frac{1}{2}{\left(\frac{\Delta i-{\mu }^{{\prime} }}{{\sigma }^{{\prime} }}\right)}^{2}}}{1-\frac{1}{2}\left(1+{\rm{erf}}\left(\frac{-{\mu }^{{\prime} }}{{\sigma }^{{\prime} }\sqrt{2}}\right)\right)}$$
(8)

and our second choice of hyperprior draws from a log-uniform distribution ranging from 0.01 to 100:

$$p(\Delta i)=\frac{1}{\Delta i}.$$
(9)

We apply a uniform hyperprior:

$$\begin{array}{cc}f(\Delta i|{x}_{0},{x}_{1})=\frac{1}{{x}_{1}-{x}_{0}}, & {x}_{0}\le x\le {x}_{1},\end{array}$$
(10)

for the truncated Gaussian underlying model, with μ ranging from –1,000 to 1,000 and σ from 0 to 1,000. Each MCMC run consists of 80 walkers for 6 × 104 steps with a burn-in fraction of 50%. For both parametric models, we perform a visual inspection of the trace plots to ensure that the chains have properly converged. Each of the best-fit models of the underlying distribution of Δi yields similar results, indicating that the stellar obliquity distribution is broad (Extended Data Fig. 4). We provide the best-fit parameters and confidence ranges for the Rayleigh, Gaussian and truncated Gaussian models in Extended Data Table 3.

Characterization of systematics and biases

The distribution of MAP values of i* shows that 14 out of 49 stars in our sample are equator-on with inclinations that are likely to be >80°. If the stellar orientation was randomly distributed–which is a reasonable assumption for isolated stars but may not be valid for this sample with resolved disks–the probability of i* > 80° is \({\int }_{{i}_{* }={80}^{\circ }}^{{i}_{* }={90}^{\circ }}\sin {i}_{* }{\rm{d}}{i}_{* }=0.174\). This points to an expectation value of about 8 for a sample of 49 stars, suggesting that there may be a preference towards equator-on stars in the sample population above what would be expected by chance. Using binomial statistics, we can quantify the significance of this discrepancy by computing the probability of an event occurring that is at least as extreme as these measurements (k = 14 out of n = 49 systems). The probability of a success is P = 0.174 and so the probability of observing at least 14 stars out of 49 with i* > 80° can be computed by taking 1 minus the probability of observing fewer than 14 stars with i* > 80°: \(P(k\ge 14| p=0.174,\,n=49)=1-P(k < 14| p=0.174,\,n=49)\,=\,1-\)\({\sum }_{k=0}^{13}\left(\genfrac{}{}{0ex}{}{n}{k}\right){p}^{k}(1-p{)}^{(n-k)}=0.054\). There is thus a probability of about 5% of there being at least 14 equator-on stars in our sample. The overrepresentation of high-inclination stars is mild, exceeding the expectation value by only 6.

Computational tools used

This research has made use of the VizieR (ref. 100) catalogue access tool, CDS Strasbourg, France101 and the following open-source software: ePop! (ref. 97), Lightkurve68, Astropy102, NumPy103, SciPy104 and Matplotlib105.