Abstract
Metabolism enables life to sustain dynamics and to repeatedly interact with the environment by storing and consuming chemical energy. A major challenge for artificial molecular machines is to find a universal energy source akin to ATP for biological organisms and electricity for electromechanical machines. More than 20 years ago, DNA was first used as fuel to drive nanomechanical devices1,2 and catalytic reactions3. However, each system requires distinct fuel sequences, preventing DNA alone from becoming a universal energy source. Despite extensive efforts4, we still lack an ATP-like or electricity-like power supply to sustain diverse molecular machines. Here we show that heat can restore enzyme-free DNA circuits from equilibrium to out-of-equilibrium states. During heating and cooling, nucleic acids with strong secondary structures reach kinetically trapped states5,6, providing energy for subsequent computation. We demonstrate that complex logic circuits and neural networks, involving more than 200 distinct molecular species, can respond to a temperature ramp and recharge within minutes, allowing at least 16 rounds of computation with varying sequential inputs. Our strategy enables diverse systems to be powered by the same energy source without problematic waste build-up, thereby ensuring consistent performance over time. This scalable approach supports the sustained operation of enzyme-free molecular circuits and opens opportunities for advanced autonomous behaviours, such as iterative computation and unsupervised learning in artificial chemical systems.
Similar content being viewed by others
Main
Nucleic acid circuits using polymerases can maintain dynamic steady states by consuming nucleoside or deoxynucleoside triphosphates7,8, demonstrating diverse functions, such as multistate memories9 and nonlinear classification10. However, with a few exceptions11, they continuously consume energy even without input changes, leading to energy waste and limited operation times12. Enzyme-free nucleic acid circuits use only rationally designed components, making them more robust to environmental changes, such as temperature and salt conditions13, while performing complex information processing tasks, including Boolean logic14,15 and neural computation16,17. Yet, beyond equilibrium computation18,19, these systems cannot sustain information processing and respond to new inputs once the energy from unpaired bases or out-of-equilibrium concentrations is depleted. This limitation has hindered the development of enzyme-free circuits capable of advanced behaviours, such as iterative computation20 and learning21.
Several strategies have been explored to achieve more sustainable computations in enzyme-free nucleic acid circuits, but the complexity remains limited to simple logic circuits with fewer than a dozen distinct molecular species18,22,23,24,25,26. Buffering schemes can maintain set species concentrations22,23,27 but require buffers in large excess, making it difficult to mitigate faulty outputs from spurious interactions. Each gate also relies on a distinct buffer, which limits scalability, and, furthermore, circuit performance decays as buffers are consumed. Another strategy uses reversible reactions18,24,25. These systems are either non-catalytic18,24, lack signal amplification and thus limiting scalability or require new fuels for new inputs25 and thus sacrificing autonomy. Waste build-up further causes performance decay.
Instead of relying on chemical energy stored in specific molecules, universal energy sources, such as magnetic28 or electrical fields29, light30,31 and heat26, have shown potential to sustain the performance of artificial molecular machines. For example, a reusable DNA logic gate was designed to operate at a lower temperature and reset at a higher temperature by exploiting the temperature-dependent balance of enthalpy and entropy in associative strand displacement26. However, its operating and reset temperatures are sensitive to molecular sequences and concentrations, limiting scalability.
Here we developed an enzyme-free circuit architecture for sustainable computation that uses a universal, accessible energy source, avoids problematic waste build-up, maintains consistent performance, incorporates signal amplification, scales to complex circuits and supports autonomous behaviours in artificial molecular machines.
Concept
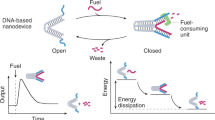
Consider a molecular circuit that stays out of equilibrium using kinetic traps (Fig. 1a), in which some monomers capable of forming dimers cannot do so because their partners are already bound elsewhere. Each input catalyses a distinct reaction, breaking an existing dimer and enabling new dimerization. This produces a unique monomer output and selectively pushes part of the system towards equilibrium, whereas unreacted molecules remain kinetically trapped. Because the input acts catalytically, the outputs remain active even after the input has been changed (for example, removed) by an upstream process, making the circuit one-time use. Heating and cooling the system normally drive it to thermodynamic equilibrium. However, if strong, flexible linkages are introduced between kinetically trapped monomers (Fig. 1b), dimerization can be favoured at high temperatures when entropy dominates, allowing the system to reset the kinetic traps after input removal. Upon cooling, the circuit returns to its initial state, ready for new inputs. Unlike reusability through reversible reactions18,24,25 and other forms of equilibrium computation19,32, reusability through kinetic traps does not rely on input to provide energy for computation but uses heat alone to reach a higher energy state that leads to the recharged state at a local but not global minimum (Extended Data Fig. 1).
a, A use-once molecular circuit. Balls with distinct colours indicate monomers with distinct identities. Free monomers can bind to each other if they have the same colour. Dimers with two colours indicate the kinetically trapped monomers. Through transient interactions, input monomers can break bonds in dimers that have a monomer with a matching colour. b, A reusable molecular circuit. The dashed lines indicate strong and flexible linkages between monomers, which are independent of weak bonds. Heat can break any weak bonds but not strong linkages. Inputs are low-concentration catalysts, which are removed when heat is applied. c, A use-once DNA catalyst. d, A reusable DNA catalyst. Coloured lines indicate strands with arrowheads marking their 3′ ends. S, T and Y are domain names, and S*, T* and Y* indicate their complementary domains. T indicates a toehold for initiating strand displacement. S and Y indicate two distinct long domains that specify the identities of the input and output, respectively.
The above abstract principle can be implemented in DNA. Toehold exchange33 enables catalytic control over DNA hybridization, which is a form of molecular dimerization. In ‘seesaw circuits’14, a use-once DNA circuit architecture, an output strand is initially bound to a gate strand, creating a kinetic trap that prevents a fuel strand from binding (Fig. 1c). An input strand catalyses output release through toehold-mediated strand displacement1, allowing the fuel to bind to the gate instead. A small amount of input triggers the production of a large amount of output, thereby achieving signal amplification. However, heating and cooling cannot reset the kinetic trap because all duplexes would simply equilibrate to their thermodynamically favoured states.
Nucleic acids with strong secondary structures can reach kinetically trapped states during heating and cooling, a principle previously used to reset polymers to monomers, as in the hybridization chain reaction5,6. Temperature and cooling rate have also been used to control the hybridization outcomes34,35. Building on these principles, we covalently linked the output and gate strands into a hairpin structure (Fig. 1d). The input still catalysed hybridization exchange between the output, fuel and gate, but the output remained tethered to the gate:fuel complex. Upon heating, all molecules became single-stranded. As the system cooled, unimolecular gate–output hybridization formed first, favoured by a lower entropic cost over bimolecular binding. Although further cooling thermodynamically favoured gate–fuel binding at high fuel concentrations, it was kinetically suppressed because the gate was already occupied. Thus, after input removal and a heat–cool cycle, the system reset to its initial kinetic trap. However, balancing circuit performance and reset efficiency required further refinements, as discussed below.
A reusable catalyst
Linking the output and gate into a hairpin biases the output release backward at typical concentrations because the reverse reaction becomes unimolecular, resulting in slow forward kinetics. To address this, we developed mechanisms to accelerate the overall reaction (Fig. 2a). First, we introduced a one-nucleotide bulge loop (B*) between the long domain (S*) and the toehold (T*) in the gate strand. The input was modified with a complementary nucleotide to bind to the bulge. The bulge acted like a mismatch36,37, slowing the reverse branch migration and biasing the second reaction step forward, providing a hidden drive without increasing undesired output production. Toehold dissociation (third step) was slower than unimolecular hybridization and was thus biased backward. We added another toehold within the hairpin loop, creating a fourth step that closed a smaller hairpin loop, resulting in an approximately 10-fold speed-up compared with the reverse reaction in the third step and further driving the reaction forward. When the toehold of the output became available, it reacted with a reporter complex, displacing a quencher strand and increasing fluorescence (fifth and sixth steps). The toehold of the fluorophore strand then opened the hairpin (seventh step), enabling the fuel strand to free the input for further catalytic cycles (eighth step). Although the number of base pairs remained unchanged, the seventh step was biased forward by the entropic gain from opening the hairpin. Unlike the use-once seesaw catalyst14, the catalytic behaviour required a downstream drain, such as the reporter. Nonetheless, an 82-fold turnover was achieved within 24 h for 1 nM input (Extended Data Fig. 2).
a, Reaction pathway. The thickness of the arrows indicates the relative forward and backward rates for each reversible reaction step; thicker arrows indicate faster rates. b, Reactions and simulation of reset. Reactions in black and grey indicate the desired and undesired reactions, respectively. c,d, Total concentrations of fluorescent molecules after heating and cooling (c) and 90% reaction completion times with 1× input (d) for eight distinct designs predicted by simulations and measured by experiments. Bar labels 0, 6 and 7 indicate the size of the loop toehold and its matching reporter toehold, whereas 6:7 indicates a 6-nt loop toehold and 7-nt reporter toehold. The bar charts are on the basis of the data in Supplementary Figs. 13–16. Error bars indicate the standard deviation for four sets of repeated experiments. e, Key design choices. T′ indicates T with a nucleotide deletion at the 3′-end. f, Simulations and fluorescence kinetics experiments of a reusable DNA catalyst. Here and in the following figures, the standard concentration 1× denotes 100 nM. The solid and dotted trajectories represent simulations and experiments, respectively. The hairpin gate (GY), fuel (F) and reporter (RQ) are at 1×, 2× and 2×, respectively. A full list of the DNA sequences is provided in Supplementary Table 2.
To evaluate how well the DNA catalyst using a hairpin gate can be recharged by heat, we developed a biophysical model (Supplementary Note 2.1) and simulated the reset behaviour using mass action kinetics (Fig. 2b). The main competing reaction during cooling is the binding between the reporter strand and the single-stranded gate–output (G–Y + R ⇌ G–YR) because G–YR has seven more base pairs than the hairpin gate GY. Simulations predicted that approximately 18 nM of the hairpin gate would fail to restore, corresponding to an 82% reset success rate (Supplementary Fig. 17a). To reduce the impact of the competing reaction, we deleted one nucleotide from the loop toehold, creating a bulge when the reporter bound to the output (Fig. 2b), which decreased the binding energy and melting temperature of G–YR. As hairpins closed quickly, the concentration of the single-stranded G–Y dropped rapidly, and even a small (1–2 °C) decrease in the melting temperature substantially limited the G–YR formation. With the deletion, the simulations predicted an improved reset success rate of 96% (Fig. 2b and Supplementary Fig. 17b). Overall, kinetics plays a more important role than thermodynamics for reset: slower hairpin closing rates can decrease reset success by more than 50% without affecting the melting temperature (Extended Data Fig. 3).
To systematically understand the trade-off between circuit performance (signal amplification speed) and reset efficiency (percentage of molecules restored), we compared simulations with fluorescence experiments for eight designs with varying bulge and toehold configurations (Fig. 2c,d). The simulations revealed three main conclusions, as confirmed by experiments: (1) a bulge in the hairpin gate promotes faster kinetics but compromises reusability; (2) an extra toehold in the hairpin loop similarly promotes faster kinetics but reduces reusability; and (3) a nucleotide deletion in the loop toehold introduces a bulge upon output–reporter binding, rescuing reusability with a mild cost to reaction speed. On the basis of these insights, we selected a design that balances performance and reset (Fig. 2e). The resulting catalyst achieved a 10-fold signal amplification within 2 h (Fig. 2f, left). A complementary inhibitor strand was used to inactivate the input, simulating the input change caused by upstream processes. After input inactivation and reset by heating to 95 °C and cooling to 20 °C in 1 min, the output returned to near zero (Fig. 2f, middle), and the circuit function was reproduced upon the reintroduction of the input (Fig. 2f, right). Although fast cooling, also known as quenching, is often considered necessary for reaching kinetic traps35, our design is robust to the rate of cooling. The reset success rate remained above 90% even with slow cooling for more than 75 min (Extended Data Fig. 4), and the circuit function was largely preserved even after 100 rounds of reset, with DNA degradation at high temperatures identified as the main limiting factor for circuit reusability (Extended Data Fig. 5).
Next, we investigated key questions for creating complex reusable DNA circuits. How precisely can hairpin gate kinetics be controlled for rate-dependent computation? How effectively can hairpin gates cascade in multilayer circuits? What design principles enable several types of circuit components to reset simultaneously in one tube? A reusable winner-take-all DNA neural network provided a case study to address these questions and serves as a foundation for synthetic molecular systems to repeatedly recognize complex patterns and improve future responses.
Kinetics and cascading
In theory, rate-independent computations offer a robust framework for molecular information processing38. However, most experimental demonstrations still rely on precise rate control to achieve complex computations and dynamics. Winner-take-all DNA neural networks exemplify this challenge, in which an accurate molecular pattern classification depends on equal rates across competing reaction pathways16,39,40. In a two-input winner-take-all function (Fig. 3a), the output turns on if and only if the corresponding input has a larger concentration. An annihilator (Anh1,2) converts both inputs into wastes through cooperative hybridization41 until only one remains, and restoration gates (GY1 and GY2) and fuels (YF1 and YF2) amplify the winner to a standard on state. Equal amplification rates are critical for avoiding biased competition. However, unlike in standard bimolecular strand displacement reactions, we found that two hairpin gates sharing the same toehold but differing in long domains showed more than a 10-fold difference in kinetics (Fig. 3b and Supplementary Fig. 20).
a, Implementation of a two-input winner-take-all (WTA) function. Here and in the following figures, red numbers within a node or on a wire in the DNA circuit diagrams indicate distinct species and their relative initial concentrations. b,c, Sequence-level diagrams, simulations and fluorescence kinetics experiments of a pair of DNA catalysts without (b) and with (c) a loop toehold. A full list of the DNA sequences is provided in Supplementary Table 3. d, Simulation of the reset. Half of the species (G–Y1, GY1, F1 and so on) are shown, and their trajectories are identical to the other half (G–Y2, GY2, F2 and so on). e, Implementation of weighted sum function. f,g, Domain-level diagrams, simulations and fluorescence kinetics experiments of a two-layer cascade with a hairpin (f) and a two-stranded (g) downstream gate. The DNA sequences are listed in Supplementary Table 4. h, Cascade with alternating layers of hairpin gates and two-stranded gates for implementing catalytic and stoichiometric reactions, respectively. Variables xi (input), wij (weight), pij (weighted input), sj (weighted sum), and yj (output) in the abstract functions are implemented with concentrations of DNA species Xi, GPij, Pij, Sj, and Yj, respectively (i = 1 to n and j = 1 to 2). Weight fuel XFi, summation gate GSj, and restoration fuel YFj facilitate weight multiplication, summation, and signal restoration, respectively. Reporter:quencher RQj detects output Yj and releases quencher Qj for fluorescence readout. Subscripts in species names are omitted when a single species per type is used for testing purposes.
To investigate the cause of the kinetics difference, we evaluated five hypotheses: strand purity (Supplementary Fig. 22), reporter reversibility (Supplementary Fig. 23), linker sequence (Supplementary Fig. 24), branch migration sequence (Supplementary Fig. 25) and loop sequence (Supplementary Fig. 26). Experimental evidence rejected the first four hypotheses but supported the last. NUPACK42 analysis further confirmed that within both hairpin gates the output domains (Y1 and Y2) had spurious interactions with the open toehold (T*) when the input was bound to the gate (Fig. 3b and Supplementary Fig. 21), competing with the T*–T binding. Stronger spurious interactions increased toehold availability for downstream reactions. Although a more stringent sequence design could reduce spurious binding (Supplementary Fig. 27), introducing a loop toehold provided a simpler and more effective solution; it replaced spurious interactions with a designed binding (Fig. 3c), forming more base pairs and a smaller loop, which enabled similar kinetics of the two hairpin gates. The desired kinetics was preserved after reset, whether the two catalysts were heated and cooled separately or together (Extended Data Fig. 6).
Combining an annihilator with two hairpin gates completed the two-input winner-take-all circuit. The annihilator, composed of two long domains and presented at a 4-fold higher concentration than the gates, was expected to have a similar melting temperature and reset at roughly the same time as the hairpin gates during cooling (Fig. 3d). Although single-stranded gates and fuels could bind to the annihilator and compete with its reset, such binding is expected to occur at lower temperatures after the annihilator has been restored. The fluorescence kinetics experiments confirmed the correct circuit computation for six input combinations, with similar behaviour observed after reset (Extended Data Fig. 7).
Implementing the weighted sum function in a winner-take-all neural network requires composing upstream gates for weight multiplication with downstream gates for summation (Fig. 3e). A weight gate uses the same hairpin gate design described above, whereas a summation gate can also be a hairpin gate but without fuel (Fig. 3f). Because the loop toehold in the weight gate becomes double-stranded when bound to the summation gate, the summation reaction is driven forward without the need for a bulge or loop toehold. However, in this two-layer circuit, only approximately 60% reaction completion was achieved at high input concentration (Fig. 3f). Replacing the downstream hairpin gate with a two-stranded gate restored the full reaction completion (Fig. 3g). This problem arose from the intramolecular toehold occlusion (Supplementary Fig. 28). When the weighted sum signal was released, it remained tethered to the input-bound gate with an open toehold, occluding the toehold of the signal and inhibiting it from participating in downstream reactions. Cascades with more layers would exacerbate this issue, reducing the kinetic control and reaction completion.
A solution to scalable cascades is to use hairpin gates and two-stranded gates in alternating layers of catalytic and stoichiometric reactions (Fig. 3h). Hairpin gates are essential for catalytic reactions, favouring gate–output over gate–fuel binding during reset. Stoichiometric reactions use two-stranded gates without fuels, in which reset competes only with binding to upstream outputs and downstream gates. Because both the upstream and downstream reactions are catalytic, their hairpin gates reset at higher temperatures, minimizing interference with the two-stranded gate reset at lower temperatures. To evaluate this strategy, we constructed a 9-bit, two-memory winner-take-all neural network for classifying ‘L’ and ‘T’ patterns. The network demonstrated reusability with alternating test patterns over ten rounds of computation, maintaining consistent performance over time (Extended Data Fig. 8).
Scalability
To assess scalability, we constructed a 100-bit, two-memory winner-take-all neural network for classifying handwritten digits ‘6’ and ‘7’ from the Modified National Institute of Standards and Technology (MNIST) database (Fig. 4a). The full system involved up to 289 distinct DNA strands; for the input patterns tested, 213 strands were present in one tube. Upon heating to 95 °C, all molecules became single-stranded. During cooling, hairpin gates (GPij and GYj) and annihilators (Anhjk) reset at higher temperatures, whereas two-stranded gates (GSj) and reporters (RQj) reset at lower temperatures. Fuels (XFi and YFj) remained single-stranded after hairpin gates have formed. The simulations predicted reset success rates of 93% for the annihilators and 85% for the summation gates (Fig. 4b). However, because both were in excess, their reduced concentrations would still support the correct computation. The reset success rate was expected to remain constant for subsequent resets.
a, Abstract circuit diagram, DNA implementation and number of strands. 1 ≤ i ≤ 100; 1 ≤ j,k ≤ 2 (k ≠ j). For the input, input inhibitor and total number of strands, the two values to the left and right sides of the vertical line correspond to the specific input patterns shown in this figure and all possible inputs, respectively. Grey bars next to species names correlate with their reset temperatures; darker means reset at a higher temperature. b, Simulation of the reset. For simplicity, only the desired product species are shown; the concentrations of other species can be inferred from the conservation laws and are shown in Supplementary Fig. 11. c, Steps for testing the reusability of the system. Each reset involves input inactivation, heating and cooling and introduction of a new test pattern. d, Weighted sum analysis of ten representative Modified National Institute of Standards and Technology digits. A test pattern closer to the diagonal line is harder, and one farther from the diagonal line is easier to classify. e, Simulations and fluorescence kinetics experiments for classifying ten test patterns sequentially added to the same test tube. The DNA sequences are listed in Supplementary Table 5.
The central question for scalability is whether stringent sequence design criteria are necessary to minimize crosstalk during reset. In use-once DNA circuits, the excellent specificity of strand displacement allows long domains to share up to 70% of their sequences14,16. By contrast, hybridization specificity is limited, except near the melting temperature. Because the temperature ramp during reset covers the full melting range of all species, it is conceivable that specificity remains sufficient. To investigate this, we used sequence design criteria developed for use-once circuits. Ten representative tests were selected on the basis of positions in the weighted sum space (Fig. 4d) and sequentially added to the reusable DNA neural network (Fig. 4c). The simulations assumed an ideal reset without errors, allowing for a comparison with the experiments to assess the reset performance. The fluorescence kinetics data closely matched the simulations (Fig. 4e), indicating that the neural network reliably processed distinct inputs over time. Initially, the tube contained approximately 100 distinct molecular species; each test added up to 20 distinct inputs, and each reset added up to 20 inhibitors. After ten rounds, more than 200 distinct strands accumulated, demonstrating robust scalability and reset.
We further demonstrated the distinct roles of input and heat in a 100-bit neural network (Extended Data Fig. 9). Partial patterns with missing specific inputs were misclassified as the opposite digit class. Once activated, the outputs could not revert to off even after the missing inputs were added, leading to a faulty computation with both outputs on. Heating and cooling reset the network, restoring the correct computation on the basis of all present inputs. Similarly, adding specific inhibitors to full input patterns converted them into partial patterns but did not flip the outputs until after heating and cooling. These experiments illustrate that changes in inputs alone are insufficient to update circuit decisions; instead, heat is required to recharge the system and reestablish the desired kinetic traps (Extended Data Fig. 1).
Versatility
Finally, we explored whether the reusable circuit architecture can implement a broader range of functions. Specifically, we aimed to create a reusable threshold and combine it with a reusable catalyst to demonstrate signal restoration in deeper circuits. Unlike the annihilator in winner-take-all neural networks, the function of a threshold precisely depends on concentration; signals below the threshold are cleaned up, whereas those above are amplified. This thresholding enables the restoration of noisy analogue inputs into robust digital outputs14.
We explored two reusable threshold designs: a hairpin (Supplementary Fig. 29) and a two-stranded complex (Supplementary Fig. 30). In both cases, the circuit performance degraded slightly after reset. We propose that threshold restoration could be improved if the reset requirements for other, less critical components were slightly relaxed. Revisiting the eight reusable catalyst designs (Fig. 2c,d), we selected the design with no bulge but a 7-nt loop toehold (Fig. 5a). This design was expected to improve the threshold reset by allowing the upstream hairpin gate (G1,3 in Fig. 5b) to reset at a higher temperature, freeing more summation gate strands (G3) to participate in strand displacement reactions that help correct undesired waste products. With this design, we demonstrated reusable logic gates that maintained a similar performance after reset (Fig. 5c,d).
a, Implementation of a two-input logic gate with signal restoration. A two-stranded gate G3,4 sums the inputs together. A hairpin threshold Th3,4 keeps the output off if the sum is below 0.8 (when both inputs are off) for logic OR and below 1.6 (when at most one input is on) for logic AND. A hairpin gate G4,5 and fuel F4 amplify and restore the signal to an ideal on state if the sum exceeds the threshold. Another hairpin gate (G1,3 or G2,3) and fuel (F1 or F2) are needed for each input (X1 or X2), upstream of the two-stranded summation gate; otherwise, the input inactivation would interfere with the reset of the summation gate as they occur at similar temperatures during cooling. b, Reactions and simulation of reset. A representative set of reactions are shown here, and the full set of reactions is listed in Supplementary Note 2.7. The reactions in black and grey indicate the desired and undesired reactions, respectively. The dark grey box highlights a strand displacement reaction that helps restore the threshold and summation gate. c,d, Simulations and fluorescence kinetics experiments of the OR (c) and AND (d) gates before and after rest. The DNA sequences are listed in Supplementary Table 8.
To evaluate logic gate composability, we constructed a three-layer circuit that computes the first 16 elements of the infinite Fibonacci word (Fig. 6a), a binary sequence with rich combinatorial properties43. Although the Fibonacci word can be generated iteratively, our circuit is feedforward and designed from a truth table, requiring inputs indicating the element index for each computation round. Composing arbitrary logic circuits naturally enforces the alternating hairpin and two-stranded gate rule (Fig. 6b). In a previous study14, fan-out required extra gates for shared inputs. Here owing to input inactivation, every input connects to an extra first-layer gate, preserving the alternating rule when counting two-stranded input wastes as the 0th layer. The resulting seven-layer DNA circuit maintained a consistent performance across 16 rounds of computation, exhibiting reliable responses after 15 resets over 640 h (Fig. 6c).
a, Logic circuit diagram. Because the ith and (i + 8)th elements are identical, the most significant bit x1 in the 4-bit input is not connected to any logic gates. b, DNA circuit diagram. A dual-rail technique was used; each signal was replaced by a pair of signals representing logic on and off separately, whereas each logic gate was combined with its upstream NOT gates and translated into a pair of AND and OR gates. Five types of species were involved, and one example of each is shown. c, Simulations and fluorescence kinetics experiments for 16 rounds of computation with all possible input combinations. The simulations indicate the expected circuit behaviour without the impact of reset. To preserve the generality and predictive power of the simulation, common rate constants and nominal concentrations were used to model the reactions involved in all logic gates. The difference between the simulations and experiments was probably because of the impact of varying sequences and effective concentrations across distinct circuit components. The DNA sequences are listed in Supplementary Table 9.
Discussion
We showed that heating and cooling can restore complex molecular systems from equilibrium to out-of-equilibrium states within minutes, thereby enabling heat-powered DNA logic circuits and neural networks. These systems operate at room temperature, consume energy stored in kinetic traps to process inputs and recharge at higher temperatures after input inactivation. The reset principle is simple: a strong, flexible linkage connects the molecules that should form a kinetic trap. Flexibility preserves the desired molecular interactions during operation, whereas strength ensures that the linkage survives heating that breaks weaker bonds for reset. Accordingly, the kinetic trap is reliably restored after each cycle. This principle, with adjusted temperature ranges, can be extended to engineered systems involving proteins and small molecules.
However, the abstract principle alone is not sufficient to guarantee a successful circuit reset. The temperature-dependent and concentration-dependent kinetics of all hybridization events must be considered, including both desired kinetic traps and competing reactions that lead to undesired equilibrium products. For example, catalysed hairpin assembly44, which is widely used for molecular signal amplification45, satisfies the abstract principle but would achieve only approximately 50% reset success on the basis of our simulations (Extended Data Fig. 10).
A key property of our approach is that operation and reset produce no waste build-up, except for input wastes. These wastes result from input inactivation used to simulate environmental signal changes and do not reflect how the DNA circuits would respond to natural input turnover, such as endonuclease degradation6. In principle, reusability is limited only by DNA degradation at high temperatures (Extended Data Fig. 5). In practice, applications without natural input turnover, such as molecular diagnostics46 with distinct patient samples, are constrained by the need to track previous inputs and accumulation of stoichiometric errors in input inactivation. More effective inactivation mechanisms are therefore needed to better mimic natural degradation. On the other hand, reusability offers a simple solution to storage; all DNA strands can be kept in a single tube for extended periods, and although leak reactions drive the system towards equilibrium, a heat–cool cycle restores the desired out-of-equilibrium state before processing any inputs.
Could a heat-powered reset be built into an autonomous molecular environment? Naturally occurring temperature cycles have been proposed as drivers of early evolution. For example, cold seawater circulating through hot volcanic rocks could supply energy for chemical reactions47. Inspired by this, we envisioned ‘heat stations’ for molecules where they diffuse to recharge themselves. It is even conceivable that a simple heat gradient could sustain complex computations, with molecules performing tasks in cool regions and regenerating fuels in hot regions.
Reusability is central to enabling more sophisticated behaviours in artificial molecular machines than previously demonstrated. Building on the heat-powered DNA circuit architecture, it is now possible to create molecular systems that spontaneously learn from their environment. Instead of complete resets that erase previous responses, tasks such as unsupervised learning require continuous updates that retain environmental information. Future studies must address selective reset, potentially by combining the current mechanism with templated synthesis processes, such as primer exchange reactions48 or strand displacement polymerization49. With further development, programmable molecular machines could compute, learn and evolve in a more sustainable manner than other artificial systems.
Methods
Sequence design
All DNA strands consisted of short toehold domains and long branch migration domains. Sequence design was performed at the domain level and was guided by several design principles experimentally validated in previous studies14,50. The domain sequences used a three-letter code (A, T and C) to minimize secondary structures and unwanted strand interactions. Other principles included no more than four consecutive As or Ts and no more than three consecutive Cs to reduce synthesis errors. To fulfil the need for similar melting temperatures, all domain sequences maintained a C content within the range of 30–70%. Furthermore, precautions were taken to prevent extensive sequence matches among pairs of domain sequences. The longest matching domain sequences were limited to 35% of the domain length. A 20-nt sequence pool was used for the input domains (Xi domain in Fig. 4a) in the winner-take-all neural networks, whereas a 15-nt sequence pool was used for all other long domains (such as Pj, Sj, Sk and Yj domains in Fig. 4a). An extra sequence design criterion for reducing the toehold occlusion in threshold molecules is explained in Supplementary Fig. 1 and Supplementary Note 1.1. A full list of the DNA sequences is shown in Supplementary Tables 1–9.
DNA oligonucleotide synthesis
All DNA strands were purchased from Integrated DNA Technologies (IDT). The reporter strands modified with fluorophores and quenchers were purified using high-performance liquid chromatography, and the input and inhibitor strands in logic circuits were purified using polyacrylamide gel electrophoresis (PAGE). All purified strands were shipped LabReady at a 100 μM concentration in 1× Tris–EDTA buffer (10 mM Tris and 0.1 mM EDTA) (pH 8.0). All other strands were not purified (standard desalting) and shipped lyophilized. They were then resuspended at 100 μM in 1× Tris–EDTA buffer (pH 8.0). One exception occurred in the experiments shown in Extended Data Fig. 2, in which the impact of strand purity on catalytic turnover was specifically investigated. All strands were stored at 4 °C. The concentrations of the strands were verified using a NanoDrop spectrophotometer (Thermo Fisher Scientific). Three measurements of absorbance at 260 nm using a 1-μl sample were averaged to determine the concentration. A Take3 microvolume plate and a Synergy H1 (BioTek) microplate reader were used for high-throughput absorbance measurements, including measuring the concentrations of inputs and input inhibitors for the 100-bit winner-take-all neural network.
Annealing protocol and buffer condition
The hairpin gates and hairpin thresholds were annealed at 90 μM. Two-stranded gates and annihilators were annealed at 45 μM, with a 1:1 ratio between the two strands. Reporters were annealed at 20 μM with 20% extra quencher strands. The buffer used in all the annealing and fluorescence kinetics experiments was 1× Tris–EDTA and 12.5 mM Mg2+. Annealing was performed in a Mastercycler nexus thermal cycler (Eppendorf) by heating to 90 °C for 5 min and then cooling to 20 °C at a rate of 0.1 °C per 6 s.
Complex purification
The annealed hairpin gates, hairpin thresholds and two-stranded complexes were purified using 12% PAGE. A single band for each sample was excised from the gel, fragmented into small pieces and incubated at room temperature in 1× Tris–EDTA buffer supplemented with 12.5 mM Mg2+ for 24 h. The resulting solution containing the purified complexes was retrieved, and their concentrations were quantified using a NanoDrop spectrophotometer (Thermo Fisher Scientific). The weight gates in each memory of the 100-bit winner-take-all neural network underwent individual annealing before being combined for a one-pot purification. The mixture was subsequently purified following the above procedure, and its concentration was determined on the basis of the average extinction coefficient of all weight gates.
Reset protocol
Reset was performed by adding input inhibitors of the same amount as the previous input strands, heating to 95 °C for 5 min, cooling to 20 °C in 1 min and staying at 20 °C for 3 min. The equal concentration of inputs and inhibitors is important to avoid errors in subsequent computations. The method used for the quantification of effective concentration is provided in Supplementary Note 1.4. Reset in the 100-round experiments shown in Extended Data Fig. 5 and Supplementary Figs. 18 and 19 involved only heating and cooling but not input inactivation. As a result, the same initial input was repeatedly processed for all subsequent computations.
Thermal cycling experiments with fluorescence readout
The 100-round reset experiments were performed using the temperature control and fluorescence readout features of a Stratagene Mx3005P quantitative polymerase chain reaction system. Each reset began at 25 °C, followed by heating to 95 °C with a holding time of 2 min or 5 min, as specified in the figures. The temperature was then lowered to 25 °C within 1 min, and the reaction kinetics was monitored for 40 min at 25 °C, with fluorescence measurements every 2 min using 180 μl of 100 nM sample in an optical tube strip (Agilent; 401428). No input inactivation was involved; reusability was evaluated with the same input across 100 rounds of computation. These experiments allowed for the performance of reset to be separated from the inevitable stoichiometric errors in input inactivation, an imperfect mechanism for simulating environmental signal changes.
Fluorescence kinetics experiments
Fluorescence kinetics data were recorded at intervals of 2 min or 4 min on a microplate reader (Synergy H1; BioTek) at 25 °C. The excitation and emission wavelengths were set to 496 nm and 525 nm for dye ATTO488, and 598 nm and 629 nm for dye ATTO590, respectively. The experiments were conducted in 96-well clear-bottom non-binding surface plates (Corning; 3651), with a reaction mixture volume of 180 μl per well and a standard concentration of 100 nM. The relative concentrations of distinct species for each experiment are shown in the figures or captions. The input patterns for testing the 100-bit winner-take-all neural network were prepared using an acoustic liquid handler (Echo 525).
For experiments that demonstrated several rounds of computation, a parallel procedure was used for efficient data collection (Supplementary Fig. 2). For n rounds of computation, instead of taking a sample in and out of a microplate reader for n times, we prepared n samples in parallel, each of which underwent 0 to n − 1 rounds of reset, and collected data once for all samples simultaneously when they received the first to the nth inputs. This way, not only was the time of data collection on a microplate reader dramatically reduced, but the accuracy of the data was also improved for the following reasons. The fluorescence signal obtained on a microplate reader depends on both the concentration and volume of the sample. A linear function of raw fluorescence to concentration can only be applied (see ‘Data normalization’ below) if the volume remains constant. Because the clear-bottom plates used for the fluorescence kinetics experiments cannot be used on a thermal cycler, if a single sample is used for several rounds of computation, it must be transferred out of and back into the plate for each reset. Multiple transfers would result in volume loss, which affects the accuracy of the data. More details about the parallel procedure and comparison with a single-sample procedure are explained in Supplementary Figs. 3 and 4 and Supplementary Note 1.2. Reproducibility of the experiments is discussed in Supplementary Note 1.5.
Data normalization
Each set of experiments that investigated the behaviour of a circuit with varying input concentrations was performed with negative and positive controls using aliquots of samples from a single master mix that contains all components of the circuit. The negative control was the circuit with no input, and the positive control was the circuit with an excess trigger strand added to the final gate directly connected to a reporter. Unlike a regular input strand, the trigger strand contains an extra toehold for irreversibly reacting with the gate. The first five data points of the negative control were averaged to determine the minimum raw fluorescence signal that corresponds to a 0× output concentration. For several rounds of computation, the negative control for the first round was used to normalize the data for all subsequent rounds, allowing for the evaluation of the reset performance. An exception was made for the logic gates, where the reset negative control was used to normalize the reset data, allowing for more accurate quantification of the on and off states for subsequent computation, where the reset baseline is expected to remain unchanged. The last five data points of the positive control were averaged to determine the maximum raw fluorescence signal that corresponds to a 1× output concentration. For several rounds of computation, the positive control for each round was used to normalize the data for the specific round, accounting for evaporation and volume change. The raw fluorescence data were converted to concentration data on the basis of a linear function using the reference data for the 0× and 1× output concentrations. We call this method an internal control. An alternative data normalization method, which we call an external control, and a comparison between the two are explained in Supplementary Fig. 5 and Supplementary Note 1.3.
Quantification of effective concentration
In this study, the change in input concentrations from a molecular environment was simulated by adding a strand with a complementary sequence for each input strand, functioning as an inhibitor to inactivate the inputs from a previous round of computation before new inputs for the subsequent round were introduced. A technical challenge involves the concentration errors in the inputs and their inhibitors. If the effective concentration of an inhibitor strand is lower or higher than that of the input strand, excess input or excess inhibitor will alter the output for subsequent computations, leading to undesired behaviour that interferes with the experimental demonstrations of how the reusable DNA circuits respond to a changing molecular environment. To address this challenge, perfecting the techniques for concentration measurements on a NanoDrop and Take3 microvolume plate was necessary (Methods, ‘DNA oligonucleotide synthesis’). Additionally, we established a simple method for quantifying the effective concentration of the input inhibitors using fluorescence measurements (Supplementary Fig. 6). This method is particularly useful when the effective concentration differs from the nominal concentration measured by ultraviolet absorbance. More details about this method are explained in Supplementary Note 1.4.
Biophysical model for reset by heating and cooling
All molecular interactions during heating and cooling were modelled as reversible hybridization, in which the forward rate was either bimolecular (kh2) or unimolecular (kh1). In both cases, the reverse rate was the same rate of dissociation (kd), which depends on the length of the hybridized domains (l), the size of the bulge loop (s) if there is any and the temperature (T). There are controversial results about how the rate of hybridization depends on temperature but a general agreement that the impact of temperature to hybridization rate is insignificant compared with that to dissociation rate51. For simplicity, we used a constant value for bimolecular hybridization33,52 and estimated the dissociation and unimolecular hybridization rates on the basis of equilibrium constants derived from thermodynamic parameters for base pairs, bulges and hairpin loops53. Because the energies of the base pairs and bulges exist in the equilibrium constants for both bimolecular and unimolecular hybridizations, they cancel out, and the unimolecular hybridization rate only depends on the size of the hairpin loop (n). More details about the model are explained in Supplementary Fig. 7 and Supplementary Note 2.1. More details about modelling the components of the reusable winner-take-all neural networks and logic circuits are explained in Supplementary Figs. 8–12 and Supplementary Notes 2.2–2.8.
Data availability
All data supporting the findings of this study are available within the paper and its Supplementary Information. Additional data files are available at CaltechDATA (https://doi.org/10.22002/q9350-kvd05). Source data are provided with this paper.
Code availability
The code for simulation and data analysis is available at CaltechDATA (https://doi.org/10.22002/q9350-kvd05).
References
Yurke, B., Turberfield, A. J., Mills Jr, A. P., Simmel, F. C. & Neumann, J. L. A DNA-fuelled molecular machine made of DNA. Nature 406, 605–608 (2000).
Yan, H., Zhang, X., Shen, Z. & Seeman, N. C. A robust DNA mechanical device controlled by hybridization topology. Nature 415, 62–65 (2002).
Turberfield, A. J. et al. DNA fuel for free-running nanomachines. Phys. Rev. Lett. 90, 118102 (2003).
Simmel, F. C. DNA nanotechnology out of equilibrium. in Visions of DNA Nanotechnology at 40 for the Next 40: A Tribute to Nadrian C. Seeman (eds Jonoska, N. & Winfree, E.) 17–29 (Springer, 2023).
Dirks, R. M. & Pierce, N. A. Triggered amplification by hybridization chain reaction. Proc. Natl Acad. Sci. USA 101, 15275–15278 (2004).
Bois, J. S. Analysis of Interacting Nucleic Acids in Dilute Solutions (California Institute of Technology, 2006).
Kim, J., White, K. S. & Winfree, E. Construction of an in vitro bistable circuit from synthetic transcriptional switches. Mol. Syst. Biol. 2, 68 (2006).
Montagne, K., Plasson, R., Sakai, Y., Fujii, T. & Rondelez, Y. Programming an in vitro DNA oscillator using a molecular networking strategy. Mol. Syst. Biol. 7, 466 (2011).
Schaffter, S. W. et al. Standardized excitable elements for scalable engineering of far-from-equilibrium chemical networks. Nat. Chem. 14, 1224–1232 (2022).
Okumura, S. et al. Nonlinear decision-making with enzymatic neural networks. Nature 610, 496–501 (2022).
Montagne, K., Gines, G., Fujii, T. & Rondelez, Y. Boosting functionality of synthetic DNA circuits with tailored deactivation. Nat. Commun. 7, 13474 (2016).
Simpson, Z. B., Tsai, T. L., Nguyen, N., Chen, X. & Ellington, A. D. Modelling amorphous computations with transcription networks. J. R. Soc. Interface 6, S523–S533 (2009).
Zhang, D. Y. & Winfree, E. Robustness and modularity properties of a non-covalent DNA catalytic reaction. Nucleic Acids Res. 38, 4182–4197 (2010).
Qian, L. & Winfree, E. Scaling up digital circuit computation with DNA strand displacement cascades. Science 332, 1196–1201 (2011).
Lv, H. et al. DNA-based programmable gate arrays for general-purpose DNA computing. Nature 622, 292–300 (2023).
Cherry, K. M. & Qian, L. Scaling up molecular pattern recognition with DNA-based winner-take-all neural networks. Nature 559, 370–376 (2018).
Xiong, X. et al. Molecular convolutional neural networks with DNA regulatory circuits. Nat. Mach. Intell. 4, 625–635 (2022).
Genot, A. J., Bath, J. & Turberfield, A. J. Reversible logic circuits made of DNA. J. Am. Chem. Soc. 133, 20080–20083 (2011).
Wang, B., Chalk, C., Doty, D. & Soloveichik, D. Molecular computation at equilibrium via programmable entropy. Preprint at bioRxiv 10.1101/2024.09.13.612990v1 (2024).
Vasić, M., Soloveichik, D. & Khurshid, S. CRN++: molecular programming language. Nat. Comput. 19, 391–407 (2020).
Lakin, M. R. & Stefanovic, D. Supervised learning in adaptive DNA strand displacement networks. ACS Synth. Biol. 5, 885–897 (2016).
DelRosso, N. V., Hews, S., Spector, L. & Derr, N. D. A molecular circuit regenerator to implement iterative strand displacement operations. Angew. Chem. Int. Ed. Engl. 56, 4443–4446 (2017).
Scalise, D., Dutta, N. & Schulman, R. DNA strand buffers. J. Am. Chem. Soc. 140, 12069–12076 (2018).
Garg, S. et al. Renewable time-responsive DNA circuits. Small 14, 1801470 (2018).
Eshra, A., Shah, S., Song, T. & Reif, J. Renewable DNA hairpin-based logic circuits. IEEE Trans. Nanotechnol. 18, 252–259 (2019).
Hahn, J. & Shih, W. M. Thermal cycling of DNA devices via associative strand displacement. Nucleic Acids Res. 47, 10968–10975 (2019).
Lakin, M. R., Youssef, S., Cardelli, L. & Phillips, A. Abstractions for DNA circuit design. J. R. Soc. Interface 9, 470–486 (2012).
Lauback, S. et al. Real-time magnetic actuation of DNA nanodevices via modular integration with stiff micro-levers. Nat. Commun. 9, 1446 (2018).
Kopperger, E. et al. A self-assembled nanoscale robotic arm controlled by electric fields. Science 359, 296–301 (2018).
Liang, X., Nishioka, H., Takenaka, N. & Asanuma, H. A DNA nanomachine powered by light irradiation. ChemBioChem 9, 702–705 (2008).
Song, X., Eshra, A., Dwyer, C. & Reif, J. Renewable DNA seesaw logic circuits enabled by photoregulation of toehold-mediated strand displacement. RSC Adv. 7, 28130–28144 (2017).
Doty, D., Rogers, T. A., Soloveichik, D., Thachuk, C. & Woods, D. Thermodynamic binding networks. In Proc. DNA Computing and Molecular Programming: 23rd International Conference (eds Brijder, R., Qian, L.) 249–266 (Springer, 2017).
Zhang, D. Y. & Winfree, E. Control of DNA strand displacement kinetics using toehold exchange. J. Am. Chem. Soc. 131, 17303–17314 (2009).
Takinoue, M. & Suyama, A. Hairpin-DNA memory using molecular addressing. Small 2, 1244–1247 (2006).
Viasnoff, V., Meller, A. & Isambert, H. DNA nanomechanical switches under folding kinetics control. Nano Lett. 6, 101–104 (2006).
Machinek, R. R., Ouldridge, T. E., Haley, N. E., Bath, J. & Turberfield, A. J. Programmable energy landscapes for kinetic control of DNA strand displacement. Nat. Commun. 5, 5324 (2014).
Haley, N. E. et al. Design of hidden thermodynamic driving for non-equilibrium systems via mismatch elimination during DNA strand displacement. Nat. Commun. 11, 2562 (2020).
Chen, H.-L., Doty, D., Reeves, W. & Soloveichik, D. Rate-independent computation in continuous chemical reaction networks. J. ACM 70, 1–61 (2023).
Kim, J., Hopfield, J. & Winfree, E. Neural network computation by in vitro transcriptional circuits. In Advances in Neural Information Processing Systems 17 (NIPS 2004) (eds Saul, L. K., et al.) 681–688 (MIT Press, 2004).
Genot, A. J., Fujii, T. & Rondelez, Y. Scaling down DNA circuits with competitive neural networks. J. R. Soc. Interface 10, 20130212 (2013).
Zhang, D. Y. Cooperative hybridization of oligonucleotides. J. Am. Chem. Soc. 133, 1077–1086 (2011).
Zadeh, J. N. et al. NUPACK: analysis and design of nucleic acid systems. J. Comput. Chem. 32, 170–173 (2011).
Lothaire, M. Algebraic Combinatorics on Words, Vol. 90 (Cambridge Univ. Press, 2002).
Yin, P., Choi, H. M., Calvert, C. R. & Pierce, N. A. Programming biomolecular self-assembly pathways. Nature 451, 318–322 (2008).
Chen, X., Briggs, N., McLain, J. R. & Ellington, A. D. Stacking nonenzymatic circuits for high signal gain. Proc. Natl Acad. Sci. USA 110, 5386–5391 (2013).
Simmel, F. C., Yurke, B. & Singh, H. R. Principles and applications of nucleic acid strand displacement reactions. Chem. Rev. 119, 6326–6369 (2019).
Martin, W., Baross, J., Kelley, D. & Russell, M. J. Hydrothermal vents and the origin of life. Nat. Rev. Microbiol. 6, 805–814 (2008).
Kishi, J. Y., Schaus, T. E., Gopalkrishnan, N., Xuan, F. & Yin, P. Programmable autonomous synthesis of single-stranded DNA. Nat. Chem. 10, 155–164 (2018).
Song, T. et al. Fast and compact DNA logic circuits based on single-stranded gates using strand-displacing polymerase. Nat. Nanotechnol. 14, 1075–1081 (2019).
Thubagere, A. J. et al. Compiler-aided systematic construction of large-scale DNA strand displacement circuits using unpurified components. Nat. Commun. 8, 14373 (2017).
Ouldridge, T. E., Šulc, P., Romano, F., Doye, J. P. & Louis, A. A. DNA hybridization kinetics: zippering, internal displacement and sequence dependence. Nucleic Acids Res. 41, 8886–8895 (2013).
Srinivas, N. et al. On the biophysics and kinetics of toehold-mediated DNA strand displacement. Nucleic Acids Res. 41, 10641–10658 (2013).
SantaLucia Jr, J., & Hicks, D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 33, 415–440 (2004).
Acknowledgements
We are grateful to A. Genot for his pioneering work on reversible DNA circuits, which was one of the earliest explorations on sustainable computation in engineered molecular systems. We thank X. Zhao, K. M. Cherry, M. Plazola and E. Winfree for discussions and suggestions; F. Dannenberg for designing the abstract Fibonacci logic circuit; Y. Du for help in setting up experiments on a quantitative PCR machine; and R. M. Murray for sharing an acoustic liquid handler. This research received support from Schmidt Sciences. T.S. and L.Q. were supported by two NSF grants (1908643 and 2212546).
Author information
Authors and Affiliations
Contributions
T.S. came up with the key mechanisms and designed and performed the experiments. T.S. and L.Q. developed the model, performed the simulations, analysed the data and wrote the paper. L.Q. initiated and guided this project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Tom de Greef, Anthony Genot, Thomas Ouldridge and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Conceptual energy landscape for computation and reset.
a, Free energy states of a reusable molecular system. When the system is recharged, it will remain in a local energy minimum (state 2) until an input becomes present. As a catalyst, the input reduces the kinetic barrier and creates a smoother pathway for producing the desired output while reaching a lower energy state that is another local minimum (state 3). After computing the input-output function, the system will remain in the local minimum that has a higher free energy than the equilibrium state of global minimum (state 4). When heat is applied, the system will transition to a denatured state with a free energy higher than any other states (state 1). When heat is removed (cooling applied), the system will return to the recharged state if the input is absent or the output state if the input is present. b, Multiple output states for computing distinct input-output functions. Each input will reduce the kinetic barrier for reaching a specific output state. Heat will bring the system to the same denatured state regardless of the output state, and cooling will allow the system to return to the same recharged state when the input is absent. c, DNA implementation of a reusable molecular system with two output states. The denatured state involves eight single strands, two of which fold into two hairpins in the recharged state, four form two duplexes, and the other two remain single-stranded. Compared to the denatured state, the recharged state has two fewer separated molecules (lower entropy) but substantially more base pairs (lower enthalpy), resulting in a lower energy state. One of the two possible output states is illustrated as state 3, where a hairpin unfolds and becomes bound to two other strands, separating a duplex. Compared to the recharged state, the output state has one fewer separated molecules but 7 more base pairs. With sufficiently high concentration, the gain in enthalpy will exceed the loss in entropy and result in a lower energy state. The unfolding of the hairpin also comes with a gain in entropy, contributing to the lower energy state. The equilibrium state has both hairpins unfolded and each converted to a three-stranded complex, doubling the energy difference between the recharged and the output state.
Extended Data Fig. 2 Turnover of the reusable catalyst.
a-b, Simulations and fluorescence kinetics experiments of a reusable DNA catalyst (a) compared with a use-once DNA catalyst (b). Four distinct combinations of strand purities were investigated. Gate strands and input strands were ordered from IDT DNA either unpurified (standard desalting) or PAGE purified. In both cases, we annealed and then PAGE purified the hairpin gate in the reusable catalyst and the double-stranded gate in the use-once catalyst in our lab. For double-stranded gates, in-house purification is necessary to reduce stoichiometry errors. For hairpin gates, we expect in-house purification to help reduce malformed structures. In modeling the reusable catalyst, kd = 5 and 2 per second were applied to IDT unpurified and purified input strand, respectively, accounting for synthesis errors within the invading toehold on the input strand; kd1 = 0.02 and 0.05 per second were applied to IDT unpurified and purified gate strand, respectively, accounting for synthesis errors within the dissociation toehold on the gate strand. A 58-fold and 82-fold catalytic turnover were observed at 24 hours with 0.01 × input when both gate and input strands were IDT unpurified and purified, respectively. In modeling the use-once catalyst, effective strand displacement rate k = 1.1 to 3.2 × 105 per molar per second were estimated based on the experimental data. A 95-fold and 90-fold catalytic turnover were observed at 24 hours with 0.01 × input when both gate and input strands were IDT unpurified and purified, respectively. In general, purified input strand resulted in slightly faster kinetics whereas purified gate strand resulted in slower kinetics. This is counterintuitive but consistent with our prior observation shown in Fig. S18 of the logic circuit construction using the seesaw gate motif14. The benefit of IDT purified gate strand is evident for the reusable catalyst but not for the use-once catalyst, presumably due to the strand length difference: the two strands in the use-once gate are 29 and 35 nucleotides, whereas the hairpin strand in the reusable gate is 74 nucleotides. With a 99.4% nucleotide coupling efficiency by IDT, 81 to 84% full-length products are expected for the two strands but only 64% full-length product is expected for the hairpin strand.
Extended Data Fig. 3 Principles of reset success.
a, Desired and competing reactions during the reset of a catalytic circuit. b, NUPACK melting analysis of the desired (GY) and undesired (GF and YR) products. For analysis of the undesired products, the single strand G–Y was separated into a strand G (before the linker domain L) and a strand Y (after the linker domain L). Concentration of G–Y, G, and Y was set to 100 nM. Concentration of F and R was set to 200 nM. The difference in melting temperature between the desired and undesired products is roughly 4 °C. c, Simulations for exploring the impact of kinetics without changing the melting temperatures. Compared to the original rate constants (top plot), the forward and reverse rates for the desired hairpin closing reaction were slowed down simultaneously by a factor of 100 (middle plot) and 1000 (bottom plot). With a 100 times slowdown, the desired unimolecular reaction remains 3.9 times faster than the undesired bimolecular reactions, resulting in a small 6.2% decrease in the reset success rate of GY. With a 1000 times slowdown, the desired unimolecular reaction becomes 2.6 times slower than the undesired bimolecular reactions, resulting in a large 56.4% decrease in the reset success rate. d-f, Simulations for exploring the impact of cooling time (d), concentration (e), and linker size (f) on reset success. A 9.7% decrease in the reset success rate is observed when the cooling time is increased by 4 orders of magnitude from 1 to 104 seconds. A much larger decrease in the reset success rate (84.6% or 97.1%, respectively) is observed when the concentration is increased to result in 4 orders of magnitude increase in the undesired bimolecular rates or when the linker size is increased to result in similar orders of magnitude decrease in the desired unimolecular reaction rate.
Extended Data Fig. 4 Reset performance with varying cooling time.
a, Fluorescence kinetics experiments of resetting a DNA catalyst by heating to 95 °C for 5 minutes and then cooling to 20 °C in 1, 12.5, 37.5 and 75 minutes. The input was inactivated by adding an inhibitor (a strand with complementary sequence) at the same concentration as the input. Standard concentration 1 × = 100 nM. b, Comparison of baseline output concentration without any input before and after reset. Two replicated trajectories after reset are taken from the experiment with 0 × input in the second and third plots in (a). c, Simulations and experimental data of reset success rate indicated by the baseline output concentration after reset. Average of the first 5 data points from the two replicated trajectories in (b) are shown in the bar chart. d, Simulations of reset success rate with up to 10 days of cooling time and with varying concentration.
Extended Data Fig. 5 Robustness of reusability.
a-d, Fluorescence kinetics experiments of a reusable catalytic DNA circuit with 100 rounds of reset using two distinct protocols that heat for 2 minutes (a,b) or 5 minutes (c,d) at 95 °C before cooling to 25 °C in 1 minute. Experiments were performed on a quantitative PCR machine and a single sample was used for all data shown in (a,b) and (c,d), respectively. Standard concentration 1× = 100 nM. The performance of the DNA circuit remained roughly the same for the first 10 rounds of reset (a). However, the output concentration decreased by 9, 29.3, and 27.5 nM for 1×, 0.2×, and 0.1× input, respectively, and increased by 12.3 nM for 0× input after 100 rounds of reset (b). Increasing the time at 95 °C from 2 to 5 minutes resulted in worse reset performance: a similar level of decrease in signal amplification with 0.1× to 1× input and increase in reset baseline with 0× input were observed after 40 rounds of reset (c). The total time at 95 °C for 100 rounds in (b) is the same as that for 40 rounds in (c). This observation suggested that DNA degradation at high temperature played a major role in the robustness of the reusability. The reset performance continued to worsen with longer total time at 95 °C: after 100 rounds of reset using the protocol that heats for 5 minutes, the output concentration for 0× input became indistinguishable from that for 0.1× input, reaching roughly half the output concentration for 1× input. Predictably, the output concentration would no longer change with input after 1,000 minutes of heating at 95 °C. This limits the maximum number of reset to on the order of 1,000 rounds if a protocol with 1-minute heating is applied.
Extended Data Fig. 6 A pair of reusable DNA catalysts.
a,b, Design, simulations, and fluorescence kinetics experiments of two distinct DNA catalysts before and after reset. c, Simulations and experiments of the two DNA catalysts in one test tube. Two reporters with distinct fluorophores and quenchers were used to simultaneously measure the two output signals. Reset was done by heating to 95 °C for 5 minutes and cooling to 20 °C in one minute. Compared to the design shown in Fig. 3c, the hairpin gates here have two nucleotides removed from the open toehold (changed from T to t), leading to slower kinetics that allows for faster annihilation and desired winner-take-all behavior in neural networks. Toehold dissociation rate kd1 = 0.018 and 0.03 per second were used in simulations for GY1 and GY2, respectively, to explain the kinetics observed in the experimental data. The small difference between the two rates can be explained by the sequence-dependent variations in spurious binding between the hairpin loop and the toehold. A 90% and 86% reset success rate were applied in simulations for GY1 and GY2, respectively, to explain the reset performance observed in experimental data. The initial concentrations of the hairpin gates, fuel strands, and reporters were decreased by 10 and 14 nM, respectively, whereas the initial concentrations of the output-reporter complexes and quencher strands were increased accordingly after reset. This non-ideal reset behavior was due to historical reasons, where reporters with a 6-nt toehold near the quencher and fluorophore modifications were used. As shown in Fig. 2c, compared to the design with a mismatched reporter (6-nt loop toehold and 7-nt reporter toehold) that result in a 1-nt bulge in the output-reporter complex, the design with a matching reporter exhibited a roughly 3.6-fold worse reset performance. Nonetheless, the kinetics was sustained after reset: simulations using the same set of rate constants before and after reset quantitatively agreed with the experimental data. When the two gates operated and reset simultaneously in one test tube, the observed kinetics was slightly slower than simulations, indicating the impact of increased toehold occlusion in a larger circuit.
Extended Data Fig. 7 A reusable two-input winner-take-all circuit.
a, Abstract circuit diagram and molecular implementation (same as shown in Fig. 3a). Red numbers within a node or on a wire in the abstract circuit diagram indicate distinct species and their relative initial concentrations. Input (S1 or S2) with a higher concentration will survive the competition facilitated by the annihilator (Anh1,2), and the remaining signal will be amplified by the downstream restoration gate (GY1 or GY2) facilitated by the fuel (YF1 or YF2). Sequences of the input strands, hairpin gates, and fuel strands are the same as shown in Extended Data Fig. 6. b, Simulations and fluorescence kinetics experiments of the circuit with various combinations of two inputs before and after reset. The reset process included input inactivation, heating to 95 °C for 5 minutes and cooling to 20 °C in one minute, and input reintroduction. Two-bit gray scale pattern to the left of the arrow in each plot indicates the input concentrations (white represents 0, black represents 1, and a shade of gray represents an analog number in between); one-bit colored pattern to the right of the arrow indicates the output (dark green represents Y1 is on and yellow represents Y2 is on). As in Extended Data Fig. 6, a 90% and 86% reset success rate were applied in simulations for GY1 and GY2, respectively. A small bias toward output Y2 was observed (higher Y2 concentration for S1 = 0.4 × and S2 = 0.6 × than Y1 concentration for S1 = 0.6 × and S2 = 0.4×), consistent with the small kinetics difference in the two gates shown in Extended Data Fig. 6.
Extended Data Fig. 8 A reusable 9-bit two-memory winner-take-all neural network.
a,b, Simulations and fluorescence kinetics experiments of the neural network with a universal input inhibitor (a) and unique input inhibitors (b). All input strands can be extended with a common domain R, and a universal input inhibitor can be designed to bind to the extension while covering up the toehold on the input. When the universal inhibitor was used to inactivate the previous test pattern during each circuit reset, reduced on-off separation between the two output signals was observed with more rounds of computation. The performance decay can be partially explained by the effective concentration of the inhibitor being 5% lower than expected, resulting in leftover inputs that accumulate in subsequent rounds. However, this explanation does not account for the increased long-term leak observed in the experiments. As only the toehold but not the branch migration domain is covered up in the waste product, it can participate in toeless strand displacement, resulting in increased leak with accumulated wastes. By contrast, when each input strand is inactivated by a distinct inhibitor that is fully complementary to the input, the waste product is fully double-stranded and not expected to cause increased leak. Experiments agreed with the expectation, demonstrating consistent off state of the output over 10 rounds of computation. The small decrease in the on state of the output can be explained by the effective concentration of the inhibitor being 5% higher than expected.
Extended Data Fig. 9 Distinct roles of input and heat in a 100-bit winner-take-all DNA neural network.
a, Weighted sum analysis of four example test patterns and a partial version of each test. When a fraction of inputs are missing, the pattern can be classified as the opposite class compared to when the full set of inputs are present. In the four examples shown here, all input bits that exist in the corresponding memory were taken out from the original tests to create the partial tests. The absence of those inputs decreased the test’s similarity to both memories in a biased fashion, reducing one weighted sum all the way to zero while maintaining a positive value for the other weighted sum. As a result, the positions of the tests moved across the diagonal line in the weighted sum space, switching the expected output from class 1 to 2 and vice versa. b, Fluorescence kinetics experiments that demonstrated incorrect output classification when inputs were presented in two subsequent batches and restored correct classification when heat was applied. Similarly, when input inhibitors were introduced to inactivate specific inputs, converting the full tests to partial tests, the output of the DNA neural network was unable to switch until heat was applied.
Extended Data Fig. 10 Simulations of heating and cooling two hairpins in catalyzed hairpin assembly.
a, Reactions involved in the simulations, where n = 6 is the number of nucleotides in each domain shown in Fig. S10 in the Supplementary Information of Yin et al., 200844. b-d, If bimolecular hybridization rate does not depend on the length of the hybridization domain, the hairpin reset success rate is expected to be 85.1% for 20 nM hairpins heated to 95 °C for 5 minutes and cooled to 20 °C in 1 minute (b), 53.6% for 100 nM hairpins cooled in 1 minute (c), and 42.3% for 20 nM hairpins cooled in 10 minutes (d). e-g, If bimolecular hybridization rate depends on the length of the hybridization domain, the hairpin reset success rate is expected to be 42.5% for 20 nM hairpins heated for 5 minutes and cooled in 1 minute (e), 13.6% for 100 nM hairpins cooled in 1 minute (f), and 10.2% for 20 nM hairpins cooled in 10 minutes (g). The poor reset performance can be explained by the substantially longer hybridization domain in the undesired product AB compared to the desired hairpins A and B. A higher concentration results in both higher melting temperature of the undesired product and smaller kinetics difference between the desired and undesired reactions, worsening the reset performance. Length-dependent bimolecular hybridization rate further favors the undesired reaction. A longer cooling time allows for more undesired product AB to form before desired hairpin B and then A starts to form, resulting in worse reset. These observations are consistent with the principles discussed in Extended Data Fig. 3.
Supplementary information
Supplementary Information
This file contains 30 Supplementary figures and more notes for materials and methods, modelling and simulations, data analysis and discussion on problems encountered with preliminary designs. It also contains nine Supplementary tables of DNA sequences and seven more references.
Supplementary Tables
This file contains nine Supplementary tables of DNA sequences in editable format.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Song, T., Qian, L. Heat-rechargeable computation in DNA logic circuits and neural networks. Nature 646, 315–322 (2025). https://doi.org/10.1038/s41586-025-09570-2
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-025-09570-2