Localization microscopy at doubled precision with patterned illumination

Abstract

MINFLUX offers a breakthrough in single molecule localization precision, but is limited in field of view. Here we combine centroid estimation and illumination pattern induced photon count variations in a conventional widefield imaging setup to extract position information over a typical micrometer-sized field of view. We show a near two-fold improvement in precision over standard localization with the same photon count on DNA-origami nanostructures and tubulin in cells, using DNA-PAINT and STORM imaging.

Main

Single-molecule localization microscopy^1,2,3 circumvents the diffraction limit using centroid estimation of sparsely activated, stochastically switching, single-molecule fluorescence images. Improvement over state-of-the-art image resolutions of around 20 nm toward values below 5 nm is desired for truly imaging at the molecular scale. Achieving 5 nm resolution requires improvements in labeling strategy to reduce linker sizes^4,5,6,7 and methods to overcome low labeling density such as data fusion⁸, but also a step forward in localization precision. Efforts so far have targeted an increase in the number of detected photons, N, by chemical engineering of brighter fluorophores⁹, or by avoiding photo-bleaching via cryogenic techniques^10,11,12. These improvements scale localization precision according to $\lambda /\left( {{\mathrm{NA}}\sqrt N } \right)$, where λ is the fluorescence emission wavelength and NA is the microscope objective numerical aperture¹³.

Recently, a new concept called MINFLUX was proposed¹⁴, in which a doughnut illumination spot is shifted over an area of size L, of ~5 nm, and the position of a single molecule in the scan range is determined by triangulation based on the detected photon count for the different doughnut positions. The localization precision of this procedure scales as $L/\sqrt N$, which is advantageous compared to $\lambda /\left( {{\mathrm{NA}}\sqrt N } \right)$, as the scan range L can in principle be chosen to be arbitrarily small. Drawbacks of MINFLUX are the limited field of view (FOV), and the low throughput, as the molecules are imaged one molecule at a time in the tiny region of interest (ROI) of size L. Balzarotti et al. suggested the use of sinusoidal illumination patterns¹⁴, similar to those used in structured illumination microscopy (SIM)¹⁵ and used earlier for single-molecule tracking¹⁶. The extension of the triangulation procedure to spatially extended illumination patterns, however, remains a challenge.

Here, we propose to extract the molecule’s position in a combined estimation from both the relative position with respect to the shifting sinusoidal illumination pattern during all camera frames within the molecule’s ‘on-event’ and from the estimated centers of the detected spots on the camera. This solves the challenge of photon count-based localization with spatially extended illumination patterns. Our method, which we call SIMFLUX, overcomes the limited FOV and throughput of MINFLUX, and is compatible with standard widefield imaging on a camera. SIMFLUX is realized by an optical architecture for fast millisecond time scale switching of orthogonally oriented sinusoidal illumination patterns, and by a bespoke data processing strategy for spatiotemporal localization in relation to the shifting illumination patterns.

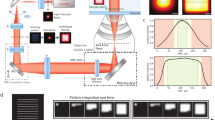
Figure 1a shows our optical architecture. A fast operable Pockels-cell switches between the two arms of a polarizing beam splitter in which piezo mounted gratings are placed that deliver the diffraction orders for interference based sinusoidal illumination patterns along two orthogonal directions (see Methods for details). This enables cycling through six patterns (two orientations, three phase steps) on the millisecond time scale with sufficient power throughput. Only two orientations are needed, because this suffices for a Fisher matrix that gives rise to an isotropic region of confidence for localization in the xy plane (see Supplementary Note). This differs from SIM, where three or five orientations are needed for a near isotropic filling up of the support in image Fourier space¹⁵.

Fig. 1: Principle of SIMFLUX.

a, A sinusoidal illumination pattern is created in a total internal reflection–SIM setup by two counter propagating evanescent waves. Fast switching between two orthogonal line patterns is achieved by placing two piezo mounted gratings in the two arms of a polarizing beam splitter, selecting the operational arm by a polarization switching Pockels cell. b, A total of six images are recorded with three shifted patterns per orthogonal orientation of the line pattern. Combining the centroid estimates of the six frames with precision σ_centroid (σ_cen) with the photon count in relation to the pattern shift improves the localization precision with a factor of around two compared to the standard centroid estimate on the sum of the six frames.

The processing pipeline (see Methods) requires the detection of single-molecule emission events in space as well as in time, in combination with a retrieval of the illumination pattern parameters (pitch, orientation, modulation depth and three phases per orientation, and relative intensity of the two beam splitter arms). First, the entire set of acquired images is processed using a standard single-molecule localization microscopy (SMLM) pipeline for selecting ROIs per frame and for an initial localization fitting. This is done on the moving sum of six frames to enhance signal-to-noise ratio for robust initial on-event detection. Next, the photon count is estimated for all individual frames within the six frame blocks. Then, the pitch and orientations of the patterns are estimated using Fourier domain peak finding¹⁷ on the localization reconstruction. The pattern phases are subsequently retrieved by fitting the sinusoidal illumination pattern to the estimated single-frame photon counts. Blocks where a molecule is not in the on-state in all six frames are filtered out by comparing the estimated single-frame photon counts to the expected values from the retrieved illumination patterns. Next, the ROIs in the frames belonging to molecular on-events are fitted with a maximum likelihood estimation (MLE) routine, taking into account the centroid positions in each frame and the fluorescence signal strengths in relation to the shifting illumination pattern. The difference in the average position of these SIMFLUX localizations and the corresponding SMLM localizations is indicative for an error in the estimation of the pattern pitch and orientations, and can therefore be used to adjust the estimates. After updating them, a next round of pattern phase estimation and SIMFLUX fitting can start. This iterative procedure converges in three to four rounds.

The Cramér–Rao lower bound (CRLB) for the localization precision (see Supplementary Note) is given by:

$${\mathrm{\Delta }}x_0 = \frac{\sigma }{{\sqrt N \sqrt {1 + 2\pi ^2\sigma ^2/p^2} }}$$

(1)

with σ ≈ λ/4NA being the width of the point spread function (PSF) and N the total number of collected photons during the on-event of the molecule. The smallest pitch (p) of the standing wave illumination pattern is p ≈ λ/2NA, indicating that the improvement factor over the SMLM precision $\sigma /\sqrt N$ can reach values up to around $\sqrt {1 + \pi ^2/2} \approx 2.4$. An imperfect modulation depth m (between 0.90 and 0.95) indicates a lower improvement factor of close to 2 (see Supplementary Note). Simulations with Gaussian and vector PSFs show that our method achieves the CRLB for a wide range of realistic photon counts and background photon levels (Supplementary Figs. 1 and 2). It appears further that background has the same relative impact as in conventional SMLM, indicating that SIMFLUX can be used under the same experimental conditions as conventional SMLM¹³ (Supplementary Fig. 3). Simulations further show that to reach a two-fold improvement in localization precision the modulation must be at least 0.9, and must be known with a precision of around 0.04; for the pattern phases, a precision of ~2° is required (Supplementary Figs. 4 and 5). We meet these conditions in our experiments. Supplementary Fig. 6 shows that there are small variations in localization precision depending on the position of the molecules with respect to the minima of the illumination patterns, leading to improvement factors compared to conventional SMLM that range between 1.6 and 2.3, with an average of 2.1 (for p/σ ≈ 2 and m ≈ 0.95). These variations can be reduced by increasing the number of phase steps (Supplementary Fig. 7 and Supplementary Note).

We have tested our method on DNA-origami nanostructures imaged with DNA-PAINT¹⁸ (see Methods). Figure 2a shows the SIMFLUX reconstruction over the full 26 × 26 μm² FOV of nano-rulers with binding site spacing of 80 nm and Fig. 2b–d show five selected SIMFLUX nano-ruler images across the FOV, with improved precision compared to the SMLM images. The latter uses the fits from the sum of six frames used for SIMFLUX, which effectively provides a spatially uniform illumination. The projections of the localizations in Fig. 2d,e on the x axis provides localization histograms (Fig. 2f,g), indicating an improvement in localization precision with a factor of around 2. The localization error, measured from the accumulated data of 420 segmented binding sites across the whole FOV, improves from 17.3 to 9.6 nm (Fig. 2h–k), an improvement factor of 1.8. The achieved precision, determined from repeated localizations of long-lasting on-events (Fig. 2l,m), is 2.3 times better for SIMFLUX, close to the expected improvement factor of 2.1 (for p/σ = 1.85, m = 0.92). The localization precision values determined in this way are slightly greater than the CRLB, as opposed to the precision values from the cluster analysis, that exceed the CRLB more (Supplementary Fig. 9). We attribute this difference to a residual drift after correction of around 4 nm, a level that is reasonable in view of the difficulty for precise estimation on the sparse sample. Drift may also be the root cause for the washing out of the dependence of the precision on global phase, anticipated by theory and for an improvement factor that is less than the theoretical value 2.1. The histogram of nearest neighbor localizations (Fig. 2n,o) shows the expected peaks at the single and double binding site distance for the origami, indicating that SIMFLUX does not compromise accuracy. The Fourier ring correlation (FRC) resolution¹⁹ improves from 16.4 to 8.6 nm (Fig. 2p), an improvement factor of 1.9, comparable to the improvement factor 1.8 found from cluster analysis. A precision improvement of 2.0 can also be achieved for the case of four phase steps (Supplementary Fig. 10), which can provide more robustness against errors in detecting the on-off transitions. Figure 2q–t and Supplementary Fig. 11 show further results on DNA-origami grids with binding site spacing of 40 and 20 nm, revealing similar resolution improvements.

Fig. 2: Demonstration of SIMFLUX on DNA-origami nanostructures.

a, Full 26-μm wide FOV SIMFLUX image of sparsely distributed nano-rulers with 80-nm spacing. Four independent imaging experiments were done with similar outcome. Scale bar, 5 μm. b,c, Zoom-in on four conventional SMLM (b) and SIMFLUX (c) nano-ruler instances color indicated as boxes in a, both reconstructions are based on the same underlying data. Scale bars, 50 nm. d,e, SMLM (d) and SIMFLUX (e) image of nano-ruler instance of box in a. Scale bars, 50 nm. f,g, Histograms of localizations in d,e projected on the x axis. h,i, Two-dimensional histograms of SMLM (h) and SIMFLUX (i) localizations in the image plane, assembled from 420 segmented binding sites. Scale bars, 15 nm. j,k, Histograms of of SMLM (j) and SIMFLUX (k) localizations projected onto the x direction. l,m, Localization error Δ_loc and CRLB (mean and s.d.) determined from repeated localizations of long-lasting on-events. Number of localizations per data point are given in the Supplementary Table. n,o, Histogram of nearest neighbor localizations for SMLM (n) and SIMFLUX (o) and bimodal Gaussian fits. p, FRC curves for dataset of a with resolution values R. q,r, SMLM (q) and SIMFLUX (r) images of DNA-origami grids with 40 nm spacing between binding sites. Two independent imaging experiments were done with similar outcome. s,t, SMLM (s) and SIMFLUX (t) images of DNA-origami grids with 20 nm spacing between binding sites. Two independent imaging experiments were done with similar outcomes. Scale bars in q–t, 50 nm.

Next, we imaged tubulin filaments in cells with DNA-PAINT (Fig. 3a–c), resulting in better visibility of the filaments and the hollow structure of tubulin²⁰ (Fig. 3d,e). The improvement in localization precision determined from long-lasting on-events is a factor 2.5 (Fig. 3f), and an FRC-resolution improvement factor of 2.1 is obtained (Fig. 3g). We also experimented with (d)STORM imaging of tubulin in cells (Fig. 3h–l), giving a relative improvement of precision with a factor 2.3 (Fig. 3m) and an improvement of FRC resolution with a factor 1.4 (Fig. 3n). The improvement in (d)STORM imaging is less than the improvement in PAINT imaging, possibly due to larger fluctuations in the intensity during the molecule’s on-time (Supplementary Fig. 12).

Fig. 3: Demonstration of SIMFLUX on cellular tubulin with DNA-PAINT and (d)STORM.

a, Full 26-μm wide FOV SIMFLUX image of tubulin sample imaged with DNA-PAINT. Three independent imaging experiments were done with similar outcome. Scale bar, 5 μm. b–d, Zoom-in on SMLM and SIMFLUX images of boxes in a; all reconstructions are based on the same underlying data. Scale bar in b (for b and c), 1 μm; in d, 2.5 μm. e, Cross-section histogram of the tubulin segment in d with bimodal Gaussian fit. f, Localization error Δ_loc and CRLB (mean and s.d.) determined from repeated localizations of long molecular on-events in the dataset of a. g, FRC curves for dataset of a with resolution values R. h, Full 26-μm wide FOV SIMFLUX image of tubulin sample imaged with (d)STORM. Four independent imaging experiments were done with similar outcome. Scale bar, 5 μm. i–k, Zoom-in on SMLM and SIMFLUX images of boxes in h, both reconstructions are based on the same underlying data. Scale bar in i (for i and j), 1 μm; in k, 2.5 μm. l, Cross-section histogram of the tubulin segment in k with bimodal Gaussian fit. m, Localization error Δ_loc and CRLB (mean and s.d.) determined from repeated localizations of long molecular on-events in the dataset of h. n, FRC curves for dataset of h with resolution values R. Number of localizations per data point in f and m are given in the Supplementary Table.

In conclusion, we have demonstrated a practical way to extend the MINFLUX concept to sinusoidal illumination patterns, improving FOV and throughput to standard SMLM experimental settings. We envision that our technique can also be used to achieve the same precision as SMLM but with four-fold less light, enabling either faster imaging or imaging with dimmer fluorophores. Our optical setup can potentially achieve the same resolution gain as MINFLUX over a small FOV in a neighborhood of size L of crossing illumination pattern minima, if we shift dark fringes of the pattern over a small total translation range L instead of the full pattern pitch p (see Supplementary Note and Supplementary Fig. 13). Another next step for SIMFLUX would be the extension to three-dimensional interference patterns for an improvement in both lateral and axial localization precision (see Supplementary Note). Similar results as reported here have been demonstrated recently²¹, using a more complex setup for very fast pattern switching and for multiplexing the phase images on two separate cameras for readout within a single camera frame, and a localization algorithm based on the modulation by the shifting illumination pattern alone.

Methods

Experimental setup

A custom total internal reflection–SIM microscope was built to implement the SIMFLUX method (Supplementary Fig. 14). The setup uses a 200 mW, 640 nm, diode laser (Toptica, CLUP-640) that is spectrally filtered with a 640/20 nm (Chroma, ET640/20 m) bandpass filter and spatially filtered by coupling into a polarization maintaining single mode fiber (ThorLabs, PM630-HP) via a numerical aperture (NA)-matched aspheric lens, L1 (focal length, f = 3.3 mm, ThorLabs, C340TMD-A). The output of the fiber is collimated by an objective, L2 (0.45/20X A-PLAN, Zeiss). SIMFLUX uses two orthogonal sinusoidal modulation patterns in the focal plane of the objective lens. The optical architecture overcomes drawbacks of typical SIM architectures. Rotating gratings are too slow to generate multiple illumination patterns for a typical molecular on-event (tens of milliseconds), spatial light modulators are sufficiently fast, but too power-inefficient to generate a sufficiently high illumination intensity (~kW cm⁻²) over an extended FOV (tens of micrometers). A simple way to generate these is to build an interferometer and self-interfere a laser at the sample plane. The approach is a modification of an earlier architecture, where two pairs of diffraction orders are generated with two orthogonally oriented gratings and combined with a polarizing beam splitter²². In our setup, custom etched binary phase gratings (HOLOOR, DS-281-1-Y-A) with pitches of 8.496 µm are used to generate plus or minus first diffraction orders with near theoretical diffraction efficiency limits of around 79%. Distinct and orthogonal interference patterns at the focal plane with controllable phase are generated using a fluid filled KD*P Pockels cell (Leysop, EM508-2T-F-AR640) to alternate the laser between two beam paths and piezoelectric stages (PI) (P-753.1CD) to phase shift the binary phase gratings. Before being sent through the Pockels cell and diffraction gratings, the laser intensity is controlled via a half wave plate (ThorLabs, DS-281-1-Y-A) and a Glan–Taylor polarizer (GL10-A) to attenuate when needed while maintaining at least a 1,000/1 intensity extinction ratio between each path. The beam then passes through the Pockels cell that is aligned such that applying a half wave voltage switches the beam between s and p polarizations. Two mirrors (ThorLabs, PF10-03-G01) then align the laser to the main optical axis of the system. A quarter wave plate and half wave plate (ThorLabs, WPQ05M-633 and WPH05M-633) are placed after the second mirror to reduce any elliptical polarization induced by reflection. A cube polarizing beam splitter (ThorLabs, CCM1-PBS252/M) selects the beam path based on s or p polarization entry. A high extinction ratio Glan–Taylor polarizer (ThorLabs, GL10-A) is then placed in each beam path after the polarizing beam splitter to ensure at least 10⁴ polarization purity in each beam path. A binary phase grating is then placed in both beam paths. Each grating is mounted on a nanometer resolution piezoelectric translation stage to induce phase shifting. The stages have a step and settle time of 3–4 ms, giving an upper limit to the frame-rate of 250 Hz. The gratings are aligned on the piezoelectric stages so that their main diffraction axes are orthogonal to one another. The azimuthal alignment of the gratings is chosen such that the polarization of the interfering diffraction orders is parallel in the objective focal plane for each beam path. After light is diffracted from each binary phase grating, a second polarizing beam splitter recombines the two paths into the main system illumination path. Two more beam steering mirrors are needed to recombine the beam path that is reflected off the first beam splitter. After recombining into a single optical axis, the diffracted orders are collimated by L3 (ThorLabs, ACA254-075-A) and sent through a spatial filter mask to filter all but the plus or minus first diffraction orders. From there, a 4f system L4,5 (Edmund Optics/ThorLabs, 49-395-INK/AC508-180-A-ML) relays the spatial filter to the rear focal plane of the objective (Nikon, CFI Apo 1.49 total internal reflection (TIRF) 100XC Oil) after reflecting off a long pass dichroic mirror (Semrock, Di03-R660-t1-25.2x35.6). If the light from the plus or minus first orders is well focused in the rear focal plane, collimated light will emerge from the objective and be incident on the sample plane. Careful alignment is needed here, as a defocus at the rear focal plane will result in a distortion of the sinusoidal illumination pattern. The plus or minus first orders enter at opposite edges of the back focal plane at a radius of ±2.91 mm from the optical axis, corresponding to an illumination NA (NA_ill) = 2.91/2.0 = 1.455 (the focal length of the Nikon ×100 objective lens is 2.0 mm). NA_ill exceeds the sample refractive index of n_med = 1.33 and therefore provides TIRF illumination. A TIRF illumination system is chosen to reduce background fluorescence by providing an interface bound optical sectioning of 100–200 nm, and to be compatible with DNA-PAINT-based localization. The sample plane is illuminated with a power density of ~600 W cm⁻² over an 80 µm illumination diameter. Control of the sample plane and system focus is achieved with an XYZ 100 × 100 × 100 µm³ travel range piezoelectric slide stage (Mad City Labs, 1D100). Emitted fluorescence is collected by the same Nikon objective in an epi-illumination configuration and passes through the long pass dichroic mirror and a bandpass 690/50 nm emission filter (Chroma, ET690/50 m) before being imaged by an infinity corrected tube lens (ThorLabs, TTL200-A) onto an sCMOS camera (Hamamatsu, ORCA Flash 4.0V2). The pixel size of our camera in the sensor plane is 6.5 µm giving a back-projected pixel size in the sample plane equal to 65 nm. Image acquisition was controlled using a standard desktop workstation equipped with a camera link frame grabber (Hamamatsu, AS-FBD-1XCLD-2PE8). Micro-manager serves as the main image acquisition software, but is integrated with a custom Python script to control an Arduino that triggers the PI piezoelectric stage controllers and the Pockels cell to iterate through imaging states. Micro-manager also controls the piezoelectric sample stage from Mad City Labs. The PI piezoelectric stages were initialized to receive triggers from the Arduino via the program MikroMove.

A second set of hardware was incorporated into the system to facilitate (d)STORM imaging. These alterations included replacing the original sCMOS camera (Hamamatsu, ORCA Flash 4.0V2) with another sCMOS camera (Andor, Zyla 4.2) for better pixel blanking between subsequent frames. The laser was replaced with a 200 mW, 638 nm, laser diode (Omicron, PhoxX+638-200) in a fiber-less free space configuration to achieve an appropriate power density at the sample plane of ~1.5 kW cm⁻² for (d)STORM imaging. Micro-manager was also replaced with the Andor Solis frame capture software to facilitate high speed spooling to hard disk without data loss.

The modulation contrast of the system was characterized by imaging a pre-prepared slide of 20 nm GATTA-beads (GattaQuant, Bead R) and finely phase shifting the illumination pattern over the sample. By imaging after each phase shift, a direct measurement of the sinusoidal wave can be traced over the image series duration (Supplementary Fig. 15). Median values of the modulation contrast of 0.91 and 0.92 in the two pattern directions were measured. The observed values for the modulation contrast may be related to polarization impurity at the back focal plane. An analysis of the electromagnetic evanescent wave at the sample results in a modulation contrast $m \approx 1 - 2\left( {{\mathrm{NA}}_{\mathrm{ill}}^2/n_{{\mathrm{sample}}}^2} \right)R$, with R being the intensity ratio of undesired (p) to desired (s) polarization at the back focal plane. Excluding other causes, a value of R around 3–4% is consistent with the observed modulation contrast. A contributing factor to polarization impurity could be the reflection of the beams converging to the back focal plane of the objective after reflection at the dichroic. The polarization purity may also be affected by the quality of the dichroic. According to the specification of the manufacturer, the reflection for s-polarized light is at almost 100%, and the reflection for p-polarized light is about 98% at a laser wavelength of 640 nm.

The pitch of the interference pattern in the sample plane was calibrated by imaging high density, blinking, fluorophores that are evenly distributed in the sample plane and localizing the fluorophores under static standing wave illumination conditions. The illumination pattern arises from the interference of evanescent waves and is therefore not directly visible, however, super-resolved localization images show it clearly (Supplementary Fig. 16), giving a pitch equal to 219.94 nm. This estimate of the pitch agrees well with the expected value λ_ex/(2NA_ill) = 640/(2 × 1.455) = 219.9 nm. The direct calibration of stage translation to phase for the piezo mounted diffraction gratings can be calculated from this data as well, giving a sample plane pattern shift to grating translation ratio of 51.6 nm µm⁻¹.

Samples

Gattaquant nano-rulers based on DNA-PAINT, GATTA-PAINT (PAINT 80 R ATTO 655), were used as the main samples for our imaging experiments. They consist of three equally spaced binding sites separated by 80 nm between each with an approximate surface density of 1 µm^–2. Other DNA-PAINT based nanostructures were imaged with uniformly decreasing structure sizes: 2 × 2 grids with 40 nm binding site distance and 4 × 3 grids with 20 nm binding site distance (see Supplementary Fig. 17 for designs) were synthesized and prepared according to the protocols provided by Schnitzbauer et al.¹⁸ employing 5′-TTATACATCTA-3′ as DNA-PAINT docking strand (positions marked in red in Supplementary Fig. 17) and 5′-CTAGATGTAT-3′-Cy3B as DNA-PAINT imager sequence. Both nanostructures were imaged using 5 nM imager strand concentration.

For the tubulin imaging with DNA-PAINT in Fig. 3, COS-7 cells were passaged every other day and used between passage numbers 5 and 20. The cells were maintained in DMEM supplemented with 1% sodium pyruvate and 10% fetal bovine serum. Passaging was performed using 1× PBS and Trypsin-EDTA 0.05%. Then, 24 h before immunostaining, cells were seeded on ibidi eight-well glass coverslips at 30,000 cells per well. For fixation, the samples were pre-fixed and pre-permeabilized with 0.4% glutaraldehyde and 0.25% Triton X-100 for 90 s. Next, the cells were quickly rinsed with 1× PBS once followed by fixation with 3% glutaraldehyde for 15 min. Afterward, samples were rinsed twice (5 min) with 1× PBS and then quenched with 0.1% NaBH₄ for 7 min. After rinsing four times with 1× PBS for 30 s, 60 s, and twice for 5 min, samples were blocked and permeabilized with 3% BSA and 0.25% Triton X-100 for 2 h. Then, samples were incubated with 10 μg ml⁻¹ of primary antibodies (1:100 dilution) in a solution with 3% BSA and 0.1% Triton X-100 at 4 °C overnight. Cells were rinsed three times (5 min each) with 1 × PBS. Next, they were incubated with 10 μg ml⁻¹ of labeled secondary antibodies (1:100 dilution) in a solution with 3% BSA and 0.1% Triton X-100 at room temperature for 1 h. For the fiducial-based drift correction, the samples were incubated with gold nanoparticles with a 1:1 dilution in 1 × PBS for 5 min. Finally, samples were rinsed three times with 1× PBS before adding imager solution. Imaging was carried out using an imager strand (P1–8 nucleotides, 5-AGATGTAT-Atto655-3′; P1–7 nucleotides, 5-GATGTAT-Atto655-3′) concentration of 2 nM in imaging buffer (1× PBS supplemented with 500 mM NaCl).

For the tubulin imaging with (d)STORM in Fig. 3, COS-7 cells were seeded onto 18 mm coverslips. After 24 h of incubation, the cells underwent extraction with 0.1% glutaraldehyde and 0.2% Triton X-100 in PEM80 for 1 min and were fixed with 4% PFA in PEM80 for 10 min. The cells were then rinsed three times in 1× PBS for 5 min and permeabilized with 0.2% Triton X-100 in PEM80 for 15 min. Cells were again rinsed three times in 1× PBS for 5 min, after which blocking was performed in 3% BSA for 45 min at room temperature. Next, the cells were incubated in primary antibody mouse anti-alpha-Tub (Sigma, 1 1,000) overnight at 4 °C. The following day the cells were rinsed three times in 1× PBS for 5 min and incubated with anti-mouse Alexa647 (Life Technologies, 1/500) for 1 h at room temperature. After three rinses, the cells were mounted on 80 μl cavity slides with AbbeLight STORM buffer.

Data acquisition

A simple data acquisition sequence was defined to acquire six (or any other arbitrary number) phase shifted images during the on-time of a single blinking event of a fluorophore (Supplementary Fig. 18). For the DNA-origami samples in this experiment, the average on-time of blinking events is ~100–200 ms for the GattaQuant nano-rulers, ~1 s for the 40 nm 2 × 2 grids and ~100 ms for the 20 nm 4 × 3 grids. For the DNA-PAINT tubulin and STORM tubulin samples the average on-time is ~400–500 and ~100 ms, respectively. All DNA-PAINT origami samples were imaged at 70 frames per second with 10 ms exposure time per frame, the DNA-PAINT tubulin samples at 14 frames per second with 40 ms exposure time per frame, and the (d)STORM samples at 200 frames per second with 4 ms exposures. These settings ensured that typically a full phase cycle of each pattern orientation was captured. The nano-ruler dataset consists of ~30,000 frames, the origami grid samples of ~100,000 frames, the DNA-PAINT tubulin dataset of ~13,000 frames and the (d)STORM tubulin dataset of ~150,000 frames.

Simulation setup

Simulated PSFs are generated according to a vectorial PSF model²³. The NA is taken to be 1.49, the wavelength 680 nm, the refractive index 1.515 (medium, cover slip and immersion fluid assumed to be matched), with a pixel size of 65 nm in object space and the ROI is 11 × 11 pixels large. The PSF coordinates within the ROI are drawn from a uniform distribution with a width of half the illumination pattern pitch. Unless stated otherwise, we take 6,000 detected signal photons and 30 background photons per pixel, and we add noise according to Poisson statistics. The simulations are run for 5,000 randomized instances. The pitch of the excitation pattern is taken to be 243.75 nm, which is set equal to about twice the spot width for the sake of simplicity. The number of signal photons reported corresponds to the number of photons captured over the entire FOV, that is taking into account the spatially extended tail of the PSF that falls outside the ROI²⁴.

We have also used simulations of blinking emitters over a full FOV (Supplementary Fig. 19). A filamentous structure, similar in appearance to microtubules, is generated using the worm-like chain model. The simulated filaments fill a FOV of several micrometers. Binding sites along the filaments are randomly generated at an average separation distance of ~5 nm. At each binding site flexible linkers are simulated using a normal distribution with a standard deviation of 3 nm. Randomly switching fluorophores are simulated at the end of the linkers, using an average on-time of nine frames and an average off-time of 54,000 frames. Random transitions between both states were simulated at a rate of 1× the frame-rate. The illumination pattern is shifted in three steps over the pitch of 220 nm with a modulation depth of 0.95 in both the x and y directions to match the expected experimental values. The locations of the resulting set of emitters that are in the on-state in a frame are blurred with the vectorial PSFs as described above. Shot noise is subsequently added, using 2,000 detected signal photons per spot and ten background photons per pixel. The entire simulation consists of 120,000 camera frames. Localizations with fitted background more than two times the average background and/or signal photon count more than twice the average (mainly occurring due to nearby fluorophores that are on simultaneously) are designated as outliers.

Processing pipeline

Supplementary Fig. 20 gives a schematic overview of the entire processing pipeline. First, the set of acquired images were first offset and gain-corrected to convert analog-digital units (ADUs) into photons^25,26. The total set of acquired images is $I_p^{lk}$ with l = 1,…,L being the pattern orientations, k = 1,…,K the pattern phases and p = 1,…,P the label for the groups of L × K frames, giving a total of L × K × P acquired frames. The detection of isolated emitting molecules is aided by first applying a sum over the L × K blocks of frames; that is, the set of $I_p^{lk}$ is summed to $J_p = \mathop {\sum }\limits_{lk} I_p^{lk}$. This averages out the effect of the shifting and rotating illumination pattern, and increases the signal-to-noise ratio for spot detection. ROIs of size 9 × 9 pixels are identified by a two-stage filtering process to reduce photon noise and local background followed by an intensity threshold^27,28. In short, we apply uniform filters to the raw images with filter sizes of 4 and 8 pixels and take the difference. We then compute the local maximum in a 5 × 5-pixel neighborhood for all pixels and accept the central pixel as candidate for a single-molecule spot if its value is the local maximum and is higher than a threshold of ten (for the nano-ruler dataset of Fig. 2 and Supplementary Fig. 11) or 20 (for the grid DNA-origami datasets of Fig. 2 and Supplementary Fig. 11). Now a 9 × 9 pixel ROI is segmented out for all candidates, and each ROI, labeled with index s, is extracted and fitted for emitter position ${\bf r}_s = \left( {x_s,y_s} \right)$, signal photon count N_s and background b_s using established MLE fitting^29,30 using a Gaussian PSF model. The fits are done with a fixed Gaussian spot width of 119 nm, determined from a separate fit on the first few frames of the entire dataset.

In a next step the signal photon count and background in the ROI with label s in the L × K original individual frames $I_p^{lk}$ are analyzed for estimating the signal photon count $N_s^{lk}$ and background $b_s^{lk}$ given the estimate of the emitter position (x_s, y_s) obtained from fitting the moving sum images J_p. The underestimation of the signal photon count²⁴ by ~30% due to the use of the Gaussian PSF model has a limited impact on the subsequent analysis, as only the relative signal photon count for different phases and orientations of the illumination pattern is used. The single-frame localizations within the sequences of L × K frames are kept and merged into a single localization estimate, according to standard practices¹³. The resulting SMLM estimates are stored for later comparison to the SIMFLUX estimate.

The next step is the estimation of the illumination pattern parameters. First, we make an initial estimate of the spatial frequency vectors ${q}_l = \left( {\cos \beta _l,\sin \beta _l} \right)/p_l$ (with pitch p_l and orientation β_l) of the patterns. The set of molecular on-events with label s contains L × K single-frame localizations with estimated coordinates (x_s, y_s), signal count $N_s^{lk}$ and background $b_s^{lk}$. The entire collection of these single-frame localizations is split into subsets corresponding to the l = 1,…,L orientations and k = 1,…,K phases of the illumination patterns. The L × K subsets of single-frame localizations are used to generate super-resolution reconstructions $S_n^{lk}$ defined on a grid of super-resolution pixels ${\bf r}_n$, with n being the index of the super-resolution pixels. We have used Gaussian blob rendering with a width equal to the average localization precision from the single-frame localizations, and a zoom factor of six compared to the detector pixel grid to make the super-resolution pixel size comparable to the single-frame localization precision¹⁹. For the data of Fig. 2 we have used a super-resolution pixel size equal to 10.8 nm, comparable to the CRLB in the single-frame localizations of around 12 nm. Each Gaussian blob is multiplied with a weight factor equal to the estimated signal photon count $N_s^{lk}$. The spatial frequencies ${\bf q}_l$ are then detected by finding the peak in the Fourier domain of the reconstructions $S_n^{lk}$.

In a next step, sequences of L × K single-frame localizations where the molecule under consideration is partially in the off-state are rejected by application of a modulation error filter. Sequences are selected where the prediction error is below a user set maximum relative error:

$$\mathop {{{\mathrm{max}}}}\limits_{k,l} \left( {\frac{{N_s^{lk}}}{{N_s}} - P_l\left( {\varphi _{lk}\left( {{\bf r}_s} \right)} \right)} \right)^{\!2} < \gamma _{{\mathrm{max}}}$$

(2)

where $P_l\left( {\varphi _{lk}\left( {{\bf r}_s} \right)} \right)$ is the expected illumination pattern. The choice for the threshold γ_max is based on a simulation study of realistic filamentous objects (see Supplementary Fig. 19). It appears that a Jaccard index of approximately 65% is achieved, where the Jaccard index is defined as the fraction TP/(TP + FP + FN) (where true positive localizations are TP, false positive localizations are FP and false negative localizations are FN). The false positive rate and false negative rate depend smoothly on γ_max (Supplementary Fig. 19h), but not so much on signal photon count and background level. For the experimental data a value in the range between 0.01 and 0.06 is selected such that about 30% of originally detected events is rejected. For the DNA-origami nano-rulers of Fig. 2 a setting γ_max = 0.012 is used, for the tubulin-PAINT dataset of Fig. 3 a setting γ_max = 0.05 is used, and for the tubulin-STORM dataset of Fig. 3 a setting γ_max = 0.04 is used.

This first estimate of pitch and orientation of the patterns is improved by an iterative refinement procedure. The first step here is to estimate the illumination pattern phases ψ_lk, as well as the modulation depths m_l and relative intensity η_l for illumination patterns with orientation l (normalized as $\mathop {\sum}\nolimits_l {\eta _l} = 1$, nominally η_l = 1/L). These estimates are obtained by a least-squares fit of the illumination pattern to the detected photon counts $N_s^{lk}$ with the error metric:

$$E_{lk} = \mathop {\sum }\limits_s \left| {N_s^{lk} - \eta _l\frac{{N_s}}{K}\left( {1 + m\cos \left( {\varphi _{lk}\left( {{\bf r}_s} \right)} \right)} \right)} \right|^2$$

(3)

with $\varphi _{lk}\left( {{\bf r}_s} \right) = 2\pi {q}_l \cdot {r}_s - \psi _{lk}$ the phase at localization position ${r}_s$. Illumination pattern phase estimation biases originating from the structure of the underlying fluorescently labeled structure are mitigated by taking into account the sum of all detected photon counts $N_s = \mathop {\sum}\nolimits_{lk} {N_s^{lk}}$ as weight factor for the illumination pattern in the error metric. The minimization of equation (3) with respect to the zeroth and first order Fourier coefficients (η_l,η_lm_l cosψ_lk, η_lm_l sinψ_lk) of the sinusoidal illumination results in:

$$\begin{array}{l}\left[ {\begin{array}{*{20}{c}} {\mathop {\sum }\limits_s \frac{{N_s^2}}{{K^2}}} & {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\cos \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} & {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\sin \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} \\ {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\cos \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} & {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\cos \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)^2} & {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\sin \left( {2\pi {\bf q}_l \cdot {\bf r}_n} \right)\cos \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} \\ {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\sin \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} & {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\sin \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)\cos \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} & {\mathop {\sum }\limits_s \frac{{{N_s}^2}}{{K^2}}\sin \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)^2} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {\eta _l} \\ {\eta _lm_l\cos \psi _{lk}} \\ {\eta _lm_l\sin \psi _{lk}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathop {\sum }\limits_s \frac{{N_s^{lk}N_s}}{K}} \\ {\mathop {\sum }\limits_s \frac{{N_s^{lk}N_s}}{K}\cos \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} \\ {\mathop {\sum }\limits_s \frac{{N_s^{lk}N_s}}{K}\sin \left( {2\pi {\bf q}_l \cdot {\bf r}_s} \right)} \end{array}} \right]\end{array}$$

(4)

which can be solved in a straightforward way. The robustness of the fit is further enhanced by an iterative procedure in which the median of the quadratic error distribution over the localizations in equation (3) is determined, and the localizations with errors less than the median are kept for a second phase estimation. After this second phase estimation, the median of the quadratic error of the original set of localizations is determined again and the localizations with error less than the median are kept for a third phase estimation and so on. This procedure converges within three iterations. We apply this procedure on the set of localizations that is obtained before application of the modulation error filter. In this way blocks of frames in which the molecule is partially in the on-state (say in the last three but not in the first three frames) aid in the fitting. The phase estimation has a standard error of the mean typically between 0.5 and 1.0° (Supplementary Fig. 8). The modulation depths m_l are typically estimated around 0.95, in agreement with the calibration measurements on beads. The modulation depth is typically underestimated for nonsparse datasets. In that case, it is better kept fixed to 0.95, the typical value obtained for sparse datasets. The relative intensity η₁ = 1 − η₂ is found to be around 0.455 in our setup.

Next, an MLE based estimate is made of the molecule’s position, using both image centroid information and photon count information. The PSF model, log-likelihood and relevant derivatives with respect to the fit parameters are defined in the Supplementary Note. Initial values for the parameter estimation are taken from the analyses on single-frame and moving sum frame data, the optimization uses the Levenberg–Marquardt algorithm. The previously estimated illumination pattern parameters are assumed to be constant throughout the experiment.

This SIMFLUX estimate differs $\delta {\bf r}_s$ from the corresponding SMLM localization, where s labels the different localization events. An improved estimate of the spatial frequencies can now be made by minimizing the overall error in the illumination pattern phases $\varphi _{lk}\left( {{\bf r}_s} \right) = 2\pi {\bf q}_l \cdot {\bf r}_s - \psi _{lk}$. The average phase error per orientation is:

$$\delta \varphi _l\left( {{\bf r}_s} \right) = 2\pi {\bf q}_l \cdot \delta {\bf r}_s + 2\pi \delta {\bf q}_l \cdot {\bf r}_s - \delta \psi _l$$

(5)

where $\delta {\bf q}_l$ is the error in the spatial frequency vector, and where δψ_l is the average error in the pattern phase. These errors can be estimated by linear regression; that is, by minimizing:

$$F_l = \mathop {\sum}\nolimits_s {\left| {\delta \varphi _l\left( {{\bf r}_s} \right)} \right|} ^2$$

(6)

This results in a linear set of equations for $\delta {\bf q}_l$ and $\delta \psi _l$:

$$\mathop {\sum }\limits_s 2\pi \left( {\delta {\bf q}_l \cdot {\bf r}_s} \right){\bf r}_s - \mathop {\sum }\limits_s \delta \psi _l{\bf r}_s = - \mathop {\sum }\limits_s 2\pi \left( {{\bf q}_l \cdot \delta {\bf r}_s} \right){\bf r}_s$$

(7a)

$$\mathop {\sum }\limits_s 2\pi \left( {\delta {\bf q}_l \cdot {\bf r}_s} \right) - \mathop {\sum }\limits_s \delta \psi _l = - \mathop {\sum }\limits_s 2\pi \left( {{\bf q}_l \cdot \delta {\bf r}_s} \right)$$

(7b)

which can be solved in a straightforward way. After updating the spatial frequency vectors to ${\bf q}_l\prime = {\bf q}_l + \delta {\bf q}_l$ the estimation of the pattern phases ψ_lk as explained above is repeated, as well as the SIMFLUX MLE fit. This procedure converges in three to four iterations.

The quality of convergence can be assessed by the root mean squared (r.m.s.) value of the SMLM-SIMFLUX localization difference $\delta r_{{\mathrm{r.m.s.}}}$. It appears that at convergence this r.m.s. value is about 13.0 nm for the nano-ruler dataset of Fig. 2 (see Supplementary Fig. 21). This value is on the order of the localization uncertainty, which seems physically reasonable. It implies an error in the overall pattern phase of about $\delta \varphi \approx 2\pi \delta r_{{\mathrm{r.m.s.}}}/p\sqrt {N_s} = 1.0^{\circ}$ with N_s = 431 the number of imaged binding sites used in the analysis and p = 220 nm the nominal pitch. This can be related to the final precision in the pitch estimation δp, which scales with the precision of the overall pattern phase estimation according to $\delta \varphi \approx 2\pi {\delta q_l} \times R_{{\mathrm{FOV}}} = 2\pi \delta pR_{{\mathrm{FOV}}}/p^2$, with R_FOV = 13 μm the FOV size. This gives a precision in the pitch estimation of about δp ≈ 0.01 nm. The distribution of SMLM-SIMFLUX localization differences in x and y for the other datasets is unbiased as well, with a width that increases with the localization precision. No correlation with the position in the FOV is observed in all cases.

Sample drift is corrected on the localization data following the method of Schnitzbauer et al.¹⁸, implemented using the Picasso software tool, available at https://github.com/jungmannlab/picasso. We note that sample drift does not influence the pattern parameter estimation as the projected pattern is static under sample drift. Therefore, we do not need to re-estimate the pattern parameters after drift correction is applied to the localizations.

All images are rendered by histogram binning on a grid with a 0.52 nm (Fig. 2d,e,p–s and Supplementary Fig. 11) or 0.52 nm (Fig. 2b,c) super-resolution pixel size with additional Gaussian blurring with kernel size (sigma) equal to one super-resolution pixel. The overview image Fig. 2a and Fig. 3a,k are rendered with a super-resolution pixel size of 33.85 nm and a Gaussian pixel blur of 19.5 nm. The subimages in Fig. 3b–e,h and l–o are rendered with a super-resolution pixel size of 3.25 nm and a Gaussian pixel blur of 3.25 nm.

Data analysis

The spread of localizations is estimated using the FRC¹⁹ of the entire super-resolution reconstruction. The two image halves are found by randomly selecting localizations to the two subsets. This gives rise to FRC curves largely determined by the localization precision, eliminating correlations arising from having multiple localizations from the same binding site (spurious correlations) would result in an FRC curve determined by the structure of the sparsely distributed binding sites¹⁹. The split datasets are used to generate reconstructions on a 2 nm super-resolution pixel grid (super-resolution pixel size must be smaller than about 0.25× the FRC resolution for a valid FRC estimation) by the histogram binning method. The spread of localizations for the DNA-origami nano-ruler dataset of Fig. 2 is also assessed with a cluster analysis of the localization point clouds around each binding site. A kernel density estimate of the histograms is used to measure the full-width half-maximum of the histograms.

These estimates are based on localizations accumulated over the entire duration of the acquisition, and therefore take into account the impact of residual drift. A more direct estimate of localization uncertainty is based on repeated localizations of the same molecule during long-lasting on-events, which are short compared to the time scale of drift. These extended on-events are detected by linking localizations in subsequent six frame blocks that are spatially proximate¹³. Two localizations are assumed to arise from the same emitting molecule if the distance between the localizations is shorter than r times the largest localization uncertainty value of the two localizations. A heuristic choice is r = 3. Small values of r will lead to an underestimation of the localization uncertainty, as the localizations are restricted to a (too) small region in space, large values of r will lead to an overestimation of the localization uncertainty, as localizations from neighboring binding sites or false positive localizations are linked into the set. For example, for the nano-ruler dataset of Fig. 2 the value for the localization uncertainty varies with about 15% in the range 2.5 ≤ r ≤ 4 around the given value 2.70 nm for r = 3. Similar variations with r are also found for the other datasets considered. The localization uncertainty is defined as the (unbiased) sample variance over the repeated localizations within the set of linked localizations. This is compared to the average CRLB value over the set of linked localizations. This analysis also provides a way to estimate the fluorophore on-time. A fit of the distribution of the number of linked localization events as a function of the run length with an exponential distribution can then be made, the fitted time constant is the estimate for the on-time. Analysis of the nano-ruler dataset of Fig. 2 gives an estimated on-time of 19.1 frames. The tubulin datasets of Fig. 3 reveal an average on-time of 7.4 frames (DNA-PAINT) and 11.8 frames (STORM).

We analyzed long-lasting on-events for intensity fluctuations above the level expected from shot noise statistics (Supplementary Fig. 12). To this end we imaged an 80 nm DNA-PAINT nano-ruler as well as a COS-7 Alexa647 (d)STORM sample with a static illumination pattern to image spots with a wide range of intensities. Well isolated spots corresponding to on-events that last at least ten frames were extracted (see Supplementary Fig. 12a,d for examples) and fitted with a standard Gaussian PSF model. For DNA-PAINT, the unbiased variance of the estimated signal photon count during the on-events as a function of the time separation of the photon count estimates T is about 27% above the level expected from the CRLB, where the deviation increases with only about 3% with T (Supplementary Fig. 12b). The variance in the fitted intensities follow the CRLB if the emitted number of photons follows the assumed Poisson statistics (Supplementary Fig. 12c), and is larger than the CRLB in case there are additional sources of intensity fluctuations such as subframe blinking events. For (d)STORM, the unbiased variance of the estimated signal photon count during the on-events as a function of the time separation of the photon count estimates T is about 125% above the level expected from the CRLB, where the deviation varies with about 12% with T (Supplementary Fig. 12e). The overall higher level of the error could come from model errors in the fitting (nonconstant background, simplified Gaussian PSF model, aberrations, error in gain calibration and so on) and from intensity fluctuations above the shot noise level.

We have analyzed the impact of intensity fluctuations on the outcome of the fitting routines by a simulation study. To that end we modified the image formation model of the Supplementary Note by replacing the overall photon count N by N′ = N (1 + E), where E is a variable that takes random values from a normal distribution with zero mean and standard deviation σ_E in each camera frame. This variable describes intrinsic intensity fluctuations of the emitter during the on-time, giving rise to an apparent variance $\Delta N^{\prime 2} = \Delta N^2 + \left( {N^2 + \Delta N^2} \right)\sigma _E^2$, with N the average photon count, a variance that is higher than the variance ΔN² according to the CRLB. The experimental values for PAINT are ΔN = 47 and ΔN′ = 60. This results in σ_E = 0.031, for an average fitted photon count N = 1,180. The experimental values for (d)STORM are ΔN = 49 and ΔN′ = 111. This results in σ_E = 0.093, for an average fitted photon count N = 1,062. With the simulations we have computed the relative improvement of SIMFLUX over conventional SMLM as a function of σ_E (Supplementary Fig. 12f). This implies an improvement factor for PAINT that is practically at the value 2.2 simulated with zero intensity fluctuations, and an improvement factor in the range 1.6–2.0 for (d)STORM, depending on signal photon count. These values are below the optimum, in agreement with the relative improvement in apparent image quality and FRC of the (d)STORM data in comparison to the PAINT data. It also turns out that the sensitivity to intrinsic intensity fluctuations is larger for higher average photon counts. This can possibly be attributed to the photon count errors of the Gaussian PSF model, which are graver for higher signal photon counts²⁴.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.