Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Universal inverse modeling of point spread functions for SMLM localization and microscope characterization

Nature Methods volume 21, pages 1082–1093 (2024)Cite this article

Subjects

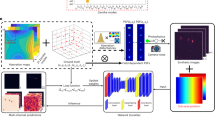
Abstract

The point spread function (PSF) of a microscope describes the image of a point emitter. Knowing the accurate PSF model is essential for various imaging tasks, including single-molecule localization, aberration correction and deconvolution. Here we present universal inverse modeling of point spread functions (uiPSF), a toolbox to infer accurate PSF models from microscopy data, using either image stacks of fluorescent beads or directly images of blinking fluorophores, the raw data in single-molecule localization microscopy (SMLM). Our modular framework is applicable to a variety of microscope modalities and the PSF model incorporates system- or sample-specific characteristics, for example, the bead size, field- and depth- dependent aberrations, and transformations among channels. We demonstrate its application in single or multiple channels or large field-of-view SMLM systems, 4Pi-SMLM, and lattice light-sheet microscopes using either bead data or single-molecule blinking data.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Concept and modalities of uiPSF.
Fig. 2: Application of uiPSF to multichannel ratiometric dual-color SMLM and 4Pi-SMLM.
Fig. 3: In situ PSF modeling from single blinking fluorophores.
Fig. 4: Ratiometric three-color imaging of the SC using an in situ PSF model.
Fig. 5: FD-PSF modeling.

Similar content being viewed by others

Data availability

The data that support the findings of this study are publicly available at Zenodo. Data for Fig. 2 are available at https://doi.org/10.5281/zenodo.10823308 (ref. 78). Data for Fig. 3 are available at https://doi.org/10.5281/zenodo.10823244 (ref. 79). Data for Fig. 4 are from ref. 60. Bead data and the first 800 frames of cell data for Fig. 5 are available at https://doi.org/10.5281/zenodo.10824517 (ref. 80). Example data for uiPSF are available at https://doi.org/10.5281/zenodo.10602740 (ref. 81). Source data are provided with this paper. Other datasets are available from the corresponding author upon reasonable request.

Code availability

uiPSF software is available at https://github.com/ries-lab/uiPSF, which includes source codes, example Jupyter notebooks and tutorials for localization analysis using the PSF models generated from uiPSF. The uiPSF software package is also available in Supplementary Software 1. The microscope acquisition software for single-objective systems was developed with Micro-Manager v2.0 (https://micro-manager.org/) and EMU v1.1 (https://github.com/jdeschamps/htSMLM/). The control software for the 4Pi-SMLM microscope is available at https://github.com/kiwibogo/Microscope-Control/tree/master/. The custom localization data analysis and rendering software is available at https://github.com/jries/SMAP/. The localization software for large FOV data is available at https://github.com/Li-Lab-SUSTech/FD-DeepLoc/.

References

  1. Theer, P., Mongis, C. & Knop, M. PSFj: know your fluorescence microscope. Nat. Methods 11, 981–982 (2014).

    Article  CAS  PubMed  Google Scholar 

  2. Faklaris, O. et al. Quality assessment in light microscopy for routine use through simple tools and robust metrics. J. Cell Biol. 221, e202107093 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  3. Nelson, G. et al. Monitoring the point spread function for quality control of confocal microscopes. Protoc. io https://doi.org/10.17504/protocols.io.bp2l61ww1vqe/v1 (2022).

  4. Qiao, C. et al. Zero-shot learning enables instant denoising and super-resolution in optical fluorescence microscopy. Preprint at bioRxiv https://doi.org/10.1101/2023.02.24.529803 (2023).

    Article  PubMed  PubMed Central  Google Scholar 

  5. Guo, M. et al. Rapid image deconvolution and multiview fusion for optical microscopy. Nat. Biotechnol. 38, 1337–1346 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  6. Li, Y., Wu, Y. -L., Hoess, P., Mund, M. & Ries, J. Depth-dependent PSF calibration and aberration correction for 3D single-molecule localization. Biomed. Opt. Express 10, 2708–2718 (2019).

    Article  PubMed  PubMed Central  Google Scholar 

  7. Hulleman, C. N. et al. Simultaneous orientation and 3D localization microscopy with a Vortex point spread function. Nat. Commun. 12, 5934 (2021).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  8. Zhang, O. et al. Six-dimensional single-molecule imaging with isotropic resolution using a multi-view reflector microscope. Nat. Photonics 17, 179–186 (2023).

    Article  CAS  PubMed  Google Scholar 

  9. Tsang, M., Nair, R. & Lu, X. -M. Quantum theory of superresolution for two incoherent optical point sources. Phys. Rev. X 6, 031033 (2016).

    Google Scholar 

  10. Shechtman, Y., Weiss, L. E., Backer, A. S., Lee, M. Y. & Moerner, W. E. Multicolour localization microscopy by point-spread-function engineering. Nat. Photonics 10, 590–594 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  11. Lelek, M. et al. Single-molecule localization microscopy. Nat. Rev. Methods Primers 1, 39 (2021).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  12. Huang, B., Wang, W., Bates, M. & Zhuang, X. Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy. Science 319, 810–813 (2008).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  13. Pavani, S. R. P. et al. Three-dimensional, single-molecule fluorescence imaging beyond the diffraction limit by using a double-helix point spread function. Proc. Natl Acad. Sci. USA 106, 2995–2999 (2009).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  14. Shechtman, Y., Sahl, S. J., Backer, A. S. & Moerner, W. E. Optimal point spread function design for 3D imaging. Phys. Rev. Lett. 113, 133902 (2014).

    Article  PubMed  PubMed Central  Google Scholar 

  15. Juette, M. F. et al. Three-dimensional sub-100 nm resolution fluorescence microscopy of thick samples. Nat. Methods 5, 527–529 (2008).

    Article  CAS  PubMed  Google Scholar 

  16. Ram, S., Prabhat, P., Chao, J., Sally Ward, E. & Ober, R. J. High accuracy 3D quantum dot tracking with multifocal plane microscopy for the study of fast intracellular dynamics in live cells. Biophys. J. 95, 6025–6043 (2008).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  17. Legant, W. R. et al. High-density three-dimensional localization microscopy across large volumes. Nat. Methods 13, 359–365 (2016).

    Article  PubMed  PubMed Central  Google Scholar 

  18. Shtengel, G. et al. Interferometric fluorescent super-resolution microscopy resolves 3D cellular ultrastructure. Proc. Natl Acad. Sci. USA 106, 3125–3130 (2009).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  19. Aquino, D. et al. Two-color nanoscopy of three-dimensional volumes by 4Pi detection of stochastically switched fluorophores. Nat. Methods 8, 353–359 (2011).

    Article  CAS  PubMed  Google Scholar 

  20. Smith, C. S., Joseph, N., Rieger, B. & Lidke, K. A. Fast, single-molecule localization that achieves theoretically minimum uncertainty. Nat. Methods 7, 373–375 (2010).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  21. Mlodzianoski, M. J., Juette, M. F., Beane, G. L. & Bewersdorf, J. Experimental characterization of 3D localization techniques for particle-tracking and super-resolution microscopy. Opt. Express 17, 8264–8277 (2009).

    Article  PubMed  Google Scholar 

  22. Babcock, H. P. & Zhuang, X. Analyzing single molecule localization microscopy data using cubic splines. Sci. Rep. 7, 552 (2017).

    Article  PubMed  PubMed Central  Google Scholar 

  23. Li, Y. et al. Real-time 3D single-molecule localization using experimental point spread functions. Nat. Methods 15, 367–369 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  24. Bates, M. et al. Optimal precision and accuracy in 4Pi-STORM using dynamic spline PSF models. Nat. Methods 19, 603–612 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  25. Li, Y. et al. Accurate 4Pi single-molecule localization using an experimental PSF model. Opt. Lett. 45, 3765–3768 (2020).

    PubMed  Google Scholar 

  26. Goodman, J. W. Introduction to Fourier Optics, Third Edition (Roberts and Company Publishers, 2005).

  27. Wolf, E. Electromagnetic diffraction in optical systems - I. An integral representation of the image field. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 253, 349–357 (1959).

    Google Scholar 

  28. Siemons, M., Hulleman, C. N., Thorsen, R. Ø., Smith, C. S. & Stallinga, S. High precision wavefront control in point spread function engineering for single emitter localization. Opt. Express 26, 8397–8416 (2018).

    Article  PubMed  Google Scholar 

  29. Noll, R. J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 66, 207–211 (1976).

    Article  Google Scholar 

  30. Niu, K. & Tian, C. Zernike polynomials and their applications. J. Opt. 24, 123001 (2022).

    Article  Google Scholar 

  31. Hanser, B. M., Gustafsson, M. G. L., Agard, D. A. & Sedat, J. W. Phase-retrieved pupil functions in wide-field fluorescence microscopy. J. Microsc. 216, 32–48 (2004).

    Article  CAS  PubMed  Google Scholar 

  32. Liu, S., Kromann, E. B., Krueger, W. D., Bewersdorf, J. & Lidke, K. A. Three-dimensional single-molecule localization using a phase retrieved pupil function. Opt. Express 21, 29462 (2013).

    Article  PubMed  PubMed Central  Google Scholar 

  33. McGorty, R., Schnitzbauer, J., Zhang, W. & Huang, B. Correction of depth-dependent aberrations in 3D single-molecule localization and super-resolution microscopy. Opt. Lett. 39, 275–278 (2014).

    Article  PubMed  PubMed Central  Google Scholar 

  34. Aristov, A., Lelandais, B., Rensen, E. & Zimmer, C. ZOLA-3D allows flexible 3D localization microscopy over an adjustable axial range. Nat. Commun. 9, 2409 (2018).

    Article  PubMed  PubMed Central  Google Scholar 

  35. Petrov, P. N., Shechtman, Y. & Moerner, W. E. Measurement-based estimation of global pupil functions in 3D localization microscopy. Opt. Express 25, 7945–7959 (2017).

    Article  PubMed  PubMed Central  Google Scholar 

  36. Ferdman, B. et al. VIPR: vectorial implementation of phase retrieval for fast and accurate microscopic pixel-wise pupil estimation. Opt. Express 28, 10179–10198 (2020).

    Article  PubMed  Google Scholar 

  37. Ferdman, B., Saguy, A., Xiao, D. & Shechtman, Y. Diffractive optical system design by cascaded propagation. Opt. Express 30, 27509–27530 (2022).

    Article  PubMed  Google Scholar 

  38. Zhang, P. et al. Analyzing complex single-molecule emission patterns with deep learning. Nat. Methods 15, 913–916 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  39. Möckl, L., Petrov, P. N. & Moerner, W. E. Accurate phase retrieval of complex 3D point spread functions with deep residual neural networks. Appl. Phys. Lett. 115, 251106 (2019).

    Article  PubMed  PubMed Central  Google Scholar 

  40. Cumming, B. P. & Gu, M. Direct determination of aberration functions in microscopy by an artificial neural network. Opt. Express 28, 14511–14521 (2020).

    Article  PubMed  Google Scholar 

  41. Xu, F. et al. Three-dimensional nanoscopy of whole cells and tissues with in situ point spread function retrieval. Nat. Methods 17, 531–540 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  42. Fu, S. et al. Field-dependent deep learning enables high-throughput whole-cell 3D super-resolution imaging. Nat. Methods 20, 459–468 (2023).

    Article  CAS  PubMed  Google Scholar 

  43. TensorFlow Developers. TensorFlow. Zenodo https://doi.org/10.5281/zenodo.4724125 (2023).

  44. Liu, D. C. & Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 45, 503–528 (1989).

    Article  Google Scholar 

  45. Thevathasan, J. V. et al. Nuclear pores as versatile reference standards for quantitative superresolution microscopy. Nat. Methods 16, 1045–1053 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  46. Axelrod, D. Fluorescence excitation and imaging of single molecules near dielectric-coated and bare surfaces: a theoretical study. J. Microsc. 247, 147–160 (2012).

    Article  CAS  PubMed  Google Scholar 

  47. Vahid, M. R., Hanzon, B. & Ober, R. J. Effect of pixelation on the parameter estimation of single molecule trajectories. IEEE Trans. Comput. Imaging 7, 98–113 (2021).

    Article  PubMed  Google Scholar 

  48. Deschamps, J., Rowald, A. & Ries, J. Efficient homogeneous illumination and optical sectioning for quantitative single-molecule localization microscopy. Opt. Express 24, 28080–28090 (2016).

    Article  PubMed  Google Scholar 

  49. Chen, B. -C. et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346, 1257998 (2014).

    Article  PubMed  PubMed Central  Google Scholar 

  50. Sapoznik, E. et al. A versatile oblique plane microscope for large-scale and high-resolution imaging of subcellular dynamics. eLife 9, e57681 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  51. Yang, B. et al. DaXi—high-resolution, large imaging volume and multi-view single-objective light-sheet microscopy. Nat. Methods 19, 461–469 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  52. Quirin, S., Pavani, S. R. P. & Piestun, R. Optimal 3D single-molecule localization for superresolution microscopy with aberrations and engineered point spread functions. Proc. Natl Acad. Sci. USA 109, 675–679 (2012).

    Article  CAS  PubMed  Google Scholar 

  53. Bossi, M. et al. Multicolor far-field fluorescence nanoscopy through isolated detection of distinct molecular species. Nano Lett. 8, 2463–2468 (2008).

    Article  CAS  PubMed  Google Scholar 

  54. Testa, I. et al. Multicolor fluorescence nanoscopy in fixed and living cells by exciting conventional fluorophores with a single wavelength. Biophys. J. 99, 2686–2694 (2010).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  55. Gahlmann, A. et al. Quantitative multicolor subdiffraction imaging of bacterial protein ultrastructures in three dimensions. Nano Lett. 13, 987–993 (2013).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  56. Backlund, M. P., Joyner, R., Weis, K. & Moerner, W. E. Correlations of three-dimensional motion of chromosomal loci in yeast revealed by the double-helix point spread function microscope. Mol. Biol. Cell 25, 3619–3629 (2014).

    Article  PubMed  PubMed Central  Google Scholar 

  57. Nehme, E. et al. Learning optimal wavefront shaping for multi-channel imaging. IEEE Trans. Pattern Anal. Mach. Intell. 43, 2179–2192 (2021).

    Article  PubMed  Google Scholar 

  58. Backlund, M. P., Lew, M. D., Backer, A. S., Sahl, S. J. & Moerner, W. E. The role of molecular dipole orientation in single-molecule fluorescence microscopy and implications for super-resolution imaging. Chemphyschem 15, 587–599 (2014).

    Article  CAS  PubMed  Google Scholar 

  59. Huang, F. et al. Ultra-high resolution 3D imaging of whole cells. Cell 166, 1028–1040 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  60. Li, Y. et al. Global fitting for high-accuracy multi-channel single-molecule localization. Nat. Commun. 13, 3133 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  61. Liu, S., Hoess, P. & Ries, J. Super-resolution microscopy for structural cell biology. Annu. Rev. Biophys. 51, 301–326 (2022).

    Article  CAS  PubMed  Google Scholar 

  62. LocMoFit quantifies cellular structures in super-resolution data. Nat. Methods 20, 44–45 (2023).

  63. Douglass, K. M., Sieben, C., Archetti, A., Lambert, A. & Manley, S. Super-resolution imaging of multiple cells by optimized flat-field epi-illumination. Nat. Photonics 10, 705–708 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  64. Ries, J. SMAP: a modular super-resolution microscopy analysis platform for SMLM data. Nat. Methods 17, 870–872 (2020).

    Article  CAS  PubMed  Google Scholar 

  65. Speiser, A. et al. Deep learning enables fast and dense single-molecule localization with high accuracy. Nat. Methods 18, 1082–1090 (2021).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  66. Yan, R., Moon, S., Kenny, S. J. & Xu, K. Spectrally resolved and functional super-resolution microscopy via ultrahigh-throughput single-molecule spectroscopy. Acc. Chem. Res. 51, 697–705 (2018).

    Article  CAS  PubMed  Google Scholar 

  67. Mlodzianoski, M. J., Curthoys, N. M., Gunewardene, M. S., Carter, S. & Hess, S. T. Super-resolution imaging of molecular emission spectra and single molecule spectral fluctuations. PLoS ONE 11, e0147506 (2016).

    Article  PubMed  PubMed Central  Google Scholar 

  68. Gu, L. et al. Molecular resolution imaging by repetitive optical selective exposure. Nat. Methods 16, 1114–1118 (2019).

    Article  CAS  PubMed  Google Scholar 

  69. Cnossen, J. et al. Localization microscopy at doubled precision with patterned illumination. Nat. Methods 17, 59–63 (2020).

    Article  CAS  PubMed  Google Scholar 

  70. Jouchet, P. et al. Nanometric axial localization of single fluorescent molecules with modulated excitation. Nat. Photonics 15, 297–304 (2021).

    Article  CAS  Google Scholar 

  71. Balzarotti, F. et al. Nanometer resolution imaging and tracking of fluorescent molecules with minimal photon fluxes. Science 355, 606–612 (2017).

    Article  CAS  PubMed  Google Scholar 

  72. Kukura, P. et al. High-speed nanoscopic tracking of the position and orientation of a single virus. Nat. Methods 6, 923–927 (2009).

    Article  CAS  PubMed  Google Scholar 

  73. Wang, J. et al. Implementation of a 4Pi-SMS super-resolution microscope. Nat. Protoc. 16, 677–727 (2021).

    Article  CAS  PubMed  Google Scholar 

  74. Antonello, J., Wang, J., He, C., Phillips, M. & Booth, M. Interferometric calibration of a deformable mirror. Zenodo https://doi.org/10.5281/ZENODO.3714951 (2020).

  75. Deschamps, J. & Ries, J. EMU: reconfigurable graphical user interfaces for Micro-Manager. BMC Bioinformatics 21, 456 (2020).

    Article  PubMed  PubMed Central  Google Scholar 

  76. Fu, S. et al. Deformable mirror based optimal PSF engineering for 3D super-resolution imaging. Opt. Lett. 47, 3031–3034 (2022).

    Article  PubMed  Google Scholar 

  77. Wu, Y. -L. et al. Maximum-likelihood model fitting for quantitative analysis of SMLM data. Nat. Methods 20, 139–148 (2023).

    Article  CAS  PubMed  Google Scholar 

  78. Liu, S., Chen, J., Li, Y., & Ries, J. uiPSF datasets for Figure 2. Zenodo https://doi.org/10.5281/zenodo.10823308 (2024).

  79. Liu, S., Chen, J., Li, Y., & Ries, J. uiPSF datasets for Figure 3. Zenodo https://doi.org/10.5281/zenodo.10823244 (2024).

  80. Liu, S., Chen, J., Li, Y., & Ries, J. uiPSF datasets for Figure 5. Zenodo https://doi.org/10.5281/zenodo.10824517 (2024).

  81. Liu, S. et al. Example data for uiPSF. Zenodo https://doi.org/10.5281/zenodo.10602740 (2024).

Download references

Acknowledgements

We thank Y. E. Katrukha and L. C. Kapitein from Utrecht University, the Netherlands; B. Hajj and L. Regnier from Institut Curie, France; K. J. A. Martens from Bonn University, Germany; A. Tschanz from the European Molecular Biology Laboratory, Germany; S. Khan and S. Pani from the University of New Mexico; Y. Li from Purdue University; J. A. Camarena from Arizona State University for testing the software. We thank X. Liu from the University of Hong Kong for valuable suggestions on inverse modeling. We thank A. M. E. Pacheco for preparing the Nup96-mMaple sample. This work was supported by the European Research Council (grant no. CoG724489 to J.R., no. 802567 to Y.S.) and the European Molecular Biology Laboratory. This work was conducted with support from the University of New Mexico Office of the Vice President for Research Program for Enhancing Research Capacity. This research was supported by grants from NVIDIA and utilized an NVIDIA A6000 GPU. S.L. was supported by EMBL ARISE fellowship no. 945405. S.L. and K.A.L. were supported by National Institutes of Health grant 1R01GM140284. Y.L. was supported by National Natural Science Foundation of China (62375116); Key Technology Research and Development Program of Shandong (2021CXGC010212); Shenzhen Medical Research Fund (B2302038); Shenzhen Science and Technology Innovation Commission (grant no. JCYJ20220818100416036 and KQTD20200820113012029); Guangdong Provincial Key Laboratory of Advanced Biomaterials (2022B1212010003); a startup grant from Southern University of Science and Technology. L.-R.M. was supported by the German Federal Ministry of Education and Research (BMBF; project SIMALESAM, FKZ 01|S21055A-B). R.H. was supported by the German research foundation (Deutsche Forschungsgemeinschaft, project TR 1278, TP C04, 316213987) and the Leibniz science campus Infecto-Optics, project HotAim 2.0. C.K. was supported by the German research foundation (Deutsche Forschungsgemeinschaft, project SFB TR166 ‘Receptorlight’, TP B05). This project has received funding from the Israel Science Foundation (grant no. 450/18 to Y.S). Y.S. was supported by the Zuckerman Foundation, and by the Donald D. Harrington fellowship.

Author information

Author notes

  1. Christian Karras

    Present address: JENOPTIK Optical Systems, Jena, Germany

  2. These authors contributed equally: Sheng Liu, Jianwei Chen.

Authors and Affiliations

  1. Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM, USA

    Sheng Liu & Keith A. Lidke

  2. European Molecular Biology Laboratory, Cell Biology and Biophysics, Heidelberg, Germany

    Sheng Liu, Jonas Hellgoth, Lucas-Raphael Müller & Jonas Ries

  3. Department of Biomedical Engineering, Guangdong Provincial Key Laboratory of Advanced Biomaterials, Southern University of Science and Technology, Shenzhen, China

    Jianwei Chen & Yiming Li

  4. Collaboration for joint PhD degree between Southern University of Science and Technology and Harbin Institute of Technology, Harbin, China

    Jianwei Chen

  5. Faculty of Biosciences, Collaboration for joint PhD degree from EMBL and Heidelberg University, Heidelberg, Germany

    Jonas Hellgoth

  6. Machine Learning in Science, Excellence Cluster Machine Learning, University of Tübingen, Tübingen, Germany

    Lucas-Raphael Müller

  7. Department of Biomedical Engineering, Technion-Israel Institute of Technology, Haifa, Israel

    Boris Ferdman & Yoav Shechtman

  8. Leibniz Institute of Photonic Technology, Jena, Germany

    Christian Karras & Rainer Heintzmann

  9. Russell Berrie Nanotechnology Institute, Technion-Israel Institute of Technology, Haifa, Israel

    Dafei Xiao

  10. Institute of Physical Chemistry and Abbe Center of Photonics, Friedrich-Schiller-University Jena, Jena, Germany

    Rainer Heintzmann

  11. Department of Mechanical Engineering, The University of Texas at Austin, Austin, TX, USA

    Yoav Shechtman

  12. Max Perutz Labs, Vienna Biocenter Campus, Vienna, Austria

    Jonas Ries

  13. Department of Structural and Computational Biology, Center for Molecular Biology, University of Vienna, Vienna, Austria

    Jonas Ries

  14. Faculty of Physics, University of Vienna, Vienna, Austria

    Jonas Ries

Authors
  1. Sheng Liu
    View author publications

    Search author on:PubMed Google Scholar

  2. Jianwei Chen
    View author publications

    Search author on:PubMed Google Scholar

  3. Jonas Hellgoth
    View author publications

    Search author on:PubMed Google Scholar

  4. Lucas-Raphael Müller
    View author publications

    Search author on:PubMed Google Scholar

  5. Boris Ferdman
    View author publications

    Search author on:PubMed Google Scholar

  6. Christian Karras
    View author publications

    Search author on:PubMed Google Scholar

  7. Dafei Xiao
    View author publications

    Search author on:PubMed Google Scholar

  8. Keith A. Lidke
    View author publications

    Search author on:PubMed Google Scholar

  9. Rainer Heintzmann
    View author publications

    Search author on:PubMed Google Scholar

  10. Yoav Shechtman
    View author publications

    Search author on:PubMed Google Scholar

  11. Yiming Li
    View author publications

    Search author on:PubMed Google Scholar

  12. Jonas Ries
    View author publications

    Search author on:PubMed Google Scholar

Contributions

J.R., Y.L., R.H. and Y.S. conceived the project. J.R., Y.L. and K.A.L. provided supervision. S.L., J.H., J.C., C.K. and L.-R.M. wrote the software. S.L. and J.C. analyzed the data. S.L., J.C., J.R., B.F. and D.X. acquired the data. S.L., J.C., Y.L. and J.R. wrote the paper with input from all authors.

Corresponding authors

Correspondence to Yiming Li or Jonas Ries.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Methods thanks Ryan McGorty and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Rita Strack, in collaboration with the Nature Methods team. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 In situ PSF model reduces the local deformation in z measured by the ring distance of Nup96.

(a) A subregion of the reconstructed Nup96 using the in situ PSF model. (b, c) XZ view of selected region in (a) from bead and in situ PSF models. (d) and (e) are the ring distance of Nup96 as a function of z-position at different depth reconstructed by using beads PSF model and in situ PSF model respectively. The points of various colors represent different imaging depths of Nup96. The straight lines represent the linear regression of the ring distance versus z-position (of the NPC center) for each imaging depth, with k representing the corresponding slope. An oil immersion objective lens (NA = 1.43) was used for imaging. (f) and (g) have the same meaning as (d) and (e), respectively, but imaged by a silicone oil immersion objective lens (NA = 1.35). Standard imaging buffer (n = 1.35) were used. Scale bars, 1 µm (a), 500 nm (b).

Source data

Extended Data Fig. 2 Effect of pixelation using the vectorial PSF modelling method.

(a) Test on simulated data. Data were simulated from vectorial PSF model, with a binning of 5 in both x and y dimensions, and without extra blurring to the PSF model. (b) Test on experimental data. The estimated blur factor is slightly smaller when adding a binning of 5 in the forward model. However, the estimated PSF model and the localization bias are nearly identical with or without additional binning in the forward model. In contrast, under the same blur factor but without binning (bin=1), the axial bias increases dramatically and the estimated PSF model differs substantially. The z/x/y bias vs. z are defined as in SI Note 2 Eqs. 2.37 and 2.38. Black lines and shaded areas in localization plots indicate mean and standard deviation of the x, y and z biases over >20 beads. Scale bar, 1 µm. A.U., arbitrary unit.

Source data

Extended Data Fig. 3 Estimation of voxel-based PSF model of a lattice light-sheet system from bead data.

The data were collected by imaging beads in agarose gel at sample stage positions from −50 µm to 50 µm, with a step size of 50 nm. Translation of the sample stage will translate the beads both in x and z dimensions in the coordinate of the detection objective. For this data, translating the sample stage by 50 nm, will translate the beads by 40.8 nm in x and 28.9 nm in z relative to the detection objective. (a) Localization in x of the deskewed data used for inverse modelling. (b) The raw data stack of each bead was deskewed using the above translation relationship between x and z dimensions. Only shifts of integer pixels were applied to maintain the photon statistics of the raw data. The deskewed bead stacks were used for inverse modelling. The sub-pixel shifts were incorporated in the forward model so that the estimated PSF model has no skew as in (d). (c) localization of the data used for inverse modelling, sub-pixel shifts were applied to the localization result in (a) to remove the skew effect. The z/x/y bias vs. z are defined as in SI Note 2 Eqs. 2.37 and 2.38. Black lines and shaded areas in localization plots indicate mean and standard deviation of the x, y and z biases over >20 beads. (d) Estimated PSF model. (e) Comparison of an example bead stack and its corresponding forward model. Scale bars, 1 µm (b,d,e).

Source data

Extended Data Fig. 4 Incorporating refractive index mismatch aberrations in the estimated PSF model.

Bead data at different imaging depth were collected by imaging beads in agarose gel at stage positions from −1 µm to 5 µm, with a step size of 20 nm. Bead data at the coverslip were collected at stage positions from −1.5 µm to 1.5 µm, with a step size of 10 nm. (a) Localization of beads in agarose gel using the PSF model estimated from beads at the coverslip. (b) Localization of beads in agarose gel using the PSF model estimated from beads at the coverslip and modified by adding an index mismatch aberration at the estimated imaging depth of each bead. Therefore, each bead stack was localized by its own modified PSF model. Depth is defined as the estimated emitter’s z position to the coverslip. The z/x/y bias vs. z are defined as in SI Note 2 Eqs. 2.37 and 2.38. (c) Comparison of the PSF model at the coverslip, bead data at different imaging depth and their corresponding PSF models. With increasing depth, the pupil size slightly decreases as the effective numerical aperture (NA) decreases from 1.43 to 1.33 (the refractive index of water), and the pupil phase shows larger spherical aberration kind of patterns. Scale bars, 1 µm (c).

Source data

Extended Data Fig. 5 Validation of in situ PSF estimation using bead data in agarose gel.

The images of these beads were collected at stage positions from −1 µm to 25 µm. For each bead, the per-frame z position was used as an independent variable to simulate the in situ single molecule data. (a) The PSF estimated from the beads on the cover glass was used to localize the bead data at different depths. (b) The in situ PSF estimated by uiPSF was used to localize the bead data at different depths. Compared to the PSF model estimated from the beads on the cover glass, the in situ PSF model fitted z-positions exhibit a good linear relationship with the objective stage positions.

Extended Data Fig. 6 Comparison of Zernike-based PSF modelling using uiPSF and INSPR.

Comparison between the input amplitude and the estimated amplitude from the in situ PSF modelling using uiPSF (a) and INSPR (b) for 21 Zernike modes (fringe indices) applied by a deformable mirror (DM). Single-molecule data were collected at each of the 21 Zernike modes and were analyzed by uiPSF and INSPR. Panel b reproduced from ref. 41, Springer Nature America. As shown in (a) and (b), the Zernike aberrations returned by uiPSF have lower residual aberrations, compared to INSPR. Comparison of uiPSF (c) with INSPR (d) for fitted z-position versus objective z-position. We imaged the single fluorophores (AF647) immobilized on a coverslip at different objective z-positions. The fluorophores’ z-position fitted by uiPSF is linear relative to the objective z-position (c), while there is a discontinuity at −300 nm for INSPR (d), indicating a mismatch between the INSPR PSF model and the single-molecule patterns.

Source data

Extended Data Fig. 7 Comparison of pixelated and Zernike pupil based in situ PSF estimation of Tetrapod blinking patterns generated from a phase plate.

(a) Comparison of estimated PSF and pupil from bead data and single molecule blinking patterns. The phase patten generated from a phase plate is more complex than the ones from a deformable mirror, both the pixelated and Zernike pupil based modelling methods can retrieve the pupil function from single molecule blinking data. However, the Zernike-based method requires accurate initial values of the Zernike coefficients, otherwise, it fails to retrieve the accurate pupil. (b, c) Estimated Zernike coefficients from Zernike-based in situ PSF modelling with (b) or without (c) accurate initial values of the Zernike coefficients. (d) Example raw camera frame used for in situ PSF modelling. Scale bar, 1 µm (a), 10 µm (d). ADU, analog to digital unit.

Extended Data Fig. 8 Validation of in situ PSF modelling for imaging a thick sample.

Imaging of Nup96-SNAP-AF647 in U2OS cells was performed using an oil immersion objective lens (NA = 1.5) and imaging buffer (n = 1.406, Methods) on a single-channel SMLM system equipped with a deformable mirror (DM). (a) A sandwiched sample of U2OS cells was prepared for an imaging depth of 25 µm. (b) Top view of the reconstructed Nup96 using the in situ PSF model. (c) Enlarged XY view of the selected region in (b). (d) XZ view of the selected region in (c) reconstructed from bead and in situ PSF models, respectively. Scale bars, 2 µm (b), 1 µm (c), and 0.5 µm (d).

Extended Data Fig. 9 Application of uiPSF for aberration correction using a deformable mirror.

Imaging of Nup96-SNAP-AF647 in U2OS cells was performed using an oil immersion objective lens (NA = 1.5) and imaging buffer (n = 1.406, Methods) on a single-channel SMLM system equipped with a deformable mirror (DM). (a) Top view of the reconstructed Nup96 using the in situ PSF model with and without uiPSF guided aberration correction by AO. (b) Zernike aberrations calculated from single molecule data using uiPSF with and without AO correction. (c, d) XZ view of the selected region in (a) for samples with and without AO correction. After uiPSF guided aberration correction, the reconstructed image quality improved notably as demonstrated by the resolved double ring structure. Scale bars, 1 µm (a), 500 nm (c-d).

Source data

Supplementary information

Supplementary Information

Supplementary Figs. 1–21, Supplementary Notes 1–7 and Supplementary Tables 1–3.

Reporting Summary

Peer Review File

Supplementary Software 1

uiPSF software package, including source codes, example Jupyter notebooks and tutorials for localization analysis using the PSF models generated from uiPSF.

Source data

Source Data Fig. 1

Statistical source data.

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Fig. 5

Statistical source data.

Source Data Extended Data Fig. 1

Statistical source data.

Source Data Extended Data Fig. 2

Statistical source data.

Source Data Extended Data Fig. 3

Statistical source data.

Source Data Extended Data Fig. 4

Statistical source data.

Source Data Extended Data Fig. 6

Statistical source data.

Source Data Extended Data Fig. 9

Statistical source data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, S., Chen, J., Hellgoth, J. et al. Universal inverse modeling of point spread functions for SMLM localization and microscope characterization. Nat Methods 21, 1082–1093 (2024). https://doi.org/10.1038/s41592-024-02282-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41592-024-02282-x

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing