Various distance between generalized Diophantine fuzzy sets using multiple criteria decision making and their real life applications

Abstract

This paper describes a generalized Diophantine fuzzy sets, which can be seen as a generalization of both Diophantine fuzzy sets and Pythagorean fuzzy sets. We define the basic properties of generalized Diophantine fuzzy set, as well as their relationships and distances. We compare Diophantine fuzzy sets with other Diophantine Pythagorean fuzzy sets to demonstrate their importance in the literature. We introduce new operators including necessity, possibility, accuracy function and score function. Furthermore, we discuss the new distance between normalized Euclidean distance and normalized Hamming distance. For a generalized Diophantine fuzzy relation, image and inverse image functions are defined. Numerous real-world applications can be found for the prevalent ideas of intuitionistic fuzzy sets, Pythagorean fuzzy sets, Diophantine fuzzy sets and q-rung orthopair fuzzy sets. Regretfully, these theories about the membership and non-membership grades have their own limits. We provide a new idea the generalized Diophantine fuzzy set that eliminates these limitations by including reference parameters. Compared to other kinds of fuzzy sets, there are more applications for generalized Diophantine fuzzy sets. We offer practical examples that show how different enhanced distances might be used in everyday situations. Additionally, to demonstrate the effectiveness of the suggested approach, flowchart based multi-criteria decision-making is provided and used to a numerical example. The outcomes are assessed for various parameter values. Furthermore, a comparative analysis developed to demonstrate the superiority of the suggested technique over current methodologies.

Introduction

Determining the optimal solution becomes more challenging for decision-makers due to the intricacy of real-world systems. It can be challenging to choose the greatest option amongst options, but it is achievable. Finding possibilities, accomplishing goals, and taking into account limits on viewpoints are difficult tasks for many organizations. Decision-makers, either individually or in groups, should therefore take into account several goals at once. Every day, a variety of difficulties pertaining to multi-attribute decision-making (MADM) must be resolved. As a result, strengthening decision-making (DM) skills is essential. Numerous researchers have conducted research in this area using a range of techniques. Uncertainty characterizes real-world challenges everywhere. Among the most productive structures utilized in daily life is decision-making (DM). Multi-criteria decision-making (MCDM) models have been utilized extensively to define real DM situations because of its power in depicting the DM process. There is no set rule for handling many challenges attributed to distinct uncertainties in real-life situations. However, complexity characterizes the behavior of an entity whose components communicate in multiple ways and follow different logical concepts in any real-life problem-solving method. It appears that MCDM management strategies have been extensively studied by many researchers from around the entire world. It also generated an abundant number of innovative responses to challenging real-world problems. A synopsis of the related issues provides the basis for most of the frameworks for this objective. Several mathematical strategies have been proposed to the researchers to deal with uncertainties. Real-world systems become more complex as time goes on, making determining the optimal solution more difficult for decision makers. Although choosing the best option can be challenging, there is still a way to make the right decision. A number of firms face challenges due to opportunities, objectives and viewpoint constraints. The aim of DM is to consider multiple objectives simultaneously when individuals or groups decide. On a daily basis, we deal with a wide range of issues related to multi attribute decision-making (MADM). Therefore, it is necessary to improve the abilities of DMs. Numerous researchers have investigated this field of study using different methods. Classical or crisp approaches may not always be appropriate for DM scenarios that involve ambiguity and uncertainty. MCDM or multi criteria decision analysis (MCDA) is a technique for DM that is highly accurate, and it has revolutionized this field¹. Benjamin Franklin was one of the first scientists to write on moral algebra research, having developed MCDM procedures. Since the 1950s, a number of empirical and theoretical scientists have investigated MCDM methods due to their capacity for mathematical modeling that can provide suggestions for how to organize DM problems and provide preferences. We discussed MCDM differs from other approaches in several ways^2,3.

In addition to fuzzy sets (FS)⁴, intuitionistic FS (IFS)⁵, Pythagorean FS (PFS)⁶ and spherical FS (SFS)⁷ have numerous applications in various fields of real life, but these theories have their own limitations related to the membership grade (MG) and non-membership grade (NMG). Several uncertain theories have also been proposed to uncertainties. Associative and non-associative structures serve as the basis for fuzzy mathematics, which also offers scientists, engineers, and mathematicians practical tools. Partially composing a set can involve elements from the universe. MG is measured for every element of a set. As a result of the extension principle, researchers were able to compute linguistic variables, calculate linguistic probabilities, arithmetic fuzzy numbers and extend relations within their domains. Nowadays, FSs are used practically exclusively in mathematical applications. IFS introduced by Atanassov⁵ contains the sum of MG and NMG, which is less than or equal to one. A DM approach is sometimes used to discuss a single issue, and sum of MG and NMG sometimes exceeds 1, when we use a DM approach to discuss the one issue. So, Yager⁶ developed the PFS which is characterized by the sum of the squares of MGs and NMGs and does not exceed one. Cuong et al.⁸ discussed the concept of a picture FS with the condition that sum of positive grade, neutral grade and negative grade is not greater than one. As a result, it can support a wider range of applications than IFS and PFS. Yang et al. discussed interval-valued PFN information with AOs for MADM⁹. Khan et al.¹⁰ introduced a PFS that incorporates the integral operator for Einstein. The fuzzy c-number can be clustered based on fuzzy clustering techniques and regression prediction can be performed using fuzzy clustering techniques. We rarely utilize the DM approach to solve problems in which the sum of the three grades exceeds 1. The SFSs were introduced by Ashraf et al.⁷ based on the premise that the sum of the squares of the three grades should not exceed 1. Fatmaa et al.¹¹ introduced SFSs using TOPSIS method.

Atanassov¹² two independent capacities such as MG and NMG, FSs are generalized to the IFS to deal with uncertainty in information. The neutrosophic set (NSS) introduced by Smarandache¹³ have three independent attributes such as truth, indeterminacy and falsity grades. In addition to Pythagorean fuzzy numbers (PFNs) and interval-valued PFNs (IVPFNs) with higher uncertainties are modeled with PFS. Cruz et al.¹⁴ discussed the concept of generalized PFS. Peng et al.¹⁵ discussed the concept of NSS with MADM using the MABAC and TOPSIS approaches. Zhang et al.¹⁶ presented a generalization of PFS using TOPSIS. The spherical vague normal operator is discussed by Palanikumar et al.¹⁷. For the q-rung orthopair FS (q-ROFS), both MG and NMG have power q, but their sum can never be greater than 1. PFSs and IFSs are generalized q-ROFSs, therefore they can be considered special cases of q-ROFSs. If q increases, there is a larger number of orthopair that satisfy the bounding constraint. The q-ROFSs can express fuzzy information over a broader range. Because parameter q can be adjusted, q-ROFSs are flexible and better suited to uncertain environments. The fuzzy information cannot be described by IFNs and PFNs, but q-ROFNs can be described if the parameter q is increased. Therefore, the q-ROFS is more flexible and suitable for describing uncertain data. Rahman et al.¹⁸ proposed a Pythagorean fuzzy aggregation operator. A bipolar FS using TOPSIS is proposed by Akram et al.¹⁹. Several authors have discussed different types of aggregation operators^20,21,22. This involves obtaining a ranking of preferences based on proximity to the ideal solution, calculating distances to those solutions and combining them. Recently, many researchers discussed the concept of new aggregating operator using extension of FS and IFS^23,24.

Hwang et al.²⁵ described the MADM concept. NSS can be considered as a generalization of the FS, IFS and picture FS. A Pythagorean neutrosophic with interval values was introduced by Smarandache et al.²⁶. Medical diagnoses can be made using single-valued NSS²⁷ and NSS²⁸. IFSs have been expanded with Hamming distance (HD), Euclidean distance (ED), normalized HD and normalized ED are discussed by Ejegwa²⁹. Chakraborty et al.³⁰ investigated Fermatean fuzzy Bonferroni AOs in the context of healthcare waste treatment. Fermatean fuzzy soft set were used to treatment COVID-19 symptoms by Zeb et al.³¹. An AO constructed using MADM was presented by Khan et al.³². An analysis of algebraic structures and their applications has been undertaken by Palanikumar et al.³³. There has been recent discussion about PFS interaction AOs and their application to MADM by Wei³⁴. An AO based on a sine trigonometric fermatean normal FS is presented by Palanikumar et al.³⁵. The TOPSIS algorithm was extended for use in a fuzzy environment by Chen et al.³⁶. A large number of IFSs and PFSs can be generalized. The mathematical treatment of a number of physical processes and systems has been studied using generalized fuzzy set (GFS). The models of such systems can be studied with the help of the present generalization of FSs. Linear Diophantine FS (LDioFS) with reference parameters was discussed by Riaz et al.³⁷. For the purpose to eradicate these constraints, we present the new idea of LDioFS along with reference parameters. Because reference parameters are used, the suggested LDioFS model is more flexible and efficient than previous methods. Additionally, by modifying the physical sense of reference parameters, LDioFS classifies the data in MADM problems. With the help of reference parameters, this set extends the space for MG and NMG while maintaining the spaces of the current structures. A LDioFS is a strong model to relax the limitations of MG and NMG due to existence of reference/control parameters. Riaz et al.³⁸ extended LDioFS to the idea of soft rough LDioFS sets with application to sustainable material handling equipment. Riaz et al.³⁹ introduced spherical LDioFSs with modeling uncertainties in MCDM. Kausar et al. discussed the concept of GFS and their applications⁴⁰. The Euclidean, Hausdorff, Minkowski and Hamming methods are a few of the widely used distance measurement techniques. Palanikumar et al.^41,42 discussed the new type of aggregating operators such as spherical fuzzy set. The literature currently in publication indicates that one technique that can be applied to the staff selection process is the Hamming distance^43,44. Recently, many researchers discussed in the extension of FS and q-ROFS^45,46 and new aggregating operators^47,48. Wei et al.⁴⁹ discussed the concept of generalized dice similarity measures for picture fuzzy sets and their applications. Nowadays, many researches discussed the concepts of linguistic q-rung orthopair fuzzy Archimedean aggregation operators⁵⁰, score function-based CoCoSo method⁵¹ and Incorporating Score and Accuracy Functions for Comprehensive Assessment⁵². Recently, Ozlu discussed the new approach towards hesitant fuzzy sets⁵³, aggregating operator⁵⁴ and neutrosophic type-2 hesitant fuzzy sets⁵⁵.

Motivation and objectives

The LDioFS is more flexible and effective because it uses reference parameters. The LDioFS also classifies the data in MADM problems based on changes in the physical meaning of the reference parameters. LDioFS more effective and adaptive than alternatives approaches. The theory of generalized fuzzy set (GFS) fails to account for the case when we choose (0.95, 0.85), leading us to conclude that $0.95^{2} + 0.85^{2} > 1$, but the concept of Diophantine GFS (GDioFS) does. Accordingly, the reference parameters (0.65, 0.55) were chosen in this study which implies $(0.95^{2})\cdot (0.65) + (0.85^{2}) \cdot (0.55) =0.9840 < 1$. We presented GDioFSs and their properties to make it easy for the reader to understand their properties and applications. The layout of this paper is systematized as follows: In “Preliminaries” section, We use the concepts collected to develop the PFS, GFS and q-rung FS. The GDioFS is defined and its properties are discussed in “Generalized Diophantine fuzzy sets (GDioFSs)” section. “Relations on GDioFSs” section explores Diophantine generalized fuzzy relations (GDioFRs), demonstrating how these relations can be applied in an example. A number of studies on the GDioFS distances are presented in “Distances between GDioFRs” section, including their application to the diagnosis of diseases in the medical field using MCDM. We present a numerical example concerning to the selection of real-life applications and analyze its result by using two different algorithms under GDioFS rules and its associated score functions and various distances. In “Comparing new methods with existing ones” section, we present a brief comparison between the proposed model and the existing approaches and see the influence of score functions as well as a sensitivity analysis on the final decision in the aggregated outcomes. Finally, the conclusion of this research is summarized in “Conclusions and future studies” section. The purpose of this study was to clarify the significance of GDioFS. GDioFS data are extracted using procedures. For example, we developed a rating for DM issues based on these operators. As a result, these studies make the following contributions:

• 1. The DioPFS can be used to analyze uncertainty problems. A GDioFS is a generalization of a GFS.

• 2. The GDioFS performs all DioFS and DioPFS functions by changing the indices m and p.

• 3. Certain limitations apply to GDioFS. By selecting the correct numerical values for m and p, we are selecting the correct values to solve the problem.

• 4. There is a significant improvement in accuracy and effectiveness over existing techniques when using the proposed method.

Preliminaries

We use the concepts collected to develop the PFS, GFS and q-rung FS. We utilize these basic components for the construction of a hybrid structure called GDioFS. We use ${\mathcal {X}}$ as a fixed sample space or as the universe.

Definition 2.1

Let ${\mathcal {X}}$ be a universal set. An IFS ${\mathcal {I}}=\{\langle \epsilon ,\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon )\rangle | \epsilon \in {\mathcal {X}}\}$ and mapping $\zeta _{\mathcal {I}}(\epsilon ): {\mathcal {X}} \rightarrow [0, 1]$ and $\xi _{\mathcal {I}}(\epsilon ): {\mathcal {X}} \rightarrow [0, 1]$ be a MD and NMD, respectively and satisfying $0 \le \zeta _{\mathcal {I}}(\epsilon )+\xi _{\mathcal {I}}(\epsilon ) \le 1$, $\pi _{\mathcal {I}}(\epsilon ) = 1-\zeta _{\mathcal {I}}(\epsilon )-\xi _{\mathcal {I}}(\epsilon )$. Since $\pi _{\mathcal {I}}(\epsilon )$ denotes the degree of indeterminacy of $\epsilon \in {\mathcal {X}}$ to ${\mathcal {I}}$ and $\zeta _{\mathcal {I}}(\epsilon ) + \xi _{\mathcal {I}}(\epsilon ) + \pi _{\mathcal {I}}(\epsilon ) = 1.$

Definition 2.2

The PFS ${\mathcal {I}}=\{\langle \epsilon ,\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon )\rangle |$ $\epsilon \in {\mathcal {X}}\}$, where $\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon ): {\mathcal {X}} \rightarrow [0, 1]$ and satisfying $0 \le (\zeta _{\mathcal {I}}(\epsilon ))^2+(\xi _{\mathcal {I}}(\epsilon ))^2 \le 1$ $\forall$ $\epsilon \in {\mathcal {X}}$, $\pi _{\mathcal {I}}(\epsilon )$ is defined as $\pi _{\mathcal {I}}(\epsilon ) = \sqrt{1-(\zeta _{\mathcal {I}}(\epsilon )^2+\xi _{\mathcal {I}}(\epsilon ))^2}$ and $(\zeta _{\mathcal {I}}(\epsilon ))^2 + (\xi _{\mathcal {I}}(\epsilon ))^2 + (\pi _{\mathcal {I}}(\epsilon ))^2 = 1.$

Definition 2.3

The DioPFS ${\mathcal {I}}=\{\langle \epsilon ,(\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon )),(\varrho _{\mathcal {I}}(\epsilon ), \sigma _{\mathcal {I}}(\epsilon ))\rangle | \epsilon \in {\mathcal {X}}\}$ where $\zeta _{\mathcal {I}}(\epsilon ),\xi _{\mathcal {I}}(\epsilon ): {\mathcal {X}} \rightarrow [0, 1]$ and $0 \le (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^2+(\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ))^2 \le 1$ $\forall$ $\epsilon \in {\mathcal {X}}$, where

$\pi _{\mathcal {I}}(\epsilon ) = \sqrt{1-(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^2+(\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ))^2}$ and $(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^2 + (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ))^2 + (\pi _{\mathcal {I}}(\epsilon ))^2 = 1.$

Definition 2.4

The Fermatean FS ${\mathcal {I}}=\{\langle \epsilon ,\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon )\rangle |$ $\epsilon \in {\mathcal {X}}\}$, where $\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon ): {\mathcal {X}} \rightarrow [0, 1]$ and satisfying $0 \le (\zeta _{\mathcal {I}}(\epsilon ))^3+(\xi _{\mathcal {I}}(\epsilon ))^3 \le 1$ $\forall$ $\epsilon \in {\mathcal {X}}$ and $\pi _{\mathcal {I}}(\epsilon ) = \sqrt{1-(\zeta _{\mathcal {I}}(\epsilon )^3+\xi _{\mathcal {I}}(\epsilon ))^3}$ and $(\zeta _{\mathcal {I}}(\epsilon ))^3 + (\xi _{\mathcal {I}}(\epsilon ))^3 + (\pi _{\mathcal {I}}(\epsilon ))^3 = 1.$

Definition 2.5

The GFS ${\mathcal {I}}$ in ${\mathcal {X}}$ is of the form: ${\mathcal {I}}=\{\langle \epsilon ,\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon ) \rangle : \epsilon \in {\mathcal {X}} \};$ where $\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon ):{\mathcal {X}} \rightarrow [0, 1]$ and $0 \le \big (\zeta _{\mathcal {I}}(\epsilon )\big )^m + \big (\xi _{\mathcal {I}}(\epsilon )\big )^p \le 1.$ In this case, the GFS index or hesitation value is defined as: $\pi _{\mathcal {I}}(\epsilon ) =\root lcm(m,p) \of { 1-\Big (\big (\zeta _{\mathcal {I}}(\epsilon )\big )^m+\big (\xi _{\mathcal {I}}(\epsilon )\big )^p\Big )},$ and $\big (\zeta _{\mathcal {I}}(\epsilon )\big )^m + \big (\xi _{\mathcal {I}}(\epsilon )\big )^p + \big (\pi _{\mathcal {I}}(\epsilon )\big )^{lcm(m,p)} = 1$, where m and p are non-negative integers.

Definition 2.6

The q-rung FS ${\mathcal {I}}=\{\langle \epsilon ,\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon ) \rangle : \epsilon \in {\mathcal {X}} \};$ where $\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon ):{\mathcal {X}} \rightarrow [0, 1]$ and $0 \le \big (\zeta _{\mathcal {I}}(\epsilon )\big )^q + \big (\xi _{\mathcal {I}}(\epsilon )\big )^q \le 1$ and hesitation value $\pi _{\mathcal {I}}(\epsilon ) = 1-\Big (\big (\zeta _{\mathcal {I}}(\epsilon )\big )^q+\big (\xi _{\mathcal {I}}(\epsilon )\big )^q\Big )$, where q is a non-negative integer.

Definition 2.7

The square root FS ${\mathcal {I}}=\{\langle \epsilon ,\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon )\rangle | \epsilon \in {\mathcal {X}}\}$, where $\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon ): {\mathcal {X}} \rightarrow [0, 1]$ and satisfying $0 \le \sqrt{\zeta _{\mathcal {I}}(\epsilon )}+(\xi _{\mathcal {I}}(\epsilon ))^2 \le 1$ $\forall$ $\epsilon \in {\mathcal {X}}$, $\pi _{\mathcal {I}}(\epsilon )$.

Here GFSs of ${\mathcal {X}}$ is represented by $GFS_{(m,p)}({\mathcal {X}})$ and GDioFSs over ${\mathcal {X}}$ is represented by $GDioFS_{(m,p)}({\mathcal {X}})$.

Generalized Diophantine fuzzy sets (GDioFSs)

The GDioFS is defined and its properties are discussed in “Generalized Diophantine fuzzy sets (GDioFSs)” section.

Definition 3.1

The GDioFS ${\mathcal {I}}$ in ${\mathcal {X}}$ is structure as follows:

$$\begin{aligned} {\mathcal {I}}=\{\langle \epsilon ,(\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon )),(\varrho _{\mathcal {I}}(\epsilon ), \sigma _{\mathcal {I}}(\epsilon ))\rangle : \epsilon \in {\mathcal {X}} \}; \end{aligned}$$

(3.1)

where $\zeta _{\mathcal {I}}(\epsilon ),\xi _{\mathcal {I}}(\epsilon ):{\mathcal {X}} \rightarrow [0, 1]$ and $\varrho _{\mathcal {I}}(\epsilon )+\sigma _{\mathcal {I}}(\epsilon ) \le 1$, the MG and NMG of $\epsilon \in {\mathcal {X}}$ to ${\mathcal {I}}$ respectively. Then

$$\begin{aligned} 0 \le \big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m + \big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p \le 1. \end{aligned}$$

(3.2)

where m and p are non-negative integers. The degree of indeterminacy is defined as

$$\begin{aligned} \pi _{\mathcal {I}}(\epsilon ) =\root lcm(m,p) \of { 1-\Big (\big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m+\big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p\Big )}, \end{aligned}$$

(3.3)

Since $\pi _{\mathcal {I}}(\epsilon )\in [0, 1]$ denotes the degree of indeterminacy of $\epsilon \in {\mathcal {X}}$ to ${\mathcal {I}}$ and

$$\begin{aligned} \big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m + \big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p + \big (\pi _{\mathcal {I}}(\epsilon )\big )^{lcm(m,p)} = 1. \end{aligned}$$

(3.4)

If $\pi _{\mathcal {I}}(\epsilon )=0$, then $\big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m + \big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p = 1$.

Remark 3.2

Here $\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )+\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\ge 1$ and $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^2+\Big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^2<1$, however, the GDioFSs as $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^m+\Big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p<1$, for $m\ge 2$ and $p\ge 2$ or vice versa. For Example, $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^3+\Big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^2<1$ and $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^3+\Big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^3<1$. Suppose $\zeta _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {I}}(\epsilon )=1$ and $\varrho _{\mathcal {I}}(\epsilon ), \sigma _{\mathcal {I}}(\epsilon )=0.5$, hence $(1\times 0.5) +(1\times 0.5) = 1$ and $(1\times 0.5)^{2} +(1\times 0.5)^{2} = 0.25+0.25=0.5<1$ and $(1\times 0.5)^{3} +(1\times 0.5)^{2} <1$ and $(1\times 0.5)^{3} +(1\times 0.5)^{3} <1.$

Remark 3.3

• 1. Both m and p are equal to 1, and we obtain DioFSs. Thus, DioFSs are a special type of GDioFSs.

• 2. If $m=2$ and $p=2$, we get the DioPFSs.

• 3. If m and p are different values, then $\hbox {GDioFS}_{(m,p)}$ is obtained.

Table 1 shows that difference between various GDioFSs.

Table 1 Difference among different GDioFSs.

Whenever m and p are positive integers. Every DioFS(IFS) is a GDioFS, also every $GDioFS_{(m,p)}({\mathcal {X}})$ is $GDioFS_{(n,q)}({\mathcal {X}})$, $n \ge m$ and $q \ge p$. Converse is not true, for ${\mathcal {I}} \in GDioFS_{m,p}(\epsilon )$, $\zeta _{{\mathcal {I}}}(\epsilon ) = 0.97$ and $\xi _{{\mathcal {I}}}(\epsilon ) = 0.95$, $\varrho _{{\mathcal {I}}}(\epsilon )= 0.7$ and $\sigma _{{\mathcal {I}}}(\epsilon )= 0.3$ and $(0.97 \times 0.7)^2 + (0.95 \times 0.3)^2< 1$. Moreover, $(0.97 \times 0.7)^m + (0.95 \times 0.3)^p< 1$, where $m\ge 2$ and $p\ge 2$, hence ${\mathcal {I}}\in GDioFS_{(m,p)}({\mathcal {X}})$. Hence, ${\mathcal {I}}$ is not an IFS.

Theorem 3.4

Let ${\mathcal {X}}$ be a universal and ${\mathcal {I}}\in GDioFS_{(m,p)}({\mathcal {X}})$. If $\pi _{\mathcal {I}}(\epsilon _i )=0$, then

• 1.
  $$\begin{aligned} |\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}}(\epsilon _i)|=\root m \of {|1-\sigma _{\mathcal {I}} (\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)^p|}. \end{aligned}$$
• 2.
  $$\begin{aligned} |\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)|=\root p \of {|1-\varrho _{\mathcal {I}} (\epsilon _i)\cdot \zeta _{\mathcal {I}}(\epsilon _i)^m|}. \end{aligned}$$

Proof

• 1. Since $\pi _{\mathcal {I}}(\epsilon _i )=0$, By Equation 3.4, $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^m + \Big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p = 1$. This implies that

  $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^m =1-\Big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p$, $|\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )|^m =|1-\Big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p|$ and

  $|\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )| =\root m \of {|1-\Big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p|}$. (2) Similar to prove.

A GDioFS can be operated using a union, intersection, complementation, sum, or product operations.

Definition 3.5

Let ${\mathcal {I}} \in GDioFS_{(m,p)}({\mathcal {X}})$. The complement of ${\mathcal {I}}$ is defined as $\langle \epsilon ,\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ), \varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ) \rangle$, for $\epsilon \in {\mathcal {X}}$. Also ${\mathcal {I}}^{c} \in GDioFS_{(m,p)}({\mathcal {X}})$ and $({\mathcal {I}}^c)^c = {\mathcal {I}}$.

Definition 3.6

Let ${\mathcal {I}},{\mathcal {J}} \in GDioFS_{(m,p)}({\mathcal {X}})$. The union and intersection are as follows:

• 1.
  $$\begin{aligned} {\mathcal {I}}\Cup {\mathcal {J}}= \big \{\big \langle \epsilon , \Big (\max \big (\zeta _{\mathcal {I}}(\epsilon ),\zeta _{\mathcal {J}}(\epsilon )\big ), \min \big (\xi _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {J}}(\epsilon )\big )\Big ),\\ \Big (\max \big (\varrho _{\mathcal {I}}(\epsilon ),\varrho _{\mathcal {J}}(\epsilon )\big ), \min \big (\sigma _{\mathcal {I}}(\epsilon ), \sigma _{\mathcal {J}}(\epsilon )\big )\Big )\big \rangle : \epsilon \in {\mathcal {X}} \big \}. \end{aligned}$$
• 2.
  $$\begin{aligned} {\mathcal {I}}\Cap {\mathcal {J}}= \big \{\big \langle \epsilon , \Big (\min \big (\zeta _{\mathcal {I}}(\epsilon ),\zeta _{\mathcal {J}}(\epsilon )\big ), \max \big (\xi _{\mathcal {I}}(\epsilon ), \xi _{\mathcal {J}}(\epsilon )\big )\Big ),\\ \Big (\min \big (\varrho _{\mathcal {I}}(\epsilon ),\varrho _{\mathcal {J}}(\epsilon )\big ), \max \big (\sigma _{\mathcal {I}}(\epsilon ), \sigma _{\mathcal {J}}(\epsilon )\big )\Big )\big \rangle : \epsilon \in {\mathcal {X}} \big \}. \end{aligned}$$

Definition 3.7

Let ${\mathcal {I}}, {\mathcal {J}} \in GDioFS_{(m,p)}({\mathcal {X}})$. The sum and product are as follows:

• 1.
  $$\begin{aligned} & {\mathcal {I}} \oplus {\mathcal {J}}= \big \langle \epsilon , \Big (\big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m+\big (\varrho _{\mathcal {J}} (\epsilon )\cdot \zeta _{\mathcal {J}}(\epsilon )\big )^p-\big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m \cdot \big (\varrho _{\mathcal {J}}(\epsilon )\cdot \zeta _{\mathcal {J}}(\epsilon )\big )^p,\\ & \quad \big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big ) \big (\sigma _{\mathcal {J}}(\epsilon )\cdot \xi _{\mathcal {J}}(\epsilon )\big )\Big )\big \rangle , \end{aligned}$$

  for $\epsilon \in {\mathcal {X}}.$

• 2.
  $$\begin{aligned} & {\mathcal {I}} \otimes {\mathcal {J}}=\big \{\big \langle \epsilon , \Big (\big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^m+\big (\sigma _{\mathcal {J}} (\epsilon )\cdot \xi _{\mathcal {J}}(\epsilon )\big )^p-\big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^m \cdot \big (\sigma _{\mathcal {J}}(\epsilon )\cdot \xi _{\mathcal {J}}(\epsilon )\big )^p,\\ & \quad \big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big ) \big (\varrho _{\mathcal {J}}(\epsilon )\cdot \zeta _{\mathcal {J}}(\epsilon )\big )\Big )\big \rangle : \epsilon \in {\mathcal {X}} \big \}. \end{aligned}$$

Remark 3.8

For ${\mathcal {I}}, {\mathcal {J}} \in GDioFS_{(m,p)}({\mathcal {X}})$. Then De Morgans laws as follows:

• 1.
  $$\begin{aligned} & ({\mathcal {I}} \Cap {\mathcal {J}})^c = {\mathcal {I}}^c \Cup {\mathcal {J}}^c,\\ & \quad ({\mathcal {I}} \Cup {\mathcal {J}})^c = {\mathcal {I}}^c \Cap {\mathcal {J}}^c. \end{aligned}$$
• 2.
  $$\begin{aligned} & ({\mathcal {I}} \oplus {\mathcal {J}})^c = {\mathcal {I}}^c \oplus {\mathcal {J}}^c,\\ & \quad ({\mathcal {I}} \otimes {\mathcal {J}})^c = {\mathcal {I}}^c \otimes {\mathcal {J}}^c. \end{aligned}$$

Definition 3.9

Let ${\mathcal {I}} \in GDioFS_{(m,p)}({\mathcal {X}})$. The score function of ${\mathcal {I}}$ is defined as $s({\mathcal {I}})=(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m -(\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ))^p, s({\mathcal {I}})\in [-1,1]$.

Definition 3.10

Let ${\mathcal {I}} \in GDioFS_{(m,p)}({\mathcal {X}})$. The accuracy function of ${\mathcal {I}}$ is defined as $a({\mathcal {I}}) = \big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m +\big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p$, $a({\mathcal {I}}) \in [0, 1]$.

Theorem 3.11

Let ${\mathcal {I}} \in GDioFS_{(m,p)}({\mathcal {X}})$. Then

• 1. $s({\mathcal {I}}) = 0$ $\iff$ $\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ) = \sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )$.

• 2. $s({\mathcal {I}}) = 1$ $\iff$ $\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ) =\root p \of {(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m-1)}$.

• 3. $s({\mathcal {I}}) =-1$ $\iff$ $\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ) = \root p \of {(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m+1)}$.

Proof

• (1) if $s({\mathcal {I}})= 0$, then, $(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m-(\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon ))^p=0$. Hence, $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^m=\Big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p$   $\forall \epsilon \in {\mathcal {X}}$ implies that $\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ) = \sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )$. Conversely, if $\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )=\sigma _{\mathcal {I}}(\epsilon ) \cdot \xi _{\mathcal {I}}(\epsilon )$,   $\forall \epsilon \in {\mathcal {X}}$, then $(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m=(\sigma _{\mathcal {I}}(\epsilon ) \cdot \xi _{\mathcal {I}}(\epsilon ))^p$. Hence, $(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m-(\sigma _{\mathcal {I}}(\epsilon ) \cdot \xi _{\mathcal {I}}(\epsilon ))^p=0.$ Therefore, $s({\mathcal {I}})=0$.

• (2) Assume that $s({\mathcal {I}})=1$. Now, $1=\big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m-\big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p$. Therefore, $\big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p=\big (\varrho _{\mathcal {I}} (\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m-1$. Thus, $\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )=\root p \of {\big (\varrho _{\mathcal {I}} (\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m-1}$, $\forall \epsilon \in {\mathcal {X}}$. Converse is also true.

• (3) Suppose $s({\mathcal {I}})=-1$. Now, $-1=\big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m-\big (\sigma _{\mathcal {I}} (\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p$, $\Rightarrow \big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\big )^p=\big (\varrho _{\mathcal {I}} (\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m+1$ and $\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )=\root p \of {\big (\varrho _{\mathcal {I}} (\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\big )^m+1}$, $\forall \epsilon \in {\mathcal {X}}$. Similar to prove the converse part.

Theorem 3.12

Let ${\mathcal {I}} \in GDioFS_{(m,p)}({\mathcal {X}})$. Then

• 1.
  $$\begin{aligned} a({\mathcal {I}}) = 1 \iff \pi _{\mathcal {I}}(\epsilon ) = 0, \end{aligned}$$
• 2.
  $$\begin{aligned} a({\mathcal {I}}) = 0 \iff |\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )| = |\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )|^{p/m}. \end{aligned}$$

Proof

• (1) Suppose $a({\mathcal {I}}) = 1$. Now, $(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m+(\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _ {\mathcal {I}}(\epsilon ))^p=1.$ Since $\pi _{\mathcal {I}}(\epsilon )=\root lcm(m,p) \of {1-[\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ) \Big )^m+\Big (\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p]}$. Hence $\pi _{\mathcal {I}}(\epsilon )=0$.

  Conversely, assume that $\pi _{\mathcal {I}}(\epsilon )=0$. Now, $(\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ))^m+(\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _ {\mathcal {I}}(\epsilon ))^p=1$. This implies that $a({\mathcal {I}})=1.$

• (2) Suppose $a({\mathcal {I}})=0$, then $\Big (\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )\Big )^m=-\Big (\sigma _{\mathcal {I}}(\epsilon ) \cdot \xi _{\mathcal {I}}(\epsilon )\Big )^p$. $|\varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon )|=|\sigma _{\mathcal {I}}(\epsilon ) \cdot \xi _{\mathcal {I}}(\epsilon )|^{p/m}.$

Definition 3.13

Let ${\mathcal {I}}, {\mathcal {J}} \in GDioFS_{(m,p)}({\mathcal {X}})$. Then

• (1) ${\mathcal {I}} = {\mathcal {J}} \iff \varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ) = \varrho _{\mathcal {J}}(\epsilon )\cdot \zeta _{\mathcal {J}}(\epsilon )$, and, $\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _ {\mathcal {I}}(\epsilon ) = \sigma _{\mathcal {J}}(\epsilon )\cdot \xi _{\mathcal {J}}(\epsilon ),$ $\forall \epsilon \in {\mathcal {X}}$.

• (2) ${\mathcal {I}} \subseteq {\mathcal {J}} \iff \varrho _{\mathcal {I}}(\epsilon )\cdot \zeta _{\mathcal {I}}(\epsilon ) \le \varrho _{\mathcal {J}}(\epsilon )\cdot \zeta _{\mathcal {J}}(\epsilon )$ and $\sigma _{\mathcal {I}}(\epsilon )\cdot \xi _ {\mathcal {I}}(\epsilon ) \ge \sigma _{\mathcal {J}}(\epsilon )\cdot \xi _{\mathcal {J}}(\epsilon )$ or $\sigma _{\mathcal {I}}(\epsilon ) \cdot \xi _{\mathcal {I}}(\epsilon ) \le \sigma _{\mathcal {J}}(\epsilon )\cdot \xi _{\mathcal {J}}(\epsilon )$, $\forall \epsilon \in {\mathcal {X}}$.

• (3) ${\mathcal {I}} \subset {\mathcal {J}} \iff {\mathcal {I}} \subseteq {\mathcal {J}}$ and ${\mathcal {I}}\ne {\mathcal {J}}$.

• (4) ${\mathcal {I}} = {\mathcal {J}} \iff {\mathcal {I}}\subseteq {\mathcal {J}}$ and ${\mathcal {J}} \subseteq {\mathcal {I}}$.

Theorem 3.14

Let ${\mathcal {I}}, {\mathcal {J}} \in GDioFS_{(m,p)}({\mathcal {X}})$. Then

• 1. $s({\mathcal {I}}) = s({\mathcal {J}}) \big (a({\mathcal {I}}) = a({\mathcal {J}})\big ) \iff {\mathcal {I}} = {\mathcal {J}} \big ({\mathcal {I}} = {\mathcal {J}}\big ),$

• 2. $s({\mathcal {I}}) \le s({\mathcal {J}}) \big (a({\mathcal {I}})\le a({\mathcal {J}})\big ) \iff {\mathcal {I}}\subseteq {\mathcal {J}} \big ({\mathcal {I}} \subseteq {\mathcal {J}}\big )$,

• 3. $s({\mathcal {I}})< s({\mathcal {J}}) \big (a({\mathcal {I}}) < a({\mathcal {J}})\big ) \iff {\mathcal {I}} \subseteq {\mathcal {J}}{ and } {\mathcal {I}} \ne {\mathcal {J}} \big ({\mathcal {I}} \subseteq {\mathcal {J}}{ and }{\mathcal {I}}\ne {\mathcal {J}}\big )$.

Definition 3.15

Let ${\mathcal {I}}\in GDioFS_{(m,p)}({\mathcal {X}})$. Then

• 1. necessity operator $(\square {\mathcal {I}})$ of ${\mathcal {I}}$ is defined as

  $\square {\mathcal {I}} =\{\big \langle \epsilon , \Big (\zeta _{\mathcal {I}}(\epsilon ), \root p \of {1-\big (\zeta _{\mathcal {I}}(\epsilon )\big )^m}\Big )$, $\Big (\varrho (\epsilon ), 1-\varrho (\epsilon )\Big ) \big \rangle : \epsilon \in {\mathcal {X}} \}.$

• 2. possibility operator $(\Diamond {\mathcal {I}})$ of ${\mathcal {I}}$ is defined as

  $\Diamond {\mathcal {I}} =\{\big \langle \epsilon , \Big (\root m \of {1-(\xi _{\mathcal {I}}(\epsilon ))^p}, \xi _{\mathcal {I}}(\epsilon )\Big ),$ $\Big (1-\sigma (\epsilon ), \sigma (\epsilon )\Big ) \big \rangle : \epsilon \in {\mathcal {X}} \}.$

Using Definition 3.15, we prove the following theorem.

Theorem 3.16

Let ${\mathcal {I}}, {\mathcal {J}} \in GDioFS_{(m,p)}$. Then

• 1. ${\mathcal {I}} \subseteq \square {\mathcal {J}} \iff \square {\mathcal {I}}\subseteq \square {\mathcal {J}}$,

• 2. ${\mathcal {I}}\subseteq \Diamond {\mathcal {J}} \iff \Diamond {\mathcal {I}}\subseteq \Diamond {\mathcal {J}}$.

Proof

(1)

$$\begin{aligned} \begin{aligned} \square {\mathcal {J}}=&\big \{\big \langle \epsilon , \Big (\zeta _{\mathcal {J}}(\epsilon ), \root p \of {1-\big (\zeta _{\mathcal {J}}(\epsilon )\big )^m}\Big ), \Big (\varrho (\epsilon ), 1-\varrho (\epsilon )\Big ) \big \rangle : \epsilon \in {\mathcal {X}}\big \},\\&=\big \{\big \langle \epsilon , \Big (\zeta _{\mathcal {J}}(\epsilon ), \xi _{\mathcal {J}}(\epsilon )\Big ), \Big (\varrho (\epsilon ), \sigma (\epsilon )\Big ) \big \rangle : \epsilon \in {\mathcal {X}} \big \},\\&={\mathcal {J}}. \end{aligned} \end{aligned}$$

(3.5)

Similarly, $\square {\mathcal {I}}={\mathcal {I}}$. Now, if ${\mathcal {I}}\subseteq \square {\mathcal {J}}$, then $\square {\mathcal {I}}\subseteq \square {\mathcal {J}}$.

Conversely, if $\square {\mathcal {I}}\subseteq \square {\mathcal {J}}$, then ${\mathcal {I}}\subseteq \square {\mathcal {J}}$. (2)

$$\begin{aligned} \begin{aligned} \Diamond {\mathcal {J}}=&\big \{\big \langle \epsilon , \Big (\root m \of {1-\big (\xi _{\mathcal {J}}(\epsilon )\big )^p}, \xi _{\mathcal {J}}(\epsilon ) \Big ),\Big (1-\sigma (\epsilon ), \sigma (\epsilon )\Big ) \big \rangle : \epsilon \in {\mathcal {X}} \big \},\\&=\{\langle \epsilon , \Big (\zeta _{\mathcal {J}}(\epsilon ),\xi _{\mathcal {J}}(\epsilon )\Big ),\Big (\varrho (\epsilon ), \sigma (\epsilon )\Big ) \rangle : \epsilon \in {\mathcal {X}} \},\\&={\mathcal {J}}. \end{aligned} \end{aligned}$$

(3.6)

Similarly, $\Diamond {\mathcal {I}}={\mathcal {I}}$. Now, if ${\mathcal {I}}\subseteq \Diamond {\mathcal {J}}$, then $\Diamond {\mathcal {I}}\subseteq \Diamond {\mathcal {J}}$. $\square$

Conversely, if $\Diamond {\mathcal {I}}\subseteq \Diamond {\mathcal {J}}$, then ${\mathcal {I}}\subseteq \Diamond {\mathcal {J}}$.

Relations on GDioFSs

The relation ${\mathcal {R}}$ is a subset of ${\mathcal {X}} \times {\mathcal {Y}}$, where ${\mathcal {X}}$ and ${\mathcal {Y}}$ are non-empty sets. The generalized Diophantine fuzzy relation (GDioFR) is a GDioFS. The GDioFS ${\mathcal {I}} \subseteq {\mathcal {X}}$ divided by GDioFS ${\mathcal {J}} \subseteq {\mathcal {Y}}$ is the cartesian product ${\mathcal {I}} \times {\mathcal {J}}$. Two-dimensional tables or matrices are used to represent the GDioFR. In all cases, GDioFS is well established, regardless of whether DioFSs or DioPFSs are used. By extending the DioFS and DioPFS concepts to the GDioFS, we extended the fuzzy relations.

Definition 3.17

The function $h:{\mathcal {X}} \rightarrow {\mathcal {Y}}$ and ${\mathcal {L}}\in GDioFS_{(m,p)}({\mathcal {X}})$ and ${\mathcal {M}}\in GDioFS_{(m,p)}({\mathcal {Y}})$. Then

• 1. the image is defined as

  $$\begin{aligned} & \zeta _{h({\mathcal {L}})}(\upsilon )= {\left\{ \begin{array}{ll} \underset{\epsilon \in h^{-1}(\upsilon )}{\vee }\zeta _{\mathcal {L}}(\epsilon ),\quad h^{-1}(\upsilon ) \ne \emptyset ,\\ \quad \quad 0, \quad \quad \text {otherwise,} \end{array}\right. }\\ & \quad \xi _{h({\mathcal {L}})}(\upsilon )= {\left\{ \begin{array}{ll} \underset{\epsilon \in h^{-1}(\upsilon )}{\wedge }\xi _{\mathcal {L}}(\epsilon ),\quad h^{-1}(\upsilon ) \ne \emptyset ,\\ \quad \quad 1, \quad \quad \text {otherwise,} \end{array}\right. } \\ & \quad \varrho _{h({\mathcal {L}})}(\upsilon )= {\left\{ \begin{array}{ll} \underset{\epsilon \in h^{-1}(\upsilon )}{\vee }\varrho _{\mathcal {L}}(\epsilon ),\quad h^{-1}(\upsilon ) \ne \emptyset ,\\ \quad \quad 0, \quad \quad \text {otherwise,} \end{array}\right. }\\ & \quad \sigma _{h({\mathcal {L}})}(\upsilon )= {\left\{ \begin{array}{ll} \underset{\epsilon \in h^{-1}(\upsilon )}{\wedge }\sigma _{\mathcal {L}}(\epsilon ),\quad h^{-1}(\upsilon ) \ne \emptyset ,\\ \quad \quad 1, \quad \quad \text {otherwise,} \end{array}\right. } \end{aligned}$$

  for each $\upsilon \in {\mathcal {Y}}$. Also, $0 \le \Big (\varrho _{h({\mathcal {L}})}(\upsilon )\cdot \zeta _{h({\mathcal {L}})}(\upsilon )\Big )^m +$ $\Big (\sigma _{h({\mathcal {L}})}(\upsilon )\cdot \xi _{h({\mathcal {L}})}(\upsilon )\Big )^p \le 1.$

  Degree of indeterminacy of $\upsilon \in {\mathcal {Y}}$ to $h({\mathcal {L}})$ is defined as

  $$\begin{aligned} \pi _h({\mathcal {L}})(\upsilon ) = \root lcm(m,p) \of {1-\Big (\Big (\varrho _{h({\mathcal {L}})}(\upsilon )\cdot \zeta _{h({\mathcal {L}})}(\upsilon )\Big )^m + \Big (\sigma _{h({\mathcal {L}})}(\upsilon )\cdot \xi _{h({\mathcal {L}})}(\upsilon )\Big )^p\Big )}. \end{aligned}$$

• 2. the inverse image of ${\mathcal {M}}$ is defined as

  $$\begin{aligned} & \zeta _{h ^{-1}({\mathcal {M}})}(\epsilon ) = \zeta _{\mathcal {M}}\big (h(\epsilon )\big ), \varrho _{h ^{-1}({\mathcal {M}})}(\epsilon ) = \varrho _{\mathcal {M}}\big (h(\epsilon )\big ),\\ & \quad \xi _{h^{-1}({\mathcal {M}})}(\epsilon ) = \xi _{\mathcal {M}}\big (h(\epsilon )\big ),\sigma _{h^{-1}({\mathcal {M}})}(\epsilon ) = \sigma _{\mathcal {M}}\big (h(\epsilon )\big ),\\ & \quad \forall , \, \epsilon \in {\mathcal {X}}. \end{aligned}$$

  Also, $\Big (\varrho _{h ^{-1}({\mathcal {M}})}(\epsilon )\cdot \zeta _{h ^{-1}({\mathcal {M}})}(\epsilon )\Big )^m + \Big (\sigma _{h^{-1}({\mathcal {M}})}(\epsilon )\cdot \xi _{h^{-1}({\mathcal {M}})}(\epsilon )\Big )^p \in [0,1]$.

  Degree of indeterminacy

  $$\begin{aligned} \begin{aligned} \pi _{h^{-1}({\mathcal {M}})}(\epsilon ) = \root lcm(m,p) \of {1- \Big (\varrho _{h ^{-1}({\mathcal {M}})}(\epsilon )\cdot \zeta _{h ^{-1}({\mathcal {M}})}(\epsilon )\Big )^m + \Big (\sigma _{h^{-1}({\mathcal {M}})}(\epsilon )\cdot \xi _{h^{-1}({\mathcal {M}})}(\epsilon )\Big )^p}. \end{aligned} \end{aligned}$$

  (3.7)

Definition 3.18

Let ${\mathcal {X}}$ and ${\mathcal {Y}}$ be any two non-empty sets. Then GDioFR ${\mathcal {R}}({\mathcal {X}} \rightarrow {\mathcal {Y}})$ is a $GDioFS_{(m,p)}$ of ${\mathcal {X}} \times {\mathcal {Y}}$ satisfying the condition

$$\begin{aligned} 0 \le \Big (\varrho _{\mathcal {R}}(\epsilon ,\upsilon )\cdot \zeta _{\mathcal {R}}(\epsilon ,\upsilon )\Big )^m + \Big (\sigma _{\mathcal {R}}(\epsilon ,\upsilon )\cdot \xi _{\mathcal {R}}(\epsilon ,\upsilon )\Big )^p \le 1. \end{aligned}$$

It is defined that the indeterminacy degree ${\mathcal {X}} \times {\mathcal {Y}}$ to ${\mathcal {R}}$ can be expressed as follows:

$$\begin{aligned} \pi _{\mathcal {R}}(\epsilon ,\upsilon )=\root lcm(m,p) \of {1-\Big (\Big (\varrho _{\mathcal {R}} (\epsilon ,\upsilon )\cdot \zeta _{\mathcal {R}}(\epsilon ,\upsilon )\Big )^m +\Big (\sigma _{\mathcal {R}}(\epsilon ,\upsilon )\cdot \xi _{\mathcal {R}}(\epsilon ,\upsilon )\Big )^p\Big )}. \end{aligned}$$

(3.8)

where ${\mathcal {R}}({\mathcal {X}} \rightarrow {\mathcal {Y}})$ is a generalized fuzzy relation (GFR) ${\mathcal {R}}$ instead of ${\mathcal {R}}({\mathcal {X}} \rightarrow {\mathcal {Y}})$.

Definition 3.19

Suppose that ${\mathcal {L}} \in GDioFS_{(m,p)}({\mathcal {X}})$. Then we define the composition relation ${\mathcal {R}}({\mathcal {X}} \rightarrow {\mathcal {Y}})$ and ${\mathcal {L}}$, ${\mathcal {M}} \in GDioFS_{(m,p)}({\mathcal {Y}})$ denoted by ${\mathcal {M}} = {\mathcal {R}}\circ {\mathcal {L}}$.

$$\begin{aligned} \varrho _{\mathcal {M}}(\upsilon )\cdot \zeta _{\mathcal {M}}(\upsilon )= \underset{x}{\max }\left( \min \Big [\Big (\varrho _{\mathcal {L}}(\epsilon )\cdot \zeta _{\mathcal {L}} (\epsilon )\Big ),\Big (\varrho _{\mathcal {R}}(\epsilon )\cdot \zeta _{\mathcal {R}}(\epsilon , \upsilon )\Big )\Big ]\right) \end{aligned}$$

(3.9)

and

$$\begin{aligned} \sigma _{\mathcal {M}}(\upsilon )\cdot \xi _{\mathcal {M}}(\upsilon )= \underset{x}{\min }\left( \max \Big [\Big (\sigma _{\mathcal {L}}(\epsilon )\cdot \xi _{\mathcal {L}} (\epsilon )\Big ),\Big (\sigma _{\mathcal {R}}(\epsilon )\cdot \xi _{\mathcal {R}}(\epsilon , \upsilon )\Big ) \Big ]\right) \end{aligned}$$

(3.10)

$\forall$ $\epsilon \in {\mathcal {X}}$ and $\upsilon \in {\mathcal {Y}}$.

Definition 3.20

A max–min–max combination of two GDioFRs is define by ${\mathcal {R}} \circ {\mathcal {Q}}$, where ${\mathcal {Q}} ({\mathcal {X}} \rightarrow {\mathcal {Y}})$ and ${\mathcal {R}}({\mathcal {Y}} \rightarrow {\mathcal {Z}})$ are the DioGFRs. In this case, GDioFR forms the set ${\mathcal {X}}$ to ${\mathcal {Z}}$ and ${\mathcal {R}} \circ {\mathcal {Q}}$ defines MG and NMG as follows:

$$\begin{aligned} \big (\varrho _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \zeta _{{\mathcal {R}}\circ {\mathcal {Q}}}\big )(\epsilon ,\varpi )= \underset{y}{\max }\left( \min [\big (\varrho _{\mathcal {Q}}\cdot \zeta _{\mathcal {Q}}\big ) (\epsilon , \upsilon ), \big (\varrho _{\mathcal {R}} \cdot \zeta _{\mathcal {R}}\big )(\upsilon , \varpi )]\right) \end{aligned}$$

(3.11)

and

$$\begin{aligned} \big (\sigma _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \xi _{{\mathcal {R}}\circ {\mathcal {Q}}}\big )(\epsilon ,\varpi )=\underset{y}{\min }\left( \max [\big (\sigma _{\mathcal {Q}}\cdot \xi _{\mathcal {Q}}\big )(\epsilon , \upsilon ), \big (\sigma _{\mathcal {R}} \cdot \xi _{\mathcal {R}}\big )(\upsilon , \varpi )]\right) \end{aligned}$$

(3.12)

$\forall$ $(\epsilon , \varpi ) \in {\mathcal {X}} \times {\mathcal {Z}}$ and $\forall \upsilon \in {\mathcal {Y}}$ and satisfying the condition

$0 \le \Big (\big (\varrho _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \zeta _{{\mathcal {R}}\circ {\mathcal {Q}}}\big )(\epsilon ,\varpi )\Big )^m +$ $\Big (\big (\sigma _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \xi _{{\mathcal {R}}\circ {\mathcal {Q}}}\big )(\epsilon ,\varpi )\Big )^p \le 1.$

The indeterminacy degree is defined as

$$\begin{aligned} \pi _{{\mathcal {R}}\circ {\mathcal {Q}}}(\epsilon ,\varpi ) = \root lcm(m,p) \of {1-\Big (\Big (\big (\varrho _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \zeta _{{\mathcal {R}}\circ {\mathcal {Q}}}\big )(\epsilon ,\varpi )\Big )^m + \Big (\big (\sigma _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \xi _{{\mathcal {R}}\circ {\mathcal {Q}}}\big )(\epsilon ,\varpi )\Big )^p\Big )}. \end{aligned}$$

Theorem 3.21

If ${\mathcal {R}}_1 \in GDioFR({\mathcal {L}},{\mathcal {M}})$ and ${\mathcal {R}}_2 \in GDioFR({\mathcal {M}},C)$, then ${\mathcal {R}}_1 \circ {\mathcal {R}}_2 \in GDioFR({\mathcal {L}},C)$.

The composition formula is defined as follows:

$$\begin{aligned} {\mathcal {R}} \circ {\mathcal {Q}} = \Big (\varrho _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \zeta _{{\mathcal {R}}\circ {\mathcal {Q}}}\Big )(\epsilon ,\varpi )-\Big (\sigma _{{\mathcal {R}}\circ {\mathcal {Q}}}\cdot \xi _{{\mathcal {R}}\circ {\mathcal {Q}}}\Big )(\epsilon , \varpi )\cdot \Big (\pi _{{\mathcal {R}} \circ {\mathcal {Q}}}(\epsilon , \varpi )\Big ), \forall (\epsilon , \varpi ) \in {\mathcal {X}} \times {\mathcal {Z}}. \end{aligned}$$

(3.13)

Distances between GDioFRs

The Euclidean, Hausdorff, Minkowski and Hamming methods are a few of the widely used distance measurement techniques. The literature currently in publication indicates that one technique that can be applied to the staff selection process is the Hamming distance^43,44. In order to evaluate inaccuracy in telecommunication, Hamming (1950) advocated counting the number of flipping bits in a fixed-length binary word. It is well known that the Hamming distance can be used to determine the difference between two sets or elements. For instance, the separation of fuzzy sets with interval values. As a result, it has been used in a variety of domains outside of decision-making, including communication, iris identification, and engineering. The distances between different GDioFSs are defined in this section. The difference between two elements or sets can be determined using the Hamming distance. The Hamming distances between the two GDioFSs are described in this section.

Definition 3.22

Let ${\mathcal {X}} =\{\epsilon _1, \epsilon _2,\ldots \epsilon _n\}$ be a universal set, ${\mathcal {I}}$ and ${\mathcal {J}}$ be two $GDioFS_{(m,p)}({\mathcal {X}})$. The Hamming distance between ${\mathcal {I}}$ and ${\mathcal {J}}$ is defined as follows:

$$\begin{aligned} \begin{aligned}{}&d^1_{(m,p)}({\mathcal {I}},{\mathcal {J}}) \\&\quad =\frac{1}{2}\biggl (\sum _{i=1}^n \Bigl (|\Big (\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}}(\epsilon _i)\Big )^m- \Big (\gamma _{\mathcal {J}}(\epsilon _i)\cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m| + |\Big (\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p-\Big (\delta _{\mathcal {J}}(\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p|\\&\qquad +|\pi _{\mathcal {I}}(\epsilon _i)^{lcm(m,p)}-\pi _{\mathcal {J}}(\epsilon _i)^{lcm(m,p)}|\Bigr )\biggr ). \end{aligned} \end{aligned}$$

(3.14)

Since

$$\begin{aligned} \pi _{\mathcal {I}}(\epsilon _i)=\root lcm(m,p) \of {1-\Big (\Big (\varrho _{\mathcal {I}}(\epsilon _i )\cdot \zeta _{\mathcal {I}}(\epsilon _i)\Big )^m+\Big (\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p\Big )} \end{aligned}$$

(3.15)

and

$$\begin{aligned} \pi _{\mathcal {J}}(\epsilon _i)=\root lcm(m,p) \of {1-\Big (\Big (\gamma _{\mathcal {J}}(\epsilon _i) \cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m+\Big (\delta _{\mathcal {J}}(\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p\Big )} \end{aligned}$$

(3.16)

for $i=1,2,\ldots ,n$, the values of $\pi _{\mathcal {I}}(\epsilon _i)$ and $\pi _{\mathcal {I}}(\epsilon _i)$ from Equation 3.15, and Equation 3.16 in Equation 3.14. We get

$$\begin{aligned} \begin{aligned}{}&d^1_{(m,p)}({\mathcal {I}},{\mathcal {J}}) \\&\quad = \frac{1}{2}\biggl (\sum _{i=1}^n \Bigl (\big |\Big (\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}} (\epsilon _i)\Big )^m- \Big (\gamma _{\mathcal {J}}(\epsilon _i)\cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m\big |+ \big | \Big (\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p- \Big (\delta _{\mathcal {J}} (\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p\big |\\&\qquad + \big |\bigl (\Big (\gamma _{\mathcal {J}}(\epsilon _i)\cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m +\Big (\delta _{\mathcal {J}}(\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p\bigr ) -\bigl (\Big (\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}}(\epsilon _i)\Big )^m+ \Big (\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p\bigr )\big |\Bigr )\biggr ). \end{aligned} \end{aligned}$$

(3.17)

Definition 3.23

In order to find the normalized Hamming distance between ${\mathcal {I}}$ and ${\mathcal {J}}$. The following equation must be considered:

$$\begin{aligned} \begin{aligned}{}&d^{1n}_{(m,p)}({\mathcal {I}},{\mathcal {J}})\\&\quad = \frac{1}{2n}\biggl (\sum _{i=1}^n ( | \Big (\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}} (\epsilon _i)\Big )^m- \Big (\gamma _{\mathcal {J}}(\epsilon _i)\cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m| +| \Big (\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p- \Big (\delta _{\mathcal {J}} (\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p\\&\qquad + |(\Big (\gamma _{\mathcal {J}}(\epsilon _i)\cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m+ \Big (\delta _{\mathcal {J}}(\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p) -(\Big (\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}}(\epsilon _i)\Big )^m+\Big (\sigma _{\mathcal {I}} (\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p)|\Bigr )\biggr ). \end{aligned} \end{aligned}$$

(3.18)

Remark 3.24

• 1. If $m=1$ and $p=1$, then normalized HD can be obtained between the two DioFSs.

• 2. If $m=2$ and $p=2$, then normalized HD can be obtained between the two DioPFSs.

• 3. If different integers m and p, then normalized HD can be obtained between the two $GDioFS_{(m,p)}({\mathcal {X}})$.

Definition 3.25

Let ${\mathcal {I}}$ and ${\mathcal {J}}$ be two $GDioFS_{(m,p)}({\mathcal {X}})$. Then ED between ${\mathcal {I}}$ and ${\mathcal {J}}$ is defined as

$$\begin{aligned} \begin{aligned}{}&d^2_{(m,p)}({\mathcal {I}},{\mathcal {J}})\\&\quad = \biggl \{\frac{1}{2}\sum _{i=1}^n \Bigl (\Bigl (\Big (\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}}(\epsilon _i)\Big )^m- \Big (\gamma _{\mathcal {J}}(\epsilon _i)\cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m\Bigr )^2 +\Bigl (\Big (\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p-\Big (\delta _{\mathcal {J}} (\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p\Bigr )^2\\&\qquad + \Bigl (\pi _{\mathcal {I}}(\epsilon _i)^{lcm(m,p)}-\pi _{\mathcal {J}}(\epsilon _i)^{lcm(m,p)}\Bigr )^2\Bigr )\biggr \}^{\!1/2}. \end{aligned} \end{aligned}$$

(3.19)

Normalized ED between ${\mathcal {I}}$ and ${\mathcal {J}}$ is defined as

$$\begin{aligned} \begin{aligned}{}&d^{2n}_{(m,p)}({\mathcal {I}},{\mathcal {J}})\\&\quad = \biggl \{\frac{1}{2n}\sum _{i=1}^n \Bigl (\Bigl (\Big (\varrho _{\mathcal {I}}(\epsilon _i)\cdot \zeta _{\mathcal {I}}(\epsilon _i)\Big )^m- \Big (\gamma _{\mathcal {J}}(\epsilon _i)\cdot \zeta _{\mathcal {J}}(\epsilon _i)\Big )^m\Bigr )^2 +\Bigl (\Big (\sigma _{\mathcal {I}}(\epsilon _i)\cdot \xi _{\mathcal {I}}(\epsilon _i)\Big )^p -\Big (\delta _{\mathcal {J}}(\epsilon _i)\cdot \xi _{\mathcal {J}}(\epsilon _i)\Big )^p\Bigr )^2\\&\qquad + \Bigl (\pi _{\mathcal {I}}(\epsilon _i)^{lcm(m,p)}-\pi _{\mathcal {J}}(\epsilon _i)^{lcm(m,p)}\Bigr )^2\Bigr )\biggr \}^{\!1/2}. \end{aligned} \end{aligned}$$

(3.20)

where ${\mathcal {X}} =\{\epsilon _1, \epsilon _2,\ldots \epsilon _n\}$.

MCDM methods

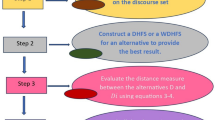
In an MCDM problem, a number of criteria are taken into consideration in the process of selecting the optimum alternative. There are several ways to apply MCDM to different fields, including finance and engineering design. An explanation of the MCDM application concepts, categories and methods is provided in this entry. There are also some of the main methods listed in this section. A MCDM approach involves evaluating the performance of objects based on several contradictory quantitative and/or qualitative criteria to achieve a consensus solution. However, these methods do not provide recommendations about which decision you should make, rather they assist decision makers in choosing the best alternative based on their needs. The MCDM method avoids trial-and-error practices in contrast to conventional trial-and-error practices. The world in which technology and competition are advancing is complex. They provide the basis for the assessment, selection, sorting and prioritization of objectives. An important component of MCDM is the evaluation and selection of the best processes, as well as the planning and design of experiments. Figure 1 shows that flowchart of the our method.

Figure 1

Flowchart of the our method.

Selection of colleges

DM can be applied in many fields including selecting a washing machine, laptop, engineering and two wheeler motor bike, as well as choosing a college for education. Expert standards were used to evaluate teacher education when selecting a college. Parents have conducted various studies mainly to discover, what drives their choice of college, which is best suited to their needs and aspirations. An academic factor considered by parents is academic quality, cost, campus environment and student/faculty relationship, all of which are grouped into four distinct elements. By assessing alternatives against these criteria, we aimed to select the optimal one. Parents prioritize college education. Five colleges were chosen for this study. Campus environment, overall cost, academic quality, relationship between students and faculty and career development are the factors (F) that determine the score of college education by experts. Five students were considered such as $S=\{S_{1}, S_{2}, S_{3}, S_{4}, S_{5}\}.$ Our study focused on five colleges: ${\mathcal {M}}=\{$College-1, College-2, College-3, College-4, College-5 $\}$. To prioritize their choices, parents make decisions based on their choices. The four college features are important to each student, according to their satisfaction, as described in the set ${\mathcal {F}}$. Table 2 presents the results. A Cartesian product is formed by taking the GDioFR of the sets S and ${\mathcal {F}}$ and denoting it by the following formula: $S \circ {\mathcal {F}}$. The decision table contains four types of entries: $r_{ij}=\langle \varrho _{ij}\zeta _{ij}, \sigma _{ij}\xi _{ij}, \pi _{ij}\rangle ,\, i=1,2,3,\ldots ,5,\,\, j=1,2,3,4.$ A college with MG $\zeta _{ij}$ represents the points that students $c_i$ assign to its features $f_j$. $\xi _{ij}$ shows the NMG, which shows that students left for the feature $f_j$. $\pi _{ij}$ indicates the degree of indeterminacy of the students $c_i$ in the feature $f_j$. The Table 3, which is the GDioFR of ${\mathcal {F}}$ and ${\mathcal {M}}$ represent as ${\mathcal {F}}\circ {\mathcal {M}}$ and $t_{jk}=\langle \varrho '_{ij}\zeta '_{jk}, \sigma _{ij}'\xi '_{jk}, \pi '_{jk}\rangle$, $j=1,2,3,4$ and $k=1,2,3,\ldots ,5$, where $\zeta '_{jk}$ denotes the feature $f_j$ in $m_k$.

Table 2 GDioFR ${\mathcal {Q}}(S \rightarrow {\mathcal {F}})$.

Table 3 GDioFR ${\mathcal {R}}({\mathcal {F}}\rightarrow {\mathcal {M}})$.

Table 4 Max–min–max composition of GDioFRs ${\mathcal {Q}}$ and ${\mathcal {R}}$, denoted by ${\mathcal {R}}\circ {\mathcal {Q}}$, and defined in Equation  3.13.

For $m=3$ and $p=3$, we find the values $\pi _{{\mathcal {C}}\circ {\mathcal {F}}}$ and $\pi _{{\mathcal {F}}\circ {\mathcal {M}}}$ using Equation 3.3. The DioFS and DioPFS values were calculated. We derive our decisions from Table 4 in two ways.

• 1. Each students to college As a result of this decision, the college is satisfied with the student. As a result, college-2 with the highest satisfaction level for $S_{1}$. $S_{2}$ is located in college-5. A college-5 student was satisfied with $S_{3}$. It is college-3 that provides $S_{4}$ satisfaction. In college-5 with satisfaction with student $S_{5}$ was found.

• 2. Each college students This decision indicates how suitable a particular college is for the student. $S_{5}$ satisfaction according to college-1. Satisfaction with $S_{4}$ with college-2. $S_{4}$ satisfaction with college-3. That is the satisfaction of $S_{1}$ with college-4. Level of satisfaction of $S_{4}$ with college-5.

Figure 2 shows that students have a variety of college choices.

Figure 2

students have a variety of college choices.

Medical diagnosis problem

In recent year, natural language processing and machine learning methods have been applied for the prediction of diagnoses from medical notes and electronic health records (EHRs). Educational, economic, management, engineering, and hospital fields deal with DM problems. At some point in the DM process, uncertainty plays a dominant role in science and technology development. A medical diagnosis system application is developed based on the symptoms provided by the user to diagnose their probable disease. Hospitals, clinics, and diagnostic centers were located using this application. Users can also order and deliver medicines directly to their location. In a medical diagnosis, symptoms and signs are evaluated to determine which diseases or conditions explain the symptoms and signs. Medicine is prescribed by doctors using MCDM procedures. A recently developed method is used in this study to diagnose a patient’s true disease based on the information provided by the symptoms he/she exhibits. Four patients were diagnosed with various diseases. Among the four patients in the P set, we have: $P= \{P_{1}, \,P_{2}, \,P_{3}, \, P_{4}\}$. Each of the patients in the set P, $p_{1}, p_{2}, p_{3}, p_{4}$ has five symptoms of each disease; $s_{1}, s_{2}, s_{3}, s_{4}, s_{5}$. Set S which contains five symptoms for a patient: $S=\{$ high temperature, fatigue, vomiting, running nose, burning sensation in eyes $\}$ and the set of diagnose $D=\{$ viral fever, malaria, typhoid, stomach problem, chest problem $\}$. Thus, we can compare the results obtained using GDioFSs with those obtained using DioFSs and DioPFSs. Patient symptoms are measured by physicians as shown in Table 5. There are four types of entry in this table.

Let $e_{ij}=\langle \zeta _{ij}, \xi _{ij}, \pi _{ij}\rangle$ i vary from 1 to 4 and j vary from 1 to 5. Each $e_{ij}$ consists of three sub-entries $\zeta _{ij}$, $\xi _{ij}$ and $\pi _{ij}$. A patient’s membership value is the first sub-entry, whereas $\zeta _{ij}$ represents the patient’s symptoms. The second sub-entry $\xi _{ij}$ represents the absence of the disease, that is, its non-membership. To keep the table concise, the third sub-entry $\pi _{ij}$ denotes the indeterminacy of $p_i$ with respect to $s_j$. As in the previous table, each entry also contains a third sub-entry $\pi _{ij}$ based on Equation 3.3. The patients symptoms are $s_j, j=1, 2, 3, 4, 5$ and their diagnoses are $d_{1}, d_{2}, d_{3}, d_{4}, d_{5}$ in Tables 6 and 7. This table has the following entry where j and k vary from 1 to 5. Let $b_{jk}=\langle \varrho '_{ij}\zeta '_{jk}, \sigma '_{ij}\xi '_{jk}, \pi '_{jk}\rangle$, symptom $s_j$ is present in disease $d_k$ as evidenced by $\zeta '_{jk}$. Each patient must be diagnosed properly. We can calculate the distances using Equations 3.17, 3.18, 3.19 and 3.20. According to Equation 3.18, these distances were calculated using the normalized Hamming distance formula. Table 8 provides a table of distances. The distance between the two FSs is represented by the distances between patient set P and symptom set S and patients/circle S respectively, as shown in Table 5. Based on the S and the diagnosis set D, the relation $S \circ D$ is presented in Tables 6 and 7.

Table 5 GDioFR of ${\mathcal {I}}(P\rightarrow S)$.

Table 6 GDioFR of ${\mathcal {J}}(S\rightarrow D)$.

Table 7 GDioFR of ${\mathcal {J}}(S\rightarrow D)$.

From Table 8, it can be seen that for malaria patients, the normalized Hamming of Equation 3.18 is the lowest. As a result, we say that Patient-1 has a stomach problem. In Patient-2 there had a stomach problem, Patient-3 there had a chest problem and Patient-4 had malaria. The results of the different diagnostic methods are compared in Table 8. $GDioFS_{(1,1)}$ is analogous to the DioFS. GDioFS is similar to DioPFS can be observed in the $GDioFS_{(2,2)}$. In addition, $m=3$ and $p=3$ were also validated to provide accurate results. Similar results were also obtained using Equations 3.17, 3.19 and 3.20.

Table 8 Normalized Hamming distance among GDioFR in Equation 3.18.

The patients are diagnosed with different diseases as shown in Fig. 3.

Figure 3

Patients are diagnosed with different diseases.

Comparing new methods with existing ones

Comparing existing models with the proposed models is the purpose of this section. As a result, it can be demonstrated to be valuable and advantageous. A discussion of generalized fuzzy sets (GFSs) and their applications was presented by Kausar et al.⁴⁰. The existing methods are presented in Tables 9 and 10. A review of the proposed concepts is presented in this study, along with their advantages and benefits. In terms of fuzzy sets, generalized Diophantine fuzzy sets are a generalization of Diophantine fuzzy sets. This method has the advantage of being able to objectively and subjectively analyze data with the help of several experts. The options and alternatives derived from DM values are shown in several illustrative examples. The options and alternatives available can be compared. They introduce distance and composite functions, which is their main advantage. Comparing an optimal choice to alternatives or options can provide a better understanding of a decision maker’s choice. This part covers the following topics: the proposed method’s validity; its aggregation flexibility to handle a variety of inputs and outputs; the impact of score functions; sensitivity analysis; superiority; and, lastly, a comparison of the suggested approach with the current approaches.

Table 9 Max–min–max composition of GFRs ${\mathcal {Q}}$ and ${\mathcal {R}}$, denoted by ${\mathcal {R}}\circ {\mathcal {Q}}$, and defined in Equation  3.13.

Table 10 Normalized Hamming distance among GFR in Equation 3.18.

Analysis of the methods

Each student to college From Table 9, the college were satisfied with the student as a result of this choice. As a result, college-2 with the highest satisfaction levels for $S_{1}$. $S_{2}$ is located in college-3. A college-3 had the highest satisfaction for student $S_{5}$.

Each college student This decision indicates how suitable a particular college is for the student. $S_{5}$ satisfaction according to college-1. Satisfaction with $S_{4}$ with college-3. $S_{2}$ satisfaction with college-5. From Table 10, it can be observed that for the patient for which diseases, the normalized Hamming is the lowest. As a result, we concluded that Patient-1 had a typoid. Patient-2 had a typoid, Patient-3 had a viral problem and Patient-4 had malaria. By comparing the above values with those in Tables 9 and 10, we can determine whether the proposed or existing models are applicable and valid. Accordingly, the optimal choice is determined by these values. Each method produced the best results with the highest value.

Validity and simplicity of the method The recommended approach is correct and suitable for any kind of input data. The suggested model works well for handling uncertainties. With reference parameters added, it covers the scope of IFS, PFS, and GDioFS. These parameters expand the MG and NMG the environment, and by changing their actual significance, we may adapt our model to work well in various scenarios. Depending on the circumstances, we face various criteria and input data in some MADM challenges. The suggested GDioFS is straightforward, easy to comprehend, and adaptable to a variety of options and qualities.

Flexibility of aggregation with different inputs and outputs The provided algorithms are flexible and straightforward to apply to a variety of input and output scenarios. The different score functions of the suggested algorithms do not significantly affect their ranking. Because reference criteria expand the range of grades and can be varied based on the circumstances in MADM approaches, this approach is more adaptable than others.

The influence of score function Several IFS score functions are provided by Nasreen et al.⁴⁰, along with a comparison of them. We present many kinds of score functions. In order to compare the GDioFNs, we also develop equivalent accuracy functions. To deal with the relatively distinct effects by Tables 9 and 10, each score function has a unique ordering strategy and computing. However, its interesting to note that the outcomes of the two methods are approximately comparable for all different kinds of score functions.

Sensitivity analysis The suggested techniques sensitivity analysis is shown in Tables 9 and 10. The identical outcome is obtained by both GDioFS and GFS algorithms. The modification of scoring functions is the cause of the shift in attribute rankings. It follows that only the score functions can affect both methods. We note that while the rankings produced by the two suggested methods differ slightly, the best outcome is the same.

Superiority and comparison of proposed method with other approaches In addition to their ability to deal with parameterizations, IFSs, PFSs, and GDioFS have certain restrictions on MG and NMG. GDioFS fulfills this research gap. GDioFS provides more space than IFSs, PFSs and DioFSs. The MG/NMG limitations have been reduced and the role of reference parameters has been established by GDioFS. The decision maker has complete flexibility to select the grades under the suggested model, which improves upon the current techniques. The suggested model and MADM difficulties have a strong connection. In this model, the pair of reference parameters is essential. They give us parameterizations for the model and contribute in expanding the MG and NMG domain. For demonstrating the superiority and validity of the recommended methods, the existing tools were used. It is more accurate and reliable than existing methods.

Conclusions and future studies

Fuzzy information can be handled by the IFSs, PFSs, DioFSs and GFSs. However, GDioFSs are more general; their outstanding ability is to relax the strict constraints of IFSs, PFSs, DioFS and GFSs by considering reference/control parameters. GDioFS is a new approach towards uncertainty and DM problems which incorporate pair of reference or control parameters against MGs and NMGs. We have developed a new fuzzy set extension called GDioFS, which offers a more adaptable and effective framework for handling uncertainty. The additional properties of reference parameters $\varrho$ and $\sigma$ are provided by GDioFS. In order to evaluate GDioFS against other current FS extensions, we have provided an overview of its geometrical characteristics. GDioFSs have more space than IFSs, PFSs, DioFSs, and GFSs together. We have included several scoring functions and accuracy functions for the GDioFN. Several Hamming, Euclidean, normalized Hamming and normalized Euclidean distance formulas have been developed and used in the real life applications. The GDioFS field has certain limitations. Choosing the numerical values for m and p is a matter of selecting the correct values based on the problem. The GDioFSs constrained m and p to non-negative integers, but the sets can be analyzed for all m and p. For MADM, we suggested algorithms. We have provided a numerical example to illustrate the application of the suggested MADM approaches. Furthermore, we present an algorithm and a numerical example that demonstrate the flexibility of our approach. Our findings show strong agreement on their own for many choices of $\varrho$ and $\sigma$, and the provided comparative analyses clarify the flexibility, reality and accessibility of our approach.

Further details on the following subjects will be covered, including GFS and the use of generalized neutrosophic sets to investigate soft and expert sets. Spherical cubic FS and Pythagorean cubic FS were applied to GFS. A complex GFS and a generalized Fermat FS can be used to solve MADM problems. We applied to logarithmic and square root FSs using our GDioFS application. We expect that the information in this publication will be useful to decision-makers and researchers in their efforts to address a range of real-life problems. Future research will focus on investigating practical applications of ideas derived from interval valued Diophantine fuzzy sets (IVDioFS), Diophantine Hesitant fuzzy sets (DioHFS), and Diophantine fuzzy rough sets (DioFRS). We will also formulate this kind of similarity measures for spherical fuzzy sets⁵⁶, T-spherical fuzzy sets, picture fuzzy sets, neutrosophic sets and Diophantine fuzzy sets.