Abstract
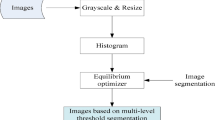
Multilevel thresholding image segmentation will subdivide an image into several meaningful regions or objects, which makes the image more informative and easier to analyze. Optimal multilevel thresholding approaches are extensively used for segmentation because they are easy to implement and offer low computational cost. Multilevel thresholding image segmentation is frequently performed using popular methods such as Otsu’s between-class variance and Kapur’s entropy. Numerous researchers have used evolutionary algorithms to identify the best multilevel thresholds based on the above approaches using histogram. This paper uses the Energy Curve (EC) based thresholding method instead of the histogram. Chaotic Bidirectional Smell Agent Optimization with Adaptive Control Strategy (ChBSAOACS), a powerful evolutionary algorithm, is developed and employed in this paper to create and execute an effective method for multilevel thresholding segmentation of breast thermogram images based on energy curves. The proposed algorithm was tested for viability on standard breast thermogram images. All experimental data are examined quantitatively and qualitatively to verify the suggested method’s efficacy.
Similar content being viewed by others
Introduction
Breast cancer is the most frequently detected type of cancer in females worldwide. Studies indicate that 2 in 5 women are prone to breast cancer throughout their lifetime. Breast cancer1 has been the second leading cause of death in women since 2013.Similarly, multiple studies have shown that women have a greater chance of surviving from breast cancer if the disease is detected and treated early2,3. The Nitric Oxide generated by cancer cells is responsible for the local temperature rise, which has been documented in several investigations4,5. The vasodilation process caused by nitric oxide causes breast tissue to heat up over its typical temperature because it interrupts the regular blood vessel flow in the area. An increase in skin temperature has been linked to deep breast malignant tumors. The relationship between an object’s energy output and its temperature has been described by Stefan Boltzmann’s Law6. As a result, the distribution of body temperature can be determined by observing infrared radiation.
Hence screening methods are essential in the detection and diagnosis of early stages of cancer. Ultrasound, Positron Emission Tomography (PET), Computed Tomography (CT), Magnetic Resonance Imaging (MRI), and Mammography are some of the medical imaging techniques that have been heavily used to detect early signs of breast cancer. Ultrasound7 is another important breast screening method to reduce a woman’s lifetime radiation exposure. However, due to noise levels and the technician’s expertise, this method has some limitations. This technique fails to detect micro-calcifications and deep breast tissue. Despite the stressful and painful process involved in getting a mammogram, it has become the most extensively utilized diagnostic imaging technology for breast cancer screening8,9. Mammography uses X-ray radiation, which is harmful to human tissue. Furthermore, mammography has accuracy issues with small tumors, with a 4%–34% percent false negative ratio. Another diagnostic method commonly used for breast cancer screening is magnetic resonance imaging (MRI). MRI has a number of disadvantages compared to mammography and ultrasound, such as a higher probability of false positives and a longer data gathering time10.
Physiological or vascular alterations in the breasts are seen in thermographic11 pictures. The use of thermal imaging for monitoring purposes is risk-free since it is nonionizing, noninvasive, painless, passive, and real-time. This technique is safe for pregnant and nursing women since it does not employ ionizing radiation. It’s especially helpful for young women since their tissues are thick, making X-ray screening more challenging and potentially dangerous. Authors12,13suggest that CADs might benefit doctors in making diagnoses by highlighting anomalies or diseases in medical imaging.
However, the segmentation method has been used to many problems with great success. Identifying aberrant areas or categorizing the elements in digital pictures requires the use of image segmentation14. The fundamental objective of segmentation is to ease the analysis process by dividing an image into discrete parts according to predetermined criteria such as texture, color, or brightness. After segments have been extracted, visualization, detection, identification, and quantitative analysis are often performed. Thresholding has also been widely employed in the last decade to aid clinicians in the diagnosis process through the medical image processing automation. The complexity of structures with similar characteristics, low contrast, noise conditions, and unclear boundaries typical of medical images15,16,17 make interpretation and analysis of image details difficult even though many works on automatic and semiautomatic segmentation have been done.
Medical digital images need to be segmented for a variety of purposes, including pre- and post-operative evaluation, diagnosis, and therapy planning. Despite thermography screening’s limited clinical utility, enhancing its application and automated detection is crucial to bringing it to widespread clinical acceptability18,19.
An eight-step semi-automatic procedure for segmenting thermal images was proposed by the authors. According to the authors, the inframammary fold and edge detection issues account for the vast majority of the malfunctions. After having a human expert segment the photos by hand, the authors employed a fuzzy rule-based system to identify the segmented regions20. A hybrid version of the snake optimization (SO) algorithm combined with the opposite-based learning (OBL) mechanism. Then, it is used to segment CT liver images.The imaged thresholding technique is used for this purpose and employed SO-OBL to identify the best, or optimal, thresholding values for gray levels in real cases with liver disease images21 .
In22, an algorithm was introduced that uses automated thresholding and boundary detection to partition thermal breast images. Despite encouraging findings, it’s possible that the area of interest being discovered may not encompass all of the upper breasts. Therefore, there is need for further study into the creation of an automated approach that may aid in the diagnosis of breast cancer using thermograms and has a cheap computing cost and high degree of resilience. Thus, reliable thresholding of breast thermograms could be used to quickly assess clinical diagnoses. The swarm algorithm is used to analyze breast thermograms in this paper.
Utilization of swarm intelligence algorithms in the selection of multi-level thresholding segmentation of medical images is not a new concept. Several authors implemented various optimization algorithms to find the optimal threshold values for brain MRI image segmentation23,24,25,26 based on different objective functions such as Otsu’s between class variance and Kapur’s entropy etc. A multi-level image segmentation technique using HRO-based Renyi’s entropy algorithm for microscopic images of cement is proposed. Taking Renyi’s entropy as the objective function, HRO is used to search the optimal threshold values and compared with other optimization algorithms27 .
The authors used a novel swarm technique called Dragonfly Algorithm (DA)28 based on the Otsu method and Kapur entropy as objective functions on the DA in the designed methodology. The method presented uses the energy curve29,30,31 instead of the histogram to solve this issue. The energy function (EF) first described in32,33 is used to derive the energy curve. The EF determines the power of each pixel’s intensity level by considering its position. Energy curves offer advantages in terms of noise reduction, feature detection, spatial information representation, and integration with other image processing techniques. These advantages make energy curves particularly useful in applications requiring detailed and smooth analysis of intensity variations, such as medical imaging and advanced image processing tasks. However, histograms remain valuable for their simplicity and effectiveness in summarizing the global intensity distribution and for tasks like thresholding.
“The No-Free Lunch Theorem” states that there is no single modern optimization strategy that can effectively tackle all real-world optimization issues. Furthermore, since every real-world issue has a unique characteristic that can be compared to the actions of one specific optimization method. For example, in image processing edge and lane detection problems can be used to describe ant systems’ behavior toward pheromone deposits. This analogy can be applied to the route planning problem in robotics, which can likewise be represented as an agent following the scent of an unknown substance. An agent’s olfactory organ (nose) is filled with smell molecules that move through the air and into the specialized cells (receptors) that deliver the message to the brain for proper interpretation. This paper gives a detailed implementation and validation of a new metaheuristic algorithm termed the chaotic smell agent optimization with adaptive control strategy (ChBSAOACS) in light of these interactions between an agent and its surrounding environment.
From the literature, it is observed that SAO showed superior performance over the other algorithms on CEC benchmark functions and many authors have utilized Otsu and Kapur’s objective approaches for multilevel image thresholding using various optimization algorithms based on energy curve. An improved version of SAO34 algorithm has been developed and implemented for the optimal multilevel thresholding of breast thermographic images based on energy curve.
The important contributions of this paper are:
-
Chaotic Bidirectional Smell Agent Optimization with Adaptive Control Strategy is developed and implemented to multi-level thresholding for the first time.
-
To find the best thresholds for different breast thermographic images, ChBSAOACS algorithm maximizes the between class-variance and entropy described by Otsu and Kapur functions.
-
Qualitative and quantitative examination for eight different breast thermographic images using proposed approach.
-
A detailed validation of ChBSAOACS with other optimization algorithms proved the efficacy of the proposed approach.
Methodology
This section provides an overview of the optimization method for olfactory agents and shows how it may be implemented in multilevel thresholding scenario. In place of the image histogram, the chosen swarm and evolutionary algorithm learn the search space defined by the Otsu and Kapur methods, both of which are based on the energy curve.
Energy curve
Histogram-based multilevel thresholding is a widely employed method due to its convenience and effectiveness. An alternative to histogram-based segmentation is energy curve-based image segmentation35. The energy curve method, in contrast to the histogram method, maintains peaks and valleys in its plotted curve. In order to separate the objects in an image, segmentation algorithms must first find threshold values in the energy curve’s midpoint. Each valley is located between two nearby modes, and each mode stands in for a different feature of the image.
Consider \(E_g \)is an EC of the image I. where \(I=\left( g_{ij},1\le i\le M,\;\;1\le i\le N\right\} \). \(g_{ij} \) is the imaging value of I at pixel location \(\left( i,j\right) \) defined under the interval \(\left( 0,\;L-1\right] \;where\;L=256 \). The energy of I is computed at grey level \(g\left( 0\le g\le L-1\right) b_{ij} \) are the elements of a two-dimensional matrix \(B_g.B_g=\left( b_{ij},1\le i\le M,\;\;1\le i\le N,\;b_{ij}=1,\;if\;g_{ij}>g;else\;b_{ij}=-1\;\right\} \). To ensure \(E_g>0 \) constant C is added to Eq. 1.Special correlation between adjacent pixels of an image I is \(N_{ij}^{d}=\left( \left( i+u,\;j+v\right) ,\left( u,v\right) \in N^{d}\right\} . \) In this paper d is considered a second-order system i.e., \(\left( u,v\right) \in \left( \left( \pm \;1,0\right) ,\left( 0,\pm 1\right) ,\left( 1,\pm 1\right) ,\left( -1,\pm 1\right) \right\} . \)
Otsu’s between class variance
Otsu’s method36 takes a bi-modal histogram and separates foreground and background pixels by computing the best threshold that minimizes the two classes’ combined spread (intra-class variance). For the multi-level thresholding expansion of the Otsu method, the term “Multi Otsu” was coined. Otsu presented a nonparametric thresholding technique that uses the maximum variance of the distinct classes as a criterion for segmenting the image.
nt thresholds are required to divide the original image into \(nt+1 \) classes for the multi-level technique. As a result, \(th\;=\;\left( {th}_1,\;{th}_2,\dots .{th}_{nt}\right\} \)encodes the collection of thresholds used for image segmentation. In this way, the grey value \(E_i \) of each pixel generates a probability \({PE}_i=\frac{E_i}{NP} \) where \({\sum _{i=1}^{NP}{{PE}_i}}=\;1\; \)and NP is the total number of pixels in the image.In order to calculate the variance \(\sigma ^{2} \) and the means \(\mu _k \) for each of the produced classes, the following formulae are used:
By optimizing the following equation, the best thresholds may be selected:
Kapur’s entropy
Kapur37 presented another nonparametric method for determining the best threshold values. It is based on the image histogram’s probability distribution and entropy. The approach seeks to determine the ideal ’th’ in terms of overall entropy. Entropy is a measure of an image’s separability and compactness between classes. In this view, entropy is maximized when the optimal ‘th’ values correctly separate the classes using Eq. 6.
Smell agent optimization (SAO)
It is through the sense of smell that most people get their first impressions of the world. The majority of living creatures can detect the presence of toxic chemicals in their surroundings utilizing their sense of smell. It’s natural to think about creating SAO with the help of human olfaction. However, as it turned out, olfaction is used by the majority of biological agents for the same main function in the process of hunting, mating, and avoiding danger. This caused a widespread smell agent to be developed as a result of an algorithm for maximizing efficiency38.
Sense of smell (olfaction)
Olfactory nerves, which are located in the nose, are responsible for allowing us to detect the scent of a material. Chemicals with molecular weights smaller than 300 Dalton are present in the smell, which diffuses from a source unevenly. Most agents need to be able to detect and distinguish these scent molecules. Among olfactory-capable agents, the process of olfaction is nearly identical. The ability to follow the scent plume is a crucial part of identifying remote odors. Several creatures, including humans, rely on this skill for survival. A person’s ability to identify potentially dangerous items such as iron tablets, household cleaners, and button batteries is based on their ability to detect the odor.
Steps of the SAO algorithm
The SAO has structured around three unique modes. Using the processes outlined in the previous paragraph, these modes are derived. Detecting odor molecules and determining whether or not to look for the source is the initial phase of operation for the agent. In \({2\text{nd}}\) mode, the agent uses the \({1\text{st}}\) mode’s choice to follow the smell molecules in search of the smell’s source. Using the third option prevents the agent from becoming confined within a small area if its trail is lost.
Sniffing mode
Since scent molecules tend to scatter in the direction of the agent, we begin the method by assigning them a randomly generated initial position. Using Eq. 7, we can find the total number of thresholds ‘d’ in the search space given the total number of smell molecules, ‘N’.
To find its optimal position in the search space, the agent uses Eq. 7 to build a position vector. \(x_{max,d} \) and \(x_{min,d} \) are maximum and minimum limits for the decision variable and rand () is a random number between 0 and 1 in case of SAO. A cubic map has been used to initialize the position vector based on Eq. 18 in the case of ChBSAOACS. It is determined that the molecules of odor will diffuse from the source/origin at an initial velocity determined by Eq. 8.
Each molecule of a smell is a potential solution in the search space that may be used to solve a problem. These potential solutions (smell molecules) may be located using the location vector in Eq. 7 and the velocities of the molecules in Eq. 8. Since the smell molecules disperse in a Brownian fashion, their velocities may be updated using Eq. 12.
Since it is assumed that the agent optimizes in increments of one step at a time, t is set to 1. For instance, until the last iteration is achieved, the algorithms keep increasing the iteration by 1 until they reach the end of the process. Therefore, the new position of the odor molecules is given by Eq. 10.
Each smell molecule evaporates at a different rate, shifting its location in the search space at a rate proportional to its diffusion velocity. Since the molecules of smell travel in a path-dependent way to the agent’s position, Eq. 10.
In Eq. 12,\(\;v \) denotes the component of the velocity that is updated throughout time. Temperature and mass of smell particles, T and m, respectively; affect molecules’ momentum in the sense of smell. The normalizing constant for the sense of smell is denoted by the sign k. The technique is robust regardless of the starting parameters used for fragrance molecules, including temperature T and mass m. The ideas of mass and temperature (m and T) are derived from the ideal theory of gas. The values of m and T have been empirically determined to be 0.175 and 0.825, respectively, to facilitate efficient use of time. Eq. 10 tests the viability of the rearranged smell molecule’s potential binding areas. This means that we can now find the \(x_{best}^{d} \) agent (best fitness position) and exit sniffing mode.
Trailing mode
When an agent is tasked with locating the source of an unpleasant odor, this mode mimics the actions of the agent. If the agent is searching for a smell source and it detects a new place with a higher concentration of scent molecules than its present position, the agent will move to that location using Eq. 13.
\(r_2 \) and \(r_3 \) are random numbers in the (0,1) range. Relatively speaking, both \(r_2 \) and \(r_3 \) penalizes the impact of olf on \(x_{gbest}^{d}\left( t\right) \) and \(x_{worst}^{d}\left( t\right) \).
Sniffing mode provides a way for the agent to decide its current position \(x_{gbest}^{d}\left( t\right) \) agent and the point with the worst fitness \(x_{worst}^{d}\left( t\right) \). This allows the agent to track the scent’s route more effectively. The relationship between exploration and exploitation in the algorithm is seen in Eq. 13. Olfaction ability is largely influenced by the size of one’s olfactory lobes, as well as one’s psychological and physical state, therefore the value of olf should be carefully chosen. Local searches benefit from low values of olf, while global searches benefit from high values of olf, since the former shows more strength in SAO’s ability to detect scents on a global search.
Random mode
Due to the discrete nature of smell molecules, their concentrations and intensities can change over time if they are spread out over a vast area relative to the search space. Because of this, trailing becomes more difficult and the scent is lost, making it difficult for an agent to follow. The agent may be unable to continue trailing at this moment, resulting in a local minimum. When this occurs, the agent enters a random mode, as follows:
Random number \(r_4 \) penalizes the value of SL by stochastically increasing the steplength of SL. If the agent loses its trail or the trailing mode is unable to get the greatest fitness or identify the smell source, the agent will take a random step using Eq. 14.
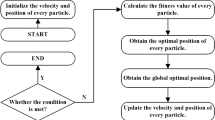
This means that the agent will constantly want to stay where the scent molecules are most concentrated throughout the route. The agent uses its knowledge of its present position, \(x_{gbest}^{d}\left( t\right) \) agent, and its worst positions, \(x_{worst}^{d}\left( t\right) \) agent, throughout the trailing process described in Eq. 14. Although the agent can only look in the feasible region because of the optimization problem. In the flowchart shown in Figure 1, ChBSAOACS’s comprehensive implementation is explained.
The proposed ChBSAOACS
In this section, an improved version of the SAO algorithm is proposed, and the one-dimensional cubic map is introduced in SAO initialization and an adaptive (non-linear) parameter control strategy is also performed.
Chaotic Map
Chaos occurs frequently in nonlinear systems. The formula for the fundamental cubic map39 is as follows:
When the chaos factors, denoted by \(\alpha \) and \(\beta \), \(\beta \) in the range [2.3,3], the cubic map is chaotic. The interval of the cubic map is (− 2, 2) for \(\alpha \) = 1, while the interval of the series is (− 1, 1) for \(\alpha \) = 4. The cubic map is also possible as:
Where the \(\rho \) denotes a tunable variable. In Eq. 18, the cubic map sequence is in (0, 1), and the ergodicity of the produced chaotic variable \(Z_n \)improves when \(\rho \) = 2.595.
During the search phase, the chaotic map can arbitrarily disperse the population of olfactory agents throughout the interval [0, 1]. In the proposed technique, the agents’ positions are first determined using a cubic map, with z (0) set to 0.315 to guarantee that the initialized interval lies within the range (0, 1).
Concept of bidirectional search
The bidirectional adjustment can enhance the algorithms’ searching performance by enabling the parameters to conduct local searches in both forward and backward directions given in Eq. 17.
Where x, f(x) and S represents the current position of butterfly, objective fitness function value and step length respectively.
Adaptive control strategy
From Eq. 13, we may deduce that the olf contributes significantly to ChBSAOACS’s optimal solution finding performance. The value of olf should be carefully chosen since olfactory capability is mostly determined by olfactory lobe size, agent psychology and health40. So, whereas a low value of olf suggests weak olfaction, which favors local searching, a high value of olf shows greater olfaction, which prefers global searching of SAO. However, in standard SAO, olf = 0.75, and setting a to a constant does not allow for a good compromise between global and local search. As a result, we suggest the following method of adaptive parameter control:
Parameter olf has the initial value and final value, \(\mu \) tuning parameter, and maxit is maximum number of iterations. The parameters used in this study were \(\mu \;=\;2 \) maxit = 200/800, \({olf}_{min}=0.1 \) and\({olf}_{max}=0.9 \). It’s important to remember that as the parameter gets bigger, the improvement technique starts to backfire.
Performance evaluation of ChBSAOACS
To demonstrate the effectiveness of the proposed ChBSAOACS in locating the global solution, it is applied to a large number of complicated test functions; sample test results for unimodal and multimodal functions from CEC14 and CEC17 are shown in Table 1. High Conditioned Elliptic, Discuss, Rosen Brocks, Weierstrass, Griewanks, Rastrigins’, Zakharov, Happy Cat, Ackley’s, power Functions, etc. pass the CEC14 tests, as do the planned ChBSAOACS. The performance of the SAO, DA, KH, GA, and PSO algorithms are compared with the test results. Table 1 displays the findings, which demonstrate that the ChBSAOACS performed better than the other algorithms in determining the global best fitness values for the designated test functions. Figure 2 depicts the plots of convergence for a few chosen functions. As can be seen in Figure 2, ChBSAOACS has outperformed the other algorithms when it comes to finding the optimum global fitness values.
Experimental evaluation and discussion
In order to compare the performance of several optimization techniques for multi-level image thresholding, a standard collection of breast thermogram images has been employed. The initial step in solving any optimization issue is to set the parameters of the method to be used. Prior to execution the SAO and ChBSAOACS algorithms, values are assigned based on a sensitivity study of the parameters (parameter tuning), as indicated in Table 2. Energy curve-based Otsu and Kapur techniques are used to evaluate the performance of ChBSAOACS using a collection of eight widely used breast thermogram images from literature. Figure 3 gives information about the test images under consideration and their corresponding histogram and energy curve. The outcomes are compared and analyzed with other methods based on Dragonfly Algorithm (DA), Kill Herd Algorithm (KHA), Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) algorithms24,25,41 from the literature.
Results of ChBSAOACS-based algorithms for multilevel image thresholding are evaluated using post-execution evaluations of picture quality such as Root Mean Square Error (RMSE), Peak Signal to Noise Ratio (PSNR), Structural Similarity Index (SSIM)42, Feature Similarity Index (FSIM)and43,44. Wilcoxon’s rank-sum test is a prominent non-parametric statistical analysis method for evaluating the performance of optimization algorithms. Self-written MATLAB algorithms running on an Intel Core i5-10310U2.21 GHz Dual Processor with 8 GB RAM are used in all simulations.
Test 10, test 11, test 2, test 3, test 30, test 31, test 4, and test 5 breast thermogram images45 from EC-Otsu-ChBSAOACS and EC-Kapur-ChBSAOACS are displayed in Figs. 4, 5, 6, 7, 8, 9, 10 and 11. Input image, segmented output images at ideal threshold levels, and corresponding energy curve information for Otsu-ChBSAOACS and Kapur-ChBSAOACS are all provided in each Figure. Images segmented using either method may be easily distinguished from one another. The reason for this is that Otsu’s between-class variance and Kapur’s entropy serve as the basis for two distinct methods. Therefore, it is necessary to rely on picture quality measures to evaluate the results. The optimal threshold values achieved using EC-Otsu-ChBSAOACS are compared in Table 3 with those obtained using other methods, including EC-Otsu-based SAO, DA, KHA, GA, and PSO algorithms41.
Table 4 presents the comparison of optimal threshold values obtained byEC-Kapur-ChBSAOACS with various existing approaches such as EC-Kapur-based DA, KHA, GA and PSO algorithms24,25,41. To our knowledge, no algorithms have produced the same set of solutions for the matching image as shown in Tables 3 and 4 for a given value of ’th’. Therefore, it is clear that different optimization algorithms use different evolutionary processes to arrive at the optimal solution. The PSNR values for all images at each threshold setting are compared across several Otsu and Kapur-based methods in Table 5. When compared to other current methods, the PSNR values produced using the EC-Otsu-ChBSAOACS and EC-Kapur-ChBSAOACS procedures are consistently superior (see Table 6). The quality of the segmented image increases as PSNR rises. The EC-Otsu-PSO method yields the lowest average PSNR value, at 15.91, while the EC-Kapur-ChBSAOACS method yields the highest, at 20.03.
The suggested Otsu-ChBSAOACS and Kapur-ChBSAOACS methods, as well as other methods, are compared to FSIM values produced by other methods in Table 6. According to common knowledge, an FSIM value near to ‘1’ implies that the input images was segmented effectively with little loss of features in the output image. Average FSIM values range from 0.7188 when using EC-Otsu-PSO to 0.8135 when using EC-Otsu-ChBSAOACS, a significant increase. Table 7 compares the SSIM values found using several methods, including the proposed Otsu-ChBSAOACS and Kapur-ChBSAOACS methods. The SSIM result close to ’1’ implies that the input image was segmented efficiently and structurally comparable to the input image with little loss of information content. Average FSIM values range from 0.6908 for EC-Otsu-PSO to 0.7536 for EC-Otsu-ChBSAOACS, which indicates a significant increase. Based on the quantitative analysis of results for the investigated approaches it is clear that the overall performance of the EC-based thresholding approach using Kapur’s entropy is better than all other approaches for the tested images. However, it appears that image thresholding ability was better with the EC-Otsu approach than the EC-Kapur approach based on qualitative results.
Methods of statistical analysis are compared and contrasted using Wilcoxon’s rank-sum test, which takes into account both alternative and null hypotheses. The lack of a substantial difference is represented by the null hypothesis, whereas its presence is shown by the alternative. The alternative hypothesis is accepted if and only if the null hypothesis is rejected at a significant level (P>0.05). Each method has been executed for 30 times to perform the test. Wilcoxon’s rank-sum test results are shown in Table 8 for each technique. In addition, the computing complexity of each approach is evaluated to maintain a level playing field. ChBSAOACS and SAO has an O(t(N D)) computational complexity, where t is the number of iterations, D is the number of variables, and N is the population size of the solutions. There is no difference in computational complexity between GA, PSO, and DA. However, KHA has a worst-case computational complexity of O(t(Nlog(N))) and an average complexity of O(t(N2)). This means that the computational complexity of KHA is worse than those of GA, PSO, DA, and variants of SAO due to the need to sort the solutions in each iteration.
With each repetition, the ChBSAOACS algorithm’s adaptive mechanism enhances the convergence speed. It’s also crucial for maintaining a healthy balance between exploration and exploitation so that selection issues don’t generate too many local solutions and so that an accurate estimate of the best solution can be found. Sniffing mode (Gases Brownian Motion), trailing mode and random mode is used to calculate the new position of a molecule in ChBSAOACS. The fitness values are taken into account when the ChBSAOACS algorithm is updated (the fitness value is related to the molecule mass and temperature). Because of the high velocities of molecules, the ChBSAOACS algorithm can scan the search space more quickly than other algorithms. The local search and global search capabilities of the ChBSAOACS algorithm may be better exploited and explored using this approach. As a result, ChBSAOACS outperformed the other algorithms in this research by a wide margin. The average execution time for investigated ChBSAOACS, SAO, DA, KH, GA and PSO optimization algorithms at 5 threshold levels is 31s, 27s, 28s, 26s, 47s and 29s respectively.
However, the ChBSAOACS algorithm presents a novel and potentially powerful approach to optimization, it has certain limitations related to complexity, computational cost, parameter sensitivity, scalability, and dependence on initial conditions. Addressing these limitations through future research directions such as optimizing computational efficiency, developing robust parameter tuning methods, exploring hybrid approaches, and enhancing scalability and robustness can further improve the algorithm’s performance and broaden its applicability.
Conclusions
Breast thermogram image segmentation based on multilevel thresholding was proposed in this article. More image information was retained while using EC-based multi-level thresholding with Otsu and Kapur objective functions. Experiments have shown that the suggested approach is simple and superior to existing segmentation methods in terms of segmenting breast thermogram images. There are a variety of quantitative indicators used to estimate the suggested method’s performance. The likelihood between the original image and the segmented image is reflected in these quality characteristics. Quantitative evidence demonstrates that EC-based thresholding using Kapur’s entropy yields accurate picture segments. Compared to other approaches, the proposed algorithm produces output images with well-delimited parts that may be evaluated qualitatively. The preliminary findings are encouraging and warrant further investigation on image classification, remote sensing, image denoising and enhancement, and other computational difficulties are only some of the many image processing problems that benefit from the EC-Kapur approach. Due to its speed and robustness, the suggested technique can also be used for other types of applications like control system design, wireless sensor networks, feature selection, data mining, clustering, etc. The hybridization of ChBSAOACS with other metaheuristic algorithms can also improve the algorithm’s performance. The method may be used with various local and global search strategies, such as Pareto distribution, Lévy flight random walk, mutation operators, and more.
Data availibility
The images used in the study are publicly available in DMR—Database For Mastology Research https://visual.ic.uff.br/dmi.
References
How Common Is Breast Cancer? http://www.cancer.org/cancer/breastcancer/detailedguide/breast-cancer-key-statistics (2022).
Gautherie, M., Thermopathology, Breast, Vivo & Flow, B. Thermal Chara (1980).
Lee, H. & Chen, Y. P. P. Image based computer aided diagnosis system for cancer detection. Expert Syst. Appl. 42, 5356–5365 (2015).
Anbar, M. Hyperthermia of the cancerous breast: Analysis of mechanism. Cancer Lett. 84, 90354–90363 (1994).
Anbar, M. Detection of cancerous breasts by dynamic area telethermometry. IEEE Eng. Med. Biol. Mag. 20, 80–91 (2001).
Kermani, S., Samadzadehaghdam, N. & Etehadtavakol, M. Automatic color segmentation of breast infrared images using a Gaussian mixture model. Optik (Stuttg) 126, 3288–3294 (2015).
Kuhl, C. K. Mammography, breast ultrasound, and magnetic resonance imaging for surveillance of women at high familial risk for breast cancer. J. Clin. Oncol. 23, 8469–8476 (2005).
Kolb, T. M., Lichy, J. & Newhouse, J. H. Comparison of the performance of screening mammography, physical examination, and breast US and evaluation of factors that influence them: an analysis of 27,825 patient evaluations. Radiology 225, 165–175 (2002).
Huynh, A. M. J. S. D. P. T. The false-negative mammogram. Radiographics 18, 1137–1154 (1998).
Port, E. R., Park, A., Borgen, P. I., Morris, E. & Montgomery, L. L. Results of MRI screening for breast cancer in high-risk patients with LCIS and atypical hyperplasia. Ann Surg Oncol 14, 1051–1057 (2007).
Etehadtavakol, M. N. E. Y. K. BREAST thermography as a potential non-contact method in the early detection of cancer: a review. J Mech Med Biol 13, 1330001–1330001 (2013).
Arakeri, M. P. & Reddy, G. R. Computer-aided diagnosis system for tissue characterization of brain tumor on magnetic resonance images. Signal Image Video Process 9, 409–425 (2015).
Moghbel, M. & Mashohor, S. A review of computer assisted detection/diagnosis (CAD) in breast thermography for breast cancer detection. Artif Intell Rev 39, 305–313 (2013).
Elaziz, M. A., Oliva, D., Ewees, A. A. & Xiong, S. Multi-level thresholding-based grey scale image segmentation using multi-objective multi-verse optimizer. Expert Syst. Appl. 125, 112–129 (2019).
Sathya, P. D. & Kayalvizhi, R. Optimal segmentation of brain MRI based on adaptive bacterial foraging algorithm. Neurocomputing 74, 2299–2313 (2011).
Joliot, M. & Mazoyer, B. M. Three-dimensional segmentation and interpolation of magnetic resonance brain images. IEEE Trans. Med. Imaging 12, 269–277 (1993).
Johnston, B., Atkins, M. S., Mackiewich, B. & Anderson, M. Segmentation of multiple sclerosis lesions in intensity corrected multispectral MRI. IEEE Trans. Med. Imaging 15, 154–169 (1996).
Ng, E. Y. & Etehadtavakol, M. (eds) Application of Infrared to Biomedical Sciences (Springer, Singapore, 2017).
Shehab, A. Secure and robust fragile watermarking scheme for medical images. IEEE Access 6, 10269–10278 (2018).
Scales, N., Kerry, C. & Prize, M. Automated image segmentation for breast analysis using infrared images. In The 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society 1737–1740 (2004).
Houssein, E. H., Abdalkarim, N., Hussain, K. & Mohamed, E. Accurate multilevel thresholding image segmentation via oppositional Snake Optimization algorithm: Real cases with liver disease. Comput. Biol. Med. 169, 107922. https://doi.org/10.1016/j.compbiomed.2024.107922 (2024).
Motta, L. S., Conci, A., Lima, R. C. F. & Diniz, E. M. Automatic Segmentation on Thermograms in Order to Aid Diagnosis and 2D Modeling (2010).
Manikandan, S., Ramar, K., Iruthayarajan, M. W. & Srinivasagan, K. G. Multilevel thresholding for segmentation of medical brain images using real coded genetic algorithm. Measurement (Lond) 47, 558–568 (2014).
Kotte, S., Pullakura, R. K. & Injeti, S. K. Optimal multilevel thresholding selection for brain MRI image segmentation based on adaptive wind driven optimization. Measurement (Lond) 130, 340–361 (2018).
Sathya, P. D. & Kayalvizhi, R. Amended bacterial foraging algorithm for multilevel thresholding of magnetic resonance brain images. Measurement (Lond) 44, 1828–1848 (2011).
Maitra, M. & Chatterjee, A. A novel technique for multilevel optimal magnetic resonance brain image thresholding using bacterial foraging. Measurement (Lond) 41, 1124–1134 (2008).
Liu, W. et al. Renyi’s entropy based multilevel thresholding using a novel meta-heuristics algorithm. Appl. Sci. 10, 3225. https://doi.org/10.3390/app10093225 (2020).
Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 27, 1053–1073 (2016).
Díaz-Cortés, M. A. A multi-level thresholding method for breast thermograms analysis using Dragonfly algorithm. Infrared Phys. Technol. 93, 346–361 (2018).
Oliva, D., Hinojosa, S., Elaziz, M. A. & Ortega-Sánchez, N. Context based image segmentation using antlion optimization and sine cosine algorithm. Multimed. Tools Appl. 77, 25761–25797 (2018).
Kandhway, P. & Bhandari, A. K. Spatial context-based optimal multilevel energy curve thresholding for image segmentation using soft computing techniques. Neural Comput. Appl. 32, 8901–8937 (2020).
Ghosh, S., Bruzzone, L., Patra, S., Bovolo, F. & Ghosh, A. A context-sensitive technique for unsupervised change detection based on hopfield-type neural networks. IEEE Trans. Geosci. Remote Sens. 45, 778–788 (2007).
Patra, S., Gautam, R. & Singla, A. A novel context sensitive multilevel thresholding for image segmentation. Appl. Soft Comput. J. 23, 122–127 (2014).
Li, J., Tang, W., Wang, J. & Zhang, X. Multilevel thresholding selection based on variational mode decomposition for image segmentation. Signal Process. 147, 80–91 (2018).
Kandhway, P. & Bhandari, A. K. Spatial context-based optimal multilevel energy curve thresholding for image segmentation using soft computing techniques. Neural Comput. Appl. 32, 8901–8937 (2020).
Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 9, 62–66 (1979).
Kapur, J. N., Sahoo, P. K. & Wong, A. K. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 29, 273–285 (1985).
Salawudeen, A. T., Mu’azu, M. B., Sha’aban, Y. A. & Adedokun, A. E. A novel Smell Agent Optimization (SAO): An extensive CEC study and engineering application. Knowl. Based Syst. 232, 107486 (2021).
Palacios, A. Cycling chaos in one-dimensional coupled iterated maps. Int. J. Bifurc. Chaos 12, 1859–1868 (2002).
Rottstaedt, F. Size matters—The olfactory bulb as a marker for depression. J. Affect. Disord. 229, 193–198 (2018).
Díaz-Cortés, M. A. A multi-level thresholding method for breast thermograms analysis using Dragonfly algorithm. Infrared Phys. Technol. 93, 346–361 (2018).
Ren, L. Gaussian kernel probability-driven slime mould algorithm with new movement mechanism for multi-level image segmentation. Measurement (Lond) 192, 110884 (2022).
Aziz, M. A., Ewees, A. A. & Hassanien, A. E. Whale Optimization Algorithm and Moth-Flame Optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 83, 242–256 (2017).
Sowjanya, K. & Injeti, S. K. Investigation of butterfly optimization and gases Brownian motion optimization algorithms for optimal multilevel image thresholding. Expert Syst. Appl. 182, 115286 (2021).
DMR—Database For Mastology Research. https://visual.ic.uff.br/dmi .
Acknowledgements
The KSU author acknowledges the funding from Researchers Supporting Project number (RSPD2024R674), King Saud University, Riyadh, Saudi Arabia.
Author information
Authors and Affiliations
Contributions
All the authors have contributed equally to this article.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kotte, S., Injeti, S.K., Thunuguntla, V.K. et al. Energy curve based enhanced smell agent optimizer for optimal multilevel threshold selection of thermographic breast image segmentation. Sci Rep 14, 21833 (2024). https://doi.org/10.1038/s41598-024-71448-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-71448-6