A novel intelligent fault diagnosis method for gearbox based on multi-dimensional attention denoising convolution

Abstract

In the field of intelligent fault diagnosis, particularly concerning rotating machinery, convolutional neural networks (CNNs) face significant challenges when applied to real industrial vibration data. These data are not only contaminated by various types of noise but also exhibit fault features that vary across different scales. Consequently, the effective suppression of extraneous noise and accurate extraction of multi-scale fault features are crucial issues. To address these challenges, this study proposes a novel deep neural network framework, termed the Multidimensional Fusion Residual Attention Network (MFRANet), for gearbox fault diagnosis. The MFRANet employs a multi-scale deep separable convolution module to thoroughly investigate the fundamental characteristics of the original vibration signals in both the time and time-frequency domains. To enhance the detailed analysis of diagnostic data and mitigate the risks of overfitting and noise interference, an efficient residual channel attention module is incorporated to weight and denoise the feature maps. Additionally, an external attention module is introduced to create implicit connections between the denoised multi-scale feature maps and to highlight potential correlations within the sample data, thereby improving the accuracy of fault diagnosis. Experimental evaluations on a gearbox fault dataset demonstrate that the proposed method surpasses several benchmark and state-of-the-art techniques in terms of diagnostic performance, exhibiting robust noise resilience across various noise levels. This indicates enhanced reliability and accuracy in gearbox fault diagnosis, providing an innovative and efficient solution for fault diagnosis in rotating machinery. The study underscores the contributions of artificial intelligence through the innovative structure of the method and the integration of advanced deep learning modules, while its engineering application is evidenced by addressing practical challenges in rotating machinery fault diagnosis. This work meets the urgent need for reliable diagnostic methods in industrial environments.

Introduction

The heavy equipment manufacturing industry is not only a critical pillar of the industrial sector but also a strategic industry vital to national security and development. Within this sector, the operational safety of mechanical equipment is particularly important, as it directly impacts production efficiency and safety. Approximately 70% of failures in rotating machinery are related to rotors, highlighting the complexity and challenges in this field^1,2. The gearbox, as a core transmission component, is especially crucial for enhancing the efficiency and stability of the entire mechanical system in the context of industrial automation³. However, faults in the gearbox can lead to significant property damage and even casualties. Therefore, accurately diagnosing the faults in gearboxes is essential for ensuring the safe operation of equipment and preventing major safety accidents^4,5.

Traditional fault diagnosis methods, such as envelope analysis⁶, sparse decomposition⁷, variational mode decomposition (VMD)⁸, empirical mode decomposition (EMD)⁹, and wavelet decomposition (WD)¹⁰, can extract fault features. However, due to the complexity and diversity of mechanical equipment, these methods heavily rely on expert knowledge and have stringent requirements for parameter selection. To address these limitations, some recent advancements have made significant breakthroughs. For instance, the frequency matching demodulation transform (FMDT) technique enhances the diagnostic accuracy of weak bearing fault features under variable speed conditions by adaptively setting demodulation parameters¹¹; the adaptive synchronous demodulation transform (ASDT) method improves frequency resolution of nonlinear signals without requiring prior knowledge¹²; gear meshing modulation analysis identifies local gearbox faults and enhances fault detection intuitiveness through the mesh modulation frequency index (MFM)¹³; the fault diagnosis method based on multi-source information fusion for PMSM effectively reduces computational complexity¹⁴; and the radial air gap magnetic flux density method maintains robustness under complex working conditions, showing good adaptability to varying loads and dynamic speeds¹⁵.

In this context, data-driven intelligent fault diagnosis methods have emerged, utilizing algorithms such as support vector machines (SVM)¹⁶ or adaptive nearest neighbor reconstruction¹⁷ to differentiate various machine health conditions through feature extraction and fault classification. Deep learning methods, in particular, have become a research hotspot due to their powerful feature extraction and learning capabilities.

In recent years, significant progress has been made in applying deep learning to fault diagnosis in rotating machinery. For instance, Chen et al.¹⁸ proposed a method combining convolutional neural networks (CNN) and discrete wavelet transforms (DWT) for identifying faults in wind turbine gearboxes. Similarly, Liu et al.¹⁹, Yang et al.²⁰, and Li et al.²¹ have utilized multi-scale CNNs, wavelet neural network algorithms, and continuous wavelet convolutional networks, respectively, to improve the accuracy of fault diagnosis in bearings and gearboxes. Yu et al.²² introduced a one-dimensional residual convolutional autoencoder (1-DRCAE) that demonstrated superiority in signal denoising and feature extraction, while Azamfar et al.²³ achieved more efficient fault diagnosis through motor current feature analysis and a two-dimensional CNN architecture. Shi et al.²⁴ proposed a novel deep neural network fault diagnosis method based on a bidirectional convolutional long short-term memory (BiConvLSTM) network.

However, noise pollution remains a significant challenge for deep learning models in fault diagnosis. To address this, researchers have proposed various improved methods, including Feng et al.’s²⁵ rotating encoder signal analysis approach, Yao et al.’s²⁶ hybrid fault diagnosis method, and CNN models specifically designed for denoising developed by Zhang et al.²⁷. Wang et al.²⁸ enhanced the identification of critical features by integrating channel and spatial attention mechanisms. Additionally, Zhang et al.²⁹ developed a multi-scale sparse frequency-frequency distribution model using short-time Fourier transform, sparse decomposition, and orthogonal matching pursuit techniques to suppress Gaussian noise and accurately detect early-stage gear faults.

Furthermore, researchers have leveraged attention mechanisms and transfer learning methods to further improve diagnostic performance in noisy environments. For instance, Zhang et al.³⁰ proposed a multimodal cross-domain fusion network that combines vibration signals and thermal images to achieve more comprehensive and robust fault diagnosis. Han et al.³¹ introduced an Attention Mechanism-driven Domain Adversarial Network (AMDAN), which combines convolutional neural networks with attention mechanisms to diagnose gear faults under varying speed and load conditions, demonstrating high classification accuracy and generalization capabilities. Overall, while current research has made some progress in enhancing CNNs’ noise robustness, there remains considerable room for improvement.

As the complexity of industrial equipment increases, fault diagnosis in rotating machinery, especially gearboxes, under noisy conditions becomes increasingly important. However, existing deep learning models often exhibit insufficient accuracy and robustness when processing high-noise vibration signals, leading to unreliable fault diagnosis results. Therefore, developing a novel fault diagnosis method that effectively handles noise interference is urgently needed. This study aims to improve the performance of convolutional neural networks (CNNs) in rotating machinery fault diagnosis, particularly in terms of noise robustness. We propose a novel deep learning architecture that combines multi-scale data fusion and attention mechanisms to enhance the extraction of critical features and effectively suppress noise interference. Experimental results demonstrate that this method exhibits excellent fault diagnosis capabilities under various operating conditions, particularly in high-noise environments, where it shows superior accuracy and robustness.

This paper proposes a novel deep neural network framework for fault diagnosis, termed the Multidimensional Fusion Residual Attention Network (MFRANet). The proposed model incorporates three key modules: the Multiscale Depthwise Separable Convolution Module (MDSCMod), the Efficient Residual Channel Attention Feature Extraction Module (ERCAMod), and the External Attention Module (EAMod). The MDSCMod captures detailed features of fault signals across different scales through effective multiscale feature learning. The ERCAMod extracts information-rich features using an efficient residual and channel attention mechanism, ensuring the accurate capture of critical fault information. The EAMod enhances the connections between samples, improving the correlation and information transfer among features. The synergy of these modules enables MFRANet to fully leverage fault-related information, effectively reducing redundancy and irrelevant noise in complex vibration signals, thereby improving the accuracy and robustness of fault diagnosis. Compared to traditional convolutional neural network models, MFRANet significantly enhances fault diagnosis performance in noisy environments by incorporating these three key modules. Unlike previous studies, MFRANet not only identifies and extracts key fault features of gearboxes across multiple scales but also reduces computational complexity and enhances model robustness through the efficient residual channel attention mechanism and external attention module.

The main contributions of this paper include:

• Proposing the Multidimensional Fusion Residual Attention Network (MFRANet): This novel deep neural network framework effectively integrates various advanced feature extraction modules, improving the model’s fault diagnosis capability in complex noise environments.

• Design and Application of MDSCMod: Through multiscale depthwise separable convolutions, the MDSCMod module overcomes the limitations of traditional CNNs with small receptive fields, significantly enhancing the feature extraction capability for gearbox fault signals.

• Innovative ERCAMod: This module optimizes the learning process of multiscale features through parallel channel and spatial attention mechanisms, improving the accuracy of fault type recognition.

• Introduction of the Low-Complexity EAMod: The external attention module significantly reduces computational complexity while maintaining high accuracy, providing effective support for real-time fault diagnosis.

The structure of this paper is as follows: “Primary methodology” section details the proposed Multi-dimensional Fusion Residual Attention Network (MFRANet), including its MDSCMod, ERCAMod, and EAMod components. “Experimental verification” section verifies the superiority and generalization of the proposed method through experiments, visualization, and comparison with five advanced methods using both the gearbox fault diagnosis dataset and the bearing fault diagnosis dataset. Ablation study” section presents extensive ablation studies conducted to verify the noise resistance of the three key components. Finally, “Conclusion” section summarizes the contributions of this paper.

Primary methodology

This document introduces a novel attention-based approach aimed at effective noise reduction, coupled with a comprehensive Convolutional Neural Network (CNN) model, designated as the Multi-dimensional Fusion Residual Attention Network (MFRANet). This section will elaborate on the proposed MFRANet, encompassing the Multi-scale Depthwise Separable Convolution Module (MDSCMod), the Efficient Residual Channel Attention Module (ERCAMod), the External Attention Module (EAMod), the fault classification mechanism, and its comprehensive architecture.

Multi-dimensional fusion residual attention network

The MFRANet model, designed for the diagnosis of faults in rotating machinery, is constructed by integrating MDSCMod and ERCAMod modules in a sequential layering approach. The comprehensive structure of MFRANet is illustrated in Fig. 1, encompassing three primary phases: data gathering, feature extraction via the sequential stacking of MDSCMod and ERCAMod, and feature categorization employing EAMod and SoftMax. The procedure for executing fault diagnosis with the MFRANet model entails the following steps:

In Step 1, the Data Acquisition system systematically collects vibration signals through accelerometers, ensuring the acquisition of essential data for subsequent analysis. Moving to Step 2, the collected vibration data undergoes meticulous preprocessing. This involves segmenting the data into predefined lengths, followed by normalization. The segmented data is then partitioned into distinct training and validation sets, essential for model training, with a reserved test set used for evaluating the model’s performance. Proceeding to Step 3, Offline Training involves the processing of signals from the training set through stages of feature learning and classification. The computation of cross-entropy loss occurs, and the gradient descent optimization technique is applied to iteratively adjust weights during the backpropagation procedure. Finally, in Step 4, Online Testing involves inputting signals from the test set into the trained MFRANet model. The embedded classifier evaluates and determines the final health condition of the bearings, providing a comprehensive assessment of the model’s performance.

Fig. 1

Overall architecture of MFRANet.

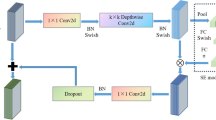
Multi-scale depthwise separable convolution module

The Multi-scale Depthwise Separable Convolution Module (MDSCMod) encompasses three main elements: a foundational convolutional layer, a multi-scale strategy, and a depthwise separable convolution mechanism. As depicted in Fig. 2, the MDSCMod’s complex structure is detailed. For a given vibration signal, the input $x$ is first processed through the foundational convolutional layer, producing a feature map. In this map, the $C$ channels are representative of the “basic” scale. Since the kernel used in the base convolutional layer is of the same size, the feature mapping $Y_{m}^{i}$ in $Y_{m}$ is on the same scale. Next, multi-scale properties are provided for MDSCMod through a hierarchical structure. In this structure, $Y_{m}$ is equally divided into $s$ subsets of feature mappings, denoted as $Y_{m}^{i},$ where $i\in \left\{ 1,2,\cdots ,s \right\}$.Each $Y_{m}^{i}$ represents a unique scale of features.

In each subset $Y_{m}^{i}\in R^{L\times w}$, There are $w= \left( C/s \right)$ channels , denoted as $Y_{m}= \left[ y_{m}^{1},y_{m}^{2},\cdots ,y_{m}^{s} \right] ^{T} \in R^{C\times L}$. Within the hierarchical multi-scale block, the scale $s$ and width $w$ serve as hyperparameters. Each $Y_{m}^{i}$ is paired with a depthwise separable convolution block (DSC), as referenced in³². This block utilizes depthwise separable convolution, a method comprising two components: depthwise (DW) and pointwise (PW), for feature map extraction. Depthwise Convolution operates on a per-channel basis, where each channel is processed by a distinct convolution kernel, ensuring that a single kernel is dedicated to a single channel. The kernel size for the channel-specific convolution is set at 3, while for pointwise convolution, the kernel size is 1, denoted by $K_{i} \left( \bullet \right)$.

The aggregate output from the feature subsets $Y_{m}^{i}$ and $K_{i-1} \left( \bullet \right)$ is input into $K_{i} \left( \bullet \right)$. The resultant output from $K_{i} \left( \bullet \right)$ is symbolized as $Y_{n}^{i}$ which can be articulated as

$$\begin{aligned} Y_{n}^{i}= \left\{ \begin{array}{lc} K_{i}\left( Y_{m}^{i} \right) , & i= 1 \\ K_{i}\left( Y_{m}^{i}+ Y_{n}^{i} \right) , & 2\le i\le s\\ \end{array} \right. \end{aligned}$$

(1)

In summary, the innovative feature representation $Y_{n}= \left[ y_{n}^{1},y_{n}^{2},\cdots ,y_{n}^{s} \right] ^{T} \in R^{C\times L}$, identified by scale $S,$ is subjected to processing through stages of batch normalization (BN)³³ and activation by rectified linear unit (ReLU)³⁴. Diverging from the traditional MLMod approach³⁵, the enhanced MDSCMod incorporates a depthwise separable convolution layer within the initial split group, thereby expanding the receptive fields across various scales. Furthermore, to reduce redundant calculations, the BN and ReLU layers within each $K_{i} \left( \bullet \right)$ are eliminated.The output $Y= \left[ y^{1},y^{2},\cdots ,y^{C} \right] ^{T} \in R^{C\times L}$ of the MDSCMod is

$$\begin{aligned} Y= ReLU\left( BN\left( Y_{n} \right) \right) \end{aligned}$$

(2)

In the MDSCMod framework, the utilization of a base kernel (BK) convolution layer is pivotal. The employment of small kernels typically restricts the extent of the receptive field. On the other hand, the wide kernel of the BK convolution layer aids in capturing both local and global information through its effective receptive field³⁶. Within the MDSCMod, the DSC provides two key benefits. Firstly, the layered multi-scale strategy using depthwise separable convolution enables more powerful multi-scale feature extraction capabilities with fewer parameters compared to parallel CNNs (as in methods¹⁹ and³⁷). Furthermore, the tiered architecture promotes interconnectivity across varying scales, enhancing the integration of features.

The convolution layer based on the BK (Base Kernel) extends the receptive field for feature learning. Simultaneously, the stratified multi-scale approach diversifies the feature scale. Evidence suggests that feature mappings derived from multi-scale kernels offer a more comprehensive representation of the input signal compared to those obtained from single-scale kernels. The integration of the BK layer with a multi-scale strategy that employs depthwise separable convolution renders the MDSCMod an effective feature extraction tool.

Fig. 2

Structure of MDSCMod.

Efficient residual channel attention module

The MDSCMod-derived feature map $Y$ exhibits significant redundancy. To address this, the ERCAMod has been developed to enable the model to selectively emphasize more critical segments while diminishing the impact of non-essential data. ERCAMod integrates both channel and spatial attention mechanisms. The architecture of ERCAMod is detailed in Fig. 3, where the multi-scale feature representation is labeled as $Y= \left[ y^{1},y^{2},\cdots ,y^{C} \right] ^{T} \in R^{C\times L}$, indicating $C$ as the channel count, $L$ as the data points per channel, and $y^{i}= \left[ y_{1}^{i},y_{2}^{i},\cdots ,y_{L}^{i} \right] ^{T} \in R^{1\times L}$ as the $i$th channel’s feature map. An initial operation compresses $Y$ across the channel dimension through the Efficient Channel Attention (ECA) module³⁸, producing the channel descriptor $D_{C}= \left[ d_{C}^{1},d_{C}^{2},\cdots ,d_{C}^{C} \right] ^{T} \in R^{C\times 1}$. $D_{C}$ of the $i$th element can be depicted as the

$$\begin{aligned} d_{C}^{i}= ECA\left( Y \right) = \frac{1}{L} \sum _{k=1}^{L}w_{i}y_{k}^{i} \end{aligned}$$

(3)

The feature mapping $Y$, which consists of multiple channels, is then condensed into a single channel by employing a depthwise separable convolution module that utilizes the spatial descriptor $D_{L}= \left[ d_{L}^{1},d_{L}^{2},\cdots ,d_{L}^{L} \right] ^{T} \in R^{1\times L}$. $D_{L}$ of the $k$th element can be characterized by the

$$\begin{aligned} d_{L}^{k}= \sum _{i=1}^{C}w_{i}y_{k}^{i} \end{aligned}$$

(4)

where $w_{i}$ denotes the weight associated with the convolution process. Following this, the information from both channel and spatial attention is amalgamated through matrix multiplication, culminating in the creation of an attention mask $F\in R^{C\times L}$. This mask mirrors the dimensions of $Y$ and is expressed as

$$\begin{aligned} F= \sigma \left( BN\left( D_{C}D_{L} \right) \right) \end{aligned}$$

(5)

where $\sigma$ represents an s-type activation function. It is important to highlight that this mask adjusts the multiscale feature map $Y$ through elementwise multiplication, serving as the input for the feature mapping model, thereby significantly influencing ERCAMod’s output. In this study, the SC of mask $M$ is identified as ’ARL’. As a result, the output generated by the ERCAMod is defined accordingly.

$$\begin{aligned} Z= F\otimes Y\oplus F\oplus Y \end{aligned}$$

(6)

where $\oplus$ symbolizes the operation of elementwise summation, and $\otimes$ represents the process of elementwise multiplication.

Unlike the methodology outlined in²⁸, our approach obviates the need for separate development of the channel attention module and the spatial attention module, as well as the examination of their sequence for different tasks. An additional advantage of the ERCAMod is that the attention mask $M$ retains the same dimensions as the initial feature map $Y$. This congruence facilitates attention residual learning, enhancing the output mapping’s information content through the integration of a shortcut connection (SC).

Consider $Y$ as the original feature mapping and $M$ as the attention mask. In the conventional residual attention framework³⁹, the output is typically defined as

$$\begin{aligned} Z= F\otimes Y\oplus Y \end{aligned}$$

(7)

In the traditional setup, the attention module is designed to learn $F\otimes Y$. Conversely, our ERCAMod is engineered to assimilate the feature $F\otimes Y\oplus F$. This capability allows ERCAMod to directly acquire the attentional mask $F$, rather than being limited to learning $F\otimes Y$ alone. The enriched data contained within $F$ elevates ERCAMod’s representational capacity and efficacy beyond that of conventional attention techniques, thereby opening novel pathways for enhancing the attention mechanism.

Fig. 3

Structure of ERCAMod.

External attention module

A newly introduced attention framework, termed External Attention⁴⁰, exhibits a computational complexity of $O\left( n \right)$; it is adept at substituting the self-attention component within current structures. This innovative approach has the potential to reveal latent correlations throughout the entire dataset, thereby imposing a robust regularization influence and augmenting the attention mechanism’s ability to generalize.

Initially, we examine the self-attention mechanism, as illustrated in Fig. 4a. For an input feature map $F\in R^{N\times d}$, with $N$ representing the total elements (or image pixels) and $d$ denoting the feature dimensions, self-attention linearly maps this input to three distinct matrices: a query matrix $Q\in R^{N\times {d}' }$, a key matrix $K\in R^{N\times {d}' }$, and a value matrix $V\in R^{N\times d}$⁴¹. The process of self-attention is then articulated as

$$\begin{aligned} & A= \left( \alpha \right) _{i,j}= softmax\left( QK^{T} \right) \end{aligned}$$

(8)

$$\begin{aligned} & F_{out} = AV \end{aligned}$$

(9)

where $A\in R^{N\times N}$ represents the attention matrix, and $\alpha _{i,j}$ stands for the pairwise affinity between the $i$th and $j$th elements.

A widely recognized simplified version of self-attention, depicted in Fig. 4b, derives the attention map directly from the input features $F$ by employing

$$\begin{aligned} & A= softmax\left( FF^{T} \right) \end{aligned}$$

(10)

$$\begin{aligned} & F_{out} = AF \end{aligned}$$

(11)

In this context, the attention map is produced by assessing similarity on a per-pixel basis throughout the feature space, leading to a more refined representation of the input features.

Despite attempts at simplification, the substantial computational demand, characterized by a complexity of $O\left( dN^{2} \right)$, remains a major limitation for the deployment of self-attention. The complexity, which grows quadratically with the quantity of input pixels, renders the direct application of self-attention to images impractical. As a result, prior research⁴² has chosen to implement self-attention on patches instead of individual pixels, aiming to reduce the computational load.

Fig. 4

Self-attention mechanism.

Self-attention is frequently perceived as augmenting input features through a linear combination of self-derived values. However, the requirement for an $N\times N$ self-attention matrix, coupled with an N-element self-value matrix for this linear combination, is not immediately obvious. Moreover, self-attention is restricted to examining relationships among elements within individual data samples, overlooking possible interconnections among elements across varied samples. Such oversight might limit the effectiveness and flexibility of the self-attention mechanism.

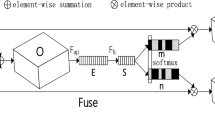
As a result, we propose a new attention module named external attention, illustrated in Fig. 5. This module determines the attention between the input pixel and the external memory cell $M\in R^{S\times d}$ by

$$\begin{aligned} & A= \left( \alpha \right) _{i,j}= Norm\left( FM^{T} \right) \end{aligned}$$

(12)

$$\begin{aligned} & F_{out} = AM \end{aligned}$$

(13)

In Eq. (12), $\alpha _{i,j}$ diverges from the self-attention mechanism by representing the similarity between the $i$th pixel and the $j$th row of $M$, with $M$ being an input-independent, learnable parameter retained throughout the training dataset. The attention map $A$, derived from acquired dataset-level prior knowledge, is normalized akin to self-attention practices. Ultimately, the input features of $M$ are updated based on the similarity encapsulated in $A$.

In practical applications, we employ two distinct storage units, $M_{k}$ and $M_{v}$ , for keys and values, respectively, to augment the network’s capacity. This modification subtly alters the calculation of external attention.

$$\begin{aligned} & A= Norm\left( FM_{k}^{T} \right) \end{aligned}$$

(14)

$$\begin{aligned} & F_{out} = AM_{v} \end{aligned}$$

(15)

The computational complexity of the external attention mechanism is represented as $O\left( dSN \right)$; owing to $d$ and $S$ functioning as hyperparameters, the algorithm demonstrates linear scalability in relation to the number of pixels. Consequently, external attention offers superior efficiency compared to self-attention, making it more feasible for application to inputs of large scale. Moreover, the computational requirements of external attention are comparable to those of a 1 × 1 convolution, further highlighting its practicality for extensive datasets.

Fig. 5

Structure of external attention module.

Fault classification

The process of fault classification, which essentially addresses fault diagnosis under multiple health conditions, constitutes multivariate classification problem. Assuming the final output from the combination of MDSCMod and ERCAMod is $Z_{F} = \left[ Z_{F}^{1},Z_{F}^{1},\cdots ,Z_{F}^{C_{F} } \right] ^{T}\in R^{C_{F}\times L_{F} }$, where $C_{F}$ represents the channel count, $L_{F}$ signifies the length of the signal for each channel, and $Z_{F}^{i}$ denotes the $i$th channel’s feature mapping. The dimension corresponding to signal length is condensed via the Global Average Pooling layer (GAP), subsequently, the $i$th element of the terminal feature vector $V= \left[ v_{1},v_{2},\cdots ,v_{C_{F} } \right] \in R^{1\times C_{F} }$ can be articulated as

$$\begin{aligned} v_{i} = GAP\left( Z_{F} \right) = \frac{1}{L_{F} } \sum _{k=1}^{L}Z_{F}^{i}\left( k \right) \end{aligned}$$

(16)

The downscaled signal is then fed into EAMod to learn implicit association features between different samples.

To differentiate among various fault types, a SoftMax layer transforms the ultimate feature vector $V\in R^{C_{F} }$ into a predictive distribution. Assuming there exist $h$ health states, the quantity of unscaled logarithms, denoted as $Q= \left[ Q_{1},Q_{1},\cdots ,Q_{h} \right] \in R^{1\times h}$, is expressed as

$$\begin{aligned} Q= VW+ b \end{aligned}$$

(17)

In the context of dense layers within neural networks, the weight matrices and bias vectors are denoted by $W\in R^{C_{F}\times h }$ and $b\in R^{1\times h }$ , respectively. The probability output corresponding to the $j$th fault type, as produced by the SoftMax layer, is represented as

$$\begin{aligned} P_{j}= \frac{\exp \left( Q_{j} \right) }{ {\textstyle \sum _{i=1}^{h}}\exp \left( Q_{j} \right) } \end{aligned}$$

(18)

The cross-entropy loss function, denoted by $L$, is employed to quantify the divergence between the predicted probabilities $P_{j}$ and the true labels $\hat{P}_{j}$ across the training dataset. It is formulated as

$$\begin{aligned} L= - \frac{1}{N}\sum _{j=1}^{N}\hat{P}_{j}\log {P_{j} } \end{aligned}$$

(19)

where $N$ symbolizes the total count of samples within the dataset.

Experimental verification

In this section, the performance of the proposed MLA-CNN model is evaluated using the US-University of Connecticut gearbox dataset⁴³ and the Southeast University gearbox dataset⁴⁴.

Dataset description

UoC dataset: The test rig mainly consists of a motor, a two-stage gearbox with replaceable gears, an electromagnetic brake, accelerometers, and a tachometer. Experimental data were acquired from a benchmark two-stage gearbox featuring interchangeable gears. The gear’s rotational speed is regulated by a motor, while torque is supplied through a magnetic brake, whose input voltage adjustments allow for torque modulation. The first-stage input shaft is equipped with a 32-tooth pinion and an 80-tooth gear. For the second stage, a 48-tooth pinion and a 64-tooth gear are employed. The speed of the input shaft is monitored by a tachometer, and vibrations from the gears are captured by accelerometers. The recording of these signals is facilitated by a dSPACE system (DS1006 Processor Board from dSPACE GmbH), with a sampling rate set at 20 kHz. As illustrated in Fig. 6, nine distinct conditions were simulated on the input shaft’s pinion, encompassing five wear severity levels, missing teeth, root cracks, spalling, and shaving. The dynamic response of systems involving gear mechanisms is angularly periodic. In practice, although gearbox systems record data at a fixed sampling rate, the time-domain response is often not time-periodic due to speed variations caused by factors such as load disturbances, geometric tolerances, and motor control errors. To address the non-stationary issue and eliminate uncertainties arising from speed variations, the Time Synchronous Averaging (TSA) method⁴⁵ is employed. This method resamples the time-uniform signal based on the shaft speed measured by the tachometer and averages it in the angular domain. Since TSA transforms the signal from a time-uniform representation to an angle-uniform representation, it can significantly reduce incoherent components in the system response. It is worth noting that TSA is a standard, unbiased technique that facilitates effective pattern recognition across various datasets, thereby ensuring to some extent that the data reflects genuine industrial gear defects.

There are two types of data: time-domain vibration signals of gears under nine conditions (fault types) (DataForClassification_TimeDomain.mat) and gear fault data after synchronous analysis in the angular frequency domain (DataForClassification_Stage0.mat). The nine conditions are: healthy condition, missing tooth, root crack, spalling, and chipping tip (five different levels of severity). The DataForClassification_TimeDomain.mat dataset is a 3600×936 matrix, where each column represents a vibration signal sample, each sample contains 3600 sampling points, and each fault type has 104 samples, making 936 = 104×9 in total. The arrangement of samples is as follows: columns 1-104 for healthy condition; 105-208 for missing tooth; followed in sequence by root crack, spalling, and chipping tip (five different levels of severity)⁴⁶. The training and test sets contain 749 and 187 samples, respectively, as shown in Table 1.

Fig. 6

Faulty gear of the two-stage reducer.

Table 1 Data segmentation.

SEU Dataset: This dataset is from Southeast University in China⁴⁷. The transmission dataset is derived from the drivetrain dynamic simulator (DDS) shown in Fig. 7. Two different working conditions are studied: the speed system load is set to 20 Hz-0 V or 30 Hz-2 V. Within each file, there are 8rows of signals which represent: 1-motor vibration, 2,3,4-vibration of planetary gearbox in three directions: x, y, and z, 5-motor torque, 6,7,8-vibration of parallel gear box in three directions: x, y, and z. Signals of rows 2,3,4 are all effective. The different fault types of bearings and gearboxes are listed in Table 2. The dataset contains bearing and gearbox data for five different working conditions, including four fault types and one healthy state, making the fault diagnosis of DDS a 5-class classification task. Each fault type includes 1,000 training samples, resulting in a total of 5000 training data samples for both gear and bearing faults. The test dataset is of the same size as the training dataset. To evaluate the effectiveness of the proposed method in handling mixed faults, gear faults and bearing faults were combined into a mixed dataset. This mixed dataset includes four gear faults, four bearing faults, and one healthy state. Each working state contains 1000 training samples and 1000 test samples, with both the training and test datasets comprising 9000 samples each.

Fig. 7

Drivetrain Dynamic Simulator (DDS).

Table 2 Type of bearing and gearbox failure.

Politecnico di Torino aero-engine bearing dataset: The dataset was collected from the test rig at Turin Polytechnic University⁴⁸, under a load of 1000 N and a motor speed of 3 × 104 r/min. The experimental platform mainly consists of a high-speed spindle, test bearings, and XYZ three-axis sensors. The dataset includes three states: inner ring fault, roller fault, and normal state. Vibration signals were divided into 256 samples, with each sample containing 2000 data points. The sampling frequency was set at 51.2 kHz, with a sampling duration of 10 seconds. The fault bearings are labeled with fault types, fault sizes, super-class labels, and sub-class labels, as shown in Table 3.

Table 3 Seven health conditions of the aero-engine bearing dataset.

Harbin Institute of Technology aero-engine bearing dataset: The test rig consists primarily of a modified aero-engine, motor drive system, and lubrication system⁴⁹. The faults include outer ring faults and inner ring faults. Aero-engine bearing data was collected under a motor speed condition of 1800 r/min. The sampling rate was set at 25 kHz, and the sampling duration was 12 seconds. Data from Channel 4 was used for this experiment. Vibration signals were divided into 184 samples, with each sample containing 2000 data points. Fault bearings are labeled with fault types, fault sizes, super-class labels, and sub-class labels, as shown in Table 4.

Table 4 Four conditions of the aero-engine bearing dataset.

Implementation details and evaluation indicators

The methodology was implemented on the Pytorch 1.12.1 platform and operated within the Windows 11 environment, utilizing a GeForce RTX 2060 Super GPU to perform computational duties. This study utilizes Z-score Normalization⁵⁰ for data normalization, where the raw signal’s mean is initially subtracted from it, and the resulting zero-mean signal is then divided by its standard deviation. For a raw signal denoted by $x_{i}$, the normalized signal $\hat{x}_{i}$ is expressed as

$$\begin{aligned} \hat{x}_{i} = \dfrac{x_{i} - \textrm{mean}(x_{i})}{\textrm{std}(x_{i})} \end{aligned}$$

(20)

where $mean\left( x_{i} \right)$ denotes the calculation of the mean and $std\left( x_{i} \right)$ denotes the calculation of the standard deviation.

During the training phase, the cross-entropy loss function was utilized, with the Adam algorithm selected for optimization. The batch size was established at 64, and the model underwent training for a total of 50 epochs. To expedite convergence, a basic learning rate decay approach was adopted, diminishing the initial learning rate by a factor of 0.1 every 10 epochs. The research began with a learning rate of 0.001, eventually reducing to a minimal rate of 0.000001.

To manage randomness and facilitate a more effective and transparent comparison of model performance across different evaluation metrics, this study applies random seed control within the neural network model’s training process. This approach guarantees the repeatability of each experiment, setting the random seed value to 42. In this study, model evaluation is conducted using four key metrics: accuracy, precision, recall, and the F1-score.

Vibration signals gathered from actual machinery are commonly affected by severe environmental conditions. Consequently, the incorporation of a distinct type of Gaussian noise into the original signal is proposed to make the experiment more practical, as suggested in^51,52. The Signal-to-Noise Ratio (SNR), measured in decibels (dB), is defined as

$$\begin{aligned} snr= 10\log _{10}{\left( \frac{P_{sig} }{P_{noi} } \right) } \end{aligned}$$

(21)

In the discussed context, $P_{sig}$ represents the signal’s power, while $P_{noi}$ signifies the power of the noise introduced. A diminished signal-to-noise ratio indicates a predominance of noise. Specifically, a 0 dB signal-to-noise ratio signifies that the signal and noise are of equal power. This study evaluates nine distinct noise levels, corresponding to signal-to-noise ratios of 8, 6, 4, 2, 0, $-$2, $-$4, $-$6, and $-$8 dB respectively.

Model architecture and hyperparameter studies

The performance of a Convolutional Neural Network (CNN) model is significantly affected by the choice of hyperparameters. The architecture of the model discussed herein comprises 12 layers: this includes five MDSCMod layers, five ERCAMod layers, one Global Average Pooling layer (GAP), one EAMod layer, and a final SoftMax layer. For the MDSCMod layers, the configuration parameters include the size of the kernel and the stride for the BK convolution layers, alongside the quantity of scales and the widths of these scales within its hierarchical architecture. The ERCAMod layers, in contrast, do not necessitate the determination of specific hyperparameters. Although the input signal is predefined as 1024 × 1, the model is designed with the flexibility to accommodate multi-channel vibration signals, extending its applicability. In every MDSCMod layer, the stride is consistently set to 2, effectively halving the signal length across each channel. As the signal dimensions are reduced, the kernel size diminishes as the network delves into deeper layers. The count of scales in all hierarchical multi-scale blocks remains constant at 4. However, to enhance feature extraction, the quantity of sub-channels escalates from 16 to 64.

Table 5 MFRANet internal hyperparameter.

Based on experience³⁵, four sets of hyperparameters are further considered, comprising: (A) the kernel size and (B) stride of the BK convolution layer, (C) the scale and (D) width within the MDSCMod’s hierarchical structure. The standard parameters for the standard model are selected as [32,16,16,8,4] for kernel size, [2,2,2,2,2] for stride, [4,4,4,4,4] for scale, and [16,16,32,32,64] for width (refer to Table 5). The justification for selecting specific hyperparameters is grounded in the observation that increasing the kernel size to 1.5 times the size utilized in the standard model does not result in improved accuracy, yet it substantially augments both the parameter count and computational complexity, measured in floating-point operations per second (FLOPs). Conversely, halving the kernel size leads to a reduction in average accuracy. Moreover, maintaining consistent kernel sizes across layers has been linked to decreased accuracy in models characterized by higher FLOPs and an increased number of parameters. The stride parameter plays a crucial role in reducing dimensionality; a larger stride diminishes FLOPs without altering the parameter count. For example, a stride of 1 can lead to a tenfold increase in FLOPs relative to the baseline model, complicating the training process and diminishing average accuracy. Conversely, a stride that is too large can significantly reduce the feature map size, leading to notable losses in information.

In terms of the scale parameter within MDSCMod, an increase in scale directly correlates with higher FLOPs and a greater number of parameters. Research findings, as indicated in³⁵, suggest that setting the scale to 4 yields optimal accuracy. Additionally, the width of the hierarchical structure in MDSCMod, similar to kernel size, was assessed in three different scenarios: 1.5 times, 0.5 times the size of the standard model, and uniform widths across all layers. It was found that a configuration with widths set to [24,24,48,48,96] doubles the parameters and FLOPs but does not significantly enhance accuracy, likely due to overfitting. A model with uniform layer widths of 32 exhibited lower accuracy compared to the standard model. Thus, these observations have informed the selection of the four hyperparameters for the standard model.

Visual analytics

Fig. 8

Time waveforms and spectra of vibration signals in the UoC gearbox failure dataset. (a) Time waveform of the noise-free raw vibration signal. (b) Frequency spectrum of the noise-free raw vibration signal. (c) Time waveform of the noise-containing vibration signal (SNR = 0). (d) Frequency spectrum of the noise-containing vibration signal (SNR = 0).

To investigate how MFRANet learns multi-scale features and suppresses noise, a faulty sample was selected from the UoC gearbox dataset. Gaussian white noise, characterized by a Signal-to-Noise Ratio (SNR) of 0 dB, was introduced into the vibration signal sample.

Figure 8a,c illustrate the time waveforms of the clean and noise-affected vibration signals, respectively. To conduct a more detailed examination of the model’s performance within the frequency domain, their respective spectra are displayed in Fig. 8b,d. In the time domain, the amplitude of the signal is noted to fluctuate periodically. These fluctuations, especially evident in Fig. 8a, are attributed to impulses generated by bearing defects, serving as crucial diagnostic indicators. The frequency domain analysis reveals distinct spectral peaks in Fig. 8b, indicative of these features. However, the introduction of noise, as depicted in Fig. 8c,d, obscures these amplitude fluctuations and muddles the spectral clarity. Thus, the periodic impulses shown in Fig. 8a play a vital role in the model’s diagnostic process, showcasing the ability of MFRANet to effectively mitigate noise interference.

Fig. 9

Spectrum of bearing fault original signal and gear fault original signal in SEU data set. (a) Bearing ball fault original signal spectrum. (b) The original signal spectrum of gear sharpening fault.

We conducted a detailed spectral analysis of the raw signals from the SEU dataset for both bearing faults and gear faults, focusing primarily on the amplitude and frequency characteristics of the signals to assess the severity of different faults, as shown in Fig. 9.

Amplitude Analysis: When comparing the amplitude of the raw signals for the two types of faults, we observed that the signal amplitude in the bearing ball fault dataset is significantly higher, while the signal amplitude in the gear tooth chipping fault dataset is relatively lower. The amplitude of a signal is typically associated with the energy level present in the system; hence, a larger amplitude may indicate more intense vibration or impact within the system, which is often linked to more severe mechanical faults. Therefore, the fault corresponding to the bearing ball fault dataset may be more severe than the fault in the gear tooth chipping fault dataset.

Frequency Characteristic Analysis: In terms of frequency characteristics, the spectrum of the bearing ball fault dataset exhibits concentrated frequency peaks, primarily distributed in the low- and mid-frequency ranges. This frequency distribution may reflect pronounced mechanical misalignment or bearing damage, which are types of faults usually accompanied by lower frequency characteristics. In contrast, the spectrum of the gear tooth chipping fault dataset shows multiple frequency peaks spread across a broader frequency range, but with relatively lower amplitudes. This distribution may indicate minor imbalances or surface defects, which typically generate higher vibration frequencies with lower amplitudes, suggesting that the severity of the fault might be relatively minor.

Fault Severity Comparison: Based on the combined analysis of amplitude and frequency characteristics, the faults in the bearing ball fault dataset exhibit higher vibration amplitudes and concentrated low-frequency peaks, indicating more severe mechanical faults, such as bearing damage or misalignment issues. Conversely, the faults in the gear tooth chipping fault dataset are characterized by lower amplitudes and more dispersed frequency peaks, likely corresponding to milder faults such as surface wear or minor imbalances.

Therefore, from the perspective of signal amplitude and frequency characteristics, the fault severity in the bearing ball fault dataset is clearly higher than in the gear tooth chipping fault dataset. This analysis supports the effectiveness of the proposed method in handling faults of varying severity, especially in more complex and severe fault scenarios.

Comparison with state-of-the-art methods

Table 6 Comparison results of Accurac, Recall, Precision and F1-score of various methods without noise (UoC dataset).

Table 7 Comparison results of Accurac, Recall, Precision and F1-score of various methods without noise (SEU dataset).

To verify the superior performance of our model, we compared the proposed MFRANet with five state-of-the-art (SOTA) methods on the University of Cincinnati (UoC) gearbox dataset and the SEU gearbox dataset. The comparative analysis encompasses five distinct methodologies: a foundational approach as detailed in reference⁵³, three methodologies based on Convolutional Neural Networks (CNNs) cited in references^21,27, and⁵⁴, and an attention-driven CNN technique outlined in reference³⁵. In replicating these methodologies for benchmarking purposes, two principal guidelines were rigorously followed to guarantee equitable comparison. Firstly, the length of the samples for each method was standardized to 1024, mirroring the specification utilized in MFRANet, as introduced in our study. Secondly, the training protocols for the models, encompassing both the optimizer and learning rate, were meticulously aligned with the specifications delineated in their original scholarly articles.

Fig. 10

Confusion matrix of each model (UoC dataset).

For the UoC dataset, Table 6 presents a comparison of the Accuracy, Recall, Precision, and F1-score of various methods in the absence of noise (Table 7, 8). Figure 10 illustrates the confusion matrix for each model (Fig. 11). Figure 12 depicts the changes in training test accuracy and loss for MFRANet across training epochs under Gaussian noise conditions ranging from 8 dB to − 8 dB (Fig. 13). Figure 14 provides a comparison of the Accuracy, Recall, Precision, and F1-score for each method under varying intensities of Gaussian noise (SNR = 0 8 dB). Table 9 details the comparative results of Accuracy, Precision, Recall, and F1-score between state-of-the-art methods and MFRANet under Gaussian noise conditions (SNR = 0 dB). The findings indicate that MFRANet consistently achieves the highest test accuracy across all tested Signal-to-Noise Ratio (SNR) conditions, particularly excelling in low-noise environments (SNR = 8 dB) where the accuracy of the MRA-CNN method reached 93.61%. In contrast, under high-noise conditions (SNR = −8 dB), the accuracy decreased to 20.85%. However, even in such conditions, MFRANet’s performance exceeded that of MRA-CNN by 2.43% in low-noise scenarios. Despite a gradual decrease in performance with increasing noise intensity, MFRANet maintained its leading position across all noise levels evaluated.

Fig. 11

Confusion matrix of each model (SEU dataset).

For the SEU dataset, Table 7 compares the Accuracy, Recall, Precision, and F1-score of various methods in the absence of noise. The confusion matrix for each model is displayed in Fig. 11. Figure 13 shows the changes in training test accuracy and loss for MFRANet across training epochs under Gaussian noise conditions ranging from 8 dB to − 8 dB. Table 10 presents the comparative results of Accuracy, Precision, Recall, and F1-score between state-of-the-art methods and MFRANet under Gaussian noise conditions (SNR = 4 dB). Similar to its performance on the UoC dataset, MFRANet achieved leading results in Accuracy, Recall, Precision, and F1-score. Additionally, as indicated by the confusion matrices in Fig. 11, MFRANet demonstrated strong performance in fault diagnosis and classification of bearing fault data within the SEU dataset, highlighting its robust generalization ability.

Fig. 12

(a)$\sim$(i) shows the training test accuracy, loss variation curves of MFRANet under Gaussian noise with signal-to-noise ratios of 8 dB$\sim$− 8 dB in turn (UoC dataset).

The superior performance of MFRANet under a broad spectrum of noise conditions can be ascribed to its innovative design, which incorporates multi-scale feature fusion and sophisticated noise reduction capabilities. This contrasts with other approaches like Resnet18-1d⁵³, which performs feature extraction at a singular scale, and WDCNN²⁷, which yields stable yet suboptimal classification results. MRA-CNN³⁵ enhances the model’s multi-scale capabilities through the utilization of convolution kernels of varying sizes to extract essential multi-scale features, yet its effectiveness diminishes significantly under high-noise conditions compared to MFRANet. Additionally, the limitations of QCNN⁵⁴ and WKNet1_Inception²¹ in addressing Gaussian noise and multi-scale learning further underscore MFRANet’s adeptness at sustaining high accuracy within complex noisy environments.

Fig. 13

(a)$\sim$(i) are the variation curves of MFRANet’s training test accuracy and loss under Gaussian noise with SNR of 8 dB$\sim$−8 dB (SEU dataset).

In comparison with the latest research by Zhao et al., who proposed a hierarchical health monitoring model based on adaptive threshold and coordinate attention network (ATCATN)⁵⁵, we conducted comparative experiments using the same datasets. Specifically, Dataset A is the Turin Polytechnic University Aero-Engine Bearing Dataset, and Dataset B is the Harbin Institute of Technology Aero-Engine Bearing Dataset. The experiments were carried out under different signal-to-noise ratio (SNR) conditions (SNR = 5 and SNR = 0), with five independent repeated experiments. The results are shown in Table 8. At low noise levels (SNR=5), the average classification accuracy of MFRANet was slightly lower than that of ATCATN, but the difference did not exceed 1%. However, under high noise levels (SNR=0), the average classification accuracy of MFRANet was significantly higher than that of ATCATN, indicating that MFRANet has higher fault diagnosis accuracy in high-noise environments.

Table 8 Average classification accuracy (%).

This study introduces MFRANet, thereby demonstrating the superiority of this novel fault diagnosis framework, particularly in the context of diagnosing faults in rotating machinery within Gaussian noise environments. This achievement not only furnishes a highly precise diagnostic tool at the technical level but also suggests the potential for widespread application in the health monitoring and maintenance of critical rotating machinery, such as rolling bearings, motors, and water pumps. Looking ahead, the scope of MFRANet’s application could extend to a broader array of industrial scenarios and condition monitoring tasks, encompassing conditions with more intricate noise patterns or where data is scant. Moreover, the observed performance decline of MFRANet under extreme noise conditions prompts future investigations into more efficacious noise reduction techniques and more adaptable multi-scale feature extraction methodologies to enhance the model’s robustness and precision further.

Table 9 Comparison results of Accuracy, Recall, Precision and F1-score of various methods with noise (SNR = 0 dB) (UoC dataset).

Ablation study

Table 10 Comparison results of Accuracy, Recall, Precision and F1-score of various methods with noise (SNR = 4 dB) (SEU dataset).

It is important to note that in all ablation experiments, we did not simply remove or replace the corresponding module from the trained model; instead, we retrained the entire network. This approach ensures that each experimental model undergoes the same initial conditions and training process, thereby eliminating potential biases introduced during training and ensuring the fairness and scientific integrity of the results. By following this method, we can more accurately assess the actual impact of individual modules on model performance and further validate the superiority of DSC in reducing computational complexity while maintaining or enhancing model performance.

Effectiveness of the MDSCMod

Fig. 14

Comparison results of Accuracy, Recall, Precision and F1-score of various methods under Gaussian noise (SNR = 0$\sim$8 dB) (UoC dataset).

The significance of the Deeply-Separable Convolution (DSC) block is rigorously validated using the University of Connecticut (UoC) dataset, with its impact assessed through an ablation study that replaces DSC with a 5×5 convolution. The choice of the 5×5 convolution kernel is based on several considerations: Firstly, compared to the smaller 3×3 convolution kernel, the 5×5 convolution kernel has a larger receptive field and enhanced feature extraction capability. This allows it to capture a broader range of spatial information, providing more contextual information and detailed features for the model, thereby better demonstrating the advantages of DSC. Secondly, using the 5×5 convolution kernel allows for a more intuitive evaluation of the advantages of DSC, including its performance and computational complexity, through direct comparison. Finally, employing the 5×5 convolution kernel as the basis for comparison ensures a more rigorous and controllable experimental design. This approach enhances the reliability and interpretability of the experimental results.

The classification results under Gaussian noise are presented in Table 12 and Fig. 15a. Additionally, the FLOPs (Floating Point Operations) and the number of parameters for the ablation model are detailed in Table 11 for comparison. Specifically, the FLOPs and the number of parameters for MFRANet are 52.59 million and 686.11 thousand, respectively. The findings underscore DSC’s pivotal role in enhancing the accuracy of fault diagnosis. Notably, at a Signal-to-Noise Ratio (SNR) of − 8 dB, incorporating DSC improved model accuracy by approximately 2.43%, alongside a reduction in computation and parameter count by 14.11MMac and 181.89K, respectively. Furthermore, at an SNR of 0 dB, DSC’s contribution to performance enhancement was even more pronounced, achieving a 7.91% improvement. These comparisons reveal that the DSC module’s share in the model’s total parameters and computations is relatively modest, accounting for only 7.537% and 8.225% respectively, evidencing its efficiency. The DSC’s architecture, a synergy of depthwise (DW) and pointwise (PW) convolutions, markedly diminishes the model’s parameter and computation footprint while preserving performance. DW convolution is tasked with feature extraction within channels, whereas PW convolution amalgamates information across channels. This configuration is adept at capturing the multi-scale features essential for fault diagnosis, while concurrently minimizing resource consumption. Performance analysis across various noise levels demonstrates DSC’s enhanced efficiency in low noise conditions, signifying its adeptness at extracting valuable features amidst noise interference. This underscores the criticality of equilibrating computational resource allocation and model performance in design considerations, with DSC offering a viable solution to this challenge.

This study corroborates that DSC markedly optimizes computational resource utilization while elevating the accuracy of fault diagnosis, reinforcing the integral role of DSC in the architecture of lightweight deep learning models. This not only substantiates the efficacy of integrating DSC into the model but also underscores its prospective utility in practical deployments, particularly within resource-limited settings. Looking ahead, DSC’s characteristics lay the groundwork for its broader application in scenarios such as real-time fault monitoring on IoT devices and edge computing applications. While some experimental outcomes may diverge from expectations, this discrepancy is attributed to the complexities of feature extraction amidst noise interference. Future research could delve into DSC’s performance under varied conditions and its optimization for an expanded array of noisy environments and application requisites, thereby further enhancing model accuracy without compromising efficiency.

Effectiveness of the ERCAMod

In evaluating the efficacy of ERCAMod, three distinct ablation protocols were developed to assess the individual and combined impacts of the Deeply-Separable Convolution (DSC) module and the Enhanced Channel Attention Module (ECAMod). The Flops, number of parameters, and precision results for the three ablation structures are shown in Tables 11 and 12, and Fig. 15b. The analysis across nine varying noise levels demonstrates that omitting either the DSC or ECAMod module detracts from the model’s classification prowess. Specifically, within the University of Connecticut (UoC) dataset, a decrement in the signal-to-noise ratio (SNR) from 0 to − 8 dB led to a reduction in model accuracy by approximately 1.67% upon the exclusion of the DSC module, 1.37% with the removal of ECAMod, and 1.52% when both were omitted. Additionally, it was observed that integrating DSC and ECAMod significantly curtails the FLOPs and parameter count, with the ERCAMod’s computational and structural metrics constituting merely 0.656% and 1.251% of those of a standard model, respectively. These findings affirm the critical role of both the DSC module and ECAMod in bolstering model performance, as well as the lightweight architecture of ERCAMod.

Table 11 The number of calculations and parameters before and after MFRANet ablation.

The investigation reveals that the DSC module and ECAMod are pivotal in enhancing classification accuracy within noisy settings, with their importance escalating as noise levels decrease, particularly within low noise scenarios. This enhancement is crucial for diagnosing faults in bearings and gears. The exclusion of the DSC module was simulated by substituting it with a 1x1 convolution operation, whereas the omission of ECAMod was replicated using a global averaging pooling layer. These substitutions underscore the intrinsic link between module functionality and model performance under various ablation strategies. The analysis further illustrates that while the absence of either module compromises performance, their synergistic integration is imperative for maintaining and elevating model efficacy, thus underscoring the value of ERCAMod’s unique residual attention and short connection design features.

Table 12 Ablation results of MFRANet under Gaussian noise (%).

This study not only corroborates the effectiveness of ERCAMod but also accentuates its practical merit in the design of lightweight networks. Through meticulous ablation experiments, the instrumental roles of the DSC modules and ECAMod in augmenting performance amidst complex noise conditions were demonstrated, aligning with the proposed lightweight and efficient design principle of ERCAMod. Moving forward, these findings furnish a novel perspective and methodological foundation for subsequent research in bearing and gear fault diagnosis. Moreover, in light of the performance shifts observed in the ablation studies, we hypothesize that the model’s lightweight design not only reduces computational demands but may also enhance diagnostic accuracy in low SNR settings through more sophisticated feature extraction processes. Future endeavors could delve into exploring an array of module combinations and configurations to further refine the model’s performance and efficiency.

Effectiveness of the EAMod

Fig. 15

Ablation results of MDSCMod, ERCAMod and EAMod under Gaussian noise.

This study delves into the impact of the External Attention Module (EAMod) on fault diagnosis performance, employing ablation experiments that entail the removal of EAMod from models trained on the University of Connecticut (UoC) datasets. The classification results under Gaussian noise are shown in Table 12 and Fig. 15c. The Flops and the number of parameters for the ablation model are also presented in Table 11 for comparison. The findings underscore EAMod’s substantial contribution to enhancing classification accuracy in low-noise environments, whereas its absence slightly benefits the model’s accuracy in high-noise settings. Specifically, models devoid of EAMod exhibit diminished classification accuracy at Signal-to-Noise Ratios (SNR) above 0 dB, yet show improved accuracy at SNRs below 0 dB. The study also sheds light on the differences in computational capacity and parameter count between the ablation model and the intact original model, further elucidating EAMod’s efficiency and impact.

EAMod’s primary role is to bolster the model’s discriminative capabilities by elucidating the latent associations among samples. In environments characterized by low noise, EAMod proficiently underscores and amplifies the connections between pivotal fault features, thereby elevating classification accuracy. Conversely, in scenarios fraught with high noise levels, EAMod may erroneously interpret noise as salient information, impairing model performance. This observation suggests that the utility of external attention mechanisms is nuanced in complex noise conditions, with their effectiveness markedly influenced by the ambient noise level. The removal of EAMod in high-noise contexts could yield better outcomes by preventing the model from overemphasizing noise features. However, excluding EAMod in low-noise scenarios results in the loss of focus on critical fault features, consequently degrading performance.

The outcomes of this investigation elucidate the variable impacts of EAMod on fault diagnosis efficacy across different noise environments. EAMod significantly boosts classification accuracy in low-noise settings by reinforcing the interrelationships among valuable features, yet its utility diminishes or even becomes counterproductive in high-noise contexts. This insight is pivotal for the development of efficient fault diagnosis models tailored to varying noise levels. Future endeavors could aim to refine the external attention module to preserve its beneficial effects under diverse noise conditions or devise new strategies for dynamically adjusting the module’s focus based on noise level fluctuations. Furthermore, these findings advocate for the consideration of environmental noise impacts when deploying attention mechanisms in practical applications, ensuring optimal model performance across varying conditions.

Conclusion

The proposed MFRANet not only provides a novel and efficient solution for fault diagnosis of rotating machinery under Gaussian noise, but also demonstrates significant advantages in high-noise environments. This innovation represents a major advancement in the field, addressing the critical challenge of accurately detecting faults in noisy conditions. Compared with traditional methods, MFRANet shows stronger robustness in handling complex noise, especially with significantly higher diagnostic accuracy under high-noise conditions (e.g., SNR=0) than existing technologies. This suggests that it has the potential to provide reliable fault diagnosis in scenarios where traditional methods are less effective.

This achievement not only provides an effective tool for accurate gearbox fault diagnosis but also expands its application prospects in the health monitoring and maintenance of key rotating equipment such as rolling bearings, motors, and pumps. Through detailed ablation experiments, this study further validates the critical roles of the Depthwise Separable Convolution (DSC) and ERCAMod modules. Their introduction not only improves diagnostic accuracy but also optimizes the use of computational resources, making it particularly suitable for resource-constrained industrial environments. These findings reinforce the practicality of lightweight deep learning models in resource-limited scenarios, laying the foundation for broader industrial applications.

Looking ahead, further optimization and expansion of MFRANet will provide more accurate and robust solutions for industrial maintenance, especially in cases involving complex noise and scarce data. This study not only offers a new tool for existing fault diagnosis technologies but also points to future research directions, particularly in expanding the application potential of MFRANet across various industries. Additionally, the study found that the model’s performance decreases under extreme noise conditions, and future work will focus on developing more efficient noise reduction techniques and flexible multi-scale feature extraction strategies. Meanwhile, the research results of the External Attention Module (EAMod) suggest that there is still room for optimization of its performance under different noise levels, providing new insights and technical routes for designing more efficient fault diagnosis models.

In conclusion, this study not only advances technological progress in the field of fault diagnosis but also opens up new possibilities for the practical application of these technologies in industrial environments. It ensures that MFRANet and its related innovations will play a key role in future predictive maintenance and health monitoring systems.