WGAN-based multi-structure segmentation of vertebral cross-section MRI using ResU-Net and clustered transformer

Abstract

The vertebral foramen, lamina, and vertebral body are three critical components of the spine structure, essential for maintaining spinal connectivity and stability. Accurately segmenting lumbar structures such as the vertebral body, vertebral foramen, and lamina in MRI cross-sections helps doctors better understand and diagnose the pathological causes of spine-related diseases. This study presents a multi-structure semantic segmentation method for vertebral transverse section MRI slices using WGAN with a residual U-Net and clustered Transformer. The generator network was replaced with a combination of a residual U-Net and a clustered Transformer-based segmentation network. The enhanced U-Net encoder, utilizing dilated convolutions and residual structures, improved multi-scale feature extraction capabilities. Meanwhile, the clustered Transformer structure, with reduced progressive linear complexity, ensured the extraction of global positional information. The results of multiple experiments show that the Dice coefficient for vertebral body segmentation increased by 3.1%, the Hausdorff distance decreased by 0.6 mm, mIOU improved by 4.1–96.2%, and PPV increased by 2.0–98.8% compared to mainstream segmentation models. These improvements are statistically significant (p < 0.05).Ablation experiments further validated the effectiveness of the proposed enhanced modules in improving segmentation accuracy for the three target structures.

Introduction

Lumbar disc herniation (LDH) symptoms are a common cause of severe low back and leg pain, often due to disc degeneration and herniation affecting specific nerve roots. A typical sign is the involvement of specific nerve roots. The common solution is lumbar spine surgery, and computed tomography(CT) and magnetic resonance imaging (MRI) imaging techniques are generally used to assess the extent of spinal and disc pathologies in surgical patients¹. While CT has significant advantages in diagnosing LDH by clearly showing lumbar spine calcification and vacuum phenomena, MRI not only offers high-resolution imaging but also provides multi-directional views to reveal the extent of disc pathology, physiological morphology, and the relationship with nerve roots and dural sac surrounding tissues.

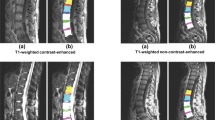
As shown in Fig. 1, conventional MRI scanning sequences include sagittal and axial views, providing a straightforward representation of the lumbar structures. However, these sequences lack a 3D view of key anatomical structures like the intervertebral foramina, posterior arch, and intervertebral disc, limiting the ability to fully assess the shape of disc herniation and the extent of nerve compression². MRI scanning sequences demonstrating cross-sectional views of lumbar spine structures are deficient in comprehensively assessing disc protrusion patterns and severity of nerve compression in lumbar disc herniation (LDH) requiring physicians to manually locate the lesion sequences. At the same time conventional 2D scanning views of tissues such as foramina and discs do not provide 3D details of the overall anatomy. Therefore, medical image segmentation techniques for lumbar spine structures have important clinical research value and can provide more precise spatial anatomical details for outpatient diagnosis and clinical surgical precautions.

Fig. 1

(a), (b), and (c) show MRI slices of the lumbar spine in the sagittal and transverse views. (b) and (c) depict the cross-sectional morphology of the lumbar spine at different locations. The factors and indicators associated with lumbar spine diseases primarily concentrate in the vertebral body, vertebral foramen, and lamina, as indicated by the three different colored areas in the images. Due to the staged progression of the condition, even cross-sections from the same area of the lumbar spine can display significant differences.

Additionally, segmenting these physiological structures from conventional MRI can provide clinical information for quantitative assessment of nerve damage and disease mechanisms in LDH, with broad applications in generating radiology reports for lumbar disc herniation³.

Manual segmentation of medical images usually requires the operator to label the boundaries or contours of the image, relying on the operator’s subjective judgement, which can lead to a loss of consistency and accuracy in the results. This approach is prone to individual operator bias, affecting the consistency and accuracy of segmentation results. This issue is particularly significant with large datasets or complex image structures, where factors such as image quality, noise interference, or complex image structures make segmentation of local areas extremely challenging. Manual segmenters, under excessive workload, might struggle to accurately identify fine structures or local features in the image, leading to imprecise segmentation results.

Certain medical images, like MRI, contain complex structures and multimodal information, with various sequences and tissue types, which might be difficult to accurately identify and segment manually. To improve efficiency and accuracy when processing large-scale data, complex structures, and multimodal information, automatic segmentation algorithms combined with manual assistance are needed to enhance medical image segmentation outcomes⁴.

Current state of research on spinal segmentation

No studies have proposed a complete segmentation of spinal structures. Currently, segmentation mainly includes manual segmentation, semi-automatic detection and segmentation, and fully automatic segmentation based on neural networks.

Manual clinical evaluation of lumbar disc pathologies

Lumbar disc herniation involves various disc pathologies, including but not limited to biomechanical causes, lumbar degeneration, and osteophyte formation at the vertebral margins. Biomechanically, as people age, the water content in the intervertebral discs decreases, and their viscoelasticity reduces, leading to stress concentration and resulting in disc deformation⁵. Lumbar degeneration involves the simultaneous deterioration of vertebral bone, soft tissue, facet joints, and intervertebral discs. Disc degeneration, atrophy, annular relaxation, vertebral body misalignment, and changes in the annulus fibrosus during vertebral movement, as well as increased tension on the vertebral edge cartilage from external factors⁶, are primary causes of LDH. Lee et al.‘s⁷ study evaluated the pathological connections between vertebrae, intervertebral discs, and neural foramina. Their work made important contributions to understanding spinal pathology, but the assessment method selected during the experiments showed inconsistencies among different clinicians. The mentioned assessment method is only suitable for small-scale case studies. In large-scale clinical applications, where the number of patients is significant, subjective evaluation methods, compared to systematic automated tools, may reduce efficiency and diagnostic accuracy. Future research should focus on developing standardized assessment methods to reduce misdiagnosis and missed diagnosis rates. Park et al.⁸, based on their experimental results, found inconsistencies in manual assessments of neural foramina among different doctors under the same medical standards. Cinotti and Peck’s teams⁹ made significant breakthroughs in understanding spinal diseases, showing that conditions like LDH result from a combination of factors, including deformities and neural foraminal stenosis, with disc pathology being a key contributing factor. Manual assessments face challenges in terms of efficiency and repeatability, often demonstrating lower efficiency and high subjectivity.

Semi-automatic segmentation methods based on ensemble algorithms

Concentration algorithms in statistical algorithms are widely used in the task of image segmentation of spine, including Bagging and Boosting techniques. Common methods are Random Forests (Random Forests) and Adaptive Boosting algorithm (Adaboost).

Zhan et al.¹⁰. achieved significant results using the Adaboost cascade classification framework and Haar wavelet features. However, the model’s robustness is weakened due to its reliance on Haar features, especially when dealing with complex spinal anatomy. When the image resolution is low, the performance of the classifier shows a significant decline. Future research should focus on exploring more generalized feature extraction techniques to address this issue. Huang et al.¹¹ proposed an Adaboost-based vertebral detection method, achieving 98% vertebral body detection efficiency. Korez et al.¹² used Random Forests and Canny operators to segment the vertebral boundary geometrically, achieving an average Dice score of 90. Cheng et al.¹³ segmented spinal CT images using localization and predicted the grayscale intensity trend of vertebral boundary changes through the Adaboost algorithm, with an average error of 1.6 mm across multiple datasets.

Suzani et al.¹⁴ leveraged multilayer perceptrons (MLPs) to extract contextual information for spinal images. They localized vertebrae by measuring the distance between geometric centroids, then used contour segmentation to extract individual vertebrae. Ebrahimi et al.¹⁵ proposed a method based on shape modeling, Random Forest classifiers, and dedicated visual features to detect spinal corner points in sagittal X-ray images. This method trains specialized Random Forest classifiers to locate each spinal region and corner point type, allowing for fast and accurate localization of individual vertebrae in both normal and pathological situations with the precision and robustness needed for clinical diagnosis and therapeutic decision-making.

Research on fully automatic methods

Fully automatic methods based on CNN

Current research on fully automatic segmentation of spinal MR images mainly includes, but is not limited to, improving deep learning network frameworks, integrating information from different types of MR images, introducing attention mechanisms, and incorporating cross-layer connections. Hwang et al.‘s¹⁶ U-Net-based fully automatic segmentation method surpassed earlier semi-automatic methods. However, the model still faces challenges such as boundary blurring, resolution variations, and high-frequency texture inconsistencies when segmenting different spinal structures. Due to the limited receptive field of convolutional kernels in the U-Net framework, it has restricted capability in extracting high-frequency regions such as complex structural boundaries and textures. To improve performance, future work should consider integrating models or utilizing multi-view data to enhance the model’s ability to capture spatial information for complex anatomical structures. Gong and colleagues¹⁷ proposed an end-to-end network framework (ResAttenGAN) to address significant differences in resolution, position, and shape within the same spinal structure, as well as boundary blurring between different structures, and overfitting due to insufficient training data. This network framework consists of full-feature fusion modules, attention modules, and adversarial learning modules, achieving simultaneous and accurate segmentation of multiple spinal structures. Liu et al.¹⁸ introduced a federated learning-based vertebral body segmentation framework (FLVBSF), incorporating a novel attention mechanism based on local dual attention gates (DAGs) and a global federated learning framework. Utilizing DAGs can improve the model’s sensitivity to vertebral body pixels and segmentation accuracy, significantly enhancing the accuracy of spinal segmentation models.

Pang and colleagues¹⁹ proposed a detection-guided hybrid supervised segmentation network (DGMSNet) for automatic spinal segmentation. This approach uses a hybrid supervised learning strategy in the segmentation network to achieve accurate and robust segmentation of spinal MR images. Wang et al.²⁰ proposed using multi-view features and graph convolutional networks to infer the relationships between vertebral bodies and intervertebral discs to achieve automatic segmentation of the spine and intervertebral discs in MR images. Pang and colleagues²¹ proposed a new two-stage framework (SpineParseNet) for vertebral body and intervertebral disc segmentation. SpineParseNet consists of a 3D graphical convolutional segmentation network (GCSN) for coarse 3D segmentation and a 2D residual network (ResUNet) for fine 2D segmentation, achieving accurate automatic segmentation of spinal MR images.

Li et al.²² proposed an MRI spinal segmentation algorithm based on a cross-attention mechanism and keypoint identification-assisted learning, effectively extracting multi-scale features from MRI, balancing inter-class similarity and intra-class diversity to enhance the network’s generalization capability and further improve the precision of intervertebral disc and vertebral body segmentation.

Fully automatic segmentation methods based on attention mechanisms

Although the attention mechanism also belongs to the branch of deep learning methods, we will discuss it separately from convolutional neural networks due to its performance enhancement in specific scenarios.The previous sections primarily covered fully automatic segmentation methods based on convolutional neural networks. Its remarkable sequence modeling capabilities and flexibility in self-attention mechanisms have introduced new performance improvements for spinal MRI image segmentation tasks. Tao et al.²³proposed a two-stage method to label and segment vertebrae. The first stage uses Spine-Transformers, treating the automatic labeling of vertebrae in arbitrary field-of-view (FOV) spinal CT scans as a one-to-one set prediction problem. This is achieved by designing a global loss function and a lightweight Transformer architecture for unique prediction and learnable positional embedding.

You et al.²⁴introduced a network model called EG-Trans3DUNet, which applies supervision to the edges of the vertebrae and incorporates additional global information via a global information extraction module, infusing global information from the entire case into the model, thereby enhancing the performance of identifying all vertebrae. This helps resolve issues with the similar appearance of adjacent vertebrae, improving the model’s segmentation consistency.

Zhang et al.²⁵ proposed a fully automatic method using 3D Swin Transformer as the backbone network, combined with the multi-scale feature fusion mechanism of the YoloX network and YoloHead. The article also discusses some traditional methods for spinal image segmentation and deep learning-based methods, pointing out their limitations. Finally, the study demonstrates the proposed method’s effectiveness and superiority in spinal segmentation tasks through experiments. Zhang and colleagues²⁶ presented a 3D lumbar vertebral cancellous bone localization and segmentation method based on a hybrid of CNN and Swin-Transformer. This method combines CNN and Swin-Transformer as two different encoders and introduces a loss function called LumAnatomy, designed to constrain the order and curvature of predicted vertebral centroids. This approach improves the accuracy of vertebral body localization. Additionally, a new multi-scale attention feature fusion module (MSA-FFM) was proposed to enhance feature fusion between parallel CNN and Swin-Transformer encoders. This module can effectively leverage the feature representation capabilities of different encoders to improve the model’s performance.

Contributions

Our study’s contributions include:

• (1) While mainstream research focuses primarily on regions such as vertebrae and intervertebral discs, there is relatively less emphasis on detailed structures like vertebral bodies, vertebral foramina, and laminae. Compared to traditional spinal vertebral segmentation, our research can analyze the pathological causes of spine-related diseases (including but not limited to the lumbar region) and identify internal pathological structures in vertebrae at various stages. This can effectively assist doctors in pathological analysis and research.

• (2) We innovatively use a segmentation network that combines WGAN with U-Net and Transformer structures. By modifying the generator, we transformed the conventional GAN generator network into an enhanced U-Net-based segmentation network with an embedded clustered Transformer structure. We also applied the k-means clustering method to optimize the Query matrix within the Transformer structure, reducing the computational complexity of the attention mechanism. This approach maintains the same segmentation accuracy as full attention scores, while improving boundary continuity and reducing semantic under-segmentation in complex structures, thereby enhancing segmentation accuracy in smoother regions.

Methodology

Data collection and organization

Our data is sourced from the public dataset provided by the Spark “Digital Human Body” AI Challenge Spine Disease Intelligent Diagnosis Competition organized by Aliyun. The dataset consists of T1 and T2 sagittal and axial images (FSE/TSE) from 200 cases, with the focus on T2 axial images of the thoracic and lumbar spine. The T2-weighted MRI image parameters include a resolution of 512 × 512 pixels and a pixel pitch of 0.3906 × 0.3906 mm. To preprocess the data, we first applied wavelet denoising to reduce noise in the original MRI images. Then, we used adaptive histogram equalization to enhance the contrast in localized regions of the lumbar structures. For segmentation, thresholding was performed based on histogram analysis using the Medical Imaging Interaction Toolkit (MITK), where grayscale histograms were visualized, and thresholds were manually selected to differentiate between target and background regions. After segmentation, the images were cropped to focus on the regions of interest, resized, and filled with zeros to ensure a uniform size of 512 × 512 × 1 pixels. Finally, Z-score normalization was applied to each pixel by calculating the mean and standard deviation, preserving the original feature distribution and minimizing the impact of variation across images.For target annotation, two radiologists utilized ITK-SNAP, with the final validation conducted by the head of the radiology department to ensure accuracy. To address the issue of sparse data, we performed rotational transformations and cropping operations on the data slices, and employed a 5-fold cross-validation approach for training and testing. The dataset was split into 60% training, 10% validation, and 30% testing. We also removed non-essential steps, such as complex manual visual inspection of histograms, to streamline the pipeline and enhance transparency and reproducibility.

Overall structure of the segmentation network

The overall framework of our proposed segmentation network for vertebral bodies, vertebral foramina, and laminae uses the WGAN architecture²⁷, addressing issues like gradient vanishing or explosion during training and low-quality samples caused by overly strong constraints in the generator. To overcome these challenges, we designed a feature generator network based on residual U-Net and a self-attention-based Transformer structure. In this paper, U-Net is chosen as a benchmark model for the following considerations: firstly, U-Net is used as one of the standard models in medical image segmentation tasks due to the effectiveness and robustness of its encoder-decoder structure in feature extraction. Secondly, the U-Net structure is highly scalable and allows for the effective fusion of various networks such as WGAN and Transformer modules to be combined to build innovative network structures.nnU-Net shows strong learning ability in multiple tasks, and its advantage lies in the automatic adjustment of hyper-parameters to different datasets, but its main network of segmentation is dominated by 2D U-Net and 3D U-Net. The focus of this study is to propose a new segmentation network architecture that combines WGAN, residual U-Net and clustering Transformer, and to verify the effectiveness of the network structure.

The overall structure of the generator and discriminator network is shown in Fig. 2. The network consists of (1) a residual U-Net encoder²⁸; (2) a cluster-based Transformer structure; (3) a residual U-Net decoder; and (4) a discriminator network.The residual U-Net encoder in the generator network extracts 2D features for the vertebral body, vertebral foramina, and laminae, while the decoder reconstructs detailed feature maps of these structures. WGAN, unlike traditional GAN, uses the Wasserstein distance as its objective function, making training more stable. The generator’s input is an MRI image of vertebrae, which is feature-extracted by the residual U-Net encoder and then reconstructed by the residual U-Net decoder to yield the predicted segmentation results.

To further improve the accuracy of target region segmentation, we expanded the region of interest by including additional background information from the neighbouring regions in the input image. A larger input is provided to the generator, allowing the network to capture more spatial information from the neighbouring regions. We introduce a discriminator network to evaluate the differences between the generated segmentation and the ground truth. The discriminator’s objective is to distinguish between real samples and generated samples. By alternately training the generator and discriminator, we can continuously optimize the generator’s segmentation capability to produce results that closely resemble the actual segmentation.In summary, the segmentation network structure for vertebrae, using a residual U-Net as the generator in the WGAN network, includes an encoder, decoder, and discriminator. The encoder extracts features, the decoder reconstructs images, and the discriminator assesses the generated segmentation results. By alternately training the generator and discriminator, we can achieve accurate segmentation of vertebral bodies, vertebral foramina, and laminae.

Fig. 2

The overall structure of the network is primarily composed of two parts: the generator and the discriminator. Since conventional GAN network generators often produce less effective predictions, we use a U-Net-based backbone network to predict and segment three types of structures: vertebral bodies, vertebral foramina, and laminae. By incorporating dilated convolutions and a cluster-based Transformer module (CTM), we further enhance boundary-capturing ability and improve pixel-level segmentation accuracy in the foreground. The role of the CTM module is to reduce the computational complexity of the attention mechanism by clustering feature vectors in the Query matrix, allowing the model to improve computational efficiency while maintaining accuracy. The purpose of the segmentation network is to boost the accuracy of the predicted labels by mixing the generator’s predictions with true labels to deceive the discriminator. This setup enables the generator to improve its performance through feedback from the discriminator.

Loss function

The overall network primarily consists of two structures: the generator network and the discriminator network. Hence, the total loss function comprises the loss functions from both the generator and discriminator networks. The generator network has a hybrid structure, so a polynomial-based loss function is used in the experiments. The composition formula for the generator network loss ${L_G}$, Eq. (1), is as follows:

$${L_G}=\alpha {L_{WG}}+\beta {L_{CE}}+\gamma {L_{Dice}}$$

(1)

where ${L_{WG}}$ is the loss for the generator in the Wasserstein GAN, and its calculation formula, Eq. (2), is as follows:

$${L_{WG}}= - {\mathbb{E}}[{D_{disc}}(G(I))]$$

(2)

In Eq. (2) the ${D_{disc}}$ parameter represents the discriminator.For the quality loss of the generated results, we choose a weighted combination of the cross-entropy loss function and the Dice loss function. The calculation formulas for the cross-entropy loss function and the Dice loss function, Eqs. (3) and (4), are as follows:

$${L_{CE}}= - \frac{1}{N}\sum\limits_{{i=1}}^{N} {\sum\limits_{{c=1}}^{C} {{Y_{i,c}}} } \cdot \log (G({I_{i,c}}))$$

(3)

$${L_{Dice}}=1 - \frac{{2 \times |G({I_i}) \cap {Y_i}|}}{{|G({I_i})|+|{Y_i}|}}$$

(4)

In Eq. (17), N represents the number of samples, C represents the number of classes, ${Y_{i,c}}$is the one-hot encoded representation of class c for the i sample in the target, and $G({I_{i,c}})$is the generator’s predicted probability for class c for the i sample. For the discriminator’s loss function, we use the Sigmoid cross-entropy loss${L_{sce}}$, with its structure described in Eq. (5):

$${L_D}=\frac{1}{m}\sum\limits_{{i=1}}^{m} {({L_{sce}}(} D({Y_i}),1)+{L_{sce}}(D({F_i}),0))$$

(5)

where m represents the total number of pixels, ${Y_i}$represents the ground truth labels, and ${F_i}$represents the predicted results from the generator network.

Generator network

Generator

We use the Wasserstein Generative Adversarial Network (WGAN), which aims to address the issues of training instability and mode collapse commonly found in traditional GANs. The generator and discriminator in a conventional GAN are defined by Eq. (6):

$${\hbox{min} _G}\,{\hbox{max} _{{D_{disc}}}}{{\mathbb{E}}_{x\sim {{\mathbb{P}}_d}}}[\log {D_{disc}}(x)] - {{\mathbb{E}}_{z\sim {{\mathbb{P}}_g}}}[\log (1 - {D_{disc}}(G(z)))]$$

(6)

In Eq. (6) the ${D_{disc}}$ parameter represents the discriminator. Where ${{\mathbb{P}}_d}$and ${{\mathbb{P}}_g}$represent the real data distribution and the generated data distribution, respectively. As can be seen from Eq. (6), traditional GANs use the Jensen-Shannon divergence as the objective function, which can lead to gradient vanishing or exploding problems during training, causing overall model instability. Additionally, traditional GANs create a competitive relationship between the generator and the discriminator. When there’s a significant difference in capabilities between the generator and the discriminator, the generator might fail to learn effective methods for generating samples, leading to mode collapse.

Our choice to use WGAN is primarily due to its use of the Wasserstein distance to measure the difference between the generator and the discriminator. The definitions for the generator and discriminator in WGAN are given in Eq. (7) as follows:

$${\hbox{min} _G}\,{\hbox{max} _{{D_{disc}}}}{{\mathbb{E}}_{x\sim {{\mathbb{P}}_d}}}[{D_{disc}}(x)] - {{\mathbb{E}}_{z\sim {{\mathbb{P}}_g}}}[{D_{disc}}(G(z))]+\lambda \cdot {D_{KL}}$$

(7)

where-${D_{KL}}$ denotes the K-Lipschitz constraint for the discriminator. $\lambda$ stands for the regularisation parameter. Compared to Eq. (6), the Wasserstein distance is more stable and can provide better training results. WGAN optimizes the Wasserstein distance by introducing ${D_{disc}}$ as a constraint, requiring that the discriminator’s gradient does not exceed a predefined threshold. This constraint can be achieved by weight clipping or gradient penalty in the discriminator.

Residual U-Net encoder

To improve the feature extraction performance of the encoder, we designed and enhanced it with specific improvements, which are detailed below. The U-Net-based encoder consists of four downsampling layers. Each downsampling layer comprises convolution layers, pooling layers, and activation functions. To address gradient vanishing as the number of downsampling layers increases, we embedded residual structures between the downsampling layers. This allows the shallow features extracted from the upper layer to be fused with the deeper features extracted from the lower layer, ensuring better stability during downsampling. The formula for the residual structure is given in Eq. (8):

$$F{(x)_{i+1}}=x+F{(x)_i}$$

(8)

where x represents the input to each downsampling layer, and $F(x)$ represents the output after processing through the downsampling layer. To address the traditional U-Net encoder’s limited ability to model longer distances, we designed an embedded self-attention-based Transformer structure between each downsampling layer. The self-attention mechanism allows dynamic allocation of attention weights, effectively focusing on positional information of complex target structures with smaller cross-sectional areas, such as vertebral bodies, laminae, and vertebral foramina, thereby enhancing regional segmentation accuracy.

However, the self-attention-based Transformer has slower convergence when resolving high-resolution shallow features, particularly in its Query, Key, and Value matrices. Inspired by²⁹, we propose clustering operations on the Query matrix to reduce the progressive complexity of the attention mechanism. The improvements related to this are detailed in section “Downsampling layer module”.

The structure of the residual U-Net encoder is shown in Fig. 3. To increase the receptive field size of the convolutional layers, we used dilated convolutions instead of traditional convolutions. This improvement is analyzed in detail in section “Residual U-Net encoder”.

Fig. 3

The structure of the residual U-Net encoder in the generator network primarily consists of residual structures and dilated convolutions. The downsampling layers, made up of these components, can extract features at different scales while reducing the risk of gradient vanishing. Because the areas of vertebral bodies, vertebral foramina, and laminae are relatively small compared to the background and show diversity, the use of a cluster-based Transformer structure improves the capture of positional information in foreground regions while reducing the progressive linear complexity.

Downsampling layer module

To segment the target structures of vertebral bodies, laminae, and vertebral foramina, we use axial slices during segmentation. The focus area for feature extraction mainly relates to extracting information from cross-sections. However, the downsampling convolution operations in the original residual U-Net encoder can lose some pixel-level detail when extracting smaller structures like intervertebral discs and laminae after multiple convolutions. Additionally, the limited receptive field size inherent to convolution operations results in a significant lack of global interaction information in the foreground region, leading to false-positive areas in segmentation predictions.To address these issues, we introduce a dilated convolution structure³⁰ to replace traditional convolution operations. The calculation formula for dilated convolution, Eq. (9), is as follows:

$${O_{i,j,k}}=\sum\limits_{{u=0}}^{{h - 1}} {\sum\limits_{{v=0}}^{{w - 1}} {\sum\limits_{{c=0}}^{{c - 1}} {{I_{(i \cdot s+u \cdot r),(j \cdot s+v \cdot r),c}} \times {K_{u,v,c,k}}} } }$$

(9)

${O_{i,j,k}}$ represents the output value at the i-th row, j-th column, and k-th channel, while ${I_{(i \cdot s+u \cdot r),(j \cdot s+v \cdot r),c}}$represents the input value at the $(i \cdot s+u \cdot r)$ row, $(j \cdot s+v \cdot r)$ column, and c channel. ${K_{u,v,c,k}}$ is the value of the convolutional kernel at the u-th row, v-th column, c-th input channel, and k-th output channel. h represents the height of the convolutional kernel, and w represents the width of the convolutional kernel. According to Eq. (10), dilated convolution increases the spacing between elements in the convolutional kernel (i.e., the dilation rate), thus enlarging the receptive field without increasing the number of parameters. Based on the residual U-Net encoder, this allows for capturing broader spatial information at multiple scales, enhancing the perception of intervertebral discs, laminae, and vertebrae’s overall structure.

As shown in Fig. 3, we introduce 3 × 3 convolutional kernels with different dilation rates in the four-layer downsampling convolutions. This allows the encoder structure to better capture contextual information in the foreground region while preserving the detail information of the intervertebral discs, laminae, and vertebrae target structures. The formula for calculating the receptive field, Eq. (10), is as follows:

$$N={\left( {{k_s}+({k_s}+1) \times (r - 1)} \right)^2}$$

(10)

where k represents the kernel size, r represents the dilation rate, and s represents the stride.By setting the dilation rates to 1, 2, 4, and 8, we can achieve receptive field sizes of 3 × 3, 7 × 7, 15 × 15, and 31 × 31, providing multi-scale receptive fields without increasing the kernel size. This approach increases the receptive field while reducing the overall parameter count and progressive complexity of the model.

Improvements to the attention mechanism based on self-expressive clustering

For segmentation of lumbar structures such as vertebral bodies, vertebral foramina, and laminae, the foreground regions are typically smaller compared to background regions, and the differences in grayscale values of structural features are often not significant. To capture the positional information and key feature patterns of labeled areas, we apply sequence modeling based on a self-attention mechanism—a local Transformer structure—to the deep features extracted by the residual U-Net encoder. Although Transformers with self-attention mechanisms can effectively extract features from foreground regions, the computational complexity of self-attention is proportional to the square of the length of the input image’s dimension vector. To reduce overall computational complexity, we apply subspace-based clustering to the query matrix in the attention mechanism, transforming overall attention scores into the attention scores of central points within each cluster. This approach reduces the progressive computational complexity of the local Transformer.

For a sequence with a length of N, the standard Transformer structure primarily uses dot-product-based multiplication attention. The calculation formula for dot-product attention, Eq. (11), is as follows:

$$\widehat {V}=AV=soft\hbox{max} \left(\frac{{Q{K^T}}}{{\sqrt {{D_k}} }}\right)V$$

(11)

where $A \in {{\mathbb{R}}^{N \times N}}$, Q represents the Query matrix and $Q \in {{\mathbb{R}}^{N \times {D_k}}}$, K represents the Keys matrix and $K \in {{\mathbb{R}}^{N \times {D_k}}},$ V represents the Value matrix and $V \in {{\mathbb{R}}^{N \times {D_v}}},$ ${D_k}$ represents the feature dimension of the query matrix, ${D_v}$represents the feature dimension of the Value matrix, and $\widehat {V}$represents the new value computed from the attention weights A. The progressive linear complexity for calculating traditional attention mechanisms is ${\rm O}({N^2}{D_k}+{N^2}{D_v})$. To reduce the randomness when calculating the attention weights A and improve the speed of linear fitting, we avoid calculating the dot product between the entire Query matrix and the transposed Keys matrix. Instead, we group the Query matrix into C clusters, and for each cluster, we calculate the attention weight of the cluster’s centroid, then backpropagate the calculated attention weight to each sample within the cluster to ensure the overall gradient doesn’t vanish. The calculation formula for the clustered Query matrix, Eq. (12), is as follows:

$${Q_c}=\frac{{\sum\nolimits_{{i=1}}^{N} {{W_{ij}}Q} }}{{\sum\nolimits_{{i=1}}^{N} {{W_{ij}}} }}$$

(12)

where ${Q_c}$ represents the set of centroids for each cluster after clustering, and ${W_{ij}} \in {\left\{ {0,1} \right\}^{N \times C}}$ represents the cluster weight matrix derived from partitioning the initial Q matrix into C clusters using the k-means algorithm. If the i-th Query matrix belongs to the j-th cluster, then ${W_{ij}}$ is set to 1. The W index matrix allows the calculation of cluster-based attention. The new formula for calculating the attention weights after clustering, Eq. (13), is as follows:

$${A^c}=soft\hbox{max} \left(\frac{{{Q^c}{K^T}}}{{\sqrt {{D_k}} }}\right)$$

(13)

The new formula for calculating the Value matrix, Eq. (14), is as follows:

$${\widehat {V}^c}={A^c}V \in {{\mathbb{R}}^{C \times {D_v}}}$$

(14)

The new Value matrix ${\widehat {V}^c}$ is calculated by first determining the attention weight ${A^c}$ from the cluster centroids ${Q_c}$ and the Key matrix, and then backpropagating the result to the corresponding samples in each cluster. During the clustering process, we first apply the k-means algorithm to the sample space in the Query matrix, assigning different samples to distinct cluster centers, thereby simplifying the calculation of attention weights. All feature vectors within each cluster share the same central attention calculation, further reducing computational cost. The clustered attention weights in Eq. 13 are used to update the weights of each sample, ensuring the transmission of overall information. This approach enables the model to achieve the same attention accuracy while reducing computational complexity, even on high-resolution medical images. The progressive linear complexity for calculating attention weights after clustering is ​${\rm O}(NC{D_k}+CN{D_v})$, which is reduced from the original ​${\rm O}({N^2}{D_k}+{N^2}{D_v})$. This shift in complexity changes the dependency from a quadratic correlation with the input sequence length N to a linear correlation. The cluster-based improved local Transformer structure, with reduced computational complexity, allows for greater focus on the positional information of deep feature pixels, facilitating the extraction of fine structures like intervertebral discs and vertebral bodies. The computational flowchart for the clustered Transformer is shown in Fig. 4.

Fig. 4

The clustered Transformer structure primarily uses k-means clustering on the Query matrix within the attention scores, then broadcasts the attention scores derived from the cluster centroids to each cluster. This approach approximates the full attention scores using multiple cluster centroids. The yellow, green, red, and blue colours of the Q matrix in the figure represent the clustering categories to which each sample of the data belongs.

Discriminator network

In the generator, we use a combination of residual U-Net and Transformer structures to generate predicted segmentation results. These predicted results, along with the ground truth labels, are simultaneously fed into the discriminator for learning and discrimination. Through adversarial learning, this approach can overcome the limitations of small-scale datasets for structures like vertebral foramina, vertebral bodies, and laminae, further enhancing the semantic segmentation performance of the model.The structure of the discriminator network is shown in Fig. 5. Unlike the encoder part in the generator, the discriminator’s main structure consists of convolution operations, normalization operations, and the activation function Leaky_ReLU. It has six convolutional layers, each with a kernel size of 3 × 3 and a stride of 2 × 2. We unified the input size for both the real labels and the predicted results to ensure consistency.

Fig. 5

By feeding real labels and predicted labels into the discriminator network, which consists of convolutional layers, the network judges the final result, promoting the learning of the segmentation network through adversarial learning. This process enhances the receptive field and reduces global forgetting in higher-level contexts.

Experiments

Segmentation evaluation metrics

To evaluate the segmentation performance of vertebral foramina, vertebral bodies, and laminae, we chose four metrics to measure segmentation accuracy and boundary precision for the three foreground targets. These four metrics are Dice segmentation accuracy, Hausdorff Distance (HD), mean Intersection over Union (mIOU), and Positive Predictive Value (PPV). The Dice coefficient measures the segmentation accuracy of smooth regions in the vertebral foramina, vertebral bodies, and laminae, while HD is used to assess the boundary segmentation accuracy for the foreground regions. By combining Dice and HD metrics, we can comprehensively evaluate the overall accuracy of foreground segmentation. The calculation formulas for these two metrics, Eqs. (15) and (16), are as follows:

$${\text{Dice}}=\frac{{2 \times {T_p}}}{{2 \times {T_p}+{F_p}+{F_n}}}$$

(15)

where ${T_p}$ represents the number of samples predicted as positive that are actually positive, ${F_p}$ represents the number of samples predicted as positive that are actually negative, and ${F_n}$ represents the number of samples predicted as negative that are actually positive.

$$H(A,B)=\hbox{max} \left\{ {\mathop {\sup }\limits_{{a \in A}} \mathop {\inf }\limits_{{b \in B}} d(a,b),\mathop {\sup }\limits_{{b \in B}} \mathop {\inf }\limits_{{a \in A}} d(a,b)} \right\}$$

(16)

where A represents the ground truth labels, and B represents the predicted labels. The mIOU metric measures the average degree of pixel overlap between the predicted result and the actual target area, while PPV reflects the proportion of correct positive predictions among the samples predicted as positive, primarily used to evaluate the accuracy of segmentation results for vertebral foramina, vertebral bodies, and laminae. The computation process for mIOU is outlined in Eq. (17):

$${\text{mIOU}}=\frac{1}{N}\sum\limits_{{i=1}}^{N} {\frac{{|{A_i} \cap {B_i}|}}{{|{A_i} \cup {B_i}|}}}$$

(17)

where N represents the number of classification categories, and ${A_i}$ and ${B_i}$ are the sets of predicted and actual values, respectively. The formula for computing the PPV, Eq. (18), is as follows:

$${\text{PPV}}=\frac{{{T_p}}}{{{T_p}+{F_p}}}$$

(18)

Experimental results and analysis

Comparison of segmentation results in experiments

For this experiment we chose five types of networks, U-Net, nnU-Net, SegNet, DeepLab v3 + and Spine-GAN, as comparison models. We chose these models for the following reasons: U-Net is a benchmark model for medical segmentation tasks due to its excellent performance in classification and segmentation tasks on medical datasets due to its encoder-decoder structure and hopping connectivity. nnU-Net model is an optimised model with automated tuning scheme for data preprocessing, which belongs to the U-Net structure, and achieves SOTA in a number of segmentation tasks. performance. The segmentation performance of this paper’s model is compared with the current automated optimisation methods by introducing the nnU-Net model. segNet, because of its simple and efficient way of decoding and feature map up-sampling, proves its effective feature learning capability in multiple tasks. deepLab v3+ is improved in the convolutional layer in a similar way to the method proposed in this paper, by inducing the spatial pyramid pooling and null convolution, which makes it more effective in The overall structure of Spine-GAN is similar to the model proposed in this paper, which incorporates generative adversarial network and LSTM structure. The performance of similar network structures on segmentation tasks is investigated by comparing Spine-GAN with the model in this paper.

To validate our model’s segmentation performance for the three target structures—vertebral foramina, vertebral bodies, and laminae—we conducted a comparative experimental study. The experimental dataset used the spinal MRI cross-sectional slices we collected, with a training set of 1018 slices and a test set of 170 slices. The comparative algorithms include six classical segmentation networks, with detailed information provided in Table 1.

Table 1 Structural information and training details of 6 comparative segmentation networks.

Experimental results for vertebral body segmentation

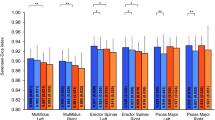
The results of repeated comparative experiments were collated and analyzed, with the experimental results for vertebral foramina, vertebral bodies, and laminae shown in Tables 2, 3 and 4. The experimental results were quantitatively analyzed using four indicators: Dice, HD, mIOU, and PPV. In the segmentation results for vertebral bodies, our model achieved the best results in all four metrics. The Dice score reached 92.6 ± 2.8, which is a 13.7% improvement compared to the traditional U-Net segmentation network. Additionally, compared to the four cutting-edge segmentation networks—nnU-Net, SegNet, DeepLab v3+, and Spine-GAN—our model improved the Dice score by an average of 7%, effectively demonstrating the effectiveness and accuracy of our model in segmenting smooth areas in vertebral bodies.

Regarding HD (95% confidence interval) results, our model achieved the shortest average HD distance of 1.7 ± 0.4 mm. This represents a 2.1 mm reduction in HD compared to the other five models, indicating significant improvement in boundary segmentation for vertebral bodies. In the mIOU and PPV metrics, our model reached 96.2 ± 1.5 and 98.8 ± 0.2, respectively, further showing that our model has a small gap between the predicted results and the true labels, indicating a higher accuracy in pixel classification. Figure 6 shows the visualization of the predicted results versus the ground truth. Analyzing the red labels representing the vertebral body segmentation, we can see that the U-Net and SegNet models exhibit slight under-segmentation in the smooth areas, indicating that pure convolutional neural network models might struggle to learn features in areas with no significant grayscale gradient differences, especially when the dataset is limited. Compared to Spine-GAN and our proposed model, the discriminator in the GAN structure aids in further feature discrimination and merging in smooth areas, contributing to improved segmentation of vertebral bodies.

In boundary segmentation tasks for vertebral bodies, the nnU-Net model, Spine-GAN model, and our proposed model all performed well, with our model achieving a boundary precision of 1.7 ± 0.4 mm. The visualization results in Fig. 6 further highlight the superior performance of our model in boundary segmentation tasks.

Table 2 Quantitative results of segmentation experiments on vertebral body structures for 6 segmentation networks

Experimental results for vertebral foramina segmentation

In the segmentation task for vertebral foramina, our model demonstrated optimal performance in both the Dice segmentation accuracy and mIOU metrics. The Dice score reached 91.5 ± 2.4, representing an average improvement of 7.08% compared to the other five models, indicating our model’s accuracy in segmenting smooth regions in vertebral foramina. In the mIOU metric, our model achieved a segmentation accuracy of 92.6 ± 1.5, reflecting a 7.5% average increase compared to the other five segmentation models, suggesting that our model has the highest degree of overlap with the ground truth, further validating its effectiveness in vertebral foramina segmentation tasks.Although our model didn’t achieve the shortest average HD distance in the HD metric, the difference between our model and Spine-GAN’s shortest distance was only 0.1 mm, indicating comparable precision in boundary segmentation.

Table 3 Quantitative results of segmentation experiments on vertebral foramina structures for 6 segmentation networks.

Experimental results for laminae segmentation

Lamina segmentation in medical imaging, particularly in MRI, is a highly technical task with multiple challenges. MRI images typically have high resolution and sensitivity to soft tissues, but low contrast between bone tissue and soft tissue makes accurate lamina segmentation quite difficult. Additionally, the laminae can vary in shape due to differences in the number of layers in cross-sectional slices, adding to the complexity of image segmentation.For the Dice metric in lamina segmentation, our model achieved an accuracy of 75.3 ± 4.2, representing an average increase of 6.18% compared to the other five models. The average shortest HD distance was 4.8 ± 0.4 mm, 0.4 mm shorter than the second-best Spine-GAN model. For the mIOU and PPV metrics, our model achieved optimal values of 81.9 ± 1.8 and 90.5 ± 3.6, respectively.

Comparing the predicted lamina segmentation results with the ground truth in Fig. 6, it is evident that the smooth regions of the laminae are relatively small and irregularly arranged, while the boundary curves are complex with multiple internal indentations. This complexity in the lamina’s boundary contributes to lower accuracy in the segmentation tasks among the three segmentation tasks, leading to lower pixel overlap and evaluation metrics like mIOU and PPV. Despite these challenges, our proposed model still achieved relatively optimal segmentation accuracy and outcomes. Compared to other segmentation models, our model demonstrated improved continuity in boundary segmentation.

Table 4 Quantitative results of segmentation experiments on laminae structures for 6 segmentation networks.

Fig. 6

The visualization of semantic segmentation results for the three target structures—vertebral bodies, vertebral foramina, and laminae—using our proposed segmentation network and five comparative segmentation networks. Areas marked in red indicate false positive regions, where the predicted segmentation includes excess segmentation in those areas.

Ablation study analysis

To validate the completeness of our proposed network structure, we conducted ablation experiments to test various modifications to the original network structure. The quantitative results for the segmentation experiments are detailed in Tables 5 and 6. To verify the significance of performance differences from various improvement measures in the segmentation experiments, we conducted t-tests on the Dice coefficient and HD metrics in the ablation study.We used U-Net as the base structure, set as the control group, with experimental groups consisting of U-Net with residual structures, U-Net with traditional Transformer modules, and U-Net with clustered Transformer modules. Additionally, we tested a residual U-Net with a combination of the clustered Transformer module and dilated convolution structures. Finally, our proposed model, a combination of WGAN, residual U-Net, and clustered Transformer, was evaluated.As shown in Table 5; Figs. 7 and 8, the original U-Net network with added residual structures improved by an average of 1.9% in the Dice metric and reduced the average HD distance by 1.25 mm. This indicates that the residual structure effectively enhances the segmentation accuracy in smooth areas and the continuity in boundary regions for vertebral bodies and vertebral foramina.

In comparing our proposed clustered Transformer module with the traditional Transformer module, the average difference in the Dice metric was only 0.15%, and the HD metric achieved similar segmentation accuracy. This demonstrates that the clustered Transformer module can achieve the same segmentation accuracy while reducing linear progressive complexity compared to the traditional Transformer module.When combining the dilated convolution structure with the residual U-Net and the clustered Transformer module, the Dice score for vertebral bodies increased by an average of 8.05%, while for vertebral foramina and laminae, the average increase was 4.7% and 6.5%, respectively. This demonstrates that our proposed improved modules effectively enhance the segmentation accuracy in smooth areas across the entire network.

Table 5 Results of ablation comparative experiments for segmentation networks with different modules.

Fig. 7

Comparison of dice results in ablation experiments with different modules (such as residual, transformer module, and clustered transformer module).

Fig. 8

Comparison of HD results in ablation experiments.

Table 6 Results of ablation comparative experiments for segmentation networks with four different modules.

Compared to the residual U-Net network with dilated convolutions and the clustered Transformer module, our proposed WGAN-based network model achieved average Dice improvements of 4.5% for vertebral bodies and 0.4% for vertebral foramina, while also reaching similar segmentation accuracy for the lamina segmentation task. This demonstrates that our proposed segmentation network achieves relatively optimal overall segmentation performance in smooth areas. Furthermore, in the HD metric, our model obtained the shortest HD distance across all three structures: vertebral bodies, vertebral foramina, and laminae, with an overall average reduction of 0.9 mm. This indicates the superiority of our model in boundary segmentation accuracy for these structures.

From the visualized segmentation results in Fig. 9, our proposed model (i) showed significant improvements in smooth region segmentation and boundary segmentation for vertebral bodies, vertebral foramina, and laminae compared to the base model (c), U-Net. Models with added Transformer modules (e), (f), and (h) demonstrated noticeable improvements in boundary segmentation continuity, indicating the effectiveness of Transformer structures based on attention mechanisms in enhancing boundary segmentation performance.

Analyzing Table 6, which includes the mIOU and PPV metrics, our model showed the highest overlap and similarity between the predicted segmentation results and the ground truth for vertebral bodies, vertebral foramina, and laminae. We achieved an average mIOU of 90.25 and a PPV of 94.5%.In summary, the experiments with various improved modules demonstrate that our proposed improvements significantly enhance the segmentation accuracy for the three target structures: vertebral bodies, vertebral foramina, and laminae. From Table 5, U-Net + Res + CTM compared with U-Net group, U-Net + Res group, and U-Net + TM group, there was a significant improvement in the indexes of Dice and HD.U-Net + Res + CTM showed a 3.3% improvement in Dice score in the disc segmentation task, and showed a significant improvement in boundary segmentation (HD), with the HD index reaching an average of 4.1 mm. the effect is especially prominent in the processing of fine structures.

However, compared with the clustered TM module, the TM module did not significantly improve HD while maintaining the improved Dice score. combined with the mIOU and PPV results of U-Net + Res + CTM in Table 6, it can be seen that adding the TM module to the residual structure can improve the segmentation performance to a certain extent, especially in the mIOU, but its processing of the boundary details still falls short of the ideal level. There are some limitations on the segmentation accuracy for smooth regions and boundary continuity segmentation. The experimental results show that, on the Dice coefficient and HD metrics, the model with the added clustered Transformer module demonstrates significant improvement over the baseline model at a significance level of p < 0.05, indicating that this module effectively enhances the model’s boundary segmentation accuracy.

From the visualised segmentation results in Fig. 9, it can be seen that the U-Net + Res + CTM experimental group (g) is better than the U-Net + TM experimental group (f) in boundary continuity segmentation. It proves to outperform the original models such as U-Net + Res and U-Net + TM in Dice metrics and HD metrics, and the experimental results show that the model with the addition of the clustering Transformer is able to improve the overall segmentation performance more efficiently, especially in the boundary continuity and small region segmentation.

In order to verify the statistical significance of our proposed 3 categories of improvements, we subsequently plan to test the results of multiple experiments for statistical significance. A t-test is used to verify whether the differences in segmentation performance between different modules such as Residual Structure, Transformer module and Clustering Transformer module are statistically significant. Verifying that the differences in model performance are not just due to random factors ensures the robustness and reliability of the experimental results.

Fig. 9

Visualization of the ablation experiment segmentation results. The areas marked in red indicate false-positive regions, while those marked in yellow indicate false-negative regions.

We plan to further explore comparative experiments with state-of-the-art models such as nnU-Net in future research, especially to optimise the model performance using the hardware resources of modern 24GB large memory GPUs.

Summary and discussion

Current research on spinal segmentation focuses on the segmentation of the vertebral body, with less attention paid to the segmentation of specific localized structures such as the vertebral bodies, foramina and vertebral plates. However, these localized structures of the spine have important clinical significance in diagnosis. In MRI image segmentation, segmentation of the vertebral plate is particularly challenging, requiring fine labeling during segmentation to avoid mistaking adjacent muscles, nerves, or other tissues for bones. Although artificial intelligence and machine learning techniques can help in this area, the adaptability and generalization ability of the technique to different local structures has not been fully validated, especially when the model needs to be generalized to more complex anatomical regions, where its performance may be limited. In addition, this method lacks a discussion of generalization to other spinal structures or other parts of the human body, which may make it difficult to generalize its application to different medical imaging scenarios.

We address the problem of efficient segmentation of vertebral bodies, foramina, and vertebral plates by designing a WGAN-based multi-objective adversarial network. Our approach combines the residual U-Net and Transformer structures in a generator network, aiming to improve the low accuracy of traditional generator networks and the problem of blurred boundaries in segmentation results. However, although the Transformer’s self-attention mechanism is effective in extracting local structural features, its computational complexity is still high, which may negatively affect the training speed of the model and real-time applications. Although we simplified the Query matrix by k-means clustering to reduce the computational complexity of Transformer, the generalization ability of the method in different imaging modalities (e.g., CT) has not been validated. Therefore, although the method performs well on MRI data, its adaptability and stability to other image data still need further research and validation.