Fast moving table tennis ball tracking algorithm based on graph neural network

Abstract

The key object tracking in sports video scenarios poses a pivotal challenge in the analysis of sports techniques and tactics. In table tennis, due to the small size and rapid motion of the ball, identifying and tracking the table tennis ball through video is a particularly arduous task, where the majority of existing detection and tracking algorithms struggle to meet the practical application requirements in real-world scenarios. To address this issue, this paper proposes a combined technical approach integrating detection and discrimination, tailored to the unique motion characteristics of table tennis. For the detector, we utilize and refine a common video differential detector. As for the discriminator, we introduce GMP (a Graph Max-message Pass Neural Network), which is designed specifically for tracking table tennis balls or similar objects. Furthermore, we enhance an existing dataset for table tennis tracking problems by enriching its scenarios. The results demonstrate that our proposed technical solution performs impressively on both the dataset and the intended real-world environments, showcasing the good scalability of our algorithms and models as well as their potential for application in other scenarios.

Introduction

The application of AI technology in sports has emerged as one of the recent research hotspots, with AI-based sports analysis already finding its way into various sports such as football, tennis and billiards. These intelligent analysis systems deployed in sports scenarios typically leverage multiple advancements in AI fields as their core technological components, adapting them to cater to the specific needs of sports analysis. For instance, human body key point extraction and pose recognition techniques are employed to identify athletes’ movements, while object detection and tracking technologies are utilized to record and analyze match scenarios. Additionally, anomaly detection and recognition techniques based on video and motion image features are used to extract key frames. These technologies aid athletes and coaches in making rational plans and decisions, reducing the cost of training and teaching, and enhancing the popularity of sports, thereby developing and elevating the overall performance level of the sport.

Similarly, table tennis is a widely popular sport globally, and video-based intelligent analysis systems for table tennis can assist a vast number of enthusiasts and athletes in evaluating their tactical characteristics, providing standardized movement guidance¹, and planning scientific training, thereby effectively enhancing their skill levels. Consequently, video-based intelligent analysis systems for table tennis techniques possess broad application prospects and ample demand. Within these intelligent analysis systems, ball tracking is an indispensable key technology. It can assist the system in determining the point of contact², delineating the start and end moments of movements to aid in action classification and standardization³, and supporting the action recognition system in segmenting rounds and scoring. However, the small size, rapid motion, and insignificant and unstable image features of the table tennis ball bring many difficulties to the tracking algorithm. Further more, well-researched target detection and tracking algorithm recently,including pedestrian tracking (primarily focused on larger targets with clear image features), and unmanned aerial vehicle (UAV) detection and tracking algorithms (where targets are small but feature-stable, making motion easier to track) are inapplicable in our scenario for these difficulties. Examples of table tennis balls to be detected and tracked are shown in Figure 1.

Fig. 1

Examples of table tennis balls to be detected and tracked.

In the context of small object detection, research represented by⁴suggests that leveraging contextual information and adjacent video frames can enhance tracking capabilities. On the other hand, studies focusing on high-speed moving object tracking, exemplified by⁵, propose the utilization of frame differences and analysis of differential images to separate the target from the background. Inspired by these two perspectives, our proposed approach combines detection and discrimination to track table tennis balls. Similar ideas have been explored in existing research, where⁶and⁷achieved good detection results using similar concepts. However, due to the processing of unstructured data, their discriminators tend to have numerous parameters, complex structures, and slow runtimes. Although existing Graph Neural Networks (GNNs) can handle unstructured data, they do not adapt well to the demands of tracking problems. The vast majority of research employing graph neural networks for tracking tasks has focused on Multiple Object Tracking (MOT) datasets, which emphasize the construction of relationships between targets while rarely considering the presence of erroneous, false, or even uncertain targets. While numerous similar studies have also prioritized handling severe occlusion and target loss scenarios⁸, these methods still rely on inferences based on relatively good detection results, rather than operating from the outset under the challenging conditions encountered in table tennis videos. Therefore, we introduce a novel Graph Max-message Pass Neural Network (GMP) as a new discriminator specifically designed for tracking and filtering table tennis balls or similar targets. The overall approach of the proposed algorithm will be detailed in Section 3, with a focus on the analysis of the discriminator GMP in Section 3.5.

To train effective models and validate the efficiency of our method, we build a dataset with rich scenarios based on existing research⁵⁶⁷⁹and conduct comparisons with various general-purpose algorithms on this dataset. The general-purpose algorithms we compared against include YOLOv8, which performs object detection based directly on single-frame image features¹⁰¹¹¹², Single Object Tracking (SOT), which relies on user annotations and image features for tracking¹³, and a scheme that utilizes the generic Graph Attention Network (GAT)¹⁴ as a discriminator. Our findings indicate that our method outperforms all the comparison algorithms and holds the potential to address other object tracking problems. In Section 4, we will delve into the detailed analysis of the performance of our proposed method. In Section 2, we will review related works, and in Section 5, we will provide a brief summary and outline future research directions.

In practical training and match analysis, our algorithm can directly provide information such as the image location and trajectory of the table tennis ball. These direct data assist the analysis system in segmenting rounds and actions. With subsequent analysis and processing, we can obtain the land point and hit point of the table tennis ball and estimate its approximate speed (shown in Figure 2). During training and matches, by analyzing these data, we can quantify players’ stability, offensive, and defensive capabilities, and use the data to arrange corresponding tactics and targeted training. For instance, in training, by analyzing players’ ball-striking speed and trajectory direction, coaches can correct their force generation method and angle during ball striking, thereby improving their hitting quality. During matches, coaches can formulate reasonable counter-tactics for their own players based on data such as the trajectory and land point of the opponent’s table tennis ball. Compared to commonly used match result analysis, scoring and losing statistics, the results provided by the table tennis tracking algorithm are more precise, detailed, and rigorous.

Fig. 2

Further analysis of the tracking results of table tennis can yield many useful technical and tactical information (including land point, hit point, approximate ball speed, etc. ). In particular, we roughly calculate the average pixel distance of the table tennis ball between a trajectory frame, and then roughly estimate the ball speed of the table tennis ball based on the pixel length of the center line of the table, the actual length (2.74m), and the video frame rate (in this case, the frame rate of the video is 30 fps).

Related works

In our previous research⁶, we leveraged a tree structure to establish contextual relationships among potential table tennis ball targets. Initially, we employed a differential detection method to filter out numerous potential targets, ensuring a sufficiently high recall rate. Subsequently, based on the proposed tree structure and the kinematic characteristics of table tennis, we refined the targets to identify the table tennis ball through trajectory analysis associated with the leaf nodes in the tree. This approach achieved certain success in terms of accuracy and adaptability across different scenarios. However, it relied heavily on manually tuned empirical parameters and operated relatively slowly. Consequently, we have further delved into this field and present the method proposed in this thesis. Our related work revolves around four aspects: the significance of table tennis tracking algorithms for intelligent analysis systems, object detection methods, traditional object tracking methods, and graph neural network-based object tracking methods.

The significance of table tennis tracking algorithms for intelligent analysis systems

Currently, there have been a number of studies, achievements, and datasets related to intelligent analysis systems for table tennis⁹, yet the tracking of table tennis balls in complex scenarios remains limited. This is due to the high technicality of table tennis, which has led most research to focus on motion guidance and standardization. These studies typically utilize deep learning methods to extract human body keypoints, employing them to model and estimate human poses¹⁵. Algorithms can then determine the start and end of actions based on the pose skeletons of individuals in video frames¹⁶, classify technical actions¹⁷, and design rules for evaluating technique execution. Similar technical solutions do not require table tennis ball detection as they rely solely on human skeletons and keypoints; however, analyzing actions based only on skeletons remains a challenging task¹⁸¹⁹. This approach is only effective in relatively standardized training environments. In less standardized training and competition scenarios, the movement of the table tennis ball is highly variable²⁰, and players need to adjust their actions accordingly. Without effective table tennis ball tracking technology, intelligent analysis systems may fail to adapt to such changes, leading to useless or even erroneous analysis and guidance, significantly reducing the accuracy and recall rates of motion guidance³. Tracking results for table tennis balls can assist in precisely dividing action stages for motion analysis and guidance, aiding in the assessment of the standardization and rationality of actions.

Object detection methods

With the development of object detection techniques in computer vision, detecting objects directly from images based on their edges, morphology, color, and other features, and regressing the bounding boxes of these objects, has become one of the primary methods for object detection. Representative methods include YOLO and FASTER-RCNN. Among them, YOLO¹²has gained widespread popularity due to its simple structure, strong adaptability, and fast operation¹⁰¹¹. Previous studies have found that applying these methods directly to table tennis ball detection is not ideal due to the small size and excessive blurring of the ball⁷. Some scholars have used an improved FASTER-RCNN algorithm to detect table tennis balls based on their small size characteristics, achieving good results²¹. However, there is still room for improvement in terms of the method’s performance metrics and adaptability to complex scenarios.

Some scholars have chosen to focus on the rapid movement characteristics and shape of table tennis balls, attempting to extract the rapidly moving balls in the foreground based on differential images⁵. Other studies have tried to directly segment blurred table tennis balls in the foreground using deep learning techniques²²⁹, while some have considered relying on background information from the table tennis table to separate the balls in the foreground²³. These methods perform well in scenarios with uncomplicated backgrounds, but table tennis sports videos in real-world are full of various noises, background clutter, and interference caused by athlete movements. Under such circumstances, the aforementioned approaches often fail to function properly. Some studies have proposed using local images for detection and excluding most image regions based on the ball’s motion characteristics to avoid background interference²⁴. However, table tennis sports videos in real-world contain a large number of invalid segments where the ball is not present, which limits the direct application of the aforementioned methods.

Traditional object tracking methods

Since relying solely on single-frame images cannot effectively solve the problem of table tennis ball tracking, a natural approach is to leverage the contextual and spatio-temporal information from videos for detection. The conventional idea behind such methods is to extract all potential candidate regions and targets from images or video frames, aggregate these targets, and then screen them based on image features, motion characteristics, and spatio-temporal information to obtain the final tracking results²⁵.

In⁴, researchers extracted all potential targets from single-frame images and then filtered out the best results based on video context, improving the detection effectiveness for blurred small objects. In²⁶, researchers successfully tracked vehicles in videos with significant distortion by combining the motion characteristics of vehicles. In²⁷, researchers achieved billiards tracking and 3D reconstruction by proposing all possible positions and shapes of the cue ball.

Furthermore, table tennis ball tracking can also be considered as part of the Single Object Tracking (SOT) problem²⁸. However, due to SOT’s heavy reliance on stable image features and feature extraction networks²⁹, its application to table tennis ball tracking is limited. Nevertheless, in this context, researchers often focus on the Region Proposal Network (RPN) responsible for candidate region generation¹³. The role of this network is to analyze all potential candidate regions and select the optimal tracking results. This aspect of the work essentially involves analyzing and discriminating all potential targets from a global perspective, assessing the confidence of each target based on prior information, and filtering out the results.

However, since the relationships among all potential targets are unstructured data, it is difficult to vectorize prior information and decision-making conditions. Therefore, most of the aforementioned studies did not use deep learning methods in addressing tracking problems, which limited their ability to extract deeper and more essential information, resulting in poor adaptability.

Graph neural networks based tracking method

In deep learning, to handle non-Euclidean space data, researchers proposed Graph Neural Networks (GNNs)³⁰. With the gradual development of deep learning and its applications, researchers have found that GNNs can adapt to various unstructured data. Currently, apart from the original GNNs, Graph Attention Networks (GATs) are also mainstream in the industry¹⁴. Some scholars have even suggested that Transformer is essentially a fully connected GNN³¹. GNNs are widely used in prediction, optimization, feature learning, and other problems due to their adaptability to unstructured data³².

³³employed GNNs to improve prediction results in latent spaces, while³⁴used GNNs to learn feature information from unstructured data in multi-agent motion. In³⁵and³⁶, GNNs were utilized to study team collaboration mechanisms in football and select the best combinations or players for the game³⁷. applied GNNs to merge and group targets in tracking problems. GNNs can adapt to unstructured data, converting traditional methods such as traversal, screening, and matching in tracking problems into regression and classification tasks in deep learning, thereby enhancing tracking performance³⁸. They have also improved the performance of tracking problems in general³⁹.

In the context of SOT, the application of graph attention mechanisms effectively integrates image feature information, leading to improved tracking performance⁴⁰. For tracking problems involving objects with distinct motion patterns and characteristics, such as vehicles and high-speed particles, GNNs can process unstructured trajectory information, predict target positions, assist in target search and reconstruction, and enhance tracking performance⁴¹⁴². In multi-target tracking problems involving pedestrians and robots, GNNs primarily facilitate message passing among objects, enabling potential targets to refine their features and learn patterns from videos or contextual images⁴³⁴⁴. used message passing in GNNs to determine the consistency among potential targets, while⁴⁵directly matched target features obtained from GNNs. Both methods achieved superior tracking results compared to traditional methods with the assistance of GNNs. During this process, some studies have attempted to modify the structure and frameworks of graph neural networks to enhance information aggregation capabilities and tracking efficiency within graphs^46,47. These methods have demonstrated promising results and improvements in pedestrian tracking and matching for Multiple Object Tracking (MOT) scenarios.

Summary

Despite the abundance of detection and tracking algorithms proposed in current research, which have achieved remarkable performance in tracking feature-rich targets such as pedestrians, they cannot be directly applied to the context and problems of table tennis analysis in our study. A single detection scheme fails to provide satisfactory accuracy and recall rates, while most tracking methods primarily focus on relationship matching issues similar to those in MOT datasets, rendering them unsuitable for our required scenarios. Although graph neural networks excel at handling unstructured data, neither GNNs nor GATs yield satisfactory results for our purposes. Notably, we recognize that the tracking tasks we envision for graph neural networks under numerous false target conditions extend beyond mere relationship matching and information fusion; they necessitate a reinterpretation (detailed in Section 3). To better accomplish this reinterpreted graph task, we propose the Graph Max-message Pass Neural Network (GMP), which we demonstrate to effectively address the challenges of table tennis tracking.

Method

Problem formulation

Fig. 3

Video frames and table tennis balls to be tracked.

The input data processed by the method proposed in this paper is a video $\Phi$, which consists of n video frames (Image, I), i.e., $\Phi = [I_{1},I_{2},\ldots ,I_{n}]$. Each frame image may or may not contain a table tennis ball, and there also may be one or multiple table tennis balls in each frame image. Therefore, we assume that there are k table tennis balls $(k = 0\ or\ k \in N^{+})$ in each frame image. We collect all these k table tennis balls in the $t^{th}$ frame image into a set $B^{t}$, where the balls are sequentially numbered as $\ b_{i}^{t}$. Specifically, $b_{i}^{t}$ denotes the $i^{th}$ table tennis ball in the $t^{th}$ frame. It should be noted that if $k = 0$, then $B^{t}$ is an empty set. In this way, we obtain a total of n sets: $B^{1},B^{2},\ldots ,B^{n}$.

The continuous movement of table tennis balls in multiple frame images is called a trajectory T. Obviously, there may be multiple trajectories throughout the video, which we assume to be $T_{1},T_{2},\ldots ,T_{u},\ldots ,T_{s}$. Any trajectory $T_{u}$ represents an ordered sequence of table tennis balls $[b_{i_{1}}^{j_{1}},b_{i_{2}}^{j_{2}},\ldots ,b_{i_{m}}^{j_{m}} ]$, where $j_{1}< j_{2}< \ldots < j_{m}$. We know that $b_{i_{1}}^{j_{1}} \in B^{j_{1}},b_{i_{2}}^{j_{2}} \in B^{j_{2}},\ldots ,b_{i_{m}}^{j_{m}} \in B^{j_{m}}$. It should be noted that, in $T_{1},T_{2},\ldots ,T_{s}$, the table tennis balls subordinated to different trajectories $T_{u}$ are all distinct. That is to say, for any given real table tennis ball $b_{i}^{t}$, it can only belong to a specific trajectory $T_{u}$ and cannot be simultaneously associated with two trajectories. Additionally, we assume that every table tennis ball $b_{i}^{t}$ will appear in the form of a trajectory, indicating that $T_{1} \cup T_{2} \cup \ldots \cup T_{s} = B_{1} \cup B_{2} \cup \ldots \cup B_{n}$.

Our ultimate task is to identify all the trajectories $T_{1},T_{2},\ldots ,T_{s}$ within the frame images $[I_{1},I_{2},\ldots ,I_{n}]$ from video $\Phi$. An example is shown in Figure 3.

Frameworks and processes

Firstly, we will outline the entire process of the proposed method:

Step 1: Each video frame image $\{ I_{1},I_{2},\ldots ,I_{n}\}$ will be processed through the object detector $h_{real}$, resulting in a set of potential objects for each frame. Consequently, we obtain n sets of potential objects, denoted as ${[O}^{1},O^{2},\ldots ,O^{t},\ldots ,O^{n}]$. These sets are similar to the sets of ping-pong balls $B^{t}$ in each frame, except that $B^{t}$ represents the actual table tennis targets, whereas $O^{t}$ comprises potential table tennis targets. Specifically, $O^{t} = \{ o_{1}^{t},o_{2}^{t},\ldots ,o_{k}^{t}\}$, where $o_{i}^{t}$ represents the i-th potential table tennis target in the t-th frame. Section 3.3 will provide a detailed introduction to the object detector $h_{real}$.

Step 2: Utilizing a sliding window (Window, w) and a gap (Gap, g), we sequentially select the potential target sets $O^{t},O^{t + 1},\ldots ,O^{t + w - 1}$ obtained from Step 1 to construct a set of graphs $G = \{ G_{1},G_{2},\ldots ,G_{r}\}$ for further discrimination. Each graph $G:\{ V,E\}$ comprises a set of nodes V and a set of edges E. The definitions of nodes and edges, as well as the specific construction method of the graphs, will be elaborated in Section 3.4.

Step 3: Each graph in the set $G = \{ G_{1},G_{2},\ldots ,G_{r}\}$ will be fed into the discriminator $f_{real}(\theta ,G_{r})$ to obtain a set of graphs $G^{p} = \{ G_{1}^{p},G_{2}^{p},\ldots ,G_{r}^{p}\}$, where both nodes and edges have associated probabilities. If the input graph to the discriminator is $G:\{ V,E\}$, then the output probability graph is defined as $G^{p}:\left\{ V^{p},E^{p} \right\} \ \ where\ V^{p} = \left\{ (v,p(v))|v \in V,p(v) \subset [0,1]\right\} \ ,E^{p} = \left\{ (e,p(e))|e \in E,p(e) \subset [0,1]\right\}$. In Section 3.5, we will introduce the discriminator $f_{real}(\theta ,G)$ in detail.

Step 4: Finally, based on all the probability graphs $G^{p}(G_{1}^{p},G_{2}^{p},\ldots ,G_{r}^{p})$, we derive a set of trajectories ${[T}_{1},T_{2},\ldots ,T_{s}]$ as the final result. Section 3.6 will explain the method of obtaining the final trajectories ${[T}_{1},T_{2},\ldots ,T_{s}]$ from the probability graphs $G^{p}$.

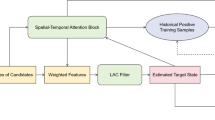
The whole process of the proposed method is illustrated in Figure 4.

Fig. 4

Flowchart of the proposed method, Step 1 extract potential targets, Step 2 organize these potential goals into a graph, Step 3 compute the confidence of each potential target and the relationship between them (i.e., gives the confidence of the nodes and edges in the graph), Step 4 organize the results of the track based on the confidence of these goals and relationships.

In the proposed method, the two core steps are the detector and the discriminator. Below, we briefly introduce our thought of the design about these two core steps, which is important to understand following detail description of each step of the proposed method.

For the problem of trajectory tracking of a specific target in a video, the most straightforward solution is to train a detector specifically for that target. In the case of table tennis trajectory tracking, this detector is represented as $p\left( b_{i}^{t}|I_{t} \right)$, which detects table tennis balls from each video frame image based on the detector. Subsequently, all detected table tennis balls, denoted as $b_{i}^{j}$, are linked together. However, due to the sparse and easily blurred features of a single table tennis ball in the image, directly construct the detector $p\left( b_{i}^{t}|I_{t} \right)$ for table tennis faces numerous challenges and yields unsatisfactory results. For instance, Figure 5 demonstrates an example of the results obtained from a table tennis ball detector (YOLOv8), which is trained by the dataset mentioned in Section 4 based. It can be observed that there are numerous missed detections and false detections.

Fig. 5

Object detection results of the trained detector YOLOv8.

To solve this problem, we need to approach it from a different way. Since the result trajectories ${[T}_{1},T_{2},\ldots ,T_{s}]$ to be output are independent of each other, we can simply analyze the detection process of a specific trajectory $T_{u}$. In the existing video stream $\phi = \{ I_{1},I_{2},\ldots ,I_{n}\}$, when we do not know $T_{u}$, we can arbitrarily designate potential targets $o_{i}^{j}$ in different frames of the video $\phi$. Subsequently, we concatenate them in the order of their appearance to obtain $T_{{possible}_{v}} = [o_{i_{1}}^{j_{1}},o_{i_{2}}^{j_{2}},\ldots ,o_{i_{m}}^{j_{m}} ]$. Evidently, we can obtain $T_{u}$ sooner or later by endlessly proposing $T_{{possible}_{v}}$. Let’s assume that all proposed $T_{{possible}_{v}}$ form $T_{\Sigma }$, i.e., $T_{\Sigma } = {\{ T}_{{possible}_{1}},T_{{possible}_{2}},\ldots ,T_{{possible}_{v}},\ldots \}$. Now, considering the posterior probability of $T_{u}$ from the perspective of $T_{\Sigma }$ we have $p\left( T_{u} \bigg | \phi \right) = \ \frac{p\left( T_{u} \right) p\left( \phi \bigg | T_{u} \right) }{p(\phi )}$. Since $p(\phi )$ does not participate in the posterior calculation of $T_{u}$, according to the maximum posterior criterion, $\underset{T_{u}}{argmax}{p\left( T_{u}|\phi \right) } = \underset{T_{u}}{argmax}{(\log \left( p\left( T_{u} \right) \right) + log(p(\phi |T_{u})))}\ where\ T_{u} \in T_{\Sigma }$.

Then, we delve into a detailed analysis of the above expression. Assuming that the two terms in the expression are largely independent during the optimization process (or have minimal mutual influence), we can optimize them individually:

• (1) The term $\log \left( p\left( T_{u} \right) \right)$ can be regarded as a probabilistic model that discriminates whether $T_{u}$ is sufficiently close to the prior of table tennis motion characteristics. To estimate $p\left( T_{u} \right)$, we need to build a discriminator based on a dataset of table tennis motions.

• (2) For the second term $log(p(\phi |T_{u}))$, we can consider a generative model of $\phi$ as $\phi = \phi _{Inital} \oplus T_{u}$, where $\phi _{Inital}$ can be interpreted as the background component (or video prior) of the image stream under analysis. The relationship between these components is expressed as $p\left( \phi |T_{u} \right) p(T_{u})p(\phi _{Inital}|\phi ,T_{u}) = p(\phi )p(T_{u}|\phi _{Inital},\phi )p(\phi _{Inital}|\phi )$. This simplifies to $p\left( \phi |T_{u} \right) = \ \frac{p(\phi )p(T_{u}|\phi _{Inital},\phi )p(\phi _{Inital}|\phi )}{p(T_{u})p(\phi _{Inital}|\phi ,T_{u})}$. Given that we primarily focus on the relationship between $T_{u}$ and $\phi$ in this generative model of $\phi$, terms like $p(T_{u})$ and other independent factors can be ignored, resulting in $p\left( \phi |T_{u} \right) \propto p(T_{u}|\phi _{Inital},\phi )$. Since we can estimate $\phi _{Inital}$ through contextual information in the video stream, $p(T_{u}|\phi _{Inital},\phi )$ points to a detector using the estimation of scene as a prior. That is, the proposed $T_{u}$ should yield a favorable output from the detector $p(T_{u}|\phi _{Inital},\phi )$.

Through the above derivation, we have decomposed the tracking problem into finding $T_{u}$ that maximizes the relatively independent discriminator $\log \left( p\left( T_{u} \right) \right)$ and detector $log(p\left( T_{u} \bigg | \phi _{Inital},\phi \right) )$. Let’s denote the discriminator as $f(\theta ,T_{u})$ and the detector as $h(T_{u}|\mu ,\phi )$. Then, $T_{u} = \underset{T_{possible}}{argmax}(f\left( \theta ,T_{possible} \right) + h(T_{possible}|\mu ,\phi ))$, where $\theta$ and $\mu$ are parameters. In practical scenarios, the preliminary detector often only provides a basic reliable threshold and cannot effectively regress. Moreover, since the detector typically operates on single-frame images, we incorporate all outputs from the single-frame detector into the discriminator. In essence, our approach can be described as following formula:

$$\begin{aligned} & T_{u} = \underset{T_{possible}}{argmax}\left( f\left( \theta ,T_{possible} \right) \right) \ \ where\ T_{possible} = [o_{i_{1}}^{j_{1}},o_{i_{2}}^{j_{2}},\ldots ,o_{i_{m}}^{j_{m}} ]\ \left( j_{1}< j_{2}< \ldots < j_{m} \right) ,\\ & \ \ o_{i}^{j} \in O^{j}\left( O^{j} = \left\{ o_{i}^{j} \bigg | h_{real}\left( o_{i}^{j} \bigg | \mu ,I_{j} \right)> threshold \right\} \right) . \end{aligned}$$

Notably, $h_{real}$ here is still a discriminator with a prior estimation of $\phi _{Inital}$, rather than a simple single-frame image detector $p( o_{i}^{j}|I_{j} )$. Additionally, we can implicitly learn the features of all known table tennis trajectories $T_{known}^{\Sigma } = [T_{known1},T_{known2},\ldots ]$ through parameterized deep learning methods, obtaining the discrimination function $f(\theta ,T_{possible})$, where $T_{possible}$ is the feature to be discriminated and $\theta = Train(T_{known}^{\Sigma })$ represents the parameters learned from all known table tennis trajectories $T_{known}^{\Sigma }$. Practically, due to the vast number of potential $T_{possible}$, we compose the set of potential targets ${[O}^{1},O^{2},\ldots ,O^{t},\ldots ,O^{n}]$ into a graph G, and our discriminator is reformulated as $f_{real}(\theta ,G)$, whose output is the previously mentioned probabilistic graph $G^{p}$.

Detector

Based on Section 3.2, we know that the detector $h_{real}$,which detects potential targets from video frame images, originates from the probabilistic model $p(T_{u}|\phi _{Inital},\phi )$. This model points to a detector that uses scene estimation as a prior. Considering a frame image $I_{t}$ belonging to the source video $\phi$, during the derivation process, we label $I_{t\_ Inital}$ as the scene for the video frame image $I_{t}$ under detection. Given that the background of an image changes relatively slowly and stably compared to high-speed moving objects, adjacent frames in the temporal domain, such as $I_{t - \Delta t},I_{t},I_{t + \Delta t}$, can be considered to have the same scene $\ I_{t\_ Initial}$. Within these images, a high-speed moving object $b_{i}^{t}$ represents the table tennis ball that we aim to detect. Assuming that the foreground images of the table tennis ball in these three frames are non-overlapping, denoted as ${I\_ b}_{i}^{t - \Delta t},{I\_ b}_{i}^{t},{I\_ b}_{i}^{t + \Delta t}$ (if there is overlap among ${I\_ b}_{i}^{t - \Delta t},{I\_ b}_{i}^{t},{I\_ b}_{i}^{t + \Delta t}$ in the video, we can increase $\Delta t$ to eliminate any overlap).

Then, we have $I_{t - \Delta t} = I_{t\_ Initial} \oplus {I\_ b}_{i}^{t - \Delta t},I_{t} = I_{t\_ Initial} \oplus {I\_ b}_{i}^{t},I_{t + \Delta t} = I_{t\_ Initial} \oplus {I\_ b}_{i}^{t + \Delta t}$. Since our goal is to extract ${I\_ b}_{i}^{t}$, we need to perform subtraction to eliminate $I_{t\_ Initial}$. Calculating $\Delta ^{-} = absdiff(I_{t - \Delta t},I_{t})$ results in $\Delta ^{-} = {I\_ b}_{i}^{t} \oplus {I\_ b}_{i}^{t - \Delta t}$. Similarly, calculating $\Delta ^{+} = absdiff(I_{t + \Delta t},I_{t})$ gives $\Delta ^{+} = \ {I\_ b}_{i}^{t} \oplus {I\_ b}_{i}^{t + \Delta t}$. Finally, calculating $\Delta = absdiff(I_{t + \Delta t},I_{t - \Delta t})$ gives $\Delta = {I\_ b}_{i}^{t - \Delta t} \oplus {I\_ b}_{i}^{t + \Delta t}$.

Considering the binarized images $\Delta _{b}^{+}, \Delta _{b}, \Delta _{b}^{-}$ corresbounding to $\Delta ^{+}, \Delta , \Delta ^{-}$, we define $M{\_ b}_{i}^{t} = {(\Delta }_{b}^{+}\hat \Delta _{b}^{-})\backslash (\Delta _{b})$. This binarized image $M{\_ b}_{i}^{t}$ serves as the position mask for ${I\_ b}_{i}^{t}$. This method, first proposed in the⁵ article, is an effective approach for detecting high-speed moving objects. Figure 6 illustrate this process.

In an ideal scenario, extracting and analyzing the connected components of the binarized image ${I\_ b}_{i}^{t}$ would yield the target set $B^{t}$ at time t. However, due to noise in practical scenarios, $M{\_ b}_{i}^{t}$ contains numerous false targets within its connected components. We denote the set of all potential targets derived from the analysis of $M{\_ b}_{i}^{t}$ as $O^{t}$. It is certain that the set of table tennis balls we seek to find, $B^{t}$, is a subset of $O^{t}$. In reality, the number of potential targets $o_{i}^{t}$ directly obtained from this method for each frame can be hundreds or even thousands. To minimize the number of potential targets $o_{i}^{t}$, we propose three methods: noise reduction, filtering, and connected component analysis.

Fig. 6

The process of differential detector $h_{real}$.

Noise reduction: We notice that the modeling of $I_{t\_ Initial}$ is often crude, and in practical videos, due to camera motion or sensor noise, $I_{t\_ Initial\_ real} = \ I_{t\_ Initial} \oplus \sigma$, where $\sigma$ represents the ghosting and noise introduced by camera movement or sensor jitter. Taking $\Delta ^{-}$- as an example, $\Delta ^{-} = absdiff(I_{t - \Delta t},I_{t}) = ( {I\_ b}_{i}^{t} \oplus {I\_ b}_{i}^{t - \Delta t} ) \oplus \sigma$. This can lead to the detection of excessive false $o_{i}^{t}$, which should originally belong to $I_{t\_ Initial}$. Considering that camera motion and sensor noise are typically sensitive to the edge regions of an image, we can estimate the distribution of $\sigma$ across the entire image, $\sigma ^{'}$, by computing the gradient of each pixel in $I_{t}$ using the Sobel operator and subtracting it accordingly: $\Delta ^{-} = ( {I\_ b}_{i}^{t} \oplus {I\_ b}_{i}^{t - \Delta t} ) \oplus \sigma \oplus ( - \sigma ^{'}) \approx ( {I\_ b}_{i}^{t} \oplus {I\_ b}_{i}^{t - \Delta t} )$. However, directly using $I_{t}$ to compute $\sigma ^{'}$ would result in the edges of ${I\_ b}_{i}^{t}$ being eroded into $\sigma ^{'}$, leading to missed detections. Therefore, when actually computing $\sigma ^{'}$, we use the images $I_{t - \Delta t}$ and $I_{t + \Delta t}$ instead.

Filtering: Although much noise is removed during the noise reduction step, there are still numerous isolated noise points present in $M{\_ b}_{i}^{t}$. The table tennis balls $b_{i}^{t}$ that we aim to extract typically belong to a larger connected component. Therefore, we can filter out these isolated noise points by applying an “erosion” followed by a “dilation” process, while barely altering the connected component where $b_{i}^{t}$ resides. Through this approach, we can significantly reduce the number of connected components and potential targets $o_{i}^{t}$, greatly reducing the computational burden without compromising the final output accuracy.

Connected Component Analysis: To further reduce the number of $o_{i}^{t}$, we can utilize some prior knowledge about the table tennis balls $b_{i}^{t}$ to conduct a simple analysis and filtering of $o_{i}^{t}$. For instance, we can predefine the shape and color characteristics of the table tennis balls. By analyzing the shape, size of the connected component where $o_{i}^{t}$ resides, as well as the color of the corresponding region in $I_{t}$, we can further filter out a portion of $o_{i}^{t}$.

The above method does not improve the effect of the method significantly, but it can greatly increase the speed of the method by reducing the number of false targets (Table 1 gives two examples). Figure 7 is an example to show all the potential targets $o_{i}^{t}$ on an image. Up to this point, we do not have sufficient information to distinguish whether these potential targets $o_{i}^{t}$ are part of the final trajectory $T_{u}$. The subsequent steps will involve screening and stitching them together to form the final output trajectory $T_{u}$.

Fig. 7

An example of all the potential targets $o_{i}^{t}$ from $I_{t}$.

Table 1 The Average number of potential targets $o_{i}^{t}$ in Video $\phi$.

Construct graph

After obtaining the potential targets ${[O}^{1},O^{2},\ldots ,O^{t},\ldots ,O^{n}]$ throughout the entire video, we sequentially select consecutive frame sets based on the window length, w, and stride, g, which is specified in Section 3.2. The range of set are: $[0,\ w - 1],\ [g,\ g + w - 1],\ \ldots ,\ [k_{1} \cdot g,\ k_{1} \cdot g + w - 1],\ \ldots ,\ [k*g,\ n]$, and the total number of such sets is $\left\lfloor \frac{n - w}{g} \right\rfloor +$1. Using the detector described in Section 3.3, we obtain the target sets corresponding to these consecutive frames, ${[O}^{t},O^{t + 1},\ldots ,O^{t + w - 1}]$. We consider all targets $o_{i}^{j}$ belonging to this set as nodes and connect all nodes belonging to different target sets $O^{t_{i}}$ as edges. The resulting graph can be described as $G:\left\{ V,E \right\} \ where\ V = \{ v_{x}|{potential\ target\ o}_{i_{x}}^{j_{x}} \},E = \{ e_{xy} =(o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}})|o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}},j_{x} \ne j_{y}\}$.

After obtaining all the potential targets $o_{i}^{t}$, a straightforward approach would be to iterate through all possible $T_{possible}$ and then select the tracking result $T_{u}$ using a learned discriminator $f(\theta ,T_{possible})$. Researchers in the⁶ have proposed similar ideas. The study revealed that directly iterating through all possible $T_{possible}$ without any filtering is completely unrealistic due to the astronomical number of potential combinations. However, it is straightforward to observe that every $T_{possible} = [o_{i_{1}}^{j_{1}},o_{i_{2}}^{j_{2}},\ldots ,o_{i_{m}}^{j_{m}} ]$ can be summarized by two essential elements: the target $o_{i_{x}}^{j_{x}}$ and the relationship between two targets $o_{i_{x}}^{j_{x}}$ and $o_{i_{y}}^{j_{y}}$.

After the construction of graph G, any potential trajectory in $T_{possible}$ can be uniquely mapped to a subgraph $G_{T_{possible}}:\{ V_{T_{possible}},E_{T_{possible}} \}\ where\ V_{T_{possible}} = \{ v_{x}| o_{i_{x}}^{j_{x}} \in T_{possible} \}, E_{T_{possible}}$$= \{ e_{xy} = ( o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}} ) | o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}} \in T_{possible} \}$. By arranging the nodes according to the frame order of the targets and adding edges connecting them, $T_{possible}$ corresponds to a path in the graph, $[v_{1},e_{12},v_{2},e_{23},v_{3},\ldots ,v_{x},e_{xy},v_{y},\ldots ,v_{m}]$, where the sequence of nodes represents the trajectory we aim to output. Notably, if $e_{xy} = ( o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}} ) \in T_{possible}$, then $j_{x} \ne j_{y}$, indicating that two potential targets do not belong to the same frame. This is the reason why we require $j_{x} \ne j_{y}$ when constructing the edges of graph G. Furthermore, if the distance between $o_{i_{x}}^{j_{x}}$ and $o_{i_{y}}^{j_{y}}$ in the image plane or the difference in their sizes is excessively large, based on priors and preset conditions, the existence of the edge $e_{xy}$ connecting $o_{i_{x}}^{j_{x}}$ and $o_{i_{y}}^{j_{y}}$ becomes unnecessary. These priors and preset conditions significantly reduce the complexity of graph G. Since node $v_{x}$ corresponds to a target $o_{i_{x}}^{j_{x}}$ that belongs to only one of the sets ${[O}^{t},O^{t + 1},\ldots ,O^{t + w - 1}]$, specifically $O^{t_{j}}$, and all nodes $o_{i}^{t_{j}}$ belonging to the same set $O^{t_{j}}$ are not connected to each other. Therefore, graph G is an N-partite graph, where N = w (window length).

Discriminator

Tasks of discriminator

Inspired by the applications of graph neural networks discussed in Chapter 2, we employ a graph neural network to implement the discriminator $f_{real}(\theta ,G)$. We design the following task for it: Suppose the result trajectory $T_{u}$ have a path in graph G, represented as $\left[v_{u_{1}},e_{u_{1}u_{2}},v_{u_{2}},e_{u_{2}u_{3}},v_{u_{1}},\ldots ,v_{u_{x}},e_{u_{x}u_{y}},v_{u_{y}},\ldots ,v_{u_{m}} \right]$. The function $f_{real}(\theta ,G)$ maps graph G to a probabilistic graph $G^{p}$, where each node v and edge e has an associated probability. Specifically, $G^{p}:\{ V^{'},E^{'} \}\ where\ V^{'} = \left\{ (v,p(v))|v \in V,p(v) \subset [0,1]\right\} \ ,E^{'} = \left\{ (e,p(e))|e \in E,p(e) \subset [0,1]\right\}$$\ with\ V,E\ \in G$. The task requires that for all v or e, if v or e belongs to $T_{u}$, then in the probabilistic graph $G^{p}$, $p(v) = 1$ or $p(e) = 1$; otherwise, $p(v) = 0$ or $p(e) = 0$. It is noteworthy that if there are multiple paths between two nodes that are not completely overlapping and a node $v_{u_{x}} \in T_{u}$ exists on these paths, such as $[v_{u_{1}},e_{u_{1}u_{2}},v_{u_{2}},e_{u_{2}u_{3}},v_{u_{3}}]$ and $[v_{u_{1}},e_{u_{1}u_{3}},v_{u_{3}}]$, then all nodes v and edges e on these paths should have $p(v) = 1$ and $p(e) = 1$ in the probabilistic graph $G^{p}$. Figure 8 illustrates the relationship between the trajectory $T_{u}$ and the probabilistic graph $G^{p}$ using an example of four consecutive image frames (with a window length w=4).

Fig. 8

The correspondence between trajectory $T_{u}$ and the probabilistic graph $G^{p}$ (Red color represents nodes v and edges e with $p(v) = 1$ or $p(e) = 1$, while blue color represents nodes and edges with p(v) =0 or $p(e) = 0$.). Those nodes and edges marked red are part of the trajectory, while the blue nodes and edges are not.

Structure of discriminator

In Section 3.4, we mentioned that the discriminator of our algorithm will be a graph neural network, denoted as $f_{real}(\theta ,G)$. Prior to this, we need to compute the initial features for both nodes v and edges e. The features of a node v are composed of the local image HOG features, position, and shape information corresponding to its underlying object $o_{i}^{t}$. Due to the sparsity of HOG features, a full-connect layer (also called Linear Layer in pytorch) is applied to compress the features before inputting them into the graph neural network. The initial features of an edge $e_{xy} = (o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}})$ are jointly determined by the position and shape information, as well as the initial features of $o_{i_{x}}^{j_{x}}$ and $o_{i_{y}}^{j_{y}}$ (Figure 9 illustrate this process).

Fig. 9

The computation process for the initial features $p^{0}$ of a node v.

After initializing the node features $p^{0}$ and edge features $q^{0}$, we pass them through a custom three-layer graph neural network, GMP (Graph Max-message Pass Neural Network). The steps and details of each layer of this model will be explained in detail later. The GMP graph neural network performs feature propagation and embedding to obtain the final node features $p^{'}$ and edge features $q^{'}$. Subsequently, we design two multi-layer perceptrons, $w_{1}$ and $w_{2}$, to score the final feature $p^{'}$ and $q^{'}$ of each node and edge, respectively. This allows us to obtain p(v) and p(e) in the probabilistic graph $G^{p}$. The specific process is illustrated in Figure 10.

Fig. 10

The structure and computation process of the discriminator, with the computation layer by layer, the characteristics of each node and edge are constantly changing, until the confidence level is finally obtained by the classifier $w_{1}(p)$ and $w_{2}(q)$.

GMP layer

Like all graph neural networks (GNNs), the Graph Message Passing (GMP) network also relies on message passing to update node and edge feature vectors. However, unlike other GNNs, the GMP network operates as follows: Firstly, each node $v_{x}$ in the GMP network collects all messages Mes from its neighbors and concatenates them into a “message tensor” $Mes_{Ax}$. Secondly, it scores the edges $e_{xy}$ connected to neighboring nodes based on the neighbors’ messages Mes, yielding $gra_{xy}$. Thirdly, it applies max-pooling to the “message tensor” $Mes_{Ax}$ to obtain a node-specific message $Mes_{x}$, which is used to update the node features. Finally, it updates the edge features based on the feature vector of the edge $e_{xy}$, the feature vectors of its adjacent nodes $v_{x}$,$v_{y}$, and the scores $gra_{xy}$, $gra_{yx}$ assigned by nodes $v_{x}$ and $v_{y}$ to the edge.

The four main steps outlined above correspond to the four primary operations f, l, g, h in each layer of GMP, each containing learned parameter sets $\theta _{1},\theta _{2},\theta _{3},\theta _{4}$. Detailed steps are elaborated below, which readers may skip if not seeking specifics. Assuming the input data consists of previous or initial node and edge features $p^{n} \in R^{i}$, $q^{n} \in R^{j}$, the “message tensor” $Mes \in R^{k}$, updated node features $p^{n + 1} \in R^{ii}$, and edge features $q^{n + 1} \in R^{jj}$:

The predefined inputs and outputs for f,l,g,h can be defined as follows:

$f(x,\theta _{1})$: Takes features $In \in R^{2i + j}$ where $In =(p_{x}^{n},q_{xy}^{n},p_{y}^{n})$ as input and produces a message $Mes \in R^{k}$ as output.

$l(x,\theta _{2})$: Takes a message $Mes \in R^{k}$ as input and outputs a real-valued score $gra \in R$.

$g(x,\theta _{3})$: Takes features $(Mes,p^{n}_{x}) \in R^{k + i}$ as input and produces new node features $p_{x}^{n + 1} \in R^{ii}$ as output.

$h(x,\theta _{4})$: Takes a tuple $(p_{x}^{n+1},gra_{xy},p_{y}^{n+1},gra_{yx},q_{xy}^{n})$ as input and outputs new edge features $q_{xy}^{n + 1} \in R^{jj}$.

Considering the feature update processes for nodes and edges separately, GMP primarily comprises two parts, Step A and Step B, focused on updating node features pn and edge features qn, respectively (The whole update process is illustrate in Figure 11).

Step A: Calculate the “message tensor” Mes, the “message passing strength” gra, and update all node features.

for each node $v_{x} \in V$:

• 1. Iterate over all adjacent nodes $v_{y_{1}},v_{y_{2}},\ldots ,v_{y_{g}},\ldots v_{y_{h}}$ and their corresponding edges $e_{xy_{1}},e_{xy_{2}},\ldots ,e_{xy_{g}},\ldots ,e_{xy_{h}} \in E$, each iterate get a triplet, all of them can be noted as ${(v}_{x}{,v}_{y_{1}},e_{xy_{1}}),\left( v_{x},v_{y_{2}},e_{xy_{2}} \right) ,\ldots ,(v_{x}{,v}_{y_{g}},e_{xy_{g}}),\ldots ,{(v}_{x}{,v}_{y_{h}},e_{xy_{h}})$. Then, concatenate their corresponding feature vectors $\left( p_{x}^{n},q_{xy_{1}}^{n}, p_{y_{1}}^{n} \right) ,\left( p_{x}^{n},q_{xy_{2}}^{n}, p_{y_{2}}^{n} \right) ,\ldots ,(p_{x}^{n},q_{xy_{g}}^{n}, p_{y_{g}}^{n}),\ldots ,\left( p_{x}^{n},q_{xy_{h}}^{n}, p_{y_{h}}^{n} \right)$. Each iteration yields results ${In}_{xy_{1}},{In}_{xy_{2}},\ldots ,{In}_{xy_{g}},\ldots {In}_{xy_{h}}$.

• 2. Concatenate all ${In}_{xy_{g}}$ to obtain the tensor ${Mes}_{Ax} \in R^{m \times k}$ (using ${\textbf{0}}^{{\textbf{k}}}$ for non-adjacent node tensors).

• 3. ${Mes}_{x} = \ max\left( {Mes}_{Ax},dim = 0 \right)$ to obtain the “message” for node $v_{x}$.

• 4. ${gra}_{xy_{g}} = \ l\left( {Mes}_{xy_{g}},\theta _{2} \right) ,{gra}_{xy_{g}} \in R$. Pass ${Mes}_{xy_{1}},{Mes}_{xy_{2}},\ldots ,{Mes}_{xy_{g}},\ldots ,{Mes}_{xy_{h}}$ through $l(x,\theta _{2})$ to obtain ${gra}_{xy_{1}},{gra}_{xy_{2}},\ldots ,{gra}_{xy_{g}},\ldots ,{gra}_{xy_{h}}$, which are the “message” weights for each triplet $(v_{x},v_{y_{g}},e_{xy_{g}})$. Associate these weights with the respective edges $e_{xy_{g}}$, where edge $e_{xy_{g}}$ receives ${gra}_{xy_{g}}$ (the “message” weight obtained through node $v_{y_{g}}$) is ${gra}_{y_{g}x}$).

• 5. $p_{x}^{n + 1} = g(({Mes}_{x},p_{x}^{n}),\theta _{3})$ to update the feature vector for node $v_{x}$.

Step B: Update edge features based on the “message passing strength” gra.

• 1. After completing Step A, each edge $e_{xy_{g}}$ possesses “message” weights $e_{xy_{g}}({gra}_{xy_{g}},{gra}_{y_{g}x})$. Each node $v_{x}$ finds all its adjacent edges $e_{xy_{1}},e_{xy_{2}},\ldots ,e_{xy_{g}},\ldots ,e_{xy_{h}}$. As mentioned earlier, graph G exhibits an n-partite structure due to the window length w (n = window length), and adjacent nodes $v_{y_{1}},v_{y_{2}},\ldots ,v_{y_{g}},\ldots v_{y_{h}}$ belong to n-1 parts among them. Assume without loss of generality that $v_{y_{g}^{1}},v_{y_{g}^{2}},\ldots ,v_{y_{g}^{n}}$ are the same node located in the same part, and the adjacent edges connecting to the same part, $e_{xy_{g}^{1}},e_{xy_{g}^{2}},\ldots ,e_{xy_{g}^{n}}$, have their respective $e_{xy_{g}}({gra}_{xy_{g}},{gra}_{y_{g}x})$. Perform a SoftMax mapping on ${[gra}_{xy_{g}^{1}},{gra}_{xy_{g}^{2}},\ldots ,{gra}_{xy_{g}^{n}}]$ to obtain ${[gra}_{xy_{g}^{1}}^{1},{gra}_{xy_{g}^{2}}^{1},\ldots ,{gra}_{xy_{g}^{n}}^{1}]$. For each edge $e_{xy}$, after completing the above steps, we obtain thresholded values that regress to (0,1), namely $({gra}_{xy_{g}}^{1},{gra}_{y_{g}x}^{1})$.

• 2. for each edge $e_{xy} \in E$ in the graph:

  $q_{xy}^{n + 1} = h((p_{x}^{n + 1},{gra}_{xy}^{1},p_{y}^{n + 1},{gra}_{yx}^{1},q_{xy}^{n}),\theta _{4})$ to update the feature vector of edge $e_{xy}$.

Fig. 11

The feature updating process in each layer of the GMP. We illustrate the feature update process for node $v_{x}$ and edge $e_{xy}$.

Message Vectors and Node features Update

Here, we focus on explaining the design rationale for the feature p component of our discriminator related to node v. In essence, within the designed tracking task framework, table tennis nodes belonging to the same trajectory should be able to identify each other through a message-passing process. While updating their features based on these “messages,” they should actively “reject” messages from other nodes. Consequently, we have devised a message-passing framework as illustrated in Figure 11 (characterized by the use of max-pooling to process all messages received by the nodes). This section provides a detailed mathematical explanation. Readers may skip this part if they are not seeking in-depth details.

Returning to the graph task we set out in Section 3.4, if node $v_{u_{x}}$ belongs to the graph path $\left[v_{u_{1}},e_{u_{1}u_{2}},v_{u_{2}},e_{u_{2}u_{3}},v_{u_{1}}, \ldots ,v_{u_{x}},e_{u_{x}u_{y}},v_{u_{y}},\ldots ,v_{u_{m}} \right]$ corresponding to trajectory $T_{u}$, let’s assume under ideal conditions that the node and edge features belonging to trajectory $T_{u}$ are $[p_{u_{1}}^{'},q_{u_{1}u_{2}}^{'},p_{u_{2}}^{'},q_{u_{2}u_{3}}^{'}, p_{u_{3}}^{'},\ldots ,p_{u_{x}}^{'},q_{u_{x}u_{y}}^{'},p_{u_{y}}^{'},\ldots ,p_{u_{m}}^{'}]$. The output of classifier $w_{1}$ is $p(T_{u}|p_{u_{1}}^{'}),p(T_{u}|p_{u_{2}}^{'}),\ldots ,p(T_{u}|p_{u_{m}}^{'}$); and the output of classifier $w_{2}$ is $p(T_{u}|q_{u_{1}u_{2}}^{'}),p(T_{u}|q_{u_{2}u_{3}}^{'}),\ldots ,p(T_{u}|q_{u_{m - 1}u_{m}}^{'})$. This implies that after message passing through the GMP network, the features $p_{u_{x}}^{'}$ and $q_{u_{x}u_{y}}^{'}$ exhibit consistency within the feature space and are highly relevant to $T_{u}$. Let’s assume that $T_{u}$ corresponds to the core features $p_{u}^{'}$ and $q_{u}^{'}$ in the feature space. Then, the final output features $p_{u_{x}}^{'}$ and $q_{u_{x}u_{y}}^{'}$ of the node $v_{u_{x}}$ and edge $e_{u_{x}u_{y}}$ belonging to $T_{u}$ should be as close as possible to $p_{u}^{'}$ and $q_{u}^{'}$. Simultaneously, the output features $p_{x}^{'}$ and $q_{xy}^{'}$ of other nodes $v_{x}$ and edges $e_{xy}$ should be as far away as possible from $p_{u}^{'}$ and $q_{u}^{'}$. Revisiting graph G, if we desire specific node features $p_{x}^{n}$ and edge features $q_{xy}^{n}$ along a certain path, targeted message passing between nodes is necessary. Nodes $v_{ux}$ belonging to the path corresponding to $T_{u}$ engage in message passing with other nodes $v_{u_{y}}$ also belonging to $T_{u}$, mutually recognizing their membership in $T_{u}$ and estimating $p_{u}^{'}$ based on messages ${Mes}_{ux}$ from neighboring nodes. This allows for consistency correction and, after multiple iterations of message passing, results in $p_{u_{x}}^{'}$.

Due to the presence of numerous false targets in graph G, node $v_{u_{x}}$ belonging to $T_{u}$ should ideally only receive messages from nodes $v_{u_{y}}$ that also belong to $T_{u}$. We observe that since table tennis exhibits specific motion pattern across multiple video frames, the triplets $(v_{u_{x}},e_{u_{x}u_{y}},{\ v}_{u_{y}})$ between nodes $v_{u_{x}}$ and $v_{u_{y}}$ in $T_{u}$ should also possess these motion pattern. Therefore, our previously designed function $f(x,\theta _{1})$ must possess the ability to recognize these pattern. Let’s design $f(x,\theta _{1})$ such that the higher the input x aligns with the characteristic pattern, the higher the output function value. Considering that graph G contains a significant number of false target nodes v, node $v_{ux}$ should filter them out. As a result, the message it receives from neighboring nodes is ${Mes}_{ux} = \underset{y_{g}}{\arg \max }{f((v_{x},v_{y_{g}},e_{xy_{g}}),\theta _{1})}$. Notably, the motion of table tennis may exhibit multiple patterns ${pattern}_{k}$, thus ${Mes}_{ux} \in R^{k}$.

For any given node $v_{x}$, the message ${Mes}_{x}$ received informs it of the specific patterns ${pattern}_{k}$ exhibited by its neighboring nodes. Node $v_{x}$ can then use ${Mes}_{x}$ to modify its node feature $p_{x}^{n}$ and record the details of this message passing, resulting in $p_{x}^{n + 1}$. That is, $p_{x}^{n + 1} = g(({Mes}_{x},p_{x}^{n}),\theta _{3})$. Figure 12 illustrates that our algorithm gradually distinguish different classes of nodes through feature update processes. Figure 13 illustrates the detail step of $g(x,\theta _{3})$ and $h(x,\theta _{4})$, where $h(x,\theta _{4})$ will be shown in Section 3.5.5.

Fig. 12

The PCA clustering results of node features at different levels demonstrate that, as message passing and feature updating proceed, the difference in features between positive samples (orange) and negative samples (blue) becomes increasingly significant.

Fig. 13

Schematic Diagram of the Node and Edge Update Functions $g(x,\theta _{4})$ and $h(x,\theta _{4})$.

Edge features update and grading edge with SoftMax

In updating edge features, we observe that in graph neural networks, edges serve as the carriers of message passing, and their properties are primarily determined by the nodes they connect. Furthermore, within the designed task framework, there exists a mutual exclusion relationship among some of the edges connected to the same node. Based on this observation, we employ softMax to score the edges and utilize these scores for updating edge features. This section primarily elaborates on the design rationale and provides a mathematical explanation. Readers who are not seeking detailed derivations may skip this part.

Similarly, if an edge $e_{u_{x}u_{y}}$ belongs to the graph path $\left[v_{u_{1}},e_{u_{1}u_{2}},v_{u_{2}},e_{u_{2}u_{3}},v_{u_{1}},\ldots ,v_{u_{x}},e_{u_{x}u_{y}},v_{u_{y}},\ldots ,v_{u_{m}} \right]$ corresponding to $T_{u}$, then the triplet $(v_{u_{x}},e_{u_{x}u_{y}},v_{u_{y}})$ composed of the edge $e_{u_{x}u_{y}}$ and its two endpoint nodes $v_{u_{x}}$ and $v_{u_{y}}$ should possess a motion pattern. Furthermore, if $e_{u_{x}u_{y}}$ belongs to the graph path corresponding to $T_{u}$, then $v_{u_{x}}$ and $v_{u_{y}}$ should exchange messages through $e_{u_{x}u_{y}}$ to bring their respective features $p_{u_{x}}^{'}$ and $p_{u_{y}}^{'}$ closer to the feature vector $p_{u}^{'}$ corresponding to $T_{u}$.

Then, a straightforward approach would be to determine the feature $q_{xy}^{n + 1}$ of the edge $e_{xy}$ based on the neighbor node features $p_{x}^{n + 1}$ and $p_{y}^{n + 1}$ after the message passing process, i.e., $q_{xy}^{n + 1} = h(p_{x}^{n + 1},p_{y}^{n + 1},\theta _{4})$. However, if our goal is to achieve the targeted and specific message passing mentioned earlier, this simple approach falls short as it treats the edge $e_{xy}$ as an appendage to the nodes $v_{x}$ and $v_{y}$, ignoring the relationships between edges in the graph structure.

Given the n-partite structure of graph G and the absence of nodes belonging to the same part in the graph path $\left[v_{u_{1}},e_{u_{1}u_{2}},v_{u_{2}},e_{u_{2}u_{3}},v_{u_{1}},\ldots ,v_{u_{x}},e_{u_{x}u_{y}},v_{u_{y}},\ldots ,v_{u_{m}} \right]$ corresponding to $T_{u}$, there exist numerous mutual exclusion relationships among the edges incident to a given node $v_{x}$, such as $e_{xy_{1}},e_{xy_{2}},\ldots ,e_{xy_{g}},\ldots ,e_{xy_{h}}$. For instance, if nodes $v_{y_{g}^{1}}$ and $v_{y_{g}^{2}}$, both neighbors of node $v_{x}$, belong to the same part, then the edges connecting them, $e_{xy_{g}^{1}}$ and $e_{xy_{g}^{2}}$, exhibit a mutual exclusion relationship.

Assuming that the node $v_{u_{x}}$ belonging to $T_{u}$ has neighboring nodes $v_{u_{y}},v_{y_{g}^{1}},v_{y_{g}^{2}},\ldots ,v_{y_{g}^{n}}$ from the same part, where only $v_{u_{y}}$ belongs to $T_{u}$, we cannot distinguish based on the available information whether $v_{u_{y}},v_{y_{g}^{1}},v_{y_{g}^{2}},\ldots ,v_{y_{g}^{n}}$ belong to $T_{u}$. Since we know that only one of them belongs to $T_{u}$, it follows that only one of the edges connecting them belongs to $T_{u}$. This leads to the constraint $p( T_{u}|e_{u_{x}u_{y}} ) + p( T_{u}|e_{u_{x}y_{g}^{1}} ) + p( T_{u}|e_{u_{x}y_{g}^{2}} ) + \ldots + p( T_{u}|e_{u_{x}y_{g}^{n}} ) \le 1$.

We implement the constraint and the probability $p( T_{u}{|e}_{xy} )$ using SoftMax and a scoring function $l(x,\theta _{2})$, respectively. Consequently, the edge $e_{xy}$ receives two weights, ${gra}_{xy}^{1}$ and ${gra}_{yx}^{1}$, which we refer to as “message passing strengths”. Based on these weights and the updated node features $p_{x}^{n + 1}$ and $p_{y}^{n + 1}$ after message passing, we update the feature of edge $e_{xy}$ as $q_{xy}^{n + 1} = h(( p_{x}^{n + 1},{gra}_{xy}^{1}{,p}_{y}^{n + 1},{gra}_{yx}^{1},q_{xy}^{n} ),\theta _{4})$.

If $e_{xy} \in T_{u}$, $p_{x}^{n + 1}$ and $p_{y}^{n + 1}$ provide specific information about $T_{u}$ to the edge $e_{xy}$, and through $h(x,\theta _{4})$, $q_{xy}^{'}$ is steered towards $q_{n}^{'}$. Conversely, if $e_{xy}$ does not belong to $T_{u}$, $h(x,\theta _{4})$ uses the tuple $( p_{x}^{n + 1},{gra}_{xy}^{1}{,p}_{y}^{n + 1},{gra}_{yx}^{1},q_{xy}^{n} )$ to determine that $e_{xy} \notin T_{u}$ and steers $q_{xy}^{'}$ away from $q_{n}^{'}$.

Alternatively, if a significant amount of “message passing” occurs between nodes $v_{x}$ and $v_{y}$ through $e_{xy}$, resulting in $p_{x}^{n + 1}$ and $p_{y}^{n + 1}$, the simplest approach is to record this information in $q_{xy}^{n + 1}$. In this case, $h(x,\theta _{4})$ needs to utilize the tuple $( p_{x}^{n + 1},{gra}_{xy}^{1}{,p}_{y}^{n + 1},{gra}_{yx}^{1},q_{xy}^{n} )$ to make the necessary judgments and maintain an accurate “record”. Figure 14 illustrates that our algorithm gradually distinguish different classes of edge through process above.

Fig. 14

The PCA clustering results of edge features at various levels indicate that, as message passing and feature updating progress, the differences in features between positive samples (orange) and negative samples (blue) become increasingly pronounced.

Training method and loss function

According to the graph tasks we have previously defined, the multi-layer perceptron, $w_{1}$ and $w_{2}$, perform supervised learning on the outputs p(v) and p(e) based on the final features $p^{'}$ and $q^{'}$ of nodes v and edges e, respectively, comparing them with the pre-defined labels $p_{GT}(v)$ and $p_{GT}(e)$. However, during the training process, the large number of false targets $o_i^t$ in the original video often results in a large-scale graph G. Taking the scenario of Image Window=8 as an example, a single graph in the Ground Truth dataset for training may contain up to hundreds of nodes and tens of thousands of edges, leading to significant resource consumption that precludes training on most GPUs.

Drawing from our discussions in Sections 3.5.3 and 3.5.4, message passing in the GMP model is typically targeted, with negative samples or messages passed between nodes belonging to different categories often being less significant. Therefore, we can randomly sample negative samples or nodes from other categories while preserving positive samples or a specific category of nodes⁴⁸. A large-scale graph G can be sampled to generate multiple small-scale graphs, and combined with randomization and the setting of hyperparameters such as batch size during training, the training process becomes more stable, often leading to more ideal results. Additionally, we can re-sample the graph G between training epochs to obtain different outcomes, effectively implementing a form of data augmentation that can effectively mitigate overfitting in the model. An example of sampling is shown in Figure 15.

Fig. 15

Schematic Diagram of the Graph Sampling Process. Red represents the Positive Sample while Blue represents Negative one. (Note: We Retain All Positive Samples and Only Sample on Negative Samples).

Interestingly, our graph neural network does not consume excessive memory during the inference mode due to the elimination of the need to store gradients, computation graphs, and intermediate results. Consequently, the algorithm does not require sampling the graph G during inference.

In terms of loss function selection, we have chosen the cross-entropy loss function. For the graph $G\left\{ V,E \right\}$, we compute the average loss across all nodes and edges and then directly sum them up:

$$\begin{aligned} & loss = - ~\frac{1}{V(G)}{\sum {\left. \left( p \right. _{GT}\left( v_{x} \right) { \log \left( {p\left( v_{x} \right) } \right) } + \left( 1 - p \right. _{GT}\left( v_{x} \right) \right) log\left( 1 - p\left( v_{x} \right) \right) )}} \\ & + \frac{1}{E(G)}{\sum {\left. \left( p \right. _{GT}\left( e_{xy} \right) { \log \left( {p\left( e_{xy} \right) } \right) } + \left( 1 - p \right. _{GT}\left( e_{xy} \right) \right) log\left( 1 - p\left( e_{xy} \right) \right) )~}} \\ & where~v_{x} \in V,~e_{xy} \in E;~V,E \in G\left\{ V,E \right\} \end{aligned}$$

Now let us revisit the cross-entropy loss function, which is expressed as $l = - \sum {ylogx + (1 - y)log(1 - x)}$ where y represents the label of the sample and x is the output result. Assuming in practical scenarios that the average correct prediction rate for positive samples is p and for negative samples is q, with the respective numbers of positive and negative samples being m and n, the total loss can be expressed as $l = - \frac{1}{m + n}(mlogp + n\log q)$.

We can calculate the derivatives of the loss function with respect to p and q as $\frac{\partial l}{\partial p} = - \frac{1}{p}\frac{m}{m + n},\frac{\partial l}{\partial q} = - \frac{1}{q}\frac{n}{m + n}$. Since p and q are generated by the Sigmoid function, the gradients passed back to the classifier are $\frac{\partial l}{\partial w} = \frac{\partial l}{\partial p}\frac{\partial p}{\partial w} + \frac{\partial l}{\partial q}\frac{\partial q}{\partial w} = - \frac{m}{m + n}\frac{1}{p}p(1 - p) - \frac{n}{m + n}\frac{1}{q}q(1 - q) = - \frac{1}{m + n}(m(1 - p) + n(1 - q))$. Here, the gradient ratio contributed by p and q, $\frac{\nabla p}{\nabla q}$, is $\frac{m(1 - p)}{n(1 - q)}$.

Furthermore, we can compute precision (pre) and recall as $pre = \frac{\frac{m}{m + n}p}{\frac{n}{m + n}(1 - q) + \frac{m}{m + n}p} = \frac{pm}{pm + (1 - q)n}$ and $recall = \frac{mp}{m} = p$. When $pre = recall$, we have $\frac{m(1 - p)}{n(1 - q)} = 1$ and $\nabla p = \nabla q$, and the model evenly improves the performance of both positive and negative samples. When $pre> recall$, $\frac{m(1 - p)}{n(1 - q)} < 1$, $\nabla p < \nabla q$, and the model tends to improve the performance of negative samples more, emphasizing recall. Conversely, when $pre < recall$, $\frac{m(1 - p)}{n(1 - q)}> 1$, $\nabla p> \nabla q$, and the model favors improving the performance of positive samples, emphasizing pre.

The original cross-entropy function aims to achieve $pre = recall$. However, when $m \ll n$, we have $1 - p \gg 1 - q$, meaning the model tends to improve q to a higher level before improving p. This can result in a low precision pre for a significant portion of the training process, and positive samples may not receive sufficient attention.

To address this, we consider a weighted loss function: $l = - \sum {a_{1}y\log x + a_{2}(1 - y)log(1 - x)}$ where $a_{1}$ and $a_{2}$ are weighting coefficients. When $a_{1} = a_{2} = 1$, it becomes the original cross-entropy function. Setting $a_{1}> a_{2}$ allows the model to focus more on positive samples, emphasizing the improvement of p and recall. Conversely, $a_{2}> a_{1}$ directs the model’s attention to negative samples, emphasizing the enhancement of q and pre.

At the initial stage of our model training, we set $a_{1}> a_{2}$. As the loss function decreases and p and q improve, we gradually decrease $a_{1}$ until $a_{1} \approx a_{2} \approx 1$. In practice, we use the following expressions for $a_{1}$ and $a_{2}$: $a_{1} = \frac{m + n}{2Max((loss + 0.15)\sqrt{mn} + ( - loss + 0.85)(\frac{m + n}{2}),\sqrt{mn})}$ and $a_{2} = \frac{m + n}{2(m + n - Max((loss + 0.15)\sqrt{mn} + ( - loss + 0.85)(\frac{m + n}{2}),\sqrt{mn}))}$, In this expression, loss refers to the value of loss function from the previous epoch, and the initial loss can be considered as positive infinity or a large number.

Organize and output results

In Section 3.4, we constructed several graphs using the potential targets $o_{i}^{j}$ from the set ${[O}^{1},O^{2},\ldots ,O^{t},\ldots ,O^{n}]$. For each probability graph $G^{p}$, we obtained the probabilities $p(v_{x})$ and $p(e_{xy})$ that each node $v_{x}$ and edge $e_{xy}$ belongs to a particular trajectory $T_{u}$ in the graph G. These probabilities correspond to the likelihood of a potential target $o_{i_{x}}^{j_{x}}$ belonging to a trajectory $T_{u}$, denoted as $p(o_{i_{x}}^{j_{x}})$, and the probability of two potential targets $o_{i_{x}}^{j_{x}}$ and $o_{i_{y}}^{j_{y}}$ belonging to the same trajectory, denoted as $q(o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}})$. It is worth noting that during the process of graph construction based on Image Window and Gap, some targets $o_{i_{x}}^{j_{x}}$ and connections $(o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}})$ may appear in multiple probability graphs $G^{p}$. In such cases, we simply select the maximum values of $p(o_{i_{x}}^{j_{x}})$ and $q(o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}})$ as the output of the Discriminator.

Subsequently, we utilize the output results $p(o_{i_{x}}^{j_{x}})$ and $q(o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}})$ to derive the resulting trajectories $T_{1},T_{2},\ldots ,T_{s}$. The specific process is outlined as follows:

Step 1.

• Set threshold values $p_{\min }$ and $q_{\min }$ for $p(o_{i_{x}}^{j_{x}})$ and $q(o_{i_{x}}^{j_{x}},o_{i_{y}}^{j_{y}})$, respectively (where $p_{min},q_{min}> 0$).

Step 2.

• Filter out all potential targets $o_{i_{x}}^{j_{x}}$ with $p\left( o_{i_{x}}^{j_{x}} \right) < p_{\min }$.

Step 3.

• For each remaining potential target $o_{i_{x}}^{j_{x}}$ with $p\left( o_{i_{x}}^{j_{x}} \right) \ge p_{\min }$, we establish a trajectory $T_{x}$ containing only that particular target, i.e., $T_{x} = [o_{i_{x}}^{j_{x}}]$. The set T is composed of all such trajectories $T_{x}$, $T = \{{T_{1},T_{2},\ldots ,T}_{x},\ldots ,T_{y},\ldots \}$.

Step 4.

• Identify the two most suitable trajectories $T_{x}$ and $T_{y}$ for merging in T.

  Initial $q_{temp} = 0,temp\_ x = - 1,temp\_ y = - 1;$

  For $(T_{x},T_{y})$ in T (where $x \ne y$):

  • Where $T_{x} = [o_{i_{x_{1}}}^{j_{x_{1}}},o_{i_{x_{2}}}^{j_{x_{2}}},\ldots ,o_{i_{x_{n}}}^{j_{x_{n}}}]$, $T_{y} = [o_{i_{y_{1}}}^{j_{y_{1}}},o_{i_{y_{2}}}^{j_{y_{2}}},\ldots ,o_{i_{y_{m}}}^{j_{y_{m}}}]$

    Initial $count = 0$ , $q_{result} = 0$

    For $(o_{i_{x_{k}}}^{j_{x_{k}}},o_{i_{y_{l}}}^{j_{y_{l}}})$ in ($T_{x},T_{y}$):

    • If any $j_{x_{k}} = \ j_{y_{l}}$:

      • $q_{result} = 0$

        Break

    • Elif $q(o_{i_{x_{k}}}^{j_{x_{k}}},o_{i_{y_{l}}}^{j_{y_{l}}})$ doesn’t exist:

      • Continue

    • Else:

      • $q_{result}\ + = \ q(o_{i_{x_{k}}}^{j_{x_{k}}},o_{i_{y_{l}}}^{j_{y_{l}}})$

        $count + +$

  • End For

• If count != 0:

  • $q_{result}$ = $\frac{q_{result}}{count}$

• If $q_{result}> q_{temp}:$

  • $q_{temp} = q_{result},temp\_ x = x,temp\_ y = y;$

• Else:

  • Continue

• End For

  Goto Step 5.

Step 5.

• If $q_{temp}> q_{\min }$:

  • 1. Merge $T_{temp\_ x}$ and $T_{temp\_ y}$ into $T_{new}$ by combining all potential targets from $T_{temp\_ x}$ and $T_{temp\_ y}$ into a single sequence and arranging them in ascending order based on the values of $j_{x_{1}},j_{x_{2}},\ldots ,j_{x_{n}}$ and $j_{y_{1}},j_{y_{2}},\ldots ,j_{y_{m}}$;

  • 2. Remove $T_{temp\_ x}$ and $T_{temp\_ y}$ from T and add $T_{new}$ to T (update T);

  • 3. Then, Return to Step 4.

• Else:

  • Goto Step 6.

Step 6.

• For the set $T = {\{ T}_{1},T_{2},\ldots ,T_{s}\}$, filter out all trajectories with a length of 1, i.e., remove all $T_{u}$ from T where $T_{u} = [o_{i_{u}}^{j_{u}}]$.

Finish Process

The final set $T = {\{ T}_{1},T_{2},\ldots ,T_{s}\}$ obtained at the end of the algorithm represents the final output result.

Evaluation and results

To train a useful model and validate effectiveness of the algorithm in a real-world, it is imperative to collect table tennis match videos that closely resemble the intended usage scenarios. These videos must be annotated according to the requirements of tactical analysis, serving as the dataset for algorithm training and evaluation. Additionally, to verify the algorithm’s effectiveness and advancement, a comparison with similar solutions is necessary. Such comparisons can also assist in identifying any issues within the algorithm.

Datasets

We have augmented the⁶⁷ dataset with a significant number of videos, resulting in a comprehensive collection encompassing 20 independent videos as the dataset. Each video is a continuous recording under a fixed scenario, totaling 13,950 frames and 6,027 annotated table tennis balls. In selecting and annotating the videos, we took into account their diversity: our dataset includes scenarios such as competition, training, and warm-up; players ranging from amateurs, student athletes, to professional athletes; and various camera perspectives including side-facing (viewing the table tennis table from the side), directly-facing (viewing the table tennis table from the back), and player-facing (viewing the player directly). In subsequent text, we will refer to the side-facing, directly-facing, and player-facing perspectives as Side-Facing, Directly-Facing, and Player-Facing, respectively. Scenes captured from different perspectives are illustrated in Figure 16. Over 45% of the dataset comes from videos recorded on mobile phones, while more than 30% originates from competition replays sourced from online and televised broadcasts on platforms such as Migu video and CCTV. Additionally, we have appropriately referenced some open-source datasets⁵⁹ to provide horizontal comparisons and references. An example frame from the dataset is shown in Figure 17, and the specific details of the videos in the dataset are summarized in Table A1 of Appendix A.

Fig. 16

Illustrations of Images from Different Perspectives: Side-Facing (Left), Directly-Facing (Middle), Player-Facing (Right).

Fig. 17

Original Video Images from the Dataset.

Results and comparison

Training and results

We selected the first 17 out of the 20 videos from the dataset for training and testing purposes, while reserving the last 3 videos for validation. It is worth noting that while the last 3 videos share similar scenarios, only one of the 17 videos used for training and testing exhibits a comparable setting. This approach was adopted because the perspectives and scenarios of the last 3 videos are the most popular among current table tennis broadcasts and tactical analyses, and are also the most likely scenarios for the application of our algorithm. Given the diversity of video scenarios and the inconsistency in the number of video frames and table tennis balls captured from different perspectives, we took extra care in dividing the training and testing sets to minimize the impact of data imbalance. For some videos, we chose the first 70% of consecutive frames as the training set, while for others, we selected the first 50%. The remaining 50% of consecutive frames from each video were designated as the testing set. (Specific ranges are detailed in Table A2. of Appendix A.)

During training, we employed the sampling scheme mentioned in Section 3.5.6 to sample the graph G constructed from the training set, while no sampling was performed on the testing set. The final counts of nodes v and edges e in the entire training set are presented in Table 2.

Table 2 Number of Nodes v and Edges e in the Test Set and Training Set.

For training, we set the learning rates for the three-layer message-passing graph neural network GMP and the classifiers $w_{1}$, $w_{2}$ to 0.005 and 0.002, respectively. In analyzing the results, we simply used a threshold of 0.5 to categorize nodes v and edges e into positive and negative samples. The performance criteria are precision, recall, and F1-score, which are calculated by TP/(TP + FP), TP/(TP + FN), and 2TP/(2TP + FN + FP), respectively. Here, TP, FP, and FN stand for the number of true positives, false positives, and false negatives, respectively.

The variation of the loss function (Section 3.5.5) and classification accuracy during the entire training process are depicted in Figure 18. Training was conducted using two NVIDIA Tesla-T4 GPUs. After sampling the training set, each epoch comprised approximately 1000 steps, resulting in rapid model convergence. The optimal model was obtained at epoch=8. Additionally, we re-sampled the training set every two training rounds, as described in Section 3.5.6. The initial learning rate for the GMP component was set to $5 \times 10^{- 4}$ with a minimum decay of $2 \times 10^{- 4}$, while the initial learning rates for the classifiers $w_{1}$ and $w_{2}$ were set to $2 \times 10^{- 4}$ with a minimum decay of $1 \times 10^{- 4}$.

Experimental results demonstrate the stability of our training approach, with good performance after model convergence. Only minor overfitting and jittering phenomena were observed.

Fig. 18

The variation curves of loss function and model performance during training.

Recalling to the problem definition in Section 3.1, we need to compare the differences between the set of trajectories $\{ T_{1},T_{2},\ldots ,T_{s}\}$ output by the algorithm and the Ground Truth set $T_{1}^{GT},T_{2}^{GT},\ldots ,T_{s}^{GT}$. For the i-th table tennis ball $b_{i}^{t}$ in the t-th frame belonging to the Ground Truth set, if $b_{i}^{t}$ is also present in the output trajectory set $\{ T_{1},T_{2},\ldots ,T_{s}$, it will be labeled as a true positive sample. Conversely, $b_{i}^{t}$ will be labeled as a false negative sample if it is not in the output set. Similarly, any sample belonging to the output trajectory set $\{ T_{1},T_{2},\ldots ,T_{s}\}$ but not to the Ground Truth set $T_{1}^{GT},T_{2}^{GT},\ldots ,T_{s}^{GT}$ will be labeled as a false positive sample. We will calculate the precision, recall, and F1-score for table tennis ball targets (Target) based on the number of these samples.

Apart from analyzing the table tennis balls $b_{i}^{t}$, we also need to assess the trajectories $T_{u}$. Consider the Ground Truth trajectory $T_{u}^{GT} = \left[b_{i_{1}^{GT}}^{j_{1}^{GT}},b_{i_{2}^{GT}}^{j_{2}^{GT}},\ldots ,b_{i_{m}^{GT}}^{j_{m}^{GT}} \right]$, where all adjacent table tennis balls $(b_{i_{x}^{GT}}^{j_{x}^{GT}},b_{i_{y}^{GT}}^{j_{y}^{GT}})$ with $(\ j_{1}^{GT}< j_{2}^{GT}< \ldots< j_{x}^{GT}< j_{y}^{GT}< \ldots < j_{m}^{GT})$ are identified. In total, $m - 1$ pairs of adjacent table tennis balls $(b_{i_{x}^{GT}}^{j_{x}^{GT}},b_{i_{y}^{GT}}^{j_{y}^{GT}})$ can be extracted from $T_{u}^{GT}$, denoted as the relationship $R(b_{i_{x}^{GT}}^{j_{x}^{GT}},b_{i_{y}^{GT}}^{j_{y}^{GT}})$. Next, we investigate whether the pair $(b_{i_{x}^{GT}}^{j_{x}^{GT}},b_{i_{y}^{GT}}^{j_{y}^{GT}})$ belongs to the same trajectory $T_{u}$ within the output trajectory set $\{ T_{1},T_{2},\ldots ,T_{s}\}$. If the pair is indeed present in the same trajectory $T_{u}$, it is labeled as a true positive sample. Otherwise, $R(b_{i_{x}^{GT}}^{j_{x}^{GT}},b_{i_{y}^{GT}}^{j_{y}^{GT}})$ is labeled as a false negative sample.

Finally, we examine all relationships $R(b_{i_{x}}^{j_{x}},b_{i_{y}}^{j_{y}})$ within the output trajectory set $\{ T_{1},T_{2},\ldots ,T_{s}\}$. If $b_{i_{x}}^{j_{x}}$ and $b_{i_{y}}^{j_{y}}$ do not belong to the same trajectory in the Ground Truth set $\{ T_{1}^{GT},T_{2}^{GT},\ldots ,T_{s}^{GT} \}$, then $R(b_{i_{x}}^{j_{x}},b_{i_{y}}^{j_{y}})$ is labeled as a false positive sample. Similarly, we calculate the precision, recall, and F1-score for all relationship groups $R(b_{i_{x}}^{j_{x}},b_{i_{y}}^{j_{y}})$ (Relationship) based on the sample counts. This analysis provides insights into the effectiveness of the algorithm in reconstructing table tennis ball trajectories.

Based on the content of Section 3.6, the manually set thresholds $p_{\min }$ and $q_{\min }$ can influence the final test results. To assess this impact, we varied $p_{\min }$ within the range of [0.05, 0.7] with a step size of 0.05. For each setting of $p_{\min }$, we ran the algorithm with three different values of $q_{\min }$: $p_{\min }$, $p_{\min } - 0.05$, and $p_{\min } + 0.05$. By averaging the output results, we obtained the mean average precision , mean average recall, and mean average F1-score.

Furthermore, we calculated the average values of these metrics across different threshold ranges. When annotating the results, we used parentheses to indicate the threshold ranges, such as (0.40–0.60) and (0.30–0.70). These ranges represent the $p_{\min }$ values tested within the specified intervals with a step size of 0.05, and the results were averaged accordingly.

The final results on our dataset are presented in Table 3. The data indicate that our proposed algorithm is not highly sensitive to the manually set thresholds $p_{\min }$ and $q_{\min }$, and it achieves good performance on most datasets.

Compare with other methods

To validate the performance and advancement of our algorithm, we examined other object tracking algorithms and potential alternative solutions, and compared them one by one. The results indicated that our algorithm excels in overall performance.

Comparison with Directly Applying Object Detection Algorithms (YOLOv8)¹²: We filtered out all images containing table tennis balls from the training and testing sets, and converted the annotated table tennis ball trajectories ${\{ T}_{1}^{GT},T_{2}^{GT},\ldots ,T_{s}^{GT}\}$ into the dataset format required by YOLOv8. Subsequently, we divided the YOLOv8 dataset into training and testing sets in the ratio of 85% and 15%, respectively. We then trained the default YOLOv8n model for 100 epochs to obtain the best-performing model. In the data evaluation, if the confidence score of a candidate bounding box inferred by the YOLOv8 model exceeded a certain threshold (conf > threshold) and its IOU(Intersection over Union) with any original annotation box of a table tennis ball in the dataset was greater than 0.4, the target was labeled as True Positive. Conversely, it was labeled as False Negative. All candidate boxes with confidence scores above the threshold (conf > threshold) but with IOU values less than 0.4 with all original annotation boxes of table tennis balls in the dataset were labeled as False Positive.

Comparison with Tracking Algorithms: SOT (Step Mode)¹³: In SOT algorithms, target tracking in videos relies on manual annotations in the first frame. However, the videos in our dataset contain numerous segments without table tennis balls, making it inappropriate to directly apply the SOT algorithm to accurately assess its tracking capability. Therefore, we disassemble the trajectories $T_{u}^{GT} = \left[b_{i_{1}^{GT}}^{j_{1}^{GT}},b_{i_{2}^{GT}}^{j_{2}^{GT}},\ldots ,b_{i_{m}^{GT}}^{j_{m}^{GT}} \right]$ in the dataset into relationships $R(b_{i_{x}^{GT}}^{j_{x}^{GT}},b_{i_{y}^{GT}}^{j_{y}^{GT}})$ between adjacent table tennis balls. This approach allows us to evaluate the algorithm’s ability to detect a table tennis ball $b_{i_{x}^{GT}}^{j_{x}^{GT}}$ when another ball $b_{i_{y}^{GT}}^{j_{y}^{GT}}$ has already been annotated.

Given that the algorithm uses ResNet as its backbone network, resulting in relatively coarse image granularity, we define a relationship $R(b_{i_{x}^{GT}}^{j_{x}^{GT}},b_{i_{y}^{GT}}^{j_{y}^{GT}})$ as True Positive if the bounding box of a detected table tennis ball $b_{i_{y}}^{j_{y}}$ with a confidence score above a threshold has an IOU(Intersection over Union) greater than 0.3 with the annotated bounding box of $b_{i_{y}^{GT}}^{j_{y}^{GT}}$. Conversely, the relationship is labeled as False Positive if the IOU is below this threshold. If no table tennis ball $b_{i_{y}}^{j_{y}}$ is detected, the relationship is marked as False Negative. It is worth noting that we did not retrain the SOT model and instead used the published open-source model directly.

Comparison with Direct Use of Graph Attention Networks (GAT): As an alternative to our GMP message-passing network, we selected a three-layer GAT model for comparison and trained and evaluated it using the same approach as described in Section 4.2.1. It is noteworthy that, due to the slightly faster computation speed of the GAT model compared to our GMP model, we allocated more feature dimensions to the GAT model. Specifically, the input node feature dimensions for each layer of the three-layer GMP model were 70, 96, and 128, respectively. In contrast, the input node feature dimensions for the three-layer GAT model were 438, 502, and 566, respectively.

Furthermore, we compared the performance of the T-FORT algorithm with the FMO algorithm on a subset of videos from the dataset. We compiled statistics on the metrics of these videos and included them in the tables for reference. All the results are presented in Table 4.

Table 3 Experimental Results of the Algorithm on our datasets.

Table 4 Experimental Results of the Algorithm on our datasets.

Analysis

Experimental Factors and Error Sample Analysis: Reviewing the hypothesis proposed in Section 3.2, our discriminator is effectively regressing $\log \left( p\left( T_{u} \right) \right)$, making decisions on potential table tennis balls in videos based on both image and motion features. In practical experiments, we observed significant differences in the trajectories and visual morphologies of table tennis balls captured from different camera angles, which are clearly reflected in our experimental data. Taking GMP(0.4–0.6) as an example, we analyzed the average results from three camera angles: Side-Facing, Player-Facing, and Directly-Facing, as summarized in Table 5.

In the Player-Facing view, the table tennis balls appear large in size, with distinct image features and significant contrast against the background due to the proximity to the table tennis table, making them easier to track. In the Side-Facing view, the movement of the table tennis balls exhibits strong regularity (primarily lateral movement). Although the balls may appear small and their image features blurry in some videos, the algorithm still achieves good tracking performance. However, in the Directly-Facing view, the trajectory of the table tennis balls is irregular, and due to interference and occlusion from the players, the balls have low contrast with the background noise, making them the most challenging to track. Consequently, the algorithm performs the worst in this view. The table tennis ball samples successfully detected from the three perspectives of Directly-Facing, Player-Facing, and Side-Facing are shown in Figure 19, 20, and 21, respectively.

Table 5 Tracking Performance under Different Views.

Analysis of False Negative Targets: The algorithm simply utilizes the HOG image operator, focusing solely on local image features of candidate targets without considering more peripheral or even global image features. The lack of semantic image features results in some table tennis balls that are not distinct from the background or are interfered with by the players’ movements lacking the necessary features for detection, leading to them being missed by the algorithm. Additionally, due to the limitations of the differential detection algorithm, some table tennis balls fail to be accurately outlined with candidate boxes, resulting in the calculation of image features deviating from normal values and causing the subsequent algorithm to overlook these balls. Examples of table tennis balls falsely labeled as negative is shown Figure 22 .

Fig. 19

Successfully detected table tennis balls in Directly-Facing view (marked with green boxes).

Fig. 20

Successfully detected table tennis balls in Player-Facing view (marked with green boxes).

Fig. 21

Successfully detected table tennis balls in Side-Facing view (marked with green boxes).

Fig. 22

Some examples of table tennis balls falsely labeled as negative (marked with blue boxes).

Analysis of False Positive Targets: These targets primarily arise from background noise, local image features and motion trajectories generated by athletes’ movements that closely resemble table tennis balls. Relying solely on local image and motion features of the table tennis balls makes it difficult to discern them accurately. Utilizing sufficiently discriminated data and image features with deep semantic information can assist in resolving some of these issues. Examples of table tennis balls falsely labeled as positive is shown Figure 23. Notably, the occurrence of these False Positive targets and trajectories is typically brief. Therefore, directly filtering out trajectories $T_{u}$with shorter lengths can significantly reduce the number of such targets. Similar strategies have also been proposed in⁶and⁷. Results of Filtering Out Short Trajectories is shown in Table A3 of Appendix A.

Fig. 23

Some examples of table tennis balls falsely labeled as positive (marked with red boxes).

Model Parameters and Inference Speed: Our proposed method not only exhibits excellent performance but also boasts a significantly small number of parameters, totaling merely 0.8M. In contrast, the YOLOv8n model possesses a substantial parameter count of 3.2M. This is partly due to our simplified approach of utilizing the HOG operator as the image feature extractor, without designing a specialized feature extraction network for small targets. Another contributing factor is the nature of graph neural networks, where model parameters are reused across nodes and edges during inference, potentially leading to the neglect of challenging and infrequently occurring samples.

Regarding inference speed, we conducted tests on Side-Facing Professional athlete Competition videos in both 1080P and 720P resolutions. The testing environment consisted of a docker container equipped with a Teala T4 graphics card (Memory 16GB), CPU limitations ranging from 4–16 cores, and memory restrictions between 8192-32768MB. The running time for each component of our algorithm is summarized in Table 6.

Table 6 Tracking Performance under Different Views.

Overall, inference speed is not a strength of our approach. Under the same testing conditions, YOLOv8’s preprocess, inference, and postprocess stages averaged 1.8ms, 16.2ms, and 2.1ms, respectively, resulting in an average frame time of 20.1ms and an inference performance exceeding 45fps (49.7fps). Furthermore, the running time of our solution is sensitive to the resolution of the video images, as the time spent by the detector is directly proportional to the image resolution. Nevertheless, the current performance of our algorithm is sufficient to meet the needs of offline inference services for users. If we consider only the Graph Inference component, our model can achieve a performance of approximately 10-20fps (without utilizing half-precision acceleration for inference in our tests). With optimizations to the detector, such as employing separate processes or adopting alternative faster solutions, our approach has the potential to achieve real-time tracking and detection.

Feasibility of Widespread Application:We downloaded a brief tennis match video (consisting of 155 frames) from the Wimbledon Tennis Championships official website⁴⁹. We brutally applied the model previously used for table tennis tracking and the same environment utilized for table tennis tactical analysis to detect tennis balls in the video, subsequently analyzing them in a similar manner. The analysis results presented in Table 7 demonstrate that even with a model, method, and technical solution specifically designed for table tennis, a certain level of effectiveness can be achieved in a tennis scenario (Examples of successfully detected tennis ball is shown in Figure 24). Based on this, we can boldly hypothesize that our proposed technical solution, with targeted modifications and training, can be applied to other ball sports such as tennis, badminton, football, basketball, volleyball, and so on. Additionally, the GMP model itself can be utilized for similar problems such as link discovery in graphs.

Fig. 24

The tennis ball successfully detected in a tennis match scenario.

Table 7 Analysis Results for Tennis Match Scenarios.

Conclusion and future works

In this paper, we addressed the challenging problem of tracking fast-moving table tennis balls, which are small-sized, rapidly moving, and have non-significant image features. To tackle this, we employed a combined approach of detection and discrimination. Specifically, for the discriminator, we proposed a novel graph neural network called GMP, which features a unique message passing mechanism tailored to address the target tracking problem. Our experimental results demonstrated that our algorithm performs well in various scenarios within the dataset and holds promise for application to other high-speed target tracking problems.

For the future works,we may improve some details in our method considering some problems and limitations. Firstly, consider the aspect of image features. We solely utilized simple HOG features. It is evident that the use of image features containing semantic information could further enhance performance. In terms of target detection, simple difference detection and connected component analysis may not work effectively in all scenarios and are susceptible to interference from athletes and video noise within the scene. Therefore, more accurate scene modeling and target detection algorithms could help improve the algorithm’s effectiveness. Further more, it would be a promising research topic to track high-speed targets such as table tennis balls using the state-of-the-art Segment Everything⁵⁰ as a detector, while incorporating contextual information. Additionally, modifying and enhancing the performance of the algorithm proposed in this paper or directly applying it to other ball sports or tracking problems are viable research directions or tasks for future exploration.