Mine water inflow prediction model based on variational mode decomposition and gated recurrent units optimized by improved chimp optimization algorithm

Abstract

Water damage accidents occur frequently in mines in China, and accurate prediction of incoming water has become an important guarantee for the safe and efficient mining of coal resources. To improve the accuracy of mine water prediction, this paper proposes the VMD-iCHOA-GRU mine water prediction model by selecting and improving it according to the previous research results in decomposition method, time series prediction model and optimization algorithm. After processing the raw data and setting the model parameters, MAE, RMSE, MAPE and R² are selected as the evaluation indexes of prediction accuracy, and VMD-GRU model, iCHOA-GRU model, CHOA-GRU model and GRU model are selected as the comparison models to validate the advantages of the VMD-iCHOA-GRU model in the prediction of mine inrush water. The results show that the VMD-iCHOA-GRU model has the best prediction effect on the trend of water inflow, with the evaluation index values of 0.00862, 0.01059, 0.02189%, 0.87079, respectively, and with the smallest MAE, RMSE, MAPE, and the largest R², and the highest prediction accuracy of the VMD-iCHOA-GRU model.

Introduction

Coal is a vital mineral resource in China, and the task of extracting it safely and efficiently poses significant challenges that mining operations must confront^1,2,3,4,5. Mine water hazards pose a severe threat to the safe extraction of coal resources, with the degree of water hazard risk being assessable by the magnitude of mine water inflow^{6,7,8,9,10,11}. Mine water inflow prediction involves utilizing existing mine water inflow data to develop a predictive model through the application of a particular algorithm, aimed at predicting the trend in mine water inflow data over a future period. Based on these predictions, measures can be devised to address potential water inrush risks, ensuring the safety of mining operations^12,13,14,15.

Commonly employed models for mine water inflow prediction encompass classical statistical models, shallow machine learning models, and deep learning models. However, both the former two categories have notable drawbacks. Classical statistical models are prone to substantial influence from random factors and generally exhibit weaker capability in handling complex scenarios. Shallow machine learning models, on the other hand, fall short in effectively extracting features from large-scale datasets^{16,17,18,19,20}. Compared to their counterparts, deep learning models possess stronger expressive capabilities, enabling them to uncover a wealth of latent information within vast amounts of data. Furthermore, they feature adaptable, flexible model architectures that seamlessly align with specific application contexts. Consequently, deep learning models emerge as the preferred choice for constructing mine water inflow prediction models^21,22,23,24. Currently, among the commonly utilized deep learning models for various tasks are Convolutional Neural Networks²⁵, Gated Recurrent Units²⁶, Long Short-Term Memory Networks²⁷, Graph Convolutional Networks²⁸ and Deep Belief Networks²⁹, These models have played significant roles and have seen widespread application in the prediction of mine water inflow.

To accurately predict the mine water inflow, related scholars have optimized the original deep learning model or introduced other models to improve the accuracy of the model prediction and have achieved abundant research results. Liang et al.³⁰ proposed a Deep Residual Network with a Bidirectional Long Short-Term Memory Networks (DRN-BiLSTM) model, which enhances the capture of complex trend features in water inflow variations; Li et al.³¹ proposed a Complementary Ensemble Empirical Mode Decomposition with Gated Recurrent Units Networks (CEEMDGRU) model, addressing modal aliasing phenomena and improving the accuracy of original signal reconstruction; Liu et al.³² proposed a Variational Mode Decomposition with Deep Belief Networks (VMD-DBN) model, mitigating the strong oscillatory nature and instability of the original time series; Li et al.³³ proposed a Chaos Theory with Generalized Regression Neural Networks (Chaos-GRNN) model, overcoming the shortcomings of previous models in insufficient consideration of factors affecting water inflow and their inherent difficulty in quantification; Wang et al.³⁴ proposed a Variational Modal Decomposition and Bidirectional Long Short-Term Memory Networks (VMD-BiLSTM) model, enhancing the capture of long-term dependencies in sequential data; Hou et al.³⁵ proposed a Complete Ensemble Empirical Mode Decomposition with Adaptive Noise-Bayesian Optimization-Bidirectional Gated Recurrent Units Networks (CEEMDAN-BO-BiGRU) model, enhancing the capability to filter data noise and enabling iterative optimization of multiple parameters.

There are also many important research results from researchers in different fields in the study of related decomposition methods, prediction models and optimization algorithms. Yin et al.³⁶ applied the spatio-temporal data feature extraction capability of the Convolutional Long Short-Term Memory (ConvLSTM) model to similar material simulation experiments, which provided valuable spatio-temporal information on stratigraphic behavioural patterns induced by mining activities, and the information obtained provided an accurate guide to predicting the formation of water inflow channels; Sun et al.³⁷ propose an Service Function Chain Deployment Optimization (SFCDO) algorithm based on a Breadth-First Search (BFS), and the experiment results show that the proposed algorithm is optimized in terms of end-to-end delay and bandwidth resource consumption; Jin et al.³⁸ propose a Boids Model-based DRL Approach for Pursuit and Escape (Boids-PE), and the overall results demonstrate that Boids-PE significantly enhance the efficiency and reliability of unmanned aerial vehicles pursuit-evasion tasks, providing a practical and robust solution for the real-world application of unmanned aerial vehicles pursuit-evasion missions; Zhou et al.³⁹ propose a Field-Programmable Gate Array (FPGA)-based improved Gaussian full-waveform decomposition method, and the experimental results show that the accuracy of the FPGA-based processing is equivalent to that of Personal Control (PC)-based processing, and the processing speed of the FPGA-based processing is 292 times faster than that of PC-based processing; Yang et al.⁴⁰ propose a novel Hierarchical Convolutional Neural Network and Gated Recurrent Unit (HCG) framework to model both spatial and temporal relations, termed as HCG, for structural damage detection, and the research results shown that the HCG outperforms other existing methods for structural damage detection significantly.

The inflow data series researched in this paper is nonlinear and oscillatory, so the corresponding methods should be selected and combined into a prediction model according to the actual situation. The oscillatory nature of the inflow data series can make the prediction results inaccurate, this paper refers to the decomposition methods used in previous studies and concludes that the adaptive and strong robustness of the Variational Modal Decomposition (VMD) method is more appropriate in decomposing the inflow data series compared to other methods. The inflow data series belongs to the time series, Gated Circulation Units (GRU) neural network solves the problem of gradient disappearance that Recurrent Neural Network is prone to when dealing with long sequence data and simplifies the gating structure compared to Long Short-Term Memory, which maintains good performance with lower computational complexity. Optimization algorithms can help predictive models to find the optimal hyperparameters. Currently, the commonly used optimization algorithms are meta-heuristic algorithms, and based on the No Free Lunch (NFL) theory⁴¹, no single meta-heuristic algorithm can universally solve all real-world problems. Therefore, according to the actual situation of the research, it is considered that the Chimpanzee Optimization Algorithm (CHOA) among the meta-heuristic algorithms has certain advantages in dealing with optimization problems in dynamic environments, and on the basis of previous research, the Sobol sequence is chosen to initialize the population, and the brand-new cosine dynamics factor is improved in order to enlarge the search range of the attacker. Based on the above analysis and selection of decomposition methods, time series prediction models and optimization algorithms, this paper constructs the Variational Mode Decomposition and Gated Recurrent Units Optimized by Improved Chimp Optimization Algorithm (VMD-iCHOA-GRU) prediction model, which provides new choices and references in the aspect of mine inflow prediction models.

Overview of the study area

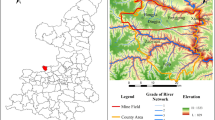
This paper takes a coal mine in Huainan City, Anhui Province, China, as the research object. The coal mine belongs to the central enterprise China Coal Xinji Energy Co., Ltd, with a design annual production capacity of 3.2 million tons, a design recoverable reserve of 20,262,800 tons, and a service life of 47 years. The shaft field is about 6.0 kms long from east to west and 4 to 7 kms wide from north to south, with a total area of about 33.6 square kilometres. The main mineable coal seams are No. 8 seam, No. 5 seam and No. 1 seam, and the average total thickness of the three seams is 12.83 m. The location of the mine is shown in Fig. 1.

Fig. 1

Illustration of mine location. This map was created by Mingjin Fan using PPT and is copyrighted by Mingjin Fan. The map shows the location of Anhui Province on a map of China on the left, the location of the city of Huainan and the coal mine in Anhui Province on the right, and the mine’s return face below.

The mine is currently mining coal seam 5, which is mainly affected by the top plate Neoproterozoic Miocene IV aquifer, Paleoproterozoic sandstone conglomerate aquifer and Permian sandstone fissure aquifer, and the Neoproterozoic Miocene III aquiclude can play a better water isolation effect on the Neoproterozoic Miocene IV aquifer, so there is no hydraulic connection between the Neoproterozoic Miocene IV aquifer and Neoproterozoic Upper Neoproterozoic III aquifer in the natural state. According to the ground hydrological borehole pumping data, it can be seen that the fourth aquifer of the Neocene system is controlled by the original sedimentary action, and it is dominated by powder and fine sand, with the water inflow per unit of q = 0.0951–0.6354L·s⁻¹·m⁻¹, weakly to moderately water-rich, and there is no continuous thick layer of clay water isolation layer at the bottom of the aquifer; the Paleocene system sandstone and conglomerate aquifer is basically without influence on the water filling of mines, due to its unstable distribution and limited scope of development. The Permian sandstone fissure aquifer is weakly water-rich in the original state with q = 0.0005–0.0989L·s⁻¹·m⁻¹, but the water-rich nature is obviously strengthened by the hydraulic connection of the fourth aquifer of the Neoproterozoic system at its hidden outcrop. The main roof aquifers and aquitard in the study area are shown in Fig. 2.

Fig. 2

Schematic diagram of the main roof strata containing aquifers and aquitard layers in the study area. Gray-green rectangles represent coal seams; blue rectangles represent major aquifers; yellow rectangles represent major aquicludes.

Methods

VMD method

The VMD⁴² works essentially by finding an optimal solution to a variational problem and involves the solution process of the variational problem, the basic flow of which is as follows:

• (1) For each mode $v_{k} (t)$, the bandwidth of the demodulated signal is estimated using Gaussian smoothing technique by using the resolved signals and their one-sided spectra obtained by Hilbert transform and adjusting the centre frequency of each signal with the addition of an exponential term. The constrained variational problem can be expressed in the form shown in Eq. (1) below:

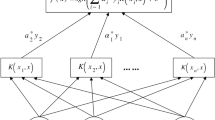
  $$\left\{ \begin{gathered} \min_{{\{ v_{k} \} ,\{ \omega_{k} \} }} \left\{ {\sum\limits_{k} {\left\| {\partial_{t} \left[ {\left( {\delta (t) + \frac{j}{\pi t}} \right)*v_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|^{2} } } \right\} \hfill \\ s \cdot t \cdot \sum\limits_{1}^{k} {v_{k} (t) = s(t)} \hfill \\ \end{gathered} \right.$$

  (1)

  where $k$ is the number of decomposed modes; $v_{k} (t)$ is the $k$ th first decomposed mode; $\omega_{k}$ is the $k$ th centre frequency; $\delta (t)$ is the impulse signal; and the constraints are described as the superposition of all decomposed modes and equal to the original signal $s(t)$

• (2) The Lagrange multiplier $\tau (t)$ as well as the quadratic penalty term α^[99] are introduced to construct the Lagrange function as shown in Eq. (2):

  $$\begin{aligned} L\left( {\left\{ {v_{k} } \right\},\left\{ {\omega _{k} } \right\},\tau } \right) = & \alpha \sum\limits_{k} {\left\| {\partial _{t} \left[ {\left( {\delta (t) + \frac{j}{{\pi t}}} \right)*v_{k} (t)} \right]e^{{ - j\omega _{k} t}} } \right\|^{2} } \\ & + \left\| {s(t) - \sum\limits_{k} {v_{k} (t)} } \right\|^{2} + \left\langle {\tau (t),s(t) - \sum\limits_{k} {v_{k} (t)} } \right\rangle \\ \end{aligned}$$

  (2)

• (3) Iteratively update each IMF component and its centre frequency using the alternating direction multiplier method (ADMM) to solve the optimal solution of the original problem. The updating process is shown in Eqs. (3) and (4):

  $$\mathop {v^{\prime}}\nolimits_{k}^{n + 1} (\omega ) = \frac{{s^{\prime}(\omega ) - \sum\limits_{i \ne k} {v^{\prime}_{i} (\omega )} + \tau ^{\prime}(\omega )/2}}{{1 + 2\alpha (\omega - \omega_{k} )^{2} }}$$

  (3)
  $$\mathop \omega \nolimits_{k}^{n + 1} = \frac{{\int_{0}^{\infty } {\omega \left| {\mathop v\nolimits_{k}^{n + 1} (\omega )} \right|^{2} d\omega } }}{{\int_{0}^{\infty } {\left| {\mathop v\nolimits_{k}^{n + 1} (\omega )} \right|^{2} d\omega } }}$$

  (4)

where $s^{\prime}(\omega )$, $v^{\prime}_{i} (\omega )$, and $\tau ^{\prime}(\omega )$ represent the Fourier transform forms of $s(t)$, $v_{k} (t)$, and $\tau (t)$, respectively.

The VMD method searches for the optimal solution by minimizing the objective function, and solves the objective function iteratively through ADMM, and when the iteration converges, the modes obtained are the decomposition results of the original water inflow data, including the low-frequency component, middle-frequency component and high-frequency component, which can reveal the intrinsic structure and change rule of the data, and improve the accuracy of the prediction of the inflow.

iCHOA

CHOA⁴³ is an intelligent optimization algorithm proposed because of the social behaviour of chimpanzee populations, including four phases of repelling, chasing, encircling and attacking. Aiming at the problems of uneven initial population distribution and easy to fall into local optimum in CHOA, iCHOA is improved by introducing Sobol sequence and cosine dynamic factor, and the specific principles are shown as follows:

• (1) Define the possible interval of the global solution as, introduce the Sobol sequence-generated random variable, and the population initialization position as shown in Eq. (5):

  $$X_{n} = lb + S_{i} \cdot (ub - lb)$$

  (5)

  where $lb$ is the left boundary of the interval; $ub$ is the right boundary of the interval; and $S_{i}$ is the $i$ th random variable generated by the Sobol sequence, $S_{i} \subseteq [0,1]$.

  Assuming that the search space is two-dimensional, and the upper and lower bounds are 0 and 1 respectively population size is 50, comparing the randomly initialized population spatial distribution and the Sobol sequence initialized population spatial distribution is shown in Fig. 3.

  Fig. 3

  

  Distribution of initialization for two different methods. (a) represents the effect of random initialization distribution; (b) represents the effect of Sobol sequence initialization distribution; in contrast the Sobol sequence initialization is more evenly distributed.

  As can be seen in Fig. 3, the Sobol sequence initialization distribution is more uniform and extensive compared to the random initialization distribution, with good results.

• (2) After the initialization of the population, chimpanzees are divided into four categories: Attacker, Barrier, Chaser and Driver, where the Attacker leads the population in searching for prey, and the other three categories are responsible for assisting. Attacker predation according to the position of the prey changes its position accordingly, its position is updated as shown in Eq. (6), and the calculation of each position vector is shown in Eqs. (7–10):

  $$X_{chimp} (t + 1) = X_{prey} (t) - a \cdot d$$

  (6)
  $$a = 2 \cdot f \cdot r_{1} - f$$

  (7)
  $$d = \left| {c \cdot X_{prey} (t) - m \cdot X_{chimp} (t)} \right|$$

  (8)
  $$c = 2 \cdot r_{2}$$

  (9)
  $$m = Chaotic.value$$

  (10)

  where $X_{chimp}$ is the coordinate vector of the current chimpanzee group; $X_{prey}$ is the coordinate position of the current target prey; $t$ is the current number of iterations; $a$ is a random vector used to measure the relative distance between the chimpanzee group and the prey; $f$ is the convergence factor, whose magnitude decreases nonlinearly from 2.5 to 0 with the number of iterations; $r_{1}$ is a random number with the value of [0,1]; $d$ is the distance between the chimpanzee and the prey; $c$ is the distance during the hunting process obstacle influence factor on chimpanzee hunting; $r_{2}$ is a random number taking the value of [0,1]; $m$ is a chaotic mapping vector; and $Chaotic.value$ is the value of the chaos factor.

• (3) To enable the attacker to search in a wider range, which enhances the ability of the algorithm to get rid of the local optimum, this paper improves the water wave dynamic factor chosen by the previous research to obtain the cosine dynamic factor with a wider search range⁴⁴. Among them, the mathematical model of the water wave dynamic factor is shown in Eq. (11) and the mathematical model of the cosine dynamic factor is shown in Eq. (12):

  $$\omega = 1 - \sin \left( {\frac{\pi }{2} \cdot \frac{t}{{t_{\max } }} + 2\pi } \right)$$

  (11)
  $$\varepsilon = \cos \left( {\frac{10\pi }{9} \cdot \frac{t}{{t_{\max } }} - \frac{\pi }{9}} \right)$$

  (12)

where $t$ represents the present iteration count, $t_{\max }$ signifies the utmost iteration, $\varepsilon$ is the cosine dynamics factor, $\omega$ is the water wave dynamics factor respectively.

The maximum number of iterations $t_{\max }$ = 10 is set, and the current number of iterations $t$ ranges from 1 to 10, and a comparison of the search ranges of the two methods is shown in Fig. 4.

Fig. 4

Comparison of the search ranges of the two methods. The blue line indicates the distribution of the dependent variable corresponding to the water-wave dynamics factor when the number of iterations is from 1 to 10; the orange line indicates the distribution of the dependent variable corresponding to the cosine dynamics factor when the number of iterations is from 1 to 10; the distribution of the cosine dynamics factor is much more uniform in comparison.

As shown in Fig. 4, when the search range is in [0,1], the water wave dynamic factor is distributed with three, while the cosine dynamic factor is uniformly distributed with five, and the search range of the cosine dynamic factor is wider and more uniform in the range of the interval; when the search range is in [−1,0], there exists an overlapping part of the search range of the water wave dynamic factor, while the distribution of the cosine dynamic factor is more uniform, and the search range is more extensive. In summary, it is believed that the cosine dynamic factor enables the attacker to search in a wider area and more uniformly, which is more effective.

The mathematical model of chimpanzee prey attack after introducing cosine dynamic factor is shown in Eqs. (13) to (15):

$$\left\{ \begin{gathered} X_{1} = \varepsilon X_{Attacker} - a_{1} \cdot d_{Attacker} \hfill \\ X_{2} = X_{Barrier} - a_{2} \cdot d_{Barrier} \hfill \\ X_{3} = X_{Chaser} - a_{3} \cdot d_{Chaser} \hfill \\ X_{4} = X_{Driver} - a_{4} \cdot d_{Driver} \hfill \\ \end{gathered} \right.$$

(13)

$$\left\{ \begin{gathered} d_{Attacker} = \left| {c_{1} \cdot X_{Attacker} - m_{1} \cdot x} \right| \hfill \\ d_{Barrier} = \left| {c_{2} \cdot X_{Barrier} - m_{2} \cdot x} \right| \hfill \\ d_{Chaser} = \left| {c_{3} \cdot X_{Chaser} - m_{3} \cdot x} \right| \hfill \\ d_{Driver} = \left| {c_{4} \cdot X_{Driver} - m_{4} \cdot x} \right| \hfill \\ \end{gathered} \right.$$

(14)

$$X(t + 1) = \frac{{X_{1} + X_{2} + X_{3} + X_{4} }}{4}$$

(15)

where $X_{Attacker}$, $X_{Barrier}$, $X_{Chaser}$, and $X_{Driver}$ denote the position vectors of the Attacker, Barrier, Chaser and Driver, and pursuer, respectively; $X_{1}$, $X_{2}$, $X_{3}$, and $X_{4}$ denote the updated coordinate vectors of the attacker, Attacker, Barrier, Chaser and Driver, respectively; and $X(t + 1)$ denotes the updated localization vectors of the individual chimpanzee after iteration.

Compared with the unimproved CHOA, the population initialization of iCHOA is more uniform, the attacker searches more widely, avoids falling into the local optimum, and can effectively perform hyperparameter optimization, apply the optimal hyperparameter values to the model prediction, and improve the prediction accuracy of the model.

GRU model

GRU is a simplified neural network that contains only update gates and reset gates, which can greatly improve the prediction speed while maintaining a better fitting effect. The internal structure of GRU neural network is shown in Fig. 5.

Fig. 5

Schematic diagram of the internal structure of GRU. All colors in this chart are used only to enhance the comparative charts of the sections within the chart for the reader’s convenience.

The GRU neural network calculation formulas are shown in Eqs. (16) to (19):

$$r_{t} = \sigma (W_{r} \left[ {h_{{^{t - 1} }} ,x_{{^{t} }} } \right] + b_{r} )$$

(16)

$$z_{t} = \sigma (h^{t - 1} \cdot W_{z} \left[ {h_{{^{t - 1} }} ,x_{{^{t} }} } \right] + b_{z} )$$

(17)

$$\widehat{h} = \tanh \left( {W_{z} \left[ {(r_{t} \odot h_{{^{t - 1} }} ),x_{{^{t} }} } \right] + b_{z} } \right)$$

(18)

$$h_{{^{t} }} = (1 - z_{t} ) \odot h_{{^{t - 1} }} + z_{t} \odot \widehat{h}$$

(19)

where $r_{t}$ is the reset gate; $z_{t}$ is the update gate; $\sigma$ is the activation function; $W_{r}$ and $W_{z}$ are the weight matrices of the reset and update gates, respectively; $b_{r}$ and $b_{z}$ are the bias matrices of the reset and update gates, respectively; $h_{{^{t - 1} }}$ is the implied state; $x_{{^{t} }}$ is the input of the current time step; $\widehat{h}$ mainly contains the input information of the current time step $x_{{^{t} }}$; $\tanh$ is the activation function, which restricts the $\widehat{h}$ range to the range of [-1,1]; and $(1 - z_{t} ) \odot h_{{^{t - 1} }}$ denotes a selective memory for the control of the previous implicit state selective forgetting; $z_{t} \odot \widehat{h}$ denotes selective memorization of the information containing the current node.

The GRU neural network can construct a high-performance inflow prediction model by capturing the long and short-term dependencies in time-series data through rational data preprocessing, model construction and training.

VMD-iCHOA-GRU prediction model construction

Mine inflow is often affected by multiple factors, resulting in unsatisfactory prediction results of a single algorithm, so choosing a composite algorithm to predict mine inflow is an important means to improve the accuracy of prediction. Using the advantages of VMD method in time series decomposition and iCHOA-GRU model in searching the spatial and temporal characteristics of mine water inflow data, this paper adopts the VMD-iCHOA-GRU model obtained from the composite of VMD method and iCHOA-GRU model to establish the composite prediction model of mine water inflow and realize the accurate prediction of mine water inflow. The detailed steps for prediction are outlined as follows:

Step 1: Preprocessing of mine water inflow data, including Outlier testing & processing and Handling of missing values.

Step 2: The pre-processed data are normalized, and the data are divided into training set and test set in the ratio of 7:3, and the data are decomposed into multiple IMFs with limited bandwidth using the VMD method to obtain the modal components of different frequency bands.

Step 3: After the iCHOA optimization algorithm is parameterized, the GRU model hyperparameters are optimized, and the optimal solution is obtained.

Step 4: The decomposed training set and test set data are imported into the iCHOA-GRU model for training and testing, and the predicted values of each modal component are superimposed.

Step 5: Perform denormalization on the superimposed predicted values and select reasonable indicators to evaluate the prediction accuracy of the model.

Step 6: Output the final prediction results.

The flow of the VMD-iCHOA-GRU prediction model is shown in Fig. 6:

Fig. 6

Flowchart of VMD-iCHOA-GRU composite prediction model. The left side is the regular prediction process of data sequence; the right side is the optimization seeking process of iCHOA; the color of the picture is only used for the convenience of readers.

Data processing

The mine mined the No. 5 seam 110,502 face from December 2, 2023, to May 30, 2024, and the water ingress data were obtained from the underground borehole water ingress data monitored by the mine from January 10, 2024 at 00:00 to January 12, 2024 at 00:00 h. The monitoring system recorded data every 1 min, with a total of 2880 data recorded over the two days.

Data preprocessing

• (1) Outlier testing and processing

  For time series, there may be some obvious deviations from the normal data points, whose values are outliers. Hydrological observation data set is generally larger, generally more convenient and simpler Lajda criterion to test these outliers, and the outliers will be deleted. The specific calculations are shown in Eqs. (20) and (21).

  $$\sigma = \sqrt {\frac{{\sum\limits_{i = 1}^{d} {\left( {x_{i} - x} \right)^{2} } }}{d - 1}}$$

  (20)
  $$\left| {x_{i} - \overline{x} } \right| > 3\sigma$$

  (21)

  where $x_{i}$ is any of the original data; $d$ is the number of original data; $\overline{x}$ is the mean of the original data; $\sigma$ is the standardized variance of the original data. When the absolute difference between $x_{i}$ and $\overline{x}$ is greater than 3 $\sigma$, it is considered an outlier and the outlier should be deleted.

• (2) Handling of missing values.

  After the removal of the outliers, the vacant part becomes the missing values, which together with the original missing values in the original data constitute the whole set of missing values. The missing values are processed by linear interpolation, and the specific calculation process is shown in Eqs. (22)

  $$f(t_{1} ) = f(t_{0} ) + (t_{1} - t_{0} )\frac{{f(t_{2} ) - f(t_{0} )}}{{t_{2} - t_{0} }}$$

  (22)

  where $t_{0}$ and $t_{2}$ are the two moments on either side of the missing value moment; $f(t_{0} )$ and $f(t_{2} )$ are the corresponding original values, respectively; $t_{1}$ is the missing value moment; and $f(t_{1} )$ is the value at the moment $t_{1}$ after the difference.

Data normalization and denormalization

Normalization is a data preprocessing technique commonly used in machine learning, data analysis, and other fields. It transforms data from different ranges to a similar range, usually to ensure that a feature does not dominate the results due to a larger range of values. In this paper, we choose the commonly used min–max normalization method, and the denormalization is to restore the data that has been normalized to the original scale, and the calculation formula is shown in Eqs. (23) and (24), respectively.

$$x^{\prime} = \frac{x - \min (x)}{{\max (x) - \min (x)}}$$

(23)

$$x = x^{\prime}\left( {\max (x) - \min (x)} \right) + \min (x)$$

(24)

where $x$ is the original value; $x^{\prime}$ is the normalized value, and $\min (x)$ and $\max (x)$ are the minimum and maximum values among all the values, respectively.

Data grouping

After data preprocessing, in the process of verifying the effect of dividing the training set and test set according to different ratios on the prediction results, it was found that when dividing the training set and test set according to the ratio of 7:3, the fit of the model reached the highest of 87.4%, which indicates that the predicted values of the training set of the model are highly close to the real values, so the ratio of the training set and the test set was set to 7:3. the training set and the test set were imported into the prediction model, which was used for 60 min of inflow. The prediction model uses 60-min inflow data to predict the next 4-min inflow, i.e., the model uses 15 consecutive time-steps of inflow data as inputs, and then extrapolates the next 1 time-step of inflow. The inflow data is shown in Fig. 7, where the blue portion indicates the training set data, and the orange portion indicates the test set data.

Fig. 7

Mine water inflow data. Blue sections indicate training set data; orange sections indicate test set data.

Model parameter optimization and evaluation

The model was built based on Matlab R2022b platform and trained and predicted under the operating system Windows 11, CPU Intel i3 12,100, and memory 16 GB 3200 MHz.

Model parameters

There are three hyperparameters in the GRU model that need to be optimized: InitialLearnRate, L2Regularization and NumOfUnits. The iCHOA and the unimproved CHOA are chosen to optimize the parameters of the GRU model, and the parameter settings of the two algorithms need to achieve the best optimization effect. The parameter settings of the two algorithms are shown in Table 1.

Table 1 Parameterization of the algorithm itself.

After 100 iterations of optimization, the accuracy of the iCHOA reaches the maximum value of 93.21% and converges at the 17th iteration; the accuracy of the CHOA reaches the maximum value of 92.16% and converges after 22 iterations. This indicates that the iCHOA is superior to the unimproved CHOA. The relationship between the number of iterations and the accuracy of the two algorithms is shown in Fig. 8, and the hyperparameters of the optimized GRU model are shown in Table 2.

Fig. 8

Iterative optimization accuracy of the two algorithms. The blue line indicates the iterative accuracy change of the iCHOA; the green line indicates the iterative accuracy change of the CHOA.

Table 2 GRU parameter optimum after iterative optimization of two algorithms.

Evaluation indicators

In this paper, four evaluation indexes, i.e., mean absolute error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE) and coefficient of determination (R²), are selected to evaluate the prediction accuracy of the model. Among them, MAE is the average of the absolute difference between the predicted value and the true value, RMSE is the square root of the average of the squares of the differences between the predicted value and the true value, MAPE is the average of the absolute percentage errors between the predicted value and the true value , and the smaller the value, the smaller the error, and the better the prediction effect; R² is the proportion of the model’s predicted value relative to the true value of the dependent variable, and the value range is usually from 0 to 1, and the larger the value, the better the model fit. The larger the value, the better the model fit. The calculation of each evaluation index is shown in Eqs. (25) to (28).

$$MAE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\widehat{{y_{i} }} - y_{i} } \right|}$$

(25)

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {y_{i} - \widehat{{y_{i} }}} \right)^{2} } }$$

(26)

$$MAPE = \frac{100\% }{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{y_{i} - \widehat{{y_{i} }}}}{{y_{i} }}} \right|}$$

(27)

$$R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{n} {\left( {\widehat{{y_{i} }} - y_{i} } \right)^{2} } }}{{\sum\limits_{i = 1}^{n} {\left( {\overline{y} - y_{i} } \right)^{2} } }}$$

(28)

where $n$ is the sample size, $\widehat{{y_{i} }}$ is the predicted value, $y_{i}$ is the true value, is the average of the predicted values, and $\overline{y} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\widehat{{y_{i} }}}$.

Comparison model

According to the existing studies, compared to CHOA, iCHOA has faster convergence and higher accuracy in algorithm optimization. Therefore, in this paper, the unoptimized Variational Mode Decomposition with Gated Recurrent Units (VMD-GRU) model, the undecomposed Gated Recurrent Units Optimized by Improved Chimp Optimization Algorithm (iCHOA-GRU) model, the unimproved Gated Recurrent Units Optimized by Chimp Optimization Algorithm (CHOA-GRU) model, and the Gated Recurrent Units (GRU) model are selected as the comparison models for the prediction experiments and the ablation experiments as a means of verifying the stability and accuracy of the VMD-iCHOA-GRU prediction model for the prediction of the water level of the aquifers of the mine.

Results of the experiment

Results of decomposition experiment

The water inflow data fluctuates and oscillates with time, and the modal decomposition of the water inflow data using the VMD method can reduce the degree of fluctuation and oscillation of the data and improve the accuracy of the prediction. To ensure that the decomposition is sufficient and not excessive, the centre frequency method is used to determine the value of the decomposition modal number K. In this paper, the modal decomposition of water inflow data starts from K = 1, and the number of decomposition modes is increased continuously to calculate the centre frequency of each Intrinsic Mode Function (IMF) under different decomposition mode numbers. The results are shown in Table 3.

Table 3 Centre frequency of each decomposition mode for different number of decomposition modes.

When K = 9, the centre frequency of 0.4620 for IMF8 is more than 90% close to the centre frequency of 0.4869 for IMF9. The very close proximity of the centre frequencies between consecutive decomposition modes indicates that the decomposition modal number K was chosen too large, resulting in the modes being unnecessarily subdivided. Therefore, the optimal number of decomposition modes for this water level data series was determined to be K = 8. The VMD decomposition results of the water level data from the three observation holes are shown in Fig. 9.

Fig. 9

VMD decomposition results. The black line is the low-frequency component, which indicates the overall trend of the data series; the light blue line is the medium-frequency component, which indicates the impact of various types of activities on the data series in a medium time scale; and the dark blue line is the high-frequency component, which indicates the impact of sudden events on the data series in a short period of time.

As shown in Fig. 9, IMF1 is the low frequency component, representing the overall trend of incoming water, and it can be seen that IMF1 basically depicts the overall trend of water inflow, i.e., it is small and gradually becomes larger in fluctuation; IMF2 is the middle frequency component, containing more significant fluctuation or vibration information in the signal, and it can be seen that the change of IMF2 is more uniform and presents certain periodic characteristics, and the corresponding overall change of water inflow also conforms to this characteristic; IMF3 ~ IMF8 is the high frequency component, representing the rapid change part of the signal in a short period of time. IMF3 ~ IMF8 are high-frequency components, representing the part of the signal that changes rapidly in a short period of time. Since the water inflow is affected by the disturbance of mining in the working face, there are often transient changes in a short period of time, so the transient changes of the signal in IMF3 ~ IMF8 are more and more rapid, which corresponds to the fluctuation and oscillation in the water inflow in a short period of time.

Results of predicting experimental

The prediction results of the test set of VMD-iCHOA-GRU model, VMD-GRU model, iCHOA-GRU model, CHOA-GRU model, and GRU model were compared with the actual values to verify the accuracy of each model in predicting the trend of the inflow volume. Due to the large amount of data in the test set of each model, which is more complicated to be presented in the picture, the data are selected uniformly every 20 data intervals starting from the first data of the test set of each model (including the first data) until the 860th data. The comparison of the prediction results for each model is shown in Fig. 10.

Fig. 10

Comparison of prediction results of each model. The black line represents the true value; the red line represents the predicted value of the VMD-iCHOA-GRU model; the green line represents the predicted value of the VMD-GRU model; the blue line represents the predicted value of the iCHOA-GRU model; the cyan line represents the predicted value of the CHOA-GRU model; and the pink line represents the predicted value of the GRU model.

As shown in Fig. 10, the VMD-iCHOA-GRU model has the best prediction effect; the VMD-GRU model lacks the algorithm for optimization of GRU hyperparameters, which leads to its prediction effect is slightly worse than that of the VMD-iCHOA-GRU model; the iCHOA-GRU model and the CHOA-GRU model lack the decomposition of the original data sequence by the VMD method, and are unable to capture the latest changes of data timely, resulting in the prediction value lagging behind the real value. The iCHOA-GRU model and the CHOA-GRU model are unable to capture the latest changes in the data in time, resulting in the predicted values lagging behind the real values, which can easily mislead the technicians to make opposite judgments in the actual production of mines, reducing the production efficiency or causing safety accidents; the GRU model that is not decomposed and optimized has the worst prediction effect due to the above reasons.

Results of ablation experiment

In this paper, four indicators, MAE, RMSE, MAPE and R², are selected to quantitatively analyse the prediction accuracy of each model, and the evaluation results are shown in Fig. 11.

Fig. 11

Comparison of evaluation results of each model. Shows the values of the evaluation metrics for each model, where the red color represents the VMD-iCHOA-GRU model; the green line represents the VMD-GRU model; the blue line represents the iCHOA-GRU model; the cyan line represents the CHOA-GRU model; and the pink line represents the VMD-GRU model.

As shown in Fig. 11, the VMD-iCHOA-GRU model has the highest accuracy in the prediction of water inflow; and the indexes of the VMD-GRU model are better than those of the iCHOA-GRU model, which indicates that the decomposition of the VMD method is stronger than the optimization of the iCHOA method in improving the accuracy of the prediction of water inflow, and that the data sequences should be decomposed by the VMD first before being imported into the VMD-iCHOA model. The data series should be decomposed by VMD first and then imported into the optimized GRU model for prediction. The indicators of iCHOA are better than those of CHOA, which indicates that the iCHOA improved by Sobol series and cosine dynamic factor is more advantageous in improving the prediction accuracy; the indicators of the original GRU model are the worst, which indicates that the adoption of the improved model for the prediction of inflow volume is reasonable.

Discussion

The aim of this study is to investigate the prediction of mine inflow using the VMD-iCHOA-GRU model, which is a combination of the VMD method, the iCHOA algorithm, and the GRU neural network, and to select a control model to investigate the effect of different modules of the model on the prediction of inflow. The main results show that the VMD-iCHOA-GRU model has the highest accuracy in the prediction of water inflow; and the indexes of the VMD-GRU model are better than those of the iCHOA-GRU model, which indicates that the decomposition of the VMD method is stronger than the optimization of the iCHOA method in improving the accuracy of the prediction of water inflow, and that the data series should be decomposed by VMD first, and then imported into the optimized GRU model of iCHOA. The data series should be decomposed by VMD first and then imported into the optimized GRU model for prediction. The indicators of iCHOA are better than those of CHOA, which indicates that the iCHOA improved by Sobol series and cosine dynamic factor is more advantageous in improving the prediction accuracy; the indicators of the original GRU model are the worst, which indicates that the adoption of the improved model for the prediction of inflow volume is reasonable.

These results have important theoretical implications for the prediction of future mine inflow. With the VMD method, the oscillating inflow data series can be feature extracted to reduce the influence of cluttered signals on the prediction; with the improved iCHOA, the hyperparameters of the prediction model can be better optimized to improve the prediction performance of the GRU model. In fact, this knowledge can be used to improve the inflow prediction method and predict the mine inflow more accurately, which plays an important role in the safe production of mines and the safety of people’s lives and properties.

The findings in the manuscript are consistent with previous studies of complex versus single prediction model predictions (Liang et al., 2023; Li et al., 2021; Liu et al., 2023; Wang et al., 2022; Hou et al., 2023), which all concluded that complex prediction models outperform single prediction models, the They all concluded that complex prediction models are better than single prediction models, and that modal decomposition of the oscillatory inflow data series can help to improve the prediction accuracy. However, our study extends the research methodology in this area by proposing an improved iCHOA optimization algorithm using Sobol series and cosine dynamic factors and combining it with the more mature VMD method and GRU neural network to obtain the VMD-iCHOA-GRU model. This model has better prediction accuracy than other models lacking optimization algorithms.

Despite the strengths of our study, there are some limitations. The model parameters used in this study are only applicable to the prediction of inflow under the geological conditions of this mine, and feature extraction was only considered for a single inflow data series. In future research and application, the relevant parameters of the model should be adjusted in time according to the actual hydrogeological conditions of the mine so that the model maintains a better prediction effect; at the same time, the effects of other factors such as aquifer water level, micro seismic energy level, micro seismic magnitude and other factors on the changes of the inflow volume should also be considered, and the multifactorial coupled prediction model should be constructed to further improve the prediction accuracy of the model.

When the prediction results show that the water inflow in the coming period exceeds the normal drainage capacity of the mine working face, the mining speed should be slowed down in time, the mining height of the working face should be lowered, and the change of the water level in the water level holes should be paid close attention to, and if necessary, the mining of the working face should be stopped and the report should be submitted to the dispatching office, and the meeting should be held to determine the countermeasure plan.

Conclusion

In this study, a new mine water inflow prediction model based on “variational mode decomposition and gated recurrent units optimized by improved chimp optimization algorithm” is introduced and applied to make high-precision prediction of mine inflow data series with oscillatory nature. The model has excellent decomposition and prediction functions to accurately predict the water inflow data. The main conclusions are as follows:

• 1. The VMD-iCHOA-GRU model can predict the trend of water inflow with minimum MAE, RMSE, MAPE and maximum Ryy², which illustrates the important role of the VMD method and the iCHOA optimization algorithm in improving the prediction accuracy.

• 2. The similarity of each index of VMD-GRU model and VMD-iCHOA-GRU model is higher than that of each index of iCHOA-GRU model and VMD-iCHOA-GRU model, which indicates that the decomposition method is more useful than the optimization method in predicting the oscillatory data series such as the water inflow. Therefore, the oscillatory data series should be decomposed first, and the prediction effect will be better after extracting all kinds of features of the data series.

• 3. In the field application, the model hyperparameters should be adjusted according to the actual trend of water inflow in the past period to ensure that the model always has the optimal prediction effect.