Introduction

In the modern digital world, due to technological advancements the intensity and diversification of cyber-attacks has reached an unexpected level. Challenges to network security has increased due to these malicious activities performed by attackers. Unlike network users, intruders also utilize technological advancements and perform various attacks to create financial losses1, operational disruptions, and data breaches2. Attack complexity and its frequency increases every day. Thus, it is essential to develop an adaptive and robust model to secure the networks. Recent studies estimate that global cybercrime costs will reach to approximately $10.5 trillion annually by 2025 from $3 trillion in 2015. This financial burden is coupled with severe operational disruptions, reputational damages, and potential national security risks. Additionally, with over 30 billion devices projected to connect to the Internet by 2030 the attack continues to expand. This makes traditional centralized methods as insufficient for detecting cyber-attacks.

Traditional approaches evolved so far are centralized which typically collects and analyze data at central location to detect different types of threats3. Though the centralized approaches are effective, but it has limitations in maintaining data privacy. Since centralized systems process huge amount of data in a central repository it leads to potential vulnerabilities and becomes an easy target to attackers4. Also, the data transfer process introduces latency and reduces the effectiveness of real time attack detection. When the network complexity and scalability increase, computational burden increases and the effectiveness in detecting threats becomes more critical in a centralized system. Centralized models face critical challenges, such as data privacy vulnerabilities, high latency, and limited scalability in dynamic network environments. Furthermore, as attackers adopt advanced strategies like distributed denial-of-service (DDoS) and advanced malware so that the conventional detection methods struggle to handle these attacks in real-time. These limitations necessitate the development of adaptive, robust, and privacy-preserving frameworks capable of addressing diverse cyber threats efficiently. Deep learning models are utilized in a wide range of applications5,6,7,8. Specifically for network security, numerous models are developed based on convolutional neural network and recurrent neural network9,10. Though the attack detection models developed based on CNN and RNN shows significant detection performance it has constraints in computational capabilities while detecting diverse attack patterns11.

To overcome this limitations, decentralized approaches are developed which utilizes the principle of federated learning. Multiple entities are allowed collaboratively to train a global model without sharing the local data. A decentralized approach provides more advantage in terms of reduced communication overhead, improved scalability, and enhanced data privacy. Privacy issues are reduced in decentralized approaches due to securing the local data while developing global model. Utilizing these benefits, an innovative approach is developed in this research work for detecting cyber-attacks through federated learning. The major objective of this research work is to create a model to address the issues of data privacy, communication efficiency and attain enhanced detection accuracy.

To attain this objective, a hybrid federated learning model is proposed by incorporating a novel spatio-temporal attention network (STAN) and a quantum inspired federated averaging optimization technique. The proposed hybrid model is designed to detect attacks and overcomes the limitations of traditional methods. Specifically, the novel spatio-temporal attention network captures the complex patterns in the network traffic data. Unlike the traditional model the proposed STAN utilizes attention mechanisms to capture the critical attack patterns in the network. This enhances accuracy and reliability in detecting a wide range of cyber threats.

Another feature of the proposed work is the quantum inspired federated learning optimization technique which overcomes the limitation of traditional federated averaging method. The proposed QIFA utilizes quantum computing principles and attain better convergence in attack detection. The quantum entanglement inspired aggregation procedure ensures the proposed model update its parameters from different nodes and improves the global model overall performance. The quantum tunneling procedure effectively avoids local optimal allows the optimization model to find best solutions which is not obtained through conventional methods.

To improve the federated learning process effectiveness the proposed model includes a hierarchical model aggregation procedure that dynamically groups nodes into regions based on the network condition and data similarity. By using an adaptive clustering algorithm, the local models are aggregated at regional servers to create an intermediate model. The intermediate models are then aggregated at central server to produce global model. Due to this, the communication overhead reduces, and detection accuracy increases in the attack detection process. Additionally, a multi- stage model refinement procedure is presented to fine tune the global model using a subset of the most relevant local model. This ensures the final model’s robustness and accuracy. The privacy preserving procedure used in the proposed utilizes advanced privacy preserving technique like differential privacy and secure multiparty computation to ensure data confidentiality in the federated learning process.

The proposed hybrid quantum-inspired federated learning network introduces an innovative detection model by integrating advanced quantum principles with federated learning for decentralized model training. Unlike traditional methods, the proposed approach employs a hierarchical model aggregation mechanism which dynamically grouping nodes based on data similarity and network conditions. This enhances the scalability and efficiency across diverse environments. The proposed spatio-temporal attention network (STAN) allows for the precise extraction of complex temporal and spatial patterns, a feature adaptable to various datasets and applications beyond network security. Moreover, the quantum-inspired federated averaging (QIFA) technique utilizes quantum superposition and entanglement principles to achieve superior convergence and global model optimization. Also, it avoids local minima that hinder conventional optimization methods. These advancements collectively offer enhanced adaptability, privacy preservation, and performance efficiency, making the proposed methodology applicable across domains such as healthcare, IoT networks, and large-scale distributed systems, where data heterogeneity and privacy are critical challenges.

The contributions made in this research work are summarized as follows.

  • Presented a novel spatio-temporal attention network to capture complex spatio-temporal patterns in network traffic data for cyberattack detection.

  • Presented a quantum inspired federated averaging optimization technique to improve the efficiency and convergence of the federated learning process by incorporating quantum inspired principles.

  • Presented a hierarchical model aggregation model that dynamically groups nodes into regions to reduce communication overhead and improve detection accuracy.

  • Presented a detailed experimental analysis to evaluate the proposed model performance through metrics like accuracy, precision, recall and f1-score.

The remaining discussion in the article are presented as follows. Section “Related works” presents a brief literature review of existing research works; Sect. “Proposed work" presents the proposed hybrid model for cyber-attack detection. Section “Results and discussion” presents the experimental results and discussion, and Section “Conclusion” highlights the conclusion section.

Related works

This section presents a brief literature review of existing works on cyber security models. A detailed analysis made in12,13,14 considered different deep learning techniques like convolutional neural network, recurrent neural network, deep belief network and autoencoders in detecting cyber-attacks like phishing and malware detection. The analysis utilizes benchmark datasets like UNSW-NB15 and CSECICIDS2018 to evaluate the deep learning model performances. Results summarizes that the analyzed deep learning models have high computational requirements and brings challenges like overfitting due to its complex architectures.

A detailed analysis of machine learning and deep learning models presented in15 for attack detection utilizes deep neural networks and support vector machines to detect different types of attacks. The feature from the benchmark KDD cup 99 dataset is extracted and classified through both deep neural network and SVM models. The results describes that the detection performance of deep neural network is better than SVM but both models require high computational cost and lags in detection performance while analyzing encrypted traffic. The attack detection model presented in16 utilizes graph neural network (GNN) for analyzing malicious network traffic to detect attack. The presented model captures the complex relationships between the network entities to detect the anomalies. The experimental results indicates that GNN are effective in anomaly pattern detection, but it requires labeled graph dataset which is challenging in real time attack detection scenarios. The deep learning-based attack detection model presented in17 developed a four layer deep fully connected network to detect different types of attacks like blackhole, DDoS, sinkhole, and wormhole attacks. The presented model demonstrates its detection performance through its high accuracy metric over traditional deep learning models.

The cyber-attack detect strategy presented in18 utilizes techniques like deep Q-Networks and Q-learning to detect different types of attacks in a network. The presented model considers the past and present traffic statistics while analyzing the network data to detect the attacks. Results demonstrate the presented model performance in various attack detection scenarios. However, it requires a precisely formulated reward functions to detect attacks with high accuracy which is challenging in real time attack detection. The attack detection model presented in19 includes a deep reinforcement learning model to dynamically adjust security policies for cyber-attack detection. The presented model utilizes an adaptive policy management procedure that fine tunes and modifies the policies based on the traffic changes to detect the threats. The adaptive procedure continuously evaluates the model and allocates suitable reward function to detect diverse attack patterns. However, providing suitable reward function has significant challenges while implementing in real time attack detection scenarios.

Attack detection through Long short-term memory (LSTM) network presented in20 captures the temporal dependencies in network traffic to detect the threats in a network. The experimentation of the presented model utilizes CTU-13 dataset to evaluate the attack detection performance and summarize that LSTM requires long training time and high memory requirements compared to traditional methods. Similar LSTM based attack detection is performed in21 through federated learning concept. The presented model aggregates the LSTM parameters from different locations and generates a global model to ensure data confidentiality and privacy. The results demonstrate the presented federated concept enhances the security, but it has high tradeoff between privacy preservation and overall performance.

An ensemble learning based attack detection presented in22 considered techniques like gradient boosting, random forest, and convolutional neural network. The ensemble model classifies the extracted network data features and finally selects the best through voting mechanism. Experimentations of the presented model utilize Bot-IoT dataset to demonstrate better detection accuracy and reduced false positives. However, due to integration of multiple models the computational overhead and complexity increases compared to traditional models.

A hybrid deep learning model presented in23 utilizes techniques like recurrent neural network and autoencoder to detect DDoS attacks in a network. The presented model extracts the attack features from network traffic through autoencoder and predicts the attack patterns through RNN. The experiments utilize CICIDS2017 dataset to evaluate the hybrid model’s better detection performance over traditional deep learning models. An attention based recurrent neural network is presented in24 to detect insider attack in a network. The presented model extracts the key features that indicate the presence of insider attack in a network through the attain based RNN model. Experimentation utilizes CERT insider threat dataset to evaluate the model performance and summarizes its better accuracy and reduced false positives. However, the presented approach has limitations in interpreting attention weights and requires precise tuning of models while detecting attacks.

The hybrid deep learning model presented in25 extracts the spatial features from the network traffic through CNN and extracts the temporal features through RNN for advanced attack detection in a network. The extracted features are fused and then classified through machine learning model to attain better detection performance. Experimentations utilizes UNSW-NB15 dataset to evaluate the model performance and from that the model better accuracy and high computation cost is identified as the major merit as well the demerit. The hybrid model presented in26 integrates the quantum principles with machine learning technique for attack detection in a network. The presented quantum support vector machine utilizes quantum entanglement and superposition principles while extracting the features and classifies them into different attack patterns. The experimental results demonstrate that the performance of quantum SVM is better than the traditional machine learning models. The hybrid attack detection model presented in27 utilizes multi-layer perceptron and convolutional neural network to detect IoT specific attacks in a network. The presented model extracts the features from network traffic using CNN and classifies them using multilayer perceptron. However, the presented model requires further optimization to attain enhanced detection performance over existing hybrid models.

A cybersecurity model presented in28 considered techniques like restricted Boltzmann machine and generative adversarial network for spam detection and insider attack identification. However, the results indicates that these deep learning model requires further enhancement in attack detection to detect different types of attack as it is limited to specific attack detection procedure. A deep convolutional generative adversarial network-based attack detection procedure presented in29 generates synthetic training data through GAN to increase the number of samples in the training process. The existing NSL-KDD dataset is augmented through the proposed model to demonstrate that increased training samples will simultaneously increase the accuracy and robustness in attack detection. Similar GAN based attack detection presented in30 generates attack patterns to improve the robustness of attack detection model. The experimental results highlight the enhanced performance attained due to the increased training samples.

A detailed evaluation of deep learning algorithms is presented in31 for cyberattack detection and multi-class classification in IoT networks. The presented approach considers approaches like DNN, CNN, and RNN models and utilize benchmark dataset to evaluate the model performance. The experimental analysis exhibit that highest accuracy of RNN model over other deep learning models. The cyber threat detection model presented in32 includes ML random forest algorithm to detect anomalies from cyber network. The presented model experimental analysis exhibits the better accuracy of random forest model over existing KNN and Naïve Bayes algorithms. To overcome the limitations in traditional ML based cyber security detection process, hybrid models are evolved. The hybrid model presented in33 incorporates ML and optimization techniques to detect different types of cyber-attacks. The presented optimized ML model attains high detection performance over traditional approaches. However, the presented model has high computational complexity and requires high quality of data for processing.

The cybersecurity model presented in34 for healthcare provides a centralized multi-source transfer learning procedure to detect DDoS and ransomware. The presented model extracts the features using PCA and utilizes advanced transfer learning to classify the attacks. The experimental results validate the model better accuracy but it has limitation in terms of high execution time. A hybrid model presented in35 combines Deep CNN with BiLSTM network to provide authentication in user application. The presented security model evaluates the trust based on Bayes theorem and process the features through hybrid deep learning model. The experimental evaluations highlight the model superior performance compared to conventional deep learning models. Similar security module presented in36 for user application detects threats using a hybrid ensemble learning approach in addition to hybrid optimization algorithm. The hybrid model combines sigmoid cosine with pigeon optimization for feature selection and classifies them using the ensemble model. Experimentations using benchmark dataset validates the better accuracy of presented model over traditional ML models.

The hybrid model presented in37 for intrusion detection combines reinforcement learning with deep Q neural network. The presented model extracts the features using the hybrid model and obtains optimal decision using Markov decision process. The experimentation that includes binary and multi attack classification evaluates different benchmark datasets and exhibits its better performance over traditional approaches. The anomaly detection model presented in38 for cyber-attack detection combines CNN with gaussian mixture model. The presented approach estimates the anomalous and legitimate event probabilities to detect different types of attacks. However, the presented model is computationally intensive and requires domain specific knowledge.

A federated learning-based IDS presented in39 utilizes convolutional neural network to train the models across different locations. The presented model shares the parameters of CNN to different nodes and generates a global model without sharing the user data. This enhances data privacy against cyber-attacks in a modern network. However, it requires a robust aggregation algorithm while generating the global model. The federated learning-based attack detection model presented in40 utilizes blockchain for secure model aggregation. The presented model ensures secure and transparent model updates across distributed nodes using block chain. However, it increases the computational overhead. Additionally, the complexity increases in addition to attack detection due to complexity of block chain systems.

Research gaps

From the literature analysis the following research gaps are identified.

  • Deep learning models like CNN, RNN, and autoencoder are better in detecting attacks and threats over machine learning algorithms. Various cyber-attacks are effectively detected by deep learning models. However, it requires more computation cost, training samples and sometimes face overfitting issues.

  • The utilization of recurrent networks in attack detection requires precise reward function which is critical to provide in real time applications.

  • The hybrid models evolved so far exhibit their better detection performance, however it requires significant computational resources while processing huge network traffic data.

  • Federated learning-based detection procedures provides enhanced data privacy and security but face issues while aggregating local models to generate global model. Integration of quantum principles can provide better accuracy and robust performance in attack detection.

Thus, in this research work federated learning is incorporated with quantum computing to attain enhanced performance in cyber-attack detection.

Proposed work

The proposed hybrid federated learning based cyber-attack detection model includes a hierarchical model aggregation procedure to group the nodes into regions based on the network data similarity and network condition. The spatio-temporal attention network used in the proposed work effectively captures the spatio-temporal patterns in network traffic data to detect wide range of cyber-attacks. The quantum inspired federated averaging model enhances the learning process through quantum inspired principles thus it improves the convergence and avoids local minima in finding optimal solution for the attack detection problem. Federated learning is a decentralized method in which multiple nodes or clients collaboratively train a model without sharing their local data. This method avoids the necessity of central data storage and thus enhances the privacy of the network. The major aim of FL is to minimize the global objective function. In general, the average of local objective function of all the participating nodes are formulated to obtain the global objective which is mathematically described as

$$F\left(w\right)=\frac{1}{K}{\sum }_{k=1}^{K}{F}_{k}\left(w\right)$$
(1)

where \(K\) indicates the total number of nodes or clients, \(w\) indicates the global model parameters, and \({F}_{k}\left(w\right)\) indicates the loss function of the \({k}^{th}\) node. In the initialization of FL process, the central server initializes the global model parameters and distributes that as initial parameters to the remaining nodes. This is mathematically represented as \(\left({w}_{0}\to \{{w}_{\text{0,1}},{w}_{\text{0,2}},\dots ,{w}_{0,K}\}\right)\) in which the initial model parameter for the \({k}^{th}\) node is indicated as \({w}_{0,k}\) and the global model parameter is indicated as \({w}_{0}\). Then each node in the network receives the global model parameters and utilizes them to update the local model. The local model is then trained to minimize the local objective function. This is performed by using gradient descent or other optimization algorithms. In the proposed work, the optimization utilizes quantum inspired federated averaging optimization procedure to minimize the local objective function. Mathematically the local objective function is formulated as

$${w}_{k}^{\left(t+1\right)}={w}_{k}^{\left(t\right)}-\eta \nabla {F}_{k}\left({w}_{k}^{\left(t\right)}\right)$$
(2)

where \({w}_{k}^{\left(t\right)}\) are the model parameters at node \(k\) at iteration \(t\), local loss function is indicated as \(\nabla {F}_{k}\left({w}_{k}^{\left(t\right)}\right)\) and \(\upeta \) indicates the learning rate. After successive local training, the nodes send its updated model parameters to the central server which is mathematically described as \(\left(\{{w}_{k,1},{w}_{k,2},\dots ,{w}_{k,K}\}\to Central Server\right)\). Finally in the global model aggregation, the central server aggregates updates from all the nodes and generates a global model. The global model update is mathematically formulated as

$${w}^{\left(t+1\right)}=\frac{1}{K}{\sum }_{k=1}^{K}{w}_{k}^{\left(t+1\right)}$$
(3)

This process is repeated till convergence and in each round the central server updates the global model and distributes the parameters to local nodes. Through these procedures FL performs collaborative training across multiple nodes and preserves the data privacy.

Hierarchical model aggregation (HMA)

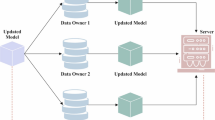
In the proposed hybrid federated learning network, a novel hierarchical model aggregation (HMA) procedure is presented to enhance the stability, accuracy, and efficiency in a decentralized learning environment. In the hierarchical model aggregation procedure, each node trains its network using its own dataset. However, to manage the scalability and to improve the efficiency of the aggregation process, the nodes are then grouped into regions based on network condition and data similarity. For this an adaptive clustering algorithm is used in the HMA process. A complete overview of HMA is depicted in Fig. 1.

Fig. 1
figure 1

Hierarchical model Aggregation.

Full size image

Consider \({\mathcal{R}}_{\mathcal{m}}\) be the set of nodes in a region \(m\), then clustering is performed based on data similarity which is measured through cosine similarity. Let \({D}_{k}\) and \({D}_{j}\) be the data distributions at nodes \(k\) and \(j\) respectively, then cosine similarity between these two data points is mathematically expressed as

$${Sim}_{data}\left(k,j\right)=\frac{{D}_{k}\cdot {D}_{j}}{|{D}_{k}||{D}_{j}|}$$
(4)

where \({Sim}_{data}\) indicates the data similarity, \((\cdot )\) indicates the dot product and \((|.|)\) indicates the norm of the vector. Further the network conditions are evaluated based on the parameters like packet loss rate, bandwidth, and latency metrics. Consider \({L}_{kj}\) be the latency between the nodes, then network efficiency is measured by inversing the latency which is mathematically formulated as

$${Sim}_{net}\left(k,j\right)=\frac{1}{{L}_{kj}}$$
(5)

where \({\text{Sim}}_{\text{net}}\) indicates the network conditions, \({L}_{kj}\) indicates the latency between nodes \(k\) and \(j\) respectively. Finally, to create a region, a combined similarity score is calculated considering the network condition and data similarity which is mathematically expressed as

$${Sim}_{combined}\left(k,j\right)=\alpha \cdot {Sim}_{data}\left(k,j\right)+\left(1-\alpha \right)\cdot {Sim}_{net}\left(k,j\right)$$
(6)

where \({\text{Sim}}_{\text{combined}}\) indicates the combined similarity score, weighting factor is indicated as \(\alpha\) and it is used to balance the data similarity and network condition. Further considering the similarity score, clustering is performed using k-means clustering algorithm. The clustering algorithm randomly initializes \(M\) cluster centroids as \((\{{C}_{1},{C}_{2},\dots ,{C}_{M}\})\) and assign each node to the cluster whose centroid has highest similarity score. For each node, the cluster assignment is mathematically formulated as

$${r}_{k}=\mathit{arg}\underset{m}{\mathit{max}}{Sim}_{combined}\left(k,{C}_{m}\right)$$
(7)

After cluster assignment, the centroids of the clusters are recomputed based on the current cluster assignment. The new centroid of cluster is the mean of nodes assigned to the cluster which is mathematically formulated as

$${C}_{m}=\frac{1}{\left|{R}_{m}\right|}{\sum }_{k\in {R}_{m}}{X}_{k}$$
(8)

where \({R}_{m}\) indicates the set of nodes assigned to cluster \(m\) and \({X}_{k}\) indicates the feature vector of the node. This procedure is repeated till all the cluster assignments are done. Then the final output of the clustering algorithm provides a set of regions \((\{{R}_{1},{R}_{2},\dots ,{R}_{M}\})\), in which each region \({\mathcal{R}}_{\mathcal{m}}\) contains a group of nodes with high data and network similarity. In each region, the nodes collaboratively train the local model by sharing its local updates. The regional server aggregates the updates from local models and creates an intermediate regional model \({w}_{m}\) which is mathematically expressed as

$${w}_{m}^{\left(t+1\right)}={\sum }_{k\in {R}_{m}}\frac{{n}_{k}}{{\sum }_{i\in {R}_{m}}{n}_{i}}{w}_{k}^{\left(t+1\right)}$$
(9)

where \({n}_{k}\) is the number of data samples at node \(k\) and \({\sum }_{i\in {\mathcal{R}}_{\mathcal{m}}}{n}_{i}\) is the total number of data samples in region \(m\). In the global aggregation process, the regional models are sent to the central server which is given as \(\left(\{{w}_{1}^{\left(t+1\right)},{w}_{2}^{\left(t+1\right)},\dots ,{w}_{M}^{\left(t+1\right)}\}\to Central Server\right)\) and it combines the regional models to update the global model parameters which is mathematically formulated as

$${w}^{\left(t+1\right)}={\sum }_{m=1}^{M}\frac{{\sum }_{k\in {\mathcal{R}}_{\mathcal{m}}}{n}_{k}}{n}{w}_{m}^{\left(t+1\right)}$$
(10)

where \(n\) is the total number of data samples across all nodes. The process of local model training and global model aggregation is repeated for several rounds until the global model parameters converge to the solution that minimizes the objective function. Through the hierarchical model aggregation, the proposed model provides an accurate and efficient federated learning environment.

Spatio-temporal attention network (STAN)

In the proposed work, the anomalies in the network are detected by analyze the spatial and temporal patterns in the network traffic data using a novel spatio-temporal attention network (STAN). The proposed STAN analyzes the network traffic feature vectors over time. Consider \(X\in {R}^{T\times N}\) is the input network traffic data to the STAN in which \(N\) indicates the number of features and \(T\) indicates the time steps. At time step \(t\), each element \({X}_{t,n}\) indicates the value of \({n}^{th}\) feature. Figure 2 depicts the process overview of proposed STAN.

Fig. 2
figure 2

Spatio-Temporal Attention Network (STAN).

Full size image

The temporal attention mechanism in the proposed STAN captures the temporal dependencies by calculating the attention score for each time step. Mathematically the process to compute temporal vector for each time step is formulated as

$${h}_{t}=ReLU\left({W}_{t}{X}_{t}+{b}_{t}\right)$$
(11)

where \({h}_{t}\) indicates the temporal vector, \({W}_{t}\in {R}^{d\times N}\) indicates the temporal attention mechanism weight matrix, \({X}_{t}\) indicates the feature vector, \({b}_{t}\in {R}^{d}\) indicates the bias vector and the activation function is indicated as \(ReLU\). Then the attention score is calculated using a SoftMax function which is mathematically expressed as

$$ \alpha_{t} = \frac{{\exp \left( {h_{t} } \right)}}{{\mathop \sum \nolimits_{{t^{\prime} = 1}}^{T} \exp \left( {h_{t\prime } } \right)}} $$
(12)

where \(\alpha_{t}\) indicates the attention score. Based on the attention score, the weighted sum of input feature is computed to obtain the temporal attention output. Mathematically it is expressed as

$$ \tilde{X} = \mathop \sum \limits_{t = 1}^{T} \alpha_{t} X_{t} $$
(13)

where \(\tilde{X}\) indicates the temporal attention output. Similarly, the proposed STAN includes a spatial attention mechanism to capture the spatial dependencies over each time step. The spatial vector for each feature is calculated as

$${g}_{n}=ReLU\left({W}_{s}{X}_{n}+{b}_{s}\right)$$
(14)

where \({g}_{n}\) indicates the spatial vector, \(n\) indicates the feature, \({W}_{s}\in {R}^{d\times T}\) indicates the spatial attention mechanism weight matrix, \({X}_{n}\) indicates the sequence of features, \({b}_{s}\in {R}^{d}\) indicates the bias vector. Then for each feature, an attention score is calculated as follows.

$${\beta }_{n}=\frac{\mathit{exp}\left({g}_{n}\right)}{{\sum }_{{n}{\prime}=1}^{N}\mathit{exp}\left({g}_{{n}{\prime}}\right)}$$
(15)

where \({\beta }_{n}\) indicates the attention score. Based on the attention score, the weighted sum of input features is computed to obtain the spatial attention output. Mathematically it is expressed as

$$\widehat{X}={\sum }_{n=1}^{N}{\beta }_{n}{X}_{n}$$
(16)

where spatial attention output is indicated as \(\widehat{X}\). After computing the spatial and temporal features, the final output is obtained by combining both attention outputs which is mathematically formulated as

$$\overline{X }=\widetilde{X}\odot \widehat{X}$$
(17)

where \(\odot \) indicates the element-wise multiplication. The spatio-temporal attention output in Eq. (17) is processed through a fully connected layers and SoftMax function to classify features as normal or anomalous. Mathematically the process to compute the logits using a fully connected layer is formulated as

$$z={W}_{f}\overline{X }+{b}_{f}$$
(18)

where \({W}_{f}\in {R}^{C\times \left(T\cdot N\right)}\) indicates the fully connected layer weight matrix, \({b}_{f}\in {R}^{C}\) indicates the bias vector and \(C\) indicates the number of classes. Finally, by applying SoftMax function the probabilities of each class is obtained which is mathematically expressed as

$$p={\text{softmax}}\left(z\right)$$
(19)

Thus, the novel STAN effectively captures the spatio-temporal patterns in the network traffic and enhances the detection accuracy in the proposed hybrid federated learning network.

Quantum-inspired federated averaging (QIFA)

In the proposed hybrid federated learning network, the learning process is enhanced by adapting a quantum inspired federated averaging procedure which is based on the principles of quantum computing. The major aim of incorporating the quantum principle is to enhance the aggregation and convergence of the federated learning model. The first step in the proposed QIFA is quantum inspired initialization in which the federated learning process is started from a different set of model parameters. To initialize the model parameters, quantum inspired random number generation techniques is used as it provides high randomness in initializing the model parameters. Then for each node in the federated learning network, updates its model parameters based on its local data. Further the quantum principles are incorporated in the aggregation process to enhance the federated averaging process. The traditional steps in the federated averaging are modified using the quantum superposition and entanglement concepts.

In quantum superposition-based aggregation, the systems can be considered in multiple states to create diverse aggregation of local models. Mathematically it is expressed as

$${w}^{\left(t+1\right)}={\sum }_{k=1}^{K}\frac{{n}_{k}}{n}{w}_{k}^{\left(t+1\right)}+\uplambda Q\left(w\right)$$
(20)

where \(K\) indicates the total number of nodes, \({n}_{k}\) indicates the number of data samples at node \(k\), \(n\) indicates the total number of data samples across all nodes, \(\uplambda \) indicate the scaling factor which is used to balance the traditional averaging and quantum adjustment factor \(Q\left(w\right)\). This adjustment factor \(Q\left(w\right)\) incorporates the superposition principles in the aggregation process which is mathematically formulated as

$$Q\left(w\right)=\frac{1}{K}{\sum }_{k=1}^{K}{\upepsilon }_{k}{w}_{k}^{\left(t+1\right)}$$
(21)

where \({\upepsilon }_{k}\) is the quantum inspired coefficient that introduces diversity based on the entangled states of the parameters. In order to avoid local minima in the optimization process, the proposed QIFA includes quantum inspired perturbations. The perturbations are periodically introduced to the global model parameters to avoid local minima which is mathematically formulated as

$${w}^{\left(t+1\right)}={w}^{\left(t+1\right)}+\updelta \mathcal{N}\left(0,{\upsigma }^{2}\right)$$
(22)

where \(\updelta \) indicates the perturbation magnitude and \(\mathcal{N}\left(0,{\upsigma }^{2}\right)\) indicates the Gaussian noise term with mean 0 and variance \(({\upsigma }^{2})\). The process from local model training to quantum inspired aggregation is repeated for several communication rounds. During each round, the global model parameters are updated and distributed them to the nodes as \(\left({w}^{\left(t+1\right)}\to \left\{{w}_{k,1}^{\left(t+1\right)},{w}_{k,2}^{\left(t+1\right)},\dots ,{w}_{k,K}^{\left(t+1\right)}\right\}\right)\). The global model is updated by the central server by aggregating parameters and quantum inspired adjustment. Mathematically it is formulated as

$${w}^{\left(t+1\right)}={\sum }_{k=1}^{K}\frac{{n}_{k}}{n}{w}_{k}^{\left(t+1\right)}+\uplambda Q\left(w\right)+\updelta \mathcal{N}\left(0,{\upsigma }^{2}\right)$$
(23)

where \(w\) indicates the global model parameters. By updating the model parameters, the QIFA in the proposed model enhances the learning process of federated learning model.

Privacy-preserving techniques

In order to ensure privacy in the federated learning, the proposed work incorporated differential privacy and secure multiparty computation techniques. Differential privacy decides the inclusion or exclusion of data points while secure multiparty computation allows multiple parties to compute a function by keeping the inputs private. To implement differential privacy the local model updates are added with a noise factor before it shares the updates with central server. Mathematically the process of adding noise factor to the local model parameters is formulated as

$${w}_{k}^{\left(t+1\right)}={w}_{k}^{\left(t+1\right)}+\mathcal{N}\left(0,{\upsigma }^{2}I\right)$$
(24)

where \({w}_{k}^{\left(t+1\right)}\) indicates the local model parameters after training at node \(k\), the Gaussian noise is indicated as \(\mathcal{N}\left(0,{\upsigma }^{2}I\right)\) in which \(I\) indicates the identity matrix and variance is indicated as \({\upsigma }^{2}\). To measure the privacy level, a privacy budget \(\upepsilon \) is used in which the lower value of \(\upepsilon \) provides higher privacy and vice versa. Based on this privacy budget, the noise scale is determined and formulated as

$$\upsigma =\frac{\Delta f}{\upepsilon }$$
(25)

where \(\Delta f\) indicates the function sensitivity which defines the changes in the output function.

While employing secure multiparty computation, each node divides its local model update into multiple portions and distribute them to other nodes. Consider the node \(k\) divides its model update \({w}_{k}^{\left(t+1\right)}\) as \(({s}_{k,1},{s}_{k,2},\dots ,{s}_{k,n})\) and sends a portion \({s}_{k,i}\) to node \(i\). Mathematically it is expressed as

$${w}_{k}^{\left(t+1\right)}={s}_{k,1}+{s}_{k,2}+\dots +{s}_{k,n}$$
(26)

where \({s}_{k,i}\) indicates the portions which divided from local model update. Each node in the network receives the divided portion from other nodes and aggregates them to obtain global model update. The central server combines the divided portions and obtains an aggregated model without learning the individual updates. Mathematically it is formulated as

$${\sum }_{k=1}^{K}{s}_{k,i}={w}_{i}^{\left(t+1\right)}$$
(27)

The central server reconstructs the global model update by combing all the split portions which is mathematically formulated as follows.

$${w}^{\left(t+1\right)}={\sum }_{i=1}^{n}\left({\sum }_{k=1}^{K}{s}_{k,i}\right)$$
(28)

Thus, by integrating differential privacy and secure multiparty computation the proposed model ensures robust privacy in the federated learning process. The integration ensures that individual data remains private while enabling collaborative model training the federated learning process.

The summarized pseudocode of the proposed hybrid federated learning network is presented as follows.

figure a

Results and discussion

The proposed hybrid federated learning network performance is evaluated using python tool. The implementation includes essential library functions to implement the federated learning model. The simulation hyperparameters used in the proposed model experimentation is listed in Table 1. The experimentation utilizes benchmark UNSW-NB15 dataset to evaluate the proposed model performance. The dataset has diverse features that describes network traffic and suitable for anomaly detection and cyber security. Details like packet counts, byte counts, protocol details, connection states, etc., are provided in the dataset as labeled instances of normal and attack traffic. A total of 2,540,044 samples in the dataset is divided in the ratio of 80:20 for training and testing. A total of 2,032,035 samples are used for the training and 508,009 samples are used for testing. Complete details of the dataset used in the training and testing process is presented in Table 2.

Table 1 Simulation hyperparameters.
Full size table
Table 2 UNSW-NB15 Dataset description.
Full size table

The proposed model utilizes metrics like accuracy, precision, recall, f1-score, Specificity, and Matthews Correlation Coefficient (MCC) for performance evaluation. Mathematical formulations for the evaluation metrics are presented as follows.

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
(29)
$$Log-Loss=-\frac{1}{N}{\sum }_{i=1}^{N}\left[{y}_{i}\mathit{log}\left({p}_{i}\right)+\left(1-{y}_{i}\right)\mathit{log}\left(1-{p}_{i}\right)\right]$$
(30)
$$Precision=\frac{TP}{TP+FP}$$
(31)
$$Recall=\frac{TP}{TP+FN}$$
(32)
$$F1-Score=2\times \frac{Precision\times Recall}{Precision+Recall}$$
(33)
$$Specificity=\frac{TN}{TN+FP}$$
(34)
$$MCC=\frac{TP\times TN-FP\times FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}$$
(35)

where \(N\) indicates the number of samples, \({y}_{i}\) indicates the actual label, and \({p}_{i}\) indicates the predicted probability. Figure 3 depicts the accuracy and loss curves of the proposed HFLN for the training and validation process. The accuracy graphs clearly presents that the proposed model training and validation accuracy increases gradually in the initial epochs. This indicates the proposed model significantly learns the features and the model aggregation continuously adjusts the parameters to become optimal. After crossing 20 epochs, the accuracy of the proposed model saturates to its maximum of 98.3% which indicates the model proficiency in classifying the anomalies. The validation accuracy follows the training accuracy with slight difference which indicates the proposed model generalization ability. Similarly in the loss curve, the training and validation curves gradually decreases and reaches a minimum when epochs are increased. In the last, the loss values stabilize which confirms that the model reached its optimal state. The accuracy and loss curves clearly present the proposed model’s high performance and stability in detecting anomalies in the network.

Fig. 3
figure 3

Accuracy and loss analysis.

Full size image

Figure 4 presents the ROC curve of proposed model training and validation process. The plot considered the false positive and true positive values. From the graph it can be observed that AUC are high for both training and validation process. In the training process, the obtained AUC is 0.9869 and for validation AUC is obtained as 0.9808. This high AUC value indicates that the proposed model is highly effective in detecting anomalies with minimum false positives. The confusion matrix obtained for the training and testing process is depicted in Fig. 5. The proposed model correctly predicted the attack and normal instances in training as well as the testing process. In the training process, the proposed model correctly classified 1,377,432 instances as non-anomalous and 397,157 instances as anomalous. Similarly in the testing process, the proposed model correctly classified 344,518 instances as non-anomalous and 99,172 instances as anomalous.

Fig. 4
figure 4

ROC curve for training and validation.

Full size image
Fig. 5
figure 5

Confusion matrix obtained for the training and test data.

Full size image

From the confusion matrix elements, the other metrics like precision, recall, f1-score, specificity and Mathew correlation coefficient are obtained for both training and testing process. The overall performance of the proposed model for all the metrics in the training and testing process is presented in Table 3. It can be observed that the proposed model exhibited maximum accuracy of 98.34% in the training process and 98.31% in the test process. similarly, the precision obtained during training is 98.20% and the test precision is 98.15%. The recall during the training is 98.45% and for the test process the recall is obtained as 98.50%. From the results the better detection performance of the proposed HFLN is observed.

Table 3 Performance metrics of proposed model.
Full size table

Further to evaluate the proposed model performance, some traditional machine learning and deep learning models are considered. Models like random forest, convolutional neural network (CNN), Long Short-Term Memory (LSTM), Recurrent Neural Network (RNN), Federated Learning (FL), Semi-supervised Spatio-Temporal Deep Learning (SSTDL) and Spatio-Temporal Graph Neural Network (STGNN)41,42 models are considered for comparative analysis. The comparative analysis utilizes the same dataset and evaluation metrics. For each model, the experimentation is performed with standard hyperparameters, and the results are finally summarized to perform this comparative analysis. The simulation hyperparameters of the traditional models are listed in Table 4.

Table 4 Simulation hyperparameters of traditional models used for comparative analysis.
Full size table

Figure 6 depicts the precision comparative analysis of proposed model with existing techniques. The results clearly present the proposed HFLN model consistent performance over other algorithms. The precision improves gradually and reaches maximum of 0.98 by 160th epoch which indicates that the proposed model learns the features more effectively and maintains high accuracy in differentiating different classes. The precision of SSTDL and STGNN are 0.970 and 0.969 which is lesser than the proposed model. The federated learning model shows a better precision of 0.96 which is closer but lesser than the proposed HFLN. The LSTM shows a maximum precision of 0.95 while CNN and RNN exhibit precisions as 0.94 and 0.935 respectively which is lesser than the proposed HFLN. The least performance is exhibited by the random forest model with 0.935 as precision. This indicates that the existing models are not efficient in managing the data complexities while detecting anomalies compared to the proposed HFLN model.

Fig. 6
figure 6

Precision comparative analysis.

Full size image

The recall metric is comparatively analyzed in Fig. 7 for all the algorithms and the results highlights the proposed model’s better performance with maximum recall of 0.9815. The proposed HFLN model superior performance demonstrates its ability in correctly identifying the positive instances which is essential for intrusion detection application. The recall of SSTDL and STGNN are 0.973 and 0.971 which is lesser than the proposed model. Similarly existing federated learning exhibit recall as 0.96, LSTM as 0.955, RNN as 0.935, CNN as 0.94 and random forest as 0.935 which is lesser than the proposed HFLN model.

Fig. 7
figure 7

Recall comparative analysis.

Full size image

Since the performance of the proposed model is better in terms of precision and recall, it is reflected in the f1-score comparative analysis given in Fig. 8. The proposed model exhibits a maximum f1-score of 0.9832 whereas existing SSTDL exhibit 0.971, STGNN exhibit 0.970, federated learning exhibit 0.970, LSTM exhibit 0.965, CNN exhibit 0.965, RNN exhibit 0.955, and random forest exhibit 0.950, as f1-score which is lesser than the proposed HFLN model. Overall, the f1-score comparative analysis highlights the proposed model better performance and its accurate predictions in the anomaly classification process.

Fig. 8
figure 8

F1-score comparative analysis.

Full size image

The specificity analysis of proposed model with other algorithms presented in Fig. 9 highlights the superior performance of proposed HFLN model. The proposed model exhibits a maximum specificity of 0.9817 whereas existing SSTDL exhibit 0.969, STGNN exhibit 0.968, federated learning exhibits 0.969 as its specificity which is lesser than the proposed model. Similarly, the specificity of LSTM is 0.963 which is approximately 2% lesser than the proposed. The specificity of CNN and RNN are 0.958 and 0.953 which is approximately 3% lesser than the proposed model. The specificity of random forest model is 0.945 which is approximately 4% lesser than the proposed model.

Fig. 9
figure 9

Specificity comparative analysis.

Full size image

The MCC analysis of proposed model with other algorithms is presented in Fig. 10. The proposed model exhibits a maximum MCC of 0.9665 whereas existing SSTDL and federated learning exhibits 0.940 as its MCC which is 2% lesser than the proposed model. STGNN exhibit 0.938 as MCC which is 4% lesser than the proposed. Similarly, the MCC of LSTM is 0.930 which is approximately 3% lesser than the proposed. The MCC of CNN and RNN are 0.920 and 0.910 which is approximately 4% and 5% lesser than the proposed model. The MCC of random forest model is 0.90 which is approximately 6% lesser than the proposed model.

Fig. 10
figure 10

MCC comparative analysis.

Full size image

Figure 11 presents the accuracy comparative analysis of proposed model with existing algorithms. The figure clearly presents the superior accuracy of the proposed model over existing techniques. The proposed model exhibits a maximum accuracy of 0.983 which is 2% better than SSTDL and STGNN model, 3% better than RNN and random forest and 2% better than LSTM and CNN models. Table 5 presents the overall performance comparative analysis considering all the metrics for proposed and existing algorithms. The proposed model exhibits its superior performance for all the metrics and provides enhanced protection against attacks in the network.

Fig. 11
figure 11

Accuracy comparative analysis.

Full size image
Table 5 Overall comparative analysis.
Full size table

Conclusion

A novel hybrid quantum spired federated learning network is presented in this research work for cyber-attack detection in a network. The proposed model incorporates techniques like spatio-temporal attention network and quantum inspired federated averaging to attain superior performance in attack detection. The proposed model experimentation utilizes benchmark UNSW-NB15 to evaluate the performance of detection model. The proposed model attains maximum accuracy of 98.34% which is much better than the traditional models like Federated learning, long short-term memory, recurrent neural network, convolutional neural network, and random forest algorithms. The proposed model reached this maximum performance due to its ability in grouping nodes, hierarchical model aggregation, and effective utilization of spatial and temporal features. Though the proposed model attained better performance in attack detection, the model computational complexity increases due to multiple techniques. However, this minor limitation can be neglected as the proposed model provides superior accuracy over existing techniques in attack detection. In future, this research work can be extended by considering adaptive learning mechanisms to enhance the detection ability, reliability, and overall performances.