Abstract
The monkeypox virus (MPXV), which is a member of the Orthopoxvirus genus in the class Poxviridae, is the causative agent of the zoonotic viral infection MPXV. The disease is similar to smallpox, but it is usually less dangerous. This study examines the evolution of the MPXV epidemic in Canada with an emphasis on the effects of control employing actual data. The main challenge is accurately estimating the virus’s rate of transmission and assessing the effectiveness of vaccination campaigns. By taking into account the modified Atangana–Baleanu–Caputo (mABC) fractional difference operator, we develop an analytical framework for an outbreak caused by MPXV and broaden it to accommodate the fractional scenario. The non-negativity and boundedness are guaranteed by the computation of the fractional-order MPXV system. At the disease-free equilibrium (DFE) \(\mathcal {P}_{0}\), we perform a local asymptotical stability analysis (LAS) and display the outcome for \(\mathbb {R}_{0}<1\). When \(\mathbb {R}_{0\textrm{r}}>1\) and \(\mathbb {R}_{0\hbar }<1\), the single endemic equilibrium point (EEP) of infectious rodents is globally asymptotically stable (GAS). Lyapunov’s approach and LaSalle’s invariant criterion demonstrate that the GAS in terms of EEP for infectious persons occurs when \(\mathbb {R}_{0\textrm{r}}<1\) and \(\mathbb {R}_{0\hbar }>1\). Through the application of nonlinear least squares, we determine the parameter values applying actual cases collected from Canada. To further bolster the operator’s effectiveness, a number of tests of this novel kind of operator were conducted. We remark that in various time scale domains \(\mathbb {N}_{\ell }\), the investigated discrete formulations will be \(\rho ^{2}\)-nonincreasing or \(\rho ^{2}\)-nondecreasing by examining \(\rho\)-monotonicity formulations and the basic properties of the suggested operator. Algorithms are constructed in the discrete generalized Mittag–Leffler (GML) kernel for mathematical simulations, emphasizing the effects of the infection resulting from multiple factors. The dynamical technique used to build the MPXV framework was significantly impacted by fractional-order. In order to lessen the infections, severity, five time-dependent control factors are also implemented. The optimality criteria are produced by applying Pontryagin’s maximal argument to prove the validity of the most effective control. Various combos of control factors are offered to reduce the incidence of MPXV. The results of the current research provide governmental officials and healthcare professionals with practical steps to take in order to establish efficient and ideal preventive approaches to reduce the MPXV outbreaks.
Similar content being viewed by others
Introduction
Recently, a new re-emerging disease was caused by the MPXV. The prompt identification of this illness among Africans leads to its eventual transmission to various regions of the globe. Animals can transmit the infection to individuals, but it remains less virulent than smallpox and shares many of the same indications. Additionally, this viral infection may harm a variety of species. The sources, potential dissemination, and nature of the MPXV are shown in1,2. There are additionally numerous ways that the illness could propagate. Such techniques include ecological transfer, human-to-human dissemination, and human-to-infected rodent virus. We direct viewers to3 for further information regarding the means of transmission channel described over here. In addition, inappropriate cooking of the contaminated creature might spread the viral infection4,5. For additional research on the spread of the disease from person to person, see6,7,8,9,10.
Comprehending and efficiently handling MPXV epidemics is now dealing with a number of difficulties. Understanding the fact of the many pathways of propagation for MPXV disease is essential. One can become contaminated by having immediate contact via infectious individuals or contaminated settings. Implementing effective preventative techniques requires understanding the broader relevance of each transmitting mechanism and its components11. Because MPXV is similar to various infections like smallpox and chickenpox, diagnosing it can be challenging often. It needs quick and accurate screening tools to identify MPXV immediately as well as separate its presence from other illnesses so that prevention and management may begin right away12. MPXV vaccines are available on marketplaces, although they are difficult to distribute, make available, and use effectively. Increasing vaccination rates are necessary, especially in areas where outbreaks are likely, in order to develop collective antibodies and prevent worldwide propagation13. For MPXV, there are currently several distinguished medicines available, but no specifically authorized medication exists. In order to improve outcomes for those who are contaminated, preventative therapies and complementary therapies have recently been investigated14. Gathering a great deal of information about an infection is essential to responding to an occurrence effectively. Evaluating community susceptibility, relevant probabilities for severe disease outcomes, and the role of undiagnosed persons in propagation are all included. MPXV is not confined to one area and is being reported in other countries worldwide. Rapid recognition and management of outbreaks need the deployment of robust surveillance infrastructures to document and adapt to them globally15,16,17. Creating and carrying out preventive measures, such as confinement, interaction monitoring, and incident solitary existence, is essential to controlling outbreaks and preventing future propagation. With similar infectiousness caused by viruses, MPXV can have genetic mutations that affect vaccine response, virulence, and propagation. It is vital to monitor and appreciate these variations when adjusting approaches to control18,19,20.
Moreover, the infectious agent that caused MPXV was first discovered on the western continent and has since been linked to other epidemics worldwide. The disease was detected in the USA in 202221.
The initial outbreak of instances has been reported via the United Kingdom, while the initial manifestation of the disease was discovered in London, wherein the individual who developed it was discovered to be a Nigerian tourist. The United Kingdom Health Security Agency subsequently identified and verified a handful of additional incidents of the infection22. Until December 2023, a total of 93,967 occurrences of MPXV have been documented throughout 116 states, including 182 documented fatalities. Gays, bisexuals, and men who engage in sexual activity with someone else without providing documentation and travel across borders to prevalent nations have made up the majority of occurrences in Canada23. By the end of January 2023, Canada had 3298 instances documented, compared to 127 occurrences confirmed from February to November of 202323.
Besides that, the threat posed by transmissible ailments to the wellness of humans remains high, underscoring the need for innovative scientific methods to effectively understand and manage these illnesses. Prominent examples of contagious infections include COVID-19, salmonellosis, schistosomiasis, bovine spongiform encephalopathy, influenza, ebola, HIV/AIDS and measles. The researchers in24 investigated the accumulation of human-adapting mutations during circulation of influenza virus in humans in the United Kingdom. Jackson et al.25 expounded the expression of mouse interleukin-4 by a recombinant ectromelia virus suppresses cytolytic lymphocyte responses and overcomes genetic resistance to mousepox. Singh et al.26 investigated the fractional diabetes model with exponential law. Modern strategies are required to increase our understanding, prevention, and therapeutic choices due to the swift advancement and propagation of illnesses. Recent advances in technology, particularly in neural machine learning and machine intelligence, have opened up novel possibilities for research on communicable infections.
These developments offer powerful instruments for assessing significant search engines, predicting outbreaks, and developing targeted treatments27,28,29,30,31.
However, the obstacles of preventing and handling outbreaks due to critical interactions are highlighted in32, where the author highlights the importance of tackling basic addresses concerning the spread of transmissible illnesses, including pathways for transfer and the impact of ecological factors. Other obstacles include providing accurate data, developing suitable forecasting techniques, and conquering barriers to medical facilities. The scientific community has offered a number of mathematical frameworks to investigate the mechanisms of the MPXV. To study the behavior of MPXV in the presence of dissemination, for instance, the researchers in33 established a mathematical framework. One benefit of this approach is that the ecological pathway in disease evolution was examined. But in order to more fully explain the unpredictable nature of the ailments, the mathematical framework lacks actual data. Significant inconsistencies in the illness eradication outcomes predicated on the hypersensitive criteria. In5, the mechanisms of and in-depth interactions between people and rodents are examined. In34, the effect on therapy and immunization is taken into account when modeling MPXV. The framework is well-designed to examine the effects of vaccination and intervention. Nevertheless, noteworthy outcomes pertaining to the therapy and immunization are absent from the proposed approach. The framework is straightforward and only adds to a limited number of quantitative findings. Don’t include accurate information and proven outcomes about the eradication of infection. In35, the researchers investigated how to represent MPXV using a mathematical framework and produced their behavioral findings. The conventional prevalence rate had been employed for each category with respect to an infection, while this approach incorporates the illness characteristics absent vaccination. In35, the researchers investigated how to simulate MPXV using a mathematical model and produced their behavioral findings. The conventional prevalence rate had been applied to both communities with respect to a virus, and basic epidemic patterns lacking vaccination are included in this framework. The simulation is devoid of actual data, and illness eradication suggestions have not been adequately considered. A mathematical framework that incorporates both human and animal propagation of transmission is being developed in36 to investigate the fluctuations in the MPXV. The real information is not taken into account, and a simulation fails to generate enough findings for the unpredictable nature of the sickness. Employing the documented instances in the USA, a fractional derivative algorithm is built to get outcomes relating to the MPXV illness37. The characteristics of immunization and an additional control criterion to examine the effect of the vaccine on the illness are absent from the framework. In order to determine the values of variables and the outcomes for the illness eradication in the USA, real information from the country was taken into account. At this point certain findings from mathematical frameworks that examined the evolution of MPXV are taken into consideration38,39. In40, the fluctuations of the condition are examined using actual data from the United Kingdom. Considering specific input situations, the predictive findings for non-pharmaceutical intervention were produced. Since the vaccination research is absent from the hypothetical scenario, no suggestions regarding how vaccination might affect the evolutionary process of the infection have been suggested. The scientists used actual United Kingdom facts and took into consideration a MPXV model that included vaccinations. The mathematical framework has been solved numerically using a formulation in fractional derivative. A mathematical framework for MPXV with nonlinear prevalence and inadequate vaccine was examined in40. But the hypothesis is missing actual information, and the findings don’t go far enough in terms of curing the illness. A previously presented approach is expanded to include fractional derivatives using United Kingdom investigations in41. Durski et al.42 addressed the emergence of MPXV in west and central Africa.
For a variety of factors, including memory impact, hereditary qualities, and crossover behaviors, fractional-order derivatives or mathematical representations are regarded to be more trustworthy in research. These benefits and other characteristics of mathematical frameworks generated using fractional-order contributed to the documentation of multiple mathematical frameworks for multiple viral illnesses in scientific journals43,44 and elsewhere. As an illustration, consider the fractional-order for the COVID-19 virus with the singular and non-singular fractional derivatives that were created in45.
The influence of the Mittag–Leffler function was taken into consideration by the researchers in46 when examining the COVID-19 disease virus. Subsequently, they demonstrated innovative conceptual and computational findings and offered an innovative numerical technique for addressing it practically. Modified fractional continuous and discrete operators with Mittag–Leffler kernels are particularly intriguing as discrete analogues because of their distinctive features47,48. A fractional-order model of bovine Brucellosis was produced by Farman et al.49 using a mABC fractional difference operator. They adapted the Lipschitz requirement to ensure novelty and assessed the Volterra-type Lyapunov function’s global stability. Results were developed in the discrete generalized form for computational modelling, highlighting the effects of the diseases attributed to multiple factors50. They used recursive techniques, fixed point techniques, and the robustness of the outcome in the Hyers–Ulam sense to carry out analysis and obtain a vague response given in sequence.
Motivated by an analysis of research on MPXV, we introduced the control strategies and came up with an innovative framework. Furthermore, by utilizing the mABC derivative, the framework is expanded to a fractional difference equation. Using actual data from Canada, the formerly studied algorithms were in integer-order derivative. In this article, we discuss MPXV in Canada and offer helpful advice on the illness. Several writers examined the instances of MPXV in other states according to the previously mentioned material, and they additionally tackled some of the disease’s suggestions. To the best of our knowledge, no one has addressed the MPXV for the real data for Canada. This one is the main motivating part of this study.
The corresponding model outcomes will be examined in this paper, first qualitatively and then quantitatively to provide justification. We will go into considerable length on a number of control-related findings and how they affect the behavior of the framework.
The article is organized as follows: section “Preliminaries” contains significant research on discrete fractional-order calculus. Section “Model configuration” consists of model configuration and illustrates the framework’s description and conceptualization of the stability analysis. Section “Explore discrete fractional order ABC MPXV model” provided the MPXV system in terms of mABC fractional difference operators, and based on the conclusions, several new formulations are presented. Also, the nonlinear least squares methodology for factor prediction is demonstrated in depth. Results and their unique dynamics were provided with the comparison of human-to-human, rodents-to-humans, human-to-rodents, and rodents-to-rodents transmission along with a description of the numerical solutions. In section “Optimal control scheme”, an optimal control model is provided. It focuses on the control design using the five strategic approaches. Section “Conclusion” offers the concluding section of the epilogue.
Preliminaries
In the context of system evaluation, you could find the following fundamental terms useful:
Definition 2.1
(51,52) Assume that \(\Im (\xi )=\xi -1\) represent the reversed jump operator.
-
For \(\wp >0,\) there is a nabla left fractional sum is described by taking into consideration a mapping \(\textrm{V}:\mathbb {N}_{\ell }=\big \{\ell ,\ell +1,\ell +2,\ldots \big \}\mapsto \mathbb {R}\) as
$$\begin{aligned} \,_{\ell }\nabla ^{-\wp }\big [\textrm{V}(\xi )\big ]=\frac{1}{\Gamma (\wp )} \sum \limits _{\phi =\wp +1}^{\xi }\textrm{V}(\phi ) \big (\xi -\Im (\phi )\big )^{\overline{\wp -1}},~~~\xi \in \mathbb {N}_{\ell +1}. \end{aligned}$$(2.1)For \(\wp >0,\) the nabla left fractional difference of \(\textrm{V}(\xi )\) is stated as
$$\begin{aligned} \,_{\ell }\nabla ^{\wp }\big [\textrm{V}(\xi )\big ]=\nabla ^{\kappa }\nabla _{\ell }^{-(\kappa -\wp )} =\frac{\nabla ^{\kappa }}{\Gamma (\kappa -\wp )}\sum \limits _{\phi =\wp +1}^{\xi }\textrm{V}(\phi ) \big (\xi -\Im (\phi )\big )^{\overline{\kappa -\wp -1}},~~~\xi \in \mathbb {N}_{\ell +1}. \end{aligned}$$ -
For \(\wp >0,\) there is a nabla left fractional sum is described by taking into consideration a mapping \(\textrm{V}:\,_{\textrm{p}}\mathbb {N}_{\ell }=\big \{\textrm{p},\textrm{p}-1,\textrm{p}-2,\ldots \big \}\mapsto \mathbb {R}\) as
$$\begin{aligned} \nabla _{\textrm{p}}^{-\wp }\big [\textrm{V}(\xi )\big ]=\frac{1}{\Gamma (\wp )} \sum \limits _{\phi =\xi }^{\textrm{p}-1}\textrm{V}(\phi ) \big (\phi -\Im (\xi )\big )^{\overline{\wp -1}},~~~\xi \in \,_{\textrm{p}-1}\mathbb {N}. \end{aligned}$$For \(\wp >0,\) the nabla left fractional difference of \(\textrm{V}(\xi )\) is stated as
$$\begin{aligned} \nabla _{\textrm{p}}^{\wp }\big [\textrm{V}(\xi )\big ]=\,_{\ominus } \Delta ^{\kappa }\nabla _{\textrm{p}}^{-(\kappa -\wp )}=\frac{(-1)^{\kappa } \Delta ^{\kappa }}{\Gamma (\kappa -\wp )}\sum \limits _{\phi =t_{q}}^{\textrm{p}-1}\textrm{V}(\phi )\big (\xi -\Im (\phi )\big )^{\overline{\kappa -\wp -1}},~~~\xi \in \,_{\textrm{p}-1}\mathbb {N}. \end{aligned}$$
Definition 2.2
(51,53) The nabla discrete Mittag–Leffler (DML) function of three parameters is stated as follows for \(\chi \in \mathbb {R}:\vert \chi \vert <1\) and \(\sigma ,\upsilon ,\gamma \in \mathbb {C}\) possessing \(\Re (\wp )>0,\) then
The DML function with two parameters for \(\gamma =1\) is computed as
The DML function with one parameter for \(\gamma =\upsilon =1\) is obtained as
Remark 2.1
(53) For \(0<\wp <1/2\) and \(\chi =-\frac{\wp }{1-\wp },\) the initial terms of \(\mathcal {E}_{\overline{\wp }}(\chi ,\xi )\) for \(\xi =0,1,2,3\) are articulated as:
In general, it is clear that \(0<\mathcal {E}_{\overline{\wp }}(\chi ,\xi )<1,~~~\xi =1,2,3,\ldots .\) On the other hand, \(\mathcal {E}_{\overline{\wp }}(\chi ,\xi )\) is monotonically non-increasing for every \(\xi =1,2,3.\)
Lemma 2.1
(51,52) A mapping \(\textrm{V}\) specified on \(\mathbb {N}_{\ell }\) for (2.1) has a discrete Laplace transform \((\mathfrak {L})\), which can be represented as
Considering a mapping \(Z_{1}\) that is further described on \(\mathbb {N}_{\ell }\), the discrete Laplace transform of the convolution of \(Z_{1}\) and \(\textrm{V}\) is as follows:
Lemma 2.2
(51,52) For a mapping \(\textrm{V}\) described on \(\mathbb {N}_{\ell }\), the result is as follows:
Specifically,
Lemma 2.3
(48,51,54) For a real number \(\wp ,\) then we have
Lemma 2.4
(48,51,54) For \(\wp ,\upsilon ,\chi ,\phi \in \mathbb {C}\) having \(\Re (\upsilon )>0,\) we have
whenever \(\vert \chi \phi ^{-\wp }\vert <1\) having \(\Re (\phi )>0.\) Moreover, ones obtain
Next, we present the definition of discrete generalized Atangana–Baleanu (DGAB) of the Liouville–Caputo fractional difference operator, which is mainly due to48,51,54.
Definition 2.3
(48,51,54) For \(\wp \in (0,1/2)\) and \(\chi =-\frac{\wp }{1-\wp }.\) Suppose \(\textrm{V}\) is specified on \(\mathbb {N}_{\ell }\cap \,_{\textrm{p}}\mathbb {N},~where~\textrm{p}>\ell .\) The left DGAB context fractional difference is obtained as
where \(AB(\wp )>0\) indicate to be normalized mapping and satisfying \(AB(\wp )\vert _{0}^{1}=1.\) Moreover, the fractional difference of the Liouville–Caputo type right DGAB is outlined as follows:
The left discrete Atangana–Baleanu fractional sum is defined as:
Definition 2.4
(54) For \(\wp \in (0,1/2)\) and \(\chi =-\frac{\wp }{1-\wp }.\) Suppose \(\textrm{V}\) is specified on \(\mathbb {N}_{\ell }\cap \,_{\textrm{p}}\mathbb {N},~\textrm{p}>\ell ,\) then we have
Additionally, the fractional difference of the right discrete modified Atangana–Baleanu Liouville–Caputo (mABC) form is given by
Definition 2.5
(54) Assuming \(w_{1}\in \mathbb {N}_{0},~\wp \in \big (w_{1},w_{1}+\frac{1}{2}\big )\) and \(\chi _{w_{1}}=-\frac{\wp -w_{1}}{w_{1}+1-\wp }\), the left discrete mABC sense fractional difference of a higher order is determined by:
Additionally, the fractional difference of the right mABC form for higher order is given by
Theorem 2.1
(55,56) Assume that the following fractional-order discrete system
containing \(\textrm{x}\in \mathbb {R}^{\textrm{n}},~\underline{\wp }=\inf \wp\) and \(\bar{\wp =\sup \wp },\) where \(0<\underline{\wp }<\wp<\bar{\wp }<1.\) The results that correspond to the expression \(\textrm{f}(\textrm{x})=0\) are the framework’s equilibrium values (2.9).
Assuming each of the eigenvalues \(\lambda _{\iota },~(\iota =1,2,\ldots ,\textrm{n})\) of the Jacobian matrix \(\mathcal {J}=\Delta \textrm{f}\) computed at the equilibrium fulfill then the equilibrium is LAS, if
Otherwise, if \(\big \vert \arg (\lambda _{\iota })\big \vert >\frac{\Lambda }{2}\overline{\wp },\) then the equilibrium point is unstable.
Theorem 2.2
(57) Assume that the polynomial equation
-
1.
If \(\textrm{n}=1,\) the criterion for stability is \(\gimel _{1}>0.\)
-
2.
If \(\textrm{n}=2,\) the Routh–Hurwitz requirements58 are fulfilled for stability (\(\gimel _{1}>0,~\gimel _{2}>0\)) or \(\gimel _{1}<0\), \(4\gimel _{2}>\gimel _{1}^{2},~~arctan(4\gimel _{2}-\gimel _{1}^{2})>\frac{\Lambda }{2}\overline{\wp }.\)
Definition 2.6
(59) Assuming the following system of characteristic equations in the configuration of \(\textrm{n}\)-order polynomials:
When every real component of the formula commencing at the root is negative, then
Assume that \(d_{\kappa }\) is a positive number and that \(\kappa =0,1,2,\ldots ,2\textrm{n}-1\) are real numbers. A square matrix of size \(\textrm{n}\times \textrm{n}\) can be described as the Hurwitz matrix for (2.12) in the following way:
Hence, for \(\kappa <0\) or \(\kappa >\textrm{n}\) with \(d_{\kappa }=0\). Consequently, either the negative index needs to be changed to zero, or a matrix component’s index is excessively large \(\textrm{n}\). The Hurwitz matrix (2.14), which forms the \(\kappa\)-level Hurwitz determinant, \(\det \mathcal {H}_{\kappa };~\kappa =1,2,\ldots ,\textrm{n}\) is described in the following manner:
Theorem 2.3
(59) The real component of the polynomial root (2.12) is negative if and only if the condition (2.10) is satisfied and
For all \(\jmath =1,2,\ldots ,\textrm{n}\), the equilibrium point \(z_{1}\) is stable if and only if \(\det \mathcal {H}_{\jmath }>0\).
Model configuration
We describe a deterministic mathematical framework for the evolution of MPXV propagation in two distinct populations of individuals and rodents, taking into account the framework of nonlinear differential equations (NDEs). The subsequent presumptions form the framework of composition:
-
(i)
continual mobilization into the vulnerable community;
-
(ii)
close interactions with infectious individuals, rodents, and polluted settings are the mechanisms by which susceptible individuals contract contracted MPXV;
-
(iii)
exclusively diseased rodents can transmit the MPXV to vulnerable rodents60;
-
(iv)
before exhibiting the therapeutic manifestations and indications of the MPXV infection, people and rodents require an extended period.
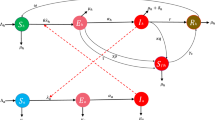
It will also be anticipated that there is homogeneous interaction among communities of individuals and rodents. Seven categories make up an individual’s subgroup: susceptible \(\textrm{X}_{\hbar },\) exposed \(\textrm{Y}_{\hbar },\) isolated \(\textrm{Q}_{\hbar },\) asymptomatic infected \(\mathcal {I}_{\mathcal {A}}\), indicative contagious \(\mathcal {I}_{\mathcal {B}}\), hospitalized \(\textrm{U}_{\hbar }\) and recuperated \(\textrm{R}_{\hbar }\) categories. The animal demographic group is made up of the vulnerable \(\textrm{X}_{\textrm{r}},\) contaminated \(\mathcal {I}_{\textrm{r}}\) and revealed \(\textrm{Y}_{\textrm{r}},\) respectively. The infected habitat is the source of undetected dissemination (\(\textrm{C}_{\epsilon }\)). These sections are shown in Fig. 1. People who have the MPXV but do not exhibit any indications or have no knowledge that the pathogenic organism is in their systems are considered inactive, whereas those who exhibit the evidence and consequences of getting infected are considered operational.
However, the acquisition levels for rodents and vulnerable individuals are \(\Lambda _{\hbar }\) and \(\Lambda _{\textrm{r}}\), respectively. The duration of interaction and connection between vulnerable individuals and people with an infection is \(\alpha _{\hbar \hbar }\), where \(\alpha _{\textrm{r}\hbar }\) represents the duration of rodent-to-human interaction, rodent-to-rodent interaction incidence is \(\alpha _{\textrm{r}\textrm{r}}\), while the hazardous habitat human interaction incidence is \(\alpha _{g_{1}\hbar }\), respectively. The presumed fatalities of rodents and people are \(\mu _{\textrm{r}}\) and \(\mu _{\hbar }\), correspondingly. The illness MPXV affects people and rodents at speeds of \(\delta _{\hbar }\) and \(\delta _{\textrm{r}}\). Furthermore, persons confronted with the virus advance at levels of \(\vartheta _{1}\), \(\vartheta _{2}\), and \(\vartheta _{3}\) to the noticeable, restricted, and un-diagnosed categories, respectively. People exhibiting serious illnesses are admitted to hospitals at an incidence of \(\beta _{2}\), whereas those exhibiting moderate indications recuperate at a rate of \(\beta _{1}\). The rates at which individuals placed under confinement develop symptoms \(\chi _{1}\), uninfected \(\chi _{2}\), and vulnerable \(\chi _{3}\) are the rates at which people placed under confinement change. Receiving treatment, patients recuperate at an intensity of \(\nu\), while rodent exposure causes infection at a rate of \(\theta\). At levels \(\phi _{1}\) and \(\phi _{2}\), the MPXV infection is released throughout the setting by afflicted individuals and infectious rodents. The pace at which the infectious agent degrades in the ambient atmosphere is \(\mu _{\epsilon }\). The system representation in Fig. 1 illustrates the processes of MPXV pathogen dissemination is \(\lambda _{\hbar }=\alpha _{\textrm{r}\hbar }\mathcal {I}_{\textrm{r}}+\alpha _{\hbar \hbar }(\theta _{\textrm{m}}\mathcal {I}_{\mathcal {A}}+\mathcal {I}_{\mathcal {B}})+\alpha _{g_{1}\hbar }\textrm{C}_{\epsilon }.\) The structure of NDEs is obtained as follows, utilizing the schematic Fig. 1, framework explanation and the following five time-varying controller measures:
supplemented with the initial values:
Schematic flow for depicting the MPXV model (3.1).
The aforesaid MPXV system includes five time-varying control measures. Among the prevention measures are:
-
(i)
A prophylactic strategy designed to lessen the risk of MPXV infection among vulnerable individuals when \(0\le \textrm{g}_{1}(\xi )\le 1\). This is capable of being accomplished by means of privately funded enlightenment.
-
(ii)
A precautionary strategy meant to lessen the spread of viruses from the surroundings to people. Using appropriate protection and cleaning your hands can help accomplish this if \(0\le \textrm{g}_{2}(\xi )\le 1\).
-
(iii)
If \(0\le \textrm{g}_{3}(\xi )\le 1,\) then a prophylactic strategy meant to lower the incidence of people being exposed to the MPXV infection. You can accomplish these by being vaccinated.
-
(iv)
The prophylactic strategy \(0\le \textrm{g}_{4}(\xi )\le 1\) attempts to minimize the pace at which the infectious pathogen sheds throughout its surroundings. This is easily achieved by treating the MPXV manifestations and donning a protective covering.
-
(v)
If \(0\le \textrm{g}_{5}(\xi )\le 1,\) then a precautionary step meant to lower the environmental prevalence of the MPXV pathogen. Antibacterial agents and appropriate disposal of leftovers consumed by people afflicted with MPXV can help attain this.
For the purpose of examining memory impacts and disease behaviors on a specific data set, mathematical frameworks using discrete fractional differences offer more versatility. Therefore, following the left discrete mABC type fractional difference with \(\wp \in (0,1]\), the nonlinear fractional difference equations provided below are employed for constructing the novel discrete fractional-order MPXV model as:
subject to the initial values defined in (3.2).
Properties of discrete fractional mABC MPXV model
Within this part, we shall examine some characteristics pertaining to the positivity and boundedness of the proposed solution of model (3.3).
Theorem 3.1
For every given starting point \(\big (\textrm{X}_{\hbar }(0),\textrm{Y}_{\hbar }(0),\textrm{Q}_{\hbar }(0),\mathcal {I}_{\mathcal {A}}(0),\mathcal {I}_{\mathcal {B}}(0), \textrm{U}_{\hbar }(0),\textrm{R}_{\hbar }(0),\textrm{X}_{\textrm{r}}(0),\textrm{Y}_{\textrm{r}}(0),\mathcal {I}_{\textrm{r}}(0), \textrm{C}_{\epsilon }(0)\big )\in (0,0,0,0,0,0,0,0,0,0,0)\)\(\cup \mathbb {R}_{+}^{11}\) and every possible solution of model (3.3) is positive. The feasible domain of model (3.3) can be expressed as \(\Omega =\Big \{\big (\textrm{X}_{\hbar },\textrm{Y}_{\hbar },\textrm{Q}_{\hbar },\mathcal {I}_{\mathcal {A}},\mathcal {I}_{\mathcal {B}}, \textrm{U}_{\hbar },\textrm{R}_{\hbar },\textrm{X}_{\textrm{r}},\textrm{Y}_{\textrm{r}},\mathcal {I}_{\textrm{r}}, \textrm{C}_{\epsilon }\big )\in \mathbb {R}_{+}^{11}\ge 0:\mathbb {N}_{\hbar }\le \frac{\Lambda _{\hbar }}{\mu _{\hbar }},~~\mathbb {N}_{\textrm{r}}\le \frac{\Lambda _{\textrm{r}}}{\mu _{\textrm{r}}},~~\textrm{C}_{\epsilon }\)\(\le \frac{(1-g_{4})\phi _{1}\Lambda _{\hbar }+\phi _{2}\Lambda _{\textrm{r}}}{\mu _{\textrm{r}}(\mu _{\epsilon +g_{5}})}\Big \}.\)
Proof
Let us consider a mABC fractional MPXV system (3.3) with the following assumptions:
It is simple to conclude that the outcomes for \(\textrm{X}_{\hbar }(\xi ),\textrm{Y}_{\hbar }(\xi ),\textrm{Q}_{\hbar }(\xi ),\mathcal {I}_{\mathcal {A}}(\xi ),\mathcal {I}_{\mathcal {B}}(\xi ), \textrm{U}_{\hbar }(\xi ),\textrm{R}_{\hbar }(\xi ),\textrm{X}_{\textrm{r}}(\xi ),\textrm{Y}_{\textrm{r}}(\xi ),\mathcal {I}_{\textrm{r}}(\xi )\) and \(\textrm{C}_{\epsilon }(\xi )\) are positive based on the outcomes described previously. Following that, we must demonstrate the boundedness of framework (3.3)’s solution for human sub-population, we have
Based on the fractional-order comparison hypothesis in61, we are able to
Hence, \(\Omega _{\mathbb {N}_{\hbar }}=\big \{\mathbb {N}_{\hbar }(\xi )\in \mathbb {R}_{+}^{7}\ge 0\vert \mathbb {N}_{\hbar }(\xi )\le \frac{\Lambda _{\hbar }}{\mu _{\hbar }}\big \}.\)
Analogously, by considering the rodent sub-population, we have
According to the fractional-order comparison hypothesis in61, we are able to
So that, \(\Omega _{\mathbb {N}_{\textrm{r}}}=\big \{\mathbb {N}_{\textrm{r}}(\xi )\in \mathbb {R}_{+}^{3}\ge 0\vert \mathbb {N}_{\textrm{r}}(\xi )\le \frac{\Lambda _{\textrm{r}}}{\mu _{\textrm{r}}}\big \}.\)
In addition, when \(\mathcal {I}_{\mathcal {A}}\le \mathbb {N}_{\hbar },~\mathcal {I}_{\mathcal {B}}\le \mathbb {N}_{\hbar }\) and \(\mathcal {I}_{\textrm{r}}\le \mathbb {N}_{\textrm{r}}\),
According to the fractional-order comparison theorem in61, we are able to
So that, \(\Omega _{\textrm{C}_{\epsilon }}=\bigg \{\textrm{C}_{\epsilon }(\xi )\in \mathbb {R}_{+}^{1}\ge 0\vert \textrm{C}_{\epsilon }(\xi )\le \frac{(1-\textrm{g}_{4})\phi _{1}\frac{Pi_{\hbar }}{\mu _{\hbar }}+\phi _{2}\frac{Pi_{\textrm{r}}}{\mu _{\textrm{r}}}}{(\mu _{\epsilon }+\textrm{g}_{5})}\bigg \}.\)
Hence, by combining \(\Omega _{\mathbb {N}_{\hbar }},\Omega _{\mathbb {N}_{\textrm{r}}}\) and \(\phi _{\textrm{C}_{\epsilon }}\), we get \(\phi =\Big \{\big (\textrm{X}_{\hbar },\textrm{Y}_{\hbar },\textrm{Q}_{\hbar },\mathcal {I}_{\mathcal {A}},\mathcal {I}_{\mathcal {B}}, \textrm{U}_{\hbar },\textrm{R}_{\hbar },\textrm{X}_{\textrm{r}},\textrm{Y}_{\textrm{r}},\mathcal {I}_{\textrm{r}}, \textrm{C}_{\epsilon }\big )\in \mathbb {R}_{+}^{11}\ge 0:\mathbb {N}_{\hbar }\le \frac{\Lambda _{\hbar }}{\mu _{\hbar }},~~\mathbb {N}_{\textrm{r}}\le \frac{\Lambda _{\textrm{r}}}{\mu _{\textrm{r}}},~~\textrm{C}_{\epsilon }\)\(\le \frac{(1-g_{4})\phi _{1}\Lambda _{\hbar }+\phi _{2}\Lambda _{\textrm{r}}}{\mu _{\textrm{r}}(\mu _{\epsilon +g_{5}})}\Big \}\) has become positively invariant for \(\mathbb {R}_{+}^{11}\) in relation to framework (3.3). Therefore, the framework (3.3) is both scientifically and biologically viable in the domain. \(\square\)
Initially, we began attempting to find equilibria in the framework (3.3), wherein \(\Xi =\big (\textrm{X}_{\hbar },\textrm{Y}_{\hbar },\textrm{Q}_{\hbar },\mathcal {I}_{\mathcal {A}},\mathcal {I}_{\mathcal {B}}, \textrm{U}_{\hbar },\textrm{R}_{\hbar },\textrm{X}_{\textrm{r}},\textrm{Y}_{\textrm{r}},\mathcal {I}_{\textrm{r}}, \textrm{C}_{\epsilon }\big )^{\textbf{T}}\). For this, we take
We derive the mathematical scheme that follows:
Therefore, we determine two responses to problem (3.3) employing appropriate arithmetic computations. We possess a disease-free steady states \(\mathcal {P}_{0}=\bigg (\frac{\Lambda _{\hbar }}{\mu _{\hbar }+\Phi \textrm{g}_{3}},0,0,0,0,0,\frac{\Phi \Lambda _{\hbar }\textrm{g}_{3}}{\mu _{\hbar }(\mu _{\hbar }+\Phi \textrm{g}_{3})},\frac{\Lambda _{\textrm{r}}}{\mu _{\textrm{r}}},0,0,0,0\bigg ).\)
Exclusively EEP with infectious rodents occur when MPXV contamination persists within the animal community alone while there are not any infections from rodents to humans or humans to humans. An endemic equilibrium point, \(\mathcal {P}^{*}\), is provided in this case study as:
where \(\mathcal {I}_{\textrm{r}}^{*}=\frac{\mu _{\textrm{r}}(\mathbb {R}_{0\textrm{r}}-1)}{\theta \alpha _{\textrm{r}\textrm{r}}}.\) This demonstrates that an EEP exclusive to rodents exists if \(\mathbb {R}_{0\textrm{r}}>1\) and \(\mathbb {R}_{0\hbar }<1.\)
Furthermore, the EEP for contaminated individuals is the threshold at which the MPXV disease persists within just humans alone and does not spread from rodent to rodent or from rodent to people. An EEP \(\mathcal {P}_{1}^{*}\) is provided via this setting and is offered by
where
Now, applying the consequence and description of62 of the next generation matrix operator, we employ the concept of evaluating the Jacobian at the DFEP with the rate of the implementation of freshly acquired viruses into disease categories \(\mathcal {F}\) versus the disparity between the speed of transmission of infectious agents into respective illness categories \(\mathcal {V}\), we have
and
Using (3.16) and (3.17), we have
where
Consequently, the spectral radius of \(\mathcal {F}\mathcal {V}^{-1}\) is used to determine the fundamental reproductive number of the representation in (3.3) and is provided by
where \(\mathbb {R}_{0\hbar }=\mathbb {R}_{0\hbar }^{\epsilon }+\mathbb {R}_{0\hbar }^{\textrm{s}}+\mathbb {R}_{0\hbar }^{\textrm{a}}\) and
and
The cutoff amount \(\mathbb {R}_{0}\) calculates the mean proportion of subsequent infections that result from an individual, rodent, or unhealthy setting infested with MPXV during the course of the infection in a community. \(\mathbb {R}_{0}\) is a very helpful number for explaining how an outbreak spreads. \(\mathbb {R}_{0}<1\) indicates the end of the illness (see Fig. 2a–d). An outbreak is created if \(\mathbb {R}_{0}>1\) for (3.3). The basic reproduction number \(\mathbb {R}_{0\textrm{r}}\) for rodent-to-rodent propagation is represented by the parameters. The expressions \(\mathbb {R}_{0\hbar }^{\textrm{a}}\), \(\mathbb {R}_{0\hbar }^{\textrm{s}}\) and \(\mathbb {R}_{0\hbar }^{\epsilon }\) denote the fundamental reproductive values associated with infections from humans to other people, while \(\mathbb {R}_{0\hbar }^{\epsilon }\) represents the fundamental reproductive number associated with infections from polluted environments to humans.
Behavior of \(\mathbb {R}_{0}\) for different values of MPXV model (3.3).
Stability analysis
If every framework approach that starts wherever in and stays close to the steady state for an indefinite amount of time is considered globally stable is the DFEP. The hypothesis shown next, as explained by63, establishes this. The representation of the structure of discrete fractional difference equations (3.3) for MPXV is expressed as:
where \(Y_{1}=(\textrm{X}_{\hbar },\textrm{R}_{\hbar },\textrm{X}_{\textrm{n}})\) and \(Y_{2}=(\textrm{Q}_{\hbar },\mathcal {I}_{\mathcal {A}},\mathcal {I}_{\mathcal {B}},\textrm{U}_{\hbar },\textrm{Y}_{\textrm{r}},\mathcal {I}_{\textrm{r}},\textrm{C}_{\epsilon })\) represent the total quantity of unaffected people \(\mathcal {F}_{1}\in \mathbb {R}_{+}^{3}\) and \(\mathcal {F}_{2}\in \mathbb {R}_{+}^{8}\) represents the population of contaminated people. \(\widetilde{E}_{0}=(\mathcal {P}_{0},0)\) is the notation for the DFEP. Asymptotic global stability is ensured provided that the subsequent requirements are met.
\(B_{1}\): \(\mathcal {P}_{0}\) is GAS, for \(\,_{\ell }^{mABC}\nabla ^{\wp }Y_{1}(\xi )=\mathcal {F}_{1}(Y_{1},0).\)
\(B_{2}\): The Jacobian matrix \(U_{1}=\,_{\ell }^{mABC}\nabla ^{\wp }\mathcal {F}_{2}(Y_{2})\) is a structure which has all of its off-diagonal elements positive (Metzler-matrix), and represents the domain wherein the MPXV system is scientifically possible for \(\mathcal {F}_{2}(Y_{1},Y_{2})=U_{1}Y_{2}-\widetilde{\mathcal {F}_{2}}(Y_{1},Y_{2})\) containing \(\widetilde{\mathcal {F}_{2}}(Y_{1},Y_{2})>0\) and \((Y_{1},Y_{2})\in \Omega .\)
Theorem 3.2
If \(\mathbb {R}_{0}<1,\) then GAS at DFEP \(\mathcal {P}_{0}\) is achieved and satisfying the supposition of \(B_{1}\) and \(B_{2}.\)
Proof
By interpreting the framework (3.3) as (3.21), we obtain \(Y_{1}=\big [\textrm{X}_{\hbar },\textrm{R}_{\hbar },\textrm{X}_{\textrm{r}}\big ]^{\textbf{T}}\) and \(Y_{2}=\big [\textrm{Y}_{\hbar },\textrm{Q}_{\hbar },\mathcal {I}_{\mathcal {A}}, \mathcal {I}_{\textrm{r}}, \textrm{U}_{\hbar }, \textrm{Y}_{\textrm{r}},\mathcal {I}_{\textrm{r}},\textrm{C}_{\epsilon }\big ]^{\textbf{T}}.\) Taking \(\textrm{Y}_{\hbar }=\textrm{Q}_{\hbar }=\mathcal {I}_{\mathcal {A}}=\mathcal {I}_{\textrm{r}}=\textrm{U}_{\hbar }=\textrm{Y}_{\textrm{r}}=\mathcal {I}_{\textrm{r}}=\textrm{C}_{\epsilon }=0,\) then uncontaminated MPXV system (3.3) yields
The following are the outcomes to (3.22) as:
Therefore, the contagious component \(\big [\textrm{Y}_{\hbar },\textrm{Q}_{\hbar },\mathcal {I}_{\mathcal {A}}, \mathcal {I}_{\textrm{r}},\textrm{U}_{\hbar }, \textrm{Y}_{\textrm{r}},\mathcal {I}_{\textrm{r}},\textrm{C}_{\epsilon }\big ]\) in (3.23) using \(\mathcal {P}_{0}=\bigg (\frac{\Lambda _{\hbar }}{\mu _{\hbar }+\Phi \textrm{g}_{3}},\frac{\Lambda _{\hbar }\textrm{g}_{3}\Phi }{(\mu _{\hbar }+\Phi \textrm{g}_{3})\mu _{\hbar }},\frac{\Lambda _{\textrm{r}}}{\mu _{\textrm{r}}}\bigg ),\) thus verified to be GAS, meaning that the requirement \(B_{1}\) is satisfied for the MPXV framework containing \(\lambda _{\hbar }=(1-\textrm{g}_{1})\big (\alpha _{\textrm{r}\hbar }\mathcal {I}_{\textrm{r}}+\alpha _{\hbar \hbar }(\theta _{\textrm{m}}\mathcal {I}_{\mathcal {A}}+\mathcal {I}_{\mathcal {B}})\big )+(1-\textrm{g}_{2})\alpha _{g_{1}\hbar }\textrm{C}_{\epsilon }\) and \(\lambda _{\textrm{r}}=\alpha _{\textrm{r}\textrm{r}}\mathcal {I}_{\textrm{r}}\) provided by
Thus, (3.24) can be expressed as follows:
similar to supposition \(B_{2}\) containing
and
When \(Y_{2}(0)>0\), then \(Y_{2}(\xi )\ge 0\). Assuming \(U_{1}\) is a Metzler matrix, a modified technique could potentially be used to get
Since \(U_{1}\) possesses a negatively dominating eigenvalue if \(\mathbb {R}_{0}<1\), we find \(Y_{2}(\xi )=0.\) Consequently, if \(\mathbb {R}_{0}<1\), the DFEP remains GAS. If not, it is unsteady. \(\square\)
Our upcoming result is the global stability analysis based on the infectious rodents for EEP.
Theorem 3.3
There exists an exclusive EEP \(\mathcal {P}^{*}\) for rodents \(\textrm{Y}_{\textrm{r}}\) exclusively, which is GAS, if \(\mathbb {R}_{0\textrm{r}}>1\) and \(\mathbb {R}_{0\hbar }<1.\)
Proof
Assume that the Lyapunov function can be expressed as
By applying Definition 2.5, we have
The following represent the EEP criteria for infectious rodents exclusively:
Plugging the aforesaid values of (3.28) and (3.29) in (3.30), we have
Simple computation yields
By applying the formula \(1-\bar{\rho }+\ln \bar{\rho }\le 0\), then (3.32) yields
As a consequence, the first requirement in Theorem 3.5 of64 is satisfied by (3.33). The related scaled matrix \(\varphi _{3}\theta \textrm{Y}_{\textrm{r}}^{*}=0\) is provided by criterion (\(B_{2}\)), as it indicates a single phase in which the rodents directly contract the disease. Thus, by selecting \(\varphi _{1}=\varphi _{2}=1\) and \(\varphi _{3}=\alpha _{\textrm{r}\textrm{r}}\mathcal {I}_{\textrm{r}}^{*}\textrm{X}_{\textrm{r}}^{*}/\theta \textrm{Y}_{\textrm{r}}^{*},\) one attains \(\,_{\ell }^{mABC}\nabla ^{\wp } \digamma (\xi )\le 0\) and equality is maintained if \(\textrm{X}_{\textrm{r}}=\textrm{X}_{\textrm{r}}^{*},~\textrm{Y}_{\textrm{r}}=\textrm{Y}_{\textrm{r}}^{*},~\mathcal {I}_{\textrm{r}}=\mathcal {I}_{\textrm{r}}^{*}\) and \(\textrm{C}_{\epsilon }=\textrm{C}_{\epsilon }^{*}.\) Consequently, \(\{\mathcal {P}^{*}\}\) is an exclusive persistent group wherein \(\,_{\ell }^{mABC}\nabla ^{\wp } \digamma (\xi )=0\) exists inside the affected rodentonly environment. According to LaSalle’s invariant hypothesis, \(\{\mathcal {P}^{*}\}\) is GAS iff \(\mathbb {R}_{0\textrm{r}}>1\), making it unique. \(\square\)
In an analogous manner, the GAS of infected persons alone at the EEP \(\mathcal {P}_{1}^{*}\) can be examined. In addition to the challenges in maintaining a steady state for the factors employed to calculate the fundamental reproductive number and DFE, as well as the fact that MPXV is notoriously challenging to oversight, one possible solution is to combine optimal control with time-based controls to devise strategies for minimizing both govern and inadvertent dissemination of the infection.
Explore discrete fractional order ABC MPXV model
First, we evoke the concept of \(\rho ^{2}\)-monotonicity.
\(\rho ^{2}\)-monotonicity analysis
In this part, we apply the \(\wp\)-monotonicity analysis with respect to discrete nabla fractional operators. We begin by reviewing over the descriptions of \(\wp\)-monotones for all \(\wp \in (0,1]\) and a mapping \(\rho :\mathbb {N}_{\ell }\mapsto \mathbb {R}\) satisfying \(\rho (\ell )=0,\) as stated in54.
-
(i)
In this particular scenario, \(\rho\) is called an \(\wp\)-monotone rising function on \(\mathbb {N}_{\ell }\) as
$$\begin{aligned} \wp \rho (\tau )\le \rho (\tau +1),~~\forall ~\tau \in \mathbb {N}_{\ell }. \end{aligned}$$(4.1) -
(ii)
In this particular scenario, \(\rho\) is called an \(\wp\)-monotone falling function on \(\mathbb {N}_{\ell }\) as
$$\begin{aligned} \wp \rho (\tau )\ge \rho (\tau +1),~~\forall ~\tau \in \mathbb {N}_{\ell }. \end{aligned}$$(4.2) -
(iii)
It is known that the function on \(\mathbb {N}_{\ell }\) is an \(\wp\)-monotonically rising function if
$$\begin{aligned} \wp \rho (\tau )<\rho (\tau +1),~~\forall ~\tau \in \mathbb {N}_{\ell }. \end{aligned}$$(4.3) -
(iv)
It is known that the function on \(\mathbb {N}_{\ell }\) is an \(\wp\)-monotonically falling function if
$$\begin{aligned} \wp \rho (\tau )>\rho (\tau +1),~~\forall ~\tau \in \mathbb {N}_{\ell }. \end{aligned}$$(4.4)
Remark 4.1
Considering \(0<\wp \le 1\), it is obvious that if \(\rho (\hbar )\) is rising or falling on \(\mathbb {N}_{\ell }\), therefore we have
or
This shows that \(\rho (\tau )\) is either rising or falling on \(\mathbb {N}_{\ell }\) for \(\wp\)-monotone.
Theorem 4.1
For \(0<\wp \le \frac{1}{2},\) the mapping \(\Xi :\mathbb {N}_{\ell }\mapsto \mathbb {R}\) satisfies
for all \(\xi \in \mathbb {N}_{\ell },\) then \(\Xi (\xi )>0.\) Furthermore, \(\Xi (\xi )\) are \(\wp\)-monotone rising functions.
Proof
By means of Definition 2.3 and Remark 2.1, for all \(\xi \in \mathbb {N}_{\ell },\) we have
Using the fact of (2.2) and implementing on the first compartment of (3.3), we have
It is worth mentioning that \(\frac{AB(\wp )}{1-\wp }>0\) with \(\,^{AB}_{\ell }\nabla ^{\wp }\big [\textrm{X}_{\hbar }(\xi )\big ]\ge 0,\) we have
To demonstrate that \(\textrm{X}_{\hbar }(\xi )>0\) for any \(\xi \in \mathbb {N}_{\jmath }\), mathematical induction is utilized. Additionally, assuming that \(\textrm{X}_{\hbar }(\xi )>0\) for any \(\xi \in \mathbb {N}_{\jmath }^{\phi }=\big \{\ell ,\ell +1,\ldots ,\phi \big \},\) while \(\textrm{X}_{\hbar }(\xi )>0\) is the underpinning supposition, we are able to determine from (4.11) that certain \(\phi \in \mathbb {N}_{\jmath },\) thus we have
In view of Remark 2.1, we have
Consequently, we conclude that \(\textrm{X}_{\hbar }(\xi )>0\) for \(\xi \in \mathbb {N}_{\ell }\), as necessary. The \(\rho ^{2}\)-monotonicity of \(\textrm{X}_{\hbar }\) is shown by rewriting (4.11) with the following modifications:
for every \(\xi \in \mathbb {N}_{\ell +1}\). It is shown that \(\textrm{X}_{\hbar }(\xi )>0\) for all \(\xi \in \mathbb {N}_{\jmath }\). Furthermore, we understand that \(\mathcal {E}_{\bar{\wp }}(\chi ,\xi )\) is monotonically decreasing for each \(\xi =0,1,\ldots\) considering Remark 2.1. As a result, (4.14) suggests that
This exhibit \(\textrm{X}_{\hbar }\) is \(\rho ^{2}\)-monotonically increasing on \(\mathbb {N}_{\ell }\). We are also able to prove it for \(\textrm{Y}_{\hbar },~\textrm{Q}_{\hbar },~\mathcal {I}_{\mathcal {A}},~\mathcal {I}_{\mathcal {B}},~\textrm{U}_{\hbar },~\textrm{R}_{\hbar }, \textrm{X}_{\textrm{r}},~\textrm{Y}_{\textrm{r}},~\mathcal {I}_{\textrm{r}}\) and \(\textrm{C}_{\epsilon }.\) \(\square\)
Remark 4.2
By restricting the criteria in Theorem 4.1 and \(\textrm{X}_{\hbar }(\ell ),\textrm{Y}_{\hbar }(\ell ),~\textrm{Q}_{\hbar }(\ell ),~\mathcal {I}_{\mathcal {A}}(\ell ),~\mathcal {I}_{\mathcal {B}}(\ell ),~\textrm{U}_{\hbar }(\ell ),~\textrm{R}_{\hbar }(\ell ), \textrm{X}_{\textrm{r}}(\ell ),~\textrm{Y}_{\textrm{r}}(\ell ),~\mathcal {I}_{\textrm{r}}(\ell ),~\textrm{C}_{\epsilon }(\ell ),\) we may deduce that \(\textrm{X}_{\hbar },\textrm{Y}_{\hbar },~\textrm{Q}_{\hbar },~\mathcal {I}_{\mathcal {A}},~\mathcal {I}_{\mathcal {B}},~\textrm{U}_{\hbar },~\textrm{R}_{\hbar },~\textrm{X}_{\textrm{r}},~\textrm{Y}_{\textrm{r}},~\mathcal {I}_{\textrm{r}}\) and \(\textrm{C}_{\epsilon }\) are \(\rho ^{2}\)-monotonicity strictly increasing on \(\mathbb {N}_{\ell }\). Additionally, for every \(\xi \in \mathbb {N}_{\ell +1}\), \(\,_{\ell }^{AB}\nabla ^{\wp }\textrm{X}_{\hbar }(\xi )>0,\,_{\ell }^{AB}\nabla ^{\wp }\textrm{X}_{\hbar }(\xi )>0,\,_{\ell }^{AB}\nabla ^{\wp }\textrm{X}_{\hbar }(\xi )>0,~\,_{\ell }^{AB}\nabla ^{\wp }\textrm{Y}_{\hbar }(\xi )>0,\,_{\ell }^{AB}\nabla ^{\wp }\textrm{Q}_{\hbar }(\xi )>0,\,_{\ell }^{AB}\nabla ^{\wp }\mathcal {I}_{\mathcal {A}}(\xi )>0,\)\(~\,_{\ell }^{AB}\nabla ^{\wp }\mathcal {I}_{\mathcal {B}}(\xi )>0,~\,_{\ell }^{AB}\nabla ^{\wp }\textrm{U}_{\hbar }(\xi )>0,~\,_{\ell }^{AB}\nabla ^{\wp }\textrm{R}_{\hbar }(\xi )>0,~\,_{\ell }^{AB}\nabla ^{\wp }\textrm{X}_{\textrm{r}}(\xi )>0,~\,_{\ell }^{AB}\nabla ^{\wp }\textrm{Y}_{\textrm{r}}(\xi )>0,~\,_{\ell }^{AB}\nabla ^{\wp }\mathcal {I}_{\textrm{r}}(\xi )>0,~\textrm{C}_{\epsilon }\) are documented.
Theorem 4.2
Assume that \(\textrm{X}_{\hbar }(\ell )=\textrm{Y}_{\hbar }(\ell )=\textrm{Q}_{\hbar }(\ell )=\mathcal {I}_{\mathcal {A}}(\ell )=\mathcal {I}_{\mathcal {B}}(\ell )=\textrm{U}_{\hbar }(\ell )=\textrm{R}_{\hbar }(\ell )=\textrm{X}_{\textrm{r}}(\ell )=\textrm{Y}_{\textrm{r}}(\ell )=\mathcal {I}_{\textrm{r}}(\ell )=\textrm{C}_{\epsilon }(\ell )=0\) and let \(\textrm{X}_{\hbar },~\textrm{Y}_{\hbar },~\textrm{Q}_{\hbar },~\mathcal {I}_{\mathcal {A}},~\mathcal {I}_{\mathcal {B}},~\textrm{U}_{\hbar },~\textrm{R}_{\hbar },~\textrm{X}_{\textrm{r}},~\textrm{Y}_{\textrm{r}},~\mathcal {I}_{\textrm{r}},~\textrm{C}_{\epsilon }\) be characterized on \(\mathbb {N}_{\ell }\) and non-decreasing on \(\mathbb {N}_{\ell +1}\). Therefore, for \(\wp \in (0,1]\), we have
Proof
By means of Theorem 4.1, we have
Using Remark 2.1 and rising function \(\textrm{X}_{\hbar }\) on \(\mathbb {N}_{\ell +1}\), it becomes clear that
This leads to
Since \(\textrm{X}_{\hbar }(\ell )=0\) and \(\textrm{X}_{\hbar }\) is non-decreasing on \(\mathbb {N}_{\ell +1}\), we can deduce
This suggests that
This completes the proof. We could potentially demonstrate it regarding the leftover cohorts in our proposed system. \(\square\)
Remark 4.3
Most of the preceding results can additionally be obtained for non-decreasing (or strictly non-increasing) mappings by using similar criteria in conjunction with the corresponding difference formulations.
Further extensions of mABC MPXV model
Theorem 4.3
Regarding \(\wp \in (0,1/2)\), the subsequent findings are valid:
and
for all \(\xi \in \mathbb {N}_{\ell +1}.\)
Proof
Let us define the following for all \(\xi \in \mathbb {N}_{\ell +1}:\)
Implementing Laplace transform \(\mathfrak {L}_{\ell }\) on first formula of (4.24) both sides and employing Lemma 2.4, we have
It follows that
After calculating \(\textrm{X}_{\hbar }(\phi )\), we get
According to47, we have
By applying the discrete inverse Laplace transform to each component of (4.27), we obtain
Furthermore, we obtain
The theorem meets all requirements in its initial part.
Furthermore, assume that for all \(\xi \in \mathbb {N}_{\ell +1},\) we have
Implementing discrete Laplace transform \(\mathfrak {L}_{\ell }\) on \(\,_{\ell }^{mABC}\nabla ^{\wp }\Upsilon _{1}\), we get
Combining (4.27) and (4.28), we have
Furthermore, we derive from (2.2) as
Thus, (4.33) reduces to
By performing the inverse Laplace transform to both sides of (4.36), we arrive at the following conclusion:
Moreover, we have
The theorem’s second part has been fulfilled in accordance with (4.31). \(\square\)
Theorem 4.4
For \(\wp \in (0,1/2)\), the resulting series provides an alternative description of the discrete mABC type fractional difference, which is:
for all \(\xi \in \mathbb {N}_{\gimel _{1}+1}.\)
Proof
By means of Definitions 2.2 and 2.4, we have
Using similar techniques, we are capable of demonstrating it for each of the cohorts in our proposed scheme. \(\square\)
Solution of MPXV model
We propose a framework that can be stated as
Using the fact of Theorem 4.2, we have
It follows that
The aforesaid formulation can be articulated as
Finally, we have
Results and discussion
In this part, we explore the stated system (3.3) computationally with the settings given in Table 1 . Furthermore, the approach described in the preceding section is applied to numerically address the suggested framework of mABC fractional derivative in discrete time. The input data collection is fitted to a framework containing characteristics provided by the framework of NLDs using the nonlinear least squares approach. This method is applied to the estimate of factors in computational frameworks that depict the evolution of infectious diseases in a variety of domains, most notably epidemiological. The aim of this approach is to identify the characteristic settings that may minimize the total squared difference between real and forecasted statistics. The following are the computational illustrations:
where \(w_{\kappa }\) is the actual information at moment \(t_{\kappa }\), \(\varsigma (t_{\kappa },\varrho )\) is the system’s estimate result at \(t_{\kappa }\) according to the specified feature set \(\varrho\) and \(\Theta (\varrho )\) is the suggested objective function’s sum of squares. The reference65 provided the everyday cumulative instances of MPXV detected in Canada through May 24, 2022 to December 31, 2023.
The supplied document states that May 24, 2022, was the inaugural recorded instance of MPXV in Canada. This is shown in the technique below, where \(\mathcal {I}_{\mathcal {A}}\)=1. The procedures below should be followed in order to begin using the current technique:
-
(a)
Development of the mathematical framework describing our situation, which is given in (3.1), whenever \(\beta =1\).
-
(b)
Within this point, we require a first estimate regarding the system variables and criteria, whether it can be derived from literary work, earlier research, or by making specific predictions that pertain to the challenge at hand.
-
In Canada, the mean lifetime is 1/(81.65\(\times 365\)) per day66.
-
The daily fertility rate of humans is \(\Lambda _{\hbar }={d}_{\hbar }\times \mathbb {N}_{\hbar }(0)=2265\), wherein \(\mathbb {N}_{\hbar }(0)=67,508,936\).
-
Rodent fertility rate is given by \(\Lambda _{\textrm{r}}={d}_{\textrm{r}}\times \mathbb {N}_{\textrm{r}}(0)\), wherein \(\mathbb {N}_{\textrm{r}}(0)=12150\).
-
Following are a few of the initial values in this instance: \(\textrm{X}_{\hbar }=1000,~\textrm{Y}_{\hbar }=100,~\textrm{Q}_{\hbar }=0,~\mathcal {I}_{\mathcal {A}}=1,~\mathcal {I}_{\mathcal {B}}=50,~\textrm{U}_{\hbar }=0,~\textrm{X}_{\textrm{r}}=1350,~\textrm{Y}_{\textrm{r}}=1,~\mathcal {I}_{\textrm{r}}=1,~\textrm{C}_{\epsilon }=20\) with the weighting variables that are utilized throughout the case study are \(W_{1}=W_{2}=W_{3}=1,~U_{1}=1,~U_{2}=50,~U_{3}=100,~U_{4}=100\) and \(U_{5}=50.\)
-
-
(c)
Creating the objective function that assesses the discrepancy between the framework’s predicted values and real information. At this point we take into account Canada’s actual information, that was accessible by67, for the period of May 24, 2022, to December 31, 2023.
-
(d)
Offering a mathematical strategy for reducing the objective function.
-
(e)
The objective function is minimized at the beginning of the technique’s repetitions to modify the setting of the variables unless the intended outcomes are achieved.
-
(f)
Lastly, a comparison between the estimated and real data validates the framework. The model’s mathematical correctness is determined by residual research and goodness of fit.
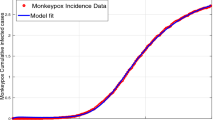
The above-discussed approach is used, and Fig. 3 and Table 1 display the outcomes. The figure 75.0735 represents the root mean square error. Table 1 provides an estimate to earn the basic reproduction number, \(\mathbb {R}_{0}=0.3489\), based upon the estimated factors. The closest correspondence with the predicted outcome and the empirical information is displayed schematically in Fig. 3, which displays the results of data-adjusting findings. Evidence vs. the model fitting is shown in Fig. 3a, and the matching residual is shown in Fig. 3b, respectively.
Applying the numerical approach presented in the preceding part, we analyze the discrete fractional-order MPXV problem. In the scenario, a day is used as a temporal unit. Consider the essence of the simulation’s time system, which is each day. The modeling process employs the parameter settings given in Table 1, and the intended outcomes are displayed dynamically. The outcomes for different assumptions of the discrete fractional-order \(\wp =1\) are shown in Fig. 4a for \(\textrm{X}_{\hbar }\) and \(\textrm{R}_{\hbar }\). We find that a decline in \(\wp =[0.95 ~0.9~0.85~0.75]\) is correlated with a reduction in people overall and a spike in the community that is not infested. This indicates that the suggested technique can be extended for additional real-world scientific and technical challenges and is dependable for resolving the identified issue for the case of human-to-human paring up in Fig. 4a,b \(\textrm{X}_{\hbar }\) and \(\textrm{R}_{\hbar },\) Fig. 4c,d \(\textrm{X}_{\hbar }\) and \(\mathcal {I}_{\mathcal {A}},\) and Fig. 4e,f \(\textrm{Y}_{\hbar }\) and \(\mathcal {I}_{\mathcal {B}},\) respectively.
Furthermore, with fixed \(\wp =1\), Fig. 5a,b depict the general number of \(\textrm{Y}_{\hbar }\) and \(\mathcal {I}_{\mathcal {A}}\) and Fig. 5c,d analyze the \(\mathcal {I}_{\mathcal {A}}\) and \(\textrm{R}_{\hbar },\) while altering \(\wp =[0.95~0.9~0.85~0.75]\). When the fractional factor \(\wp =[0.95~0.9~0.85~0.75]\) is decreased, there is a considerable decrease in the overall amount of human interactions. The Fig. 5a,b, and c,d demonstrate this better than Fig. 5e,f, which show additional scenarios with the various other suppositions of discrete fractional-order.
Thus, when modeling such an outbreak, the memory impact yields significant findings for the interaction of animal and human populations.
When exposed humans and asymptotic infectious communicate, the interaction value \(\vartheta _{3}\) enhances the proportion of asymptotic infectious. This leads to a spike in the overall number of infested humans and, consequently, an increase in the infections of individuals through the animal-to-human spread way. The effect is depicted in Fig. 6a,b. The overall amount of infectious rodents is expected to rise due to a boost in the number of interactions between susceptible humans, which will expand the overall number of humans affected by the disease for discrete fractional-order \(\wp =[0.95~0.9~0.85~0.75]\) (see Fig. 6c).
Therefore, decreasing the amount of time that \(\textrm{Y}_{\hbar }\) spends with \(\textrm{C}_{\epsilon }\) will lower the quantity of individual occurrences. For constant \(\wp =1\), the equivalent outcomes are displayed in Fig. 6d when \(\wp =[0.95~0.9~0.85~0.75]\) is varied. Figure 6e,f depict individual communities impacted by indirect transmission.
Figure 6e displays the effects of exposed humans and the indirect transmission of contaminated environments under multiple parameter predictions for discrete fractional-order \(\wp =1\). The impact of the environment on unprotected animal communities is depicted in Fig. 6f for \(\wp =[0.95~0.9~0.85~0.75]\). The outcome comparisons for constants \(\wp =1\) and \(\phi _{1}=0.04\) and \(\phi _{2}=0.02\) indirect environment are shown in Fig. 6e,f, where \(\textrm{g}_{4}=0.05\). We took into account the environmental effective quarantine rate, and a relatively slower decline in hospitalization rates. There is an apparent distinction between the patients with and without quarantine, as shown by the results in Fig. 6. This demonstrates the efficacy of quarantine, as increasing numbers of people are protected by MPXV, which will result in a better decline in instances. It is evident from analyzing the discrete fractional-order estimates that \(\wp =[0.95~0.9~0.85~0.75]\) is efficient.
To examine the effect of the \(\textrm{X}_{\textrm{r}}\) on the overall number of \(\mathcal {I}_{\textrm{r}}\) for constant \(\wp =1\), we provide Fig. 7a. By adjusting \(\theta\), which represents the pace at which persons in quarantine acquire vulnerability to a varying \(\wp =[0.95~0.9~0.85~0.75]\), the quantity of revealed and contaminated individuals is reduced (see Fig. 7b). These findings suggest that a lower hospitalization rate \(\beta _{2}\) will end up in a greater decrease in the total number of infected people. Consequently, an improved decline in the number of infections will result from quarantine’s efficacy. Furthermore, we plot the impact of \(\textrm{Y}_{\textrm{r}}\) and \(\mathcal {I}_{\mathcal {B}}\) for fractional-order \(\wp =1\) and \(\wp =[0.95~0.9~0.85~0.75]\) in Fig. 7c,d and e,f show the impact of \(\textrm{Y}_{\textrm{r}}\) and \(\textrm{C}_{\epsilon },\) respectively. The quarantine and the discrete fractional-order \(\wp\) both greatly lower the likelihood of occurrences of MPXV within coming generations in the community. As a result, in order to lower the overall number of occurrences in the coming years, it is critical to hospitalized more people. It might be challenging to hospitalized a particular percentage of individuals in developing economies due to vaccine expenses, but in advanced economies, this becomes more practical. Furthermore, vaccine effectiveness plays a significant part in the management of illness. A quarantine with an elevated level of effectiveness will prove less unsuccessful in preventing new infections.
Time evolutionary process depicted for the discrete fractional-order MPXV model (3.3) with respect to \(\wp =1\) and \(\wp =[0.95 ~0.9~0.85~0.75]\) for paring up (a,b) \(\textrm{X}_{\hbar }\) and \(\textrm{R}_{\hbar },\) (c,d) \(\textrm{X}_{\hbar }\) and \(\mathcal {I}_{\mathcal {A}},\) and (g-i) \(\textrm{Y}_{\hbar }\) and \(\mathcal {I}_{\mathcal {B}},\) respectively.
Time evolutionary process depicted for the discrete fractional-order MPXV model (3.3) with respect to \(\wp =1\) and \(\wp =[0.95 ~0.9~0.85~0.75]\) for paring up (a,b) \(\textrm{Y}_{\hbar }\) and \(\mathcal {I}_{\mathcal {A}},\) (c,d) \(\mathcal {I}_{a}\) and \(\textrm{R}_{\hbar },\) and (e,f) \(\mathcal {I}_{s}\) and \(\textrm{R}_{\hbar },\) respectively.
Time evolutionary process depicted for the discrete fractional-order MPXV model (3.3) with respect to \(\wp =1\) and \(\wp =[0.95 ~0.9~0.85~0.75]\) for paring up (a,b) \(\textrm{X}_{\hbar }\) and \(\textrm{Q}_{\hbar },\) (c,d) \(\textrm{X}_{\hbar }\) and \(\mathcal {I}_{\textrm{r}},\) and (e,f) \(\textrm{Y}_{\hbar }\) and \(\textrm{C}_{\epsilon },\) respectively.
Time evolutionary process depicted for the discrete fractional-order MPXV model (3.3) with respect to \(\wp =1\) and \(\wp =[0.95 ~0.9~0.85~0.75]\) for paring up (a,b) \(\textrm{X}_{\textrm{r}}\) and \(\mathcal {I}_{\textrm{r}},\) (c,d) \(\textrm{Y}_{\textrm{r}}\) and \(\mathcal {I}_{\mathcal {B}},\) and (e,f) \(\textrm{Y}_{\textrm{r}}\) and \(\textrm{C}_{\epsilon },\) respectively.
Optimal control scheme
Optimal control testing can be employed to evaluate the influence of various treatment methods on the MPXV system. The objective function aims to minimize the transmission of the MPXV infection and the associated therapeutic costs as
where \(W_{\iota },~(\iota =1,2,3)\) and \(U_{\iota },~(\iota =1,2,\ldots ,5)\) are non-negative weights assigned to the benefits of suppressing MPXV within a given period \(\mathcal {N}\). To minimize MPXVs whilst minimizing control costs, we want to find the most effective control \((g_{1}^{*},g_{2}^{*},g_{3}^{*},g_{4}^{*},g_{5}^{*})\) as
corresponding to (5.1), where
Pontryagin’s maximal theory70 outlines the essential criteria for optimal control. Mugabi et al.71 propose showing the presence of optimum control and identifying the optimality mechanism.
In order to explore the existence of optical control, suppose that \(\tilde{g}=\big (g_{1}(\xi ),g_{2}(\xi ),g_{3}(\xi ),g_{4}(\xi ),g_{5}(\xi )\big )\in \mathbb {N}\) and \({I}_{ast}=(\textrm{Y}_{\hbar },\mathcal {I}_{\mathcal {B}},\textrm{C}_{\epsilon }),\) then (5.2) can be expressed as
The optimal control couple settings are calculated employing an optimization technique70. This requires establishing a Hamiltonian framework, as illustrated as follows:
where \(\alpha _{1},\alpha _{2},\alpha _{3},\alpha _{4},\alpha _{5},\alpha _{6},\alpha _{7},\alpha _{8},\alpha _{9},\alpha _{10},\alpha _{11}\) represent the co-state characteristics associated to the state cohorts \(\textrm{X}_{\hbar },~\textrm{Y}_{\hbar },\textrm{Q}_{\hbar },~\mathcal {I}_{\mathcal {A}},~\mathcal {I}_{\mathcal {B}},~\textrm{U}_{\hbar },\textrm{R}_{\hbar },\textrm{X}_{\textrm{r}},~\textrm{Y}_{\textrm{r}},~\mathcal {I}_{\textrm{r}}\) and \(\textrm{C}_{\epsilon }.\) The control system’s co-state formulas (3.3) are derived employing the Hamiltonian (5.5) and the following hypothesis.
Theorem 5.1
Assume that there is an optimal control \((g_{1}^{*},g_{2}^{*},g_{3}^{*},g_{4}^{*},g_{5}^{*})\) to (5.1) throughout \(\mho\), including accompanying optimal configurations \(\textrm{X}_{\hbar }^{\tilde{g}^{*}},~\textrm{Y}_{\hbar }^{\tilde{g}^{*}},\textrm{Q}_{\hbar }^{\tilde{g}^{*}},~\mathcal {I}_{\mathcal {A}}^{\tilde{g}^{*}},~\mathcal {I}_{\mathcal {B}}^{\tilde{g}^{*}},~\textrm{U}_{\hbar }^{\tilde{g}^{*}},\textrm{R}_{\hbar }^{\tilde{g}^{*}},\textrm{X}_{\textrm{r}}^{\tilde{g}^{*}},~\textrm{Y}_{\textrm{r}}^{\tilde{g}^{*}},~\mathcal {I}_{\textrm{r}}^{\tilde{g}^{*}}\) and \(\textrm{C}_{\epsilon }^{\tilde{g}^{*}}\) of the MPXV model (3.3) that minimizes (5.1) on \(\mho\). The co-state functions \(\alpha _{1},\alpha _{2},\ldots ,\alpha _{11}\) interact the following:
the transversality state, which serves as a constraint for the ending outcomes of the co-state characteristics, is defined as \(\alpha _{\iota }=0,~\xi \mathbb {N}_{\ell }\), where \(\iota\) ranges from 1 to 11. The characterization of this prerequisite is as follows:
where
Proof
Considering an optimal control Hamiltonian with a particular format, the Pontryagins maximal criterion ensures
utilizing the condition formula
The co-state formulas are provided by
and stationary requirements are
Applying (5.5) to the optimal control \(\mathbb {H}\) and then applying (5.11) to it yields
and when applying the Definition 2.4 to the optimal control Hamiltonian (5.5) in reference to the acceptable control systems, considering the transversality constraint \(\alpha _{1}=\alpha _{2}=\cdots =0,~\xi \in \mathbb {N}_{\ell }\), result is obtained
The potential outcomes \(\hat{g_{1}},\hat{g_{2}},\hat{g_{3}},\hat{g_{4}},\hat{g_{5}}\) of the optimal controllers \({g_{1}^{*}},{g_{2}^{*}},{g_{3}^{*}},{g_{4}^{*}},{g_{5}^{*}}\) are obtained by implementing (5.12) on (5.14) as
According to71, the regular controlling considerations are as follows:
where \(\jmath =1,2,3,4,5\) and a totally successful oversight procedure is represented by the number \(g^{*}_{\jmath }\). Thus, it is evident based on typical reasoning that
The framework (3.3) including its initial values, the co-state structure (5.13) containing its transversality criteria, and the optimal criterion (5.17) combine to generate the optimality structure.
Consider the outcomes of the state’s (3.3), the co-state (5.13) and the optimality criteria (5.17) as
for \({\xi }_{\kappa }=\kappa \hbar\) having \(\kappa =0,1,2,\ldots ,v_{1}+1,\) \(v_{1}\) represents the step size and \(\kappa\) is the number of sub-intervals within the domain \(\mathbb {N}_{\ell }\). As a result, the optimal control mechanism is provided by Table 2.
For the purpose of determining the most effective control for the processes of governance and contextual propagation of MPXV diseases, which include asymptomatic and exhibiting symptoms of contamination in an individual subgroup, the optimality mechanism is addressed quantitatively in the following phase using the aforesaid procedure. \(\square\)
Control effects
Numerical experiments of the parameterized MPXV control approach, as well as without control, are shown in this subsection. The purpose of such scenarios is to support the empirical insights presented in Sections 4 and 5. The five tactics with the labels show how control groups affect the frequency of infections in an individual community.
-
I
This entails merging only the control factors \(g_{1}\) and \(g_{3}\) with \(g_{2}=g_{4}=g_{5}=0\).
-
II
This involves merging the control factors \(g_{1},~g_{2},~g_{4}\) and \(g_{5}\) with \(g_{3}=0\).
-
III
This is the process of adding the control factors \(g_{1},~g_{3},~g_{4}\) and \(g_{5}\) with \(g_{2}=0\).
-
IV
The process involves merging the control factors \(g_{2},~g_{4},~g_{5}\) with \(g_{1}=g_{3}=0\).
-
V
This involves incorporating every control factor.
I: Impact of immunization and community awareness
Here, controllers \(g_{1},g_{2},g_{4}\) and \(g_{5}\) remain zero, whereas controlling \(g_{1}\) and \(g_{5}\) are turned on and employed to mimic the MPXV controlling system (3.3). The behavior of individual cohorts determined by the application of tactics I is displayed in Fig. 8a–f. Meanwhile, Fig. 8a–f shows the associated ideal control settings. These modeling outcomes demonstrate that, when approach I is applied, the amount of revealed, insulated, and contaminated (both un-diagnosed and acute contagious) would decrease, albeit not a lot. The number of individuals that recuperated will develop as vaccinations provide immunity against MPXV infections. By using I, the \(\mathbb {R}_{0\hbar }\) would be reduced from 1.6001 without intervention to 0.1123. This demonstrates a considerable influence on the ratios of exposure to infection.
Impact of exclusively employing vaccine and outreach efforts, that is, \(g_{1}\ne g_{3}\ne 0\), whereas \(g_{2}=g_{4}=g_{5}=0\). The scenario lacking controls and including controls adopting approach I in view of discrete fractional-order for mABC difference operator when \(\wp =[0.95~0.9~0.85~0.75]\).
II: Impact of employing personal safeguard resources and outreach to the public
In this instance, despite maintaining \(g_{3}\) zeros, controllers \(g_{1},g_{2},g_{4}\) and \(g_{5}\) are engaged and utilized to replicate the MPXV controlling system (3.3). When vaccination is not used as a control strategy, Fig. 9 illustrates the patterns of MPXV transmission in individual cohorts, while Fig. 9a–f shows the comparable control patterns. The outcomes of the modeling indicate that there is a greater effect in decreasing transmission in the pathogenic classifications while increasing the recovery group. There is a reduction in \(\mathbb {R}_{0\hbar }=1.6002\) to \(\mathbb {R}_{0\hbar }=1.3045\). This is significant precisely because the majority of the biological channels via which MPXV infections affect humans will be affected by this technique. The control patterns utilized in method II are displayed in Fig. 9a–f along with the strength of every controlling therapy.
Impact of including all control factors excluding vaccination, that is, \(g_{1}\ne g_{2}\ne g_{4}\ne g_{5}\ne 0\) and \(g_{3}=0\). The scenario lacking controls and including controls adopting approach II in view of discrete fractional-order for mABC difference operator when \(\wp =[0.95~0.9~0.85~0.75]\).
III: Impact of applying disinfectant agents and adequate disposal of waste
Despite retaining \(g_{2}\) zero, strategy III engages controllers \(g_{1},g_{3},g_{4}\) and \(g_{5}\), using these individuals to imitate the MPXV controlling mechanism (3.3). As seen in Fig. 10, the simulations conducted excluding \(g_{2}\) demonstrate a notable decrease in the amount of viruses in the individual compartments. This suggests that the incidence of MPXV is much decreased whenever vaccination is administered in conjunction with additional interventions that are effective on both the direct and ecological spread, as opposed to methods I and II, respectively. Meanwhile, \(\mathbb {R}_{0\hbar }=1.6002\) decreased from \(\mathbb {R}_{0\hbar }=1.1078.\) Adopting technique III, which reflects this. Figure 10a–f displays the appropriate control description, which uses strategy III to indicate the degree of effectiveness for every controller.
Effects of merging the control factors with the exception of \(g_{2}\) yielded the following results: \(g_{1}\ne g_{3}\ne g_{4}\ne g_{5}\ne 0\) whilst \(g_{2}=0.\) The scenario lacking controls and including controls adopting approach III in view of discrete fractional-order for mABC difference operator when \(\wp =[0.95~0.9~0.85~0.75]\).
IV: Impact of precautionary measures
In assertion IV, which simulates the MPXV controlling mechanism (3.3), controls \(g_{2},g_{4}\) and \(g_{5}\) are enabled whenever \(g_{1}=g_{3}=0\). At this point, the model findings in Fig. 11 indicate an insignificant effect in lowering the prevalence of MPXV if the concentration is on minimizing the spread of infection via the setting exclusively and disregarding the source of infection. Then, \(\mathbb {R}_{0\hbar }\) being lowered from 1.6002 to 1.1324. In comparison to assertions I, II and III, there is a smaller decrease in the percentage of susceptible to detached contaminated (unaffected and chronically contagious) persons. The amplitude of the restrictions employed in assertion IV is displayed in Fig. 11a–f compartment wise.
Effects of merging the control factors with the exception of \(g_{2}, g_{4},g_{5}\) yielded the following results: \(g_{2}\ne g_{4}\ne g_{5}\ne 0\) whilst \(g_{1}=g_{3}=0\). The scenario lacking controls and including controls adopting approach IV in view of discrete fractional-order for mABC difference operator when \(\wp =[0.95~0.9~0.85~0.75]\).
V: Impact of employing every control factor
The activation of controls \(g_{1},g_{2},g_{3},g_{4}\) and \(g_{5}\) is utilized to replicate (3.3) of the MPXV controlling system. When every control is combined, Fig. 12 demonstrates a noteworthy decrease in the quantity of vulnerable, hospitalized and isolated individuals. There was a notable rise in the quantity of people within the recovering category. Then, the value of \(\mathbb {R}_{0\hbar }=1.6023\) decreases to \(\mathbb {R}_{0\hbar }=1.4391\). According to approach V, Fig. 12a–f displays the ideal control characteristics for every function.
Conclusion
This investigation offers an extensive review of the dynamics of MPXV with respect to environmental contamination and indirect transmission with the aid of discrete GML kernel. In light of the epidemiological description of MPXV, a comprehensive model was created and bolstered by an extensive presentation that emphasized the public health issues related to the virus and included an analysis of the scientific literature. Nonlinear evolutionary differential equations constitute the cornerstone of the system’s composition, and the propagation methods of its features are discussed. The classical model has been discrete fractional-order mABC difference equations. The fractional model’s qualitative analysis and other important findings were examined. The DFEP and EEP have been determined. Examining the DFE’s stability showed that the suggested framework is LAS when the \(\mathbb {R}_{0}<1.\) Considering upon their essential characteristics and \(\rho\)-monotonicity terms, the research showed that the suggested discrete fractional differences will show \(\rho ^{2}\)-nonincreasing or nondecreasing influence in particular time scale regions, enabling effective oversight of MPXV.
Real data on cases of MPXV in Canada were analyzed for the purpose of research. The framework fitting was accomplished via a methodical procedure utilizing the nonlinear least squares technique; certain parameters have been estimated during the model fitting procedure, while others were obtained from the previous research. In graphical representation, the fit efficiency and associated results are displayed. Significant factors were examined and their effects on the mathematical framework were graphically shown. Various numerical findings were obtained by assuming various values of the fractional-order \(\wp\) and the framework’s parameters. There was an apparent decrease in the number of instances of MPXV in the future when the interaction settings were studied despite having the fractional-order \(\wp\) fixed.
Therefore, the significance of control in accomplishing pathogen extinction was highlighted by examining the impact of control procedures on the framework and the situation in which oversight was not present. Additionally, it was shown that the fading rate has a major impact on the overall number of occurrences of MPXV, either raising or lowering it. More rigorous restrictions on population growth can significantly lower the number of incidents. Contrary to earlier research, the findings reported here provide more trustworthy perspectives on the evolution of MPXV. Compared to earlier reports in the scientific literature, the study of actual information within control methods showed greater significance for the infection.
The results imply that it’s critical to reduce encounters involving healthy people and rodents that are diseased. Controlling rodent infestations via better hygiene, general awareness campaigns, and preventative interventions to shield individuals from rodent contamination ought to constitute the main goals of health safety precautions. The goal of prevention efforts ought to comprise decreasing the spread of zoonotic infections by putting into implementation efficient rodent prevention means, like utilizing pesticides, regulating the availability of nutrition, and modifying ecosystems. Moreover, administering a vaccine having more potency and slower rates of decline might improve attempts to eliminate infection. Reducing the percentage of humanity that is under control can aid in the decrease of viral infection incidents that arise from rodent-human contacts. An improved comprehensive of the present technique will be created by reanalyzing actual Canadian data and adding an age-structured strategy. These developments in fractional and stochastic analysis will lead to the proposal of further cost-effectiveness-supported optimum control techniques. Its objective is to pinpoint the effects on people at multiple ages so that preventative plans for the general population can be developed.
Data availability
The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.
References
World health organization, 2023, https://www.who.int/news-room/fact-sheets/ detail/monkeypox, (Accessed 05 March 2023).
Jezek, Z., Szczeniowski, M., Paluku, K. M., Mutombo, M. & Grab, B. Human monkeypox: confusion with chickenpox. Acta Tropica 45, 297–307 (1988).
Monkeypox signs and symptoms. CDC, 2022, Available online at: https://www. cdc.gov/poxvirus/monkeypox/.
Emmanuel, A., UgoMoens, G. N. & Okeke, M. I. Monkeypox virus in Nigeria: Infection biology. Epidemiology Evol. Vir 12, 1257 (2020).
Rimoin, A. W. et al. Major increase in human monkeypox incidence 30 years after smallpox vaccination campaigns cease in the Democratic Republic of Congo. Proc. Natl. Acad. Sci. USA 107, 16262–16267 (2010).
Peter, O. J., Fahrani, N. D. & Chukwu, C. W. A fractional derivative modeling study for measles infection with double dose vaccination. Healthcare Anal 4, 100231 (2023).
Jitsinchayakul, S., Zarin, R., Khan, A., Yusuf, A., Zaman, G., Humphries, U.W. & Sulaiman, T.A. Fractional modeling of COVID-19 epidemic model with harmonic mean type incidence rate. Open Phy, 19, 693-709 (2021).
Addai, E., Adeniji, A., Peter, O. j., Agbaje, J. O. & Oshinubi. Dynamics of Age-Structure Smoking Models with Government Intervention Coverage under Fractal-Fractional Order Derivatives. Fractal-Fractional Order Derivatives. Fractal Fract, 7, 370 (2023).
Zarin, R. Numerical study of a nonlinear COVID-19 pandemic model by finite difference and meshless methods. Partial Diff. Equ. Appl. Math 6, 100460 (2022).
Yadav, P., Jahan, S., Shah, K., Peter, O. J. & Abdeljawad, T. Fractional-order modelling and analysis of diabetes mellitus: Utilizing the Atangana-Baleanu Caputo (ABC) operator. Alexandria Eng J 81, 200–209 (2023).
Mpox (monkeypox)-Democratic Republic of the Congo, 2024, Available at: https://www.who.int/emergencies/disease-outbreak-news/item/2023-DON493 (Accessed 18 July 2024).
Sklenovska, N., Ranst, M. V. Emergence of monkeypox as the most important orthopoxvirus ’ infection in humans, Front. Public Health, 241, (2018). https://doi.org/10.3389/fpubh.2018.00241
Information on the smallpox vaccination, 2024, Available at: https: //www.gov.canada/government/publications/monkeypox-vaccination-resources, (Accessed 24 May 2024).
Mpox treatment information for healthcare professionals, 2024, Available at: https://www.cdc.gov/poxvirus/mpox/clinicians/treatment.html, (Accessed 24 May 2024).
Zarin, R., Khan, A., Akgül, A. & Akgül, E. K. Fractional modeling of COVID-19 pandemic model with real data from Pakistan under the ABC operator. AIMS Math 7, 15939–15964 (2022).
Abioye, A. I., Peter, O. J., Ogunseye, H. A., Oguntolu, F. A., Ayoola, T. A. & Oladapo, A. O. A fractional-order mathematical model for malaria and COVID-19 co-infection dynamics, Healthcare Anal. 4 , (2023).
Zarin, R. & Humphries, U. W. A robust study of dual variants of SARS-CoV-2 using a reaction-diffusion mathematical model with real data from the USA. Eur. Phys. J. Plus. 138, 1057 (2023).
Peter, O. J. et al. A mathematical model analysis of meningitis with treatment and vaccination in fractional derivatives. Inter J. Appl. Comput. Math 8, 117 (2022).
Alqhtani, M., Saad, K. M., Zarin, R., Khan, A. & Hamanah, W. M. Qualitative behavior of a highly non-linear Cutaneous Leishmania epidemic model under convex incidence rate with real data. Math. Biosci. Eng 21, 2084–2120 (2024).
Peter, O. J., Oguntolu, F. A., Ojo, M. M., Olayinka, O, A., Jan, R. & Khan, I. Fractional order mathematical model of monkeypox transmission dynamics. Physica Scr, 97, 084005 (2022).
Singapore Ministry of Health, Europe, US on alert over detection of Monkeypox cases: What is the virus, symptoms and its transmission across the globe. Available from: https://news.knowledia.com/IN/en/articles/europe-us-on-alert-over-detection-of-monkeypoxcases-what-is-the-virus-5.
So, have you heard about monkeypox? 2024, https://www.theatlantic. com/health/archive/2022/05/monkeypox-outbreak-covid-pandemic/629920/, (Accessed 24 January 2024).
Mpox (monkeypox) outbreak: epidemiological overview, 2023, https: //www.gov.canada/government/publications/monkeypox-outbreak-epidemiologicaloverview/ mpox-monkeypox-outbreak-epidemiological-overview-7-december- 2023, (Accessed 24 May 2024).
Elderfield, R. A. et al. Accumulation of human-adapting mutations during circulation of A (H1N1) pdm09 influenza virus in humans in the United Kingdom. J. Virol. 88, 13269–13283. https://doi.org/10.1128/JVI.01636-14 (2014).
Jackson, R. J. et al. Expression of mouse interleukin-4 by a recombinant ectromelia virus suppresses cytolytic lymphocyte responses and overcomes genetic resistance to mousepox. J. Virol. 75, 1205–1210 (2001).
Singh, J., Kumar, D. & Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ 2018, 231 (2018).
Peter, O. J. et al. Analysis and dynamics of fractional order mathematical model of COVID-19 in Nigeria using Atangana-Baleanu operator. Comp. Materials Continua 66, 1823–1848 (2021).
Peter, O. J. et al. Fractional order of pneumococcal pneumonia infection model with Caputo Fabrizio operator. Resu Phy 29, 104581 (2021).
Zarin, R., Khaliq, H., Khan, A., Ahmed, I. & Humphries, U. W. A numerical study based on haar wavelet collocation methods of fractional-order antidotal computer virus model. Symmetry 15, 621 (2023).
Peter, O. J. Transmission dynamics of fractional order brucellosis model using Caputo-Fabrizio operator. Inter J. Diff. Equ 2020, 2791380 (2020).
Kobe, J. et al. A game theoretic model of cholera with optimal personal protection strategies. Bull. Math. Bio. 80, 2580–2599. https://doi.org/10.1007/s11538-018-0476-5 (2018).
Antonovics, J. Transmission dynamics: critical questions and challenges. Phil. Trans. R. Soc. 372, 20160087 (2017).
Madubueze, C., Onwubuya, I. O., Godwin, N., Nkem, G. Z. & Chazuka, Z. On the transmission dynamics of the monkeypox virus in the presence of environmental transmission, Front. Appl. Math. Stat. 114, (2022).
Usman, S. & Adamu, I. I. Modeling the transmission dynamics of the monkeypox virus infection with treatment and vaccination interventions. J. Appl. Math. Phys. 5, 2335 (2017).
Peter, O. J. et al. Transmission dynamics of monkeypox virus: a mathematical modelling approach. Model. Earth Syst. Environ. 8, 3423–3434 (2022).
Emeka, P., Ounorah, M., Eguda, F. & Babangida, B. Mathematical model for monkeypox virus transmission dynamics. Epidemiol Open Access 8, 1000348 (2018).
Hutson, C. L. et al. Transmissibility of the monkeypox virus clades via respiratory transmission: investigation using the prairie dog-monkeypox virus challenge system. PLoS ONE. 8, e55488 (2013).
Okposo, N. I., Addai, E., Apanapudor, J. S. & Gómez-Aguilar, J. F. A study on a monkeypox transmission model within the scope of fractal-fractional derivative with power-law kernel. Eur. Phys. J. Plus. 138, 684 (2013).
Elsonbaty, A., Adel, W., Aldurayhim, A. & El-Mesady, A. Mathemati cal modeling and analysis of a novel monkeypox virus spread integrating imperfect vaccination and nonlinear incidence rates. Ain Shams Eng J. 15, 102451 (2024).
Ngungu, M., Addai, E., Adeniji, A., Adam, U. M. & Oshinubi, K. Mathematical epidemiological modeling and analysis of monkeypox dynamism with nonpharmaceutical intervention using real data from United Kingdom. Front. Publ. Health 11, 1101436 (2023).
Hobson, G. et al. Family cluster of three cases of monkeypox imported from Nigeria to the United Kingdom. Euro Surveill. 26, 2100745 (2021).
Durski, K. N. et al. Emergence of Monkeypox - West and Central Africa, 1970–2017. MMWR Morb Mortal Wkly Rep. 67, 306–310 (2018).
Khan, H., Tunc, C., Chen, W. & Khan. A. Existence theorems and Hyers-Ulam stability for aclass of hybrid fractional differential equations with \(p\)-Laplacian operator. J. Appl. Anal. Comput, 8, 1211-26 (2018).
Khan, H., Alzabut, J., Gómez-Aguilard, J. F. & Alkhazan, A. Essential criteria for existence of solution of a modified-ABC fractional order smoking model, Ain. Shams. Eng. J. l15, 102646 (2024).
Kumar, S., Chauhan, R. P., Momani, S. & Hadid, S. Numerical investigations on COVID-19 model through singular and non-singular fractional operators. Numer. Meth. Partial. Differ. Equ. 40, e22707 (2024).
Bonyah, E., Sagoe, A. K., Kumar, D. & Deniz, S. Fractional optimal control dynamics of coronavirus model with Mittag-Leffler law. Ecological Complexity, 45, (2020).
Abdeljawad, T. & Baleanu, D. Discrete fractional differences with nonsingular discrete Mittag- Leffler kernels. Adv. Differ. Eq. 2016, 1–18 (2016).
Abdeljawad, T. Fractional difference operators with discrete generalized Mittag-Leffler kernels. Chaos Soliton. Fract. 126, 315–324 (2019).
Farman, M. et al. Analysis of a fractional order Bovine Brucellosis disease model with discrete generalized Mittag-Leffler kernels. Res. Phys. 52, 106887 (2023).
Narayanan, G., Ali, M. S., Rajchakit, G., Jirawattanapanit, A. & Priya, B. Stability analysis for Nabla discrete fractional-order of Glucose-Insulin Regulatory System on diabetes mellitus with Mittag-Leffler kernel. Biomed. Signal Proces. 80, 104295 (2023).
Abdeljawad, T. & Baleanu, D. Discrete fractional differences with nonsingular discrete Mittag- Leffler kernels. Adv. Differ. Eq. 2016, 1–18 (2016).
Abdeljawad, T., Jarad, F. & Baleanu, D. A semigroup-like property for discrete Mittag-Leffler functions. Adv. Diff. Eq. 2012, 1–7 (2012).
Abdeljawad, T. & Baleanu, D. Monotonicity analysis of a nabla discrete fractional operator with discrete Mittag-Leffler kernel. Chaos Soliton. Fract. 102, 106–110 (2017).
Mohammed, P. O., Srivastava, H. M., Baleanu, D. & Abualnaja, K. M. Modified fractional difference operators defined using Mittag-Leffler kernels. Symmetry 14, 1519 (2022).
Ghaziani, R. K., Alidousti, J. & Eshkaftaki, A. B. Stability and dynamics of a fractional order Leslie-Gower prey-predator model. Appl. Math. Model. 40, 2075–2086 (2016).
Petras, I. Fractional-Order Nonlinear Systems: MODELING (Berlin, Germany, Analysis and Simulation; Springer Science & Business Media, 2011).
Ahmed, E., El-Sayed, A. M. A. & El-Saka, H. A. A. Equilibrium points, stability and numerical solutions of fractional-order predator prey and rabies models. J. Math. Anal. Appl. 325, 542–553 (2007).
Tsvetkov, D. P. & Angelova-Slavova, R. Positive periodic solutions for periodic predator-prey systems of Leslie-Gower or Holling Tanner type. Nonlinear Stud. 27, 991–1002 (2020).
Erawaty, N. & Amir, A. K. Stability analysis for routh-hurwitz conditions using partial pivot. J. Phys. Conf. Ser. 1314, 062017 (2019).
Madubueze, C., Onwubuya, I., Nkem, G. N. & Chazuka, Z. On the transmission dynamics of the monkeypox virus in the presence of environmental transmission. Front. Appl. Math. Stat, 114, (2022).
Li, H. L., Zhang, L., Hu, C., Jiang, Y. L. & Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 54, 435–449 (2017).
Driessche, P. & Watmough, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 180, 29–48 (2002).
Chien, F. & Shateyi, S. Volterra-lyapunov stability analysis of the solutions of babesiosis disease model. Symmetry 13, 1272 (2021).
Shuai, Z. & Driessche, P. Global stability of infectious disease models using Lyapunov functions. SIAMJ. Appl. Math. 73, 1513–1532 (2013).
Mathieu, E., Spooner, F., Dattani, S., Ritchie, H. & Roser, M. Mpox. Our World Data. (2022) https://ourworldindata.org/mpox.
Canada. life expectancy 1950-2024, 2024, https://www.macrotrends.net/countries/ GBR/Canada/life-expectancy, (Accessed 10 January 2024).
Mathieu, E., Spooner, F., Dattani, S., Ritchie, H. & Roser, M. Mpox. (monkeypox), 2024, https://ourworldindata.org/monkeypox.
Bhunu, C. P. & Mushayabasa, S. Modelling the transmission dynamics of pox-like infections, (2011).
Madubueze, C., Onwubuya, I., Nkem, G. N. & Chazuka, Z. On the transmission dynamics of the monkeypox virus in the presence of environmental transmission. Front. Appl. Math. Stat. 114, (2022).
Pontryagin, L. Mathematical Theory of Optimal Processes (CRC Press, Boca Raton, FL, English, 1987).
Mugabi, F., Mugisha, J., Nannyonga, B., Kasumba, H. & Tusiime, M. Parameter-dependent transmission dynamics and optimal control of foot and mouth disease in a contaminated environment. J. Egypt. Math. Soc. 27, 1–21 (2019).
Acknowledgements
The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TUDSPP-2024-127).
Funding
This research was funded by Taif University, Taif, Saudi Arabia (TU-DSPP-2024-127).
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Rashid, S., Bariq, A., Ali, I. et al. Dynamic analysis and optimal control of a hybrid fractional monkeypox disease model in terms of external factors. Sci Rep 15, 2944 (2025). https://doi.org/10.1038/s41598-024-83691-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-83691-y
Keywords
This article is cited by
-
Stochastic modeling for the transmission of hepatitis B virus with multiple time-delays and vaccination effect
Arabian Journal of Mathematics (2025)