Magnetization and superparamagnetic behavior of FeCu nanoalloys at room temperature via synthesis and simulation

Abstract

Bimetallic nanoalloys combining magnetic and noble metals are promising for magnetic sensors, catalysis, optical detection, and biomedical imaging applications. Their development relies on understanding morphology, electronic structure, and crystallography. This study explores iron-based magnetic nanoalloys using efficient synthesis and advanced characterization. Molecular dynamics (MD) simulations examined atomic-scale morphology and structural features, linking them to magnetic behavior. A spin-lattice dynamics algorithm simulated iron–copper (FeCu) nanoalloys of varying sizes and compositions. FeCu nanoalloys were synthesized via a one-step reduction reaction and analyzed using multiple techniques, yielding nanoparticles with high saturation magnetization and an 11 nm average size. Simulations and experiments confirmed core-shell (CS) and Janus morphologies, where copper shells an iron core. Findings suggest that composition, rather than morphology alone, predominantly influences magnetic properties, while the core-shell morphology enhances oxidation resistance due to the noble copper metal employed. This study is the first to integrate the spin-lattice algorithm with experimental analysis, providing consistent insights into design and accurate characterization. Thus, it confirms the practical and novel synthesis of low-size FeCu nanoparticles with ideal superparamagnetic properties—exhibiting no hysteresis—suitable for various research and industrial applications.

Introduction

Nanoparticles (1–100 nm) are key to nanotechnology, exhibiting unique properties due to their small size, large surface area, and quantum effects. These traits enable advanced applications in medicine, electronics, energy, and environmental science, surpassing bulk materials. Their high surface-area-to-volume ratio boosts chemical reactivity and catalysis, while quantum effects influence conductivity, magnetism, and optics.

The class of magnetic nanoparticles (MNPs) has distinct properties shaped by size, uniformity, surface area, and biocompatibility. By adjusting synthesis parameters, traits like superparamagnetism and adsorption kinetics can be tailored for applications in biology, catalysis, data storage, spintronics, sensors, and MRI contrast^{1,2,3,4,5,6,7,8,9,10}. Their large surface area enhances superparamagnetism, making MNPs a dynamic focus of theoretical and experimental nanoscience research.

These MNPs are classified as diamagnetic, paramagnetic, ferromagnetic, ferrimagnetic, or antiferromagnetic based on magnetic dipole interactions. Among them, superparamagnetic nanoparticles, which exhibit zero magnetization in the absence of an external field, are particularly useful in drug delivery and MRI enhancement. Since they do not retain magnetization once the field is removed, interparticle attraction is eliminated, influencing surface properties and biological applications. Their high sensitivity to magnetic fields allows precise control over their behavior.

Controlling MNP size and morphology is essential for tailoring their physicochemical properties. Reaction parameters must be carefully adjusted to achieve desired size distributions^11,12. For example, nanoparticles below the single-domain limit (~ 20 nm for iron oxide) often exhibit superparamagnetism at room temperature, making them valuable for ferrofluids, data storage, and medicine^11,12. Nanoparticle size significantly impacts properties such as coercivity, magnetization, and magnetic structure, which are shaped by intrinsic composition and surface effects. Below 20 nm, thermal fluctuations typically prevent permanent magnetization^12,13. For example, ε-Fe₂O₃ nanoparticles transition from ferromagnetic to superparamagnetic around 6 nm due to surface effects and weakened exchange interactions. Larger particles (~ 20 nm) exhibit higher coercivity than smaller ones (~ 6 nm) due to an increased surface-to-volume ratio, impacting magnetic stability and ordering^11,14.

At temperatures higher than room temperatures, thermal energy overcomes magnetic interactions, reducing effective magnetization, particularly in smaller nanoparticles, where high surface-to-volume ratios amplify thermal fluctuations^13,15,16. In magnetic alloys, exchange coupling between core and shell atoms affects magnetic properties. This coupling, arising from atomic magnetic moment interactions, results in diverse magnetic behaviors based on materials and structure. Differences in atom arrangement and cooling rates during synthesis yield varied phase diagrams and thermal behaviors^13,17.

Magnetic bimetallic nanoparticles (MBNPs) offer enhanced properties over monometallic particles due to synergistic effects between two metals, improving magnetic response for applications like magnetic separation and targeted drug delivery. MBNPs enable efficient separation from solutions via external magnetic fields, which is critical for catalytic processes and environmental remediation^7,8. Core-shell interactions in MBNPs lead to diverse exchange coupling mechanisms, with differences in atomic number and coupling type (core vs. shell) influencing thermal stability and magnetic behavior¹³.

Notably, core@shell nanoparticles exhibit stability against oxygen, water, and chemicals. Copper and iron combinations yield multifunctional nanoparticles with high catalytic activity and ferromagnetic properties, enabling magnetic separation from reaction systems¹⁸. Bimetallic FeCu nanoparticles, made from cost-effective metals, exhibit notable magnetic properties despite the immiscibility of iron and copper. These alloys are traditionally produced via vapor deposition and mechanical alloying^9,10, balancing iron’s magnetism with copper’s diamagnetic behavior. Despite synthesis challenges like oxidation, FeCu nanoparticles offer noble-metal catalyst alternatives. Their structures—random alloys, ordered alloys, core-shell, or Janus—depend on synthesis methods, composition, and temperature^19,20,21. They achieve saturation magnetization of ~ 15 µWb·m·kg⁻¹ via mechanical milling²² and ~ 18 emu·g⁻¹ through chemical reduction²³.

Because Cu and Fe are immiscible at equilibrium, FeCu solid solutions require non-equilibrium techniques like mechanical alloying^24,25,26 or vapor deposition²⁷. FeCu nanoparticles have also been synthesized through chemical reduction, involving sodium borohydride in oxygen-free conditions. These nanoparticles exhibit superparamagnetic behavior at low temperature ~ 10 K²⁸.

Synthesis methods significantly influence nanoparticle size and magnetic properties. In nickel ferrite nanoparticles (NiFe₂O₄), synthesis variations can result in differences in particle size, which in turn affect magnetic behavior. Nanoparticles synthesized via sol-gel methods tend to be ferromagnetic, while those produced by sputtering are superparamagnetic²³. FeCu alloy preparation via redox reactions, such as using sodium borohydride and activated carbon, produces nanoparticles with average sizes around 20 nm and chain-like arrangements²⁹. Also, the preparation of FeCu nanoparticles through a redox reaction of mixed aqueous salts was reported. The analysis included structure, morphology, and magnetic properties, though the magnetic loop’s hysteresis did not confirm a strong superparamagnetic FeCu alloy formation³⁰.

Computational studies have been crucial in designing and characterizing FeCu bimetallic nanoparticles using molecular dynamics (MD) simulations^19,20. These studies identified two structural types: a core-shell structure at low Cu concentrations and a Janus-like morphology at higher levels¹⁹. The cooling rate is key, with Janus morphology forming at lower rates. Different crystalline phases are observed, and the cooling rate strongly influences liquid-to-crystalline transitions. Structural characterization and potential energy assessments have been conducted²⁰. However, a broader simulation framework is needed to fully understand MNPs, as molecular and spin dynamics alone cannot capture magnetic and atomic excitations³¹. Atomistic spin-lattice simulations integrate spin and lattice dynamics using classical equations like the Landau-Lifshitz-Gilbert equation for spins and Newton’s equations for lattice atoms, incorporating exchange interactions, magnetic anisotropy, and magnetoelastic coupling. By combining the MD, Monte Carlo, and spin-dynamics methods³², the MD simulation is generalized to magnetic materials. These studies are vital for magnetism, spintronics, and materials science, aiding the design of magnetic materials and devices. A unified molecular and spin dynamics model³³ enables simulations without phenomenological spin damping, enhancing the understanding of magnetic relaxation and energy transfer between lattice and spins^33,34. Studies also examine compressed iron’s magnetic properties using Langevin equations³⁴ and first-principles methods integrating spin and molecular dynamics for solids and clusters³⁵. Ma and Dudarev³⁶ reviewed spin-lattice coupling, simulation methods, and DFT-based approaches for various materials.

MNPs, including FeCu nanoparticles, are used in recovering valuable materials from waste streams and separating biological components^37,38. FeCu nanoparticles excel in electrochemical applications, improving battery and fuel cell performance by enhancing conductivity and stability^38,39. Their magnetic behavior depends on structural phase, composition, and grain size. These alloys have soft magnetic characteristics, ideal for data storage, biomedical devices, and catalysis. Understanding how size, surface effects, exchange coupling, and structure influence magnetic behavior is key to optimizing their applications. Advances in synthesis and characterization will continue to refine magnetic properties.

The goal is to synthesize and study the alloying process, thermodynamic stability, chemical composition, and structural and magnetic properties of FeCu-based magnetic nanoalloys. FeCu alloys are produced via redox reactions and characterized to examine nanoparticle structure and magnetism. Molecular dynamics simulations complement experiments by exploring atomic-level phenomena. These simulations heat nanoclusters with varying Cu/Fe ratios to 2000 K, then cool them stepwise to 300 K, while also assessing the effects of an external magnetic field during cooling. Uniformly small nanoparticles are essential. Comparing experimental magnetization curves with simulations shows how size and structure (core-shell vs. Janus) influence magnetic behavior, highlighting room-temperature superparamagnetism in these durable nanoparticles.

Simulation methodology

Molecular dynamics simulations were carried out to investigate the structural and magnetic properties of FeCu bimetallic nanoparticles. The Embedded Atom Method (EAM) potential by Bonny et al.⁴⁰ modeled inter- and intra-atomic interactions. Besides EAM—the most trusted potential for metallic systems—other commonly used force fields include ReaxFF, INTERFACE Force Field (IFF), AMOEBA, DREIDING, and CHARMM^41,42.

MD simulations were performed in the canonical ensemble (NVT) using LAMMPS (stable version, March 3, 2020)⁴³, while spin-lattice simulations used the SPIN package per Tranchida et al.⁴⁴. The canonical ensemble computed total energies, magnetizations, magnetization energies, and optimized structures. Atomic visualization and trajectory analysis employed OVITO (Open Visualization Tool, version 2.9.0⁴⁵), and VMD⁴⁶. First, energy and spin minimization used the conjugate gradient algorithm. Fe and Cu atoms equilibrated at 2000 K—well above their melting points—for 20 ns to reach equilibrium. Subsequently, the FeCu nanoparticle system was cooled gradually from 2000 K to 300 K at a rate of 0.34 K/ps. This low to moderate cooling rate²⁰ was chosen to promote the distinct immiscibility between Fe and Cu, allowing the development of their respective crystalline structures. Minimization calculations applied both the conjugate gradient and FIRE algorithms. Temperature control combined a Langevin thermostat with the Velocity-Verlet algorithm. All simulations used a 1 fs time step, no boundary conditions, and a 400 × 400 × 400 ų supercell.

We explored various FeCu nanocluster sizes and concentrations. Initial spherical core-shell nanoclusters with 5,601 Fe atoms (~ 5 nm diameter) and varying Cu amounts were constructed (see Fig. 1; Table 1). Data for Janus FeCu nanoparticle construction appear in Fig. 2; Table 1.

Also, we prepared MNPs that experienced an external magnetic field (of 1000 Tesla) during the gradual cooling process from 2000 K to 300 K under the simulation procedures explained above. The results were analyzed for the possible improvement of the extent of magnetic properties at 300 K.

Fig. 1

The initial structures of core-shell FeCu nanoparticle alloys.

Table 1 Number of Fe and Cu atoms and radius (Å) for the simulation of core-shell and Janus FeCu nanoparticles.

Fig. 2

The initial structures of Janus FeCu nanoparticles.

Experimental procedure

Chemicals: FeSO₄⋅7H₂O (99.5%, Merck), CuSO₄⋅5H₂O (99.0%, Merck), de-ionized water, Argon gas (local agents), NaOH (99.0%, Merck), NaBH_4, (96.0%, Merck) acetone (99.8%, Merck).

Instruments: Bruker AXS D8 Avance X-Ray Diffraction (XRD), MIRA3 TESCAN-XMU Scanning electron microscope (SEM), FEI TECNAI F20 High-Resolution Transmission Electron Microscopy (HRTEM), Energy Dispersive Analysis of X-ray (EDAX), Kavir Vibrating Sample Magnetometer (VSM).

The stoichiometric FeCu nano-alloy was synthesized following the procedure by Morales-Luckie et al.³⁰. A 5 mM aqueous solution of FeSO₄·7H₂O and CuSO₄·5H₂O was prepared using deionized water. Both 500 ml metal salt solutions were mixed, degassed, and kept under an argon atmosphere. After stirring for 20 min, the pH was adjusted to 7.0 with 1 M NaOH. Then, 100 ml of a 10 mM NaBH₄ solution was added dropwise to the metal salt mixture over 60 min at room temperature. The fine dark precipitate was filtered, washed three times with deionized water, and dried with acetone.

For the FeCu nanoparticle sample, room temperature powder XRD patterns were obtained using a Siemen D-5000 diffractometer with Cu Kα radiation at 1.54 Å. FE-SEM analysis, X-ray energy dispersive spectroscopy, and elemental mapping were performed using the MIRA3 TESCAN-XMU model. The HRTEM studies were conducted at an accelerating voltage of 200 kV. For HRTEM, a small amount of powder was subjected to ultrasonic waves in absolute ethanol for homogeneous dispersion. One drop of this FeCu/ethanol-suspended solution was applied to the copper grid and allowed to dry before imaging. Magnetic properties were analyzed with a VSM. The sample was examined as a solid powder without additional preparation.

Results and discussion

This study examines FeCu nanoparticles via MD simulations, starting with core-shell and Janus morphologies. Both structures were optimized with and without a magnetic field applied. The simulations explored how varying core/shell size ratios influence the nanoparticles’ structural and magnetic properties. The next section presents comprehensive experimental studies on synthesized FeCu nanoparticles, focusing on their structure and magnetization.

Simulation results

Structural properties of nanoparticles simulated at B_ext=0

Figure 3 shows simulated core-shell FeCu nanoparticles heated above their melting point (2000 K) and cooled to 300 K without a magnetic field. The nanoparticles retain their core-shell structure, with Cu atoms forming the shell due to their lower surface energy.

The atom-atom radial distribution function (RDF, g(r)) characterizes the morphology of bimetallic nanoparticles, revealing their structural and coordination properties. Figure 4 presents the calculated g(r) for optimized core-shell clusters. Pronounced short-range peaks indicate strong local coordination, while longer distances show weaker interactions. In the CS(25,30) cluster, Cu⋯Cu correlations are weaker than Fe⋯Fe, whereas other morphologies show the opposite trend, influenced by core-shell size ratios (Figs. 2 and 3). In CS(25,30), copper forms a thin shell around the iron core, similar to phenomena reported for other bimetallic alloys like cesium-sodium nanoclusters⁴⁷. A similar morphological variation has been discussed as arising from van der Waals interactions and modeled using double-wall carbon nanotubes⁴⁸.

Fig. 3

Structures of core-shell FeCu nanoparticles equilibriated at 300 K simulated in the absence of an external magnetic field.

Fig. 4

RDFs for FeCu atoms of different-sized core-shell nanoparticles (Fig. 1) simulated at 300 K without an external magnetic field.

A comparison of RDFs (Figure S1, Supporting Information) shows major interatomic correlations from Fe⋯Fe and Cu⋯Cu interactions, with minor Fe⋯Cu correlations. This reflects the thermodynamic stability of uniform Fe and Cu phases within alloy cluster patches and limited Fe-Cu interaction at patch interfaces. The higher Cu atom count at r = 50 leads to less dynamic behavior and a more ordered Cu crystal structure. Fe atoms in the core are similarly organized, minimally affecting the Cu shell, which remains stable despite excess Cu. The first minimum in Figure S1a indicates a solid-like Fe⋯Fe structure, contrasting with the liquid-like Cu⋯Cu structure in Figure S1c. These RDF-derived features guide magnetic nanoparticle (MNP) synthesis for targeted applications. As discussed in the experimental section, factors like thermodynamics, surface energy, and redox rates determine which metal forms the shell.

Crystalline phases of FeCu nanoalloys are identified using common neighbor analysis (CNA) via the OVITO algorithm⁴⁵ (Table 2). In core-shell and Janus nanoparticles, crystalline proportions (excluding icosahedral coordination, ICO) increase with the Fe/Cu ratio. Recognizable crystalline structures remain minor, with all phases sensitive to nanoparticle size.

Controlling thermodynamic and kinetic factors during synthesis is key to achieving desired bimetallic morphologies. Core-shell structures form when one metal exhibits stronger self-affinity and lower surface energy, leading to encapsulation, whereas Janus morphologies arise from metal repulsion or unmet thermodynamic equilibrium. Radial RDFs (Figure S2, Supporting Materials) show Janus nanoparticles, like core-shell systems, with strong Fe⋯Fe and Cu⋯Cu correlations but weak Fe⋯Cu correlations. Increasing the Cu/Fe ratio strengthens Cu⋯Cu correlations while Fe⋯Fe retains its solid-like character and Cu⋯Cu remains liquid-like.

Applying a magnetic field during MNP synthesis significantly affects Fe₃O₄ crystallinity and magnetic properties. Such studies highlight their potential in hyperthermia therapies, leveraging heat generated under an alternating magnetic field^49,50. While primarily used in cancer treatment, this approach can be adapted for controlled warming in hypothermia therapy. Heat output is precisely regulated by adjusting field parameters and nanoparticle properties, enabling safe, localized temperature elevation. External fields during synthesis further enhance magnetization, and combined with functionalization, enable biocompatible, minimally invasive warming^49,50,51.

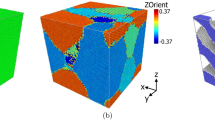
Figure 5 presents the influence of the external field (1000 Tesla) on the simulated core-shell FeCu nanoparticles at 300 K (cooled from 2000 K). A visual comparison of Figs. 3 with 5 unravels the increased core iron atom ordering under the field. Furthermore, to quantitatively assess the effect of the external magnetic field on the cluster size within the Fe core, we performed a cluster analysis on the core region of the core-shell NPs using OVITO software⁴⁵. The results indicate that as the core size increases, the influence of the external magnetic field on iron clustering becomes more significant. As shown in Table 3, for larger NPs—such as FeCu-CS(30,45) and FeCu-CS(35,50)—the number of iron clusters decreases under the applied magnetic field, suggesting that the iron clusters grow in size significantly when exposed to an external magnetic field.

Similar behavior appears in imidazolium-based ionic liquids with (FeCl₄)⁻ anions⁵². Magnetic properties of [C₄mim][FeCl₄] were confirmed as paramagnetic, with a 5.8 µB per Fe atom magnetic moment via SQUID magnetometry⁵³.

Nanoparticle magnetization stems from electron spin alignment, typically short-range at the nanoscale due to strong local exchange interactions. In well-ordered systems, alignment extends longer-range, producing collective magnetization. This alignment—governed by crystalline structure, particle size, and synthesis conditions—is enhanced by external fields. Structural improvements in MNPs are evidenced by increased RDF peak heights at both short and long ranges (Figure S3).

Table 2 Common neighbor analysis (CNA) for FeCu nanoparticles, simulated in the absence of an external magnetic field at 300 K.

Table 3 The influence of an external field applied during cooling process on core-shell FeCu nanoparticles of varying sizes was quantitively analyzed by OVIT software⁴⁵.

Simulation of magnetic properties of nanoparticles

Spin-lattice dynamics simulations of core-shell MNPs prepared without an external magnetic field show notable magnetization and magnetic energy variations. The magnetization spectrum across magnetic fields (−1000 to 1000 Tesla) was calculated for all (core-shell and Janus) simulated NPs at 300 K. Figure 6 displays a sigmoid-shaped spectrum with a sharp zero-field transition. The plateaus indicate the attainable saturation magnetization and also allow the evaluation of the magnetization’s size dependence quantitatively. Following the spectra, Fig. 7 shows that as the Fe/Cu ratio increases, magnetization rises nonlinearly at high- (saturation and) mid-range fields. Around zero external fields, FeCu NPs exhibit convergence behavior, producing a unified crossing point near  -3 T. Collecting more data near zero shifts this point closer to zero, as shown in Fig. 8 for CS(25,30), highlighting the simulation’s accuracy. Notably, this confirms simulation is capable of identifying the true superparamagnetic behavior, and superparamagnetic is shown by all NP independent of their size.

Therefore, superparamagnetic NPs exhibit no residual magnetism after field removal, preventing attraction to nearby materials and reducing aggregation. This property is vital for drug delivery and enhanced MRI imaging. Furthermore, superparamagnetic NPs offer better magnetic control due to their strong yet reversible response to external fields.

Figure 9 shows Janus FeCu nanoparticle structures equilibrated at 300 K. The final Janus (25,25) NP structure, achieved via the same simulation procedure, suggests FeCu systems may evolve into core-shell structures over longer simulations. As depicted in Figs. 6 and 8, Janus structures generally exhibit lower magnetization than core-shell counterparts, depending on nanoparticle size and Fe/Cu ratio. Although their spectra appear indistinguishable, Janus NPs’ lower magnetization stems from their premature geometry, differing from the more developed core-shell configurations.

Fig. 5

Core-shell FeCu nanoparticles equilibrated at 300 K and in the presence of an external magnetic field with a magnitude of 1000 Tesla.

Fig. 6

Magnetization spectrum of core-shell and Janus FeCu nanoparticles as a function of the external magnetic field at 300 K. Lines and broken lines facilitate trend analysis.

Fig. 7

Magnetization of core-shell FeCu nanoparticles as a function of Fe/Cu atoms ratio in different external magnetic fields. Lines facilitate trend analysis.

Fig. 8

The magnified magnetization spectrum (Fig. 6) provides detailed insights into the magnetic behavior near zero external fields. The blue arrow indicates the external field (approximately  -3 Tesla) where zero magnetization is observed for all NPs studied. Similarly, the red arrow highlights the zero magnetization point (achieved at -1 Tesla) in the CS(25,30) NP. For this NP specifically, additional simulated data points closer to zero external fields were incorporated to refine the spectrum, providing a basis for identifying true superparamagnetic NPs through spin-lattice simulation. Lines and broken lines facilitate trend analysis.

Fig. 9

FeCu nanoparticles simulated from Janus’s initial structure, equilibriated at 300 K in the absence of an external magnetic field.

Similar to FeCu core-shell NPs, Janus NPs exhibit non-linear magnetization increases with the Fe/Cu ratio (Figure S4). Magnetization trends nonlinearly at higher external fields but remains linear at lower ones. Table 4 summarizes magnetization energy variations for Janus NPs with and without an external field. Magnetic structural similarities are inferred from magnetization energy values: CS (25, 50) ~ J (25, 45) and CS (25, 40) ~ J (25, 35). At equilibrium, magnetization primarily depends on size, regardless of initial structure.

Analyzing magnetization vector components under external fields reveals the magnetization behavior of NPs. These components represent projections along the x-, y-, and z-axes, influenced by NP shape, size, anisotropy, and field strength. Table S1(A) and S1(B) compare simulated magnetization vectors of core-shell and Janus FeCu NPs at 300 K, under zero external field and fields up to 1000 Tesla along the z-axis. Higher Fe/Cu ratios correspond to stronger magnetic components, while lower ratios significantly reduce magnetization, aligning it along the z-axis. Notably, the results suggest that NPs exhibit magnetization isotropy in the absence of external fields but develop anisotropic magnetization under moderate to strong fields, independent of morphology or Fe/Cu ratio.

Table 4 Total magnetization and magnetic energy of FeCu core-shell and Janus nanoparticles at 300 K simulated in the absence and presence of an external magnetic field.

Effect of the external magnetic field during the cooling process

To investigate the structural and magnetic behavior of FeCu core-shell NPs prepared under an external magnetic field, we analyzed a representative CS(30,45) NP with initial core-shell configuration simulations under two conditions: (1) equilibration at 2000 K without an external field and (2) equilibration at 2000 K with a 1000 Tesla external field. Both systems were then cooled from 2000 K to 300 K, as detailed in the simulation methodology. Figure 10 compares the two scenarios, showing that the structure cooled under the external field (Fig. 10b) exhibits enhanced atomic ordering, with iron atoms preferentially aggregating in the core.

The corresponding correlation functions (Fig. 11) reveal significant structural differences, confirming the external field’s impact. Notably, these differences extend to long distances, reflecting effective long-range correlations governed by both exchange and dipolar interactions. Exchange interactions, typically short-ranged, include (1) direct exchange between neighboring atoms and (2) super-exchange mediated by non-magnetic atoms, allowing longer-range effects. This spin-lattice simulation effectively captures intrinsic spin-spin correlations, accurately representing the magnetic properties of FeCu NPs.

Dipolar interactions, arising from magnetic dipole moments, can align or anti-align neighboring spins depending on orientation. While weaker than exchange interactions, they extend over longer ranges and significantly affect systems with moderately separated magnetic moments. Both interaction types are encompassed by the simulation algorithm applied to these FeCu nanoalloys.

Fig. 10

Structure of FeCu-CS(30,45), (a) cooled from 2000 K to 300 K in the absence of external magnetic field and then equilibriated at 300 K in the presence of 1000 Tesla external magnetic field, (b) cooled gradually from 2000 K to 300 K and equilibriated (at 300 K) while the 1000 Tesla external magnetic field is on.

Fig. 11

Radial distribution functions of Fe atoms for FeCu-CS (30,45), illustrate how the external field affects the cooling process, (a) condition 1, (b) condition 2 (see text). The difference in behavior is extended to long ranges up to 25 Å (not shown for clarity).

Heat of mixing

We have calculated the heat of mixing for FeCu nanoalloys using the simulated potential energy data:

$$\Delta H_{{mix}} = E_{{FeCu}}^{{\left( {per\;atom} \right)}} - \left( {x_{{Fe}} E_{{Fe}}^{{\left( {per\;atom} \right)}} + x_{{Cu}} E_{{Cu}}^{{\left( {per\;atom} \right)}} } \right)$$

(1)

Here, $\:{E}_{FeCu}^{\left(per\:atom\right)}$​ represents the potential energy per atom of the FeCu nanoalloy, while $\:{E}_{Fe}^{\left(per\:atom\right)}\:$​ and $\:{E}_{Cu}^{\left(per\:atom\right)}\:$​ denote the potential energies per atom of pure Fe and Cu nanoparticles of the same size and structure, respectively. The variable x refers to the atomic fraction of the components. According to the calculated heat of mixing for the selected MNPs (Table 5), an increase in shell size leads to a reduced tendency for mixing, whereas an increase in core size enhances it. In the case of Janus FeCu nanoparticles, the mixing tendency decreases as the size of the Cu domain increases. Furthermore, based on the data presented in Tables 3 and 5, it can be concluded that increasing the amount of the magnetic element Fe—and consequently the overall magnetization of the nanoparticles—correlates with a reduction in the number of clusters (Table 3). This supports the idea that an excess of free electrons enhances inter-cluster interactions, thereby contributing to the formation of a lower-entropy MNP system.

Table 5 Simulated heats of mixing for selected MNPs.

Experimental results

In synthesizing these nanoparticle materials, the optimal concentration of the reducing agent is crucial for achieving complete reduction while preventing agglomeration and uncontrolled growth. Maintaining a stable inert gas atmosphere is essential to avoid oxidation of the metal nanoparticles. Additionally, precise control of pH and minimizing temperature fluctuations are critical for ensuring product homogeneity.

Several experimental techniques, such as X-ray diffraction (XRD), field-emission scanning electron microscopy (FE-SEM), energy-dispersive X-ray analysis (EDAX), elemental mapping, and high-resolution transmission electron microscopy (HRTEM), can be employed to characterize the crystal structure, morphology, and electronic properties of the as-synthesized FeCu nanoparticles. The magnetic properties of the material can be assessed using vibrating sample magnetometry (VSM).

XRD analysis

The crystal structure of the synthesized FeCu alloy was analyzed using XRD to monitor the reduction process and detect phase separation. Bragg reflections (Figure S5) corresponding to the [(104), (110), (113), (024), (116), (214), and (300)] planes were observed at 2θ values of 35.6°, 38.7°, 43.4°, 49.1°, 53.5°, 62.8°, and 66.0°, respectively, which align well with reported results for this alloy⁵⁴. Furthermore, a comparison of the crystal planes of Fe(0) (JCPDS card No. 01–087-0721)³⁷ and Cu(0) (JCPDS card No. 003–1018)⁵⁵ with those of the synthesized FeCu nanoalloy revealed a shift of approximately 0.2°, confirming the successful alloying of iron and copper.

Lattice expansion or contraction occurs when Cu is added to Fe, shifting XRD peaks (Figure S5) to higher or lower angles, directly influenced by atomic metallic radii. The larger metallic radius (Cu) expands the lattice, shifting peaks to lower angles, while the smaller radius (Fe) contracts it, shifting peaks higher. Since Cu’s radius exceeds Fe’s, its peaks appear at lower angles.

A second set of peaks marked with an asterisk (*) in Figure S5a confirms alloy formation. FeCu’s Bragg reflections differ from pure Fe or Cu but fall between them, supporting FeCu nanostructure formation⁵⁶. Peak broadening indicates small nanostructure size, while strong, sharp peaks reflect high crystallinity.

The nanoparticle size is approximately calculated using the Scherrer equation (Eq. 2) based on the corresponding XRD pattern.

$$\:d=\frac{9\lambda\:}{\beta\:\text{cos}\theta\:}$$

(2)

where d is the average diameter of the structure and λ (= 1.54 Å) is the wavelength of the X-ray source in the presence of copper metal. The width of the peak, β (in radian), is estimated at half maximum. For Bragg angle $\:\theta\:=35.66$^o and β = 0.778, the average diameter of the synthesized nanostructures (Eq. 2) can be estimated to be 10.74 nm. Figures S5b and S5c present the XRD analysis generated using VESTA (Visualization for Electronic and Structural Analysis, version 3.4.7⁵⁶) software for Cu(0) and Fe(0), derived from the experimental XRD patterns. These serve as standard calibration references for Cu(0) and Fe(0).

Field emission scanning electron microscope (FE-SEM) analysis

To examine the morphology and composition of the synthesized FeCu nanoalloy, FE-SEM, EDAX, and elemental mapping were employed. FE-SEM revealed highly homogeneous spherical particles averaging ~ 11 nm in diameter (Figure S6), closely aligning with the 10.74 nm size from XRD analysis (Eq. (2)). EDAX was conducted by directing an electron beam onto the sample, collecting emitted X-rays characteristic of the elements present, thus providing bulk material insights due to deep beam penetration.

It is worth noting that TEM typically offers superior spatial resolution and enhanced contrast, making it a preferred technique for evaluating nanoparticle size and morphology. However, in this particular case, performing statistical analyses of the size distribution is impractical due to significant nanoparticle aggregation. This aggregation is primarily attributed to the compound’s intrinsic magnetic properties. The agglomeration may be further influenced by electron interactions among interconnected particles. Despite these challenges, the mean particle size, as estimated using the TEM scale bar, is approximately 20 nm.

The nanoparticle size distribution obtained from FE-SEM is centered around 11 nm (Figure S6c), placing it within the lower range reported in the literature and suggesting strong superparamagnetic potential. As shown in Table 6, the magnetic properties of the nanoparticles are influenced not only by their size and synthesis method but also by the type of metal alloyed with Fe. Among the studied magnetic nano-alloys, the co-metal Co enhances magnetization more significantly than Ag, with Cu and Ni following.

Although the simulated magnetization spectrum exhibits a trend similar to that observed in experimental studies, several factors contribute to the substantially lower magnetization values seen in MD simulations compared to experiments. First, MD simulations typically operate on nanosecond timescales, whereas magnetic phenomena often evolve over much longer durations, resulting in an incomplete depiction of nanoparticle magnetic behavior. Additionally, the simulations were performed on smaller system sizes (~ 5 nm) relative to the experimentally observed particles (~ 11 nm) (see Fig. 1 and Figure S6c). Another limitation arises from the use of approximated interatomic potentials in MD simulations, which may not fully capture the electronic structure and magnetic interactions of the material. Furthermore, in experimentally prepared samples, nanoparticles interact through magnetic dipolar interactions, which significantly influence the measured magnetization. These interactions are absent in the current simulations, as only a single, isolated nanoparticle is modeled. Despite these limitations, the spin-lattice method remains capable of capturing magnetization effects due to dipolar interactions—particularly if, during simulation optimization, the aggregated Fe core atoms separate and form islands embedded within the Cu shell.

EDAX (via FE-SEM, Figure S7) confirms Fe and Cu presence and detects 32% oxygen (Table 7). Elemental mapping shows a uniform Fe, Cu, and O distribution (Figure S8).

Table 6 A comparison with the properties of synthesized (bimetallic) magnetic nanoparticles in the literature. Although the magnetization of nanoparticles out of precious metals (Co and Ag) is high, using cheaper Cu (this work) produces acceptable magnetization while superparamagnetic.

Table 7 Mass ratio of the elements in the FeCu synthesized Nanoalloy.

High-resolution transmission electron microscope analysis

The morphology of FeCu nanostructures was thoroughly investigated using high-resolution transmission electron microscopy (HR-TEM). As shown in Fig. 12a–d, the nanostructures predominantly exhibit a core-shell configuration, albeit with a range of morphological variations. TEM analysis confirms the coexistence of both core-shell and Janus-type structures. The core-shell architecture is visualized in the TEM images, where the iron core and copper shell can be distinguished by contrast differences, as evident in Fig. 12e–g. Particularly noteworthy is the observation of off-centered core-shell structures, which offer valuable insights into interatomic interactions influenced by the relative sizes of the core and shell components. To further validate the core-shell structure, UV-Vis spectroscopy was employed^60,61. Copper nanoparticles typically exhibit a characteristic surface plasmon resonance (SPR) absorption peak near 585 nm in the visible region⁶². The intensity and position of this SPR band are affected by intrinsic properties such as particle size, shape, solvent environment, and the nature of reducing agents used during synthesis. Additionally, copper oxide nanoparticles display a distinct absorption peak around 298 nm⁶³, while iron nanoparticles present a primary absorption peak near 290 nm and a secondary peak around 350 nm, attributed to electronic transitions and surface plasmon oscillations of iron residues⁶⁴. In the present study, an absorption peak at approximately 312 nm was observed (Fig. 12h), suggesting the formation of FeCu core-shell structures. Due to the low intensity of the specific SPR peak of copper at 585 nm, a previously synthesized FeCu alloy sample—where a significant portion of copper had oxidized to copper oxide—was also analyzed. This allowed for clearer spectroscopic interpretation. Notably, a red shift in the copper oxide absorption peak from 298 nm to 312 nm was detected, providing further evidence of the core-shell configuration in the original FeCu nanostructures.

It is worth noting that TEM typically offers superior spatial resolution and enhanced contrast, making it a preferred technique for evaluating nanoparticle size and morphology. However, in this particular case, performing statistical analyses of the size distribution is impractical due to significant nanoparticle aggregation. This aggregation is primarily attributed to the compound’s intrinsic magnetic properties and may be further influenced by electron interactions among interconnected particles. Despite these challenges, the mean particle size, as estimated using the TEM scale bar, is approximately 20 nm.

Additionally, electron diffraction patterns obtained from arbitrary surfaces reveal bright spots, confirming the crystalline structure of the sample (Fig. 12i–j). The chemical characterization of the sample via EDAX analysis verifies the presence of iron, copper, oxygen, and carbon, suggesting partial oxidation of the sample under the reaction media (Figure S9). Based on the elemental composition, an empirical formula such as FeCuO₃.₆ can be estimated.

Fig. 12

(a–g) HR-TEM analysis, (e–g) visualization of morphological details of core-shell contrast, (h) UV-Vis absorption spectrum of FeCu nanoalloy, and (i–j) electron diffraction patterns of arbitrary surfaces of iron-copper nanoalloy.

Mechanism of FeCu nanoalloy formation

The formation of FeCu core-shell nanoalloy is significantly influenced by precursor and reducing agent concentrations, reaction medium pH, and the reducing agent addition rate, collectively affecting precursor reduction, nucleation, and growth. Dropwise NaBH₄ addition to an alkaline copper and iron precursor solution (Fig. 13a) facilitates metal precursor reduction according to their standard electrode potentials. Copper (${E^{\circ}}_{\rm Cu^{2+}/Cu}$ = + 0.34 V) reduces first, forming primary copper nanoparticle nuclei (Fig. 13b) and initiating growth. In contrast, Fe²⁺ reduction with NaBH₄ alone is challenging due to its more negative potential (${E^{\circ}}_{\rm Fe^{2+}/Fe}$ = −0.44 V). However, in an alkaline medium, copper presence, and a favorable Cu–Fe synergistic effect promote faster Fe²⁺ reduction. pH control influences hydrogen production, with NaBH₄ hydrolysis enhancing the reducing hydrogen availability. As Fe atoms form the core, Cu atoms arrange around it to form the shell (Fig. 13c). Notably, both newborn Fe and Cu atoms may oxidize partly while this shelling is self-catalyzed by Cu’s lower surface energy, protecting Fe core atoms of the FeCu nanoparticles from fracture and oxidation after the nanoparticle’s formation⁶⁵. Subsequent crystal growth and diffusion produce FeCu nanostructures with an off-centric core-shell morphology (Fig. 13d). The reduction reaction with NaBH₄ is shown in Eq. 3.

$$4{\text{Fe}}^{{2 + }} + 4{\text{Cu}}^{{2 + }} + 3{\text{BH}}_{4} ^{ - } + 12{\text{H}}_{2} {\text{O}} \to 4{\text{Fe}}^{0} {\text{Cu}}^{0} + 3{\text{B}}\left( {{\text{OH}}} \right)_{4} ^{ - } + 24{\text{H}}^{ + }$$

(3)

Fig. 13

The detailed mechanism of FeCu nanoalloy Formation: (a) gradual addition of NaBH₄ to the alkaline solution containing CuSO₄ and FeSO₄, (b) reduction of Cu(II) precursor, (c) reduction of Fe(II) and the generation of Fe(0) atoms, and (d) core-shell structure formation of FeCu through the crystal growth process, completing the nanoalloy formation.

Magnetic property analysis

VSM analyzed the magnetic property of synthesized FeCu nanoalloy at ambient temperature within an external field of ± 10 kOe. The obtained spectrum (Fig. 14) has a sinusoidal shape, having a saturation magnetization value of 27.50 emu/g, indicating the magnetic moment per unit mass and reflecting the degree of alignment of magnetic domains. Since the saturation magnetization for the single nanoparticle(s) has been simulated under no effective boundary condition, implying no interparticle-induced magnetization contribution, the big difference between the synthesized and the simulated single NP represents the surface effect, particle size, and superparamagnetic extension.

The inset in Fig. 14 (magnifies the spectrum and) shows the existence of an ignorable hysteresis of about 1 Oe in zero external fields, on the reversal of the external field, for the synthesized FeCu NP. The forward magnetization hysteresis loop indicates zero magnetization at zero external fields, revealing the strict superparamagnetic properties of the synthesized FeCu nanoalloy.

Fig. 14

Magnetization property of a sample of FeCu nanoalloy synthesized. The inset magnifies the trend of magnetization near zero external fields, showing that zero magnetization is attainable at zero external fields. The saturation magnetization decreases by 3% after 20 days.

Conclusions

The properties of bimetallic FeCu nanoalloys were investigated through experimental synthesis, characterization, and MD simulations. The spin-lattice algorithm, incorporating spin coupling and magnetic dipole interaction into classical MD, successfully simulates magnetic properties consistent with real-world experiments. For both core-shell and Janus FeCu nanoparticles, no direct correlation was found between morphology and magnetic properties; however, magnetization depends only on the Fe/Cu mass ratio. Correlation function analysis confirms that Cu atoms form a shell around Fe cores, with persisting long-range atom-atom correlations indicating direct and indirect spin-spin coupling, effectively captured by the spin-lattice algorithm. This first-time simulation of the magnetization spectrum accurately identifies saturation magnetization and achieves near-zero magnetization at zero external fields, evidencing FeCu’s superparamagnetic behavior. Multi-technique analysis verified the core-shell morphology of the synthesized FeCu nanoalloy. The average particle size of 11 nm from FE-SEM closely matches the 10.74 nm calculated from XRD data, aligning with the lower bound of reported sizes and supporting the observed superparamagnetism. The Fe magnetic core, shelled by the noble Cu metal, is protected from oxidation after the nanoparticle formation while maintaining a high saturation magnetization of 27.50 emu/g. The precise attainment of zero magnetization at zero fields, combined with the novel spin-lattice simulation, compellingly demonstrates the room-temperature superparamagnetic nature of synthesized FeCu under controlled conditions.