Introduction

Debris flows are rapidly moving mixtures of water and debris that pose serious geohazard risks, particularly in mountainous regions1,2,3. Triggered by landslides, earthquakes, or intense runoff, they involve complex interactions between geological, climatic, and hydrological factors4,5. Their high velocity and capacity to transport large volumes of material down steep slopes cause severe damage to infrastructure and landscapes6,7. Understanding the mechanisms governing viscous debris flows is essential for accurate prediction and risk mitigation. Unlike dilute flows, viscous debris flows exhibit non-Newtonian behavior due to their high solid content, making them difficult to model. With solid volume fractions ranging from 0.5 to 0.8, these flows behave as viscoplastic fluids, requiring specialized modeling approaches8,9,10. However, due to the uncertainties in debris flow dynamics, numerical simulations based on physical models have become vital for capturing their behavior and improving hazard assessment11,12,13,14,15.

In geotechnical engineering, slope deformation and failure have traditionally been analysed using continuum-based methods, such as the finite element method (FEM). While effective for small-scale problems, FEM struggles with large deformations like debris flows due to mesh distortion, often leading to numerical instabilities16. To overcome this, depth-averaged shallow flow models have been used, but they oversimplify the problem into two dimensions, failing to capture the full nonlinear behavior throughout the flow depth8,17,18,19. Discrete methods, including the Material Point Method (MPM) and Discrete Element Method (DEM), have shown promise in simulating landslides and soil flows20. However, DEM’s complexity in representing individual soil grains makes it less practical for large-scale debris flow modeling21,22,23.

For more realistic three-dimensional simulations, mesh-free methods such as Smoothed Particle Hydrodynamics (SPH) offer a powerful alternative24,25. SPH discretizes the continuum into particles, avoiding the mesh distortion issues of FEM and providing a robust solution for large deformation problems. Its ability to simulate scale-dependent, highly dynamic flows makes it increasingly popular for debris flow modeling. Unlike DEM, SPH uses conservation laws of mass, momentum, and energy, making it more suitable for capturing landslide dynamics. Researchers have successfully applied SPH to simulate flow-like landslides, lahars, and avalanches, making it a reliable tool for modeling real-world debris flow behavior26,27,28. Before applying numerical models to field-scale events, physical model tests are essential for calibration and validation. Controlled flume experiments provide accurate initial and boundary conditions, helping refine the rheological parameters for debris flow simulations29. Kong et al.30 reported that the rheological properties of interstitial fluid (i.e., Newtonian and non-Newtonian fluids) strongly influence the behavior of particle-laden geophysical flows, so it is crucial to consider its value during simulation. Field-scale flume or geotechnical centrifuge models offer the most relevant insights for real-world applications as they replicate geomorphological processes under controlled conditions. Validating numerical models through experimental setups, followed by field-based verification, ensures better accuracy and reliability. There is a pressing need to study geophysical flows in the hazard-prone Western Ghats of India, as the region has experienced frequent debris flow events over the past decade yet remains poorly understood due to limited research.

This paper presents a simplified depth-averaged debris flow model using the open-source DualSPHysics tool in a controlled setting. The model incorporates Herschel-Bulkley (H-B) rheology to account for internal friction. Calibration is performed using experimental data, and the model is initially tested through a lab-scale dam break simulation. Numerical results are then validated against existing experimental data to evaluate accuracy. The smooth particle hydrodynamics formulation and corresponding numerical schemes are detailed to ensure stable and precise solutions. Additionally, a case study of a real debris flow event in Kerala, India, is analyzed and validated with field data and prior studies. A detailed analysis of Pettimudi debris flow was performed considering it as a viscous flow and its applicability in the future was assessed.

Materials and methods

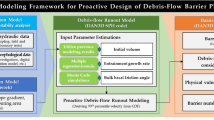
This study investigates the behavior of nonlinear viscoplastic materials, specifically Herschel–Bulkley fluids, which transition between solid-like and fluid-like states depending on the applied stress. These materials are widely used to model natural geophysical flows such as snow avalanches, mudflows, debris flows, and submarine landslides. While real-world debris flow behavior involves complex two-phase interactions—such as pore pressure diffusion, dilatancy, and particle migration—single-phase models like the Herschel–Bulkley equation provide a practical approximation for capturing bulk flow dynamics. We first conducted numerical simulations using the Smoothed Particle Hydrodynamics (SPH) method to establish boundary conditions and refine model parameters. This initial modeling phase helped identify key rheological parameters and constraints necessary for experimental validation. Following this, large-scale flume experiments were carried out to validate the numerical findings by replicating debris flow initiation, propagation, and deposition under controlled conditions. The integration of numerical and experimental approaches allowed for a comprehensive evaluation of debris flow mechanisms (Fig. 1).

Fig. 1
figure 1

Flowchart summarizing the methodology used in the present study.

Full size image

DualSPHysics model

DualSPHysics is an open-source computational tool designed to model fluid dynamics using the Smoothed Particle Hydrodynamics (SPH) method. Released under the GNU General Public License, it is freely available and built upon the original FORTRAN-based SPH formulation developed in SPHysics. While it excels in handling large-scale simulations, DualSPHysics maintains robustness and reliability in various fluid dynamics applications31. The core of DualSPHysics is based on the SPH method, a mesh-free Lagrangian particle technique where particles represent the state of the fluid. These particles interact with each other and structures, allowing the approximation of governing equations such as mass, momentum, and energy conservation. The mesh-free nature of SPH is particularly advantageous in simulations involving large deformations, as it avoids the mesh distortions commonly encountered in grid-based methods32. The particles’ interactions are governed by a smoothing kernel function that defines their influence on one another, enabling accurate modeling of complex flows and interactions between fluids and structures33,34.

DualSPHysics allows for detailed simulations of both fluid and solid phases, where particles can behave as a continuum when the system reaches a steady state. This makes it highly applicable in cases where particle concentration distributions, such as sediment transport or debris flows, need to be predicted. The Lagrangian approach used by DualSPHysics tracks the motion of individual particles, offering a computationally effective way to capture dynamic processes that would otherwise be difficult with Eulerian grid-based methods. While the Lagrangian method may require more computation time due to the need to track the behavior of each particle, it avoids the challenges associated with mesh distortions and enables simulations of volatile processes like landslides, debris flows, and free-surface flows over complex terrains35. Recent advancements have allowed DualSPHysics to deliver reliable results in various applications, from hydraulic engineering and wave dynamics to environmental modeling. Its ability to simulate large deformations and versatility in GPU and CPU computing make DualSPHysics a powerful tool for researchers and engineers aiming to model fluid-structure interactions with high accuracy and computational efficiency.

Simulation configuration

In the present work, we created a simulation setup in the FreeCAD module of DualSPHysics. Figure 2 schematically shows the simulation setup used in this study based on our experimental flume setup (Sect. 3). We kept fluid volume per unit weight at 0.03 m2 and density was varied between 1400 kg/m3 and 1800 kg/m3 to model a dense fluid in lines with slurries. We recreated this setup numerically and set \(\:{L}_{h}\)= 300 mm θ = 230 and 26 to keep flume channel in two parts. Figure 2a shows the profile view of the entire setup which consists of debris mass, a flume channel, and a deposition surface to catch runout deposits. The width of the flume channel was kept at 0.6 m whereas vertical and horizontal heights were kept at 3 m each (Fig. 2b). The debris mass was set at 0.6 m*0.3 m*0.2 m (Fig. 2c). Since the simulations are being performed for viscous flows hence the initial parameters for rheological and boundary conditions were taken from previous research11,36,37. The Herschel-Bulkley rheological model was applied for numerical simulation where the specific yield stress and kinematic viscosity were taken as per the experimental results in the present study and previous research38,39,40,41. The Courant–Friedrichs–Levy (CFL) coefficient was kept at 0.2 to ensure the capturing of high-energy fluid behavior42. The remaining input parameters are mentioned in Table 1.

Fig. 2
figure 2

Numerical model used in the present study for the simulation (a) schematic diagram, (b) plan view, (c) profile view.

Full size image
Table 1 Input parameters for dam break simulation in numerical modeling.
Full size table

Experimental validation

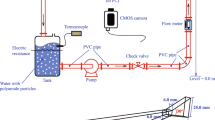
The experimental setup featured four straight, rectangular channels, each measuring 1 m in length and 0.6 m in width, which connected to a lower-angle outflow plain. The first channel, where debris flow initiation occurred, was 1 m tall to capture the rapid flow dynamics, while the remaining channels were designed with a height of 0.6 m. The channel slopes ranged from 23° to 26° (Fig. 3a) to replicate gullies in the Western Ghats region of Peninsular India43,44. An upstream mixing tank equipped with 2-horsepower motors (Fig. 3a) enabled the rapid release of a well-mixed debris slurry via a manually controlled gate. Sediment and water were mixed for about 20 s in a hopper before the gate was opened, allowing simultaneous flow. Several cameras were employed for monitoring, including a Nikon PowerShot A640 for deposit analysis, a GoPro mini 11 (Fig. 3a), and a smartphone-based scanner for capturing deposit morphology. Additionally, an ultrasonic sensor with a 100-millisecond response time was used to monitor fluctuations in flow height (Fig. 3b). The Hero GoPro mini 11 camera (Fig. 3c) was used to analyze debris flow initiation, with the overall setup shown in Fig. 3d and e.

A nonwoven polyester/PP geotextile sheet was utilized to capture the runout deposits. Flow depth near the channel apex was validated by combining video footage with manual tape measurements. A high-precision point cloud was generated using a handheld smartphone-based45 scanner and processed using a post-processing imaging tool46. This data was transformed into a 2 mm resolution Digital Elevation Model (DEM) via Kriging interpolation, using the nine closest neighboring pixels. The DEM provided measurements of geometrical features of the deposit like length, width, and thickness, which were then verified manually with a tape measure. The maximum debris flow length, width, and runout distance were calculated, as well as lobe thickness, levee height, and deposit area. The gate was operated using a latch mechanism connected to a rotating steel shaft and opened by a slow-turning electric motor. Upon the latch release, the gate quickly lifted to an angle of 35° due to the pressure from the debris, stabilizing at 25° through coordinated electric motor operation. This method ensured accurate and thorough data collection throughout the experiment. Experimental flume details used in the current study were mentioned in our previous work47. The material composition used is given in Appendix A in the supplementary file.

Fig. 3
figure 3

Description of experimental flume setup used for analysis (a) Schematic sketch of setup, (b) flow height measurement sensor, (c) GoPro camera, (d) planer view of flume setup, (e) actual flume setup used in the study.

Full size image

Rheological parameterization

Previous studies48,49,50 explored the shear thinning and thickening behavior of debris-flow mixtures with varying soil and water compositions. In response to these findings, the HBP model was developed as a more generalized approach, offering a better representation of the rheological characteristics of debris flows. In the study of38,39, it was expressed as in Eqs. (1–4).

$$\:\tau\:=\:\:{\tau\:}_{y}+\mu\:\dot{\gamma\:}n$$
(1)
$$\:{\mu\:}_{eff}={\:K\left(\dot{\gamma\:}\right)}^{n-1}+\:\frac{{\tau\:}_{y}}{2\dot{\gamma\:}}$$
(2)
$$\:K={2}^{n-1}\cdot\:\mu\:$$
(3)

Where \(\:\tau\:\) is shear stress, \(\:{\tau\:}_{y}\) is yield stress, \(\:{\mu\:}_{eff}\) is effective viscosity and \(\:\dot{\gamma\:}\) is shear rate. In geotechnical engineering, the yield stress is often characterized by the Mohr-Coulomb yield criterion, defined by the material’s cohesion (c) and friction angle (φ)36,51, providing a foundational framework for understanding the material’s failure conditions as in Eq. (4)

$$\:{\tau\:}_{y}=c+\sigma\:\text{tan}\phi\:$$
(4)

To determine the initial rheological parameters, such as viscosity and yield stress, of a debris mixture containing clay, silt, and fine sand (d < 0.2 mm) (Fig. 4a and b), a small-scale rheometer test with a parallel plate configuration was performed. The debris mixture was combined with water, and the rheological tests followed the method outlined in previous studies38,39,40. The material was agitated in a hopper-type mixer at an rpm greater than 120 (Fig. 4c) to ensure the particles remained suspended in the sample. The bulk density was maintained between 1400 and 1800 kg/m³ to retain a semi-fluid texture, similar to the approach taken in water-soil suspension studies40,41. The standard procedure52,53 for determining the rheological properties of non-Newtonian fluids, such as the debris mixture in this study, was followed. The sample was placed between two parallel plates in the rheometer (Fig. 4d) to conduct the tests. A 2 mm gap, 10 times the maximum particle size, was maintained between the plates to avoid localized shear near the spindle surface and prevent shear weakening due to low shear rates (γ)54. The obtained results after the tests were curve-fitted for the Herschel-Bulkley model. The parameters obtained from these tests are listed in Appendix A and were later applied in a numerical dam-break model using DualSPHysics (Sect. 2.1).

Fig. 4
figure 4

Rheological testing comprising of (a) finer particles (d < 75 microns), (b) fine sands (75 microns < d < 200 microns), (c) homogenization of samples under preparation, (d) parallel plate rheometer used in the study.

Full size image

Result and analysis

The similarity between the numerical and experimental results obtained from the current work demonstrates a high degree of accuracy in modeling debris flow behavior under consistent boundary and rheological conditions. Both simulations were conducted under identical parameters, which allowed for a direct comparison between the SPH numerical model and the corresponding experimental outcomes. Simulations having similar bulk densities were selected to provide a detailed analysis of the similarities observed between the two methods. Figure 5 presents the variation in flow height during the initiation phase for six selected cases with bulk densities ranging from 1400 kg/m³ to 1860 kg/m³. In these cases, it was observed that flows with lower densities reached their peak flow height earlier than those with higher densities. Interestingly, the maximum flow height was exhibited by the less dense flows, both in the numerical and experimental setups. This observation suggests that bulk density has a direct influence on the timing and magnitude of peak flow height, with less dense materials demonstrating quicker, more significant responses. However, the comparison between computed and measured flow heights revealed multiple discontinuities, particularly in peak height and time duration. The computed flows exhibited higher flow heights and earlier peaks compared to the experimental results. This discrepancy could be attributed to the greater homogeneity in the yielding process within the numerical model, whereas the experimental flows were more heterogeneous and involved a slight delay in initiation due to the dam-break mechanism. This limitation highlights challenges in accurately calibrating flow height in SPH simulations.

Figure 6 compares the shape of runout deposits at the flat area (the end of the flow) between the computed and measured results. Selected cases with varying densities (1420 kg/\(\:{m}^{3}\) – 1820 kg/\(\:{m}^{3}\)) were taken into consideration to analyze the accuracy of computed results with lab-scale flume observations. The runout deposits in the numerical simulation aligned closely with the experimental results, particularly in cases with lower densities, where the runout patterns were almost identical. However, some inconsistencies were noted in the higher-density cases, indicating that the DualSPHysics tool struggled to simulate real-time dam break flows accurately at these higher densities. This suggests a limitation of the tool in handling high-density flows under certain conditions, which could be attributed to challenges in capturing the exact dynamics of denser debris flows.

To further investigate the morphology of the deposited material, Fig. 7 shows a side-by-side comparison of the computed and measured results for 13 cases with varying densities. It was observed that, for both the experimental and numerical simulations, the deposition length decreased and the width increased as the bulk density rose. This trend is consistent with our previous findings47, which demonstrated that denser materials tend to spread laterally more than they extend longitudinally. The agreement between the numerical and experimental results across different density conditions provides strong evidence for the accuracy of the SPH model in simulating debris flow deposition, particularly at lower densities.

Fig. 5
figure 5

The variation of flow height with time at the initiation of debris flow (a) numerical analysis, (b) experimental result.

Full size image

In summary, the numerical tool effectively replicated the key dynamics of debris flow behavior observed in the experimental dam break results. The simulation parameters used, as detailed in Table 1, played a crucial role in the calibration of the DualSPHysics simulation tool, ensuring the model’s reliability in various conditions. Although some discrepancies were observed at higher densities, where the numerical model struggled to fully capture the dam break behavior, the overall similarity between the numerical and experimental results is significant. The validated parameters from these controlled experiments were later applied to field-based debris flow simulations in Kerala, India, where the same rheological parameters and boundary conditions were used to model a real debris flow event. This validation demonstrates the robustness of the SPH numerical model for simulating debris flow in both experimental and real-world cases.

Fig. 6
figure 6

Comparison of deposition pattern for debris flow runout at the end of flume for varying density.

Full size image
Fig. 7
figure 7

Comparison of dimensions of runout deposit at the flat surface of the numerical model and flume setup.

Full size image

Case study of pettimudi landslide

On the night of August 6, 2020, a devastating landslide occurred in the Pettimudi village, located in the Munnar region of Idukki district, Kerala, India. Triggered by torrential rains, the landslide struck at 10:45 PM (UTC + 5:30), causing massive destruction and loss of life55. Pettimudi, situated approximately 10 km north of Munnar town, lies amidst tea plantations and densely forested areas56,57. This remote setting, deep within the Western Ghats, is particularly vulnerable to landslides due to its steep terrain and monsoon-prone climate (Fig. 8). The catastrophic event resulted in the sudden movement of a massive volume of loose debris and associated materials down the slope. The debris flow followed a long runout path, destroying everything in its course, including a row of temporary houses of workers known locally as ‘layams’ (Fig. 9). These homes were built for estate workers living near the tea plantations. The force of the debris flow obliterated four of these structures, wiping them out completely. Along with the layams, estate roads that cut across the valley’s toe were also demolished, further isolating the affected area. The debris flow, laden with large volumes of water, descended at high speed and caused immense damage to the infrastructure downstream. Vehicles parked in the vicinity were either buried or severely damaged, while large trees were uprooted from the hillsides. Unfortunately, 66 lives were lost in the disaster, with four individuals still missing56. This tragic event now stands as one of the most devastating landslides in Kerala’s history.

Fig. 8
figure 8

Detailed study area showing (a) location of debris flow event in peninsular India, (c) slope geometry of runout area, (c) satellite imagery of affected area, (d) daily rainfall in Pettimudi at the time of the event. (Source- IMD58).

Full size image

Post-Disaster field investigation

In the aftermath of the Pettimudi landslide, the authors conducted a field investigation between September 15 and 20, 2020, after the completion of rescue operations. The investigation aimed to assess the extent of damage, and determine the sub-surface of the gully using a standard penetration test (SPT) and velocity electrical sounding (VES) type geotechnical test (Fig. 10). Upon arriving at the landslide site, the terrain was steep and unstable, with two topographic hollows prominently visible in the affected area. These hollows, located beneath the barren hillcrest, played a crucial role in initiating the landslide. Reports55,59 showed that the landslide scar measured approximately 1200 m in length, with a width varying between 30 and 120 m, a depth of 3 to 7 m, and a height difference of 125 m. The total area affected by the landslide was estimated at 70,125 square meters, with the dislodged material amounting to an approximate volume of 280,500 cubic meters. The debris had immense kinetic energy as it traveled downhill, further contributing to the destruction in the village below. The investigation revealed that the landslide was largely confined to a steep segment of the landscape within the shola forest, located beneath a barren hillcrest. Sholas are small patches of stunted tropical montane forests found in valleys interspersed with grassland, a characteristic feature of the higher regions of South India. The heavy rains that had fallen during the monsoon season led to significant runoff from the hill’s crest, which eventually triggered the landslide. This runoff was funnelled into topographic hollows covered in loose debris, creating the perfect conditions for a mass movement of soil and rock. The dislodged debris, mixed with stormwater, traveled through the first-order stream channel connected to the hollows. This sudden influx of material led to severe bank erosion, widening the stream and creating a high-energy flow of debris. As the debris moved downhill, it continued to erode the stream banks, increasing its destructive force. The four layams that were situated along the streambank were destroyed as the debris flow surged through the area, leaving nothing in its path. The debris flow consisted of mostly sand-water slurry with almost complete erosion at the upstream of flow (Fig. 9a).

Fig. 9
figure 9

Post debris flow scenarios from Pettimudi (a) upstream erosion of gully validated by exposed bedrock (men for scale), (b) observed entrainment in gully along with scouring of side banks, (c) vegetation (tea gardens) destroyed due to flow, (d) destroyed layams due the flow in zone-2, (e) runout deposition at flat terrain.

Full size image

Preliminary assessment of slope failure mechanism

A preliminary assessment of the failed slope was carried out based on field observations and Google Earth imagery. It was determined that the landslide was initiated in the steep upper segment of the shola forest, just below the barren hilltop. The combination of heavy rains and runoff from the hill’s crest caused the debris-mantled hollows to become saturated, leading to the landslide. The material dislodged during the slide consisted of loose soil, highly weathered rocks, and vegetation, all of which were funnelled into the stream channel below. The obtained sub-surface profile from the deposition profile in the borehole validates the presence of finer particles up to 3 m (Fig. 10b and d) depth followed by coarser particles till bedrock (Fig. 10e). As the debris flow progressed, the bed load in the stream increased dramatically, leading to intense bank erosion and a widening of the channel. The widened stream, carrying a mixture of stormwater and debris, reached the village with devastating force, destroying homes and roads. The stream channel’s alteration due to the debris flow increased the velocity and intensity of the event, exacerbating the damage to the village infrastructure and surrounding landscape. Looking at the severity of destroyed households, the affected area was divided into zones 1 and 2 to better analyze the debris flow movement in the present study. This landslide event, like many others in the Western Ghats during the monsoon season60, emphasizes the vulnerability of the region to natural disasters. Moreover, the growing number of settlements and infrastructure developments in these fragile landscapes increases the potential for human and economic loss during such events. Considering the role of sandy particles in the present case, a suitable rheological model like H-B was proposed to model the debris flow. With respect to the rheological parameters like yield stress and viscosity, the flow’s predominant grain size was 1 cm, and the slurries were dominated by sand and its fragments. Therefore, the power law index n was initially determined to be 1.062. Experimental results show that n ≥ 1.0 for strongly sheared sandy slurries are consistent with this value of n. It was empirically found that the coefficient ‘m’ was 100. The simulation considers the input boundary parameters the same as from the dam break simulation excluding rheological parameters. The density of flow was kept at 1800 \(\:kg/{m}^{3}\), with kinematic viscosity at 0.1 \(\:{m}^{2}/\)s after converting from dynamic viscosity. The fluid and boundary particles were 35,893 and 5,91,333 respectively. The input rheological and boundary condition parameters are mentioned in Table 2. A 12.5 m input digital elevation model (DEM) from ALOS PALSAR (Advanced Land Observing Satellite – Phased Array type L-band Synthetic Aperture Radar)62 for Pettimudi debris flow was used for delineating the source area62.

Fig. 10
figure 10

Field-based survey showing (a) SPT setup in the depositional zone to collect samples at varying depths, (b) 1 m, (b) 3 m, (d) 6 m, (e) 9.5 m.

Full size image

Runout modeling

The debris flow took approximately 300 s to reach the flat lands near the layams, where it eventually merged into a nearby stream. Over its path, the flow traveled a total distance of 1200 m, achieving a peak velocity of 18 m/s (Fig. 11). The debris flow first reached zone-1 within 150 s, and it took an additional 120 s to advance to zone-2, where it caused the most significant damage. The flow height and velocity observed are consistent with the findings of Jain et al.56. During the initial stages of the flow (from t = 0 to 20 s), the velocity remained relatively low, but the flow quickly reached its maximum velocity between t = 20 s to t = 40 s, before beginning to slow down as it approached zone-1. Between zone-1 and zone-2, the velocity stabilized between 3 and 6 m/s and became nearly stagnant after reaching zone-2. Since there are no field measurements during the process, these results are assumed.

The velocity gradient at flow initiation, as illustrated in Fig. 12, shows a distinct upward trend as time progresses, aligning with the results of Goodwin et al.37, further validating the initiation of the flow under field conditions. An increase in flow height was observed in the early stages, but it subsequently diminished, following a pattern similar to a dam-break simulation11. A Herschel-Bulkley (H-B) model-based debris flow study observed comparable trends in Japan, where velocity increased upstream before decreasing due to topographical variations in the flow path49. Using a Bingham model for the same case study, noted an immediate surge in flow velocity during initiation which could be attributed to the shear-thickening behavior in the H-B model (where n > 1)62; resulting in a smaller velocity gradient compared to the Bingham model. Our study aligns with the H-B model, which accounts for the delayed velocity increase at the onset of flow (Fig. 11). Real debris flow like Pettimudi can introduce inertial effects for sand (collisions) and water (turbulence)63 which were not taken into account in the present study. Liang64 reported similar velocity trends in granular flow using SPH modeling. Similarly, studies by Kong et al.65,66 have demonstrated the value of modeling debris flows as multiphase mixtures using coupled CFD-DEM approaches, where the fluid phase is represented by a non-Newtonian slurry (e.g., Herschel–Bulkley model) and the boulders by polydisperse solid particles. Their work has shown improved impact assessment on barriers by capturing discrete particle effects and their interactions with viscous fluids.

The downstream flow caused significant damage to multiple layams, with hydrodynamic impact pressures documented in Fig. 13. Zone-1 experienced relatively minor impacts compared to zone-2, where the entire built-up area was submerged under the debris flow. The hydrodynamic impact pressure peaked just after the debris flow struck the houses in zone-1, but gradually decreased as the flow surges passed through. However, in zone 2, the impact pressure remained elevated for an extended duration due to the lower elevation and greater flow volume passing over the area (Fig. 13b). The pressure values ranged between 100 and 200 kPa, which is in line with the trends observed by Dai et al.49. The hydrodynamic pressure increased exponentially with greater flow depths (Fig. 13c) in both zones, with the deepest flow causing the most significant impacts. The toe of the debris flow in this study was measured at 110 m, which is 10 m shorter than the physical measurement reported by Achu et al.55. This 10-meter discrepancy could be attributed to differences in boundary conditions between the current study and the real-world field case. Figure 13d shows a flow depth of 3.2 m over the buildings in zone-2 at t = 300 s, which is sufficient to fully submerge existing infrastructure. This flow depth aligns with the modeling results of Jain56. The flow depth visualization in this study was performed separately using a Python library, and the overall flow kinematics and dynamics were found to be consistent with previous case studies from other regions. The simulation of the Pettimudi debris flow, which considered the fluid phase of the slurry mixture, was closely related to granular-viscous or plain granular flows, indicating that the model effectively captured the flow’s complex behavior. The Reynolds number (Re = U·h/\(\:\nu\:\)) for our flows ranged from 2.5 to 27 (for U = 5–18 m/s, h = 1–3 m, ν = 2 m²/s), confirming laminar dominance (Re ≪ 1000). This aligns with viscous debris flows where high kinematic viscosity (ν = 2 m²/s) suppresses turbulence, even at densities of 1400–1800 kg/m³4,61. Turbulence effects were thus justifiably neglected.

Table 2 Input parameters for pettimudi debris flow simulation.
Full size table
Fig. 11
figure 11

Variation of debris flow in Pettimudi at different time steps.

Full size image
Fig. 12
figure 12

Depiction of flow gradient at the initiation of Pettimudi debris flow for different time steps.

Full size image

Debris flow deposition and validation

The movement of material from the main deposition zone into the layams of zone-2 has been thoroughly analyzed. The final results were compared with deposited material heights measured using Soil Penetration Test (SPT) and Vertical Electrical Sounding (VES) profiles. The simulated results indicate a deposition depth of 1.5–2 m in zone 1, located at the transition between steep and mild slopes. In the field-based study, it was observed that coarser particles, such as boulders, were prevalent in this zone (Fig. 9d). This can be attributed to the reduced capacity of the debris flow to transport these larger particles as they move into flatter terrain67 explains this phenomenon, noting that as a viscous debris flow reaches a mildly sloping area, its ability to disperse coarse particles decreases due to the reduced velocity of the flow (Fig. 11). As a result, the flow loses its competence to carry larger debris, leading to their deposition in such transitional zones. This aligns with the observed field conditions in the current study. The present analysis used a consistent profile position across the numerical simulation, geotechnical (SPT), and geophysical (VES) investigations to ensure accuracy68. Figure 14 illustrates these comparative profiles, along with the final depths observed in the SPH models within the deposition zone. The SPH model recorded a maximum runout deposit of 3.7 m in zone 2, primarily consisting of clay-sand mixtures, as most of the coarser particles were deposited earlier in zone (1) In contrast, field-based measurements indicated a deposition height of around 3 m in zone (2) Supporting this, the literature using the finite volume method (FVM) suggests a similar deposit height of 3.5 m56. This variation between the SPH model and field-based data can be attributed to slight differences in model assumptions and real-world conditions but remains within an acceptable range of agreement.

The debris flow deposits between zone-1 and zone-2 displayed varying heights, with higher deposition in the flatter regions near zone-2, predominantly affecting the layams (temporary buildings), which were destroyed by the flow. The materials deposited were primarily sand and clay mixtures up to 3 m in height, with highly weathered gravel forming the base layer. These depositions were validated using borehole data and VES surveys in both zones (Fig. 15a). In Zone 1, the deposits largely consisted of clay-sand mixtures, which extended up to a depth of 2.5 to 3 m, as confirmed by the VES survey conducted after the debris flow event. This also validated the results of the current numerical simulations. Although it remains challenging to assess the exact impact load on the buildings without factoring in granular particles, the current sand-slurry setting suggests that the hydrodynamic impact load aligns with natural debris flow conditions, as shown in previous studies69,70.

The cross-section analysis revealed different deposit thicknesses depending on the location of the VES and borehole log. For the VES profile, the thickness is relative to the lower surface, which represents the depth of the channel as predicted by the geophysical investigations (Fig. 15a). On the other hand, the modeling results were from DualSPHysics defined thickness based on the input surface of the Digital Elevation Model (DEM). The numerical model predicted greater material deposition on the left side of the flow deposition compared to the borelog and VES profiles in both zone-1 and zone-2 (Fig. 15b and c). While the SPH model showed thicker deposition across the entire area, it was more representative in that the majority of the material remained within the deposition zone. In contrast, field-based observations indicated a significant amount of overflow material, with highly weathered gravel at the base, particularly noted in Fig. 9. This overflow material was much greater than the amount of material deposited in the numerical model. The overall deposition pattern observed in the numerical model closely mirrors the results of Achu et al.55 and was further validated through field-based studies. This study provides an accurate depiction of the debris flow dynamics in zones 1 and 2, particularly highlighting the destruction of the layams and the varying deposition heights throughout the region.

Fig. 13
figure 13

The hydrodynamic impact pressure along the residential zones in Pettimudi debris flow (a) at t = 300 s the deposition pattern along zone-1 and zone-2, (b) the variation of pressure with time during flow-structure interaction in zone-1 and 2, (c) the variation pressure gradient during flow-structure interaction, (d) flow height in zone-2 at t = 300 s.

Full size image
Fig. 14
figure 14

Flow height variation along zone-1 at different time steps.

Full size image

Discussion

This paper presents a fully three-dimensional, Herschel-Bulkley (HBP) model-based Smoothed Particle Hydrodynamics (SPH) method to simulate debris flow behavior. The governing equations are based on Navier-Stokes type equations, which are numerically solved using the SPH scheme in 3D. The HBP model is integrated to define the constitutive relationship between particles, enabling the simulation of both dilatant and pseudoplastic fluids. To validate the proposed HBP method, a dam-break experiment was created using a flume setup, followed by a set of numerical simulations with similar boundary conditions. The results showed that the method accurately captured the debris flow dynamics, including deposition, flow velocity, and depth. Previous studies11,36,37 have already shown the efficacy of utilizing the HBP model over simple Bingham or Cross models, hence the proposed approach delivered superior performance in simulating debris-flow processes. To calibrate the numerical model, rheometrical tests were performed and fitted parameters were determined. Later a comparison between computed and measured features was done to analyse the DualSPHysics model. During the calibration, we did not encounter tensile instability in numerical simulations unlike previous research33,37 thus making further analysis precise with respect to its performance at upscale. The method was further applied to model the 2020 Pettimudi debris flow in Kerala, India. Key parameters, such as flow velocity, depth, and pressure during the runout, were determined, and field surveys validated the deposition patterns over the damaged infrastructure. The simulation closely matched the characteristics described in previous studies55,56 and was corroborated by in-situ tests like the Soil Penetration Test (SPT) and Vertical Electrical Sounding (VES) (Fig. 15b and c). Erosion and entrainment71,72 were not accounted for in this study, limiting the ability to achieve a perfect match with the real debris flow. However, the methodology successfully modeled the debris flow through proper calibration using the SPH formulation. The results for hydrodynamic impact pressure, deposition profiles, and affected areas aligned well with findings from previous studies.

Fig. 15
figure 15

Validation via geophysical testing at deposition zone (a) comparison between VES and bore log data for deposition in zone-2, (b) VES profile at zone-1 and zone-2, (c) deposition profile at zone 1 and zone 2.

Full size image

Scaling considerations

Scaling issues are inherent when translating laboratory-scale results to real-world scenarios, especially in complex phenomena like debris flows29,73,74. This study ensured geometric, kinematic, and dynamic similarity between the flume experiments and the real-world Pettimudi debris flow. Geometric scaling was maintained with a runout length ratio of approximately 1:1000. For kinematic similarity, the velocity ratio between the lab-scale maximum values and real-world debris flows was approximately 1:10, ensuring that the kinematic of the flow was reasonably represented. The dynamic similarity was addressed using the Froude number (\(\:{F}_{r}\)), a critical dimensionless parameter representing the ratio of inertial to gravitational forces. In the lab experiments, \(\:{F}_{r}\) was calculated as 1.864, indicating a better calibration compared to previously reported small-scale studies, such as Zhou et al.75,76, which reported a significantly higher Fr of 7.56 due to the overestimation of physical forces. For the Pettimudi debris flow case, \(\:{F}_{r}\) values were between 2.55 and 2.7, aligning well with typical field observations where \(\:{F}_{r}\) ranges from 0 to 3, as noted by Kwan et al.77 and McArdell et al.78.

Despite these efforts, scaling limitations remain. The model calibration revealed significant discrepancies in flow height between lab-scale simulations and field observations, as shown in Fig. 6, though better agreement was achieved during the deposition phase. Since this study primarily focuses on deposition impacts, particularly over buildings (layams) in the Pettimudi case, the calibration was deemed acceptable. However, these scaling challenges should be acknowledged as a limitation, and future studies may benefit from advanced scaling techniques or field-based validation to enhance accuracy further.

Limitations of the present study

However, the methodology has some limitations. The rheology model could be enhanced by incorporating granular-viscous properties to better reflect soil material characteristics. The H-B model in DualSPHysics simplifies debris flow as a single-phase viscoplastic fluid, neglecting two-phase interactions like pore pressure dynamics, particle segregation, and air entrapment. The delayed peak in flow velocity and height can be credited to ductile yield behavior40 of clay-sand suspension of debris flow which can be improved by considering frictional characteristics along with viscous flow. The current model was trained using a small-scale flume, and performance could improve with a large-scale setup73,79. Additionally, rheological parameters were derived from experiments and empirical formulas, but future studies could benefit from a large-scale rheometer for improved training. The lack of well-documented case studies poses another challenge, although empirical formulas from Von Boetticher80 and Majors and Pierson61 can be used in cases with limited data, especially when fine particles and clay mineral composition are involved. Researchers69,81 have demonstrated the use of flume model tests to determine hydrodynamic impact pressure in viscous debris flows. The present study follows a similar approach, applied to a different study area However, the hydrodynamic impact pressure observed in the present study shows a limitation when it comes to real debris flow which is wet granular generally with very high impact due to a coarser load81. Since the present study incorporates viscous slurry-type flow, adding boulder particles would have increased the accuracy of impact pressure65,66. However, the proposed method effectively analyzed the Pettimudi debris flow disaster and its impact on nearby infrastructure. This study offers valuable insights for land-use planning and emphasizes the importance of analyzing past debris flows to better understand the underlying mechanisms.

Conclusion

The study effectively demonstrates the use of Smoothed Particle Hydrodynamics (SPH), specifically the Herschel-Bulkley-Papanastasiou (HBP) model, to simulate and understand the complex behavior of viscous debris flows. By conducting both experimental and numerical analyses under consistent boundary conditions, the study analyzed the reliability of SPH for replicating the dynamics of debris flows, especially in highly viscous cases where conventional models have limitations. The following conclusions can be drawn from the research work as listed below-.

  • Key findings from the study, such as the maximum flow velocity of 16 m/s during initiation and the hydrodynamic impact pressures ranging from 80 to 200 kPa, align closely with the real-world behavior of the Pettimudi debris flow. This validates the robustness of the SPH approach when applied to the simulation of viscoplastic fluids, particularly debris flows consisting of clay-sand mixtures. The runout distance, flow depth, and deposition width obtained from the SPH simulations were closely matched with field observations and experimental data, further confirming the method’s applicability for modeling large-scale debris flows.

  • The comparative analysis between experimental data and numerical simulations showed a significant correlation, particularly in flow initiation and deposition patterns. Although the numerical model struggled with higher-density flows, the overall consistency of results demonstrated that SPH, when combined with appropriate rheological models, is capable of accurately predicting debris flow behavior. The contours used to assess the deposition zones further supported the similarities between experimental and numerical outcomes, providing additional confidence in the methodology.

  • The delayed increase in velocity observed in the model was consistent with the behavior of highly viscous flows, further validating the use of this rheological approach. Importantly, the study highlighted that denser debris flows tend to spread laterally, rather than extending longitudinally, a finding that aligns with previous research and provides critical insights for understanding how debris flows behave in different conditions. The inclusion of erosion and entrainment however could better match the real debris flow scenarios.

  • Despite its strengths, the study also identified limitations in the SPH model, particularly when dealing with high-density flows. The observed discrepancies in flow dynamics suggest that further refinement of the model’s ability to handle dense granular flows is needed. In addition, while the experimental flume setup provided a valuable platform for calibrating the SPH model, the study suggests that future work should consider larger-scale flume experiments to better simulate real-world debris flow conditions.

  • Finally, the field validation of the Pettimudi case study illustrates the practical applicability of the SPH method for disaster risk mitigation and land-use planning. The study’s findings provide valuable insights for engineers and planners tasked with developing strategies to mitigate the impact of debris flows on vulnerable infrastructure. By incorporating numerical modeling with field-based data, this approach offers a powerful tool for predicting debris flow behavior and improving preparedness for future events.

In summary, this research highlights the potential of SPH, combined with HBP rheology, to simulate and analyze debris flows, offering significant insights into their behavior. The Pettimudi landslide serves as a tragic reminder of the risks posed by such natural phenomena, especially in the context of climate change, which is predicted to exacerbate the frequency and intensity of extreme weather events. Future mitigation efforts will need to focus on better understanding the complex interactions between land-use practices, slope stability, and rainfall patterns in the region to prevent similar disasters from occurring again.