Introduction

Dengue hemorrhagic fever (DHF) is a disease caused by infection with the dengue virus, which is transmitted via the bite of an infected female Aedes mosquito. This disease occurs in tropical and subtropical regions worldwide, with most cases occurring in urban and semi-urban areas that infecting all age groups. In mild cases, the disease causes a high fever and symptoms similar to the flu. Meanwhile, for severe cases, this disease can cause serious bleeding, shock from a sudden fast drop in blood pressure, and even death. The four dengue virus serotypes that cause DHF are DENV-1, DENV-2, DENV-3, and DENV-4, and they can be identified using serological techniques. After recovering from an infection with one of these serotypes, a person acquires lifelong immunity against reinfection from the same serotype. But it is possible for subsequent infections by different serotypes with a more severe risk than before1.

Sex differences can affect the severity, prevalence and pathogenesis of infections caused by viruses, bacteria, parasites and fungi. Males are more susceptible to infectious diseases than females, regardless of how the infection is spread whether from person to person, vectors, blood, food, or through water2. Women possess two X chromosomes which contribute to the enhancement of their immune system, despite the possibility of one of the X chromosomes being inactive. The immune system is regulated by a gene coded X on the chromosome controls the immune system, causing females to have higher amounts of CD4+ T cells and less susceptibility to inflammation and not easily infected with viruses3.

The mathematical model may play an essential role for understanding the dynamics of infectious disease transmission, allowing for the prediction and management of infectious disease4,5,6,7,8. In addition, the availability of real data on a disease will improve the estimation of model parameters. Thus, the mathematical models can explain the spread of disease in a region using these parameter values. Meanwhile, time dependent control strategies have been utilized to determine the optimal ways in eliminating the spread of disease. The researchers have been developed the mathematical models to investigate the spread dynamics of DHF. Buonomo and Marca9 analyzed the control in the form of spraying campaigns and ITN adoption on the DHF model. Authors in10 have studied a mathematical model to investigate the transmission dynamics of DHF in Pakistan. Zhang and Lui11 discussed DHF model with a control in the form of releasing the Wolbachia-infected mosquitoes. The work in12 proposed a mathematical model of DHF with hospitalization based the monthly real data of East Java province, Indonesia. Ndi et al.13 developed DHF model with observing two different serotype infections and including a control in the form of vaccination. Puspita et al.14 proposed DHF model with four-age structure classification, i.e., children, youngsters, productive adults, and elders. Aldila et al.15 formulated a mathematical model for DHF control program in Jakarta, Indonesia. The authors in16 constructed model’s time-varying effective reproduction number to capture trends the dengue transmission in Palu, Indonesia. Recently, the authors in17 introduced an optimal control deterministic model of DHF dynamics by accounting for the asymptomatic, isolated, and vigilant compartments in the human population.

A number of researchers have studied the effect of sex classification on infectious diseases. For instance, Fatmawati et al.18 have analyzed a mathematical model of HIV/AIDS transmission by classifying sex in human populations. Taghikhani et al.19 studied a mathematical model for the spread of dengue by classifying sex in the adult Aedes Aegypti mosquito population. Rathinasamy et al.20 constructed a mathematical model for the spread of HIV/AIDS by classifying the sex of a population that is susceptible and infected with HIV, while the population infected with AIDS is not classified based on sex. No previous study has addressed the mathematical model of DHF transmission by classifying the sex of the human population. This study set out to understand the dynamic transmission of DHF by considering the sex of the human population. We then estimate the DHF model parameters using the cumulative number of annual DHF cases reported in West Java Province from 2014 to 2020. Next, this research provide the optimal control strategy to examine the impact of fumigation and prevention for the most effective control measures of DHF transmission.

The rest of this paper is laid out as follows. The mathematical model formulation is presented in section “DHF model transmission”. The estimation of the DHF model parameters is given in section “Parameter estimation”. The stability analysis of the equilibria and parameter sensitivity are devoted in sections “Stability analysis of equilibrium point” and “Sensitivity analysis” respectively. The completion of the optimal control and the numerical simulation is performed in section “Optimal control problem”. In addition, section “Cost effectiveness analysis” focuses on the calculation of cost analysis to determine the most effective optimal control strategy. Furthermore, section “Sex classification impact in optimal control” discuss the impact of differing prevention efforts on male and female humans. Ultimately, the paper is concluded in section “Conclusion”.

DHF model transmission

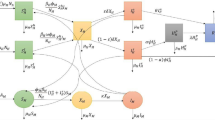
In this section, we describe the host-vector model of dengue hemorrhagic fever (DHF) transmission by considering sex in the human populations. The host (human) population is devide to six subpopulations, namely susceptible male subpopulation \(\left( S_m\right)\), susceptible female subpopulation \(\left( S_f\right)\), infectious male subpopulation \(\left( I_m\right)\), infectious female subpopulation \(\left( I_f\right)\), recovery male subpopulation \(\left( R_m\right)\), and recovery female subpopulation \(\left( R_f\right)\). The vector (mosquito) is divided to two subpopulations, namely susceptible subpopulation \(\left( S_v\right)\) and infectious subpopulation \(\left( I_v\right)\).

The total human population can be represented by \(N_h=N_m+N_f\), with the total of male human populations \(N_m=S_m+I_m+R_m\) and the total of female human populations \(N_f=S_f+I_f+R_f\). The formulation for the total population of mosquitoes can be described by \(N_v=S_v+I_v\). The assumptions of the constructing for the mathematical model of the DHF transmission can be stated as following.

  1. 1.

    Susceptible humans can become infected with DHF if they are bitten by an infected mosquito, while the susceptible mosquitoes can become infected with DHF if they are bitten an infected human.

  2. 2.

    The incubation period is ignored so that the infected population can directly transmit DHF.

  3. 3.

    Mosquito populations are unable to recover.

  4. 4.

    There is no reinfection of DHF.

  5. 5.

    The transmission rate of DHF for the male populations is greater than the female populations.

The notation and description of parameters of the mathematical model of DHF transmission is displayed in Table 1. Based on the assumptions and descriptions of the variables and parameters, the transmission diagram of the DHF model is given in Fig. 1.

Table 1 Parameters description.
Full size table
Fig. 1
figure 1

DHF transmission diagram.

Full size image

The mathematical representation of the transmission of DHF is described by an eight-dimensional nonlinear autonomous system of ordinary differential equations.

$$\begin{aligned} \frac{dS_v}{dt}= & {\mathrm {\Lambda }}_v\mathrm {-}\frac{{\beta }_v\left( I_m\mathrm {+}I_f\right) }{N_h}S_v\mathrm {-}{\mu }_vS_v,\nonumber \\ \frac{dI_v}{dt}= & \frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vI_v,\nonumber \\ \frac{dS_m}{dt}= & {\mathrm {\Lambda }}_{hm}-\frac{{\beta }_hI_v}{N_h}S_m-{\mu }_{hm}S_m,\nonumber \\ \frac{dS_f}{dt}= & {\mathrm {\Lambda }}_{hf}-\gamma \frac{{\beta }_hI_v}{N_h}S_f-{\mu }_{hf}S_f,\\ \frac{dI_m}{dt}= & \frac{{\beta }_hI_v}{N_h}S_m-\left( {\theta }_m+{\tau }_m+{\mu }_{hm}\right) I_m,\nonumber \\ \frac{dI_f}{dt}= & \gamma \frac{{\beta }_hI_v}{N_h}S_f-\left( {\theta }_f+{\tau }_f+{\mu }_{hf}\right) I_f, \nonumber \\ \frac{dR_m}{dt}= & {\theta }_mI_m-{\mu }_{hm}R_m, \nonumber \\ \frac{dR_f}{dt}= & {\theta }_fI_f-{\mu }_{hf}R_f.\nonumber \end{aligned}$$
(1)

All parameters of the model (1) are assumed to be positive. Furthermore, the DHF transmission rate of the male population is greater than the female. We assume that \(\gamma\) as the additional immunity level for female population to reduce the rate of DHF transmission with \(0<\gamma <1\). The model (1) subject to the initial conditions by \(S_v\left( 0\right)\), \(S_m\left( 0\right)\), \(\ S_f\left( 0\right) >0\) and \(I_v\left( 0\right)\), \(I_m\left( 0\right)\), \(I_f\left( 0\right)\), \(R_m\left( 0\right)\), \(R_f\left( 0\right) \ge 0\), with the solutions of system (1) remain non-negative for all time \(t>0\) and defined in closed set \(\mathrm {\Omega }\) (positively invariant) is given by

$$\begin{aligned} \mathrm {\Omega }={\mathrm {\Omega }}_v\cup {\mathrm {\Omega }}_m\cup {\mathrm {\Omega }}_f\subset {\mathbb {R}}^2_+\times {\mathbb {R}}^3_+\times {\mathbb {R}}^3_+, \end{aligned}$$
(2)

with

$$\begin{aligned} {\mathrm {\Omega }}_v&=\left\{ \left( S_v\left( t\right) ,I_v\left( t\right) ,\ R_v\left( t\right) \right) \in {\mathbb {R}}^2_+:N_v=\frac{{\mathrm {\Lambda }}_v}{{\mu }_v}\right\} ,\\ {\mathrm {\Omega }}_m&=\left\{ \left( S_m\left( t\right) ,I_m\left( t\right) ,\ R_m\left( t\right) \right) \in {\mathbb {R}}^3_+:N_m\le \frac{{\mathrm {\Lambda }}_m}{{\mu }_m}\right\} ,\\ {\mathrm {\Omega }}_f&=\left\{ \left( S_f\left( t\right) ,I_f\left( t\right) ,\ R_f\left( t\right) \right) \in {\mathbb {R}}^3_+:N_f\le \frac{{\mathrm {\Lambda }}_f}{{\mu }_f}\right\}. \end{aligned}$$

Next, we demonstrate the positive nature of finding a solution to the system (1) based on the theorem presented below.

Theorem 2.1

Let \(S_v\left( 0\right)\), \(I_v\left( 0\right)\), \(S_m\left( 0\right)\), \(S_f\left( 0\right)\), \(I_m\left( 0\right)\), and \(I_f\left( 0\right)\) be the initial conditions of the system. If \(S_v\left( 0\right) \ge 0\), \(I_v\left( 0\right) \ge 0\), \(S_m\left( 0\right) \ge 0\), \(S_f\left( 0\right) \ge 0\), \(I_m\left( 0\right) \ge 0\), and \(I_f\left( 0\right) \ge 0\) then all solutions are positive for every \(t>0\).

Proof

  1. 1.

    Take the first equation of the system (1) is as follows:

    $$\begin{aligned}\frac{dS_v\left( t\right) }{dt}={\mathrm {\Lambda }}_v-\frac{{\beta }_v\left( I_m\left( t\right) +I_f\left( t\right) \right) }{N_h\left( t\right) }S_v\left( t\right) -{\mu }_vS_v\left( t\right) .\end{aligned}$$

    Let \(\eta \left( t\right) =\frac{{\beta }_v\left( I_m\left( t\right) +I_f\left( t\right) \right) }{N_h\left( t\right) }\), so it is obtained as follows:

    $$\begin{aligned}\frac{dS_v\left( t\right) }{dt}\mathrm {=}{\mathrm {\Lambda }}_v\mathrm {-}\eta \left( t\right) S_v\left( t\right) \mathrm {-}{\mu }_vS_v\left( t\right) \end{aligned}$$
    $$\begin{aligned}\mathrm {\Longleftrightarrow }\frac{dS_v\left( t\right) }{dt}\mathrm {\ge }\mathrm {-}\eta \left( t\right) S_v\left( t\right) \mathrm {-}{\mu }_vS_v\left( t\right) \end{aligned}$$
    $$\begin{aligned}\mathrm {\Longleftrightarrow }\frac{d\left( e^{{\mu }_vt\mathrm {+}\int ^t_0{\eta }\left( s\right) ds}S_v\left( t\right) \right) }{dt}\mathrm {\ge }\textrm{0}\end{aligned}$$
    $$\begin{aligned}\mathrm {\Longleftrightarrow }S_v\left( t\right) \mathrm {\ge }ke^{\mathrm {-}{\mu }_vt\mathrm {-}\int ^t_0{\eta \left( s\right) } ds}.\end{aligned}$$

    Substitute the initial condition \(S_v(0)\) at \(t=0\), we get

    $$\begin{aligned}S_v\left( t\right) \ge S_v\left( 0\right) e^{-{\mu }_vt-\int ^t_0{\eta \left( s\right) }\ ds}.\end{aligned}$$

    Hence, \(S_v(t)\) is positive for \(t\ge 0\). Then using the same steps, we can prove the \(S_m(t)\) and \(S_f\left( t\right)\) are also positive for \(t\ge 0\).

  2. 2.

    Take the second equation of the system (1) is as follows:

    $$\begin{aligned}\frac{dI_v\left( t\right) }{dt}=\frac{{\beta }_v\left( I_m\left( t\right) +I_f\left( t\right) \right) }{N_h\left( t\right) }S_v\left( t\right) -{\mu }_vI_v\left( t\right) \end{aligned}$$
    $$\begin{aligned}\Longleftrightarrow \frac{dI_v\left( t\right) }{dt}\ge -{\mu }_vI_v\left( t\right) \end{aligned}$$
    $$\begin{aligned}\Longleftrightarrow \frac{d\left( e^{{\mu }_vt}I_v\left( t\right) \right) }{dt}\ge 0\end{aligned}$$
    $$\begin{aligned}\Longleftrightarrow I_v\left( t\right) \ge ke^{-{\mu }_vt}.\end{aligned}$$

    By using the initial condition \(I_v(0)\) at \(t=0\), we get

    $$\begin{aligned}I_v\left( t\right) \ge I_v\left( 0\right) e^{-{\mu }_vt}.\end{aligned}$$

    So \(I_v(t)\) is positive for \(t\ge 0\). Then using the same steps we can prove the \(I_m(t)\), \(I_f\left( t\right)\), \(R_m\left( t\right)\), and \(R_f\left( t\right)\) are also positive for \(t\ge 0\).

\(\square\)

Parameter estimation

In this section, we estimate the value of parameter on model (1). First, we collect data from21,22,23,24, which are DHF cases of humans, DHF mortality of humans, total human populations, and life expectancy in West Java Province, Indonesia by sex in 2014–2023, respectively. The DHF cases of male and female humans population in West Java Province, Indonesia is compared in Fig. 221.

Fig. 2
figure 2

DHF cases in West Java, Indonesia.

Full size image

Based on Fig. 2, the case of DHF in West Java Province, Indonesia in both of male and female populations are fluctuate. Hence, we use cumulative DHF case data every years from 2014 to 2023 as data in estimating parameters. In parameter estimation, we use the least-squares fitting method25 except for parameter \({\mu }_v,\ {\mu }_m,\ {\mu }_f,{\mathrm {\Lambda }}_m,{\mathrm {\Lambda }}_f,{\tau }_m,\) and \({\tau }_f\) are obtained from demographic. The natural death rate is obtained from inverse from the average of life expectancy. Based on26, the average of life expectancy of Aedes mosquitoes is 25 days. The average life expectancy of male and female human populations are 71.048 years and 74.864 years, respectively24. Hence, we have \({\mu }_v=14.6\), \({\mu }_{hm}=0.0141\), and \({\mu }_{hf}=0.0134\) per year. Next, the growth rate of human is obtained from the average of multiplying the total population by the natural death. Using the data in23,24, we have \({\mathrm {\Lambda }}_{hm}=328,323\) and \({\mathrm {\Lambda }}_{hf}=301,673\) population per year. Furthermore, for DHF mortality rate we approach it with Case Fatality Rate (CFR) that is obtained from the proportion of all individuals who die from DHF among all individuals infected with DHF. Based on the data in22, we have \({\tau }_m=0.0068\) and \({\tau }_f=0.0087\) per year.

The estimation of the remaining parameters in the model (1) is carried out by minimizing the following objective function

$$\begin{aligned}{\mathop {\textrm{min}}_{{\mathrm {\Lambda }}_v,{\beta }_v,{\beta }_h,\gamma ,{\theta }_m,{\theta }_f} \sum ^{t_f}_{i=0}{\left( {\left( I_{m_i}-I^{data}_{m_i}\right) }^2+{\left( I_{f_i}-I^{data}_{f_i}\right) }^2\right) }\ },\end{aligned}$$

with \(t_f\) is the final time, \(I^{data}_{m_i}\) and \(I^{data}_{f_i}\) are the cumulative DHF cases data of male and female humans respectively, as well \(I_{m_i}\) and \(I_{f_i}\) are the cumulative numerical solutions of infected male and female humans population respectively, for \(i=0,1,2,\dots ,t_f\). In order the estimation process, we set the initial population as

$$\begin{aligned}\left( S_{v_0};I_{v_0};S_{m_0};S_{f_0};I_{m_0};I_{f_0};R_{m_0};R_{f_0}\right) =\left( 50,000,000;\ 500;\ 21,788,900;\ 20,641,524;\ 10320;\ 8819;\ 0;\ 0\right) .\end{aligned}$$

The initial parameter values for estimation are given by

$$\begin{aligned}\left( {\mathrm {\Lambda }}_{v_0};{\beta }_{v_0};{\beta }_{h_0};{\gamma }_0;{\theta }_{m_0};{\theta }_{f_0}\right) =\left( 9\times {10}^8;\ 0.5;\ 0.9;\ 0.5;\ 0.3;\ 0.3\right) ,\end{aligned}$$

with lower bound parameter values are

$$\begin{aligned}\left( {10}^8;{10}^{-3};{10}^{-3};\ {10}^{-3};{10}^{-3};{10}^{-3}\right) \end{aligned}$$

and upper bound parameter values are

$$\begin{aligned}\left( {10}^{10};\ 2;\ 2;\ 1;\ 1;\ 1\right) ,\end{aligned}$$

The comparison of the reported data and the model solution is displayed in Fig. 3. The result of the parameters estimation can be seen in Table 2.

Fig. 3
figure 3

Comparison of the model solution and the reported data of DHF cases on the infected male and female humans population.

Full size image
Table 2 Fitted and estimated value of the parameters.
Full size table

According to the outcome of the estimation, the mean absolute percentage error (MAPE) between the data and the model solution in male population is \(4.28\%\) and female population is \(4.66\%\). Then the average MAPE from the comparison of the two data and the model solution is \(4.47\%\).

Stability analysis of equilibrium point

This section focuses on examining the stability of disease-free equilibria of the model (1), both at a local and global level. Initially, we ascertain the state of equilibrium together with its conditions of existence and the basic reproduction number. By considering model (1), we are able to derive two equilibria, specifically the disease-free equilibrium and the endemic equilibrium. The disease-free equilibrium is defined as.

$$\begin{aligned}E_0=\left( S^0_v,I^0_v,S^0_m,S^0_f,I^0_m,I^0_f,R^0_m,R^0_f\right) =\left( \frac{{\mathrm {\Lambda }}_v}{{\mu }_v},0,\frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}},\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}},0,0,0,0\right) .\end{aligned}$$

Next, we calculate the basic reproduction number (\(R_0\)) which quantifies the potential for infectious spread within a population27,28. By employing the Next Generation Matrix method29, we calculate the basic reproduction number as

$$\begin{aligned} R_0=\sqrt{\frac{{\beta }_h{\beta }_v{\mathrm {\Lambda }}_v{\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+\gamma {\mathrm {\Lambda }}_{hf}m_1{\mu }_{hm}\right) }{m_1m_2{\mu }^2_v{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2}}, \end{aligned}$$
(3)

where \(m_1={\theta }_m+{\tau }_m+{\mu }_{hm}\) and \(m_2={\theta }_f+{\tau }_f+{\mu }_{hf}\).

Next, assuming \(R_{0m}=\frac{{\beta }_h{\beta }_v{\mathrm {\Lambda }}_v{\mathrm {\Lambda }}_{hm}{\mu }_{hm}{\mu }^2_{hf}}{m_1{\mu }^2_v{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2}\) and \(R_{0f}=\frac{\gamma {\beta }_h{\beta }_v{\mathrm {\Lambda }}_v{\mathrm {\Lambda }}_{hf}{\mu }^2_{hm}{\mu }_{hf}}{m_2{\mu }^2_v{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2}\), we have the equation \(R^2_0=R_{0m}+R_{0f}\). Since all parameters are assumed to be positive, so \(R_{0m}<R^2_0\) and \(R_{0f}<R^2_0\).

Local stability of the disease-free equilibrium

The stability of the disease-free equilibrium point is obtained by substituting the value of the non-endemic equilibrium point \(E_0 = \left( \frac{{\mathrm {\Lambda }}_v}{{\mu }_v},0,\frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}},\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}},0,0,0,0\right)\) into the Jacobian matrix as follows:

$$\begin{aligned}J_{E_0}=\left( \begin{array}{cccccccc} -{\mu }_v & \quad 0 & \quad 0 & \quad 0 & \quad -b_v & \quad -b_v & \quad 0 & \quad 0 \\ 0 & \quad -{\mu }_v & \quad 0 & \quad 0 & \quad b_v & \quad b_v & \quad 0 & \quad 0 \\ 0 & \quad -b_m & \quad -{\mu }_{hm} & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad -b_f & \quad 0 & \quad {-\mu }_{hf} & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad b_m & \quad 0 & \quad 0 & \quad -m_1 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad b_f & \quad 0 & \quad 0 & \quad 0 & \quad -m_2 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad {\theta }_m & \quad 0 & \quad -{\mu }_{hm} & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad {\theta }_f & \quad 0 & \quad -{\mu }_{hf} \end{array} \right) ,\end{aligned}$$

where \(b_v=\frac{{\beta }_v{\mathrm {\Lambda }}_v}{\left( \frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}+\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}\right) {\mu }_v},\ b_m=\frac{{\beta }_h{\mathrm {\Lambda }}_{hm}}{\left( \frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}+\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}\right) {\mu }_{hm}},\) and \(b_f=\frac{\gamma {\beta }_h{\mathrm {\Lambda }}_{hf}}{\left( \frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}+\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}\right) {\mu }_{hf}}.\)

From the matrix \(J_{E_0}\), we will look for the characteristic equation with \({\textrm{det} \left( \lambda I-J_{E_0}\right) =0\ }\), such that we obtain

$$\begin{aligned} \left( \lambda +{\mu }_v\right) {\left( \lambda +{\mu }_{hm}\right) }^2{\left( \lambda +{\mu }_{hf}\right) }^2\left( {\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3\right) =0 \end{aligned}$$
(4)

where

$$\begin{aligned} a_1&=m_1+m_2+{\mu }_v,\\ a_2&=m_1m_2+{\mu }_vm_1\left[ 1-R_{0m}\right] +{\mu }_vm_2\left[ 1-R_{0f}\right] ,\\ a_3&={\mu }_vm_1m_2\left[ 1-R^2_0\right]. \end{aligned}$$

From the Eq. (4), we have the eigenvalues \(-{\mu }_v\), \(-{\mu }_{hm}\), and \(-{\mu }_{hf}\), which are negative and the remainder are the roots of the following equation:

$$\begin{aligned} {\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0. \end{aligned}$$
(5)

By using Routh–Hurwitz criterion, the characteristic Eq. (5) will have roots with negative real parts if and only if \(a_1,\ a_2, \ a_3, \ a_1a_2-a_3>0\). It is clear that the coefficient \(a_1>0\), while \(a_2>0\) if \(R_{0m}<1\) and \(R_{0f}<1\), and the coefficient \(a_3>0\) if \(R^2_0<1\).

Using some algebraic calculation, we have

$$\begin{aligned} a_1a_2-a_3&=\left( m_1+m_2\right) \left( m_1m_2+{\mu }_vm_1\left( 1-R_{0m}\right) +{\mu }_vm_2\left( 1-R_{0f}\right) \right) +{\mu }_v\left( {\mu }_vm_1\left( 1-R_{0m}\right) +{\mu }_vm_2\left( 1-R_{0f}\right) \right) \\&+{\mu }_vm_1m_2R^2_0. \end{aligned}$$

Hence, the coefficient \(a_1a_2-a_3\) is positive if \(R_{0m}<1\) and \(R_{0f}<1\). Since \(R_{0m}<R^2_0\), \(R_{0f}<R^2_0\), and \(R^2_0<1\), then \(R_{0m}<1\) and \(R_{0f}<1\) are fulfilled. Thus, all roots of Eq. (5) have negative real parts, when \(R^2_0<1\Longleftrightarrow R_0<1\). Therefore, the disease-free equilibrium \(\left( E_0\right)\) will be locally asymptotically stable for \(R_0<1\) and unstable whenever \(R_0>1\). The foregoing discussion could be summarized in the following theorem.

Theorem 4.1

The disease-free equilibrium \(\left( E_0\right)\) of the system (1) is locally asymptotically stable in region of interest \(\Omega\) if \(R_0<1\) and unstable if \(R_0>1\).

Global stability of the disease-free equilibrium

The global asymtotic stability of the disease-free equilibrium will be investigated using the method described by Castillo-Chavez et al. in30. Let \(X={\left( S_v,S_m,S_f,R_m,R_f\right) }^T\in {\mathbb {R}}^5\) and \(Z={\left( I_v,I_m,\ I_f\right) }^T\in {\mathbb {R}}^3\), so the system (1) can be represented by:

$$\begin{aligned} \frac{dX}{dt}&=F\left( X,Z\right) \nonumber \\ \frac{dZ}{dt}&=G(X,Z), G\left( X,0\right) =0, \end{aligned}$$
(6)

where \(E_0=\left( X_0,0\right)\) denotes the disease- free equilibrium of the system.

Based on30, the fixed point \(E_0=\left( X_0,0\right)\) is globally asymptotically stable provided that \(R_0<1\) and the two conditions bellow are satisfied

\(\left( \textrm{H1}\right)\) For \(\frac{dX}{dt}=F\left( X,0\right)\), \(X_0\) is globally asymptotically stable,

\((\textrm{H2})\) \(G\left( X,Z\right) =AZ-\hat{G}\left( X,Z\right)\), \(\hat{G}\left( X,Z\right) \ge 0\) for \(\left( X,Z\right) \in \mathrm {\Omega }\),

where \(A=D_ZG\left( X_0,0\right)\) is the M-matrix (the off diagonal elements of A are non-negative).

From the system (1), the Eq. (6) can be stated as follows:

$$\begin{aligned}F\left( X,Z\right) =\left( \begin{array}{c} {\mathrm {\Lambda }}_v-\frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vS_v \\ {\mathrm {\Lambda }}_{hm}-\frac{{\beta }_hI_v}{N_h}S_m-{\mu }_{hm}S_m \\ {\mathrm {\Lambda }}_{hf}-\gamma \frac{{\beta }_hI_v}{N_h}S_f-{\mu }_{hf}S_f \\ {\theta }_mI_m-{\mu }_{hm}R_m \\ {\theta }_fI_f-{\mu }_{hf}R_f \end{array} \right), G\left( X,Z\right) =\left( \begin{array}{c} \frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vI_v \\ \frac{{\beta }_hI_v}{N_h}S_m-m_1I_m \\ \gamma \frac{{\beta }_hI_v}{N_h}S_f-m_2I_f \end{array} \right) .\end{aligned}$$

Furthermore, we obtain

$$\begin{aligned}A=\left( \begin{array}{ccc} -{\mu }_v & \frac{{\beta }_vS^0_v}{N^0_h} & \frac{{\beta }_vS^0_v}{N^0_h} \\ \frac{{\beta }_h}{N^0_h}S^0_m & -m_1 & 0 \\ \gamma \frac{{\beta }_h}{N^0_h}S^0_f & 0 & -m_2 \end{array} \right), \hat{G}\left( X,Z\right) =\left( \begin{array}{c} \frac{{\beta }_v\left( I_m+I_f\right) S^0_v}{N^0_h}\left( 1-\frac{S_vN^0_h}{N_hS^0_v}\right) \\ \frac{{\beta }_hS^0_mI_v}{N^0_h}\left( 1-\frac{S_mN^0_h}{N_hS^0_m}\right) \\ \frac{\gamma {\beta }_hS^0_fI_v}{N^0_h}\left( 1-\frac{S_fN^0_h}{N_hS^0_f}\right) \end{array} \right), \end{aligned}$$
$$\begin{aligned}F\left( X,0\right) =\left( \begin{array}{c} {\mathrm {\Lambda }}_v-{\mu }_vS_v \\ {\mathrm {\Lambda }}_{hm}-{\mu }_{hm}S_m \\ {\mathrm {\Lambda }}_{hf}-{\mu }_{hf}S_f \\ -{\mu }_{hm}R_m \\ -{\mu }_{hf}R_f \end{array} \right) .\end{aligned}$$

By solving \(\frac{dX}{dt}=F\left( X,0\right)\), we have

$$\begin{aligned} \left( \begin{array}{c} S_v\left( t\right) \\ S_m\left( t\right) \\ S_f\left( t\right) \\ R_m\left( t\right) \\ R_f\left( t\right) \end{array} \right) =\left( \begin{array}{c} \frac{{\mathrm {\Lambda }}_v}{{\mu }_v}+\left( S_v\left( 0\right) -\frac{{\mathrm {\Lambda }}_v}{{\mu }_v}\right) e^{-{\mu }_vt} \\ \frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}+\left( S_m\left( 0\right) -\frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}\right) e^{-{\mu }_{hm}t} \\ \frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}+\left( S_f\left( 0\right) -\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}\right) e^{-{\mu }_{hf}t} \\ R_m\left( 0\right) e^{-{\mu }_{hm}t} \\ R_f\left( 0\right) e^{-{\mu }_{hf}t} \end{array} \right). \end{aligned}$$
(7)

Then, from Eq. (7), when \(Z=0\) yields \({\mathop {\textrm{lim}}_{t\rightarrow \infty } S_v\left( t\right) \ }=\frac{{\mathrm {\Lambda }}_v}{{\mu }_v}=S^0_v\), \({\mathop {\textrm{lim}}_{t\rightarrow \infty } S_m\left( t\right) \ }=\frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}=S^0_m\), \({\mathop {\textrm{lim}}_{t\rightarrow \infty } S_f\left( t\right) \ }=\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}=S^0_f\), \({\mathop {\textrm{lim}}_{t\rightarrow \infty } R_m\left( t\right) \ }=0=R^0_m\), and \({\mathop {\textrm{lim}}_{t\rightarrow \infty } R\left( t\right) \ }=0=R^0_f\) that ensuring the global asymptotic stability of the equilibrium \(X_0=\left( \frac{{\mathrm {\Lambda }}_v}{{\mu }_v},\frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}},\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}},0,0\right)\) hence \(\textrm{H1}\) is satisfied.

Next, it is clear that \(S_v\le N_v=\frac{{\mathrm {\Lambda }}_v}{{\mu }_v}=S^0_v\), \(S_m\le N_m\le \frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}=S^0_m\), and \(S_f\le N_f\le \frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}=S^0_f\), hence \(S_v\le S^0_v\), \(S_m\le S^0_m\), and \(S_f\le S^0_f\). However, to have \({\hat{G}}_1\left( X,Z\right) \ge 0\), \({\hat{G}}_2\left( X,Z\right) \ge 0\), and \({\hat{G}}_3\left( X,Z\right) \ge 0\) some conditions are required. For example, we could let the total human population be at equilibrium level \(\left( N_h=\frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}+\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}=N^0_h\right)\) and this condition will be achieved when we assume to ignore the disease-induced death rate. This ensures that \(1-\frac{S_vN^0_h}{N_hS^0_v}\ge 0\), \(1-\frac{S_mN^0_h}{N_hS^0_m}\ge 0\), and \(1-\frac{S_fN^0_h}{N_hS^0_f}\ge 0\). Hence \(\textrm{H2}\) is satisfied. Since two conditions are fulfilled, the disease-free equilibrium is globally asymptotically stable if we assume to ignore the disease-induced death rate. The foregoing discussion could be summarized in the following theorem.

Theorem 4.2

Suppose that in system (1) the disease-induced death rate is ignored \(\left( {\tau }_m={\tau }_f=0\right)\). If \(R_0<1\), then the non-endemic equilibrium point is globally asymptotically stable.

Endemic equilibrium

The endemic equilibrium of the system (1) will be determined using the conditions of the force infection \((\kappa _v, \kappa _h)\), with

$$\begin{aligned} {\kappa }_v=\frac{{\beta }_v\left( I_m+I_f\right) }{N_h},\ \ \ \ \ \ \ \ {\kappa }_h=\frac{{\beta }_hI_v}{N_h}. \end{aligned}$$
(8)

Hence, we obtain the endemic equilibrium as follows:

$$\begin{aligned}E_1=\left( S^*_v,I^*_v,S^*_m,S^*_f,I^*_m,I^*_f,R^*_m,R^*_f\right) \end{aligned}$$

where

$$\begin{aligned} S^*_v&=\frac{{\mathrm {\Lambda }}_v}{{\kappa }^*_v+{\mu }_v}, \ \ I^*_v=\frac{{\kappa }^*_v}{{\mu }_v}S^*_v, \ \ S^*_m =\frac{{\mathrm {\Lambda }}_{hm}}{{\kappa }^*_h+{\mu }_{hm}}, \ \ S^*_f=\frac{{\mathrm {\Lambda }}_{hf}}{\gamma {\kappa }^*_h+{\mu }_{hf}},\nonumber \\ I^*_m&=\frac{{\kappa }^*_h}{m_1}S^*_m, \ \ I^*_f =\frac{\gamma {\kappa }^*_h}{m_2}S^*_f, \ \ R^*_m=\frac{{\theta }_m}{{\mu }_{hm}}I^*_m, \ \ R^*_f =\frac{{\theta }_f}{{\mu }_{hf}}I^*_f. \end{aligned}$$
(9)

Subtitute Eqs. (9) into (8) in steady state and after algebraic simplification, we have

$$\begin{aligned}{\kappa }^*_v=\frac{{{\kappa }^*_h}^2\left( {\beta }_v\gamma \left( {{\mathrm {\Lambda }}_{hm}m_2\mathrm {+}\mathrm {\Lambda }}_{hf}m_1\right) \right) +{\kappa }^*_h\left( {\beta }_v\left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+\gamma {\mathrm {\Lambda }}_{hf}m_1{\mu }_{hm}\right) \right) }{{{\kappa }^*_h}^2\left( \gamma m_1m_2N^*_h\right) +{\kappa }^*_h\left( m_1m_2N^*_h\left( \gamma {\mu }_{hm}+{\mu }_{hf}\right) \right) +m_1m_2{\mu }_{hm}{\mu }_{hf}N^*_h},\end{aligned}$$

and \({\kappa }^*_h\) satisfying the following quadratic equation

$$\begin{aligned} b_0{{\kappa }^*_h}^2+b_1{\kappa }^*_h+b_2=0, \end{aligned}$$
(10)

with

$$\begin{aligned} b_0&=N^*_h{\mu }_v{\beta }_v\gamma \left( {{\mathrm {\Lambda }}_{hm}m_2\mathrm {+}\mathrm {\Lambda }}_{hf}m_1\right) +N^{2^*}_h{\mu }^2_v\gamma m_1m_2,\\ b_1&=N^*_h{\mu }_v{\beta }_v\left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+\gamma {\mathrm {\Lambda }}_{hf}m_1{\mu }_{hm}\right) +N^{2^*}_h{\mu }^2_vm_1m_2\left( \gamma {\mu }_{hm}+{\mu }_{hf}\right) -{{\mathrm {\Lambda }}_v{\beta }_v\beta }_h\gamma \left( {{\mathrm {\Lambda }}_{hm}m_2\mathrm {+}\mathrm {\Lambda }}_{hf}m_1\right) ,\\ b_2&=N^{2^*}_h{\mu }^2_vm_1m_2{\mu }_{hm}{\mu }_{hf}\left( 1-\frac{{\beta }_h{\beta }_v{\mathrm {\Lambda }}_v\left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+\gamma {\mathrm {\Lambda }}_{hf}m_1{\mu }_{hm}\right) }{N^2_h{\mu }^2_vm_1m_2{\mu }_{hm}{\mu }_{hf}}\right). \end{aligned}$$

The total number of human population in steady state condition is given by

$$\begin{aligned}N^*_h=S^*_m+I^*_m+R^*_m+S^*_f+I^*_f+R^*_f\end{aligned}$$
$$\begin{aligned} \Longleftrightarrow N^*_h&=\frac{{\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {{\kappa }^*_h}^2\left( \gamma \left( {\mu }_{hm}+{\theta }_m\right) \right) +{\kappa }^*_h\left( {\mu }_{hf}\left( {\mu }_{hm}+{\theta }_m\right) +\gamma {\mu }_{hm}m_1\right) +{\mu }_{hm}{\mu }_{hf}m_1\right) }{m_1m_2\left( {{\kappa }^*_h}^2\left( \theta \right) +{\kappa }^*_h\left( \theta {\mu }_{hm}+{\mu }_{hf}\right) +{\mu }_{hm}{\mu }_{hf}\right) }\nonumber \\& \quad +\frac{{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( {{\kappa }^*_h}^2\left( \gamma \left( {\mu }_{hf}+{\theta }_f\right) \right) +{\kappa }^*_h\left( \gamma {\mu }_{hm}\left( {\mu }_{hf}+{\theta }_f\right) +{\mu }_{hf}m_2\right) +{\mu }_{hm}{\mu }_{hf}m_2\right) }{m_1m_2\left( {{\kappa }^*_h}^2\left( \theta \right) +{\kappa }^*_h\left( \theta {\mu }_{hm}+{\mu }_{hf}\right) +{\mu }_{hm}{\mu }_{hf}\right) }. \end{aligned}$$
(11)

By substituting Eq. (11) into (10) and after algebraic simplification, the force infection \({\kappa }^*_h\) meet the quartic equation

$$\begin{aligned} c_0{{\kappa }^*_h}^4+c_1{{\kappa }^*_h}^3+c_2{{\kappa }^*_h}^2+c_3{\kappa }^*_h+c_4=0, \end{aligned}$$
(12)

with \(c_0, c_1, c_2, c_3\), and \(c_4\) are given by

$$\begin{aligned} c_0&=\left( {\mu }_v\gamma {\beta }_v{\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_{hm}m_2+{\mathrm {\Lambda }}_{hf}m_1\right) +{\mu }^2_v\gamma \left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hm}+{\theta }_m\right) +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( {\mu }_{hf}+{\theta }_f\right) \right) \right) \\& \quad \times \left( {\mathrm {\Lambda }}_{hm}\gamma {\mu }_{hf}m_2\left( {\mu }_{hm}+{\theta }_m\right) +{\mathrm {\Lambda }}_{hf}\gamma {\mu }_{hm}m_1\left( {\mu }_{hf}+{\theta }_f\right) \right) ,\\ c_1&=\left( {\mu }_v\gamma {\beta }_v{\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_{hm}m_2+{\mathrm {\Lambda }}_{hf}m_1\right) +{\mu }^2_v\gamma \left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hm}+{\theta }_m\right) +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( {\mu }_{hf}+{\theta }_f\right) \right) \right) \\& \quad \times \left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hf}\left( {\mu }_{hm}+{\theta }_m\right) +\gamma {\mu }_{hm}m_1\right) +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( \gamma {\mu }_{hm}\left( {\mu }_{hf}+{\theta }_f\right) +{\mu }_{hf}m_2\right) \right) \\& \quad +\left( {\mathrm {\Lambda }}_{hm}\gamma {\mu }_{hf}m_2\left( {\mu }_{hm}+{\theta }_m\right) +{\mathrm {\Lambda }}_{hf}\gamma {\mu }_{hm}m_1\left( {\mu }_{hf}+{\theta }_f\right) \right) \left( {\mu }_v{\beta }_v{\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_ {hm}m_2{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}\gamma m_1{\mu }_{hm}\right) \right. \\& \quad \left. +{\mu }^2_v{\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hf}\left( {\mu }_{hm}+{\theta }_m\right) +\gamma {\mu }_{hm}m_1\right) +{\mu }^2_v{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( \gamma {\mu }_{hm}\left( {\mu }_{hf}+{\theta }_f\right) +{\mu }_{hf}m_2\right) \right) \\& \quad -{\mathrm {\Lambda }}_v{\beta }_v{\gamma }^2{\beta }_h{\mu }^2_{hm}{\mu }^2_{hf}m_1m_2\left( {\mathrm {\Lambda }}_{hm}m_2+{\mathrm {\Lambda }}_{hf}m_1\right) ,\\ c_2&=\left( {\mu }_v\gamma {\beta }_v{\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_{hm}m_2+{\mathrm {\Lambda }}_{hf}m_1\right) +{\mu }^2_v\gamma \left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hm}+{\theta }_m\right) +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( {\mu }_{hf}+{\theta }_f\right) \right) \right) \\& \quad \times \left( {\mu }_{hm}{\mu }_{hf}m_1m_2\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) \right) \\& \quad +\left( {\mu }_v{\beta }_v{\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}\gamma m_1{\mu }_{hm}\right) +{\mu }^2_v{\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hf}\left( {\mu }_{hm}+{\theta }_m\right) +\gamma {\mu }_{hm}m_1\right) \right. \\& \quad \left. +{\mu }^2_v{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( \gamma {\mu }_{hm}\left( {\mu }_{hf}+{\theta }_f\right) +{\mu }_{hf}m_2\right) \right) \left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hf}\left( {\mu }_{hm}+{\theta }_m\right) +\gamma {\mu }_{hm}m_1\right) \right. \\& \quad \left. +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( \gamma {\mu }_{hm}\left( {\mu }_{hf}+{\theta }_f\right) +{\mu }_{hf}m_2\right) \right) \\& \quad +\left( {\mathrm {\Lambda }}_{hm}\gamma {\mu }_{hf}m_2\left( {\mu }_{hm}+{\theta }_m\right) +{\mathrm {\Lambda }}_{hf}\gamma {\mu }_{hm}m_1\left( {\mu }_{hf}+{\theta }_f\right) \right) \left( {\mu }^2_v{\mu }_{hm}{\mu }_{hf}m_1m_2\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}\right. \right. \\& \quad \left. \left. +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) \right) -{\mathrm {\Lambda }}_v{\beta }_v\gamma {\beta }_h{\mu }^2_{hm}{\mu } ^2_{hf}m_1m_2\left( \left( {\mathrm {\Lambda }}_{hm}m_2+{\mathrm {\Lambda }}_{hf}m_1\right) \left( \gamma {\mu }_{hm}+{\mu }_{hf}\right) +\left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}\gamma m_1{\mu }_{hm}\right) \right) ,\\ c_3&=\left( {\mu }_v{\beta }_v{\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}\gamma m_1{\mu }_{hm}\right) +{\mu }^2_v{\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hf}\left( {\mu }_{hm}+{\theta }_m\right) +\gamma {\mu }_{hm}m_1\right) \right. \\& \quad \left. +{\mu }^2_v{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( \gamma {\mu }_{hm}\left( {\mu }_{hf}+{\theta }_f\right) +{\mu } _{hf}m_2\right) \right) \left( {\mu }_{hm}{\mu }_{hf}m_1m_2\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) \right) \\& \quad +\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}m_2\left( {\mu }_{hf}\left( {\mu }_{hm}+{\theta }_m\right) +\gamma {\mu }_{hm}m_1\right) \right. \\& \quad \left. +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}m_1\left( \gamma {\mu }_{hm}\left( {\mu }_{hf}+{\theta }_f\right) +{\mu }_{hf}m_2\right) \right) \left( {\mu }^2_v{\mu }_{hm}{\mu }_{hf}m_1m_2\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf} +{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) \right) \\& \quad -{\mathrm {\Lambda }}_v{\beta }_v{\beta }_h{\mu }^2_{hm}{\mu }^2_{hf}m_1m_2\left( \left( {\mathrm {\Lambda }} _{hm}m_2{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}\gamma m_1{\mu }_{hm}\right) \left( \gamma {\mu }_{hm}+{\mu }_{hf}\right) +\gamma {\mu }_{hm}{\mu }_{hf}\left( {\mathrm {\Lambda }}_{hm}m_2+{\mathrm {\Lambda }}_{hf}m_1\right) \right) ,\\ c_4&={\mu }^2_v{\mu }^2_{hm}{\mu }^2_{hf}m^2_1m^2_2{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2\left( 1-R^2_0\right). \end{aligned}$$

Since all parameters assumed to be positive, then we have \(c_0>0\). Additionally, the model (1) always has an endemic equilibrium whenever \(\frac{c_4}{c_0}<0\Leftrightarrow c_4<0\Leftrightarrow R^2_0>1\Leftrightarrow R_0>1\). The foregoing discussion could be summarized in the following theorem.

Theorem 4.3

System (1) always has an endemic equilibrium whenever \(R_0>1\).

Since Eq. (12) is a fourth-order polynomial, it is possible to have more than one endemic equilibrium. To explore this possibility, we use Descartes’ rule of signs to determine the criteria for the number of positive equilibria, which corresponds to the number of positive roots of the polynomial in (12). The results are provided in Tables 3 and 4. It is clearly shown in Table 3 that when \(R_0>1\), there will always be at least one endemic equilibrium. In cases 3, 5, 6, and 7, it is possible to have three endemic equilibria when \(R_0>1\). Conversely, as shown in Table 4, when \(R_0<1\), there is always a possibility for a dengue-free situation. However, except for case 1, the other cases in Table 4 indicate that while a dengue-free situation is possible, there is also a possibility of the emergence of a dengue-endemic equilibrium. When this endemic equilibrium appears with \(R_0<1\) it is never unique; there are always multiple endemic equilibria-either 2 or 4. Therefore, based on this analysis, a condition of \(R_0<1\) does not always guarantee the extinction of dengue from the population.

Table 3 Possible positive roots of polynomial in (12) using descartes rules of signs for the case of \(R_0>1\).
Full size table
Table 4 Possible positive roots of polynomial in (12) using descartes rules of signs for the case of \(R_0<1\).
Full size table

Special case of the endemic equilibrium

Based on Theorem 4.2, the disease-free equilibrium is globally asymptotically stable, which means that the existence of backward bifurcation will not occur when the disease-induced death rate is zero. We employ the special case for assume to ignore the disease-induced death rate \(\left( {\tau }_m={\tau }_f=0\right)\). Hence, we represent \(N^*_h=\frac{{\mathrm {\Lambda }}_{hm}}{{\mu }_{hm}}+\frac{{\mathrm {\Lambda }}_{hf}}{{\mu }_{hf}}\) and substitute into Eq. (10), the force infection \({\kappa }^*_h\) fulfill the quadratic equation

$$\begin{aligned} d_0{{\kappa }^*_h}^2+d_1{\kappa }^*_h+d_2=0, \end{aligned}$$
(13)

with

$$\begin{aligned} d_0&=\frac{{\mu }_v{\beta }_v\gamma \left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) \left( {\mathrm {\Lambda }}_{hm}m_2+{\mathrm {\Lambda }}_{hf}m_1\right) }{{\mu }_{hm}{\mu }_{hf}}+\frac{{\mu }^2_v\gamma m_1m_2{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2}{{\mu }^2_{hm}{\mu }^2_{hf}},\\ d_1&=\frac{{\mu }_v{\beta }_v\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) \left( {\mathrm {\Lambda }}_{hm}m_2{\mu }_{hf}+\gamma {\mathrm {\Lambda }}_{hf}m_1{\mu }_{hm}\right) }{{\mu }_{hm}{\mu }_{hf}}+\frac{{\mu }^2_vm_1m_2\gamma {\mu }_{hm}{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2}{{\mu }^2_{hm}{\mu }^2_{hf}}\left( 1-R_{0m}\right) \\& \quad +\frac{{\mu }^2_vm_1m_2\gamma {\mu }_{hf}{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2}{{\mu }^2_{hm}{\mu }^2_{hf}}\left( 1-R_{0f}\right) ,\\ d_2&=\frac{{\mu }^2_vm_1m_2{\mu }_{hm}{\mu }_{hf}{\left( {\mathrm {\Lambda }}_{hm}{\mu }_{hf}+{\mathrm {\Lambda }}_{hf}{\mu }_{hm}\right) }^2}{{\mu }^2_{hm}{\mu }^2_{hf}}\left( 1-R^2_0\right). \end{aligned}$$

Suppose \(d_2>0\Leftrightarrow R^2_0<1\Leftrightarrow R_0<1\). Since \(R_{0m}<R^2_0\) and \(R_{0f}<R^2_0\), we can conclude \(R_{0m}<R^2_0<1\Leftrightarrow R_{0m}<1\) and \(R_{0f}<R^2_0<1\Leftrightarrow R_{0f}<1\). It is clear that we have \(1-R_{0m}>0\) and \(1-R_{0f}>0\). Furthermore, when \(d_2>0\) is fulfill, then \(d_1>0\). This indicates the model never has two endemic equilibrium and also the backward bifurcation does not occur when we ignore the disease-induced death rate. Thus, we obtain the following results.

Theorem 4.4

Suppose the disease-induced death rate of the system (1) is ignored \(\left( {\tau }_m={\tau }_f=0\right)\). Then the system (1) has:

  1. 1.

    A unique endemic equilibrium that exist in \(\Omega\) if \(d_2<0\) \((\mathrm {i.e.}\ R_0>1)\).

  2. 2.

    A unique endemic equilibrium that exist in \(\Omega\) if \(d_1<0\) and either \(d_2=0\) \((\mathrm {i.e.\ }R_0=1)\) or \(d^2_1-4d_0d_2=0\).

  3. 3.

    No endemic equilibrium otherwise.

Global stability analysis of endemic equilibrium

Suppose

$$\begin{aligned}{\mathrm {\Omega }}_0=\left\{ M\in \mathrm {\Omega }:I_v=I_m=I_f=0\right\} ,\end{aligned}$$

with \(M=\left( S_v\left( t\right) ,I_v\left( t\right) ,S_m\left( t\right) ,S_f\left( t\right) ,I_m\left( t\right) ,I_f\left( t\right) ,R_m\left( t\right) ,R_f\left( t\right) \right)\) and \({\mathrm {\Omega }}_0\) is defined as the stable manifold of non-endemic equilibrium \(\left( E_0\right)\). The global stability of endemic equilibrium is given in the following theorem.

Theorem 4.5

The endemic equilibrium \(\left( E^*\right)\) in special case is globally asymptotically stable in the interior of region \(\Omega \backslash { \Omega }_0\) if \(R_0>1\).

Proof

We use Goh-Volterra type Lyapunov function \(\mathcal {L}\ :\ \Omega \backslash { \Omega }_0\rightarrow \mathbb {R}\) defined as

$$\begin{aligned} \mathfrak {L}&=\left( S_v-S^*_v-S^*_v{\textrm{ln} \frac{S_v}{S^*_v}\ }\right) +\left( I_v-I^*_v-I^*_v{\textrm{ln} \frac{I_v}{I^*_v}\ }\right) + k_1 \left( S_m-S^*_m-S^*_m{\textrm{ln} \frac{S_m}{S^*_m}\ }\right) + k_2 \left( S_f-S^*_f-S^*_f{\textrm{ln} \frac{S_f}{S^*_f}\ }\right) \\& \quad + k_1 \left( I_m-I^*_m-I^*_m{\textrm{ln} \frac{I_m}{I^*_m}\ }\right) + k_2 \left( I_f-I^*_f-I^*_f{\textrm{ln} \frac{I_f}{I^*_f}\ }\right), \end{aligned}$$

with

$$\begin{aligned} k_1= \frac{\beta _v I_m^* S_v^*}{\beta _h I_v^* S_m^*}, \, \, \, k_2= \frac{\beta _v I_f^* S_v^*}{\gamma \beta _h I_v^* S_f^*}. \end{aligned}$$

The time derivative of \(\mathcal {L}\) is

$$\begin{aligned} \frac{d\mathfrak {L}}{dt}=&\left( \frac{dS_v}{dt}-\frac{S^*_v}{S_v}\frac{dS_v}{dt}\right) +\left( \frac{dI_v}{dt}-\frac{I^*_v}{I_v}\frac{dI_v}{dt}\right) +k_1\left( \frac{dS_m}{dt}-\frac{S^*_m}{S_m}\frac{dS_m}{dt}\right) +k_2\left( \frac{dS_f}{dt}-\frac{S^*_f}{S_f}\frac{dS_f}{dt}\right) + \\& \quad k_1\left( \frac{dI_m}{dt}-\frac{I^*_m}{I_m}\frac{dI_m}{dt}\right) +k_2\left( \frac{dI_f}{dt}-\frac{I^*_f}{I_f}\frac{dI_f}{dt}\right) \end{aligned}$$
$$\begin{aligned} \Longleftrightarrow \frac{d\mathfrak {L}}{dt}=\left( 1-\frac{S^*_v}{S_v}\right) \frac{dS_v}{dt}+\left( 1-\frac{I^*_v}{I_v}\right) \frac{dI_v}{dt}+k_1\left( 1-\frac{S^*_m}{S_m}\right) \frac{dS_m}{dt}+k_2\left( 1-\frac{S^*_f}{S_f}\right) \frac{dS_f}{dt}+k_1\left( 1-\frac{I^*_m}{I_m}\right) \frac{dI_m}{dt}+k_2\left( 1-\frac{I^*_f}{I_f}\right) \frac{dI_f}{dt}. \end{aligned}$$
(14)

Subtituted system (1) into Eq. (14) we get

$$\begin{aligned} \frac{d\mathfrak {L}}{dt}&=\left( 1-\frac{S^*_v}{S_v}\right) \left[ {\mathrm {\Lambda }}_v-\frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vS_v\right] +\left( 1-\frac{I^*_v}{I_v}\right) \left[ \frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vI_v\right] \\& \quad +k_1\left( 1-\frac{S^*_m}{S_m}\right) \left[ {\mathrm {\Lambda }}_{hm}-\frac{{\beta }_hI_v}{N_h}S_m-{\mu }_{hm}S_m\right] +k_2\left( 1-\frac{S^*_f}{S_f}\right) \left[ {\mathrm {\Lambda }}_{hf}-\frac{\gamma {\beta }_hI_v}{N_h}S_f-{\mu }_{hf}S_f\right] \nonumber \\& \quad +k_1\left( 1-\frac{I^*_m}{I_m}\right) \left[ \frac{{\beta }_hI_v}{N_h}S_m-m_1I_m\right] +k_2\left( 1-\frac{I^*_f}{I_f}\right) \left[ \frac{\gamma {\beta }_hI_v}{N_h}S_f-m_2I_f\right] .\nonumber \end{aligned}$$
(15)

At equilibrium, from system (1) we have relation:

$$\begin{aligned}&{\mathrm {\Lambda }}_v=\frac{{\beta }_v\left( I^*_m+I^*_f\right) }{N^*_h}S^*_v+{\mu }_vS^*_v, \ \ {\mu }_v=\frac{{\beta }_v\left( I^*_m+I^*_f\right) }{N^*_hI^*_v}S^*_v, \ \ {\mathrm {\Lambda }}_{hm}=\frac{{\beta }_hI^*_v}{N^*_h}S^*_m+{\mu }_{hm}S^*_m, \nonumber \\& \quad {\mathrm {\Lambda }}_{hf}=\frac{\gamma {\beta }_hI^*_v}{N^*_h}S^*_f+{\mu }_{hf}S^*_f, \ \ m_1=\frac{{\beta }_hI^*_v}{N^*_hI^*_m}S^*_m, m_2=\frac{\gamma {\beta }_hI^*_v}{N^*_hI^*_f}S^*_f. \end{aligned}$$
(16)

Replacing relation at steady state (16) into Eq. (15) and after some simplification we have:

$$\begin{aligned} \frac{d\mathfrak {L}}{dt}&=\frac{{\beta }_v I^*_m}{N^*_h}S^*_v\left( 2-\frac{S^*_v}{S_v}+\frac{I_m N^*_h}{I^*_m N_h}-\frac{I_m S_v I^*_v N^*_h}{I^*_m S^*_v I_v N_h}-\frac{I_v}{I^*_v}\right) +\frac{{\beta }_v I^*_f}{N^*_h}S^*_v\left( 2-\frac{S^*_v}{S_v}+\frac{I_f N^*_h}{I^*_f N_h}-\frac{I_f S_v I^*_v N^*_h}{I^*_f S^*_v I_v N_h}-\frac{I_v}{I^*_v}\right) \\& \quad +{\mu }_vS^*_v\left( 2-\frac{S^*_v}{S_v}-\frac{S_v}{S^*_v}\right) +k_1\frac{{\beta }_hI^*_v}{N^*_h}S^*_m\left( 2-\frac{S^*_m}{S_m}-\frac{I_v N^*_h}{I^*_v N_h}-\frac{I^*_m S_m I_v N^*_h}{I_m S^*_m I^*_v N_h}-\frac{I_m}{I^*_m}\right) +k_1{\mu }_{hm}S^*_m\left( 2-\frac{S^*_m}{S_m}-\frac{S_m}{S^*_m}\right) \\& \quad +k_2\frac{\gamma {\beta }_hI^*_v}{N^*_h}S^*_f\left( 2-\frac{S^*_f}{S_f}-\frac{I_v N^*_h}{I^*_v N_h}-\frac{I^*_f S_f I_v N^*_h}{I_f S^*_f I^*_v N_h}-\frac{I_f}{I^*_f}\right) +k_2{\mu }_{hf}S^*_f\left( 2-\frac{S^*_f}{S_f}-\frac{S_f}{S^*_f}\right) \end{aligned}$$

Subtitute \(k_1\) and \(k_2\), we get

$$\begin{aligned} \frac{d\mathfrak {L}}{dt}&=\frac{{\beta }_v I^*_m}{N^*_h}S^*_v\left( 4-\frac{S^*_v}{S_v}-\frac{I_m S_v I^*_v N^*_h}{I^*_m S^*_v I_v N_h}-\frac{S^*_m}{S_m}-\frac{I^*_m S_m I_v N^*_h}{I_m S^*_m I^*_v N_h}+\frac{I_m N^*_h}{I^*_m N_h}-\frac{I_m}{I^*_m}+\frac{I_v N^*_h}{I^*_v N_h}-\frac{I_v}{I^*_v}\right) \\& \quad +\frac{{\beta }_v I^*_f}{N^*_h}S^*_v\left( 4-\frac{S^*_v}{S_v}-\frac{I_f S_v I^*_v N^*_h}{I^*_f S^*_v I_v N_h}-\frac{S^*_f}{S_f}-\frac{I^*_f S_f I_v N^*_h}{I_f S^*_f I^*_v N_h}+\frac{I_f N^*_h}{I^*_f N_h}-\frac{I_f}{I^*_f}+\frac{I_v N^*_h}{I^*_v N_h}-\frac{I_v}{I^*_v}\right) \\& \quad +{\mu }_vS^*_v\left( 2-\frac{S^*_v}{S_v}-\frac{S_v}{S^*_v}\right) +\frac{\beta _v I_m^* S_v^*}{\beta _h I_v^* S_m^*}{\mu }_{hm}S^*_m\left( 2-\frac{S^*_m}{S_m}-\frac{S_m}{S^*_m}\right) +\frac{\beta _v I_f^* S_v^*}{\gamma \beta _h I_v^* S_f^*}{\mu }_{hf}S^*_f\left( 2-\frac{S^*_f}{S_f}-\frac{S_f}{S^*_f}\right) \end{aligned}$$

Since arithmetic mean is greater than or equal to geometric mean, then it is guaranteed

$$\begin{aligned}\left( 4-\frac{S^*_v}{S_v}-\frac{I_m S_v I^*_v N^*_h}{I^*_m S^*_v I_v N_h}-\frac{S^*_m}{S_m}-\frac{I^*_m S_m I_v N^*_h}{I_m S^*_m I^*_v N_h}+\frac{I_m N^*_h}{I^*_m N_h}-\frac{I_m}{I^*_m}+\frac{I_v N^*_h}{I^*_v N_h}-\frac{I_v}{I^*_v}\right) \le 0,\end{aligned}$$
$$\begin{aligned}\left( 4-\frac{S^*_v}{S_v}-\frac{I_f S_v I^*_v N^*_h}{I^*_f S^*_v I_v N_h}-\frac{S^*_f}{S_f}-\frac{I^*_f S_f I_v N^*_h}{I_f S^*_f I^*_v N_h}+\frac{I_f N^*_h}{I^*_f N_h}-\frac{I_f}{I^*_f}+\frac{I_v N^*_h}{I^*_v N_h}-\frac{I_v}{I^*_v}\right) \le 0\end{aligned}$$

if we assume \((N_h=N^*_h)\) which is a special case of endemic equilibrium. Suppose this assumption hold, we have

$$\begin{aligned} \frac{d\mathfrak {L}}{dt}&=\frac{{\beta }_v I^*_m}{N^*_h}S^*_v\left( 4-\frac{S^*_v}{S_v}-\frac{I_m S_v I^*_v}{I^*_m S^*_v I_v}-\frac{S^*_m}{S_m}-\frac{I^*_m S_m I_v}{I_m S^*_m I^*_v}\right) +\frac{{\beta }_v I^*_f}{N^*_h}S^*_v\left( 4-\frac{S^*_v}{S_v}-\frac{I_f S_v I^*_v}{I^*_f S^*_v I_v}-\frac{S^*_f}{S_f}-\frac{I^*_f S_f I_v}{I_f S^*_f I^*_v}\right) \\& \quad +{\mu }_vS^*_v\left( 2-\frac{S^*_v}{S_v}-\frac{S_v}{S^*_v}\right) +\frac{\beta _v I_m^* S_v^*}{\beta _h I_v^* S_m^*}{\mu }_{hm}S^*_m\left( 2-\frac{S^*_m}{S_m}-\frac{S_m}{S^*_m}\right) +\frac{\beta _v I_f^* S_v^*}{\gamma \beta _h I_v^* S_f^*}{\mu }_{hf}S^*_f\left( 2-\frac{S^*_f}{S_f}-\frac{S_f}{S^*_f}\right) \end{aligned}$$

Hence, its clear that

$$\begin{aligned}\left( 4-\frac{S^*_v}{S_v}-\frac{I_m S_v I^*_v}{I^*_m S^*_v I_v}-\frac{S^*_m}{S_m}-\frac{I^*_m S_m I_v}{I_m S^*_m I^*_v}\right) \le 0, \left( 4-\frac{S^*_v}{S_v}-\frac{I_f S_v I^*_v}{I^*_f S^*_v I_v}-\frac{S^*_f}{S_f}-\frac{I^*_f S_f I_v}{I_f S^*_f I^*_v}\right) \le 0,\end{aligned}$$
$$\begin{aligned}\left( 2-\frac{S^*_v}{S_v}-\frac{S_v}{S^*_v}\right) \le 0,\left( 2-\frac{S^*_m}{S_m}-\frac{S_m}{S^*_m}\right) \le 0,\left( 2-\frac{S^*_f}{S_f}-\frac{S_f}{S^*_f}\right) \le 0.\end{aligned}$$

Therefore, \(\frac{d\mathcal {L}}{dt}\le 0\) since all the parameters are positive, with \(\frac{d\mathcal {L}}{dt}=0\) if only if \(S_v=S^*_v\), \(I_v=I^*_v\), \(S_m=S^*_m\), \(S_f=S^*_f\), \(I_m=I^*_m\), and \(I_f=I^*_f\). The endemic equilibrium point \(E_1\) in special case is unique and exists if \(R_0>1\) and the singleton set \(\left\{ E^*\right\}\) is the biggest compact invariant set in \(\left\{ \left( S_v,\ I_v,S_m,\ S_f,\ I_m,I_f\right) \in \mathrm {\Omega }\mathrm {\ :}\frac{d\mathcal {L}}{dt}=0\right\}\). According to LaSalle’s invariance principle31 the endemic equilibrium point \(E_1\) in special case globally asymptotically stable in the interior of region \(\mathrm {\Omega }\mathrm {\backslash }{\mathrm {\Omega }}_0\) if \({\textrm{R}}_0\mathrm {>1}\). \(\square\)

Sensitivity analysis

In this section, we consider the sensitivity analysis to determine which parameter has the potential to affect the basic reproduction number as state in32. Utilising the sensitivity index, one can quantify the sensitivity analysis associated with variables. The sensitivity index \(R_0\) with respect to some parameter, say a is given by \({\mathrm {\Upsilon }}^{R_0}_a=\frac{\partial R_0}{\partial a}\times \frac{a}{R_0}\). The sensitivity indices for \(R_0\) in Table 5 can now be calculated using the parameter values from Table 2.

Table 5 Sensitivity index of the parameters in \(R_0\).
Full size table

According to Table 5, the positive sensitivity index indicates that increasing the parameter values will also increase the value of \(R_0\). Conversely, the negative sensitivity index indicates that increasing the value of the parameter will result in a drop in the value of \(R_0\). The largest and smallest index from sensitivity index shows the most influential parameters on changes in \(R_0\), that is \({\mu }_v,{\mathrm {\Lambda }}_v,\ {\beta }_v,\ {\mathrm {\Lambda }}_{hm},\) and \({\beta }_h\). Furthermore the simulation of the change of \(R_0\) to the parameters \({\mu }_v\) with \({\beta }_v\) and \({\beta }_h\) with \({\mathrm {\Lambda }}_{hm}\) as follows.

Fig. 4
figure 4

Contour plot of \(R_0\) in plane \({\mu }_v-{\beta }_v\) and plane \({\beta }_h-{\mathrm {\Lambda }}_{hm}\).

Full size image

Based on contour plot in Fig. 4, it can be seen that the parameter \({\beta }_v\) and \({\beta }_h\) has a positive relation, however the parameter \({\mu }_v\) and \({\mathrm {\Lambda }}_{hm}\) has a negative relation. This corresponds to the sign of index sensitivity in Table 5.

Optimal control problem

In this section, we investigate the optimal control strategy on DHF model (1). Two control variables are implemented, namely fumigation (\(u_1\)) and prevention (\(u_2\)). Prevention efforts comprise using mosquito nets, mosquito repellent, and clothes that cover the body as possible, while insecticides enclose spraying and fumigation against mosquitoes.

The DHF model with control variables is state as follows.

$$\begin{aligned} \frac{dS_v}{dt}&={\mathrm {\Lambda }}_v-\frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vS_v-\delta u_1S_v, \nonumber \\ \frac{dI_v}{dt}&=\frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vI_v-\delta u_1I_v,\nonumber \\ \frac{dS_m}{dt}&={\mathrm {\Lambda }}_{hm}-\left( 1-u_2\right) \frac{{\beta }_hI_v}{N_h}S_m-{\mu }_{hm}S_m,\nonumber \\ \frac{dS_f}{dt}&={\mathrm {\Lambda }}_{hf}-\left( 1-u_2\right) \gamma \ \frac{{\beta }_hI_v}{N_h}S_f-{\mu }_{hf}S_f,\nonumber \\ \frac{dI_m}{dt}&=\left( 1-u_2\right) \frac{{\beta }_hI_v}{N_h}S_m-\left( {\theta }_m+{\tau }_m+{\mu }_{hm}\right) I_m,\nonumber \\ \frac{dI_f}{dt}&=\left( 1-u_2\right) \gamma \frac{{\beta }_{hf}I_v}{N_h}S_f-\left( {\theta }_f+{\tau }_f+{\mu }_{hf}\right) I_f,\nonumber \\ \frac{dR_m}{dt}&={\theta }_mI_m-{\mu }_{hm}R_m,\nonumber \\ \frac{dR_f}{dt}&={\theta }_fI_f-{\mu }_{hf}R_f. \end{aligned}$$
(17)

The control function \(u_1\) and \(u_2\) are defined on interval \(\left[ 0,t_f\right]\), where \(0\le u_i\left( t\right) \le 1\), \(t\in \left[ 0,t_f\right]\), \(i=1,2\), and \(t_f\) denotes the end time of the controls. Our goal is to minimize the number of infected mosquitoes, infected male and female humans populations, also the cost of applying fumigation and prevention controls as low as possible. For this, we consider the objective function

$$\begin{aligned} J\left( u_1,u_2\right) =\int ^{t_f}_0{\left( A_1I_v+A_2I_m+A_3I_f+\frac{1}{2}C_1u^2_1+\frac{1}{2}C_2u^2_2\right) dt}, \end{aligned}$$
(18)

with \(A_1\), \(A_2\), and \(A_3\) are weights of the objective function for \(I_v\), \(I_m\), and \(I_f\) respectively, \(C_1\) and \(C_2\) are weight parameters for fumigation and prevention respectively. We use the quadratic cost function for J to describe the cost of control efforts33,34. This quadratic function can represent a non-linear increase in costs associated with the implementation of control measures in the field.

To solve the optimal control problem, we use Pontryagin’s Maximum Principle35. This principle convert the minimizing of the cost function (18) with constraint (17) into the problem of minimizing the Hamiltonian function H that provided by

$$\begin{aligned} H = A_1I_v+A_2I_m+A_3I_f+\frac{1}{2}C_1u^2_1+\frac{1}{2}C_2u^2_2 + \Sigma _{i=1}^8 \lambda _i f_i, \end{aligned}$$
(19)

where \(f_i\) asserts the right-hand side of the model (17) and \(\lambda _i, i=1, 2,..., 8\) represents the adjoint or co-state variables.

The co-state equations are obtained from the negative derivative of the Hamilton function that shown by the following equations.

$$\begin{aligned} \dot{{\lambda }_1}&=\left( {\lambda }_1-{\lambda }_2\right) \frac{{\beta }_v\left( I_m+I_f\right) }{N_h}+{\lambda }_1\left( {\mu }_v+\delta u_1\right) ,\\ \dot{{\lambda }_2}&=-A_1+\left( {\lambda }_3-{\lambda }_5\right) \left( 1-u_2\right) \frac{{\beta }_hS_m}{N_h}+\left( {\lambda }_4-{\lambda }_6\right) \left( 1-u_2\right) \frac{\gamma {\beta }_hS_f}{N_h}+{\lambda }_2\left( {\mu }_v+\delta u_1\right) ,\\ \dot{{\lambda }_3}&=\left( {\lambda }_2-{\lambda }_1\right) \frac{{\beta }_v\left( I_m+I_f\right) S_v}{N^2_h}+\left( {\lambda }_3-{\lambda }_5\right) \left( 1-u_2\right) \frac{{\beta }_hI_vN_h-{\beta }_hI_vS_m}{N^2_h}+\left( {\lambda }_6-{\lambda }_4\right) \left( 1-u_2\right) \frac{\gamma {\beta }_hI_vS_f}{N^2_h}+{\lambda }_3{\mu }_{hm},\\ \dot{{\lambda }_4}&=\left( {\lambda }_2-{\lambda }_1\right) \frac{{\beta }_v\left( I_m+I_f\right) S_v}{N^2_h}+\left( {\lambda }_5-{\lambda }_3\right) \left( 1-u_2\right) \frac{{\beta }_hI_vS_m}{N^2_h}+\left( {\lambda }_4-{\lambda }_6\right) \left( 1-u_2\right) \frac{\gamma {\beta }_hI_vN_h-\gamma {\beta }_hI_vS_f}{N^2_h}+{\lambda }_4{\mu }_{hm},\\ \dot{{\lambda }_5}&=-A_2+\left( {\lambda }_1-{\lambda }_2\right) \frac{{\beta }_vS_vN_h-{\beta }_v{I_mS}_v}{N^2_h}+\left( {\lambda }_2-{\lambda }_1\right) \frac{{\beta }_vI_fS_v}{N^2_h}+\left( {\lambda }_5-{\lambda }_3\right) \left( 1-u_2\right) \frac{{\beta }_hI_vS_m}{N^2_h}\\& \quad +\left( {\lambda }_6-{\lambda }_4\right) \left( 1-u_2\right) \frac{\gamma {\beta }_hI_vS_f}{N^2_h}+\left( {\lambda }_5-{\lambda }_7\right) {\theta }_m+{\lambda }_5\left( {\tau }_m+{\mu }_{hm}\right) ,\\ \dot{{\lambda }_6}&=-A_3+\left( {\lambda }_1-{\lambda }_2\right) \frac{{\beta }_vS_vN_h-{\beta }_v{I_fS}_v}{N^2_h}+\left( {\lambda }_2-{\lambda }_1\right) \frac{{\beta }_vI_mS_v}{N^2_h}+\left( {\lambda }_5-{\lambda }_3\right) \left( 1-u_2\right) \frac{{\beta }_hI_vS_m}{N^2_h}\\& \quad +\left( {\lambda }_6-{\lambda }_4\right) \left( 1-u_2\right) \frac{\gamma {\beta }_hI_vS_f}{N^2_h}+\left( {\lambda }_6-{\lambda }_8\right) {\theta }_f+{\lambda }_6\left( {\tau }_f+{\mu }_{hf}\right) ,\\ \dot{{\lambda }_7}&=\left( {\lambda }_2-{\lambda }_1\right) \frac{{\beta }_v\left( I_m+I_f\right) S_v}{N^2_h}+\left( {\lambda }_5-{\lambda }_3\right) \left( 1-u_2\right) \frac{{\beta }_hI_vS_m}{N^2_h}+\left( {\lambda }_6-{\lambda }_4\right) \left( 1-u_2\right) \frac{\gamma {\beta }_hI_vS_f}{N^2_h}+{\lambda }_7{\mu }_{hm},\\ \dot{{\lambda }_8}&=\left( {\lambda }_2-{\lambda }_1\right) \frac{{\beta }_v\left( I_m+I_f\right) S_v}{N^2_h}+\left( {\lambda }_5-{\lambda }_3\right) \left( 1-u_2\right) \frac{{\beta }_hI_vS_m}{N^2_h}+\left( {\lambda }_6-{\lambda }_4\right) \left( 1-u_2\right) \frac{\gamma {\beta }_hI_vS_f}{N^2_h}+{\lambda }_8{\mu }_{hf}, \end{aligned}$$

with the transversality conditions \({\lambda }_i\left( t_f\right) =0,\ i=1,2,...,8\).

The optimal solutions of \(u_1\) and \(u_2\) are given by

$$\begin{aligned} u^*_1&={\textrm{min} \left\{ 1,{max \left( 0,\delta \left( \frac{{\lambda }_1S_v+{\lambda }_2I_v}{C_1}\right) \right) \ }\right\} \ },\\ u^*_2&={\textrm{min} \left\{ 1,{max \left( 0,\left( {\lambda }_5-{\lambda }_3\right) \frac{{\beta }_hI_v}{C_2N_h}S_m+\left( {\lambda }_6-{\lambda }_4\right) \frac{\gamma {\beta }_hI_v}{C_2N_h}S_f\right) \ }\right\} \ }. \end{aligned}$$

By assuming \(A_1=A_2=A_3=1\), \(C_1=20000\), \(C_2=100000\), \(\delta =0.7\), and the other parameters are refer to Table 3, we solve the numerical optimal control simulation using backward and forward sweep as described in36. Hence, the optimally of the model is yielded, which are comprised of the model without control, the adjoint system and the optimality conditions. To ascertain which strategy or combination gives the efficient methods of controlling DHF, we considered the following strategies for our simulation. Strategy 1 use the fumigation only \((u_2=0)\), Strategy 2 employ the prevention only \((u_1=0)\), and Strategy 3 utilise the combination of fumigation and prevention. The result of the simulation for the comparison \(I_v\), \(I_m\), and \(I_f\) without and with control are demonstrated in Fig. 5. Looking at Fig. 5, it is apparent that when the control strategies are implemented, there is a prominent reduction in the number of infected mosquito populations compared to no control. Likewise, in both infected male and female human populations, there are a significant reduction when control strategies are implemented compared to no intervention. The control profiles of each strategy are given in Fig. 6.

Fig. 5
figure 5

Comparison of the populations \(I_v\), \(I_m\), and \(I_f\) without and with control of each strategies.

Full size image
Fig. 6
figure 6

Control Profiles of Strategy 1, Strategy 2, and Strategy 3, respectively.

Full size image

Cost effectiveness analysis

In this section, we will assess and compare the advantages and disadvantages of control measures for each method implemented in the previous section. We will use the Infection Averted Ratio (IAR), Average Cost-Effectiveness Ratio (ACER), and Incremental Cost-Effectiveness Ratio (ICER) as metrics for evaluation. These economic evaluations are mathematically defined in9,37 as follows.

$$\begin{aligned}\mathrm {IAR=}\frac{\mathrm {Cumulative\ infected\ averated}}{\mathrm {Cumulative\ recovered}}.\end{aligned}$$

The cumulative infected average is calculated as the difference between the total number of infectious individuals in the uncontrolled case and the total number of infectious individuals with control, summed over time. To be more precise

$$\begin{aligned}\textrm{IAR}=\frac{\int ^{t_f}_0{\left( \left( I_m\left( t\right) -I^*_m\left( t\right) \right) +\left( I_f\left( t\right) -I^*_f\left( t\right) \right) \right) \ dt}}{\int ^{t_f}_0{\left( R^*_m\left( t\right) +R^*_f\left( t\right) \right) \ dt}},\end{aligned}$$

with the subscript notation * is used to indicate the optimal solutions linked with the appropriate approach. The optimal approach for utilising IAR is the technique with the highest ratio.

$$\begin{aligned}\mathrm {ACER=}\frac{\mathrm {Total\ cost\ invested\ on\ the\ intervention}}{\mathrm {Total\ number\ of\ infectious\ averted}}.\end{aligned}$$

The total cost invested on the intervention is assumed as the value of the objective function of each strategies based on Eq. 18. The most cost-effective strategy when using ACER is the strategy with the lowest ratio.

$$\begin{aligned}\mathrm {ICER=}\frac{\mathrm {Difference\ in\ cost\ produced\ by\ strategies\ }i\mathrm {\ and\ }j}{\mathrm {Difference\ in\ the\ total\ number\ of\ infections\ averted\ i}\mathrm {n\ strategies\ }i\mathrm {\ and\ }j}.\end{aligned}$$

Hence, ICER is employed to evaluate and compare two distinct tactics, denoted as i and j. The ICER numerator includes the disparities in intervention cost, averted illness cost, costs of prevented case, and saved productivity losses, if relevant. The denominator is the difference in health outcomes. We calculate the cost of a strategy designed for ACER. When comparing multiple intervention options, they are evaluated incrementally by comparing each intervention with the next less effective alternative in terms of the overall number of infections prevented38,39,40.

The result of calculation IAR and ACER is presented on Table 6. Based on Table 6, the Strategy 2 and 3 have a very close value to averts the highest number of infections and produces the highest ratio (IAR = 0.6) and lowest average cost-effectiveness ratio (ACER = 2.3). Hence, they are the most effective. Given the uncertainty in determining the most efficient approach to implement, we turned to the incremental cost-effectiveness ratio (ICER) to identify the most cost-effective option.

Table 6 Comparison of IAR and ACER for each intervention strategies.
Full size table
Table 7 Comparison of ICER for each intervention strategies.
Full size table

The ICER indexes, as reported in Table 7, are obtained as follows.

$$\begin{aligned} \textrm{ICER}\left( \textrm{1}\right)&=\frac{492,440-0}{1.3661\times {10}^4-0}= 31.435, \\ \textrm{ICER}\left( 2\right)&=\frac{336,550-492,440}{1.4328\times {10}^5-1.3661\times {10}^4}= - 0.717,\\ \textrm{ICER}\left( 3\right)&=\frac{335,160-336,550}{1.4386\times {10}^5-1.4328\times {10}^5}= - 0.240. \end{aligned}$$

Comparing Strategy 1 and Strategy 2, the use of strategy 2 is cost saving over Strategy 1. This indicate the Strategy 1 is less effective and more costly than the other strategy. Hence, Strategy 1 is removed. Furthermore we recalculation the index of ICER as follows.

$$\begin{aligned} \textrm{ICER}\left( 2\right)&=\frac{336,550-0}{1.4328\times {10}^5-0}=2.349,\\ \textrm{ICER}\left( 3\right)&=\frac{335,160-336,550}{1.4386\times {10}^5-1.4328\times {10}^5}= - 0.240. \end{aligned}$$

Comparing Strategy 2 and Strategy 3, the use of Strategy 3 is cost saving over Strategy 2. This indicate the Strategy 2 is less effective and more costly than the other strategy. Hence, Strategy 2 is removed. Our result suggest that Strategy 3 is the most cost-effective intervention associated with the incremental cost-effectiveness ratio (ICER). This finding supports the work of9,12 that the integration of the prevention and fumigation is the best strategy to minimize the number of dengue-infected hosts and vector in the population.

Sex classification impact in optimal control

In this section we try to simulate optimal control by differentiated prevention control to male and female human populations. Prevention in the male human population will be increased because the male population is more susceptible to infection. Next, model (17) will be reconstructed as follows.

$$\begin{aligned} \frac{dS_v}{dt}&={\mathrm {\Lambda }}_v-\frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vS_v-\delta u_1S_v, \nonumber \\ \frac{dI_v}{dt}&=\frac{{\beta }_v\left( I_m+I_f\right) }{N_h}S_v-{\mu }_vI_v-\delta u_1I_v,\nonumber \\ \frac{dS_m}{dt}&={\mathrm {\Lambda }}_{hm}-\zeta \left( 1-u_2\right) \frac{{\beta }_hI_v}{N_h}S_m-{\mu }_{hm}S_m,\nonumber \\ \frac{dS_f}{dt}&={\mathrm {\Lambda }}_{hf}-\left( 1-u_2\right) \gamma \ \frac{{\beta }_hI_v}{N_h}S_f-{\mu }_{hf}S_f, \nonumber \\ \frac{dI_m}{dt}&=\zeta \left( 1-u_2\right) \frac{{\beta }_hI_v}{N_h}S_m-\left( {\theta }_m+{\tau }_m+{\mu }_{hm}\right) I_m,\nonumber \\ \frac{dI_f}{dt}&=\left( 1-u_2\right) \gamma \frac{{\beta }_{hf}I_v}{N_h}S_f-\left( {\theta }_f+{\tau }_f+{\mu }_{hf}\right) I_f,\nonumber \\ \frac{dR_m}{dt}&={\theta }_mI_m-{\mu }_{hm}R_m,\nonumber \\ \frac{dR_f}{dt}&={\theta }_fI_f-{\mu }_{hf}R_f. \end{aligned}$$
(20)

with \(\zeta\) is an additional parameter aimed at increasing prevention in the male human population. The control application that will be simulated is strategy 3 (combination of fumigation and prevention). The results of this comparison are presented in Fig. 7.

Fig. 7
figure 7

Comparison of infected human population with and without differentiated prevention.

Full size image

Based on Fig. 7, the differentiated in prevention between male and female human populations has very significant in eliminating the infected human population. It can be seen that when we do not differentiate the treatment, the optimal application of controls \(u_1\) and \(u_2\) can reduce the number of sufferers by \(1.4386\times 10^5\) populations. However, if we differentiate the treatment efforts, the application of these controls can reduce the number of sufferers by \(1.5247\times 10^5\) populations. Therefore, we suggest that prevention efforts should be differentiated for male and female, as male are more susceptible to DHF. For example, one potential approach is to adjust the formulation of mosquito repellents for males and females to enhance their effectiveness.

Conclusion

We constructed a sex clasification model to explore the DHF transmission dynamics in West Java Province, Indonesia. Based on the values of parameter estimation, the basic reproduction number is 1.0959. This finding indicate that DHF transmission is still endemic in West Java Province, Indonesia. Next, in analyzing the model, we obtained two equilibrria, namely a free-disease equilibrium \(\left( E_0\right)\) and an endemic equilibrium \(\left( E_1\right)\). The free-disease equilibrium is locally asymptotical stable if \(R_0<1\) and globally asymptotical stable if \(R_0<1\) in the condition of disease-induced death rate was ignored. Then, the endemic equilibrium in the condition of disease-induced death rate is globally asymptotically stable if \(R_0>1\). Based on ICER calculation, we conclude that implementing combination strategies of fumigation and prevention is the most effective and cost-efficient approach to controlling and reducing DHF cases. Furthermore, we recommend that prevention efforts be designed to address the differences between males and females. Differentiating prevention strategies based on sex could have a significant impact on reducing the DHF cases, as males and females may have different risk profiles and responses to preventive measures. Adapting prevention efforts to these differences could enhance the overall effectiveness of control programs and contribute to better disease management.

This study was limited by the absence of age classification, multi-strain infections, multi-region to capture human mobility, and seasonal factors. Although our model has demonstrated the importance of considering sex differences in dengue transmission, there is still room for improvement in other research directions. It is well known that children are more at risk of dengue exposure compared to adults. For example, in Indonesia, elementary school children typically wear short-sleeved shirts, making them more exposed to mosquito bites than adults, who often wear long sleeves at work. Hence, incorporating age classification into future models would be a valuable extension. Another possible research direction is the inclusion of individual-specific factors. As mentioned in41, people with larger body sizes, higher metabolic rates, and distinct odors may be more attractive to mosquitoes. Additionally, human mobility can be integrated into the model using a meta-population approach to capture spatial heterogeneity in dengue transmission dynamics. These extensions could enhance the model’s accuracy and applicability in public health planning.