Quantitative structure property relationship and multiattribute decision analysis of antianginal drugs using topological indices

Abstract

Angina is a condition characterized by chest pain or discomfort due to insufficient blood flow to the heart muscle. Effective management focuses on reducing symptoms and preventing disease progression through lifestyle modifications, medications, and interventional procedures. Timely diagnosis and treatment are crucial for enhancing patient quality of life. Designing and developing experimental drugs is challenging and costly, which makes mathematical and computational methods essential for efficient drug discovery. In this article, we introduce a novel molecular descriptor based on a graph theory-driven degree partitioning technique, integrated into a quantitative structure-property relationships (QSPR) framework. Using quadratic regression, we determine the optimal predictors for four key properties boiling point, enthalpy of vaporization, flash point, and index of refraction for sixteen anti-angina drugs based on nine degree-based topological indices. Furthermore, by combining these descriptors with the multi-attribute decision-making additive ratio assessment technique, we achieve robust and reliable drug rankings. Our innovative integration of a new molecular descriptor with advanced statistical and decision-making methods not only improves predictive accuracy but also provides a novel and efficient approach for the development and optimization of angina drug therapies.

Introduction

Graph theoretical applications in chemistry have increased significantly in the recent years. Chemical graph theory is a branch of mathematical chemistry based on topology and applies graph theory to the mathematical explanation of chemical procedures. In many areas of chemistry, graphs play an important part in the modeling of chemical compounds through the use of molecular structure. A molecular descriptor offers a more precise mathematical representation of a possible molecular structure. Molecular descriptors that are most frequently utilized are chemical bonding indices. The term topological indices is commonly utilized to characterize these chemical bonds. Since the concepts behind topological indices are derived from the concepts of graph theory, these are viewed as graph invariants. These molecular descriptors can be distance, degree, and neighborhood-based, as discussed by Balaban¹; Gutman²; Mondal et al.³.

To create novel medications, research is constantly conducted to treat angina patients and cure the illness. Although the procedure of designing and developing experimental drugs is expensive, time-consuming, and difficult. Mathematical and computational methods are crucial to accomplishing this objective in the best possible way. Topological indices: one of these computational and mathematical methods is widely employed in the medications utilized to treat different diseases. The topological index is a useful part or the result of specific standardized tests that are produced through a logical and computational method that transforms the chemical data given within a graphical representation of a molecules, as explained by Arockiaraj et al.⁴ and Paul et al.⁵.

The rising resistance of angina to existing medical treatments has discovered novel angina drugs as a significant topic to study in pharmaceutical research. QSPR modeling is essential for forecasting the biological impact of these medications based on the molecules. Using topological descriptors, which summarize the molecular structure in terms of connectivity and can significantly simplify drug property estimation is a crucial component of QSPR modeling. Imani et al.⁶ examined the quantitative structure activity relationship modeling of molecular properties for alzheimers disease using random forest. Abubakar et al.⁷ evaluated the QSPR analysis of 15 antituberculosis medicines using support vector regression and computed the neighborhood degree-based topological indices of these medications. Support vector regressions effectiveness was calculated by comparing it with classical linear regression. Awan et al.⁸ explained the topological indices and linear regression models of various compounds with potential antimalarial compounds, including quinine, primaquine, artemether, artelinic acid, modified triazoles, and others. Different beta-blockers used to treat cardiac disease and computed degree-based topological indices for each based on the M-polynomial were explored by Hasani and Ghods⁹. Kirana et al.¹⁰ analyzed Quinolone antibiotics using curvilinear regression models and the computation of eleven topological indices through QSPR analysis. The application of topological indices for estimating the usefulness of various medications utilized to treat blood cancer was the main objective of Zhang et al.¹¹. For a family of benzenoid hydrocarbon molecules, Ravi and Desikan¹² computed the reduced reverse degree based indices in the QSPR analysis. Hui et al.¹³ utilized topological descriptors as independent variables in both linear and multiple regression models to assess the chemical and physical properties of antiemetic medications. Degree-based topological descriptors and curvilinear regression models for thirteen skin cancer medications were analyzed by Khan et al.¹⁴.

An essential field of decision science that deals with difficult decision issues involving several different factors is multi-attribute decision-making. This method is crucial in scenarios where judgments cannot be made using a single criterion and substitutes for taking into consideration many variables to get a reasonable result. Applications of multi-attribute decision-making are found in many fields, such as public policy, engineering, business, and healthcare, where decisions frequently have important and far-reaching effects. For example, in the healthcare industry, multi-attribute decision-making can help choose the best course of action by weighing patient preferences, expenses, adverse reactions, and efficient implementation. The additive ratio assessment technique eliminates the influence of different measurement units and simplifies complex decision-making problems by using a relative indicator (utility degree) to identify the best alternative. This indicator can indicate the differences between the alternatives and the optimal solution. Zavadskas and Turskis¹⁵ introduced the additive ratio assessment method in 2010. Junior et al.¹⁶ developed a decision support system that used the additive ratio assessment method to calculate criteria, sub-criteria, and alternative assessment data to provide appropriate housing for potential purchasers. Arshad¹⁷ utilized the additive ratio assessment and entropy methodologies to help decision-makers evaluate potential warehouse locations that best satisfy the organizations operational and strategic goals. To determine a final ranking of company assessment data on supplier services, Wahyudi¹⁸ purposed to measure the extent of company experience with supplier services by applying the additive ratio assessment approach.

Recent advances in molecular descriptor development have significantly contributed to the field of QSPR modeling. For instance, innovative descriptor optimization techniques have enhanced the prediction of chemical properties^30,31. Other recent works have successfully integrated graph theory-based methodologies to capture complex molecular topologies, thereby improving model accuracy^32,33. Furthermore, the potential of degree partitioning techniques in representing finite graphs has been underscored in contemporary research^{34,35,36,37,38}. In our study, we build on these developments by introducing a new molecular descriptor based on a graph theory-based degree partitioning technique, which provides a robust and efficient representation of molecular topology. Comparative analysis with these recent studies confirms the enhanced predictive performance and novelty of our approach in the context of anti-angina drug evaluation.

Motivation

We used nine degree based topological indices to develop the QSPR model and evaluated the physiochemical properties of sixteen different medications. For the first time, angina drugs are being studied using degree based topological indices. We emphasize the importance of selecting medications for treating angina with prioritization based on factors such as patient preferences, cost-effectiveness, efficacy, safety, and accessibility. The results of the study may help determine which drug is most effective for helping angina patients in managing their symptoms, improving their quality of life, and taking better care of their illness. This study also identify the best-ranked angina medications that have not been previously studied.

Contribution

The following points summarize our work contribution to this study:

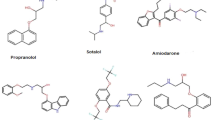
• There are nine topological indices and sixteen drug structures. By comparing topological indices with four physicochemical properties of the medications, QSPR models were developed to evaluate reliability. The computation procedure is carried out for angina drugs such as Acebutolol, Ranolazine, Metoprolol, Amlodipine, Atenolol, Carvedilol, Nitroglycerin, Nadolol, Amyl nitrite, Nicorandil, Propranolol, Molsidomine, Nicardipine, Nifedipine, Diltiazem, and Ivabradine. Then, using linear and quadratic regression analysis, the obtained values are assessed through QSPR modeling to investigate different physicochemical properties of the medications, including boiling point, enthalpy of vaporization, flash point, and index of refraction.

• The analysis of the graphical data is conducted using Microsoft Excel and Matlab to make a graph.

• We examined the relationship between the rankings produced by the multi-attribute decision-making technique and the computed topological indices.

Basic definitions

The structure of the medications is represented as a network known as a molecular graph, where every vertex represents an atom and every edge represents a chemical bond between the atoms, to compute topological indices. Consider a molecular graph G = (V, E) with vertex set V(G) and edge set E(G). In graph G, the numbers |V(G)| and |E(G)| stand for the number of vertices and edges, respectively. The degree of vertex u $\in$ V(G) is expressed by deg(u) or d(u) and is the number of vertices that are adjacent to u. The expression e = uv, where e $\in$ E(G), represents the edge between the vertices u and v. Hydrogen atoms are often not included in chemical graphs because they have a valence of one since they only make one bond in many organic molecules, as presented by Kirmani et al.¹⁹. The following degree-based topological indices are utilized in this paper:

First and second Zagreb index

The Zagreb indices developed by Das and Gutman²⁰, Gutman and Trinajsti$\acute{c}$²¹ and Gutman et al.²²:

$$\begin{aligned} M_{1}(G) = \sum \limits _{uv\in E(G)}[d_{u}+d_{v}]. \end{aligned}$$

$$\begin{aligned} M_{2}(G) = \sum \limits _{uv\in E(G)}[d_{u}.d_{v}]. \end{aligned}$$

Harmonic index

Fajtlowicz²³ was the one who initially introduced the harmonic index.

$$\begin{aligned} H(G) = \sum \limits _{uv\in E(G)}\frac{2}{d_{u}+d_{v}}. \end{aligned}$$

Forgotten index

The forgotten topological index was introduced by Furtula and Gutman²⁴ in 2015.

$$\begin{aligned} F= \sum \limits _{uv\in E(G)}[d_{u}^{2}+d_{v}^{2}]. \end{aligned}$$

Inverse sum indeg index

The inverse sum index was presented by Vuki$\check{c}$evi$\acute{c}$ and Ga$\check{s}$perov²⁵ in 2010. Extreme inverse sum index values were discovered in 2015 by Sedlar et al.²⁶ for various kinds of graph types, such as chemical trees, connected graphs, molecular graphs, and trees. The inverse sum index is defined as follows:

$$\begin{aligned} ISI(G)= \sum \limits _{uv\in E(G)}\frac{d_{u}d_{v}}{d_{u}+d_{v}}. \end{aligned}$$

Augmented Zagreb index

$$\begin{aligned} AZI(G)= \sum \limits _{uv\in E(G)}\left( \frac{d_{u}d_{v}}{d_{u}+d_{v}-2}\right) ^{3}. \end{aligned}$$

Atom bond connectivity index

Estrada et al.²⁷ created the degree-based topological index atom bond connectivity index, which is defined as follows:

$$\begin{aligned} ABC(G)= \sum \limits _{uv\in E(G)}\sqrt{\frac{d_{u}+d_{v}-2}{d_{u}d_{v}}}. \end{aligned}$$

Hyper Zagreb index

An enhanced form of the Zagreb index, the hyper Zagreb index was proposed by Shirdel et al.²⁸ in 2013. The hyper Zagreb index formula is defined as follows:

$$\begin{aligned} HM(G) = \sum \limits _{uv\in E(G)}(d_{u}+d_{v})^{2}. \end{aligned}$$

Geometric arithmetic index

Vukicevic and Furtula²⁹ described the geometric arithmetic index in 2009. The geometric arithmetic index has the following computational definition:

$$\begin{aligned} GA(G)= \sum \limits _{uv\in E(G)}\frac{2\sqrt{d_{u}d_{v}}}{d_{u}+d_{v}}. \end{aligned}$$

Methods and materials

In this section, we evaluate the topological indices of angina drugs. We analyze sixteen drugs: Acebutolol, Ranolazine, Metoprolol, Amlodipine, Atenolol, Carvedilol, Nitroglycerin, Nadolol, Amyl nitrite, Nicorandil, Propranolol, Molsidomine, Nicardipine, Nifedipine, Diltiazem, and Ivabradine. The values of the topological indices shown in Table 1 are calculated using the described mathematical techniques. The data in Table 2 are obtained from ChemSpider. Fig 1 displays the corresponding drug structures. Additionally, we evaluated various topological indices, including the first and second Zagreb index, harmonic index, forgotten index, inverse sum indeg index, augmented index, atom-bond connectivity index, hyper Zagreb index, and geometric arithmetic index, based on the physicochemical properties of angina medications. These properties include boiling point ($\mathcal{B}\mathcal{P}$), enthalpy of vaporization ($\mathcal{E}\mathcal{V}$), flash point ($\mathcal{F}\mathcal{P}$), and index of refraction ($\mathcal{I}\mathcal{R}$). We utilized analytical approaches, edge partition techniques, degree-counting processes, and theoretical graph utilities to complete the mathematical computations. ChemDraw software is a useful tool for drawing chemical structures in two dimensions. Microsoft Excel and Matlab are effective tools for constructing line or correlation graphs. Matlab is used to create 2D graphs that compare topological indices and drug properties.

Fig. 1

Chemical structures of the drugs that help fight angina disease.

Table 1 Sixteen angina drugs and the values of nine topological indices.

Table 2 Sixteen angina drugs and their physicochemical properties.

Regression models

A regression model is a statistical method used to estimate the relationships between a dependent variable and one or more independent variables. It can be used to predict the future strength of the relationship between variables and to measure the degree of that relationship. A linear regression model is used to predict the value of one variable depending on the value of another variable. The factors we used to predict the value of the dependent variable are known as independent or explanatory variables, while the variable we seek to forecast is known as the dependent variable. This model assumes that the relationship is linear, meaning that changes in the independent variables produce proportional changes in the dependent variable. A quadratic regression model is used when the relationship between the variables is expected to be curved rather than linear. This model fits a parabolic curve to the data by incorporating squared terms of the independent variables, allowing it to capture more complex, non-linear relationships. In this section, we examined the connection between computed topological indices and physicochemical properties using regression models. We summarized the calculations of topological indices and physicochemical properties of molecular structures in Table 1 and Table 2, respectively. The resulting values can be used to develop regression models. To establish a connection between the dependent and independent variables, we have two regression models for each considered property. For these models, we typically have an equation.

$$\begin{aligned} X= B(Y_{i})+A \end{aligned}$$

$$\begin{aligned} X= C(Y_{i})^{2}+B(Y_{i})+A \end{aligned}$$

where X is dependent variable, Y$_{i}$(i = 1, 2, 3,...) are independent variables, A is the regression model constant, and B and C are the coefficients for descriptor.

First Zagreb index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 2.8813[\textrm{M}_{1}(\textrm{G})]+160.267\\&\mathcal{E}\mathcal{V}= 0.345[\textrm{M}_{1}(\textrm{G})]+38.4867\\&\mathcal{F}\mathcal{P}= 1.7309[\textrm{M}_{1}(\textrm{G})]+52.6224\\&\mathcal{I}\mathcal{R}= 0.0008141[\textrm{M}_{1}(\textrm{G})]+1.4663\\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -0.0220[\textrm{M}_{1}(\textrm{G})]^{2}+7.785[\textrm{M}_{1}(\textrm{G})]-71.9402\\&\mathcal{E}\mathcal{V}= -0.0028[\textrm{M}_{1}(\textrm{G})]^{2}+0.9697[\textrm{M}_{1}(\textrm{G})]+8.9052\\&\mathcal{F}\mathcal{P}= -0.0135[\textrm{M}_{1}(\textrm{G})]^{2}+4.7389[\textrm{M}_{1}(\textrm{G})]-89.8173\\&\mathcal{I}\mathcal{R}= 0.0000[\textrm{M}_{1}(\textrm{G})]^{2}+0.0033[\textrm{M}_{1}(\textrm{G})]+1.3473\\ \end{aligned}$$

Second Zagreb index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 2.2579[\textrm{M}_{2}(\textrm{G})]+195.8964 \\&\mathcal{E}\mathcal{V}= 0.2693[\textrm{M}_{2}(\textrm{G})]+42.891 \\&\mathcal{F}\mathcal{P}= 1.3551[\textrm{M}_{2}(\textrm{G})]+74.1823 \\&\mathcal{I}\mathcal{R}= 0.0006473[\textrm{M}_{2}(\textrm{G})]+1.4752 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -0.0150[\textrm{M}_{2}(\textrm{G})]^{2}+6.0844[\textrm{M}_{2}(\textrm{G})]-4.708\\&\mathcal{E}\mathcal{V}= -0.0019[\textrm{M}_{2}(\textrm{G})]^{2}+0.7634[\textrm{M}_{2}(\textrm{G})]+16.9859\\&\mathcal{F}\mathcal{P}= -0.0091[\textrm{M}_{2}(\textrm{G})]^{2}+3.6873[\textrm{M}_{2}(\textrm{G})]-48.0778\\&\mathcal{I}\mathcal{R}= 0.0000[\textrm{M}_{2}(\textrm{G})]^{2}+0.0027[\textrm{M}_{2}(\textrm{G})]+1.3698\\ \end{aligned}$$

Harmonic index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 34.9958[\textrm{H}(\textrm{G})]+112.6942 \\&\mathcal{E}\mathcal{V}= 4.2065[\textrm{H}(\textrm{G})]+32.6182 \\&\mathcal{F}\mathcal{P}= 21.0229[\textrm{H}(\textrm{G})]+24.0447 \\&\mathcal{I}\mathcal{R}= 0.009857[\textrm{H}(\textrm{G})]+1.4532 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -3.2839[\textrm{H}(\textrm{G})]^{2}+104.1444[\textrm{H}(\textrm{G})]-209.1402\\&\mathcal{E}\mathcal{V}= -0.4077[\textrm{H}(\textrm{G})]^{2}+12.7911[\textrm{H}(\textrm{G})]-7.3365\\&\mathcal{F}\mathcal{P}= -2.0149[\textrm{H}(\textrm{G})]^{2}+63.45[\textrm{H}(\textrm{G})]-173.4218\\&\mathcal{I}\mathcal{R}= -0.0016[\textrm{H}(\textrm{G})]^{2}+0.0433[\textrm{H}(\textrm{G})]+1.2977\\ \end{aligned}$$

Forgotten index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 1.0558[\textrm{F}(\textrm{G})]+183.8097 \\&\mathcal{E}\mathcal{V}= 0.1259[\textrm{F}(\textrm{G})]+41.4652 \\&\mathcal{F}\mathcal{P}= 0.6344[\textrm{F}(\textrm{G})]+66.7236 \\&\mathcal{I}\mathcal{R}= 0.000291[\textrm{F}(\textrm{G})]+1.4751 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -0.0031[\textrm{F}(\textrm{G})]^{2}+2.8319[\textrm{F}(\textrm{G})]-26.5146\\&\mathcal{E}\mathcal{V}= -0.0004[\textrm{F}(\textrm{G})]^{2}+0.3563[\textrm{F}(\textrm{G})]+14.1782\\&\mathcal{F}\mathcal{P}= -0.0019[\textrm{F}(\textrm{G})]^{2}+1.724[\textrm{F}(\textrm{G})]-62.3027\\&\mathcal{I}\mathcal{R}= 0.0000[\textrm{F}(\textrm{G})]^{2}+0.0012[\textrm{F}(\textrm{G})]+1.3653\\ \end{aligned}$$

Inverse sum indeg index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 11.9335[\textrm{ISI}(\textrm{G})]+168.7892 \\&\mathcal{E}\mathcal{V}= 1.4302[\textrm{ISI}(\textrm{G})]+39.4728 \\&\mathcal{F}\mathcal{P}= 7.1637[\textrm{ISI}(\textrm{G})]+57.8769 \\&\mathcal{I}\mathcal{R}= 0.003456[\textrm{ISI}(\textrm{G})]+1.4665 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -0.3874[\textrm{ISI}(\textrm{G})]^{2}+32.2857[\textrm{ISI}(\textrm{G})]-56.5686\\&\mathcal{E}\mathcal{V}= -0.0490[\textrm{ISI}(\textrm{G})]^{2}+4.0046[\textrm{ISI}(\textrm{G})]+10.967\\&\mathcal{F}\mathcal{P}= -0.2365[\textrm{ISI}(\textrm{G})]^{2}+19.59[\textrm{ISI}(\textrm{G})]-79.7183\\&\mathcal{I}\mathcal{R}= -0.0002[\textrm{ISI}(\textrm{G})]^{2}+0.0139[\textrm{ISI}(\textrm{G})]+1.3514\\ \end{aligned}$$

Augmented Zagreb index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 1.5949[\textrm{AZI}(\textrm{G})]+188.9077 \\&\mathcal{E}\mathcal{V}= 0.1908[\textrm{AZI}(\textrm{G})]+41.9405 \\&\mathcal{F}\mathcal{P}= 0.9558[\textrm{AZI}(\textrm{G})]+70.2513 \\&\mathcal{I}\mathcal{R}= 0.0004742[\textrm{AZI}(\textrm{G})]+1.4701 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -0.0079[\textrm{AZI}(\textrm{G})]^{2}+4.5234[\textrm{AZI}(\textrm{G})]-37.8644\\&\mathcal{E}\mathcal{V}= -0.0010[\textrm{AZI}(\textrm{G})]^{2}+0.5618[\textrm{AZI}(\textrm{G})]+13.214\\&\mathcal{F}\mathcal{P}= -0.0047[\textrm{AZI}(\textrm{G})]^{2}+2.7209[\textrm{AZI}(\textrm{G})]-66.4361\\&\mathcal{I}\mathcal{R}= 0.0000[\textrm{AZI}(\textrm{G})]^{2}+0.002[\textrm{AZI}(\textrm{G})]+1.3522\\ \end{aligned}$$

Atom bond connectivity index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 20.8665[\textrm{ABC}(\textrm{G})]+122.3617 \\&\mathcal{E}\mathcal{V}= 2.5058[\textrm{ABC}(\textrm{G})]+33.8211 \\&\mathcal{F}\mathcal{P}= 12.5447[\textrm{ABC}(\textrm{G})]+29.685 \\&\mathcal{I}\mathcal{R}= 0.005819[\textrm{ABC}(\textrm{G})]+1.4569 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -1.0740[\textrm{ABC}(\textrm{G})]^{2}+57.5397[\textrm{ABC}(\textrm{G})]-151.3737\\&\mathcal{E}\mathcal{V}= -0.1348[\textrm{ABC}(\textrm{G})]^{2}+7.1075[\textrm{ABC}(\textrm{G})]-0.5269\\&\mathcal{F}\mathcal{P}= -0.6626[\textrm{ABC}(\textrm{G})]^{2}+35.1703[\textrm{ABC}(\textrm{G})]-139.1967\\&\mathcal{I}\mathcal{R}= -0.0005[\textrm{ABC}(\textrm{G})]^{2}+0.0239[\textrm{ABC}(\textrm{G})]+1.3218\\ \end{aligned}$$

Hyper Zagreb index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 0.5399[\textrm{HM}(\textrm{G})]+194.4627 \\&\mathcal{E}\mathcal{V}= 0.06431[\textrm{HM}(\textrm{G})]+42.7621 \\&\mathcal{F}\mathcal{P}= 0.3246[\textrm{HM}(\textrm{G})]+73.0241 \\&\mathcal{I}\mathcal{R}= 0.0001532[\textrm{HM}(\textrm{G})]+1.4756 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -0.0007[\textrm{HM}(\textrm{G})]^{2}+1.2694[\textrm{HM}(\textrm{G})]+41.0841\\&\mathcal{E}\mathcal{V}= -0.0001[\textrm{HM}(\textrm{G})]^{2}+0.1575[\textrm{HM}(\textrm{G})]+23.17\\&\mathcal{F}\mathcal{P}= -0.0004[\textrm{HM}(\textrm{G})]^{2}+0.7752[\textrm{HM}(\textrm{G})]-21.7045\\&\mathcal{I}\mathcal{R}= 0.0000[\textrm{HM}(\textrm{G})]^{2}+0.0005[\textrm{HM}(\textrm{G})]+1.3932\\ \end{aligned}$$

Geometric arithmetic index

Linear regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= 14.854[\textrm{GA}(\textrm{G})]+138.9602 \\&\mathcal{E}\mathcal{V}= 1.7853[\textrm{GA}(\textrm{G})]+35.7787 \\&\mathcal{F}\mathcal{P}= 8.9204[\textrm{GA}(\textrm{G})]+39.8867 \\&\mathcal{I}\mathcal{R}= 0.00427[\textrm{GA}(\textrm{G})]+1.4586 \\ \end{aligned}$$

Quadratic regression

$$\begin{aligned}&\mathcal{B}\mathcal{P}= -0.5762[\textrm{GA}(\mathrm {G)}]^{2}+41.393[\textrm{GA}(\mathrm {G)}]-125.5436\\&\mathcal{E}\mathcal{V}= -0.0718[\textrm{GA}(\mathrm {G)}]^{2}+5.0924[\textrm{GA}(\mathrm {G)}]+2.8184\\&\mathcal{F}\mathcal{P}= -0.3528[\textrm{GA}(\mathrm {G)}]^{2}+25.1725[\textrm{GA}(\mathrm {G)}]-122.0911\\&\mathcal{I}\mathcal{R}= -0.0003[\textrm{GA}(\mathrm {G)}]^{2}+0.0174[\textrm{GA}(\mathrm {G)}]+1.3278\\ \end{aligned}$$

Computed statistical parameters

Different parameters in a regression model have different purposes. The number of items (population) in a sample is represented by the quantity N. The constant and coefficient of topological index are represented by A, B, and C, respectively. The correlation coefficient between the predicted and actual values of the physicochemical properties is represented by r. The r values can indicate a direct relationship (positive value) or an inverse relationship (negative value). The r$^{2}$ provides an assessment of the relationship between independent variables changes and dependent variables. The regression model with the highest r$^{2}$ value is considered highly efficient. When the F value in any test is greater than 2.5, it is considered significant. The significance of the obtained data is indicated by the value of p. If the value of p$\le$ 0.05, than the result is significant, otherwise insignificant. The regression model Tables 3-11 included the coefficients, the correlation coefficients, square of the correlation coefficients (r$^{2}$), F-ratio test, p values, and significance level.

Table 3 The QSPR model of M$_{1}$(G) utilized statistical parameters.

Table 4 The QSPR model of M$_{2}$(G) utilized statistical parameters.

Table 5 The QSPR model of H(G) utilized statistical parameters.

Table 6 The QSPR model of F(G) utilized statistical parameters.

Table 7 The QSPR model of ISI(G) utilized statistical parameters.

Table 8 The QSPR model of AZI(G) utilized statistical parameters.

Table 9 The QSPR model of ABC(G) utilized statistical parameters.

Table 10 The QSPR model of HM(G) utilized statistical parameters.

Table 11 The QSPR model of GA(G) utilized statistical parameters.

Implementation of the ARASS (Additive Ratio Assessment) method

The additive ratio assessment method simplifies complex decision-making by selecting the best alternative based on a relative indicator, or utility degree. This indicator shows the difference between alternatives and the ideal solution while eliminating the influence of varying measurement units. It is a compensatory method in which both beneficial and non-beneficial attributes are considered to achieve a feasible solution. The advantage of this type of multi-attribute group decision-making method is that it requires minimal computing time, is easy to use, and maintains the independence of attributes. The steps involved in evaluating the alternatives are as follows:

• Step 1: Decision-making matrix. The first step is establishing decision-making matrix as shown in Table 12.

  $$X = \begin{bmatrix} X_{o1} & \cdots & X_{oj} & \cdots & X_{0n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ X_{i1} & \cdots & X_{ij} & \cdots & X_{in} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ X_{m1} & \cdots & X_{mj} & \cdots & X_{mn} \\ \end{bmatrix}$$

• Step 2: Identify the optimal performance rating for each attribute. The next step is to identify the best performance evaluation for each attribute. When there are no preferences among decision-makers, the following formula is used to determine the ideal performance ratings:

  $$\begin{aligned} x_{0j}=\max \limits _{i}x_{ij}, \text {if} \max \limits _{i}x_{ij} \text {is preferable}; \end{aligned}$$

  (1)
  $$\begin{aligned} x_{0j}=\min \limits _{i}x_{ij}^{*}, \text {if} \max \limits _{i}x_{ij}^{*} \text {is preferable}. \end{aligned}$$

  (2)

• Step 3: Compute a normalized decision matrix. The attribute, whose preferable values are maximum are normalized as follows:

  $$\begin{aligned} x_{ij}=\frac{x_{ij}}{\sum \limits _{i=0}^{m}x_{ij}}. \end{aligned}$$

  (3)

  The attribute, whose preferable values are minimum are normalized by applying two step procedure:

  $$\begin{aligned} \overline{x_{ij}}=\frac{1}{x_{ij}^{*}}; \end{aligned}$$

  (4)
  $$\begin{aligned} x_{ij}=\frac{x_{ij}}{\sum \limits _{i=0}^{m}x_{ij}}. \end{aligned}$$

  (5)

  See Table 13

• Step 4: Compute a weighted normalized decision matrix. The weighted normalized performance evaluation are determined as follows:

  $$\begin{aligned} v_{ij}=x_{ij}.w_{j}. \end{aligned}$$

  (6)

  where $w_{j}$ is the weight (importance) of the j attribute and $x_{ij}$ is the normalized rating of the j attribute as shown in Table 14.

• Step 5: Compute the overall performance index for every alternative. The total of the weighted normalized performance evaluation can be used to determine the overall performance index for every alternative, as shown following.

  $$\begin{aligned} S_{i}=\sum \limits _{i=1}^{n} v_{ij}. \end{aligned}$$

  (7)

  See Table 15.

• Step 6: Determine the utility degree.

  $$\begin{aligned} K_{i}=\frac{s_{i}}{s_{0}} \end{aligned}$$

  (8)

  where s$_{i}$ and s$_{0}$ are the optimality attributes values as shown in Table 15.

• Step 7: Rank the alternatives and select the most effective one. After calculating K$_{i}$, the alternatives are ranked accordingly. For the given attribute, the alternative with the highest K$_{i}'$ value is considered the best compromise solution and is ranked first, with the remaining alternatives ranked in descending order as shown in Table 15 and graphically shown in Fig. 2.

Table 12 Decision matrix.

Table 13 Normalized decision matrix.

Table 14 Weighted normalized decision matrix.

Table 15 Optimality function, utility degree and ranking.

Fig. 2

Ranking of angina treatment medications via ARASS.

Graphical analysis of correlation coefficients

The correlation coefficient is a crucial measure because it indicates how well the theoretical models align with actual experimental data. This information can be valuable for chemists and pharmacists in developing effective treatments, including medications for angina. The P-value indicates the significance of the correlation coefficients. For results to be considered statistically significant, the P-value must be less than or equal to 0.05, and the correlation coefficients should lie within the range of −1 to 1. Values of the correlation coefficient for linear and quadratic regression models are shown in Table 16. Various types of graphs can be used to represent the data, including bar charts, line graphs, area graphs, curved graphs, scatter plots, pie charts, pictographs, column charts, and bubble charts. Fig. 3 and 4 show the relationship between properties and topological indices using curved graphs. The x-axis displays the names of the nine topological indices, while the y-axis shows the corresponding correlation values. Boiling point, enthalpy of vaporization, flash point, and index of refraction are physical properties of substances that often exhibit strong correlations with one another. All of the graphs have a positive x-axis because the topological indices (predicted values) and the properties (experimental values) are positively correlated. Ultimately, we find that the correlation coefficients and topological indices are significant.

Table 16 Correlation coefficient of linear and quadratic regression models.

Fig. 3

Graphs of the correlation coefficient of the linear regression model.

Fig. 4

Graphs of the correlation coefficient of the quadratic regression model.

Applications of multi-attribute group decision-making

Multi-attribute group decision-making is a field within decision science that focuses on decision-making processes where a group of decision-makers evaluates multiple attributes. Multi-attribute group decision-making is widely applied across various fields because it effectively manages complex decision problems that involve multiple attributes and the input of various experts. Here are several key applications of multi-attribute group decision-making:

• In drug formulation, multi-attribute group decision-making techniques can be used to balance factors like drug stability, release rate, and patient compliance. This helps in designing formulations that meet both scientific and practical requirements. Multi-attribute group decision-making can assist in evaluating potential drug targets by assessing various attributes such as biological relevance, drug ability, and potential for off-target effects. This allows researchers to prioritize targets that are most promising for drug development. Multi-attribute group decision-making methods can help rank compounds based on multiple factors like biological activity, toxicity, and pharmacokinetics. This helps in selecting the most promising leads for further development.

• In transportation networks, communication networks, or supply chain logistics, multi-attribute group decision-making can be used to select the optimal path based on multiple criteria like distance, cost, time, and reliability. For designing transportation systems, such as road networks or public transit systems, multi-attribute group decision-making helps in selecting routes and connections by weighing factors like travel time, distance, cost, and safety. In designing communication networks (such as telecommunication or computer networks), multi-attribute group decision-making can be used to decide on the optimal network structure by considering multiple criteria like cost, bandwidth, latency, and reliability. Suppliers and manufacturers form a network, and multi-attribute group decision-making can help in selecting the best suppliers by considering criteria such as cost, quality, delivery time, and reliability. The network of suppliers is analyzed using graph theory, and decision-makers evaluate potential suppliers to optimize the supply chain. Decision-makers evaluate different paths (edges) and nodes (vertices) to determine the best route that satisfies all individuals.

• In data analysis, graphs can represent relationships between data points, and multi-attribute group decision-making can be applied to cluster these data points based on multiple attributes like similarity, distance, or connectivity. Decision-makers evaluate different clustering options to find the most meaningful grouping. In large networks, identifying communities or clusters is crucial for understanding network dynamics. Multi-attribute group decision-making helps in partitioning the network into clusters by considering criteria like modularity, density, and edge.

• In education, multi-attribute group decision-making techniques are used to rank universities or academic programs based on criteria like academic performance, research output, faculty quality, and student satisfaction. Educational institutions apply multi-attribute group decision-making to design curricula that balance theoretical knowledge, practical skills, and industry relevance.

• Governments and organizations use multi-attribute group decision-making to develop energy policies by considering criteria like sustainability, cost, energy security, and public acceptance. Multi-attribute group decision-making is applied in evaluating renewable energy projects (e.g., wind, solar) by assessing environmental impact, cost, and energy output.

Results and discussion

QSPR models provide an overview of the relationship between chemical structures and biological activity, aiding in chemical analysis. QSPR models can predict the properties of novel molecular structures. This section discusses the relationship between physicochemical properties and chemical invariants as well as the results of linear and quadratic regression analyses. The approach developed in this study employs QSPR analysis to correlate the physical and chemical properties of angina drugs with specific topological descriptors. We analyzed the drugs using the assigned topological indices to achieve optimal outcomes. The goal is to identify the numerical values that exhibit a strong correlation.

In Table 17, we compare our degree-based topological indices with other commonly used molecular descriptor sets such as RDKit, Mordred, and alvaDesc. The table summarizes key aspects including the number of descriptors, computational complexity, interpretability, and predictive accuracy. Our approach uses only 9 descriptors, resulting in low computational complexity and high interpretability while achieving comparable predictive performance. In contrast, RDKit and alvaDesc offer approximately 300 and 500 descriptors respectively, with medium levels of complexity and interpretability, whereas Mordred provides around 1800 descriptors, which can lead to higher computational demands and reduced interpretability. Figure 5 graphically illustrates these differences by depicting the number of descriptors for each descriptor set, further emphasizing the streamlined and efficient nature of our method.

Table 17 Comparison of Molecular Descriptor Sets.

Fig. 5

Bar chart comparing the number of descriptors across different molecular descriptor sets.

Conclusions

This research observed the properties of sixteen angina drugs, namely Acebutolol, Ranolazine, Metoprolol, Amlodipine, Atenolol, Carvedilol, Nitroglycerin, Nadolol, Amyl Nitrite, Nicorandil, Propranolol, Molsidomine, Nicardipine, Nifedipine, Diltiazem, and Ivabradine. One effective technique employed by scientists to reduce unnecessary laboratory costs is QSPR analysis, which uses topological descriptors for medications treating various diseases. A QSPR model was developed using linear and quadratic regression analysis to estimate properties such as boiling point, enthalpy of vaporization, flash point, and index of refraction. All topological indices demonstrated a strong correlation with these properties of the angina drugs. The prioritization of drugs can be viewed as a multi-attribute group decision-making challenge. The ARAS method is particularly flexible in addressing diverse decision-making scenarios, especially when decision-makers possess varying levels of expertise or when criteria weights may change. The method is designed to be robust, ensuring that the final rankings are consistent and reflect the collective preferences of the group. This approach facilitates the integration of both qualitative and quantitative criteria, making it particularly suitable for complex decision-making scenarios that involve multiple factors. To demonstrate the application of this effective multi-attribute group decision-making technique, sixteen angina medications were evaluated. The methodology relies heavily on thorough evaluations and has been successfully applied within the framework of topological indices. We identified ivabradine as the most suitable medication, closely aligning with the optimal solution. Future research in the field of angina treatment should focus on advancing personalized medicine, developing innovative pharmacological therapies, and leveraging regenerative medicine. The potential of regenerative medicine, including stem cell therapy and tissue engineering, should be a priority to restore damaged cardiac tissue. Integrating digital health technologies and artificial intelligence to improve real-time patient monitoring and personalized treatment plans will also be crucial in shaping the future of angina care.