Optimization of tribocorrosion performance for SUS casted AZ91D Mg composites reinforced with ZrB₂ using an entropy integrated TODIM approach

Abstract

AZ91D composites are ideal for weight-sensitive, high-stress aerospace applications because of their improved mechanical properties and corrosion resistance. This study focuses on the microstructural, physical, and mechanical characterization of newly developed AZ91D composites reinforced with Zirconium diboride (ZrB₂) and explores their optimal performance in tribocorrosion conditions. The metal matrix composites (MMCs) were fabricated using the stir-ultrasonication-squeeze (SUS) casting technique. Additionally, an innovative approach called entropy-integrated TODIM, an MCDM method, was employed to determine the optimal process conditions. Based on the TODIM results, the optimized tribocorrosion parameters were found to be a wt.% reinforcement of 15%, an ageing temperature of 230 °C, an applied load of 30 N, and a pH value of 10. Furthermore, the desirability approach showed significant deviations in responses. Using the desirability approach and optimizing process parameters minimized corrosion pits and peak generation in the surface profile.

Introduction

In recent decades, engineers have focused on developing lightweight, energy-efficient materials to reduce vehicle fuel consumption and CO₂ emissions, supporting the ‘dual carbon’ goal^1,2. Magnesium (Mg), being the eighth most abundant material on the Earth, offers a promising solution³. With a density of only 1.74 g/cc, Mg alloys are 35% lighter than aluminum (Al), 61% lighter than titanium (Ti), and 71% lighter than stainless steel (SS)⁴. These alloys offer high specific strength, excellent damping capacity, good machinability, and remarkable mechanical properties, making them suitable alternatives to Al, Ti, and SS in various industries such as aerospace, automotive, and structural applications^5,6. Among commercially used Mg alloys, AZ91 stands out for its excellent castability and strengthening capabilities⁷. However, due to its hexagonal close-packed (HCP) crystal structure-which has fewer operational slip systems compared to other materials-Mg alloys face certain limitations, including poor wear resistance, low corrosion resistance, and reduced creep strength^8,9. In marine environments, the corrosion rate of commercial Mg alloys is higher than that of pure Mg. This increased corrosion can be attributed to several factors, such as its highly electronegative potential (-2.37V_vs.SHE)¹⁰, the formation of an unstable quasi-passive hydroxide (OH) film, and the presence of impurity elements like iron (Fe), copper (Cu), and nickel (Ni)^11,12,13. Additionally, due to its highly reactive nature and low standard electrode potential, Mg alloys are prone to rapid galvanic corrosion in aqueous environments, especially when secondary phases are present¹⁴.

One of the most promising approaches for eliminating limitations of Mg alloy is to add an alloying element such as Cu, Fe, Gd, etc., or reinforcing particles such as oxides, nitrides, silicate, and boride into the matrix¹⁵. Zirconium Boride (ZrB₂) is a well-known hard ceramic reinforcement particle that is frequently used in Mg matrices to achieve high hardness and strength, which in turn provides wear-resisting properties¹⁶. The crystal structure of ZrB₂ has a hexagonal, densely packed structure with boron atoms forming graphite-like layers. Its metallic (Zr-Zr), covalent (B-B), and ionic (Zr-B) bonds provide high thermal and electrical conductivity, along with superior hardness, stiffness, and chemical stability¹⁷. And ZrB₂ also has an outstanding combination of properties, which encompasses a high melting point, elevated electrical and thermal conductivity, chemical inertness when exposed to molten metals or non-basic slags, and robust thermal shock resistance¹⁸. These features make it an ideal material for high-temperature applications that require corrosion, wear, or oxidation resistance¹⁹. Zhang et al.²⁰ investigated the effect of ZrB₂ particles on the microstructure and mechanical properties of Mg-Zn-Y-Mn alloys. They found that incorporating 0.0075 wt.% ZrB₂ led to grain structure refinement and the formation of a long-period stacking ordered (LPSO) structure with a grain size of 24.87 μm. Additionally, this enhancement resulted in significant improvements in the ultimate tensile strength (UTS) and elongation of the alloy, achieving values of 225 MPa and 17.5%, respectively, compared to the as-cast Mg alloy. Morampudi et al.²¹ investigated the mechanical and corrosion behaviour of an Al6061 alloy reinforced with nano ZrB₂. The research findings demonstrated that increasing the amount of nano ZrB₂ in the alloy matrix resulted in improved mechanical properties. Additionally, the inclusion of 2 wt.% ZrB₂ led to a substantial 86% reduction in the rate of corrosion compared to the unmodified alloy.

El-Khair et al.²² examined the wear behaviour of AM100-ZrB₂-C hybrid composites and observed that composites reinforced with ZrB₂ exhibited superior wear resistance compared to both hybrid composites and as-cast alloys due to their high load-bearing capacity.

Mg composites were fabricated through both liquid metallurgy and powder metallurgy. Among them, commonly liquid casting processes, including squeeze casting, disintegrated melt deposition technique, stir casting, spray deposition, etc., were utilized to make Mg composites. The properties of the composites can deteriorate if an inappropriate casting process is selected²³. So, stir-squeeze casting is one of the cost-effective casting methods for the fabrication of Mg composites. Despite the effectiveness of stirring in distributing reinforcements in the matrix, the drawback of stir casting technology is the prolonged stirring time required. This extended stirring time can lead to oxidation of the Mg matrix, diminishing the overall performance of the composites²⁴. To address this issue, ultrasonic treatment (UST) is used as an efficient technique for achieving uniform dispersion of reinforcement by using ultrasonic cavitation to disrupt the formation of clusters and bubbles during casting²⁵. Using squeeze pressure can enhance mechanical and tribological properties by reducing porosity and refining grains through recrystallization²⁶. Nevertheless, UST alone is inadequate for composite production. Hence, the ultrasonication coupled stir-squeeze casting technique was developed to improve the microstructure and mechanical properties of the composites²⁷.

The mechanical and corrosion properties of Mg-MMCs are influenced by various parameters, including normal load, frequency, sliding distance, heat treatment, pH value, electrolyte concentration, and volume fraction of reinforcements. For instance, thermomechanical processes like heat treatment (solutionizing & ageing) play a crucial role in determining the mechanical and corrosion properties of Mg composites^28,29. Antony et al.³⁰ examined the effect of aging temperature on the mechanical and corrosion properties of AZ91D/SiC/Gr hybrid composites. Their findings revealed that the ageing heat treatment condition led to improved mechanical properties, specifically a 5.46% increase in UTS, an 18.66% increase in YS, and a 19.27% increase in elongation. Additionally, the corrosion behaviour of the T6 heat-treated samples showed a lower I_corr (3.24 µA/cm²) compared to the T4 heat-treated samples (7.84 µA/cm²). Gnanavelbabu et al.³¹ investigated the salt spray corrosion behavior of Mg composites reinforced with ultra-high-temperature ceramic (UHTC) particles under various ageing conditions. Their study found that composites reinforced with TaC and HfC particles exhibited better corrosion resistance compared to those reinforced with TiC, TiN, and TiB₂, particularly after up to 48 h of exposure at 230 °C. This improvement was attributed to the formation of a robust and compact protective layer and a reduction in the amount of secondary phase. Siqin Liu et al.³² investigated the tribocorrosion behaviour on AZ31 Mg alloy coated with single micro-arc oxidation (MAO) by Tafel and Nyquist plot under varying normal loads (5, 10, and 15 N). They found that the material started to wear and the open circuit potential (OCP) began to decrease after a load of 10 N. In an electrochemical test, Li Yang et al.³³ examined the corrosion performance of Mg /carbon fiber composites, using pH as the variable. The findings of the study revealed that as the pH value decreased, the corrosion current density of the composites increased. Moreover, the maximum corrosion resistance was observed at a pH of 13. The authors attributed the increased cathodic reaction and subsequent corrosion to the heightened H⁺ concentration in acidic solutions. According to Kumar et al.⁴⁵ increasing the amount of wt.% of ZrB₂ (0 to 15%) particulates on aluminum matrix AA7178 enhances the mechanical and corrosion resistance of the composite. The addition of 10% wt.% ZrB₂ particulates in the AA7178 matrix increased hardness by 26% and ultimate tensile strength by 15%. The composite containing 15 wt.% ZrB₂ showed superior corrosion resistance to other composites.

The conducted studies show that optimal composite properties depend on varying process parameters, making traditional trial-and-error methods inadequate for modern productivity demands. Efficient optimization is crucial for achieving high performance while saving time, resources, and cost. Therefore, using advanced statistical tools within defined process ranges is essential for effective experimental design³⁵. Nowadays many optimization tools such as Grey Relational Analysis (GRA), Response Surface Analysis (RSM), and Multiple Objective Decision Making (MODM) techniques like COmbinative Distance-based ASsessment (CODAS), Evaluation based on Distance from Average Solution (EDAS), Additive Ratio Assessment Approach (ARAS), etc. are used to optimize the process parameters. Among several MODM approaches, the TODIM technique incorporates prospect theory. Existing MODM techniques are primarily based on the premise that decision-makers should strive to identify a solution that maximizes a global measure of value. In contrast, the TODIM technique gives a modified global measurement of value derived from the prospect theory paradigm. Sunil Kumar et al. optimized the CrN/TiAlSiN coating using the BWM-TODIM technique, and concluded that the optimal process parameters are 100 ^oC of temperature, 0.05 m/s of velocity, 5 N of load and 2000 m of sliding distance exhibit the outcome of wear rate of 5.67 × 10^− 6 mm³Nm^-1, COF of 0.51, surface roughness of 5.4 μm, wear depth of 0.67 μm and hardness after wear 2781 HV³⁴.

As per the existing literature survey, incorporating ZrB₂ particles in the Mg matrix was anticipated to function as a load carrier and form a defensive layer that restricts contact with the counterpart and reduces Cl^- ion attack on the metal surface. Besides, the corrosive behavior of the material is significantly impacted by ageing temperature, as it results in the reprecipitation of the β-Mg phase, and the pH value of the environment has a considerable effect on the corrosion behavior of the material, as it leads to the formation of Mg (OH)₂. Nevertheless, only a scant amount of research has delved into the meticulous exploration of optimal parameter combinations for refining the tribocorrosion behavior of materials. To address this gap, this study utilizes an innovative ultrasonic-assisted stir-squeeze casting technique with optimized parameters to fabricate ZrB₂-reinforced Mg composites.

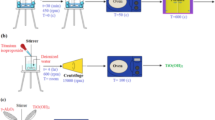
A tribocorrosion test was conducted using an L16 orthogonal array experimental design, evaluating four parameters: wt% of reinforcement (0–15%), ageing temperature (170–260 °C), applied load (15–60 N), and pH value (3, 10). The responses measured included corrosion potential (E_corr), corrosion current (I_corr), corrosion rate, wear depth, and post-corrosion hardness. The entropy-integrated TODIM technique was applied to identify the optimal process parameters, while ANOVA and 3D surface plots were used to analyze the effects of individual parameters and their interactions on tribocorrosion responses. Finally, a desirability and confirmation test were conducted to validate the optimal conditions, providing deeper insights into the tribocorrosion behaviour of Mg composites. Figure 1 illustrates a visual overview of the entire study along with its significant outcomes.

Fig. 1

Graphical representation of the overall study.

Experimental details

Materials

A 99.9% purified AZ91D Mg alloy (obtained from Exclusive Mg Private Ltd., Hyderabad, India) was utilized as the matrix material. The elemental composition and ratio of each element in the AZ91D alloy are presented in Table 1, while the microstructure and chemical composition of the alloy, determined through Scanning Electron Microscope (SEM) and Energy-Dispersive X-ray Spectroscopy (EDS) are depicted in Fig. 2. To fabricate the composites, ZrB₂ with a particle size of 5 μm and 99.9% purity level, supplied by Ultra-Nanotech, Bangalore, India, was utilized as reinforcement. The EDS analysis confirms the ratio of intermetallic materials stated in Table 1. The basic properties of the AZ91D Mg alloy and ZrB₂ are displayed in Table 2, while the notations for the fabricated alloy and composites are presented in Table 3.

Table 1 Elements present in AZ91D Mg alloy³¹.

Fig. 2

SEM and EDAX of AZ91D and ZrB₂.

Table 2 Properties of matrix and reinforcement materials^36,37.

Table 3 Material composition and notation.

Fabrication of AZ91D/ZrB₂ composites

Due to the environmental sensitivity of Mg alloys, it is imperative to employ a reliable casting method for fabricating Mg composites. Therefore, a specially designed stir-squeeze casting furnace coupled with UST setup was utilized for the casting of Mg composites³⁸. To achieve faster melt conditions, 1.065 kg of AZ91D Mg alloy was taken and cut into 50 × 50 × 20 mm billets using an abrasive cutting machine. To achieve a liquidized form, these billets are added to the furnace, which was kept at an 800 ^oC temperature. Since Mg material is reactive to oxygen, it is highly inflammable. To prevent the material from oxidation, a protective gas environment of 90% argon and 10% sulfur hexafluoride was maintained throughout the process. A mechanical stirrer coated with graphite was used to stir the molten metal at 400 rpm, to reduce amalgamation during casting. The preheated reinforcement particles (at 300 ^oC) were added to the molten slurry and stirred for 5 min. This was followed by the immersion of a titanium probe into the molten metal to produce UST vibration. This vibration was maintained at 2500 W power and 20 kHz frequency for 5 min using a UST power controller. The procedure ended by pouring the molten slurry into a preheated (300 ^oC) split-type squeeze die, followed by applying a squeeze pressure of 120 MPa for 1 min. Figure 3 displays the flow process of fabricating AZ91D/ZrB₂ composites.

Heat treatment process

Following fabrication, the alloy and composites were heat-treated in a muffle furnace as per ASTM B116-06 standards. The fabricated alloy and composites were initially placed in a furnace using fire clay bricks under an argon gas environment to prevent oxidation. Then, the solutionizing process (T4 heat treatment) was performed from ambient temperature to 415 ^oC for 16 h at a temperature rise of 1.5 ^oC/min. After finishing this heat treatment process, the specimens were quenched with water to improve mechanical strength by preventing grain slippage. Subsequently, the ageing process (T6 heat treatment) was performed at different temperatures (170, 200, 230 & 260 ^oC) for 16 h, followed by cooling to room temperature through air cooling. Figure 3 illustrates the T4 and T6 heat treatment process, as well as the heat-treated specimens.

Fig. 3

Illustration for fabrication of AZ91D/ZrB₂ composites.

Microstructure analysis

Microstructure analysis of the alloy and composites was done using an optical microscope (OM) (Olympus-BX51M) and SEM (Hitachi). A square sample with a dimension of 10l ×10b × 5t mm was made by a slow-speed cutter. After preparation, the samples underwent polishing with various SiC sandpapers (120, 220, 600, 800, 1200, 1600, & 2000), followed by the use of 1μm diamond paste to attain an ultra-smooth surface. Following that, the polished samples were subjected to etching according to the ASTM E407 standards. For the etching of Mg, a picral reagent composed of 5ml CH₃COOH, 10ml H₂O, 100ml C₂H₆O, and 2–4 g picric acid was used as the designated etchant. To examine the crystalline phases that exist in Mg composites, X-Ray Diffraction (XRD) analysis was conducted using PANalytical X’pert, with a scan rate of 2°/min and a wavelength of λ = 1500 Å.

Density and porosity measurement

To study the physical properties, mainly density, and porosity, the specimens of all the composites and alloy were calculated with the help of a solid material density kit (Make: OHAUS). The specimen was to be cleaned with acetone solution to avoid impurities and dust present on their surfaces. The theoretical density of any such composite material can be determined using the rule of mixture equation, as shown in Eq. (1). The specimens were initially measured for their weight in the air (W_air) and then in water (W_water) with an accuracy of ± 0.00001 g. Five such observations for all the samples were taken and the average value has been recorded. Then the actual density was measured with the help of a solid material density kit using Eq. (2).

$$\begin{array}{l}\:Theoretical\:density = \left( {\:Volume\:fraction\:of\:matrix} \right)\:\left( {density\:\:of\:matrix} \right)\\\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\,\,\, + \left( {Volume\:fraction\:of\:reinforcement} \right)\left( {density\:of\:reinforcement} \right)\:({\rm{g}}/{\rm{c}}{{\rm{m}}^3})\end{array}$$

(1)

$$\:Actual\:density\:=\left(\frac{{W}_{air}\:}{{W}_{air}\:-{W}_{water}}\right)\times\:\:{\rho\:}_{water}(\text{g}/{\text{c}\text{m}}^{3})$$

(2)

Through density values, its porosity value was calculated using Eq. (3)

$$\:Porosity=1-\frac{Actual\:density}{Theoretical\:density}\left(\%\right)$$

(3)

Micro Vickers hardness

The mechanical properties of the fabricated materials were assessed through hardness tests. Following the ASTM E384-16 standard, the hardness of the material was measured using a Micro Vickers hardness tester (Model: leitzminiload, Make: Leitz Wetzlar) with a 500 gf load of indentation and a 15s dwell time. The average of 5 readings was used to determine the hardness value.

Selection of process parameters and their levels

The selection of process parameters and their levels for tribocorrosion testing plays a crucial role. Insufficiently large or small ranges can lead to incomplete or impractical solutions. One key factor to consider is the aging temperature, as higher temperatures promote the formation of secondary β-phase, which enhances the mechanical properties of the composites, while lower ageing temperatures may not be sufficient for such formations. The pH value is another vital parameter, as increasing pH values result in reduced corrosion rates due to lower concentrations of H⁺ ions Conversely, lower pH values increase corrosion rates due to higher concentrations of these H⁺ ions reacting with metal surfaces. The magnitude of the applied load is also an important consideration. Larger loads result in increased material removal rates due to greater contact between the pin and sample surfaces, while smaller loads tend to decrease removal rates. Furthermore, the wt.% of reinforcement used in the composites should be carefully chosen. Higher wt.% values can lead to particle agglomeration, while lower percentages generally have no significant impact on the microstructure or mechanical properties. The selection of parameter ranges is based on a combination of trial experiments, information obtained from previous literature, and standard parametric combinations commonly used in tribocorrosion testing. Table 4 presents the selected process parameters and their levels of the experiments designed using the Taguchi L16 orthogonal array.

Table 4 Process parameters and their levels.

Tribocorrosion test

As per the ASTM G119-09 standards, the tribocorrosion test was performed on the Linear Reciprocating Tribometer (Make: Ducom) coupled with an electrochemical workstation (Make: IVIUM). Initially, the test samples, shaped as per specifications (22 × 24 mm), were obtained using a slow-speed cutter. Surface roughness, measured with a portable surface roughness tester (Made: Mitutoyo), was found to be less than 0.3 μm for all samples. The illustration of the tribocorrosion setup and testing samples is presented in Fig. 4(a-c). The reference, counter, and working electrodes attached to the fixture were saturated calomel, graphite, and test samples, respectively. EN8, with dimensions of ⌀6 × 15l mm was used as the counter pin material. The pin was affixed to the transducer and reciprocated with a stroke length of 10 mm at a frequency of 3 Hz for 30 min. The OCP testing commenced 15 min. before sliding and concluded 15 min. after sliding, resulting in a total OCP testing time of 1 h. Tafel plots were obtained after conducting the OCP testing, and the I_corr value was determined. The amount of material removed is calculated in grams after performing the tribocorrosion test.

Fig. 4

(a)Tribocorrosion illustration, (b) Tribocorrosion setup, (b) Testing samples.

Implementation of entropy integrated TODIM method

Entropy method

The Entropy Weighted Method (EWM) was proposed by Shannon and Weaver in 1947, and later developed by Zeleny in 1982. It is a technique that uses probability theory to measure the level of uncertainty or randomness (entropy) in a system. The EWM then utilizes this information to evaluate the significance of various attributes or responses without considering the preference of the decision-maker. The EWM is based on the idea that not all types of information are equally valuable or informative. It assigns lower weights to indicators that are less informative and higher weights to those that provide more important or helpful information. This allows the technique to rank and prioritize different attributes or responses based on their relative relevance, enabling decision-makers to make better-informed and more sensible choices. To implement the EWM, the first step is to identify the decision matrix or objectives. The normalized decision matrix is then calculated, and the probability and entropy value of each attribute and response are determined. The degree of divergence for each response is calculated by assessing the average information contained. Finally, the entropy weight is calculated, which is used to determine the goal weights. Using the original decision matrix, the Shannon entropy approach determines the weights of the decision criteria.

Step 1

Calculate project outcome (P_ij), by normalizing the decision matrix using Eq. (4).

$$\:{\varvec{P}}_{\varvec{i}\varvec{j}}=\frac{{\varvec{X}}_{\varvec{i}\varvec{j}}}{{\sum\:}_{\varvec{i}=1}^{\varvec{m}}{\varvec{X}}_{\varvec{i}\varvec{j}}}$$

(4)

Step 2

Calculation of the entropy measure of P_ij by Eq. (5).

$$\:{\varvec{E}}_{\varvec{j}}=-\varvec{k}{\sum\:}_{\varvec{i}=1}^{\varvec{m}}{\varvec{P}}_{\varvec{i}\varvec{j}}\:\mathbf{ln}{\varvec{P}}_{\varvec{i}\varvec{j}\:}$$

(5)

Step 3

Defining the weights for criteria based on the concept of entropy method using Eq. (6), Always $\:\sum\:(1-{E}_{j})$ is 1.

$$\:{\varvec{W}}_{\varvec{j}}=\frac{1-{\varvec{E}}_{\varvec{j}}}{{\sum\:}_{\varvec{j}=1}^{\varvec{n}}1-{\varvec{E}}_{\varvec{j}}}$$

(6)

TODIM method

According to the Multi-Objective Decision-Making (MODM) principle, decision-makers should strive to find the optimal option that best aligns with the values of all relevant factors. However, the TODIM method is designed to account for the need to determine a global measurement value while applying prospect theory. Research has shown that people can make wise judgments even in the face of risk through the use of a descriptive technique. The function that defines the relationship between value and outcome has certain characteristics that resemble the function proposed by Prospect Theory, which describes the relationship between loss or gain and outcome. This function mimics the loss or gain function of Prospect Theory because its mathematical representation corresponds to intrinsic properties. The multi-attribute function calculates the overall impact of all criteria by summing the individual losses and gains of each criterion. To solve the multi-criteria problem, a set of ‘n’ possibilities is compared using a collection of ‘m’ criteria, which can be qualitative or quantitative. The TODIM method, which is effective for managing both qualitative and quantitative criteria, requires the normalization of criterion values. One criterion is selected to serve as the reference standard for the evaluation process. Next, each alternative is compared to every other alternative to determine which has the relative advantage. This procedure is done for every single set of alternatives. The sum of all criteria is used to calculate the relative profit and loss of each option. Depending on how well each choice meets the relevant condition, the computed summed result can be a gain, a loss, or zero. The final and partial dominance matrices are constructed using the criteria weight matrix and normalized decision matrix. These matrices help to evaluate the relative importance of each criterion about others and identify the most dominant alternatives based on decision criteria. Reference standards are defined at this point to make further computations easier. The TODIM technique often assigns the most weight to reference criteria. Using the value function of prospect theory, the TODIM method aims to determine the extent to which each choice dominates the others. The primary idea behind the TODIM approach is to rank the options based on their partial and overall dominance over the others. While the TODIM method has only recently been used to optimize wear parameters, it has the potential to be implemented in a wide range of management decision-making processes, including material selection and stock investment analysis. To rank the alternatives, the TODIM approach involves several mathematical steps, which are depicted in Fig. 5 which displays the flow of entropy and the TODIM method.

Step 1

Construct the decision matrix for n criteria and m alternatives as per Eq. (7)

$$\:\text{X}=\left(\begin{array}{cccc}{x}_{01}&\:{x}_{02}&\:\cdots\:&\:{x}_{0n}\\\:{x}_{11}&\:{x}_{12}&\:\dots\:&\:{x}_{1n}\\\:\vdots&\:\vdots&\:\vdots&\:\vdots\\\:{x}_{m1}&\:{x}_{m2}&\:\cdots\:&\:{x}_{mn}\end{array}\right)$$

(7)

Where, X_ij is the performance of i^th criteria and j^th alternatives.

Step 2

The decision matrix is then normalized to make all criteria values a dimensionless matrix. Depending upon the objective of the criteria either to maximization or minimization, the following Eqs. (8) & (9) are used.

$$\:\text{F}\text{o}\text{r}\:\text{B}\text{e}\text{n}\text{e}\text{f}\text{i}\text{c}\text{i}\text{a}\text{l},\:\:{P}_{ij}=\frac{{x}_{ic}}{\sum\:_{i=1}^{n}{x}_{ic}}$$

(8)

$$\:\text{F}\text{o}\text{r}\:\text{N}\text{o}\text{n}-\text{B}\text{e}\text{n}\text{e}\text{f}\text{i}\text{c}\text{i}\text{a}\text{l},\:\:\:{P}_{ij}=\frac{1/{x}_{ic}}{\sum\:_{i=1}^{n}{1/x}_{ic}}$$

(9)

where $\:{x}_{ic}$ represents the value of i^th criteria compared to j^th alternative. P_ij represents the normalized value for the i^th criteria and j^th experimental run, and generally, this value ranges from 0 to 1. A greater normalization score indicates more helpful criteria, while a lower value indicates less beneficial criteria.

Step 3

The Entropy approach is used to calculate the criteria weights (W_c). The relative weight (W_cr) of each criterion is also computed using Eq. (10). W_r is the maximum weight among the criteria.

$$\:{W}_{cr}=\frac{{W}_{c}}{{W}_{r}}$$

(10)

Step 4

Calculate the dominance degree of alternative (E_ri) over another alternative (E_rj) using Eqs. (11) & (12).

$$\:\delta\:({Er}_{i},{Er}_{j})=\:\sum\:_{Wr=1}^{n}\varnothing\:{W}_{r}({Er}_{i},{Er}_{j})\:\forall\:(\:\text{i},\text{j})\:$$

(11)

$$\varnothing {W_r}\left( {E{r_i},E{r_j}} \right) = \left\{ \begin{array}{l}\sqrt {\frac{{{W_{cr}}\left( {{P_i}{W_r},{P_j}{W_r}} \right)}}{{\sum {\:_{c = 1}^m} {W_{cr}}}}} \:\:\:\:\:\quad \quad \quad \quad\quad {\rm{if}}\:\left( {{P_i}{W_r} - {P_j}{W_r}} \right) > 0\\0\:\:\:\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\rm{if}}\:({P_i}{W_r} - {P_j}{W_r}) = 0\\\frac{{ - 1}}{{\theta \:}}\sqrt {\frac{{\left( {\sum {\:_{c = 1}^m} {W_{cr}}} \right)\left( {{P_i}{W_r} - {P_j}{W_r}} \right)}}{{{W_{cr}}}}} \:\:\quad\,\, {\rm{if}}\:({P_i}{W_r} - {P_j}{W_r}) < 0\end{array} \right.$$

(12)

(P_iW_r − P_jW_r > 0) represent the loss and (P_iW_r − P_jW_r < 0) represents the gain of ith alternative over the j^th alternative respectively.

Step 5

Calculate overall dominance degree for the alternative by Eq. (13), i.e.,

$$\:{\upxi\:}\text{i}=\frac{\sum\:_{j=1}^{n}\delta\:({Er}_{i},{Er}_{j})-min\sum\:_{j=1}^{n}\delta\:({Er}_{i},{Er}_{j})}{max\sum\:_{j=1}^{n}\delta\:({Er}_{i},{Er}_{j})-min\sum\:_{j=1}^{n}\delta\:({Er}_{i},{Er}_{j})}$$

(13)

Step 6

Based on their dominance value the alternatives are ranked. The alternative with the maximum dominance rank is the optimum.

Fig. 5

Flow diagram of the proposed methodology.

Result and discussion

Microstructure analysis

Figure 6(a-d) illustrates the OM images of the fabricated materials. Figure 6(a) shows the microstructure of the AZ91D Mg alloy, referred to as ‘AZ0’. This alloy is characterized by extended primary α-Mg dendritic arms, which exhibit a high aspect ratio. Surrounding these dendritic structures is a notable presence of intermetallic phases, specifically β-Mg₁₇Al₁₂. This phase forms due to the significant amounts of Al and Mg in the AZ91D alloy, reflecting its eutectic nature. In contrast, Fig. 6(b-d) shows a finer and more uniform grain structure resulting from the application of ultrasonication. The ultrasonication process produces a cavitation effect, collapsing the reinforcement particles and dispersing them throughout the matrix. The microstructures of the composites vary depending on the amount of ZrB₂ particles added, with increasing wt.% of reinforcement leading to greater grain refinement. This refinement is attributed to the presence of ZrB₂ particles, which act as heterogeneous nucleation sites, inhibiting excessive grain growth during solidification. Additionally, the squeezing procedure during fabrication reduces porosity and further refines the grain structure³⁷. During this process, the β-Mg₁₇Al₁₂ intermetallic precipitates become well-developed and continuous within the finer grains, enhancing the mechanical properties of the composites as also observed in³⁹. Overall, the microstructure of both the alloy and composites appears clean and flawless, with no visible defects, due to the effective application of the SUS casting process. Figure 6 also provides information on the grain size of the fabricated alloy and composites. The grain size of the AZ0 alloy is 80 μm. The graph shows a decrease in grain size as the wt.% of ZrB₂ particles increases. The average grain sizes for the AZ5, AZ10, and AZ15 composites are 73 μm, 65 μm, and 58 μm, respectively, with the most significant grain size reduction observed at the highest wt.%. According to Zhang et al., the addition of ZrB₂ particles to the matrix significantly contributes to the reduction in grain size²⁰.

Fig. 6

(a-d). OM image and grain size of fabricated materials.

Fig. 7

(a-d). Microstructural morphology of materials using SEM analysis.

Figure 7(a-d) presents the dispersion SEM images of the fabricated materials. In Fig. 7(a), the SEM image of the AZ0 material reveals a dendritic structure with the β-Mg₁₇Al₁₂ phase, primarily located at the grain boundaries and surrounded by α-Mg. It is evident from the image that the β-Mg₁₇Al₁₂ precipitates, which formed after T6 heat treatment, appear in a discontinuous pattern¹⁶. This heat treatment significantly influences the microstructure of the AZ91D alloy. During solutionizing (T4), most of the β-Mg₁₇Al₁₂ precipitates dissolve into the α-Mg phase, as the temperature during heating surpasses the solvus line. Consequently, solutionizing results in a smaller number of β-Mg₁₇Al₁₂ precipitates of very fine size, dispersed within a large volume of eutectic mixture⁴⁰. However, the subsequent ageing process promotes the growth of β-Mg₁₇Al₁₂ precipitates due to the long-range diffusion of atoms. As a result, the precipitates that dissolve during solutionizing grow and appear in a discontinuous form during ageing⁴¹. Figure 7(b-c) shows the distribution of ZrB₂ reinforcements at a lower content of 5 and 10 wt%, exhibiting a uniform and homogeneous dispersion of ZrB₂ particles throughout the matrix. This even distribution is attributed to the vigorous stirring and UST processes used during fabrication. UST effectively shortened the stirring time, which was essential for preventing the formation of clusters and reducing oxidation in the Mg matrix⁴². The UST process generates high temperature and pressure gradients in the melt due to rapid compression and expansion cycles. Particle clusters disintegrate as ultrasonic waves propagate, and transient bubbles within the melt rapidly collapse²⁴. This process breaks up the clusters, ensuring a uniform distribution of reinforcement particles in the matrix. Additionally, UST improves the wettability of the particles by cleaning their surfaces. The application of squeeze pressure during solidification further enhanced the microstructure of the composites²⁶. However, in the case of AZ15 (Fig. 7(d)), some agglomeration was observed, likely due to the higher addition of 15 wt% ZrB₂ particles, which tend to form clusters at higher concentrations.

XRD analysis of alloy and composites

The XRD pattern for the fabricated alloy and composites is presented in Fig. 8. The spectra for the AZ0, AZ5, AZ10, and AZ15 composites show peaks corresponding to the α-Mg and β-Mg₁₇Al₁₂ phases of the AZ0 alloy. The ageing process regenerates Mg₁₇Al₁₂ precipitates from the supersaturated α-Mg solid solution. These peaks align with JCPDS card 89-5003 for α-Mg and 01-1128 for β-Mg₁₇Al₁₂⁴³. Additionally, JCPDS card 89-3930 verifies the presence of ZrB₂ peaks in the AZ5, AZ10, and AZ15 composites⁴⁴. Notably, the intensity of ZrB₂ peaks increases as its wt.% rises in the matrix, with the AZ15 composite showing the highest peak intensity due to the larger amount of ZrB₂. Furthermore, intermetallic β-Mg₁₇Al₁₂ precipitates are more prominent in AZ10 and AZ15 compared to AZ5, especially around the grain boundaries as a result of heat treatment. The XRD analysis confirms the absence of any adverse chemical reactions between the matrix and reinforcement particles at all levels of inclusion, with only beneficial intermetallic phases present. These precipitates contribute to the improved mechanical strength of the composites⁴⁵.

Fig. 8

XRD analysis of AZ0 alloy and composites.

Density and porosity measurement

The physical properties of the fabricated alloy and composites are shown in Fig. 9. The inclusion of harder UHTC ceramic ZrB₂ greatly influences the density of the fabricated composites. It clearly shows that the measured actual density of the composites is increases with an increase in the composition of ZrB₂ wt.% of 5, 10, and 15 respectively. It can be inferred that the alloy which has been fabricated without any reinforcements exhibits lower porosity than all the other composites. The porosity of manufactured materials increases as ZrB₂ reinforcing content increases. It is always known that the inclusion of any foreign particle in an alloy will tend to increase the chances of dislocation or any gas entrapment which will simultaneously result in the increase in a defect called porosity. Among that, AZ15 has been observed as a highly porous material having a porosity of about 1.48%. This may be due to the presence of some slight agglomerations that were observed in its microstructure.

Fig. 9

Physical properties of the fabricated materials.

Hardness measurement

The hardness values for the alloy and composites are shown in Fig. 10. It was observed that the AZ0 alloy has a lower hardness (93 HV) compared to the composites, primarily due to the softer nature of the non-reinforced matrix. Additionally, the coarse grain structure contributes to its brittleness, reducing the load-bearing capacity. The incorporation of a small amount of ZrB₂ in the matrix (AZ5) increased hardness by approximately 4.3%, a result of adding a smaller quantity of high-density ZrB₂ particles to the matrix. As the ZrB₂ content increased to 10 wt.% and 15 wt.%, the hardness of the AZ10 and AZ15 composites rose by 7.5% and 13%, respectively. The improvement in hardness is attributed to several factors, including (i) the uniform distribution of ZrB₂ particles achieved through the stir-UST process, (ii) grain refinement, (iii) enhanced degassing and improved wettability via UST, and (iv) the elimination of pores and voids due to the squeeze pressure applied during solidification⁴⁶.

The evenly dispersed ceramic ZrB₂ particles acted as nucleation sites for the α-Mg phase during solidification, further refining the grain structure. These hard ZrB₂ particles enhanced the load-bearing capacity of the composites, significantly contributing to the increase in hardness⁴². The ZrB₂ particles also resisted local matrix deformation during indentation, leading to a higher hardness in the reinforced matrix. Moreover, the presence of hard and brittle β-Mg₁₇Al₁₂ precipitates, regenerated by the T6 heat treatment, further contributed to the improvement in the hardness of the materials⁴⁷.

Fig. 10

Hardness of the fabricated materials.

Optimization of AZ91D/ZrB₂ composites using entropy integrated TODIM method

The optimization process began by creating an experimental setup using the Taguchi L16 orthogonal array, which was prepared by using Minitab software. Table 5 displays the corresponding responses for each combination of parameters. It is important to note that the experiments were conducted with one replication.

Table 5 Parameter response table for L₁₆ orthogonal array.

Calculation of weight using entropy

The significance of the experiment’s responses was evaluated using the entropy method. Firstly, a decision matrix was created based on the experimental results, as presented in Table 5. Equation (4) was then used to normalize the decision matrix, standardizing the responses to a common scale and range. Table 6 displays the normalized matrix, including all the responses.

Table 6 Normalized matrix and entropy measure of the process outcomes.

After the normalization process, the overall measure of the project outcomes’ entropy was calculated using Eq. (5). Additionally, for each response, Eq. (5) was employed to compute its entropy. The entropy measure of the project outcome is presented in Table 6.

Next, Eq. (6) was utilized to compute the weight of each response, considering the corresponding entropy measure. The resulting values, as displayed in Table 7, represent the optimal weight assigned to each response, with a total sum of 1. Notably, the corrosion current response obtained the highest weight, reaching a maximum value of 78%. This highlights its significance within the overall experiment.

Table 7 Weight of the responses.

Optimization using TODIM technique

Using the TODIM approach, the task is to choose the most suitable combination of tribocorrosion parameters for AZ91D/ZrB₂. For the ‘n’ number of designed alternative experimental runs and ‘m’ number of chosen criteria, as shown in Table 5 construct the decision matrix. But before proceeding to the steps for optimization, the different units of the chosen criteria have to be made to a common scale and range, eliminating the large difference in the magnitude of the criteria. Table 8 shows the normalized matrix of criteria considering a min-max formula as given in Eqs. (8) & (9). From the entropy weight method, the weights of all criteria are taken and the relative weight for the criteria is calculated using Eq. (10). The weight of the corrosion current is to be the maximum and taken as W_r. In the TODIM method, the alternative experimental runs are compared with other alternative experimental runs. Using Eq. (12) the dominance degree φwr (Eri, Erj) is calculated. The degree of dominance Eri, Erj of one experimental alternative Eri over another experimental alternative Erj was also computed. Table 8 shows the dominance degree of each alternative to all other alternatives. It is for the experimental run Er1 compared to all the other alternative experimental runs. Similarly, the degree of dominance for all remaining alternatives was also calculated using Eq. (13), the overall degree of dominance alternatives was calculated, and then the alternatives were ranked.

From Table 9, it is clear the alternative Er15 (A – 15%, B – 230 °C, C – 30 N, and D – 10) showed the highest value of the overall degree of dominance and Er4 (A – 0%, B – 260 °C, C – 60 N, and D – 3) showed the lowest value. The decreasing order of experimental runs based on their ranking: Er15 > Er10 > Er11 > Er9 > Er14 > Er6 > Er1 > Er7 > Er16 > Er13 > Er12 > Er8 > Er3 > Er5 > Er2 > Er4. In each experimental trial, the TODIM grade value indicates a single qualitative feature for all five response characteristics. The processing variables with the greatest TODIM grade value were used to define optimal processing settings within the designated experimental domain. The TODIM grade value for various experimental trials are illustrated in Fig. 11. Significantly, the 15th experimental trial displayed the highest TODIM grade value, indicating the proximity of the processing conditions to the optimal settings of the process variables.

Table 8 Normalization matrix and degree of dominance alternatives.

Table 9 Overall degree of dominance and ranking.

Fig. 11

TODIM grade and rank.

ANOVA

The ANOVA was used to identify the key factors influencing the TODIM grade, with the detailed results presented in Table 10. This analysis is essential for determining which variables have the most significant impact on the TODIM model and helps assess the interactions between these factors. The factors (model terms) evaluated in this study were labelled as A, B, C, and D, with interaction terms such as AB, AC, AD, BC, and BD. All these factors and their interactions were found to significantly contribute to the development of the regression equation for TODIM, as formulated in Eq. (14). The ANOVA results revealed that the wt.% of reinforcement (Factor A) had the most significant impact on the TODIM grade, contributing 34%. This considerable contribution highlights the importance of ZrB₂ reinforcement, as it plays a critical role in strengthening the grain structure and reducing Cl⁻ ion attack, which enhances the material’s properties. The second most influential factor was the ageing temperature (Factor B), contributing 14%. This temperature affects the material strength by encouraging the reprecipitation of the secondary phase, which also acts as a cathodic region during casting⁴⁸. The normal load (Factor C) contributed 8%, reflecting its role in influencing the wear behaviour of the composites under testing conditions. Lastly, the pH value (Factor D) contributed 6%, demonstrating that the chemical environment during testing, particularly for corrosion and degradation behaviour, significantly affects the TODIM grade. These contributions were visually represented in Fig. 12, making it clear which factors had the greatest influence on the outcome.

The derived regression equation showed a high R² value of 0.93, indicating a strong correlation between the predicted and actual experimental data. This high R² value suggests that the regression model provides an excellent fit for the performance characteristics being evaluated. Furthermore, the predicted R² value (0.90) and adjusted R² value (0.92) were closely aligned, supporting the reliability of the model. The proximity of these values confirms that the model is not overfitted and that it generalizes well to new data. In addition to the R² values, the analysis also reported an adequate precision value of 4.30, as shown in Table 11. Adequate precision measures the signal-to-noise ratio, with values greater than 4 considered desirable. A value of 4.30 indicates that the model has good discrimination capabilities, allowing it to distinguish between significant and insignificant effects, further validating the accuracy and robustness of the regression model. The combination of a high R² value, close alignment between the predicted and adjusted R² values, and a strong adequate precision value underscores the suitability of the developed quadratic model for predicting the TODIM value.

Table 10 Analysis of variance on TODIM grade.

Fig. 12

Percentage of the contribution of process parameters.

Table 11 Model summary.

Regression equation:

$$\begin{array}{l}\:{\rm{TODIM}}\:{\rm{Grade}} = 0.566 + 0.290 \times \:{\rm{A}} + 0.050 \times \:{\rm{B}} + 0.085 \times \:{\rm{C}}\: - 0.085\\\quad \quad \quad \quad \quad \quad \quad\quad \times \:{\rm{D}}\: - 0.045 \times \:{\rm{AB}} + 0.263 \times \:{\rm{AC}} + 0.115 \times \:{\rm{AD}} + 0.072 \times \:{\rm{BC}}\: - 0.083 \times \:{\rm{BD}}\end{array}$$

(14)

The residual plots in Fig. 13(a-e) validate the quadratic mathematical models developed for predicting TODIM grade values based on all experimental trials. A closer examination of each sub-figure offers valuable insights into the model’s accuracy and reliability. Figure 13(a) presents the relationship between the predicted and actual TODIM values, displaying a strong linear correlation. The proximity of most data points to the line of equality indicates that the model can predict TODIM values with high accuracy, confirming its robustness and reliable fit between experimental and predicted results. Figure 13(b) shows the normal probability plot of externally studentized residuals. The fact that most points align closely with the reference line suggests that the residuals follow an approximately normal distribution. This confirms that the assumption of normally distributed errors is valid, a critical requirement for ensuring model accuracy. By adhering to this assumption, the likelihood of bias in the predictions is minimized.

Figure 13(c) illustrates the externally studentized residuals plotted against the predicted TODIM values. The residuals are scattered randomly around zero with no apparent patterns, indicating that the model does not exhibit heteroscedasticity (non-constant variance). This random distribution further supports the appropriateness of the prediction model, as it confirms that the residuals do not deviate systematically. Figure 13(d) depicts the residuals versus experimental runs. Similar to the previous plot, there is no discernible pattern, and the residuals remain within the expected range. This lack of trends affirms that the errors are independent, ensuring that the model accurately captures the random variability in the data without introducing bias throughout the experimental trials. Figure 13(e) highlights the standardized effects of various process parameters on the tribocorrosion properties of the fabricated MMCs. Parameters that exceed the critical threshold, represented by the vertical dotted line at a 95% significance level (α = 0.05), are considered statistically significant. The analysis identifies four key process variables that significantly influence the tribocorrosion behaviour of the MMCs. These critical factors provide valuable insights into which parameters must be carefully controlled to optimize the tribocorrosion properties of the material.

Fig. 13

(a) Actual Vs, Predicted TODIM value, (b) Normal % Probability Vs. Externally studentized Residuals, (c) Externally Studentized Residuals Vs. Predicted TODIM, (d) Externally Studentized Residuals Vs. Experimental Runs, (e) Pareto Chart.

Effect of parameter on responses

The main effects plots presented in Fig. 14(a-e) provide a comprehensive analysis of how various process parameters, such as wt.% of reinforcement, ageing temperature, and applied load, influence the tribocorrosion behaviour and material responses. The wt.% of reinforcement (Fig. 14(a)) stands out as the most significant factor impacting key responses like corrosion potential and hardness after tribocorrosion. As the wt.% of reinforcement increases, these properties improve, primarily due to the beneficial effect of ZrB₂, which forms a protective β-phase that shields the material from Cl⁻ ions. This protective film results in enhanced corrosion resistance and material hardness-similar to how ceramic coatings exhibit enhanced corrosion protection in aggressive subcritical and supercritical aqueous systems due to their thermal stability and chemical inertness⁴⁹​. However, as the reinforcement content continues to rise, other responses such as corrosion current, corrosion rate, and wear depth decrease, since the additional reinforcement particles reduce free electron emission and slow down material removal, thus limiting the transformation of Mg into Mg⁺ ions.

The ageing temperature also plays a crucial role in shaping the material’s response, as seen in Fig. 14(b). As the temperature increases, the formation of the β-phase further boosts corrosion potential and hardness. However, at temperatures beyond 230 °C, the melting of this protective β-phase allows Cl⁻ ions to easily attack the material, leading to increased corrosion current, corrosion rate, and wear depth. Therefore, the optimal ageing temperature for achieving the best corrosion resistance and hardness appears to be around 230 °C. Beyond this point, the dissolution of the β-phase results in diminished protective capabilities, which inversely impacts the tribocorrosion performance.

Figure 14(c) highlights the interaction between wt.% of reinforcement and applied load on corrosion rate. The effect of reinforcement on corrosion rate is straightforward; increased reinforcement reduces the rate. However, the impact of the applied load is more nuanced. At lower loads, the ZrB₂ tribolayer formed during the process protects the material, resulting in a decreased corrosion rate. As the load increases, the tribolayer gets worn away, leading to an increase in both corrosion rate and material removal due to the higher corrosion current.

The influence of applied load on wear depth is evident in Fig. 14(d). As the applied load rises, the wear depth increases due to the depletion of the tribolayer in the fabricated composites. A similar load-sensitive wear behavior has been observed in LPBF-fabricated WC-12Co cemented carbides, where scanning speed and substrate compatibility influenced microstructural integrity and wear characteristics⁵⁰. This depletion allows for greater material removal, highlighting the sensitivity of the composite material to higher applied loads.

Lastly, Fig. 14(e) illustrates how an increase in wt.% of reinforcement, ageing temperature, and pH value enhances hardness after corrosion. The presence of reinforcement and elevated temperatures promotes the formation of a protective ZrB₂ and β-Mg₁₇Al₁₂ tribolayer, which offers resistance to wear and corrosion from chloride ions. Additionally, a higher pH value facilitates the presence of OH⁻ ions, encouraging the formation of corrosion-resistant by-products. However, this improvement in hardness is counteracted by an increase in applied load, which leads to more material deformation and removal, ultimately reducing the material’s hardness.

Fig. 14

Main Effect Plot: (a) corrosion potential (V), (b) corrosion current (A cm^− 2), (c) corrosion rate (mm/yr.), (d) wear depth (µm), (e) Hardness after tribocorrosion (HV).

3D- surface plot

The 3D surface plots illustrated in Fig. 15(a-e) provide a clear understanding of the variation in TODIM grade an index measuring tribocorrosion and wear resistance based on changes in critical process parameters such as wt.% of reinforcement, ageing temperature, applied load, and pH value. In Fig. 15(a), it is evident that both the wt.% of reinforcement and the ageing temperature positively influence the TODIM grade. As the ageing temperature increases, the formation of the β-Mg phase becomes more pronounced, which serves to shield the primary Mg phase from corrosive attacks. The optimal ageing temperature is around 230 °C, beyond which the protective β-Mg₁₇Al₁₂ phase begins to dissolve into the Mg matrix, thus reducing its effectiveness. Furthermore, an increase in the wt.% of ZrB₂ reinforcement enhances the material’s wear and corrosion resistance. However, this trend does not persist indefinitely; further increments in reinforcement lead to the agglomeration of particles, which detracts from the composite’s overall effectiveness. The study identifies 15% ZrB₂ as the optimal reinforcement level, showing superior results compared to other percentages.

In Fig. 15(b), a similar trend is observed in the wt.% of reinforcement, where an increase in reinforcement boosts the TODIM grade. However, increasing the applied load has the opposite effect, leading to a reduction in the TODIM grade. This is because higher applied loads result in more material being removed from the surface of the fabricated composites, thereby increasing wear and reducing tribocorrosion resistance. The increased load creates greater friction between the material’s surface and external asperities, hastening the wear process, and consequently, lowering the TODIM grade.

Moving on to Fig. 15(c), it is demonstrated that an increase in both wt.% of reinforcement and pH value results in an improved TODIM grade. This can be explained by the chemical dynamics of the environment: at lower pH values, chloride ions (Cl⁻) are more aggressive due to the abundance of H⁺ ions, which react with Mg to form MgCl₂, thereby accelerating corrosion. In contrast, at higher pH levels, the presence of OH⁻ ions promote the formation of corrosion-resistant by-products such as Mg (OH)₂, which enhances the material’s resistance to corrosion and wear, thereby increasing the TODIM grade.

Figure 15(d) presents the relationship between ageing temperature, applied load, and TODIM grade. As ageing temperature increases and the applied load decreases, the TODIM grade improves. This can be attributed to the fact that a lower applied load reduces frictional forces and prevents the erosion of the protective layers, thereby preserving the integrity of the material. Conversely, higher loads cause greater contact between hard asperities and the material, leading to an increase in friction and facilitating the removal of protective layers, which exposes the material to chloride ion attacks.

Finally, Fig. 15(e) shows that increasing both the ageing temperature and pH value leads to an increase in the TODIM grade. This is consistent with the previous findings: at higher ageing temperatures, the formation of the β-Mg₁₇Al₁₂ phase enhances corrosion resistance, and at higher pH values, the presence of OH⁻ ions lead to the formation of corrosion-resistant layers, such as Mg (OH)₂, which further protects the material from wear and corrosion.

Fig. 15

3D surface plot of different combinations of process parameters (a) AB, (b) AC, (c) AD, (d) BC, (e) BD.

Desirability plot

The desirability function is an effective mathematical modeling tool used to identify optimal conditions from a set of specified parameters, aiming to maximize or minimize outcomes based on defined criteria. Each parameter is assigned a value between 0 and 1, where 1 represents the most desirable or optimal outcome. This approach helps manage multiple objectives by combining various response measures into a single composite desirability score. The score enables the determination of the ideal combination of process parameters that produce the best overall performance for the system under study. In this particular desirability analysis, two distinct optimization objectives were applied, depending on the nature of the variables. For corrosion potential and post-corrosion hardness, the “larger-the-better” criterion was applied, meaning higher values were preferred due to their positive contribution to material performance. Conversely, for corrosion current, corrosion rate, and wear depth, the “smaller-the-better” principle was adopted, as lower values signify reduced material degradation and improved durability.

The process variables analyzed such as the wt% of reinforcement, ageing temperature, applied load, and pH value were selected within a predefined range, as illustrated in the figure. Each of these input variables plays a critical role in influencing the tribocorrosion behavior of the material system. The optimal sequence of these parameters corresponds to the highest desirability score, indicating the best balance of parameters to achieve superior performance. The ram function graph in Fig. 16 visually represents the results, clearly indicating the preferred desirability levels for each process variable. The horizontal axis shows the range of each variable, while the dots highlight the points within that range that achieve the highest desirability. The vertical axis represents the combined desirability score for all parameters, with higher altitudes indicating more favorable results. From the analysis, the optimal tribocorrosion parameters were identified as 15 wt.% reinforcement, an ageing temperature of 230 °C, an applied load of 5 N, and a pH value of 10. These specific settings correspond to the highest desirability score in the study, demonstrating an ideal balance between maximizing material performance (corrosion potential and hardness) and minimizing degradation (corrosion current, corrosion rate, and wear depth).

The ram function graph helps visualize the optimal desirability levels for each process variable, determined by the weight assigned to each. The altitude on the graph reflects the overall desirability, accounting for the combined influence of all variables. The dots on the graph represent the exact parameter levels that yield the highest desirability score. For instance, 15 wt.% reinforcement optimizes the material’s wear resistance and mechanical strength. An ageing temperature of 230 °C provides the best thermal condition for enhancing material properties. A load of 5 N minimizes wear without compromising performance, while a pH value of 10 promotes an alkaline environment that enhances corrosion resistance.

The analysis presented in Fig. 17(a-d) provides critical insights into the relationship between key processing variables and the resulting performance of the material, as measured by both desirability and TODIM grade. The 3D surface plot and contour map in.

Figure 17(a) and 17(b) indicate that the peak desirability level, represented by a score of 0.904, is achieved under conditions of higher reinforcement content, higher ageing temperature, and lower applied load. This peak suggests that the combination of these variables delivers optimal material properties by enhancing both corrosion resistance and mechanical performance. The sharp incline of the surface plot toward the area of higher desirability demonstrates strong coherence between the chosen target values and the actual performance of the system, ensuring that the materials maintain their integrity while minimizing wear and corrosion.

Similarly, Fig. 17(c) and 17(d) illustrate the relationship between the TODIM grade and the process variables. The TODIM plot shows that the highest grade is achieved when the material is processed with higher levels of reinforcement and lower loading conditions. This result emphasizes the importance of reinforcement content in improving overall material durability and highlights the detrimental effect of excessive loading, which can accelerate wear and degradation. The gradual increase in the TODIM value as the reinforcement percentage rises and the load decreases further supports this interpretation. These findings demonstrate that reinforcing the material with higher percentages and subjecting it to lower mechanical stresses leads to a more favorable balance of properties, improving both the corrosion and wear resistance.

Confirmation test

The confirmation test was performed to determine the efficiency of entropy-integrated TODIM in predicting the optimal level of squeeze casting parameter. An initial setting is considered with expert opinion. The values of responses obtained at the optimal setting arrived from TODIM are compared with that of the initial values. Table 12 displays the results and comparison of the confirmation test. The TODIM value improves from 0.5661 to 0.9047 when predicted at the optimal condition. The confirmation test gave an acceptable outcome as significant improvements were found with the TODIM grade as well as the responses.

Fig. 16

Desirability plot.

Fig. 17

(a) 3D Surface plot of Desirability, (b) 2D surface plot of desirability, (c) 3D Surface plot of TODIM grade, (d) 2D surface of TODIM grade.

The results shown in Fig. 18 indicate that optimal conditions resulted in minimal surface damage and fewer corrosion pits compared to the initial conditions. Additionally, the 3D photographs revealed fewer surface peaks under these optimized parameters. In contrast, the higher surface damage and increased corrosion pit formation observed under initial conditions were due to insufficient ageing and high load, which caused greater electron discharge on the sample surfaces. These corrosion pits led to localized stress concentrations in the material and are recognized as critical inducing factors for the initiation of fatigue cracks^51,52. However, under optimal conditions—particularly at an ageing temperature of 230 °C the corrosion rate and corrosion current were significantly reduced. This improvement is attributed to the precipitation of a secondary phase, which acted as a cathodic region, thereby lowering electron activity and minimizing corrosion pit formation.

Table 12 Confirmation test.

Fig. 18

Tribocorrosion test at initial and optimal conditions.

Corrosion mechanism

The corrosion mechanism of Mg/ZrB₂ composites changes notably with increasing ZrB₂ content, as illustrated in Fig. 19(a-d). This is primarily attributed to the formation of a protective ZrB₂ layer beneath the naturally occurring Mg(OH)₂ passive film, which enhances the composite’s corrosion resistance. In the 0% ZrB₂ strengthened Mg matrix, the corrosion rate is fast due to magnesium’s reactivity in chloride-rich environments. The corrosion product is a loosely bound Mg(OH)₂ layer that provides minimal protective abilities. This porous layer allows aggressive Cl⁻ to easily form micro-pitting and localized corrosion. With the high and continued release of Mg²⁺ ions during aggressive pitting corrosion, there is also a high evolution of trapped H₂ gas, which is indicative of a high rate of corrosion. With an addition of 5% ZrB₂, a minor ZrB₂-rich protective layer will develops underneath the Mg(OH)₂ layer, acting as a secondary sub-barrier. This second barrier limits direct electrolyte penetration to the Mg surface, producing noticeable shifts in the amount of Mg²⁺ released and H₂ gas evolution. As the ZrB₂ concentration increases to 10%, its protective barrier increases in tenacity, which further strengthens the corrosion barrier system. The continuous and uniformly distributed ZrB₂ particles will further pad/muffle and block existing micro-galvanic sites at the Mg surface, and thereby continue to stabilize the integrity of the passive layer. Further reductions of both Mg²⁺ and H₂ are present due to increased corrosion resistance.

Fig. 19

(a-d). Corrosion Mechanism with respect to reinforcement.

Corrosion behaviour in Mg-15% ZrB₂ composites is influenced by the formation and activity of a reprecipitated secondary phase layer during ageing, as displayed in Fig. 20(a-d).

At 170 °C ageing temperature, the primary occurrence of the reprecipitated secondary phase layer starts, but the layer is thin, not continuous, and weakly adhered to the matrix. This immature secondary phase layer provides minimal barrier protection, allowing the corrosive medium to easily penetrate the surface. Consequently, the rate of release of Mg²⁺ ions is high, and the rate of evolution of H₂ gas is also high, which suggests a vigorous corrosion process characterized by extensive anodic dissolution of magnesium and water reduction reactions at cathodic locations. When the ageing temperature is increased to 200 °C, the secondary phase layer becomes more prominent and moderately uniform. The heightened precipitate density starts to limit direct exposure of the Mg matrix to the corrosive environment, thus breaking corrosion pathways. At this point, the microstructure is fine and the formation of the passive layer is enhanced, resulting in lower Mg²⁺ ion release and less H₂ gas evolution than at 170 °C. Nevertheless, complete precipitation hardening has not yet been achieved, and thus corrosion protection is still moderate.

Fig. 20

(a-d). Corrosion Mechanism of AZ15 with respect to ageing temperature.

At the ideal ageing temperature of 230 °C, the composite achieves maximum formation of a dense, continuous, and well-bonded reprecipitated secondary phase layer.

The layer, homogeneously distributed in the matrix and at the Mg/ZrB₂ interfaces, serves as an effective corrosion-resistant barrier, sealing out aggressive Cl⁻ ions and minimizing micro-galvanic activity. The structural integrity and compactness of this layer significantly enhance corrosion resistance, resulting in very low Mg²⁺ release and very low H₂ evolution. This indicates low metal dissolution and high passivation efficiency. However, when the ageing temperature is further increased to 260 °C, over-ageing leads to coarsening of the reprecipitated phases due to over-ageing. The secondary phase particles become larger and segregate at grain boundaries, breaking the continuity and efficiency of the protective layer. The coarse precipitates also create microstructural stress and interfacial defects, which act as initiation sites for localized corrosion. Accordingly, the corrosion resistance decreases abruptly, exhibiting very high Mg²⁺ ion release and very high H₂ gas evolution, suggesting accelerated degradation of the passive film and an aggressive corrosion environment.

Conclusions

By using a linear reciprocating tribometer with an L16 orthogonal array, the material’s tribocorrosion behaviour was examined. The entropy-integrated TODIM method was utilized to optimize process variables such as wt% of reinforcement (%), ageing temperature (^oC), applied load (N), and pH value based on corrosion potential, corrosion current, corrosion rate, wear depth, and hardness of the corroded sample as responses. The statistical analysis and individual and combined contributions of each process parameter were analyzed through ANOVA and a 3D surface plot. The following conclusions are drawn below:

• 1. Morphological examination through OM and SEM revealed that the composites fabricated using stirring, UST, and squeezing techniques showed uniform dispersion of ZrB₂ particles in the matrix. However, the AZ15 composites exhibited agglomeration due to cluster formation during casting. XRD analysis confirmed the presence of α-Mg and β-Mg₁₇Al₁₂ phases, without any intermetallic formation, indicating non-reactivity between the matrix and reinforcements.

• 2. The inclusion of ZrB₂ in the fabricated composites leads to an increase in both density and porosity, with higher ZrB₂ content correlating to greater porosity, particularly in AZ15, which exhibits the highest porosity at 1.48% due to possible agglomerations.

• 3. The hardness of the fabricated composites (AZ5, AZ10, and AZ15) showed significant improvement compared to the base alloy AZ0, with increases of approximately 4.30%, 7.52%, and 12.9%, respectively. This enhancement was attributed to the addition of denser ZrB₂ reinforcements into the AZ91D Mg alloy. The AZ15 composites, containing 15 wt.% of ZrB₂ reinforcements, achieved the highest hardness value of 105 VHN.

• 4. The TODIM method successfully transformed the multi-response optimization problem into a single response. The highest TODIM grade (1.000) was obtained in experiment 15 (A4B3C2D2). The coefficient of determination (R² = 0.9397) indicated a strong correlation between the predicted and experimental results.

• 5. The Analysis of Variance (ANOVA) showed that all process parameters (A, B, C, and D) significantly influenced the responses. Additionally, significant interactions were observed between parameter pairs AB, AC, AD, BC, and BD. Among the parameters, the wt.% of reinforcement (A) had the most significant effect, contributing 37.4% to the responses.

• 6. The 3D surface plots demonstrated that the TODIM grade increased with higher wt.% of reinforcement, ageing temperature, and pH value, while it decreased with increasing applied load. The optimal responses were achieved with the parameters set at 15% wt.% of reinforcement (A), 230 °C ageing temperature (B), 15 N applied load (C), and pH 10 (D).

• 7. The optimal settings determined using the TODIM method were 14.9% for wt.% of reinforcement (A), 229 °C for ageing temperature (B), 30.50 N for applied load (C), and pH 9.99 (D). The corresponding optimal response values were − 1.39 V for corrosion potential (E_corr), 0.005 A/cm² for corrosion current (I_corr), 0.964 mm/yr for corrosion rate, 249.62 μm for wear depth, and 100.94 Hv for hardness of the corroded sample. A confirmation test revealed an improvement of 0.338 in the TODIM grade.