Improving computational drug repositioning through multi-source disease similarity networks

Abstract

Computational drug repositioning seeks to identify new therapeutic uses for existing or experimental drugs. Network-based methods are effective as they integrate relationships among drugs, diseases, and target proteins/genes into prediction models. However, traditional approaches often rely on a single phenotype-based disease similarity network, limiting the diversity of disease information. In this study, we constructed three disease similarity networks—phenotypic, ontological, and molecular—using data from OMIM, Human Phenotype Ontology annotations, and gene interaction network, respectively. These were integrated into disease multiplex networks and multiplex-heterogeneous networks. We applied a tailored Random Walk with Restart (RWR) algorithm to predict novel drug-disease associations. Experimental results show that both disease multiplex and multiplex-heterogeneous networks outperform their single-layer counterparts in leave-one-out cross-validation. Using 10-fold cross-validation, our method, MHDR, outperformed the state-of-the-art methods TP-NRWRH, DDAGDL and RGLDR, demonstrating the advantage of integrating multiple disease similarity networks. We predicted novel drug-disease associations by ranking candidates, identifying 68 associations supported by shared proteins/genes, 1,064 by shared pathways, and 84 by shared protein complexes, with many validated by clinical trials, underscoring the practical impact of our approach.

Introduction

Drug repositioning, which identifies new clinical indications for existing or experimental drugs, offers a cost-effective alternative to traditional drug discovery, known for being time-consuming and expensive¹. Historically, clinical observations have driven successful repositioning cases. For instance, bevacizumab, initially developed for metastatic colon cancer and non-small cell lung cancer by targeting angiogenesis, has been repurposed to treat exudative macular degeneration by slowing abnormal retinal vascularization². Similarly, sildenafil now addresses erectile dysfunction and pulmonary hypertension, thalidomide treats severe erythema nodosum leprosum, and retinoids are used for acute promyelocytic leukemia^3,4. Studies by Ashburn et al. and Sardana et al. further highlight successful examples of drug repositioning^5,6. To scale this process, computational methods—including machine learning, network-based, and matrix-based approaches—have emerged for in silico prediction of drug-disease associations^7,8.

Network-based methods are particularly effective, as they integrate known relationships among drugs, diseases, and target proteins/genes into prediction models⁹. These methods often rely on the principle that similar drugs can treat diseases with shared pathogenesis or symptoms, constructing heterogeneous networks where drug and disease similarity networks are linked via drug-disease associations. For example, Wu et al. used network clustering to identify drug-disease modules in a heterogeneous network¹⁰, while Luo et al. applied a Bi-Random Walk with Restart (MBiRWR) algorithm on a similar network¹¹. RLSDR employed semi-supervised learning to rank candidate diseases¹², and TP-NRWRH introduced a two-pass random walk with restart approach to predict new drug indications¹³. More recent methods, such as DDAGDL¹⁴ and RGLDR¹⁵, leverage advanced techniques like graph attention networks and regulation-aware learning within complex heterogeneous information networks (HINs), incorporating drug-protein and protein-disease associations to enhance prediction accuracy.

Despite these advancements, a key limitation persists: most methods use a single phenotype-based disease similarity network, typically derived from MimMiner¹⁶, which computes similarity using MeSH terms from OMIM disease descriptions¹⁷. This approach overlooks diverse disease relationships, such as molecular and ontological similarities, limiting prediction accuracy¹⁸. Early methods relied on MeSH vocabularies¹⁶ or shared genes¹⁹, but recent developments, including the Human Phenotype Ontology (HPO), enable more comprehensive semantic similarity measures^20,21,22. Recognizing that diseases are characterized by multiple dimensions—phenotypic, molecular, and ontological—integrating these perspectives can improve disease relationship modeling.

In this study, we constructed three disease similarity networks: DiSimNet_O (phenotypic, based on MimMiner/OMIM), DiSimNet_H (ontological, using HPO annotations), and DiSimNet_G (molecular, derived from HumanNet gene interactions). These were integrated into disease multiplex networks (e.g., DiSimNet_OHG) and multiplex-heterogeneous networks (e.g., DrSimNet_P-DiSimNet_OHG) using known drug-disease associations. We adapted a Random Walk with Restart (RWR) algorithm to rank candidate diseases, predicting novel drug-disease associations. Our approach outperformed single-layer networks in leave-one-out cross-validation (LOOCV) and surpassed state-of-the-art methods like TP-NRWRH, DDAGDL, and RGLDR in 10-fold cross-validation, demonstrating the value of multi-source disease similarity integration. We further validated predictions with clinical evidence, identifying numerous drug-disease associations supported by shared genes, pathways, and protein complexes.

Materials and methods

Here, we first introduce how networks of drugs and diseases (including single/monoplex drug/disease similarity networks, disease multiplex networks, heterogeneous networks of drugs and diseases, and multiplex-heterogeneous networks of drugs and diseases) were constructed. Then, we described how the random walk with restart (RWR) algorithm was adapted to rank candidate diseases on these networks, ultimately to predict novel drug-disease associations.

Network construction

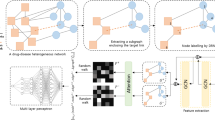
In this section, we describe the construction of drug and disease networks. First, we constructed single/monoplex drug/disease similarity networks. Then, we combined them to form multiplex, heterogeneous and multiplex-heterogeneous networks using known drug-disease associations (Fig. 1).

Fig. 1

Network construction. First, single/monoplex drug/disease similarity networks are constructed, including: (a) DrSimNet_C, a drug similarity network constructed by computing the chemical structure-based similarity between two drugs; (b) DiSimNet_O, a disease similarity network constructed based on a disease vocabulary database, MeSH, which is used to annotate diseases in OMIM medical description records; (c) DiSimNet_H, a disease similarity network constructed using a disease annotation database, HPO, by a semantic similarity measure; and (d) DiSimNet_G, a disease similarity network built based on known associated genes and interactions in a gene network, HumanNet. Second, (e) a disease multiplex network is constructed using two or three monoplex disease similarity networks (e.g., DiSimNet_OHG). Finally, (f) a heterogeneous network of drugs and diseases is constructed by connecting a drug similarity network and a disease similarity network through known drug-disease associations (e.g., DrSimNet_C-DiSimNet_O), and (g) a multiplex-heterogeneous network is formed by connecting a drug similarity network with a disease multiplex network using known drug-disease associations (e.g., DrSimNet_C-DiSimNet_OHG).

Construction of monoplex drug/disease similarity networks

Drug similarity networks

First, we collected a drug similarity network from a previous study PREDICT²³. This network includes 593 drugs and 175,528 associations between them (shortly called DrSimNet_P). This network covers only a small set of drugs available in public databases. Therefore, we additionally constructed a larger one under the hypothesis that drugs with similar chemical structures would have similar therapeutic functions and can be used to treat similar diseases. More specifically, we computed the similarity between each pair of drugs based on their chemical structures using the SIMCOMP tool²⁴ for 7,838 drugs collected from the KEGG database²⁵. We eventually obtained 887,883 interactions with a positive similarity between every pair of the drugs to construct a drug similarity network (shortly called DrSimNet_C) (Fig. 1(a)).

Disease similarity networks

First, we constructed a disease similarity network using a disease phenotype similarity matrix collected from MimMiner¹⁶. This matrix was constructed based on the similarity between disease phenotypes represented by OMIM records¹⁷, which describe diseases as genetic disorders using natural language. Each element of the matrix represents the degree of phenotypic similarity between two diseases, normalized to [0,1]. To ensure a reliable and sparse network, we selected the five nearest neighbors (kLN = 5) with the highest similarity scores for each disease, resulting in a phenotypic disease similarity network with 19,791 interactions among 5,080 phenotypes (shortly called DiSimNet_O) (Fig. 1(b)). The choice of kLN = 5 balances network connectivity with specificity, prioritizing the most robust associations. To explore the impact of this parameter, we constructed alternative DiSimNet_O networks with kLN = 10, kLN = 15, and a similarity threshold (sim ≥ 0.3), evaluating their performance in Supplementary Figures S1–S4, as discussed in the Results section.

Second, we constructed another disease similarity network based on the Human Phenotype Ontology (HPO). To this end, we first mapped each disease to one OMIM record, then annotated the OMIM with HPO terms using the HPO annotation database²⁶. The similarity between two HPO terms was calculated based on the information content (IC) of each term, defined as follows:

$$\:IC\left(t\right)=\:-\text{l}\text{o}\text{g}\left(p\left(t\right)\right)$$

where $\:p\left(t\right)$ is the probability of term ttt occurring in the HPO annotation database, computed as $\:p\left(t\right)=\frac{f\left(t\right)}{f\left(root\right)}$​, with $\:f\left(t\right)=Annot\left(t\right)+\:\sum\:_{c\in\:Children\left(t\right)}f\left(c\right)$. Here, Annot(t) is the number of phenotypes annotated with term ttt, and Children(t) is the set of child terms of ttt in the HPO graph. The semantic similarity between two HPO terms t_i and t_j is calculated using the most informative common ancestor approach²⁷:

$$\:simTerm\left({t}_{i},{t}_{j}\right)=\underset{c\in\:P\left({t}_{i},{\:t}_{j}\right)}{\text{max}}\left(IC\left(c\right)\right)$$

where $\:P\left({t}_{i},{t}_{j}\right)$ is the set of shared ancestors. The similarity between diseases d_i and d_j ​ is:

$$\:sim\left({d}_{i},{d}_{j}\right)=\underset{{t}_{i}\in\:T\left({d}_{i}\right),\:{\:t}_{j}\in\:T\left({d}_{j}\right)}{\text{max}}\left(simTerm\left({t}_{i},{t}_{j}\right)\right)$$

This value is normalized to [0,1]:

$$\:simDis\left({d}_{i},{d}_{j}\right)=\frac{2\times\:sim\left({d}_{i},{d}_{j}\right)}{sim\left({d}_{i},{d}_{i}\right)+sim\left({d}_{j},{d}_{j}\right)}$$

By selecting the five nearest neighbors for each node, we constructed an HPO-based disease similarity network with 34,476 interactions among 6,521 disease phenotypes (DiSimNet_H) (Fig. 1(c)).

Finally, we constructed a disease similarity network based on known disease-associated genes and a gene network²⁸. Using 3,229 diseases from OMIM and the HumanNet gene-gene similarity network²⁹, we defined the similarity between diseases d_i and d_j as the similarity between their associated gene sets G₁ and G₂:

$$\:simDis\left({d}_{i},{d}_{j}\right)=simGeneSet\left({G}_{1},{G}_{2}\right)=\frac{{\sum\:}_{{g}_{i}\in\:{G}_{1}}\text{m}\text{a}\text{x}\left(sim\right({g}_{i},{G}_{2}\left)\right)+{\sum\:}_{{g}_{j}\in\:{G}_{2}}\text{m}\text{a}\text{x}\left(sim\right({g}_{j},{G}_{1}\left)\right)}{\left|{G}_{1}\right|+\left|{G}_{2}\right|}$$

This resulted in a disease similarity network (DiSimNet_G) with 82,241 interactions among 3,229 diseases (Fig. 1(d)).

Construction of multiplex disease similarity networks

To enhance the prediction of drug-disease associations, we constructed a disease multiplex network by integrating three distinct disease similarity networks—phenotypic (DiSimNet_O), molecular (DiSimNet_G), and HPO-based (DiSimNet_H)—as layers, allowing Random Walk with Restart (RWR) to capture complementary disease relationships across multiple biological perspectives. Each layer shares the same set of disease nodes, but edges are weighted by different similarity measures, reflecting phenotypic, molecular, and ontological relationships, respectively. Two or three disease similarity networks can be connected to form a multiplex disease similarity network with two or three layers, respectively (Table 1).

Table 1 List of single/monoplex disease similarity and multiplex disease networks.

Construction of heterogeneous and multiplex-heterogeneous networks

Heterogeneous and multiplex-heterogeneous networks were constructed by connecting a drug similarity network with a monoplex and multiplex disease similarity network, respectively, using known drug-disease associations. Thus, we collected the known associations from PREDICT²³. There are 1,933 associations between 593 drugs and 313 diseases. Each drug similarity network can be connected with a monoplex disease similarity network (Fig. 1(f)); thus, six heterogeneous networks were finally obtained. Similarly, each drug similarity network can be connected with a disease multiplex network to form a multiplex-heterogeneous network; thus, a total of eight multiplex-heterogeneous networks can be obtained (Fig. 1(g)). (Table 2).

Table 2 A list of heterogeneous and multiplex-heterogeneous networks constructed by connecting disease networks with a drug similarity network (e.g., DrSimNet_P and DrSimNet_C).

Random walk with restart algorithm on networks of drugs and diseases

In this section, we describe the Random Walk with Restart (RWR) algorithm adapted to rank candidate diseases for a given drug, predicting novel drug-disease associations. The RWR algorithm simulates a walker traversing a network, starting from source nodes (e.g., a drug and its known associated diseases), moving to neighboring nodes with probabilities defined by edge weights, and occasionally restarting at the source nodes. This process ranks nodes (diseases) based on their steady-state probabilities, reflecting their relevance to the source nodes. We apply RWR to monoplex and multiplex disease similarity networks, as well as heterogeneous and multiplex-heterogeneous networks, to leverage diverse disease and drug similarity information.

RWR algorithm on monoplex and multiplex networks of diseases

For a monoplex disease similarity network (Fig. 1(b-d)), the RWR algorithm ranks diseases based on their proximity to a set of source nodes (S), which includes all diseases known to be associated with a drug of interest, dr. The algorithm balances exploration (moving to adjacent nodes) and exploitation (returning to source nodes) to identify diseases likely to be associated with dr.

Parameters and variables

• $\:{A}_{D}$: Adjacency matrix of the monoplex disease similarity network (n ⋅ n), where $\:{{(A}_{D})}_{i,j}$ represents the similarity between diseases $\:{d}_{i}$ and$\:\:{d}_{j}$.

• $\:{M}^{D}$: Transition matrix, obtained by column-normalizing $\:{A}_{D}$, where $\:{{{\left({M}^{D}\right)}_{i,j\:=}\:(A}_{D})}_{i,j}/\sum\nolimits_{k}{{(A}_{D})}_{k,j}$ denotes the probability of moving from disease $\:{d}_{i}$ and$\:\:{d}_{j}$.

• $\:{P}_{t}^{D}$: Probability vector (n ⋅ 1) at step t, where $\:{\left({P}_{t}^{D}\right)}_{i}$ is the probability of the walker being at disease $\:{d}_{i}$.

• $\:{P}_{0}^{D}$: Initial probability vector (n ⋅ 1), defined as:

$$\:{P}_{0}^{D}=\left\{\begin{array}{c}\frac{1}{\left|S\right|}\:\:\:\:\:\:\:if\:{d}_{i}\in\:S\\\:0\:\:\:\:\:\:\:otherwise\end{array}\right.$$

where (|S|) is the number of source nodes.

• $\:\gamma\:$: Restart probability (γ ∈ (0, 1)), controlling the likelihood of the walker returning to the source nodes at each step. A higher γ emphasizes the influence of source nodes, while a lower γ allows more exploration.

• $\:{P}_{\infty\:}^{D}$: Steady-state probability vector, where $\:{\left({P}_{\infty\:}^{D}\right)}_{i}$ represents the relative importance of disease $\:{d}_{i}$ to the source nodes.

RWR equation and derivation

The RWR algorithm updates the probability vector iteratively until convergence. At each step, the walker either moves to a neighboring node with probability $\:1-\gamma\:$ or restarts at the source nodes with probability $\:\gamma\:$. The update rule is:

$$\:{P}_{t+1}^{D}=\left(1-\gamma\:\right){M}^{D}{P}_{t}^{D}+{\gamma\:P}_{0}^{D}$$

• Step 1: Initialize $\:{P}_{0}^{D}$ based on the source nodes (S).

• Step 2: Compute the transition matrix $\:{M}^{D}$ by normalizing $\:{A}_{D}$.

• Step 3: At each iteration, calculate $\:{P}_{t+1}^{D}$:

  • The term $\:\left(1-\gamma\:\right){M}^{D}{P}_{t}^{D}$ represents the probability of moving to neighboring nodes, weighted by the transition probabilities in $\:{M}^{D}$.

  • The term $\:{\gamma\:P}_{0}^{D}$ represents the probability of restarting at the source nodes.

• Step 4: Repeat until $\:{P}_{t}^{D}$ converges to $\:{P}_{\infty\:}^{D}$, where (||$\:{P}_{t+1}^{D}$ - $\:{P}_{t}^{D}$|| < $\:\epsilon\:$) (e.g., $\:\epsilon\:$ = 10⁻⁶).

• Step 5: Rank diseases based on $\:{\left({P}_{\infty\:}^{D}\right)}_{i}$, with higher values indicating stronger associations with dr.

For a multiplex disease similarity network (Fig. 1(e)), multiple disease similarity networks (layers) are integrated, sharing the same set of diseases but with different similarity measures (e.g., DiSimNet_O, DiSimNet_H, DiSimNet_G). The walker can move within a layer or jump between layers.

Additional parameters for multiplex networks

• L: Number of layers in the multiplex network.

• $\:{A}_{D}^{\left[i\right]}$: Adjacency matrix of the disease similarity network at layer i (i = 1,…, L).

• $\:\delta\:$: Between-disease-disease-network jumping probability ($\:\delta\:$∈ [0,1]), controlling the likelihood of the walker jumping between layers.

• $\:\tau\:$: Weight vector ($\:\left[{\tau\:}_{1},\dots\:,{\tau\:}_{L}\right]$), where $\:{\tau\:}_{i}$ represents the importance of layer i. We set $\:{\tau\:}_{i}$ = 1/L for equal contribution.

• $\:{A}_{D}^{M}$: Adjacency matrix of the multiplex network, defined as:

$$\:{A}_{D}^{M}=\left[\begin{array}{ccc}(1-\delta\:){A}_{D}^{\left[1\right]}&\:\dots\:&\:\frac{\delta\:}{(L-1)}I\\\:\dots\:&\:\dots\:&\:\dots\:\\\:\frac{\delta\:}{(L-1)}I&\:\dots\:&\:(1-\delta\:){A}_{D}^{\left[L\right]}\end{array}\right]$$

where I is the identity matrix, and off-diagonal blocks allow inter-layer transitions.

• $\:{M}^{M}$: Transition matrix of the multiplex network, derived by column-normalizing $\:{A}_{D}^{M}$.

• $\:{P}_{t}^{M}$: Probability matrix (n ⋅ L) at step t, where $\:{P}_{t}^{i}$ is the probability vector for layer i.

• $\:{P}_{0}^{M}$: Initial probability matrix, set as $\:{P}_{0}^{M}=\tau\:{P}_{0}^{D}$.

RWR equation for multiplex networks

The update rule for the multiplex network is:

$$\:{P}_{t+1}^{M}=\left(1-\gamma\:\right){M}^{M}{P}_{t}^{M}+{\gamma\:P}_{0}^{M}$$

• Step 1: Initialize $\:{P}_{0}^{M}$ using $\:\tau\:$ and $\:{P}_{0}^{D}$.

• Step 2: Construct $\:{A}_{D}^{M}$ and compute $\:{M}^{M}$.

• Step 3: Update $\:{P}_{t}^{M}$ iteratively, where the walker moves within or between layers based on $\:{M}^{M}$.

• Step 4: Compute the steady-state probability $\:{P}_{\infty\:}^{M}$. The final score for each disease is the geometric mean of steady-state probabilities across layers.

• Step 5: Rank diseases based on their scores.

RWR algorithm on heterogeneous and multiplex-heterogeneous networks

In a heterogeneous network (Fig. 1(f)), a drug similarity network and a disease similarity network are connected via known drug-disease associations (bipartite network). The RWR algorithm ranks both drugs and diseases simultaneously, using the drug of interest dr and its known associated diseases as source nodes. The multiplex-heterogeneous network (Fig. 1(g)) extends this by integrating a drug similarity network with a multiplex disease similarity network.

Parameters and variables for heterogeneous networks

• $\:{A}_{Dr}$: Adjacency matrix of the drug similarity network (m ⋅ m), where $\:{\left({A}_{Dr}\right)}_{i,j}$ is the similarity between drugs $\:d{r}_{i}$ and$\:\:d{r}_{j}$.

• $\:{A}_{D}$: Adjacency matrix of the disease similarity network (n ⋅ n).

• B: Adjacency matrix of the bipartite drug-disease network, where $\:{\left(B\right)}_{i,j}=1$ if drug $\:d{r}_{i}$ is associated with disease d_j, and 0 otherwise.

• $\:{A}^{H}$: Adjacency matrix of the heterogeneous network:

$$\:{A}^{H}=\left[\begin{array}{cc}{A}_{Dr}&\:B\\\:{B}^{T}&\:{A}_{D}\end{array}\right]$$

• $\:{M}^{H}$: Transition matrix of the heterogeneous network, defined as:

$$\:{M}^{H}=\left[\begin{array}{cc}{M}_{Dr}^{H}&\:{M}_{DrD}^{H}\\\:{M}_{DDr}^{H}&\:{M}_{D}^{H}\end{array}\right]$$

• where:

  • $\:{\:M}_{Dr}^{H}$: Intra-subnetwork transition matrix for the drug similarity network.

  • $\:{M}_{D}^{H}$: Intra-subnetwork transition matrix for the disease similarity network.

  • $\:{M}_{DrD}^{H}$, $\:{M}_{DDr}^{H}$: Inter-subnetwork transition matrices for drug-to-disease and disease-to-drug transitions.

• $\:\lambda\:$: Between-drug-disease-network jumping probability ($\:\lambda\:$∈[0,1]), controlling the likelihood of the walker jumping between drug and disease networks.

• $\eta$: Importance weight ($\eta$ ∈ [0,1]), balancing the contribution of the drug and disease networks in the initial probability vector.

• $\:{P}_{t}^{H}$: Probability vector ((m + n) ⋅ 1) at step t.

• $\:{P}_{0}^{H}$: Initial probability vector, defined as:

$$\:{P}_{0}^{H}=\left[\begin{array}{c}\left(1-\right){P}_{0}^{D}\\\:{P}_{0}^{Dr}\end{array}\right]$$

where

$$\:{P}_{0}^{Dr}=\left\{\begin{array}{c}1\:\:\:\:\:\:\:if\:{d}_{i}\equiv\:dr\\\:0\:\:\:\:\:\:\:otherwise\end{array}\right.$$

Transition matrix derivation

The transition matrix $\:{M}^{H}$ is computed as follows:

• For $\:{M}_{DrD}^{H}$:

$$\:{\left({M}_{DrD}^{H}\right)}_{i,j}=p\left({d}_{j}|d{r}_{i}\right)=\left\{\begin{array}{c}\frac{{\left(B\right)}_{ij}}{{\sum}_{j}{\left(B\right)}_{ij}}\:\:\:\:\:if\:\:{\sum}_{j}{\left(B\right)}_{ij}\ne\:0\\\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

• For $\:{M}_{DDr}^{H}$:

$$\:{\left({M}_{DDr}^{H}\right)}_{i,j}=p\left(d{r}_{j}|{d}_{i}\right)=\left\{\begin{array}{c}\frac{{\left(B\right)}_{ji}}{{\sum}_{j}{\left(B\right)}_{ji}}\:\:\:\:\:\:if\:\:{\sum}_{j}{\left(B\right)}_{ji}\ne\:0\\\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

• For $\:{\:M}_{Dr}^{H}$:

$$\:{\left({\:M}_{Dr}^{H}\right)}_{i,j}=\left\{\begin{array}{c}\frac{{\left({A}_{Dr}\right)}_{ij}}{{\sum}_{j}{\left({A}_{Dr}\right)}_{ij}}\:\:\:\:\:\:if\:\:{\sum}_{j}{\left(B\right)}_{ij}=0\\\:\frac{{(1-)\left({A}_{Dr}\right)}_{ij}}{{\sum}_{j}{\left({A}_{Dr}\right)}_{ij}}\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

• For $\:{M}_{D}^{H}$:

$$\:{\left({M}_{D}^{H}\right)}_{i,j}=\left\{\begin{array}{c}\frac{{\left({A}_{D}\right)}_{ij}}{{\sum}_{j}{\left({A}_{D}\right)}_{ij}}\:\:\:\:\:\:\:\:\:\:if\:\:{\sum}_{j}{\left(B\right)}_{ji}=0\\\:\frac{{(1-)\left({A}_{D}\right)}_{ij}\:}{{\sum}_{j}{\left({A}_{D}\right)}_{ij}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

RWR equation for heterogeneous networks

The update rule is:

$$\:{P}_{t+1}^{H}=\left(1-\gamma\:\right){M}^{H}{P}_{t}^{H}+{\gamma\:P}_{0}^{H}$$

• Step 1: Initialize $\:{P}_{0}^{H}$ using $\:{P}_{0}^{D}$, $\:{P}_{0}^{Dr}$, and $\eta$.

• Step 2: Compute $\:{M}^{H}$ using the above transition matrices.

• Step 3: Update $\:{P}_{t}^{H}$ iteratively, allowing the walker to move within or between subnetworks.

• Step 4: Rank diseases based on the disease-related portion of $\:{P}_{\infty\:}^{H}$.

Multiplex-Heterogeneous networks

For a multiplex-heterogeneous network (Fig. 1(g)), the drug similarity network is connected to each layer of a multiplex disease similarity network via L identical bipartite networks. The bipartite adjacency matrix is:

$$\:{B}^{MH}=\left[\begin{array}{c}\begin{array}{c}{B}^{\left[1\right]}\\\:\dots\:\end{array}\\\:{B}^{\left[L\right]}\end{array}\right]$$

The adjacency matrix is:

$$\:{A}^{MH}=\left[\begin{array}{cc}{A}_{Dr}&\:{B}^{MH}\\\:{\left({B}^{MH}\right)}^{T}&\:{A}_{D}^{M}\end{array}\right]$$

The transition matrix $\:{M}^{MH}$ and RWR equation follow the same structure as the heterogeneous case:

$$\:{M}^{MH}=\left[\begin{array}{cc}{M}_{Dr}^{MH}&\:{M}_{DrD}^{MH}\\\:{M}_{DDr}^{MH}&\:{M}_{D}^{MH}\end{array}\right]$$

$$\:{P}_{t+1}^{MH}=\left(1-\gamma\:\right){M}^{MH}{P}_{t}^{MH}+{\gamma\:P}_{0}^{MH}$$

where $\:{P}_{t+1}^{MH}$, $\:{P}_{t}^{MH}$, and $\:{P}_{0}^{MH}$ are of dimension (n⋅L + m), and $\:{P}_{0}^{MH}=\left[\begin{array}{c}\left(1-\right){P}_{0}^{H}\\\:{P}_{0}^{Dr}\end{array}\right]$.

The final disease scores are computed as the geometric mean across layers, similar to the multiplex case.

Performance evaluation

The prediction performance was assessed using a leave-one-out cross-validation (LOOCV) scheme for each drug, structured as a binary classification task where positive instances are known drug-disease associations, and negative instances are all other diseases not known to be associated with the drug. Given a drug dr, let D be the set of its known associated diseases (positive samples) and C be the set of candidate diseases (negative samples, i.e., all diseases not in D). For each disease s∈D, we perform the following steps:

• 1. Hold-Out: Remove the association between dr and s, treating s as a test sample.

• 2. Seed Nodes: Set the remaining known associated diseases D\{s} as seed nodes (S).

• 3. Ranking: Apply the Random Walk with Restart (RWR)-based ranking method to score all diseases in C∪{s}.

• 4. Evaluation: Repeat this process for each s∈D, evaluating the ranking of s relative to C.

LOOCV was chosen over k-fold cross-validation to maximize the number of drugs included in the evaluation. In the PREDICT dataset (1,933 associations between 593 drugs and 313 diseases), 171 drugs have only one known associated disease. In k-fold cross-validation, each drug requires at least k associated diseases to be split into k folds, excluding these 171 drugs for k > 1. LOOCV, requiring only one associated disease, ensures all 593 drugs are evaluated, providing a more comprehensive assessment.

Performance is evaluated using two metrics: the Area Under the Receiver Operating Characteristic Curve (AUROC) and the Area Under the Precision-Recall Curve (AUPRC). For a given threshold τ, we compute true positives (TP), false negatives (FN), false positives (FP), and true negatives (TN) as follows:

$$\:TP=\sum\limits_{s\in\:S}I(rank\left(s\right)\le\:\tau\:)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:FN=\sum\limits_{s\in\:S}I(rank\left(s\right)>\tau\:)$$

$$\:FP=\sum\limits_{c\in\:C}I(rank\left(c\right)\le\:\tau\:)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:TN=\sum\limits_{c\in\:C}I(rank\left(c\right)>\tau\:)$$

where rank(s), rank(c) denote the rank of the held-out disease s and candidate disease c in C∪{s}, and I(⋅) is the indicator function. The True Positive Rate (TPR) and False Positive Rate (FPR) are defined as:

$$\:TPR=\frac{TP}{TP+FN}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:FPR=\frac{FP}{FP+TN}$$

By varying τ from 1 to the size of C∪{s}, we plot the ROC curve (TPR vs. FPR) and compute AUROC.

Additionally, we compute precision and recall to plot the Precision-Recall curve and calculating AUPRC.

$$\:Precison=\frac{TP}{TP+FP}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:Recall=\frac{TP}{TP+FN}$$

AUROC measures overall discriminative ability, while AUPRC is particularly informative for our highly imbalanced dataset, where positive associations (~ 0.07% of all drug-disease pairs, or ~ 1:1,428 positive-to-negative ratio) are sparse. AUPRC emphasizes the model’s ability to correctly identify true positives among the minority class, complementing AUROC.

Results

Parameter settings

The prediction performance of the RWR-based methods on different types of drug and disease networks depends on their parameters. The RWR-based methods have been studied for predicting disease-associated biomarkers, such as the prediction of disease-associated genes^30,31,32. Thus, its parameters, including the restart probability ($\:\gamma\:$), the between-drug-disease-network jumping probability ($\:\lambda\:$), and the importance weight ($\:)$ of layers in a heterogeneous network, have been well studied, and the prediction performance was shown to be stable to changes in these parameters.

The goal of this study is to prove that the integration of multiple disease similarity networks can improve the prediction of drug-disease associations. Therefore, we only investigated the change of the restart probability ($\:\gamma\:)$ (i.e., the core parameter of the RWR-based methods) and the between-disease-disease-network jumping probability ($\:\delta\:$). In particular, two networks were considered: a disease multiplex network (DiSimNet_OHG) and a multiplex-heterogeneous network (DrSimNet_P-DiSimNet_OHG). All monoplex disease networks were considered equal in contributing to the prediction performance; thus, we set $\:{\tau\:}_{1}={\tau\:}_{2}=\dots\:{\tau\:}_{L}=1/L$.

Firstly, to investigate $\:\gamma\:,$ we varied it in [0.1, 0.3, 0.5, 0.7, 0.9] and kept other parameters constants, i.e., $\:\delta\:$ = $\:\lambda\:$ =$\eta$= 0.5, then we assessed the prediction performance of the RWR-based algorithm on the two investigated networks. Figure 2(a) shows that the performance of the multiplex-heterogeneous network is nearly unchanged; meanwhile, that of the multiplex network was slightly worse when $\:\gamma\:$ increased.

Finally, we varied $\:\delta\:$ in [0.1, 0.3, 0.5, 0.7, 0.9] and kept other parameters constants, i.e., $\:\gamma\:$ = $\:\lambda\:$ =$\eta$= 0.5, to investigate its effect on the prediction performance on the two networks. As a result, we observed similar results that when the $\:\delta\:$ increases the prediction performance of the multiplex-heterogeneous network remains stable; meanwhile, that of the multiplex network slightly decreases (Fig. 2(b)).

Taken together, the prediction performance of the RWR-based methods is stable with respect to changes in parameters; thus, we set $\:\gamma\:$ = $\:\delta\:$ = $\:\lambda\:$ =$\eta$= 0.5 for all other experiments.

Fig. 2

Prediction performance of the RWR-based methods on a disease multiplex network and a multiplex-heterogeneous network according to the change of (a) restart probability ($\:{\upgamma\:}$), and (b) between-disease-disease-network jumping probability ($\:\delta\:$).

Integration of multiple disease similarity networks improves the prediction performance

Impact of neighbor selection in disease similarity network construction

To assess the impact of the neighbor selection parameter in constructing the DiSimNet_O network, we evaluated four variants: the original DiSimNet_O with kLN = 5 (19,791 interactions among 5,080 phenotypes), and three alternatives with kLN = 10, kLN = 15, and a similarity threshold (sim ≥ 0.3). These variants were tested across monoplex, multiplex, heterogeneous (with DrSimNet_P), and multiplex-heterogeneous (with DrSimNet_P) networks, using AUROC and AUPRC metrics (Supplementary Figures S1–S4). For monoplex networks (Figure S1), DiSimNet_O (kLN = 10) achieved the highest performance (AUROC = 0.835, AUPRC = 0.016), while DiSimNet_O (kLN = 15) had the lowest AUROC (0.659) and DiSimNet_O (sim ≥ 0.3) had the lowest AUPRC (0.006). In multiplex networks (Figure S2), DiSimNet_OHG (kLN = 15) yielded the highest AUROC (0.871), and DiSimNet_OHG (kLN = 5, 10) tied for the highest AUPRC (0.019). For heterogeneous networks (Figure S3), DrSimNet_P-DiSimNet_O (kLN = 10) matched the original kLN = 5 for the highest AUROC (0.979), with kLN = 15 achieving the highest AUPRC (0.116). In multiplex-heterogeneous networks (Figure S4), all DiSimNet_OHG networks have similar AUROC (0.987–0.988), and DiSimNet_OHG (kLN = 10) the highest AUPRC (0.271). Across all scenarios, multiplex and multiplex-heterogeneous networks outperformed their monoplex and heterogeneous counterparts, consistent with our main findings. The original choice of kLN = 5 performed competitively (e.g., AUROC = 0.987, AUPRC = 0.269 for DrSimNet_P-DiSimNet_OHG), supporting its use, though kLN = 10 or 15 slightly improved performance in some cases. The similarity threshold (sim ≥ 0.3) generally underperformed, likely due to reduced network connectivity.

Disease multiplex and single/monoplex disease similarity networks

We compared the prediction performance of RWR-based methods on three monoplex disease similarity networks (DiSimNet_O, DiSimNet_H, DiSimNet_G) and four multiplex networks (DiSimNet_OH, DiSimNet_OG, DiSimNet_HG, DiSimNet_OHG). Figure 3(a) shows AUROC results, with DiSimNet_O achieving the highest monoplex performance (AUROC = 0.815) compared to DiSimNet_H (AUROC = 0.762) and DiSimNet_G (AUROC = 0.743). Multiplex networks outperformed monoplex networks, with DiSimNet_OH achieving AUROC = 0.866 and DiSimNet_OG achieving AUROC = 0.777, DiSimNet_HG at AUROC = 0.748, and DiSimNet_OHG at AUROC = 0.841. Figure 3(b) presents AUPRC results, reflecting the imbalanced nature of the dataset (baseline AUPRC ~ 0.0007). DiSimNet_O achieved the highest monoplex AUPRC of 0.011 (~ 16 times the baseline), followed by DiSimNet_H (AUPRC = 0.003, ~ 4 times) and DiSimNet_G (AUPRC = 0.002, ~ 3 times). Multiplex networks showed superior performance: DiSimNet_OH (AUPRC = 0.020, ~ 29 times), DiSimNet_OG (AUPRC = 0.012, ~ 17 times), DiSimNet_HG (AUPRC = 0.003, ~ 4 times), and DiSimNet_OHG (AUPRC = 0.019, ~ 27 times). These results confirm that integrating multiple disease similarity networks enhances the ability to identify true positives, particularly in sparse settings.

Fig. 3

Performance comparison between single/monoplex disease similarity networks and multiplex disease networks. (a) AUROC curves for monoplex (DiSimNet_O, DiSimNet_H, DiSimNet_G) and multiplex (DiSimNet_OH, DiSimNet_OG, DiSimNet_HG, DiSimNet_OHG) networks. (b) AUPRC curves, highlighting performance on the imbalanced dataset (baseline AUPRC ~ 0.0007).

Multiplex-heterogeneous and heterogeneous networks

We evaluated heterogeneous and multiplex-heterogeneous networks constructed with two drug similarity networks (DrSimNet_P and DrSimNet_C). For DrSimNet_P, Fig. 4(a) shows that all multiplex-heterogeneous networks achieved AUROC ≥ 0.98, outperforming heterogeneous networks (e.g., DrSimNet_P-DiSimNet_O, AUROC = 0.979). Figure 4(c) presents AUPRC results, with heterogeneous networks ranging from AUPRC = 0.030 (~ 43 times the baseline) for DrSimNet_P-DiSimNet_H to AUPRC = 0.066 (~ 94 times) for DrSimNet_P-DiSimNet_G. Multiplex-heterogeneous networks performed significantly better: DrSimNet_P-DiSimNet_OH (AUPRC = 0.169, ~ 241 times), DrSimNet_P-DiSimNet_OG (AUPRC = 0.224, ~ 320 times), DrSimNet_P-DiSimNet_HG (AUPRC = 0.219, ~ 313 times), and DrSimNet_P-DiSimNet_OHG (AUPRC = 0.269, ~ 384 times). For DrSimNet_C, Fig. 4(b) shows multiplex-heterogeneous networks with AUROC ≥ 0.97, surpassing heterogeneous networks (e.g., DrSimNet_C-DiSimNet_G, AUROC = 0.953). Figure 4(d) reports AUPRC values, with heterogeneous networks from AUPRC = 0.027 (~ 39 times) for DrSimNet_C-DiSimNet_H to AUPRC = 0.062 (~ 89 times) for DrSimNet_C-DiSimNet_G, and multiplex-heterogeneous networks ranging from AUPRC = 0.158 (~ 226 times) for DrSimNet_C-DiSimNet_OH to AUPRC = 0.321 (~ 459 times) for DrSimNet_C-DiSimNet_OHG. These AUPRC results highlight the superior performance of multiplex-heterogeneous networks in distinguishing true positives, complementing the AUROC findings and confirming the benefit of integrating multiple disease similarity networks.

Fig. 4

Performance comparison between heterogeneous and multiplex-heterogeneous networks. (a) AUROC curves for networks with DrSimNet_P. (b) AUROC curves for networks with DrSimNet_C. (c) AUPRC curves for networks with DrSimNet_P. (d) AUPRC curves for networks with DrSimNet_C.

Impact of the integration of disease similarity networks on prediction performance

The disease multiplex network integrates DiSimNet_O, DiSimNet_G, and DiSimNet_H as layers, where each layer is a weighted graph with diseases as nodes and edges weighted by similarity scores. DiSimNet_O uses MimMiner phenotypic similarities based on OMIM records. DiSimNet_G measures molecular similarity using gene sets from OMIM and interactions from HumanNet. DiSimNet_H computes semantic similarity using HPO annotations, normalized via Resnik’s method.

In the multiplex network, all layers share the same set of disease nodes, corresponding to the union of nodes across DiSimNet_O, DiSimNet_G, and DiSimNet_H. This results in 7,496 diseases for DiSimNet_OHG (Table 1), combining all unique diseases from the individual networks. Diseases present in one layer but not others have edges in those layers weighted as zero (i.e., no connection). For instance, a disease present in DiSimNet_H but not DiSimNet_G will have no neighbors in the DiSimNet_G layer. Each disease node exists in all layers, connected by intra-layer edges (weighted by the respective similarity measure) and inter-layer edges (connecting the same disease across layers). We constructed four multiplex networks (Table 1), with DiSimNet_OHG combining all three layers. Inter-layer connections are weighted by a jumping probability ($\:\delta\:$), tuned to 0.5, balancing intra-layer and cross-layer propagation in RWR (see “Materials and Methods” section).

The multiplex framework enables RWR to traverse both within and between layers, capturing diverse disease relationships that a single layer might miss. Intra-layer edges reflect similarity within a specific perspective (e.g., phenotypic similarity in DiSimNet_O), while inter-layer edges (weighted by $\:\delta\:$) allow the walker to jump between layers, integrating complementary signals. For example, two diseases with low phenotypic similarity in DiSimNet_O might be strongly connected in DiSimNet_G due to shared genes, and inter-layer jumps enable RWR to combine these signals, improving the ranking of related diseases. This cross-layer interaction is crucial for identifying indirect relationships, such as when a third disease bridges two diseases phenotypically in DiSimNet_O and molecularly in DiSimNet_G, enhancing the overall connectivity and robustness of disease similarity estimates.

Mathematically (see “Materials and Methods” section), the multiplex adjacency matrix ($\:{A}_{D}^{M}$) incorporates both intra-layer adjacency matrices (e.g., $\:{A}_{D}^{\left[1\right]}$ for DiSimNet_O) and inter-layer transitions, with off-diagonal blocks weighted by ($\:\frac{\delta\:}{(L-1)}$). The transition matrix $\:{M}^{M}$ normalizes these weights, and RWR updates probabilities across layers, with the final disease score computed as the geometric mean of steady-state probabilities across layers. This integration ensures that diseases are ranked based on a holistic view of their similarities, leveraging all available data sources.

The multiplex network’s ability to integrate diverse similarity measures significantly improves prediction performance, as shown in Figs. 3 and 4. For example, compared to monoplex networks, DiSimNet_OHG achieved an AUROC of 0.841 and AUPRC of 0.019 (27 times the baseline of 0.0007), outperforming DiSimNet_O (AUROC 0.815, AUPRC 0.011), DiSimNet_G (AUROC 0.743, AUPRC 0.002), and DiSimNet_H (AUROC 0.762, AUPRC 0.003) (Fig. 3). In addition, the prediction of drug valsartan (KEGG ID: D00400) for hypertension (MIMID: 145500) benefited from DiSimNet_G’s molecular similarity (shared gene AGTR1) (Table 3). This demonstrates that the multiplex framework, by leveraging interactions across layers, enhances the identification of novel drug-disease associations, aligning with clinical evidence and improving practical utility.

Compare with other methods

Recently, a state-of-the-art network-based method, TP-NRWRH³³, was proposed, utilizing a heterogeneous network of drugs and diseases based on the PREDICT dataset. TP-NRWRH employs a two-pass random walk with restart on this network, predicting potential drug-disease associations based on the mean probability of the two passes. In their study, TP-NRWRH outperformed methods for drug-disease association prediction (e.g., MBiRWR¹¹ and DrugNet³⁴) and drug-target interaction prediction (e.g., NBI³⁵, HGBI³⁶, KBMF2 K³⁷ and DT-Hybrid³⁸) using 10-fold cross-validation on PREDICT. For a fair comparison, we evaluated our best method, MHDR—using the RWR-based approach on the multiplex-heterogeneous network DrSimNet_P-DiSimNet_OHG—with the same 10-fold cross-validation scheme on PREDICT. MHDR achieved an AUROC of 0.965 and an AUPRC of 0.158, surpassing TP-NRWRH’s reported AUROC of 0.9394. The enhanced performance is due to the integration of two additional disease similarity networks (DiSimNet_H and DiSimNet_G) in DrSimNet_P-DiSimNet_OHG, demonstrating that incorporating more disease similarity networks improves prediction accuracy.

To further validate MHDR’s performance, we compared it with recent state-of-the-art methods, including DDAGDL¹⁴ and RGLDR¹⁵. DDAGDL constructs a heterogeneous information network (HIN) of drugs, diseases, and proteins using known drug-disease, drug-protein, and protein-disease associations. It employs an autoencoder to generate initial representations from SMILES for drugs, MeSH structures for diseases, and protein sequences for proteins, followed by a graph attention network (GAT)³⁹ to learn high-quality representations of drugs and diseases, and XGBoost for prediction. In contrast, MHDR relies solely on drug-disease associations, a drug similarity network (constructed based on chemical structure similarity), and disease similarity networks (constructed using phenotypic similarities from OMIM records and HPO terms, as well as molecular data), using a tailored Random Walk with Restart (RWR) algorithm. For a fair comparison, we adapted MHDR by using GAT to learn high-quality representations of drugs and diseases, followed by XGBoost for prediction. Although MHDR does not use an autoencoder to derive initial representations from SMILES, MeSH structures, or protein sequences, the process of constructing drug and disease similarity networks inherently embeds this information into the similarities between drugs and between diseases. Using the same negative sample selection and 10-fold cross-validation, DDAGDL achieved an AUROC of 0.9593 and an AUPRC of 0.0396, while MHDR outperformed it with an AUROC of 0.965 and an AUPRC of 0.158.

Similarly, RGLDR constructs a heterogeneous biological network of drugs, diseases, and proteins, using random walks with metapaths (e.g., drug → protein → disease) to build regulation graphs and a regulation-aware graph representation learning approach to learn representations of drugs and diseases, followed by XGBoost for prediction. To enable a fair comparison, we adapted MHDR by defining metapaths within the drug and disease similarity networks (e.g., drug → drug → drug, disease → disease → disease, due to the absence of protein data in our similarity networks). We then learned the representations of drugs and diseases based on these metapaths, followed by XGBoost for prediction. Using the same negative sample selection and evaluation scheme, RGLDR achieved an AUROC of 0.9633 and an AUPRC of 0.044, showing a comparable AUROC to MHDR (0.965) but a lower AUPRC (0.158 vs. 0.044). These results suggest that MHDR’s integration of multiple disease similarity networks enhances prediction performance.

Prediction of novel drug-disease associations

In the previous section, we demonstrated that our Random Walk with Restart (RWR)-based methods, particularly on the multiplex-heterogeneous network DrSimNet_P-DiSimNet_OHG, achieved superior prediction performance, with stable results across parameter variations and high AUROC and AUPRC scores. Here, we leverage this network to predict novel drug-disease associations and validate their practical relevance through clinical evidence. For each drug, we used known associated diseases as seed nodes, ranked other diseases in the disease multiplex network, and selected the top 10 highly ranked diseases as promising candidates for evidence search (Table S1 in Supporting Information). To demonstrate the model’s real-world utility, we provide case studies for associations supported by shared genes/proteins and shared pathways/protein complexes, validated by clinical trials from ClinicalTrials.gov using “rclinicaltrials” R package, addressing the need for practical effectiveness beyond theoretical metrics.

Case studies: associations supported by shared genes/proteins

We identified 68 drug-disease associations with shared genes/proteins, where disease-associated genes from OMIM¹⁷ and drug targets from KEGG²⁵ overlap, indicating potential drug repositioning opportunities⁴⁰ (Table S2). Of these, 16 were supported by clinical trials. Below, we highlight three representative case studies from Table 3, showcasing their biological grounding and clinical trial support.

• Testosterone (KEGG ID: D00075) and Prostate Cancer (MIMID: 176807): Testosterone activates the androgen receptor (AR), driving prostate cancer proliferation. However, bipolar androgen therapy uses high-dose testosterone to disrupt AR signaling, offering a novel treatment for castration-resistant cases. Clinical trials, such as NCT04558866, confirm its therapeutic potential by demonstrating efficacy in advanced prostate cancer. The shared gene AR provides a strong biological basis for this association.

• Argatroban (KEGG ID: D00181) and Ischemic Stroke (MIMID: 601367): Argatroban inhibits thrombin (F2), preventing clot propagation in ischemic stroke caused by thromboembolism. Trials like NCT03552354 validate its efficacy in reducing stroke progression, aligning with F2’s role in coagulation pathways. This association highlights the model’s ability to identify clinically relevant treatments.

• Risperidone (KEGG ID: D00426) and Obsessive-Compulsive Disorder (OCD) (MIMID: 164230): Risperidone’s antagonism of the serotonin 5-HT2 A receptor (HTR2 A) enhances SSRI efficacy in treatment-resistant OCD. NCT00389493 demonstrates significant symptom improvement, supporting its off-label use. The shared gene HTR2 A underpins the biological rationale for this prediction.

These cases, detailed in Table 3 and Table S2, illustrate how our model’s predictions are supported by clinical trial evidence, demonstrating practical utility.

Table 3 A list of 10 out of 16 drug-disease associations supported by shared genes/proteins and clinical trials.

Case studies: associations supported by shared pathways and protein complexes

Another indirect approach that can also support evidence for drug repositioning is based on shared protein complexes^41,42 or pathways^43,44,45,46 between a drug of interest and its candidate diseases. It has been proposed that the targeted protein complexes that drugs and diseases share can be used to estimate the possibility of a drug-disease association⁴⁷. Furthermore, a drug’s biological pathway may indicate the presence of a disease caused by its target. If targets of a drug and genes underlying a disease not currently treated by the drug are involved in the same pathway, it may indicate a promising association between the drug and the disease. Therefore, protein complexes or pathways that the drug of interest and its candidate diseases share could be exploited as evidence supporting drug repositioning. Here, we identified 1,064 and 84 drug-disease associations supported by shared KEGG pathways (Table S3) and CORUM⁴⁸ protein complexes (Table S4), respectively, with 73 supported by both (Tables S5). Of these, 30 were validated by clinical trials. Below, we present case studies for these nine associations from Table 4, each backed by shared molecular mechanisms and clinical evidence.

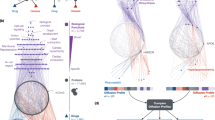
• Estrone (KEGG ID: D00067) and Breast Cancer (MIMID: 114480): Estrone promotes breast cancer growth through estrogen signaling pathway (map04915) and receptor complexes (Er-alpha-p53-hdm2 complex and ESR1-MAGEA2-TP53 complex). Trials like NCT01089049 validate its role in hormone therapy, supporting strategic therapeutic applications. Figure 5 (a) visualizes the connection between the Estrone and breast cancer via shared pathways and protein complexes.

• Testosterone (KEGG ID: D00075) and Prostate Cancer (MIMID: 176807): Testosterone drives prostate cancer via androgen pathways (map05215) and receptor complexes, but bipolar androgen therapy disrupts tumor growth. NCT04558866 confirms efficacy in advanced cases, consistent with shared gene (AR) evidence (Table 3).

• Argatroban (KEGG ID: D00181) and Ischemic Stroke (MIMID: 601367): Argatroban inhibits coagulation cascades (map04610), preventing stroke-related clots. NCT03552354 validates its efficacy in acute stroke, aligning with shared gene (F2) findings.

• Dexamethasone (KEGG ID: D00292) and Schizophrenia (MIMID: 181500): Dexamethasone modulates neuroactive ligand-receptor interactions (map04080), potentially reducing schizophrenia’s stress-related symptoms. NCT01310140 supports its therapeutic potential in early psychosis.

• Valsartan (KEGG ID: D00400) and Hypertension (MIMID: 145500):

• Valsartan blocks renin-angiotensin signaling (map04614), effectively lowering blood pressure. NCT01878201 confirms its efficacy in hypertension, consistent with shared gene (AGTR1) evidence. Figure 5(b) visualizes the association between Valsartan and Hypertension via shared pathways and protein complexes.

• Risperidone (KEGG ID: D00426) and Obsessive-Compulsive Disorder (MIMID: 164230): Risperidone modulates serotonergic pathways (map04726), enhancing OCD treatment. NCT00389493 confirms symptom improvement, aligning with shared gene (HTR2 A) findings.

• Olanzapine (KEGG ID: D00454) and Attention Deficit-Hyperactivity Disorder (MIMID: 143465): Olanzapine targets dopaminergic pathways (map04728), reducing ADHD impulsivity. NCT00205699 validates its efficacy in severe cases, consistent with shared gene (DRD4).

• Prednisolone (KEGG ID: D00472) and Schizophrenia (MIMID: 181500): Prednisolone modulates stress-related pathways (map04080), potentially alleviating schizophrenia symptoms. NCT03340909 supports its exploration as a novel treatment.

• Prochlorperazine (KEGG ID: D00493) and Schizophrenia (MIMID: 181500): Prochlorperazine blocks dopaminergic pathways (map04728), reducing psychotic symptoms. NCT02600741 confirms its efficacy in acute schizophrenia.

These nine associations, supported by shared pathways, protein complexes, and clinical trials, highlight the practical impact of our DrSimNet_P-DiSimNet_OHG network. Estrone drives breast cancer growth via estrogen signaling (map04915), with trials like NCT01089049 supporting its use in hormone therapy. Testosterone and argatroban excel in prostate cancer and ischemic stroke, with NCT04558866 and NCT03552354 confirming efficacy, mirroring shared gene findings. Dexamethasone and prednisolone offer novel schizophrenia treatments by targeting stress pathways (map04080), validated by trials like NCT01310140 and NCT03340909. Valsartan tackles hypertension through renin-angiotensin signaling (map04614), with NCT01878201 proving effectiveness. Risperidone and olanzapine enhance OCD and ADHD treatments via serotonin and dopamine pathways (map04726, map04728), backed by NCT00389493 and NCT00205699. Prochlorperazine controls schizophrenia symptoms, with NCT02600741 supporting its role. These cases, detailed in Table 4 and Table S5, show our model’s predictions translate to clinical applications.

To validate practical relevance, we confirmed that clinical trial outcomes align with our predictions. For risperidone in OCD, NCT00389493 demonstrates significant symptom reduction, supporting its predicted role in HTR2 A-driven efficacy. In prostate cancer, NCT04558866’s therapeutic benefits validate testosterone’s predicted disruption of AR signaling. Argatroban’s predicted stroke benefit (pathway map04610, gene F2) is supported by NCT03552354’s efficacy in reducing progression. These alignments, cross-referenced with shared gene associations, confirm that our model identifies clinically actionable drug-disease links, enhancing its real-world utility.

This section, supported by case studies and clinical trial validations, demonstrates that our multiplex-heterogeneous network not only achieves high predictive performance (AUROC/AUPRC) but also identifies drug-disease associations with tangible clinical impact, paving the way for innovative drug repositioning.

Fig. 5

Visualization of drug-disease associations via shared KEGG pathways and CORUM protein complexes, predicted by the DrSimNet_P-DiSimNet_OHG network. (a) The drug Estrone (KEGG ID: D00067) and breast cancer (MIMID: 114480) are linked by six shared pathways (e.g., estrogen signaling pathway, pathways in cancer) and two protein complexes (e.g., ER-alpha-p53-HDM2 complex, ESR1-MAGEA2-TP53 complex), supported by clinical trials like NCT01089049. (b) The drug Valsartan (KEGG ID: D00400) and Hypertension, Essential (MIMID: 145500) are connected by 14 shared pathways (e.g., renin-angiotensin system, neuroactive ligand-receptor interaction) and two protein complexes (e.g., AGTR1-AGTR2 complex, AGTR1-MAS1 complex), validated by trials such as NCT01878201. Diseases, drugs, pathways, and protein complexes are represented as nodes in blue squares, red circles, pink triangles, and purple diamonds, respectively. Green solid lines indicate associations, with edge weights reflecting the strength of connectivity between nodes.

Table 4 A list of 10 out of 30 promising drug-disease associations supported by shared pathways and protein complexes, and clinical trials.

Conclusions and discussion

Drug repositioning seeks to identify new indications for existing drugs, a process often limited by the scarcity of off-label uses discovered in clinical practice. Computational methods, particularly network-based approaches, offer a scalable solution by leveraging relationships among drugs, diseases, and target proteins/genes. These methods typically assume that similar drugs can treat similar diseases, using drug and disease similarity networks to predict associations. However, reliance on single disease similarity networks restricts the diversity of disease information, limiting prediction accuracy. As diseases often share molecular causes and phenotypic markers, integrating multiple disease similarity perspectives can enhance prediction performance.

In this study, we constructed three disease similarity networks—DiSimNet_O (phenotypic, OMIM), DiSimNet_H (ontological, HPO), and DiSimNet_G (molecular, HumanNet)—and integrated them into multiplex disease similarity networks (e.g., DiSimNet_OHG) and multiplex-heterogeneous networks (e.g., DrSimNet_P-DiSimNet_OHG). Using a tailored Random Walk with Restart (RWR) algorithm, we predicted novel drug-disease associations. Experimental results demonstrate that these integrated networks outperform single-layer networks in leave-one-out cross-validation. In 10-fold cross-validation, our method, MHDR, surpassed the state-of-the-art method TP-NRWRH, DDAGDL and RGLDR, highlighting the benefit of multi-source disease similarity integration. The practical utility of our approach is evidenced by the prediction of 68 drug-disease associations supported by shared proteins/genes, 1,064 by shared pathways, and 84 by shared protein complexes, with many associations validated by clinical trials (e.g., testosterone for prostate cancer, NCT04558866; valsartan for hypertension, NCT01878201).

Recent methods like DDAGDL and RGLDR leverage advanced representation learning within complex heterogeneous information networks. DDAGDL uses graph attention networks to learn high-quality drug and disease representations, while RGLDR employs regulation-aware graph learning with metapaths, both integrating drug-protein and protein-disease associations. Their approaches have been extended to predict lncRNA-miRNA interactions, expanding their utility in bioinformatics⁴⁹. However, their dependence on protein data can limit applicability to datasets, which lacks such associations. In contrast, MHDR’s integration of diverse disease similarity networks—embedding phenotypic, ontological, and molecular information—offers greater adaptability while achieving superior performance.

Other recent methods also advance drug discovery and treatment innovation. 3DSMILES-GPT⁵⁰ facilitates drug discovery by generating three-dimensional molecular structures based on target profiles, aiding the design of novel therapeutics. AMP-Designer⁵¹ uses large language models to design antimicrobial peptides, providing new avenues for addressing infectious diseases. These innovations complement network-based methods like ours, offering diverse strategies for drug repositioning and development.

Our predictions, supported by molecular evidence (shared genes, pathways, protein complexes) and clinical trials, underscore the potential of our method for practical drug repositioning⁵². Looking ahead, drug similarities—crucial for understanding therapeutic mechanisms—can be further explored by constructing diverse drug similarity networks and integrating them into a multiplex-heterogeneous framework, potentially enhancing prediction accuracy⁵³.