Introduction

Recently, the application of AI in various fields has garnered attention, particularly in STEM education, where it is fostering a transformative shift paradigms1,2,3,4. With the advancement of machine learning and large language models (LLMs), artificial intelligence technologies offer interactive learning opportunities that significantly enhance students’ creativity, critical thinking, collaboration, and problem-solving skills skills5,6,7,8. This convergence of artificial intelligence and STEM education redefines the roles of educators from mere knowledge transmitters to effective learning facilitators and collaborators1,9,10. while empowering students to become active participants in constructing and applying knowledge independently.

However, the successful integration of AI into education ultimately depends on teachers’ acceptance and willingness to adopt these technologies6,11,12,13,14. Mathematics, as the foundation of all STEM disciplines, is critical in this transformation; however, mathematics is often underrepresented in STEM education research15,16,17,18. Current research primarily focuses on assessing mathematics teachers’ readiness to adopt technology19,20,21. However, there is a notable gap in attention to their acceptance of artificial intelligence specifically within an interdisciplinary STEM framework. Consequently, this study seeks to address the significant research gap by examining the principal factors that influence mathematics teachers’ acceptance and adoption of artificial intelligence technologies in the field of STEM education.

Extensive research has explored the adoption and continued use of educational technology by higher education faculty. For example, Jeyaraj et al.22 integrated the TAM, TPACK, and UTAUT models to analyze the factors influencing sustained technology use among higher education instructors in emerging economies. Similarly, Al-Adwan et al.23 focused on educators’ perceptions, experiences, and barriers to using educational technologies. However, the present study shifts the focus to the Chinese context, specifically investigating K–12 mathematics teachers’ initial intentions to adopt and use artificial intelligence (AI) technologies within STEM education. At present, the application of AI in STEM teaching at the K–12 level in China remains in its early stages, and teachers generally lack sufficient understanding, application skills, and integration capabilities related to AI2,24. Therefore, identifying the key factors that influence mathematics teachers’ adoption of AI technologies is of great theoretical and practical significance for promoting innovation in STEM education and achieving effective integration of AI technologies.

This study aims to address two core research questions: (1) What are the key determinants of K–12 mathematics teachers’ intention to adopt AI technologies in STEM education? (2) What factors influence their actual acceptance behavior when integrating AI into interdisciplinary STEM teaching?

To explore these underlying mechanisms, this study adopts the Unified Theory of Acceptance and Use of Technology 2 (UTAUT2), a comprehensive theoretical framework that has been widely validated in educational research contexts25,26. UTAUT2 extends the original UTAUT model27 and is particularly well-suited for understanding voluntary technology adoption in learning environments28.

This study aims to contribute to the field in three ways: (1) identifying the key factors that influence mathematics teachers’ adoption of AI technologies in STEM education; (2) providing theoretical support for targeted professional development programs to enhance the application of AI in STEM teaching; and (3) offering practical recommendations for policymakers and technology developers to better support mathematics teachers in AI-driven educational environments.

Literature review and hypothesis development

The role and application of AI in STEM education

In today’s digital landscape, artificial intelligence (AI) is emerging as a transformative force in education, particularly within STEM education29. AI integration in STEM education reshapes traditional teaching by incorporating intelligent technologies and data-driven methods strategies6,30,31,32,33. AI and STEM education are inherently connected: while STEM provides a context for technological literacy development, AI serves as a catalyst that enhances interdisciplinary learning and supports critical and computational thinking34,35. This synergy enables students to actively engage with AI tools to explore cross-disciplinary concepts and apply knowledge in practical, meaningful ways.

Research has examined AI in STEM education. Xu and Ouyang2 reviewed 71 studies from 2011 to 2021, identifying six application areas: learning prediction, intelligent tutoring systems, behavior monitoring, automated assessment, personalized learning recommendations, and teaching management. Their findings revealed that most applications target higher education, especially in computing and engineering, enhancing student engagement and critical thinking. However, K–12 implementation, particularly in mathematics and science, faces challenges like inadequate infrastructure, low teacher proficiency, and insufficient long-term effectiveness data. Similarly, Yang et al.3 analyzed 186 papers from 2013 to 2023, outlining four integration paths: enhancing inquiry-based learning, merging with emerging technologies (e.g., AR/VR), applying practical AI tools, and improving student motivation. Yet, they noted that K–12 research is sparse and regionally uneven due to technological constraints.

Mathematics teachers’ perceptions and adoption of AI in STEM

Research shows that the adoption of AI among mathematics teachers is shaped by personal psychological factors (such as self-efficacy and attitudes toward AI) as well as external conditions (including policy support, availability of infrastructure, and cultural context) contexts)11,12. Wang et al.36 noted that self-efficacy and perceived usefulness strongly affect teachers’ adoption behaviors. Furthermore, differences across educational settings and countries are evident, as indicated by Xu and Ouyang2who found K–12 mathematics classrooms significantly lag behind higher education in AI implementation due to limited teacher readiness and institutional support.

Despite generative AI’s promising potential in personalized learning and student engagement37mathematics teachers often face ongoing challenges, such as inadequate training, insufficient technical literacy, limited awareness of AI applications, and resource constraints38,39,40,41. These challenges are especially pronounced in K–12 contexts, emphasizing a significant gap in existing research, which has largely overlooked AI integration within this educational level and discipline.

Teachers’ acceptance of emerging technologies significantly influences their successful integration into classroom teaching. Previous research frequently employs theoretical frameworks such as the Technology Acceptance Model (TAM) and the Unified Theory of Acceptance and Use of Technology 2 (UTAUT2) to explore teachers’ adoption behaviors towards Artificial Intelligence (AI). For instance, Nikou and Economides42 found that perceived ease of use—a core TAM factor—significantly affects teachers’ intention to use AI, alongside external support and outcome quality. Wang et al.36indicated that teachers’ self-efficacy, expected benefits, and attitudes toward AI strongly influence their adoption decisions. Using the UTAUT2 model, Wijaya et al.43 identified performance expectancy as the primary factor shaping Chinese pre-service mathematics teachers’ intention to use AI chatbots, indicating a focus on practical teaching benefits over social influences or habitual factors. Similarly, Al Darayseh44applying TAM, concluded that teachers generally show high acceptance of classroom AI integration, with minimal impact from anxiety.

As generative AI evolves, mathematics teachers increasingly recognize its potential in STEM education. Generative AI can enhance learner engagement, provide personalized learning experiences, track student performance, and alleviate anxiety, thereby promoting inclusive education37. However, teachers remain concerned about AI tools’ maintenance and costs, especially in budget-limited institutions. Additionally, integrating AI with STEM teaching significantly improves students’ capability development compared to traditional methods34indicating AI’s critical role in transforming STEM educational practices.

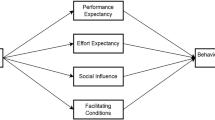
The literature review shows that various factors influence mathematics teachers’ acceptance of AI technologies in STEM education. This study utilizes the Unified Theory of Acceptance and Use of Technology 2 (UTAUT2) as its framework. Developed by Venkatesh et al.45 UTAUT2 extends the original UTAUT model and is widely employed to examine technology adoption in educational contexts. The model has been extensively used to analyze user behavior across various technologies28,46. This study examines key UTAUT2 constructs—Performance Expectation, Effort Expectation, Social Influences, Hedonic Motivation, Habit, Facilitating Conditions, and Price Value—on mathematics teachers’ behavioral intentions and usage behavior regarding AI in STEM education. Figure 1 illustrates the theoretical model.

Research hypotheses

The hypotheses proposed in this study are shown in Fig. 1.

Fig. 1
figure 1

Research framework.

Full size image

Performance Expectancy (PE) is considered one of the core predictors in the UTAUT model47. Performance expectancy refers to the extent to which an individual believes that using technology will enhance their job performance or tasks45. This interpretation closely relates to the concept of perceived usefulness found in the Technology Acceptance Model48. Previous research on technology acceptance consistently demonstrates that Performance Expectancy significantly influences an individual’s willingness to embrace new technologies49. Therefore, this study hypothesizes that performance expectancy positively influences mathematics behavioral intentions (H1a) and usage behavior (H2a) when adopting AI technologies in STEM education.

Effort Expectancy (EE) refers to the ease of use associated with technology27. Research has shown that when teachers view artificial intelligence as easy to use, they are more likely to integrate it into their teaching practices50. AI helps teachers identify students’ needs and optimize strategies via data analysis and feedback, encouraging adoption51. Therefore, this study hypothesizes that effort expectancy positively influences mathematics teachers’ behavioral intentions (H1b) and usage behavior (H2b) regarding the adoption of AI technologies in STEM education.

Social Influences (SI) refers to how individuals believe that important others, such as colleagues or supervisors, think they should adopt new technology27. Social norms and peer pressure significantly influence technology adoption. This study defines social influence as the extent to which teachers feel encouraged by peers and leaders to incorporate artificial intelligence into STEM teaching. It is a critical factor affecting technology usage behavior and positively impacts users’ willingness to adopt new technologies52. Therefore, this study hypothesizes that social influences positively affect mathematics teachers’ behavioral intentions (H1c) and usage behavior (H2c)in adopting AI technologies in STEM education.

Hedonic Motivation (HM) is a newly introduced variable in the UTAUT2 model, reflecting the enjoyment or satisfaction users experience when interacting with technology27. If using technology is enjoyable, it can strongly motivate its use26. The integration of AI into STEM education is emerging as a novel teaching approach for mathematics teachers, potentially offering a more enjoyable teaching experience for them and creating a more engaging and lively classroom for students6,53. Therefore, this study hypothesizes that hedonic motivation positively influences mathematics teachers’ behavioral intentions (H1d) and usage behavior (H2d) in adopting AI technologies in STEM education.

Perceived Risk (PR) refers to users’ subjective assessment of potential negative consequences or losses linked to the adoption of new technology. Many studies indicate that aspects related to perceived risk are variables that negatively affect consumers’ intentions to use technology54. Individuals perceive uncertainty before adopting a behavior, believing that it will not increase expected benefits55. Research shows that perceived risk significantly affects users’ behavioral intentions to use technology, and this impact is often negative56. Therefore, this study hypothesizes that Perceived Risk (PR) negatively influences mathematics teachers’ behavioral intentions (H1e) and usage behavior (H2e) in adopting AI technologies in STEM education.

Habit (HT) is defined as the degree to which an individual instinctively engages in certain behaviors as a result of prior learning27. It can also be viewed as user behavior that is directed toward future actions, representing a perceptual structure shaped by past experiences and outcomes47. The more familiar a person becomes with using technology, the more likely they are to continue its use57. Therefore, this study hypothesizes that Habit (HT) positively influences mathematics teachers’ behavioral intentions (H1f) and usage behavior (H2f) in adopting AI technologies in STEM education.

Facilitating Conditions (FC) refer to an individual’s perception of the availability of technical and organizational resources that enable and support the effective use of technology45. Research indicates that FC is a key factor influencing users’ behavioral intentions and actual usage behaviors. Organizations or environments that provide technical support and timely assistance can increase users’ acceptance of technological products, thereby fostering the adoption of new technologies25. Therefore, this study hypothesizes: Habit (HT) positively influences mathematics teachers’ behavioral intentions (H1g) and usage behavior (H2g) in adopting AI technologies in STEM education.

Price Value (PV) refers to the belief that the amount paid for a technological tool is matched by the benefits received. If the perceived benefits outweigh the Price Value (PV), this will positively influence Behavioral Intention (BI)45. In the integration of AI into STEM education, teachers often do not have to pay direct costs, but the “price” they pay is in terms of time spent learning, creating, and applying these materials. In this scenario, it is assumed that teachers will carefully weigh the relationship between benefits and costs. Since Price Value (PV) applies to voluntary practitioners58this concept is suitable for scenarios involving the integration of AI into STEM education. Therefore, this study hypothesizes that Price Value (PV) positively influences mathematics teachers’ behavioral intentions (H1h) and usage behavior (H2h) in adopting AI technologies in STEM education.

Behavioral Intentions (BI) refer to the extent to which an individual is inclined, prepared, or willing to adopt and use a particular technology45. When users exhibit Behavioral Intentions (BI) while using innovative technologies, they are likely to engage in usage behaviors59. Behavioral Intentions can reasonably and accurately predict consumers’ future behaviors60. In this study, Behavioral Intentions represent the extent to which mathematics teachers are willing to integrate AI into their STEM teaching practices. Ultimately, Use Behavior pertains to the actual interaction with technology, reflecting how an individual’s intent to use the technology translates into practical application45. UTAUT2, developed by Venkatesh, explains how Use Behavior (UB) is influenced by Behavioral Intentions.

Use Behavior (UB) refers to the actual behavior of using AI in STEM Education, which can also be measured by the frequency of AI usage in STEM Education over a given period of time. In this study, Use Behavior is defined as mathematics teachers’ actual implementation and application of AI in their STEM education practices.

Previous research indicates that behavioral intention is a crucial determinant in predicting the actual use behavior of technology in education27. This relationship has been confirmed in studies examining teachers’ adoption of artificial intelligence in education61. Therefore, this study further suggests that Mathematics teachers’ behavioral intentions significantly and positively influence their actual use of AI in STEM education(H3).

Methodology

This study employs quantitative research methods to explore how to enhance K-12 mathematics teachers’ willingness and use behavior in integrating Artificial Intelligence (AI) into STEM education. In our experiments, informed consent was obtained from all participants, and all methods were performed in accordance with relevant guidelines and regulations.

Sampling

The sample included K–12 mathematics teachers from various age groups, education levels, and teaching stages (primary, junior high, Vocational School (Junior), and high school), providing a diverse representation of frontline educators in China’s basic education system. This study conducted an online questionnaire survey to explore the attitudes and perceptions of Chinese mathematics teachers regarding the integration of Artificial Intelligence (AI) into STEM education. The survey was designed and distributed using the Wenjuanxing(https://www.wjx.cn) platform and was disseminated to mathematics teachers in four provinces—Qinghai in Northwest China, Henan and Beijing in Central China, and Hainan in Southern China—via social media tools such as WeChat. The study selected four provinces—Beijing, Henan, Hainan, and Qinghai—to ensure geographic diversity and include perspectives from various economic development levels. Convenience sampling recruited mathematics teachers in each province. Although convenience sampling was used, the inclusion of economically diverse provinces helps mitigate regional bias and increases the generalizability of findings across different educational contexts in China. Data collection occurred from October to December 2024, covering groups of mathematics teachers who have used AI in STEM teaching activities and those who have not. To ensure participants fully understood the context of the survey, the questionnaire began with a video introduction and a written explanation about integrating AI in STEM education, asking participants to answer after reading the full explanation. A total of 503 questionnaires were retrieved. After excluding responses with missing data on core items or uniform answers (e.g., selecting “1” for all items), 474 valid samples were retained, resulting in a 94.2% effective response rate. Participants were grouped by age in ten-year intervals and were recruited voluntarily basis. This exceeds the minimum sample size recommended for SEM and ensures sufficient power for analyzing the model’s eight latent constructs and 30 indicators62. In this study sample, there was a significant gender imbalance, with female teachers dominating (398) and fewer male teachers (76). This gender imbalance trend is consistent with the overall population distribution in China’s teaching industry. In China, women hold the majority of teaching positions, especially in elementary and middle schools63. All respondents submitted their questionnaires digitally, and demographic details are provided in Table 1.

Table 1 Demographic characteristics of the respondents.
Full size table

Questionnaire design

A questionnaire survey method was used to meet the research objectives. The final questionnaire was organised into two sections: the first part collected demographic information, including teacher gender, age, region, K-12 education level, and frequency of AI usage (refer to Table 1). The second part, which is the main section of the questionnaire, based on the modified UTAUT2 model, included 30 items (3 items per construct) designed to assess mathematics teachers’ perceptions of the factors influencing their behavioural intentions and actual usage behaviours when using AI in STEM education. The survey employed a 5-point Likert scale, ranging from 1 (strongly disagree) to 5 (strongly agree). Drawing on previous research, all variables and the questionnaire were meticulously refined and revised43,45,64. The full list of questionnaire items is provided in the Supplementary Information.

Results

The preliminary data underwent screening using IBM SPSS 27, including tests for normality, reliability analysis, and exploratory factor analysis. Subsequently, confirmatory factor analysis and structural equation modeling were conducted using IBM AMOS 24 to validate the measurement model and examine the proposed relationships. The findings confirm that the reliability and validity of all constructs align with the recommended standards, ensuring the robustness of the measurement model. AMOS is software designed for Structural Equation Modeling65. SEM is a statistical method that allows researchers to explore intricate relationships between observed and latent variables. This study utilized AMOS software and embraced a covariance-based structural equation modeling approach, particularly suited for validating established theories. CB-SEM necessitates stringent compliance with data assumptions, making it well-suited for hypothesis testing and theory validation. Conversely, PLS-SEM provides greater flexibility and is frequently employed for exploratory research and theory development66. If the goal of the research is to test and validate theories, then CB-SEM is the appropriate method to use. In contrast, for objectives focused on prediction and theory development, PLS-SEM is the better choice. Conceptually and practically, PLS-SEM resembles multiple regression analysis. Its primary aim is to maximize the explained variance in causal constructs while evaluating the data quality based on the measurement characteristics model67.

Descriptive statistics and normality assessment

Descriptive statistics, including means, standard deviations, skewness, and kurtosis, examined the distribution properties of the observed variables and assessed normality. Mean values ranged from 2.97 to 3.82, indicating general agreement with questionnaire statements. Standard deviations varied from 0.564 to 0.918, reflecting differing response dispersion across constructs. Skewness ranged from − 0.808 to − 0.057, and kurtosis from − 0.545 to 1.01, all within accepted thresholds of |skewness| < 1 and |kurtosis| < 268,69. These results suggest approximate univariate normality and meet assumptions for covariance-based structural equation modeling (CB-SEM), making the dataset suitable for further confirmatory modeling.

Table 2 Normality test of data.
Full size table

Reliability analysis

Table 3 presents the findings from the reliability analysis. The results show that all items have Corrected Item-Total Correlation (CITC) values exceeding 0.5, which indicates that scores for all items within the different constructs are reliably grouped within a comparable range, reflecting solid internal consistency70. All constructs have a Cronbach’s alpha value greater than 0.7, indicating good reliability of the questionnaire71. Furthermore, the Cronbach’s alpha for individual constructs does not improve upon removing any items, indicating good internal consistency in the data72. Therefore, the collected data are highly reliable and suitable for further analysis. The assessment of Common Method Bias (CMB) adhered to Kock’s73 framework, which indicates that CMB in Structural Equation Modeling (SEM) primarily stems from measurement methods utilized. To evaluate this, a comprehensive collinearity test was conducted on all latent variables within the model, as shown in Table 3. The Variance Inflation Factors (VIF) derived from this analysis are below the critical threshold of 3.3, as set by Kock73signifying that Common Method Bias (CMB) is not a major concern for this study. This result indicates that our model is not notably affected by Common Method Bias (CMB), which reinforces the strength of our research methodology.

Table 3 Results of reliability analysis.
Full size table

Exploratory factor analysis

Exploratory Factor Analysis. We conducted principal component analysis using the varimax rotation method for our exploratory factor analysis (see Table 4). The Kaiser–Meyer–Olkin (KMO) test returned a value exceeding 0.5, while Bartlett’s test of sphericity produced a p-value of under 0.05. These findings indicate a strong partial correlation among the items, allowing us to reject the null hypothesis that the correlation matrix is an identity matrix, thereby confirming that the collected data is suitable for factor analysis analysis74. The exploratory factor analysis findings indicated that each item’s communality value was above 0.5 within its construct, confirming that all items had strong correlations with others in the same construct75. Upon extracting the new factors, each construct revealed one factor with an eigenvalue above 1, and the cumulative variance explained was over 50%. Additionally, every item exhibited factor loadings exceeding 0.6. Thus, the data fulfills the unidimensionality requirement as indicated in previous research76.

Table 4 Results of exploratory factor analysis.
Full size table

Confirmatory factor analysis

Confirmatory Factor Analysis (CFA) was performed to evaluate the model’s reliability and validity (Table 5). Compared to the benchmarks suggested by Hair et al.77the model fit indices in this study satisfied the recommended thresholds, indicating a good model fit. The RMSEA and SRMR decreased by less than 0.05, whereas GFI, AGFI, NFI, and CFI saw an increase that stayed within 0.1. These results indicate that Common Method Bias (CMB) does not pose a significant problem in the dataset78.

Table 6 presents the results of the Confirmatory Factor Analysis (CFA). The findings show that all items had factor loadings greater than 0.6, and the squared multiple correlations (SMC) surpassed 0.4, satisfying the recommended criteria established in the study by Taylor and Todd79. The Average Variance Extracted (AVE) and Composite Reliability (CR) for each construct were calculated based on factor loadings. The results indicated that the AVE for each construct exceeded 0.4, while the CR values surpassed 0.6, suggesting that the data demonstrated sufficient convergent validity80.

Table 5 Model fit indices of confirmatory factor analysis.
Full size table
Table 6 Results of confirmatory factor analysis.
Full size table

The Fornell–Larcker criterion was used to assess discriminant validity, as shown in Table 7. This table displays the diagonal elements as each construct’s square root of the Average Variance Extracted (AVE). In contrast, the off-diagonal elements represent the Pearson correlation coefficients between various constructs. According to the results, the square root of AVE for each construct exceeds its highest correlation with any other construct, suggesting that each construct exhibits more significant shared variance with its indicators than those of different constructs. Furthermore, all correlation coefficients remain below 0.8, a threshold frequently referenced in prior research to confirm discriminant validity81. This ensures that the constructs in the study maintain sufficient conceptual distinction, preventing excessive overlap and reinforcing the integrity of the measurement model82.

Table 7 Correlation analysis and discriminant validity.
Full size table

Structural equation model

This study utilized maximum likelihood estimation to build the structural equation model (SEM). To ensure robust results, 2000 bootstrap samples were utilized, with 95% confidence intervals calculated for parameter estimation. The model fit indices shown in Table 8 demonstrate that all values meet the recommended thresholds from previous research, affirming that the model shows a strong fit to the data. These findings validate the appropriateness of the SEM framework for analyzing the relationships among the study variables77.The calculation results of the structural equation model are shown in Fig. 2; Table 9.

The results indicate that only performance expectancy, hedonic motivation, and price value have a direct and significant effect on teachers’ behavioral intentions. In contrast, factors like effort expectancy, social influence, perceived risk, habit, and facilitating conditions do not significantly impact behavioral intention. Consequently, hypotheses H1a, H1d, and H1h are validated, whereas hypotheses H1b, H1c, H1e, H1f, and H1g are not backed by the data.

The research found that effort expectancy, facilitating conditions, and price value have a significant impact on teachers’ actual usage behavior. In contrast, performance expectancy, social influence, habit, hedonic motivation, and perceived risk do not significantly affect this behavior effect. Therefore, hypotheses H2b, H2d, and H2h are upheld, affirming that ease of use, supportive conditions, and cost factors are significant in the adoption process. Conversely, hypotheses H2a, H2c, H2e, H2f, and H2g lack support, suggesting these elements may not be crucial to teachers’ technology usage behavior.

The study revealed a notable positive correlation between behavioral intention and actual usage behavior, showing that the intention to utilize AI in STEM courses significantly predicts actual usage among mathematics teachers. This supports earlier research that emphasizes behavioral intention as a vital and impactful element in technology adoption. These results highlight the need to foster positive attitudes towards technology to improve actual usage. The detailed relationships among the variables and comprehensive findings are illustrated in the final model, found in Fig. 3, titled “Path Analysis Results.”.

Table 8 Model fit indices of the structural equation model.
Full size table
Fig. 2
figure 2

Structural Equation Model.

Full size image
Table 9 The results of the direct effects hypotheses.
Full size table
Fig. 3
figure 3

Path analysis results.

Full size image

Discussion

This study examined the factors affecting K–12 mathematics teachers’ adoption of AI in STEM education using the UTAUT2 model. Results indicate that Performance Expectancy, Hedonic Motivation, and Price Value significantly influence teachers’ behavioral intentions, while Effort Expectancy, Facilitating Conditions, and Price Value impact actual use. Conversely, Social Influence, Habit, and Perceived Risk had no significant effects. These results partly support the UTAUT2 framework, suggesting some factors may behave differently in K–12 STEM contexts. The following discussion elaborates on each hypothesis.

Performance expectancy

The results support H1a, showing that performance expectancy positively influences mathematics teachers’ behavioral intention to use AI in STEM education. This aligns with previous research suggesting that when teachers believe AI can enhance instructional effectiveness, they are more likely to consider adopting it83,84,85. In the context of STEM education, mathematics teachers may be especially motivated by AI’s ability to enhance efficiency in lesson planning, assessment, and student differentiation.

H2a was unsupported; performance expectancy did not significantly affect actual usage. This suggests a gap between intention and action, likely due to limited access to AI tools, lack of school support, or perceived implementation complexity. While teachers see AI as beneficial, real-world barriers may hinder consistent use. This aligns with previous research in STEM education, which shows that positive attitudes toward technology don’t always result in classroom implementation due to practical challenges constraints86,87,88. These findings underscore the importance of addressing real-world implementation challenges while reinforcing the perceived value of AI in education.

Effort expectancy

H1b was unsupported; effort expectancy did not significantly influence mathematics teachers’ intention to use AI in STEM education. This indicates that even if AI tools seem easy to use, this alone may not drive teachers’ adoption intentions. This finding contrasts with earlier research identifying effort expectancy as a key factor in technology adoption83,84. In STEM education, mathematics teachers may prioritize pedagogical value and classroom impact over perceived ease of use when forming their intentions.

H2b was supported, indicating that effort expectancy positively affects actual usage behavior. While ease of use may not initially motivate teachers to consider AI, it becomes crucial once they try it. If AI tools are perceived as user-friendly and requiring minimal effort, teachers are more likely to continue using them. This aligns with findings highlighting usability as essential for sustained technology use in STEM, where time and cognitive load are limited89. These results emphasize the need for designing AI tools that are pedagogically meaningful and intuitive, aiding both initial use and long-term integration.

Social influence

H1c and H2c were unsupported; social influence did not significantly affect mathematics teachers’ behavioral intention or actual AI usage in STEM education. This suggests that encouragement from colleagues, administrators, or institutional culture may not decisively influence teachers’ decisions to adopt AI tools in STEM education. These findings deviate from some previous studies89,90which suggested that peer and organizational expectations could shape technology adoption, particularly in the early stages of diffusion.

In STEM education, this result may reflect the individualistic and expertise-driven nature of mathematics instruction, where teachers prioritize personal judgment over external opinions. Given the early stage of AI adoption in many schools, social norms around AI integration may not be well established, reducing their influence on teacher behavior2. Thus, creating a supportive culture around AI use—through communities of practice, peer modeling, and visible leadership—may be necessary before social influence can meaningfully affect adoption processes.

Hedonic motivation

The results support H1d, indicating that hedonic motivation significantly and positively influences mathematics teachers’ behavioral intention to use AI in STEM education. This suggests that when teachers find AI tools enjoyable or intrinsically satisfying to use, they are more likely to express a willingness to adopt them. This finding is consistent with previous studies showing that the pleasure or enjoyment derived from using new technologies can enhance adoption intentions, particularly during the early stages of diffusion83,85. In the context of STEM teaching, the novelty and interactivity of AI tools may stimulate positive emotional responses, thereby increasing teachers’ openness to technology integration.

H2d was unsupported; hedonic motivation did not significantly affect usage behavior. This shows that while mathematics teachers may be curious about AI, their classroom implementation relies more on practical factors like time constraints, curriculum fit, and technical support43,91,92. This intention–behavior gap is common in educational technology research and highlights the limitations of emotion-driven factors in overcoming real-world barriers93. Thus, to ensure sustained AI use in STEM education, it is crucial to supplement motivation-building strategies with concrete resources and implementation support.

Perceived risk

H1e and H2e were unsupported; perceived risk did not significantly affect AI usage among mathematics teachers in STEM education. Concerns about negative outcomes, like data privacy, job displacement, or ethics, may not be central to their AI adoption decisions. This finding contrasts with studies in other domains where perceived risk hinders technology uptake91.

One explanation lies in the institutional and cultural context of Chinese K–12 education. AI tools are often introduced through top-down selection by school administrators or education bureaus, who vet tools for safety and alignment with standards. Consequently, mathematics teachers are less likely to evaluate risks independently and may view approved tools as inherently trustworthy. Additionally, the controlled digital environment in schools and limited autonomy in tool selection may further reduce perceived uncertainty. This filtering may lead teachers to see AI not as disruptive, but as a sanctioned aid for instruction, particularly in structured STEM subjects, such as mathematics94.

Habit

H1f and H2f were both unsupported; habit did not significantly affect mathematics teachers’ behavioral intention or actual usage of AI in STEM education. In STEM education, particularly for mathematics teachers, AI tools are still in the early stages of integration and are not yet embedded in daily teaching practices. The limited and irregular use among teachers suggests that AI habits are not yet established. This aligns with studies indicating that when technology is new or used sporadically, habits have a minimal influence on adoption decisions45,89. Until such conditions are established, habit is unlikely to serve as a reliable driver of AI adoption in educational contexts. In STEM education, AI integration remains relatively novel, and teachers have yet to develop consistent routines for its use. Without sustained exposure and repeated application, AI tools are unlikely to become part of teachers’ automatic instructional behaviors. Therefore, habit may become more relevant in the later stages of adoption, once the technology is embedded in curriculum practices and supported by school-wide implementation structures.

Facilitating conditions

H1g was unsupported; facilitating conditions did not significantly affect mathematics teachers’ intent to use AI in STEM education. This suggests that infrastructure, training, and support may not directly shape teachers’ willingness to adopt AI tools. Teachers may prioritize perceived usefulness or motivational factors over logistical considerations when adopting AI. One possible explanation is that when teachers evaluate whether to adopt AI, they may prioritize perceived usefulness or motivational factors over logistical considerations12.

H2g support indicates that facilitating conditions significantly affect actual usage behavior. This reveals a gap between intention and action: support systems are crucial for enabling classroom use, even if they don’t drive adoption intent95. Access to reliable technology, support, and training in STEM influences mathematics teachers’ follow-through. These findings highlight the need to enhance practical support to close the gap between interest and implementation.

Price value

Both H1h and H2h were supported, showing that price value significantly impacts mathematics teachers’ intention and actual use of AI in STEM education. In China’s K–12 system, most AI tools are offered free by schools or platforms, so the perceived “value” for teachers refers to non-monetary costs like time investment, cognitive effort, and instructional alignment. When teachers believe that AI tools’ educational benefits outweigh the learning efforts, they are more likely to form a strong intention to use and apply these tools in practice40,89.

This finding indicates that AI tools must show clear instructional value while reducing the learning curve and operational complexity to gain acceptance among teachers. In STEM education, enhancing usability, integration, and pedagogical compatibility can increase perceived value and encourage classroom adoption.

Behavioral intentions and usage behavior

H3 supported the notion that behavioral intention significantly predicts actual AI usage among mathematics teachers in STEM education, confirming the UTAUT2 model’s assumption that intention drives behavior. In structured STEM classrooms, teachers intending to use AI are likely to act on that intention, given adequate support and resources. This underscores the necessity to strengthen teachers’ motivation to use AI and ensure conditions exist to translate intention into practice.

Implications

This study examined AI usage and intentions among mathematics teachers in STEM education using an adapted UTAUT2 model. The findings confirm the model’s applicability in K–12 STEM education and reveal key factors influencing teachers’ adoption of AI tools. This study provides significant contributions for researchers, educators, and technology developers to improve AI integration in STEM education.

Theoretical implications

This study offers several theoretical contributions. First, it adapts and empirically validates the UTAUT2 model within the context of K–12 mathematics teachers utilizing AI tools in STEM education, an area that has been infrequently examined in the existing literature. In contrast to prior studies that frequently identify multiple factors impacting behavioral intention40,96,97our findings suggest that only a subset of UTAUT2 constructs—specifically, Performance Expectancy, Hedonic Motivation, and Price Value—serve as significant predictors of intention, with Performance Expectancy emerging as the predominant predictor. This observation underscores the distinctive motivational framework of STEM educators, who tend to prioritize instructional effectiveness and perceived advantages over social pressure or habitual influences.

Second, the differentiation between factors affecting intention and those determining actual behavior provides deeper insights into the intention–behavior gap, a persistent challenge within technology acceptance research. The significance of constructs such as Effort Expectancy and Facilitating Conditions solely for actual usage emphasizes the necessity of distinguishing between motivational influences and implementation facilitators within the UTAUT2 framework98,99.

Lastly, by reconceptualizing Price Value in terms of time and cognitive effort rather than financial expenditure—an adjustment that is particularly pertinent to the Chinese K–12 education system, where AI tools are generally provided at no cost—this study contributes to a more contextually relevant understanding of technology acceptance constructs91. These findings not only augment the explanatory capacity of UTAUT2 in educational environments but also lay the groundwork for future cross-cultural comparisons, especially regarding the role of practical constraints in the adoption of AI by educators.

Practical implications

This study offers several significant practical implications for fostering the adoption and effective utilization of artificial intelligence tools among mathematics educators within STEM education. Firstly, the finding that performance expectancy serves as the most robust predictor of behavioral intention underscores the necessity for developers and school leaders to articulate clearly how AI tools can enhance instructional effectiveness43. Demonstrating tangible benefits, such as improved lesson efficiency, differentiated instruction, and real-time student feedback, can fortify teachers’ willingness to embrace such technologies.

Secondly, the prominence of effort expectancy and facilitating conditions in forecasting actual usage behavior highlights the critical importance of mitigating technical barriers. AI tools must be designed with simplicity, intuitive interfaces, and seamless integration into existing teaching workflows. Furthermore, educational institutions should provide continuous technical support and targeted professional development, ensuring that educators feel equipped and supported in their effective use of AI tools96,100.

Thirdly, the reconceptualization of price value as primarily indicative of time and cognitive effort rather than financial cost bears direct implications for policy and training. In light of the substantial workload faced by K–12 educators, AI tools should be perceived not as an additional burden but as time-saving, workload-reducing assistants89,91. Training programs ought to elucidate not only how to utilize AI but also demonstrate how it can alleviate teaching pressures, such as through the automation of routine tasks or the enhancement of student engagement.

Finally, collaboration between AI developers and educational institutions is imperative. Engaging educators directly in the design and feedback process can ensure that AI tools are tailored to meet real classroom needs. By involving end-users—specifically mathematics teachers—in the piloting, refinement, and contextualization of AI applications, developers can create tools that are pedagogically relevant, user-friendly, and aligned with the specific goals of STEM education. Such partnerships also foster a sense of ownership among teachers, potentially leading to more sustainable and innovative applications of AI in the classroom97.

Limitations

This study presents several limitations. First, the sample was confined to K–12 mathematics educators in China, potentially limiting the generalizability of the findings to other subjects, educational levels, or cultural contexts. Second, the cross-sectional design captures teacher perceptions and behaviors at a singular point in time, without accounting for possible changes or long-term adoption patterns. Third, the reliance on self-reported data may introduce bias, as actual classroom usage behavior may differ from what respondents reported. Furthermore, the study did not differentiate between various types of AI tools, which may exhibit variability in terms of usability and impact. Lastly, while the UTAUT2 model provided a robust framework, other potentially relevant factors—such as data privacy concerns or students’ AI readiness—were not included and necessitate further exploration in subsequent research.

Conclusion

This research applied the UTAUT2 model to assess the relationship between mathematics teachers’ intentions and their actual implementation of AI in STEM education. The findings partly validate the model’s relevance in educational technology adoption, yet indicate that certain conventional pathways are not significant in understanding how mathematics teachers use AI behavior97. To clarify, this study implemented and refined the UTAUT2 model specifically for mathematics education. It’s important to recognize that while this finding may not represent a groundbreaking advance for the theory, it does empirically demonstrate the model’s adaptability within this particular field. Furthermore, the research confirms the successful validation and implementation of the model among mathematics teachers. Importantly, the theoretical conclusions from this study depend on the current state of AI development in STEM education. As technology progresses and teachers accumulate more experience, the impact of related variables on teacher behavior might change. This study validates that Performance Expectancy, Hedonic Motivation, and Price Value have a significant effect on mathematics teachers’ behavioral intentions, whereas Effort Expectancy, Social Influence, Perceived Risk, and Habit do not significantly affect these intentions in this context study91. The study also revealed that time cost plays a crucial role in the Price Value perception among mathematics teachers. This implies that teachers prioritize whether AI tools can lessen their teaching burdens over the tools’ economic costs. Conversely, factors like Effort Expectancy, Facilitating Conditions, and Price Value greatly influence actual usage behavior. This suggests that when mathematics teachers consider the long-term use of AI tools, the usability of the technology and the potential time savings are pivotal. Additionally, while teachers’ intentions to use these tools do impact their actual usage behavior, the influence is limited. This limitation may be linked to the current ubiquity of AI tools and the ongoing adaptation process teachers undergo with technology. Finally, the study proposes that the key factors affecting mathematics teachers’ AI usage may continue to change as technology improves, policies evolve, and teacher training deepens. Future research could investigate how mathematics teachers across various educational stages or cultural contexts adapt to and embrace AI tools technology.