Introduction

Recently, uncertainty has become more pronounced in numerous domains, including science, technology, and daily life. The growing amount of big data increases the complexity and diversity of uncertain information, rendering its management and interpretation more difficult. The increase in data and its associated uncertainty poses distinct issues in decision-making and problem-solving across various sectors. To tackle these issues, Zadeh1 presented the technique of fuzzy sets (FSs), which have demonstrated significant efficacy in managing uncertainty across several domains2,3. Bukhari et al.4 stated a unique Adaptive Fuzzy Particle Swarm Optimization strategy that promotes green logistical and supply chain management. Atanassov extended the concept by formulating intuitionistic fuzzy sets (IFSs)5, which improve the capacity to handle ambiguous and imprecise data. Yager6 suggested the Pythagorean fuzzy sets (PFS), which broadens the concept by generalizing the link between PM and NM degrees. In a PFS, the sum of squares of PM and NM is \(\le 1.\)

Compared to IFSs, PFSs offer more relaxed constraints, enhancing their capacity to manage uncertainty. Peng and Yang7 developed the idea of interval-valued PFS (IVPFSs), which enable interval-based PM and NM degrees. Senapati and Yager8 established Fermatean fuzzy sets (FFS), further relaxing the conditions to generalize PFS. Jeevaraj9 proposed the interval-valued FFSs (IVFFS), a generalization of both IVFS and FFS. The IVFFS is especially useful for handling uncertainty because it allows PM and NM degrees to be represented as intervals. The important aspect of the IVFFS is that the total of the cubes of the upper boundaries of these intervals must be \(\le 1\). Although earlier models improved our capacity to manage uncertainty, they continued to falter in decision-making situations, necessitating several answer alternatives, including “yes,” “refusal,” “no,” and “neutral.” Traditional fuzzy sets and intuitionistic FS are ineffective in adequately addressing these issues. Cuong10 presented Picture fuzzy sets (PFS) to address this difficulty. This advanced methodology enhances traditional fuzzy logic by integrating three distinct membership functions: positive membership \(\hbar_\mathcal{R}\left(\varkappa \right)\), neutral membership \(\eta \mathcal{R} \left(\varkappa \right)\), and negative membership \(\varrho_\mathcal{R}\left(\varkappa \right)\) degrees while maintaining the condition \(0\le \hbar_\mathcal{R}\left(\varkappa \right)+ \eta_\mathcal{R}\left(\varkappa \right)+ \varrho_\mathcal{R}\left(\varkappa \right)\le 1\).

Kutlu and Kahraman11 presented spherical fuzzy sets (SFSs), which reduce the usual PFS requirement \(0\le \hbar_\mathcal{R}^{2}\left(\varkappa \right)+ \eta_\mathcal{R}^{2}\left(\varkappa \right)+ \varrho_\mathcal{R}^{2}\left(\varkappa \right)\le 1\), allowing for a greater range of membership values. This advancement enables greater adaptability in managing intricate, ambiguous information, particularly in decision-making scenarios involving multiple forms of uncertainty. There has been a significant rise in practical applications and research projects involving advanced fuzzy systems12,13. Riaz et al.14 developed the aggregation operators for q-rung orthopair fuzzy soft sets and established a multi-attribute decision-making methodology to resolve uncertain problems in sustainable logistics. These methods have been extensively utilized in many disciplines, i.e., energy management, reliability assessment, and IoT implementation15,16, demonstrating their adaptability and increasing influence. Alrasheedi et al.17 stated the FF-SPC-RS-MARCOS structure that utilizes the MARCOS method using Sugeno–Weber weighted averaging operators and Fermatean fuzzy sets to analyze reliable vendors in the pharmaceutical supply chain.

The study of aggregation operators (AOs) has been a major focus of MADM research, particularly in fuzzy contexts. Researchers have become more interested in fuzzy AOs due to their potential for building more robust decision-making algorithms. Ma et al.18 proposed an ordered weighted interactive AOs combined with an entropy weighting method based on IVPFSs. Yazar Okur et al.19 explored and determined particular industry sustainable development metrics for logistical services, emphasizing the economic, ecological, and interpersonal aspects using the implementation of Fermatean fuzzy entropy and the WASPAS strategy. Akram et al.20 established a triangular form of IVFFNs and investigated its arithmetic features. Senapati and Chen21 developed numerous novel IVPF aggregation operators based on Hamacher triangular norms, providing answers to MCDM problems. Kishorekumar et al.22 proposed the IVPF Bonferroni mean operator, demonstrating its practical use in real-world applications such as CTY. Li and Wang23 analyzed the universal interactions of an outbreak of HIV through logistical fission for infected cells and explicit between cells infection.

Rani et al.24 used Einstein AOs to solve MADM problems in an IVFPS framework. Several researchers have made additional advancements in aggregation and MCDM techniques, including Zhao et al.25, Khan et al.26, Liu et al.27, Abu-Lail et al.28, and Bihari et al.29, who have proposed diverse techniques for various application domains. Akhtar30 described a novel fuzzy methodology implementing IVFF with hybrid IVFF-PIPRECIAS and IVFF-WASPAS strategies to detect an effective, responsive, resilient, and ecologically conscious logistics company inside the manufacturing market. Baranidharan et al.31 stated a strategy for an optimal fuzzy fractional three-stage transport network to eliminate transport expenses and exhausts, implementing generalized pentagonal fuzzy numbers. Hussain et al.32 constructed a multi-attribute group decision-making strategy using Frank aggregation operators within a complex picture fuzzy environment to analyze and classify environmentally friendly power facilities.

Fan et al.33 established a novel MADM technique to look for logistical providers in an interval-valued picture fuzzy context. Ali and Rehman34 investigated the Schweizer–Sklar operational rules for IVPFS. They defined prioritized aggregation operators for MADM, with them in the context of virtual ecological innovation and managerial theory for Industry 5.0. Rehman et al.35 presented Einstein aggregation methodologies for interval-valued intuitionistic fuzzy sets (IVPFS) and created a MAGDM approach to solve decision-making obstacles. Hernández-Torres et al.36 established a hybrid MCDM model for selecting power-generating techniques, showing gasification as the most suitable option for an abandoned economically independent operation. Shanthi et al.37 used the PFS to evaluate an efficient mobile network. This research investigates IVFPFNs and introduces a novel ordering principle designed to enhance the efficacy of MADM methods. This new framework offers improved decision-making instruments for tackling intricate real-world issues.

Research gap

In recent years, some fuzzy set models such as Fermatean FSs (FFS)8, interval-valued Fermatean FSs (IVFFS)9, picture FSs (PFS)10, and complex picture FSs (CPFS)32, have gained significant attention due to their ability to model uncertainty and hesitation in complex decision-making environments. In reviewing the current literature and based on the deep literature review, it is evident that while these methods are increasingly being applied, the integration of Einstein AOs with interval-valued Fermatean picture fuzzy sets (IVFPFS) remains an unexplored area. The identified gap creates an excellent basis for further study while serving as the fundamental driving force behind this research.

To fill these gaps, we suggest the following inquiries for research:

  • What are the few important operations of Einstein AOs within the context of interval-valued Fermatean picture fuzzy sets (IVFPFS), and how do they improve the precision and integrity of the aggregation process?

  • What is the significance of the newly introduced aggregation operators (IVFPFEWA and IVFPFEWG) within the IVFPFS framework? Which advantages do they have for advanced information aggregation?

  • How practical is the proposed method when used in real-world scenarios, such as choosing the most suitable logistics company?

Our research evaluates these questions, which fills an essential theoretical void while developing an effective decision-making instrument for complex, uncertain scenarios. Future investigations in fuzzy set applications should use the proposed IVFPFS Einstein operators as their new standard because of their advanced flexible aggregation method.

Motivation

The motivation behind researching IVFPFEWA and IVFPFEWG under interval-valued Fermatean picture fuzzy environments was to create effective decision systems for sustainable logistics management that resolve expert evaluation challenges involving uncertainty and ambiguity. Sustainable logistics must solve various competing factors, i.e., infrastructure development, economic performance in logistics, operational management, and smart technological innovation. Decision-makers must evaluate these criteria according to their opinions, which are frequently unclear or hesitant. The wide range of expert assessment variations combined with complex logistics scenarios requires a precise selection of optimal sustainable logistics strategies. IVFPFSs enhance MADM methods to deliver precise decision-maker preference modeling, particularly when working with imprecise or interval-based data. The IVFPF framework expands traditional fuzzy sets through its power to handle broader types of uncertainty and hesitation, which leads to better logistics and alternative evaluation capabilities.

These evaluation criteria need distinct consideration regarding their importance throughout different geographical areas and intervals or between stakeholder groups. Sustainability-related risk levels defined through linguistic inputs, such as low, moderate, and high, can find appropriate interpretations through the flexibility of IVFPFSs. According to existing literature, traditional decision-making models face difficulties because they encounter unreliable and inconsistent performance metrics. Advanced aggregation operators based on IVFPF need development because their comprehensive nature helps evaluate sustainable logistics strategies despite uncertain conditions. The implementation of IVFPFS in sustainable logistics management provides a strategic improvement to decision-making processes. The advanced tool provides organizations with precise sustainability-related decisions through accurate decision support that enables them to tackle uncertainty effectively, along with enhanced precision and sustained sustainability goals.

Main contributions of the study

Motivated by these research questions, this work seeks to achieve the following key goals and contributions:

  • It presents the concept of interval-valued Fermatean picture fuzzy sets and investigates the vital operational rules that control this environment.

  • The work indicates the significance of Einstein AOs in the interval-valued Fermatean picture fuzzy framework, which helps to provide consistent approximation during the aggregation process. This study introduces novel AOs, such as IVFPF Einstein weighted aggregation (IVFPFEWA) and IVFPF Einstein weighted geometric (IVFPFEWG). It discusses their characteristics, applications, and contributions to aggregation techniques.

  • A MADM algorithm is developed to deal with uncertainty and redundancy when evaluating logistics companies, and a case study is offered to illustrate its practical application.

  • Lastly, the suggested technique is compared with the existing technique to emphasize its advantages and strengths, illustrating its capacity as a more effective decision-making instrument for practical applications.

The work is structured as follows: “Preliminary“ section outlines the key concepts required to understand the proposed approach. “Interval-valued Fermatean picture fuzzy set” section discusses the unique notion of IVFPFSs, including their characteristics, score, and accuracy. “Einstein operations of Interval-valued Fermatean picture fuzzy sets” section investigates the Einstein operational laws and aggregation operators for IVFPFSs such as IVFPFEWA and IVFPFEWG operators. “Proposed MADM model based on the developed Einstein AOs” section extends the MADM model based on our developed AOs and presents the case study to evaluate the logistics company. “Supremacy of the proposed technique” section describes a comparative study that highlights the suggested method’s strengths. Lastly, “Conclusion” section provides recommendations for future research and conclusions.

Preliminary

This section presents fundamental concepts necessary for understanding this work’s innovative nature.

Definition 2.1

10 Let \(\chi\) be the undefined set; then, a picture fuzzy sets \(\mathcal{R}\) on \(\chi\) is described in the following:

$$\mathcal{R}=\left\{\varkappa , \hbar_\mathcal{R}\left(\varkappa \right), \eta_\mathcal{R}\left(\varkappa \right), \varrho_\mathcal{R}\left(\varkappa \right)|\varkappa \in \chi \right\},$$

where \(\eta_\mathcal{R}\left(\varkappa \right),\hbar_\mathcal{R}\left(\varkappa \right),\varrho_\mathcal{R}\left(\varkappa \right)\) represent the membership degrees (MDs) of neutral, positive, and negative \(,\) respectively; \(\left(\hbar_\mathcal{R}\left(\varkappa \right), \eta_\mathcal{R}\left(\varkappa \right), \varrho_\mathcal{R}\left(\varkappa \right)\right)\in \left[\text{0,1}\right],\) and \(0\le \hbar_\mathcal{R}\left(\varkappa \right)+ \eta_\mathcal{R}\left(\varkappa \right)+\varrho_\mathcal{R}\left(\varkappa \right)\le 1.\) The refusal membership function \({\pi }_\mathcal{R}\left(\varkappa \right)\) is described as: \({\pi }_\mathcal{R}\left(\varkappa \right)=1-\left(\hbar_\mathcal{R}\left(\varkappa \right)+ \eta_\mathcal{R}\left(\varkappa \right)+\varrho_\mathcal{R}\left(\varkappa \right)\right).\)

Definition 2.2

33 Let \(\chi\) be the undefined set, and an interval-valued picture fuzzy sets \(\mathcal{R}\) on \(\chi\) is described in the following:

$$\mathcal{R}=\left\{\varkappa , \left[\hbar_\mathcal{R}^{L}\left(\varkappa \right),\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right],\left[\eta_\mathcal{R}^{L}\left(\varkappa \right),\eta_\mathcal{R}^{U}\left(\varkappa \right)\right],\left[\varrho_\mathcal{R}^{L}\left(\varkappa \right),\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right]|\varkappa \in \chi \right\},$$

where \(0\le \hbar_\mathcal{R}^{L}\left(\varkappa \right)\le \hbar_\mathcal{R}^{U}\left(\varkappa \right)\le 1,\) \(0\le \eta_\mathcal{R}^{L}\left(\varkappa \right)\le \eta_\mathcal{R}^{U}\left(\varkappa \right)\le 1\) \(0\le \varrho_\mathcal{R}^{L}\left(\varkappa \right)\le \varrho_\mathcal{R}^{U}\left(\varkappa \right)\le 1,\) and \(0\le \hbar_\mathcal{R}^{U}\left(\varkappa \right)+ \eta_\mathcal{R}^{U}\left(\varkappa \right)+ \varrho_\mathcal{R}^{U}\left(\varkappa \right)\le 1.\) Here \(\hbar_\mathcal{R}\left(\varkappa \right)=\left[\hbar_\mathcal{R}^{L}\left(\varkappa \right),\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right],\) \(\eta_\mathcal{R}\left(\varkappa \right)=\left[\eta_\mathcal{R}^{L}\left(\varkappa \right),\eta_\mathcal{R}^{U}\left(\varkappa \right)\right],\) and \(\varrho_\mathcal{R}\left(\varkappa \right)=\left[\varrho_\mathcal{R}^{L}\left(\varkappa \right),\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right]\) described the positive, neutral, and negative MDs of \(\varkappa \in \chi\), respectively.

Definition 2.3

8 Let \(\chi\) be the undefined set. A Fermatean fuzzy set \(\mathcal{R}\) on \(\chi\) is identified as:

$$\mathcal{R}=\left\{\varkappa , \hbar_\mathcal{R}\left(\varkappa \right), \varrho_\mathcal{R}\left(\varkappa \right)|\varkappa \in \chi \right\},$$

where \(\hbar_\mathcal{R}\left(\varkappa \right), \varrho_\mathcal{R}\left(\varkappa \right)\) represent positive and negative MDs of \(\varkappa \in \chi\) respectively, fulfill the requirements as follows: \(\hbar_\mathcal{R}\left(\varkappa \right), \varrho_\mathcal{R}\left(\varkappa \right)\in \left[\text{0,1}\right],\) and \(0\le \hbar_\mathcal{R}^{3}\left(\varkappa \right)+ \varrho_\mathcal{R}^{3}\left(\varkappa \right)\le 1.\) The hesitancy degree of the value \(\varkappa \in \chi ,\) denoted by \({\pi }_\mathcal{R}\left(\varkappa \right),\) is described as: \({\pi }_\mathcal{R}\left(\varkappa \right)=\sqrt[3]{1-\left(\hbar_\mathcal{R}^{3}\left(\varkappa \right)+ \varrho_\mathcal{R}^{3}\left(\varkappa \right)\right)}\).

Definition 2.4

20 Let \(\chi\) be the undefined set. An interval-valued Fermatean fuzzy set \(\mathcal{R}\) on \(\chi\) has been defined as follows:

$$\mathcal{R}=\left\{\varkappa , \left[\hbar_\mathcal{R}^{L}\left(\varkappa \right),\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right],\left[\varrho_\mathcal{R}^{L}\left(\varkappa \right),\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right]|\varkappa \in \chi \right\},$$

where \(0\le \hbar_\mathcal{R}^{L}\left(\varkappa \right)\le \hbar_\mathcal{R}^{U}\left(\varkappa \right)\le 1,\) \(0\le \varrho_\mathcal{R}^{L}\left(\varkappa \right)\le \varrho_\mathcal{R}^{U}\left(\varkappa \right)\le 1,\) and \(0\le {\left(\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}+{\left(\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}\le 1.\) Here \(\hbar_\mathcal{R}\left(\varkappa \right)=\left[\hbar_\mathcal{R}^{L}\left(\varkappa \right),\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right]\) and \(\varrho_\mathcal{R}\left(\varkappa \right)=\left[\varrho_\mathcal{R}^{L}\left(\varkappa \right),\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right]\) represent the positive and negative MDs of \(\varkappa \in \chi\), respectively. The function \({\pi }_\mathcal{R}\left(\varkappa \right)=\left[{\pi }_\mathcal{R}^{L}\left(\varkappa \right),{\pi }_\mathcal{R}^{U}\left(\varkappa \right)\right]\) represent the indeterminacy degree of \(\varkappa \in \chi\), where \({\pi }_\mathcal{R}^{L}\left(\varkappa \right)=\sqrt[3]{1-\left({\left(\hbar_\mathcal{R}^{L}\left(\varkappa \right)\right)}^{3}+{\left(\varrho_\mathcal{R}^{L}\left(\varkappa \right)\right)}^{3}\right)}\) and \({\pi }_\mathcal{R}^{U}\left(\varkappa \right)=\sqrt[3]{1-\left({\left(\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}+{\left(\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}\right)}.\) To keep it simple, we describe interval-valued Fermatean fuzzy numbers (IVFFNs), \(\mathcal{R}_{i}=\left(\left[\hbar_{\mathcal{R}_{i}}^{L}\left(\varkappa \right),\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right],\left[\varrho_{\mathcal{R}_{i}}^{L}\left(\varkappa \right),\varrho_{\mathcal{R}_{i}}^{U}\left(\varkappa \right)\right]\right),\) where \(i\) is a positive integer.

Definition 2.5

20 Let \(\mathcal{R}=\left\{ \left[\hbar_\mathcal{R}^{L},\hbar_\mathcal{R}^{U}\right],\left[\varrho_\mathcal{R}^{L},\varrho_\mathcal{R}^{U}\right]\right\}\) be a IVFFN. The score \(\mathcal{S}\) and accuracy \(\text{\AA}\) functions for IVFFN are expressed as follows:

  1. (1)

    \(\mathcal{S}\left(\mathcal{R}\right)=\frac{1}{2}\left({\left(\hbar_\mathcal{R}^{L}\right)}^{3}+{\left(\hbar_\mathcal{R}^{U}\right)}^{3}-{\left(\varrho_\mathcal{R}^{L}\right)}^{3}-{\left(\varrho_\mathcal{R}^{U}\right)}^{3}\right) \in \left[-1, 1\right],\)

  2. (2)

    \(\text{\AA} \left(\mathcal{R}\right)=\frac{1}{2}\left({\left(\hbar_\mathcal{R}^{L}\right)}^{3}+{\left(\hbar_\mathcal{R}^{U}\right)}^{3}+{\left(\varrho_\mathcal{R}^{L}\right)}^{3}+{\left(\varrho_\mathcal{R}^{U}\right)}^{3}\right) \in \left[0, 1\right].\)

Interval-valued Fermatean picture fuzzy set

This section presents the concept of interval-valued Fermatean picture fuzzy sets and some of their fundamental properties.

Definition 3.1

37 Let \(\chi\) be the undefined set and an interval-valued Fermatean picture fuzzy sets (IVFPFS) \(\mathcal{R}\) on \(\chi\). It is described as

$$\mathcal{R}=\left\{\varkappa , \left[\hbar_\mathcal{R}^{L}\left(\varkappa \right),\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right],\left[\eta_\mathcal{R}^{L}\left(\varkappa \right),\eta_\mathcal{R}^{U}\left(\varkappa \right)\right],\left[\varrho_\mathcal{R}^{L}\left(\varkappa \right),\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right]|\varkappa \in \chi \right\},$$

where \(0\le \hbar_\mathcal{R}^{L}\left(\varkappa \right)\le \hbar_\mathcal{R}^{U}\left(\varkappa \right)\le 1,\) \(0\le \eta_\mathcal{R}^{L}\left(\varkappa \right)\le \eta_\mathcal{R}^{U}\left(\varkappa \right)\le 1\) \(0\le \varrho_\mathcal{R}^{L}\left(\varkappa \right)\le \varrho_\mathcal{R}^{U}\left(\varkappa \right)\le 1,\) and \(0\le {\left(\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}+{\left(\eta_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}+{\left(\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}\le 1.\) Here \(\hbar_\mathcal{R}\left(\varkappa \right)=\left[\hbar_\mathcal{R}^{L}\left(\varkappa \right),\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right],\) \(\eta_\mathcal{R}\left(\varkappa \right)=\left[\eta_\mathcal{R}^{L}\left(\varkappa \right),\eta_\mathcal{R}^{U}\left(\varkappa \right)\right],\) and \(\varrho_\mathcal{R}\left(\varkappa \right)=\left[\varrho_\mathcal{R}^{L}\left(\varkappa \right),\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right]\) represent the positive, neutral, and negative MDs of \(\varkappa \in \chi\), respectively. The function \({\pi }_\mathcal{R}\left(\varkappa \right)=\left[{\pi }_\mathcal{R}^{L}\left(\varkappa \right),{\pi }_\mathcal{R}^{U}\left(\varkappa \right)\right]\) represent the indeterminacy degree of \(\varkappa \in \chi\), where \({\pi }_\mathcal{R}^{L}\left(\varkappa \right)=\sqrt[3]{1-\left({\left(\hbar_\mathcal{R}^{L}\left(\varkappa \right)\right)}^{3}+{\left(\eta_\mathcal{R}^{L}\left(\varkappa \right)\right)}^{3}+{\left(\varrho_\mathcal{R}^{L}\left(\varkappa \right)\right)}^{3}\right)}\) and \({\pi }_\mathcal{R}^{U}\left(\varkappa \right)=\sqrt[3]{1-\left({\left(\hbar_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}+{\left(\eta_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}+{\left(\varrho_\mathcal{R}^{U}\left(\varkappa \right)\right)}^{3}\right)}.\) To keep it simple, we represent interval-valued Fermatean picture fuzzy numbers (IVFPFNs) as \(\mathcal{R}_{i}=\left(\left[\hbar_{\mathcal{R}_{i}}^{L}\left(\varkappa \right),\hbar_{\mathcal{R}_{i}}^{U}\left(\varkappa \right)\right],\left[\eta_{\mathcal{R}_{i}}^{L}\left(\varkappa \right),\eta_{\mathcal{R}_{i}}^{U}\left(\varkappa \right)\right],\left[\varrho_{\mathcal{R}_{i}}^{L}\left(\varkappa \right),\varrho_{\mathcal{R}_{i}}^{U}\left(\varkappa \right)\right]\right),\) where \(i\) is a positive integer.

Definition 3.2

Let \(\mathcal{R}_{1}=\left\{\left[\hbar_{\mathcal{R}_{1}}^{L},\hbar_{\mathcal{R}_{1}}^{U}\right],\left[\eta_{\mathcal{R}_{1}}^{L},\eta_{\mathcal{R}_{1}}^{U}\right],\left[\varrho_{\mathcal{R}_{1}}^{L},\varrho_{\mathcal{R}_{1}}^{U}\right]\right\},\) and \(\mathcal{R}_{2}=\left\{ \left[\hbar_{\mathcal{R}_{2}}^{L},\hbar_{\mathcal{R}_{2}}^{U}\right],\left[\eta_{\mathcal{R}_{2}}^{L},\eta_{\mathcal{R}_{2}}^{U}\right],\left[\varrho_{\mathcal{R}_{2}}^{L},\varrho_{\mathcal{R}_{2}}^{U}\right]\right\},\) be the IVFPFNs and \(\delta >0.\) Subsequently, the ensuing properties were fulfilled by probable fundamental operations.

  1. 1.
    $$\begin{aligned} {\mathcal{R}}_{1} \oplus {\mathcal{R}}_{2} = & \bigg(\left[ {\sqrt[3]{{\left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} + \left( {\hbar _{{{\mathcal{R}}_{2} }}^{L} } \right)^{3} - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} \left( {\hbar _{{{\mathcal{R}}_{2} }}^{L} } \right)^{3} }},\sqrt[3]{{\left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} + \left( {\hbar _{{{\mathcal{R}}_{2} }}^{U} } \right)^{3} - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} \left( {\hbar _{{{\mathcal{R}}_{2} }}^{U} } \right)^{3} }}} \right], \\ & \left[ {\eta _{{{\mathcal{R}}_{1} }}^{L} \eta _{{{\mathcal{R}}_{2} }}^{L} ,\eta _{{{\mathcal{R}}_{2} }}^{U} \eta _{{{\mathcal{R}}_{1} }}^{U} } \right],\left[ {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} {\varrho }_{{{\mathcal{R}}_{2} }}^{L} ,{\varrho }_{{{\mathcal{R}}_{2} }}^{U} {\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right]\bigg) \\ \end{aligned}$$
  2. 2.
    $${\mathcal{R}}_{1} \otimes {\mathcal{R}}_{2} = \left( {\begin{array}{*{20}c} {\left[ {\hbar _{{{\mathcal{R}}_{1} }}^{L} \hbar _{{{\mathcal{R}}_{2} }}^{L} ,\hbar _{{{\mathcal{R}}_{1} }}^{U} \hbar _{{{\mathcal{R}}_{2} }}^{U} } \right],\left[ \begin{gathered} \sqrt[3]{{\left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} + \left( {\eta _{{{\mathcal{R}}_{2} }}^{L} } \right)^{3} - \left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} \left( {\eta _{{{\mathcal{R}}_{2} }}^{L} } \right)^{3} }}, \hfill \\ \sqrt[3]{{\left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} + \left( {\eta _{{{\mathcal{R}}_{2} }}^{U} } \right)^{3} - \left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} \left( {\eta _{{{\mathcal{R}}_{2} }}^{U} } \right)^{3} }} \hfill \\ \end{gathered} \right],} \\ {\left[ {\sqrt[3]{{\left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} + \left( {{\varrho }_{{{\mathcal{R}}_{2} }}^{L} } \right)^{3} - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} \left( {{\varrho }_{{{\mathcal{R}}_{2} }}^{L} } \right)^{3} }},\sqrt[3]{{\left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} + \left( {{\varrho }_{{{\mathcal{R}}_{2} }}^{U} } \right)^{3} - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} \left( {{\varrho }_{{{\mathcal{R}}_{2} }}^{U} } \right)^{3} }}} \right]} \\ \end{array} } \right)$$
  3. 3.
    $$\delta \mathcal{R}_{1}=\left(\left[\sqrt[3]{\left(1-{\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{\delta }\right)},\sqrt[3]{\left(1-{\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{\delta }\right)}\right],\left[{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{\delta },{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{\delta }\right],\left[{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{\delta },{\left(\varrho_{\mathcal{R}_{1}}^{U}\right)}^{\delta }\right]\right)$$
  4. 4.
    $$\begin{aligned} {\mathcal{R}}_{1}^{\delta } = &\bigg( \left[ {\left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{\delta } ,\left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{\delta } } \right],\left[ {\sqrt[3]{{\left( {1 - \left( {1 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } } \right)}},\sqrt[3]{{\left( {1 - \left( {1 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } } \right)}}} \right], \\ & \left[ {\sqrt[3]{{\left( {1 - \left( {1 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } } \right)}},\sqrt[3]{{\left( {1 - \left( {1 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } } \right)}}} \right]\bigg). \\ \end{aligned} .$$

We present the score and accuracy numbers as tools for testing two IVFPFNs. Using these data, we create comparable rules for IVFPFNs, as discussed below.

Definition 3.3

Let \(\mathcal{R}=\left\{ \left[\hbar_\mathcal{R}^{L},\hbar_\mathcal{R}^{U}\right],\left[\eta_\mathcal{R}^{L},\eta_\mathcal{R}^{U}\right],\left[\varrho_\mathcal{R}^{L},\varrho_\mathcal{R}^{U}\right]\right\}\) be an IVFPFN, then score \(\mathcal{S}\) and accuracy \(\text{\AA}\) values of IVFPFNs is expressed as shown.

  1. (1)
    $$\mathcal{S}\left(\mathcal{R}\right)=\frac{1}{2}\left({\left(\hbar_\mathcal{R}^{L}\right)}^{3}+{\left(\hbar_\mathcal{R}^{U}\right)}^{3}-{\left(\eta_\mathcal{R}^{L}\right)}^{3}-{\left(\eta_\mathcal{R}^{U}\right)}^{3}-{\left(\varrho_\mathcal{R}^{L}\right)}^{3}-{\left(\varrho_\mathcal{R}^{U}\right)}^{3}\right) \in \left[-1, 1\right],$$
  2. (2)
    $$\text{\AA} \left(\mathcal{R}\right)=\frac{1}{2}\left({\left(\hbar_\mathcal{R}^{L}\right)}^{3}+{\left(\hbar_\mathcal{R}^{U}\right)}^{3}+{\left(\eta_\mathcal{R}^{L}\right)}^{3}+{\left(\eta_\mathcal{R}^{U}\right)}^{3}+{\left(\varrho_\mathcal{R}^{L}\right)}^{3}+{\left(\varrho_\mathcal{R}^{U}\right)}^{3}\right) \in \left[0, 1\right].$$

Definition 3.4

Let \(\mathcal{R}_{1}=\left\{\left[\hbar_{\mathcal{R}_{1}}^{L},\hbar_{\mathcal{R}_{1}}^{U}\right],\left[\eta_{\mathcal{R}_{1}}^{L},\eta_{\mathcal{R}_{1}}^{U}\right],\left[\varrho_{\mathcal{R}_{1}}^{L},\varrho_{\mathcal{R}_{1}}^{U}\right]\right\},\) and \(\mathcal{R}_{2}=\left\{ \left[\hbar_{\mathcal{R}_{2}}^{L},\hbar_{\mathcal{R}_{2}}^{U}\right],\left[\eta_{\mathcal{R}_{2}}^{L},\eta_{\mathcal{R}_{2}}^{U}\right],\left[\varrho_{\mathcal{R}_{2}}^{L},\varrho_{\mathcal{R}_{2}}^{U}\right]\right\},\) are the IVFPFNs, the comparison among \(\mathcal{R}_{1}\) and \(\mathcal{R}_{2}\) is shown as.

  1. I.

    If \(\mathcal{S}\left({\mathcal{R}}_{1}\right)<\mathcal{S}\left({\mathcal{R}}_{2}\right),\) then \({\mathcal{R}}_{1}<{\mathcal{R}}_{2}.\)

  2. II.

    If \(\mathcal{S}\left({\mathcal{R}}_{1}\right)>\mathcal{S}\left({\mathcal{R}}_{2}\right),\) then \({\mathcal{R}}_{1}>{\mathcal{R}}_{2}.\)

  3. III.

    If \(\mathcal{S}\left({\mathcal{R}}_{1}\right)=\mathcal{S}\left({\mathcal{R}}_{2}\right),\) then

    1. 1.

      if \(\text{\text{\AA} }\left({\mathcal{R}}_{1}\right)<\text{\text{\AA} }\left({\mathcal{R}}_{2}\right),\) then \({\mathcal{R}}_{1}<{\mathcal{R}}_{2}.\)

    2. 2.

      if \(\text{\text{\AA} }\left({\mathcal{R}}_{1}\right)>\text{\text{\AA} }\left({\mathcal{R}}_{2}\right),\) then \({\mathcal{R}}_{1}>{\mathcal{R}}_{2}.\)

    3. 3.

      if \(\text{\text{\AA} }\left({\mathcal{R}}_{1}\right)=\text{\text{\AA} }\left({\mathcal{R}}_{2}\right),\) then \({\mathcal{R}}_{1}={\mathcal{R}}_{2}.\)

Proposition 3.5

Let \(\mathcal{R}, \mathcal{R}_{1}, \mathcal{R}_{2}\) are the three IVFPFNs and \(\delta , {\delta }_{1}, {\delta }_{2},\) then we have

  1. 1.

    \({\mathcal{R}_{1}\oplus \mathcal{R}}_{2}={\mathcal{R}_{2}\oplus \mathcal{R}}_{1}\)

  2. 2.

    \({\mathcal{R}_{1}\otimes \mathcal{R}}_{2}={\mathcal{R}_{2}\otimes \mathcal{R}}_{1}\)

  3. 3.

    \(\delta \left({\mathcal{R}_{1}\oplus \mathcal{R}}_{2}\right)=\delta {\mathcal{R}_{1}\oplus \delta \mathcal{R}}_{2}\)

  4. 4.

    \({\delta }_{1}\mathcal{R}\oplus {\delta }_{2}\mathcal{R}=\left({\delta }_{1}\oplus {\delta }_{2}\right)\mathcal{R}\)

  5. 5.

    \(\mathcal{R}^{{\delta }_{1}}\otimes \mathcal{R}^{{\delta }_{2}}=\mathcal{R}^{\left({\delta }_{1}+{\delta }_{2}\right)}\)

  6. 6.

    \(\mathcal{R}_{1}^{\delta }\otimes \mathcal{R}_{2}^{\delta }={\left({\mathcal{R}_{1}\otimes \mathcal{R}}_{2}\right)}^{\delta }\)

Proof

Straightforward.

Einstein operations of interval-valued Fermatean picture fuzzy sets

This section explores the key principles of Einstein’s operational laws and the aggregation operators, such as IVFPFEWA and IVFPFEWG operators, and their properties.

Definition 4.1

Let \(\mathcal{R}_{1}=\left\{\left[\hbar_{\mathcal{R}_{1}}^{L},\hbar_{\mathcal{R}_{1}}^{U}\right],\left[\eta_{\mathcal{R}_{1}}^{L},\eta_{\mathcal{R}_{1}}^{U}\right],\left[\varrho_{\mathcal{R}_{1}}^{L},\varrho_{\mathcal{R}_{1}}^{U}\right]\right\},\) and \(\mathcal{R}_{2}=\left\{ \left[\hbar_{\mathcal{R}_{2}}^{L},\hbar_{\mathcal{R}_{2}}^{U}\right],\left[\eta_{\mathcal{R}_{2}}^{L},\eta_{\mathcal{R}_{2}}^{U}\right],\left[\varrho_{\mathcal{R}_{2}}^{L},\varrho_{\mathcal{R}_{2}}^{U}\right]\right\},\) be the IVFPFNs, and \(\delta >0\) be the real number; according to def. 3.2, the following results hold.

  1. 1.

    \({\mathcal{R}_{1}{\oplus }_{e}\mathcal{R}}_{2}=\left(\begin{array}{c}\left[\sqrt[3]{\frac{{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}+{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}}},\sqrt[3]{\frac{{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}+{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}}}\right],\left[\frac{\eta_{\mathcal{R}_{1}}^{L}\eta_{\mathcal{R}_{2}}^{L}}{\sqrt[3]{1+\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}},\frac{\eta_{\mathcal{R}_{1}}^{U}\eta_{\mathcal{R}_{2}}^{U}}{\sqrt[3]{1+\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}}\right], \\ \left[\frac{\varrho_{\mathcal{R}_{1}}^{L}\varrho_{\mathcal{R}_{2}}^{L}}{\sqrt[3]{1+\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}},\frac{\varrho_{\mathcal{R}_{1}}^{U}\varrho_{\mathcal{R}_{2}}^{U}}{\sqrt[3]{1+\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}}\right]\end{array}\right)\)

  2. 2.

    \({\mathcal{R}_{1}{\otimes }_{e}\mathcal{R}}_{2}=\left(\begin{array}{c}\left[\frac{\hbar_{\mathcal{R}_{1}}^{L}\hbar_{\mathcal{R}_{2}}^{L}}{\sqrt[3]{1+\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)\left(1-{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}},\frac{\hbar_{\mathcal{R}_{1}}^{U}\hbar_{\mathcal{R}_{2}}^{U}}{\sqrt[3]{1+\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)\left(1-{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}}\right],\left[\sqrt[3]{\frac{{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}}{1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}}},\sqrt[3]{\frac{{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}}{1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}}}\right], \\ \left[\sqrt[3]{\frac{{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}}{1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}}},\sqrt[3]{\frac{{\left(\varrho_{\mathcal{R}_{1}}^{U}\right)}^{3}+{\left(\varrho_{\mathcal{R}_{2}}^{U}\right)}^{3}}{1+{\left(\varrho_{\mathcal{R}_{1}}^{U}\right)}^{3}{\left(\varrho_{\mathcal{R}_{2}}^{U}\right)}^{3}}}\right]\end{array}\right)\)

  3. 3.

    \(\delta {\mathcal{R}}_{1} = \left( {\begin{array}{*{20}c} \begin{gathered} \left[ {\sqrt[3]{{\frac{{\left( {1 + \left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } - \left( {1 - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}{{\left( {1 + \left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } + \left( {1 - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}}},\sqrt[3]{{\frac{{\left( {1 + \left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } - \left( {1 - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}{{\left( {1 + \left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } + \left( {1 - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}}}} \right], \hfill \\ \left[ {\frac{{\sqrt[3]{2}\left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{\delta } }}{{\sqrt[3]{{\left( {2 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } + \left( {\left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}}},\frac{{\sqrt[3]{2}\left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{\delta } }}{{\sqrt[3]{{\left( {2 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } + \left( {\left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}}}} \right], \hfill \\ \end{gathered} \\ {\left[ {\frac{{\sqrt[3]{2}\left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{\delta } }}{{\sqrt[3]{{\left( {2 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } + \left( {\left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}}},\frac{{\sqrt[3]{2}\left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{\delta } }}{{\sqrt[3]{{\left( {2 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } + \left( {\left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}}}} \right]} \\ \end{array} } \right)\)

  4. 4.

    \({\mathcal{R}}_{1}^{\delta } = \left( {\begin{array}{*{20}c} \begin{gathered} \left[ {\frac{{\sqrt[3]{2}\left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{\delta } }}{{\sqrt[3]{{\left( {2 - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } + \left( {\left( {\hbar _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}}},\frac{{\sqrt[3]{2}\left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{\delta } }}{{\sqrt[3]{{\left( {2 - \left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } + \left( {\left( {\hbar _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}}}} \right], \hfill \\ \left[ {\sqrt[3]{{\frac{{\left( {1 + \left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } - \left( {1 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}{{\left( {1 + \left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } + \left( {1 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}}},\sqrt[3]{{\frac{{\left( {1 + \left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } - \left( {1 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}{{\left( {1 + \left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } + \left( {1 - \left( {\eta _{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}}}} \right], \hfill \\ \end{gathered} \\ {\left[ {\sqrt[3]{{\frac{{\left( {1 + \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } - \left( {1 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}{{\left( {1 + \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } + \left( {1 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{L} } \right)^{3} } \right)^{\delta } }}}},\sqrt[3]{{\frac{{\left( {1 + \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } - \left( {1 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}{{\left( {1 + \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } + \left( {1 - \left( {{\varrho }_{{{\mathcal{R}}_{1} }}^{U} } \right)^{3} } \right)^{\delta } }}}}} \right]} \\ \end{array} } \right)\)

Proposition 4.2

Let \(\mathcal{R}_{1}=\left\{\left[\hbar_{\mathcal{R}_{1}}^{L},\hbar_{\mathcal{R}_{1}}^{U}\right],\left[\eta_{\mathcal{R}_{1}}^{L},\eta_{\mathcal{R}_{1}}^{U}\right],\left[\varrho_{\mathcal{R}_{1}}^{L},\varrho_{\mathcal{R}_{1}}^{U}\right]\right\},\) and \(\mathcal{R}_{2}=\left\{ \left[\hbar_{\mathcal{R}_{2}}^{L},\hbar_{\mathcal{R}_{2}}^{U}\right],\left[\eta_{\mathcal{R}_{2}}^{L},\eta_{\mathcal{R}_{2}}^{U}\right],\left[\varrho_{\mathcal{R}_{2}}^{L},\varrho_{\mathcal{R}_{2}}^{U}\right]\right\},\) are the IVFPFNs and \(\delta >0\) be a real number, so

  1. 1.

    \({\mathcal{R}_{1}{\oplus }_{e}\mathcal{R}}_{2}={\mathcal{R}_{2}{\oplus }_{e}\mathcal{R}}_{1}\)

  2. 2.

    \(\delta \left({\mathcal{R}_{1}{\oplus }_{e}\mathcal{R}}_{2}\right)=\delta {\mathcal{R}_{1}{\oplus }_{e}\delta \mathcal{R}}_{2}\)

  3. 3.

    \({\mathcal{R}_{1}\otimes \mathcal{R}}_{2}={\mathcal{R}_{2}{\otimes }_{e}\mathcal{R}}_{1}\)

  4. 4.

    \({\delta }_{1}\mathcal{R}_{1}{\oplus }_{e}{\delta }_{2}\mathcal{R}_{1}=\left({\delta }_{1}{\oplus }_{e}{\delta }_{2}\right)\mathcal{R}_{1}\)

  5. 5.

    \({\mathcal{R}_{1}}^{{\delta }_{1}}{\otimes }_{e}{\mathcal{R}_{1}}^{{\delta }_{2}}={\mathcal{R}_{1}}^{\left({\delta }_{1}+{\delta }_{2}\right)}\)

  6. 6.

    \(\mathcal{R}_{1}^{\delta }{\otimes }_{e}\mathcal{R}_{2}^{\delta }={\left({\mathcal{R}_{1}{\otimes }_{e}\mathcal{R}}_{2}\right)}^{\delta }\)

Proof

See Appendix I (cc supplementary material).

Definition 4.3

Let \(\mathcal{R}_{i}=\left\{\left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right],\left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right],\left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\right\},\) \(\left(i=\left\{\text{1,2},\dots ,p\right\}\right)\) be the IVFPFNs with an associated weight vector (WV) \(\zeta =\left\{{\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{p}\right\},\) satisfying \({\zeta }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{p}{\zeta }_{i}=1.\) The IVFPFEWA operator denoted as \(FPFEWA : \mathcal{R}^{p}\to \mathcal{R}\) is described as follows:

$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)={{\zeta }_{1}\mathcal{R}}_{1}{\oplus }_{e}{{\zeta }_{2}\mathcal{R}}_{2}{\oplus }_{e}\cdots {\oplus }_{e}{\zeta }_{p}\mathcal{R}_{p}={\oplus }_{i=1}^{p}{\zeta }_{i}\mathcal{R}_{i}.$$

Theorem 4.4

Let \(\mathcal{R}_{i}=\left\{\left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right],\left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right],\left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\right\},\) \(\left(i=\left\{\text{1,2},\dots ,p\right\}\right)\) be the set of IVFPFNs, then the IVFPFEWA operator determines the aggregated value that follows:

$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\left(\begin{array}{c}\left[\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{array}\right)$$
(1)

Proof

To illustrate the IVFPFEWA operator, we will employ mathematical induction.

Step (1). If \(\zeta =2\), so

$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2}\right)={{\zeta }_{1}\mathcal{R}}_{1}{\oplus }_{e}{{\zeta }_{2}\mathcal{R}}_{2}.$$

Using Definition 4.1, we have

$${{\zeta }_{1}\mathcal{R}}_{1}=\left(\begin{array}{c}\left[\sqrt[3]{\frac{{\left(1+{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}-{\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}{{\left(1+{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}},\sqrt[3]{\frac{{\left(1+{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}-{\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}{{\left(1+{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left(1-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right], \\ \left[\frac{\sqrt[3]{2}{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}},\frac{\sqrt[3]{2}{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right], \\ \left[\frac{\sqrt[3]{2}{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}},\frac{\sqrt[3]{2}{\left(\varrho_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left(\varrho_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left(\varrho_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right]\end{array}\right)$$
$${\zeta }_{2} \mathcal{R}_{2}=\left(\begin{array}{c}\left[\sqrt[3]{\frac{{\left(1+{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}},\sqrt[3]{\frac{{\left(1+{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right], \\ \left[\frac{\sqrt[3]{2}{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}},\frac{\sqrt[3]{2}{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right], \\ \left[\frac{\sqrt[3]{2}{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}},\frac{\sqrt[3]{2}{\left(\varrho_{\mathcal{R}_{2}}^{U}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left(\varrho_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left(\varrho_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right]\end{array}\right)$$
$$\begin{aligned}IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2}\right)&={{\zeta }_{1}\mathcal{R}}_{1}{\oplus }_{e}{{\zeta }_{2}\mathcal{R}}_{2}=\left(\begin{array}{c}\bigg[{\left(\frac{\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}+\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}{1+\left(\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}\right)\left(\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}\right)}\right)}^\frac{1}{3}, \\ {\left(\frac{\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}+\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}{1+\left(\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}\right)\left(\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}\right)}\right)}^\frac{1}{3}\bigg],\\ \bigg[\frac{\left(\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}{\sqrt[3]{1+\left(1-\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(1-\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}}, \\ \frac{\left(\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}{\sqrt[3]{1+\left(1-\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(1-\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}}\bigg],\\ \bigg[\frac{\left(\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}{\sqrt[3]{1+\left(1-\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(1-\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}}, \\ \frac{\left(\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}{\sqrt[3]{1+\left(1-\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}}}\right)\left(1-\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\right)}}\bigg]\end{array}\right)\\ & =\left(\begin{array}{c}\bigg[\sqrt[3]{\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}, \\ \sqrt[3]{\frac{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}-{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}{{\left(1+{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1+{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left(1-{\left({\hbar}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(1-{\left({\hbar}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\bigg],\\ \bigg[\frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(2-{\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\eta}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left({\left({\eta}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}, \\ \frac{\sqrt[3]{2}{\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}{\left({\eta}_{\mathcal{R}_{2}}^{U}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(2-{\left({\eta}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\eta}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left({\left({\eta}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\bigg], \\ \bigg[\frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{{\zeta }_{1}}{\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(2-{\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}+{\left({\left({\varrho}_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\zeta }_{1}}{\left({\left({\varrho}_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\zeta }_{2}}}}, \\ \frac{\sqrt[3]{2}{\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{{\zeta }_{1}}{\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{{\zeta }_{2}}}{\sqrt[3]{{\left(2-{\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left(2-{\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}+{\left({\left({\varrho}_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\zeta }_{1}}{\left({\left({\varrho}_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\zeta }_{2}}}}\bigg]\end{array}\right)\\ & =\left(\begin{array}{c}\bigg[\sqrt[3]{\frac{\prod_{i=1}^{2}{\left(1+{\left({\hbar}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{2}{\left(1-{\left({\hbar}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{2}{\left(1+{\left({\hbar}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{2}{\left(1-{\left({\hbar}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}, \sqrt[3]{\frac{\prod_{i=1}^{2}{\left(1+{\left({\hbar}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{2}{\left(1-{\left({\hbar}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{2}{\left(1+{\left({\hbar}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{2}{\left(1-{\left({\hbar}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\bigg],\\ \bigg[\frac{\sqrt[3]{2} \prod_{i=1}^{2}{\left({\eta}_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{2}{\left(2-{\left({\eta}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{2}{\left({\left({\eta}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}, \frac{\sqrt[3]{2} \prod_{i=1}^{2}{\left({\eta}_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{2}{\left(2-{\left({\eta}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{2}{\left({\left({\eta}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\bigg], \\ \bigg[\frac{\sqrt[3]{2} \prod_{i=1}^{2}{\left({\varrho}_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{2}{\left(2-{\left({\varrho}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{2}{\left({\left({\varrho}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{2}{\left({\varrho}_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{2}{\left(2-{\left({\varrho}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{2}{\left({\left({\varrho}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\bigg]\end{array}\right)\end{aligned}$$

Consequently, the results are applicable for \(p=2\).

Step (2). Assuming that the outcome is results for \(p={\mathtt{k}}^{*}\), then

$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\left(\begin{array}{c}\left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{array}\right).$$

Step (3). We demonstrate that the result is valid to \(p={\mathtt{k}}^{*}+1\).

$$\begin{aligned}IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{{\mathtt{k}}^{*}+1}\right)&=\left(\begin{array}{c}\left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{array}\right)\\ & \quad {\oplus }_{e}\left(\begin{array}{c}\left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{array}\right)\end{aligned}$$
$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{{\mathtt{k}}^{*}+1}\right)=\left(\begin{array}{c}\left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{array}\right)$$

in which the result for \(p={\mathtt{k}}^{*}+1\) is demonstrated. Hence, the result is valid \(\forall p\).

Theorem 4.5

Let \(\mathcal{R}_{i}=\left\{\left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right],\left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right],\left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\right\},\) \(\left(i=\left\{\text{1,2},\dots ,p\right\}\right)\) be the IVFPFNs with an associated weight vector (WV) \(\zeta =\left\{{\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{p}\right\},\) satisfying \({\zeta }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{p}{\zeta }_{i}=1.\) The IVFPFEWA operator has the following characteristics

Idempotency: if \(\mathcal{R}_{i}=\mathcal{R}_{0}=\left(\left[\hbar_{\mathcal{R}_{0}}^{L},\hbar_{\mathcal{R}_{0}}^{U}\right],\left[\eta_{\mathcal{R}_{0}}^{L},\eta_{\mathcal{R}_{0}}^{U}\right],\left[\varrho_{\mathcal{R}_{0}}^{L},\varrho_{\mathcal{R}_{0}}^{U}\right]\right),\) \(i=\left\{\text{1,2},3,\dots ,p\right\},\) then

$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\mathcal{R}_{0}$$

Proof

We know that

$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\left(\begin{array}{c}\left[\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right],\\ \left[\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{{\zeta }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{array}\right)$$
$$IVFPFEWA\left(\mathcal{R}_{0},\mathcal{R}_{0},\dots ,\mathcal{R}_{0}\right)=\left(\begin{array}{c}\left[\sqrt[3]{\frac{\left(1+{\left(\hbar_{\mathcal{R}_{0}}^{L}\right)}^{3}\right)-\left(1-{\left(\hbar_{\mathcal{R}_{0}}^{L}\right)}^{3}\right)}{\left(1+{\left(\hbar_{\mathcal{R}_{0}}^{L}\right)}^{3}\right)+\left(1-{\left(\hbar_{\mathcal{R}_{0}}^{L}\right)}^{3}\right)}},\sqrt[3]{\frac{\left(1+{\left(\hbar_{\mathcal{R}_{0}}^{U}\right)}^{3}\right)-\left(1-{\left(\hbar_{\mathcal{R}_{0}}^{U}\right)}^{3}\right)}{\left(1+{\left(\hbar_{\mathcal{R}_{0}}^{U}\right)}^{3}\right)+\left(1-{\left(\hbar_{\mathcal{R}_{0}}^{U}\right)}^{3}\right)}}\right],\\ \left[\frac{\sqrt[3]{2} \eta_{\mathcal{R}_{0}}^{L}}{\sqrt[3]{\left(2-{\left(\eta_{\mathcal{R}_{0}}^{L}\right)}^{3}\right)+{\left(\eta_{\mathcal{R}_{0}}^{L}\right)}^{3}}},\frac{\sqrt[3]{2} \eta_{\mathcal{R}_{0}}^{U}}{\sqrt[3]{\left(2-{\left(\eta_{\mathcal{R}_{0}}^{U}\right)}^{3}\right)+{\left(\eta_{\mathcal{R}_{0}}^{U}\right)}^{3}}}\right],\\ \left[\frac{\sqrt[3]{2} \varrho_{\mathcal{R}_{0}}^{L}}{\sqrt[3]{\left(2-{\left(\varrho_{\mathcal{R}_{0}}^{L}\right)}^{3}\right)+{\left(\varrho_{\mathcal{R}_{0}}^{L}\right)}^{3}}},\frac{\sqrt[3]{2} \varrho_{\mathcal{R}_{0}}^{U}}{\sqrt[3]{\left(2-{\left(\varrho_{\mathcal{R}_{0}}^{U}\right)}^{3}\right)+{\left(\varrho_{\mathcal{R}_{0}}^{U}\right)}^{3}}}\right]\end{array}\right)$$
$$IVFPFEWA\left(\mathcal{R}_{0},\mathcal{R}_{0},\dots ,\mathcal{R}_{0}\right)=\left(\left[\hbar_{\mathcal{R}_{0}}^{L},\hbar_{\mathcal{R}_{0}}^{U}\right],\left[\eta_{\mathcal{R}_{0}}^{L},\eta_{\mathcal{R}_{0}}^{U}\right],\left[\varrho_{\mathcal{R}_{0}}^{L},\varrho_{\mathcal{R}_{0}}^{U}\right]\right)=\mathcal{R}_{0}$$

Boundedness: if \(\mathcal{R}^{-}=\left\{\left[min\hbar_{\mathcal{R}_{i}}^{L},min\hbar_{\mathcal{R}_{i}}^{U}\right],\left[max\eta_{\mathcal{R}_{i}}^{L}, max\eta_{\mathcal{R}_{i}}^{U}\right],\left[max\varrho_{\mathcal{R}_{i}}^{L},max\varrho_{\mathcal{R}_{i}}^{U}\right]\right\}\) and \(\mathcal{R}^{+}=\left\{\left[max\hbar_{\mathcal{R}_{i}}^{L},max\hbar_{\mathcal{R}_{i}}^{U}\right],\left[min\eta_{\mathcal{R}_{i}}^{L}, min\eta_{\mathcal{R}_{i}}^{U}\right],\left[min\varrho_{\mathcal{R}_{i}}^{L},min\varrho_{\mathcal{R}_{i}}^{U}\right]\right\},\) then

$$\mathcal{R}^{-}\le IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\mathcal{R}^{+}$$

Proof

Let us consider a function \(f\left(t\right)=\frac{1-t}{1+t},\) \(t\in \left[\text{0,1}\right].\) Then \(f\left(t\right)\) is a dec-function if \({f}{\prime}\left(t\right)<0.\) If take that \(min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\le {\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\le max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3},\) \(\forall i=\text{1,2},3,\dots ,\mathsf{n}\). Then,

$$f\left(max{\left({\hbar}_{{\mathcal{R}}_{i}}^{L}\right)}^{3}\right)\le f\left({\left({\hbar}_{{\mathcal{R}}_{i}}^{L}\right)}^{3}\right)f\left(min{\left({\hbar}_{{\mathcal{R}}_{i}}^{L}\right)}^{3}\right), \forall i$$
$$\Rightarrow \left(\frac{1-max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le \left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le \left(\frac{1-min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)$$

For WV \({\zeta }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{p}{\zeta }_{i}=1\), Then,

$$\Rightarrow {\left(\frac{1-max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le {\left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le {\left(\frac{1-min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}$$
$$\Rightarrow \prod_{i=1}^{p}{\left(\frac{1-max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \prod_{i=1}^{p}{\left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \prod_{i=1}^{p}{\left(\frac{1-min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}$$
$$\Rightarrow {\left(\frac{1-max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{\sum_{i=1}^{p}{\zeta }_{i}}\le \prod_{i=1}^{p}{\left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le {\left(\frac{1-min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{\sum_{i=1}^{p}{\zeta }_{i}}$$
$$\Rightarrow \left(\frac{1-max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le \prod_{i=1}^{p}{\left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \left(\frac{1-min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)$$
$$\Rightarrow \left(\frac{2}{1+max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le 1+\prod_{i=1}^{p}{\left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \left(\frac{2}{1+min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)$$
$$\Rightarrow \left(\frac{1+min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{2}\right)\le \frac{1}{1+\prod_{i=1}^{p}{\left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}}\le \left(\frac{1+max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{2}\right)$$
$$\Rightarrow \left(min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)\le -1+\frac{2}{1+\prod_{i=1}^{p}{\left(\frac{1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}{1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}}\le \left(max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)$$
$$\Rightarrow min{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\le \frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}\le max{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}$$
$$\Rightarrow min\hbar_{\mathcal{R}_{i}}^{L}\le \sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le max\hbar_{\mathcal{R}_{i}}^{L}$$
(2)

Similarly,

$$\Leftrightarrow min\hbar_{\mathcal{R}_{i}}^{U}\le \sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le max\hbar_{\mathcal{R}_{i}}^{U}$$
(3)

Let us now consider a function \(g\left(t\right)=\frac{2-t}{t},\) \(t\in \left[\text{0,1}\right].\) Then \(g\left(t\right)\) is a dec-function if \({g}{\prime}\left(x\right)<0.\) If we suppose that \(min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le {\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3},\) \(\forall i=\left\{\text{1,2},3,\dots ,p\right\}\). Then,

$$g\left(max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)\le g\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)\le g\left(min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right), \forall i$$
$$\Rightarrow \left(\frac{2-max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le \left(\frac{2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le \left(\frac{2-min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)$$

For WV \({\zeta }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}=1\), then the above inequality can be written as follows:

$$\Rightarrow {\left(\frac{2-max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le {\left(\frac{2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le {\left(\frac{2-min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}$$
$$\Rightarrow \prod_{i=1}^{p}{\left(\frac{2-max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \prod_{i=1}^{p}{\left(\frac{2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \prod_{i=1}^{\mathsf{n}}{\left(\frac{2-min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}$$
$$\Rightarrow {\left(\frac{2-max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{\sum_{i=1}^{p}{\zeta }_{i}}\le \prod_{i=1}^{p}{\left(\frac{2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le {\left(\frac{2-min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{\sum_{i=1}^{p}{\zeta }_{i}}$$
$$\Rightarrow \left(\frac{2-max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le \prod_{i=1}^{p}{\left(\frac{2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \left(\frac{2-min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{min{\eta_{\mathcal{R}_{i}}^{L}}^{3}}\right)$$
$$\Rightarrow \left(\frac{2}{max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)\le 1+\prod_{i=1}^{p}{\left(\frac{2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}\le \left(\frac{2}{min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)$$
$$\Rightarrow \left(\frac{min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{2}\right)\le \frac{1}{1+\prod_{i=1}^{p}{\left(\frac{2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}\right)}^{{\zeta }_{i}}}\le \left(\frac{max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}}{2}\right)$$
$$\Rightarrow min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le \frac{2 \prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}\le max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}$$
$$\Rightarrow min\eta_{\mathcal{R}_{i}}^{L}\le \sqrt[3]{\frac{2 \prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le max\eta_{\mathcal{R}_{i}}^{L}$$
(4)

Similarly,

$$\Rightarrow min\eta_{\mathcal{R}_{i}}^{U}\le \sqrt[3]{\frac{2 \prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(2-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le max\eta_{\mathcal{R}_{i}}^{U}$$
(5)

One may similarly prove the non-membership by applying the same logic described for the neutral membership. That is,

$$\begin{aligned} \Rightarrow \left[ {min{\varrho }_{{{\mathcal{R}}_{i} }}^{L} ,min{\varrho }_{{{\mathcal{R}}_{i} }}^{U} } \right] & \le \left[ {\sqrt[3]{{\frac{{2\prod\limits_{{i = 1}}^{p} {\left( {\left( {{\varrho }_{{{\mathcal{R}}_{i} }}^{L} } \right)^{3} } \right)^{{\zeta _{i} }} } }}{{\prod\limits_{{i = 1}}^{p} {\left( {2 - \left( {{\varrho }_{{{\mathcal{R}}_{i} }}^{L} } \right)^{3} } \right)^{{\zeta _{i} }} } + \prod\limits_{{i = 1}}^{p} {\left( {\left( {{\varrho }_{{{\mathcal{R}}_{i} }}^{L} } \right)^{3} } \right)^{{\zeta _{i} }} } }}}},\sqrt[3]{{\frac{{2\prod\limits_{{i = 1}}^{p} {\left( {\left( {{\varrho }_{{{\mathcal{R}}_{i} }}^{L} } \right)^{3} } \right)^{{\zeta _{i} }} } }}{{\prod\limits_{{i = 1}}^{p} {\left( {2 - \left( {{\varrho }_{{{\mathcal{R}}_{i} }}^{L} } \right)^{3} } \right)^{{\zeta _{i} }} } + \prod\limits_{{i = 1}}^{p} {\left( {\left( {{\varrho }_{{{\mathcal{R}}_{i} }}^{L} } \right)^{3} } \right)^{{\zeta _{i} }} } }}}}} \right] \\ & \le \left[ {max{\varrho }_{{{\mathcal{R}}_{i} }}^{L} ,max{\varrho }_{{{\mathcal{R}}_{i} }}^{U} } \right] \\ \end{aligned}$$
(6)

Based on inequalities (2–6), it is evident that if \(IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\left(\left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right],\left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right],\left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\right),\) then \(\left[min\hbar_{\mathcal{R}_{i}}^{L},min\hbar_{\mathcal{R}_{i}}^{U}\right]\le \left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right]\le \left[max\hbar_{\mathcal{R}_{i}}^{L},{max \hbar}_{\mathcal{R}_{i}}^{U}\right],\) \(\left[min\eta_{\mathcal{R}_{i}}^{L},min\eta_{\mathcal{R}_{i}}^{U}\right]\le \left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right]\le \left[{max\eta}_{\mathcal{R}_{i}}^{L},{max\eta}_{\mathcal{R}_{i}}^{U}\right]\left[min\varrho_{\mathcal{R}_{i}}^{L},min\varrho_{\mathcal{R}_{i}}^{U}\right]\le \left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\le \left[max\varrho_{\mathcal{R}_{i}}^{L},{max \varrho}_{\mathcal{R}_{i}}^{U}\right],\) which can be described in terms of score value, such that \(\mathcal{S}\left(\mathcal{R}^{-}\right) < \mathcal{S}\left(\mathcal{R}\right)\) and \(\mathcal{S}\left(\mathcal{R}\right) <\mathcal{S}\left(\mathcal{R}^{+}\right)\). So,

$$\mathcal{R}^{-}\le IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)\le \mathcal{R}^{+}.$$

Monotonicity: If \({\mathcal{R}}_{i}\le {\mathcal{R}}_{i}{{^{\prime}}},\) for \(i=\left\{\text{1,2},3,\dots ,p\right\},\) so

$$IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)\le IVFPFEWA\left(\mathcal{R}_{1}{\prime},\mathcal{R}_{2}{\prime},\dots ,\mathcal{R}_{p}{\prime}\right)$$

Proof

Let us consider a function \(f\left(t\right)=\sqrt[3]{\frac{1-t}{1+t}},\) \(t\in \left[\text{0,1}\right].\) Then \(f\left(t\right)\) is a dec-function on \(\left[\text{0,1}\right].\) if \(\mathcal{R}_{p}<\mathcal{R}_{p}{\prime},\) then \(f\left(\mathcal{R}_{p}\right)<f\left(\mathcal{R}_{p}{\prime}\right) \forall p.\)

$$1-\hbar_{\mathcal{R}_{i}}^{L}\ge 1-{\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\Rightarrow 1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\ge 1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}$$
$$\Rightarrow \left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)-\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)\le \left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)-\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)$$
$$\Rightarrow \frac{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)-\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)+\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}\le \frac{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)-\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)+\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}$$

For WV \({\zeta }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{p}{\zeta }_{i}=1\), above inequality is represented as follows:

$$\Rightarrow \frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}\le \frac{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}$$
$$\Rightarrow \sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le \sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}$$

Similarly,

$$\Rightarrow \sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le \sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}$$
$$\begin{aligned} &\left[\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\\ & \quad \le \left[\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}-\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left(1-{\left({\hbar{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{aligned}$$

Let us now consider a function \(g\left(t\right)=\sqrt[3]{\frac{2-t}{t}},\) \(t\in \left[\text{0,1}\right].\) Then \(g\left(t\right)\) is a dec-function if \({g}{\prime}\left(x\right)\) on \(\left[\text{0,1}\right].\) if \(\mathcal{R}_{p}<\mathcal{R}_{p}{\prime},\) then \(f\left(\mathcal{R}_{p}\right)<f\left(\mathcal{R}_{p}{\prime}\right) \forall p.\) If we suppose that \(min{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le {\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le max{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3},\) \(\forall i=\left\{\text{1,2},3,\dots ,p\right\}\)

Now \(\eta_{\mathcal{R}_{i}}^{L}\le {\eta{\prime}}_{\mathcal{R}_{i}}^{L}\Rightarrow {\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le {\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}.\) For WV \({\zeta }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}=1,\) so

$${\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}\le {\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}\Rightarrow 2{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}\le 2{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}$$

As \(2-\eta_{\mathcal{R}_{i}}^{L}\le 2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\Rightarrow {\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le {\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\)

$$\Rightarrow {\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\le {\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}+{\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}$$
$$\Rightarrow {\left({\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}+{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}\le {\left({\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}+{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}$$
$$\Rightarrow \frac{2{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}}{{\left({\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}+{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}}\le \frac{2{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}}{{\left({\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}+{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{\sum_{i=1}^{\mathsf{n}}{\zeta }_{i}}}$$
$$\Rightarrow \frac{2\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}\le \frac{2\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}$$
$$\Rightarrow \sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le \sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}$$

Similarly,

$$\Rightarrow \sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}\le \sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}$$
$$\begin{aligned}&\left[\sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\\ & \quad \le \left[\sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\zeta }_{i}}}},\sqrt[3]{\frac{2\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}{\prod_{i=1}^{p}{\left({\left(2-{\eta{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}+\prod_{i=1}^{p}{\left({\left({\eta{\prime}}_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\zeta }_{i}}}}\right]\end{aligned}$$

Hence, it proves the inequality.

Definition 4.6

Let \(\mathcal{R}_{i}=\left(\left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right],\left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right],\left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\right),\) \(\left(i=\left\{\text{1,2},3,\dots ,p\right\}\right)\) be the sets of IVFPFNs with connected WV \({\kappa }_{i}=\left\{{\kappa }_{1},{\kappa }_{2},\dots ,{\kappa }_{\mathsf{n}}\right\},\) satisfying \({\kappa }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{p}{\kappa }_{i}=1.\) The IVFPFEWG operator \(FPFEWG : \mathcal{R}^{p}\to \mathcal{R}\) is illustrated as

$$IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)={\otimes }_{i=1}^{p}{\left(\mathcal{R}_{i}\right)}^{{\kappa }_{i}}.$$

Theorem 4.7

Let \(\mathcal{R}_{i}=\left(\left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right],\left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right],\left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\right),\) \(\left(i=\left\{\text{1,2},3,\dots ,p\right\}\right)\) be the data of IVFPFNs. Afterward, the IVFPFEWG operator generates the aggregated value in the following format:

$$IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\left(\begin{array}{c}\left[\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{p}{\left({\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{p}{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{p}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{p}{\left({\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{p}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{p}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{p}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{p}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right]\end{array}\right)$$
(7)

Proof

To demonstrate the IVFPFEWG operator, we employ mathematical induction.

Step (1). If \(\kappa =2\), so

$$IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2}\right)=\mathcal{R}_{1}^{{\kappa }_{1}}{\otimes }_{e}\mathcal{R}_{2}^{{\kappa }_{2}}.$$
$$\mathcal{R}_{1}^{{\kappa }_{1}}=\left(\begin{array}{c}\left[\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{{\kappa }_{1}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}},\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{{\kappa }_{1}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}}\right], \\ \left[\sqrt[3]{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}},\sqrt[3]{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}}\right], \\ \left[\sqrt[3]{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}},\sqrt[3]{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}}\right]\end{array}\right)$$
$$\mathcal{R}_{2}^{{\kappa }_{2}}=\left(\begin{array}{c}\left[\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}},\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}}\right], \\ \left[\sqrt[3]{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}},\sqrt[3]{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}}\right], \\ \left[\sqrt[3]{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}},\sqrt[3]{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}\right]\end{array}\right)$$
$$\begin{aligned}IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2}\right)&=\mathcal{R}_{1}^{{\kappa }_{1}}{\otimes }_{e}\mathcal{R}_{2}^{{\kappa }_{2}}=\left(\begin{array}{c}\bigg[\frac{\left(\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{{\kappa }_{1}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}}\right)\left(\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}\right)}{\sqrt[3]{1+\left(1-\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{{\kappa }_{1}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}}\right)\left(1-\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}\right)}}, \\ \frac{\left(\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{{\kappa }_{1}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}}\right)\left(\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}}\right)}{\sqrt[3]{1+\left(1-\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{{\kappa }_{1}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}}\right)\left(1-\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}}\right)}}\bigg],\\ \bigg[{\left(\frac{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}+\frac{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}{1+\left(\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}\right)\left(\frac{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}\right)}\right)}^\frac{1}{3}, \\ {\left(\frac{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}+\frac{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}}{1+\left(\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}}\right)\left(\frac{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}\right)}\right)}^\frac{1}{3}\bigg],\\ \bigg[{\left(\frac{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}+\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}{1+\left(\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}\right)\left(\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}\right)}\right)}^\frac{1}{3}, \\ {\left(\frac{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}+\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}{1+\left(\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}}\right)\left(\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}\right)}\right)}^\frac{1}{3}\bigg]\end{array}\right)\\& =\left(\begin{array}{c}\bigg[\frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{{\kappa }_{1}}{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left({\left(\hbar_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}, \\ \frac{\sqrt[3]{2}{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{{\kappa }_{1}}{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{{\kappa }_{2}}}{\sqrt[3]{{\left(2-{\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(2-{\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left({\left(\hbar_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}{\left({\left(\hbar_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}}\bigg],\\ \bigg[\sqrt[3]{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}, \\ \sqrt[3]{\frac{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\eta_{\mathcal{R}_{1}}^{U}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\eta_{\mathcal{R}_{2}}^{U}\right)}^{3}\right)}^{{\kappa }_{2}}}}\bigg], \\ \bigg[\sqrt[3]{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}, \\ \sqrt[3]{\frac{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}-{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}{{\left(1+{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1+{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}+{\left(1-{\left(\varrho_{\mathcal{R}_{1}}^{L}\right)}^{3}\right)}^{{\kappa }_{1}}{\left(1-{\left(\varrho_{\mathcal{R}_{2}}^{L}\right)}^{3}\right)}^{{\kappa }_{2}}}}\bigg]\end{array}\right)\\ & =\left(\begin{array}{c}\left[\frac{\sqrt[3]{2} \prod_{i=1}^{2}{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{2}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{2}{\left({\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{2}{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{2}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{2}{\left({\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{2}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{2}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{2}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{2}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{2}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{2}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{2}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{2}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{2}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{2}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{2}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{2}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{2}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{2}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{2}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{2}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right]\end{array}\right)\end{aligned}$$

Hence, the results are true to \(p=2\).

Step (2). Assuming that the results are true to \(p={\mathtt{k}}^{*}\), then

$$IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{{\mathtt{k}}^{*}}\right)=\left(\begin{array}{c}\bigg[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}}, \\ \frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\bigg],\\ \bigg[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}}, \\ \sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\bigg],\\ \bigg[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}}, \\ \sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\bigg]\end{array}\right).$$

Step (3). We demonstrate that the result is valid to \(p={\mathtt{k}}^{*}+1\).

$$\begin{aligned}IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{{\mathtt{k}}^{*}+1}\right)&=\left(\begin{array}{c}\left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}}{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left({\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right]\end{array}\right)\\ & \quad {\otimes }_{e}\left(\begin{array}{c}\left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right]\end{array}\right)\end{aligned}$$
$$IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{{\mathtt{k}}^{*}+1}\right)=\left(\begin{array}{c}\left[\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\hbar_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\frac{\sqrt[3]{2} \prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{{\kappa }_{i}}}{\sqrt[3]{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(2-{\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left({\left(\hbar_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\eta_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right],\\ \left[\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{L}\right)}^{3}\right)}^{{\kappa }_{i}}}},\sqrt[3]{\frac{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}-\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}{\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1+{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}+\prod_{i=1}^{{\mathtt{k}}^{*}+1}{\left(1-{\left(\varrho_{\mathcal{R}_{i}}^{U}\right)}^{3}\right)}^{{\kappa }_{i}}}}\right]\end{array}\right)$$

in which the result for \(p={\mathtt{k}}^{*}+1\) is demonstrated. Hence, the result is valid \(\forall p\).

Theorem 4.8

Let \(\mathcal{R}_{i}=\left\{\left[\hbar_{\mathcal{R}_{i}}^{L},\hbar_{\mathcal{R}_{i}}^{U}\right],\left[\eta_{\mathcal{R}_{i}}^{L},\eta_{\mathcal{R}_{i}}^{U}\right],\left[\varrho_{\mathcal{R}_{i}}^{L},\varrho_{\mathcal{R}_{i}}^{U}\right]\right\},\) \(\left(i=\left\{\text{1,2},\dots ,p\right\}\right)\) be the IVFPFNs with an associated WV \({\kappa }_{i}=\left\{{\kappa }_{1},{\kappa }_{2},\dots ,{\kappa }_{\mathsf{n}}\right\},\) satisfying \({\kappa }_{i}\in \left[\text{0,1}\right]\) and \(\sum_{i=1}^{p}{\kappa }_{i}=1.\) The IVFPFEWG operator has the following characteristics.

Idempotency: if \({\mathcal{R}}_{i}={\mathcal{R}}_{0}=\left(\left[{\hbar}_{{\mathcal{R}}_{0}}^{L},{\hbar}_{{\mathcal{R}}_{0}}^{U}\right],\left[{\eta}_{{\mathcal{R}}_{0}}^{L},{\eta}_{{\mathcal{R}}_{0}}^{U}\right],\left[{\varrho}_{{\mathcal{R}}_{0}}^{L},{\varrho}_{{\mathcal{R}}_{0}}^{U}\right]\right),\) \(i=\left\{\text{1,2},3,\dots ,p\right\},\) then

$$IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\mathcal{R}_{0}$$

Boundedness: if \({\mathcal{R}}^{-}=\left\{\left[min{\hbar}_{{\mathcal{R}}_{i}}^{L},min{\hbar}_{{\mathcal{R}}_{i}}^{U}\right],\left[max{\eta}_{{\mathcal{R}}_{i}}^{L}, max{\eta}_{{\mathcal{R}}_{i}}^{U}\right],\left[max{\varrho}_{{\mathcal{R}}_{i}}^{L},max{\varrho}_{{\mathcal{R}}_{i}}^{U}\right]\right\},\) \({\mathcal{R}}^{+}=\left\{\left[max{\hbar}_{{\mathcal{R}}_{i}}^{L},max{\hbar}_{{\mathcal{R}}_{i}}^{U}\right],\left[min{\eta}_{{\mathcal{R}}_{i}}^{L}, min{\eta}_{{\mathcal{R}}_{i}}^{U}\right],\left[min{\varrho}_{{\mathcal{R}}_{i}}^{L},min{\varrho}_{{\mathcal{R}}_{i}}^{U}\right]\right\},\) then

$$\mathcal{R}^{-}\le IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)=\mathcal{R}^{+}$$

Monotonicity: If \({\mathcal{R}}_{i}\le {\mathcal{R}}_{i}{{^{\prime}}},\) for \(i=\left\{\text{1,2},3,\dots ,p\right\},\) so

$$IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)\le IVFPFEWG\left(\mathcal{R}_{1}{\prime},\mathcal{R}_{2}{\prime},\dots ,\mathcal{R}_{p}{\prime}\right)$$

Proof

The proof is identical to that of Theorem 4.5.

Proposed MADM model based on the developed Einstein AOs

In this section, we design an algorithm to illustrate the efficacy of the proposed approach in evaluating MADM problems. We also explore its application in advancing a sustainable logistics management system.

Let \(\acute{Y} =\left\{{\acute{Y} }_{1},{\acute{Y} }_{2},\dots ,{\acute{Y} }_{\mathcal{n}}\right\}\) represent a set of \(\mathsf{n}\)-alternatives and \(\mathcal{C}=\left\{{\mathcal{C}}_{1},{\mathcal{C}}_{2},\dots ,{\mathcal{C}}_{m}\right\}\) represent the collection of \(m\)-attributes. Let \(\mathcal{w}=\left\{{\mathcal{w}}_{1},{\mathcal{w}}_{2},\dots , {\mathcal{w}}_{n}\right\}\) describe the set of WVs associated with the attributes where \({\mathcal{w}}_{j}\in \left[\text{0,1}\right]\) and \(\sum_{j=1}^{n}{\mathcal{w}}_{j}=1.\) Let \(\upepsilon =\left\{{\upepsilon }_{1},{\upepsilon }_{2},\dots ,{\upepsilon }_{t}\right\}\) represent the data of decision-makers, each of which has associated weights, where \(\varpi =\left\{{\varpi }_{1},{\varpi }_{2},\dots ,{\varpi }_{t}\right\},\) where \({\varpi }_{k}\in \left[\text{0,1}\right]\) and \(\sum_{k=1}^{t}{\varpi }_{k}=1.\) We present the next algorithm for addressing the MADM problem and determining the definitive ranking of the alternatives.

Algorithm

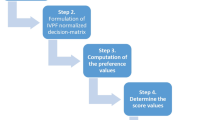
We created an algorithm for the MADM technique to process the intricate information that was obtained from our approach. The following stages of this method, which are also illustrated in Fig. 1, are outlined below, providing a clear and intuitive guide for both experts and readers.

Fig. 1
figure 1

Flowhat of proposed MADM approach.

Full size image

Based on suggested AOs, a multi-attribute group decision-making method.

Input: DMs evaluation information \({D}^{k}={\left({{\aleph }}_{\text{ij}}^{\text{k}}\right)}_{n\times m}\) for each expert \(k\)

1: Obtain the assessment information from DMs.

2: Normalize the DM:

  • For benefit-type criteria, apply: \(\left(\left[\hbar_{\mathcal{R}_{jk}}^{L},\hbar_{\mathcal{R}_{jk}}^{U}\right],\left[\eta_{\mathcal{R}_{jk}}^{L},\eta_{\mathcal{R}_{jk}}^{U}\right],\left[\varrho_{\mathcal{R}_{jk}}^{L},\varrho_{\mathcal{R}_{jk}}^{U}\right]\right)\)

  • For non-benefit-type criteria, apply the complement of the above.

    $${{\aleph }}^{\text{n}}=\left\{\begin{array}{c}\left(\left[\hbar_{\mathcal{R}_{jk}}^{L},\hbar_{\mathcal{R}_{jk}}^{U}\right],\left[\eta_{\mathcal{R}_{jk}}^{L},\eta_{\mathcal{R}_{jk}}^{U}\right],\left[\varrho_{\mathcal{R}_{jk}}^{L},\varrho_{\mathcal{R}_{jk}}^{U}\right]\right) for benefit type\\ {\left(\left[\hbar_{\mathcal{R}_{jk}}^{L},\hbar_{\mathcal{R}_{jk}}^{U}\right],\left[\eta_{\mathcal{R}_{jk}}^{L},\eta_{\mathcal{R}_{jk}}^{U}\right],\left[\varrho_{\mathcal{R}_{jk}}^{L},\varrho_{\mathcal{R}_{jk}}^{U}\right]\right)}^{\text{c}} for non-benefit type\end{array}\right.$$
    (8)

3: Calculate and Aggregate the IVFPF information using the following:

  • \({{\aleph }}_{\text{jk}}=IVFPFEWA\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)\),

  • \({{\aleph }}_{\text{jk}}=IVFPFEWG\left(\mathcal{R}_{1},\mathcal{R}_{2},\dots ,\mathcal{R}_{p}\right)\)

4: Compute the score value of each alternative using

$$\mathcal{S}\left(\mathcal{R}\right)=\frac{1}{2}\left({\left(\hbar_\mathcal{R}^{L}\right)}^{3}+{\left(\hbar_\mathcal{R}^{U}\right)}^{3}-{\left(\eta_\mathcal{R}^{L}\right)}^{3}-{\left(\eta_\mathcal{R}^{U}\right)}^{3}-{\left(\varrho_\mathcal{R}^{L}\right)}^{3}-{\left(\varrho_\mathcal{R}^{U}\right)}^{3}\right)$$

5: Compare all score values and select the alternative with the highest score as the best option.

Output: Optimal alternative.

Application

A company seeks to enhance material delivery and logistics operations by combining intelligent technologies into its existing framework. The company requires external logistics service partnerships to achieve automation since their operations need increased efficiency and reduced expenses. The company must choose an appropriate logistics partner from several qualified service providers, making the decision process vital for connecting its strategic objectives with actual results. This necessitates the assessment of many logistics firms based on conventional and novel performance indicators. The modern logistics environment presents growing complexities that require real-time tracking features alongside predictive analytics and automated systems. To select the best logistics provider, organizations must evaluate infrastructure capability alongside financial stability and operational competence together with apparent technological innovation capacity.

The decision criteria were meticulously selected after conducting a thorough examination of pertinent literature and industry practices in intelligent logistics:

  • Infrastructure Development \(\left({\mathcal{C}}_{1}\right)\): The organization conducts an assessment of physical assets alongside technological infrastructure that contains warehouses alongside transport systems and IT infrastructure since these elements determine operational flexibility and scalability potential.

  • Economic Performance in Logistics \(\left({\mathcal{C}}_{2}\right)\): A sustainable partnership depends on three key factors: cost efficiency, profit margins, and financial stability measurements.

  • Operational Management \(\left({\mathcal{C}}_{3}\right)\): Assesses the logistics provider’s ability to handle daily logistics operations, including routing, scheduling, and managing disruptions effectively.

  • Smart Innovation Technological \(\left({\mathcal{C}}_{4}\right)\): Reflects the provider’s adoption of smart technologies like IoT, big data, and automation, which are key for optimizing logistics processes in the long term.

These criteria were weighted based on expert input, ensuring a balanced representation of operational and strategic factors relevant to modern logistics management. Figure 2 provides a full explanation of each factor.

Fig. 2
figure 2

Explanation of factors and alternatives.

Full size image

The results of the evaluation, derived from the IVFPF-based MADM method, offer a structured and transparent process for selecting the most suiF logistics partner. In real-world decision-making, this model helps. Experts evaluate criteria with interval-valued fuzzy numbers to enhance both evaluation accuracy and reliability. By implementing fuzzy logic, the assessment method better understands the irregularities in expert evaluations while understanding provider abilities more precisely. This ranking serves decision-makers to prove their selection choices by demonstrating they follow factual evidence instead of subjective opinions and missing information. Once the choice of logistics provider is made, the company can achieve operational excellence, technological advancement, and long-term profitability. By implementing this approach, the company selects a partner who satisfies both current operational requirements and develops capabilities to overcome future technological and market-related challenges. This methodology allows for a more nuanced understanding of each candidate’s strengths and shortcomings, facilitating informed decision-making for selecting the best logistics supplier.

Numerical example

This experimental case study in logistics management assesses four logistics service providers to identify the most effective option based on critical performance metrics. The companies \({\acute{Y} }_{1},{\acute{Y} }_{2},{\acute{Y} }_{3},\) and \({\acute{Y} }_{4}\) have been chosen for further evaluation because they are considered to have the most potential. Three specialists were invited to evaluate these companies, allocating weights to critical variables according to their knowledge. The assessment criteria comprise infrastructure development \(\left({\mathcal{C}}_{1}\right)\), economic performance in logistics \(\left({\mathcal{C}}_{2}\right)\), operational management \(\left({\mathcal{C}}_{3}\right)\), and smart technological innovation \(\left({\mathcal{C}}_{4}\right)\), with respective weightings of 0.58, 0.15, 0.20, 0.07. Utilizing the MADM method algorithm within the IVFPF framework to identify the ideal alternative.

Step 1 The decision-makers’ structured knowledge from diverse emergency management sources in the form of IVFPFNs is given in Table 1.

Table 1 Decision-matrix of IVFPFN.
Full size table

Step 2 The standard decision matrices do not require conversion to normalized matrices, as the experimental case study only entails a single type of criterion.

Step 3 We employ the proposed IVFPFEWA and IVFPFEWG operators, as described in Eqs. (1) and (7), respectively. Table 2 displays the results derived from the IVPFFWA and IVPFFWG operators.

Table 2 Resulting aggregation values of IVFPFEWA and IVFPFEWG.
Full size table

Step 4 Definition 3.3 is used for determining the score value \(\mathcal{S}\), which is shown in Table 3.

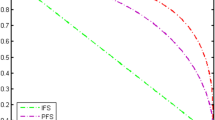
Table 3 Score values of IVFPFEWA and IVFPFEWG.
Full size table

Step 5 Rearrange the computed score values to identify the best alternative by ranking them in order and described in Fig. 3. The results acquired with the IVFPFEWA and IVFPFEWG operators are listed below:

Fig. 3
figure 3

Resulting of the proposed methods.

Full size image
$${\acute{\text{Y} }}_{4}>{\acute{\text{Y} }}_{2}>{\acute{\text{Y} }}_{3}>{\acute{\text{Y} }}_{1} and {\acute{\text{Y} }}_{4}>{\acute{\text{Y} }}_{2}>{\acute{\text{Y} }}_{3}>{\acute{\text{Y} }}_{1}.$$

Supremacy of the proposed technique

A highly practical and efficient method for managing MADM problems operates inside the IVFPFS environment. The methodology introduces MADM model innovation through IVFPFEWA and IVFPFEWG operators to achieve superior results than classic approaches. The model provides adaptable features that enable effective performance to deliver needed decision results under changing situations. The main difficulty with MADM models appears through the variations that occur when different models provide their assessment rankings. According to our research, standalone conventional approaches produce dissimilar results when researchers analyze them compared to hybrid analysis structures. Hybrid approaches consisting of IVIFS, IVPFS, and IVFFS have become popular because they effectively handle ambiguity and uncertain information during decision-making. Our proposed approach excels above all existing mixed fuzzy set frameworks since it offers better efficiency and effectiveness in managing uncertain and imprecise data.

The paper examines the strengths of our method and how it compares to established aggregation operators through Table 4. The creation of this approach emerged due to a requirement for customized solutions that would suit complex business applications. Our method stands out from existing hybrid models because it unifies an extensive range of fuzzy set types, including FS, IFS, IVIFS, PFS, IVPFS, FFS, and IVFFS, to provide an improved decision-making solution. The current hybrid structures show inadequacy in completely replicating complex decision contexts. We develop a new MADM operational framework based on interaction aggregation operators within IVFPFS to improve decision-making capabilities. The model features parameters that accept decision-making elements assessed through membership degrees, non-membership degrees, and neutrality degrees that maintain values between 0 and 1. The system delivers a sophisticated way of representing uncertain information with greater depth of understanding. The hybrid framework delivers substantially superior performance compared to traditional MADM approaches, according to Table 4 data.

Table 4 Feature analysis of different models with a proposed model.
Full size table

Comparative analysis

The proposed technique shows major differences with current methods by providing better uncertain data processing capabilities according to the comparison results. The ability of this process decreases information loss risks that arise from assigning fixed scores to parameters without factoring in their influence on other variables. The recommended MADM method effectively measures alternative similarity and interpretability while excluding unreliable data, which results in outcomes that are superior to those of conventional methods. According to our study, various current decision-making procedures by Cuong10 encounter limitations when addressing scenarios involving MD, NeD, and NMD. These methods are grounded in frameworks like Picture FSs and Pythagorean Picture FSs. Consequently, they struggle to effectively handle cases where \(\text{MD }+\text{ NeD }+\text{ NMD }> 1\) or \((\text{MD})^{2} + (\text{NeD})^{2} + (\text{NMD})^{2} > 1\), limiting their applicability in more intricate decision-making environments. These methods demonstrate restricted capabilities when employed to interval value decisions that require high power assessment of MD, neuD, and NMD.

To highlight the effectiveness of our proposed strategy, a comparative analysis was conducted using several existing methods, including the IVPFWA33, IVPFWG33, IVPFSSPOA34, IVPFSSPOG34, IVPPFWA35, and IVPPFWG35 operators, as illustrated in Table 5. We strictly adhered to their original parameter settings, mathematical formulations, and procedural steps without introducing any modifications or adjustments. This approach allowed us to evaluate each method in its intended form and ensured that any performance differences observed were not due to experimental bias or tuning. This analysis offers significant insights into the efficacy of the proposed approach. As illustrated in Table 5, all techniques consistently rank as the greatest option and \({\acute{Y} }_{1}\) as the worst.

Table 5 Comparison analysis with different existing techniques.
Full size table

The proposed method displays superior consistency in how scores are distributed, and alternatives are ranked according to Table 5, and a graphical representation of the obtained results is presented in Fig. 4.

Fig. 4
figure 4

Comparison with the existing methods.

Full size image

Different tests reveal that the proposed method consistently assigns the top ranking to \({\acute{Y} }_{4}\) and the lowest position to \({\acute{Y} }_{1}\) through scores that exhibit minimal variation. Our method generates score evaluations (Score 4 = 0.0215 and − 0.0084), which demonstrate more stability in comparison to Rehman et al.35, where the scores fluctuate to (Score 4 = 0.0245 and − 0.0344). Stability analysis and reduced sensitivity to minor input variations emerge from the experimental outcomes.

The proposed method improves interpretability by maintaining accuracy in decision-maker preferences and variable interrelations. The proposed method maintains reliable results when used as an aggregation operator for IVFPFEWA and IVFPFEWG, demonstrating its adaptable functionality in various decision-making environments. Both numerical outcomes and conceptual reasoning show that the proposed method demonstrates practical effectiveness with superior performance due to its newfound value.

Advantages and limitations of the proposed method

The following comparative evaluation will emphasize the proposed model’s strengths and limitations.

  • IVFPFSs improve the ability to manage two-dimensional information, providing a more detailed and insightful knowledge of objects in the context of decision-making. A more complex and complete strategy than earlier techniques is achieved by aggregating IVFPF data.

  • The suggested evaluation model integrates both angular and distance variables, providing a comprehensive and nuanced perspective on the proximity of decision objects. This method facilitates a comprehensive knowledge of their relationships.

  • The aggregation approach facilitates experts’ decision-making process by providing a variety of data processing methods.

It is essential to recognize several limitations related to the presented research:

  • While the suggested IVFPFN algorithms are distinct, they have weaknesses and might benefit from further modification to improve their accuracy, computing efficiency, and robustness in large-scale datasets.

  • Although the MADM technique offers a thorough assessment of our strategies, the method’s results are significantly influenced by the selection of criteria and the assignment of weights. Variations in these aspects may influence the total efficacy of the decision-making process.

  • The system has not been applied to large-scale logistics networks in practice. Problems related to heavy computing, the mix of different data, and fluctuating environmental aspects make it difficult to scale distributed supply chain systems effectively.

  • While our model successfully addresses several layers of complexity, it is important to recognize that the comprehensive nature of decision-making in sustainable logistics management cannot be fully captured within the scope of a single study or methodological approach.

  • The framework was created for use in sustainable logistics, but we still need to examine if it could be applied to different areas such as healthcare, finance, or urban planning. It may be necessary to modify the system to fit different limitations and stakeholder expectations.

  • The model does well at identifying complex steps, yet it cannot perfectly demonstrate the interactive processes that occur in real-world sustainable logistics. Future work needs to investigate ways to use both machine learning and simulation as part of validation processes.

Conclusions

In this work, we presented interval-valued Fermatean picture fuzzy sets (IVFPFSs). We investigated their key features and the essential functional laws that lay the basis for understanding them. We thoroughly investigated and evaluated IVFPFS features using Einstein methodologies. We also presented several aggregation methods integrating Einstein operations with averaging and geometric approaches, including the IVFPF Einstein weighted-averaging and weighted-geometric techniques. To illustrate the practical applications of these techniques, we created a MADM model for data gathering and processing. A numerical illustration of logistics management decision-making demonstrated The method’s utility. Ultimately, we examined our suggested model against existing ones to determine its efficacy. The findings demonstrate that our approach improves flexibility and adaptation, allowing decision-makers to select the optimal alternative across diverse contexts.

Future research can investigate a variety of options by expanding upon this investigation. The operation-related and rules principles of IVFPFNs could be developed in fundamental theory. Future research can integrate dynamic systems evaluation strategies38,39,40,41,42,43, which include the stability and higher-order evaluation drawn from differential equations, into the IVFPFS structure to boost the agility, security, and real-time management of sustainable logistical administration approaches.