An efficient swarm evolution algorithm with probability learning for the black and white coloring problem

Abstract

There is a graph G = (V, E), which has n vertices and l edges. Color the vertices of G black or white, ensuring no black vertex is adjacent to any white vertex, thus partitioning them into disjoint black and white sets. The optimal solution of the black and white coloring (BWC) problem is defined as the coloring scheme that maximizes the number of white vertices in the corresponding set, given a fixed number of black vertices. This problem is a NP-complete problem, widely used in reagent product storage in chemical industry and the solution to the problem of black and white queens in chess. The paper presents a swarm evolution algorithm based on improved simulated annealing search and evolutionary operation with probability learning mechanism. Furthermore, crossover operation, perturbation operation, and tabu search strategy improve the search ability of the algorithm, while evolutionary operation with probability learning mechanism increases the probability of the algorithm finding better solutions. Using Cayley graphs, random graphs, semi-random graphs, and benchmark DIMACS graphs, experiments are conducted to compare the finding results from swarm evolution algorithm and other classical heuristic algorithms. Experimental results show that the swarm evolution algorithm outperforms other heuristic algorithms in solving the BWC problem, and the swarm evolution algorithm can improve the known best results of the BWC problem.

Introduction

The Black and White Coloring (BWC) problem is initially described in¹. There is an undirected graph G = (V, E), where V is a set containing n vertices, and E is a set containing l edges. The vertices in graph G are colored in white or black, the black vertices constituting set B and the white vertices constituting set W. The two sets meet the following conditions:

(i1) B = {v_i|v_i ∈ V, 0 ≤ i < b}, in which v_i is black vertex, b is the number of vertices in set B.

(i2) W = {w_j|w_j ∈ V, 0 ≤ j < e}, in which w_j is white vertex, e is the number of vertices in set W.

(i3) ∀ v_i ∈ B, ∀ w_j ∈ W, (v_i, w_j)$\notin$ E, 0 ≤ i < b, 0 ≤ j < e.

(i4) When |B| is established, |W| is the maximized.

When conditions i1, i2, and i3 are met, it is found in graph G that set B and set W are referred to as the BWC problem of graph G. Besides conditions i1, i2 and i3 are satisfied, i4 is met at the same time, the solution (B, W) is the optimal solution of BWC problem, and |W| is the optimal value of BWC problem.

In¹, an application of the BWC problem is proposed: On an n × n chessboard, B black queens and W white queens are placed. A placement scheme is designed to make black and white queens mutual attack unavailable, there being white queens as many as possible. It has been proved that BWC is a NP-complete problem in¹. In², the BWC problem is applied to the design of chemical storage. Since chemical drugs have a certain toxicity, to ensure the safety of chemical storage, a reasonable segregated storage scheme should be designed to avoid unsafe factors such as toxicity, flammability, and causticity of chemicals.

The paper presents an efficient swarm evolution algorithm for the BWC problem. The algorithm consists of three parts. In the first part, an improved simulated annealing search strategy is adopted to explore the search space. This strategy incorporates tabu search and crossover operation to enhance the algorithm’s ability to find better solutions. In the second part, a perturbation operation is introduced to increase the likelihood of finding better solutions during the search process. Finally, in the third part, a probability learning mechanism is utilized to dynamically record the algorithm’s search history. This mechanism informs the reconstruction of the search space, guiding the swarm evolution operation. By leveraging this knowledge, the algorithm further improves its chances of finding better solutions.

We evaluate the performance of the swarm evolution algorithm on Cayley graphs (which includes “kings” graphs and “rooks” graphs), random graphs, semi-random graphs, and benchmark DIMACS graphs. The evaluation results show that the swarm evolution algorithm has a stronger search ability than the variable neighborhood search algorithm, simulated annealing algorithm, greedy algorithm, simulated annealing algorithm with configuration checking³, and local search algorithm⁴. In particular, the swarm evolution algorithm improves the known best results of 3 graphs in⁵ and 22 graphs in⁴.

The main structure of this paper is organized as follows. Section “Related work” introduces the current research work of heuristic algorithms. Section “A Swarm evolution algorithm for BWC” describes the design of the swarm evolution algorithm for solving the BWC problem. Section “A variable neighborhood search algorithm for BWC” describes the variable neighborhood search algorithm for solving BWC problem. Section “A simulated annealing algorithm for BWC” describes the simulated annealing algorithm for solving BWC problem. Section “The greedy algorithm for BWC” describes the greedy algorithm for solving BWC problem. Section “Experimental results” describes the performance analysis of the swarm evolution algorithm and comparative experiments of different algorithms.

Related work

In⁶, a fast algorithm for tree was presented to solve the BWC problem. In⁷, a linear time approximation algorithm was presented to solve the BWC problem. On the other hand, some heuristic algorithms were presented to solve BWC problems in relevant literatures. For example, two tabu algorithms were used to solve the BWC problem in⁵, a simulated annealing algorithm with configuration checking was used to solve the BWC problem³, and a local search algorithm was used to solve the BWC problem⁴.

Furthermore, some heuristic algorithms were presented to solve other combinatorial optimization problems. In⁸, an iterated k-opt local search algorithm was presented to solve the maximum clique problem. In⁹, a reactive local search algorithm was presented to solve the maximum clique Problem. In¹⁰, a phased local search algorithm was presented to solve the maximum clique problem. In¹¹, a k-opt local search algorithm was presented to solve the maximum clique problem. In¹², an iterated local search algorithm was presented to solve the traveling salesman problem. In^{13,14,15,16,17,18}, tabu search algorithms were presented to solve different combinatorial problems. In^19,20, variable neighborhood search algorithms were presented to solve different combinatorial problems. In^{21,22,23,24,25,26}, simulated annealing algorithms were presented to solve different combinatorial problems. In²⁷, a greedy algorithm was presented to solve the small dominating set problem in graphs. In^28,29, memetic algorithms were presented to solve the minimum sum coloring problem. In^30,31, local search algorithms with probability learning were presented to solve the coloring problems. In³², tabu search algorithm with probability learning was presented to solve the minimum load coloring problem. In³³, an improved whale algorithm was presented to solve the flexible job shop scheduling problem. In³⁴, a novel monarch butterfly optimization algorithm was presented to solve the Large-Scale 0–1 Knapsack problem. In³⁵, an improved firefly algorithm was presented to solve the constrained optimization engineering design problem. In³⁶, different crossover and mutation operators were identified as critical components that enable evolutionary algorithms to find better solutions. Consequently, asymptotic analyses were carried out on some well-known and recent crossover and mutation operators, and the convergence of the recent evolutionary algorithms was also analyzed. Based on these foundations, a genetic algorithm framework was proposed to effectively solve the graph coloring problem (GCP). In³⁷, three evolutionary operation algorithms combined with tabu search strategy were proposed to solve the graph coloring problem, and their effectiveness was verified on the DIMACS graphs. In³⁸, a novel evolutionary algorithm with central-value-based conflict gene crossover and mutation operators was proposed for solving the graph coloring problem, and its effectiveness was demonstrated on DIMACS benchmark graphs.

A swarm evolution algorithm for BWC

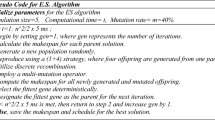
In the paper, we present a swarm evolution algorithm to solve the BWC problem of graphs. The swarm evolution algorithm is summarized in Swarm_BWC (Algorithm 1). The flowchart of the algorithm is shown in (Fig. 1).

Fig. 1

Flowchart of the swarm evolution algorithm to solve BWC.

Algorithm 1

Swarm_BWC (G, b, p, M, D, Y).

The algorithm first generates p initial probability matrices to construct a probability matrix group M (see Section “Construction of probability matrix group”). Using each probability matrix in M, it generates an initial individual, and p probability matrices generate p initial individuals, thus constructing a swarm D composed of p individuals (see Section “Swarm initialization”). Then the algorithm completes four steps of operation in one iteration.

In the first step, an improved simulated annealing search is applied to each individual in swarm D, and the obtained search results are stored in swarm Y. If a better solution to the BWC problem is found, it is saved as the current best solution. After searching, new individuals are evolved from each individual in swarm D, thus constructing swarm Y (see Section “Crossover operation” and Section “Improved simulated annealing search”).

In the second step, swarm Y is perturbed to further enhance the likelihood of finding a better solution. If a better solution to the BWC problem is found after the perturbation operation, it is saved as the current best solution (see Section “Perturbation operation”).

In the third step, based on the dynamic changes within swarms D and Y, a probability learning mechanism modifies each probability matrix value in the probability matrix group M, thereby capturing the dynamic changes of the swarm (see Section “Update operation of probability matrix group”).

In the fourth step, the modified probability matrix group M is used to further evolve swarm D, resulting in the newly evolved swarm D (see Section “Evolutionary operation of swarm”).

The swarm evolution algorithm iterates multiple times to find better solutions before the end condition is met. The W₁ represents the best solution found for the BWC problem within the search. The best represents the best value found for the BWC problem within the search, and it is also the objective function value for the best solution of the BWC problem in the algorithm search.

The search space and objective function of algorithm

There is an undirected graph G = (V, E), in which V is the vertex set of graph G and E is the edge set of graph G. Select b vertices and color them black from set V to generate a black vertex set B, |B|= b, and the remaining vertices with gray color to generate a gray vertex set V_grey, V_grey = V \ B. Then, a search space S for the BWC problem of graph G is constructed, which is a binary coloring scheme (B, V_grey) of graph G. That is:

$$S = \{ (B,V_{grey} )|B \subset V,|B| = b,V_{grey} = V\backslash B\}$$

(1)

When a bipartite coloring scheme (B, V_grey) of graph G is given, search for vertices in the set V_grey that comply with the rules (i1) ~ (i3) in Section “Introduction”, color these vertices white, and move these white vertices from the set V_grey to the set W, thereby generating a white vertex set W. Here, W is defined as:

$$W = \{ v|v \in V_{grey} ,\forall w \in B,(v,w) \notin E\}$$

(2)

From the definition, W ⊆ V_grey, thus constructing a solution (B, W) for the BWC problem in graph G.

According to the rule (i4) in Section “Introduction”, the goal of finding the best solution for the BWC problem in graph G is to find the best value from all the solutions (B, W)_j (1 ≤ j ≤ k) that can be obtained by the swarm evolution algorithm. Therefore, the objective function f_max(G) searched by the swarm evolution algorithm is defined as:

$$\left\{ \begin{gathered} f_{*} ((B,W)) = |W| \hfill \\ f_{\max } (G) = \mathop {\max }\limits_{1 \le j \le k} \{ (f_{*} ((B,W)_{j} ))\} \hfill \\ \end{gathered} \right.$$

(3)

In formula 3, it can be seen that k is the number of solutions (B, W) to the BWC problem obtained by the swarm evolution algorithm in S, and f_max(G) is the best value obtained by the swarm evolution algorithm from k solutions.

In Fig. 2, there is an undirected graph G = (V, E), where n =|V|= 8, l =|E|= 9. We first color the vertices in graph G black and gray, thereby constructing a set of black vertices B and a set of gray vertices V_grey. After determining the black vertices, search for vertices that can be colored white from the set of gray vertices V_grey, and construct the set of white vertices W. It is assumed that the number of black vertices is 2 (b = 2), and two schemes for coloring the vertices are shown in (Figs. 3, 4). In Fig. 3, the set B = {v₀, v₇} while the set W = {v₂, v₅}, so that |W|= 2. In Fig. 4, the set B = {v₅, v₆} while the set W = {v₀, v₁, v₂, v₃}, resulting in |W|= 4. After analysis, W = {v₀, v₁, v₂, v₃} has been identified as the optimal solution to the BWC problem in graph G when b = 2. Additionally, the corresponding cardinality of W, denoted as |W|= 4, represents the best value obtained for the BWC problem.

Fig. 2

An undirected graph instance.

Fig. 3

A BWC with |B|= 2 and |W|= 2.

Fig. 4

An optimal BWC with |B|= 2 and |W|= 4.

Construction of probability matrix group

To solve the BWC problem, it is necessary to color each vertex in graph G black or gray, and then search for vertices that can be colored white among the gray ones. Correctly coloring the vertices of graph G is crucial. References^30,31,32 propose heuristic algorithms with a probability learning mechanism to solve graph coloring problems. Therefore, inspired by the ideas of these references, we introduce a probability learning mechanism into the swarm evolution algorithm to solve the BWC problem in graphs.

There is a graph G = (V, E), where |V|= n, and each vertex in graph G is colored black or gray based on the coloring probability value. For each vertex v_i (0 ≤ i < n), we define c_i0 to denote the probability that v_i is black, and c_i1 to denote the probability that v_i is gray, with the constraint that c_i0 + c_i1 = 1.

For the coloring of vertex v_i, if the randomly generated coloring probability value c ≤ c_i0, then vertex v_i is colored black; otherwise, it is colored gray. The coloring probability values of the n vertices are combined to construct a probability matrix A of size n × 2. Therefore, using this probability matrix A, a binary coloring scheme for graph G can be constructed, as follows:

$$A = \left( \begin{gathered} c_{00} ,c_{01} \hfill \\ c_{10} ,c_{11} \hfill \\ ...... \hfill \\ c_{i0} ,c_{i1} \hfill \\ ...... \hfill \\ c_{(n - 1)0} ,c_{(n - 1)1} \hfill \\ \end{gathered} \right)$$

(4)

A probability matrix can construct a bipartite coloring scheme for graph G, and a bipartite coloring scheme can be identified as an individual. In the swarm evolution algorithm, multiple individuals are generated to construct the swarm. Therefore, multiple probability matrices are constructed in this algorithm. When the algorithm generates p individuals, p probability matrices are constructed. Thereby a probability matrix group M is constructed, where M = {A₀, A₁,…, A_j,…, A_p-1}. The jth (0 ≤ j < p) probability matrix A_j in the probability matrix group is used to generate the jth initial individual. To perform initial random coloring on the vertices of graph G, the initial coloring probability value of each vertex in the probability matrix A_j is set to 1/2.

After constructing the probability matrix group, the swarm evolution algorithm continuously modifies the probability matrix values based on changes in individual search results, achieving probability learning of the current search results. In the later phase, evolutionary operation is implemented based on the probability learning results (see Section “Update operation of probability matrix group” and Section “Evolutionary operation of swarm”).

Swarm initialization

There is a graph G = (V, E), where |V|= n and |E|= l. The jth (0 ≤ j < p) individual is generated in the probability matrix group based on the jth probability matrix A_j (0 ≤ j < p). During the process of generating the jth individual, a vertex v_i (0 ≤ i < n) is randomly selected from the vertex set V of graph G. When the randomly generated coloring probability value is less than A_j(c_i0), the vertex v_i is added to set B, indicating that the vertex is colored black. Otherwise, the vertex v_i is added to the set V_grey, indicating that the vertex is colored gray. This vertex selection process is repeated until b black vertices are selected. The remaining vertices of graph G are colored gray and added to the set V_grey, thus constructing the jth individual (B, V_grey)_j (also represented as a binary coloring scheme of graph G ), where |B|= b and V_grey = V \B. Using this method, p initial probability matrices in the probability matrix group are used to generate p initial individuals, constructing a swarm D = {(B, V_grey)_j|0 ≤ j < p, |B|= b, V_grey = V \B}, where |D|= p.

Crossover operation

The crossover operation is a very important operational procedure in swarm evolution algorithm, which enables swarm evolution algorithm to evolve into new search spaces during individual search, in order to find better values. We propose two crossover operation strategies.

The first crossover operation

The first crossover operation is implemented through the following three steps.

First step: Get an individual (B, V_grey), in which |B|= b, V_grey = V \ B. Based on set B and set V_grey, a set Uncontrol is constructed by vertices in set V_grey, which are nonadjacent with arbitrary vertex in set B. That is:

$$Uncontrol = V_{grey} - \{ v|v \in V_{grey} ,\exists u \in B,(v,u) \in E\}$$

(5)

Uncontrol ⊆ V_grey in here.

Second step: A set UnConnectNodes is constructed, whose initial status is: UnConnectNodes = ∅. We first randomly choose a vertex v_i in the set Uncontrol, 0 ≤ i <|Uncontrol|, and then add vertex v_i to the set UnConnectNodes. Next, add all vertices in set V_grey that are not adjacent to vertex v_i to the UnConnectNodes. That is:

$$UnConnectNodes = \{ v_{i} \} \cup \{ w|w \in V_{grey} ,(w,v_{i} ) \notin E\}$$

(6)

UnConnectNodes ⊆ V_grey in here.

Third step: We choose at random a vertex v_j in the set B, 0 ≤ j < b. And we choose successively every vertex u_i from set UnConnectNodes (vertex u_i is also in set V_grey), the values of i ranging successively from 0 to |UnConnectNodes|− 1. Hence, one by one, we exchange vertex v_j in set B with vertex u_i in set V_grey to produce multiple temporary binary coloring schemes (B^', V^'_grey)_i.

When there are as many as x (1 ≤ x ≤|UnConnectNodes|) vertices in the set UnConnectNodes, x temporary binary coloring schemes {(B^', V^'_grey )_i| 0 ≤ i < x, 1 ≤ x ≤|UnConnectNodes|} will be obtained. From x temporary binary coloring schemes, we choose an optimal scheme as the new final binary coloring scheme in this crossover.

The optimal scheme (B^*,V ^*_grey) is the one where the number of vertices in set V ^*_grey , dominated by the vertices in set B^*, is minimized (when vertex v is adjacent to vertex w, we say that vertex v dominates vertex w).

That is:

$$f((S_{a} ,S_{b} )) = |\{ u|u \in S_{b} ,\exists w \in S_{a} ,(u,w) \in E\} |$$

(7)

Here, f((S_a, S_b)) indicates the number of vertices in set S_b that are dominated by vertices in set S_a.

$$\begin{gathered} f((B^{*} ,V_{grey}^{*} )) = \mathop {\min }\limits_{0 \le i < x} (f((B^{'} ,V_{grey}^{'} )_{i} )) \hfill \\ s.t.\left\{ \begin{gathered} 1 \le x \le |UnConnectNodes| \hfill \\ |B^{'} | = b \hfill \\ B^{'} \subseteq V \hfill \\ V_{grey}^{'} = V\backslash B^{'} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(8)

When multiple binary coloring schemes can obtain f((B^*, V ^*_grey)), randomly choose one to make it the new final binary coloring scheme after crossover. The process has a time complexity of O(b × (n − b)²).

In a graph G = (V, E), where V = {v₀, v₁, v₂, v_3, v_4, v_5, v_6, v_7, v_8, v_9, v_10, v₁₁}, suppose the number of black vertices is 4. When we obtain a binary coloring scheme (B, V_grey) as shown in Fig. 5(1), let B = {v₁, v₅, v₇, v₉} and V_grey = {v₀, v₂, v₃, v₄, v₆, v₈, v₁₀, v₁₁}. Then, let Uncontrol = {v₂, v₈, v₁₀, v₁₁}. A new binary coloring scheme needs to be generated. So, if we choose a vertex v₂, at random from the set Uncontrol, then UnConnectNodes = {v₂, v₃, v₁₀, v₁₁}. Choose vertex v₅ at random from set B, and exchange vertex v₅ successively with every vertex of set UnConnectNodes. This process results in 4 temporary binary coloring schemes, denoted as {(B^', V^'_grey)_i|0 ≤ i < 4}. From these 4 temporary schemes, the one satisfying formula 8 is selected as the result of this crossover. In Fig. 5(2), the new final binary coloring scheme (B^*, V ^*_grey) after crossover is shown: B^* = {v₁, v₃, v₇, v₉}, V ^*_grey = {v₀, v₂, v₄, v₅, v₆, v₈, v₁₀, v₁₁}. This is because, after exchanging v₅ with v₃, the vertices in set B^* dominate the vertices in set V ^*_grey to the least extent (here, the vertices in set B^* only dominate the vertices v₀, v₅, v₆ in set V ^*_grey, achieving the smallest number of dominating vertices).

Fig. 5

Crossover process of binary coloring scheme (the first crossover operation).

When vertex v₅ and vertex v₂ are swapped, a temporary binary coloring scheme (B^', V^'_grey)₁ is generated, where B^' = {v₁, v₂, v₇, v₉} and V^'_grey = {v₀, v₃, v₄, v₅, v₆, v_8, v₁₀, v₁₁}. In this scheme, f((B^', V^'_grey)₁) = 6. The white vertex set W = {v₁₀, v₁₁}, and |W|= 2.

When vertex v₅ and vertex v₃ are swapped, a temporary binary coloring scheme (B^', V^'_grey)₂ is generated, where B^' = {v₁, v₃, v₇, v₉} and   V^'_grey = {v₀, v₂, v₄, v₅, v₆, v₈, v₁₀, v₁₁}. In this scheme, f((B^', V^'_grey)₂) = 3. The white vertex set W = {v₂, v₄, v₈, v₁₀, v₁₁}, and |W|= 5. This is the optimal solution chosen after the current crossover operation.

When vertex v₅ and vertex v₁₀ are swapped, a temporary binary coloring scheme (B^', V^'_grey)₃ is generated, where B^' = {v₁, v₇, v₉, v₁₀} and V^'_grey = {v₀, v₂,v₃, v₄, v₅, v₆, v_8, v₁₁}. In this scheme, f((B^', V^'_grey)₃) = 5. The white vertex set W = {v₂, v₈, v₁₁}, and |W|= 3.

When vertex v₅ and vertex v₁₁ are swapped, a temporary binary coloring scheme (B^', V^'_grey)₄ is generated, where B^' = {v₁, v₇, v₉, v₁₁} and V^'_grey = {v₀, v₂, v₃, v₄, v₅, v₆, v_8, v₁₀}. In this scheme, f((B^', V^'_grey)₄) = 6. The white vertex set W = {v₂, v₁₀}, and |W|= 2.

In Fig. 5(1) (before crossover), the binary coloring scheme for graph G is (B, V_grey), where B = {v₁, v₅, v₇, v₉} and V_grey = {v₀, v₂, v₃, v₄, v₆, v₈, v₁₀, v₁₁}. In this scheme, f((B, V_grey)) = 4. The white vertex set W = {v₂, v₈, v₁₀, v₁₁}, and |W|= 4. After the crossover operation, the binary coloring scheme of graph G changes to (B^*, V ^*_grey), where B^* = {v₁, v₃, v₇, v₉} and V ^*_grey = {v₀, v₂, v₄, v₅, v₆, v₈, v₁₀, v₁₁}. In this scheme, f((B^*, V ^*_grey)) = 3. The white vertex set W = {v₂, v₄, v₈, v₁₀, v₁₁}, and |W|= 5. Therefore, after crossover operation, a better solution can be found.

The second crossover operation

We propose a second crossover operation, which is implemented through the following two steps.

Step 1: For an individual (B, V_grey), |B|= m, V_grey = V \ B. Find the degree value of each vertex in the set V_grey.

Step 2: We choose a vertex u_j with the lowest degree value in the set V_grey, where degree[u_j] =  $\mathop {\min }\limits_{{0 \le i < |V_{grey} |}} (degree[u_{i} ])$. That is:

$$\left\{ \begin{gathered} {degree}[u_{i} ] = |\{ (u_{i} ,w)|u_{i} \in V_{grey} ,\exists w \in V_{grey} ,(u_{i} ,w) \in E\} | \hfill \\ {degree}[u_{j} ] = \mathop {\min }\limits_{{0 \le i < |V_{grey} |}} ({degree}[u_{i} ]) \hfill \\ 0 \le i < |V_{grey} |,0 \le j < |V_{grey} | \hfill \\ \end{gathered} \right.$$

(9)

If there are multiple vertices with the lowest degree value, randomly choose one vertex u_j, from among these vertices. Randomly choose a vertex v_j from set B and proceed to exchange two vertices v_j and u_j between set B and V_grey. Specifically, B^* ← B\{v_j} ∪ {u_j}, V ^*_grey ← V_grey\{u_j} ∪ {v_j}. Thus, a new binary coloring scheme (B^*, V ^*_grey) is generated through the crossover operation. The process has a time complexity of O(n × (n − b)).

In a graph G = (V, E), where V = {v₀, v₁, v₂, v_3, v_4, v_5, v_6, v_7, v_8, v_9, v_10, v₁₁}, suppose the number of black vertices is 4. When we obtain a binary coloring scheme (B, V_grey), as shown in Fig. 6(1), let B = {v₁, v₅, v₇, v₉} and V_grey = {v₀, v₂, v₃, v₄, v₆, v₈, v₁₀, v₁₁}. In this scheme, f((B, V_grey)) = 4. The white vertex set W = {v₂, v₈, v₁₀, v₁₁}, and |W|= 4. According to formula 9, the degree values of vertices v₀, v₂, v₃, v₄, v₆, v₈, v₁₀, v₁₁ (in the set V_grey) are 2, 4, 0, 4, 1, 2, 1, 2, respectively. Among these, vertex v₃ has the smallest degree value. We randomly select vertex v₁ from set B and definitely select vertex v₃ from set V_grey to perform a crossover operation, generating a new binary coloring scheme (B^*, V ^*_grey) , as shown in Fig. 6(2), where B^* = { v₃, v₅, v₇, v₉} and V ^*_grey = {v₀, v₁, v₂, v₄, v₆, v₈, v₁₀, v₁₁}. In this coloring scheme, f((B^*, V ^*_grey)) = 2. The white vertex set W = {v₁, v₂, v₆, v₈, v₁₀, v₁₁}, and |W|= 6. Therefore, after crossover operation, a better solution can be found.

Fig. 6

Crossover process of binary coloring scheme (the second crossover operation).

Improved simulated annealing search

A crucial process in swarm evolution algorithm is to search for each individual in swarm D to find the best solution to the BWC problem. Simulated annealing algorithm is used to search for each individual in the swarm. Due to the phenomenon of repeated searches during the process of searching for individuals in the simulated annealing algorithm, the search efficiency is reduced. In order to improve the search efficiency of the simulated annealing algorithm, we added a tabu search strategy to the simulated annealing algorithm, thus using an improved simulated annealing algorithm to search for all individuals in swarm D.

The improved simulated annealing algorithm is summarized in Improved_SA_Search (Algorithm 2). In Algorithm 2, an initial temperature T₀ and a cooling coefficient α are determined. Temperature cooling is achieved by using T = α × T, where α ∈ (0, 1). When the temperature T gradually cools to T_e (the end temperature), i.e., T ≤ T_e, or after meeting the end condition, the search of algorithm 2 is terminated.

For a given jth individual D_i in swarm D (here, (B, V_grey)_j represents the jth individual D_i), the vertices in set B are black vertices. According to the given set B, the strategy for Algorithm 2 to search for white vertices is to search in set V_grey all the vertices that are not adjacent to any vertex in set B, and the vertex set obtained is the white vertex set W. In order to maximize the number of vertices in the set of white vertices, we should minimize the number of vertices in V_grey that are dominated by set B.

During each iteration of Algorithm 2, the value of the currently searched individual D_j is first obtained from swarm D, that is, (B, V_grey)_temp ← (B, V_grey)_j. Then, the crossover operation method described in Section “Crossover operation” is used to perform crossover on (B, V_grey)_temp, generating a new binary coloring scheme (B^', V^'_grey)_temp. If f((B^', V^'_grey)_temp) = 0, it indicates that the maximum value of W is found, which is W = V^'_grey, and the current best solution (B^', V^'_grey )_temp and the value of |V^'_grey| are stored in S_best and W_best, respectively. If f((B^', V^'_grey )_temp) < f((B, V_grey) _temp), the new binary coloring scheme (B^',V^'_grey)_j is accepted, that is (B,V_grey)_temp ← (B^', V^'_grey ) _temp, and the current best solution (B^', V^'_grey )_temp and the value of |V^'_grey|- f((B^', V^'_grey)_temp) are stored in S_best and W_best, respectively. Otherwise, a new binary coloring scheme (B^', V^'_grey)_temp is accepted based on some probability. Here, the objective function f is defined in formula 7.

When the end condition set by Algorithm 2 is met, S_best and W_best are the best solution and value for Algorithm 2 search. If Algorithm 2 can find new and better values, it will accept the current better scheme and serve as the new state Y_j (i.e., (Bⁿ, Vⁿ_grey)_j) of individual D_j after evolution, that is: (Bⁿ, Vⁿ_grey)_j ← (B,V_grey)_temp (see code line 13 or 19); otherwise, Y_j is the same as D_j, meaning that the second line of code in Algorithm 2 stores the initial state of Y_j as the current new individual, that is: (Bⁿ, Vⁿ_grey)_j ← (B, V_grey)_j.

Algorithm 2

Improved_SA_Search (G, D_j, Tabulist, T₀, α, T_e, L).

To find white vertices, individual (B^', V^'_grey)_temp can be searched using (Algorithm 2). We use a tabu list in Algorithm 2 to implement a tabu search strategy. The tabu list is implemented using a two-dimensional data structure called Tabulist, with a length set to L. This list is used to store the current iteration values ies of Algorithm 2’s run. If (ies − Tabulist[v][w]) < L, then, based on the crossover operation, vertex v and vertex w are reselected for exchange, thereby obtaining a non-tabu binary coloring scheme (B^', V^'_grey)_temp. Otherwise, the ies value is stored in Tabulist.

Perturbation operation

To increase the probability of finding better values in the swarm evolutionary algorithm, we have added the perturbation operation. The perturbation operation is summarized in Perturbation_operation (Algorithm 3). We introduce a startup parameter d for Algorithm 3, and when the swarm evolution algorithm runs d iterations per interval, we start the perturbation operation (Algorithm 3).

There are two methods for perturbation operation. One method involves randomly selecting an individual Y_j from set Y to obtain a binary coloring scheme (Bⁿ, Vⁿ_grey)_j. Then, a vertex is randomly chosen from set Bⁿ and another from set Vⁿ_grey to exchange, generating a new binary coloring scheme (B^n', V ^n'_grey)_j. Algorithm 2 is employed to search for (B^n', V ^n'_grey)_j, and if a better solution is found, the better solution is obtained, and it is adopted as the evolving new individual Y_j, that is, Y_j ← temp (line 7 in Algorithm 3). The second method follows a similar procedure, with the exception that two vertices are randomly selected from each of set Bⁿ and set Vⁿ_grey to exchange, resulting in a new binary coloring scheme (B^n'', V^n''_grey)_j. Algorithm 2 is again utilized to explore (B^n'', V^n''_grey)_j, and if a better solution is found, it becomes the new Y_j, namely, Y_j ← temp (see code line 14 in Algorithm 3). Both perturbation operation methods are then randomly chosen.

Algorithm 3

Perturbation_operation(Y, d₁, d, best).

Update operation of probability matrix group

From Sections “Construction of probability matrix group” and “Swarm initialization”, it can be seen that the binary coloring scheme (B, V_grey) corresponding to the individual in the swarm is generated based on the vertex coloring probability matrix. From Sections “Crossover operation” to “Improved simulated annealing search”, it can be seen that in the binary coloring scheme (B, V_grey), by selecting black vertices from set B and gray vertices from set V_grey for exchange purposes, the black vertices are moved from set B to set V_grey, and the gray vertices are moved from set V_grey to set B, generating new search spaces to find better solutions for the BWC problem. When a better solution is found, the swarm evolution algorithm will accept the binary coloring scheme (B^', V^'_grey) corresponding to the better solution as the currently found solution. To record the changes in vertex movement in set B and set V_grey, we need to modify the vertex coloring probability value based on the initial and changed coloring states of the vertices, thereby updating the vertex coloring probability matrix A and realizing probability learning of vertex coloring changes. Based on the learning results of vertex coloring changes, we provide a basis for later swarm evolution operations.

For the update process of a single probability matrix A_j, we compared the binary coloring scheme (B, V_grey)_j of the jth individual D_j in swarm D and the binary coloring scheme (Bⁿ, Vⁿ_grey)_j of the jth individual Y_j in swarm Y and updated the vertex coloring probability matrix in four different cases.

The first case: When the black vertex v_i (0 ≤ i < n) in set B is in set Bⁿ, it indicates that the color of the vertex has not changed. We reward the probability of the vertex being black, where the reward factor is set to σ₁ (0 < σ₁ < 1), and synchronously update the probability value of this vertex being gray. That is:

$$\left\{ \begin{gathered} c_{i0} = \sigma_{1} + (1 - \sigma_{1} ) \times c_{i0} \hfill \\ c_{i1} = (1 - \sigma_{1} ) \times c_{i1} \hfill \\ 0.15 \le c_{i0} \le 0.85 \hfill \\ 0.15 \le c_{i1} \le 0.85 \hfill \\ 0 < \sigma_{1} < 1 \hfill \\ v_{i} \in B,v_{i} \in B^{n} ,0 \le i < n \hfill \\ \end{gathered} \right.$$

(10)

After changing c_i0 and c_i1 according to formula 10, when c_i0 > 0.85, we set c_i0 to 0.85; when c_i0 < 0.15, we set c_i0 to 0.15; when c_i1 > 0.85, we set c_i1 to 0.85; when c_i1 < 0.15, we set c_i1 to 0.15. (Here, to prevent the corrected vertex coloring probability values c_i0 and c_i1 from being excessively large or small, we directly set the lower bound of the probability values to 0.15 and the upper bound to 0.85.)

The second case: When the black vertex v_i (0 ≤ i < n) in set B is in set Vⁿ_grey, it means that the vertex has changed from originally black to gray. We penalize the probability of the vertex being black and compensate for the probability of the vertex being gray. The penalty factor is set to σ₂ (0 < σ₂ < 1), the compensation factor is set to σ₃ (0 < σ₃ < 1). That is:

$$\left\{ \begin{gathered} c_{i0} = (1 - \sigma_{2} ) \times (1 - \sigma_{3} ) \times c_{i0} \hfill \\ c_{i1} = \sigma_{3} + (1 - \sigma_{3} ) \times \sigma_{2} + (1 - \sigma_{3} ) \times (1 - \sigma_{2} ) \times c_{i1} \hfill \\ 0.15 \le c_{i0} \le 0.85 \hfill \\ 0.15 \le c_{i1} \le 0.85 \hfill \\ 0 < \sigma_{2} < 1 \hfill \\ 0 < \sigma_{3} < 1 \hfill \\ v_{i} \in B,v_{i} \in V_{grey}^{n} ,0 \le i < n \hfill \\ \end{gathered} \right.$$

(11)

After changing c_i0 and c_i1 according to formula 11, when c_i0 > 0.85, we set c_i0 to 0.85; when c_i0 < 0.15, we set c_i0 to 0.15; when c_i1 > 0.85, we set c_i1 to 0.85; when c_i1 < 0.15, we set c_i1 to 0.15. (Here, the rules for setting the upper and lower bounds of c_i0 and c_i1 values are as described above.)

The third case: When the gray vertex v_i (0 ≤ i < n) in the set V_grey is in the set Vⁿ_grey, it indicates that the color of the vertex has not changed. We reward the probability of the vertex being gray, where the reward factor is set to σ₁ (0 < σ₁ < 1), and synchronously update the probability value of the vertex being black. That is:

$$\left\{ \begin{gathered} c_{i1} = \sigma_{1} + (1 - \sigma_{1} ) \times c_{i1} \hfill \\ c_{i0} = (1 - \sigma_{1} ) \times c_{i0} \hfill \\ 0.15 \le c_{i1} \le 0.85 \hfill \\ 0.15 \le c_{i0} \le 0.85 \hfill \\ 0 < \sigma_{1} < 1 \hfill \\ v_{i} \in V_{grey} ,v_{i} \in V_{grey}^{n} ,0 \le i < n \hfill \\ \end{gathered} \right.$$

(12)

After changing c_i0 and c_i1 according to formula 12, when c_i0 > 0.85, we set c_i0 to 0.85; when c_i0 < 0.15, we set c_i0 to 0.15; when c_i1 > 0.85, we set c_i1 to 0.85; when c_i1 < 0.15, we set c_i1 to 0.15. (Here, the rules for setting the upper and lower bounds of c_i0 and c_i1 values are as described above.)

The fourth case: When the gray vertex v_i (0 ≤ i < n) in the set V_grey is in the set Bⁿ, it indicates that the vertex has changed from gray to black. We penalize the probability of the vertex being gray and compensate for the probability of the vertex being black. Here, the penalty factor is set to σ₂ (0 < σ₂ < 1), the compensation factor is set to σ₃ (0 < σ₃ < 1). That is:

$$\left\{ \begin{gathered} c_{i1} = (1 - \sigma_{2} ) \times (1 - \sigma_{3} ) \times c_{i1} \hfill \\ c_{i0} = \sigma_{3} + (1 - \sigma_{3} ) \times \sigma_{2} + (1 - \sigma_{3} ) \times (1 - \sigma_{2} ) \times c_{i0} \hfill \\ 0.15 \le c_{i1} \le 0.85 \hfill \\ 0.15 \le c_{i0} \le 0.85 \hfill \\ 0 < \sigma_{2} < 1 \hfill \\ 0 < \sigma_{3} < 1 \hfill \\ v_{i} \in V_{grey} ,v_{i} \in B^{n} ,0 \le i < n \hfill \\ \end{gathered} \right.$$

(13)

After changing c_i0 and c_i1 according to formula 13, when c_i0 > 0.85, we set c_i0 to 0.85; when c_i0 < 0.15, we set c_i0 to 0.15; when c_i1 > 0.85, we set c_i1 to 0.85; when c_i1 < 0.15, we set c_i1 to 0.15. (Here, the rules for setting the upper and lower bounds of c_i0 and c_i1 values are as described above.)

Using the single probability matrix update strategy described above, we sequentially update each probability matrix in the probability matrix group. The update operation of the probability matrix group is summarized in Probability_matrices_updating (Algorithm 4).

Algorithm 4

Probability_matrices_updating (M, Y, D, p, σ₁, σ₂, σ₃).

In the swarm evolution algorithm, each individual corresponds to a probability matrix. Therefore, in Algorithm 4, the probability matrix is modified for each individual to realize the update operation of the probability matrix group. The process has a worst time complexity of O(p × (n − 1)²).

Evolutionary operation of swarm

The evolutionary operation of a swarm is an important process in the swarm evolution algorithm, which involves implementing evolutionary operation on individuals in the swarm to generate new and better individuals, thereby increasing the probability of the swarm evolution algorithm finding better solutions on new individuals. According to the updated probability matrix group M, the jth individual (B, V_grey)_j (0 ≤ j < p) in swarm D is subjected to evolutionary operation.

The evolutionary operation process comprises two steps. In the first step, vertex v_i is sequentially selected from set (B)_j, where i ranges from 0 to b-1. If the randomly generated coloring probability value is less than A_j (c_i0), v_i is colored black and added to set B_temp. Once this step is completed, if |B_temp|= b, it indicates that the black vertex set B_temp has been fully constructed. Otherwise, if |B_temp|< b, the second step is followed. In the second step, vertex w_k is randomly selected from set (V_grey)_j, where k ranges from 0 to |(V_grey)_j|-1. If the randomly generated coloring probability value is less than A_j (c_k0), w_k is colored black and added to set B_temp until |B_temp|= b. After evolution, a new individual (B_temp, V_{grey_temp})_j is generated. Here, B_temp represents the set of black vertices and V_{grey_temp} represents the set of gray vertices, with V_{grey_temp} = V \B_temp. Thus, the new individual is accepted, namely, (B, V_grey)_j ← (B_temp, V_{grey_temp})_j. According to the evolutionary operation strategy, each individual in swarm D undergoes evolutionary operation, realizing the evolution of the swarm. This process involves swarm evolution and has a time complexity of O(p × n × b).

The evolutionary operation is summarized in Swarm_recombination (Algorithm 5).

Algorithm 5

Swarm_recombination (D, M).

Stochastic convergence analysis of the swarm evolution algorithm

Crossover operation is a key operational step in swarm evolution algorithm to find better solutions. When the algorithm searches for an individual, a new binary coloring scheme is generated by applying crossover operation to the individual to find better solutions.

Case 1: In Fig. 5(1) in Section “The first crossover operation”, the white vertex set W₁ = {v₂, v₈, v₁₀, v₁₁}, |W₁|= 4. We randomly select vertex v₅ from set B and apply the first crossover operation strategy to choose vertex v₃ from set V_grey, generating a new binary shading scheme (B^*, V ^*_grey), where B^* = {v₁, v₃, v₇, v₉} and V ^*_grey = {v₀, v₂, v₄, v₅, v₆, v₈, v₁₀, v₁₁}. The white vertex set W₂ = { v₂, v₄, v₈, v₁₀, v₁₁}, and |W₂|= 5.

Case 2: In Fig. 6(1) in Section “The second crossover operation”, the white vertex set W₁ = {v₂, v₈, v₁₀, v₁₁}, |W₁|= 4. We randomly select vertex v₁ from set B and apply the second crossover operation strategy to choose vertex v₃ from set V_grey, generating a new binary shading scheme (B^*, V ^*_grey), where B^* = {v₃, v₅, v₇, v₉} and V ^*_grey = {v₀, v₁, v₂, v₄, v₆, v₈, v₁₀, v₁₁}. The white vertex set W₂ = {v₁, v₂, v₆, v₈, v₁₀, v₁₁}, and |W₂|= 6.

Therefore, during the algorithm iteration process, crossover operations are performed based on probability to select vertices such that |W₁| <|W₂|< … <|W_t|< …, thereby finding better solutions. In addition, after testing the graphs “home.col” and “le450_25d.col”, we find that the algorithm’s search results can remain stable at the best solution after a certain number of iterations.

In the swarm evolution algorithm, the improved simulated annealing search operation described in Section “Improved simulated annealing search” is used to search for better solutions for individuals. In this operation, we use the tabu table Tabulist to avoid the search process getting stuck in local optima, unable to find global better solutions. If (ies − Tabulist[v][w]) < L, reselect the non-tabu vertices that the algorithm can find better global solutions. The code for using the tabu table can be found on lines 7 and 8 of (Algorithm 2).

In the improved simulated annealing search operation, the number of operation iterations is controlled by the temperature cooling method T = α × T to reduce the temperature. At the same time, specific end condition is set (to find the optimal solution or reach the end time of search consumption) to control the number of iterations of the operation. When T ≤ T_e or a specific termination condition is met, the iterative run of the improved simulated annealing search operation is terminated. The code to end the operation is shown in line 25 of (Algorithm 2). In addition, in the swarm evolution algorithm, a specific end condition is still set (the end condition is set to find the optimal solution, or the search time reaches the end time) to control the number of iterations of the algorithm. The code for ending the algorithm iteration is shown in line 16 of (Algorithm 1).

A variable neighborhood search algorithm for BWC

Variable neighborhood search algorithm is a classic heuristic algorithm that mainly explores a new solution space by exchanging vertices in the search space to find the best global solution to the problem.

For a graph G = (V, E), V will be divided into two sets B and S₂, in which set B is set of black vertices, and |B|= b, S₂ = V \B. The initial status is b black vertices are generated at random to construct set B, the remaining vertices in the graph G construct set S₂. Here, b is the determined number of black vertices in BWC problem. The searched white vertices are in set S₂, and the white vertices are constructed into the white vertices set W. The initial number of vertices in set W is |W₀| =|{v|v ∈ S₂, ∀w ∈ B, (v,w)$\notin$ E}|.

In the algorithm, set B and S₂ are designated as the neighborhood region, and we search for white vertices in set S₂. If all the vertices in set S₂ are white, it indicates that the optimal solution for the set of white vertices has been found, and the algorithm execution will be terminated. If the number of white vertices is greater than what was previously searched, it indicates that a better solution has been found, and the new, better solution is accepted. A new neighborhood is then generated, and the search is repeated until the algorithm reaches its end condition.

The strategies adopted in the dynamic change of the neighborhood are mainly exchanging multiple vertices in neighborhood. The method of generating a neighborhood is to exchange k vertices between set B and set S₂. Here, N_k (k = 1, 2,…, k_max) is defined as pre-generated finite neighborhood, and k is the number of vertices exchanged in neighborhood region. N_k ((B, S₂)) is defined as the neighborhood region obtained when (B, S₂) has exchanged k vertices. For positive integer k (k < min(|B|, |S₂|)), B_k(B) is obtained when set B has exchanged k vertices, and B_k(S₂) is obtained when set S₂ has exchanged k vertices. Thus, when the neighborhood (B, S₂) changes to the new neighborhood (B^', S^'₂), it is defined as:

$$N_{k} ((B,S_{2} )) = \{ (B \cup X_{2} \backslash X_{1} ,S_{2} \cup X_{1} \backslash X_{2} )|X_{1} \in B_{k} (B),X_{2} \in B_{k} (S_{2} )\}$$

(14)

Formula 14 shows that variable neighborhood search algorithm is to exchange at random k vertices between set B and set S₂ to generate a new neighborhood (B^', S^'₂).

In the algorithm, employing neighborhood state accepting condition, the new neighborhood (B^', S^'₂) is accepted, that is: (B, S₂) ← (B^', S^'₂). The condition for accepting the state is that there are more white vertices searched in set S^'₂. The process of neighborhood change has a time complexity of O(b × (n − b)).

The procedure of finding the best solution by the algorithm is shown in formula 15, which is:

$$\left\{ \begin{gathered} |W_{0} | = |\{ v|v \in S_{2} ,\forall w \in B,(v,w) \notin E\} | \hfill \\ |W_{i} | = \mathop {\max }\limits_{i} (|\{ v|v \in S_{2}^{'} ,\forall w \in B^{'} ,(v,w) \notin E\} |,|W_{i - 1} |) \hfill \\ W_{best \, } = W_{i} \hfill \\ \end{gathered} \right.$$

(15)

Here, i represents the number of iterations of the algorithm.

The algorithm is summarized in VNS (Algorithm 6).

Algorithm 6

VNS(G, k_max, b).

In the algorithm, k_max is used to control the number of vertices exchanged during algorithm operation. The W₂ represents the best solution found for the BWC problem within the search. The best represents the best value found for the BWC problem within the search, and it is also the objective function value for the best solution of the BWC problem in the algorithm search.

A simulated annealing algorithm for BWC

The simulated annealing algorithm is a classic heuristic approach that primarily employs the principles of solid-state annealing, incorporating probabilistic jumps to identify the global optimal solution within the search space. The core strategy involves gradually decreasing a “temperature” parameter while iteratively executing the algorithm to explore the best solution to the problem.

In the algorithm, through the gradual change of state, the final result is obtained probabilistically. Given a graph G = (V, E), the vertex set V is divided into two sets, B and S₂, where |B|= b and S₂ = V \ B. The initial states of sets B and S₂ are generated, and new set states (B^', S^'₂) are continuously generated based on the current states of B and S₂. The algorithm aims to find a better solution for W (where W is the set of white vertices) in the new set states until the termination condition of the algorithm is met.

The initial state process to generate set B and S₂ is: first, b black vertices are selected at random in V to construct set B, then construct set S₂ = V \ B, thus set B and S₂ are generated, in which |B|= b.

We consider the current sets B and S₂ to be the current set state (B, S₂). We randomly select t vertices, where 1 ≤ t ≤ 3, from both sets B and S₂ to exchange, thereby obtaining a new set state (B^', S^'₂). If g(B^', S^'₂) < g(B, S₂), the new set state (B^', S^'₂) will be accepted, or be accepted with a certain probability, i.e., (B, S₂) ← (B^', S^'₂). Otherwise, the new state may be rejected, and the current state (B, S₂) remains unchanged. If g(B^', S^'₂) = 0, it indicates that set S^'₂ may be an optimal solution for set W, and therefore the algorithm execution will be terminated. The function g(U₁, U₂) is defined as follows:

$$g(U_{1} ,U_{2} ) = |\{ v|v \in U_{2} ,\exists w \in U_{1} ,(w,v) \in E\} |$$

(16)

Function g(U₁, U₂) denotes the number of vertices in set U₂ that are adjacent to the vertices in set U₁. The process of changing the set state operates with a time complexity of O(b × (n − b)).

Based on the initial temperature T₀, end temperature T_e, and cooling coefficient α (0 < α < 1), the algorithm generates a new state (B^', S^'₂) after the cooling process, where T represents the current temperature and is updated according to the formula T = α × T. This new state is then used to search set W, until the temperature T is lowered to T_e or the end condition of the algorithm is met.

The algorithm is summarized in SA (Algorithm 7).

Algorithm 7

SA(G, T₀, T_e, α, b).

The W₃ represents the best solution found for the BWC problem within the search. The best represents the best value found for the BWC problem within the search, and it is also the objective function value for the best solution of the BWC problem in the algorithm search.

The greedy algorithm for BWC

Greedy algorithm is a classic heuristic algorithm that iteratively runs with the locally optimal operation at each step, searching for the best solution in the search space.

For a graph G = (V, E), V is a set containing n vertices, and E is a set containing l edges. To solve the BWC problem using a greedy algorithm, the key lies in how to select black vertices to add to set B. Initially, the vertex set V is divided into two sets B and S₂, with S₂ = V, B = ∅. Set B represents the set of black vertices. Utilizing specific strategies, choose a black vertex from set S₂, add it to set B, and subsequently remove it from set S₂. Repeat this addition phase until |B|= b. Then, based on the currently determined sets B and S₂, search for the white vertices in set S₂, thereby constructing the white vertex set W. There are two strategies to choose black vertices, hence two kinds of greedy algorithms are realized.

The first greedy algorithm

In this greedy algorithm, first, from set S₂, choose the vertex v_i (0 ≤ i <|S₂|) with the minimum degree value. If there are multiple vertices with the minimum degree value, randomly select one and delete it from set S₂, adding it as a black vertex to set B. Second, following a defined vertex selection method, choose a black vertex w from set S₂, delete it from set S₂, and add it to set B. Third, continue performing the second step until the number of black vertices in set B reaches b. Fourth, search for the white vertex set W in set S₂ based on the currently obtained sets B and S₂. If the number of vertices in set W is greater than the number of currently determined white vertices, it indicates that a better solution has been found and is accepted as the new set W. Fifth, initialize sets B and S₂, and then repeat the implementation from the first step until the end condition of the algorithm is met. Once the end condition is met, the algorithm will be terminated.

The method for selecting black vertices is to select vertex w from set S₂ and add it to set B, so that the number of vertices in set B that can dominate the vertices in set S₂ is minimized (if there are multiple vertices with the minimum value, then choose one at random). The objective function of vertex w is defined as:

$$f(B \cup \{ w\} ) = \mathop {\min }\limits_{{0 \le j < |S_{2} |}} (|\{ v|v \in S_{2} \backslash \{ w_{j} \} ,\exists u \in B \cup \{ w_{j} \} ,(u,v) \in E\} |)$$

(17)

In the algorithm, if B = ∅, the process of selecting a black vertex from the set S₂ has a time complexity of O(n²). Conversely, if B ≠ ∅, the process of selecting black vertices from the set S₂ has a worst time complexity of O(b × (n − 1)²).

The first algorithm is summarized in Greedy_One (Algorithm 8).

Algorithm 8

Greedy_One(G, B, S₂, b).

The W₄ represents the best solution found for the BWC problem within the search. The best represents the best value found for the BWC problem within the search, and it is also the objective function value for the best solution of the BWC problem in the algorithm search.

The second greedy algorithm

In this greedy algorithm, the method of selecting black vertices is to select vertex w from set S₂, so that the sum of the greedy degrees of vertex w in set S₂ is minimized (If there are multiple vertices with the minimum value, then choose one at random). The objective function f ^'(B ∪ {w}) for selecting vertex w is:

$D(v_{i} ) = |\left\{ {e|\exists e \in S_{2} ,v_{i} \in S_{2} ,(v_{i} ,e) \in E} \right\}|$,

$$f^{'} \left( {B \cup \{ w\} } \right) = \mathop {\min }\limits_{\begin{subarray}{l} h = \{ v_{i} |\exists v_{i} \in S_{2} ,w_{j} \in S_{2} ,(v_{i} ,w_{j} ) \in E\} \\ 0 \le i < |S_{2} | \\ 0 \le j < |S_{2} | \end{subarray} } \left( {\sum\limits_{{v_{i} \in h}} {\left( {1/\left( {1 + D\left( {v_{i} } \right)} \right)} \right)} } \right)$$

(18)

Here, v_i is the vertex to which vertex w_j is adjacent in set S₂. The greedy degree of v_i, denoted as D(v_i), represents the number of vertices in set S₂ that are adjacent to v_i. In the algorithm, the process of selecting black vertices from set S₂ has a worst time complexity of O(n³).

The second algorithm is summarized in Greedy_Two (Algorithm 9).

Algorithm 9

Greedy_Two(G, B, S₂, b).

The W₅ represents the best solution found for the BWC problem within the search. The best represents the best value found for the BWC problem within the search, and it is also the objective function value for the best solution of the BWC problem in the algorithm search.

Experimental results

We implemented the swarm evolution algorithm, variable neighborhood search algorithm, greedy algorithm, and simulated annealing algorithm using C+  + . All algorithms were executed on a platform equipped with an Intel Pentium G630 (R) processor running at 2.70 GHz, 8 GB of memory, and Windows 7 (64 bits) operating system. All algorithms were tested using Cayley graphs, random graphs, semi-random graphs, and benchmark DIMACS graphs. We compared the results of the swarm evolution algorithm, variable neighborhood search algorithm, greedy algorithm, and simulated annealing algorithm, and conducted corresponding data analysis. In addition, we also compared the results of the swarm evolution algorithm with algorithms proposed in existing literature, such as tabu search algorithms⁵, simulated annealing with configuration checking³, and local search algorithm⁴.

In the experiment, the swarm evolution algorithm has two versions, namely, “Swarm-E-1” and “Swarm-E-2”. “Swarm-E-1” represents the swarm evolution algorithm implemented using the first crossover operation. “Swarm-E-2” represents the swarm evolution algorithm implemented using the second crossover operation. “VNS1” represents the variable neighborhood search algorithm (k_max = 1). “VNS2” represents the variable neighborhood search algorithm (k_max = 2).

In the paper, we used four types of graphs to test all algorithms.

The first type of graphs is Cayley graphs, which are further divided into “kings” graphs (Cartesian strong product, C_m ${ \boxtimes }$ C_n) and “rooks” graphs (Cartesian product, K_m□K_n). The generation methods of these graphs were proposed in⁵.

The second type of graphs is random graphs (G_m,p), and the generation method of these graphs was proposed in⁵.

The third type of graphs is semi-random graphs (SR_m,B,W), and the generation method of these graphs was proposed in⁵, where the generation probability of semi-random graphs is 1/3.

The fourth type of graphs is benchmark DIMACS graphs, which were proposed in³².

Setting of algorithm parameter

The swarm evolution algorithm has multiple control parameters, including the number of individuals of swarm p, tabu table length L, perturbation operation startup parameter d, initial temperature T₀, temperature cooling coefficient α, end temperature T_e, reward factor σ₁, penalty factor σ₂, and compensation factor σ₃. In order to conduct later testing of the swarm evolution algorithm, first set the parameter values of p, L, d, T₀, α, and T_e to 5, 10, 4, 1000, 0.9997, and 0.0001, respectively. On this basis, we conducted experiments to investigate the impact of parameter settings such as reward factor σ₁, penalty factor σ₂, and compensation factor σ₃ on the search capability of the algorithm. We first set the parameter values of σ₁, σ₂, and σ₃ to 18 groups, which are {σ₁ = 0.1, σ₂ = 0.1, σ₃ = 0.1}, {σ₁ = 0.1, σ₂ = 0.1, σ₃ = 0.2}, {σ₁ = 0.1, σ₂ = 0.1, σ₃ = 0.3}, {σ₁ = 0.1, σ₂ = 0.2, σ₃ = 0.1}, {σ₁ = 0.1, σ₂ = 0.2, σ₃ = 0.2}, {σ₁ = 0.1, σ₂ = 0.2, σ₃ = 0.3}, {σ₁ = 0.1, σ₂ = 0.3, σ₃ = 0.1}, {σ₁ = 0.1, σ₂ = 0.3, σ₃ = 0.2}, {σ₁ = 0.1, σ₂ = 0.3, σ₃ = 0.3}, {σ₁ = 0.2, σ₂ = 0.1, σ₃ = 0.1}, {σ₁ = 0.2, σ₂ = 0.1, σ₃ = 0.2}, {σ₁ = 0.2, σ₂ = 0.1, σ₃ = 0.3}, {σ₁ = 0.2, σ₂ = 0.2, σ₃ = 0.1}, {σ₁ = 0.2, σ₂ = 0.2, σ₃ = 0.2}, {σ₁ = 0.2, σ₂ = 0.2, σ₃ = 0.3}, {σ₁ = 0.2, σ₂ = 0.3, σ₃ = 0.1}, {σ₁ = 0.2, σ₂ = 0.3, σ₃ = 0.2}, {σ₁ = 0.2, σ₂ = 0.3, σ₃ = 0.3}. Using the “Swarm-E-1” algorithm, we conducted tests on multiple graphs, including “C₅₁ ${ \boxtimes }$ C₅₀”, “K₇₅□K₇₀”, “inithx.i.1.col”, “fpsol2.i.1.col”, “inithx.i.2.col”, “le450_5b.col”, “le450_15c.col”, “le450_25a.col”, “school1.col”, and “zeroin.i.3.col”. Each graph was tested 10 times, with each test lasting 30 min, and the test results are summarized in (Table 1).

Table 1 Experiments with parameters σ₁, σ₂ and σ₃.

In Table 1, the “id” column represents the sequence number of the set parameter values, while the “parameters” column displays the specific values of σ₁, σ₂, and σ₃. The “b” column stands for the number of black vertices in the graphs, which is fixed at 20 for all test graphs. The “Best” column indicates the best value among the test results for each graph, and the “Avg” column provides the average of the test results for each graph. In Table 1, we use bold italics to indicate the best values of the algorithm, as well as the best average values.

To determine the optimal values of parameters σ₁, σ₂, and σ₃, we employed the optimal vector method proposed in³⁹ to analyze the sample data presented in (Table 1). The core principle of this method involves first constructing a vector group that comprises multiple vectors from the sample data. These vectors are created for each column or row (selected based on the problem description and test results). Subsequently, the maximum and minimum values of these vectors are normalized, and the lengths of each vector are calculated. The column or row number corresponding to the vector with the maximum length value represents the optimal parameter value for obtaining the sample value. Based on this concept, we implemented the method in two steps.

Step 1: Based on the test results in “parameters” (presented in Table 1), construct a column vector incorporating the “Best” results of all graphs in each row. Subsequently, assemble a vector group VT_Best comprised of 18 such column vectors, where the column numbers correspond to the sequence number “id” of the parameter values.

$$VT_{Best} = \left( {\begin{array}{*{20}c} {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} & {2508} \\ {4620} & {4620} & {4620} & {4620} & {4615} & {4615} & {4620} & {4620} & {4620} & {4615} & {4620} & {4615} & {4550} & {4620} & {4554} & {4620} & {4620} & {4620} \\ {476} & {476} & {476} & {476} & {476} & {476} & {434} & {476} & {476} & {476} & {476} & {476} & {476} & {476} & {476} & {476} & {476} & {476} \\ {844} & {844} & {844} & {844} & {804} & {844} & {844} & {844} & {844} & {799} & {844} & {844} & {815} & {801} & {844} & {844} & {814} & {814} \\ {625} & {625} & {625} & {625} & {625} & {625} & {606} & {625} & {625} & {625} & {625} & {625} & {625} & {625} & {625} & {625} & {603} & {625} \\ {281} & {284} & {284} & {281} & {284} & {281} & {281} & {284} & {284} & {284} & {284} & {284} & {281} & {281} & {281} & {284} & {281} & {284} \\ {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} & {152} \\ {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} \\ {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} & {354} \\ {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {186} \\ \end{array} } \right)$$

Then perform maximum and minimum normalization on VT_best to obtain the vector group VT ^'_Best.

$$VT_{Best}^{'} = \left( {\begin{array}{*{20}c} {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} \\ {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} \\ {1.0} & {1.0} & {1.0} & {1.0} & {0.93} & {0.93} & {1.0} & {1.0} & {1.0} & {0.93} & {1.0} & {0.93} & {0.0} & {1.0} & {0.06} & {1.0} & {1.0} & {1.0} \\ {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {0.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} \\ {1.0} & {1.0} & {1.0} & {1.0} & {1.11} & {1.0} & {1.0} & {1.0} & {1.0} & {0.0} & {1.0} & {1.0} & {0.36} & {0.04} & {1.0} & {1.0} & {0.33} & {0.33} \\ {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {0.14} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {0.0} & {1.0} \\ {0.0} & {1.0} & {1.0} & {0.0} & {1.0} & {0.0} & {0.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {0.0} & {0.0} & {0.0} & {1.0} & {0.0} & {1.0} \\ {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} \\ {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} \\ {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} \\ \end{array} } \right)$$

Finally, based on the optimal vector method, a set of data set VT_{Best_result} is obtained, namely, VT_{Best_result} = {3.00, 3.16, 3.16, 3.00, 2.98, 2.98, 2.65, 3.16, 3.16, 2.98, 3.16, 3.14, 2.67, 2.83, 2.83, 3.16, 2.67, 3.02}.

Step 2: Based on the test results in “parameters” (data in Table 1), construct the “Avg” results of all graphs in each row into a column vector, and thus construct a vector group VT_Avg composed of 18 column vectors (whose column numbers correspond to the sequence number “id” of the parameter values).

$$VT_{Avg} = \left( {\begin{array}{*{20}c} {2506} & {2504} & {2506} & {2506} & {2506} & {2508} & {2505} & {2505} & {2505} & {2504} & {2506} & {2506} & {2506} & {2507} & {2503} & {2508} & {2507} & {2505} \\ {4544} & {4569} & {4569} & {4570} & {4570} & {4562} & {4557} & {4571} & {4570} & {4555} & {4597} & {4536} & {4542} & {4556} & {4543} & {4563} & {4556} & {4569} \\ {421} & {422} & {432} & {412} & {434} & {416} & {411} & {409} & {411} & {414} & {426} & {439} & {417} & {416} & {440} & {415} & {411} & {427} \\ {808} & {801} & {807} & {813} & {795} & {801} & {810} & {807} & {807} & {793} & {813} & {800} & {800} & {797} & {808} & {822} & {799} & {800} \\ {598} & {605} & {606} & {602} & {600} & {600} & {595} & {599} & {601} & {605} & {602} & {610} & {599} & {600} & {599} & {603} & {596} & {606} \\ {277} & {277} & {278} & {274} & {279} & {275} & {277} & {278} & {275} & {278} & {275} & {276} & {274} & {275} & {277} & {280} & {276} & {277} \\ {149} & {149} & {150} & {151} & {150} & {150} & {149} & {151} & {150} & {149} & {150} & {148} & {150} & {150} & {150} & {150} & {151} & {149} \\ {384} & {384} & {384} & {383} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} & {384} \\ {294} & {303} & {293} & {322} & {302} & {284} & {303} & {283} & {303} & {264} & {304} & {284} & {274} & {264} & {284} & {304} & {303} & {314} \\ {186} & {186} & {183} & {180} & {182} & {186} & {186} & {186} & {183} & {186} & {186} & {186} & {186} & {186} & {186} & {186} & {183} & {183} \\ \end{array} } \right)$$

Then perform maximum and minimum normalization on VT_Avg to obtain the vector group VT ^'_Avg.

$VT_{Avg}^{'} = \left( {\begin{array}{*{20}c} {0.60} & {0.20} & {0.60} & {0.60} & {0.60} & {1.00} & {0.40} & {0.40} & {0.40} & {0.20} & {0.60} & {0.60} & {0.60} & {0.80} & {0.00} & {1.0} & {0.80} & {0.40} \\ {0.13} & {0.54} & {0.54} & {0.56} & {0.56} & {0.43} & {0.34} & {0.57} & {0.56} & {0.31} & {1.0} & {0.00} & {0.10} & {0.33} & {0.11} & {0.44} & {0.33} & {0.54} \\ {0.39} & {0.42} & {0.74} & {0.10} & {0.81} & {0.23} & {0.06} & {0.00} & {0.06} & {0.16} & {0.55} & {0.97} & {0.26} & {0.23} & {1.0} & {0.19} & {0.06} & {0.58} \\ {0.52} & {0.28} & {0.48} & {0.69} & {0.07} & {0.28} & {0.59} & {0.48} & {0.48} & {0.00} & {0.69} & {0.24} & {0.24} & {0.14} & {0.52} & {1.0} & {0.21} & {0.24} \\ {0.20} & {0.67} & {0.73} & {0.47} & {0.33} & {0.33} & {0.00} & {0.27} & {0.40} & {0.67} & {0.47} & {1.0} & {0.27} & {0.33} & {0.27} & {0.53} & {0.07} & {0.73} \\ {0.50} & {0.50} & {0.67} & {0.00} & {0.83} & {0.17} & {0.50} & {0.67} & {0.17} & {0.67} & {0.17} & {0.33} & {0.00} & {0.17} & {0.50} & {1.0} & {0.33} & {0.50} \\ {0.33} & {0.33} & {0.67} & {1.00} & {0.67} & {0.67} & {0.33} & {1.0} & {0.67} & {0.33} & {0.67} & {0.00} & {0.67} & {0.67} & {0.67} & {0.67} & {1.0} & {0.33} \\ {1.0} & {1.0} & {1.0} & {0.00} & {1.00} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} \\ {0.52} & {0.67} & {0.50} & {1.00} & {0.66} & {0.34} & {0.67} & {0.33} & {0.67} & {0.00} & {0.69} & {0.34} & {0.17} & {0.00} & {0.34} & {0.69} & {0.67} & {0.86} \\ {1.0} & {1.0} & {0.50} & {0.00} & {0.33} & {1.0} & {1.0} & {1.0} & {0.50} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {1.0} & {0.50} & {0.50} \\ \end{array} } \right)$

Finally, based on the optimal vector method, a set of data set VT_{Avg_result} is obtained, namely, VT_{Avg_result} = {1.86, 1.96, 2.09, 1.84, 2.02, 2.00, 1.85, 2.08, 1.74, 1.78, 2.30, 2.14, 1.74, 1.84, 2.04, 2.54, 1.90, 1.93}.

Step 3: Set the weight of the data in VT_{Best_result} to 0.5, set the weight of the data in VT_{Avg_result} to 0.5, and sum the corresponding components of the two sets weighted by their respective weights to obtain the data set VT_result, namely, VT_result = {2.43, 2.56, 2.63, 2.42, 2.5, 2.49, 2.25, 2.62, 2.45, 2.38, 2.73, 2.64, 2.21, 2.34, 2.44, 2.85, 2.29, 2.48}. That is:

VT_result = {vt_i| vt_i = vtb_i × 0.5 + vta_i × 0.5, vtb_i ∈ VT_{Best_result}, vta_i ∈ VT_{Avg_result}, 0 < i <|VT_{Best_result} |}.

Step 4: Select the maximum value of 2.85 from VT_result, which corresponds to the 16th sample column vector.

Therefore, according to the decision rule of the optimal vector method, we determine the parameter values σ₁ = 0.2, σ₂ = 0.3, and σ₃ = 0.1, which correspond to the 16th sample column vector (id = 16), as the parameter values for the swarm evolution algorithm.

Finally, the parameter values of the swarm evolution algorithm are determined as shown in (Table 2). In addition, the parameters T₀, α, and T_e in SA algorithm are set to 1000, 0.9997, and 0.0001, respectively. We conducted algorithm testing using these parameter values in the later stage.

Table 2 Parameter setting of the swarm evolution algorithm.

Test results on swarm evolution algorithm and other algorithms

We first evaluated the performance characteristics of various algorithms, including swarm evolution algorithms (Swarm-E-1 and Swarm-E-2), variable neighborhood search algorithms (VNS1 and VNS2), the simulated annealing algorithm (SA), and greedy algorithms (Greedy_One and Greedy_Two). Testing was conducted on graphs belonging to different categories, such as “C₃₁ ${ \boxtimes }$ C₃₀ (b = 150)”, “C₅₁ ${ \boxtimes }$ C₅₀ (b = 250)”, “K₁₅□K₁₀ (b = 40)”, “homer.col (b = 25)”, “le450_15d.col (b = 25)”, “le450_25d.col (b = 25)”, “G_500,0.1 (b = 40)”. The running curves of these algorithms are presented in (Fig. 7). In Fig. 7, the X-axis represents the data collection time for the algorithms running on each graph, with results collected every 10 s of running time. The Y-axis depicts the results obtained by the algorithms at the corresponding collection run time for each graph. Analysis of the curves reveals that under graphs (b) and (c), the swarm evolution algorithms exhibit significantly superior search capabilities compared to other algorithms, leading to better results. Under graphs (a), (e), (f), and (g), the swarm evolution algorithms perform slightly better than the SA algorithm, achieving superior results compared to SA, but still outperforming other algorithms. Finally, under graph (d), the swarm evolution algorithms demonstrate marginally improved search capabilities compared to other algorithms.

Fig. 7

The running curves of algorithms.

To compare the differences in search results among the swarm evolution algorithm, simulated annealing algorithm, variable neighborhood search algorithm, and the greedy algorithm, we conducted four groups of comparative tests, with each graph tested 20 times for 30 min each.

In the first group of tests, multiple graphs are used for testing, such as Cayley graphs, random graphs, and semi-random graphs. The test results of the algorithms are summarized in (Table 3). In Table 3, “Instance” represents the graph for the test, “|V|” represents the number of vertices in this graph, “b” represents the number of black vertices in the graph, “best” represents the best value of the number of white vertices in the algorithm search, and “avg” represents the average value of the number of white vertices in the algorithm search, “time (s)” represents the average time (in seconds) consumed by the algorithm to obtain the best value.

Table 3 The test results of the algorithms on Cayley graphs, random graphs, and semi-random graphs.

In Table 3, we use bold italics to indicate the best values of the algorithms, as well as the minimum time values spent on obtaining these best values. The swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of all graphs. The SA algorithm can obtain the best values of 16 graphs (approximately 62% of the total number of graphs). The Greedy_One algorithm can obtain the best values of 9 graphs (approximately 35% of the total number of graphs). The Greedy_Two algorithm can obtain the best values of 3 graphs (approximately 12% of the total number of graphs). The VNS1 and VNS2 algorithms can respectively find the best value for one graph (approximately 4% of the total number of graphs). In addition, the swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of 17 graphs (approximately 65% of the total number of graphs) by consuming the minimum time value. The SA algorithm can find the best values of 4 graphs by consuming the minimum time value (approximately 15% of the total number of graphs). The Greedy_One algorithm can find the best values of 3 graphs by consuming the minimum time value (approximately 12% of the total number of graphs). The Greedy_Two algorithm can find the best values of two graphs by consuming the minimum time value (approximately 8% of the total number of graphs). Although VNS1 and VNS2 algorithms can find the best value of one graph, they consume more time. From this, our swarm evolution algorithms have the best search performance in the first group of tests.

The second group of test graphs used large “kings” graphs (graphs with many vertices). The test results are summarized in (Table 4).

Table 4 The test results of the algorithms on large “kings” graphs.

In Table 4, we use bold italics to indicate the best values of the algorithms. The swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of 13 graphs (approximately 87% of the total number of graphs). The Greedy_One algorithm can find the best value for two graph (approximately 13% of the total number of graphs). Other algorithms can’t find the best values for the graphs. From this, it can be seen that our swarm evolution algorithms have the best search performance in the second group of tests.

The third group of test graphs used large “rooks” graphs (graphs with many vertices). The test results are summarized in (Table 5).

Table 5 The test results of the algorithms on large “rooks” graphs.

In Table 5, we use bold italics to indicate the best values of the algorithms, as well as the minimum time values spent on obtaining these best values. The swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of 12 graphs (approximately 80% of the total number of graphs). The SA algorithm can find the best values of 9 graphs (approximately 60% of the total number of graphs). Other algorithms can not find the best values of these graphs. In addition, the swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of 10 graphs (approximately 67% of the total number of graphs) by consuming the minimum time values. The SA algorithm can find the best values of 5 graphs by consuming the minimum time values (approximately 33% of the total number of graphs). From this, our swarm evolution algorithms have the best search performance in the third group of tests.

The fourth group of test graphs used benchmark DIMACS graphs. The test results are summarized in (Table 6).

Table 6 The test results of the algorithms on benchmark DIMACS graphs.

In Table 6, we use bold italics to indicate the best values of the algorithms, as well as the minimum time values spent on obtaining these best values. The swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can obtain the best values of 59 graphs (approximately 98% of the total number of graphs). The SA algorithm can obtain the best values of 58 graphs (approximately 97% of the total number of graphs). The Greedy_One algorithm can obtain the best values of 15 graphs (approximately 25% of the total number of graphs). The Greedy_Two algorithm can obtain the best values of 18 graphs (approximately 30% of the total number of graphs). The VNS1 algorithm can obtain the best values of 26 graphs (approximately 43% of the total number of graphs). The VNS2 algorithm can obtain the best values of 28 graphs (approximately 47% of the total number of graphs).

In addition, the swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of 47 graphs (approximately 78% of the total number of graphs) by consuming the minimum time values. The SA algorithm can find the best values of 17 graphs by consuming the minimum time values (approximately 28% of the total number of graphs). The Greedy_One algorithm can find the best values of 3 graphs by consuming the minimum time values (approximately 5% of the total number of graphs). The Greedy_Two algorithm can find the best values of 3 graphs by consuming the minimum time values (approximately 5% of the total number of graphs). The VNS1 algorithm can find the best values of 10 graphs by consuming the minimum time values (approximately 17% of the total number of graphs). The VNS2 algorithm can find the best values of 10 graphs by consuming the minimum time values (approximately 17% of the total number of graphs). It should be noted that when the average time consumed by the algorithm search in Table 6 is less than 0.01, we think that the time consumption value is roughly the same. From this, our swarm evolution algorithms have the best search performance in the fourth group of tests.

Comparison of swarm evolution algorithm with other existing algorithms

In⁵, algorithms were proposed to solve the BWC problem, such as tabu algorithms (In this literature, these algorithm names were respectively “R-tabu” and “SG-tabu”), integer linear programming (In this literature, the algorithm was named “ILP”), randomized restart hill climbing (In this literature, the algorithm was named “RRHC”), greedy randomized adaptive search procedure (In this literature, the algorithm was named “GRASP”), and simulated annealing (In this literature, the algorithm was named “SA”). In³, simulated annealing with configuration checking (In this literature, the algorithm was named “SACC”) was proposed to solve the BWC problem. In⁴, a local search algorithm based on tabu table (In this literature, the algorithm was named “BTLSBWC”) was proposed to solve the BWC problem. Firstly, we compared the test results of the swarm evolution algorithms with the algorithms proposed in⁵, and the comparison results are summarized in (Table 7).

Table 7 The comparison results for swarm evolution algorithm, R-tabu, SG-tabu, ILP, SA, RRHC, and GRASP.

In Table 7, we use bold italics to indicate the best values of the algorithms. The tabu algorithms, RRHC algorithm, and GRASP algorithm can find the best values for graph “G_200,0.1(b = 10)”. The tabu algorithms can find the best values for graph “G_200,0.1(b = 40)”. Our swarm evolution algorithms can find the best values for graphs “C₂₁ ${ \boxtimes }$ C₂₀(b = 100)”, “G_500,0.1(b = 20)”, and “G_500,0.1(b = 40)”. In addition, our swarm evolution algorithms and tabu algorithms can find the best values of the same graphs and can find more of the best values of graphs than multiple algorithms such as ILP, SA (algorithm proposed in⁵), RRHC, and GRASP. From this, our swarm evolution algorithms can improve the known results of three graphs in⁵.

In³, the hardware testing environment for the SACC algorithm was PC (Intel CPU 2.7 GHz), and the algorithm was coded in C +  + . Each graph was tested 20 times, each time for 30 min. We implemented the testing of the swarm evolution algorithms based on this testing environment and compared the test results of the swarm evolution algorithms and the SACC algorithm, as shown in (Table 8).

Table 8 Comparison results for swarm evolution algorithms and SACC.

In Table 8, we use bold italics to indicate the best values of the algorithms, as well as the minimum time values spent on obtaining these best values. Our swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of 11 graphs (approximately 92% of the total number of graphs). The SACC algorithm can find the best values of 10 graphs (approximately 83% of the total number of graphs). In addition, the swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the best values of 7 graphs by consuming the minimum time values (approximately 58% of the total number of graphs). The SACC algorithm can find the best values of 5 graphs by consuming the minimum time values (approximately 42% of the total number of graphs). (Here is an explanation: in³, the graph marked by the author is K₁₅□K₁₁, but according to the content description of the reference, the graph should be K₁₅□K₁₀.) From this, our swarm evolution algorithms have better search ability than SACC algorithm.

We implemented the testing of the swarm evolution algorithms in the BTLSBWC algorithm testing environment described in⁴ (25 tests per graph, each lasting 20 min) and compared the test results of the swarm evolution algorithms with the BTLSBWC algorithm. The comparison results are summarized in (Table 9).

Table 9 The comparison results for swarm evolution algorithms and BTLSBWC.

In Table 9, we use bold italics to indicate the best values of the algorithms. Our swarm evolution algorithms (Swarm-E-1 and Swarm-E-2) can find the same best values as the BTLSBWC algorithm in multiple graphs, such as “C₁₅ ${ \boxtimes }$ C₁₁(b = 20)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 25)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 28)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 70)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 99)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 100)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 120)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 125)”, “C₁₅ ${ \boxtimes }$ C₁₁(b = 141)”, “C₂₁ ${ \boxtimes }$ C₂₀(b = 80)”, and “C₂₁ ${ \boxtimes }$ C₂₀(b = 100)”. In other graphs, the swarm evolution algorithms can find better results than the BTLSBWC algorithm. From this, our swarm evolution algorithms have better search ability than the BTLSBWC algorithm and can improve the 22 existing results for graphs “le450_25a.col” and “le450_15c.col” in⁴.

Conclusion

In the paper, we present a swarm evolution algorithm (Swarm_BWC) to solve the black and white coloring problem. This algorithm adopts an improved simulated annealing search process, combined with a perturbation operation, two crossover operations and a group evolution operation with probability learning mechanisms, to enhance the algorithm’s search ability.

We analyzed the performance of swarm evolution algorithm on 14 Cayley graphs (divided into 46 instances for testing), 2 random graphs (divided into 4 instances for testing), 6 semi-random graphs (divided into 6 instances for testing), and 60 benchmark DIMACS graphs (divided into 60 instances for testing). Compared with variable neighborhood search algorithm, greedy algorithm and simulated annealing algorithm, the swarm evolution algorithm found the best solutions for 109 test instances, with the highest number of best solutions found, so our algorithm exhibited stronger capabilities.

Furthermore, we studied the local search algorithm, simulated annealing algorithm with configuration checking and tabu search algorithm presented in the references. Through comparative experiments on Cayley graphs between swarm evolution algorithms and simulated annealing with configuration checks, it can be found that our algorithm has stronger search ability than simulated annealing with configuration checks in terms of the number of best solutions found and the time consumed in finding the best solutions. We conducted additional experimental comparisons among our swarm evolution algorithm, local search algorithm, and tabu search algorithm, revealing that our algorithm had improved the known best results for 25 graphs.

Finally, we demonstrated that the Swarm_BWC method can significantly improve other classical heuristic methods for solving BWC problem.