Enhancing breast cancer diagnosis through machine learning algorithms

Abstract

Among the most important health concerns in the world, and the number one cause of death in women, is breast cancer. Bearing in mind that there are more than 100 types of cancer, each presenting different symptoms, its early detection is indeed a big challenge. The prevalence of breast cancer indicates the prudent need for effective diagnostic and prognostic approaches. From 2016 to 2020, 19.6 deaths per 100, 000 women occurred annually due to breast cancer—a factor indicating the importance of early treatments. Machine Learning has become important for the improvement of early diagnosis and prognosis that may have the potential to reduce mortality rates. Some considerable volume of research work has been carried out on the use of Machine Learning algorithms for accurate diagnosis of breast cancer. In this research has done extensive algorithm evaluation like SVM, DT, RF, Logistic regression, KNN and ANN using datasets CDP Breast Cancer. The important performance indicators observed for each of these algorithms included accuracy, precision, recall, sensitivity, and specificity. These findings are an important step forward in the application of Machine Learning to improve diagnostic accuracy, thus enabling early detection and mitigating the major consequences of breast cancer on global health.

Introduction

Breast cancer is known as a significant global health concern, Millions of women are affected by it every year^1,2. Reducing mortality and increasing treatment efficacy depend on prompt diagnosis and precise risk assessment. The identification of breast cancer biomarkers by innovative techniques with high sensitivity, accuracy, and quicker treatment potential has been made possible by recent developments in medical technology and nanotechnology, notably in biosensors and the use of nanoparticles for therapy. On the other hand, the emergence of machine learning (ML) methods is also a strong and powerful tool for analyzing and extracting biological data. All these methods help in the early detection of cancer cells^3,4,5,6.

The integration of CDP biosensors and immunohistochemically data provides a new approach to the analysis of breast cancer biomarkers at the molecular level. The CDP Nano sensor whose mechanism of action is based on electrochemical reactions with high sensitivity and selectivity allows the identification of biomolecules, this device detects the existence or absence of cancer cells by measuring the amount of RAS in the cancer environment. Also, immunohistochemistry provides valuable histopathological information that enables the quantification of protein expression patterns in breast tissue samples^7,8,9.

In this paper, we examine the risk of breast cancer recurrence by combining CDP nano sensor data and immunohistochemistry with machine learning methods that include supervised learning. We discuss the principles of operation and mechanism of CDP nano sensors and immunohistochemical assays. We also examine their effectiveness in breast cancer research and clinical practice (Fig. 1).

Fig. 1

A comprehensive view of the CDP Nano biosensor and the overall diagnostic mechanism of the device⁵.

In addition, we review various machine learning algorithms, including supervised and unsupervised learning approaches, to analyze and interpret data generated by CDP nano sensors and immunohistochemical assays. These ML methods identify biomarkers relevant to disease progression, making it possible with high accuracy and reliability.

By examining recent studies, we clarify the application of machine learning methods in the diagnosis and classification of breast cancer cells. We also discuss the challenges and limitations associated with this method, such as data integration and model validation, and present appropriate solutions to these problems.

Finally, our study aims to provide insights to researchers and clinicians, about the potential of combining CDP biosensors, immunohistochemistry, and machine learning methods to advance breast cancer diagnosis, risk assessment, and personalized treatment strategies. By leveraging the strengths of these interdisciplinary approaches, we aim to increase our understanding of breast cancer cell pathogenesis and ultimately enhance the rate of treatment of this dangerous disease. We have illustrated the research pathway (Fig. 2).

Fig. 2

Visualizing the workflow of the proposed model.

Literature review

To diagnose breast cancer, many studies have been conducted using various methods and machine learning models to evaluate breast cancer tumors and cells. Efforts have been made to identify and introduce the best diagnostic method.

Tseng et al. in a test conducted between 2003 and 2016 on 302 patients, used the Her2 and CEA factors in blood in four methods: Support Vector Machine (SVM), Random Forest (RF), Logistic Regression (LR), and Naive Bayes (NB). The RF model was chosen as the optimal method for diagnosis¹⁰. Nindrea et al. employed the Wisconsin breast cancer dataset and utilized four models: SVM, DT, NB, and K-NN, achieving accuracies of 97.13, 95.13, 95.99, and 95.27%, respectively. This indicated that the SVM model had the highest detection¹¹. Zhou et al., employed a Convolutional Neural Network (CNN) method to predict and identify invasive ductal carcinoma in breast cancer images, achieving an approximate accuracy of 88%¹². Chaurasia, V. and Pal, S. The goal of this study was to increase the accuracy of breast cancer prediction by applying the feature selection approach and comparing different machine learning algorithms. On the Wisconsin Diagnostic Breast Cancer (WDBC) dataset, classification accuracy was enhanced to more than 90% and, in some cases, 99% by reducing features and using hybrid models such as Random Forest and Voting Classifier. Removing unnecessary features has improved accuracy and decreased overfitting¹³. Delen et al. used breast cancer patient records in a different experiment, where they were pre-classified into two groups: “survived” (93, 273) and “not survived” (109, 659). The survivorship prediction yielded results with an accuracy of approximately 93%¹⁴. Omondiagbe et al. merged the dimensionality reduction approach (LDA) with three popular machine learning techniques—SVM, ANN, and NB—and it was found that the degree of accuracy increased when these models were combined with LDA. This study also employed Wisconsin data for analysis. Model time SVM-LDA is employed at 98.82, while the SVM model alone is 96.47%¹⁵. Aruna et al. used decision trees, support vector machines, RBF networks and naïve Bayes to classify a Wisconsin breast cancer dataset. With a score of 96.99%, they were able to use support vector machines (SVM) to achieve the maximum accuracy¹⁶. Md. Murad Hossin et al. compared several machine learning techniques for detecting breast cancer in their study. Eight distinct machine learning methods were used to evaluate the WBCDc dataset: LR, DT, RF, KNN, SVM, AB, GB, and GNB. A comprehensive analysis of a number of outputs, including the confusion matrix, accuracy, sensitivity, precision, and AUC, was used to identify the best machine learning strategy. After careful analysis, the best models were found to be LR and SVM, which achieved exceptional testing accuracy of 99.12%, sensitivity of 97.73%, and specificity of 100%¹⁷. Fatih Muhammed and Ak performed a research that compared techniques for detecting and diagnosing breast cancer utilizing data visualization and machine learning. They utilized Dr. William H. Walberg’s breast tumor dataset and implemented multiple methodologies including Logistic Regression (LR), Nearest Neighbour (NN), Support Vector Machine (SVM), Naive Bayes, Decision Tree, Random Forest (RF), and Convolutional Forest. Logistic Regression using all features had the highest performance, attaining an accuracy of 98.1%. Their findings underscored the efficacy of data visualization and machine learning in cancer detection, facilitating future developments in this field¹⁸. Chaurasia, V. and Pal, S. aimed to develop a data mining-based diagnostic system for breast cancer diagnosis and survival prediction. They used three algorithms: RepTree, RBF Network, and Simple Logistic. The Simple Logistic classifier achieved the greatest accuracy of 74.47% in just 0.62 s. Chi-square, Info Gain, and Gain Ratio tests were employed to identify key parameters influencing breast cancer survival, including the degree of malignancy, number of affected nodes, and tumor size¹⁹. Kourou et al. analyzed the categorization of cancer patients into low-risk and high-risk groups. Their analysis suggests that combining multidimensional and heterogeneous data with different feature selection and classification methods might provide significant insights for cancer research. They utilized techniques like Artificial Neural Networks (ANN), Bayesian Networks (BNs), Support Vector Machines (SVM), and Decision Trees (DT) to create a model for evaluating cancer risks and predicting patient outcomes²⁰. Xiaomin zhou et al. displayed in a review article CNN algorithm was employed to detect and diagnose invasive ductal carcinoma in breast cancer images, with an accuracy of approximately 88%. This review emphasized that deep ANN approaches are useful not only in breast histopathological image analysis but also in other fields of microscopic image analysis, including cervical histopathology analysis¹². Chadaga et al. (2023) employed stacked models in conjunction with feature selection methods like Mutual Information and Harris Hawks Optimization to predict the effectiveness of hematopoietic stem cell transplantation (HSCT) in children. The STACKC model, which combines boosting algorithms with base learners, was used in this study. The Borderline-SMOTE technique was used to balance the data. With an accuracy of 89%, an AUC of 91%, and an average precision (AP) score of 92%, the outcomes were outstanding²¹. Goenka et al., developed a 3D convolutional neural network designed to analyze preprocessed T1-weighted MRI scans. By applying data augmentation techniques like slight rotations and scaling, they significantly boosted the model’s ability to generalize. Impressively, their model reached 100% accuracy in distinguishing Alzheimer’s patients from healthy individuals. This result highlights the power of using full-brain volumetric data, rather than relying on individual slices, and marks a meaningful step forward in building reliable, automated tools for Alzheimer’s detection²². Susmita et al. was presented a sophisticated framework employing machine learning and several explainable artificial intelligence (XAI) approaches. The study highlighted important risk variables including age, body mass index, and hypertension and reached a 96% prediction accuracy by combining stacked ensemble models with interpretable techniques like SHAP, LIME, and QLattice. The study’s conclusions provide important information for creating clinical decision-support systems for the early identification and prevention of stroke²³. Motarjem et al. analyzed 25 blood markers at the time of admission were utilized to predict the length of hospital stay and risk of mortality in patients with COVID-19. In addition to machine learning models like Random Forest and GLM, the Accelerated Failure Model (AFT) with log-normal distribution was employed. With a mean square error (MSE) of 9.53, the GLM model outperformed the others, demonstrating the critical importance of variables like calcium, platelets, age above 50, and underlying illnesses²⁴.

Methodology

Data collection

This analytical investigation utilized data sourced from the Motamed Cancer Institute, a clinical research center specializing in breast cancer in Tehran, Iran.

Breast cancer dataset: Initially, we gathered 300 records from individuals who had been referred to the research center in the last 3 years (2021–2024). Each record contained information on 6 features (see Table 1), all marked according to the device amp, and sorted into two groups indicating the presence, or absence of breast cancer. Out of these records, 75% were found to have cancer cells. It’s important to note that without knowing the specific model and dataset used, it’s difficult to say for certain what these features represent. However, in the context of breast cancer, these features could potentially represent:

• HER2 receptor status: HER2 stands for Human epidermal growth factor receptor 2—a protein that plays an active role in the growth and division of a certain kind of breast cancer. As it is a receptor, it is a player in signal transduction that influences key processes to facilitate growth and division. HER2 is a protein that, under some conditions, expresses in larger numbers or in amplified layers, leading unconditionally to further growth and cell division—or, in other words, promoting the process of initiation and progression of breast cancer. The HER2-positive breast cancers make up a proportion of 15% to 20% among all the cases of breast cancers and are relatively more aggressive in their nature of growth and spreading than the HER2-negative ones. Up until then, such cancers had a very bad prognosis, which radically changed with the advent of targeted therapy.

Table 1 Her2 scoring system.

Although the prognosis radically changed over the past 20 years for the better in cases of HER2-positive breast cancers, the development of more precisely targeted forms of therapeutics has otherwise significantly changed the prognosis. HER2-positive breast cancers are more aggressive, but the drugs used to treat them—trastuzumab (Herceptin), pertuzumab (Perjeta), ado-trastuzumab emtansine (Kadcyla), and lapatinib (Tykerb)—are extremely effective. Adjuvant trastuzumab regimens have been found to reduce the risk of recurrence and improve overall survival to such an extent that the prognosis of patients with HER2+ breast cancer is, in certain settings, now at least as good as—even superior to—that of patients whose disease lacks HER2 overexpression. These targeted therapies for HER2, in addition to chemotherapy and, on occasion, with radiation and surgery, are transforming one of the formerly quite ominous variants of breast cancer into a rather more manageable type under today’s paradigms of treatment²⁵. The status of HER2 in the data that we used was classified into four levels, namely 0, 1, 2, and 3. This is based upon the output recorded in the pathobiology test of the patients. This shows the frequency of each groups (Fig. 3).

• Ki-67 proliferation rate: Ki67 is considered both a predictive marker of the response to therapy and a prognostic predictor in breast cancer. The Ki67 index, representing the percentage of tumor cells positive for Ki67, represents a very important prognostic indicator of the nature and prognosis of tumors. While high levels of Ki67 usually denote higher tumor grades, features of more aggressive tumors, and worse prognosis, less aggressive tumors and better treatment outcomes are generally associated with low levels. The predictive value of Ki67, therefore, helps clinicians in treatment direction toward a more successful course. Given their penchant for fast growth, high-Ki67 tumors would logically be more susceptible to certain chemotherapies, while their low-Ki67 counterparts could be more responsive to hormone therapies or other targeted treatments²⁶.

• Estrogen Receptors (ERs): Most instances of hormone receptor-positive breast cancer demonstrate just how vital estrogen receptors, or ERs, are to the development of the disease in question. As a result of the manifestation of estrogen receptors on the cell membranes, ER-positive breast tumors have the ability to respond to estrogens—the naturally occurring hormone responsible for growth and proliferation. The state of the disease sees estrogen binding with its receptor in ER-positive breast cancer, turning on the signaling pathways that promote tumor growth.

Fig. 3

Proportion of Each Category in Her2.

Curiously, the ER status represents an important prognostic factor: generally, the prognosis for patients with ER-positive tumors is better compared to those with ER-negative tumors. The promising prognosis is explained by factors including increased sensitivity of these types of tumors to hormone treatments, reduced tumor grade, and slower growth. Second, ER status provides treatment options by serving as a predictive indicator of therapy response. For the ER-positive tumors, hormonal therapies employ either aromatase inhibitors or tamoxifen to alter estrogen signaling or to lower estrogen levels. Individuals with ER-positive tumors therefore tend to benefit from these drugs, which effectively prevent the tumor from growing and reduce the possibility of its recurrence²⁷.

• Progesterone receptor: Expression of the progesterone receptor is one major biomarker in the context of breast cancer, especially of the hormone receptor-positive types. PR, just like its counterpart—the estrogen receptor—plays a very important role in the response to hormones of breast cancer. Progesterone receptors are expressed by PR-positive breast malignancies to respond well to progesterone signaling in a manner quite similar to ER-positive tumors. Similar to estrogen, in the presence of its receptor, progesterone can stimulate cell growth and proliferation of PR-positive breast cancer cells.

In this respect, PR status is also a predictive factor in the case of breast cancer, although possibly less directly than ER. Generally, when tumors are both PR and ER positive, prognosis is better than for those cancers that are ER positive but PR negative. PR positive status generally correlates with lower tumor grade, slower tumor growth, as well as a greater likelihood of response to hormone therapy. PR status also indicates tumor responsiveness to hormone therapy in a similar manner as ER. The PR-positive tumors will most likely benefit from treatments such as tamoxifen or aromatase inhibitors, which exert their action on the tumor through a more hormonal route. When a tumor cell is PR-positive, it means that progesterone signaling is important in its proliferation—that is, it becomes all the more susceptible to treatments that disturb this very signaling pathway.

In summary, PR makes additional contributions to hormone responsiveness, determination of prognosis, and prediction of response to therapy in hormone receptor-positive breast cancer. Assessment, in addition to ER status, allows the best choices in therapy and optimal outcomes for patients with breast cancer^28,29.The frequency and distribution of each of these variables are displayed in the violin plot (Fig. 4).

• Neoadjuvant therapy: Whether or not the patient received chemotherapy before surgery, in our data, almost half of the patients had a history of chemotherapy (Fig. 5).

Fig. 4

Violin Plot of numerical feature by CDPQ (A) PR. (B) ER. (C) Ki67.

Fig. 5

Count of Each Category in Neoadjuant.

Summarizing and analyzing data characteristics using descriptive statistics:

Descriptive statistics refers to a collection of instruments and methods employed in statistics to characterize, quantify, and analyze the attributes of a data set. These features facilitate our understanding of the data and enable us to identify the significant patterns (Tables 2 and 3).

Table 2 Type of variable.

Table 3 Descriptive statistics.

It is also displayed to provide a better understanding of the distribution of each variable (Fig. 6).

Fig. 6

Density Plot for numerical features.

Preprocessing

In the first stage of data preparation, triple-negative cancers were removed. Then, based on the CDP number, a new column was formed in such a way that the positive CDP number one (indicating the presence of cancer cells) and the negative number zero (indicating the absence of cancer cells) were considered. It should be mentioned that based on the performance of the device and the explanations of its makers, numbers above 370 are considered positive numbers.

Mahalanobis distance

The distance between a point and a set is estimated by the Mahalanobis distance, an important term in statistics and data science. In this method, the distance is recognized with the use of a covariance matrix of the data. The formula to determine the Mahalanobis distance is as shown below:

$$\text{D }(\text{x},\text{ y}) = \sqrt{{\left(x-y\right)}^{T}{s}^{-1}\left(x-y\right)}$$

Using this formula, the desired ‘x’ point along with its distance from the set is computed. The ‘S’ is the covariance matrix of the data, and ‘y’ is the data set. Mahalanobis distance is the measure of the distance of a data point from the set of data points, one of the most important concepts in statistics and data science. This distance takes into account the dispersion of the data. In data science, Mahalanobis distance is very important for finding and eliminating outlier data. One can tell whether a data point deviates from the normal pattern of the data by calculating this interval for every data point. A data point could be labeled as an outlier and excluded from the model if its distance from the center of the data distribution exceeds the maximum allowable threshold. Thus, Mahalanobis distance could be used to find an outlier³⁰.

PCA

Principal Component Analysis is a statistical procedure in dimensionality reduction that involves an orthogonal transformation of a dataset—probably with correlated variables—into a set of uncorrelated variables known as the principal components. The main intention of PCA, therefore, is to retain those features that explain the maximum variance within the data so that the data can be analyzed based on reduced dimensionality quite easily and interpretation is enhanced. First, standardization is carried out on the data matrix X, consisting of n observations and p variables. It is a very crucial step since the use of variables with different scales in one analysis ensures each variable is given equal weight. A standardized data matrix Z is obtained by centering each variable—that is, subtracting the mean—and scaling, that is, dividing by the standard deviation:

$$\text{Zij}=\frac{{x}_{ij}-{\mu }_{j}}{{\sigma }_{j}}$$

where μ_j is the mean of the j-th variable and σ_j is its standard deviation.

Next, the covariance matrix C of the standardized data is computed to capture the relationships between the variables. The covariance matrix, which is a p × p symmetric matrix, is defined as:

$$C = \left( {1/\left( {n - 1} \right)} \right) \times \left( {Z^{T} \times \, Z} \right)$$

In this matrix, each element C_jk represents the covariance between variables j and k. To identify the directions of maximum variance, PCA performs an eigenvalue decomposition of the covariance matrix, which involves solving the eigenvalue equation:

$$C \times v = \lambda \times v$$

Here, v represents an eigenvector and λ is the corresponding eigenvalue. The eigenvalues provide insight into the variance captured by each principal component, while the eigenvectors indicate the directions in the original feature space along which this variance occurs.

The eigenvalues are sorted in descending order, and the top k eigenvectors corresponding to the largest eigenvalues are selected to form a new basis for the data. If the eigenvalues are denoted as λ₁, λ₂, …, λ_k, and the associated eigenvectors as v₁, v₂, …, v_k, the first principal component PC₁ can be expressed as:

$$PC_{1} = Z \times v_{1}$$

The transformation of the original standardized data into the new subspace defined by the principal components is achieved through the matrix multiplication:

$$Y = Z \times V_{k}$$

where Y is the transformed data matrix and V_k is the matrix that contains the selected eigenvectors. This transformation reduces the dimensionality of the data while preserving the essential variance.

PCA has numerous applications across various fields, such as image processing, bioinformatics, and finance, where it facilitates the identification of underlying patterns, reduces noise, and enables the exploration of high-dimensional datasets. By capturing the most critical information in fewer dimensions, PCA provides a powerful tool for researchers and analysts seeking to derive meaningful insights from complex data^31,32,33.

Illustrates the distribution of the data analyzed in this study on a PCA plot prior to balancing (Fig. 7).

Fig. 7

PCA of patient data distribution.

SMOTE

SMOTE (Synthetic Minority Over-sampling Technique) is a widely utilized and effective approach employed when machine learning datasets exhibit class imbalance. Class imbalance transpires when a class, typically the minority class, is under-represented relative to others, resulting in biased performance from the learning model. SMOTE generates synthetic instances for the minority class, thus balancing the class distribution. This method recognizes instances of the minority class and generates new synthetic examples for them. The new samples are produced along the line segments connecting each or all of the k nearest neighbours of the minority class. The newly generated imitations are produced inside the feature space, hence enhancing the representation of the minority class without introducing bias to the majority class³⁴.

SMOTE reduces issues related to imbalanced datasets by generating a greater and more equitable training set for machine learning methods. It achieves this by producing synthetic data to mitigate overfitting in the minority class and enhance the model’s generalization ability. However, it is important to recognize that this method may not be appropriate for all datasets, particularly when there is much overlap between the minority and majority class data, or when the sample space is inadequately specified. Moreover, while SMOTE may be useful in some situations, it is essential to assess its efficacy and integrate it with additional methodologies to enhance the model’s robustness and precision in managing imbalanced datasets³⁵.

In this study, the initial number of individuals in the minority group was 76, whereas the majority group comprised 224 individuals. Following the application of the SMOTE technique, utilized for class balancing, the instances in both groups became equal, each containing 179 individuals (Fig. 8).

Fig. 8

(A) Normal cell (25%) and (B). Tumor cell (75%).

Machine learning algorithm

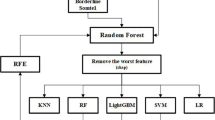
In our project, we have accomplished predictive analysis through the implementation of various machine learning supervised algorithms (Fig. 9). The machine learning algorithms utilized in our project include:

Fig. 9

Type of Machine Learning.

SVM

Support Vector Machines (SVMs) are a powerful class of supervised learning algorithms used for classification tasks. The primary objective of SVMs is to find the optimal hyperplane that separates data points of different classes in a high-dimensional feature space. The hyperplane is defined by the equation:

$$wx + b = 0$$

where w is the weight vector (normal vector to the hyperplane), x is the input feature vector, and b is the bias term.

The goal of SVM is to maximize the margin between the hyperplane and the closest data points from each class, known as support vectors. The margin is defined as the distance from the hyperplane to the nearest data points of either class. The optimization problem can be mathematically expressed as follows:

Minimize:

$$1/2\left| {\left| w \right|} \right|^{2}$$

Subject to the constraints:

$y_{i} \left( {wx_{i} + b} \right) \ge 1,\;{\text{for}}\;{\text{all}}\;i$.where y_i is the class label of the i-th training sample x_i, taking values of + 1 or − 1. The term ||w||2 represents the squared norm of the weight vector, which we seek to minimize to maximize the margin.

To solve this constrained optimization problem, we can introduce Lagrange multipliers α_i for each constraint. The Lagrangian function L is formulated as:

$$L\left( {w,b,\alpha } \right) = 1/2\left| {\left| w \right|} \right|^{2} - \sum {\left( {\alpha_{i} \left[ {y_{i} \left( {wx_{i} + b} \right) - 1} \right]} \right)}$$

where α_i ≥ 0. The dual form of the optimization problem is obtained by maximizing the Lagrangian with respect to α while minimizing it with respect to w and b.

The dual problem can be formulated as:

Maximize:

$$\sum {\left( {\alpha_{i} } \right)} \Sigma - 1/2\sum { \, \left( {\sum {\left( {\alpha_{i} \alpha_{j} y_{i} y_{j} \left( {x_{i} x_{j} } \right)} \right)} } \right)}$$

Subject to:

$$\Sigma \left( {\alpha_{i} y_{i} } \right) = 0,\alpha_{i} \ge 0$$

The dual formulation focuses on the Lagrange multipliers α and captures the relationships between data points through the kernel trick³⁶.

SVMs can be extended to handle non-linear classification problems by using kernel functions. A kernel function K (x_i, x_j) computes the dot product in a transformed feature space without explicitly mapping the input data to that space. Common kernels include:

• Linear Kernel: K (x_i, x_j) = x_i · x_j

• Polynomial Kernel: K (x_i, x_j) = (x_i · x_j + c) ⁿ

• Radial Basis Function (RBF) Kernel: K (x_i, x_j) = e^{(−γ||xi—xj||2)}

Using kernels allows SVMs to create complex decision boundaries while maintaining computational efficiency³⁷.

Once the optimal α values are determined, the decision function for a new data point x can be expressed as:

$$f\left( x \right) = {\text{sign}}\left( {\sum {\left( {\alpha_{i} y_{i} K \, \left( {x_{i} , \, x} \right)} \right)} + b} \right)$$

The support vectors, which are the data points that lie closest to the decision boundary, play a critical role in defining the hyperplane. The SVM decision boundary is influenced solely by these support vectors, making SVMs both efficient and robust.

SVMs are known for their strong performance in high-dimensional spaces and their ability to generalize well to unseen data, particularly due to the maximization of the margin. However, they can be computationally intensive, especially with large datasets or when using non-linear kernels. Additionally, careful parameter tuning (e.g., choice of kernel and regularization parameters) is essential for optimal performance.

Despite these challenges, SVMs remain a powerful tool for classification tasks across various domains, including bioinformatics, image recognition, and text classification^38,39.

Random Forest

Random Forest is a widely used ensemble learning approach in supervised machine learning, typically employed for regression and classification tasks. To enhance precision and resilience, the method constructs several decision trees during training and amalgamates their predictions. To implement randomization and reduce overfitting, each decision tree in the forest is trained on a random selection of features and a random part of the training data. During prediction, the ensemble of decision trees aggregates or votes on each other’s predictions, producing a more accurate and exact model⁴⁰.

The Random Forest method can be properly expressed as follows: The process comprises many phases employing a training dataset (D) containing (N) samples and (M) features. The procedure starts with the creation of bootstrapped datasets (D_b), each including (N) samples randomly chosen with replacement from the original dataset. A decision tree (T_b) is generated for each bootstrapped dataset (D_b) by recursively splitting the data according to randomly selected attributes at each node. The ultimate prediction is generated by consolidating the forecasts from each decision tree. This aggregation is often performed in regression tasks by averaging the predictions of all trees, but in classification tasks, it is usually achieved by picking the mode (most common class) from the predictions of all trees. This ensemble method utilizes the combined expertise of several trees to reduce overfitting and enhance the performance beyond that of singular trees^41,42.

Logistic regression

Logistic regression is a widely used statistical model for binary classification tasks, where the objective is to predict the probability that a given instance belongs to one of two classes, typically denoted as 1 (positive class) and 0 (negative class)⁴³.

This method is particularly effective in scenarios where the outcome is categorical and can be interpreted probabilistically.

At its core, logistic regression applies a logistic function, also known as the sigmoid function, to a linear combination of the input features. The mathematical formulation can be expressed as follows:

$$P\left( {y = 1|x} \right) = \sigma \left( z \right) = 1/\left( {1 + e^{( - z)} } \right)$$

where:

P (y = 1 | x) represents the probability of the instance belonging to class 1 given the input features x.

z is defined as the linear combination of the input features and their corresponding coefficients (weights):

$$z = \beta_{0} + \beta_{1} \times x_{1} + \beta_{2} \times x_{2} + ... + \beta_{n} \times x_{n}$$

In this equation:

β₀ is the intercept (bias term),

β₁, β₂, …, β_n are the coefficients associated with each input feature x₁, x₂, …, x_n.

The logistic function, represented by σ (z), maps any real-valued number into the range¹, ensuring that the predicted probabilities are valid. The output of the logistic regression model can be interpreted as the likelihood that the instance belongs to the positive class⁴⁴.

Odds and log-odds

Logistic regression is closely related to the concept of odds and log-odds (logit). The odds of an event occurring is defined as the ratio of the probability of the event occurring to the probability of it not occurring:

$${\text{Odds}} = P\left( {y = 1|x} \right)/P\left( {y = 0|x} \right) = P\left( {y = 1|x} \right)/\left( {1 - P\left( {y = 1|x} \right)} \right)$$

Taking the natural logarithm of the odds gives the log-odds, also known as the logit:

$${\text{Logit}}\left( {P\left( {y = 1|x} \right)} \right) = \log \left( {P\left( {y = 1|x} \right)/\left( {1 - P\left( {y = 1|x} \right)} \right)} \right) = z$$

This relationship shows that the log-odds are linearly related to the input features:

$$\log \left( {P\left( {y = 1|x} \right)/\left( {1 - P\left( {y = 1|x} \right)} \right)} \right) = \beta_{0} + \beta_{1} \times x_{1} + \beta_{2} \times x_{2} + ... + \beta_{n} \times x_{n}$$

Estimation of coefficients

The coefficients β₀, β₁, …, β_n are estimated using training data through a method called maximum likelihood estimation (MLE). MLE finds the parameter values that maximize the likelihood of observing the given data under the model. The likelihood function for a logistic regression model can be expressed as:

$$L\left( \beta \right) = \prod \left( {P\left( {y^{i} | \, x^{i} ;\beta } \right)} \right)$$

where N is the number of observations, and yⁱ and xⁱ are the response variable and feature vector for the i-th observation, respectively. The coefficients are found by maximizing this likelihood function, often using iterative optimization algorithms such as gradient ascent or Newton–Raphson.

During the prediction phase, an instance is classified into class 1 if the predicted probability P (y = 1 | x) exceeds a predefined threshold (commonly set at 0.5). If the predicted probability is below this threshold, the instance is classified as belonging to class 0. This threshold can be adjusted based on the specific application requirements, such as balancing false positives and false negatives^44,45.

Decision tree

In machine learning, decision trees are an effective tool for both regression and classification problems. It divides the input space recursively into smaller areas according to the characteristics of the data. In order to maximize the purity of the resulting subsets, the algorithm chooses the characteristic at each stage that best divides the data into homogenous subsets. This procedure keeps going until a predetermined point is reached, such a maximum depth, or until further splitting doesn’t materially enhance the model’s functionality^46,47.

The mathematical goal of the decision tree method is to find the best split at each node so that the most purity or information is achieved. The Gini impurity is a common way to measure how impure a node becomes. It estimates how likely it is that a randomly chosen sample would be wrongly labelled if its label were based on the node’s class distribution. Another way to measure the amount of doubt or disorder in a set of samples is to use entropy. At each node, the program picks the split that gets rid of the most impurities or adds the most information⁴⁸.

The decision tree algorithm can be represented by the following formula:

$${\text{Split}}\;{\text{feature}} = \arg \max \;{\text{features}} \left( {{\text{Impurity}}\;{\text{measure}}\left( x \right) - \sum\limits_{i = 1}^{k} {\frac{{\left| {x_{i} } \right|}}{\left| x \right|}} {\text{Impurity}}\;{\text{measure}}\left( {xi} \right)} \right)$$

where x_i is the set of samples at the current node, x_i are the subsets resulting from splitting x based on a particular feature, and k is the number of subsets.

Until a stopping requirement is satisfied, the algorithm repeats this process, creating a tree structure where each leaf node denotes a class label (in classification) or a predicted value (in regression)^37,49.

Evaluation:

To assess the effectiveness and capabilities of the utilized models, we employed three evaluation methods: accuracy, recall, and precision. The operational concepts of each method are explained below.

$$\text{Accuracy}: \frac{TP+TN}{\text{Total Number of Predictions}}$$

$$\text{Precision}: \frac{TP}{TP+FP}$$

$$\text{Recall}: \frac{TP}{TP+FN}$$

• TP: True Positive

• FP: False Positive

• TN: True Negative

• FN: False Negative

Ethics approval and consent to participate

All methods in this study were conducted in accordance with relevant guidelines and regulations and were approved by the National Ethics Committee of Iran (approval code: IR.TUMS.VCR.REC.1397.355). Informed consent was obtained from all participants (or their legal guardians), and the objectives and methods of the study were fully explained to them before the study began.

Results

A study conducted on machine learning algorithms for the classification of breast cancer evaluated four models and the evaluation results are reported for two cases: before and after applying the SMOTE technique: Decision Tree, SVM, Random Forest, Logistic Regression, KNN and ANN (Table 4). All the six gave promising results, although Random Forest showed the best results (after applying SMOTE). This is proof that among all six models, the Random Forest technique would be more efficient in finding any hidden pattern that signifies malignancy in the case of breast cancer data. This finding accentuates the role of machine learning in analyzing breast cancer data. Only with further research and improvement, these algorithms can be a useful tool in enhancing early diagnosis and detection to improve patient outcomes eventually.

Table 4 (a) The performance of the models was evaluated based on three evaluation indicators -SMOTE. (b)The performance of the models was evaluated based on three evaluation indicators + SMOTE.

Four machine learning models were compared: Decision Tree, SVM, Random Forest, Logistic Regression, KNN and ANN (Fig. 10). The table depicts the performance comparison of six classification models, namely Decision Tree, SVM, Random Forest, and Logistic Regression, ANN and KNN in terms of their precision, accuracy, and recall. Precision defines the correct classification of positive cases out of those predicted as positive. The best precision is contributed by SVM with 94%, followed by Logistic Regression with 89% precision. While performing well, Random Forest yields 86% precision and 84% recall. Meanwhile, Decision Tree has the lowest precision of 83% but the highest recall of 80%.

Fig. 10

Presents the comparison of three evaluation indicators among the models utilized. (A) comparison of precision scores (B) comparison of Recall scores (C) comparison of accuracy scores.

The choice of a proper model depends on what the unique application requires: to minimize false positives, SVM or Logistic Regression would be ideal, while for detecting positive examples, the best choice is Decision Tree. Random Forest provides a balanced performance in general. Overall, this assessment will help make valuable decisions about the most suitable model for a particular situation.

The Receiver Operating Characteristic (ROC) curve is a very powerful means to assess the strengths of classification models. The models under examination are six in number: Random Forest, Decision Tree, Support Vector Machine, Logistic Regression, KNN and ANN. True Positive Rate refers to the ratio of correctly identified positive cases, whereas the False Positive Rate conveys the percentage of negative examples that were incorrectly classified. AUC conveys the general performance of the model, and in the case of AUC, a higher magnitude is better in terms of efficacy. Specifically, the highest AUC for the Random Forest is 0.87, while that of the Decision Tree is 0.77, SVM at 0.76, and LR at 0.68.

Among them, the Random Forest model was the most successful in classification employment based on the AUC values, while the rest of the models, except for the Logistic Regression model, did quite well. The ROC curve shows the trade-off between sensitivity and specificity: models are very useful when their TPR is high and FPR low. Thus, only a model with an AUC greater than 0.5 is considered better than random guessing. Therefore, the ultimate choice of a model depends on both the performance metrics and specific application requirements (Fig. 11).

Fig. 11

ROC Curve of 6 Models.

This plot ranks the variables of the developed model in terms of their importance for classification based on the Gini coefficient (Fig. 12). However, the rank by Gini identifies the most influential variable as ‘age, ‘ followed by ‘her2, ‘ ‘k67, ‘ ‘er, ‘ ‘pr, ‘ and ‘neoadjuvant therapy’ in descending order. This may indicate that the patient’s age and the presence of certain proteins and receptors in the cancer cells will play an important role for the model to distinguish between malignant from non-malignant cases.

Fig. 12

he Gini coefficient to assess the significance of features.

Furthermore, the relationships between features were analyzed, considering that the dependencies between them may be nonlinear. So, to introduce the quantitative characteristics of such relations, the Pearson correlation coefficient was measured (Fig. 13). As a non-parametric measure of monotone dependencies, Spearman’s rank correlation describes the dependence between orders of two variables without requiring their relationship to be linear.

Fig. 13

Spearman Rank Correlation Heatmap.

This heat map visualizes these relationships through a color gradient that varies by direction and strength. Some observations from this are: Correlation analysis identifies several variables that have significant relations. PR and ER exhibit a strong positive correlation of 0.98, Ki67 and PR of 0.84, Ki67 and ER of 0.85. This shows that these factors are somewhat interrelated and possibly influenced by similar sources or mechanisms. There is also a negative association between Neoadjuvant and CDPQ, − 0.17, to suggest that the quantity of CDPQ in a patient receiving neoadjuvant treatment may vary. Most of the relationships of age and other factors were modest. These relationships will be further consolidated by checking their biological or clinical significances or by further analysis using some statistical methods such as hypothesis testing in order to bring out significances. Scatter plots or line graphs provide further insight into these relationships. Overall, the above correlation matrix is a very useful tool in assessing potential relationships between variables and also for coming up with idea developments for further studies.

Discussion

Accurate and timely prediction of breast cancer is one of the important goals of current research in the field of breast cancer. However, the data available to investigate breast mast cells in machine learning is still limited. Various machine learning techniques have been applied to improve the accuracy of prediction and detection of cancer cells. The main goal of this study was to determine the most effective machine learning methods for breast cancer risk assessment. Currently, limited data are available to the public, and most of the reviews are based on these data, which makes the results of the algorithms close to each other. In this study, we tried to use new data for the review. In breast cancer research, immunohistochemical (IHC) markers serve as essential biomarkers for diagnosis, prognosis, and treatment decision-making. These IHC markers, including estrogen receptor (ER), progesterone receptor (PR), human epidermal growth factor receptor2 (HER2), and the proliferation marker Ki-67, provide important information about tumour biology.

Ronchi et al. showed in their review that immunohistochemical factors are used not only for diagnostic purposes but also as prognostic indicators and important factors in response to specific treatments. These are useful and practical biomarkers in breast cancer management. Currently, these factors are the only means by which specific treatment strategies can be adopted⁵⁰.

Johansson et al. showed that even with modern methods of breast cancer treatment, IHC subgroups are crucial for prognosis. Tumor size, nodal status, and IHC are important factors for predicting cancer, and they operate independently of each other; therefore, it is essential to assess all of them. When these factors are combined, the probability of dying from cancer is reduced by 20 to 40 times⁵¹.

Shuai et al. evaluated IHC factors as important indicators in cancer after chemotherapy. The levels of these biomarkers change post-chemotherapy, indicating the tumor’s adaptation or response to the treatment. Changes in the expression levels of these factors are important for guiding subsequent treatments and predicting outcomes. Additionally, re-evaluating hormone and HER2 receptors after chemotherapy helps improve treatment approaches⁵².

While these IHC markers have been very important in the clinical field, their integration with Nano biosensors such as CDPs offers a new approach to increase diagnostic and prognostic accuracy. Nano biosensors have the potential to identify biomolecules in real time and with high sensitivity. This study investigated the relationship between IHC factors and the CDP Nano biosensor to evaluate whether the latter can be an effective tool in detecting IHC marker expression profiles. In this research, we showed that there is a significant relationship between these IHC factors that are related to the tumor and the CDP data that is related to the amount of RAS factor in the tissue around the tumor. This conclusion can be a clue for future research in this field in order to investigate the rate of metastasis of cancer cells in the future.

Our analysis seeks to discover the correlation between these factors with the help of machine detection methods. Among the 6 machine learning methods used in this data set, the SVM method recorded the highest precision with 94%, followed by the logistic regression method with 89% precision. In terms of accuracy, the Random Forest algorithm with it recorded 78% higher accuracy, which shows a relatively large drop in accuracy. It should be noted that one can consider that a wider data set may lead to higher levels of accuracy in the long run. By examining the results of all methods, it can be concluded that all models have a high level of ability to distinguish between cancerous and normal cells. However, it should be noted that these methods may be affected by the size and type of data, and further investigation is needed to generalize them to all data.

For the performance evaluation of the applied models, in this section, we used the K-Fold Cross Validation method, where the value of K ranged from 2 to 10. This method allowed us to judge the efficiency and accuracy of each model for various folds. In each iteration of the K-Fold process, the data was divided into K subsets, and one subset was used for testing, while the other subsets were used for the creation of a training dataset. We did that K times, sliding the test set so that eventually every portion of the data got used for testing a more complete measurement of the performance of each model (Table 5).

Table 5 Evaluation of machine learning algorithms using k-fold cross-validation.

This method facilitated a more profound understanding of the models’ stability and generalization abilities when confronted with novel data. Through the examination of average performance indicators, including accuracy and AUC, with their respective standard deviations, we conducted a more comprehensive comparison of the models. This assured us that the results due to K-Fold Cross Validation were robust and not because of a different split of the data, but instead represented a more reliable measure of how the models would perform in real-world scenarios.

From this analysis, the performance of both SVMs and Logistic Regression drastically reduced, indicating that these models do not perform effectively on the given dataset. On the other hand, Random Forest turned out to be the most robust model, yielding topmost results in terms of accuracy as well as predictive capability.

Therefore, it can be concluded that for the data at hand, Random Forest is conducive to classification tasks with better efficiency. The RF model is used to provide an estimate of the relative importance measure for each feature, as in (Fig. 12). In this case, the Gini importance method was determined by the score mean impurity reduction. The data show that age may be the most important risk factor in the assessment. These agreements with the literature review imply that the developed model correctly highlights the susceptibility to breast cancer due to high counts of CDP as well as the presence of immunohistochemical factors. From a practical point of view, the results introduced in the current study provide significant findings related to the prediction of the risk of breast cancer based on exposure parameters such as CDP numerical level, age, history of chemotherapy, and relevant immunohistochemical factors.

In this regard, it is important to recognize the limitations of this research. These are the limited availability of samples due to the novelty of the CDP device and its relatively limited usage in the operating room, and recall bias.

Conclusion

The development and use of machine learning algorithms on CDP number parameters for the prediction of risk with respect to breast cancer are presented here. Minimum above 370 the results indicate that the machines are quite efficient in distinguishing the patients suffering from breast cancer from the healthy patients with great performance metrics of mean recall at 82.5%, mean precision at 85.75%, and mean accuracy at 76.5%. Moreover, we identified the important risk factor ‘age’. Most of the patients analyzed were above 40 years; hence this ascertains that with an increase in age the likelihood of developing a malignant tumor increase, which includes the great influence of ‘Her2’ and ‘Ki67’ during the development of cancer.

In conclusion, these models are both proper and efficient for early and timely detection of cancerous cells. They can aid surgeons in assessing the requisite volume of breast tissue to excise, along with the essential postoperative medicine needed. Furthermore, the data utilized in this investigation has been applied for the initial time.

Limitations and future directions

Interpretation and generalizability of our findings should be considered in light of several potential limitations. First, the sample size of 300 participants, although providing sufficient statistical power for our initial analysis, may limit the extent to which these results can be generalized to broader populations. Second, the data were collected from a single center in Tehran, which may introduce a selection bias and limit the external validity of our findings to other geographic regions and healthcare settings. Furthermore, the novel nature of the CDP device means that its reliability and long-term consistency across settings are still under investigation, potentially introducing variability in measurements. Finally, while we used the SMOTE technique to address class imbalance in our dataset, this method can sometimes lead to overfitting on artificial minority class samples, which may have affected the performance of some machine learning models. Future research should aim to address these limitations. “This should be done through larger, multicenter studies and further validation of the CDP device.