MambaCAttnGCN+: a comprehensive framework integrating MambaTextCNN, cross-attention and graph convolution network for piRNA-disease association prediction

Abstract

Elucidating the interactions between piwi-interacting RNAs (piRNAs) and diseases is crucial for diagnosis and treatment. Although several computational approaches have been developed to investigate piRNA-disease associations, sparse datasets present challenges in capturing the complex relationships between piRNAs and diseases. To develop a more accurate prediction model for associations between piRNAs and diseases. We integrated piRNA sequence information, disease-related semantic terms, and existing piRNA-disease association networks to construct a heterogeneous graph. Utilizing the Mamba module, we developed an innovative sequence embedding model, MambaTextCNN, to extract features from piRNA sequences, which we used as node attributes within the heterogeneous graph. A heterogeneous graph convolution method was then applied to identify potential associations between piRNAs and diseases, with cross-attention mechanisms further enhancing node features. Finally, by incorporating positive unlabeled learning techniques, we developed the piRNA-disease association prediction model MambaCAttnGCN+. In 5-fold cross-validation, MambaCAttnGCN + achieved AUCs of 0.94 and 0.953 on two datasets, outperforming seven other state-of-the-art models. Additionally, a comparison of three distinct approaches for representing sequence node features, revealed through ablation experiments that features extracted by MambaTextCNN were the most effective. MambaCAttnGCN + represents a valuable predictive tool for future research on piRNA-disease associations in biomedicine.

Introduction

Piwi-interacting RNAs (piRNAs) are a class of small non-coding RNAs (ncRNAs) ranging from 24 to 32 nucleotides in length¹. piRNAs were first identified in the testes of Drosophila melanogaster in 2001² and later isolated from the vas deferens of male mice in 2006¹. To date, piRNAs have been recognized in nearly 44 species³. Although the primary function of piRNAs is to inhibit the transcription of transposons in germ cells and maintain genomic integrity^4,5 a growing body of research suggests that piRNAs are involved in diverse biological processes, includding transposon silencing, histone modification, translational regulation, DNA methylation, and immune environment regulation^6,7.

An increasing body of evidence is expanding our understanding of piRNAs. Studies have revealed the crucial role of piRNAs in the occurrence and prognosis of multiple human diseases, as well as their potential applications in the diagnosis and treatment of these conditions. This highlights the potential of these ncRNAs as valuable diagnostic markers and therapeutic targets⁸. For instance, piR-39,980 exerts an inhibitory effect on FDFT1, thereby mitigating tumorigenesis by modulating the proliferation and apoptosis of tongue squamous cell carcinoma in hypoxic environments⁹. Additionally, hsa_piR_019949 enhances chondrocyte anabolic activity by downregulating the expression of lncRNA NEAT1¹⁰, while piR-has-23,533 promotes the aggressiveness of head and neck squamous cell carcinoma via USP7 signaling pathways¹¹.

Biological experiments are essential for accurately identifying piRNAs and uncovering their associations with diseases. Numerous hypotheses have been confirmed through such experiments¹². However, with the growing number of identified piRNAs and associated diseases, traditional biological experiments such as gene knockout¹³ and RNA interference¹⁴ face challenges, including lengthy experimental timelines, complexity, and high costs¹⁵. To address these issues, researchers have developed computational analysis methods to improve the efficiency of piRNA research.

Traditional machine learning and deep learning approaches have been extensively applied in bioinformatics. Using databases such as piRDisease¹⁶, ncRPheno¹⁷ and MNDR¹⁸ a range of computational models have been proposed to elucidate piRNA-disease associations. For instance, iPiDi-PUL¹⁹ integrates piRNA and disease features, extracts key attributes through principal component analysis (PCA), and classifies unlabeled associations using machine learning techniques like random forests. It also employs positive unlabeled learning (PUL) strategies to construct reliable negative sample training models. Building on heterogeneous network integration, iPiDA-GCN²⁰ captures complex structural features via graph convolutional networks (GCN); ETGPDA²¹ uses the attention mechanism-based GCN to derive low-dimensional embedding features for piRNAs and diseases, while developing an embedding transformation module to address inconsistencies in embedding spaces. iPiDA-SWGCN²² mitigates adjacency matrix sparsity through a weighting strategy. PDA-PRGCN²³ incorporates feature enhancement techniques, such as subgraph projection and residual scaling, to improve model performance via GCN. GAPDA²⁴ leverages line graphs within heterogeneous networks to dynamically assign weights among nodes, thereby reducing noise effects in interaction networks. Additionally, iPiDA-GBNN²⁵ employs gradient boosting methods with shallow architectures to incrementally construct complex GrowNet frameworks, enhancing model robustness. Compared with traditional machine learning approaches, these advanced methods incorporate inter-node information more effectively.

However, representing sequence features solely through sequence similarity does not sufficiently capture the implicit information within local sub-sequences. To address this limitation, piRDA⁷ extracts significant and abstract information from the original sequence without relying on feature engineering. It also incorporates a two-step positive-unlabeled learning strategy and guiding techniques to reduce false negatives and bias in positive unlabeled data. Despite its simplicity, robustness, and efficiency, this approach provides limited insights when addressing the complex relationship between piRNA and diseases, resulting in suboptimal model performance. PUTransGCN²⁶ utilizes a heterogeneous graph network to reveal potential piRNA-disease associations by extracting features from the original piRNA sequence using TextCNN as node features within the heterogeneous graph framework. By leveraging an attention mechanism, it automatically adjusts and aggregates weight parameters for heterogeneous node features. This approach integrates PUL strategies to facilitate the identification of reliable negative associations. While effective, TextCNN tends to overlook global information inherent in the original piRNA sequence.

In recent years, state space models and Mamba have made significant advancements²⁷ emerging as promising backbone networks for foundational model selection. Mamba leverages linear complexity and dynamic state modeling to significantly improve the flexibility and accuracy of sequence feature extraction, all while maintaining computational efficiency. This approach shows exceptional promise in DNA sequence analysis²⁸. To develop a more accurate prediction model for piRNA-disease associations, we drew inspiration from prior research and integrated MambaTextCNN, GCN, and Cross Attention to construct our piRNA-disease association prediction framework. Additionally, we employed PUL to generate reliable negative samples for model training. Our contributions are outlined as follows:

• 1. To address the limitation of TextCNN in capturing the global information inherent in original piRNA sequences, we integrated the Mamba module with CNN to develop the MambaTextCNN model. This model leverages the Mamba module to capture global sequence information while using CNN to enhance local feature extraction.

• 2. In constructing a more accurate disease association prediction model, we used MambaTextCNN within a piRNA-disease heterogeneous network framework to embed node features from piRNA sequences. By adeptly combining MambaTextCNN, GCN, and Cross Attention, we developed the MambaCAttnGCN + model, achieving effective predictions for unknown piRNA-disease associations.

• 3. To our knowledge, this is the first application of Mamba in piRNA-disease association prediction (PDA).

Result

Comparison with existing methods

As shown in Tables 1 and 2, MambaCAttnGCN + outperforms other methods across multiple metrics, including ranking index, AUC, and AUPR.

Table 1 Evaluation of method performance on the MNDR4.0 dataset.

Table 2 Evaluation of method performance on the pirdisease v1.0 dataset.

To assess the statistical significance of these improvements, a Mann-Whitney U test was conducted on the scores obtained from these methods. Statistical tests (as shown in supplementary Tables S1 and S2) show that MambaCAttnGCN + significantly outperforms all baseline models (p < 0.05), including ETGPDA; iPiDi-PUL variants based on decision trees (DT), support vector machines (SVM), and random forests (RF); as well as iPiDA-GCN, iPiDA-SWGCN, iPiDA-GBNN, piRDA, and PUTransGCN.

Although no statistically significant difference in the AUPR was observed between MambaCAttnGCN + and PUTransGCN on the piRDisease v1.0 dataset, this result is acceptable given that no additional optimization was performed for this dataset. Moreover, an analysis of six evaluation metrics across both datasets revealed statistically significant differences in five of them, further validating the superior performance of MambaCAttnGCN+.

Ablation experiment

To rigorously evaluate the efficacy of the MambaTextCNN approach and to determine the impact of original piRNA sequence characteristics on model performance, we conducted an ablation experiment. We also assessed the influence of different PUL strategies on model outcomes.

This study evaluates three different feature extraction approaches: sequence similarity features, TextCNN, and MambaTextCNN, which are used to generate sequence-based node embeddings within multiple PUL frameworks. We developed a predictive model, SimCatGCN-PUL, which utilizes sequence similarity as the node inputs and integrates GCN with a cross-attention mechanism. The structural schematic of this model is shown in Fig. S5 of Supplementary. For comparison, we constructed CNNCatGCN-PUL, which employs original piRNA sequence features extracted via TextCNN as node embedding and likewise combines GCN with cross-attention mechanism. This model corresponds to the previously described PUTransGCN²⁶ and its schematic is provided in Fig S6 of Supplementary. It is important to note that only difference among these three models lies in their node feature representations; all other architectural components remain consistent.

The evaluated PUL strategies include PU bagging, two-step methods, spy techniques, combinations thereof, and a baseline setting without PUL. By comparing these approaches, we performed a systematic analysis of the individual and combined effects of feature extraction techniques and PUL strategies on the overall predictive performance of the models.

To further contextualize the role of global information modeling in piRNA sequence representation, we considered additional architectures known for their ability to capture long-range dependencies. Recurrent neural networks, such as Long Short-Term Memory (LSTM) networks²⁹ are capable of retaining information over extended sequences through gated memory cells, which makes them suitable for modeling sequential biological data. In contrast, Transformer architectures leverage self-attention mechanisms that allow each token in the sequence to attend to all others simultaneously, thus capturing global contextual information more effectively and efficiently³⁰. These architectures have demonstrated strong performance in various sequence modeling tasks and serve as meaningful baselines when evaluating the potential of the Mamba module as a global information encoder.

Table 3 Performance of PUL methods and original sequence feature representations interaction on MNDR v4.0.

Table 4 Performance of PUL methods and original sequence feature representations interaction on pirdisease v1.0.

Diverse representations of sequence node features

As shown in Tables 3 and 4, under identical PUL conditions, the MambaTextCNN method significantly outperforms TextCNN method in Rank index, AUC, and AUPR across both the MNDRv4.0 and piRDisease v1.0 datasets. For instance, without applying PUL on the MNDRv4.0 dataset, MambaTextCNN achieves improvements of 2.31% in the Rank index, 0.67% in AUC, and 8.23% in AUPR. Similarly, on the piRDisease v1.0 dataset, it yields gains of 1.56%, 1.64%, and 4.09% in the respective metrics. These results underscore the effectiveness of the proposed MambaTextCNN module.

Among 30 evaluation metrics across both datasets, MambaTextCNN demonstrates superior performance in 25 metrics showing comparable results. For example, without PUL on the MNDR v4.0 dataset, MambaTextCNN achieves Rank index and AUC values only 0.1% lower than those of sequence similarity, while improving AUPR by 0.09%. On the piRDisease v1.0 dataset, minor decreases of 0.12% in Rank index, 0.13% in AUC, and 0.57% in AUPR are observed. These findings suggest that MambaTextCNN extracts more comprehensive and informative features from raw piRNA sequences than the sequence similarity method.

Furthermore, as detailed in Tables 3 and 4, and 5, a comparative analysis of the three sequence-based node feature representation methods under the same PUL configurations shows that 91.67% of the scores from MambaTextCNN exceed those of sequence similarity. In contrast, 90% of the sequence similarity scores outperform those from TextCNN. These results further validate the superior capacity of MambaTextCNN in capturing nuanced and discriminative features from piRNA sequences.

Table 5 Performance comparison of different original sequence feature representation methods with varying percentages of spy incorporated into the combined method on MNDR v4.0.

Diverse approaches to PUL

As shown in Tables 3 and 4, when sequence node features are held constant, the combination of PU bagging, the two-step method, and spy technique significantly outperforms their individual applications or the absence of PUL. This improvement is evident in both Rank index and AUC metrics across datasets. The degree of enhancement varies by dataset; for instance, when original sequence features are extracted using MambaTextCNN, the spy technique achieves the best performance on the MNDR v4.0 dataset, while the two-step method yields the highest gains on piRDisease v1.0. These findings suggest that integrating multiple PUL strategies enables synergistic benefits by leveraging the strengths of each method to enhance overall model performance.

The proportion of these spies plays a critical role in determining model effectiveness. A higher spy ratio increases the number of presumed negative samples, but also raises the risk of misclassifying true positives. Conversely, a lower spy ratio yields more reliable negatives but limits their quantity, potentially impairing the model’s generalizability. Thus, selecting an optimal spy ratio is essential to balancing reliability and coverage.

As shown in Table 5, MambaTextCNN consistently outperforms TextCNN at every evaluated spy ratio. Notably, when the spy ratio is set to 6%, MambaTextCNN achieves the highest AUC score. Deviations from this optimal value, such as 5% or values above 6%, result in a noticeable decline in AUC performance.

Overall, under equivalent spy ratio settings, MambaTextCNN consistently outperforms both sequence similarity and TextCNN-based methods, further validating the effectiveness of its novel design in enhancing the performance of PUL frameworks.

Different attention mechanisms

To evaluate the impact of different attention mechanisms on model performance, we conducted a comparative analysis between models employing multi-head cross-attention and multi-head self-attention, as shown in Supplementary Table S3. The results demonstrate that multi-head cross-attention consistently outperforms self-attention, with observed improvements of 0.13% in Rank index, 0.12% in AUC, and 1.67% in AUPR. These findings underscore the superior capability of cross-attention in capturing the interdependent relationships between piRNAs and diseases, thereby enhancing overall predictive performance.

Comparison with different PiRNA sequence embedding methods

To evaluate the effectiveness of the MambaTextCNN model in capturing global and local information, we replaced the Mamba module with other commonly used sequence modeling architectures, including Transformer, LSTM, and TextCNN, while keeping all other components fixed. The results are presented in Table S4 of the Supplementary. Among all models, MambaTextCNN achieved the best overall performance. These results highlight the advantage of combining Mamba’s global context modeling with TextCNN ability to extract local sequence patterns, offering a more comprehensive feature representation than models relying solely on either global or local mechanisms.

Parameter evaluation

Using the MNDR4.0 dataset, we conducted a grid search to evaluate the effects of three key hyperparameters, as summarized in Supplementary Tables S5 and S6: (i) convolutional kernel configurations for MambaTextCNN (e.g., (1, 3), (1, 5), (1, 7), (3, 5), (3, 7), (1, 3, 5), (1, 3, 7), (1, 5, 7), and (3, 5, 7)); (ii) the state size of Mamba (14, 16, and 18); and (iii) the dropout rate (0.1, 0.2, and 0.3). The best performance was observed with a kernel configuration of (1, 5, 7), a Mamba state size of 16, and a dropout rate of 0.1.

Generalization experiment

To further evaluate the generalization ability of the proposed model, we applied it to a different type of biological association prediction task: miRNA-disease association (MDA) prediction. We used the Human MicroRNA Disease Database (HMDD v3.2), which is currently the most comprehensive repository of experimentally supported MDAs, containing 15,186 validated associations involving 901 miRNAs and 877 diseases³¹. To ensure a fair comparison with previous studies, we adopted a benchmark dataset curated and preprocessed by prior work, and compared our model against four representative methods: AMHMDA³², AGAEMD³³, MINIMDA³⁴ and MUSCLE³⁵ (supplementary Sect. 2.5 provides an overview of these models).

As shown in supplementary Table S7, our model outperformed AGAEMD in some evaluation metrics, but overall lagged behind the other competing methods. We hypothesize that this result may be attributed to several factors: (1) the proposed model was originally designed for piRNA-disease tasks, and its architecture and feature extraction mechanisms were not tailored for MDA prediction; (2) disease-specific features, which are critical in MDA prediction, were not effectively incorporated into the current model; (3) there are substantial differences in sequence length distributions between miRNAs and piRNAs, yet we did not adjust the embedding-related hyperparameters (e.g., maximum sequence length, embedding dimension) accordingly during this transfer experiment.

Although the model’s performance on this task was suboptimal, the experiment offers valuable insights into its cross-task generalizability and highlights the need for future adaptations in model structure and training strategies tailored to specific tasks.

Case study

To evaluate the predictive performance of MambaCAttnGCN + in identifying disease-associated piRNAs, we implemented a disease-agnostic validation strategy by removing all known piRNA associations for a target disease, treating it as novel. The model was then used to infer new associations and assign relevance scores, which were used to rank candidate piRNAs. This approach was applied to three representative and clinically significant diseases: renal cell carcinoma (RCC), parkinson’s disease (PD), and cardiovascular disease (CVD).

Table 6 The top five PiRNAs related to different diseases as predicted by the mambacattngcn+.

RCC is the most common form of kidney cancer, accounting for over 175,000 deaths globally each year³⁶. PD ranks as the second most prevalent age-related neurodegenerative disorder after Alzheimer’s disease, with global cases projected to reach 12 million by 2050³⁷. CVD remains the leading cause of death worldwide, increasingly affecting younger populations due to lifestyle factors such as poor sleep and diet³⁸. Investigating the role of piRNAs in these diseases offers potential for novel therapeutic strategies.

The top 5 ranked piRNAs for each disease were validated against existing literature using PubMed references. As shown in Table 6 and 15 predicted associations were supported by prior evidence. In RCC, piR-32,637, DQ598675, and piR-4580 were downregulated in tumor tissues, while hsa_piR_004153 and hsa_piR_016735 were upregulated in exosomes^36,39,40. In PD, piRNAs including DQ597484, piR-36,772, and others were differentially expressed in both cellular and postmortem samples⁴¹. For CVD, PIR58596, PIR32637, PIR36772, and PIR45809 showed reduced expression, while PIR54043 was elevated⁴².

To assess the model’s predictive capacity, we trained it on the complete dataset and generated predictions across all disease categories. To further evaluate its accuracy, we compared the predicted association scores with previously reported disease-piRNA associations documented in the literature. Predictions were considered putative positive associations if their scores exceeded 0.995 and ranked within the top 10% for a given disease. As detailed in Table S8 of Supplementary, none of the 20 associations reported by PUTransGCN²⁶ were present in the MNDR4.0 dataset used in our study. However, among the 10 associations predicted by our model with scores above 0.995, three ranked within the top 10% of their respective disease categories.

These findings demonstrate that MambaCAttnGCN + can effectively identify novel piRNA-disease associations, highlighting its potential utility in guiding future biological validation and experimental investigations.

Discussion

To advance the prediction of piRNA-disease associations, we developed MambaTextCNN, a novel network for extracting informative features directly from original piRNA sequences. By incorporating GCN and a multi-headed cross-attention mechanism, we further proposed MambaCAttnGCN+, which demonstrated superior predictive performance across two independent benchmark datasets. Ablation studies confirmed that the latent representations learned by MambaTextCNN significantly outperformed those based on conventional sequence similarity, underscoring the importance of sequence-specific features in enhancing piRNA-disease association prediction.

Traditional machine learning approaches, such as those employed by iPiDi-PUL¹⁹ have proven effective in reducing experimental costs; however, their performance in feature extraction remains limited. As presented in Tables 1 and 2, models employing deep learning techniques achieved substantially superior results (Rank index: 9–16%, AUC: 80.5–95.5%, AUPR: 32-68.5%) compared to iPiDi-PUL (Rank index: 23–45%, AUC: 56.5-75.85%, AUPR: 9-18.5%). These findings are consistent with previous studies^{7,20,21,22,25,26} highlighting the advantages of end-to-end deep learning frameworks, which facilitate automated feature extraction and enhance non-linear modeling capabilities. On the MNDR4.0 dataset, MambaCAttnGCN + outperformed iPiDi-PUL (RF) with gains of 14.41% in Rank index, 15.6% in AUC, and 44.38% in AUPR. Comparable improvements were observed on the piRDisease v1.0 dataset, reaffirming the robustness and generalizability of our proposed method.

Numerous researchers have utilized homogeneous or heterogeneous network-based approaches to predict piRNA-disease associations through machine learning and deep learning techniques^{19,20,21,22,25}. While these methods have significantly advanced the field, they often rely on sequence similarity or Gaussian kernel similarity as node features, thereby overlooking the latent information encoded in the original piRNA sequences. Recent studies have underscored the importance of such latent sequence features in enhancing model performance, particularly within ncRNAs research⁴³. For instance, PUTransGCN²⁶ employs TextCNN to extract latent features directly from piRNA sequences, incorporating them as node features within a heterogeneous graph framework. This strategy yields notable performance improvements over traditional similarity-based approaches, as reflected in the metrics presented in Tables 1 and 2. Similarly, PiRDA⁷ performs association prediction exclusively based on raw piRNA sequences, demonstrating the substantial predictive power inherent in these sequences without the need for extensive feature engineering. Our findings align with these observations. As shown in Tables 3 and 4, and 5, under identical PUL settings, the MambaTextCNN module consistently outperforms or at least matches the performance of traditional sequence similarity-based methods in extracting informative features from raw piRNA sequences. These results underscore the essential role of latent sequence features in constructing accurate and robust piRNA-disease association prediction models. Looking ahead, future studies should prioritize the integration of such latent features to further improve model interpretability and predictive capability, thereby contributing to the ongoing refinement of PDA prediction frameworks.

PUTransGCN²⁶ incorporates a piRNA sequence similarity matrix, a disease similarity mechanism, and a heterogeneous network constructed from piRNA-disease adjacency matrices. It utilizes TextCNN to extract node features from these adjacency matrices. While this approach demonstrates competitive performance, the use of TextCNN is inherently limited in capturing global contextual information within sequences, thereby constraining the model’s ability to fully leverage the latent features embedded in piRNA sequences. To address this limitation, we developed MambaCAttnGCN+, an enhanced model that builds upon the PUTransGCN architecture by integrating Mamba, a novel feature extraction module. In our design, Mamba operates in conjunction with a CNN to form MambaTextCNN, a hybrid mechanism that captures both global dependencies (via Mamba) and local patterns (via CNN). This dual-level feature representation allows for a more comprehensive extraction of sequence information. As shown in Tables 1 and 2, MambaCAttnGCN + achieves consistent improvements over PUTransGCN, with gains of 0.91%, 1.05%, and 1.05% in Rank index, AUC, and AUPR, respectively, on the MNDR4.0 dataset. Comparable enhancements are also observed on the piRDisease v1.0 dataset, further confirming the effectiveness and generalizability of our proposed model.

Additionally, under identical PUL conditions, Tables 3 and 4 reveal that MambaTextCNN outperforms its TextCNN counterpart across multiple metrics. Table 5 further substantiates this trend, demonstrating superior performance even when the spy ratio remains fixed. These findings suggest that MambaTextCNN is a promising alternative to conventional CNN-based extractors in DNA and RNA sequence analysis, offering a novel and effective framework for capturing both local and global features inherent in biological sequences.

While our work centers on piRNA–disease associations, extensive efforts have been devoted to miRNA–disease prediction using methods such as matrix factorization and GCN (e.g., IMIPMF⁴⁴, NCMD⁴⁵, SMAP⁴⁶, GCNCF⁴⁷). These models achieve high accuracy but often rely on similarity networks rather than modeling RNA sequences directly. In contrast, we focus on piRNAs (an underexplored class of ncRNAs) and introduce a novel state space framework, MambaTextCNN, to capture both local and global sequence features. This hybrid approach, when integrated with GCN and cross-attention mechanisms, consistently outperforms similarity- and CNN-based baselines. Our findings highlight the potential of sequence-level modeling in piRNA research and suggest opportunities for multi-class small RNA frameworks that incorporate both piRNA and miRNA data.

Notably, our case study revealed two novel piRNA-disease associations not previously documented in public databases: hsa_piR_004153 and hsa_piR_016735 were both found to be consistently upregulated in exosomes derived from Renal Cell Carcinoma (RCC) samples compared to normal renal tissue. This observation suggests potential involvement of these piRNAs in RCC pathogenesis, particularly in the extracellular signaling milieu.

For hsa_piR_004153, prior studies have reported downregulation in colorectal cancer tissues and serum⁴⁸ but upregulation in plasma extracellular vesicles (EVs) from smokers⁴⁹ and patients with Parkinson’s disease⁵⁰ suggesting a context-dependent expression profile. These divergent patterns highlight a possible link between elevated extracellular piR_004153 and inflammatory processes, which are frequently observed in smoking-related disorders, neurodegeneration, and renal carcinogenesis³⁶. Consistently, our mining of the exRNA-disease database⁵¹ revealed elevated piR_004153 levels in patients with subarachnoid hemorrhage and gastric cancer, both conditions associated with systemic inflammation (As shown in the supplementary Fig. S1 and S2).

Similarly, hsa_piR_016735 was also upregulated in RCC-derived exosomes and has been previously reported to exhibit downregulation in breast cancer tumors⁵² but elevated expression in rheumatoid arthritis synovial fibroblasts⁵³ and in the plasma EVs of smokers⁴⁹ and Parkinson’s patients⁵⁰. These findings again point toward a possible role in chronic inflammation or immune modulation. Data from exRNAdisease⁵¹ further demonstrate shifts in expression across inflammatory and neoplastic contexts, including subarachnoid hemorrhage and gastric cancer (As shown in the supplementary Fig. S3 and S4).

Together, these findings suggest that hsa_piR_004153 and hsa_piR_016735 may represent previously unrecognized extracellular regulators in RCC, potentially acting through inflammation-related pathways. Their consistent enrichment in RCC exosomes underscores their promise as non-invasive biomarkers, while their broader expression across inflammatory pathologies hints at conserved molecular mechanisms linking chronic inflammation and tumor progression. Functional studies are warranted to elucidate their roles and targets within the tumor microenvironment.

In recent years, the Transformer architecture has become a dominant framework across a wide range of applications. Its attention mechanism enables models to focus selectively on relevant portions of the input sequence, thereby improving contextual understanding^54,55. However, a major limitation of this architecture lies in its computational inefficiency—specifically, the attention mechanism scales quadratically with input length, posing challenges for processing very long sequences. In contrast, Mamba has recently emerged as a promising alternative, designed to efficiently model complex dependencies in sequential data with lower computational overhead²⁷. In this work, we incorporated Mamba not as a standalone global encoder, but in combination with TextCNN to form a hybrid architecture MambaTextCNN. This design integrates global context modeling with local pattern extraction, enabling a more comprehensive and efficient representation of piRNA sequences.

While our model demonstrated improved performance in predicting piRNA–disease associations, several limitations remain. First, the number of experimentally validated associations is currently limited, although we anticipate that the volume of available data will increase in the future. Second, our work to date has primarily focused on leveraging Mamba’s potential for extracting features from original sequences. In future studies, we plan to explore replacing the cross-attention classifier with Mamba to reduce computational costs and further harness its capabilities in disease association prediction. Finally, experimental validation of the predicted associations would enhance the reliability and biological significance of our findings.

Conclusion

The MambaTextCNN model proposed in this study demonstrates strong capability in extracting features from original piRNA sequences. By integrating GCN with cross-attention mechanisms, the enhanced MambaTextCNN + model significantly improves the accuracy of piRNA–disease association predictions. This advancement not only contributes to identifying piRNA-related diseases in biological research, but also enables a more comprehensive investigation into the role of piRNAs in disease progression. Furthermore, it deepens our understanding of disease mechanisms and may inform the development of more effective therapeutic strategies.

Dataset

In line with recommendations from previous studies²⁶ we evaluated our model using two benchmark datasets: MNDR4.0¹⁸ and piRDisease v1.0¹⁶. MNDR v4.0 is a comprehensive database of ncRNA-disease associations, encompassing 18 RNA types, 117 species, and 4090 diseases, with a total of 3,428,058 associations. From this resource, we extracted the piRNA-disease subset and removed duplicate entries and ambiguous entries, resulting in a dataset comprising 8,205 piRNAs and 15 diseases, including 9616 experimentally verified associations. In contrast, piRDisease v1.0 is a dedicated database for piRNA-disease associations, containing 7,939 validated associations involving 4796 piRNAs and 28 diseases. After filtering out duplicates, we retained a refined dataset comprising 4,350 piRNAs, 21 diseases, and 5,002 verified associations.

Methods

Mamba and MambaTextCNN

Mamba

The Mamba module²⁷ consists of a combination of a selective Structured State-Space Model (SSM) sequence transformation (A detailed introduction to the SSM module is provided in Supplementary Sect. 2.1) and a gated MLP mechanism. As shown in the leftmost schematic diagram in Fig. 1, the input sequence is duplicated and projected to twice its original dimension, followed by causal convolution and subsequent application of the SiLU/Swish nonlinear activation function⁵⁶ which culminates in the selective SSM process. Alternatively, a separate path applies SiLU nonlinearity to the input before gating the output from the SSM. Finally, this gated representation is projected back to its original dimension, d.

Fig. 1

Mamba module used for sequence modeling in piRNA-disease association prediction.

MambaTextCNN

As illustrated in Fig. 2, the MambaTextCNN model architecture represents a nuanced variation of the TextCNN framework⁵⁷. Let $\:{x}_{i}\in\:{\mathbb{R}}^{k}$ denote the k-dimensional vector corresponding to the i-th subsequence within the RNA sequence. A RNA of length n is expressed as:

$$\:{x}_{1:n}={x}_{1}⨁{x}_{2}⨁\cdots\:⨁{x}_{n}$$

(1)

.

Where $\:⨁$⨁\) serves as the concatenation operator. More formally, let $\:{x}_{i:i+j}$ represent the concatenation of the subsequence comprising $\:{x}_{i},{x}_{i+1},\cdots\:,{x}_{i+j}$.

Fig. 2

Architecture of the MambaTextCNN single-channel model for piRNA-disease association prediction.

The Mamba module performs feature extraction on the vector representations of RNA subsequences:

$$\:{X}_{1:n}=Mamba\left({x}_{1:n}\right)$$

(2)

.

The convolution operation involves a filter $\:W\in\:{\mathbb{R}}^{hk}$, which is applied to the window of h sub-sequences to yield a novel feature. For example, the feature $\:{c}_{i}$ is derived from the window of the sub-sequence $\:{X}_{i:i+h-1}$.

$$\:{c}_{i}=f(W\bullet\:{X}_{i:i+h-1}+b)$$

(3)

.

Where $\:b\in\:\mathbb{R}$ represents a bias term, while f denotes a nonlinear activation function, such as ReLU. The filter is systematically applied to each potential subsequence window within the RNA sequence $\:\{{x}_{1:h},{x}_{2:h+1},\cdots\:,{x}_{n-h+1:n}\}$ to generate a feature map.

$$\:C=\left[{c}_{1},{c}_{2},\cdots\:,{c}_{n-h+1}\right]$$

(4)

.

$\:C\in\:{\mathbb{R}}^{n-h+1}$. We apply a max pooling operation⁵⁸ on the feature map, designating the maximum value $\:\widehat{c}=\text{m}\text{a}\text{x}\left\{c\right\}$ as the feature associated with this specific filter. This process aims to capture the most salient feature for each feature map the one exhibiting the highest value.

The extraction method for each feature from individual filters has been detailed. This architecture employs filters with varying window sizes to generate distinct activations. These transformed outputs make up the penultimate layer before being processed through a fully connected softmax layer that outputs categorical likelihood predictions.

MambaCAttnGCN+

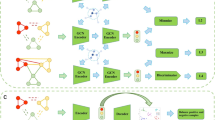
We propose a predictor, termed MambaCAttnGCN+, which integrates MambaTextCNN, GCN, and a cross-attention mechanism to predict piRNA-disease associations. To minimize the impact of positive samples on model performance during training, we employed PUL. The workflow of MambaCAttnGCN+, illustrated in Fig. 3, comprises three main steps: (a) generating embeddings for piRNA sequences using MambaTextCNN; (b) extracting piRNAs and disease features from the heterogeneous network via GCN; and (c) predicting association scores through the cross-attention mechanism.

Fig. 3

Flowchart of MambaCAttnGCN+. (A) Establishment of the piRNA-Disease Heterogeneity Network: Each piRNA sequence is segmented into multiple 3-mers, with feature vectors generated by word2vec substituting these 3-mers. Subsequently, the features of piRNA nodes are embedded using MambaTextCNN. (B) Feature extraction utilizing GCN: A heterogeneous network is constructed by integrating similarity matrices for piRNAs and diseases, along with their adjacency matrix. Graph convolutional networks (GCNs) are then applied to extract features for both node types. (C) Score prediction utilizing the cross-attention mechanism: In the encoder designed to extract piRNA features, the query (Q) matrix encodes piRNA representations, while the key (K) and value (V) matrices correspond to disease features; in the encoder for disease feature extraction, this assignment is reversed.

Embedding of PiRNA sequences for enhanced representation

Inspired by the DeepLncLoc model⁵⁹ we utilized k-mers in combination with MambaTextCNN to achieve piRNA embedding. The workflow for piRNA embedding is illustrated in Fig. 3(A), and the detailed steps are presented below:

• 1. Subsequence Division: Each piRNA sequence is divided into $\:m$ consecutive k-mer subsequences. The piRNA sequence representation is as follows:

$$\:piRNA={\tilde{P}}_{1},\cdots\:{\tilde{P}}_{2},\cdots\:,{\tilde{P}}_{m}$$

(5)

Here, $\:{\tilde{P}}_{i}$ represents the $\:i$-th subsequence of the piRNA sequence. The value of k is set to 3, with a stride window of 1. For example, the sequence “ACCAATG” is segmented into {ACC, CCA, CAA, AAT, ATG}.

• 2. Subsequence Vectorization: We utilize Word2vec⁶⁰ with a skip-gram architecture to pre-train embeddings for all 3-mer subsequences derived from piRNA sequences, thereby representing each 3-mer as a dense feature vector.

• 3. Subsequence Vector Encoding: Each piRNA sequence is divided into 31 overlapping 3-mers, which are mapped to 128-dimensional pre-trained embeddings. This process yields a matrix of shape (31, 128) per sequence. When processed in batches, the resulting tensor has shape (N, 31, 128), where N is the number of piRNA sequences.

• 4. Advanced Sequence Feature Extraction using MambaTextCNN: To capture both global and local dependencies within the piRNA sequences, we employ a multi-branch architecture consisting of three parallel pathways. Each pathway begins with a Mamba module configured with a state size of 16 and a convolution kernel size of 4. Following the Mamba module, each branch includes a 1D convolution layer with a kernel size of 1, 5, or 7, respectively, designed to extract local features at different granularities. A max pooling operation is then applied to each convolutional output to reduce dimensionality and emphasize the most salient features. Finally, the outputs from the three branches are concatenated to form a unified representation of shape (N, 384), where N is the number of piRNA sequences in the batch.

Heterogeneous piRNA-disease graph construction and GCN-based feature extraction

Establishment of the piRNA-disease heterogeneity network

We developed a heterogeneous piRNA-disease network, consisting of three types of edges (piRNA-disease edges, piRNA-piRNA edges, and disease-disease edges, denoted as $\:{E}_{piRNA-disease}$, $\:{E}_{piRNA-piRNA}$, and $\:{E}_{disease-disease}$, respectively. Here, $\:{E}_{piRNA-disease}$ is derived from the piRNA-disease associations in the original database MNDRv 4.0, while the other two edge types are based on similarities among homogeneous biological entities. The network comprises two categories of nodes (piRNAs and diseases, represented as $\:{V}_{piRNA}$ and $\:{V}_{disease}$, respectively). The piRNA-disease heterogeneous network can be formally expressed as:

$$\:{A}_{h}=\left[\begin{array}{cc}{S}_{p}^{seq+GIP}&\:{A}_{PD}\\\:{A}_{PD}^{T}&\:{S}_{d}^{sem+GIP}\end{array}\right]$$

(6)

.

In this equation, $\:{S}_{p}\in\:{\mathbb{R}}^{m\times\:m}$ denotes the piRNA similarity matrix, $\:{S}_{d}\in\:{\mathbb{R}}^{n\times\:n}$ signifies the disease similarity matrix, and $\:A\in\:{\mathbb{R}}^{m\times\:n}$ represents the piRNA-disease adjacency matrix. Here, $\:m$ indicates the number of piRNAs, while $\:n$ denotes the number of diseases.

PDA matrix

The adjacency matrix $\:{A}_{PD}$ characterizes the interrelationship between each piRNA and its corresponding disease:

$$\:{A}_{PD}=\left[\begin{array}{ccc}{a}_{11}&\:\cdots\:&\:{a}_{1n}\\\:⋮&\:\ddots\:&\:⋮\\\:{a}_{m1}&\:\cdots\:&\:{a}_{mn}\end{array}\right]$$

(7)

.

If the $\:i$-th piRNA is associated with the $\:j$-th disease, then $\:{a}_{ij}=1$; otherwise, $\:{a}_{ij}=0$.

PiRNA similarity matrix

The piRNA similarity matrix based on sequence and adjacency information is denoted as $\:{S}_{p}^{seq+GIP}\in\:{\mathbb{R}}^{m\times\:m}$. Assuming that piRNAs with similar sequences tend to share functional roles, we apply the Smith-Waterman alignment algorithm⁶¹ to quantify pairwise similarity. Sequence data are obtained from piRBase v3.0³. The normalized sequence similarity is calculated as:

$$\:{S}_{p}^{seq}\left({p}_{i},{p}_{j}\right)=\frac{SW({p}_{i},{p}_{j})}{\sqrt{SW({p}_{i},{p}_{i})\times\:SW({p}_{j},{p}_{j})}}$$

(8)

.

Here, $\:SW({p}_{i},{p}_{j})\in\:{\mathbb{R}}^{m\times\:m}$ denotes the sequence alignment score between the $\:i$-th and $\:j$-th piRNA. Additionally, Gaussian Interaction Profile (GIP) kernel similarity is computed based on the assumption that piRNAs with analogous disease interaction patterns are likely to be functionally related^{19,21,24,62,63}, defined as⁶⁴:

$$\:{S}_{p}^{GIP}\left({p}_{i},{p}_{j}\right)=\text{e}\text{x}\text{p}(-\lambda\:{‖{A}_{PD}\left({p}_{i},\right)-{A}_{PD}({p}_{j},)‖}^{2})$$

(9)

.

Where $\:{A}_{PD}\left({p}_{i},\right)$ and $\:{A}_{PD}({p}_{j},)$ denote the i-th and j-th row vectors of the adjacency matrix $\:{A}_{PD}$, respectively, while $\:{\lambda\:}_{p}$ represents the kernel width coefficient, defined as:

$$\:{\lambda\:}_{p}=\frac{1}{\frac{1}{{N}_{p}}{\sum\:}_{k=1}^{{N}_{p}}{||{A}_{PD}({p}_{k},)||}^{2}}$$

(10)

.

The piRNA similarity matrix is then constructed based on both sequence similarity and GIP kernel similarity, as follows:

$$\:{S}_{p}^{seq+GIP}=\frac{{S}_{p}^{seq}+{S}_{p}^{GIP}}{2}$$

(11)

.

Disease similarity matrix

Disease similarity is derived from the Disease Ontology (DO), which provides a standardized framework for capturing topological relationships among diseases⁶⁵ in a directed acyclic graph (DAG). The semantic similarity between the $\:i$-th and $\:j$-th diseases is calculated as follows:

$$\:{S}_{d}^{sem}\left({d}_{i},{d}_{j}\right)=\frac{{\sum\:}_{t\in\:{T}_{i}\cap\:{T}_{j}}({S}_{{d}_{i}}\left(t\right)+{S}_{{d}_{j}}\left(t\right))}{{\sum\:}_{t\in\:{T}_{i}}{S}_{{d}_{i}}\left(t\right)+{\sum\:}_{t\in\:{T}_{j}}{S}_{{d}_{j}}\left(t\right)}$$

(12)

Where $\:{T}_{i}$ represents the directed acyclic graph (DAG) of the $\:i$-th disease, while $\:{S}_{{d}_{i}}$ reflects the semantic influence of disease $\:t\in\:{T}_{i}$ on the $\:i$-th disease. The calculation methodology is outlined as follows:

$$\:\left\{\begin{array}{c}{S}_{{d}_{k}}\left(t\right)=max\left\{\theta\:\bullet\:{S}_{{d}_{k}}\left(\acute{t}\right)|\acute{t}\in\:children\:of\:(t)\right\}\:\:if\:{d}_{k}\ne\:{d}_{j}\\\:{S}_{{d}_{k}}\left(t\right)=1\:\:\:\:\:\:\:otherwise\end{array}\right.$$

(13)

.

Following prior studies²⁶ we set the attenuation parameter $\:\theta\:$ is established at 0.5. Similarly, the GIP kernel similarity among diseases is calculated as⁶⁴:

$$\:{S}_{d}^{GIP}\left({d}_{i},{d}_{j}\right)=\text{e}\text{x}\text{p}(-\lambda\:{‖{A}_{PD}\left(,{d}_{i}\right)-{A}_{PD}\left({,d}_{j}\right)‖}^{2})$$

(14)

.

Where $\:{A}_{PD}\left(,{\:d}_{i}\right)$ and $\:{A}_{PD}\left({,\:\:d}_{j}\right)$ denote the $\:i$-th and $\:j$-th column vectors of the adjacency matrix $\:{A}_{PD}$, respectively, while $\:{\:\lambda\:}_{d}$ represents the kernel width coefficient, defined as follow:

$$\:{\lambda\:}_{d}=\frac{1}{\frac{1}{{N}_{d}}{\sum\:}_{k=1}^{{N}_{p}}{‖{A}_{PD}\left({,d}_{k}\right)‖}^{2}}$$

(15)

.

The disease similarity matrix is then constructed based on both disease semantic similarity and GIP kernel similarity, as follows:

$$\:{S}_{d}^{sem+GIP}=\frac{{S}_{d}^{sem}+{S}_{d}^{GIP}}{2}$$

(16)

.

Feature extraction utilizing GCN

GCN are widely used for aggregating information from adjacent nodes and uncovering latent network structures^20,21,22,26 in network analysis tasks. Here, GCN is employed to extract piRNA-disease association features from heterogeneous graph networks. As illustrated in Fig. 3(B), the input relationship for GCN is synthesized using the similarity matrices of piRNA and diseases. Let $\:{H}^{l}\in\:{R}^{d}$ represent the node embedding at the $\:l$-th layer of GCN; thus, the computation of the node embedding $\:{H}^{l+1}\in\:{R}^{d}$ is computed as:

$$\:{H}^{l+1}=\sigma\:\left({\tilde{D}}^{-\frac{1}{2}}{\tilde{A}}_{h}{\tilde{D}}^{-\frac{1}{2}}{H}^{l}{W}^{l}\right)$$

(17)

$$\:{\tilde{A}}_{h}=I+\:{A}_{h}$$

(18)

$$\:\tilde{D}\left(i,j\right)={\sum\:}_{j}{\tilde{A}}_{h}(i,j)$$

(19)

.

Where $\:{A}_{h}$ is obtained from Eq. 6. The matrix $\:{\tilde{A}}_{h}$ denotes the adjacency matrix corresponding to the entire network, while $\:\tilde{D}$ represents the degree matrix of $\:{\tilde{A}}_{h}$. $\:I$ represents the identity matrix, $\:{H}^{l}$ refers to the node embedding at the $\:l$-th layer, and $\:{W}^{l}$ indicates the trainable parameter matrix. Additionally, $\:\sigma\:$ denotes the nonlinear activation function ReLU.

The initial embedding $\:{H}^{0}$ is formed by concatenating the piRNA embeddings obtained through MambaTextCNN with the disease embeddings $\:{S}_{d}^{sem}$ derived from the disease semantic similarity matrix. The first m rows of $\:{H}^{l}$ correspond to the piRNA embeddings, while the final n rows represent the disease embeddings, where m and n denote the respective quantities of piRNAs and diseases.

Score prediction utilizing the cross-attention mechanism

To better capture the complex relationship between piRNAs and diseases, a cross-attention mechanism is implemented (As shown in Fig. 4)³⁰. This mechanism enables the model to concentrate on relevant piRNA-disease pairs by integrating features from both piRNA and diseases. The input to the feature cross-attention module consists of the tRNA embedding and disease embedding obtained from the comprehensive view embedding $\:{H}^{l+1}$, as defined in Eq. 17.

Fig. 4

Multi-head cross-attention mechanism for modeling piRNA-disease interactions.

When extracting piRNA features, the encoder’s Q matrix input comprises piRNA embeddings, while the K and V matrices contain disease embeddings, and vice versa when extracting disease features. Scaled dot-product attention is calculated as follows:

$$\:Attention\left(\acute{Q},\acute{K},\acute{V}\right)=softmax\left(\frac{\acute{Q}{\acute{K}}^{T}}{\sqrt{{d}_{k}}}\right)\acute{V}$$

(20)

$$\:\acute{Q}=\overrightarrow{Q}{\overline{W}}^{Q}$$

(21)

$$\:\acute{K}=\overrightarrow{K}{\overline{W}}^{K}$$

(22)

$$\:\acute{V}=\overrightarrow{V}{\overline{W}}^{V}$$

(23)

.

Where $\:{\overline{W}}^{Q}$,$\:{\overline{W}}^{K}$,$\:{\overline{W}}^{V}$ are trainable parameter matrices, and $\:{d}_{k}$ as the feature vector dimension ($\:{d}_{k}$ = 256). The multi-head cross-attention mechanism aggregates information from multiple attention heads, allowing the model to capture diverse interaction patterns. The final correlation score for each piRNA-disease pair is computed as the inner product of their respective feature vectors derived from the model output.

$$\:MutilHead\left(\overrightarrow{Q},\overrightarrow{K},\overrightarrow{V}\right)=Concat({head}_{1},{head}_{2},\cdots\:,{head}_{h}){W}^{o}$$

(24)

$$\:{head}_{i}=Attention(\overrightarrow{Q}{\overline{{W}_{i}}}^{Q},\overrightarrow{K}{\overline{{W}_{i}}}^{K},\overrightarrow{V}{\overline{{W}_{i}}}^{V})$$

(25)

.

Here, h denotes the number of heads, with a default configuration set to 2.

The skip connection and normalization block that follows the MultiHead operation are designed to integrate both the original features and the aggregated features within the attention mechanism. Ultimately, the correlation score between each piRNA and disease is derived by computing the inner product of their respective feature vectors obtained from the model output.

Utilize PUL to identify reliable negative associations

In our dataset, due to factors such as cost and technical limitations, we only have ‘positive data’ validated through biological experiments and ‘unlabeled data’ that remains unverified. Unlabeled associations may contain hidden positives, so treating all unlabeled samples as negative could introduce bias, distort the dataset’s distribution, and ultimately degrade the model’s performance.

To address this issue, we applied the PUL to identify reliable negative associations⁶⁶. PUL has proven effective in tasks with substantial unlabeled data and a limited proportion of positive instances, such as data stream classification and information retrieval. In the context of piRNA-disease association prediction, several methods have employed bagging strategies to identify high-quality negative associations^7,19,62, while PUTransGCN²⁶ combines three distinct methods. Building on prior research, we employed a combination of these three methods to construct reliable negative samples.

The core idea of the spy technique is to embed known positive instances as ‘undercover agents’ within unlabeled associations, and then train an initial classifier under the assumption that all unlabeled examples are negative. For all unconfirmed negative associations, those with posterior probabilities lower than any undercover agent are classified as reliable negative associations. PU bagging involves classifying unlabeled associations using multiple relatively accurate, smaller classifiers, with associations that produce lower average scores across these classifiers being deemed reliable negative associations. The two-step approach iteratively updates the model to enhance classification accuracy and reliability. Detailed procedures are available in Supplementary Sect. 2.2.

Performance evaluation

We used 5-fold cross-validation to evaluate model performance. The results were obtained by calculating the average and variance of the final five iterations across all folds. The verified associations set $\:{\dot{\mathbb{P}}}^{+}$ and the unlabeled association sset $\:{\dot{\mathbb{P}}}^{U}$ are partitioned into five equally sized subsets as follows:

$$\:{\dot{\mathbb{P}}}^{+}={\dot{\mathbb{P}}}_{1}^{+}\cup\:{\dot{\mathbb{P}}}_{2}^{+}\cup\:{\dot{\mathbb{P}}}_{3}^{+}\cup\:{\dot{\mathbb{P}}}_{4}^{+}\cup\:{\dot{\mathbb{P}}}_{5}^{+}$$

(26)

$$\:{\dot{\mathbb{P}}}^{U}={\dot{\mathbb{P}}}_{1}^{U}\cup\:{\dot{\mathbb{P}}}_{2}^{U}\cup\:{\dot{\mathbb{P}}}_{3}^{U}\cup\:{\dot{\mathbb{P}}}_{4}^{U}\cup\:{\dot{\mathbb{P}}}_{5}^{U}$$

(27)

.

The delineation of the dataset is as follows:

$$\:{\dot{\mathbb{P}}}_{i}^{train}={\complement\:}_{{\dot{\mathbb{P}}}^{+}}{\dot{\mathbb{P}}}_{i}^{+}\cup\:{{PUL({\complement\:}_{{\dot{\mathbb{P}}}^{+}}{\dot{\mathbb{P}}}_{i}^{+}\cup\:\complement\:}_{{\dot{\mathbb{P}}}^{U}}\dot{\mathbb{P}}}_{i}^{U})$$

(28)

$$\:{\dot{\mathbb{P}}}_{i}^{test}={\dot{\mathbb{P}}}_{i}^{+}\cup\:{\dot{\mathbb{P}}}_{i}^{U}$$

(29)

.

Here, i∈[1,2,3,4,5], where $\:\complement\:$ represents the complement operation, and PUL refers to the selection of reliable negative samples. It is important to note that for each cross-validation iteration, the GIP kernel similarity matrices $\:{S}_{p}^{GIP}$ and $\:{S}_{d}^{GIP}$ must be recalculated based on a newly defined training set.

To tackle the issue of modeling with positive and unlabeled data, we incorporated three established PUL strategies (Spy, PU Bagging, and Two-Step) into the training pipeline of the MambaCAttnGCN + model. Specifically, during each fold of five-fold cross-validation, the dataset was divided into training and test sets. From the training set, we applied these PUL methods to identify a set of reliable negative samples from the unlabeled portion. These negative samples were then combined with the known positive samples to construct a training dataset $\:{\dot{\mathbb{P}}}_{i}^{train}$.

Importantly, the test set $\:{\dot{\mathbb{P}}}_{i}^{test}$contained both known positive samples and the remaining unlabeled data, which were not processed by any PUL method. This setup ensures that the model’s generalization performance is evaluated under a realistic positive-unlabeled setting. The incorporation of PUL in this manner enables the model to benefit from supervision while mitigating label noise and class imbalance.

To facilitate a more robust comparison with existing research approaches^{12,14,16,19,20}, we evaluated the performance of the predictive model using the area under the receiver operating characteristic curve (AUC), the area under the precision-recall curve (AUPR), and the ranking of positive predictions¹⁹. A lower rank index value indicates superior model performance. The formula for calculating the ranking index is as follows:

$$\:rand\:index=\frac{1}{\left|{\dot{\mathbb{T}}}_{test}^{+}\right|}\sum\:_{a\in\:{\dot{\mathbb{S}}}_{test}^{+}}\frac{{\gamma\:}_{a}}{\left|{\dot{\mathbb{T}}}_{test}\right|}$$

(30)

.

Where $\:\left|{\dot{\mathbb{T}}}_{test}^{+}\right|$ denotes the total number of known PDAs within the test subset $\:{\dot{\mathbb{T}}}_{test}^{+}$, while $\:\left|{\dot{\mathbb{T}}}_{test}\right|$ signifies the overall count of piRNA-disease pairs present in the same test subset. An association within the positive test subset $\:{\dot{\mathbb{T}}}_{test}^{+}$ is represented by $\:a$, and $\:{\gamma\:}_{a}$ indicates its rank position among all associations in this positive test set.

Implementation details

Our methodology was implemented using Python 3.10 and PyTorch 2.1, with all experiments conducted on a single NVIDIA RTX 4090 GPU equipped with 24GB of memory. The model was trained for a maximum of 220 epochs, during which all trainable parameters were optimized using the Adam optimizer at a learning rate of 0.001. A comprehensive summary of all hyperparameters is provided in Supplementary Table S9.

We performed a comparative analysis of the performance of MambaCAttnGCN + against seven state-of-the-art prediction models across two datasets. These models include ETGPDA²¹, iPiDi-PUL¹⁹, iPiDA-GCN²⁰, iPiDASWGCN²², iPiDA-GBNN²⁵, piRDA⁷ and PUTransGCN²⁶. The study referenced as²⁶ provided a comprehensive reproduction of the performance metrics for these models under configuration conditions to ours and included replicable code. Therefore, we utilized these results directly. This comparative evaluation aims to provide a clearer understanding of the effectiveness and advantages of our proposed model.