An elegant intellectual engine towards automation of blockchain smart contract vulnerability detection

Abstract

To prevent vulnerabilities and ensure app security, smart contract vulnerability detection identifies flaws in blockchain code. To overcome the limitations of traditional detection methods, this study introduces a novel approach that combines Explainable Artificial Intelligence (XAI) with Deep Learning (DL) to detect vulnerabilities in smart contracts. The proposed intellectual engine operates in multiple stages. First, a smart contract is created, and the user provides a value during the runtime phase. XAI and DL then analyze the opcodes in high-value contracts to detect potentially risky processes. If violations such as security protocol failures, insufficient funds, or account restrictions are found, the engine halts the transaction and generates an error report. If the contract passes this vulnerability assessment, it continues executing without interruption. This ensures flagged transactions remain functional while being assessed. Our proposed Hybrid Boot Branch and Bound Long Short-Term Memory (HB³LSTM) approach achieves outstanding performance, with an accuracy of 99.68%, precision of 99.43%, recall of 99.54%, and an F1-score of 99.40%, which surpasses the performance of existing methods.

Introduction

Blockchains are distributed databases with immutability and tamper-resistance¹. In smart contract systems, code is law, and conditions in smart contracts cannot be modified². Smart contracts offer multiple³. However, it can be difficult to address exploitable bugs in smart contracts written in languages like Solidity⁴. Ethereum’s open network and control of financial assets make smart contracts easy targets for attackers⁵. Bugs in smart contracts can have global effects, leading to hard forks and significant financial losses⁶. Existing methods for preventing financial losses due to flaw exploitation in smart contracts include data flow analysis, runtime monitoring, fuzzing, symbolic execution, and Satisfiability Modulo Theories (SMT) solutions⁷.

These techniques require human expertise, have long detection times, and do not cover all vulnerabilities⁸. Machine Learning (ML) has shown promise in detecting smart contract vulnerabilities, but existing solutions have limitations, requiring access to source code and being unable to identify specific vulnerability types, only classifying them as binary⁹. Smart contract vulnerabilities can be divided into four groups. Reentrancy attacks, where malicious contracts recursively call the original contract; integer overflow/underflow, causing incorrect calculations; improper access control, allowing unauthorized actions; and unchecked external calls, leading to failed or exploited interactions. Mitigations include using safe math, access controls, and handling external call errors¹⁰.

Additional risks, such as greedy contract designs and unprotected self-destruct instructions¹¹, can lead to Denial of Service (DoS) attacks. Miners can also influence transaction order, causing transaction order dependence¹². Mitigations include using safe math libraries, strong access control, error handling for external calls, and the “Checks-Effects-Interactions” pattern¹³. The use of Deep Neural Network (DNN) detectors is also gaining traction in automatically identifying and mitigating smart contract vulnerabilities¹⁴. These practices emphasize the importance of secure coding and thorough audits to prevent exploitation¹⁵.

DNN detectors can detect a variety of problems by keeping track of historical vulnerabilities¹⁶. With little data, transfer learning allows for rapid adaptability to new vulnerabilities¹⁷. It can be difficult to analyze Artificial Intelligence (AI) models and feature selection in closed systems¹⁸.

Learning-based vulnerability detection techniques have benefited from DL success in IoT security¹⁹. Effective vulnerability detection is becoming more and more necessary as smart contracts in blockchain systems proliferate in order to stop exploitation²⁰. Conventional approaches lack coverage and are labor-intensive and slow. Although machine learning, especially DL, has potential, it finds it difficult to adjust to new weaknesses. Models must retain prior knowledge while rapidly picking up new information through transfer learning. XAI integration improves smart contract security and guarantees transparency. In this study, a DL model known as HB³LSTM uses Long Short-Term Memory (LSTM) networks to identify smart contract vulnerabilities. For clear and understandable vulnerability detection, it incorporates XAI. The principal findings of this study are as follows:

• The goal is to improve finding vulnerabilities in smart contracts by using a phased approach that integrates DL and XAI to identify violations and ensure the safe execution of high-value contracts.

• HB³LSTM intellectual engine detects smart contract vulnerabilities by combining Branch and Bound Optimization algorithms (BBO) with LSTM networks. BBO is used for optimization, and LSTMs are used for sequence prediction. The model’s main goals are to spot potentially dangerous transactions and stop them.

• Improved Quantum online Portfolio Optimization (IQPO) to solve complex problems more quickly and shorten the time it takes to find vulnerabilities. This improves scalability and makes it possible to react to changes in the economy in real time by adjusting the portfolio.

• Smart contracts can be vulnerable to opcodes, causing issues like reentrancy, overflow, or access control flaws. XAI’s SHAP (SHapley Additive exPlanations) values are employed; contracts with positive values are considered invulnerable, while those with negative values are considered vulnerable.

This study is divided into five components. A review of the literature is given in “Literature Survey” Section, and the suggested model is explained in “Proposed methodology” Section. The outcomes of the suggested procedures are displayed in “Results and discussions” Section, along with a comparison of this model with a few other modern methods. The discussion is presented in “Conclusion” Section, and recommendations for additional research are made in Sect. 6.

Literature survey

In 2021, He et al.²¹ introduced a model for smart contract vulnerability detection, leveraging BERT for semantic feature extraction, BiLSTM for sequence learning, and an attention mechanism to prioritize critical features. This approach enhances detection accuracy and generalization, outperforming traditional methods in identifying security flaws in smart contracts.

In 2022, Jingya Dong et al.²² Proposed a feasible energy trading method to achieve a self-sufficient energy consumption. It provides the accurate energy transfer signals in the blockchain to attain the better self-sufficiency of transactions.

In 2022, Jingya Dong et al.²³ suggested a novel transaction processing method to protect private data using mapping algorithm to solve the privacy attacks. It also improves the performances of efficient executions of transactions using the privacy preserving decentralized energy trading scheme.

In 2022, Jingya Dong et al.²⁴ introduced a method light weight data fusion to reduce the network congestions and wastage of bandwidth with the secure analysis for IOT. Furthermore, proposed an improved hierarchical fuzzy based hashing technique to local the anomalies in the machine learning models to ensure the security of the sensitive data.

In 2023, Wu et al.²⁵ investigated the techniques for locating smart contract vulnerabilities, highlighting the shortcomings of conventional methods. They highlighted the use of machine learning, especially DL and attention processing, for improved accuracy. The paper’s conclusion noted the need for detecting methods that are more dependable and scalable.

In 2023, Yazdinejad et al.²⁶ introduced a secure, intelligent fuzzy blockchain framework to enhance threat detection in blockchain-based IoT networks, addressing uncertainty and ambiguity in IoT data. It combines a fuzzy DL model, optimized ANFIS, fuzzy matching, and a fuzzy control system to detect and mitigate network attacks.

In 2023, Chen et al.²⁷ suggested a novel method for smart contract vulnerability detection by constructing a Semantic Graph (SG) for each function, capturing both syntax and semantic relationships. It then utilizes an Edge-Attention Residual Graph Convolutional Network (EA-RGCN) to extract content and semantic features.

In 2023, Ma et al.²⁸ introduced a Hierarchical Graph Attention Network (HGAT) for smart contract vulnerability detection, addressing the inefficiencies of existing methods. It Constructs Code Graphs (CFG) from Abstract Syntax Tree (AST) and Control Flow Graph (CFG) to extract node features and applies Graph Attention Network (GAT) for feature learning.

In 2023, Jie et al.²⁹ introduced static analysis and multimodal AI techniques that have improved the detection of smart contract vulnerabilities. To define 84 efficient vulnerability-uncovering techniques, strategies make use of code and graph embeddings from word2vec, Transformer-Based Bidirectional Encoder Representation (BERT), and Graph Convolutional Network (GCN) models. In intermodal, intermodal, and multimodal contexts, this encompasses feature selection, fusion, training, and decision-making units. Bidirectional Long Short-Term Memory (BiLSTM) models, thick layers, Random Forest (RF), Max Pooling (MP), Spatial Pyramid Pooling (SPP), and text Convolutional Neural Networks (CNNs) are examples of high-accuracy jobs.

In 2023, Dong et al.³⁰ proposed a network called decentralized autonomous oracle network combined with consensus protocol and non-interactive reputation maintenance to secure the smart contract to be more reliable and tamper-proof inputs and output.

In 2024, Osei et al.³¹ suggested WIDENNET, a DL-based method using WDE and DNN to detect vulnerabilities in smart contracts. It focuses on identifying reentrancy and timestamp dependence issues by extracting byte codes and converting them into operational codes.

In 2024, Sharma et al.³² introduced two detection techniques used by the Intrusion Detection System (IDS): anomaly-based IDS, which detects known hostile activities, and signature-based IDS, which detects abnormal system behavior. Signature-based IDS is inefficient due to its reliance on pre-existing signatures and limitations in storage and computation, making it unable to detect new attacks. Anomaly-based IDS can detect novel attacks but may also produce false positives.

In 2024, Zhen et al.³³ introduced a Dual Attention Graph Neural Network (DA-GNN) for smart contract vulnerability detection. It converts Control Flow Graph (CFG) opcode sequences into feature matrices and leverages a dual attention mechanism for improved node embedding updates.

In 2024, Wu et al.³⁴ introduced a two-pronged approach to smart contract vulnerability detection. It improved detection efficiency and accuracy by combining static and dynamic analysis. The approach provided a more reliable security solution and performed better than conventional methods.

In 2024, Mothukuri et al.³⁵ suggested a novel AI-driven solution to address the DeFi credibility issue by introducing a Trust Score system that evaluates DeFi projects using four key risk factors. These include smart contract vulnerabilities, suspicious transactions, anomalous price changes, and scam sentiment from social media, two of which are novel in DeFi fraud detection.

In 2025, Dong et al.³⁶ introduced a P2P energy efficient trading system to permit the users to conduct an energy efficient transaction without the having the contribution of third party. It helps to improve the high performance and efficiency to meet the energy efficient tractions in the trading system. A comparison of recent works is presented in Table 1.

Table 1 Comparisons for recent works.

Problem statement

One of the main challenges to smart contract analysis is the dearth of open-source resources, the inability to discover vulnerabilities in bytecode, and a high false rate in detection techniques. Complexity is increased by scalability problems, lengthy vulnerability discovery times, and the requirement for ongoing IoT network monitoring. Furthermore, issues with large data quality, computational cost, and the lack of transparency of AI models undermine confidence in automated analysis, which makes it more difficult to properly protect these systems. To address these drawbacks, the proposed method, “HB³LSTM: Smart contract-based vulnerability detection using deep explainable AI,” uses an HB³LSTM intellectual engine framework to overcome these challenges. The IQPO is used to reduce vulnerability detection processing time and improve scalability. The HB³LSTM intellectual engine can improve predictive accuracy and reduce risks by efficiently resolving vulnerabilities. Furthermore, SHAP helps to improve the accuracy. Our ultimate objective is to improve the detection methods’ capacities in order to more accurately detect smart contract flaws.

Proposed methodology

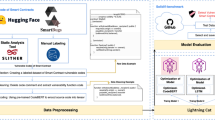
The proposed methodology for identifying smart contract vulnerabilities includes several important phases. First, data from Smart Bugs Wild Dataset uses Natural Language Processing (NLP) techniques for preprocessing, such as word segmentation, lexical analysis, word-to-vector conversion, and TF-IDF for feature extraction. To maximize processing time and scalability, feature selection is then carried out using IQPO. A new hybrid approach called the HB³LSTM intellectual engine finds and blocks risky transactions and extracts code fragments that highlight vulnerabilities. To improve vulnerability detection, the model collaborates with expert systems. The next step involves interpreting model outputs using XAI approaches like SHAP values. Negative values draw attention to aspects associated with vulnerabilities, making it easier to identify crucial opcodes influencing contract security, while positive values show characteristics that contribute to invulnerable contracts. Figure 1 describes the overall proposed methodology.

Fig. 1

Overall proposed methodology.

Dataset collection

Our study leverages the Kaggle Smart Bugs Wild Dataset³⁷, which includes over 1250 Solidity-written smart contracts, vulnerable and non-vulnerable, annotated with specific vulnerability types such as reentrancy, integer overflow/underflow, and access control issues.

Opcode extraction

Smart contracts are self-executing agreements with terms encoded in opcode. Simplifying opcode enhances efficiency and reduces transaction costs by minimizing complexity. This ensures correct operation across scenarios like caller authorization and transaction validity while preserving functionality [38]. Table 2 describes the opcode extraction from the SmartBug wild dataset.

Table 2 Opcode extraction from SmartBug wild dataset.

The input–output mechanism of SOLC is used to extract opcodes, guaranteeing consistency between compiler versions. The function name can be compared to the Application Binary Interface (ABI); a cross-check is carried out to retrieve opcodes solely from injected contracts. Algorithm (1) describes the opcode extraction algorithm in detail. An ABI and an ordered set of opcodes are both included in every contract.

$$C = \left\{ {\left( {ABI_{1} ,O_{1} } \right),\left( {ABI_{2} ,O_{2} } \right), \ldots ,\left( {ABI_{n} ,O_{n} } \right)} \right\}$$

(1)

where $C$ is the collection of contracts that SOLC returned in order to explain the sifting procedure,$ABI_{n}$ indicates the ABI for the $n^{th}$ contract and $O_{n}$ indicates the ordered list of opcode for the $n{\text{th}}$ contract. Opcodes like PUSH, which has 32 possibilities, and other operations like MSTORE, CALL VALUE, ISZERO, and JUMPI are simplified to minimize variations.

Preprocessing

In data preprocessing, smart contract code undergoes lexical analysis, symbol removal, and word segmentation; TF-IDF is applied for feature and word-to-vector conversion maps²⁵.

Lexical analysis in smart contract vulnerability identification tokenizes raw Solidity code into meaningful units like keywords, operators, identifiers, and delimiters while removing comments and whitespace. Symbol removal eliminates non-informative components like comments, blank lines, and useless code, reducing noise and computational complexity. This helps the model focus on relevant code patterns, improving accuracy and speeding up training and inference. Word segmentation divides code into discrete tokens, ensuring each component is processed independently while preserving structure. This enhances the model’s ability to detect vulnerabilities by focusing on important patterns and relationships. TF-IDF is a text vectorization method for feature extraction. It combines Term Frequency (TF), which weights words based on their frequency in a document, with Inverse Document Frequency (IDF), which reduces the weight of common terms across documents.

$$TF\left( {t,d} \right) = \frac{b}{B}$$

(2)

where $b$ represents the number of times $t$ appears in the document $d$ and $B$ represents the total number of terms in a document $d$.

$$IDF\left( {t,D} \right) = \log \,\left( \frac{a}{A} \right)$$

(3)

where $a$ denotes the total number of documents in the corpus and $A$ denotes the number of documents containing term $t$. The TF-IDF score for a term in a document is obtained by multiplying its TF and IDF scores.

$$TF - IDF\left( {t,d,D} \right) = TF\left( {t,d} \right) \times IDF\left( {t,D} \right)$$

(4)

TF-IDF transformation can be as a

$$z = \,\,encoder\,\left( X \right)$$

(5)

where $X$ denotes the input feature matrix extracted from smart contract opcode and $z$ denotes the resulting TF-IDF vector representation of the input data. This map is to the actual application of converting tokens to vector form using the TF-IDF encoder. Figure 2 shows the code for the preprocessing.

Fig. 2

Preprocessing code.

The parameter settings for the TF-IDF were selected based on a systematic hyperparameter tuning procedure. Each setting was evaluated through repeated experiments using a validation split to measure its effect on downstream model performance. The max_features parameter was set to 10,000 after testing various thresholds; this value best preserved relevant vocabulary while preventing overfitting. The choice of n-grams (1, 2) was validated through comparisons with unigram- and trigram-only setups, where (1, 2) provided optimal contextual richness. Stop word removal via NLTK improved classification accuracy by reducing noise. L₂ normalization outperformed L₁ in maintaining consistent feature scaling and stable model behavior. Smooth_IDF was enabled to handle unseen terms without destabilizing inverse frequency values. Sublinear TF scaling was included after observing improvements in model generalization and robustness. This tuning process involved grid-like evaluation and iterative refinement across these parameters, as shown in Table 3.

Table 3 TF-IDF parameter settings.

Word-to-vector conversion captures the semantic linkages between code parts by converting tokens into numerical vectors using embedding approaches. This improves the model’s capacity to identify vulnerabilities like inappropriate variable use or dangerous dependencies by helping it comprehend how the contract interacts.

Improved quantum online portfolio optimization (IQPO) for feature selection

IQPO³⁹ is a quantum computing-based framework that enhances online decision-making in financial markets by leveraging quantum algorithms such as quantum state preparation, norm estimation, and inner product estimation. It is chosen for feature selection because of its ability to process high-dimensional data efficiently, dynamically adapt to evolving datasets, and achieve a quadratic speedup in computation compared to classical methods. The key advantage of IQPO is its ability to use quantum oracles to encode feature relevance scores, perform fast probabilistic sampling using multi-sampling algorithms, and estimate importance measures through quantum inner product computations, making it ideal for selecting the most informative features in real-time machine learning tasks.

Quantum representation of feature data

Instead of classical access to feature vectors, assume quantum access through a set of unitaries $P_{{\rho^{\left( u \right)} }}$, representing the transformed feature importance values at time $u$. The input data is encoded as

$$P_{{\rho^{\left( u \right)} }} \left| j \right\rangle \left| {\vec{0}} \right\rangle = \left| k \right\rangle \left| {\rho_{j}^{\left( u \right)} } \right\rangle$$

(6)

where $\rho^{\left( u \right)} = \left( {\rho_{1}^{\left( u \right)} ,\rho_{2}^{\left( u \right)} , \ldots ,\rho_{n}^{\left( u \right)} } \right)$ is the feature vector at the time $u$, $\max_{j\varepsilon \left[ o \right]} \rho_{j}^{\left( u \right)} = 1$ ensures feature values are normalized and $\rho_{j}^{\left( u \right)} \ge s_{\min } > 0$ guarantees all features have a minimum significance level. This encoding allows efficient quantum computations on the feature space, preparing for importance ranking.

Quantum portfolio weight update rule

The weight update for each feature follows a softmax-like transformation, capturing cumulative importance over multiple time steps:

$$\omega_{j}^{{\left( {u + 1} \right)}} = \frac{{\exp \left( {\eta \sum\nolimits_{{u^{\prime } = 1}}^{u} {\frac{{\rho_{j}^{\left( u \right)} }}{{\omega^{{\left( {u^{\prime } } \right)}} \cdot \rho^{{\left( {u^{\prime } } \right)}} }}} } \right)}}{{\sum\nolimits_{j = 1}^{o} {\exp \left( {\eta \sum\nolimits_{{u^{\prime } = 1}}^{u} {\frac{{\rho_{j}^{{\left( {u^{\prime } } \right)}} }}{{\omega^{{\left( {u^{\prime } } \right)}} \cdot \rho^{{\left( {u^{\prime } } \right)}} }}} } \right)} }}$$

(7)

where $\omega \left( 1 \right) = \left( {\frac{1}{n}, \ldots ,\frac{1}{n}} \right)$ initializes all features with equal importance, $\eta$ denotes a learning rate that controls the impact of past observations, and $\rho_{j}^{\left( u \right)}$ denotes the importance score of feature $j$ at time $u$. This update ensures that the most relevant features gain higher importance while less significant features are gradually suppressed.

Quantum computations for feature selection

To efficiently compute cumulative feature importance in superposition, define the following transformations:

$$\left| j \right\rangle \left| {\vec{0}} \right\rangle \to \left| j \right\rangle \left| {\sum\limits_{{u{\prime} = 1}}^{u - 1} {\frac{{\rho_{j}^{{\left( {u{\prime} } \right)}} }}{{\tilde{J}^{{\left( {u{\prime} } \right)}} }}} } \right\rangle$$

(8)

This transformation allows encoding past feature gains into a quantum state for efficient parallel computation. Furthermore, a quantum unitary to extract feature selection scores:

$$\left| j \right\rangle \left| 0 \right\rangle \to \left| j \right\rangle r_{j}^{\left( u \right)} ,\;r_{j}^{\left( u \right)} = \exp \left( {\eta \sum\limits_{{u^{^{\prime} = 1} }}^{u - 1} {\frac{{\rho_{j}^{{\left( {u^{\prime } } \right)}} }}{{\tilde{J}^{{\left( {u^{\prime } } \right)}} }}} } \right)$$

(9)

This representation allows rapid ranking of features based on their cumulative contribution.

Quantum norm estimation for feature importance

To measure the total contribution of each feature vector $w$, estimate its norm using quantum queries:

$$\left| {\left\| w \right\|_{1} - \tilde{a}} \right| \le \varepsilon \left\| w \right\|1$$

(10)

The required query complexity for this estimation is

$$P\left( {\frac{{\left){\vphantom{1z}}\right. \!\!\!\!\overline{\,\,\,\vphantom 1{z}}}}{ \in }\log \left( {\frac{1}{\delta }} \right)} \right)$$

(11)

where $\in$ controls the approximation accuracy, $\delta$ denotes the confidence level of the estimation, and $z$ denotes the total number of features. This step ensures that feature importance scores are precisely quantified, helping to refine the selection process.

Quantum inner product estimation for feature ranking

To evaluate the correlation between feature vectors, compute the inner product using quantum estimation:

$$\left| {\tilde{J}\tilde{Q} - v \cdot w} \right| \le \varepsilon \,v \cdot w$$

(12)

where $\tilde{J}\tilde{Q}$ denotes the quantum estimate of $v.w$. This estimation is performed efficiently with a quantum complexity of

$$P\left( {\frac{\sqrt m }{{\varepsilon \sqrt {v_{\min } } }}\log \left( {\frac{1}{\delta }} \right)} \right)$$

(13)

where $\delta$ denotes the failure probability, $P$ denotes the number of quantum gates, $m$ denotes the feature vectors, $v_{\min }$ ensures that no feature has a negligible contribution. By applying inner product estimation, features undergo ranking based on their relevance.

Quantum multi-sampling for feature selection

To finalize feature selection, quantum multi-sampling identifies the top $p$ features by ensuring:

$$U \ge \left\| {qx} \right\|_{1}$$

(14)

$$\left| {U - \left\| q \right\|1} \right| \le \min \left\{ {1/\sqrt {p,\,} \varepsilon } \right\}\left\| q \right\|1$$

(15)

where $U$ denotes the inner product sum over selected features,$||q||$ denotes the expected outcome, $\sqrt p$ denotes the number of quantum gates root values, and $||qx||$ denotes the length of the vector. The expected run-time complexity for multi-sampling is

$$P\left( {\sqrt {tz} \,\log \,\left( {\frac{1}{\delta }} \right)} \right)$$

(16)

where $P$ denotes the cumulative importance of selected features, $tz$ denotes the number of features to select. This step ensures that only the most significant features are retained for vulnerability detection. Once IQPO selects the most informative features, they are used as input to the HB³LSTM model.

$$X^{\prime } = QOPO\left( X \right)$$

(17)

where $X$ denotes the original feature matrix before selection, and $X^{\prime }$ denotes the optimized and selected subset of features most relevant to vulnerability detection. This represents IQPO transforming the original feature set into a selected, optimized set. HB³LSTM processes the feature vectors and applies DL techniques to detect software vulnerabilities. This integration enhances both accuracy and computational efficiency, enabling real-time detection of potential security threats. The IQPO algorithm was tested primarily on Qiskit’s statevector simulator to emulate noiseless quantum computations. The simulation utilized 8 qubits to represent the feature space encoding and enable quantum operations such as state preparation, norm estimation, and inner product estimation. The choice of 8 qubits balances computational tractability with sufficient feature dimensionality representation for the datasets in use.

Table 4 shows the parameter settings for the IQPO. The QLR was set to 0.001 to ensure gradual convergence while maintaining stability, particularly in complex search spaces. The decay rate of 0.95 was chosen to enable adaptive learning rate reduction, helping the algorithm fine-tune its learning behavior over time. A regularization factor of 0.01 was incorporated to mitigate overfitting by penalizing overly complex solutions, which is essential for generalization. The quantum walk probability was fixed at 0.5 to strike a balance between global exploration and local exploitation. Although a systematic hyperparameter tuning procedure such as grid search or Bayesian optimization was not exhaustively applied due to computational constraints, the selected values were empirically validated through sensitivity analysis across benchmark datasets. This approach ensured that the chosen parameters provided consistently good performance, even if not globally optimal.

Table 4 Parameter settings for IQPO.

Hybrid boot branch and bound long short-term memory (HB³LSTM) for vulnerability detection

The HB³LSTM is a combination of Boot LSTM⁴⁰ and BBO. It is a novel strategy that combines the advantages of several approaches to enhance smart contract vulnerability identification. This method combines an LSTM network, which functions well for a series of prediction tasks, with algorithms that are commonly employed in optimization problems. With an emphasis on identifying potentially hazardous transactions and preventing risky behavior in smart contracts, the HB³LSTM model is especially made to extract code fragments that expose vulnerabilities.

LSTM

A specialized kind of Recurrent Neural Network (RNN) called an LSTM is employed in our study as a model to capture temporal dependencies in sequential data. LSTM learns sequence patterns by retaining knowledge across time steps through gates (input, forget, output) and a tanh layer. The cell state carries important information, enabling selective updates. This architecture is ideal for sequence prediction tasks. The typical LSTM cell structure is depicted graphically in Fig. 3.

Fig. 3

Typical LSTM cell structure.

Which data from earlier time steps should be ignored is decided by the first layer, also referred to as the forget layer. Equation (18) provides the mathematical expression of the forget gate’s output $\left( {g_{t} } \right)$.

$$g_{t} = \sigma \left( {W_{g} \cdot \left[ {n_{t - 1} ,X_{t} } \right] + b_{f} } \right)$$

(18)

where $\sigma$ denotes the sigmoid role of activation, $W_{g}$ denotes the forget gate’s weight, $b_{f}$ indicates the forget gate’s bias, $X_{t}$ denotes the time $t$_,and $n_{t - 1}$ is the hidden layer of time. In the LSTM, the input gate ($j_{t}$) is the second layer that decides whether the cell state receives fresh data. This choice, determined by applying the subsequent formula, is shown in Eq. (19).

$$j_{t} = \sigma \left( {W_{j} \cdot \left[ {n_{t - 1} ,X_{t} } \right] + b_{j} } \right)$$

(19)

where $W_{j}$ indicates input gate weight and $b_{j}$ indicates input gate bias. The tanh layer, sometimes referred to as the cell state layer ($\hat{D}_{t}$), is the third layer. Equation (20) defines the vector of new candidate values that are produced by this layer:

$$\hat{D}_{t} = \phi \left( {W_{D} \cdot \left[ {h_{t - 1} ,X_{t} } \right] + b_{D} } \right)$$

(20)

where $\varphi$ denotes the function of tanh, $W_{D}$ denotes the weight of the cell, and $b_{D}$ denotes the bias cell. The old cell state $\hat{D}_{t}$ is changed into the new cell state $D_{t}$ following the first three layers. The interplay between the input gate and the forget gate produces this update. According to Eq. (21), new data is added by the input gate, while old data is discarded by the forget gate.

$$D_{t} = g_{t} D_{t - 1} + j_{t} \hat{D}_{t}$$

(21)

where $D{}_{t}$ new cell, $J_{t}$ denotes the input gate, and $g_{t}$ denotes the output gate. The last layer, the output gate, is in charge of generating the final output in accordance with the modified cell state. The output gate operates in the following manner:

$$p_{t} = \sigma \left( {W_{p} \cdot \left[ {h_{t - 1} ,X_{t} } \right] + b_{p} } \right) \cdot \phi \left( {D_{t} } \right)$$

(22)

where $W_{p}$ denotes output gate weight and the $b_{p}$ indicates output gate bias.

Bootstrap

Bootstrap is a general statistical inference approach that builds a sampling distribution by uniformly sampling with replacements from the original data. It is widely used as a robust alternative to parametric statistical inference, which may be unreliable due to complexities in computing standard errors. Bootstrap methods are particularly useful when parametric assumptions fail or are difficult to verify. Three bootstrap techniques exist for regression analysis: pairs bootstrap, standard residuals bootstrap, and wild residuals bootstrap. Among these, pairs bootstrap is preferred for problems like SPF, where observations are correlated. This method helps preserve the dependence structure between observations, ensuring more reliable statistical inference. By resampling from the original data, it provides better estimations without relying on strict distributional assumptions. For vulnerability detection, bootstrap and LSTM integrate by leveraging bootstrap resampling to enhance training data variability and model robustness. Bootstrap helps generate diverse datasets, reducing overfitting, while LSTM captures temporal dependencies for accurate predictions. This combination improves the reliability and generalization of the vulnerability detection model.

Integrated boot LSTM

In the proposed Boot-LSTM framework for vulnerability detection, bootstrapping enhances the robustness of LSTM models by training them on multiple bootstrapped datasets. This approach is particularly beneficial in handling the variability and uncertainty in cybersecurity threat patterns caused by evolving attack techniques. Furthermore, bootstrapping facilitates the exploration of LSTM behavior on different resampled sequences of vulnerability datasets, each potentially representing diverse cyber threat scenarios. By continuously generating diverse detection outcomes during resampling and leveraging temporal correlations identified by LSTM, the model produces high-quality predictive indicators that account for the inherent uncertainty of threat evolution. To improve detection accuracy, the model’s weights are refined through the BBO algorithm, enhancing the reliability of vulnerability assessments. This hybrid approach strengthens adaptability and reduces false positives, leading to more effective cyber threat detection in dynamic environments. The optimized feature set is passed through an encoding module of HB³LSTM to generate latent representations $z$, which are further used by a classifier layer to produce vulnerability predictions $y_{pred}$.

$$y_{pred} = classifier\left( z \right)$$

(23)

Where $y_{pred}$ denotes the predicted output indicating software vulnerability status. The detection stage identifies various classes of software vulnerabilities, including time manipulation, front running, DoS, reentrancy, access control issues, arithmetic errors, unchecked low-level calls, and other types. The architecture of HB³LSTM has been shown in Fig. 4.

Fig. 4

Architecture of HB³LSTM.

Table 5 shows the hyperparameter settings for HB³LSTM. The hyperparameters were chosen based on a combination of empirical testing, and domain-specific considerations to ensure robust performance. The three-layer structure allows HB³LSTM to effectively capture hierarchical temporal features, a common practice in deep sequence models. A hidden unit size of 256 provides a balance between expressive power and computational tractability. The dropout rate of 0.3 was selected based on preliminary experiments that indicated it effectively reduced overfitting without compromising learning. A batch size of 64 was used to balance memory constraints with training stability. The BBO optimizer was chosen for its proven adaptability and fast convergence in DL tasks. The learning rate of 0.0005 was fine-tuned empirically to ensure smooth training dynamics. Overall, the selected hyperparameters reflect a pragmatic balance between experimental insight and best practices from the existing performance.

Table 5 Hyperparameter settings for HB³LSTM.

Enhancing weight update with branch and bound algorithm

An optimization technique called BBO⁴¹ has been effectively used for smart contract vulnerability detection. BBO is an optimization algorithm that systematically explores solution spaces by computing bounds and eliminating suboptimal solutions, making it effective for constrained problems. It is chosen over heuristic or greedy methods because it guarantees global optimality while efficiently navigating large solution spaces through intelligent pruning. Unlike heuristic or greedy methods, BBO avoids unnecessary computation by bounding suboptimal regions, making it scalable and practical for high-dimensional problems. Its flexibility supports complex constraints like sparsity, and it can be tailored to exploit specific problem structures. It balances optimality, efficiency, and adaptability, making it ideal for structured optimization tasks. In the optimization, the weight parameters of the Boot LSTM network are trained using BBO to enhance convergence and prevent getting stuck in local minima. By applying BBO, the model efficiently refines weight updates, prioritizing critical features related to smart contract vulnerabilities.

Initialization

For the initialization of the first and second blocks, it can be represented as

$$M^{\left( 0 \right)} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right],\;v^{\left( 0 \right)} = \left[ {\begin{array}{*{20}c} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} } \right]$$

(24)

where $M^{\left( 0 \right)}$ denotes the initialization phase of the upper bound, and $v^{\left( 0 \right)}$ denotes the initialization phase of the lower bound.

Fitness function

In the fitness function, LSTM weight parameters are optimized to minimize detection error and enhance model accuracy. It can be denoted as

$$Fitness\,\,function = Min(W_{D} )$$

(25)

where $Min(W_{D} )$ denotes the minimizing the weight from the Boot LSTM. By optimizing this function, BBO ensures that the model reduces false positives, improves convergence speed, and focuses on learning from critical opcode sequences related to smart contract vulnerabilities. The fitness evaluation continues iteratively until optimal or near-optimal values are found.

Branching process

The branching process is central to the BBO algorithm. It systematically explores the search space using a binary enumeration tree, where each node corresponds to a candidate subproblem. At each node, a pair of binary vectors is maintained. For the lower bound vector:

$${\rm M}\,\,: = \left( {M_{1} ,M_{2} ,\,.\,.\,.,M_{q + r} } \right)^{\rm T} \in \left\{ {0,1} \right\}^{q + r}$$

(26)

For the upper bound vector:

$$v: = \left( {v_{1} ,v_{2} , \ldots ,v_{q + r} } \right)^{\rm T} \in \left\{ {0,1} \right\}^{q + r}$$

(27)

Each binary variable $a_{k} \in \left\{ {0,1} \right\}$ is bounded by the corresponding entries $M_{k} \le a_{k} \le v_{k}$ for all $k \in \left\{ {1, \ldots ,p} \right\}$_.. At the root node, starts with $M = 0$ and $v = 1$, representing the unconstrained space. . The process of branching involves selecting an unfixed variable $a_{k}$ and creating two child nodes as $M_{k} = v_{k} = 0$ and $M_{k} = v_{k} = 1$.This recursive process continues until all variables are uniquely determines $a$. The feasibility of a node is ensured by a constraint that the number of non-zero entries in a subset of $a$ should lay within a desired target:

$$\sum\limits_{k = 1}^{q} {M_{k} } \le \theta_{y} \le \sum\limits_{k = 1}^{q} {v_{k} } ,\;\sum\limits_{k = 1}^{r} {M_{q + k} } \le \theta_{z} \le \sum\limits_{k = 1}^{r} {v_{q + k} }$$

(28)

where $q$ denotes the number of variables in the first block, $r$ denotes the number of variables in the second block, and $\theta_{y} ,\theta_{z}$ denotes the target sparsity level for each block. This branching structure allows for efficient pruning and ensures only feasible and promising paths are explored.

Terminal node

A terminal node is one where no further branching is necessary because the solution is either fully determined or satisfies the stopping condition. The terminal node function can be represented as:

$$ter\min al\left( {\left( {M,v} \right),\left( {t,u} \right),\theta } \right): = \left\{ {\begin{array}{*{20}c} {true} & {if\sum\nolimits_{k = t}^{u} {M_{k} = \theta ,} } \\ {true} & {f\sum\nolimits_{k = t}^{u} {v_{k} = \theta ,} } \\ {false} & {otherwise} \\ \end{array} } \right.$$

(29)

For the first block, the node is terminal if:

$$\begin{gathered} ter\min al\left( {\left( {M,v} \right),\left( {1,q} \right),\theta_{y} } \right) = true \hfill \\ \sum\limits_{k = 1}^{q} {M_{k} } = \theta_{y} \;\left( {{\text{or}}} \right)\;\sum\limits_{k = 1}^{q} {v_{k} } = \theta_{y} \hfill \\ \end{gathered}$$

(30)

_{For the second block, the node is terminal if:}

$$\begin{gathered} ter\min al\left( {\left( {M,v} \right),\left( {q + 1,q + r} \right),\theta_{y} } \right) = true \hfill \\ \sum\limits_{k = 1}^{r} {M_{q + k} = \theta_{z} } \;\left( {{\text{or}}} \right)\;\sum\limits_{k = 1}^{r} {v_{q + k} } = \theta_{z} \hfill \\ \end{gathered}$$

(31)

If both conditions are met, the solution vector xx is complete and marks the terminal node. Terminal nodes represent either optimal or bounded suboptimal solutions and are essential in concluding viable paths in the solution tree.

Lower and upper bounds

To avoid unnecessary exploration, each feasible node is evaluated by computing bounds on the objective value. An upper bound is computed by relaxing the sparsity constraint and setting all unfixed variables to their upper limit.

$$upper\left( {M,v} \right) = \lambda_{\max }^{ * } \left( v \right)$$

(32)

where $a = v$ denotes all the remaining variables active and $\lambda_{\max }^{ * }$ denotes the objective value. A lower bound is derived by greedily building a feasible solution within the sparsity constraint. Variables are selected based on descending importance measured from the first block and the second block until the sparsity limits $\theta_{y}$ and $\theta_{z}$ are met. The resulting vector $a^{LB}$ is used to compute

$$lower = \left( {M,v} \right) = \lambda_{\max }^{ * } \left( {a^{LB} } \right)$$

(33)

This provides a valid bound from a feasible configuration. These bounds help eliminate suboptimal paths early and prioritize exploration of the most promising branches. Evaluating bounds is critical for maintaining computational efficiency while ensuring the search remains on track toward optimal solutions.

Re-evaluating the fitness

The optimization process repeatedly re-evaluates the LSTM weights and feature selections to minimize detection error and refine accuracy. This cycle continues until the model converges to the most optimal and globally accurate configuration.

Termination

The process terminates once the best solution is found that satisfies all constraints with minimal error. At this point, no further branching is needed, and the optimized weights are finalized for deployment. The optimized weights from the Boot LSTM model, refined using the BBO, are fed into SHAP for interpretability. SHAP analyzes the model predictions by attributing contributions to each input feature. This integration enhances transparency and trust in smart contract vulnerability detection. Table 6 shows the pseudocode for the BBO.

Table 6 Pseudocode for BBO.

Theoretical convergence proof

The convergence of the BBO algorithm is theoretically guaranteed under standard assumptions. Specifically, BBO ensures global convergence when:

• The objective function is bounded below.

• The branching process partitions the feasible space exhaustively.

• The bounding functions compute valid lower and upper bounds for all subproblem.

The objective function is continuous and bounded. The pruning strategy in BBO eliminates suboptimal nodes using reliable bounds, and the branching process ensures exhaustive exploration of feasible regions. According to established theory, ensures that the optimal solution will eventually be found:

$$\mathop {\lim }\limits_{u \to \infty } g_{u}^{ * } = g^{opt}$$

(34)

where $g_{u}^{ * }$ denotes the best solution at iteration $u$, and $g^{opt}$ denotes the global optimum. The stopping criterion $|VC - MC| \le \in$ ensures termination when a near-optimal solution is reached within acceptable tolerance. This theoretical foundation, together with the empirical evidence in Fig. 5, validates BBO’s convergence properties for high-dimensional, constrained optimization tasks.

Fig. 5

Convergence characteristics of BBO.

On the x-axis, generations are plotted, while the y-axis shows the corresponding objective function values. Initially, at generation 0, the objective function starts at approximately − 9.5, indicating a suboptimal configuration. By generation 3, the value improves to − 10, reflecting early-stage optimization progress. At generation 5, a sharper drop is observed as the value reaches − 13.08, suggesting that BBO is effectively pruning suboptimal branches and focusing on more promising solutions. By generation 10, the objective value stabilizes between − 13.05 and − 12, demonstrating strong convergence characteristics. This smooth and monotonic decline without significant oscillations highlights BBO’s ability to avoid local minima and maintain a stable optimization path. The convergence trend also indicates that the BBO bounding mechanism effectively eliminates non-viable candidate’s early, accelerating convergence. Compared to heuristic algorithms, BBO structured search ensures global optimality by thoroughly exploring feasible solutions. The absence of erratic spikes in the graph affirms the method’s efficiency and stability. This behavior validates BBO’s suitability for high-dimensional, constrained optimization tasks.

Explainable AI interpretation of SHAP

HB³LSTM intellectual engines, highly effective, are often hard to interpret because of their black-box nature, which makes it challenging to rely on their results for vulnerability detection. To enhance trust and usability in vulnerability detection, XAI techniques such as SHAP⁴² provide insights into feature contributions, improving transparency and model reliability. For complex models like DNN, Kernel SHAP approximates each feature’s contribution using weighted linear regression. It employs a surrogate linear model that closely aligns with the original model’s predictions, ensuring interpretability. The Shapley value for a feature quantifies its influence on the final prediction:

$$g\left( {z^{\prime } } \right) = \varphi_{0} + \sum\limits_{i = 1}^{N} {\varphi_{i} z_{i}^{\prime } ,}$$

(35)

where $z_{i}^{\prime }$ indicates whether the feature $i$ is present (1) or not (0); $\varphi_{i}$ represents relative feature contribution using the Shapley value and $\phi_{0}$ is the starting value in the event that no input features are present (0). By systematically analyzing feature combinations, SHAP assigns values to each input, highlighting their impact on predictions. Summing Shapley values across all instances:

$$I_{i} = \frac{1}{m}\sum\limits_{j = 1}^{m} {\left| {\phi_{i}^{\left( j \right)} } \right|}$$

(36)

where $m$ denotes how many occurrences there are in the dataset. This method ensures model-agnostic explanations, maintaining consistency across different DL architectures.

To evaluate the interpretability of the HB³LSTM model, SHAP values were analyzed across multiple predictions. A consistent pattern emerged, showing that certain opcodes such as add, push1, call, and delegate call regularly ranked among the top contributors. These opcodes are closely associated with critical operations like arithmetic computations and external contract interactions, which are often targeted in common smart contract vulnerabilities. The repeated prominence of these opcodes in the SHAP rankings strongly indicates their significance in model decisions. Additionally, cross-referencing these findings with known vulnerability patterns from curated datasets confirmed that opcodes with higher Shapley values are indeed aligned with commonly exploited code fragments. This alignment reinforces the conclusion that SHAP not only facilitates interpretability but also effectively highlights security-relevant features that correlate with actual vulnerabilities.

Figure 6 shows the code for vulnerability identification logic of SHAP. Figure 7 illustrates the SHAP flowchart of proposed methodology, where feature-level explanations pinpoint the most significant attributes influencing vulnerability detection. This aids security teams in identifying root causes of attacks and prioritizing key metrics for faster detection with reduced false positives.

Fig. 6

Code for vulnerability identification logic of SHAP.

Fig. 7

Flowchart for proposed methodology.

The methodology uses IQPO to optimize feature selection and NLP techniques to preprocess data in order to identify smart contract vulnerabilities. In addition to identifying dangerous transactions, a hybrid HB³LSTM intellectual engine extracts vulnerable code fragments. In order to evaluate results and identify certain vulnerability types, XAI approaches such as SHAP values are employed. TF-IDF and opcode extraction help with feature extraction, and LSTM manages sequence prediction. This method increases blockchain security and strengthens vulnerability detection. Table 7 shows the code presentation of the overall proposed approach.

Table 7 Open code Presentation of Proposed Approach.

Results and discussions

To address the generalizability of the proposed model, additional experiments were conducted using smart contracts developed for the Hyperledger fabric platform. These contracts, sourced from open-access repositories and executed within a simulated Fabric chain code environment, enabled comprehensive testing within a permissioned blockchain framework. To address key limitations of Ethereum, such as potential overfitting, the model was adapted and implemented in the Hyperledger environment. The experiments conducted on Hyperledger analyzed platform-specific performance metrics, including success rate, throughput, latency, and resource consumption. The results demonstrate that the proposed method maintains strong performance across these metrics, indicating effective generalization and adaptability for vulnerability detection on diverse blockchain platforms. The approach classifies vulnerability types with high accuracy by leveraging advanced DL techniques, implemented using Python’s robust libraries and frameworks, and optimized Hyperledger ecosystems. Python’s complex DL libraries and frameworks are utilized in the method, and the implementations are done on the Hyperledger platform. The quantum feature selection algorithm IQPO was implemented on IBM Qiskit’s simulator with 8 qubits to represent feature vectors. Quantum operations such as norm and inner product estimations were executed in a noiseless simulation environment, enabling precise evaluation of feature importance rankings without noise interference. This simulation-based approach allowed us to verify IQPO’s computational advantages and scalability before deployment on physical quantum hardware. The implementation runs on a Windows 10 operating system with Python 3.12.7, utilizing a 2.15 GHz processor and 1267 GB of RAM. Visual Studio Code is used as the development environment for executing the code. The experimental findings are presented in this section, along with an examination of how the method generates classifications that are highly accurate.

Dataset description

The SmartBugs Wild dataset is a large-scale collection of 47,331 Ethereum smart contracts, curated for the purpose of analyzing and detecting real-world security vulnerabilities. It is designed for use in training and testing machine learning and DL models aimed at smart contract vulnerability detection. The dataset includes both vulnerable and non-vulnerable contracts, providing balanced data for binary and multi-class classification tasks. A subset of the dataset, which includes over 1250 Solidity-written smart contracts, is annotated with specific vulnerability types such as reentrancy, integer overflow/underflow, and access control issues. These labeled contracts allow for fine-grained vulnerability classification and supervised learning. The dataset supports empirical evaluation of security analysis tools by offering realistic and diverse samples from the Ethereum network. It enables the training of robust models capable of identifying subtle and complex flaws in contract logic. The diversity and scale of the data also help reduce model overfitting and improve generalization. Researchers can use the dataset to benchmark detection techniques across various types of smart contract vulnerabilities. Ultimately, SmartBugs Wild aims to advance the security and reliability of blockchain applications through improved vulnerability detection methodologies.

Performance metrics

Key metrics for categorization models are compiled in Table 8. While memory measures the ability to recognize good instances, precision demonstrates the consistency of favorable predictions. While accuracy denotes complete correctness, the F1-score finds a balance between recall and precision. A higher AUROC rating indicates better class distinction. TP (True Positives), TN (True Negatives), FP (False Positives), FN (False Negatives), TPR (True Positive Rate), and FPR (False Positive Rate) are key terms that help compare model performances.

Table 8 Binary classification and performance metrics.

Exploratory data analysis

Table 9 contrasts different security tools based on how well they can identify smart contract vulnerabilities using the Smart Bugs Wild Dataset. It evaluates the accuracy, recall, F1-score, and FPR of every instrument for a variety of vulnerabilities. No single tool performs better than the others, even though Mythril and Oyente are excellent in terms of recall and precision for certain vulnerabilities. While Mythril frequently has superior precision but a higher FPR, Maian and Securify exhibit balanced performance with differing strengths in recall and F1-score.

Table 9 Comparison of different tools in smart bugs wild dataset.

Taxonomical analysis of vulnerabilities in hyperledger fabric using HB³LSTM

To enhance vulnerability detection in Hyperledger Fabric, a refined taxonomy based on the HB³LSTM model is proposed, focusing on actual exploit types rather than architectural layers. The detection process identifies key vulnerability classes, including reentrancy, where repeated function calls compromise contract state, and access control issues due to improper identity verification. DoS vulnerabilities are flagged when resource exhaustion or execution blocking is detected. Arithmetic errors, such as overflows or underflows, are also recognized as critical risks. The model detects unchecked low-level calls, which may lead to unexpected behaviors and time manipulation vulnerabilities arising from misuse of temporal data. Front-running is identified when transaction ordering is exploited for gain. These categories are supplemented by other miscellaneous vulnerabilities representing less common yet dangerous flaws. This taxonomy enhances threat classification and interpretability, ensuring HB³LSTM alignment with practical security challenges in Fabric-based smart contracts.

Case study

Protect Decentralized Finance (DeFi) platforms by scanning their deployed smart contracts for vulnerabilities using the dataset.

Real-Time Application: Analyze the blockchain mempool (where unconfirmed transactions reside) to prevent attacks like front running.

Confirmed Example:

A mempool monitor detects a front running attack where an attacker tries to outbid a trade by submitting a transaction with a higher gas fee.

Steps to Apply Dataset:

• Train a model Use the dataset to train a model that identifies malicious transaction patterns, such as excessive gas usage in attacks.

• Deploy on nodes Run the model on Ethereum nodes to monitor transactions in the mempool.

• Block malicious transactions Flag and prevent suspicious transactions from being confirmed.

Dataset analysis

Figure 8 presents the distribution of vulnerability classes in the SmartBugs Wild Dataset, visualized using a pie chart. With 30.4% of the total, “arithmetic” is the largest sector, followed by “other” with 22.9%. “Unchecked_low_calls” and “reentrancy” are about equal, at about 11.8% and 11.9%, respectively. “Time manipulation” is 3.3%, “front running” is 6.6%, “access control” is 3.1%, and “denial service” is 10.0%. This graph helps prioritize security efforts by highlighting the frequency of various vulnerabilities.

Fig. 8

Class distribution in the smart bugs wild dataset.

The feature importance graph for the Smart Bugs Wild Dataset illustrates the significance of various features in the dataset. The x-axis represents the feature importance, ranging from 0.00 to 0.12, while the y-axis lists the features being evaluated. The features, from highest to lowest importance, are add, and, 0 × 0, dup2, push1, dup1, jumpdest, pop, swap1, and push2. Each feature has a corresponding horizontal bar indicating its importance, with error bars showing the uncertainty or variability in the measurement. The feature “add” has the highest importance, followed by “and” and “0 × 0,” while “push2” has the lowest importance among the listed features. This Fig. 9 helps in understanding which features are most significant in the Smart Bug Wild Dataset, potentially guiding further analysis or model development.

Fig. 9

Feature importance graph for smart bugs wild dataset.

The features in Smart Bugs Wild Dataset’s ROC curve illustrates how well classifiers work in identifying smart contract vulnerabilities, as described in Fig. 10. For different classifiers, it compares the true positive rate against the false positive rate. Effectiveness is indicated by the Area Under the Curve (AUC) values; greater values signify superior performance. The capacity of classifiers to differentiate between smart contracts that are vulnerable and those that are not is compared using this curve.

Fig. 10

ROC curve of classes in smart bugs wild dataset.

Figure 11 shows the confusion matrix for the SmartBugs. Wild Dataset shows the model’s performance in identifying smart contract vulnerabilities. The actual class is represented by each row, while the anticipated class is represented by each column. The model accurately detected instances of arithmetic, front-running, denial-of-service, time-manipulation, unchecked-low-calls, reentrancy, and access-control vulnerabilities. Better performance is indicated by higher diagonal values, which also reveal areas for improvement and areas of strength.

Fig. 11

Confusion matrix of smart bugs wild dataset.

Figure 12 shows the performance of the model in terms of accuracy and loss over 100 training epochs for the task of vulnerability detection. In (a) presents the accuracy trends, where the training accuracy reaches approximately 0.98, the testing accuracy stabilizes around 0.86, and the validation accuracy achieves about 0.78. (b) Shows the corresponding loss values, with the training loss at approximately 0.38, testing loss around 0.28, and validation loss reaching as low as 0.17. These results indicate good generalization ability of the model, with a slight performance drop in the validation phase suggesting potential areas for further optimization.

Fig. 12

Performance evaluation of training, testing, and validation phases. (a) accuracy versus epochs (b) loss versus epochs.

Figure 13 shows the computational efficiency of the proposed HB³LSTM model compared to existing methods in terms of the number of nodes processed and their corresponding running time. The existing methods like EA-RGCN²⁷, WIDENET³¹, and DA-GNN³³ demonstrate a running time of approximately 10⁴ units over 500 nodes and higher. While the proposed HB³LSTM model significantly outperforms these methods with a substantially reduced running time of approximately 10⁻¹, indicating its superior computational efficiency and scalability in handling large-scale data. This improvement is primarily attributed to the integration of BBO into the training phase of the Boot LSTM network. Within the computational graph, BBO replaces traditional gradient-based optimization by systematically evaluating candidate weight configurations to minimize detection error. By computing upper and lower bounds on the objective function, BBO prunes suboptimal paths and focuses computation on promising regions of the search space. This intelligent pruning strategy not only improves convergence and accuracy but also drastically reduces computational overhead, contributing to the superior performance.

Fig. 13

Computational efficiency comparison of the proposed model.

Figure 14 presents a SHAP summary plot illustrating the most influential TF-IDF features in predicting vulnerabilities in smart contracts from the Smart Bugs Wild dataset. Features such as “push1,” “and,” “jumpdest,” and “swap1” exhibit the highest mean SHAP values, indicating strong contributions to the model’s classification outcomes. Specifically, high SHAP values for “jumpdest” correlate with control-flow vulnerabilities like reentrancy, while “push1” is tied to arithmetic flaws such as overflows. The x-axis represents the mean SHAP values, and the color gradient indicates the original feature values, aiding in interpretability. “dup2” shows a consistent positive impact on vulnerability detection, whereas features like “add” and “and” demonstrate mixed influence. The plot provides a quantitative lens into not just feature importance but also their directional impact. SHAP thus enhances the transparency of complex models, which ensures explainable predictions. Overall, the analysis validates SHAP’s role in highlighting security-critical patterns in smart contract code.

Fig. 14

SHAP summary plot for smart bugs wild dataset.

Table 10 shows the statistical validation of SHAP feature contributions for key opcodes in HB³LSTM based vulnerability detection. The mean SHAP values for each opcode, indicating their average contribution to the model’s predictions. The opcode call has a mean SHAP value of 0.084 with a t-value of 6.41 and a highly significant p-value (< 0.001), alongside a large effect size d = 1.25, highlighting its strong influence. The opcode delegatecall has the mean of 0.079, t = 5.87, p < 0.001, and d of 1.15, and selfdestruct has the mean value of 0.075, t = 5.42, p < 0.001, and d = 1.05, also showing significant positive contributions. The add opcode contributes moderately with a mean SHAP value of 0.067, t = 4.22, p = 0.0002, and effect size d = 0.89. In contrast, opcodes like jumpdest have the mean of 0.014, t = 1.13, p = 0.26, and d = 0.21; log0 has the mean of 0.011, t = 0.97, p = 0.33, and d = 0.18; and revert has the mean of 0.008, t = 0.42, p = 0.68, and d = 0.10 have lower mean values and non-significant p-values, indicating weaker or inconsistent influence. The statistical tests confirm that most key opcodes contribute meaningfully to vulnerability detection, reinforcing the model’s interpretability via SHAP. Overall, this analysis validates the importance of these features and supports the reliability of the HB³LSTM model in identifying smart contract vulnerabilities.

Table 10 Statistical validation of SHAP feature contributions for key opcodes in HB³LSTM based vulnerability detection.

Figure 15 shows the performance comparison of the proposed HB³LSTM model on original and adversarial smart contracts using key evaluation metrics. The model achieved high values on the original dataset, with an accuracy of 0.97, precision of 0.98, recall of 0.99, and F1-score of 0.98, indicating excellent predictive capabilities. In contrast, the performance significantly declined on adversarial contracts, where accuracy dropped to 0.85, precision to 0.75, recall to 0.7, and F1-score to 0.65. This stark performance gap highlights the robustness of the original model against data perturbations. It also confirms the effectiveness of the BBO algorithm in optimizing the model’s weights.

Fig. 15

Comparative performance metrics of HB³LSTM on original vs. adversarial smart contracts.

Comparison analysis

The accuracy of three distinct approaches, like Hierarchical Attention Network (HAN), Dual-Channel Convolutional Neural Network (DC-CNN), and the suggested HB³LSTM across tenfold cross-validation, is shown in the graph in Fig. 16. The accuracy is shown on the y-axis, which ranges from 0.60 to 1.00, and the number of folds is shown on the x-axis, which ranges from 1 to 10. The accuracy of the suggested HB³LSTM approach is higher across all folds, consistently outperforming the other two techniques. This superior performance of HB³LSTM can be attributed to its hybrid architecture, which combines the strengths of Boot-LSTM with BBO. The LSTM component enables effective sequence learning and temporal pattern recognition, which is particularly beneficial for modeling contextual dependencies in sequential data. BBO adaptively optimizes model parameters, enhancing convergence and generalization. Furthermore, the hierarchical structure of HB³LSTM allows it to capture both local and global features more effectively than the flat architectures of HAN and DC-CNN. This integrated and adaptive design leads to more robust learning and explains the consistently higher accuracy observed across all folds.

Fig. 16

Cross-validation of existing and proposed methods.

Figure 17 shows the comparative convergence behavior analysis of four optimization algorithms, like Particle Swarm Optimization (PSO), Lyrebird Optimization (LBO), Single Candidate Optimization (SCO), and the BBO, over 20 iterations. The y-axis denotes the loss values, while the x-axis represents the number of iterations. Among the existing methods, PSO has the loss of 0.85, LBO has the loss of 0.75, and SCO has the loss of 0.65, respectively. While the proposed BBO achieves the lowest loss of 0.55, indicating faster and more stable convergence. This superior performance is primarily due to BBO’s structured approach to optimizing the weight parameters of the Boot LSTM network. Unlike population-based methods like PSO and LBO, which often suffer from premature convergence due to limited global coordination. But BBO employs bounding and pruning techniques. These methods eliminate suboptimal regions of the solution space early in the search, improving both convergence speed and accuracy while reducing the risk of getting trapped in local minima. Compared to SCO, which explores a single solution path at a time, BBO maintains a strategic balance between exploration and exploitation. This balance is particularly valuable in high-dimensional spaces, such as those found in smart contract analysis, where solution landscapes are often complex and filled with deceptive local optima. Overall, BBO’s systematic and scalable search strategy enhances both the robustness and precision of the optimization process, making it highly effective in minimizing loss and improving the detection of smart contract vulnerabilities.

Fig. 17

Comparative convergence analysis of optimization algorithms.

Figure 18 shows the computational analysis of BBO over the existing algorithms, addressing concerns related to computational placement and efficiency. The x-axis reflects the number of function evaluations, while the y-axis presents the function error value on a logarithmic scale. The proposed BBO algorithm maintains a consistent error around 10⁰, indicating it rapidly converges and stabilizes early in the optimization process. This stability demonstrates where BBO fits in the computational graph as an efficient optimizer with bounded weight updates. Unlike PSO, which continues to decrease error to below 10⁻², and LBO, which reaches around 10⁻¹, BBO emphasizes early convergence and conservative updates. These bounded behaviors are a result of adaptive limits placed on neural weight changes, implicitly acting as a pruning mechanism. Therefore, BBO contributes to computational efficiency by enforcing stability and reducing unnecessary exploration. This reflects its role in constraining weight space evolution and potentially aiding in implicit network pruning.

Fig. 18

Computational analysis of BBO.

Table 11 presents a comparative analysis of existing methods against the proposed HB3LSTM model using key performance metrics. Among static-based tools, Mythril shows the lowest accuracy at 39.48% and F1-score at 37.04%, while Oyente has 70.04% accuracy and a 59.41% F1-score. DL models demonstrate superior performance, with HAN achieving 94.76% accuracy and a 96.29% F1-score and a DC-CNN further improving to 96.89% accuracy and a 97.64% of F1-score. The LLM, like CodeBERT, has an accuracy of 85.42%, a precision of 75.23%, recall of 69.45, and an F1-score of 7.32%. FinBERT has the accuracy of 82.45%, precision of 79.73%, recall of 69.06%, and F1-score of 70.26%. The proposed HB3LSTM outperforms all with 99.34% accuracy, 99.52% precision, 99.28% recall, and a 99.13% F1-score. This clearly highlights the effectiveness of HB3LSTM in vulnerability detection.

Table 11 Dataset comparison of existing methods with the proposed model.

Figure 19 shows the comparative performance of the proposed HB³LSTM model against existing LLMs based on the accuracy metric. The existing models like the N-Gram²⁷ model achieved an accuracy of 40.87%, CodeBERT with 56.89%, and FinBERT with 78.35%. In contrast, the HB³LSTM model demonstrated a remarkable accuracy of 98.79%, significantly outperforming all baseline models. This superior performance is attributed to the HB³LSTM hybrid architecture that combines the optimization strength of the BBO algorithm with the sequential learning capabilities of LSTM networks. The BBO component efficiently navigates complex search spaces to enhance model precision, while LSTM excels at capturing temporal dependencies in transaction sequences. Together, they enable HB³LSTM to detect smart contract vulnerabilities more effectively. Overall, HB³LSTM offers a robust, scalable solution for identifying potentially malicious blockchain transactions.

Fig. 19

Performance comparison of the proposed HB³LSTM model with existing LLM based on accuracy.

Figure 20 shows a performance comparison between Ethereum²⁷ and Hyperledger across four key metrics. In (a), the success rate shows that Ethereum achieved 40% in Test Case (TC) 1, 20% in TC 2, 65% in TC 3, and 60% in TC 4. In contrast, Hyperledger showed much higher success rates of 96% in TC 1, 93% in TC 2, 97% in TC 3, and 96% in TC 4 in the respective test cases. In (b), the throughput shows. Ethereum recorded 50 transactions per second in Scenario (S) 1, 70 in S2, 62 in S3, and 78 in S4. Hyperledger outperformed with 65 in S1, 95 in S2, 90 in S3, and 91 transactions per second, respectively. In (c), the latency shows that Ethereum had values of 75 ms, 60, 68, and 70 across the scenarios, while Hyperledger maintained lower latency at 92, 90, 90, and 87 ms. In (d), it shows the resource utilization; Ethereum used 200% CPU and 900 Mega Bytes (MB) of memory, whereas Hyperledger consumed only 120% CPU and 550 MB of memory, showcasing its higher efficiency. Table 12 shows the example code for SHAP.

Fig. 20

Comparative metrics analysis between ethereum and hyperledger platforms. (a) success rate, (b) throughput, (c) latency, (d) resource utilization.

Table 12 Example code for SHAP.

Figure 21 illustrates the cross-platform performance evaluation of the proposed HB³LSTM model across four operating systems: Windows, Linux, Ubuntu, and macOS. The model achieved the highest accuracy on Ubuntu at 99.8%, followed closely by macOS at 99.7%, Linux at 99.2%, and Windows at 98.5%. In terms of memory usage, Ubuntu again performed best, consuming only 260 MB, followed by Linux with 280 MB, macOS at 300 MB, and Windows using the most at 320 MB. Throughput analysis revealed that Ubuntu also led in request handling, achieving 1750 requests/sec, with Linux at 1700, macOS at 1600, and Windows trailing at 1500. These results underscore Ubuntu’s superior efficiency across all three metrics. Linux and macOS also showed competitive performance, while Windows lagged slightly in comparison. This cross-platform consistency highlights the robustness and portability of the proposed model.

Fig. 21

Cross platform performance evaluation.

Ablation study

Table 13 presents an ablation study highlighting the performance of various existing methods. EA-RGCN achieved 90.47% accuracy, 91.16% precision, 89% recall, and a 90.03% F1-score. BERT showed 92.53% accuracy, 94.21% precision, 95.77% recall, and 89.47% F1-score. ANFIS reached 96.4% accuracy, 99.4% precision, 96% recall, and a 99.1% F1-score. CNN-LSTM obtained 91% accuracy, 92% precision, 99% recall, and 95% F1-score. While these methods deliver competitive results, our proposed HB³LSTM with Explainable AI significantly outperforms them all, achieving 99.68% accuracy, 99.43% precision, 99.54% recall, and 99.40% F1-score. The proposed method outperforms established baselines like CNN-LSTM and BERT. The proposed HB³LSTM + Explainable AI method demonstrates superior performance compared to other methods, highlighting its potential for effective vulnerability detection. The results suggest that the combination of HB³LSTM and Explainable AI provides a robust and accurate approach for identifying vulnerabilities.

Table 13 Ablation study of proposed method.

Discussion

Our suggested approach improves the detection of smart contract vulnerabilities in several steps. First, NLP methods are used to preprocess the input. The significance of important terms in the smart contract is then captured by applying TF-IDF for feature extraction. Improved Quantum Online Portfolio scalability is used for feature selection. In order to find vulnerabilities and stop dangerous transactions, the hybrid HB³LSTM then extracts important code fragments. Lastly, the model’s decisions are interpreted using XAI approaches, such as SHAP values, which show how particular aspects affect the vulnerability or invulnerability of a contract. This method increases detection accuracy while offering insightful information about the security of smart contracts.

To further enhance the robustness of smart contract vulnerability detection systems, future work can explore adversarial training strategies. Adversarial examples are inputs deliberately crafted to deceive the model, which poses significant threats to the reliability of security classifiers. Incorporating adversarial training could increase model resilience by exposing it to potential attack vectors during the learning phase. The integrating modular defense mechanisms, such as runtime behavior analyzers or transaction simulation engines, could serve as an added layer of protection. These modules can act in tandem with the static analysis approach, offering both proactive and reactive security coverage. Another promising direction is the fusion of semantic-aware graph representations with HB³LSTM to better model code dependencies and interactions. Combining this with adversarial robust training regimes may yield systems that are both interpretable and resistant to manipulation. Extending explainability modules to incorporate user-friendly visualizations could facilitate broader adoption by auditors and developers who may not be familiar with machine learning outputs but require actionable insights.

Conclusion

In the final analysis, by comparing several approaches, the suggested methodology successfully improves smart contract vulnerability identification. The method uses IQPO for effective feature selection, cutting down on processing time and improving scalability after preprocessing the data and extracting features using NLP and TF-IDF. By identifying important code segments and preventing dangerous transactions, the novel HB³LSTM enhances detection even further and works in combination with expert models. The final stage, which uses XAI with SHAP values, allows for the identification of critical opcodes that impact smart contract vulnerabilities and transparent decision-making. A reliable, scalable, and interpretable system for identifying and reducing smart contract risks is produced by this multi-step process.

However, adversarial testing reveals certain robustness gaps in the current model, suggesting the need for proactive defense mechanisms. Future research can explore the integration of adversarial training and lightweight defense modules to improve resilience against sophisticated evasion attempts. Additionally, extending the system to operate within decentralized or federated environments can enhance both data privacy and scalability. Embedding the approach within blockchain-native security frameworks and enabling real-time anomaly monitoring will further ensure adaptability to evolving threat landscapes. These enhancements can lay the groundwork for a more trustworthy and future-ready smart contract analysis platform.