Introduction

Terrestrial ecosystems are vital carbon reservoirs that play a key role as global carbon sinks1. Gross primary productivity (GPP) is an important indicator for evaluating the health of terrestrial ecosystems2 and reflects the total amount of organic matter produced through photosynthesis. Furthermore, it influences the rate at which plants absorb carbon dioxide from the atmosphere3. Therefore, the accurate estimation of GPP is of theoretical and practical importance for quantifying the carbon sink functions of terrestrial ecosystems4.

Due to the complexity of GPP field measurements and the limitations of observational scales5, regional-scale GPP estimation generally relies on models, such as BIOME-BGC6 and EC-LUE7, that are based on remote sensing data. However, it is challenging to represent complex nonlinear interactions between different vegetation types and the exchange rate between carbon dioxide and water vapor using these models8,9. In addition, interference from specific environmental stressors such as moisture, temperature, and extreme weather reduces the accuracy and reliability of these models10,11.

In recent years, with the development of machine learning (ML) technologies, ML-based GPP estimation methods have become a research hotspot12,13. For example, Papale et al.14 used an artificial neural network to construct a GPP estimation model suitable for Europe. Yao et al.15 generated a carbon sink dataset for Chinese terrestrial ecosystems with a spatial resolution of 1 km based on model tree regression. Subsequently, Cho et al.16 utilized a support vector machine (SVM) to estimate the national-scale GPP of South Korea from 2000 to 2018. Recently, Guo et al.17 and Sarkar et al.18 used random forest (RF) model to develop time-series GPP dataset. These models were trained using site observation data (SOD) and extrapolated using remote sensing data19,20. These ML-based methods efficiently capture the complex nonlinear relationships in a dynamic system of carbon fluxes21,22. Compared with traditional ecological process models, ML-based methods achieve superior GPP estimation accuracy23. However, most ML-based GPP estimation methods do not account for the effects of collinearity between variables, leading to low accuracy18. To address this problem, Lu et al.24 developed a deep learning method to merge 23 CMIP6 datasets to generate highly accurate monthly GPP products with a spatial resolution of \(0.25^{\circ }\). Deep learning models improve the accuracy of GPP estimation, but the complexity of network structures and large demand for training data lead to high computation and training costs. Conversely, the novel gradient-boosting algorithm CatBoost25 has lightweight network structures. It ignores the influence of collinearity between variables and overcomes gradient biases and prediction shifts, efficiently handling time-series data. CatBoost has been applied to remote sensing estimation tasks26,27. For example, Zheng et al.28 used CatBoost as a comparative model to estimate the annual GPP in Europe and North America. Additionally, Liu et al.29 integrated the extreme gradient boosting (XGBoost), CatBoost, and Shapley additive explanations (SHAP) models to estimate gross ecosystem productivity. However, the existing models fail to effectively integrate the temporal dynamics of vegetation parameters and lack adaptive modeling of terrain heterogeneity during the design process.

Shanxi Province is situated in the eastern part of the Loess Plateau (LP), within the mid-section of the Yellow River Basin in northern China. It serves as a crucial component of China’s national ecological security strategy (“Two Screens and Three Belts”) and is a key region for national soil and water erosion control projects30. The ecological environment in this region is extremely fragile. Meanwhile, Shanxi Province is an energy-intensive heavy chemical industry base that is primarily driven by coal resource development. Large-scale and frequent coal mining and the development of high-energy-consuming industries have continuously increased the concentration of greenhouse gases in the atmosphere31, negatively affecting ecological health and development. However, there is a lack of carbon flux towers in Shanxi Province, and few studies have examined long-term GPP changes in this region. Furthermore, previous research mainly focused on the Yellow River Basin32 and LP33. For example, Zhang et al.33 explored the vulnerability of the LP ecosystem based on the GPP. Meanwhile, Gong et al.34 used a modified vegetation photosynthesis model to obtain a long-term series of GPP in the LP from 2001 to 2022 and investigate the impacts of different land use patterns and meteorological factors. Previous studies35,36,37 have revealed the spatiotemporal patterns of GPP in the LP and the Yellow River Basin, as well as their climatic and ecological driving mechanisms. However, as a core component of a low-carbon economic zone, Shanxi Province exhibits unique characteristics, such as coal mining pressure, a fragile ecosystem, and a “green, low-carbon and energy economy” synergistic development model that has not yet been adequately explored in existing models. Therefore, it is crucial to comprehensively quantify the impacts of factors such as climate, topography, human activities, and their interactions on the GPP in Shanxi Province.

In this study, we developed a CatBoost-based GPP estimation method. Using this method, we aimed to achieve long-term GPP estimation and explore the driving factors of GPP in Shanxi Province. The three major contributions of this study can be summarized as follows: (1) We proposed a CatBoost-based GPP estimation model that effectively captures temporal dependence and embeds terrain constraints, achieving better results than comparative methods. (2) We applied the CatBoost GPP model to estimate long-term GPP from 2001 to 2022 in Shanxi Province, analyze the GPP spatiotemporal change trends, and identify GPP declines and potential degradation areas. (3) We further explored the driving mechanisms of GPP changes and elucidated the contributions of natural and anthropogenic factors to GPP in Shanxi Province.

Materials and methods

Study area

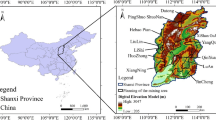
Shanxi Province, China (\(34^\circ 34.8'\)–\(40^\circ 43.4'\)N, \(110^\circ 14.6'\)–\(114^\circ 33.4'\)E) is located in the eastern LP and is bordered to the west and east by the Lvliang and Taihang mountains, respectively (Fig. 1). The natural environment within the study region is complex and includes diverse landform types. The region is characterized by uneven spatiotemporal water and heat distributions influenced by the mid-latitude temperate continental monsoon climate and geographical factors. Soil erosion and water loss are severe in Shanxi Province38,39 primarily because most areas are arid with low rainfall30 and are prone to frequent meteorological disasters. Furthermore, the coarse texture and loose structure of the soil as well as human activities weaken its erosion resistance.

Shanxi Province is known in China as the “hometown of coal” and is rich in mineral resources40. However, coal mining and steel smelting have caused severe environmental pollution in recent decades. Therefore, the Shanxi provincial government implemented ecological protection measures in 1997, and consequently, the ecological environment was gradually restored and improved. It is important to accurately monitor vegetation productivity and explore its driving forces in this region.

Fig. 1
figure 1

Location of Shanxi Province. Maps were created using ArcGIS10.2 (Environmental Systems Research Institute, USA. https://www.esri.com/).

Full size image

Data sources and preprocessing

Construction of the modeling dataset

We collected eddy covariance (EC) flux data, moderate-resolution satellite remote sensing imagery (MOD11A2, MOD13A3, MOD15A2H, and MCD12Q1), and digital elevation model (DEM) data to construct the GPP dataset.

The EC flux data were obtained from the ChinaFlux (http://www.chinaflux.org/) and FLUXNET2015 (http://fluxnet.fluxdata.org) datasets. Flux data were measured using the EC method.

For the EC flux data from ChinaFLUX, we obtained flux data measured every half hour, including net ecosystem exchange (NEE, gC\(\, \textrm{m}^{-2}\, day^{-1}\)) and ecosystem respiration (RE, gC\(\, \textrm{m}^{-2}\, \textrm{day}^{-1}\)). These data underwent standardized quality control by site researchers, including coordinate rotation, outlier filtering, Webb-Pearman-Leuning correction, gap filling, and flux partitioning41. The processed data, which have high reliability for GPP modeling42,43, were aggregated to a daily resolution in ChinaFLUX. Additional details of the data processing method can be found in Yu44. In this study, the daily GPP was derived from NEE and RE data using the following equation:

$$\begin{aligned} GPP = RE - NEE, \end{aligned}$$
(1)

The FLUXNET2015 dataset provided two GPP estimates (gC\(\, \textrm{m}^{-2}\, \textrm{day}^{-1}\)) derived from NEE partitioning using the variable Ustar (u*) threshold (VUT): (1) night-time method (GPP_NT_VUT_REF)41, and (2) day-time method (GPP_DT_VUT_REF)45. All GPP data were calculated using the average of the night- and day-time partitioning methods. Specifically, we removed data points where the day-time and night-time partitioning results differed by more than 3 gC \(\textrm{m}^{-2}\, \textrm{day}^{-1}\), and replaced them with the average of the 2 days before and after the current day46.

Furthermore, the EC flux data were excluded if less than 80% of the data were observed during the year, and stations with less than 2 years of observations were not used. Following screening, we used 14 EC ground stations, including eight ChinaFLUX sites and six FLUXNET2015 sites. Table 1 shows the EC ground station locations, vegetation information, and observation period.

We utilized MOD11A2, MOD13A3, MOD15A2H, and MCD12Q1 data products (Table 2) collected by the National Aeronautics and Space Administration from 2001 to 2022. We reclassified the land use type according to the International Geosphere-Biosphere Programme vegetation classification system (Table 3) to match the flux site observation information47,48. Simultaneously, we verified whether the land use raster pixels within 1000 m around the observation site had the same land use type as that listed on the official website of the observation site to ensure data consistency. Due to cloud coverage and instrument failures, there was noise in the data products. We processed the MOD11A2, MOD15A2H, and MOD13A3 products to ensure temporal continuity. We searched for pixels based on the image quality control information. When the quality control information indicated poor quality, the average of the previous and next image pixels were used to fill in the missing data. If the quality of both periods was poor, the average of many years with good image quality was used to fill in the data. Finally, the data were smoothed using the Savitzky-Golay filter to obtain a smoother MODIS time series dataset.

Table 1 GPP observation site information.
Full size table
Table 2 Description of MOD11A2, MOD13A3, MOD15A2H, and MCD12Q1 data. Target Band Name indicates the band of each product needed for our study.
Full size table

We collected the DEM data from the SRTM 90 m Digital Elevation Database. Subsequently, we input the DEM data into the ArcGIS slope calculation tool to generate slope data.

To reduce the effects of missing data on model accuracy, we processed the modeling data using the following steps:

  1. (1)

    The daily values of GPP were aggregated into an 8d resolution using a sum aggregation strategy to match the remote sensing data intervals. Additionally, the SOD were projected onto the WGS1984 coordinate system.

  2. (2)

    We resampled seven types of feature data, including time, temperature, Fraction of Absorbed Photosynthetically Active Radiation (FPAR), Normalized Difference Vegetation Index (NDVI), land use type, DEM, and slope, to a consistent 1000 m grid. Subsequently, we collected pixel points within a Euclidean distance of 1000 m from the observation site. Based on the aforementioned steps, invalid values were removed from the collected points. Finally, the mean of the remaining pixel values was calculated and used as the representative value for the observation site.

  3. (3)

    The temporal resolution of all feature data was converted to 8 d. We spatially matched the SOD and feature data through spatial linkages (Fig. 2). Following vectorization, the data were organized into columns to construct the GPP dataset (each column represents a unique feature). The dataset consisted of eight columns: GPP observation value, time, temperature, FPAR, NDVI, land use type, DEM, and slope. The final dataset contained 3864 samples, split into training and validation sets in a 7:3 ratio.

Table 3 Reclassification of the land use type.
Full size table

Factor data

We selected 2005, 2010, 2015, and 2020 as the key research nodes. To analyze the drivers of GPP spatial variation in Shanxi Province, we selected seven variables, including four natural variables (elevation, slope, temperature, and precipitation) and three anthropogenic variables (GDP, population, and land use type), as driving factors (Table 4). Furthermore, we performed corresponding reprojection, resampling, and clipping operations on the data of these seven factors to align their spatiotemporal resolutions.

Table 4 Sources and details of factor data.
Full size table

GPP validation dataset

To evaluate the accuracy of the proposed CatBoost GPP method, we compared the results of CatBoost GPP with those of two open-source GPP products: MODIS GPP6 and GOSIF GPP49 (Table 5). Following resampling, the spatial resolutions of the MODIS GPP and GOSIF GPP data were 1000 and 5000 m, respectively. We removed invalid values from the collected pixels and calculated the average of the remaining pixel values as the site-specific value (as described in “Construction of the modeling dataset”) to create the GPP comparison dataset.

Table 5 GPP data product sources and overview.
Full size table

Methods

The workflow of this study is illustrated in Fig. 2. First, we proposed a novel GPP estimation method based on the CatBoost technique. We used a self-constructed GPP dataset to train the proposed CatBoost GPP model and then applied the best model weights to estimate the GPP of Shanxi Province from 2001 to 2022. Second, we combined the Theil–Sen approach (TSA) and Mann–Kendall (MK) trend test to analyze GPP change trends. In addition, we utilized the Hurst exponent to explore the persistence of spatiotemporal variations in the GPP and predict future GPP trends. Third, we revealed the factors controlling the spatiotemporal variation in the GPP in Shanxi Province using a Geodetector model.

Fig. 2
figure 2

Workflow diagram for this study, with created using ArcGIS10.2 (Environmental Systems Research Institute, USA. https://www.esri.com/).

Full size image

CatBoost GPP model construction

Notably, CatBoost is a gradient boosting decision tree framework25. It employs order boosting instead of traditional gradient estimation methods to reduce gradient and prediction bias along with overfitting risks50. Previous studies have demonstrated that CatBoost outperforms other decision tree methods when dealing with high-dimensional input features and noisy data51. For GPP estimation, the data exhibit complex periodic, non-stationary, and nonlinear patterns, making CatBoost particularly suitable for model construction. The algorithm automatically encodes categorical land use features into numerical values, minimizing encoding errors and mitigating bias from low-frequency categories. Additionally, CatBoost’s feature combination mechanism effectively addresses spatiotemporal heterogeneity (e.g., between static topographic features such as elevation and dynamic variables such as NDVI), enhancing the model’s environmental driver characterization. Hence, we developed a CatBoost GPP model to estimate the GPP of Shanxi Province. The construction of CatBoost GPP consisted of the following four steps: (1) We enumerated various segmentation methods to construct trees. The CatBoost GPP model grades each tree based on the predicted result accuracy during the training phase and assigns higher weights to decision trees with better predictive performance. (2) The GPP dataset was divided into training and validation sets as follows: data beyond the 5th year were considered as the validation set when the data at a site spanned more than 5 years; otherwise, final-year data were considered as the validation set. Finally, 3864 samples, comprising 2806 training and 1058 validation samples, were collected. (3) We utilized the GPP training and validation samples to train CatBoost GPP. Guided by the loss function, root mean square error (RMSE) (Eq. 2), the proposed model gradually reduces the bias of noisy points to achieve an optimal regression tree structure. (4) We applied the best model trained by the self-generated GPP dataset to estimate the GPP of Shanxi Province. The final GPP estimation result was obtained by calculating the weighted sum of all decision trees. The RMSE was calculated as follows:

$$\begin{aligned} RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^{N}(Y_{0,i} - Y_{m,i} )^{2}}, \end{aligned}$$
(2)

where N denotes the total number of samples, and \(Y_{0,i}\) \(Y_{m,i}\) are the observed and estimated values of i, respectively.

We implemented CatBoost GPP using the CatBoost regressor library with Python 3.7 programming language. The model was optimized during training using five parameters: n_estimators, learning_rate, max_depth, l2_leaf_reg, and loss_function25. Firstly, we used “RMSE” as the loss_function. Secondly, based on prior experience, we initially set n_estimators to 400, and selected the most probable value of other parameters as the search space (Table 6). Then, we combined the grid search method with 10-fold cross-validation to determine the optimal value of the CatBoost model. Finally, we further tested all n_estimator values in the range of 50–1500 with an interval of 50 and observed that the RMSE stabilized when n_estimators = 750 (Figure 3).

Table 6 Parameter range and optimal parameters for grid search.
Full size table
Fig. 3
figure 3

Relationship among the regression error RMSE, \(R^{2}\) and \(N\_estimators\) in the CatBoost GPP model.

Full size image

Accuracy assessment and performance evaluation

We compared the results of CatBoost GPP with those of seven other models: SVM, RF, LightGBM, XGBoost, LSTM (Long Short-Term Memory), MODIS GPP, and GOSIF GPP. Three metrics were used to evaluate the accuracy of the results: \(R^{2}\), RMSE, and mean absolute error (MAE). The equations for \(R^{2}\) and MAE are as follows:

$$\begin{aligned} & R^{2} =\left[ \frac{ {\textstyle \sum _{i=1}^{N}}\left( Y_{0,i}-\overline{Y_{0} } \right) \left( Y_{m,i}-\overline{Y_{m} } \right) }{\sqrt{ {\textstyle \sum _{i=1}^{N}} \left( Y_{0,i}-\overline{Y_{0} } \right) ^{2} {\textstyle \sum _{i=1}^{N}\left( Y_{m,i}-\overline{Y_{m} } \right) ^{2}} } } \right] ^{2}, \end{aligned}$$
(3)
$$\begin{aligned} & MAE=\frac{1}{N} \sum _{i=1}^{N} \left| Y_{0,i}- Y_{m,i} \right| , \end{aligned}$$
(4)

where N denotes the total number of samples; \(Y_{0,i}\) and \(Y_{m,i}\) are the observed and estimated values of i, respectively; and \(\overline{Y_{0}}\) and \(\overline{Y_{m}}\) represent the averages of the observed and estimated data, respectively.

TSA and MK trend test

We combined the TSA52 and MK53 trend tests to assess the GPP change trends. The TSA can be computed as follows:

$$\begin{aligned} S=Median\left( \frac{x_{j}-x_{i} }{j-i} \right) \end{aligned}$$
(5)

where \(x_{j}\) and \(x_{i}\) represent the GPP in years j and i, respectively (\(2001\le i< j\le 2022\)); \(S> 0\) indicates an upward trend in the GPP in Shanxi Province during this time series, whereas \(S< 0\) indicates a downward trend.

The MK trend test is a nonparametric statistical method used for trend analysis of time-series data. The equation is as follows:

$$\begin{aligned} Z=\left\{ \begin{array}{cl} \frac{S-1}{\sqrt{\operatorname {VAR(S)}}} & S>0 \\ 0 & S=0, \\ \frac{S+1}{\sqrt{\operatorname {VAR}(S)}} & S<0 \end{array}\right. \end{aligned}$$
(6)

where Z denotes the statistic S and is the Theil–Sen median. At a given significance level \(\alpha\), \(\left| Z \right| > Z_{1-(\alpha /2 )}\) indicates a significant change in the data series at the \(\alpha\) level. We selected a significance level of \(\alpha =0.05\) to classify the GPP trend changes as shown in Table 7.

Table 7 Classification criteria of GPP temporal changes at a significance level of \(\alpha =0.05\).
Full size table

Hurst exponent

The Hurst exponent (H) quantitatively represents the persistence of time-series data. We divided H into five trends: (1) H approaches zero: greater anti-persistence; (2) \(0<H<0.5\): future trends are expected to reverse from past trends; (3) \(H = 0.5\): no change in the data; (4) \(0.5< H < 1\): the process has continuous characteristics, and the future trend is consistent with the past; and (5) H approaches 1: greater persistence54. We combined the TSA results and Hurst exponents to classify the results into five categories (Table 8). The classification results were used to analyze the sustainability of GPP changes.

Table 8 Classification of the sustainability of GPP changes.
Full size table

Geodetector model

We used a Geodetector model to quantify the effects of different variables on the spatial distribution of GPP in Shanxi Province by performing factor and interaction detection.

(1) Factor detection: We quantified the magnitude of the influence of environmental factors on GPP. A factor that significantly influences the GPP should have a spatial distribution that closely resembles that of the GPP. Suppose \(q\in \left[ 0, 1 \right]\) refers to the explanatory power of a single factor on GPP spatial variation, and h is the category of variable GPP or factor X. The number of units for layer h and the whole region is set to \(N_{h}\) and N, respectively, and \(\alpha _{h}^{2}\) and \(\alpha ^{2}\) are the strata and the study area of GPP, respectively. The value of q is calculated as follows55:

$$\begin{aligned} q=1-\frac{ {\textstyle \sum _{h=1}^{L}}N_{h} \sigma _{h}^{2} }{N\sigma ^{2} } \end{aligned}$$
(7)

(2) Interaction detection: The interactive effect of the two drivers on GPP is determined by comparing the q-values of the two environmental factors after interaction \(\left[ q(X_{1} \cap X_{2}) \right]\) with the q-values of the individual environmental factors \([q(X_{1})\) and \(q(X_{2})]\)56 (Table 9).

Table 9 Types of interaction.
Full size table

Partial and composite correlation analyses

We used partial57 and composite correlation analyses58 to establish classification criteria for climate-driven factors (Table 10) at a significance level of p = 0.05 to clarify the response mechanism of GPP to precipitation and temperature in Shanxi Province.

Table 10 Rules of climatic driving factors for GPP variation. \(PR_{GPP-T}\) is the partial correlation coefficient between GPP and temperature, \(PR_{GPP-P}\) is the partial correlation coefficient between GPP and precipitation, and \(MR_{GPP-T-P}\) is the composite correlation coefficient between GPP and temperature/precipitation.
Full size table

Results

Model performance evaluation

Figure 4 shows the results of the accuracy evaluation of each method. The CatBoost GPP achieved the highest consistency with SOD (\(R^{2}\) = 0.890, RMSE = 1.155 gC\(\textrm{m}^{-2}\, \textrm{day}^{-1}\), and MAE = 0.772 gC \(\, \textrm{m}^{-2}\, \textrm{day}^{-1}\)). Compared to traditional estimation models (MODIS GPP and GOSIF GPP), CatBoost GPP exhibited a 0.438 higher \(R^{2}\) value, 1.42 gC \(\, \textrm{m}^{-2}\, \textrm{day}^{-1}\) lower RMSE and 0.756 gC\(\, \textrm{m}^{-2}\, \textrm{day}^{-1}\) lower MAE. Furthermore, CatBoost consistently outperformed all evaluated mainstream ML methods, including RF, SVM, LightGBM, XGBoost, and LSTM. Specifically, the \(R^{2}\) of CatBoost improved by 1.14–2.53%, while the RMSE and MAE decreased by 3.91–8.48% and 3.86–7.66%, respectively. Notably, CatBoost achieved a 5.62% reduction in MAE compared to the second-best method XGBoost. This demonstrates that the proposed method effectively addresses the overestimation and underestimation issues of the comparative models. CatBoost GPP accurately captures complex nonlinear relationships between GPP and feature variables. The fitted line of our method is closest to the ideal 1:1 line, and its predictions demonstrate a more uniform distribution around this line, indicating greater reliability compared with other methods.

Fig. 4
figure 4

Scatter plots of the observed and estimated GPP from different models.

Full size image

Spatiotemporal variations in GPP in Shanxi Province from 2001 to 2022

The proposed method was applied to estimate the GPP in Shanxi Province from remote sensing images. We compared the results of CatBoost GPP with those of MODIS GPP and GOSIF GPP products to evaluate the accuracy and validity of our method. Finally, we analyzed the temporal and spatial changes in the GPP in Shanxi Province.

Temporal variations in GPP

The annual average GPP values from CatBoost GPP, MODIS GPP, and GOSIF GPP exhibited significant upward trends (Fig. 5). The CatBoost GPP values had an annual fluctuation range of 555.31–1008.14 gC\(\, \textrm{m}^{-2}\, \textrm{year}^{-1}\), with a mean value of 844.45 gC\(\, \textrm{m}^{-2}\, \textrm{year}^{-1}\) and an annual increase of \(\sim\)20.58 gC\(\, \textrm{m}^{-2}\, {year}^{-1}\). The results of CatBoost GPP were consistent with those of MODIS GPP and GOSIF GPP in terms of trends and growth. All three annual GPP curves exhibited low values in 2001, 2005, 2009, 2011, 2015, and 2019, which may have been due to extreme meteorological events59.

Fig. 5
figure 5

Annual average GPP values for Shanxi Province from 2001 to 2022.

Full size image

Spatial variations in GPP

We normalized the maximum value of GPP from 2001 to 2022 that was obtained using different methods. This decreased the discrepancies between GPP estimates, allowing us to accurately compare and analyze the spatial distribution patterns of GPP in Shanxi Province. The spatial distributions of the CatBoost GPP, GOSIF GPP, and MODIS GPP results were highly consistent (Fig. 6), exhibiting a pattern of “low in the northwest and high in the southeast,” with distinct banding characteristics. A high GPP was observed in the western Lvliang Mountains, eastern Taihang Mountains, and central and southern river valley plains. The GPP was low in the central basin, loess hilly belt along the Yellow River west of the Lvliang Mountains, and urban areas.

From the perspective of administrative regions, Jincheng had the highest GPP, followed by Yuncheng and Changzhi. The three cities with the lowest values were Xinzhou, Datong, and Shuozhou. Jincheng’s GPP was 970.15 gC\(\, \textrm{m}^{-2}\, \textrm{year}^{-1}\), whereas Shuozhou’s GPP was only 462.15 gC\(\, \textrm{m}^{-2}\, \textrm{year}^{-1}\). Spatial differences in the GPP were affected by both natural and anthropogenic factors. Shuozhou had a higher latitude, lower precipitation, and lower temperatures than Jincheng, leading to a more fragile ecosystem60. Furthermore, during the study period, Shuozhou experienced rapid GDP growth and large-scale mining activities61, leading to low GPP.

Significant differences were observed between the GPP results of different methods because of differences in data sources, parameter settings, model selection, spatial scales, and estimation timescales. MODIS GPP estimates GPP based on a light-use efficiency model, while GOSIF GPP directly estimates the GPP based on the solar-induced chlorophyll fluorescence emitted by plants during photosynthesis, reflecting the actual growth status of vegetation. As GOSIF GPP considers various environmental stressors and anthropogenic factors, it can capture the spatial distribution in greater detail62,63. The CatBoost GPP results were highly consistent with those of GOSIF GPP with respect to both temporal and spatial variations. However, CatBoost GPP yielded a more detailed spatial distribution with a spatial resolution of 1000 m. As GOSIF GPP and CatBoost GPP have different spatial resolutions, the \(R^{2}\) value between CatBoost GPP and GOSIF GPP was 0.63 (Fig. 7a). Wang et al.64, Liu et al.65, and Yu et al.66 reported that MODIS GPP underestimates the GPP, especially in northern China. The values obtained with CatBoost GPP were higher than those obtained with MODIS GPP, with an \(R^{2}\) value of 0.73 between the two models (Figure 7(b)), confirming that our method effectively addresses GPP underestimation.

Fig. 6
figure 6

Spatial distribution of the normalized mean GPP in Shanxi Province from 2001 to 2022. Maps were created using ArcGIS10.2 (Environmental Systems Research Institute, USA. https://www.esri.com/).

Full size image
Fig. 7
figure 7

Validation of CatBoost GPP against GOSIF GPP (a) and MODIS GPP (b). The red dashed line is the fit line between the CatBoost GPP and GOSIF GPP and MODIS GPP and the black solid line is the 1:1 line.

Full size image

In addition, we compared the CatBoost GPP results with the results of previous GPP estimation research (Table 11). Following cross-validation, our method obtained reasonable GPP results for Shanxi Province. Therefore, CatBoost GPP is suitable for investigating the spatiotemporal trends in and drivers of GPP in Shanxi Province.

Table 11 Estimation of GPP in Shanxi Province using different terrestrial models.
Full size table

Annual GPP trends and consistency of future GPP trends

Overall, the GPP in Shanxi Province noticeably improved from 2001 to 2022 (Fig. 8a). The percentage of areas characterized by significant improvement, slight improvement, slight degradation, and considerable degradation was 87%, 9%, 3%, and 1%, respectively. The areas of significant decline were mainly concentrated in densely populated areas of the cities. The largest proportion of the decline in GPP (8.1%) occurred in Taiyuan due to two main reasons. First, Taiyuan’s urbanization process has accelerated, and the type of land cover has changed rapidly, with large areas of vegetation being converted to construction land. Second, the increase in carbon emissions from human activities indirectly led to a decrease in GPP. Meanwhile, approximately 98% of Linfen and Lvliang had significant increases in GPP. Ecological improvement in the two cities mainly stemmed from the Chinese government’s ecological projects, such as afforestation efforts in the LP since the late 20th century75.

Fig. 8
figure 8

(a) GPP change trends in Shanxi Province, (b) the spatial distribution of the Hurst exponent for the annual average GPP time series in Shanxi Province, and (c) predicted GPP changing trends in Shanxi Province. Maps were created using ArcGIS10.2 (Environmental Systems Research Institute, USA; https://www.esri.com/).

Full size image

The spatial distribution of the Hurst exponents for the GPP time series is shown in Fig. 8b. Regions in which the GPP trend was expected to remain consistent (0.5 < Hurst exponents < 1) covered 39.54% of the study area, whereas those in which the trend was expected to reverse (0 < Hurst exponents < 0.5) covered 60.46%. The average Hurst exponent for Shanxi Province was 0.48, suggesting weak anti-persistence in GPP development. In the future, while GPP will continue to rise, the growth rate will gradually decline. Furthermore, the vegetation carbon sequestration capacity may stabilize or even decrease without human intervention.

We combined the trend analysis and Hurst exponent results to predict the sustainability of GPP variations (Fig. 8c). In Shanxi Province, 37.2% of regions exhibited continuous improvement, 58.8% exhibited degradation, 2.34% exhibited continuous degradation, and 1.67% exhibited improvement. Notably, the improved and continuously degraded areas were concentrated in the centers and surrounding areas of the municipal administrative divisions. These areas had dense populations and underwent rapid land use changes, resulting in a high stochasticity of vegetation change. The persistently improved areas were mainly distributed in the Yuncheng Basin, Datong Basin, and Yellow River area on the left side of the Lvliang Mountains. The GPP degradation area was the largest, indicating that the ecological environment in most parts of Shanxi Province was unstable. Continued vegetation protection efforts are necessary to achieve sustainable development.

Quantitative analysis of GPP changes

Effects of natural and anthropogenic factors

The degree of influence of each factor on GPP was in the following order: land use type > precipitation > temperature > slope > elevation > population > GDP (Fig. 9). The land use type, with a q-value of 0.46, had the strongest explanatory power for GPP changes, followed by precipitation, with a q-value of 0.32, which was the main natural factor influencing spatial GPP variation. The effects of various driving factors changed from 2001 to 2022. Among natural factors, the q-values of temperature and elevation increased continuously, whereas those of precipitation and slope decreased. The explanatory power of anthropogenic factors (land use type, population, and GDP) continuously increased. This indicates that human activities, such as ecological protection measures, natural resource management, and urban development, had a significant impact on GPP changes. Human activities positively contributed to the ecological development of Shanxi Province (Figs. 8a, 9).

Fig. 9
figure 9

The q-values of different factors in Shanxi Province.

Full size image

Effects of interactions between factors

The effects of the interactions between factors on the GPP were stronger than the effects of single factors, and interactions between factors were categorized as bivariable enhanced or nonlinear enhanced (Fig. 10). The interaction between land use type and precipitation yielded the highest q-value, and their respective interactions with other factors were also significant. Among these, the interaction between precipitation and temperature significantly affected the spatial distribution of GPP, evolving from nonlinear enhanced to bivariable enhanced over time. The q-values of the interactions between precipitation and elevation, precipitation and slope, temperature and elevation, and temperature and slope significantly increased compared with those of single factors. This is because elevation and slope serve as the underlying surfaces for vegetation growth, affecting sunlight and hydrothermal conditions, thereby influencing the spatial distribution of GPP. The interactions between population and elevation, as well as those between population and temperature, are complex.

Fig. 10
figure 10

Interactions between driving factors of the GPP in Shanxi Province. x1: elevation, x2: slope, x3: precipitation, x4: temperature, x5: GDP, x6: population, x7: land use type.

Full size image

Discussion

Interpretability analysis based on SHAP

We employed SHAP value-based interpretability analysis to quantitatively evaluate the relative importance of features (Fig. 11a) and their direction of influence on GPP estimation (Fig. 11b). The SHAP values effectively quantified each feature’s contribution to the model output, with higher values indicating that the feature had a more significant impact on the results76. According to the SHAP values of the driving factors (Fig. 11a), time-series features were essential for constructing the CatBoost GPP estimation model. Among them, NDVI demonstrated the most significant impact on the CatBoost GPP model, followed by FPAR. Notably, NDVI and FPAR can directly characterize the spatiotemporal heterogeneity of vegetation growth status and photosynthetic capacity77,78, thereby playing a dominant role in the model’s estimation process. As intra-annual changes in GPP vary significantly more than inter-annual changes, temporal features play a crucial role in the GPP estimation process. LST is an important environmental influencing factor in GPP estimation20, yet its influence on the model was lower than that of temporal feature. This is mainly because LST changes are not completely synchronous with vegetation growth rhythms, and they vary in impact across different growth stages79. Moreover, GPP is influenced by other environmental factors (e.g., precipitation and evapotranspiration), which reduces the effect of LST on the model. Land use changes directly affect GPP and are the most immediate manifestation of human impacts on terrestrial ecosystems80. However, as a category-type feature, land use exhibited a weaker effect on the model than the time-series feature. Meanwhile, topographic factors such as DEM and slope, which represent terrain elevation and gradient, respectively, affect vegetation spatial distribution patterns by mediating the redistribution of hydrothermal factors, thereby affecting vegetation composition and structure81. Incorporated as constraints in CatBoost GPP estimation, these prevent overestimation in steep, high-elevation areas.

In Fig. 11b, the vertical axis represents feature variables, while the horizontal axis shows the SHAP values. Each point corresponds to a real sample, and broader point distributions indicate higher sample densities. The color gradient from blue (low) to red (high) visually demonstrates the degree and direction of influence of features. Specifically, higher values of NDVI, FPAR, and LST are associated with positive SHAP values, suggesting that these features stimulate vegetation GPP. High values of these characteristics typically indicate favorable vegetation growth conditions and environments, which enhance the vegetation’s carbon sequestration capacity. Conversely, the SHAP values of DEM and slope are mostly negative at high values, indicating that high elevations and steep slopes have a significant inhibitory effect on vegetation GPP. This is because high elevations and steep slopes values suppress vegetation productivity through direct environmental stressors, such as low temperature and drought, as well as indirect resource limitations, such as soil erosion and nutrient depletion. This leads to predominantly negative SHAP values being associated with high DEM and slope values. This characteristic improves the accuracy of vegetation GPP estimation in regions with large variations in elevation and slope, such as Shanxi Province.

Fig. 11
figure 11

Feature importance and effect analysis of the CatBoost model ((a) feature importance, (b) summary plot).

Full size image

Analysis of factors affecting GPP in Shanxi Province

We utilized a Geodetector model to identify the main drivers of GPP spatiotemporal variation in Shanxi Province and found that land use type was the main driver of GPP evolution. Previous studies indicated that land use change driven by human activity has substantially altered the structure and function of natural ecosystems, affecting the terrestrial carbon flux82between 2001 and 2022, 27% of land use types in Shanxi Province underwent change (Fig. 12). The farmland area had the greatest increase (27621 km\(^{2}\)), which primarily occurred in Linfen, Yuncheng, southern Lvliang, and western Jincheng. The high carbon sequestration capacity of farmland and forest land had a notable positive impact on the GPP of Shanxi Province. Conversely, the continuous expansion of urban construction land led to a substantial decline in GPP in medium and large cities. Furthermore, considerable uncertainty surrounds future GPP trends (Fig. 8c).

Fig. 12
figure 12

(a) Spatial distribution of land use change in Shanxi province from 2001 to 2022 and (b) transform matrix of total GPP (Tg) in the context of land use change in Shanxi province from 2001 to 2022. Maps were created using ArcGIS10.2 (Environmental Systems Research Institute, USA; https://www.esri.com/).

Full size image

Despite variations in land use type, GPP increased overall, with grassland experiencing the greatest increase in GPP (29.07 Tg C). Grassland constitutes the primary land use type in Shanxi Province, accounting for approximately 53% of the region, primarily in the northwestern section (e.g., Datong and Shuozhou). These areas have been impacted by coal mining, desertification, and land degradation, resulting in a fragile ecological environment. Nevertheless, the implementation of national ecological projects, including the Beijing–Tianjin Sandstorm Source Control Project, Three-North Shelterbelt Project, and Grain for Green Program30,32, has led to improvements in the ecological environment and consequently, an increase in GPP.

The interaction detector revealed that the interaction between temperature and precipitation had a complex effect on the GPP spatial pattern in the study area. Therefore, we used partial57 and composite correlation analyses58 to establish classification criteria for climate-driven factors (Table 10) at a significance level of p = 0.05 to clarify the response mechanism of GPP to precipitation and temperature in Shanxi Province.

The results of partial and composite correlation analyses are shown in Fig. 13 The average partial correlation coefficient between GPP and temperature was 0.28, and that between GPP and precipitation was 0.37. The composite correlation coefficient was 0.44. The spatial distribution exhibited a pattern of “weak in the north and south and strong in the central region”, with climatic factors driving approximately 90.54% of GPP variation in Shanxi Province. However, the majority of areas (54.41%) were weakly driven by temperature and precipitation. Areas with significant GPP changes were primarily influenced by precipitation (23.53%) and were concentrated in the central part of the province. The regions where GPP was driven solely by temperature (4.96%) were scattered across the study area. Notably, in the southwestern and northwestern regions of Shanxi Province, GPP increases were closely related to human activities.

These findings are closely related to the geographical location of Shanxi Province. Precipitation is a major factor controlling vegetation growth and largely determines the spatial distribution of vegetation83. Shanxi is a semi-humid and semi-arid region with low rainfall. In particular, the correlation between precipitation and GPP was significantly lower in the northern areas than in other regions. Although rainfall has increased in recent years, it has historically been a key factor limiting vegetation growth in the northern part of Shanxi Province. Furthermore, Shanxi is located in the mid-latitude region, in which the temperature difference between the north and south is small and the temperature is stable. This resulted in a lower sensitivity of GPP to temperature. However, the temperature affects surface evapotranspiration. As the temperature increases, the effective water content in the soil decreases, thereby slowing the growth and development of vegetation84.

Topographic conditions such as slope and elevation generally remain stable in natural environments, and they mainly influence vegetation biomass, carbon storage, and carbon sequestration potential by regulating soil, water, and light resources85. In Shanxi Province, the explanatory power of these factors was lower than that of climatic factors; however, the interacting effect of topographic and climatic factors exerted a notable influence on the GPP. This may have been related to the local redistribution of precipitation and temperature caused by topographical factors86. In addition, areas with gradual slopes or level ground experience frequent human interference, hindering vegetation growth, but steep-sloped areas with infrequent human activity enable vegetation to grow better and therefore have a greater impact on GPP. As for elevation, in recent years, large-scale ecological restoration and afforestation projects have altered the natural vertical distribution of vegetation. The distribution of planted forests spans various elevations, which may reduce the effect of elevation on vegetation.

Fig. 13
figure 13

Correlation between GPP and climatic factors in Shanxi province and types of climatic drivers. Maps were created using ArcGIS10.2 (Environmental Systems Research Institute, USA. https://www.esri.com/).

Full size image

Study limitation

Although the proposed CatBoost GPP model showed superior performance in estimating GPP at the site scale, several issues remain that hindered its performance. The uncertainties and limitations of the proposed method were mainly attributed to the following aspects. First, owing to the difficulty and high cost of obtaining field-measured GPP data and the lack of publicly available GPP observations for Shanxi Province, we cross-validated the estimation results using data from MODIS GPP, GOSIF GPP, and previous studies. Although these datasets have been widely validated for GPP estimation, incorporating field measurements would further reduce accuracy uncertainties. Secondly, vegetation photosynthesis is a complex process influenced by multi-scale environmental, atmospheric, and physiological factors. In the future, we will consider additional drivers, such as carbon dioxide concentration87 and solar radiation16, to explore the effect of each characteristic variable on the model. Finally, we employed the dataset division method used in previous studies23, which has scientific validity. However, due to the lack of observational datasets, this division may be biased due to inter-annual variations. In future studies, we will collect more data to compare the effects of different dataset division methods on the model estimation results, and further verify the validity of dataset division.

Conclusions

We developed a novel GPP estimation framework based on CatBoost that synergistically combines ML techniques with vegetation ecophysiological mechanisms. The CatBoost GPP model exhibited superior performance (\(R^{2}\) = 0.890, RMSE = 1.155 gC \(\textrm{m}^{-2} \, \textrm{day}^{-1}\), MAE = 0.772 gC \(\, \textrm{m}^{-2}\, \textrm{day}^{-1}\)) compared with that of the RF, SVM, LightGBM, XGBoost, LSTM, GOSIF GPP, and MODIS GPP methods. We applied the CatBoost GPP model to estimate the GPP of Shanxi Province from 2001 to 2022. Based on the results, we further investigated the spatiotemporal evolution of the GPP and its driving factors. The main conclusions were as follows:

(1) Spatially, the GPP was generally low in the northwest and high in the southeast, with distinct band features. From 2001 to 2022, the GPP exhibited significant fluctuating growth at a rate of 20.58 gC \(\textrm{m}^{-2}\, \textrm{year}^{-1}\). However, the recent trend in GPP indicates weak anti-persistence, with 58.8% of the land potentially facing degradation in the future.

(2) Human activities contributed to an increase in the GPP, with land use type being the most significant factor. In the northwestern and southwestern regions of Shanxi Province, GPP changes were primarily driven by human activities, whereas GPP changes in the central region were predominantly affected by climatic factors, particularly precipitation.

(3) Factor interactions were either bivariable or nonlinear enhanced. The combined effect of precipitation and temperature had the most complex and significant impact on GPP, with an explanatory power of 46%, covering approximately 62.05% of the study area.