The adaptive dynamic programming signal control system for person in a connected vehicle environment

Abstract

Urban person delay and congestion remain persistent challenges in modern traffic systems. Leveraging Connected Vehicle (CV) data, this study proposes a novel Person-Based Adaptive Control Algorithm (PB-ACA) to minimize average person delay at isolated urban intersections. Unlike traditional vehicle-based controls, PB-ACA integrates vehicle occupancy data with real-time trajectory and speed information to assign signal priorities based on person-level delay impacts. A three-layered dynamic programming approach is adopted in PB-ACA with the objective of minimizing person delay with real time occupancy data. A signal phase transition exploration mechanism is also developed to explore all possible signal timing plans according to non-conflicting phase rules and efficient principles. The generalized vehicle trajectory and car-following model is adopted for predicting the platoon discharge times considering different cases and fleet trajectories to enhance the responsiveness to CV data. Performance evaluations using microsimulation in SUMO compare PB-ACA against three benchmark approaches: fixed-time control (FTCA), inductive loop-actuated control (ILACA), and vehicle-based adaptive CV signal control (VBACVSC). Results show that PB-ACA reduces average person delay by up to 55% compared to FTCA, by 42% compared to ILACA and by 11% relative to VBACVSC, especially benefiting high-occupancy vehicles. These findings demonstrate PB-ACA’s potential to improve individual mobility and promote equitable traffic signal control in connected environments.

Introduction

Rising traffic congestion and delays are increasingly critical issues in urban areas, largely driven by the dramatic growth in vehicle miles traveled¹. According to INRIX research, the total economic cost of congestion across the US, UK, and Germany reached nearly $461 billion in 2017, with the majority attributed to time lost by drivers and passengers². Urban traffic signal control systems play a pivotal role in alleviating congestion by dynamically managing conflicting vehicle flows and adapting to fluctuating traffic demand at intersections.

Traditional Urban Traffic Control (UTC) systems have evolved through three main stages: fixed-time control (e.g. TRANSYT³), actuated control, and traffic-responsive control utilizing fixed-location sensors (e.g. SCOOT⁴, OPAC⁵, SCAT⁶, RHODES⁷, PRODYN⁸, MOTION⁹). Fixed-time systems operate with predetermined phase sequences and durations based on offline optimizations of historical traffic data¹⁰. Actuated control strategies rely on real-time input from loop detectors and radar sensors, while traffic-responsive systems represent the most advanced form of UTC, dynamically adjusting signal timing in response to traffic conditions.

However, two significant limitations constrain the effectiveness of traffic-responsive systems. First, most sensors (e.g., inductive loops) are point-based, capturing only limited snapshots of passing vehicles¹¹. Second, current UTC strategies are inherently vehicle-based systems, which treat all vehicles equally without accounting for the number of passengers. Yet, improving personal mobility rather than vehicle throughput is increasingly emphasized in future urban mobility visions¹². Time lost per person, not per vehicle, constitutes the true economic cost of congestion, projected to reach 106 h per person annually by 2050, a threefold increase from 2018¹³. Therefore, it is critical to developing signal controllers with the objective of reducing person delay in urban signalized junctions. While this is hardly achievable in UTC systems as vehicle occupancy information cannot be acquired by loop-based sensors.

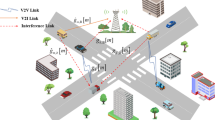
Recent advances in Connected Vehicle (CV) technologies, via vehicle-to-infrastructure (V2I) and vehicle-to-vehicle (V2V) communications, offer promising solutions. Using protocols such as Dedicated Short-Range Communication (DSRC), CVs can share real-time data on position, speed, and vehicle status with traffic controllers. While vehicle occupancy detection has not been standardized, systems like Automated Passenger Counters (APCs), in-vehicle load sensors, and roadside video analytic provide feasible methods for estimating occupancy. These advances present an opportunity to overcome both key limitations of traditional UTC systems.

This paper proposes a novel, person-based signal control strategy that utilizes real-time CV data in isolated urban intersections. Assuming full CV penetration, vehicles can transmit occupancy data and operational states to traffic controllers. Our approach assigns signal priority based on passenger load, offering a new perspective beyond conventional vehicle-based models. Inspired by transit signal priority (TSP) strategies, such as phase skipping and extension, we design a system capable of flexibly adjusting phase sequences and durations to minimize average person delay¹⁴.

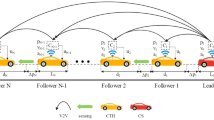
The core of the proposed Person-Based Adaptive Control Algorithm (PB-ACA) is a three-layer dynamic programming (DP) optimization framework, which integrates position, speed, and occupancy data to evaluate signal strategies. The first layer performs a forward DP to compute optimal vehicle departure times based on candidate signal plans. The second layer explores all feasible phase transitions using non-conflicting phase rules and updates departure predictions accordingly. The third layer evaluates person-based performance at the end of the horizon and uses backward DP to identify the best timing strategy.

The structure of this paper is as follows: Section 2 presents a review of related literature and identifies existing research gaps. Section 3 outlines the overall PB-ACA system framework. Sections 4 and 5 provide the methodology details of PB-ACA. Section 6 describes the simulation setup, evaluation scenarios, and benchmark models. Section 7 discusses performance results. Section 8 concludes the paper and outlines directions for future research.

Literature review

Compared to traditional loop-based sensors, connected vehicle data provide richer and more granular insights into traffic dynamics, enabling more effective signal control. Existing CV-based adaptive signal control methods can be grouped into three major categories^10,15.

In the first group, many early studies model each intersection as a decision-making agent that receives real-time CV data (e.g., speed and position). Some formulate signal optimization as mathematical programming problems aiming to minimize vehicle delay^16,17,18, minimize queue length^19,20, maximize throughput²¹ or improve efficiency^22,23. Others build on classical models like Webster’s formula²⁴, substituting historical data with live CV data to better respond to dynamic conditions^25,26,27. In parallel, researchers have introduced machine learning into signal timing optimization. Reinforcement learning (RL)-based approaches optimize signal plans via trial-and-error training^28,29. The analogy methods were also adapted by some studies, drawing lessons from the knowledge and architectures of other areas, such as artificial immune network³⁰, weighted backpressure model³¹ and game-theoretic approaches^32,33,34.

Some researchers incorporate Autonomous Vehicles (AVs) into mixed traffic environments. Methods include reservation-based strategies^35,37, which allocate intersection right-of-way in time slots based on arrival order, and trajectory-based methods^36,38,39, which compute conflict-free paths via centralized or decentralized coordination. Extensions to these models include hybrid strategies that combine traffic signal optimization with AV trajectory control⁴⁰, and hierarchical control frameworks that integrate local (intersection-level) and global (corridor-level) decision layers^41,42,43. However, all methods in these two groups remain vehicle-centric, focusing on vehicle delay rather than passenger-level outcomes.

A more recent line of research incorporates person delay into optimization. Christofa and Skabardonis⁴⁴ proposed minimizing person delay by considering buses and cars, but under rigid signal settings (fixed cycle, sequence, and stages). Later works extended this to include bus priority with minimal impact on other traffic^45,46 and flexible cycle lengths⁴⁷. Vilarinho et al.⁴⁸ introduced a bid-based priority mechanism to reduce person delay based on vehicle occupancy, though it relied on empirical pedestrian estimates. A user-based signal optimization algorithm was then designed to maximize user throughput rather than minimise person delay in a four-leg isolated junction using fixed phase sequence and stage combination settings⁴⁹.

The existing adaptive signal researches using CV information in the first two groups are vehicle-based with the objective of reducing average vehicle delays or vehicle travel times⁴⁸, neglecting the priority of high occupancy vehicles. Few papers in third groups developed signal priority systems focusing on person delays including public transport, some of which extended the person-based objectives towards a regular junction environment without the interpretation of public vehicles. This enables the signal control transitions from the vehicle-based system to the person-based system utilizing CV data. From the experiences of Transit Signal Priority strategies, flexible signal timing approaches ought to be adopted to award higher priorities to buses with more people, e.g., stage skipping, green extension, and stage recall. However, the traffic environments at junctions without public transport are more complex when aiming to achieve the total person-delay objective, since it is challenging to predict the arrival times of private cars, the lanes from which they approach, and their occupancy rates. Even though state-of-the-art researches attempted to adopt flexible cycle length, their approaches with fixed stage sequences and specific phase combinations are still not flexible enough for person delay reduction targets. Therefore, there is a critical research gap that more flexible signal plans need to be optimized for person-based signal controls to better react to passenger vehicles with a variety of occupancy levels from different directions and arrival lanes. Meanwhile, the new vehicle trajectory and car-following updating theories are required to be developed to predict vehicle arrival time under different potential signal timing plans.

In this study, a new signal control system is developed to explore the optimal signal plans for reaching maximum user delay profits from all feasible phase combinations and stage sequences, considering a variety of people occupancy in vehicles, flow demands in separate lanes and vehicle statuses. Moreover, the theories used in researches to predict the discharging time of approaching vehicles in different cases are not applicable in situations of flexible stage sequences and phase combinations due to possible high-frequency traffic light modes switch for assigning priorities to corresponding passenger vehicles.

The study attempts to fill in the research gaps. The proposed control method is a expandable framework that can be implemented in multiple junctions, and imperfect CV situations with buses. This paper proposes an Adaptive Person Based Signal Control Algorithm (PB-ACA) to minimize person delay by exploring all possible phase combinations and feasible signal plan strategies at isolated urban intersections. The extended works on how to improve the approach in more realistic traffic situations will be briefly introduced in the discussion and conclusion sections and will achieve in future works. The contributions of this paper are as follows:

• A three-layered dynamic programming person-based signal control mechanism is developed to minimize the person delay weighted by real-time occupancy data, shifting focus from vehicle-centric to people-centric signal control.

• A novel state transition mechanism is proposed, enabling flexible phase combinations and sequences beyond fixed-cycle constraints, dynamically exploring all non-conflicting phase options to optimize person throughput.

• A generalized vehicle trajectory and car-following model is proposed to accurately predict platoon discharge times under mixed traffic states (free-flow/queuing), enhancing responsiveness to CV data in adaptive control.

System overview

This section introduces the operational structure of the proposed PB-ACA system for isolated urban intersections (illustrated in Fig. 1). The control algorithm receives and processes Basic Safety Message (BSM) data from connected vehicles, including vehicle ID, position, speed, and occupancy level, broadcast at 10 Hz via DSRC under the IEEE 802.11p protocol⁵⁰. The system defines a 250-meter control perimeter, within which all CV messages can be reliably received⁵¹. A 1-second time step is used for real-time decision-making.

At the core of PB-ACA is a three-layer dynamic programming (DP) optimization procedure, which identifies the optimal signal control strategy at each decision point. As shown in Fig. 1, the algorithm receives vehicle ID, position, speed and vehicle occupancy level, and processes them to produce the vehicle state list and initial departure time list as inputs for the first layer. The first layer introduced in Sect. 5.1 performs a forward DP process, calculating sub-performance values for candidate signal plans at every second. These are derived from vehicle states and estimated departure times. The second layer in Sect. 5.2 and 5.3 incorporates a signal phase transition exploration algorithm that enumerates all feasible phase combinations in the next stage, using non-conflict phase rules and updating departure predictions based on both state and decision variables. The third layer conducts a backward DP search at the end of the planning horizon to select the signal plan that maximizes person-based performance. Additionally, a trajectory and car-following model is employed to accurately estimate vehicle discharge times under different control scenarios, accounting for free-flow and queued conditions. This rolling horizon framework executes continuously, updating signal plans as new CV data become available.

Problem formulation

This section presents the technical framework of the proposed PB-ACA, designed to optimize traffic signal operations at isolated urban intersections. Unlike conventional approaches, PB-ACA eliminates rigid phase sequencing and fixed duration constraints while prioritizing the minimization of average person delay through real-time CV data utilization. PB-ACA establishes an adaptive decision-making mechanism that dynamically associates signal plans with person-based performance metrics. The algorithm uniquely incorporates vehicle occupancy levels through continuous data exchange between the intersection controller and CVs, enabling responsive priority allocation based on actual passenger numbers. The complete mathematical formulation employs the sets, variables, and parameters detailed in Table 1.

Table 1 The variables and parameters used in PB-ACA.

The objective of PB-ACA is to minimize the average person delay in the isolated urban junction. The person delay is calculated by the product of vehicle delay and the number of people in a vehicle. The vehicle delay equals the difference value of the vehicles’ predicted departure time and virtual departure time from the downstream place of the junction. However, the summation of delays of all detected vehicles is difficult to be measured in signal optimization procedure as not all vehicles from upcoming lanes can be discharged in a limited planning duration $\:T$. The departure times of those vehicles are unknown in the current optimization. Therefore, the increment of total people time savings is adopted to replace the summation of people delay reduction. A mixed integer linear programming model is developed in PB-ACA maximizing the total number of person discharging time savings. The occupancy level factor is incorporated into the objective function to assign fairly priorities to vehicle users and their vehicles. The objective function is formulated in Eq. (1):

$$\:\text{max}\sum\:_{p=1}^{{P}^{{\prime\:}}}\sum\:_{i=1}^{{i}_{p}}A(i,p)[{T}^{{\prime\:}}+1-Tc\left(i,p\right)]$$

(1)

s.t.

$$\:0\:\le\:A\left(i,p\right)\le\:\:{A}_{0}\:\:\:\:\:\:\:\:i=1,\:2,\:\dots\:,\:{i}_{p},\:\forall\:p\:\in\:P$$

(2)

$$\:0\:\le\:Tc\left(i,p\right)\le\:\:{T}^{{\prime\:}}+1\:\:\:\:\:\:\:i=1,\:2,\:\dots\:,\:{i}_{p},\:\forall\:p\:\in\:P$$

(3)

$$\:0\:\le\:\sum\:_{p=1}^{{p}^{{\prime\:}}}{m}_{t}^{p}\le\:\:2\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:t\:\in\:T$$

(4)

$$\:{{Vc}_{t}^{p}(i,\:s}_{t})<\:{{Vc}_{t}^{p}(i+1,\:s}_{t})\:\:\:\:\:\:\:i=1,\:2,\:\dots\:,\:{i}_{p}-1,\:\forall\:p\:\in\:P,\forall\:t\:\in\:T,\forall\:{s}_{t}\:\in\:{S}_{t}$$

(5)

$$\:{{{d}_{t\:}\in\:D}_{t}(s}_{t}),\:\:{s}_{t\:}\in\:\:{S}_{t\:},\:\:\:\:\:\forall\:t\:\in\:T\:$$

(6)

where $\:A(i,p)$ represents the occupancy level of vehicle i in phase p, $\:{A}_{0}$ is the occupancy limit, $\:{T}^{{\prime\:}}$ is the planning duration, $\:Tc\left(i,p\right)$ refers to the vehicle crossing time. $\:{m}_{t}^{p}$ represents the traffic light state in phase $\:p$ at time stage $\:t$, represented by binary variables. 0 if red and 1 if green. $\:{{Vc}_{t}^{p}(i,\:s}_{t})$ is the predictive departure time of vehicle $\:\text{i}$ in phase $\:p$ at time stage $\:t$, given state variable $\:{s}_{t}$. Constraint (2) limits the value ranges of occupancy level parameters in each vehicle. Constraint (3) limits the value of time spent on the departure time of a specific vehicle starting from time step 0. This value equals $\:{T}^{{\prime\:}}+1$ if the vehicle fails to cross in planning duration. Equation (4) constraints the number of green traffic light phases $\:{m}_{t}^{p}$ available to be assigned at the same time, which should be no more than 2 to obey the rules of non-conflicting phases in a standard 8-phases isolated junction to avoid vehicle collision. Constraint (5) sets out the relationships of predictive departure time among those vehicles in the same lane assuming no lane-changing behaviours near the junction.

Fig. 1

Conceptual framework flowchart of PB-ACA.

Constraint (6) claims that all of the state variables $\:{s}_{t\:}$and decision variables $\:{d}_{t\:}$need to be selected from their separate sets $\:{S}_{t\:}$and $\:{{D}_{t}(s}_{t})$ at time $\:t$. The determinations of state set and control decision set depend on phase transition regulation and state set in last stage $\:t-1$, which are represented in Eqs. (7) and (8) respectively. The details are described in Sect. 5.2.

$$\:{S}_{t\:}=\:\left\{{s}_{t}\:\mid\:\langle{s}_{t-1},\:{s}_{t}\rangle\:\in\:L,{\:s}_{t-1}\in\:\:{S}_{t-1\:}\right\}\:\:\:\:\forall\:t\:\in\:T$$

(7)

$$\:{{D}_{t}(s}_{t})=\:\left\{\langle{s}_{t-1},\:{s}_{t}\rangle\:\mid\:\langle{s}_{t-1},\:{s}_{t}\rangle\:\in\:L,{\:s}_{t-1}\in\:\:{S}_{t-1\:}\right\}\:\:\:\:\:\:\:\:\:\:\:\forall\:t\:\in\:T$$

(8)

where $\:\langle{s}_{t-1},\:{s}_{t}\rangle$ refers to the decision made by junction controller transition from state $\:{s}_{t-1}$ at time stage $\:t-1$ to state $\:{s}_{t}$ at time stage $\:t$.

Fig. 2

Different cases of fleet trajectory representations assuming constantly green light given.

Before implementing the optimal solution algorithm, all BSMs from CVs are organized into vehicle information lists categorized by phase index. This process aims to generate initial predictive departure time lists for the vehicle fleet using vehicle trajectory theories illustrated in Fig. 2. Each connected vehicle transmits real-time data on its individual characteristics and trajectory to the junction management infrastructure. Using location information, the distances from these vehicles—traveling within the detection region and approaching the junction center—to the cross line of each lane are calculated. The location lists are then sorted so that connected vehicles are ordered by their distance to the cross line from nearest to farthest within the detection range. Instantaneous speed and occupancy level lists are compiled by recording fleet information in this distance-based order.

Given the positions and speeds of the vehicle fleet in a lane, the initial departure times for queued and arriving vehicles are predicted at the optimization start under the assumption that the lane will continuously receive green lights, as defined in Eqs. (9) and (10). This prediction method is rooted in kinematic wave theory principles adopted in person-based control [41] and [44], which models vehicle trajectories in a fleet considering adjacent vehicle influences. To reduce algorithm optimization complexity, this paper simplifies vehicle acceleration and deceleration processes during queue merging or discharge startup. The method considers four distinct fleet trajectory patterns (see Fig. 2) for arriving fleets with at least three vehicles.

The departure scenarios in Fig. 2 analyze vehicle trajectories and statuses using speed and distance-to-junction data. Blue lines represent vehicles traveling at free-flow speed, while brown lines denote queued or slowing vehicles. The primary distinction between scenarios is whether a queue exists at the junction when the green light is activated. If the speed of the first vehicle in approach fleet $\:{v}_{0}^{p}\left(i\right)$ is higher than the threshold speed parameter $\:{v}_{s}$, it is in free-flow status, with its departure time calculated as the distance to the junction cross line divided by its instantaneous speed. Following vehicles also cross the junction without stopping, as shown in Case 1 of Fig. 2. If the platoon’s first vehicle is stationary, it forms a queue at the junction. Upon receiving a green light, this vehicle incurs a start-up loss time $\:\alpha\:$ due to driver reaction time and acceleration time lost, then cross the junction with saturated flow speed $\:{v}_{s}$. Subsequential queued vehicles (Case 2) accelerate to speed $\:{\text{v}}_{\text{s}}$ and discharge with a saturation time headway $\:{\text{h}}_{\text{s}\:}$to avoid collisions. When a free-traveling vehicle approaches the queue’s end, it either merges into the queue before front vehicles discharge (Case 3) or crosses freely after queue clearance if sufficiently distant (Case 4). The decision depends on comparing the free-speed discharge time with the previous vehicle’s predicted departure time plus the saturation headway: Case 3 occurs if the latter is greater; otherwise, Case 4 applies.

As theorized in Fig. 2, the first vehicle’s initial departure time is formulated separately (Eq. 9) because its trajectory is unaffected by following vehicles, and start-up loss time must be considered. The initial departure times of subsequential vehicles are computed sequentially using Eq. (10).

$$\:{{Vc}_{0}^{p}(1,\:s}_{0})=\left\{\begin{array}{c}\alpha\:+{h}_{s}-{g}_{p},\:\:\:\:\:\:\:\:if\:{v}_{0}^{p}\left(1\right)=0\:and\:{g}_{p}\:<\:\alpha\:+{h}_{s}\\\:min[\alpha\:+{h}_{s}-{g}_{p},\:{\:l}_{0}^{p}\left(1\right)\:/\:\:{v}_{0}^{p}(1\left)\:\right],\:\:if\:{0\:\le\:v}_{0}^{p}\left(1\right)\:\le\:{v}_{s}\:and\:{g}_{p}\:<\:\alpha\:+{h}_{s}\\\:{\:l}_{0}^{p}\left(1\right)\:/\:\:{v}_{0}^{p}\left(1\right),\:\:\:\:\:\:\:if\:{v}_{0}^{p}\left(1\right)\:>\:{v}_{s}\:or\:{g}_{p}\:\ge\:\:\alpha\:+{h}_{s}\end{array}\right.\:\:\forall\:p\:\in\:P$$

(9)

$$\:{{Vc}_{0}^{p}(i,\:s}_{0})=\left\{\begin{array}{c}{{\:Vc}_{0}^{p}(i\:-1,\:s}_{0})\:+{h}_{s},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:{v}_{0}^{p}\left(i\right)\:\le\:\:{v}_{s}\:\\\:{{max}[l}_{0}^{p}\left(i\right)\:/\:\:{v}_{0}^{p}\left(i\right),\:{{\:Vc}_{0}^{p}(i\:-1,\:s}_{0})\:+{h}_{s}],\:\:if\:{v}_{0}^{p}\left(i\right)\:>\:{v}_{s}\end{array}\:\:\forall\:p\:\in\:P,\:i\:\ge\:2\right.$$

(10)

where $\:{g}_{p}$ is the total number of constantly green traffic lights time steps given for phase p before initial time stage 0, $\:{\:l}_{0}^{p}\left(i\right)$ and $\:\:{v}_{0}^{p}\left(i\right)$are instantaneous distance and speed of vehicle $\:i$ from the stop line to its location in phase p at initial time stage. The travelling status of each vehicle when it leaves the approaching lane is defined by binary variables. This variable is judged after the initial departure time is determined for the convenience of updating the departure time of the vehicle in the following steps. The transition of two status modes is an irreversible process. Once a vehicle driving in free flow speeds changes to queuing status, this status will keep constantly up to be discharged. The statuses of the first vehicle and following vehicles in the lane counted from the stop line are expressed in Formulas (11) and (12) respectively.

$$\:{{Vc}_{0}^{p}(1,\:s}_{0})=\:\left\{\begin{array}{c}1,\:\:\:\:\:\:\:\:if\:{v}_{0}^{p}\left(1\right)\:>\:{v}_{s}\:\\\:0,\:\:\:\:\:\:\:\:if\:{v}_{0}^{p}\left(1\right)\:\le\:{v}_{s}\end{array}\:\:\:\:\:\:\:\:\forall\:p\:\in\:P\right.$$

(11)

$$\:{{Vc}_{0}^{p}(1,\:s}_{0})=\:\left\{\begin{array}{c}1,\:if\:{v}_{0}^{p}\left(1\right)\:>\:{v}_{s}\:and\:{\:{{Vc}_{0}^{p}(i,\:s}_{0})\:>l}_{0}^{p}\left(i\right)/{v}_{0}^{p}\left(i\right)\\\:0,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:other\:cases\end{array}\:\:\:\:\:\:\:\forall\:p\:\in\:P\right.,\:\:\:i\:\ge\:2$$

(12)

In this section, the details of the proposed PB-ACA is introduced to minimize total person delay in urban isolated junction. PB-ACA describes the controller decision-making operational mechanism of associating traffic signal plans with the corresponding person-based performance measures, considering the occupancy level of each vehicle according to real-time information from the interaction of junction controller and CVs. Dynamic programming is adopted to divide the whole optimization problem into sub-problem in every time step with recursive structure. The optimal solution for substructure is recorded and can be retrieved in the following optimization process to avoid repetitive calculations, which is more effective than the enumeration method.

In a certain planning step $\:t\:\in\:T$ the upper layer of the three-layered DP optimization algorithm captures an optimal value function to a special traffic situation by the proposed DP framework and removes any other strategies to avoid recalculation from the initial stage. The performance measure value function at every time step should be calculated by combining junction policy and instantaneous environmental vehicle states. Junction controller awards traffic green light to discharge vehicles or traffic red light to stop and obstruct vehicle queues. In order to calculate performance measures, the middle layer of the three-layered DP optimization algorithm updates the vehicle departure time list in every stage. The middle layer also explores all kinds of possible signal plans based on the flexible traffic light state machine in Sect. 5.2 rather than a fixed stage sequence, such as a standard NEMA ring barrier signal timing structure in (13). At the lower layer, the algorithm finds the optimal person-based performance measure at the end of the planning horizon and uses a backward recursion DP to search for a signal timing plan resulting in this value function.

$$\:{{c}_{t}({s}_{t},d}_{t})=\:\left\{\begin{array}{c}{\left[a\right(1,t-1,{p}_{t}^{1},\:s}_{t-1})+{a(1,t-1,{p}_{t}^{2},\:s}_{t-1})]\left({T}^{{\prime\:}}+1-t\right),\\\:if{\:p}_{t}^{1}\in\:\left\{\text{1,3},\text{6,8}\right\},\:{p}_{t}^{2}\in\:\left\{\text{2,4},\text{5,7}\right\},\:0<{{Vc}_{t-1}^{{\:p}_{t}^{1}}(1,\:s}_{t-1})\le\:\text{1,0}<{{Vc}_{t-1}^{{\:p}_{t}^{2}}(1,\:s}_{t-1})\le\:1\\\:{\left[a\right(1,t-1,{p}_{t}^{1},\:s}_{t-1}\left)\right]\left({T}^{{\prime\:}}+1-t\right)\:,\\\:if{\:p}_{t}^{1}\in\:\left\{\text{1,3},\text{6,8}\right\}\:and\:0<{{Vc}_{t-1}^{{\:p}_{t}^{1}}(1,\:s}_{t-1})\le\:1,{p}_{t}^{2}\notin\:\left\{\text{2,4},\text{5,7}\right\}\:or\:{{Vc}_{t-1}^{{\:p}_{t}^{2}}(1,\:s}_{t-1})>1\\\:{\left[a\right(1,t-1,{p}_{t}^{2},\:s}_{t-1}\left)\right]\left({T}^{{\prime\:}}+1-t\right),\\\:if{p}_{t}^{2}\in\:\left\{\text{2,4},\text{5,7}\right\}\:and\:0<{{Vc}_{t-1}^{{\:p}_{t}^{2}}(1,\:s}_{t-1})\le\:1,{p}_{t}^{1}\notin\:\left\{\text{1,3},\text{6,8}\right\}\:or\:{{Vc}_{t-1}^{{\:p}_{t}^{1}}(1,\:s}_{t-1})>1\\\:0,\:other\:cases\end{array}\right.\:\:\:\forall\:t\:\in\:T$$

(13)

where $\:{{c}_{t}({s}_{t},d}_{t})$ represents performance measure for person delay at time stage $\:t$, given state variable $\:{s}_{t}$ and control variable $\:{d}_{t}$.

Upper layer

At the upper layer, a dynamic programming optimization algorithm is operated to figure out the optimal solution. The multi-stage DP applies a forward recursion to solve the signal timing optimization problem in the certain planning horizons. Forward recursion calculates the performance measure based on the state variables and decisions and then records the optimal value function for each stage. The forward recursion of DP is on the basis of assigning signal phase plans to each stage as a time step. Considering each time step as a stage, the optimization algorithm applies as many stages as necessary to figure out the optimal solution.

The general framework of DP is illustrated in Fig. 3. The signal timing optimization algorithm triggers at stage 0 and collects state information from connected vehicles. There are several available choices (e.g. $\:{d}_{\text{1,1}\:,\:\:}{d}_{\text{1,2}\:,\:\:}\:{d}_{\text{1,3}\:}$in stage 1 in Fig. 3) for junction controllers to implement different phase allocation schemes, transferring vehicle environments and signal phases to different states (e.g. $\:{s}_{\text{1,1}\:,\:\:}{s}_{\text{1,2}\:,\:\:}\:{s}_{\text{1,3}\:}$in stage 1 in Fig. 3) with varying people discharging benefits. The signal optimization algorithm accumulates this performance measure in every stage and figures out the optimal solutions at the final stage based on the performance value function. The three-layered DP optimization algorithm assigns flexible signal phase sequences and durations to achieve maximum value of performance value function based on predictive vehicle departure time. The stage represents the time step in the algorithm and is discretized to 1 s intervals to enable the algorithm to identify all of the possibilities and relative benefits of signal plan transition in every stage. The junction controller determines the phase allocation in every stage at the final stage by performing the optimization over a predetermined planning horizon.

Fig. 3

Multi-stage dynamic programming sketch for the signal timing optimization algorithm.

All of the feasible states $\:{s}_{t}$ and junction decisions $\:{d}_{t}$ at time step stage $\:\text{t}$ are derived from the sets of possible states $\:{S}_{t\:}$ and control decisions $\:{{D}_{t}(s}_{t})$ in Eqs. (7) and (8). The details of the forward recursion are described as follows:

Algorithm 1 Forward recursion dynamic programming algorithm in the upper and middle layer of PB-ACA

Input: Speed, location, vehicle ID and occupancy data of vehicle (car or bus)$\:\text{i}=\text{1,2},\dots\:,{\text{i}}_{\text{p}},\forall\:\text{p}\in\:\text{P}$. Junction signal information$\:{\text{s}}_{0}$at initial time step 0. Output: Optimal solution for signal timing state$\:{s}_{T{\prime\:}}^{*}$at final time step$\:T{\prime\:}$with maximum accumulated function value$\:{f(T{\prime\:},s}_{T{\prime\:}})$; dictionary with sub optimal solution path$\:{O}^{*}$. 1: predict the initial departure time$\:{Vc}_{0}^{p}(i,{s}_{0})$initial vehicle statue$\:{Sc}_{0}^{p}(i,{s}_{0})$of vehicle (car or bus)$\:i=\text{1,2},\dots\:,{i}_{p},\forall\:p\in\:P$at time step 0 using Eqs. (12)–(17) 2: set$\:t\leftarrow\:1$,$\:f{(0,s}_{0})\leftarrow\:0$,$\:{O}^{*}\leftarrow\:$empty dictionary 3: while$\:t\le\:T{\prime\:}$do: 4: for each$\:{s}_{t-1}\in\:{S}_{t-1}$: 5: get state variable set$\:{S}_{t}$and decision variable set$\:{{D}_{t}(s}_{t})$at time step$\:\text{t}$using Algorithm 2 and Table 1 6: for each$\:{s}_{t}\in\:{S}_{t}$and$\:{{d}_{t}\in\:D}_{t}{(s}_{t})$: 7: calculate sub performance measure$\:{c}_{t}({s}_{t},{d}_{t})$using Eqs. (18) and (19) 8:$\:f{(t\:,s}_{t})\leftarrow\:{max}_{{s}_{t}}$ 9: record$\:{{s}_{t-1}^{*}\leftarrow\:O}^{*}\left[{t,s}_{t}\right]$as sub optimal solution if$\:{c}_{t}({s}_{t},{d}_{t})+f{(t-1\:,s}_{t-1})=f{(t\:,s}_{t})$ 10: while$\:t<T{\prime\:}$do: 10: for each$\:p\in\:P$: 11: if$\:p$==$\:{p}_{t}^{1}$or$\:p$==$\:{p}_{t}^{2}$: 12: update$\:{{Vc}_{t}^{p}(i,\:s}_{t})$,$\:{{Sc}_{t}^{p}(i,\:s}_{t})$and$\:{a(i,t,p,\:s}_{t})$using Eqs. (20)–(22) 13: else: 14: update$\:{{Vc}_{t}^{p}(i,\:s}_{t})$,$\:{{Sc}_{t}^{p}(i,\:s}_{t})$and$\:{a(i,t,p,\:s}_{t})$using Eqs. (23)–(27) 15:$\:t\leftarrow\:t+1$ 16:$\:\:f\left({T}^{{\prime\:}},{s}_{T{\prime\:}}^{*}\right)=\text{m}\text{a}\text{x}$

The forward recursion in the upper layer starts the optimization at stage 1 by assigning cumulative value representing person-based objective function to 0. For each stage, the upper layer of DP calculates the performance measure of people discharging benefits, determining and recording the optimal solution $\:{{O}^{*}d}_{t}\left({s}_{t}\right)$ combining with the cumulative value function in the last stage for each state variable $\:{s}_{t}$. In the final stage, the optimization algorithm compares function values of different states to decide the optimal signal timing plans with the highest objective function value.

A series of phase allocations for each stage reaching to the optimal state are searched by a backward recursion in the lower layer in Sect. 5.4. The performance measure $\:{{c}_{t}({s}_{t},d}_{t})$ of people benefits from the last stage to the current stage is a function of state variables and control decisions. The performance measure is calculated in response to person-based objective function by judging whether the first index vehicle after the stop line in lanes given green traffic light in state $\:{\text{s}}_{\text{t}}$ is able to cross the stop line or not. The value $\:{{c}_{t}({s}_{t},d}_{t})$ is calculated in Eq. (13).

Vehicles and people are constantly discharging from the approaching lanes and vehicle environments are dynamic as the proceeds of optimization. The predictive departure time, travelling status and occupancy level of vehicles in each lane determining the value of $\:{{c}_{t}({s}_{t},d}_{t})$ need to be updated in the middle layer after the calculation of performance measure in the upper layer in every stage, and returned them to the upper layer for calculation in next stage.

The middle layer: signal phase transition exploration mechanism

The most common vehicle-based adaptive CV signal controls for an isolated junction propose their optimization algorithm by using National Electrical Manufacturing Association (NEMA) phase numbers. The four-leg isolated junction layout and phase allocations are used in this paper (illustrated in Fig. 4) and the phase conflicting map illustrating which phases are conflicted is graphed in the middle of Fig. 5. Notably each number with arrows indicates the phase index and corresponding vehicle movements. A dual-ring controller follows fixed pre-determined phase sequences, which failed to be adopted in person-based signal control to explore the flexibility of signal timing plans⁴⁵.

Fig. 4

Isolated junction layout and signal phase diagram adopted in this paper.

A flexible signal phase sequence and combinations machine are proposed in PB-ACA to solve this problem. In the middle layer of the DP optimization algorithm, the set for all feasible traffic signal phase states is produced in each stage depending on the signal state set in the last stage and phase transition linkages allowing junction state transfer from the last stage to the current stage in Eq. (7). The phase set is originated from real-time phase information collected by traffic light infrastructure as phase set at the initial stage.

Inspired by the theoretical flexible traffic light state machine proposed in⁵², the phase transition linkage and exploration algorithm is adopted in this research. It allows to explore all of the flexible phase transition linkage situations efficiently by obeying the rules of avoiding conflicting vehicle flow collisions based on phase conflicting map⁵³ (see Fig. 5) and eliminating unnecessary or meaningless linkages. In the phase conflicting map, the number in the first row represents the subject phase index and the number in the first column represents the compatible or conflicting phase. Value 1 means two phases are compatible and 0 means two phases are conflicting. To elaborate on the feasible adjacent relationships, several criteria need to be satisfied meanwhile to ensure junction travelling safety and limited green time resource utilization:

• At any state in an isolated junction, the junction controller assigns green traffic lights to at most two non-conflicting phases to ensure the vehicle flow can safely cross the junction centre area without collision. The non-conflicting relationships between any of the two phases in an isolated junction have been expressed in Table 1. For every phase, there are two other compatible phases that allow them to proceed with vehicle flows at the same time. More specifically, given phase $\:{p}_{t}^{1}\:\in\:P$, at state $\:{s}_{t}$, compatible phase $\:{p}_{t}^{2}\in\:E\left({p}_{t}^{1}\right)$. For example, if the index of the first phase is 1, the non-conflicting phase of it belongs to set $\:\left\{\text{2,5}\right\}$.

Table 2 Set for possible traffic phase States given state in the last stage.

Fig. 5

An example of signal phase transition and exploration mechanism.

• The transitions between two states need to experience complete intergreen interval duration, each of which incorporates two non-conflicting phases with green light and all of them are completely different. However, if one of the green light phases in one state is the same as one of those green light phases in another state, this phase should keep green lights during the intergreen time. This is because the green light phase exists in two different states and the red light is unnecessary to operate to obstruct the vehicle flows. For example, phase 1 will keep the green light during state transition $\:\left(\text{1,2}\right)$ to $\:\left(\text{1,5}\right)$.

• The traffic signal phase state with two non-conflicting phases cannot transfer to itself after an intergreen duration. This criterion is to ensure maximizing the use of green resources. For instance, state $\:\left(\text{1,2}\right)$ cannot transfer to $\:\left(\text{1,2}\right)$ by intergreen duration.

According to these rules, the steps of signal phase transition and exploration mechanism are described as follows (Fig. 5 illustrates those steps in an example):

Algorithm 2 Signal phase transition and exploration algorithm

Input: Signal timing state$\:{s}_{t-1}$at time step$\:t-1$; dictionary with sub optimal solution path$\:{O}^{*}$from Algorithm 1. Output: Signal timing state set$\:{S}_{t}$and decision set$\:{{D}_{t}(s}_{t})\:$at time step$\:t$. 1:$\:{S}_{t}$$\:\leftarrow\:$[],$\:{{D}_{t}(s}_{t})\:$$\:\leftarrow\:$[] 2: explore all possible$\:{s}_{t}=\left({p}_{t}^{1},{p}_{t}^{2}\right)$based on$\:{s}_{t-1}=\left({p}_{t-1}^{1},{p}_{t-1}^{2}\right)$and Table 1, insert each$\:{s}_{t}$into list$\:{S}_{t}$ 3: if$\:t\ge\:F+1$: 4: for each$\:{s}_{t}\in\:{S}_{t}$: 5: if$\:{p}_{t-1}^{1}\in\:\left\{\text{1,2},\text{3,4},\text{5,6},\text{7,8}\right\}$and$\:{p}_{t-1}^{2}={r}_{F}$: 6: retrieve$\:{s}_{t-F-1}$$\:\left({p}_{t-F-1}^{1},{p}_{t-F-1}^{2}\right)$from$\:{\text{O}}^{\text{*}}$ 7: remove$\:{s}_{t}$from$\:{S}_{t}$if$\:{p}_{t-F-1}^{2}={p}_{t}^{2}$: 8: elif$\:{p}_{t-1}^{1}={r}_{F}\wedge\:{p}_{t-1}^{2}={r}_{F}$: 9: retrieve$\:{s}_{t-F-1}$$\:\left({p}_{t-F-1}^{1},{p}_{t-F-1}^{2}\right)$from$\:{O}^{*}$ 10: remove$\:{s}_{t}$from$\:{S}_{t}$if$\:{p}_{t-F-1}^{1}={p}_{t}^{1}$and$\:{p}_{t-F-1}^{2}={p}_{t}^{2}$ 11: else: 12: pass 13: for each$\:{s}_{t}\in\:{S}_{t}$: 14:$\:{d}_{t}\leftarrow\langle{s}_{t-1},{s}_{t}\rangle$ 15: insert$\:{d}_{t}$into$\:{{D}_{t}(s}_{t})$

The middle layer of the DP optimization algorithm reproduces the flexible signal phase machine which satisfies all of the requirements above and modifies it as a form of the adjacent list in Table 1. Given the form of traffic phase state at the last stage, all feasible forms of state at this stage are listed in Table 1. These possible phase states constitute the set for the planned stage and enable DP to calculate different performance measures by visiting all of the elements in the set.

The middle layer: vehicle departure time update

In the middle layer of PB-ACA, the initial departure time list is updated combined with the decision of junction signal controller for lane $\:\text{i}$ to calculate the partial fragments of person delay reduction. The initial departure time list of the fleet for one lane is predicted in Sect. 4 assuming the traffic green light is always given for the current phase in the following stages. However, this assumption in a standard isolated junction is a special situation and not suitable for all cases as there are only two phases that can be given with right of way at the same stage at most to avoid vehicle collision of flows from conflicting vehicles. The different traffic phase sequences and combinations in varying states will result in different vehicle statuses, affecting the time spent arriving at the stop line. The vehicle environments are essential to be updated at every stage corresponding to every generated state in the state set given green or red traffic light.

If the traffic light for phase $\:p$ is green at stage $\:t$, the renovation of predictive departure time, travelling status and occupancy level for each vehicle in each lane are expressed in Eqs. (14)–(16). The predictive departure time of every vehicle in this lane is shortened according to Fig. 2 assuming constant green light in Eq. (14). If the algorithm realizes that the first vehicle has crossed the lane, the vehicle state list and occupancy level list are updated to remove the information of the vehicle being discharged in Eqs. (15) and (16) respectively. However, if the junction controller allocates the red traffic light to the planned phase in the current stage, the proceedings of vehicle discharging will be obstructed and none of the vehicles in this lane is able to leave. As a result, the vehicle trajectory and car-following updating theories are proposed in this paper. The different cases of fleet trajectories need to be updated to cases in Fig. 6.

$$\:If\:{g}_{t}^{p}=1:$$

$$\:{{Vc}_{t}^{p}(i,\:s}_{t})=\left\{\begin{array}{c}{{Vc}_{t-1}^{p}(i,\:s}_{t-1})-1,\:\:\:\:\:\:\:\:if\:\:{{Vc}_{t-1}^{p}(1,\:s}_{t-1})>1,i=1,\:2,\:\dots\:,\:{i}_{p}\\\:{{Vc}_{t-1}^{p}(i+1,\:s}_{t-1})-1,\:if\:0<{{Vc}_{t-1}^{p}(1,\:s}_{t-1})\le\:1,\:i=1,\:2,\:\dots\:,\:{i}_{p}-1\end{array}\right.\forall\:p\:\in\:P,\forall\:t\:\in\:T$$

(14)

$$\:{{Sc}_{t}^{p}(i,\:s}_{t})=\:\left\{\begin{array}{c}{{Sc}_{t-1}^{p}(i,\:s}_{t-1}),\:\:\:\:\:if\:\:{{Vc}_{t-1}^{p}(1,\:s}_{t-1})>1,i=1,\:2,\:\dots\:,\:{i}_{p}\\\:{{Sc}_{t-1}^{p}(i+1,\:s}_{t-1}),\:if\:0<{{Vc}_{t-1}^{p}(1,\:s}_{t-1})\le\:1,\:i=1,\:2,\:\dots\:,\:{i}_{p}-1\end{array}\right.\:\:\:\forall\:p\:\in\:P,\forall\:t\:\in\:T$$

(15)

$$\:{a(i,t,p,\:s}_{t})=\:\left\{\begin{array}{c}{a(i,t-1,p,\:s}_{t-1}),\:\:\:\:\:\:\:if\:\:{{Vc}_{t-1}^{p}(1,\:s}_{t-1})>1,i=1,\:2,\:\dots\:,\:{i}_{p}\\\:{a(i+1,t-1,p,\:s}_{t-1}),\:if\:0<{{Vc}_{t-1}^{p}(1,\:s}_{t-1})\le\:1,\:i=1,\:2,\:\dots\:,\:{i}_{p}-1\end{array}\right.\:\forall\:p\:\in\:P,\forall\:t\:\in\:T$$

(16)

$$\:If\:{g}_{t}^{p}=0:$$

$$\:{{Vc}_{t}^{p}(1,\:s}_{t})=\:\left\{\begin{array}{c}{max}\left[{{Vc}_{t-1}^{p}(1,\:s}_{t-1}\right)-1,\:\alpha\:\:+{h}_{s}],\:\:\:if\:\:{{Sc}_{t-1}^{p}(1,\:s}_{t-1})=1\\\:{{Vc}_{t-1}^{p}(1,\:s}_{t-1}),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:{{Sc}_{t-1}^{p}(1,\:s}_{t-1})=0\end{array}\right.\:\:\:\:\forall\:p\:\in\:P,\forall\:t\:\in\:T$$

(17)

.

where $\:{{Sc}_{t}^{p}(i,\:s}_{t})$ is a binary variable represents the predictive status of vehicle $\:i$ in phase p when it crosses the stop line at time stage $\:t,$ given state variable $\:{s}_{t}$, 1 represents free travelling status and 0 represents queuing/slow-down status.

In case 1 in Fig. 6, the key point is to judge whether vehicle fleets with free speed trajectories in green light given situations switch to queuing mode or not. The initial departure time for the first vehicle in fleet $\:{{Vc}_{t}^{p}(1,\:s}_{t})$ minus time step spent 1 are compared with the departure time of queuing vehicle involving start-up time loss $\:\alpha\:$. The maximum value is adopted as an updated departure time for the first vehicle because once the red light is given, it will last for at least an intergreen duration. The departure times and statuses of the following vehicles are successively decided by taking maximum value. The situations in case 2 keep unchanged as the queues have formed. The red light postpones the departure time of all vehicles as seen in case 2 in Fig. 3. The situation of case 3 is extremely similar to case 2 in Fig. 6, as the statuses of approaching vehicles to the end of the queue are judged to be queued before the departures of the front vehicles. In case 4, the departure times of those vehicles with free speed are compared again with their queuing departure time after $\:\varDelta\:\text{t}$ time left given a red light.

$$\:{{Vc}_{t}^{p}(i,\:s}_{t})=\:\left\{\begin{array}{c}{max}\left[{{Vc}_{t-1}^{p}(i,\:s}_{t-1}\right)-1,\:{{\:Vc}_{t-1}^{p}(i\:-1,\:s}_{t-1})\:+{h}_{s}],\:\:\:if\:\:{{Sc}_{t-1}^{p}(i,\:s}_{t-1})=1\\\:{{Vc}_{t-1}^{p}(i,\:s}_{t-1}),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:{{Sc}_{t-1}^{p}(i,\:s}_{t-1})=0\end{array}\right.\:i\ge\:2$$

(18)

$$\:{{\:\:\:\:\:\:Sc}_{t}^{p}(i,\:s}_{t})=\:\left\{\begin{array}{c}0,\:\:\:if\:\:{{Vc}_{t}^{p}(i,\:s}_{t})=\:{{\:Vc}_{t-1}^{p}(i\:-1,\:s}_{t-1})\:+{h}_{s}\\\:1,\:\:\:\:if\:{{Vc}_{t}^{p}(i,\:s}_{t})\ne\:\:{{\:Vc}_{t-1}^{p}(i\:-1,\:s}_{t-1})\:+{h}_{s}\end{array}\right.\:\:\:i\ge\:2,\forall\:p\:\in\:P,\forall\:t\:\in\:T$$

(19)

$$\:{{\:\:\:\:\:\:Sc}_{t}^{p}(1,\:s}_{t})=\:\left\{\begin{array}{c}0,\:\:\:if\:\:{{Vc}_{t}^{p}(1,\:s}_{t})=\:\alpha\:\:+{h}_{s}\\\:1,\:\:\:if\:{{Vc}_{t}^{p}(1,\:s}_{t})\ne\:\:\alpha\:\:+{h}_{s}\end{array}\right.\:\:\:\forall\:p\:\in\:P,\forall\:t\:\in\:T$$

(20)

$$\:{\:\:\:\:\:a(i,t,p,\:s}_{t})=\:{a(i,t-1,p,\:s}_{t-1})\:\:i=1,\:2,\:\dots\:,\:{i}_{p},\forall\:p\:\in\:P,\forall\:t\:\in\:T$$

(21)

.

Equations (17) and (18) update of vehicle predictive departure times for the first index and others consider different criteria in Fig. 6. The departure time of those vehicles recognized as queuing or slow-down vehicles remain unchanged until the green traffic light is given in the following stages. The thresholds of different vehicle travelling statuses are set for vehicles in the lane to judge the vehicle status in this stage. If vehicles are determined to be discharged following the saturated flow, the vehicle departure time and travelling status will be adjusted accordingly. Otherwise, the vehicle still travels towards the end of vehicle queues at free travelling speeds.

The adjustments for vehicle travelling status are represented in Eqs. (19) and (20). As red traffic lights cause obstacles for all of vehicles in the lane, the number of vehicles and their respective occupancy levels keep the same value during the planning stage, which is shown in Eq. (21). These traffic parameters are then accomplished updating and passed to the upper layer to calculate the performance measure for the next stage.

Fig. 6

Update for different cases of fleet trajectory representations assuming red light for next step.

The lower layer

The upper layer and middle layer execute the DP algorithm to the final stage and find the optimal solution with the highest person-based objective function in PB-ACA. In the lower layer, a backward recursion is applied to retrieve the optimal policy for the whole planning duration starting from the final stage and operating backwards. After all of the optimal decisions reacting to every state made in all stages, the optimal decision of each stage can be retrieved by backward recursion described as follows:

Algorithm 3 Backward recursion algorithm in the lower layer of PB-ACA when$\:\text{t}=\text{T}{\prime\:}$

Input: Signal timing state$\:{\text{s}}_{\text{T}{\prime\:}}^{\text{*}}$at final time step$\:\text{T}{\prime\:}$with maximum accumulated function value$\:{f(T{\prime\:},s}_{T{\prime\:}})$; dictionary with sub optimal solution path$\:{\text{O}}^{\text{*}}$from Algorithm 1. Output: Optimal signal timing plan list$\:{\text{S}\text{i}\text{g}}^{\text{*}}$reaching to signal timing state$\:{\text{s}}_{\text{T}{\prime\:}}^{\text{*}}$ 1: optimal signal timing plan list$\:{\text{S}\text{i}\text{g}}^{\text{*}}$$\:\leftarrow\:$[], insert$\:{\text{s}}_{\text{T}{\prime\:}}^{\text{*}}$into$\:{\text{S}\text{i}\text{g}}^{\text{*}}$,$\:t\leftarrow\:\text{T}{\prime\:}$ 2: while$\:t\ge\:2$do: 3: retrieve$\:{\text{s}}_{\text{t}-1}^{\text{*}}$from$\:{\text{O}}^{\text{*}}[\text{t},\:{\text{s}}_{\text{t}}^{\text{*}}]$ 4: insert$\:{\text{s}}_{\text{t}-1}^{\text{*}}$as first element in$\:{\text{S}\text{i}\text{g}}^{\text{*}}$ 5:$\:t\leftarrow\:t-1$

The optimal plan consisted by a series of junction controller decision choices in every stage is recorded after the backward algorithm. A rolling-horizon approach is applied for PB-ACA where the problem is solved again when one stage (barrier group) is executed in order to include more recent vehicle data from CVs. The proposed approach collects data at a certain time step, predicts traffic state for a certain planning duration constituted by a number of time steps, and finds optimal signal timing parameters with the highest objective function values, implementing it in an isolated intersection over the prediction period. At the end of implementation, the data collection system and three-layered optimization algorithm will be triggered again to repeat the commands.

Simulation and experiments

To validate the performance of the proposed PB-ACA, a case study was conducted using a modeled isolated junction located at New John Street West & A34 in the Newtown area of Birmingham, UK. The simulation environment was built using the open-source microscopic traffic simulator SUMO, which offers space-continuous, high-resolution modeling with multi-modal traffic capabilities⁵⁴. Figure 7(a) illustrates the geometric layout of the junction and the corresponding 8-option signal phase diagram. The simulation is operated using discrete 1-second time steps, and is controlled via a Python API, which allows for flexible implementation of custom traffic control logic. Real-world traffic data were obtained from Birmingham City Council, which provides public access to inductive loop detector data across the Birmingham and West Midlands region. For this study, traffic flow counts recorded in 2023 were extracted at 5-minute intervals and then aggregated into hourly intervals across a 24-hour period to derive daily flow profiles. An example of these daily patterns is shown in Fig. 7(b), where the grey lines represent weekday flow fluctuations for loop N51131R. The envelope bounded by ± 25% of the average flow encompasses the majority of observed variation, and this ± 25% margin is used as a threshold to define low, average, and high traffic conditions in the simulation experiments. The traffic volume diagrams of the low, average and high traffic levels during 8:00 a.m. − 9:00 a.m. peak hour period and 14:00 p.m. − 15:00 p.m. inter-peak period are illustrated in Figs. 8 and 9 respectively.

To assess the effectiveness of PB-ACA relative to existing methods, three benchmark control strategies are implemented for comparison:

• Fixed-time control algorithm (FTCA): A conventional signal timing plan with fixed phase sequences and green durations, based on historical average traffic volumes.

• Inductive loop actuated control algorithm(ILACA): A semi-dynamic approach where green times adjust in response to real-time vehicle presence detected by loop sensors.

• Vehicle-based adaptive CV signal control (VBACVSC): An adaptive signal control scheme that utilizes CV data to dynamically allocate green time based on detected queue length and vehicle arrival information, while maintaining a fixed phase sequence.

Fig. 7

(a) Geometry and signal phase diagram; (b) An example of the daily flow patterns on weekdays and average flow profile in low, average and high levels.

Fig. 8

Traffic flow diagrams of low, average, high flow level during 8:00 a.m. − 9:00 a.m. peak hour period.

Fig. 9

Traffic flow diagrams of low, average, high flow level during 14:00 p.m. − 15:00 p.m. interpeak period.

FTCA and ILACA are based on guidelines from the Federal Highway Administration’s Signal Timing Manual⁵³. VBACVSC is a connected vehicle-based control approach aimed at minimizing vehicle delay. It determines green time durations using CV-reported speeds and queue lengths and is bounded by user-defined minimum and maximum green time constraints.

The connected vehicle (CV) data are utilized to assess real-time vehicle travel status and queue length, enabling dynamic adjustment of green signal duration. At the onset of a green phase for a specific lane, the signal controller collects the speeds of vehicles in the active lane and determines whether the nearest vehicle to the stop line has come to a complete stop (i.e., speed $\:{SP}_{1}$= 0). If so, this indicates the presence of queued vehicles. The junction controller then calculates the required green duration $\:{T}_{s}$ based on the number of queued vehicles n, incorporating start-up loss time $\:\alpha\:$ and saturated headway $\:{h}_{s}$, as defined in Eq. (22). The derived green duration must not fall below the minimum threshold $\:{g}_{\text{m}\text{i}\text{n}}$; otherwise, $\:{g}_{\text{m}\text{i}\text{n}}$ is applied. Conversely, if the nearest vehicle is in motion, the lane is allocated only the minimum green time.

$$\:{T}_{s}=\:\left\{\begin{array}{c}\text{max}\left[{g}_{min},\:\alpha\:+\:n*{h}_{s}\right],\:\:if\:{\text{S}\text{P}}_{1}\:>0\:\\\:{g}_{min},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:{SP}_{1}=0\:\end{array}\right.$$

(22)

When the active lane executes the green duration assigned in Eq. (22), the signal control is triggered again to decide whether offer green extension time or switch to phases in the next stage. The distance (from the vehicle position to the cross line) and speed of the nearest vehicle travelling in the active lane are obtained as $\:{L}_{1}$ and $\:{SP}_{1}$ to calculate the time it cost to pass through the stop line. If cross time is less than extension time unit $\:{E}_{n}$, the green duration will be extended to keep the current lane active. The added green duration should also be less than the maximum green time $\:{g}_{\text{m}\text{a}\text{x}}$, otherwise the green signal switches to phases in the next stage. The related calculation and judgement for green duration extension are shown in Eq. (23):

$$\:{T}_{s}=\left\{\begin{array}{c}{T}_{s}+\frac{{L}_{1}}{{SP}_{1}},\:\:\:if\frac{{L}_{1}}{{SP}_{1}}\le\:{E}_{n}\:and\:{T}_{s}+\:{L}_{1}/{SP}_{1}\le\:{g}_{max}\\\:{T}_{s}\:in\:equation\left(6-1\right)\:for\:next\:phases,\:\:\:\:other\:cases\end{array}\right.\:$$

(23)

The Vehicle-Based Adaptive Control with CV Support (VBACVSC) iteratively applies Eq. (23) to manage green phase extensions within $\:{g}_{\text{m}\text{a}\text{x}}$ constraints. Once termination criteria are met, the junction controller leverages real-time CV data from lanes in the subsequent phase to compute a new initial green duration using Eq. (22).

The Krauss microscopic car-following model is employed to simulate vehicle dynamics, ensuring traffic flow stability and collision avoidance⁵⁵. Vehicles are randomly generated across intersection routes in each simulation run, with arrival distributions and route probabilities reflecting realistic traffic patterns. A demand rate of 2,400 vehicles per hour (veh/h) is simulated over a 20-minute period for the entire network. To mitigate randomness, 10 simulation runs are conducted per signal control scenario, each with unique random seeds. In this framework, all vehicles are assumed to be CVs capable of transmitting real-time data without latency. Each vehicle is randomly assigned an occupancy level from 1 to 4 to reflect varying passenger loads. For PB-ACA, occupancy data are incorporated as additional input parameters.

Average person delay serves as the primary performance metric, quantifying the excess travel time experienced by passengers relative to free-flow conditions. Specifically, individual vehicle delay is computed as the difference between actual travel time and free-flow travel time. The total delay for passengers in a vehicle is the product of vehicle delay and occupancy level. To assess the impact of planning horizons on PB-ACA, evaluations are conducted with incremental durations (from 10 s to 60 s with a step of 10 s). This systematic variation enables analysis of how temporal planning granularity influences control efficacy.

Results and discussions

Table 2 presents the average person delay and vehicle delay across all phases for PB-ACA and three benchmark models (FTCA, ILACA, and VBACVSC). The values in parentheses denote the percentage reduction in total average delay relative to the fixed-time control (FTCA). Notably, PB-ACA achieves a 50% reduction in average person delay compared to FTCA, outperforming both ILACA (14%) and VBACVSC (44%). Moreover, PB-ACA reduces person delay by 11% over VBACVSC, underscoring its efficacy in prioritizing high-occupancy vehicles.

Table 3 further dissects these results by vehicle occupancy levels, demonstrating that CV-based adaptive controls (VBACVSC and PB-ACA) reduce delays by over 42% across all occupancy categories compared to FTCA. This highlights the superiority of real-time CV data over conventional inductive loop detectors, which often yield imprecise estimates of queue dynamics and phase transitions. Crucially, the performances of average vehicle delay by operating PB-ACA are not significantly degraded comparing to VBACVSC. In this scenario, the average person delay of PB-ACA is lower than the average vehicle delay because high-occupancy vehicles receive higher priority, enabling them to clear the intersection more quickly. Given the varying number of occupants in vehicles, person-based traffic control strategies offer greater value and rationale compared to vehicle-based approaches. This concept is inspired by Transit Signal Priority (TSP) strategies, which prioritize high-occupancy vehicles like buses.

Table 2 Comparison of average person delay (s/per) and average vehicle delay (s/veh) for each phase under different signal controls (FTCA, ILACA, VBACVSC, PB-ACA).

Table 3 Comparison of average person delays (s/per) sorted by different vehicle occupancies under different signal controls (FTCA, ILACA, VBACVSC, PB-ACA).

Figure 10 presents the box plots of person delays across different vehicle occupancy levels, illustrating the distributions and variabilities for four distinct signal approach scenarios. To ensure comparability, the statistical data for individuals in the same vehicle occupancy level—traveling identical routes with synchronized arrival times—are consolidated into a single plot for each scenario. The figure comprises four subplots (a–d), corresponding to occupancy levels 1 through 4, respectively. In each box plot, the upper and lower bands denote the 95th and 5th percentiles, while the upper box line, orange midline, and lower box line represent the 75th, 50th, and 25th percentiles, providing a comprehensive view of delay dispersion.

Figure 11 displays a line chart comparing the average delays per person and their aggregated means across varying occupancy levels under different DP prediction horizons (10–60 s) in the PB-ACA framework. Each colored line corresponds to a specific occupancy level, with the black line indicating the summation average. A detailed discussion of these results follows in the subsequent section.

Beyond minimizing average person delays, adaptive connected vehicle (CV) signal control strategies, namely VBACVSC and PB-ACA, also reduce delay variability for both vehicle occupants and pedestrians, as evidenced by the box plots in Fig. 10. While the ILACA variants marginally outperform those of FTCA, they exhibit notable instability compared to VBACVSC and PB-ACA. The observed discrepancies in average delays and variability between ILACA and CV-based strategies can be attributed to inaccuracies in inductive loop sensors’ estimations of traffic conditions, queue lengths, discharge times, and signal phase transitions. These findings underscore the superiority of connected vehicle technology over conventional inductive loop systems in signal control optimization, particularly under 100% CV penetration scenarios.

Fig. 10

Box plots of 5th, 25th, 50th, 75th and 95th percentiles of delay per person (s/per) during simulation sorted by different vehicle occupancy levels (1, 2, 3, 4) under different signal controls (FTCA, ILACA, VBACVSC, PB-ACA).

As demonstrated in Table 3, the proposed PB-ACA achieves a reduction in average person delay of up to 13% for 4-occupancy vehicles compared to the FTCA benchmark. Notably, PB-ACA also yields slightly lower delays for 2- and 3-occupancy vehicles than VBACVSC. This trend is further supported by Fig. 10 (b–d), where PB-ACA exhibits superior performance in minimizing delay variability for 2-, 3-, and 4-occupancy vehicles. While PB-ACA shows a marginal increase (6%) in delay for 1-occupancy vehicles compared to VBACVSC, the difference is not statistically significant. Moreover, the delay variability for 1-occupancy vehicles in PB-ACA closely mirrors that of VBACVSC, as illustrated in Fig. 10 (a). These findings highlight the greater efficacy of PB-ACA in reducing delays for high-occupancy vehicles without substantially compromising performance for low-occupancy scenarios. This advantage stems from the person-based objective function and adaptive signal phase mechanism of PB-ACA, making it a promising solution for isolated urban intersections aiming to minimize person delay.

Fig. 11

Line charts of average delay per person in different occupancy level vehicles in PB-ACA and summation of different signal controls in different DP prediction horizons.

Figure 11 examines the influence of planning horizon duration (10–60 s) on average person delay in PB-ACA. As shown in Fig. 11(a), the 30 s horizon yields the lowest delays across all CV-based algorithms. Deviating from this optimal duration, whether by increasing (40–60 s) or decreasing (10–20 s) the horizon leads to higher delays. Short horizons (10s, 20 s) introduce biased function value calculations, preventing the algorithm from deriving optimal signal plans. In extreme cases (e.g., 10 s), CV-based strategies underperform even FTCA and ILACA. Long horizons (50s, 60 s) hinder real-time adaptability, as the controller lacks updated CV data for vehicles outside the communication range at decision points, leading to inaccurate travel time estimations. Figure 11(b) confirms similar behavior across different occupancy levels, reinforcing that a 30 s planning horizon strikes the best balance between responsiveness and accuracy, avoiding the pitfalls of overly short or long prediction windows.

Figures 12 and 13 present comprehensive performance comparisons between the proposed PB-ACA approach and three benchmark models (FTCA, ILACA, and VBACVSC) in terms of delay and stopping frequency metrics. To assess the priority policies and effectiveness of PB-ACA, the results are categorized by vehicle occupancy levels. As shown in Fig. 12, PB-ACA demonstrates significant improvements in person delay reduction compared to benchmark algorithms, reducing 40.2 − 51.8%, 28.2 − 38.6% and 6.8 − 9.8% of average person delay of all vehicles compared to the FTCA, ILACA and VBACVSC benchmark algorithms in the vehicular environments under three flow scenarios. Figure 13 demonstrates similar reductions of average person stop for the proposed algorithms against the benchmark algorithms, which are 46.3 − 59.7%, 36.8 − 47.9% and 5.5 − 10.7% respectively.

Fig. 12

Comparison of average person delay (s/per) and vehicle delay (s/veh) of the proposed algorithm and benchmarking algorithms under three flow scenarios.

Fig. 13

Comparison of average person stop (num/per) and average vehicle stop (num/veh) of the proposed algorithm and benchmarking algorithms under three flow scenarios.

Fig. 14

Average vehicle delay and person delay of the proposed PB-ACA against benchmarking control methods under three flow demand scenarios and various CV penetration rates.

Fig. 15

Average vehicle stop and person stop of the proposed PB-ACA against benchmarking control methods under three flow demand scenarios and various CV penetration rates.

Notably, PB-ACA maintains comparable vehicle delay and stop performance to VBACVSC while achieving these person-focused improvements. The superior performance of CV-based methods (VBACVSC and PB-ACA) stems from their ability to leverage real-time vehicle data for more accurate crossing time estimation, unlike infrastructure-dependent methods like ILACA that rely on inductive loop sensors. The limitations of ILACA in precisely estimating traffic conditions, queue dynamics, and optimal signal timing result in more frequent transitions between queuing and discharging states, ultimately increasing delays and stops.

Figures 14 and 15 present sensitivity analyses examining algorithm performance under varying CV penetration rates (10–100%) for different traffic scenarios. Figure 14 illustrates sensitivity test results of average delays (Figure Fig. 14 (a), (c) and (e) for average person delays and Figure Fig. 14 (b), (d) and (f) for average vehicle delays) respectively of different controls from 10 to 100% CV penetration rate with a step of 10%. Figure 15 illustrates how the proposed algorithm and benchmarking models change with CV penetration rates (Fig. 15 (a), (c) and (e) for average person stop and Fig. 15 (b), (d) and (f) for average vehicle stop) assuming situations of all passenger cars.

The plots in Fig. 14 show similar variation trends of average person/vehicle delays among signal controls using CV data under three traffic flow levels. The average person/vehicle delays of signal controls using CV data (VBACVSC and PB-ACA) increase as the CV penetration rate decreases regardless of their objectives or signal plan flexibility. The average person/vehicle delays of the connected control methods perform worse than ILACA when the CV penetration rate is less than 50%, and perform worse than FTCA when the CV penetration rate is less than 30%. Compared to VBACVSC, the advantage of reducing person delay in the proposed algorithm is gradually reduced by reducing the CV penetration rate. The average person/vehicle delays of PB-ACA are not significantly different to those of VBACVSC when the CV penetration rate decrease to 60-80%. Figure 15 illustrates that there are similar influences on trends of average person/vehicle stops in Fig. 14 of all operational algorithms under three flow levels. The performance decline occurs because reduced CV penetration limits the algorithms’ visibility of complete traffic conditions. Below critical penetration thresholds, the optimization cannot achieve its full potential due to incomplete information. In contrast, FTCA and ILACA maintain constant performance as they don’t rely on CV data. These results highlight the importance of sufficient CV penetration (above 50–60%) for realizing the full benefits of CV-based signal control systems, while demonstrating PB-ACA’s superior performance under favorable penetration conditions.

Conclusions

This paper develops an innovative predictive person based signal control PB-ACA in urban roads. The objective of PB-ACA is to minimize average person delay. Positions, speeds and occupancy levels of each CV from interaction of junction controller and CVs through wireless communication are required as data sources of signal timing decision optimization. An innovation three-layered dynamic programming architecture algorithm is developed as the core of PB-ACA after collecting and processing connected vehicle data. In order to search the optimal signal timing plans for minimum person delay target in planning horizon, the dynamic programming optimization algorithm is developed to count the total benefits. A signal phase transition exploration mechanism is developed in middle layer to explore all possible signal timing plans according to non-conflicting phase rules and efficient principles. The vehicle trajectory and car-following updating theories used for predicting discharging time of all vehicles in platoon is also proposed considering different cases and fleet trajectories. The three-layered DP approach is able to explore all of the possible signal timing strategies in a certain planning horizon and efficiently figure out their person based value function for determining optimal solutions.

An experiment and evaluation framework to validate the performances of PB-ACA in hypothesis urban isolated junction with three benchmarking models is also built in this paper. Simulation results demonstrate that PB-ACA achieves substantial improvements in person delay reduction—up to 55% over FTCA, 42% over ILACA and 11% over VBACVSC—without sacrificing overall traffic efficiency. These results affirm PB-ACA’s superiority in promoting equity and efficiency in urban traffic control by prioritizing person-level benefits. Additionally, The sensitivity analysis reveals that PB-ACA maintains comparable performance to VBACVSC in terms of average person delay and stops when CV penetration rates range between 60% and 80%, demonstrating its robustness under partial connectivity scenarios.

Future works will be done to extend the junction scales of person based approach in CV environments into coordinated junctions. Some realistic scenarios, such as imperfect CV penetration rates, variety flow demand and real world case study will also be considered to constructed to test the performances of proposed person based control. The functions of PB-ACA should be supported in those cases if necessary. These are achieving to enhance the performances of PB-ACA and will be introduced in following researches.