Long-distance target localization optimization algorithm based on single robot moving path planning

Abstract

To address the problem of low positioning accuracy for long-distance static targets, we propose an optimized algorithm for long-distance target localization (LTLO) based on single-robot moving path planning. The algorithm divides the robot’s movement area into hexagonal grids and introduces constraints on stopping position selection and non-redundant locations. Based on image parallelism, we propose a method for calculating the relative position of the target using sensing information from two positions. Additionally, an improved hierarchical density-Based spatial clustering of applications with noise (HDBSCAN) algorithm is developed to fuse the relative coordinates of multiple targets. Furthermore, we establish the corresponding constraints for long-distance target localization and construct a target localization optimization model based on single-robot path planning. To solve this model, we employ a double deep Q-network and propose a reward strategy based on coordinate fusion error. This approach solves the optimization model and obtains the optimal target positions and path trajectories, thereby improving the positioning accuracy for long-distance targets. Experimental results demonstrate that for static targets at distances ranging from 100 to 500 meters, LTLO outperforms traditional monocular visual localization (TMVL), monocular global geolocation (MGG) and long-range binocular vision target geolocation (LRBVTG) by obtaining an optimal path to identify target positions, maintaining a relative localization error within 4% and an absolute localization error within 6%.

Introduction

With rapid technological advancements, robotic target localization technology facilitates autonomous navigation and interaction, enabling robots to identify, locate, and reach specific targets in complex and dynamic environments. Long-distance target localization is crucial for enhancing the operational efficiency and responsiveness of robots in military, rescue, and industrial sectors^1,2. For example, in military applications, long-distance localization allows robots to accurately identify and locate enemy personnel, drones, tanks, and other targets from a safe distance, enabling reconnaissance and strike missions. This capability not only reduces the risk of injuries to friendly forces but also increases combat efficiency and safety. In rescue operations, long-distance localization enables robots to quickly search and locate targets in disaster-stricken areas, especially in hazardous or inaccessible regions, providing essential support for rescue efforts. Moreover, this technology enhances the effectiveness of robots in industrial logistics and warehousing tasks, such as automated picking and sorting, which significantly increases both productivity and operational efficiency.

Long-distance target localization technology utilizes high-precision sensors and advanced algorithms to identify and track targets across extensive areas, enabling rapid responses and dynamic adaptation through real-time data processing. Currently, long-distance target localization algorithms are mainly categorized into two types: those that utilize multiple static sensing devices and those that employ a single mobile sensing device. Algorithms utilizing multiple static sensing devices involve deploying one or more static sensors at predetermined locations. These algorithms use data interactions or information gathered from multiple devices to pinpoint the target’s location. However, this method requires fixed installations at various sites, resulting in high costs, limited flexibility, and potential coverage gaps in large or complex environments. Conversely, algorithms that utilize a single mobile sensing device take advantage of sensor mobility to collect target information from various locations, offering high flexibility and extensive coverage in determining target coordinates. However, the following challenges still remain:

• (1) Difficulty in model construction: Constructing an accurate and reliable localization model poses significant challenges, as it must account for both mobility and localization constraints. Mobility constraints pertain to the device’s movement points and trajectories, while localization constraints involve factors such as camera tilt during movement and the correlation between moving paths and target positioning. Therefore, developing a precise target localization model with a mobile device is complex and demanding.

• (2) Low precision in long-distance localization: In the context of long-distance static target localization, various factors compromise precision. Uncertainties in device moving paths, inaccurate depth estimations, and challenges in model construction all contribute to reduced localization precision, ultimately diminishing the accuracy of target positioning.

To address these issues, this paper proposes a long-distance target localization optimization algorithm based on single robot moving path planning (LTLO). The contributions of this paper are as follows:

• (1) To address the challenge of building an accurate localization model for a single mobile device, we have partitioned the robot’s movement area into uniform hexagonal grids, factoring in movement constraints like the selection of stopping positions and the avoidance of repetitive paths. Additionally, we consider constraints associated with parallel imaging and relative target positioning, proposing an optimization model for long-distance target localization that leverages the robot’s movement trajectory.

• (2) To address inaccuracies in the fusion of relative coordinates for multiple targets, we introduce a pruning operation and silhouette coefficient calculation based on multiple target relative coordinates. We propose a fusion algorithm employing an improved hierarchical density-based spatial clustering of applications with noise (HDBSCAN) to efficiently identify clusters near the true relative coordinates of the targets, thereby improving the effectiveness of coordinate fusion.

• (3) To enhance the precision of long-distance target localization, we have developed an experience replay buffer that includes state information such as grid centers and estimated target coordinates, utilizing a double deep Q-network (DDQN). We have constructed behavior and target networks, a loss function, and a reward strategy based on coordinate fusion. Through training the model during the robot’s movement and selecting the next direction, we aim to determine the optimal moving path, thereby significantly improving the accuracy of long-distance target localization.

Related work

In the field of long-distance target localization, some researchers fix static sensing devices, equipped with one or multiple sensors, at specific locations to investigate long-distance target localization algorithms using data gathered from multiple devices. For example, Wang et al.³ proposed a traditional monocular visual localization (TMVL) method that utilizes specific geometric shapes to mark the target and obtain its positional information through the similarity triangulation method. This type of monocular visual sensor localization technique requires prior knowledge of the target and shows diminishing localization performance as the detection distance increases. Mao et al.⁴ improved long-distance accuracy by optimizing the spatial layout of sensors and proposing a method that combines direction localization and time difference of arrival. Liu et al.⁵ achieved precise three-dimensional localization by integrating intelligent metasurface technology, eliminating the need for additional altitude measurement devices or complex radar networks. Gao et al.⁶ proposed a novel global localization method by fusing data from monocular cameras, inertial measurement units (IMU), and global positioning systems (GPS). This algorithm corrects camera poses using pixel mapping and IMU data, detects long-distance targets using target detection algorithms, and calculates the relative and geographic positions of the target using a monocular vision model. Fang et al.⁷ proposed a long-distance target localization algorithm by fusing binocular cameras, IMU, and GPS. They extended the baseline length between the two cameras, aligned them parallel based on IMU data, and proposed a long-baseline parallel binocular model for localizing distant targets to obtain their geographic positions. Wen et al.⁸ constructed the online visual language map and waypoint prediction module, and proposed the approach for vision-and-language navigation. The approach can enable robots to better understand the environment and navigate according to natural language instructions, especially in complex or unknown environments. Wang et al.⁹ proposed an enhanced domain confrontation neural network model to solve the problem of accuracy degradation of UWB positioning technology in dynamic NLOS environments. By combining the manually extracted channel impulse response characteristics and domain-adversarial learning, the model maintains high performance in different environments, reduces the dependence on a large number of labeled data, and improves the practicability and robustness of the system. While these studies employ data from multiple static devices for stable and continuous monitoring, they require the installation of fixed equipment at various sites, leading to high costs and limited flexibility due to fixed layouts.

To enhance flexibility and cover large areas, some researchers have considered using single devices, such as mobile robots and drones, for long-distance target localization. For example, Cai et al.¹⁰ tackled the localization issue in oblique remote sensing images by integrating deep learning with the you only look once (YOLO) algorithm to detect buildings and optimize three-dimensional positional data. Kan et al.¹¹ improved localization accuracy by utilizing a combination of drone and satellite images, applying deep learning to address differences in viewpoint and orientation. Zhang et al.¹² constructed three-dimensional maps from image sequences captured by drones and GPS data to quickly estimate target positions. Although these studies enhance localization flexibility, they primarily concentrate on target detection and tracking using single mobile devices, without addressing path planning. There remains significant potential for improving the accuracy of target localization.

To address the path planning problem, some researchers have begun optimizing it using traditional algorithms and machine learning techniques. For example, Zhang et al.¹³ improved the A* algorithm by incorporating radar threat assessment to optimize drone paths. Liu et al.¹⁴ employed a genetic algorithm combined with digital twin technology to dynamically adjust preset trajectories of robots. Sun et al.¹⁵ proposed a strategy that combines an improved elastic potential field and particle swarm optimization to address the interception of moving underwater targets by drones, significantly enhancing interception efficiency and path planning performance in complex aquatic environments. Additionally, Ma et al.¹⁶ refined the particle swarm optimization algorithm by enabling particles to autonomously adjust dimensions according to real-world conditions, thus improving the algorithm’s flexibility and adaptability and implementing varied update strategies for different particle types to optimize localization outcomes. Wu et al.¹⁷ introduced a swarm-based 4D path planning method to optimize drone paths in urban environments, using an improved ant colony optimization algorithm combined with a genetic algorithm to develop a two-level framework for solving multi-path planning and task-related issues. Zhang et al.¹⁸ integrated path planning with schedule optimization, proposed the rapidly-exploring random tree star (RRT*) algorithm to generate near-optimal paths for each robot, and used a heuristic bias-based particle swarm optimization algorithm to optimize scheduling, adjusting each robot’s arrival time using a path-time-space approach to avoid congestion and collisions. However, these studies [11-16] mostly rely on global environmental data, posing challenges in meeting real-time and high-precision requirements. To solve this problem, some researchers have investigated deep learning and reinforcement learning techniques to dynamically adjust path planning strategies, achieving efficient localization in complex and dynamic scenarios. For example, Yang et al.¹⁹ adopted a prioritized double deep Q-network to improve learning efficiency and path optimization performance, selecting useful positive experiences from the experience buffer to enhance algorithm stability and reusability. Xi et al.²⁰ optimized underwater drone path planning using the double dueling deep Q-network (D3QN) algorithm. They introduced real ocean data to build an accurate marine environment model and designed precise state transitions and reward functions to enhance the algorithm’s learning efficiency and path planning effectiveness. Li et al.²¹ proposed a path planning algorithm that combines deep Q-network (DQN) with the artificial potential field method for autonomous navigation and collision avoidance of unmanned surface vehicles in complex maritime environments. By improving the action space and reward function of DQN with the artificial potential field, they addressed the issue of sparse rewards in the traditional DQN algorithm, thereby enhancing its performance in practical applications. Salehizadeh et al.²² proposed a D3QN algorithm with an adaptive learning mechanism for path planning, integrating real-time oceanic environmental data. Chen et al.²³ introduced the transformer structure into the multi-robot path planning problem, using contrastive learning and double deep Q-network to tackle challenges associated with training policy neural networks after introducing the transformer. While these studies combine swarm intelligence, machine learning, reinforcement learning, and complex mathematical models to design optimal paths for mobile robots, there is still room for improvement in terms of precise localization of long-distance visual targets.

Principle of LTLO

Figure 1

Positioning schematic diagram of LTLO.

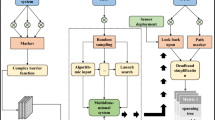
As shown in Fig. 1, a single mobile robot equipped with an IMU, camera, GPS, and other modules localizes a distant target within a movable area. To achieve efficient data acquisition, this paper divides the robot’s operational area into several identical hexagonal grids and encodes the hexagon matrix. And denote g(i, j) to be the j-th hexagon in the i-th row. Compared to traditional quadrilateral grid partitioning, hexagonal grids offer advantages in spatial coverage efficiency, directional consistency, and path smoothness. Specifically, the hexagonal grids provide higher directional symmetry, enabling the robot to sample uniformly in six equidistant directions during movement. This effectively mitigates issues such as path deflection and inconsistent cost estimation. Additionally, with the fewest edges per unit area, hexagonal grids reduce redundant movements. In terms of image acquisition, the more uniform angular variation of hexagon centers enhances disparity matching and relative position estimation. Therefore, we adopt hexagonal grids as the foundation for modeling robotic movement paths, thereby improving path planning efficiency and enhancing adaptability to complex environments. Starting from the initial grid center, the robot captures images of the distant target, then moves to an unvisited grid center within its current grid to take additional images. As it moves, the robot acquires image and distance information, utilizing this data to calculate the coordinates of the distant target. However, the LTLO still needs to address two key challenges: First, how to integrate data from the IMU, camera, and other transmission sources into a set of mathematical expressions that describe constraints on the robot’s movement trajectory and distant target localization, and then establish an optimization model to minimize target position errors. Second, how to apply a reinforcement learning algorithm to solve the optimization model, which will enable the robot to determine the optimal movement trajectory and the most accurate coordinates for distant target localization. The specific solutions to these two challenges are detailed below.

Establishment of positioning optimization model

Constraints on robot movement

A robot is stationed at the center of a hexagonal grid, where it adjusts its camera angle to capture an image of the target. Subsequently, it relocates to the center of an adjacent hexagonal grid. Let $P=\left( {{p}_{0}},...,{{p}_{k}},...,{{p}_{n}} \right)$ represent the robot’s movement trajectory, where ${p}_{i}$ is the grid center where the robot is located at time i, and ${p}_{0}$ is the robot’s initial position. Let n denote the number of grid centers visited by the robot. Considering that the robot can only select the next grid center among its neighboring locations, the constraint for selecting the staying position can be formulated as:

$$\begin{aligned} {p_{k + 1}} \in {G_k},k = 0,2,...,n - 1 \end{aligned}$$

(1)

where ${G}_{k}$ represents the neighboring grid centers of the current position ${p}_{k}$ , and can be defined as:

$$\begin{aligned} {G_k} = \left\{ \begin{array}{l} \left\{ {g\left( {1,j + 1} \right) ,g\left( {2,j} \right) ,g\left( {2,j + 1} \right) } \right\} {\hspace{15.0pt}}{p_k} = g\left( {1,j} \right) {\hspace{2.0pt}} and {\hspace{2.0pt}} j \ne m\\ \left\{ {g\left( {1,m - 1} \right) ,g\left( {2,m} \right) ,g\left( {2,m + 1} \right) } \right\} {\hspace{15.0pt}} {p_k} = g\left( {1,m} \right) \\ \left\{ {g\left( {n,j + 1} \right) ,g\left( {n - 1,j} \right) ,g\left( {n - 1,j + 1} \right) } \right\} {\hspace{15.0pt}}{p_k} = g\left( {n,j} \right) {\hspace{2.0pt}} and {\hspace{2.0pt}} j \ne m\\ \left\{ {g\left( {n,m - 1} \right) ,g\left( {n - 1,j} \right) ,g\left( {n - 1,j + 1} \right) } \right\} {\hspace{15.0pt}} {p_k} = g\left( {n,m} \right) \\ \left\{ {g\left( {i - 1,1} \right) ,g\left( {i,2} \right) ,g\left( {i + 1,1} \right) } \right\} {\hspace{15.0pt}} {p_k} = g\left( {i,1} \right) {\hspace{2.0pt}} and {\hspace{2.0pt}} i {\hspace{2.0pt}} is {\hspace{2.0pt}} even\\ \left\{ {g\left( {i - 1,1} \right) ,g\left( {i - 1,2} \right) g\left( {i,2} \right) ,g\left( {i + 1,1} \right) ,g\left( {i + 1,2} \right) } \right\} {\hspace{15.0pt}} {p_k} = g\left( {i,1} \right) {\hspace{2.0pt}} and {\hspace{2.0pt}} i {\hspace{2.0pt}} is {\hspace{2.0pt}} odd {\hspace{2.0pt}} and {\hspace{2.0pt}} i \ne 1 {\hspace{2.0pt}} or {\hspace{2.0pt}} n\\ \left\{ {g\left( {i - 1,m - 1} \right) ,g\left( {i,m - 1} \right) ,g\left( {i + 1,m - 1} \right) } \right\} {\hspace{15.0pt}} {p_k} = g\left( {i,m} \right) {\hspace{2.0pt}}and {\hspace{2.0pt}} i {\hspace{2.0pt}} is {\hspace{2.0pt}} even\\ \left\{ {g\left( {i - 1,m} \right) ,g\left( {i - 1,m - 1} \right) g\left( {i,m - 2} \right) ,g\left( {i + 1,m - 1} \right) ,g\left( {i + 1,m} \right) } \right\} {\hspace{15.0pt}} {p_k} = g\left( {i,m - 1} \right) {\hspace{2.0pt}}and {\hspace{2.0pt}} i {\hspace{2.0pt}} is {\hspace{2.0pt}} odd {\hspace{2.0pt}} and {\hspace{2.0pt}} i \ne 1 {\hspace{2.0pt}} or {\hspace{2.0pt}} n\\ \left\{ {g\left( {i - 1,j} \right) ,g\left( {i - 1,j + 1} \right) ,g\left( {i,j - 1} \right) ,g\left( {i,j + 1} \right) ,g\left( {i + 1,j} \right) ,g\left( {i + 1,j + 1} \right) } \right\} {\hspace{15.0pt}} {p_k} = g\left( {i,j} \right) {\hspace{2.0pt}}and {\hspace{2.0pt}} i {\hspace{2.0pt}} is {\hspace{2.0pt}} odd\\ \left\{ {g\left( {i - 1,j - 1} \right) ,g\left( {i - 1,j} \right) ,g\left( {i,j - 1} \right) ,g\left( {i,j + 1} \right) ,g\left( {i + 1,j - 1} \right) ,g\left( {i + 1,j} \right) } \right\} {\hspace{15.0pt}} other{\hspace{2.0pt}}{p_k} = g\left( {i,j} \right) {\hspace{2.0pt}}and {\hspace{2.0pt}} i{\hspace{2.0pt}} is {\hspace{2.0pt}} even \end{array} \right. \end{aligned}$$

(2)

where m represents the number of grids in the first row, and n represents the total number of rows in the grid, which is an odd number. The robot aims to move to unvisited grid centers whenever possible, so the movement trajectory P avoids including any repeated grid centers. This implies that:

$$\begin{aligned} {p_g} \ne {p_v},\forall {p_g},{p_v} \in P{\hspace{4.0pt}} g \ne v \end{aligned}$$

(3)

Constraints on long-distance target localization

Image parallelism   In binocular stereo vision positioning technology, two cameras capture stereo image pairs of the same scene, utilizing the disparity between these images to achieve 3D spatial localization. A standard stereo vision setup requires that the two cameras remain parallel at all times. However, maintaining this alignment consistently over extended periods can be challenging in practical applications. This paper employs a single-camera motion strategy to simulate the effects of binocular vision by changing the observation position. During movement, the camera may undergo significant angular deviation at different observation positions, resulting in non-parallel images that reduce localization accuracy. Therefore, the Bouguet algorithm is used for image rectification. By leveraging the camera’s rotation matrix and translation vector, the algorithm achieves rotational transformations for both images, mapping them onto a common imaging plane and ensuring epipolar line parallelism. In order to improve the estimation accuracy of the rotation matrix and translation vector, this paper uses IMU sensor to obtain camera pose information. Since the IMU accumulates errors over time, its bias continually increases with prolonged use. To mitigate this effect, this paper resets the IMU error after each camera movement and employs Kalman filtering to fuse the camera, IMU, and GPS data, thereby optimizing the camera pose estimation and enhancing the accuracy of the rotation matrix and translation vector. Namely, using equation (4), the rectification rotation matrices ${R_l}$ and ${R_r}$ are constructed, and both original images are reprojected to obtain two rectified images, effectively mitigating the non-parallel issue caused by camera deviations.

$$\begin{aligned} {R_l} = \left[ {\begin{array}{*{20}{c}} {\mathbf{{e}}_\mathbf{{1}}^ \top }\\ {\mathbf{{e}}_\mathbf{{2}}^ \top }\\ {\mathbf{{e}}_\mathbf{{3}}^ \top } \end{array}} \right] {{R}^{\frac{1}{2}}},{R_r} = \left[ {\begin{array}{*{20}{c}} {\mathbf{{e}}_\mathbf{{1}}^ \top }\\ {\mathbf{{e}}_\mathbf{{2}}^ \top }\\ {\mathbf{{e}}_\mathbf{{3}}^ \top } \end{array}} \right] {{R}^{ - \frac{1}{2}}} \end{aligned}$$

(4)

where,$\begin{array}{*{20}{c}} {{\mathbf{{e}}_\mathbf{{1}}} = \frac{\mathbf{{T}}}{{\left\| \mathbf{{T}} \right\| }}} \end{array}$, $\begin{array}{*{20}{c}} {{\mathbf{{e}}_\mathbf{{2}}} = \frac{{\mathbf{{T}} \times \left( {0,0, - 1} \right) }}{{\left\| {\mathbf{{T}} \times \left( {0,0, - 1} \right) } \right\| }}} \end{array}$, $\begin{array}{*{20}{c}} {{\mathbf{{e}}_\mathbf{{3}}} = \frac{{{\mathbf{{e}}_\mathbf{{1}}} \times {\mathbf{{e}}_\mathbf{{2}}}}}{{\left\| {{\mathbf{{e}}_\mathbf{{1}}} \times {\mathbf{{e}}_\mathbf{{2}}}} \right\| }}} \end{array}$. R represents the rotation matrix, which is derived from the camera’s rotation angles measured by an IMU. T represents the translation vector, which can be calculated from the distances between the central points of hexagonal grids.

Target relative position calculation based on two position sensing information   Based on the rectified images, the relative position of the target can be calculated using the principle of parallel stereo vision. However, in the hexagonal grid pattern, as shown in Figure 1, the robot’s ability to move both laterally and diagonally renders the traditional parallel binocular disparity method unsuitable for calculating depth distance. Therefore, this paper introduces a method for calculating relative position based on information from two positional sensors. The specific approach is outlined as follows:

Figure 2

Parallel binocular model.

When the robot moves laterally, as shown in Fig. 2, two parallel cameras with the same parameters simultaneously capture images of the same object from differing positions. The speeded-up robust features (SURF) algorithm matches feature points across consecutive images, determining the pixel coordinates of these points on each camera’s imaging plane. Let the horizontal pixel coordinates of the two imaging points be denoted as ${u_f}$ and ${u_b}$, respectively. The disparity, defined as the difference between the horizontal pixel coordinates ${u_f}$ and ${u_b}$, is used to compute the i-th relative coordinate ${L_i} = (x_i^c, y_i^c, z_i^c)$ of the target object through triangulation.

$$\begin{aligned} x_i^c = \frac{{\left( {{x_l} - {c_x}} \right) b}}{{{u_f} - {u_b}}},\begin{array}{*{20}{c}} {y_i^c = \frac{{\left( {{y_l} - {c_y}} \right) b}}{{{u_f} - {u_b}}},z_i^c = \frac{{fb}}{{{u_f} - {u_b}}}} \end{array} \end{aligned}$$

(5)

where, b represents the distance between the two camera positions, which also corresponds to the distance between the centers of adjacent hexagonal grid cells. f represents the camera’s focal length. ${x_l}$ and ${y_l}$ represent the pixel coordinates. ${c_x}$ and ${c_y}$ represent the offsets of the camera imaging plane’s origin in the horizontal and vertical directions, respectively.

Figure 3

In the case of oblique movement.

Figure 4

Diagonal binocular model.

When the robot moves diagonally, as shown in Fig. 3, the relative positions of the two cameras change, resulting in variations in the size of the target object’s image. In this scenario, the traditional parallel binocular disparity method is ineffective in calculating the depth distance. Therefore, this paper proposes a diagonal binocular vision model. As shown in Fig. 4, the relative coordinate ${L_j} = (x_j^c,y_j^c,z_j^c)$ of the j-th target is calculated by determining the difference in image width of the target object as captured by the cameras, as follows:

$$\begin{aligned} x_j^c = \frac{{\left( {{x_l} - {c_x}} \right) z_j^c}}{f},y_j^c = \frac{{\left( {{x_l} - {c_x}} \right) z_j^c}}{f},z_j^c = \frac{{{w_f} * bsin\theta }}{{{w_b} - {w_f}}} \end{aligned}$$

(6)

where, ${w_f}$ and ${w_b}$ are the image widths on the camera ${O_f}$ and ${O_b}$ imaging planes, respectively. $\theta$ is the angle between the two camera positions.

Target relative coordinate fusion based on improved HDBSCAN   Through the movement of the camera and the computation of relative target coordinates, multiple sets of coordinate data are generated. The HDBSCAN algorithm, known for automatically determining the number of clusters and its tolerance to varying data shapes and noise, however, the relative coordinate data tend to be sparse. During localization, they are susceptible to environmental disturbances, which can lead to outliers. Therefore, we propose an enhanced HDBSCAN-based relative coordinate fusion algorithm that incorporates pruning operations and silhouette coefficient calculations. This enhancement effectively identifies a cluster of points around the true relative target coordinates, significantly reducing the error in relative target localization. The specific methodology is detailed as follows:

First, we define the core distance of each coordinate ${L_i}$ as the Euclidean distance to its k -nearest neighbor:

$$\begin{aligned} core\left( {{L_i}} \right) = d\left( {{L_i},{L_k}} \right) \end{aligned}$$

(7)

where, ${L_k}$ is the k-nearest neighbor of point ${L_i}$ . Based on this distance, we further define the mutual reachability distance between any two points as:

$$\begin{aligned} d\left( {{L_i},{L_j}} \right) = max\left\{ {core\left( {{L_i}} \right) ,core\left( {{L_j}} \right) ,d\left( {{L_i},{L_j}} \right) } \right\} \end{aligned}$$

(8)

where, $d\left( {{L_i},{L_j}} \right)$ represents the original distance among the two points ${L_i}$ and ${L_j}$ . Using the mutual reachability distance as the edge weight, we apply Prim’s algorithm to construct the minimum spanning tree between points. Next, we sort the edges of the minimum spanning tree incrementally, starting with the smallest weight, and merge the two nodes or clusters connected by the selected edge into a new cluster. This process is continued by selecting the next edge with the smallest weight until all nodes are merged into a single cluster, forming a hierarchical tree structure. Subsequently, pruning operations are performed by iteratively selecting the mutual reachability distances, sorted in ascending order, as pruning thresholds to yield different clustering schemes. The silhouette coefficient for each clustering scheme is then calculated using the following equation (9):

$$\begin{aligned} SC = \frac{1}{N}\sum \limits _{i = 1}^N {\frac{{b\left( i \right) - a\left( i \right) }}{{\max \left\{ {a\left( i \right) ,b\left( i \right) } \right\} }}} \end{aligned}$$

(9)

where, SC represents the silhouette coefficient of the points, N represents the number of clustering schemes, $a\left( i \right)$ is the average distance from point i to other points within the same cluster, and $b\left( i \right)$ is the average distance from point i to all points in the nearest neighboring cluster. After calculating the silhouette coefficients for each scheme, we select the scheme with the most significant change in silhouette coefficient as the final clustering scheme. This is achieved by interpreting the silhouette coefficients as a curve and selecting the clustering scheme corresponding to the point where the maximum perpendicular distance to the line connecting the start and end points of the curve is. Finally, the centroid of the cluster with the largest number of points from the selected clustering scheme is chosen as the fused relative coordinate $\hat{L} = ({x^c},{y^c},{z^c})$ of the target.

Optimization model establishment

The robot follows the trajectory P, stopping at the center of each grid cell to acquire images and other data related to the long-distance target. Using the target relative position calculation method, the coordinates of the distant target are determined. Considering movement constraints and those associated with long-distance target localization, the objective is to identify an optimal movement strategy ${P^*}$, that minimizes both the path length and the target coordinate error. The optimization model is established as follows:

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _P \left( {\left\| {\hat{L} - {L_R}} \right\| /{D_P}} \right) \\ \mathrm{{s}}\mathrm{{.t}}\mathrm{{. P}} = ({p_0},...,{p_k},...,{p_n})\\ {p_{k + 1}} \in {\mathrm{{G}}_k},k = 0,2,...,n - 1\\ {p_g} \ne {p_v},\forall {p_g},{p_v} \in P{\hspace{4.0pt}} g \ne v\\ \hat{L} = IH({L_i})\\ equation (5) - (6) \end{array} \end{aligned}$$

(10)

where, $\hat{L}$ represents the estimated coordinates of the target node following fusion, ${L_R}$ represents the true coordinates of the target node, ${D_P}$ represents the length of the moving path, and $IH({L_i})$ represents the final relative coordinates obtained using the improved HDBSCAN for target relative coordinate fusion, based on all acquired ${L_i}$ .

Approximate solution of the optimization model

Swarm intelligence algorithms are optimization methods inspired by the collective behaviors observed in nature. These algorithms aim to find global optimal solutions by simulating the interactions among individuals within a group. However, they are sensitive to parameter settings and prone to premature convergence, which often results in suboptimal solutions. Reinforcement learning, on the other hand, is a machine learning approach where an agent learns an optimal policy through interacting with the environment. During this process, the agent takes actions based on its current state, calculates the Q-value for each action, and selects actions based on these values. By evaluating the outcome through rewards, the agent iteratively improves its policy to maximize cumulative rewards. Deep reinforcement learning enhances this process by utilizing neural networks to approximate Q-values, effectively addressing the challenge of high-dimensional state-action spaces and improving generalization capabilities. The DDQN algorithm, in particular, separates the target Q-value estimation from the action selection process, reducing Q-value overestimation and providing a more stable and reliable learning process. Compared to other deep reinforcement learning algorithms, DDQN features lower complexity, faster convergence, and is easier to implement, especially for problems involving discrete action spaces.

Therefore, this paper proposes the use of DDQN as the foundational framework. It incorporates a reward strategy based on coordinate fusion errors to address the optimization model described in equation (10). This approach aims to determine the optimal target locations and path trajectories. The specific details are presented below.

Solving network model construction   In the model, the state ${s_t}$ of the robot is defined as the state information at time t, which is ${s_t} = \left[ {{p_{t - 1}},{p_t},x,y,z} \right]$ , where ${p_t}$ represents the two-dimensional index of the grid center in the hexagonal grid at time t. x, y and z represent the image data obtained from ${p_{t - 1}}$ and ${p_t}$. The estimated coordinates of the target are obtained using a relative position algorithm based on these two sensor inputs, subject to the constraints of equations (5)-(6) and the constraints in model (10). The robot can move in six possible directions in the hexagonal grid, denoted as $\mathcal{A} = \left\{ {{a_1},{a_2},{a_3},{a_4},{a_5},{a_6}} \right\}$, where ${a_1}$ represents moving to the right, ${a_2}$ represents moving to the upper right, ${a_3}$ represents moving to the lower right, ${a_4}$ represents moving to the left, ${a_5}$ represents moving to the upper left, ${a_6}$ and represents moving to the lower left. However, the movement directions are constrained in boundary regions of the grid. Thus, the set of feasible movement directions for each state is determined by the movement constraints given in equations (1)-(3).

The reward function decisively influences the algorithm’s optimization performance and network convergence by guiding the robot to learn the optimal movement strategy. Specifically, if a particular movement direction brings the estimated target coordinates closer to the optimal solution, it deserves a higher reward; conversely, it gains a lower reward or even a negative reward. Thereby, this setting of the reward function encourages the robot to progressively choose paths that facilitate target localization. However, according to the optimization objective in model (10), the robot does not have access to the true target coordinate ${L_\mathrm{{R}}}$ during movement. Therefore, the approach continuously updates the estimated coordinate using a relative position computation algorithm and leverages the trend in the estimated coordinate change as the basis for optimization, enabling the algorithm to locate the optimal target coordinate. Based on these considerations of both movement strategy and localization error, the following reward function is proposed:

$$\begin{aligned} {r_t} = r_{error}^t + r_{goal}^t \end{aligned}$$

(11)

where, ${r_t}$ represents the total reward at time t, and $r_{error}^t$ represents the target localization reward at time t. $r_{error}^t$ is obtained as follows. Firstly, obtain the estimated coordinates ${IH(L_{t-1)}}$ and ${IH(L_t)}$ by the target relative position calculation algorithm at time $t-1$ and t, respectively. And then calculate the change of the reference coordinates as the reward value. The process is expressed as:

$$\begin{aligned} r_{error}^t = - \left( {{{\left\| {IH({L_t}) - L_{ref}^t} \right\| }_2} - {{\left\| {IH({L_{t - 1}}) - L_{ref}^t} \right\| }_2}} \right) \end{aligned}$$

(12)

where, $L_{ref}^t$ represents the current reference coordinates, which can be represented as:

$$\begin{aligned} L_{ref}^t = \alpha IH\left( {{L_t}} \right) + \left( {1 - \alpha } \right) L_{ref}^{t - 1} \end{aligned}$$

(13)

where, $\alpha$ is a weight coefficient used to balance the influence of the currently computed coordinate and the historical reference coordinate. If ${IH(L_t)}$ is closer to the reference coordinate than ${IH(L_{t-1)}}$, meaning the movement contributes to convergence. As a result, a positive reward is given to encourage the robot to continue moving in that direction. Conversely, if the movement leads to divergence, a negative reward is assigned to penalize the robot and discourage further movement in that direction. Denote $r_{goal}^t$ to be the reward obtained when the difference between the target’s estimated coordinate, which is acquired through the improved HDBSCAN-based target relative coordinate fusion algorithm, and the reference coordinate reaches a specified threshold $\varepsilon$. The process can be expressed as:

$$\begin{aligned} r_{goal}^t = \left\{ \begin{array}{l} 100-k\cdot {\left\| {IH({L_t}) - L_{ref}^t} \right\| _2},{\left\| {IH({L_t}) - L_{ref}^t} \right\| _2} \le \varepsilon \\ 0,{\left\| {IH({L_t}) - L_{ref}^t} \right\| _2} > \varepsilon \end{array} \right. \end{aligned}$$

(14)

To further balance exploration and exploitation, the method employs a Softmax strategy to select movement directions. This strategy uses a probability distribution to choose an action, where the distribution is based on the Q-value of each action, and can be expressed as:

$$\begin{aligned} P\left( {{s_{t - 1}}|{a_k}} \right) = \frac{{{e^{{Q_{behavior}}\left( {{s_{t - 1}},{a_k},\omega } \right) }}}}{{\sum \limits _{m = 1}^{{M_\mathcal{A}}} {{e^{{Q_{behavior}}\left( {{s_{t - 1}},{a_m},\omega } \right) }}} }} \end{aligned}$$

(15)

where, $P\left( {{s_{t - 1}}|{a_k}} \right)$ represents the probability of selecting movement direction ${a_k}$ in state ${s_{t-1}}$, and ${Q_{behavior}}\left( {{s_{t - 1}},{a_k},\omega } \right)$ represents the Q-value of ${a_k}$ in state ${s_{t-1}}$. ${Q_{behavior}}\left( {{s_{t - 1}},{a_k},\omega } \right)$ is the total number of available movement directions determining the range of possible actions. Compared to the greedy strategy, the Softmax strategy assigns higher selection probabilities to actions with higher Q-values, while still allowing actions with lower Q-values to be chosen with non-zero probability, thereby enabling better exploration.

Figure 5

Network model for moving location selection at the next time instant.

Algorithm 1

Solution process of LTLO

Based on the definitions above, we propose the network model to select the next movement position, as shown in Fig. 5. This network model includes an experience replay buffer, two networks with identical structures: the behavior network and the target network , and a loss function. The experience replay buffer is used to collect and store experience tuples (state ${s_{t - 1}}$ , direction of movement ${a_{t - 1}}$ , reward ${r_{t - 1}}$, state ${s_t}$). The behavior network and target network both take a 7-dimensional state representation, ${s_t}$ , as input, hence their input layers consist of 7 neurons. The network features two fully connected hidden layers, each containing $\lambda$ neurons. Considering the robot’s six possible movement directions, the output layer comprises 6 neurons. The hidden layers use the rectified linear unit (ReLU) activation function, enhancing the network’s capability to manage nonlinear problems.

During training, the robot first moves from the starting position, sequentially placing state ${s_{t - 1}}$ information and others into the experience replay buffer. The network uses the experience replay buffer to input the current data samples into the behavior network ${Q_{behavior}}$, where it computes the Q-values for each possible movement direction in the given state , and selects the Q-value corresponding to the chosen movement direction ${s_{t - 1}}$ as the predicted value ${y_{eval}}$. Next, the robot calculates the movement direction ${a_t}$ with the maximum Q-value for state in the behavior network ${Q_{behavior}}$. The Q-value of state ${s_t}$ in the target network ${Q_{target}}$ for each movement direction ${a_t}$ is computed, and the Q-value corresponding to movement direction is selected and substituted into equation (16) to compute the target value ${y_{target}}$:

$$\begin{aligned} {y_{target}} = {r_{t - 1}} + \gamma {Q_{target}}\left( {{s_t},{a_t},\omega '} \right) \end{aligned}$$

(16)

where, $\gamma$ represents the reward discount factor, used to measure the importance of future rewards, and $\omega '$ represents the parameters of the target network. Based on the predicted value ${y_{eval}}$ and the target value ${y_{target}}$, the loss function Loss is calculated using the mean squared error:

$$\begin{aligned} Loss =\mathbb {E} \left[ {{{\left( {{y_{target}} - {y_{eval}}} \right) }^2}} \right] \end{aligned}$$

(17)

where, $\mathbb {E}$ represents the expectation. Finally, the parameters $\omega$ of the behavior network are optimized using the gradient descent method. At the fixed training frequency $\tau$ , the parameters $\omega$ of the behavior network are copied to the parameters $\omega '$ of the target network, ensuring stable network updates and achieving iterative training.

Implementation of model solution    Based on Algorithm 1, the robot moves while searching for the optimal solution of model (10). The detailed steps are as follows:

Step 1: Randomly initialize the behavior network and the target network . Set the experience replay buffer with a capacity of 10,000, the sample batch size of 64, the update frequency of 10, the reward discount factor of 0.95, the error threshold of 0.3, and the maximum number of iterations Y of 50.

Step 2: Let $t=1$, and the robot initializes the initial position ${s_{t-1}}$ and visited path ${P_y}$.

Step 3: The robot calculates the set of movement directions $\mathcal{A}\left( {{s_{t-1}}} \right)$ in the current state ${s_{t - 1}}$ using equation (2), and excludes the directions that lead to already visited positions. If the set of movement directions is empty, it performs the following operations until $\mathcal{A}\left( {{s_{t - 1}}} \right)$ is non-empty: it backtracks along the robot’s path to previously visited grid centers, identifies unvisited neighboring grid centers, and adds them to $\mathcal{A}\left( {{s_{t - 1}}} \right)$.

Step 4: The robot uses the behavior network ${Q_{behavior}}$ to calculate the movement probabilities for the directions ${a_{t-1}}$ in set $\mathcal{A}\left( {{s_{t - 1}}} \right)$ using equation (15), and selects the direction with the highest probability.

Step 5: The robot moves to the corresponding grid center based on the selected direction. It photographs the target, uses Yolo and other target detection algorithms to detect the distant target and processes the captured image in parallel with the image taken at time $t-1$. Then it uses the SURF algorithm for feature matching of the target in the images. If the movement direction is parallel, the robot calculates the target coordinates using equation (5). If the movement direction is diagonal, it uses the equation (6) to calculate the target’s relative position, thus obtaining state ${s_t}$. Using the relative position data at each point along the robot’s path, it clusters the obtained coordinate data using the improved HDBSCAN-based relative coordinate fusion algorithm to acquire the target coordinates at time t. Then the robot calculates the immediate reward ${r_{t_1}}$ using equation (11).

Step 6: The robot stores the generated data tuple $\left( {{s_{t - 1}},{a_{t - 1}},{r_{t - 1}},{s_t}} \right)$ into the experience replay buffer D. If the number of tuples is less than $\chi$, it selects all tuples as the incremental training set for the behavior network. Otherwise, it samples the latest $\chi$ tuples as the incremental training set.

Step 7: The robot sequentially inputs the tuples $\left( {{s_k},{a_k}} \right)$ from the training set into the behavior network ${Q_{behavior}}$ for training, and calculates the predicted values to obtain set ${y_{eval}}$. It sequentially inputs ${s_{k+1}}$ into the target network ${Q_{target}}$ to calculate the target values, obtaining set ${y_{target}}$. Then, it calculates the loss function using equation (16) and updates the parameters $\omega$ of the behavior network through gradient descent. If $t\% \tau = = 0$ , it copies the parameters $\omega$ of the behavior network to the parameters $\omega '$ of the target network.

Step 8: The strategy’s effectiveness is evaluated by checking whether the absolute difference between the estimated clustered coordinates obtained after the robot’s movement and the reference clustered coordinates fall below a predefined threshold. If this condition is satisfied, it indicates that the estimated target coordinates have stabilized, and the path planning process is terminated. Otherwise, $t=t+1$, set and go back to Step 3 to continue searching. If the maximum number of iterations Y is not reached, go back to Step 2 for the next iteration. Otherwise, the robot obtains the estimated coordinates $IH({L_t})$.

According to algorithm 1, we analyze the time complexity of LTLO. The LTLO primarily involves calculating the position of a distant target and training the network. During each movement, the robot uses an improved HDBSCAN-based relative coordinate fusion method to compute the position of the distant target, which requires clustering the obtained coordinate points L. Thus, the time complexity of this part is $\Theta \left( {{L^2}} \right)$. The time complexity of the network training part mainly depends on the total number of neural network parameters and the number of tuples in the training set, resulting in a complexity of $\Theta \left( {\lambda \rho } \right)$ . Therefore, the total time complexity of LTLO is $\Theta \left( {K * \left( {{L^2} + \lambda \rho } \right) } \right)$ , where K is the number of grid cells along the robot’s path.

Experimental results

Experimental environment and parameter settings

The experimental mobile robot is shown in Fig. 6. The robot adopts a four-wheel differential drive structure, providing stable mobility with a motion control accuracy of $\pm 0.1$ meters. The robot is equipped with a high-performance ten-axis IMU sensor (WTGAHRS2) based on micro-electro-mechanical system (MEMS) technology, integrating a three-axis gyroscope, a three-axis accelerometer, and a three-axis electronic compass for real-time attitude measurement and positioning support. For image acquisition, the system uses a high-precision camera with a resolution of $3472\times 3472$ and a frame rate of 30 fps to capture long-range target images. The robot also includes a GPS-enabled positioning module, which works in conjunction with the IMU sensor to achieve multi-source fused localization. All sensor data is processed by an integrated computing unit powered by an Intel i7-12700H processor, 16 GB of RAM, and an NVIDIA GeForce GTX 4060 GPU, which handles both image processing and DDQN-based path planning computations.

Figure 6

Experimental equipment.

Figure 7

Experimental environment.

To validate the effectiveness of the proposed algorithm, experiments were conducted on an outdoor playground under clear weather conditions. During the experiment, the IMU sensor provided real-time data from GPS, gyroscope, and electronic compass, while the internal parameters of the camera were calibrated using Zhang’s calibration method. Fig. 7 shows the mobile range of the robot grid and the experimental environment for the target region of interest (ROI) 1. The mobile robot moved within a specified grid range, collecting data with each grid center spaced 10 meters apart. The experimental parameters used for target localization are listed in Table 1. The mobile robot started from grid coordinates g(3, 3) and performed target localization using relative coordinates with g(0,0) as the reference point. The experiment targeted five accessible ROIs for testing, specifically windows on buildings at distances ranging from 100 meters to 500 meters. The targets for each ROI were imaged from multiple locations. ROI 1 was located at a distance of 104.49 meters, ROI 2 at 193.75 meters, ROI 3 at 316.80 meters, ROI 4 at 379.53 meters, and ROI 5 at 494.21 meters. These distance settings ensured that the equipment captured high-quality images and allowed evaluation of the algorithm’s performance in mid-to-long-distance localization, applicable to various real-world scenarios such as drone surveillance and rescue operations.

Table 1 Experimental parameters.

Analysis of simulation results

Analysis of parameter selection

Figure 8

Target relative positioning error of LTLO.

Figure 9

Target relative positioning error of LTLO.

This paper discusses the cases under hexagonal grid widths of 5m, 8m, 10m, 12m, and 15m, and analyzes the impact of grid width on the relative localization error of LTLO based on the parameters listed in Table 1. It calculates the relative localization error for five target positions under each specific grid width. As shown in Fig. 8, the overall relative localization error of LTLO exhibits a clear decreasing trend as the hexagonal grid width increases. When the grid is overly dense, although the data sampling density improves significantly, frequent short-distance movements intensify the accumulation of sensor noise. This effect becomes especially problematic when addressing pose angle errors for nearby targets, as the accumulated noise directly degrades the accuracy of image correction, potentially increasing the overall error rate. In addition, dense path planning introduces substantial computational redundancy, which severely impacts the stability of the clustering algorithm. As the grid width increases, the baseline distance between stereo cameras also increases. This not only enhances the resolution for depth estimation of distant objects but also significantly increases the disparity in the stereo imaging system, thereby improving localization accuracy to a certain extent. However, it is worth noting that after the grid width reaches a certain threshold, further improvements in localization accuracy come at the cost of reduced path planning efficiency. Considering the trade-off between path efficiency and localization accuracy, the subsequent experiments adopt a grid width of 20 meters. This configuration effectively reduces localization errors while mitigating excessive losses in path planning efficiency.

This paper analyzes the impact of convergence threshold on the relative localization error of LMDTL. It selects convergence thresholds of 0.1, 0.2, 0.3, 0.4, and 0.5, and computes the relative localization error for five target positions under each threshold based on the parameters listed in Table 1. As shown in Fig. 9, the relative localization error tends to increase overall as the convergence threshold gradually increases. This trend occurs because a larger convergence threshold often causes the training process to converge prematurely, significantly reducing the efficiency of feature fusion. This process can be illustrated through a comparison of the cases under thresholds of 0.1 and 0.5. With a threshold of 0.1, the algorithm achieves the minimum localization error; however, such a small threshold forces the model to train for a longer duration, which increases the length of the exploration path. In contrast, when the threshold increases to 0.5, the algorithm converges too early during the initial training phase, leading to insufficient feature fusion and a substantial decline in localization accuracy. Considering the trade-off between localization accuracy and average path length, the method adopts a convergence threshold of 0.3 for subsequent experiments. This setting effectively reduces localization error while avoiding excessive increases in path length, thereby achieving a balanced performance between localization precision and movement efficiency.

Ablation experiment

To validate the contribution of the path planning module (DDQN optimization strategy) to long-range target localization accuracy and path efficiency, this paper conducts an ablation study based on LTLO. Three approaches are compared: Method A (removing DDQN path planning and using a fixed route), Method B (removing the HDBSCAN-based relative coordinate fusion algorithm and instead applying simple coordinate averaging), and Method C (the complete LTLO algorithm). These methods are tested across five ROIs, and the experimental results are shown in Table 2. The results indicate that Method A yields higher localization errors compared to Method C. This is because Method A relies on a fixed path, which leads to target image data being collected from suboptimal positions. These less accurate observations, when fused, result in increased relative and absolute errors in the estimated target coordinates. This demonstrates the critical role of dynamic path optimization in improving data quality. Method B shows lower error rates than Method A but higher than Method C. Although Method B eliminates the HDBSCAN-based relative coordinate fusion and replaces it with coordinate averaging, the independent optimization of path planning still improves the spatial distribution of observation points to some extent. However, due to its inability to effectively identify and differentiate dense coordinate clusters, its localization accuracy remains limited. In contrast, Method C achieves the lowest error rates across all ROIs. This confirms that the full LTLO algorithm, which integrates path planning with relative coordinate fusion, can generate more optimal fusion paths, thereby improving the accuracy of the final target localization. As a result, Method C consistently delivers the lowest relative and absolute errors, demonstrating the effectiveness of the proposed path planning algorithm in enhancing long-range target localization accuracy.

Table 2 Target positioning ablation experiment.

Analysis of algorithm performance

Figure 10

Target relative positioning error of LTLO.

As shown in Fig. 10, during the robot’s path-searching process, the relative positioning error of the target gradually decreases with each movement step. Initially, due to uncertainty in the fused coordinates of the target, the relative positioning error is relatively large. However, as the robot continues to move and gather new observation data, the relative positioning errors of all targets decrease significantly. Specifically, the error for ROI 1 reduces rapidly within the first 5 steps, for ROI 2 within the first 9 steps, for ROI 3 within the first 10 steps, for ROI 4 within the first 7 steps, and for ROI 5 within the first 11 steps, indicating that the algorithm can effectively adjust the initial state in the early phase. After the 10th step, the relative positioning errors of all targets gradually converge, suggesting that the estimated coordinates are approaching the actual target positions, with the final relative errors of each target fluctuating within a small range. Therefore, LTLO demonstrates good convergence properties.

Figure 11 shows the path planning results for the robot targeting different ROIs. Considering the obstacle-free scenarios, the moving path for localizing ROI 1 is shown as the blue path in Fig. 11(a), the path for localizing ROI 2 is represented by the yellow path in Fig. 11(a), and the path for ROI 3 by the red path in Fig. 11(a). In Fig. 11(b), the path for localizing ROI 4 is the blue path, and the path for ROI 5 is the red path. Consider the obstacle scenarios, as shown in Fig. 11(c), the robot successfully plans the paths to ROI1, ROI2, and ROI3, avoiding the gray regions that represent impassable areas. Similarly, Fig. 11(d) illustrates the robot’s path planning to ROI4 and ROI5, where the robot effectively bypasses obstacles while still selecting near-optimal paths and achieving accurate target localization. As shown in Fig. 11, the robot not only adapts its path flexibly based on the target locations but also demonstrates the capability to autonomously avoid interference in complex environments and complete its tasks, ensuring that it can identify optimal paths and estimate the target’s optimal coordinates across varying distances. The proposed LTLO algorithm inherently incorporates traversability constraints within the hexagonal grid during path planning. As a result, the path planning process in the presence of obstacles does not differ significantly from that in obstacle-free scenarios. Experimental results indicate that the presence of obstacles has minimal impact on the outcome analysis. Therefore, we only show the experimental results in the obstacle-free scenarios in the following.

Figure 11

Moving paths for different targets.

Positioning comparison under different moving paths

To assess the impact of different moving paths on target localization, Fig. 12 presents four different moving path schemes. Fig. 12(a) shows a path where the mobile robot starts from g(0,0), moves around the perimeter of the grid, and locates the target through image capture. Fig. 12(b) depicts a spiral outward path where the robot starts from g(3,3) and spirals outward, capturing images to locate the target. Fig. 12(c) shows the robot starting from g(0,0) and moving along each row of the grid to capture images for target localization. Fig. 12(d) illustrates the moving path of LTLO, using ROI 1 as an example. Using the parameters listed in Table 1, the relative and absolute errors between the estimated coordinates and the true coordinates of the same ROI target were calculated for different moving paths. As shown in Table 3, LTLO has the lowest relative and absolute errors for all ROIs. This is because LTLO dynamically adjusts the path based on real-time observation data and estimation results, selecting an optimal route. During clustering fusion, the collected coordinate points are more concentrated and highly correlated, effectively reducing unnecessary noise, resulting in more accurate clustering outcomes. Since LTLO avoids redundant movements and minimizes accumulated errors, it achieves high-precision localization within shorter paths. In contrast, the other three fixed-path schemes have longer paths, leading to resource waste and extended localization times. The robot needs to cover a larger area, which results in longer paths generating accumulated errors in IMU data and producing a large amount of irrelevant target image data. These higher-error data points lead to multiple inaccurate target coordinates, which, after clustering fusion, increase the relative and absolute errors of the target coordinates.

Figure 12

Different moving path schemes.

Table 3 Target Localization results under different moving paths.

Comparison of target positioning errors

Figure 13

Relative positioning error rate comparison.

Figure 14

Absolute positioning error rate comparison.

According to the parameters in Table 1, this paper compares the relative coordinates, relative errors, LLA coordinates, and absolute errors of LTLO, TMVL³, MGG⁶, and LRBVTG⁷ across ROI 1 to ROI 5. As shown in Table 4, Figs. 13, and 14, due to factors such as image quality, the degree of path optimization, clustering stability, and sensor noise, LTLO exhibits slight fluctuations across different ROIs. However, for localization targets ranging from 100m to 500m, LTLO identifies near-optimal paths consistently. It effectively maintains the relative localization error within 4% and the absolute error within 6%, which are significantly lower than those of TMVL, MGG, and LRBVTG. It is reasoned that in long-distance target localization, LTLO considers movement constraints such as stay position selection and non-repetitive positioning, as well as long-distance target localization constraints such as image parallelism and relative position calculation. It constructs an optimization model for long-distance target localization based on the robot’s movement trajectory. For this optimization model, LTLO employs a reward strategy based on coordinate fusion in the improved Double Deep Q-Network, determining the optimal moving path through model training during the movement process and selecting the next movement direction. LTLO also introduces an improved HDBSCAN-based algorithm for fusing the relative coordinates of the target, effectively identifying the set of points surrounding the true relative coordinates and enhancing the effectiveness of coordinate fusion, thereby improving the accuracy of long-distance target localization. In contrast, TMVL has significant limitations in practical applications, as it requires manually providing target height information. Accurately measuring the height of long-distance targets manually is often challenging. Therefore, TMVL has considerable errors and impacts localization accuracy. The MGG algorithm relies on IMU data for camera pose correction, but angular drift errors in the IMU cause the lateral localization error to increase linearly with distance. Additionally, the depth estimation model based on pixel height introduces increasing errors as the target distance grows. LRBVTG requires manual adjustment of the camera angle to maintain parallelism between images. However, due to the long baseline between cameras, maintaining consistent camera orientation at two positions during movement is challenging, especially in complex terrain, which results in tilting and non-parallelism. Therefore, LRBVTG reduces the accuracy of image matching, further affecting localization accuracy.

Table 4 Target localization results under different algorithms.

Discussion and conclusion

This paper presents an optimization algorithm for long-distance target localization (LTLO) that leverages the path planning of a single mobile robot. First, we construct an optimization model for long-distance targets, using the robot’s movement trajectory and dividing the operational area into hexagonal grids of equal size. Multiple movement constraints are introduced, including stay position selection and non-repetitive positioning. Then, by incorporating image parallel constraints and relative position calculations, we propose a target coordinate fusion algorithm based on the improved HDBSCAN. This algorithm effectively identifies clusters around the target’s true relative coordinates and fuses multiple target coordinate datasets to minimize positioning errors, thereby establishing long-distance localization constraints and constructing a target optimization model. Next, we propose an approximate solution for the optimization model, based on the improved double deep Q-network for training. We introduce a reward strategy based on coordinate fusion, which selects the next movement direction during the training process to find the robot’s optimal moving path, thereby improving localization accuracy for long-distance targets. Finally, we demonstrate the experimental environment, analyze the impact of different paths on target localization, and evaluate the performance of LTLO by comparing localization errors under different moving paths and algorithms. Experimental results show that, for static targets within distances of 100m to 500m, LTLO can identify effective moving paths to determine the target’s location, keeping relative positioning errors below 4% and absolute positioning errors below 6%, outperforming TMVL, MGG and LRBVTG.

The current LTLO framework primarily operates based on a single robot and targets long-range object localization under clear weather conditions, where objects can be detected using object recognition algorithms such as YOLO. In such scenarios, the image data is of high quality, and sensor outputs remain stable, supporting efficient image processing and data fusion. However, under adverse conditions such as rain, fog, and uneven lighting, as well as other complex environments, the performance of vision sensors faces greater challenges. Enhancing the feature extraction capability of vision sensors in low-light or high-noise environments and improving the robustness of target localization remain critical open problems. Future research can focus on developing more efficient image processing algorithms to improve feature extraction under low-light and high-noise conditions. Moreover, integrating multi-modal sensor fusion–combining data from visual, infrared, radar, and other types of sensors–can further enhance system perception in complex environments, thereby improving object recognition and localization accuracy. In addition, while LTLO improves localization accuracy by integrating multiple algorithms and incorporating neural network-based training, it also slightly increases algorithmic complexity. Therefore, future work will focus on optimizing the algorithm structure to maintain high localization accuracy while reducing computational overhead, thus enhancing the method’s applicability in a broader range of scenarios.