Two-layer energy scheduling of electrical and thermal smart grids with energy hubs including renewable and storage units considering energy markets

Abstract

This paper presents a two-layer energy management method designed for the operation of hubs within electrical and thermal smart grids. These energy hubs actively participate in both day-ahead and real time energy markets. Two-layer approach involves coordination at two distinct levels. In the first layer, the focus is on managing sources and storage equipment in collaboration with the hub operator. In the second layer, attention shifts to the interaction between the hub operator and the grid operator. The framework follows a two-stage formulation, where the first stage addresses the day-ahead operation model and the second stage pertains to real-time scheduling. In the first stage, a bi-level optimization strategy is employed. The upper level seeks to minimize the energy cost of smart grids while adhering to optimal power flow constraints, whereas the lower level aims to maximize hubs’ profit in the day-ahead energy market subject to the operational constraints of sources and storage systems represented in an energy hub model. The second stage mirrors this problem structure but uses a smaller time step and adopts the flexibility cost minimization as objective for the upper level. To simplify the bi-level optimization problem into a single-objective model, the Karush–Kuhn–Tucker (KKT) method is applied. Uncertainties of load, price of market, and renewable energy generation are modeled using the unscented transformation technique. Problem-solving is undertaken using a hybrid optimization solver that combines artificial bee colony and honey-bee mating optimization methods. Simulation results highlight the effectiveness of this approach, demonstrating its capability to enhance both economic and technical performance. Specifically, hubs achieve significant profitability and operational flexibility, leading to an 18% improvement in economic performance and a 18-27% enhancement in operational efficiency compared to traditional power flow studies.

Introduction

Motivation and background

To mitigate emissions, transitioning from fossil fuels to renewable energy sources (RESs) is essential. A contemporary approach involves leveraging renewable resources, combined heat and power (CHP) units, and energy storage systems (ESSs) to tackle this challenge¹. In the foreseeable future, power systems, particularly distribution systems, are expected to incorporate a growing number of these technologies. However, the complex nature of modern distribution system operations calls for innovative solutions. The smart distribution network concept suggests integrating generation units and active loads through microgrids (MGs), virtual power plants (VPPs), and energy hubs (EHs) for improved management². Given the interdependence of energy sources, it is more effective to control them collectively rather than in isolation³. Consequently, deploying a comprehensive EH framework can help synchronize renewable and non-renewable sources with active loads to enhance efficiency compared to managing each source independently³. When connected to energy networks, EHs can significantly enhance the networks’ performance⁴. By improving the coordination and control of energy sources and active loads, EHs also have the potential to boost market profitability. Achieving the optimal technical and economic conditions for energy networks and centers hinges on implementing an optimal energy management system⁵. This system relies on two-way communication between energy sources, storage facilities, and the energy hub operator⁵. To avoid exceeding technical limits within energy networks, it is imperative for the hub operator to maintain consistent two-way communication with the network operator.

A substantial body of research has been dedicated to the domain of energy management in EHs. For instance, the optimal power flow model outlined in⁶ highlights the interconnected nature of electric and thermal energy within EH systems. The primary focus of this model is to minimize the total operational costs, which include resource utilization, carbon emissions, demand response programs (DRPs), and system maintenance. This study employs an adjustable robust optimization method to handle the uncertainties inherent in renewable energy outputs and DRPs. By leveraging duality theory principles, this optimization problem is reformulated as a mixed-integer linear programming (MILP) task, which is efficiently resolved using a commercial solver. Similarly, the research in⁷ proposes a scheduling framework for EHs that incorporates a tri-generative advanced adiabatic compressed air energy storage (AA-CAES) system. The approach applies a safe deep reinforcement learning (DRL) method, combining primal–dual optimization and imitation learning, to ensure both operational safety and efficiency. The process begins with the modeling and linearization of the AA-CAES system under off-design conditions, achieved through a MILP approach. Subsequently, the study presents a comprehensive safe DRL methodology, including both training and testing stages, supported by a specific case study evaluation. In⁸, the focus shifts to energy management strategies in grid-connected flexible EHs. This framework integrates electrical and thermal networks, where renewable energy sources and storage systems operate under the coordination of a central hub. The objective is to minimize operating costs by considering an optimal power flow model alongside the mathematical representation of flexible EHs. To address uncertainties in demand levels, energy costs, and renewable power availability, the researchers implement an unscented transformation (UT) technique. This reduces computational complexity while improving solution accuracy and computation speed, effectively capturing system flexibility and addressing uncertainty factors. Further exploration is presented in⁹, which examines the management of electrical and thermal networks in renewable EHs with a focus on network flexibility regulation through flexible pricing services. These hubs encompass renewable energy sources, bio-waste units (BUs), storage devices, and responsive loads. BUs simultaneously generate electrical and thermal energy. The study seeks to balance network energy costs with revenue derived from hub flexibility by minimizing cost discrepancies. Lastly, reference¹⁰ targets the management of electricity, gas, and heating networks in flexible EHs within the day-ahead (DA) energy market using a market clearing price (MCP) model. The proposed bi-level optimization framework includes a higher-level problem that maximizes EH profits while accounting for operational constraints involving power sources, storage, and responsive loads. Meanwhile, the lower-level problem calculates energy prices and evaluates how EH performance impacts both technical and economic factors tied to MCP modeling.

The involvement of grid-connected EH in DA and real-time (RT) energy markets is elaborated in Ref.¹¹. The proposed optimization framework comprises two distinct stages. The first stage addresses EH participation in the hourly DA energy market through a two-layer energy management system, structured as a bilevel optimization problem. The second stage focuses on reducing profitability discrepancies between the DA and 5-min RT energy markets, ensuring enhanced operational alignment and financial returns. In Ref.¹², a stochastic scheduling methodology for multi-energy hub systems is introduced, aimed at simultaneously optimizing the performance of energy hubs and distribution networks. This framework integrates RESs, inherently uncertain parameters, DRPs, and emissions considerations to promote efficient and sustainable system operation. Ref.¹³ presents a scenario-based approach to optimize EH operations under the uncertainty of wind turbine (WT) and photovoltaic (PV) system outputs. The methodology is applied in environmental health contexts across various frameworks. A k-means clustering algorithm is employed to reduce computational complexity while maintaining adequate accuracy. To solve the stochastic optimization problem, a genetic algorithm (GA) is utilized, enabling effective decision-making under uncertainty. The work in Ref.¹⁴ explores the potential of harnessing excess heat from Power-to-X technologies within future energy hubs, addressing challenges such as decarbonizing the gas sector and minimizing renewable energy curtailments. Similarly, Ref.¹⁵ adopts a power-to-gas hub model in response to these challenges. To tackle uncertainties related to RESs and electricity market prices, Ref.¹⁶ employs a robust optimization framework. Monte Carlo simulations (MCS) are applied to compare the charging loads of electric vehicles (EVs) under coordinated versus uncoordinated charging modes. Additionally, this robust optimization approach extends to evaluating hybrid electrical, thermal, and cooling energy storage systems, offering comprehensive insights into their dynamic integration within future energy hub operations. In¹⁷, the energy management approach is expressed for the multi-energy rural microgrids including renewable units, aiming to satisfy the rural electricity, heat, gas networks, and irrigation demands economically. Ref.¹⁸ presents the distributed hybrid-triggered dynamic-consensus-observer-based secondary control tailored for average voltage restoration and load current sharing in general multi-bus DC microgrids over directed networks.

Table 1 is a compilation of many research articles pertaining to the subject matter being investigated.

Table 1 Classification of recent research studies.

Research gaps and contributions

Based on the previous subsection and as it is observed in Table 1, the energy management of EHs should be focused more than before because there are the following gaps:

• The literature mostly underlines a unified model for energy management, generation units, and active demand of EHs^{6,7,8,9,10,11,12,13,14,15,16}. Operators of networks receive the data from power sources and loads and send commands to them. As a result, the operators manage the energy of the energy networks even though the data received by operators significantly rise and operation becomes slow. To tackle this challenge, operators of EHs need to collaborate with generation units and active demand. Moreover, operators of EHs and networks need to work together and reduce the amount of data to accelerate the operation¹¹.

• In less research, such as^9,10,11, the economic model of EHs has been investigated with their presence in the energy or ancillary services market. However, it should be noted that since hubs contain power sources, storage devices, and responsive loads, hubs are expected to play an effective role in energy generation and storage, thus earning financial benefits from energy and ancillary services markets. In^9,10, the DA market model is considered. Yet, as RESs have uncertainty, this makes the results of DA and RT operations different. Accordingly, the balance of generation and consumption may not be established in RT operation. This condition is proportional to the lack of flexibility. To compensate for this issue, it is necessary for flexible sources such as storage devices and responsive loads to address RES power fluctuations in RT operation compared to DA operation. Therefore, there is a need to present the RT operation model, which has been included in few researches such as¹¹.

• BUs are a category of RESs capable of generating electrical energy by utilizing environmental waste as a resource. Also, if this source is equipped with CHP technology, it can operate simultaneously in the generation of electrical and thermal energy. However, in most studies such as^{6,7,10,11,12,13,14,15,16}, the presence of WT and PV renewable resources in EHs has been used, and in fewer researches such as^8,9, the importance of using CHP-based BU in hubs has been investigated. In addition, in most researches, batteries are generally utilized as storage devices. Although this element has high efficiency and power density, its installation cost is high and it has a low useful life. Also, access to their high capacity is limited. To compensate for this issue, hydrogen storage and compressed air can be used in the hub. The cost of these elements is lower than that of batteries, their useful life is longer, and access to high capacity is possible for them. These elements are also efficient. Nonetheless, the presence of these elements has been presented in less research such as⁷.

• There are various mathematical and evolutionary algorithms to solve problem of energy hub operation. But, in most studies, such as^{6,8,12,13,14,15,16}, non-hybrid evolutionary algorithms (NHEAs) and mathematical solvers suitable for modeling the problem have been used to solve the proposed scheme. These algorithms generally have a high dispersion in the final response obtained, which reduces the reliability of the optimal solution. In addition, some research has obtained a linear approximation model for the proposed design and then obtained the optimal solution from the solutions suitable for this model. However, in this process, a significant computational error occurs for some parameters. For example, based on¹⁹, the use of linear approximation has caused energy losses in the electrical network to be calculated as zero. Also, some studies such as⁷ do not provide a more realistic operation model of energy networks including EHs. For instance, in some studies, only the EH model is seen, but the performance of the hub also depends on the technical parameters of the network, such as the voltage and the allowable capacity of the distribution lines. Therefore, they are more of a linear model. With increased processes for updating decision variables, it is assumed that the optimal solution obtained will have approximately unique response conditions. This is available if the Hybrid evolutionary algorithm (HEA) is used in the proposed scheme.

• The operation of the different energy networks with EHs is specified by a high number of different uncertainties such as load and energy prices in different networks, renewable power, and energy demand of mobile storage devices. Therefore, the adoption of non-parametric methods in stochastic modeling such as scenario-based stochastic optimization (SBSO) used in some studies such as^{7,12,13,14,15} requires the extraction of a large number of scenarios. This makes solving the problem time-consuming. However, due to the imperative of minimizing the mathematical time needed for problem-solving tasks, using SBSO is not a good solution for modeling uncertainties. To compensate for this and provide appropriate modeling of uncertain quantities, some studies such as^6,11,16 have suggested the use of robust optimization. This case includes only a single scenario called the “worst-case scenario”. Although the use of this method reduces the computational time of problem-solving, the status of several scenarios must be investigated to calculate some indicators. For example, to calculate the flexibility indices, various scenarios resulting from the uncertainty of active power generation by RESs should be taken into account⁸. Therefore, parametric methods like the unscented transformation (UT) method will be used in stochastic modeling because such approaches necessitate the least number of scenarios⁸.

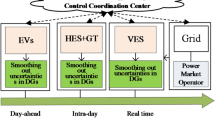
This study explores the optimal integration of EHs to address previously identified limitations. As illustrated in Fig. 1, these EHs are interconnected with both electricity and heating smart grids. They incorporate RESs, such as WT and CHP-BU, alongside flexible storage solutions including hydrogen storage (HS), thermal energy storage (TES), and compressed-air energy storage (CAES). Within this framework, EHs function as bilateral coordinators, managing the interaction between TES, CHP-BU, HS, CAES, and WT. To bridge the initial research gap, a two-layer energy management system (EMS) has been implemented. This EMS governs the operation of energy networks integrated with EHs. The first layer focuses on the cooperation between generation units and active loads with the EH operator. Meanwhile, the second layer handles coordination between the EH operator and energy network operators. A two-stage optimization approach underpins this framework: the first stage addresses the DA operation of networks in the presence of hubs, while the second stage involves RT operation. Each stage nests a bilevel optimization process. During the first stage, the upper-level optimization prioritizes minimizing energy procurement costs from upstream networks, while also factoring in the optimal power flow constraints of both electrical and thermal networks. The lower-level optimization includes EH participation in energy markets, aiming to maximize hub profits in both electrical and thermal markets. This process takes into account the operational models of RESs and storage systems configured within hubs. The second stage optimization mirrors the structure of the first, but with a distinct objective, i.e. minimizing flexibility costs, in the upper-level problem. Notably, time granularity differs between stages: the first stage operates on an hourly basis, while the second adopts a 5-min resolution. Addressing uncertainties tied to renewable generation, demand load, and energy pricing represents another critical enhancement. These are modeled using the UT technique. A single-level model is derived by applying the Karush–Kuhn–Tucker (KKT) method, enabling computational efficiency. The optimization problem is then solved by integrating honey-bee mating optimization (HBMO) with an artificial bee colony (ABC) algorithm. Ultimately, this research introduces various contributions and objectives that pave the way for more robust and efficient energy management in networks with integrated EH systems. In other words, contributions and objectives are:

• Presenting a two-stage optimization model for modeling the participation of EHs in the DA and RT energy markets to minimize the flexibility cost.

• Considering two-layer energy management to coordinate resources and storage systems with the hub operator and to coordinate the hub operator with the operators of different networks to reduce the processing speed by the network operator through reducing the volume of data delivered to this operator,

• Considering the capabilities of hydrogen and compressed air storage, as well as CHP-based BU in the energy hub.

• Achieving a reliable optimal solution with low calculation time and error in the energy management of grid-connected hubs using the combined algorithm of HBMO and ABS, and

• Using stochastic optimization based on the UT method to model uncertainties of load, renewable sources, and energy prices to reach the optimal solution in low computing time and accurate modeling of flexibility (imbalance between DA and RT operations).

Fig. 1

Two-stage optimization of the energy networks operation with EHs based on two-layer EMS.

“Incorporation of grid-connected EHs in energy markets” section describes the mathematical formula of the scheme, “Solution procedure” section presents solving method of the problem, “Findings and discussion” section reports the results, and “Conclusion” section summarizes the conclusions.

Incorporation of grid-connected EHs in energy markets

Hour-basis DA operation of energy networks with EHs (First stage)

The formulation of the problem is as follows:

$$\min \,\,\,\,\,\,F_{1} = \sum\limits_{{\omega \in \Gamma_{S} }} {\sigma_{\omega } \sum\limits_{{\tau \in \Gamma_{OH} }} {\left\{ {\xi_{\tau ,\omega }^{E} P_{o,\tau ,\omega }^{S} + \xi_{\tau ,\omega }^{H} H_{o,\tau ,\omega }^{S} } \right\}} }$$

(1)

Subject to:

$$P_{b,\tau ,\omega }^{S} + \sum\limits_{{h \in \Gamma_{H} }} {A_{b,h}^{E} P_{h,\tau ,\omega }^{H} } - \sum\limits_{{l \in \Gamma_{B} }} {B_{b,l}^{E} P_{b,l,\tau ,\omega }^{L} = P_{b,\tau ,\omega }^{C} } \,\,\,\forall b,\tau ,\omega$$

(2)

$$Q_{b,\tau ,\omega }^{S} - \sum\limits_{{l \in \Gamma_{B} }} {B_{b,l}^{E} Q_{b,l,\tau ,\omega }^{L} = Q_{b,\tau ,\omega }^{C} } \,\,\,\forall b,\tau ,\omega$$

(3)

$$P_{b,l,\tau ,\omega }^{L} = g_{b,l}^{L} \left( {V_{b,\tau ,\omega } } \right)^{2} - V_{b,\tau ,\omega } V_{l,\tau ,\omega } \left\{ {g_{b,l}^{L} \cos \left( {\phi_{b,\tau ,\omega } - \phi_{l,\tau ,\omega } } \right) + b_{b,l}^{L} \sin \left( {\phi_{b,\tau ,\omega } - \phi_{l,\tau ,\omega } } \right)} \right\}\,\,\,\,\forall b,l,\tau ,\omega$$

(4)

$$Q_{b,l,\tau ,\omega }^{L} = - b_{b,l}^{L} \left( {V_{b,\tau ,\omega } } \right)^{2} + V_{b,\tau ,\omega } V_{l,\tau ,\omega } \left\{ {b_{b,l}^{L} \cos \left( {\phi_{b,\tau ,\omega } - \phi_{l,\tau ,\omega } } \right) - g_{b,l}^{L} \sin \left( {\phi_{b,\tau ,\omega } - \phi_{l,\tau ,\omega } } \right)} \right\}\,\,\,\,\forall b,l,\tau ,\omega$$

(5)

$$H_{m,\tau ,\omega }^{S} + \sum\limits_{{h \in \Gamma_{H} }} {A_{m,h}^{H} H_{h,\tau ,\omega }^{H} } - \sum\limits_{{l \in \Gamma_{T} }} {B_{n,l}^{H} H_{m,l,\tau ,\omega }^{L} = H_{m,\tau ,\omega }^{C} } \,\,\,\,\,\,\forall m,\tau ,\omega$$

(6)

$$H_{m,l,\tau ,\omega }^{L} = \varpi_{m,l} \left( {T_{m,\tau ,\omega } - T_{l,\tau ,\omega } } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\forall m,l,\tau ,\omega$$

(7)

$$\underline{V} \le V_{b,\tau ,\omega } \le \overline{V}\,\,\,\,\,\,\,\,\,\,\,\,\,\forall b,\tau ,\omega$$

(8)

$$\left( {P_{b,l,\tau ,\omega }^{L} } \right)^{2} + \left( {Q_{b,l,\tau ,\omega }^{L} } \right)^{2} \le \left( {\overline{S}_{b,l}^{L} } \right)^{2} \,\,\,\,\,\,\,\,\,\,\,\,\forall b,l,\tau ,\omega$$

(9)

$$\left( {P_{b,\tau ,\omega }^{S} } \right)^{2} + \left( {Q_{b,\tau ,\omega }^{S} } \right)^{2} \le \left( {\overline{S}_{b}^{S} } \right)^{2} \,\,\,\,\,\,\,\,\,\,\,\,\forall b = o,\tau ,\omega$$

(10)

$$\underline{T} \le T_{m,\tau ,\omega } \le \overline{T}\,\,\,\,\,\,\,\,\,\,\,\,\,\forall m,\tau ,\omega$$

(11)

$$- \overline{H}_{m,l}^{L} \le H_{m,l,\tau ,\omega }^{L} \le \overline{H}_{m,l}^{L} \,\,\,\,\,\,\,\,\,\,\,\,\,\forall m,l,\tau ,\omega$$

(12)

$$- \overline{H}_{m}^{S} \le H_{m,\tau ,\omega }^{S} \le \overline{H}_{m}^{S} \,\,\,\,\,\,\,\,\,\,\,\,\,\forall m = o,\tau ,\omega$$

(13)

$$P^{H} ,H^{H} \in \arg \left\{ {\max \,\,\,\,\,\,F_{2} = \sum\limits_{{\omega \in \Gamma_{S} }} {\sigma_{\omega } \sum\limits_{{\tau \in \Gamma_{OH} }} {\sum\limits_{{h \in \Gamma_{H} }} {\left( {\zeta_{\tau ,\omega }^{E} P_{h,\tau ,\omega }^{H} + \zeta_{\tau ,\omega }^{H} H_{h,\tau ,\omega }^{H} } \right)} } } } \right.$$

(14)

Subject to:

$$P_{h,\tau ,\omega }^{H} = P_{h,\tau ,\omega }^{BU} + P_{h,\tau ,\omega }^{WT} + \left( {P_{h,\tau ,\omega }^{Ge} - P_{h,\tau ,\omega }^{Mo} } \right) + \left( {P_{h,\tau ,\omega }^{FC} - P_{h,\tau ,\omega }^{EL} } \right) - P_{h,\tau ,\omega }^{C} :\vartheta_{h,\tau ,\omega }^{P} \,\,\,\,\,\,\forall h,\tau ,\omega$$

(15)

$$H_{h,\tau ,\omega }^{H} = H_{h,\tau ,\omega }^{BU} + \left( {H_{h,\tau ,\omega }^{DCH} - H_{h,\tau ,\omega }^{CH} } \right) - H_{h,\tau ,\omega }^{C} :\vartheta_{h,\tau ,\omega }^{H} \,\,\,\,\,\forall h,\tau ,\omega$$

(16)

$$H_{h,\tau ,\omega }^{BU} = P_{h,\tau ,\omega }^{BU} \frac{{\left( {1 - \eta^{t} - \eta^{l} } \right)\eta^{h} }}{{\eta^{t} }}:\vartheta_{h,\tau ,\omega }^{bu} \,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(17)

$$0 \le P_{h,\tau ,\omega }^{EL} \le \,\chi_{h}^{EL} :\underline{\mu }_{h,\tau ,\omega }^{el} ,\overline{\mu }_{h,\tau ,\omega }^{el} \,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(18)

$$0 \le P_{h,\tau ,\omega }^{FC} \le \,\chi_{h}^{FC} :\underline{\mu }_{h,\tau ,\omega }^{fc} ,\overline{\mu }_{h,\tau ,\omega }^{fc} \,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(19)

$$\underline{E}_{h}^{HT} \le E_{h}^{HT} (0) + \sum\limits_{t = 1}^{\tau } {\left( {\eta^{EL} P_{h,t,\omega }^{EL} - \frac{1}{{\eta^{FC} }}P_{h,t,\omega }^{FC} } \right)} \le \overline{E}_{h}^{HT} :\underline{\mu }_{h,\tau ,\omega }^{ht} ,\overline{\mu }_{h,\tau ,\omega }^{ht} \,\,\,\,\,\,\forall h,\tau ,\omega$$

(20)

$$0 \le P_{h,\tau ,\omega }^{Mo} \le \,\chi_{h}^{Mo} :\underline{\mu }_{h,\tau ,\omega }^{mo} ,\overline{\mu }_{h,\tau ,\omega }^{mo} \,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(21)

$$0 \le P_{h,\tau ,\omega }^{Ge} \le \,\chi_{h}^{Ge} :\underline{\mu }_{h,\tau ,\omega }^{ge} ,\overline{\mu }_{h,\tau ,\omega }^{ge} \,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(22)

$$\underline{E}_{h}^{CAT} \le E_{h}^{CAT} (0) + \sum\limits_{t = 1}^{\tau } {\left( {\eta^{Mo} P_{h,t,\omega }^{Mo} - \frac{1}{{\eta^{Ge} }}P_{h,t,\omega }^{Ge} } \right)} \le \overline{E}_{h}^{CAT} :\underline{\mu }_{h,\tau ,\omega }^{cat} ,\overline{\mu }_{h,\tau ,\omega }^{cat} \,\,\,\,\,\,\forall h,\tau ,\omega$$

(23)

$$0 \le H_{h,\tau ,\omega }^{CH} \le \,\chi_{h}^{CH} :\underline{\mu }_{h,\tau ,\omega }^{ch} ,\overline{\mu }_{h,\tau ,\omega }^{ch} \,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(24)

$$0 \le H_{h,\tau ,\omega }^{DCH} \le \,\chi_{h}^{DCH} :\underline{\mu }_{h,\tau ,\omega }^{dch} ,\overline{\mu }_{h,\tau ,\omega }^{dch} \,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(25)

$$\left. {\underline{E}_{h}^{T} \le E_{h}^{T} (0) + \sum\limits_{t = 1}^{\tau } {\left( {\eta^{CH} H_{h,t,\omega }^{CH} - \frac{1}{{\eta^{DCH} }}H_{h,t,\omega }^{DCH} } \right)} \le \overline{E}_{h}^{T} :\underline{\mu }_{h,\tau ,\omega }^{t} ,\overline{\mu }_{h,\tau ,\omega }^{t} \,\,\,\,\,\,\,\forall h,\tau ,\omega } \right\}$$

(26)

Upper-level formulation (second layer of EMS)

The hour-basis DA operation of the energy networks with EHs is described here. Equations (1)-(13) states the problem and includes an objective function so that the minimum energy cost is reached⁸. Optimal power flow (OPF) equations are presented in Eqs. (2) through (13)^4,8,9, while power flow equations are presented in Eqs. (2) through (7). Equations (2)-(5), which also provide the active and reactive power balance of network buses and objects passing across lines, describe the electricity network power flow^20,21,22,23. Equations (6)–(7) give the heating network power flow⁸. Equations (8)–(13) are the operation constraints of the energy networks^8,9, representing the limitation on bus voltage magnitude, apparent power of distribution lines and substations^24,25,26,27, node temperature, and thermal power of heating pipelines and stations.

Lower layer (first layer of EMS)

The goal function, Eq. (14), maximizes the EHs profit in electricity and heat energy markets. EH’s profit is equal to the total of its revenues in the aforementioned markets. Energy price and power are multiplied to determine revenue in each market²⁸. When power has a positive value, Eq. (14) gives EH’s revenue; while for its negative value, Eq. (14) gives EH’s cost. The demand and supply balances for active and heating power are denoted by Eqs. (15)-(16). In these two equations, WT and BU are considered as electrical energy producers^{29,30,31,32,33}, and hydrogen and compressed air storages were utilized as energy storage. BU is equipped with CHP technology⁹, so in the thermal sector, only BU produces thermal energy. The power of RESs is a parameter^34,35,36,37. Also, TES has employed used as an energy store. Equations (17)–(26) provide the operational model of the ESSs and RESs in EHs. By being equipped with CHP, BU is able to produce electrical and thermal energy at the same time. This is presented in Eq. (17), which refers to the amount of thermal power produced by BU based on its active power⁸. In addition, it should be noted that in the Eqs. (15) and (16), the active power generation by WT and BUs were included as parameters, the amount of which is determined based on weather data. The functioning of EESs including HS and CAES are described in Eqs. (18)–(23)^7,38. HS has fuel cell (FC), electrolyzer (EL), and hydrogen tank (HT)³⁸. The electrolyzer is active in the HS charging mode and converts the electrical energy into hydrogen³⁹. Then hydrogen is stored in HT. In HS discharge mode, FC is active and it receives hydrogen from HT and converts it into electrical energy³⁸. HS performance model can be seen in Eqs. (18)-(20). The capacity limits of EL and FC are given in constraints (18) and (19), respectively, and the limit on the energy stored in HT is proportional to constraint (20)³⁹. In CAES, a motor stores electrical energy in the form of compressed air in a compressed air tank (CAT) in the CAES charging operation mode. In the discharge mode, CAES also receives a compressed air generator from the CAT and converts it into electrical energy. Following this, the performance model of CAES is in the form of Eqs. (21)–(23)⁷. In Eqs. (21) and (22), the motor and generator capacity limits are included, respectively. In constraint (23), the limitation of energy stored in CAT is considered⁷. The TES performance model is presented in Eqs. (24)–(26)¹. Its mathematical model is the same as EES, with the difference that thermal power is used in Eqs. (24)–(26). Constraints (24) and (25) state the charge and discharge rate limit^40,41,42,43, respectively, then the thermal energy stored in TES is limited based on (26)⁴⁴. Finally, variables ϑ and μ represent Lagrange multipliers for equality and inequality equations, respectively.

5-min RT scheduling of EHs in the energy networks (second stage)

Unexpected outcomes in terms of active power may be found when weather conditions affect the output power production of power sources. As a consequence, the supply and demand balance may no longer be maintained for RT operation, indicating inadequate system flexibility^9,11. As a solution, the research underlines the utilization of flexibility sources, such as ESSs¹. Equations (27) minimize the unbalance profit of EHs in DA and RT markets⁴⁵. This equation presents the flexibility cost. A bi-level optimization framework frames the issue. The upper level objective function is provided in Eq. (27), and its constraints include the OPF restrictions on the energy networks are shown in (2)–(13). This statement is expressed in (28). Equations (29)–(30) are used in the lower-level model to determine EH’s profit in the RT market. The model provided by Eqs. (14)–(15) is analogous to the problem as described in these equations. Finally, it should be noted that minimization of the unbalance between RT and DA operations or flexibility cost based on Eq. (27) can achieve 100% flexible EHs in energy networks so that if F₃ is zero, it means that flexibility sources including storage systems in EH resolve the oscillation of RES active/heat power in RT operation compared to DA operation. Therefore, in both modes of operation, EHs will always have the same power. This equates to 100% EH adaptability across various networks. As a result, the EHs are more flexible the lower the F3 value. On the other hand, it is anticipated that by decreasing F3, the outcomes of the RT and DA procedures for EH would be comparable.

$$\min \,\,\,\,\,\,F_{3} = \sum\limits_{{\omega \in \Gamma_{S} }} {\sigma_{\omega } \sum\limits_{{\tau^{\prime} \in \Gamma_{{OH^{\prime}}} }} {\sum\limits_{{h \in \Gamma_{H} }} {\left( {\left( {\zeta_{{\tau^{\prime},\omega }}^{E} P_{{h,\tau^{\prime},\omega }}^{H} - \zeta_{{\tau^{\prime},\omega }}^{\prime E} P_{{h,\tau^{\prime},\omega }}^{\prime H} } \right)^{2} + \left( {\zeta_{{\tau^{\prime},\omega }}^{H} H_{{h,\tau^{\prime},\omega }}^{H} - \zeta_{{\tau^{\prime},\omega }}^{\prime H} H_{{h,\tau^{\prime},\omega }}^{\prime H} } \right)^{2} } \right)} } }$$

(27)

Subject to:

$${\text{Constraints }}\,\left( {2} \right) - \left( {{13}} \right)\,{\text{ considering}}\,\tau^{\prime}\,{\text{instead }}\,{\text{of}}\,\tau ,{\text{ and}}\,{\text{ using}}\, \, (.^{\prime}){\text{for}}\,{\text{ parameters }}\,{\text{and}}\,{\text{ variables}}$$

(28)

$$P^{{\prime H}} ,H^{{\prime H}} \in \arg \left\{ {\max \,\,\,\,\,\,F_{4} = \sum\limits_{{\omega \in \Gamma _{S} }} {\sigma _{\omega } \sum\limits_{{\tau ^{\prime} \in \Gamma _{{OH^{\prime}}} }} {\sum\limits_{{h \in \Gamma _{H} }} {\left( {\zeta _{{\tau ^{\prime},\omega }}^{{\prime E}} P_{{h,\tau ,\omega }}^{{\prime H}} + \zeta _{{\tau ^{\prime},\omega }}^{{\prime H}} H_{{h,\tau ,\omega }}^{{\prime H}} } \right)} } } } \right.$$

(29)

Subject to:

$${\text{Constraints }}\,\left( {{15}} \right) - \left( {{26}} \right)\,{\text{ considering}}\,\tau^{\prime}{\text{instead }}\,{\text{of}}\,\tau ,{\text{ and}}\,{\text{ using}}\, \, (.^{\prime}){\text{for}}\,{\text{ parameters }}\,{\text{and}}\,{\text{ variables}}$$

(30)

The frequency of phenomena is determined using prediction data. The pace of the aforementioned occurrences, and eventually the production of renewable energy, does not have a deterministic value and is associated by uncertainty since the forecast of a datum is accompanied by an error. This leads to different day-ahead and real-time operations of a system with renewable resources. Therefore, generation and consumption balance may not be established in real time operation. These conditions are corresponding to the flexibility lack of the system. Therefore, numerous studies, including⁴⁵, advise using storage devices or demand response strategies in addition to renewable sources. A CHP-based BU is part of an energy hub. The thermal power in a BU is a coefficient of the active power of the BU based on Eq. (17). This also leads to a decrease in the flexibility of the energy hub in the thermal sector. Thermal storage is used with BU to address this problem. These substances have the capacity to regulate their thermal power. They will thus be able to increase the thermal part of the energy hub’s flexibility. It should be noted that this issue will be comprehensible by providing an adequate formulation that considers the system’s adaptability. Equation (27) was used in this instance. If the value of F3 is zero, this equation predicts that real-time and day-ahead operations will provide results that are quite comparable. This issue corresponds to the conditions of high flexibility in the proposed system.

Uncertainty modeling

Uncertainty parameters of the problems (1)-(3) include energy price, ζ^E, ζ^H, ξ^E, and ξ^H, load, P^C, Q^C, and H^C; renewable power, P^WT and P^BU_. These uncertainties are modeled in this study in a stochastic framework using the UT method. This method needs fewer executions than Monte Carlo Simulation (MCS) and analytic methods, helping to reduce execution time. Additionally, this approach to modeling uncertainty does not need any assumptions. The UT approach also has the benefit of being able to handle nonlinear transitions^8,9 and accurately estimate the probability distribution function (PDF) while simplifying the coding procedure. The stochastic uncertainty parameters are likewise modeled using this way. Parameter n is the dimension of the vector of input uncertainty parameters (U). In this study, n = 9 is assumed. So, there are 2n + 1 = 19 scenarios, with n = 9. There is no necessity to decrease the number of scenarios in this methodology due to the limited number of scenarios. Further information regarding this methodology can be found in the publication referenced^8,9.

The execution step in these issues is minimal. Therefore, the real-time market execution stage in the suggested strategy takes roughly 5 min. As a result, it is essential to find a quick computational solution. The magnitude of the issue is one aspect that influences how long it takes to compute. This problem causes the problem’s volume to grow, which may require a lengthy calculation and fall short of the operator’s objectives. The worst-case scenario is the sole possible outcome for this approach. Since this technique has a scenario and produces a robust solution¹⁶, it is anticipated that it will take less time to solve the issue than stochastic optimization. However, it should be emphasized that the flexibility of the issue is also taken into account in the suggested approach based on Eq. (27). Analyzing various scenarios of renewable energy production is required to determine the precise condition of flexibility. As a result, robust optimization cannot appropriately assess the flexibility issue. This work applies the UT approach to account for the aforementioned circumstances. The stochastic optimization process used here has the fewest possible situations. As a result, it is anticipated to have a short computation time, and using this approach, the level of flexibility may be thoroughly examined.

Solution procedure

Single-level formulation

A bi-level formulation has been adopted to structure the problems (1)-(26) and (27)-(30). In conventional methods, a single-level model used to found an optimal solution⁴⁶. The current study incorporates the KKT method to realize this⁴⁶. The lower level must contain the lower level confined by the KKT technique in order to offer the single-objective modeling of the issue²³. In KKT model, The Lagrangian function (L) of the lower level, which is determined in Eqs. (14)-(15) or (29)-(30), equals the sum of its objective function and penalty functions^{47,48,49,50,51}. The penalty functions for constraints a ≤ b and a = b are given by μ.max(0, a—b) and ϑ.(b—a), respectively⁴⁶.

Constraints found by the KKT method are obtained by taking the derivative of the Lagrangian function with respect to its variables (P and H in model (14)-(26) or (29)-(30), μ, and ϑ) equal to zero⁴⁶. Equations (31)-(62) shows the single-level formula of the problem described by (1)-(26). The upper level is expressed using Eqs. (31)-(32). Constraints (33)-(41) is obtained by taking the derivative of the Lagrange function with respect to the primal variable of the lower level (P^H, H^H, P^Ge, P^Mo, P^EL, P^FC, H^CH, H^DCH) equal to zero. The equation $\frac{\partial L}{{\partial \vartheta }} = 0$ is used to form constraint (42), where it includes the equality constraints in the lower-level problem such as (15)-(17). The result of $\frac{\partial L}{{\partial \mu }} = 0$ (μ is the Lagrange multiplier of an inequality constraint, i.e., a ≤ b) is subject to two conditions, where constraint (43) is found concerning its first condition. Constraint (43) contains inequality limits (18)-(26). $\mu .\left( {a - b} \right) = 0$ is achieved according to the second condition. Equations (44)-(61) present the second condition of $\frac{\partial L}{{\partial \mu }} = 0$. Finally, Eq. (62) gives the boundary on Lagrange multipliers⁴⁶.

$$\min \,\,\,\,\,\,F_{1} = \sum\limits_{{\omega \in \Gamma_{S} }} {\sigma_{\omega } \sum\limits_{{\tau \in \Gamma_{OH} }} {\left\{ {\xi_{\tau ,\omega }^{E} P_{o,\tau ,\omega }^{S} + \xi_{\tau ,\omega }^{H} H_{o,\tau ,\omega }^{S} } \right\}} }$$

(31)

Subject to:

$${\text{Constraints }}\left( {2} \right) - \left( {{13}} \right)$$

(32)

$$\vartheta_{h,\tau ,\omega }^{P} = \sigma_{\omega } \zeta_{\tau ,\omega }^{E} :\frac{\partial L}{{\partial P_{h,\tau ,\omega }^{H} }} = 0$$

(33)

$$\vartheta_{h,\tau ,\omega }^{H} = \sigma_{\omega } \zeta_{\tau ,\omega }^{H} :\frac{\partial L}{{\partial H_{h,\tau ,\omega }^{H} }} = 0$$

(34)

$$\vartheta_{h,\tau ,\omega }^{bu} - \vartheta_{h,\tau ,\omega }^{H} = 0:\frac{\partial L}{{\partial H_{h,\tau ,\omega }^{BU} }} = 0$$

(35)

$$\overline{\mu }_{h,\tau ,\omega }^{ge} - \underline{\mu }_{h,\tau ,\omega }^{ge} - \vartheta_{h,\tau ,\omega }^{P} + \sum\limits_{t = \tau }^{24} {\frac{1}{{\eta^{Ge} }}\left( {\underline{\mu }_{h,t,\omega }^{cat} - \overline{\mu }_{h,t,\omega }^{cat} } \right)} = 0:\frac{\partial L}{{\partial P_{h,\tau ,\omega }^{Ge} }} = 0$$

(36)

$$\overline{\mu }_{h,\tau ,\omega }^{mo} - \underline{\mu }_{h,\tau ,\omega }^{mo} + \vartheta_{h,\tau ,\omega }^{P} + \sum\limits_{t = \tau }^{24} {\eta^{Mo} \left( {\overline{\mu }_{h,t,\omega }^{cat} - \underline{\mu }_{h,t,\omega }^{cat} } \right)} = 0:\frac{\partial L}{{\partial P_{h,\tau ,\omega }^{Mo} }} = 0$$

(37)

$$\overline{\mu }_{h,\tau ,\omega }^{fc} - \underline{\mu }_{h,\tau ,\omega }^{fc} - \vartheta_{h,\tau ,\omega }^{P} + \sum\limits_{t = \tau }^{24} {\frac{1}{{\eta^{FC} }}\left( {\underline{\mu }_{h,t,\omega }^{ht} - \overline{\mu }_{h,t,\omega }^{ht} } \right)} = 0:\frac{\partial L}{{\partial P_{h,\tau ,\omega }^{FC} }} = 0$$

(38)

$$\overline{\mu }_{h,\tau ,\omega }^{el} - \underline{\mu }_{h,\tau ,\omega }^{el} + \vartheta_{h,\tau ,\omega }^{P} + \sum\limits_{t = \tau }^{24} {\eta^{EL} \left( {\overline{\mu }_{h,t,\omega }^{ht} - \underline{\mu }_{h,t,\omega }^{ht} } \right)} = 0:\frac{\partial L}{{\partial P_{h,\tau ,\omega }^{EL} }} = 0$$

(39)

$$\overline{\mu }_{h,\tau ,\omega }^{dch} - \underline{\mu }_{h,\tau ,\omega }^{dch} - \vartheta_{h,\tau ,\omega }^{H} + \sum\limits_{t = \tau }^{24} {\frac{1}{{\eta^{DCH} }}\left( {\underline{\mu }_{h,t,\omega }^{t} - \overline{\mu }_{h,t,\omega }^{t} } \right)} = 0:\frac{\partial L}{{\partial H_{h,\tau ,\omega }^{DCH} }} = 0$$

(40)

$$\overline{\mu }_{h,\tau ,\omega }^{ch} - \underline{\mu }_{h,\tau ,\omega }^{ch} + \vartheta_{h,\tau ,\omega }^{H} + \sum\limits_{t = \tau }^{24} {\eta^{CH} \left( {\overline{\mu }_{h,t,\omega }^{t} - \underline{\mu }_{h,t,\omega }^{t} } \right)} = 0:\frac{\partial L}{{\partial H_{h,\tau ,\omega }^{CH} }} = 0$$

(41)

$${\text{Constraints }}\;\left( {{15}} \right) - \left( {{17}} \right):\frac{\partial L}{{\partial \vartheta }} = 0$$

(42)

$${\text{Constraints}}\; \, \left( {{18}} \right) - \left( {{26}} \right):{\text{ The}}\;{\text{ first }}\;{\text{condition }}\;{\text{of}}\frac{\partial L}{{\partial \mu }} = 0$$

(43)

$$P_{h,\tau ,\omega }^{EL} \underline{\mu }_{h,\tau ,\omega }^{el} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{el} }} = 0\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(44)

$$\left( {P_{h,\tau ,\omega }^{EL} - \,\chi_{h}^{EL} } \right)\overline{\mu }_{h,\tau ,\omega }^{el} = 0:\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{el} }} = 0\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(45)

$$P_{h,\tau ,\omega }^{FC} \underline{\mu }_{h,\tau ,\omega }^{fc} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{fc} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(46)

$$\left( {P_{h,\tau ,\omega }^{FC} - \chi_{h}^{FC} } \right)\overline{\mu }_{h,\tau ,\omega }^{fc} :\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{fc} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(47)

$$\left( {\underline{E}_{h}^{HT} - E_{h}^{HT} (0) - \sum\limits_{t = 1}^{\tau } {\left( {\eta^{EL} P_{h,t,\omega }^{EL} - \frac{1}{{\eta^{FC} }}P_{h,t,\omega }^{FC} } \right)} } \right)\underline{\mu }_{h,\tau ,\omega }^{ht} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{ht} }} = 0\,\,\,\,\,\,\forall h,\tau ,\omega$$

(48)

$$\left( {E_{h}^{HT} (0) + \sum\limits_{t = 1}^{\tau } {\left( {\eta^{EL} P_{h,t,\omega }^{EL} - \frac{1}{{\eta^{FC} }}P_{h,t,\omega }^{FC} } \right)} - \overline{E}_{h}^{HT} } \right)\overline{\mu }_{h,\tau ,\omega }^{ht} :\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{ht} }} = 0\,\,\,\,\,\,\forall h,\tau ,\omega$$

(49)

$$P_{h,\tau ,\omega }^{Mo} \underline{\mu }_{h,\tau ,\omega }^{mo} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{mo} }} = 0\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(50)

$$\left( {P_{h,\tau ,\omega }^{Mo} - \,\chi_{h}^{Mo} } \right)\overline{\mu }_{h,\tau ,\omega }^{mo} = 0:\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{mo} }} = 0\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(51)

$$P_{h,\tau ,\omega }^{Ge} \underline{\mu }_{h,\tau ,\omega }^{ge} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{ge} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(52)

$$\left( {P_{h,\tau ,\omega }^{Ge} - \,\chi_{h}^{Ge} } \right)\overline{\mu }_{h,\tau ,\omega }^{ge} = 0:\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{ge} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(53)

$$\left( {\underline{E}_{h}^{CAT} - E_{h}^{CAT} (0) - \sum\limits_{t = 1}^{\tau } {\left( {\eta^{Mo} P_{h,t,\omega }^{Mo} - \frac{1}{{\eta^{Ge} }}P_{h,t,\omega }^{Ge} } \right)} } \right)\underline{\mu }_{h,\tau ,\omega }^{cat} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{cat} }} = 0\,\,\,\,\,\,\forall h,\tau ,\omega$$

(54)

$$\left( {E_{h}^{CAT} (0) + \sum\limits_{t = 1}^{\tau } {\left( {\eta^{Mo} P_{h,t,\omega }^{Mo} - \frac{1}{{\eta^{Ge} }}P_{h,t,\omega }^{Ge} } \right)} - \overline{E}_{h}^{CAT} } \right)\overline{\mu }_{h,\tau ,\omega }^{cat} = 0:\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{cat} }} = 0\,\,\,\,\,\,\forall h,\tau ,\omega$$

(55)

$$H_{h,\tau ,\omega }^{CH} \underline{\mu }_{h,\tau ,\omega }^{ch} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{ch} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(56)

$$\left( {H_{h,\tau ,\omega }^{CH} - \,\chi_{h}^{CH} } \right)\overline{\mu }_{h,\tau ,\omega }^{ch} = 0:\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{ch} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(57)

$$H_{h,\tau ,\omega }^{DCH} \underline{\mu }_{h,\tau ,\omega }^{dch} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{dch} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(58)

$$\left( {H_{h,\tau ,\omega }^{DCH} - \,\chi_{h}^{DCH} } \right)\overline{\mu }_{h,\tau ,\omega }^{dch} = 0:\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{dch} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(59)

$$\left( {\underline{E}_{h}^{T} - E_{h}^{T} (0) - \sum\limits_{t = 1}^{\tau } {\left( {\eta^{CH} H_{h,t,\omega }^{CH} - \frac{1}{{\eta^{DCH} }}H_{h,t,\omega }^{DCH} } \right)} } \right)\underline{\mu }_{h,\tau ,\omega }^{t} = 0:\frac{\partial L}{{\partial \underline{\mu }_{h,\tau ,\omega }^{t} }} = 0\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(60)

$$\left( {E_{h}^{T} (0) + \sum\limits_{t = 1}^{\tau } {\left( {\eta^{CH} H_{h,t,\omega }^{CH} - \frac{1}{{\eta^{DCH} }}H_{h,t,\omega }^{DCH} } \right)} - \overline{E}_{h}^{T} } \right)\overline{\mu }_{h,\tau ,\omega }^{t} = 0:\frac{\partial L}{{\partial \overline{\mu }_{h,\tau ,\omega }^{t} }} = 0\,\,\,\,\,\,\,\forall h,\tau ,\omega$$

(61)

$$\vartheta \,{\text{ is}}\,{\text{a free}}\,{\text{variable,}}\,{\text{and }}\mu \,{\text{is}}\,{\text{a positive}}\,{\text{variable}}{.}$$

(62)

Eventually, based on “5-min RT scheduling of EHs in the energy networks (second stage)” section , the single-level model of the 5-min RT operation problem for the proposed scheme is described as follows:

$$\min \,\,\,\,\,\,F_{3} = \sum\limits_{{\omega \in \Gamma_{S} }} {\sigma_{\omega } \sum\limits_{{\tau^{\prime} \in \Gamma_{{OH^{\prime}}} }} {\sum\limits_{{h \in \Gamma_{H} }} {\left( {\left( {\zeta_{{\tau^{\prime},\omega }}^{E} P_{{h,\tau^{\prime},\omega }}^{H} - \zeta_{{\tau^{\prime},\omega }}^{\prime E} P_{{h,\tau^{\prime},\omega }}^{\prime H} } \right)^{2} + \left( {\zeta_{{\tau^{\prime},\omega }}^{H} H_{{h,\tau^{\prime},\omega }}^{H} - \zeta_{{\tau^{\prime},\omega }}^{\prime H} H_{{h,\tau^{\prime},\omega }}^{\prime H} } \right)^{2} } \right)} } }$$

(63)

Subject to:

$${\text{Constraint }}\left( {{28}} \right)$$

(64)

$${\text{Constraints }}\,\left( {{33}} \right) - \left( {{62}} \right)\,{\text{ considering}}\,\tau^{\prime}{\text{instead }}\,{\text{of}}\,\tau ,{\text{ and}}\,{\text{ using}}\, \, (.^{\prime}){\text{for}}\,{\text{ parameters }}\,{\text{and}}\,{\text{ variables}}$$

(65)

Solution method based on HEA

This paper uses a combined HBMO⁵² and ABC⁵³ algorithm and finds an optimal reliable solution. When more steps are required for updating decision variables in evolutionary algorithms⁵⁴, finding an optimal solution^{55,56,57,58,59} with a small standard deviation will be more likely, noting that two updating stages are used for decision variables, i.e. HMBO phase and ABC process. Decision and dependent variables are two types of variables used for the problem⁶⁰. The decision variables^61,62,63 include P^Ge, P^Mo, P^EL, P^FC,, H^DCH and H^CH, and other parameters are dependent variables^64,65,66. To solve the problem, the hybrid HBMO + ABC algorithm specifies N (size of the population) random values for decision variables based on (18)-(19), (21)-(22), (24)-(25). Dependent variables that include P^S, Q^S, H^S, P^L, Q^L, H^L, V, ϕ, T, P^H, H^H, H^BU, μ and ϑ are found by constraints (2)-(7), (33)-(42), and (44)-(62). To provide a solution to the constraints, the present study employs the Newton–Raphson method. Using these variables, the fitness function (FF) is found. The fitness function (66) is calculated by adding the objective function of the main problem (31) and the penalty function (PeF) of constraints (8)-(13), (20), (23) and (26)^67,68 associated with the operational constraints on energy networks (1i)-(1r), and ESSs energy limits. The penalty function for the constraint a ≤ b will be α.max (0, a − b), where α ≥ 0 shows the Lagrangian multipliers. α is assumed as decision variables. The penalty function at the optimal point is expected to be zero, meaning that the aforementioned constraints are met. Convergence conditions are assumed to be available after a known maximum number of iterations (iter_max). Eventually, the suggested solution method based on HBMO + ABC is described in Algorithm 1. Finally, to implement the proposed design for energy networks, a smart platform needs to be installed in these networks. This platform incudes smart algorithms and telecommunication devices^{69,70,71,72,73}.

$$FF = Eq.(31) + \sum {PeF\,of\,Eqs.\,(8) - (13),(20),(23),(26)}$$

(66)

Algorithm 1

Pseudocode of the hybrid HBMO + ABC algorithm to solve the proposed scheme.

Findings and discussion

Case study

In general, the proposed design model in the second section can be applied to various data from energy networks, renewable resources, and various storage devices. The system has a 9-bus electrical network and a 7-node thermal grid, as shown in Fig. 2⁸. One MVA and one MW serve as the base power for the electricity and heating networks, correspondingly. In addition to data on the energy networks⁸, also includes information on distribution lines and conduits. Peak electricity and heat demand data are provided in⁸. The load level during other hours is determined by multiplying load factor by peak load^{74,75,76,77,78}. Figure 3⁹ depicts the daily load factor curve for electricity and thermal networks. Bus 1 in the electrical network is a reference bus where the voltage amplitude is equal to 1 p.u. and the voltage angle is zero. Also, Node 1 in the thermal network is considered as a reference node, and the temperature in this node is 1 p.u. The limit of the temperature and voltage amplitude is in the range of [0.9, 1] p.u.^{79,80,81,82,83}. Electricity price during (1:00–7:00), (8:00–16:00, and 23:00–00:00) and (17:00–22:00) is 17.6, 26.4 $/MWh and 33 $/MWh. The price of heat between 1:00 and 4:00 and between 14:00 and 00:00 (5:00–15:00) is 22 (30) $/MWh⁹.

Fig. 2

The test system with EHs, (a) electrical network, (b) thermal grid⁸.

Fig. 3

Daily curve of load factor and active power produced by RESs⁹.

A system with 7 EHs is shown in Fig. 2. Only electrical equipment, such as WT, HS, and CAES, is present in EHs 1–3 and 5. CHP-based BU, CAES, and TES are located in other hubs. In hydrogen storage, HT has a capacity of 2.5 MW, and the amount of initial energy and the minimum energy that can be stored in it is 10% of the capacity of HT. This storage has EL and FC with a capacity of 1 MW, and their efficiency is 78% and 62%, respectively³⁸. In CAES, there is a 1 MW motor and generator, whose efficiency is set at 81%⁷. The maximum energy that can be stored in CAT, the initial energy, and the minimum energy that can be stored in it are 2.5 MWh, 0.25 MWh, and 0.25 MWh, respectively. In TES, the charging and discharging rate is 1 MW. The charging and discharging efficiency is assumed to be 80%, and its capacity is 2.5 MWh. Its initial and minimum energy is 10% of TES capacity¹. The turbine, thermal, and loss efficiency in CHP-based BU is 40%, 40%, and 8% respectively^1,9. The capacity of WT and BU is 0.5 MW and 0.5 MW, respectively. Figure 2 shows the EH installation locations inside the energy networks. The power generation rate times the size of the RESs can be used to calculate the RESs hourly active power generation^{84,85,86,87,88}. The amount of power generation for BU and WT for a day is shown in Fig. 3⁹.

Results

The problem was implemented in MATLAB software and the following results were found for different cases.

HEA convergence behavior

Different solvers are employed here, including differential evolution (DE)⁸⁹, sine cosine algorithm (SCA)⁹⁰, ABC, HBMO, and the HBMO + ABC algorithm so that the suggested management system is validated^52,53,89,90. To find statistical indices like the standard StD of the objective function (1), each algorithm is executed twenty times. Table 2 lists the results. In the final convergence iteration (4000th iteration), the hybrid HBMO + ABC algorithm provides the optimal solution (lowest F1 and F3 and maximum F2). According to Table 2, this algorithm converges rapidly and reaches the convergence point in 113.2 s on the 732nd iteration. However, the same parameters for other solvers required more than one thousand iterations and 125 s, respectively. The HBMO + ABC algorithm has a StD of 0.95%, as is the least amount amongst those of DE, SCA, ABC, and HBMO solvers. Correspondingly, a negligible dispersion is obtained in the response of the hybrid algorithm and it provides a roughly unique response. As per the findings, the hybrid HBMO + ABC algorithm quickly convergences, and needs fewer iterations, shorter processing time, and fewer unique response conditions, which corresponds to the fourth novelty in section I.D. To elucidate, from the perspective of network operators who are seeking optimal planning of power sources and ESSs, the utilization of HEA is a novelty because HEA ensures that a precise and efficient solution will be obtained, as outlined in Table 2.

Table 2 Results of different algorithms.

The problem under study is non-convex and conventional solvers find a local optimum solution for it. The hybrid HBMO + ABC algorithm achieves the optimal point compared to DE, SCA, ABC, and HBMO. As a result, it finds a suboptimal point. Furthermore, the suggested algorithm has a lower StD than its counterparts. As a result, it is better than the other solvers in coming up with original solutions. The distinct procedures used to update the variables used in decision-making, as well as the consideration of different arrangements and the merging of other algorithms, as indicated by the conditions mentioned, can be credited for the superiority of the HBMO + ABC algorithm over NHEAs for the problem under investigation.

In Table 2, the results are presented for two types of uncertainty modeling; in one case, the UT method is used, and in the other, the SBSO method is examined for different scenarios. In the SBSO method, MCS first produces a large number of scenarios. In each scenario, the amount of uncertainty is determined based on their mean and standard deviation values. Then, the normal probability function is used to calculate the probability of the selected uncertainty values. The probability of each generated scenario (σ⁰) is equal to the product of the probability of uncertainties in this scenario. Then Kantorovich method is selected as a scenario reduction technique, which applies those scenarios to the problem that have the least distance to each other. The details of this method are presented in⁹¹. Finally, the probability of each new scenario is equal to σ⁰ value of this scenario divided by the sum of σ⁰ for the selected scenarios. In this section, MCS produces 2000 scenarios. In Table 2, the results of the HBMO + ABC solver are presented for different number of scenarios obtained from the Kantorovich method. As can be seen, if the number of scenarios is low, the obtained solution is much more different than the results of UT, but in the case of high number of scenarios for SBSO, the obtained solution has a slight difference with the results of UT. In other words, the UT method has been able to obtain the reliable optimal solution with a low number of scenarios, but this is obtained for SBSO with a high number of scenarios. Following that, the computing time in UT is much lower than SBSO, which indicates the ability of the latest innovation in section I.D

Two-layer EMS potential in the energy networks with EHs

In this part, the potential and ability of three EMS models is presented on the energy networks that contain EHs.

• Uncoordinated model (UM) of generating units and storage systems in the two-layer EMS: In this method, operators separately control the generation units and ESSs. Thus, the problem described in “Incorporation of grid-connected EHs in energy markets” section is solved independently for each element of the EHs. Broadly speaking, to check the potential of the CHP-based BU, Eqs. (1)–(26) incorporate the model of CHP-based BU only and excludes the models of the rest of the equipment⁸⁰.

• Coordinated model (CM) of ESSs and generation units in a two-layer EMS: In this method, an EH is utilized to coordinate storage systems and generating units. Operators of EHs, who manage power sources and ESSs, collaborate with operators of the energy networks so that the second layer of the EMS is realized. The mathematical description is analogous to that of the problem described in “Incorporation of grid-connected EHs in energy markets” section.

• Coordinated model (CM) of generating units and ESSs in a single-layer EMS: In this situation, it is assumed that energy network operators coordinate the EHs’ equipment with one another. The modeling of this case in the DA operation consists of an objective function (1) and constraints of the problem given in Eqs. (2)–(13) and (15)–(26). Correspondingly, the objective function (14) is not included in the problem (1)–(26), and the rest of the equations structure a single-stage modeling. The same situation is considered in the description given by Eqs. (27)–(30).

Table 3 and Fig. 4 contain the results obtained. In the DA and RT energy markets, the CM method obtains profit of $402.31 and $404.09 for EHs, respectively. In the uncoordinated model, the unbalance function given by Eq. (27) between these markets is $27.18 (367.76 – 340.58), whereas in the coordinated model, it is reduced to $11.78. The difference between EHs’ profit in coordinated and uncoordinated models for DA and RT energy markets is $61.73 (402.31 – 340.58) and %46.33 (414.09 – 367.76). Comparing the CM approach with single- and two-layer EMS illustrates that profits of generation units and ESSs in the EH are not very different. Table 3 shows that this is negligible compared to the profit achieved in the markets. Nonetheless, the time spent to solve the problem for the single-layer EMS is approximately 62% ((183.1–113.2)/113.2) greater than that in the two-stage EMS. Also, in comparison to the single-layer EMS, the two-layer EMS can provide a model of the objectives of EHs within the objective function of the lower layer. Thus, according to Table 3 and the above discussion, the CM scheme for generation units and storage related to the two-layer EMS is better than other EMS models from economic and computational time aspects. When the two-layer EMS is implemented, EHs may benefit economically from a range of load levels (LLs), as shown in Fig. 4. Additionally, the amplitude of the imbalance function (27) within the aforementioned markets increases in proportion to the augmentation of the LL.

Table 3 EHs Profit in different EMS methods.

Fig. 4

The unbalanced condition between DA and RT energy markets for various load levels, (a) expected profit of EHs, (b) unbalanced function (F₃) value.

EHs operation

According to Fig. 5, which depicts the daily power curve for the market-integrated EHs, the CAESs and HSs are in the charging mode when the EHs create negative active power between 1:00 and 8:00. The cost of electricity is cheap at this season, resulting in increased profits for EHs. Electricity sources and ESSs inject electricity energy into the electrical network from 9:00 to 0:00 since power is positive during this period, providing more advantage. Due to the high cost of energy during the hours of 17:00–00:00, RESs inject power into the electrical grid. In the all hours, EHs inject heat power into the heating network (Fig. 5b). Due to the low price of heat power during 1:00–4:00 and 16:00–0.00, the TES is in charging mode. It injects heat power into the heating network together with the BU between the hours of 8:00 and 15:00 and 23:00 and 0:00 in order to increase profits for EHs.

Fig. 5

Daily curve of, (a) active power, (b) heat power of EHs in DA and RT energy markets for LL = 100%.

Figure 6 depicts the daily profit curve for EHs. The profitability is determined by the pricing of active and heat power. According to Fig. 5, the EHs experience a loss in the markets from 1:00 to 8:00 due to the low levels of active power and heat power. On the other hand, profit exhibits a positive trend during different periods. Additionally, there is a greater disparity between the DA and RT operations specifically between the hours of 12:00 and 15:00 in terms of active power and profit generated by EHs. The lack of power control in RESs leads to inaccuracies in predicting power output, resulting in an imbalance. As is seen in Fig. 3, RESs contribute a significant amount of power to the energy EHs. Consequently, the disparity between DA and RT operations is expected to be more pronounced during these specific hours compared to other periods. Additionally, Figs. 5b demonstrate that the distance between the scheduling of DA and RT remains constant throughout the entire operation period for the heat power of EHs.

Fig. 6

Daily profit curve of EHs in DA and RT energy markets for LL = 100%.

The energy networks operation

The values of the operation indices for electricity and heat networks are shown in Fig. 7. Two case studies—the power flow study (Case I) and the proposed design (Case II)—use various LL values for the two-layer EMS. Case I makes the assumption that there are no energy hubs linked to energy networks. But in Case II, the networks are linked to energy hubs, and their energy management is based on the definitions given in "Incorporation of grid-connected EHs in energy markets" and "Solution procedure" sections. Equation (1)'s predicted energy cost for the energy networks is shown in Fig. 7, together with the predicted energy loss (the discrepancy between the predicted energy supply and demand), maximum voltage drop (MVD), maximum temperature drop (MTD), maximum overvoltage (MOV), and maximum over-temperature (MOT) with regard to RT operation. As per Fig. 7a, the suggested scheme reduces the operation cost of the energy networks by roughly 18.3% ((4150—3390)/4150) during the increased load with LL = 130% compared to that in Case I. Also, the expected energy loss, MVD, and MTD values are reduced by about 20%, 27%, and 18% compared to Case I, as shown in Figs. 7b–c. The realization of these circumstances, as shown in Fig. 7d, however, requires a nearly 0.006 and 0.008 p.u. increase in MOV and MOT. These parameters are below their 0.1 p.u. (1.1—1) acceptable threshold. Due to a decrease in the energy demand of passive loads, these indices for a lower LL are more advantageous than in the scenario when LL = 130%. In other words, it should be noted that in Case II, with the increase in load level, the amount of energy consumed by passive loads increases; therefore, the amount of cost, energy loss, MVD, and MTD rises. Nevertheless, the amount of MOV and MOT decreases.

Fig. 7

Operation indices in the RT scheduling of the energy networks for various cases and values of LL, (a) operating cost of energy networks, (b) energy loss in energy networks, (c) maximum drop of voltage and temperature, (d) maximum overvoltage and over-temperature values.

Conclusion

This paper introduces a two-layer energy management framework for electrical and thermal smart grids integrated with storage-based renewable energy hubs. These hubs actively participate in both the day-ahead and real-time energy markets. The proposed scheme is structured as a two-stage optimization model. In the first stage, a bievel formulation is implemented. The upper level focuses on minimizing the energy costs of the networks while adhering to optimal power flow constraints. The lower level aims to maximize the profits of energy hubs in the day-ahead market by factoring in the operational dynamics of energy sources and storage systems. The second stage addresses a similar optimization problem; however, in this stage, the objective function for the upper level shifts to minimizing the flexibility costs. To simplify this nested structure, the KKT method is applied to derive a single-level model. Additionally, the UT method is employed to account for uncertainties in load demand, renewable power generation, and energy prices. For solving the model, a hybrid algorithm combining ABC and HBMO is deployed. Numerical results demonstrate that this hybrid solver outperforms non-hybrid algorithms by achieving more optimal solutions in shorter computational times with fewer convergence iterations. Moreover, this algorithm had a lower standard deviation, which was around 0.95%. This means that the mentioned algorithm almost has a unique solution. UT method compared to SBSO required a much lower number of scenarios, which resulted in reducing the calculation time. There are greater advantages when managing generating units and active demand together, or by employing an EH, than when managing both markets independently. It is shown that compared to the single-stage EMS model, the two-stage EMS design is more computationally efficient. The suggested solution efficiently reduces the flexibility cost. The suggested design demonstrates improvements in energy cost, energy loss, MVD, and MTD of 18%, 20%, 27%, and 18% above the results of power flow studies by taking into account the permitted limits for overvoltage, and over-temperature. This proposal was successful in securing very flexible circumstances for the suggested plan. In addition to gaining financial advantages from the energy market for sources and storage devices in the form of energy hubs, the suggested strategy also managed energy hubs to create a suitable technological and economic environment for energy networks.

The proposed plan does not consider the presence of electric vehicles. However, these vehicles provide their energy through connection to the power system. Therefore, they are new loads in the power system. This issue is considered as future work in the proposed plan. Demand side management also has significant potential in improving the economic and technical conditions of energy networks. The proposed plan is considered as future work by considering demand response. In the proposed plan, only the operational status of energy hubs in the energy market and various networks has been examined. However, hubs come with various resource and storage planning costs. In other words, there is a need to consider the costs of construction, maintenance, and operation of the hub in the proposed plan. This issue was considered as future work.