3E analysis of sCO₂ recuperator cycle with multi effect desalination and organic Rankine cycle to enhance environmental sustainability

Abstract

Supercritical carbon dioxide (sCO₂) is an effective working fluid in closed-loop power conversion cycles, offering significant advantages over traditional steam-based Rankine cycles. These cycles efficiently extract heat from sources such as gas turbine exhaust and industrial waste heat, converting it into usable power. This paper presents a novel approach to enhance the performance of the sCO₂ recuperator cycle by integrating multi-effect desalination (MED) and organic Rankine cycles (ORC). This integration aims to improve both thermal efficiency and operational stability of the sCO₂ cycle. The MED process utilizes waste heat from the sCO₂ cycle to produce fresh water, thereby enhancing overall system efficiency, while the ORC optimizes energy recovery from low-grade heat sources. Through a comprehensive analysis of thermodynamic performance and system integration, this study demonstrates significant improvements in the stability and efficiency of the sCO₂ cycle. Various configurations, including simple, recuperator, and split cycles, are examined, focusing on key parameters such as gas turbine outlet temperature, smoke flow rate, and maximum cycle pressure. Results indicate that the efficiencies of the recuperator cycle, recuperator cycle with MED, recuperator cycle with ORC, and recuperator cycle with MED & ORC cycles are 19.26%, 30.89%, 25.51%, and 24.27%, respectively. The study emphasizes minimizing exergy losses to enhance environmental sustainability, leading to increased exergy efficiency and reduced emissions. The stability index correlates with exergy efficiency, indicating that higher values reflect greater stability and lower pollution levels. The sustainability indices for the different configurations are also reported, demonstrating the potential for improved output power and energy efficiency. In conclusion, this study highlights that advancements in sCO₂ cycles and the implementation of various configurations significantly enhance energy efficiency and environmental sustainability, while reducing pollution. The integration of additional cycles, such as Organic Rankine Cycle and Multi-Effect Desalination, further contributes to these improvements.

Introduction

In an era where the demand for sustainable and efficient energy sources is para-mount, supercritical carbon dioxide (sCO₂) cycles have emerged as a promising technology for power generation and energy optimization. These cycles are renowned for their high efficiency and ability to effectively harness waste heat. However, fluctuations in operational conditions can adversely affect both the efficiency and stability of these systems. In contrast, gas turbine combined cycle power plants are recognized as a leading technology for electricity generation, offering superior efficiency through the integration of gas turbines with steam cycles, resulting in a reliable power generation system. The advantages of sCO₂ energy production and heat recovery systems over traditional steam-based systems are significant. These include reduced turbine dimensions, simplified primary heat recovery exchangers, and the elimination of water treatment systems, all of which contribute to lower capital and installation costs. This study explores the potential enhancement of gas turbine combined cycle systems by substituting the steam cycle with a novel system that employs supercritical carbon di-oxide (sCO₂) as the working fluid. Optimizing sCO₂ combined cycle systems is crucial for improving environmental sustainability and operational stability. By focusing on enhancing energy efficiency, improving exergy performance. This research addresses fundamental challenges in the field of sustainable energy. The use of supercritical carbon dioxide as a working fluid presents significant advantages over conventional Rankine cycles, particularly in terms of efficiency and cost-effectiveness. Furthermore, the integration of complementary technologies, such as multi-effect desalination (MED) and organic Rankine cycles (ORC), can substantially enhance the performance and stability of the sCO₂ cycle. This paper delves into this integration, examining its impact on the efficiency and stability of the sCO₂ cycle, ultimately contributing to the advancement of sustainable energy solutions.

Literature review

The history of the supercritical carbon dioxide (sCO₂) cycle spans over fifty years, beginning with a pivotal study by Fehr in 1967, which compared the critical conditions of various fluids in supercritical cycles¹. Among the key contributors to this field is Angelino, whose extensive research highlighted that conventional carbon dioxide cycles achieve higher efficiency than steam reheating cycles when turbine inlet temperatures exceed 650 degrees Celsius. His work demonstrated the advantages of sCO₂ cycles over Brayton and Rankine cycles, particularly in terms of their simplicity and enhanced efficiency². The high efficiency, compactness, and straightforward design of carbon dioxide cycles render them highly suitable for practical applications. A significant finding from Angelino’s research was the reduction in specific volume, which leads to lower compressor work requirements. Additionally, he identified the minimization of heat capacity differences as a critical factor in improving cycle efficiency. Notably, the smaller diameter of carbon dioxide turbine rotors, even at elevated speeds, results in a volumetric flow per unit of power that is approximately 30 to 50 times smaller than that of traditional heating cycles³. In 1971, Chermanne explored cycles featuring three compressors and two intercoolers, emphasizing their compactness and high efficiency, which make them particularly advantageous for the shipping industry by reducing fuel consumption⁴. In 1977, Combs pro-posed the application of these cycles in maritime contexts, focusing on the Fehr cycle and the recombination cycle, which also indicated reduced fuel consumption⁵. In 1997, Petr conducted comprehensive studies on supercritical carbon dioxide cycles and their applications in modern power plants, particularly the Brayton cycle and the supercritical carbon dioxide cycle with re-condensation. This research also investigated the effects of reheating on the efficiency of the recompression cycle⁶. Dostal designed a carbon di-oxide cycle with re-condensation for bismuth-lead-cooled reactors in 2001⁷. In the same year, he investigated the impact of pressure drops across various components on cycle efficiency, finding that one- and two-stage reheating could enhance efficiency by 1.2% and 0.46%, respectively. His study concluded that utilizing multiple reheating stages does not significantly improve cycle efficiency and is not cost-effective⁸. In 2006, Dostal further explored indirect power cycles for helium-cooled reactors, high-lighting the favorable outcomes of the Brayton cycle with re-condensation, the Brayton helium-nitrogen cycle, and supercritical steam cycles. His research indicated that one- and two-stage reheating systems are economically unviable⁹. In 2007, Zhang examined the solar heating cycle and supercritical carbon dioxide power generation, assessing the effects of atmospheric changes and various parameters on cycle performance¹⁰. Ishiyama’s 2008 study focused on power generation systems, including the gas turbine cycle, helium turbine cycle, and supercritical carbon dioxide turbine cycle¹¹. Moisseytsev’s research in 2009 analyzed various configurations of the supercritical carbon dioxide Brayton cycle for power generation in sodium-cooled reactors, emphasizing the advantages of supercritical cycles over traditional steam Rankine cycles, including improved efficiency, fewer components, smaller dimensions (especially in turbomachines), and a simpler design¹². In 2009, Sarkar conducted an exergy analysis and optimization of the supercritical carbon dioxide cycle, exploring the influence of parameters such as exergy and component irreversibility on cycle efficiency, optimal pressure ratios, and energy efficiency¹³. Yari’s 2010 research examined wasted heat in the supercritical carbon dioxide cycle precooler with re-condensation in the organic Rankine cycle using carbon dioxide fluid, demonstrating that the combined cycle’s efficiency is approximately 5–26% higher than that of the supercritical carbon dioxide cycle¹⁴. Jiangfeng et al. investigated the thermodynamic performance of supercritical carbon dioxide power cycle components for waste heat energy recovery in 2010, emphasizing the effects of turbine inlet temperature, pressure, and ambient temperature on cycle performance¹⁵. In 2012, Halimi et al. conducted a numerical analysis of the Brayton cycle of supercritical carbon dioxide as an energy producer, revealing an efficiency of 42.44% for the recompression cycle, with a 0.69% increase in efficiency when reheating was applied¹⁶. Pichel et al. performed a thermal analysis of the supercritical carbon dioxide power cycle in the same year, exploring various configurations of the cycle with re-condensation and comparing their efficiencies, which peaked at 43.31%, comparable to the Rankine cycle¹⁷. In 2016, Kim et al. studied supercritical carbon dioxide Rankine cycles aimed at recovering waste heat from turbine exhaust gas, exploring three distinct Rankine cycles—simple, cascade, and split—and revealing the effectiveness of waste heat recovery systems in maximizing power output¹⁸.

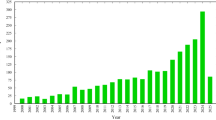
The growth of articles published after 2018 has shown a marked increase. Moreover, the topic of the supercritical carbon dioxide cycle has garnered considerable attention in recent years, alongside related cycles such as water desalination, organic Rankine cycles (ORC), geothermal energy, and solar energy. The supercritical carbon dioxide (sCO₂) technology has gained attention as an innovative method for power generation in recent decades. This technology is rapidly developing due to its unique characteristics, including high efficiency and reduced emissions. Figure 1 illustrates the growth of publications related to the term “sCO₂” from 2000 to 2025.

Fig. 1

The growth of articles related to the sCO₂ cycle between 2000 and 2025.

In 2019, Dhinest et al. investigated the thermal performance and economic analysis of the supercritical carbon dioxide cycle within a combined cycle power plant, scrutinizing maximum performance and electricity costs for five CO₂ cascade cycles¹⁹. In 2020, Eduardo et al. explored the supercritical carbon dioxide Brayton cycle utilizing geothermal sources, noting the potential of geothermal energy as a clean resource for electricity generation, particularly from high-temperature sources. The study examined four different cascades with geothermal sources, show-casing ongoing global efforts in supercritical carbon dioxide cycle research and development²⁰. Alongside this technology, water desalination through various methods, including multi-effect desalination (MED), has become increasingly important for providing fresh water in water-scarce regions. The organic Rankine cycle (ORC) has also emerged as an effective method for recovering energy from low-grade heat sources in recent years. Recent research has focused on optimizing energy systems through advanced analytical methods and innovative designs. Mohtaram et al. (2020) utilized multi-objective evolutionary optimization and 4E analysis to enhance the performance of a combined cycle power plant, emphasizing reductions in CO₂, CO, and NOx emissions while controlling costs²¹. Ahamad and Parvez (2023) introduced a novel solar-powered cogeneration system that employs a 4-E analysis for simultaneous electrical power and heating production, showcasing the potential of integrated renewable energy solutions²². Akram et al. (2022) conducted first and second law analyses of an Organic Rankine Cycle aimed at recovering waste heat from solar-operated combined cycle power plants, contributing valuable insights into efficiency improvements in hybrid systems²³. Further advancements are highlighted by Mohtaram et al. (2023), who proposed a thermodynamic analysis of waste heat utilization in a triple-pressure cogeneration cycle, demonstrating innovative applications of thermodynamic methods²⁴. Bani-Hani et al. (2023) explored the energy and exergy performance of a regenerative Brayton cycle using monochlorobiphenyl wastes as an alternative fuel, indicating the benefits of waste-to-energy approaches²⁵. Additionally, Mohtaram et al. (2023) enhanced the efficiency of ejector expansion systems and lithium bromide absorption refrigeration through transcritical CO₂ techniques²⁶. Aryanfar and Mohtaram (2024) analyzed the energy, exergy, and exergoeconomic aspects of a transcritical CO₂ cycle powered by geothermal energy, providing insights into operational efficiencies with and without economizers²⁷. Lastly, Lamagna et al. (2024) assessed and optimized single flash geothermal systems integrated with transcritical CO₂ cycles, highlighting the importance of scenario-based evaluations for sustainable energy recovery²⁸. Collectively, these studies underscore the ongoing efforts to improve energy efficiency and sustainability across various power generation technologies. In 2021, Omar et al. explored that Integrating a multi-effect distillation (MED) process with a concentrated solar power (CSP) plant can enable a sustainable solution to meet our global society’s increasing energy and freshwater demands. As such, this study can be considered a pioneering analysis of the potential of integrating a cascaded MED system with a supercritical CO2 (sCO2) cycle²⁹. In the same year, Song et al. proposed four configurations of combined SCO₂-ORC system for hybrid solar and geothermal power generation and performs detailed thermodynamic and economic assessments based on actual conditions in Seville, Spain³⁰. In recent years, significant advancements have been made in the optimization and application of supercritical carbon dioxide (sCO₂) cycles for power generation. Ahmadi and Zirak (2022) focused on enhancing the efficiency of the sCO₂ power generation cycle through comprehensive energy analysis, highlighting the cycle’s potential for improved performance³¹. Galledari and Ahmadi (2023) contributed to the thermal design aspects of a tube-shell recuperator within the sCO₂ cycle, which is crucial for maximizing heat recovery and overall system efficiency³². Furthermore, Moradi and Ahmadi (2023) explored the feasibility of integrating thermal desalination water into the sCO₂ power generation cycle, demonstrating that such integration can significantly increase the system’s efficiency³³. Collectively, these studies underscore the innovative approaches being taken to enhance the viability and efficiency of sCO₂ technologies in power generation and their potential applications in water desalination. In 2024, Tovar et al. showed that Solar energy as a thermal source has become a viable and thermo-sustainable option to generate heat, for the energy production through power cycle configurations³⁴. In 2024, Molière et al. demonstrated that supercritical CO₂ (sCO₂) cycles hold significant promise for electricity generation, outlining both their benefits and the challenges faced in industrial applications. They stress the necessity for additional engineering research and innovative designs to address the existing limitations in implementing this technology³⁵. In conclusion, the optimization of supercritical carbon dioxide combined cycle systems represents a significant step towards achieving environmental sustainability and stability in energy production. By addressing key challenges such as increasing energy efficiency, improving exergy performance, and reducing cycle costs, these systems have the potential to play a vital role in the transition towards sustainable energy practices on a global scale.

Research gap

While previous studies have thoroughly explored supercritical carbon dioxide (sCO₂) cycles, examining various analytical frameworks and their applications across different industrial sectors, a notable gap remains in the comprehensive assessment that combines energy, exergy, economic, and environmental sustainability analyses for various configurations. Additionally, the simultaneous impacts of integrating desalination cycles with organic fluids have not been sufficiently compared in the existing literature. This paper aims to address this gap by providing an in-depth and holistic analysis of these essential elements, thereby enhancing our understanding of the potential synergies and efficiencies that can be achieved through integrated systems.

Innovation

This research introduces a novel approach to integrating environmental sustainability within supercritical carbon dioxide (sCO₂) combined cycle systems. The primary objective is to mitigate environmental impacts by employing sustainable practices. A significant aspect of this study is its comprehensive optimization strategy, which not only boosts energy efficiency but also enhances exergy performance, leading to overall system improvement. The focus is on maximizing exergy efficiency while minimizing energy losses to optimize energy utilization. The originality of this work lies in its integrated methodology, which concurrently advances environmental sustainability and energy efficiency in sCO₂ combined cycle systems, making a substantial contribution to sustainable energy practices and the optimization of system performance.

Research methodology

This study employs a comprehensive and integrated methodology to address the existing gaps in supercritical carbon dioxide (sCO₂) cycles. The research begins with an extensive literature review to analyze previous studies on sCO₂ cycles and identify gaps in the integration of energy, exergy, and environmental sustainability, particularly concerning desalination processes. Following this, a comparative analysis will be conducted to evaluate different configurations of sCO₂ cycles, focusing on the integration of desalination processes with organic fluids. An important aspect of this research involves developing an innovative strategy to enhance energy efficiency and exergy performance, aimed at minimizing energy losses while maximizing overall system performance. A thorough sustainability assessment will also be conducted to evaluate the environmental impacts of the proposed integrated systems, ensuring that the suggested solutions align with sustainable energy practices. The results will be visually presented through infographics and charts to effectively summarize key insights, with Fig. 2 illustrating the sustainability analysis method employed in the project. Initially, this work will involve reviewing the existing literature and performing calculations related to thermodynamic relationships for energy, exergy, and sustainability analysis, followed by coding in the EES software. In this software, based on the data and assumptions presented in the paper, equations will be solved, and sensitivity analysis and optimization will be performed.

Fig. 2

Infographic illustrating the research methodology.

According to information provided by Foundry, achieving environmental sustainability depends on key factors such as optimizing the use of fossil fuels, eliminating waste, promoting recycling, recovering energy, saving time, and reducing pollution, all supported by the pillars of economic, social, and environmental development³⁶. Therefore, this structured methodology is designed to provide a better understanding of sCO₂ cycles and their integration with desalination processes and organic fluid cycles, contributing to advancements in sustainable energy practices and optimizing system performance.

System description

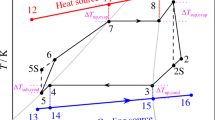
Supercritical carbon dioxide power generation cycles possess distinct characteristics that significantly influence their design and application. A key feature of this cycle is that the discharge pressure from the pump and the inlet pressure to the turbine are substantially higher than the critical pressure of 7.38 MPa. Under these conditions, the fluid transitions into a supercritical state, where it no longer exhibits distinct liquid and vapor phases. Figure 3 presents the phase transition diagram for carbon dioxide. Moreover, according to thermodynamic principles, when heat is added to the supercritical fluid, its temperature increases continuously. This contrasts with subcritical fluids, which maintain a constant temperature during the phase transition from liquid to vapor.

Fig. 3

The phase transition diagram of carbon dioxide.

Figure 4 compares the temperature changes based on the relative percentage of heat power for the combined steam cycle, the combined supercritical carbon dioxide cycle, and the organic Rankine cycle. In these cycles, heat transfer occurs in the gas turbine exhaust between gas (flue gas) and steam, toluene (an organic fluid), and supercritical carbon dioxide, respectively. This figure illustrates the advantages of supercritical carbon dioxide over other fluids under specific conditions. The superiority of supercritical carbon dioxide is evident, as steam and toluene undergo a phase change between 150 and 200 degrees Celsius, resulting in a portion of the heat power being utilized at a constant temperature for this phase transition. In contrast, supercritical carbon dioxide achieves the highest efficiency in heat transfer with flue gas, as indicated by the two parallel lines in the graph.

Fig. 4

Comparison of the thermal efficiency of CO₂ with other fluids.

One of the key advantages of supercritical carbon dioxide (sCO₂) power cycles is the compact physical size of the turbomachines, which is attributable to the high density of the working fluid and the low-pressure ratio of the cycle. This reduced size leads to lower costs, simpler turbomachine designs, and decreased installation expenses.

Advantages of carbon dioxide compared to other fluids

The use of supercritical carbon dioxide as a working fluid offers several significant benefits:

• Functional Simplicity: Carbon dioxide exhibits a favorable temperature range in its supercritical phase due to its moderate critical pressure characteristics.

• Cost-Effectiveness: The high density of supercritical carbon dioxide allows for a reduction in the size of cycle equipment. This not only lowers the construction costs of the equipment but also decreases the amount of fuel required.

• Optimal Placement and Layout: The high density of supercritical carbon dioxide enables the design of turbines and compressors with considerably smaller dimensions. This reduction in equipment size enhances the flexibility of equipment arrangements and minimizes the spatial requirements for the cycle.

• Favorable Physical and Thermodynamic Properties: Supercritical carbon dioxide is characterized by non-toxicity, thermal stability, and non-flammability, making it a safe option for various applications.

• Environmental Friendliness: The supercritical carbon dioxide cycle does not contribute to water pollution, thermal pollution, or the emission of greenhouse gases, making it an environmentally sustainable choice.

• High Efficiency: The supercritical carbon dioxide cycle achieves high efficiency at elevated operating temperatures, owing to the fluid’s high specific heat capacity near the critical point³⁷.

Cycle specification

The exhaust from the gas turbine acts as the primary heat source for the supercritical carbon dioxide (sCO₂) cycle, with a temperature of 489 °C and a mass flow rate of 89 kg/s. A pinch temperature of 30 °C is assumed, leading to a turbine inlet temperature of 459 °C for the carbon dioxide. To cool the carbon dioxide before it enters the pump, an air-cooled condenser is used, utilizing ambient air at 23 °C as the cooling medium, which allows for a maximum temperature rise of 20 °C. As a result, the inlet temperature to the pump is 28 °C, maintaining a 5 °C pinch temperature relative to the atmosphere. The surrounding air temperature of 23 °C reflects an average of both cold and hot seasons in the testing area. The isentropic efficiencies of the turbine and pump are assumed to be 90% and 80%, respectively. The pump increases the pressure of the carbon dioxide to 230 bar, a level chosen to ensure safe operating conditions within the pipeline. The carbon dioxide enters the pump as a saturated liquid. The minimum temperature at the heat recovery steam generator (HRSG), corresponding to the exit of the gas turbine exhaust, is set at 90 °C due to dew point constraints. Furthermore, pressure losses in all pipelines are not considered for this analysis.

Different cycle configurations and design inputs

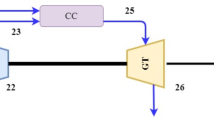
The supercritical carbon dioxide (sCO₂) cycle operates in conjunction with an industrial gas turbine, where the hot exhaust gases from the turbine serve as the heat source for the heat recovery steam generator (HRSG) of the sCO₂ cycle boiler. Figure 5 presents a schematic representation of the basic sCO₂ cycle. For this analysis, an average annual ambient temperature of 23 °C has been assumed, reflecting warm climate conditions. Consequently, the CO₂ pressure at the pump is approximately 69 bar (absolute), which aligns with the turbine outlet pressure, assuming no losses within the system. This configuration results in a turbine exit temperature of 326.8 °C, which must be subsequently cooled in a condenser. To enhance energy utilization, a recuperator has been incorporated into the cycle, as shown in Fig. 6. The recuperator reduces the load on the condenser and recovers some energy. Three distinct configurations are considered for the recuperator cycle. In one configuration, a multi-effect desalination (MED) cycle is integrated; in another, an organic Rankine cycle (ORC) is included. Finally, a more comprehensive configuration combines both the MED and ORC cycles with the sCO₂ recuperator cycle.

Cycle design procedure

The method of designing supercritical carbon dioxide cycles for increased stability and reduced pollution is described as follows:

sCO₂ simple cycle

Figure 5 illustrates the initial configuration of the simple supercritical carbon dioxide cycle. The thermodynamic properties at various nodes are provided in Table 1, taking into account the isentropic efficiencies of both the pump and the turbine. All calculations were conducted using EES software. The cycle has a mass flow rate of 67.44 kg/s, while the mass flow rate of the cooling air in the condenser is 1666 kg/s. Additionally, the mass flow rate of the turbine exhaust gases released through the stack is 89 kg/s. This simple cycle configuration exhibits an efficiency of 17.73%, indicating a relatively low cycle efficiency. Energy modeling has been performed separately for each component.

Table 1 sCO₂ simple cycle properties.

Fig. 5

Schematic of sCO₂ simple cycle.

Fig. 6

Schematic of sCO₂ recuperator cycle.

The governing energy equations are³⁸:

Turbine power and efficiency

$$\:{\dot{W}}_{T}=\dot{m}\left({h}_{in}-{h}_{out}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{1}-{h}_{2}\right)$$

(1)

$$\:{\eta }_{I,T}=\frac{\left({h}_{in}-{h}_{out}\right)}{\left({h}_{in}-{h}_{outs}\right)}=\frac{\left({h}_{1}-{h}_{2}\right)}{\left({h}_{1}-{h}_{2s}\right)}$$

(2)

Pump power and efficiency

$$\:{\dot{W}}_{P}=\dot{m}\left({h}_{out}-{h}_{in}\right)=\dot{{\dot{m}}_{{CO}_{2}}}\left({h}_{5}-{h}_{4}\right)$$

(3)

$$\:{\eta}_{I,P}=\frac{\left({h}_{outs}-{h}_{in}\right)}{\left({h}_{out}-{h}_{in}\right)}=\frac{\left({h}_{5s}-{h}_{4}\right)}{\left({h}_{5}-{h}_{4}\right)}$$

(4)

Condenser cold and hot sides

$$\:{Q}_{C,h}={\dot{m}}_{C,h}\times\:\left({h}_{C,h.in}-{h}_{C,h.out}\right)={\dot{m}}_{{co}_{2}}\times\:\left({h}_{3}-{h}_{4}\right)$$

(5)

$$\:{Q}_{C,c}={\dot{m}}_{C,c}\times\:\left({h}_{C,c.out}-{h}_{C,c.in}\right)={\dot{m}}_{Air}\times\:\left({h}_{12}-{h}_{11}\right)$$

(6)

Heat recovery steam generator (HRSG)

There is a large temperature changes of gas turbine smoke in the exhaust and HRSG, to consider the specific heat capacity changes, Eq. 7 is used at constant atmospheric air (smoke) pressure³⁹:

$$\:{{c}_{p}}_{g}=1.04841-3.8371\frac{{T}_{g}}{{10}^{4}}+9.4537\frac{{{T}_{g}}^{2}}{{10}^{7}}-5.49031\frac{{{T}_{g}}^{3}}{{10}^{10}}+7.9298\frac{{{T}_{g}}^{4}}{{10}^{14}}$$

(7)

Table 2 Specific heat capacity at constant pressure for smoke flow in the stack.

Table 2 gives specific heat capacity at constant pressure for smoke flow in the stack. As can be seen, the average value of the specific heat capacity at constant pressure is obtained by considering different temperature conditions of about 1.1 kJ/kg k, but in this study, due to the ease of calculations and based on reference⁴⁰, its value is 1.148 kJ/kg K.

Equation (8) to (11) represents the heat transfer for the hot and cold sides of HRSGs³⁸:

$$\:{Q}_{H1,h}={\dot{m}}_{H1,h}\left({h}_{H1,h.in}-{h}_{H1,h.out}\right)={\dot{m}}_{smoke}\:{{c}_{p}}_{g}\left({T}_{13}-{T}_{14}\right)$$

(8)

$$\:{Q}_{H1,c}={\dot{m}}_{H1,c}\left({h}_{H1,c.out}-{h}_{H1,c.in}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{1}-{h}_{8}\right)$$

(9)

$$\:{Q}_{H2,h}={\dot{m}}_{H2,h}\left({h}_{H2,h.in}-{h}_{H2,h.out}\right)={\dot{m}}_{smoke}\:{{c}_{p}}_{g}\left({T}_{14}-{T}_{15}\right)$$

(10)

$$\:{Q}_{H2,c}={\dot{m}}_{H2,c}\left({h}_{H2,c.out}-{h}_{H2,c.in}\right)=x\:{\dot{m}}_{{CO}_{2}}\left({h}_{10}-{h}_{9}\right)$$

(11)

sCO₂ recuperator cycle

In the second configuration, illustrated in Fig. 6, a recuperator is integrated into the cycle after the turbine. Table 3 provides the thermodynamic properties for this recuperator configuration. The cycle’s mass flow rate increases to 73.45 kg/s, while the mass flow rate of the condenser cooling air decreases to 1635 kg/s. The addition of the recuperator facilitates heat recovery, improving the cycle efficiency to 19.26%. This enhancement is primarily due to the increased temperature at Point 8, which raises the cycle mass flow rate and subsequently reduces the cooling air mass flow rate in the condenser.

Recuperator

Equations (12) and (13) represent the heat transfer for the hot and cold sides in the Recuperator³⁸:

$$\:{Q}_{R,h}={\dot{m}}_{R,h}\left({h}_{R,h.in}-{h}_{R,h.out}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{2}-{h}_{3}\right)$$

(12)

$$\:{Q}_{R,c}={\dot{m}}_{R,c}\left({h}_{R,c.out}-{h}_{R,c.in}\right)=\left(1-x\right)\:{\dot{m}}_{{CO}_{2}}\left({h}_{7}-{h}_{6}\right)$$

(13)

Table 3 sCO₂ recuperator cycle properties.

The development of the recuperator cycle is driven by the influence of the recuperator outlet temperature on various cycle parameters, particularly in relation to exhaust outlet temperatures. Figure 7 illustrates how the recuperator outlet temperature (T₈) affects the cycle parameters. For instance, at an exhaust outlet temperature of 90 degrees Celsius, T8 has a more limited permissible range. As depicted in Fig. 7a, the energy efficiency of the recuperator cycle remains independent of T8 across all exhaust outlet temperatures. The first law efficiency follows a consistent curve, indicating that the ratio of output power to input thermal energy (Q_in) stays constant. This constancy arises because output power depends on the mass flow rate of carbon dioxide, influenced by T₈, while Q_in is determined by h15. Figure 7b shows that the second law efficiency exceeds the first law efficiency, with higher second law efficiency observed at lower exhaust outlet temperatures. This occurs because minimizing exhaust temperature (just above the air dew point) allows for maximum utilization of input heat. In other words, for a given T₈, lower exhaust temperatures enhance exergy efficiency, while higher exhaust temperatures require an increase in T₈ to maintain constant efficiency.

Fig. 7

the effect of recuperator outlet temperature (T₈) on: (a) energy efficiency, (b) exergy efficiency, (c) exergy destruction.

Figure 7c highlights that exergy loss increases as exhaust temperature decreases, with maximum exergy loss occurring at an exhaust temperature of 90 degrees Celsius and minimum loss at 300 degrees Celsius. Notably, the maximum exergy loss state shows an improvement of approximately 10 megawatts compared to the minimum exhaust temperature state. This finding supports the integration of Organic Rankine Cycle (ORC) and Multi-Effect Distillation (MED) cycles with supercritical carbon dioxide cycles, which will be explored further.

sCO₂ recuperator cycle with MED

In the third configuration, illustrated in Fig. 8, a desalination cycle is integrated into the system within the exhaust path of the turbine, specifically between points 14 and 15. Table 4 provides the thermodynamic properties for this configuration. The mass flow rate of the cycle increases to 85.36 kg/s, while the mass flow rate of the cooling air in the condenser decreases to 1014 kg/s. The incorporation of this desalination cycle facilitates additional heat recovery through the recuperator, resulting in an increase in cycle efficiency to 30.89%. This enhancement is primarily due to the temperature rise at Point 8, which contributes to an increase in the cycle’s mass flow rate and, in turn, a reduction in the mass flow rate of the cooling air in the condenser.

Table 4 Thermodynamic properties for recuperator cycle with MED.

Fig. 8

Schematic of sCO₂ recuperator with MED.

sCO₂ recuperator cycle with ORC

In the fourth configuration, an organic fluid cycle is utilized instead of the desalination cycle, as illustrated in Fig. 9. The thermodynamic properties of this configuration are presented in Table 5. The mass flow rates of carbon dioxide and the cooling air in the condenser remain unchanged compared to the previous configuration. However, a new cycle has been added, featuring equipment such as a turbine, pump, and condenser related to the organic fluid, which can generate power and enhance the overall efficiency of the cycle. Therefore, as shown in Table 5, the overall efficiency of the cycle increases to 25.51%.

Table 5 Thermodynamic properties for recuperator cycle with ORC (R-123).

Fig. 9

Schematic of sCO₂ recuperator with ORC.

sCO₂ recuperator cycle with MED and ORC

In the fifth configuration, illustrated in Fig. 10, a desalination cycle and an organic fluid cycle are simultaneously integrated into the system in the exhaust path of the turbine, specifically between points 14 and 15. Table 6 presents the thermodynamic properties of this configuration. In this cycle, the mass flow rate of carbon dioxide and the cooling air in the condenser remain constant at 1014 kg/s. For the time being, we assume that the heat corresponding to the temperature range of 200 to 90 degrees Celsius is distributed equally, with part allocated to the desalination cycle and part to the organic fluid cycle. The subsequent sections of the paper will address various scenarios related to optimizing the heat recovery between the temperatures of 200 and 90 degrees Celsius.

Table 6 Thermodynamic properties for recuperator cycle with MED & ORC.

Fig. 10

Schematic of sCO₂ recuperator with MED & ORC.

The heat recovery, cycle efficiency, and system efficiency of sCO₂ cycles, as illustrated in Fig. 11, are as follows:

Fig. 11

Heat recovery, cycle and system efficiency of sCO₂ cycles based on T₁: (a) simple sCO₂ cycle, (b) recuperator sCO₂ cycle, (c) recuperator sCO₂ cycle with MED, (d) recuperator sCO₂ cycle with ORC, (e) recuperator sCO₂ cycle with MED & ORC.

Modeling of energy, exergy and environmental sustainability (3E)

Power generation facilities, including nuclear, thermal, hydropower, and solar plants, significantly impact the environment, often leading to pollution and ecological disruption. While electricity is essential for modern life, its production can harm the environment, necessitating strategies to mitigate these effects. Achieving sustainable development requires a focus on efficient resource utilization and the adoption of sustainable energy sources. Exergy methods are vital for improving efficiency, enabling society to maximize resource benefits while minimizing environmental degradation. Increased efficiency leads to reduced resource consumption and lessens the environmental burden of energy systems. The application of exergy techniques can enhance sustainable practices. According to Cornelissen, exergy analysis is crucial for sustainable development, as it quantifies the environmental impacts of emissions and resource scarcity. By reducing exergy destruction through effective fuel use, power plant systems can enhance sustainability. This section conducts an exergy analysis to evaluate system sustainability across a range of environmental temperatures from 25 °C to 45 °C, providing insights into performance and potential for reducing environmental impacts while improving energy efficiency³⁶.

Energy efficiency calculations

The general equation of Energy Balance for a Steady-Flow System is:

The cycle efficiency of the first law of thermodynamics is¹⁸:

$$\:{\eta}_{I}=\frac{{\dot{W}}_{Net}\:}{{\dot{Q}}_{in}\:}=\frac{{\dot{W}}_{T}-{\dot{W}}_{P}}{\sum\:_{i}{\dot{Q}}_{Hi}}$$

(14)

For the thermal efficiency of the cycle:

$$\:{\eta}_{CYC}=\frac{{\dot{W}}_{T}-{\dot{W}}_{P}}{\sum\:_{i}{\dot{Q}}_{Hi}}$$

(15)

The heat recovery efficiency of waste heat recovery (WHR) from a waste heat source can be defined as follows:

$$\:{\eta}_{HR}=\frac{\sum\:_{i}{\dot{Q}}_{Hi}}{{\sum\:_{i}{\dot{Q}}_{Hi}}_{max}}=\frac{\sum\:_{i}{{\dot{m}}_{smoke}\left({h}_{in}-{h}_{out}\right)}_{i}}{\sum\:_{i}{{\dot{m}}_{smoke}\left({h}_{in}-{h}_{0}\right)}_{i}}=\frac{\sum\:_{i}{\left({h}_{in}-{h}_{out}\right)}_{i}}{\sum\:_{i}{\left({h}_{in}-{h}_{surr}\right)}_{i}}$$

(16)

where Q_{H, max} is the maximum allowable heat rate from the waste heat source; The subscript 0 indicates that the properties are taken at the reference temperature and pressure (T₀, P₀) representing the dead state. The system thermal efficiency of the sCO₂ cycle for the waste heat recovery can be defined as the ratio of the net power to the maximum allowable heat rate from the waste heat source. This is expressed as follows:

$$\:{\eta}_{SYS}=\frac{{\dot{W}}_{T}-{\dot{W}}_{P}}{{\sum\:_{i}{\dot{Q}}_{Hi}}_{max}}$$

(17)

Exergy efficiency calculations

The general equation of Exergy Balance for a Steady-Flow System is^38,41:

$$\:\sum\:\left(1-\frac{{T}_{0}}{{T}_{k}}\right){\dot{Q}}_{k}-\dot{W}+\sum\:_{in}\dot{m}\psi -\sum\:_{out}\dot{m}\psi -{\dot{X}}_{des}=0$$

(18)

where:

$$\:\psi=\left(h-{h}_{0}\right)-{T}_{0}\left(s-{s}_{0}\right)$$

(19)

Turbine and pump

The exergy Balance for the turbine and pump:

$$\:{\dot{X}}_{des,T}={\dot{m}}_{{CO}_{2}}\left({\psi}_{1}-{\psi}_{2}\right)-{\dot{W}}_{T}$$

(20)

$$\:{\dot{X}}_{des,P}={\dot{m}}_{{CO}_{2}}\left({\psi}_{4}-{\psi}_{5}\right)+{\dot{W}}_{P}$$

(21)

Second law efficiency is calculated as shown:

$$\:{\eta}_{II,T}=\frac{{\dot{W}}_{out}}{{\dot{W}}_{rev,out}}=\frac{\left({h}_{1}-{h}_{2}\right)}{\left({\psi}_{1}-{\psi}_{2}\right)}=\frac{\left({h}_{1}-{h}_{2}\right)}{\left({h}_{1}-{h}_{2}\right)-{T}_{0}\left({s}_{1}-{s}_{2}\right)}$$

(22)

$$\:{\eta}_{II,P}=\frac{{\dot{W}}_{rev,in}}{{\dot{W}}_{in}}=\frac{\left({\psi}_{5}-{\psi}_{4}\right)}{\left({h}_{5}-{h}_{4}\right)}=\frac{\left({h}_{5}-{h}_{4}\right)-{T}_{0}\left({s}_{5}-{s}_{4}\right)}{\left({h}_{5}-{h}_{4}\right)}$$

(23)

Condenser

In the condenser, temperature $\:{T}_{k}\:\:\:$that gives $\:{\dot{Q}}_{k}\:\:$is equal to the ambient temperature. Therefore, the value of $\:\sum\:\left(1-\frac{{T}_{0}}{{T}_{k}}\right){\dot{Q}}_{k}$ is equal to zero. Therefore Eq. (24) shows the exergy Balance for the condenser:

$$\:{\dot{X}}_{des,C}={\dot{m}}_{{CO}_{2}}\left({\psi}_{3}-{\psi}_{4}\right)$$

(24)

The efficiency of the second law of thermodynamics for the condenser is calculated from Eq. (25):

$$\:{\eta}_{II,C}=\frac{{\dot{m}}_{cold}\:{\varDelta\:\psi}_{cold}}{{\dot{m}}_{hot}\:{\varDelta\:\psi}_{hot}}=\frac{{\dot{m}}_{air}\left({\psi}_{12}-{\psi}_{11}\right)}{{\dot{m}}_{{CO}_{2}}\left({\psi}_{3}-{\psi}_{4}\right)}=1-\frac{{\dot{X}}_{des,C}}{{\dot{m}}_{{CO}_{2}}\left({\psi}_{3}-{\psi}_{4}\right)}$$

(25)

Recuperator

In the recuperator, because both sides are in the cycle. Therefore, the value of $\:\sum\:\left(1-\frac{{T}_{0}}{{T}_{k}}\right){\dot{Q}}_{k}$ is zero. Therefore Eq. (26) shows the exergy Balance for the recuperator:

$$\:{\dot{X}}_{des,R}={\dot{m}}_{{CO}_{2}}\left({\psi}_{2}-{\psi}_{3}\right)+(1-x){\dot{m}}_{{CO}_{2}}\left({\psi}_{6}-{\psi}_{7}\right)$$

(26)

The efficiency of the second law of thermodynamics for the recuperator is calculated from Eq. (27):

$$\:{\eta}_{II,R}=\frac{{\dot{m}}_{cold}\:{\varDelta\:\psi}_{cold}}{{\dot{m}}_{hot}\:{\varDelta\:\psi}_{hot}}=\frac{\left(1-x\right)\left({\psi}_{7}-{\psi}_{6}\right)}{\left({\psi}_{2}-{\psi}_{3}\right)}=1-\frac{{\dot{X}}_{des,R}}{{\dot{m}}_{{CO}_{2}}\:\left({\psi}_{2}-{\psi}_{3}\right)}$$

(27)

Heat recovery steam generator (HRSG)

Equations (28) and (29) show the exergy Balance for the HRSGs:

$$\:{\dot{X}}_{des,H1}=\left(1-\frac{{T}_{0}}{{T}_{13}}\right){Q}_{H1\:\left(air\right)}+{\dot{m}}_{{co}_{2}}\left({\psi}_{8}-{\psi}_{1}\right)$$

(28)

$$\:{\dot{X}}_{des,H2}=\left(1-\frac{{T}_{0}}{{T}_{14}}\right){Q}_{H2\:\left(air\right)}+{\dot{m}}_{{co}_{2}}\left({\psi}_{9}-{\psi}_{10}\right)$$

(29)

The efficiency of the second law of thermodynamics for the HRSGs is calculated from Eqs. (30) and (31):

$$\:{\eta}_{II,H1}=\frac{{\dot{m}}_{cold}\:{\varDelta\:\psi}_{cold}}{{\dot{m}}_{hot}\:{\varDelta\:\psi}_{hot}}=\frac{{\dot{m}}_{{CO}_{2}}\left({\psi}_{1}-{\psi}_{8}\right)}{{\dot{m}}_{air}\left({\psi}_{13}-{\psi}_{14}\right)}=1-\frac{{\dot{X}}_{des,H1}}{{\dot{m}}_{air}\left({\psi}_{13}-{\psi}_{14}\right)}$$

(30)

$$\:{\eta}_{II,H2}=\frac{{\dot{m}}_{cold}\:{\varDelta\:\psi}_{cold}}{{\dot{m}}_{hot}\:{\varDelta\:\psi}_{hot}}=\frac{{\dot{xm}}_{{CO}_{2}}\left({\psi}_{10}-{\psi}_{9}\right)}{{\dot{m}}_{air}\left({\psi}_{14}-{\psi}_{15}\right)}=1-\frac{{\dot{X}}_{des,H2}}{{\dot{m}}_{air}\left({\psi}_{14}-{\psi}_{15}\right)}$$

(31)

Second law cycle efficiency

The cycle efficiency of the second law of thermodynamics is calculated from the lowing equation:

$$\:{\eta}_{II}=\frac{{\dot{\psi}}_{wanted}\:}{{\dot{\psi}}_{source}\:}=\frac{{\dot{\psi}}_{T}-{\dot{\psi}}_{P}}{{\dot{\psi}}_{H1}+{\dot{\psi}}_{H2}}$$

(32)

Sustainability calculations

For exploring the correlation between sustainability and environmental impact in contrast to exergy efficiency, Connelly and Koshland suggest using a depletion number (D_P) to characterize the efficiency of fossil fuel consumption³⁶:

$$\:{D}_{P}=\frac{{\dot{X}}_{d}}{{\psi}_{in}}$$

(33)

where $\:{\dot{X}}_{d}$ = exergy destruction and $\:{\psi}_{in}\:$= exergy input.

The relationship between exergy efficiency and the depletion number is as follows:

$$\:{\eta}_{II}=1-{D}_{P}$$

(34)

The relationship between the sustainability index (SI) and the depletion number is:

$$\:SI=\frac{1}{{D}_{P}}$$

(35)

The Depletion Number (D_P) and the Sustainability Index (SI) are two key metrics for evaluating the state of the environment and the impacts of human activities on natural resources. The Depletion Number serves as an environmental metric that measures the consumption of natural resources within a system or process, typically calculated as the ratio of resources consumed to the total available resources. This perspective helps us understand how and at what rate resources such as water, soil, and minerals are being depleted. For instance, in mining operations, the Depletion Number can indicate the amount extracted compared to the existing reserves. A high Depletion Number often signals the risk of resource depletion and poses a threat to ecosystems, potentially leading to environmental instability. On the other hand, the Sustainability Index is a comprehensive measure that assesses the sustainability of a system, project, or activity from environmental, social, and economic perspectives. This index is calculated based on several key factors, including energy consumption, waste generation, greenhouse gas emissions, and impacts on biodiversity and ecosystems. The Sustainability Index helps us understand the overall effects of an activity or system on the environment and identify strengths and weaknesses in natural resource management and environmental conservation. In practice, these metrics can be quantified numerically and are often derived from simulation models used to predict environmental impacts. Ultimately, utilizing the Depletion Number and the Sustainability Index allows us to gain a better understanding of environmental challenges and make informed decisions for the preservation of natural resources and the enhancement of environmental sustainability.

Result of energy, exergy and environmental sustainability (3E) analyses

The results of the energy and exergy analyses for the simple cycle, the recuperative cycle with organic fluid, and the recuperative cycle with desalination are detailed in Table 7. As previously mentioned, the isentropic efficiency of the turbine is measured at 90%, while the pump achieves an efficiency of 80%. The analysis reveals that the cycle efficiency for the simple cycle stands at 17.73%. In contrast, the recuperative cycle demonstrates an improved efficiency of 19.26%. Further enhancements are observed in the recuperative cycle with organic fluid, where the efficiency reaches 25.51%. The highest efficiency is recorded for the recuperative cycle with desalination, which achieves an impressive 30.89%. In terms of mass flow rates of carbon dioxide, the values for the respective cycles are 67.64 kg/s for the simple cycle, 73.45 kg/s for the recuperative cycle, and 85.36 kg/s for both the recuperative cycle with organic fluid and the recuperative cycle with desalination. Moreover, the second law efficiencies for these cycles are noteworthy, with values of 48.01%, 52.14%, 68.82%, and 73.07%, respectively. Despite the relatively high efficiencies of both the turbine and the pump, it is important to highlight that the exergy destruction occurring within the condenser and the heat recovery steam generators (HRSG) plays a significant role in diminishing the overall efficiencies of the cycles. This underscores the need for further optimization in these components to enhance the overall performance of the systems.

Table 7 Energy and exergy analysis of sCO₂ cycles (Simple, recuperator, recuperator with ORC, recuperator with MED).

The results of the sustainability and environmental analysis are presented in Table 8. As illustrated, the development of the supercritical carbon dioxide simple cycle has led to significant improvements in both stability and reductions in environmental pollution. Specifically, the depletion number serves as an indicator of environmental pollution, while the Sustainability index reflects the overall stability of the cycle. A decrease in the depletion number, coupled with an increase in the Sustainability index, is considered desirable for achieving a more sustainable system.

Table 8 Environmental sustainability analysis of sCO₂ cycles (Simple, recuperator, recuperator with ORC, recuperator with MED).

The sustainability index for the various cycles are as follows: 1.920 for the simple cycle, 2.090 for the recuperative cycle, 3.205 for the recuperative cycle with organic fluid, and 3.802 for the recuperative cycle with desalination. These values indicate a progressive enhancement in stability as the complexity of the cycle increases. Additionally, the depletion numbers for the same cycles are recorded as 0.520 for the simple cycle, 0.479 for the recuperative cycle, 0.312 for the recuperative cycle with organic fluid, and 0.263 for the recuperative cycle with desalination. A lower depletion number signifies a reduction in environmental pollution, which is a critical aspect of sustainability. In summary, a higher sustainability index indicates greater stability within the cycle, while a lower depletion number reflects a decrease in pollution levels. These findings underscore the importance of optimizing cycle designs to enhance both sustainability and environmental performance, ultimately contributing to more eco-friendly energy solutions. The following section delves into a comprehensive analysis of an integrated cycle that synergistically combines the supercritical carbon dioxide (sCO₂) recuperator cycle with an organic Rankine cycle (ORC) and a multi-effect desalination (MED). This innovative approach aims to optimize energy utilization and enhance the sustainability of the overall system. For the purpose of this analysis, we focus on a temperature range from 200 °C to 90 °C, which corresponds to the dew point of the exhaust gases from a gas turbine. To thoroughly evaluate the performance of this integrated system, we consider three distinct operational modes. one featuring equal temperature intervals and two employing unequal temperature intervals. These three modes give rise to a total of six scenarios, each of which will be discussed in detail in the following sections:

Scenario 1

In this scenario, we allocate energy within the temperature range of 200 °C to 90 °C. Specifically, energy is transferred from 200 °C to 145 °C for the organic fluid, while the remaining energy is directed from 145 °C to 90 °C for the thermal desalination process. This configuration allows for effective heat recovery and utilization in both the organic fluid cycle and the desalination system.

Scenario 2

Conversely, in Scenario 2, we adjust the energy allocation for the same temperature range. Here, energy is assigned from 200 °C to 145 °C for the desalinated water, while energy from 145 °C to 90 °C is utilized for the organic fluid. This reversal of energy flow highlights the flexibility of the integrated system in accommodating different operational priorities.

Scenario 3

Moving to Scenario 3, we again operate within the 200 °C to 90 °C temperature range, but this time we allocate energy from 200 °C to 170 °C for the organic fluid. The remaining energy is then directed from 170 °C to 90 °C for the thermal desalination process. This scenario emphasizes the potential for higher temperature utilization in the organic fluid cycle, which may enhance the overall efficiency of the system.

Scenario 4

In this scenario, we reverse the energy allocation approach once more. For the temperature range of 200 °C to 90 °C, energy is assigned from 200 °C to 170 °C for the desalinated water, while the energy from 170 °C to 90 °C is allocated for the organic fluid. This configuration allows us to explore the impacts of prioritizing desalination over the organic cycle.

Scenario 5

In Scenario 5, we focus on a lower temperature threshold within the same overall range. Here, energy is allocated from 200 °C to 110 °C for the organic fluid, with the subsequent energy directed from 110 °C to 90 °C for the desalinated water. This scenario examines the performance of the system when operating with lower temperature limits, which may be relevant for specific applications.

Scenario 6

Finally, in Scenario 6, we again allocate energy from 200 °C to 110 °C, but this time for the desalinated water, while energy from 110 °C to 90 °C is directed to the organic fluid. This arrangement allows for a thorough investigation of the system’s performance under varied operational conditions.

The results of comparing six scenarios are presented in Table 9.

Table 9 Thermodynamic properties for scenarios of simultaneous recuperator cycle with MED and ORC.

Following a thorough examination of the six scenarios, a comprehensive comparative analysis has been conducted, focusing on three key performance indicators: energy efficiency, exergy performance, and environmental sustainability, collectively referred to as the 3E framework. This extensive evaluation is designed to identify the optimal configuration of the integrated cycle, which ultimately aims to enhance energy utilization and promote environmental protection within multi-effect desalination (MED) and organic Rankine cycle (ORC). The results of this analysis are presented in Table 10.

Table 10 Environmental sustainability analysis of supercritical carbon dioxide cycles for recuperator cycle with MED and ORC.

These rankings indicate a clear trend: scenarios that operate at higher temperatures within the organic cycle demonstrate greater stability. In other words, the desalination cycle operates more effectively at lower temperatures, while the organic fluid cycle benefits from higher temperature conditions. This insight emphasizes the importance of optimizing the operational parameters of both cycles to enhance overall system performance and sustainability. By strategically aligning the temperature profiles of the multi-effect desalination and the organic Rankine cycle, we can achieve a more efficient and environmentally friendly integrated system.

Table 11 Thermodynamic properties for simultaneous recuperator cycle with MED and ORC.

Following the analysis and optimization of the supercritical carbon dioxide recuperator cycle, which has been integrated simultaneously with organic fluid cycles and thermal desalination processes, the focus has shifted to examining the impact of organic fluids on system performance. In this context, a detailed comparison is made among three specific organic fluids: R-123, R-245fa, and R-600. This comparative analysis aims to evaluate the thermodynamic properties and performance characteristics of each fluid within the integrated system. By assessing factors such as energy efficiency, heat transfer capabilities, and overall system stability, we can gain valuable insights into how these organic fluids contribute to the effectiveness of the cycle. To facilitate a comprehensive comparison of the effects of these three organic fluids, we have compiled a series of data and results that are presented in several tables. The thermodynamic properties of each fluid are detailed in Table 11, providing essential insights into their performance characteristics. Following this, Table 12 presents the results obtained from the energy analysis, highlighting the energy efficiency and utilization of each fluid within the integrated system.

Table 12 Energy analysis of simultaneous recuperator cycle with ORC.

Furthermore, Table 13 showcases the findings from the exergy analysis, which evaluates the quality of energy and the potential for work extraction from each fluid.

Table 13 Exergy analysis of simultaneous recuperator cycle with ORC.

Finally, Table 14 outlines the results of the environmental sustainability analysis, assessing the ecological impacts associated with the use of these organic fluids in the system.

Table 14 The impact of changing the type of organic fluid on environmental sustainability for recuperator cycle with ORC.

Together, these tables offer a comprehensive overview of the comparative performance of R-123, R-245fa, and R-600, enabling us to draw informed conclusions regarding their suitability for enhancing the efficiency and sustainability of the integrated thermal desalination and organic fluid cycles.

Sensitivity analysis

To conduct the sensitivity analysis, we consider parameters that can be controlled. These include the cycle’s upper pressure (P₁ or P_max) and turbine inlet temperature (TIT) The cycle’s lower pressure (P₂) is set to ensure that the pump’s inlet is a saturated liquid at the surrounding temperature. The following section will focus on the Pareto Chart related to the development of the supercritical carbon dioxide cycle and its impact on the analysis of energy, exergy, and environmental sustainability (3E).

Cycle upper pressure (P₁)

Fig 12 depict the effect of maximum cycle pressure on cycle parameters.

Figs. 12

Influence of cycle upper pressure (P₁) on: (a) energy efficiency, (b) exergy efficiency, (c) sustainability index..

As illustrated in Fig. 12a, the energy efficiency of all four cycles is significantly lower than that of the Carnot cycle. However, the recuperator cycles combined with the Organic Rankine Cycle and the multi-effect desalination (MED) cycle demonstrate higher efficiencies compared to the other two cycles. This improvement is primarily due to enhanced heat recovery in the recuperator cycle compared to the simple cycle, which boosts its efficiency. Similarly, the recuperator cycles with the Organic Rankine Cycle (ORC) and multi-effect desalination benefit from even greater heat recovery than the recuperator cycle alone, leading to further efficiency gains. While the efficiency of the Carnot cycle remains unaffected by turbine inlet pressure, increasing the maximum cycle pressure in supercritical carbon dioxide cycles enhances energy efficiency. This occurs because higher pressure increases the output work of the cycle while maintaining a constant input heat. Figure 12b illustrates the exergy efficiency, which behaves similarly to that of the first law, with the efficiency of the second law exceeding that of the first. Furthermore, as shown in Table 7, the greatest exergy losses in the cycles occur in the Heat Recovery Steam Generator (HRSG) and the condenser. Specifically, the total exergy losses are 17,702 kW for the simple cycle, 17,081 kW for the recuperator cycle, 18,710 kW for the recuperator with the Organic Rankine Cycle, and 8,935 kW for the recuperator with multi-effect desalination. These results indicate a reduction in exergy losses and an improvement in exergy efficiency as the cycles are developed. Figure 12c highlights the impact of increasing the maximum cycle pressure on the environmental sustainability of the cycle and environmental pollution. This figure demonstrates that the increase in stability and reduction in pollution for the recuperator cycles with multi-effect desalination (MED) and the Organic Rankine Cycle (ORC) are significantly greater than those observed in the other two cycles.

Turbine Inlet temperature (TIT)

Figure 13 illustrates the impact of turbine inlet temperature (TIT) on the parameters of the cycle

Fig. 13

Influence of turbine inlet temperature (TIT) on: (a) energy efficiency, (b) exergy efficiency, (c) sustainability index.

Figure 13a demonstrates that the efficiencies of all four cycles examined are significantly lower than that of the Carnot cycle, which serves as a theoretical benchmark for maximum efficiency. Among the cycles analyzed, the recuperator cycles that incorporate the Organic Rankine Cycle and multi-effect desalination exhibit superior efficiencies compared to the other two cycles. This improvement in efficiency can be primarily attributed to enhanced heat recovery mechanisms within the recuperator cycle. By effectively capturing and reusing waste heat, these cycles can operate more efficiently than simpler configurations. Moreover, the recuperator cycles that utilize the Organic Rankine Cycle and multi-effect desalination benefit from even more advanced heat recovery processes. This results in further enhancements in efficiency, showcasing the potential of integrating multiple technologies to optimize performance. It is important to note that while the efficiency of the Carnot cycle remains constant regardless of changes in turbine inlet temperature (TIT), increasing the TIT in supercritical carbon dioxide cycles significantly boosts energy efficiency. This is because higher inlet temperatures lead to increased output work from the cycle, all while keeping the input heat constant. Such an increase in TIT allows for better thermodynamic performance, making these cycles more effective in energy conversion. Figure 13b illustrates the concept of exergy efficiency, revealing that the efficiency derived from the second law of thermodynamics exceeds that of the first law. This finding underscores the importance of considering both energy and exergy when evaluating the performance of thermodynamic cycles. Additionally, as shown in Table 7, the most significant exergy losses occur within the Heat Recovery Steam Generator (HRSG) and the condenser. These results highlight the ongoing need to minimize exergy losses and enhance exergy efficiency as the cycles are further developed and optimized. Finally, Fig. 13c addresses the implications of increasing turbine inlet temperature on the environmental sustainability of the cycles and their associated pollution levels. The data indicate that the improvements in stability and reductions in environmental pollution for the recuperator cycles, particularly those integrated with thermal desalination and the Organic Rankine Cycle, are markedly greater than those observed in the other two cycles. This suggests that optimizing these cycles not only enhances their efficiency but also contributes positively to environmental outcomes, making them more sustainable options in energy production.

Pareto charts

The Pareto Chart is an effective analytical tool for data visualization and analysis, typically displayed as a bar chart. It enables the identification and prioritization of factors influencing a specific issue, allowing decision-makers to concentrate on the most significant contributors to a problem. This focus enhances problem-solving and resource allocation. In this study, three Pareto Charts are presented, each linked to a different objective function concerning the development of the supercritical carbon dioxide cycle. The relevant data for constructing these charts is provided in Table 15.

Table 15 Input data for the Pareto chart analyzing the impact of sCO2 type on energy efficiency, exergy, and environmental sustainability (3E).

Figure 14a illustrates the impact of the supercritical carbon dioxide cycle on energy efficiency, specifically reflecting the performance as defined by the first law of thermodynamics. This chart highlights the key factors influencing energy output and helps identify areas for potential improvement. Figure 14b demonstrates the effect of the supercritical carbon dioxide cycle on exergy efficiency, which is associated with the second law of thermodynamics. This chart provides insights into how effectively the system converts available energy into useful work, emphasizing the importance of minimizing exergy losses. Figure 14c and d depicts the influence of the supercritical carbon dioxide cycle on environmental sustainability, particularly in terms of pollution levels. This chart underscores the environmental implications of the cycle’s development, allowing stakeholders to assess its ecological impact and identify strategies for reducing emissions.

Fig. 14

Pareto chart for (3E): (a) energy efficiency, (b) exergy efficiency, (c) environmental sustainability, (d) environmental pollution.

Together, these Pareto Charts serve as a comprehensive framework for understanding the multifaceted effects of the supercritical carbon dioxide cycle, enabling researchers and engineers to prioritize their efforts in enhancing energy performance, optimizing exergy efficiency, and promoting environmental sustainability.

Conclusions

In conclusion, the supercritical carbon dioxide (sCO₂) power cycle demonstrates higher efficiency in recovering waste heat from gas turbines compared to the steam cycle, while maintaining simplicity and compactness. The energy efficiency of the simple sCO₂ cycle is 17.73%, but it experiences significant exergy losses, with the heat recovery steam generator (HRSG) accounting for 52.27% and the condenser for 43% of these losses. By expanding the cycle and incorporating a recuperator, the energy efficiency of the recuperator sCO₂ cycle increases by 1.53%, reaching 19.26%, while also reducing exergy losses to 49.09% for the HRSG and 38.38% for the condenser. The influence of the recuperator outlet temperature on various cycle parameters, along with the potential for enhanced utilization of exhaust heat, supports the integration of desalination cycles and organic fluid cycles with the recuperator cycle. The calculated exergy efficiencies for the simple cycle, recuperator cycle, recuperator cycle with organic fluid, recuperator cycle with desalination, and recuperator cycle with both organic fluid and desalination are 48.01%, 52.14%, 68.12%, 73.07%, and 70.87%, respectively. To improve exergy efficiency, modifications should focus on components with higher exergy losses. Sensitivity analysis indicates that the maximum cycle pressure has a greater impact on efficiency than the turbine inlet temperature. Sustainability analysis reveals sustainability indices of 1.92, 2.09, 3.03, 3.23, and 3.57 for the simple cycle, recuperator cycle, recuperator cycle with ORC, recuperator cycle with MED, and recuperator cycle with both ORC and MED, respectively, indicating that the development of supercritical carbon dioxide cycles contributes to environmental sustainability. Additionally, the depletion numbers for these cycles are 0.52, 0.479, 0.312, 0.263, and 0.291, respectively, suggesting that the advancement of supercritical carbon dioxide cycles aids in reducing environmental pollution. Overall, modifications to cycle components and the advancement of the recuperator cycle enhance both first and second law efficiencies and environmental sustainability. These changes must be managed effectively to ensure that technical and economic benefits are realized.