Prediction of loess collapsibility coefficient using bayesian optimized random forest model

Abstract

Accurately predicting the collapsibility coefficient of loess is crucial for mitigating the hazards associated with loess collapsibility in engineering projects, natural environment, and socio-economic activities. The traditional method for determining the collapsibility coefficient is time-consuming, labor-intensive, and expensive. In recent years, researchers have increasingly employed machine learning techniques to predict collapsibility coefficient and have obtained promising results. However, the process of hyperparameter optimization in previous studies was not sufficiently comprehensive, leading to suboptimal model performance. Therefore, in this study, Bayesian optimization was employed to fine-tune the hyperparameters of six different regressors, and the performance of these models was evaluated on both a training set and an independent testing set. The results demonstrated that the Random Forest-based model achieved the best performance, with R² values of 0.915 and 0.965 on the training and independent testing sets, respectively. These findings indicate that the proposed model is capable of reliably predicting the collapsibility coefficient of loess.

Introduction

Loess is a fundamental material widely used in engineering construction. However, it is susceptible to collapse when exposed to water. This vulnerability can result in substantial personal and property losses across national, societal, and individual levels¹. In recent decades, the study of loess collapsibility has garnered considerable academic attention. However, its underlying causes remain poorly understood due to their complexity². Although researchers have made notable progress, many aspects of loess collapsibility remain inadequately investigated. Loess subsidence is influenced by multiple factors, which can be broadly categorized into intrinsic and extrinsic factors. With respect to extrinsic factors, scholars worldwide have primarily focused on the formation and structural characteristics of loess, proposing various mechanisms and theories, including capillary action³, salt dissolution⁴, water film wedging⁵, and pressure theory⁶. Further studies have examined alterations in its physicochemical properties and internal microstructure in response to varying moisture content. Regarding intrinsic factors, researchers primarily examine loess collapsibility through the framework of spatial structural mechanics theory^7,8.

To evaluate the collapsibility of loess, laboratory compression and in-situ immersion tests are commonly employed to determine the collapsibility coefficient^9,10. During this process, loess samples are typically collected from various depths within the construction site and subsequently measured using single-line or double-line testing methods. However, the testing process is complex, time-consuming, and labor-intensive. Additionally, factors such as sample heterogeneity, equipment precision, and operator expertise may compromise the reliability of the test results. To enhance resource efficiency, researchers have investigated the relationship between the collapsibility coefficient of loess and its essential physical parameters, with the aim of estimating the collapsibility coefficient based on stable, quantifiable physical factors¹¹.

Machine learning not only reduces the need for time-consuming and expensive experiments, but also facilitates large-scale detection, rendering it a vital tool for future analyses of loess collapsibility. Researchers have conducted extensive studies aimed at predicting the collapsibility coefficient of loess using various machine learning algorithms. For instance, Chen et al. proposed a multiple linear regression model to predict the collapsibility coefficient of loess in Xinyuan County. This method explicitly represents the relationship between the collapsibility coefficient and its influencing factors. However, its predictive performance is limited. To address this issue, they also introduced a radial basis function (RBF) model for predicting the collapsibility coefficient¹². Zhao et al. classified the degree of loess collapsibility in Xining and proposed a support vector machine (SVM) model based on statistical learning methods. However, compared to the Random Forest-based model, the SVM-based model exhibits inferior predictive accuracy, and its black-box nature limits interpretability¹³. Motameni et al. introduced a multi-layer perceptron neural network (MLPNN) to predict the collapsibility coefficient of loess. However, this model is also a black box and is prone to entrapment in local minima¹⁴. Furthermore, Zhu et al. demonstrated that models based on ensemble learning, such as Random Forest (RF), achieve high predictive accuracy and offer superior interpretability.

Despite these advancements, many studies have inadequately addressed the issue of model optimization. Among the few that tackle this challenge, researchers have employed Genetic Algorithms (GA) to optimize RF and Support Vector Regression (SVR)¹¹, while Wei et al. utilized Particle Swarm Optimization (PSO) to optimize backpropagation (BP) neural networks¹⁵. However, the process of hyperparameter optimization in these studies lacked thoroughness, resulting in suboptimal model performance. Notably, model optimization is an inherently complex task that requires careful consideration of several factors, including the choice of optimization algorithm, the specific parameters being tuned, the data used for training and validation, and the model architecture. Therefore, achieving optimal model performance necessitates a systematic and rigorous approach to optimization.

Compared with GA, Bayesian optimization typically finds better approximate optimal solutions within fewer iterations due to its use of probabilistic models and Bayesian inference techniques, enabling more efficient exploration of the solution space with fewer evaluations. In contrast to PSO, which updates the search space based on particle velocity and position updates, Bayesian optimization offers greater flexibility in balancing the trade-off between exploration and exploitation¹⁶. Therefore, this study aims to predict the collapsibility coefficient of loess by integrating Bayesian optimization with machine learning methods. Initially, the collected experimental data on loess collapsibility were preprocessed. Subsequently, six machine learning models were developed, including Decision Tree, Ridge, RF, SVR, Light Gradient Boosting Machine (LGBM), and eXtreme Gradient Boosting (xGBoost). Each model underwent comprehensive parameter optimization using Bayesian optimization. Five-fold cross-validation was performed on the training dataset, followed by evaluation on an independent test dataset. Ultimately, the RF-based model demonstrated the highest predictive performance, with an R² value reaching 0.965. These results suggest that the proposed model can reliably predict the collapsibility coefficient of loess.

Methods

Dataset construction

Northwestern provinces and regions of China, such as Xinjiang and Gansu, as well as southwestern provinces including Yunnan and Tibet, contain extensive loess deposits¹⁷. The Ili River Valley, located in the northwest of Xinjiang, China, is a depressed zone within the Mesozoic–Cenozoic belt of the Tianshan Fold Belt. Due to its unique geological and geomorphic factors, the loess found in this region differs significantly from that on the Loess Plateau, being more purely of aeolian origin. The experimental data for this study were derived from a dedicated investigation into the evaluation of collapsible loess foundations in the diversion channel of the Akdala Hydropower Station project on the Tekes River in Ili, Xinjiang (Fig. 1(a-b)). To examine the effects of moisture content and dry density on loess collapsibility, a series of collapsibility experiments were conducted on remolded loess using a triple consolidation apparatus under varying moisture and density conditions (Fig. 1(c)). The experiments followed the double-line method, and soil materials used were collected from depths ranging between 1 and 7 m using the pressure sampling method. The initial moisture content was the natural value, and test samples were categorized into six groups (6.3%, 9.2%, 12.2%, 15.3%, 18.6%, and 21.3%). The dry density was set to eight distinct levels (1.24, 1.27, 1.31, 1.35, 1.39, 1.43, 1.47, and 1.55 g/cm³). This resulted in a total of 47 experimental combinations. However, the sample with a moisture content of 21.3% and a dry density of 1.24 g/cm³ failed to form properly. Ultimately, a total of 235 valid samples were obtained using this experimental design.

Fig. 1

Sample collection and experimental equipment. (a) On-site exploratory well, (b) Soil sample, (c) Triple consolidation apparatus.

Factor correlation analysis and normalization

Correlation analysis has been widely used to examine the strength and direction of associations among different factors^18,19,20. To further explore the relationships between the factors in this study, we calculated the correlation coefficients among key influencing factors (Fig. 2). The correlation coefficient between moisture content and the collapsibility coefficient is −0.14, suggesting that higher moisture content slightly reduces collapsibility. This may be because elevated moisture levels cause the soil to approach a saturated state, where increased pore-water pressure reduces the effective stress exerted by external loads. The correlation coefficient between the collapsibility coefficient and dry density is −0.6. This negative correlation can be attributed to the fact that soils with higher dry density have more tightly packed particles, leading to low porosity. As a result, when water infiltrates such soils, their structure remains more stable and is less prone to collapsible deformation. The correlation coefficient between pressure and the collapsibility coefficient is 0.5, indicating that higher pressure leads to more pronounced collapsibility.

Fig. 2

Correlation coefficient matrix of different factors, where DD represents dry density and CC represents correlation coefficient.

The experimental variables have differing units and magnitudes, leading to significant discrepancies among them. As a result, directly using raw data in modeling may cause the model to converge to local minima. To mitigate this issue and reduce potential model bias, the raw data must be normalized prior to training. In this study, the Min-Max method was employed for normalization²¹. This widely used technique linearly scales the original data to a fixed range, typically [0, 1]. The formula is as follows:

$$\:{x}_{norm}=\frac{{x}_{i}-{x}_{min}}{{x}_{max}-{x}_{min}}$$

(1)

Where: $\:{x}_{i}\:$is the original data to be normalized, $\:{x}_{norm}$ is the normalized data; $\:{x}_{min}$ is the minimum value in each column of the factor set, and $\:{x}_{max}\:$is the maximum value in each column of the factor set. This method ensures that the distribution of the original data is preserved after normalization, with only the data range being transformed. The samples were then divided into a training dataset and an independent testing dataset using an 80:20 split to construct the collapsibility coefficient prediction model, where the 80% training dataset helps prevent overfitting, and the 20% testing dataset provides a rigorous evaluation of model performance.

Classification and regression trees

The Classification and Regression Trees (CART) algorithm can handle both continuous and discrete factors with each node having at most two child nodes²². When the sample variable factors are discrete, the resulting decision tree is a classifier; when the sample variable factors are continuous, the resulting decision tree is a regressor. In this study, the loess collapsibility dataset can be represented as $\:\text{D}=\left\{\left({x}_{1},{y}_{1}\right),\left({x}_{2},{y}_{2}\right),\dots\:,\left({x}_{n},{y}_{n}\right)\right\}$, where $\:{x}_{i}$ represents the sample vector composed of detection factors for each sample, and $\:{y}_{i}$ represents the collapsibility coefficient value of each sample. By arranging the values of different factors $\:A$ in ascending order and using the median as the splitting point $\:t$ for each factor, the dataset $\:\text{D}$ can be divided into two subsets $\:{D}_{1}$​ and $\:{D}_{2}$​ for a particular factor $\:A$ and splitting point $\:t$. The mean squared error ($\:MSE$) after splitting is calculated as follows:

$$\:{MSE}_{split}\left(D,A,t\right)=\frac{{|D}_{1}|}{\left|D\right|}MSE\left({D}_{1}\right)+\frac{{|D}_{2}|}{\left|D\right|}MSE\left({D}_{2}\right)$$

(2)

Where $\:{|D}_{1}|$ and $\:{|D}_{2}|$ denote the sample sizes of subsets $\:{D}_{1}$​ and $\:{D}_{2}$​, respectively, while $\:\left|D\right|$ represents the total sample size of the dataset $\:D$. $\:MSE\left({D}_{i}\right)$ is the mean squared error between the observed and predicted collapsibility coefficients for all samples in subset $\:{D}_{i}$. The feature and splitting point that minimize the $\:MSE$ value after node splitting are selected as the optimal split. This process is recursively applied to each subset until a stopping criterion is satisfied. Additionally, pruning can be employed to enhance the model’s generalization performance.

Random forest

RF is an ensemble model constructed from CART²³. During the process of building a RF-based model, the method employs bootstrap sampling to sample the training dataset with replacement $\:\text{n}$ times, forming a new training dataset. This process is repeated $\:\text{K}$ times, corresponding to the number of decision trees to be constructed, generating $\:\text{K}$ different training datasets. Additionally, when building each CART, $\:\text{K}$ factors are randomly selected from all factors for node splitting, and out-of-bag data is used for performance evaluation. For the task of predicting loess collapsibility coefficients, each decision tree predicts the collapsibility coefficient for each sample. The final prediction of the RF-based regressor can be expressed as:

$$\:\widehat{y}\left(x\right)=\frac{1}{K}\sum_{k=1}^{K}{\widehat{y}}_{b}\left(x\right)$$

(3)

Implementation of other types of regressors

In addition to the Decision Tree and RF, Ridge, SVR, LGBM, and xGBoost were also developed in this study using Python. Among these, Ridge is a linear model²⁴, SVR is a statistical machine learning model based on the maximum margin principle²⁵, and LGBM and xGBoost are ensemble learning models^26,27. To ensure a fair comparison, Bayesian optimization was employed to tune the hyperparameters of these models using the same training dataset, with the parameters detailed in Table 1.

Table 1 The optimal hyperparameters for different regressors.

Bayesian optimization of different regressors

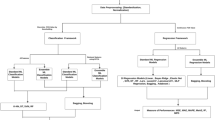
Bayesian optimization approximates the objective function using a surrogate model and then employs an acquisition function to select the next set of hyperparameters²⁸. Compared to grid search and random search, Bayesian optimization explores the hyperparameter space more efficiently, particularly when the space is large and the influence of hyperparameters on model performance is complex. This efficiency arises by utilizing prior evaluation outcomes to guide subsequent searches. To determine the optimal structure of various regressors and enhance the prediction accuracy of the loess collapsibility coefficient, Gaussian process regression was applied to approximate the $\:MSE$ function for each regressor. As shown in Fig. 3, the main steps are as follows:

Step 1: First, determine the hyperparameters for models such as Decision Tree, Ridge, RF, SVR, LGBM, and xGBoost. For each hyperparameter, define its search space, as shown in Table 1. For example, when optimizing the hyperparameters of an RF-based regressor, the search ranges for n_estimators, max_depth, min_samples_leaf, and min_samples_split are set to (10, 200), (3, 15), (1, 10), and (2, 20), respectively. Through Bayesian optimization, the goal is to identify the hyperparameters that minimize the $\:MSE$ value between the actual and predicted values of the collapsibility coefficient. This can be expressed as

$$\:{h}^{*}=arg\:\underset{h\in H}{\text{min}}\:MSE\left(h\right)$$

(4)

Where $\:{h}^{\text{*}}$ represents the optimal set of hyperparameters that minimizes the $\:MSE$ value of the model. $\:H$ denotes the defined search space for the hyperparameters, which includes all possible combinations of hyperparameter values within their search ranges. $\:MSE\left(h\right)$ refers to the mean squared error of the model when trained with a specific set of hyperparameters $\:h$.

For different regressors, we initialized their hyperparameters based on empirical values, and then we computed the corresponding $\:MSE$ on the training dataset using cross-validation. This process was repeated for multiple initializations to create a dataset of $\:({h}_{sample},{MSE}_{sample})$ pairs, which serves as the starting point for bayesian optimization.

Step 2: Assume that the mean squared error between the actual and predicted values of the collapsibility coefficient$\:\:MSE\left(h\right)$ follows a Gaussian process (GP)²⁹. This can be expressed as.

$$\:MSE\left(h\right)\sim GP\left(m\left(h\right),k(h,h^{\prime})\right)$$

(5)

Where $\:m\left(h\right)$ denotes the mean function of the Gaussian process, which is typically set to zero after standardizing the input hyperparameters. $\:k(h,h^{\prime})$ refers to the covariance function (kernel function) that measures the similarity between two sets of hyperparameters $\:h$ and $\:h^{\prime}$. Using the paired data points ​$\:({h}_{sample},{MSE}_{sample})$, we train a Gaussian process regression model to approximate the objective function $\:MSE\left(h\right).$

Step 3: Select the optimal hyperparameters for different regressors based on the acquisition function. After modeling the objective function using a Gaussian process, we evaluate the sampling points. During this process, the model may tend to sample around local optima, preventing it from finding the global optimum. The acquisition function effectively balances exploration and exploitation, enabling efficient sampling. In this study, the acquisition function $\:EI\left(h\right)$ is defined as

$$\:EI\left(h\right)=\left(\mu\left(h\right)-MSE\left({h}^{+}\right)-\xi\:\right){\varnothing}\left(\text{Z}\right)+{\upsigma\:}\left(h\right){\phi}\left(\text{Z}\right)$$

(6)

Where $\:\mu\:\left(h\right)$ represents the mean predicted by the Gaussian process for the hyperparameters $\:h$. $\:MSE\left({h}^{+}\right)$ denotes the best performance value (minimum mean squared error) observed so far during the optimization process. $\:\xi\:$ is a parameter that balances exploration and exploitation. $\:{\upsigma\:}\left(h\right)$ represents the standard deviation predicted by the Gaussian process for the hyperparameters $\:h.$ $\:\text{Z}$ can be calculated using the formula $\:\text{Z}=\frac{\mu\:\left(h\right)-MSE\left({h}^{+}\right)-\xi\:}{{\upsigma\:}\left(h\right)}$. $\:{\varnothing}\left(\text{Z}\right)$ is the cumulative distribution function of the standard normal distribution. $\:{\phi}\left(\text{Z}\right)$ stands for the probability density function of the standard normal distribution.

Step 4: The optimal hyperparameters obtained from the previous steps are applied to different regressors. The performance is measured using the following regression model evaluation metrics: $\:{R}^{2}$ (Coefficient of Determination), $\:EVS$ (Explained Variance Score), $\:MAE$ (Mean Absolute Error), $\:MSE$, $\:RMSE$ (Root Mean Squared Error), $\:PI$³⁰, $\:VAF$³¹, $\:\:RSR$ and$\:\:NMBE$³². Below are the specific formulas for these metrics:

$$\:\left\{\begin{array}{c}{R}^{2}=1-\frac{\frac{1}{N}{\sum}_{i=1}^{N}({y}_{i}-{\widehat{y}}_{i}{)}^{2}}{\frac{1}{N}{\sum}_{i=1}^{N}({y}_{i}-\stackrel{-}{y}{)}^{2}}\\\:EVS=1-\frac{Var(y-\widehat{y})}{Var\left(y\right)}\\\:\begin{array}{c}MSE=\frac{1}{N}{\sum}_{i=1}^{N}({\widehat{y}}_{i}-{y}_{i}{)}^{2}\\\:MAE=\frac{1}{N}{\sum}_{i=1}^{N}|{y}_{i}-{\widehat{y}}_{i}|\\\:\begin{array}{c}VAF=\left(1-\frac{var(y-\widehat{y}\:)}{var\left(y\right)}\right)\\\:PI={R}^{2}+\left(VAF/100\right)-RMSE\\\:\begin{array}{c}RMSE=\sqrt{\frac{1}{N}\sum_{i=1}^{N}{({\widehat{y}}_{i}-{y}_{i})}^{2}}\\\:NMBE=\frac{\sum_{i=1}^{n}{({\widehat{y}}_{i}-{y}_{i})}^{2}}{\sum_{i=1}^{n}{y}_{i}}\end{array}\end{array}\end{array}\end{array}\right.$$

(7)

Here, $\:N$ is the number of samples to be predicted, $\:{y}_{i}\:$represents the true value of the collapsibility coefficient for the $\:i\text{t}\text{h}$ sample, $\:{\widehat{y}}_{i}$ represents the predicted value of the collapsibility coefficient for the $\:i\text{t}\text{h}$ sample, $\:y$ denotes the set of true values for the test samples, $\:\widehat{y}\:$denotes the set of predicted values for the test samples, and $\:Var\left(y\right)$ represents the variance of the true values of the test samples, $\:\stackrel{-}{y\:}$ stands for the average values of the test samples. Researchers have used many methods to improve the generalization performance of the model and reduce the uncertainty of the model^33,34. In this study, five-fold cross-validation was used to evaluate the performance of each regressor³⁵. The data was divided into five folds, with each fold taking turns as the test set while the remaining four folds served as the training set for model training. The model was then evaluated on the test set. Finally, the results from the five experiments were averaged to reduce model uncertainty and enhance the model’s generalization ability.

To clearly and intuitively demonstrate the process of predicting the loess collapsibility coefficient, the modeling workflow is presented in Fig. 3. This figure illustrates the key steps involved in the prediction process, including data preprocessing, model selection, hyperparameter optimization, and performance evaluation. The workflow is designed to provide a comprehensive overview of how the prediction model is developed and validated, ensuring transparency and reproducibility in this study.

Fig. 3

The framework of the collapsibility coefficient prediction model.

Results and discussions

Relationship between collapsibility coefficient and pressure with the same moisture content but different dry densities

The experimental results of collapsibility tests on soil samples with different densities under identical moisture content conditions are presented in Fig. 4(a–f). The results indicate that when the moisture content is below 21.30%, the dry density is below 1.55 g/cm³, and the applied pressure is less than 50 kPa, the collapsibility coefficient becomes negligible. This negligible collapsibility arises from the combined effects of low moisture, low dry density, and low pressure. These findings suggest that, under certain natural or engineered scenarios, loess can remain stable without requiring extensive ground improvement. However, if any of these thresholds are exceeded (e.g., rising groundwater or increased loading), the potential for collapse may reoccur. As the pressure increased from 50 kPa to 100 kPa, the collapsibility coefficient increased significantly. This phenomenon is attributed to the relatively large pore spaces between soil particles at low pressures, which allowed compaction and resulted in a sharp increase in the collapsibility coefficient. However, the rate of increase in the collapsibility coefficient gradually slowed as pressure increased because the pore spaces between the soil particles decreased, making further compression more difficult. Consequently, the effect of pressure on the collapsibility coefficient diminished, and the collapsibility coefficient approached a stable value. Furthermore, as shown in Fig. 4(b), when the dry density of the sample was 1.55 g/cm³, the collapsibility coefficient became negative when the applied pressure was below 150 kPa, indicating that the sample underwent expansion rather than collapse due to excessive dry density. Moreover, as depicted in Fig. 4(e) and 4(f), the collapsibility coefficient-pressure relationship curves for dry densities ranging from 1.24 g/cm³ to 1.47 g/cm³ exhibit peaks with distinct inflection points at moisture contents of 18.6% or 21.3%.

Fig. 4

Variation of the collapsible coefficient with pressure and dry density under different moisture contents. (a) 6.30%, (b) 9.20%, (c) 12.20%, (d) 15.30%, (e) 18.60%, (f) 21.30%.

The observed phenomenon may be attributed to the significant softening of cementing materials (such as montmorillonite clay minerals and soluble salts like calcium carbonate) in loess at specific moisture contents (18.6% or 21.3%). When the moisture content reaches these critical thresholds, the water content becomes sufficient to disrupt the cementation structure between particles without achieving full saturation. Under these conditions, the application of pressure induces particle rearrangement, resulting in the peak behavior observed in collapsibility coefficient. When the dry density reaches or exceeds 1.55 g/cm³, the loess can be considered essentially non-collapsible. This phenomenon occurs because the compaction process fundamentally alters the pore structure: metastable macropores (e.g., overhead pores) are largely eliminated, resulting in a stabilized microstructure dominated by micropores. Simultaneously, cementing materials (carbonates and clay minerals) become more uniformly distributed, exhibiting mechanical properties similar to those of overconsolidated soils that resist further compaction under pressures below 400 kPa.

Relationship between collapsibility coefficient and pressure with the same dry density but different moisture contents

The results of collapsibility experiments on soil samples with varying moisture contents at a constant dry density are shown in Fig. 5(a–h). The experimental curves indicate that when the dry density is 1.24 g/cm³ and the applied pressure is below 300 kPa, the collapsibility coefficient increases with pressure. This phenomenon occurs because the collapsibility sensitivity of low dry-density soil under low-pressure conditions (below 300 kPa) primarily arises from the progressive failure of its initially loose structure due to the combined effects of loading and moisture. Increasing pressure accelerates particle rearrangement and pore collapse. As long as the critical pressure threshold is not reached, structural stability continues to deteriorate, resulting in an increasing trend in the collapsibility coefficient with rising pressure.

Moreover, compared to samples with other dry densities, collapsibility coefficient remains relatively high across all samples with a dry density of 1.24 g/cm³, regardless of moisture content. In contrast, for dry densities ranging from 1.27 g/cm³ to 1.47 g/cm³ and moisture contents between 6.3% and 12.2%, collapsibility coefficient rises with pressure when the applied pressure is between 50 kPa and 100 kPa. However, when the moisture content exceeds this range (18.6–21.3%), the coefficient initially increases with pressure but subsequently decreases, forming a distinct peak. This behavior may be attributed to the higher moisture content causing the sample, prepared at a lower dry density, to develop a honeycomb structure. This loose particle arrangement, upon water immersion, initially enhances collapse potential but eventually reduces it as excess moisture limits further compression.

Fig. 5

Variation of the collapsible coefficient with pressure and moisture content under different dry densities. (a) 1.24 g/cm³, (b) 1.27 g/cm³, (c) 1.31 g/cm³, (d) 1.35 g/cm³, (e) 1.39 g/cm³, (f) 1.43 g/cm³, (g) 1.47 g/cm³, (h) 1.55 g/cm³.

Using bayesian optimization to tune parameters for different regressors

Based on the above analysis, it is evident that the collapsibility coefficient of loess is closely related to factors such as dry density, moisture content, and applied pressure. Accordingly, these three variables were selected as features for predicting the collapsibility coefficient. To develop an optimal prediction model, six algorithms, Decision Tree, Ridge, RF, SVR, LGBM, and xGBoost, were implemented in this study. Compared to the traditional grid search method, Bayesian optimization significantly accelerates the hyperparameter tuning process, especially for models with multiple parameters. For models with fewer hyperparameters, such as Ridge regression, grid search can still efficiently identify optimal parameters within a short timeframe. However, for more complex models like LGBM and xGBoost, grid search often struggles to find optimized parameters promptly. In these cases, Bayesian optimization offers superior performance. Therefore, Bayesian optimization was employed to fine-tune the hyperparameters of all models in this study. Each model was trained using the training dataset, with the number of optimization iterations set to 32, and five-fold cross-validation was conducted to identify the optimal parameters. The results are summarized in Table 1.

Model performance on the training dataset

To select the optimal model for predicting the collapsibility coefficient, six regressors, Decision Tree, Ridge, RF, SVR, LGBM, and xGBoost, were trained using the best hyperparameters obtained previously. Each model underwent a five-fold cross-validation experiment on the same training dataset with identical folds, and the results are summarized in Table 2. Among these, the xGBoost model demonstrated the best predictive performance, achieving an R² of 0.932, EVS of 0.938, MAE of 0.01, RMSE of 0.014, VAF of 93.801%, PI of 1.856, RSR of 0.793, and NMBE of 0.003, all outperforming the other models. Conversely, the Ridge regression model showed the poorest performance, with an R² of 0.388, EVS of 0.401, MAE of 0.035, RMSE of 0.042, VAF of 40.128%, PI of 0.748, RSR of 2.394, and NMBE of 0.029. These results indicate that the relationship between dry density, moisture content, pressure, and the collapsibility coefficient is nonlinear, rendering linear models like Ridge unsuitable for this prediction task. Furthermore, models based on decision tree ensembles generally exhibited superior performance. The basic Decision Tree-based model achieved an R² of 0.809, EVS of 0.822, MAE of 0.016, RMSE of 0.023, VAF of 82.189%, PI of 1.608, RSR of 1.329, and NMBE of 0.009, outperforming both Ridge and SVR models. Ensemble methods such as RF, LGBM, and xGBoost further enhanced performance, with average R² values exceeding 0.92. These findings suggest that ensemble tree-based models are more suitable and effective for predicting the collapsibility coefficient of loess.

Table 2 Performance comparison among different models on the training dataset.

Model comparison on the independent testing dataset

To further compare the performance of the models, we conducted an additional evaluation using an independent testing dataset. Each model was trained on the entire training dataset with its optimal hyperparameters before being tested. The results are summarized in Table 3. Consistent with previous findings, the linear Ridge regression model exhibited the poorest performance, with an R² of 0.434, EVS of 0.462, MAE of 0.03, RMSE of 0.039, VAF of 46.212%, PI of 0.858, RSR of 2.143, and NMBE of 0.031, reaffirming the presence of nonlinear relationships between dry density, moisture content, pressure, and collapsibility coefficient. The SVR-based model demonstrated notable improvement on the independent testing dataset compared to its training performance, highlighting its strong generalization capability. Nevertheless, its predictive accuracy remained inferior to ensemble learning models such as RF, LGBM, and xGBoost. Among these ensemble methods, all achieved R² values exceeding 0.96, indicating their superior effectiveness for predicting loess collapsibility. Specifically, the XGBoost model attained an R² of 0.963, EVS of 0.963, MAE of 0.008, RMSE of 0.01, VAF of 96.335%, PI of 1.917, RSR of 0.547, and NMBE of 0.002 on the independent test set, marginally trailing the RF-based model. Considering model performance across both the training and independent testing datasets, ensemble-based models clearly outperformed others overall. Additionally, Fig. 6(a–f) presents the actual versus predicted collapsibility coefficients for each model, further demonstrating the superior linearity and prediction accuracy of the ensemble decision tree models.

Table 3 Performance comparison for different models on the independent testing dataset.

Fig. 6

Scatter plots to compare the predicted values and actual values of different models. (a) DecisionTree, (b) Ridge, (c) RF, (d) SVR, (e) LGBM, (f) xGBoost.

To further evaluate the predictive performance of the six models, we analyzed the absolute differences between their predictions and the actual test data. As shown in Fig. 7(a–f), the RF-based model exhibited the smallest absolute differences, thereby achieving the best predictive accuracy among all models. In this study, a collapsibility coefficient less than or equal to 0.01 was considered indicative of very weak or negligible collapsibility of the loess or soil upon water exposure, and such values were predicted as zero. For samples with a collapsibility coefficient greater than 0.01, the RF-based model generally produced smaller absolute errors. Specifically, 65% (17/26) of these samples had relative prediction errors below 10%, 80.76% (21/26) had errors below 20%, and 92.31% (24/26) had errors below 30%. Only two samples exhibited relative errors exceeding 30%. These samples had moisture contents of 18.6% and 21.3%, dry density of 1.35 g/cm³, and applied pressures of 100 kPa and 400 kPa, respectively. The likely cause of these larger errors, as illustrated in Fig. 4, is the rapid decline of the collapsibility coefficient when pressure exceeds 100 kPa at these specific moisture and density conditions. Overall, these findings confirm that the RF-based model can reliably and accurately predict the collapsibility coefficient.

Fig. 7

The absolute difference between the true and predicted values of each model. (a) DecisionTree, (b) Ridge, (c) RF, (d) SVR, (e) LGBM, (f) xGBoost.

Performance validation and software development

To further validate the model’s applicability in other regions, we collected experimental data from published literature and specifically used the Lanzhou Donggang dataset from Li et al. for verification³⁶. The reason for choosing only this dataset is that most published data lack the pressure parameter required by our model, typically including only water content or dry density. Their experiments provide water content, dry density, and pressure (set at 200 kPa), making their data compatible with our model. Accordingly, we retrained our model using the samples from this study and tested it on their dataset. The results show that the relative error of our model on this external dataset is less than 25% (see Table 4), indicating that the model retains reasonable predictive capability for loess collapsibility in other regions. For researchers’ convenience, we packaged the developed model into user-friendly software using wxPython and PyInstaller (The software link is provided in the Data Availability Statement). The software includes modules for feature selection, regressor selection, model construction, validation, and sample prediction. Researchers can use this software not only for prediction but also for further development, such as exploring optimized combinations of different training datasets, input features, and regressors. Due to Ridge’s relatively poor predictive performance, only five models, DecisionTree, RF, SVR, LGBM, and xGBoost, are integrated. Since the RF-based model demonstrated the best predictive accuracy, the software allows users to adjust its hyperparameters dynamically. The other four models come with pre-trained hyperparameters embedded and do not support dynamic tuning. It is worth noting that because of the use of different random seeds in partitioning training and testing datasets, the software’s prediction results may differ slightly from those reported in this paper.

Table 4 Performance comparison for different models on the independent testing dataset.

Conclusion

The prediction of the loess collapsibility coefficient is a critical task in civil engineering, as it directly influences the safety and stability of construction projects in loess regions. This study developed and optimized regression models to accurately predict the loess collapsibility coefficient, applying Bayesian optimization to six regressors: DecisionTree, Ridge, RF, SVR, LGBM, and xGBoost. A fair comparison was conducted through cross-validation on the training dataset and evaluation on an independent testing dataset. Results show that the Random Forest-based model achieved the best performance, with R² values of 0.915 and 0.965 on the training and testing datasets, respectively. Ensemble methods based on decision trees, such as LGBM and xGBoost, also demonstrated superior performance compared to other regressors, suggesting their suitability for this prediction task.

Bayesian optimization effectively fine-tunes hyperparameters within a limited computational budget, particularly for models with many hyperparameters, whereas traditional grid search becomes computationally prohibitive in such cases. Among the six models optimized, all except the linear Ridge model showed satisfactory predictive capabilities, with Ridge performing poorly on both datasets.

Due to limitations in sample preparation and dataset size, more advanced machine learning techniques like deep learning were not feasible in this study. Accurate prediction of the loess collapsibility coefficient is vital for engineers to assess collapse risks and implement mitigation strategies during design and construction. This research demonstrates the effectiveness of combining machine learning with Bayesian optimization to address complex geotechnical challenges, promoting safer and more sustainable construction in loess regions. Leveraging such data-driven models enables better understanding and management of loess collapse risks, thereby reducing the associated economic and social impacts.