Engineering oriented shape optimization of GHT-Bézier developable surfaces using a meta heuristic approach with CAD/CAM applications

Abstract

Optimization techniques are particularly useful when designing different free-form surfaces and manufacturing products in the engineering and CAD/CAM fields. Recently, many real-world problems utilize optimization techniques with objective functions to get their desired solution. In this paper, the shape optimization of GHT-Bézier developable surfaces by using a meta-heuristic technique called Improved-Grey Wolf Optimization (I-GWO, in short) technique is presented. This Grey Wolf optimization algorithm impersonates the hunting tactics of grey wolves in nature. Three optimization models arc length (AL), minimum energy (En), and curvature variation energy (CVEn) of dual and interpolation curves, are used to formulate this technique. The shape control parameters are considered as optimization variables. So, our aim is to find the optimal shape control parameters by applying the I-GWO algorithm to the optimization models through an iterative process. By using the duality principle between the points and planes, the construction of GHT-Bézier developable surfaces is formulated by the optimal choice of shape parameters obtained from I-GWO technique. Furthermore, the developability degree of GHT-Bézier developable surfaces is also determined. Some applications of the proposed method are given and the effectiveness of this method is illustrated.

Introduction

Optimization techniques have tremendous commercial success in the engineering and computer technology areas during the past three decades. Surprisingly, some bio-inspired optimization techniques, such as Particle Swarm Optimisation (PSO) technique, Ant Colony Optimisation (ACO) technique, and Genetic Algorithm (GA) technique, are not only popular in the fields of engineering and computer science, but are also well-known among scientists in a variety of disciplines. These bio-inspired optimization techniques have been applied in various research fields in the presence of natural occurrences to solve complex problems.

The I-GWO algorithm is also an emerging optimization technqiue which is related to swarm intelligence computation. The inspiration of this work is typically related to the collective behavior of animals^1,2. The hunting (optimization) is guided by three wolves having the variables $\lambda ,$ $\alpha ,$ and $\beta ,$ and which also gives the best minimum values of the fitness function. In this iterative searching space, the best position of prey is given by the best position of the wolves $Y_{\lambda },$ $Y_{\alpha },$ and $Y_{\beta }.$ In essence, the optimization process provide three best solutions and the prey is the optimal solution of the optimization which is obtained after some iteration process.

Related research

Numerous swarm intelligence algorithms (SIA) were introduced as meta-heuristic optimization techniques in recent research in^3,4,5. The Bat Algorithm (BA)⁶ is a superior swarm-based method, effective for solving small-scale engineering problems with high precision. However, for complex multi-objective tasks, hybrid approaches like MFO-ANN⁷ offer enhanced convergence and accuracy. These methods have shown excellent results, particularly in optimizing magnetic abrasive finishing (MAF) processes. Kumar et al., presented a novel multi-objective evolutionary algorithm (MOEA) named Particle swarm optimization in⁸ incorporating crowding distance (MOPSO-CD) has been applied to get the Reliability-Cost Fronts (RCFs) of this complex multi-objective reliability optimization problem. Igiri et al.⁹ found that the randomization system and parameter configurations had an impact on how well a meta-heuristic technique worked. A comprehensive overview of the research strategies on SIA and evolutionary algorithms (EA) is given. SIA saves the previous data about the search space while EA discards the information of the past generations.

It also utilizes memory to preserve the optimal result obtained so far and mostly has fewer parameters to adjust, easy to implement and has small number of operators as compared to EA. Many existing researches based on the novel nature-inspired algorithms is provided by authors for the shape optimization and various engineering designing. By using PSO-based shape parameters optimization, the quasi developable GHT-Bézier surfaces are generated by Cao et al.¹⁰. The PSO technique yields with the optimal shape parameters, gives the higher developability degree of Q-Bézier strips. Cui et al., described a new structural morphology method in¹¹ for the construction of free-form grid surfaces by using plate components. Zheng et al.¹², presented the modeling by using the exclusive parameters determined by the GWO algorithm.

BiBi et al.¹³ proposed the PSO technique to construct the family of GHT-Bézier developable surfaces with high developability degree, where the single objective function with very wide range of solution space was used as a fitness function to find the optimal solution. These optimal parameters were used to construct the optimized developable surfaces and to determine the developability degree. To solve the problem of shape adjustment for developable surfaces, Hu et al. proposed a novel method for constructing local controlled generalized developable H-Bézier surfaces with shape parameters in¹⁴ using the control planes. A novel approach which is designed specifically for developable models with curved folds is presented by Pan et al. in¹⁵ to focus on restoring the model’s developability and based on normal variation. In¹⁶, few complex reliability optimization problems are solved by using a nature-inspired metaheuristic called gray wolf optimizer (GWO) algorithm and the result had better convergence and accuracy as compared to the other optimization techniques. An algorithm is suggested for creating a general NURBS surface approximation that is piecewise developable surface¹⁷. These fabricatable surfaces have properties that make them advantageous for manufacturing from flat sheets of material without any distortion. The recent advances in the modelling of developable surfaces¹⁸ show how they permit the interactive design of arrangements of curved beams, in particular the design of so-called geometric support structures given in Fig. 1.

Figure 1

(a) Developable Strips which follow the guiding curves¹⁸, (b) Union of Developable strips with various properties¹⁸, (c) Physical demonstration of computational wrapping¹⁹.

Construction of some Bézier models and their applications in CAD/CAM modeling and manufacturing are given in²⁰. Ammad et al.²¹, constructed a family of generalized developable cubic trigonometric Bézier surfaces such as Enveloping developable surfaces, Spine developable surfaces and developable surface interpolation geodesic curve. The analysis properties and some applications are also given. BiBi et al. proposed a new approach for $G^{3}$ continuity conditions between two adjacent GHT-Bézier curves and between two GHT-Bézier developable surfaces with continuity conditions given in^22,23. The study about the basis functions, the curvature, and the tangent of the GHT-Bézier curve are given in²⁴. As for the fundamental curvature analysis of the surface in three dimension space, the mean curvature and Gaussian curvature are used in²⁵. The surface with Mean curvature is called a minimal surface while the surface with Gaussian curvature is called a developable surface. Wang and Elber²⁶ has introduced a multidimensional dynamic programming approach for fitting ruled surfaces to freeform rational surfaces. By optimizing point-pair elevations along surface normals, a GPU-accelerated solution ensures minimal fitting error.

The theory about the construction of various engineering surfaces is described by BiBi et al.^27,28. These surfaces are utilized for a variety of technical and manufacturing tasks to cut down on production costs and increase productivity. In^29,30, the analysis properties and the continuity constraints for two adjoining Bézier curves are described. To simulate the paper bending and animation applications, the developable surfaces as the envelope of rectifying plane is presented in³¹, which provides the intuitive control for modeling and paper bending. BiBi et al.³² presented the construction of GHT-Bézier curves and surfaces with symmetric designs. Some engineering applications and various curve modelings of this proposed study are also described. Construction of some engineering surfaces such as swept surfaces, ruled surfaces, swung surfaces and bilinear surfaces were presented by Ammad and Misro³³. The meta-heuristic algorithms called gravitational search algorithm (GSA) and Particle Swarm Optimization (PSO) are presented in³⁴ to resolve the new training methods for Feedforward Neural Networks.

In³⁵, an algorithm is described to draw a conclusion by using binary bat algorithm. By using PSO-based shape parameters optimization, the quasi developable GHT-Bézier surfaces are generated by Cao et al.³⁶. This PSO technique yields with the optimal shape parameters, gives the higher developability degree of Q-Bézier strips. Cui et al., described a new structural morphology method in³⁷ for the construction of free-form grid surfaces by using plate components. Wang³⁸ proposed an optimization-based methods to enhance developability in polygonal meshes. A Flattenable Laplacian mesh framework is proposed in³⁹ for efficient surface modeling. The approach enables real-time design of flattenable, manufacturable surfaces based on the constrained optimization technology. Zheng et al.⁴⁰, presented the modeling by using the exclusive parameters determined by the GWO algorithm. Chaube et al.⁴¹, presented a procedure which is introduced to construct the membership and the non-membership functions of the fuzzy reliability function, by considering the failure rates as time-dependent CBFN.

Osaba et al.⁴², presented a step-by-step methodology that covers each research phase of meta huiristic techniques while addressing that scientific topic. In⁴³, the authors exhaustively tabulated more than 500 metaheuristics from two aspects, namely, the inspirational source and the essential operators for generating solutions. The Ant Lion Optimizer (ALO) is a nature-inspired algorithm proposed in⁴⁴, known for its simplicity, scalability, and balanced exploration–exploitation. It has been widely applied and improved through various modifications. Similarly, the MaGI algorithm uses extreme candidate values for efficient search in⁴⁵ and performs well on diverse optimization problems. Shahraki et al.⁴⁶, suggested a solution to improve the GWO algorithm’s population variety, balance between exploitation and exploration, and premature convergence in order to address various engineering issues. The I-GWO algorithm benefits from a new movement strategy called dimension learning-based hunting (DLH) search strategy, which was inspired by the unique hunting habits of grey wolves in nature. This algorithm significantly enhances the original GWO by improving convergence speed and acurracy.

Traditional optimization methods for GHT-Bézier developable surfaces, which are crucial in fields like computer graphics, robotics, and aerodynamics, often suffer from slow convergence and limited accuracy. This leads to inefficiencies in designing complex surfaces such as car bodies, airplane skins, and ship hulls, where higher developability degree is essential. To address these challenges, this study introduces the Improved Grey Wolf Optimization (I-GWO) algorithm with DLH search strategy, which significantly enhances the original GWO by improving both convergence speed and accuracy. By optimizing shape control parameters, it achieves higher developability degrees with fewer iterations, providing greater accuracy and reduced computational costs. It also enhances the precision, efficiency, and functionality of complex surface designs in industries like automotive, aerospace, and shipbuilding.

The motivation behind this study is given below which stems from the critical need for precision and advanced optimization in CAD/CAM applications.

• The proposed I-GWO algorithm supports the development of GHT-Bézier surfaces, ensuring accurate and reliable design for complex shapes.

• The I-GWO algorithm enables higher degrees of developability, enhancing the effectiveness of GHT-Bézier developable surfaces in engineering applications.

• This study uses the I-GWO algorithm, a novel nature-inspired optimization approach, construct a class of GHT-Bézier developable surfaces by using dual and interpolation curves with broad range of applications in engineering field.

In this proposed work, the I-GWO algorithm is combined with a multi-objective functions to optimize shape control parameters and accurately determine the developability degree. Notably, the technique provides optimal solutions with fewer iterations, making it a highly efficient and computationally simple compared to other optimization methods.

Some technical contributions of the proposed study are given as follows:

• A study about the developability degree of GHT-Bézier developable surfaces is given.

• The shape optimization of GHT-Bézier developable surfaces is presented based on the dual curve and interpolation curve by using I-GWO algorithm.

• The GHT-Bézier developable surfaces are constructed by using the I-GWO algorithm with fewer iterations and the optimal shape parameters are obtained by multi-objective functions to determine developability degree.

• Modeling examples are also presented to show the efficiency of the proposed method with developability degree.

• The effectiveness of the I-GWO algorithm is demonstrated through a comprehensive comparison with various optimization methods, and its practical utilization is further highlighted by real-life applications in product modeling.

The whole work is summarized as follows. A review of I-GWO algorithm, the methodology, working mechanism and convergence performance of this algorithm are given, in “I-GWO algorithm”. A study about developable surfaces and the developability degree of GHT-Bézier ruled surface is given in “GHT-Bézier developable surfaces”. The fitness function in three shape optimization models for the modeling of Enveloping, Spine and Cylinder GHT-Bézier developable surfaces with higher developability degree, and the optimization models for the construction of interpolation curve on GHT-Bézier developable surfaces are described in “Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm”. The procedure is described in “Construction of GHT-Bézier developable surfaces by using I-GWO algorithm” for the shape optimization of GHT-Bézier developable surface by using the I-GWO algorithm. Results and modeling examples to show the efficiency of the proposed I-GWO algorithm and its comparison with other optimization methods are given in “Results and discussion”. The real world product modeling with higher developpability degree based on I-GWO algorithm is presented in “Application design for product modeling based on I-GWO”. Some concluding remarks and future directions are summarized in “Concluding remarks”.

I-GWO algorithm

Improved-Grey Wolf Optimization (I-GWO) algorithm is an advanced method which is proposed by Shahraki, Taghian and Mirjalili in⁴⁴, to overcome the flaws of GWO algorithm such as population diversity and premature convergence. The I-GWO algorithm is designed with new movement strategy named as Dimension Learning-based Hunting (DLH) search strategy to perform the optimization which mimics the hunting behavior of grey wolves in nature and leads with three main steps, searching of prey, encircling prey and attacking prey. The DLH search strategy in I-GWO algorithm, is used to overcome the deficiencies of GWO algorithm. Through the multi-neighbor learning, the searching space is increased and population diversity is maintained. In this work, the authors describe the I-GWO algorithm is used to construct GHT-Bézier developable surfaces by finding the optimal shape parameters. First, the parameters and population size are initialized, and three wolves $Y_{\lambda }, Y_{\alpha }$ and $Y_{\beta }$ are chosen arbitrarily which gives the minimum best values of arc length, energy and curvature variation energy. The new best position of the wolf is updated with the current position and this iteration process continued till the optimal shape parameters are achieved. In each iteration, the I-GWO has both candidate wolf which generated by the DLH and GWO search mechanism to move the wolf from the current position to the best position. The new position of the winner candidate wolf is selected and updated in each iteration. The hunting behavior of grey wolves in nature is shown in Fig. 2.

Figure 2

Hunting mechanism of Grey Wolves⁴⁷.

Methodology of I-GWO algorithm

Contemporary use of developable surfaces and their geometric manipulation with or without the use of computer software has been increasingly well documented. The application of developable surfaces is wide ranging from ship-building to manufacturing of clothing as they are suitable to the modelling of surfaces which is made out of leather, paper, fibre, and sheet metal. Developable surfaces form a very small subset of all possible surfaces. For centuries, cylinders and cones were believed to be the only ones, until studies in the eighteenth century proved that the tangent surfaces also belong to the same mathematical family.

In the proposed study, the authors presented the I-GWO algorithm for the shape optimization of GHT-Bézier developable surfaces by dual curve and interpolation curve with higher developability degree. For finding the developability degree, the optimal shape parameters are need to be determined. For the iteration process the initial shape parameters are chosen from the domain $[-1,1]$, which are referred to as wolf candidates, and the optimal shape parameters will obtained by solving three optimization models for the arc length, energy, and curvature variation energy that are described in “Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm”. Assume that $N=8$ wolf candidates are selected from a solution space, and each wolf has three distinct values for the shape parameters $(\alpha , \beta , \lambda ).$ The values of fitness function i.e arc length, energy and curvature variation energy are determined and after that three best minimum values for each of the fitness function are chosen and their corresponding wolf candidates $Y_{\lambda }, Y_{\alpha }, Y_{\beta }$ are used for further optimization process. These three elite wolves $Y_{\lambda }, Y_{\alpha }, Y_{\beta }$ are actually chosen because they provided the three best minimum values for each fitness function.

Now, for each wolf candidate’s, the three best positions are determined one by one by using Eq. (2.6). Equation (2.7) is used to obtain the updated wolf candidate, once these three values are discovered. Now by using DLH search strategy, the wolves are randomly selected from solution space and each wolf is learned by its different neighbor. The Euclidean distance $ED_{k}(\vartheta )$ is determined between the current position and updated position of the wolf candidates. The neighbouring wolves $Y_{j}(\vartheta )$ of $Y_{k}(\vartheta ),$ whose distance is less than $ED_{k}(\vartheta ),$ make another sub-solution space defined in Eq. (2.10) where the position of wolf candidate can be easily determined. The best wolf candidate is chosen on the basis of minimum values by comparing the values obtained by GWO and DLH search strategy. This iterative process is continued till the minimum best value for each wolf is obtained. The elite wolf with the lowest values of the shape parameters is at the best position to hunt its prey. These shape parameters are the optimal values and used to determine the developability degree and for the construction of GHT-Bézier developable surfaces.

Figure 3

Flowchart to describe I-GWO algorithm.

Working principle of I-GWO algorithm

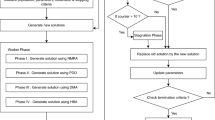
The flowchart to describe I-GWO algorithm is shown in Fig. 3. An algorithm to explain the methodology and working principle of I-GWO is described below. I-GWO algorithm includes three steps which consist of initializing, movement, and finally selecting and updating.

• Initializing: In the first step, N wolves are randomly spread in solution space in a given range $[Y_{min}, Y_{max}]$ by Eq. (2.1) as follows,

  $$\begin{aligned} Y_{kj}=Y_{min}+rand [0,1]\times (Y_{max}-Y_{min}), \quad k\in [1,N], j\in [1,D]. \end{aligned}$$

  (2.1)

  The position of kth wolf in $\vartheta$th iteration is represented in vector form as $Y_{k}(\vartheta )=\{Y_{i1}, Y_{i2}, Y_{i3},...,Y_{iD}\}$, where D is the dimension which is defined for a problem. The fitness value of $Y_{k}(\vartheta )$ can be calculated by the fitness function $f(Y_{k}(\vartheta )).$

• Movement: Individual hunting is an interesting social behavior of grey wolves in GWO algorithm. Meanwhile, the I-GWO algorithm possesses another search strategy named as DLH search strategy. In DLH, each wolf is learned by its neighbor to be another candidate wolf to get the new position of $Y_{k}(\vartheta )$. GWO and DLH search strategies generate two different wolves and can be describes as following steps:

  1. GWO search strategy:

  GWO is inspired by the hierarchy and hunting behavior of gray wolf populations. The algorithm achieves optimization by mathematically simulating the tracking, surrounding, hunting and attacking the process of gray wolf populations. The gray wolf hunting process involves three steps: social hierarchy stratification, encircling the prey and attacking the prey.

  i) Social Hierarchy: Gray wolves are social canids at the top of the food chain and follow a strict hierarchy of social dominance. In this search strategy, the first three best wolves named $Y_{\lambda }, Y_{\alpha }$, and $Y_{\beta }$ are chosen from the population. The best solution is marked as the $Y_{\lambda }$, the second-best solutions are marked as the $Y_{\alpha },$ and the third-best solutions are marked as the $Y_{\beta }.$

  ii) Encircling the Prey: Gray wolves encircle prey during the hunt, in order to mathematically model encircling behavior, the following equations are used: A decreasing coefficient a,  which is a distance control parameter and the coefficients $B_{kj}$ and $C_{kj}$ in the form of a vector can be calculated by using Eqs. (2.2–2.4),

  $$\begin{aligned} a= & 2(1-\frac{iteration}{Maxiter}), \end{aligned}$$

  (2.2)
  $$\begin{aligned} B_{kj}= & 2\times a \times r_{1}-a, \end{aligned}$$

  (2.3)
  $$\begin{aligned} C_{kj}= & 2\times r_{2}, \end{aligned}$$

  (2.4)

  where $r_{1}$ and $r_{2}$ are the random numbers between [0, 1],  and maxiter denotes the maximum number of iterations. The prey encircling is determined by considering the values of $Y_{\lambda }(\vartheta ), Y_{\alpha }(\vartheta )$ and $Y_{\beta }(z)$ with Eq. (2.5), while $Y_{\lambda }, Y_{\alpha }$ and $Y_{\beta }$ are the position of those wolf candidates which gives the minimum best values, and $Y(\vartheta )$ denotes the position of all random wolf candidates which are chooses one by one and used for iteration process.

  $$\begin{aligned} {\left\{ \begin{array}{ll} D_{\lambda }=|C_{k1} \times Y_{\lambda }-Y(\vartheta )|,\\ D_{\alpha }=|C_{k2} \times Y_{\alpha }-Y(\vartheta )|,\\ D_{\beta }=|C_{k3} \times Y_{\beta }-Y(\vartheta )|. \end{array}\right. } \end{aligned}$$

  (2.5)

  iii) Attacking the Prey: Gray wolves have the ability to recognize the location of potential prey, and the search process is mainly carried out by the guidance of $(\lambda , \alpha , \beta )$ wolves. In each iteration, the best three wolves $(\lambda , \alpha , \beta )$ in the current population are retained, and then the positions of other search agents are updated according to their position information. The following formulas are proposed in this regard:

  $$\begin{aligned} {\left\{ \begin{array}{ll} Y_{k1}(\vartheta )=Y_{\lambda }(\vartheta )-B_{k1}\times D_{\lambda }(\vartheta ),\\ Y_{k2}(\vartheta )=Y_{\alpha }(\vartheta )-B_{k2}\times D_{\alpha }(\vartheta ),\\ Y_{k3}(\vartheta )=Y_{\beta }(\vartheta )-B_{k3}\times D_{\beta }(\vartheta ). \end{array}\right. } \end{aligned}$$

  (2.6)

  After calculating the Eq. (2.6) by using above values, the first candidate of GWO can be calculated by using the following equation,

  $$\begin{aligned} Y_{k-GWO}(\vartheta +1)=\frac{Y_{k1}(\vartheta )+Y_{k2}(\vartheta )+Y_{k3}(\vartheta )}{3}. \end{aligned}$$

  (2.7)

  The main constraint in the GWO search strategy is its wide range of solution space, which increases the risk of selecting infeasible or less relevant neighboring wolves during the optimization process. This can cause the algorithm to converge slowly. The DLH strategy overcomes this by using Euclidean distance to identify the most relevant nearby wolves, effectively reducing the search space and minimizing the chances of constraint violations. This targeted approach helps in maintaining solution feasibility while accelerating the optimization process.

  2. DLH search strategy: In the DLH search strategy, the dimensions of $Y_{k}(\vartheta )$ are calculated in a different way. Each individual wolf is learned by its different neighbors and wolf are randomly selected from population space. Then apart from the wolf obtained by the GWO search strategy, i.e. $Y_{k-GWO}(\vartheta +1),$ the DLH search strategy produces another wolf candidate named $Y_{k-DLH}(\vartheta +1).$ So, the Euclidean distance between the current position $Y_{k}(\vartheta )$ and candidate position $Y_{k-GWO}(\vartheta +1)$ can be calculated by using Eq. (2.8) as follows,

  $$\begin{aligned} ED_{k}(\vartheta )=||Y_{k}(\vartheta )-Y_{k-GWO}(\vartheta +1).|| \end{aligned}$$

  (2.8)

  Then, the nearest wolves of $Y_{k}(\vartheta )$ are represented by $M_{k}(\vartheta ),$ and can be obtained by using the following Eq. (2.9)

  $$\begin{aligned} M_{k}(\vartheta )=\{Y_{j}(\vartheta )|dis_{k}(Y_{k}(\vartheta ),Y_{j}(\vartheta ))\le ED_{k}(\vartheta ),\quad Y_{j}(\vartheta ) \in P\}, \end{aligned}$$

  (2.9)

  where P represents the population and $dis_{k}$ is the Euclidean distance between $Y_{k}(\vartheta )$ and $Y_{j}(\vartheta ).$ After the adjacent wolf of $Y_{k}(\vartheta )$ is obtained, then multi-neighbor wolves can be determined by using Eq. (2.10)

  $$\begin{aligned} Y_{k-DLH,d}(\vartheta +1)=Y_{k,d}(\vartheta )+rand[0,1] \times (Y_{n,d}(\vartheta )-Y_{k,d}(\vartheta )), \end{aligned}$$

  (2.10)

  where the $d-th$ dimension of $Y_{k-DLH,d}(\vartheta +1)$ is calculated by using $d-th$ dimension of an arbitrary wolf $Y_{n,d}(\vartheta ),$ selected from $M_{k}(\vartheta ),$ and an arbitrary wolf $Y_{r,d}(\vartheta )$ from population.

• Selecting and Updating: In this step, the best wolf is chosen which is selected by comparing the fitness values of two wolf candidates $Y_{k-GWO}(\vartheta +1)$ and $Y_{k-DLH}(\vartheta +1)$ by using Eq. (2.11)

  $$\begin{aligned} Y_{k}(\vartheta +1)= {\left\{ \begin{array}{ll} Y_{k-GWO}(\vartheta +1),\quad \quad f(Y_{k-GWO})<f(Y_{k-DLH}),\\ Y_{k-DLH}(\vartheta +1), \quad \quad otherwise. \end{array}\right. } \end{aligned}$$

  (2.11)

  To update the new position of the wolf $Y_{k}(\vartheta +1),$ if the fitness value of the selected candidate is less than $Y_{k}(\vartheta ),$ then $Y_{k}(\vartheta )$ is updated by the selected candidate. Otherwise, $Y_{k}(\vartheta )$ remains unchanged in the population. This technique is performed for all the wolves one by one and the iteration process remains continuous until the optimal values of parameters are obtained.

Convergence performance

The proposed Improved Grey Wolf Optimization (I-GWO) algorithm demonstrates superior convergence performance in the shape optimization of GHT-Bézier developable surfaces. By introducing the DLH search strategy, the solution space is significantly reduced, allowing the algorithm to swiftly navigate toward the optimal or near-optimal solution. This results with the faster convergence rate compared to the standard GWO algorithm.

GHT-Bézier developable surfaces

GHT-Bernstein basis functions and GHT-Bézier curve

Definition 1

The generalized hybrid trigonometric Bernstein (GHT-Bernstein, in short) basis functions borrows from²⁷ is defined as follows in Eq. (3.1),

$$\begin{aligned} {\left\{ \begin{array}{ll} \digamma _{0,2}(\vartheta )= (1- \lambda \sin (\frac{\pi }{2}\vartheta ))(1-\sin (\frac{\pi }{2}\vartheta )) e ^{\beta \vartheta } \\ \digamma _{1,2}(\vartheta )=1-\digamma _{0,2}(\vartheta )-\digamma _{2,2}(\vartheta )\\ \digamma _{2,2}(\vartheta )= (1- \alpha \cos (\frac{\pi }{2}\vartheta ))(1-\cos (\frac{\pi }{2}\vartheta )) e ^{(1-\vartheta ) \beta }, \end{array}\right. } \end{aligned}$$

(3.1)

where $\lambda , \alpha ,\beta \in [-1, 1]$ are the shape parameters. For r $(r\ge 3),$ these basis functions can be generalized by using recursive formula as given in Eq. (3.2),

$$\begin{aligned} \digamma _{j,r}(\vartheta )=\vartheta \digamma _{j-1,r-1}(\vartheta )+(1 - \vartheta ) \digamma _{j,r-1}(\vartheta ) , ~~~\quad \vartheta \in [0,1]. \end{aligned}$$

(3.2)

Moreover, the function $\digamma _{j,r}(\vartheta )$ is defined only when $j>-1$ and $j\le q$.

Definition 2

The rth degree GHT-Bézier curve with the control points $\hbar _r$ is defined in Eq. (3.3) as,

$$\begin{aligned} \wp (\vartheta ; \lambda , \alpha ,\beta )= \sum ^{r}_{j=0} \hbar _r \digamma _{j,r}(\vartheta ), \quad \quad \vartheta \in [0,1]. \end{aligned}$$

(3.3)

Definition 3

For the control points $\hbar _r$, the tangent of rth degree GHT-Bézier curve is defined as follows,

$$\begin{aligned} \wp _{\vartheta }(\vartheta ; \lambda , \alpha ,\beta )= \sum ^{r}_{j=1} \hbar _r \digamma '_{j,r-1}(\vartheta ), \quad \quad \vartheta \in [0,1]. \end{aligned}$$

(3.4)

Developable surface

A ruled surface is a surface that can be swept out by moving a line in a space in the following way as in Eq. (3.5).

$$\begin{aligned} {\left\{ \begin{array}{ll} S(\vartheta , \vartheta _{1})= p(\vartheta )+\vartheta _{1} h(\vartheta ),\quad \quad \vartheta , \vartheta _{1} \in [0,1],\\ h(\vartheta )=q(\vartheta )-p(\vartheta ). \end{array}\right. } \end{aligned}$$

(3.5)

The formation of a ruled surface can be made possible by using the generatrix and directrix of the curve. The $q(\vartheta )$ and $p(\vartheta )$ are called the directrix of the curve while $h(\vartheta )$ is called the generatrix of the curve. The GHT-Bézier curve defined in Eq. (3.3) is used as the directrix of the curve. The $\wp _{\vartheta }(\vartheta )$ is the tangent of the GHT-Bézier curve given in Eq. (3.4). The developable surface is a special kind of ruled surface that is expandable on the plane as shown in Fig. 4.

Figure 4

The graphical representation of GHT-Bézier developable surface.

The developability condition of the surface is that the surface has zero Gaussian curvature. In mathematical representation, the developability condition of the ruled surface is given in Eq. (3.6)

$$\begin{aligned} \wp _{\vartheta }(\vartheta ) \times h(\vartheta )\cdot q_{\vartheta }(\vartheta )=0, \end{aligned}$$

(3.6)

which shows that the generatrix is the intersection between the tangent plane and the surface $S(\vartheta , \vartheta _{1})$.

By the dual principle in 3D projective space, a one-parameter family of planes are determined by considering the control points of curve (given in Eq. (3.3)) as control planes. Based on GHT-Bézier curve the one-parameter of planes are given as,

$$\begin{aligned} \{\Pi _{\vartheta }\}:L(\vartheta ,\varpi )=\sum ^{3}_{j=0} \ell _j \digamma '_{j,r}(\vartheta ), \quad \quad \vartheta \in [0,1], \end{aligned}$$

(3.7)

where $\ell _{j}=(w_{j}, x_{j}, y_{j}, z_{j}),$ are the control planes and $\varpi =(\lambda , \alpha ,\beta )$ are the shape control parameters. The above equation in vector form is written in Eq. (3.8),

$$\begin{aligned} L(\vartheta ,\varpi )=\sum ^{3}_{j=0} (w_{j}, x_{j}, y_{j}, z_{j}) \digamma '_{j,r}(\vartheta )=\{\Lambda _{0}(\vartheta ), \Lambda _{1}(\vartheta ), \Lambda _{2}(\vartheta ), \Lambda _{3}(\vartheta ) \}, \quad \quad \vartheta \in [0,1], \end{aligned}$$

(3.8)

where, $\Lambda _{j}(\vartheta )=\sum ^{3}_{j=0}\ell _{j}\digamma '_{j,r}(\vartheta ),~~(j=0,1,2,3).$ According to the duality principle, the GHT-Bézier enveloping developable surface of one parameter family of planes $\{\Pi _{\vartheta }\}$²³ is given in Eq. (3.9),

$$\begin{aligned} {\mathfrak {F}}(\vartheta ,\nu ; \varpi ) = \nu \Game (\vartheta ) + V(\vartheta ), ~~~ \nu \in (-\infty , +\infty ),~~~ \vartheta \in [0, 1]. \end{aligned}$$

(3.9)

where, the expression of above terms are given in Eq. (3.10),

$$\begin{aligned} {\left\{ \begin{array}{ll} \Lambda (\vartheta )=\{\Lambda _{0}(\vartheta ), \Lambda _{1}(\vartheta ), \Lambda _{2}(\vartheta )\},\\ \Upsilon =\Lambda '_{3}(\vartheta )\Lambda (\vartheta )-\Lambda _{3}(\vartheta )\Lambda '(\vartheta ),\\ \Game (\vartheta )=\Lambda (\vartheta ) \times \Lambda '(\vartheta )=\{\Lambda _{1}(\vartheta )\Lambda '(\vartheta )-\Lambda _{2}(\vartheta )\Lambda '_{1}(\vartheta ),\Lambda _{2}(\vartheta )\Lambda _{0}'(\vartheta )-\Lambda _{0}(\vartheta ) \Lambda '_{2}(\vartheta ), \Lambda _{0}(\vartheta )\Lambda '_{1}(\vartheta )-\Lambda _{1}(\vartheta )\Lambda '_{0}(\vartheta )\},\\ V(\vartheta )=\frac{\Game \times \Upsilon }{\Game \cdot \Game },\quad ~~\vartheta \in [0,1]. \end{array}\right. } \end{aligned}$$

(3.10)

By defining another envelope of one parameter family of planes, the expression given in Eq. (3.11) is obtained,

$$\begin{aligned} E(\vartheta )= \frac{\Lambda ''_{3}(\vartheta )[\Lambda (\vartheta )\times \Lambda '(\vartheta )]+\Lambda _{3}(\vartheta )[\Lambda '(\vartheta )\times \Lambda ''(\vartheta )]+\Lambda '_{3}(\vartheta )[\Lambda ''(\vartheta )\times \Lambda (\vartheta )]}{\Lambda (\vartheta )\cdot [\Lambda '(\vartheta ) \times \Lambda ''(\vartheta )]}. \end{aligned}$$

(3.11)

then the Spine GHT-Bézier developable surface as in²³ can be determined by using the following Eq. (3.12),

$$\begin{aligned} J(\vartheta ,\nu ;\varpi )= E(\vartheta )+\nu E'(\vartheta ), \quad \quad \nu \in (-\infty , +\infty ),~~~ \vartheta \in [0, 1]. \end{aligned}$$

(3.12)

A cylinder is traditionally three dimensional solid and one of the most basic developable surface. The cylinder GHT-Bézier developable surface is obtained by translating a GHT-Bézier dual curve a distance d, where $d\ge 0$ is along the normal vector of the plane. The expression of cylinder GHT-Bézier developable surface is given as:

$$\begin{aligned} H_{cylinder}(\vartheta ,\vartheta _{1};\varpi )= \sum _{i=0}^{3} \sum _{j=0}^{1} P_{i,j} \digamma _{i,3}(\vartheta ) \digamma _{j,1}(\vartheta _{1}) \quad \quad 0 \le \vartheta ,\vartheta _{1}\le 1, \end{aligned}$$

(3.13)

where $P_{i,j}$ are the control points.

A geodesic interpolation curve on GHT-Bézier developable surface as in²³ can be constructed by using Eq. (3.14)

$$\begin{aligned} \mathcal {Q}(\vartheta ,\nu ;\varpi )= \wp (\vartheta ;\Omega )+\nu [\gamma _{1}(\wp '(\vartheta ;\Omega ))+\gamma _{2}\{(\wp '(\vartheta ;\Omega ))\times \wp ''(\vartheta ;\Omega )\} ],\quad \quad \vartheta \in [0,1], ~~\nu \in (-\infty , +\infty ). \end{aligned}$$

(3.14)

The exact representation of geodesic interpolation GHT-Bézier curve can also be represented on the cone having the developability degree. The mathematical representation of the cone is given in Eq. (3.15),

$$\begin{aligned} \mathcal {C}(\vartheta , \nu )=(\nu \varepsilon \tan (\varrho )\cos (2\pi \vartheta ),~ \nu \varepsilon \tan (\varrho )\sin (2\pi \vartheta ),~ \nu \varepsilon ), \end{aligned}$$

(3.15)

where $\varepsilon$ is the maximum height and $\varrho$ is the half aperture angle of the cone.

Developability degree of GHT-Bézier ruled surface

The developable surface has zero Gaussian curvature at every point and a constant tangent plane along any ruling. For a ruled surface $S(\vartheta , \vartheta _{1})$, the tangent lines are not in the same plane and there exists a twisted angle at the ends of a ruling. If the boundary curves are selected in a way that the twisted angle along any ruling equals zero, namely, the surface has the common tangent plane condition everywhere, then the surface becomes developable. The twisted angle can be used to measure the developability degree of a ruled surface. The unit normal vector of the directrix $p(\vartheta )$ and $q(\vartheta )$ are $n_{p}(\vartheta )=\frac{(p(\vartheta )-q(\vartheta ))\times p_{\vartheta }(\vartheta ) }{||(p(\vartheta )-q(\vartheta ))\times p_{\vartheta }(\vartheta )||},$ and $n_{q}(\vartheta )=\frac{(p(\vartheta )-q(\vartheta ))\times q_{\vartheta }(\vartheta )}{||(p(\vartheta )-q(\vartheta ))\times q_{\vartheta }(\vartheta )||},$ respectively.

The twisted angle on the ruling of the ruled surface can be measured for a fixed value of $\vartheta$ by using Eq. (3.16),

$$\begin{aligned} \Im (\vartheta )=(n_{p}(\vartheta ), n_{q}(\vartheta ))-1, \end{aligned}$$

(3.16)

and “,” denote as the inner product between $n_{p}(\vartheta )$ and $n_{q}(\vartheta ).$ In order to determine the developability degree of a ruled surface, few rulings on the surface $S(\vartheta , \vartheta _{1})$ are taken where each of the ruling corresponds to a parameter $\vartheta _{j} \in [0,1],~(j=1,2,...,n).$ The developability degree of the ruled surface is defined as in Eq. (3.17),

$$\begin{aligned} DV=\sum _{j=1}^{K}\{(n_{p}(\vartheta _{j}), n_{q}(\vartheta _{j}))-1\}. \end{aligned}$$

(3.17)

$\Im (\vartheta ) = 0$ only if exact developability is achieved. For a ruled surface, the larger DV is, the better developability the ruled surface has.

Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm

In many industrial planning activities, the shape optimization design of developable surfaces is a crucial and challenging CAD/CAM approach. This section examines the shape optimization of GHT-Bézier developable surfaces with higher developability degree by using an Improved-Grey Wolf Optimization (I-GWO) method. The shape optimization problem is described as an arc length, energy, and curvature variation minimization problem of dual curve which is based on the duality between points and planes in 3D projective space. An I-GWO optimization algorithm is applied to the solution of GHT-Bézier shape optimization models and the optimal values of shape parameters are determined. These optimal values of shape parameters are further used to construct the developable surfaces and also to determine the developability degree. Finally, the effectiveness and performance of the proposed methods is illustrated by some representative and convictive numerical examples.

Cylinder, enveloping and spine GHT-Bézier developable surfaces by using I-GWO method

The shape of GHT-Bézier developable surfaces is very easy to adjust and obtain in²³ because it contains three different shape parameters which help to modify the shape designing’s. People usually construct developable surfaces in engineering with suitable shape and also fulfil some specific requirement according to designer’s aim. In the proposed study, the optimization model is solved to get the optimal shape parameters for the construction of GHT-Bézier developable surface with a higher developability degree. As the values of the shape parameters are chosen from this domain, $\lambda ,\alpha , \beta \in [-1,1],$ and all the values (except zero value) of the parameter $\beta$ from domain $[-1,1]$ will produce a complex and unsolvable expression. So, the power of exponential function is taken as zero, that can be made possible when $\beta =0$ is considered in the optimization models so that the exponential function will be equal to 1,  to avoid complex expression.

As the equation of GHT-Bézier developable surface is a non-linear function of its shape parameters, this equation will generate complex computational results if the equation is used in the optimization model directly. To get simple computational results, the shape optimization problem of GHT-Bézier developable surfaces is converted into a dual curve by using the duality principle. The conversion ensures that the GHT-Bézier developable surface carries the optimal shape with higher developability degree. For this reason the three mathematical models are presented to construct the Enveloping and Spine GHT-Bézier developable surfaces with higher developability degree. The dual curve of one parameter family of planes, based on the duality principle is given in Eq. (3.7).

• 1. Shape Optimization Model I

  In this model, the above-mentioned dual curve holds the shortest AL. The AL is defined as Eq. (4.1) which is based on the AL of the parametric curve.

  $$\begin{aligned} AL(\varpi )=\int _{0}^{1}||L'(\vartheta ;\varpi )||d\vartheta , \quad \varpi =(\lambda , \alpha , \beta ) \end{aligned}$$

  (4.1)

  To simplify the calculation, Eq. (4.1) is replaced with Eq. (4.2) as,

  $$\begin{aligned} \hat{AL}(\varpi )=\int _{0}^{1}||L'(\vartheta ;\varpi )||^{2}d\vartheta ,\quad (\lambda , \alpha ) \in [-1,1],~ \beta =0. \end{aligned}$$

  (4.2)

  For the dual curve having the smallest value of $\hat{AL}$, only specific values of shape parameters are needed which minimize Eq. (4.2). Furthermore, the dual curve given in Eq. (3.7) is simplified as

  $$\begin{aligned} ||L'(\vartheta ;\varpi )||^{2}=\left[ \sum ^{3}_{j=0} w_j \digamma '_{j,r}(\vartheta )\right] ^{2}+\left[ \sum ^{3}_{j=0} x_j \digamma '_{j,r}(\vartheta )\right] ^{2}+\left[ \sum ^{3}_{j=0} y_j \digamma '_{j,r}(\vartheta )\right] ^{2}+\left[ \sum ^{3}_{j=0} z_j \digamma '_{j,r}(\vartheta )\right] ^{2}, \end{aligned}$$

  (4.3)

  where prime represents the first derivative w.r.t “$\vartheta$”. For further simplification, Eq. (4.3) is written as follows

  $$\begin{aligned} ||L'(\vartheta ;\varpi )||^{2}=\sum ^{10}_{j=1} u_{j}(\vartheta ;\varpi )h_{j}, \end{aligned}$$

  (4.4)

  where

  $$\begin{aligned} u_{1}(\vartheta )= & \digamma '_{0,3}(\vartheta )\digamma '_{0,3}(\vartheta ), \quad \quad h_{1}=w_{0}^{2}+x_{0}^{2}+y_{0}^{2}+z_{0}^{2},\\ u_{2}(\vartheta )= & \digamma '_{1,3}(\vartheta )\digamma '_{1,3}(\vartheta ), \quad \quad h_{2}=w_{1}^{2}+x_{1}^{2}+y_{1}^{2}+z_{1}^{2},\\ u_{3}(\vartheta )= & \digamma '_{2,3}(\vartheta )\digamma '_{2,3}(\vartheta ), \quad \quad h_{3}=w_{2}^{2}+x_{2}^{2}+y_{2}^{2}+z_{2}^{2},\\ u_{4}(\vartheta )= & \digamma '_{3,3}(\vartheta )\digamma '_{3,3}(\vartheta ), \quad \quad h_{4}=w_{3}^{2}+x_{3}^{2}+y_{3}^{2}+z_{3}^{2},\\ u_{5}(\vartheta )= & \digamma '_{0,3}(\vartheta )\digamma '_{1,3}(\vartheta ), \quad \quad h_{5}=2(w_{0}w_{1}+x_{0}x_{1}+y_{0}y_{1}+z_{0}z_{1}),\\ u_{6}(\vartheta )= & \digamma '_{0,3}(\vartheta )\digamma '_{2,3}(\vartheta ), \quad \quad h_{6}=2(w_{0}w_{2}+x_{0}x_{2}+y_{0}y_{2}+z_{0}z_{2}),\\ u_{7}(\vartheta )= & \digamma '_{0,3}(\vartheta )\digamma '_{3,3}(\vartheta ), \quad \quad h_{7}=2(w_{0}w_{3}+x_{0}x_{3}+y_{0}y_{3}+z_{0}z_{3}),\\ u_{8}(\vartheta )= & \digamma '_{1,3}(\vartheta )\digamma '_{2,3}(\vartheta ), \quad \quad h_{8}=2(w_{1}w_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}),\\ u_{9}(\vartheta )= & \digamma '_{1,3}(\vartheta )\digamma '_{3,3}(\vartheta ), \quad \quad h_{9}=2(w_{1}w_{3}+x_{1}x_{3}+y_{1}y_{3}+z_{1}z_{3}),\\ u_{10}(\vartheta )= & \digamma '_{2,3}(\vartheta )\digamma '_{3,3}(\vartheta ), \quad \quad h_{10}=2(w_{2}w_{3}+x_{2}x_{3}+y_{2}y_{3}+z_{2}z_{3}). \end{aligned}$$

  By combining Eqs. (4.2) and (4.4), the new Eq. (4.5) is formed as follows

  $$\begin{aligned} \hat{AL}(\varpi )=\int _{0}^{1}||L'(\vartheta ;\varpi )||^{2}d\vartheta =\sum _{j=1}^{10}b_{j}(\varpi )h_{i}, \end{aligned}$$

  (4.5)

  where

  $$\begin{aligned} b_{1}= & \int _{0}^{1}u_{1}(\vartheta )d\vartheta =\frac{1792 e^{\beta }\lambda (1+\lambda )-288\pi ^{2}\lambda (1+\lambda )+18\pi ^{3}(1+2\lambda (1+\lambda ))+27\pi (20+\lambda (8+3\lambda ))}{432\pi },\\ b_{2}= & \int _{0}^{1}u_{2}(\vartheta )d\vartheta =\frac{4-4e^{\beta }+e^{\beta }}{864\pi }\bigg[36\pi ^{2}(3+11\alpha -8\lambda )(1+\lambda )-3\pi (180+392\alpha +301\alpha ^{2}+320\lambda \\ & -308\alpha \lambda +548\lambda ^{2})+32(27+56\alpha ^{2}+139\lambda +224\lambda ^{2}-\alpha (29+197\lambda )+18\pi ^{3}(2\alpha ^{2}\alpha (-2+\lambda )\\ & +2(1+\lambda +\lambda ^{2}))\bigg],\\ b_{3}= & \int _{0}^{1}u_{3}(\vartheta )d\vartheta =\frac{e^{\beta }+2\beta }{432\pi }\bigg[-36\pi ^{2}(1+\alpha )(-3+8\alpha -11\lambda )+32(27+224\alpha ^{2}+\alpha (139-197\lambda )\\ & -29\lambda +56\lambda ^{2})-3\pi (180+548\alpha ^{2}+392\lambda +301\lambda ^{2}-4\alpha (-80+77\lambda )+18\pi ^{3}(2\alpha ^{2}-\alpha (-2+\lambda )\\ & +2(1+\lambda +\lambda ^{2}))\bigg],\\ b_{4}= & \int _{0}^{1}u_{4}(\vartheta )d\vartheta =\frac{1792e^{\beta }\alpha (1+\alpha )-288\pi ^{2}\alpha (1+\alpha +18\pi ^{3}(1+2\alpha (1+\alpha ))+27\pi (20+\alpha (8+3\alpha )))}{432\pi },\\ b_{5}= & \int _{0}^{1}u_{5}(\vartheta )d\vartheta =\frac{-18\pi ^{2}(2-e^{\beta })(9+\alpha )(1+\lambda )-9\pi ^{3}(1+2\lambda (1-\alpha +\lambda ))+ 3\Psi _{1}+\Psi _{2}}{432\pi },\\ b_{6}= & \int _{0}^{1}u_{6}(\vartheta )d\vartheta =\frac{-18\pi ^{2}(2-e^{\beta })(9+\alpha )(1+\lambda )-9\pi ^{3}(1+\lambda (2+\alpha +2\lambda ))+3\pi \Psi _{3}+\Psi _{4}}{432\pi },\\ b_{7}= & \int _{0}^{1}u_{7}(\vartheta )d\vartheta =-\frac{(2e^{\beta }-1)(9\pi ^{3}\alpha \lambda +\pi (432+480\alpha +480\lambda +771\alpha \lambda ) +\Psi _{5})}{432\pi },\\ b_{8}= & \int _{0}^{1}u_{8}(\vartheta )d\vartheta =\frac{-e^{\beta }}{432\pi }\bigg[144\pi ^{2}(\alpha +\lambda +2\alpha \lambda )-3\pi (216+\alpha (232-565\lambda ) +232\lambda +438\lambda ^{2})+\Psi _{6}\bigg],\\ b_{9}= & \int _{0}^{1}u_{9}(\vartheta )d\vartheta =\frac{16e^{\beta }(27+\alpha (27+112\alpha -197\lambda )-85\lambda )-18\pi ^{2}(1+\alpha )(9+\lambda )-\Psi _{7}}{432\pi },\\ b_{10}= & \int _{0}^{1}u_{10}(\vartheta )d\vartheta = \frac{3e^{\beta }\pi (-108+\alpha (-72+110\alpha -137\lambda ))-9\pi ^{3}(1+2\alpha (1+\alpha -\lambda ))+\Psi _{8}}{432\pi }, \end{aligned}$$

  with

  $$\begin{aligned} \Psi _{1}= & \pi (-108+\lambda (-72-137\alpha +110\lambda )),\\ \Psi _{2}= & 8(-27+\alpha (85+197\lambda )-\lambda (363+448\lambda )),\\ \Psi _{3}= & (72+(160-137\lambda )\lambda +2\alpha (80+197\lambda )),\\ \Psi _{4}= & 16(27+\lambda (27+112\lambda )-\alpha (85+197\lambda )),\\ \Psi _{5}= & -108\pi ^{2}(1+\alpha )(1+\lambda )-8(-27+85\lambda +\alpha (85+197\lambda )),\\ \Psi _{6}= & 438\alpha ^{2}+8(135+448\alpha ^{2}+\alpha (23-985\lambda )+23\lambda +448\lambda ^{2})+9\pi ^{3}(2\alpha ^{2}\alpha (-2+\lambda )+2(1+\lambda +\lambda ^{2})),\\ \Psi _{7}= & 9\pi ^{3}(1+\alpha (2+2\alpha +\lambda ))+3\pi (8(9+20\lambda )+\alpha (160-137\alpha +394\lambda )),\\ \Psi _{8}= & -8(27+\alpha (363+448\alpha -197\lambda )-85\lambda )+18\pi ^{2}(1+\alpha )(3+16\alpha -5\lambda ). \end{aligned}$$

  From Eq. (4.5), three shape parameters $(\lambda ,\alpha ,\beta )$ must be different from each other if the arc length, $\hat{AL}(\varpi )$ is taken as fitness function of GHT-Bézier developable surface. So from above discussion, the optimization model is solved to get the minimum $\hat{AL}$ given in Eq. (4.6) as,

  $$\begin{aligned} min~\{\hat{AL}(\varpi )=\int _{0}^{1}||L'(\vartheta ;\varpi )||^{2}d\vartheta =\sum _{j=1}^{10}b_{j}(\varpi )h_{i}, \quad where \quad \lambda , \alpha \in [-1,1],~ \beta =0\}. \end{aligned}$$

  (4.6)

  Due to the high non-linearity of the fitness function, it is hard to find the appropriate values of the shape parameters by direct computation. Therefore, the I-GWO is used to solve the optimization model I, due to its powerful global search ability. The shortest arc length $\hat{AL}(\varpi )$ is considered as a fitness function to find the optimal values of shape control parameters for the construction of GHT-Bézier developable surface along with the developability degree. In each iteration, the value of arc length is evaluated, and for the corresponding shape parameters the value of developability degree is also determined. After successive iterations, when the minimum value of arc length is obtained, then the corresponding optimal shape parameters gives the higher developability degree. The algorithm described in “Construction of GHT-Bézier developable surfaces by using I-GWO algorithm” is follow up for getting the optimal solution.

• 2. Shape Optimization Model II

  In this model, the smoothness of the dual curve is demonstrated which can be measured by its energy value. For smaller value of En, more smoother dual curve is obtained. The shape optimization model of energy value is given as follows

  $$\begin{aligned} En(\varpi )=\int _{0}^{1}||L''(\vartheta ;\varpi )||^{2}d\vartheta ,\quad (\lambda , \alpha ) \in [-1,1], ~ \beta =0. \end{aligned}$$

  (4.7)

  Based on the mathematical representation of the dual curve given in Eq. (3.7), the following relation is obtained

  $$\begin{aligned} ||L''(\vartheta ;\varpi )||^{2}=\left[ \sum ^{3}_{j=0} w_j \digamma ''_{j,r}(\vartheta )\right] ^{2}+\left[ \sum ^{3}_{j=0} x_j \digamma ''_{j,r}(\vartheta )\right] ^{2}+\left[ \sum ^{3}_{j=0} y_j \digamma ''_{j,r}(\vartheta )\right] ^{2}+\left[ \sum ^{3}_{j=0} z_j \digamma ''_{j,r}(\vartheta )\right] ^{2}. \end{aligned}$$

  (4.8)

  Moreover, Eq. (4.8) is rewritten as follows

  $$\begin{aligned} ||L''(\vartheta ;\varpi )||^{2}=\sum ^{10}_{j=1} v_{j}(\vartheta ;\varpi )h_{j}, \end{aligned}$$

  (4.9)

  where

  $$\begin{aligned} v_{1}(\vartheta )= & \digamma ''_{0,3}(\vartheta )\digamma ''_{0,3}(\vartheta ), \quad \quad v_{2}(\vartheta )= \digamma ''_{1,3}(\vartheta )\digamma ''_{1,3}(\vartheta ),\\ v_{3}(\vartheta )= & \digamma ''_{2,3}(\vartheta )\digamma ''_{2,3}(\vartheta ), \quad \quad v_{4}(\vartheta )= \digamma ''_{3,3}(\vartheta )\digamma ''_{3,3}(\vartheta ), \\ v_{5}(\vartheta )= & \digamma ''_{0,3}(\vartheta )\digamma ''_{1,3}(\vartheta ), \quad \quad v_{6}(\vartheta )=\digamma ''_{0,3}(\vartheta )\digamma ''_{2,3}(\vartheta ), \\ v_{7}(\vartheta )= & \digamma ''_{0,3}(\vartheta )\digamma ''_{3,3}(\vartheta ), \quad \quad v_{8}(\vartheta )= \digamma ''_{1,3}(\vartheta )\digamma ''_{2,3}(\vartheta ), \\ v_{9}(\vartheta )= & \digamma ''_{1,3}(\vartheta )\digamma ''_{3,3}(\vartheta ), \quad \quad v_{10}(\vartheta )= \digamma ''_{2,3}(\vartheta )\digamma ''_{3,3}(\vartheta ). \end{aligned}$$

  By combining Eqs. (4.7) and (4.9), the relation for energy given in Eq. (4.10) is obtained,

  $$\begin{aligned} En(\varpi )=\int _{0}^{1}||L''(\vartheta ;\varpi )||^{2}d\vartheta =\sum _{j=1}^{10}g_{j}(\varpi )h_{j}, \end{aligned}$$

  (4.10)

  where

  $$\begin{aligned} g_{1}= & \int _{0}^{1}v_{1}(\vartheta )d\vartheta = \frac{e^{\beta }\pi }{864}[512\lambda (1+\lambda )-144\pi ^{2}\lambda (1+\lambda )+9\pi ^{3}(1+2\lambda +5\lambda ^{2})+54\pi (11+22\lambda +16\lambda ^{2})],\\ g_{2}= & \int _{0}^{1}v_{2}(\vartheta )d\vartheta = \frac{(2e^{\beta }-1)\pi }{864}[18\pi ^{2}(15+23\alpha -8\lambda )(1+\lambda )+9\pi ^{3}(2+5\alpha ^{2}+\alpha (2-4\lambda )+2\lambda +5\lambda ^{2})\\ & -6\pi (-333+70\alpha ^{2}-400\lambda -148\lambda ^{2}+\alpha (86+52\lambda ^{2}))+16(-135+32\alpha ^{2}-71\lambda +128\lambda ^{2}\\ & -\alpha (167+263\lambda ))],\\ g_{3}= & \int _{0}^{1}v_{3}(\vartheta )d\vartheta =\frac{\pi e^{\beta }}{864}(-18\pi ^{2}(1+\alpha )(-15+8\alpha -23\lambda )+6\pi (333+148\alpha ^{2}+\alpha (400-52\lambda )-86\lambda \\ & -70\lambda ^{2})+9\pi ^{3}(2+5\alpha ^{2}+\alpha (2-4\lambda )+2\lambda +5\lambda ^{2})+16(-135+128\alpha ^{2}-167\lambda \\ & +32\lambda ^{2}-\alpha (71+263\lambda ))), \end{aligned}$$
  $$\begin{aligned} g_{4}= & \int _{0}^{1}v_{4}(\vartheta )d\vartheta =\frac{(2e^{2\beta }-e^{\beta })\pi }{864}(512\alpha (1+\alpha )-144\pi ^{2}\alpha (1+\alpha )+9\pi ^{3}(1+2\alpha +5\alpha ^{2})\\ & +54\pi (11+22\alpha +16\alpha ^{2})),\\ g_{5}= & \int _{0}^{1}v_{5}(\vartheta )d\vartheta =\frac{\pi }{1728}[-18\pi ^{2}(3+11\alpha -16\lambda )(1+\lambda )-9\pi ^{3}(1+\lambda (2-8\alpha +5\lambda ))-12\pi (171+\\ & \lambda (342+35\alpha +181\lambda ))+8(135-\lambda (57+256\lambda )+\alpha (199+263\lambda ))],\\ g_{6}= & \int _{0}^{1}v_{6}(\vartheta )d\vartheta =\frac{e^{\beta }\pi }{1728}[-18\pi ^{2}(9+\alpha )(1+\lambda )-9\pi ^{3}(1+\lambda (2+4\alpha +5\lambda ))+12\pi (72+\lambda (232+\\ & 37\lambda )+2\alpha (44+83\lambda ))-16(135+(135-64\lambda )\lambda +\alpha (199+263\lambda ))],\\ g_{7}= & \int _{0}^{1}v_{7}(\vartheta )d\vartheta =\frac{e^{\beta }\pi }{432}[270+398\lambda -9\pi ^{3}\alpha \lambda +54\pi ^{2}(1+\alpha )(1+\lambda )+\alpha (398+526\lambda )-3\pi (88\lambda +\\ & \alpha (88+131\lambda ))],\\ g_{8}= & \int _{0}^{1}v_{8}(\vartheta )d\vartheta =\frac{\pi }{1728}[-9\pi ^{3}e^{\beta }(2+5\alpha ^{2}+\alpha (2-4\lambda )+\lambda (2+5\lambda ))-36\pi ^{2}(9+13\lambda +\alpha (13+\\ & 17\lambda ))+12\pi (-234+33\alpha ^{2}+\lambda (-146+33\lambda )-\alpha (146+79\lambda ))-8(-675+256\alpha ^{2}+\lambda (-739+\\ & 256\lambda )-\alpha (739+1315\lambda ))],\\ g_{9}= & \int _{0}^{1}v_{9}(\vartheta )d\vartheta =\frac{e^{\beta }\pi }{1728}[16(-135+\alpha (-135+64\alpha -263\lambda )-199\lambda )-18\pi ^{2}(1+\alpha )(9+\lambda )-\\ & 9\pi ^{3}(1+\alpha (2+5\alpha +4\lambda ))+12\pi (72+88\lambda +\alpha (232+37\alpha +166\lambda ))],\\ g_{10}= & \int _{0}^{1}v_{10}(\vartheta )d\vartheta =\frac{\pi e^{\beta }}{1728}[-9\pi ^{3}(1+\alpha (2+5\alpha -8\lambda ))-8(-135+\alpha (57+256\alpha -263\lambda )-199\lambda )\\ & +18\pi ^{2}(1+\alpha )(-3+16\alpha -11\lambda )-12\pi (171+\alpha (342+181\alpha +35\lambda ))]. \end{aligned}$$

  In the above discussion, the Shape Optimization Model II is solved to obtain the shape parameters which are used for the construction of GHT-Bézier developable surfaces. To get a smoother dual curve, the smaller value of the fitness function is obtained by applying the I-GWO algorithm, and the generated the optimal shape control parameters are also used to determine the developability degree,

  $$\begin{aligned} min~~\{En(\varpi )=\int _{0}^{1}||L''(\vartheta ;\varpi )||^{2}d\vartheta =\sum _{j=1}^{10}g_{j}(\varpi )h_{j}, \quad where \quad \lambda , \alpha \in [-1,1], \beta =0\}. \end{aligned}$$

  (4.11)

  In each iteration, the energy value is to be evaluated, and for the corresponding shape parameters the value of developability degree is also determined. After successive iterations when the minimum energy value is obtained given in Eq. (4.11), then the corresponding optimal shape parameters gives the higher developability degree. So, for the minimum energy value, the corresponding shape parameters gives the smoother curve of the GHT-Bézier developable surfaces with higher developability degree. The steps to solve this optimization model are given in “Construction of GHT-Bézier developable surfaces by using I-GWO algorithm”.

• 3. Shape Optimization Model III

  In this model, the dual curve with minimum CVEn value is measured by using Eq. (4.12) as follows,

  $$\begin{aligned} CVEn(\varpi )=\int _{0}^{1}||L'''(\vartheta ;\varpi )||^{2}d\vartheta ,\quad (\lambda , \alpha ) \in [-1,1], ~ \beta =0. \end{aligned}$$

  (4.12)

  For this model, the mathematical representation of the dual curve given in Equation (3.7) is used and substitute in Eq. (4.12), to get

  $$\begin{aligned} ||L'''(\vartheta ;\varpi )||^{2}=[\sum ^{3}_{j=0} w_j \digamma '''_{j,r}(\vartheta )]^{2}+[\sum ^{3}_{j=0} x_j \digamma '''_{j,r}(\vartheta )]^{2}+[\sum ^{3}_{j=0} y_j \digamma '''_{j,r}(\vartheta )]^{2}+[\sum ^{3}_{j=0} z_j \digamma '''_{j,r}(\vartheta )]^{2}. \end{aligned}$$

  (4.13)

  The above Eq. (4.13) is simplified in Eq. (4.14) as,

  $$\begin{aligned} ||L'''(\vartheta ;\varpi )||^{2}=\sum ^{10}_{j=1} t_{j}(\vartheta ;\varpi )h_{j}, \end{aligned}$$

  (4.14)

  where

  $$\begin{aligned} t_{1}(\vartheta )= & \digamma '''_{0,3}(\vartheta )\digamma '''_{0,3}(\vartheta ), \quad \quad t_{2}(\vartheta )= \digamma '''_{1,3}(\vartheta )\digamma '''_{1,3}(\vartheta ),\\ t_{3}(\vartheta )= & \digamma '''_{2,3}(\vartheta )\digamma '''_{2,3}(\vartheta ), \quad \quad t_{4}(\vartheta )= \digamma '''_{3,3}(\vartheta )\digamma '''_{3,3}(\vartheta ), \\ t_{5}(\vartheta )= & \digamma '''_{0,3}(\vartheta )\digamma '''_{1,3}(\vartheta ), \quad \quad t_{6}(\vartheta )=\digamma '''_{0,3}(\vartheta )\digamma '''_{2,3}(\vartheta ), \\ t_{7}(\vartheta )= & \digamma '''_{0,3}(\vartheta )\digamma '''_{3,3}(\vartheta ), \quad \quad t_{8}(\vartheta )= \digamma '''_{1,3}(\vartheta )\digamma '''_{2,3}(\vartheta ), \\ t_{9}(\vartheta )= & \digamma '''_{1,3}(\vartheta )\digamma '''_{3,3}(\vartheta ), \quad \quad t_{10}(\vartheta )= \digamma '''_{2,3}(\vartheta )\digamma '''_{3,3}(\vartheta ). \end{aligned}$$

  By combining Eq. (4.13) and Eq. (4.15), the following relation is obtained

  $$\begin{aligned} CVEn(\varpi )=\int _{0}^{1}||L'''(\vartheta ;\varpi )||^{2}d\vartheta =\sum _{j=1}^{10}f_{j}(\varpi )h_{j}, \end{aligned}$$

  (4.15)

  where

  $$\begin{aligned} f_{1}= & \int _{0}^{1}t_{1}(\vartheta )d\vartheta = \frac{\pi ^{3}e^{\beta }(128\lambda (1+\lambda )-576\pi ^{2}\lambda (1+\lambda )+9\pi ^{3}(1+2\lambda +17\lambda ^{2})+\Phi _{1})}{3456},\\ f_{2}= & \int _{0}^{1}t_{2}(\vartheta )d\vartheta =\frac{(2e^{\beta }-1)\pi ^{3}}{3456}(18\pi ^{2}(15+47\alpha -32\lambda )(1+\lambda )+9\pi ^{3}(2+17\alpha ^{2}+\alpha (2-16\lambda )\\ & +2\lambda +17\lambda ^{2})+16(351+8\alpha ^{2}+367\lambda +32\lambda ^{2}+\alpha (343+319\lambda ))+6\pi (855+347\alpha ^{2}+592\lambda \\ & +2584\lambda ^{2}-2\alpha (145+1328\lambda ))),\\ f_{3}= & \int _{0}^{1}t_{3}(\vartheta )d\vartheta =\frac{\pi ^{3}}{3456}[-18\pi ^{2}(1+\alpha )(-15+32\alpha -47\lambda )+9\pi ^{3}(2+17\alpha ^{2}+\alpha (2-16\lambda )+2\lambda \\ & +17\lambda ^{2})+6\pi (855+2584\alpha ^{2}+\alpha (592-2656\lambda )-290\lambda +347\lambda ^{2})+16(351+32\alpha ^{2}+343\lambda \\ & +8\lambda ^{2}+\alpha (367+319\lambda ))],\\ f_{4}= & \int _{0}^{1}t_{4}(\vartheta )d\vartheta =\frac{\pi ^{3}e^{\beta }(128\alpha (1+\alpha )-576\pi ^{2}\alpha (1+\alpha )+9\pi ^{3}(1+2\alpha +17\alpha ^{2})+\Phi _{2} )}{3456},\\ f_{5}= & \int _{0}^{1}t_{5}(\vartheta )d\vartheta =\frac{\pi ^{3}}{6912}(-18\pi ^{2} e^{\beta }(-3+29\alpha -64\lambda )(1+\lambda )-9\pi ^{3}(1+\lambda (2-32\alpha +17\lambda ))\\ & -8(351+\lambda (399+64\lambda )+\alpha (335+319\lambda ))-12\pi (279+\lambda (558-484\alpha +1591\lambda ))),\\ f_{6}= & \int _{0}^{1}t_{6}(\vartheta )d\vartheta =\frac{\pi ^{3}e^{\beta }}{6912}[18\pi ^{2}(-21+11\alpha )(1+\lambda )-9\pi ^{3}(1+\lambda (2+16\alpha +17\lambda ))\\ & +16(351+\lambda (351+16\lambda )+\alpha (335+319\lambda )+24\pi (81+\alpha (176-304\lambda )+\lambda (338+323\lambda )))],\\ f_{7}= & \int _{0}^{1}t_{7}(\vartheta )d\vartheta =-\frac{\pi ^{3}e^{\beta }(702+670\lambda +36\pi ^{3}\alpha \lambda -81\pi ^{2}(1+\alpha )(1+\lambda )+ \alpha (670+638\lambda )+\Phi _{3})}{1728},\\ f_{8}= & \int _{0}^{1}t_{8}(\vartheta )d\vartheta =\frac{-e^{\beta }\pi ^{3}}{6912}(9\pi ^{3}(2+17\alpha ^{2}+\alpha (2-16\lambda )+\lambda (2+17\lambda ))+72\pi ^{2}(3+ 11\lambda +\alpha \\ & (11+19\lambda ))+12\pi (738+993\alpha ^{2}+\alpha (386-2780\lambda )+\lambda (386+993\lambda ))+8(1755+64\alpha ^{2}\\ & +\lambda (1739+64\lambda )+\alpha (1739+1595\lambda ))),\\ f_{9}= & \int _{0}^{1}t_{9}(\vartheta )d\vartheta =\frac{e^{\beta }\pi ^{3}}{6912}[18\pi ^{2}(1+\alpha )(-21+11\lambda )+24\pi (81+\alpha (338+323\alpha -304\lambda )\\ & +176\lambda )-9\pi ^{3}(1+\alpha (2+17\alpha +16\lambda ))+16(351+335\lambda +\alpha (351+16\alpha +319\lambda ))],\\ f_{10}= & \int _{0}^{1}t_{10}(\vartheta )d\vartheta =-\frac{\pi ^{3}}{6912}(12\pi (279+\alpha (558+1591\alpha -484\lambda ))+9\pi ^{3}(1+\alpha (2+17\alpha -32\lambda ))\\ & -18\pi ^{2}(1+\alpha )(3+64\alpha -29\lambda )+8(351+335\lambda +\alpha (399+64\alpha +319\lambda ))). \end{aligned}$$

  where

  $$\begin{aligned} \Phi _{1}= & 54\pi (13+26\lambda +105\lambda ^{2}),\\ \Phi _{2}= & 54\pi (13+26\alpha +105\alpha ^{2}),\\ \Phi _{3}= & -12\pi (-88\lambda +\alpha (-88+31\lambda )). \end{aligned}$$

  For this model, the optimal shape parameters are determined by the minimum values of the fitness function given in Eq. (4.16). These shape parameters are used for the designing of GHT-Bézier developable surfaces with the higher developability degree.

  $$\begin{aligned} min~\{CVEn(\varpi )=\int _{0}^{1}||L'''(\vartheta ;\varpi )||^{2}d\vartheta =\sum _{j=1}^{10}f_{j}(\varpi )h_{j}, \quad where \lambda , \alpha \in [-1,1], \beta =0\}. \end{aligned}$$

  (4.16)

  The specific steps for solving the optimization model are given in “Construction of GHT-Bézier developable surfaces by using I-GWO algorithm”.

GHT-Bézier interpolation curve developable surfaces by using I-GWO algorithm

In this section, three new optimization models for interpolation curves are presented which are used to construct the developable surfaces. The optimization problems of GHT-Bézier developable surfaces are converted in the form of interpolation curve with 3D projective space where the minimum values of $\hat{AL}$, En, and CVEn are used as the fitness function. For the interpolation curve, the mathematical models are given as follows:

• 1. Optimization Model I

  In this model, it is presented that the GHT-Bézier geodesic interpolation curve holds the shortest arc length. The appropriate arc length used in this model is given in Eq. (4.2),

  $$\begin{aligned} \hat{AL}(\varpi )= \int _{0}^{1}||L'(\vartheta ;\varpi )|| \quad \varpi =(\lambda , \alpha , \beta ) \end{aligned}$$

  (4.17)

  Furthermore, the arc length given in Eq. (4.17) can be simplified as,

  $$\begin{aligned} ||L'(\vartheta ;\varpi )||^{2}=\left[ \sum _{j=0}^{3}w_{j}\digamma '_{j,r}(\vartheta )\right] ^{2}+[\sum _{j=0}^{3}x_{j}\digamma '_{j,r}(\vartheta )]^{2}+\left[ \sum _{j=0}^{3}y_{j}\digamma '_{j,r}(\vartheta )\right] ^{2}. \end{aligned}$$

  (4.18)

  For further simplifications, the Eq. (4.18) is written in the form of Eq. (4.19) as

  $$\begin{aligned} ||L'(\vartheta ;\varpi )||^{2}=\sum _{j=1}^{10}u_{j}(\vartheta ;\varpi )\hat{h}_{j} \end{aligned}$$

  (4.19)

  where $u_{j}$ is the same as defined previously in “Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm” and $\hat{h}_{j}$ is given below

  $$\begin{aligned} \hat{h}_{1}= & w_{0}^{2}+x_{0}^{2}+y_{0}^{2}, \quad \quad \quad \quad \quad ~~\quad \hat{h}_{2}=w_{1}^{2}+x_{1}^{2}+y_{1}^{2},\\ \hat{h}_{3}= & w_{2}^{2}+x_{2}^{2}+y_{2}^{2}, \quad \quad \quad \quad \quad ~~\quad \hat{h}_{4}=w_{3}^{2}+x_{3}^{2}+y_{3}^{2},\\ \hat{h}_{5}= & 2(w_{0}w_{1}+x_{0}x_{1}+y_{0}y_{1}), \quad \quad \hat{h}_{6}=2(w_{0}w_{2}+x_{0}x_{2}+y_{0}y_{2}),\\ \hat{h}_{7}= & 2(w_{0}w_{3}+x_{0}x_{3}+y_{0}y_{3}), \quad \quad \hat{h}_{8}=2(w_{1}w_{2}+x_{1}x_{2}+y_{1}y_{2}),\\ \hat{h}_{9}= & 2(w_{1}w_{3}+x_{1}x_{3}+y_{1}y_{3}), \quad \quad \hat{h}_{10}=2(w_{2}w_{3}+x_{2}x_{3}+y_{2}y_{3}). \end{aligned}$$

  After some simplifications, the following relation for arc length is obtained given in Eq. (4.20) as,

  $$\begin{aligned} \hat{AL}=\int _{0}^{1}||L'(\vartheta ;\varpi )||^{2} d\vartheta =\sum _{j=1}^{10}b_{j}(\varpi )\hat{h}_{j}, \end{aligned}$$

  (4.20)

  where $b_{j}(\varpi )$ is the same as defined in “Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm”. By applying I-GWO algorithm, the following model given in Eq. (4.21) is obtained with minimum value of arc length for the construction of geodesic interpolation GHT-Bézier developable surfaces.

  $$\begin{aligned} min~\{\hat{AL}=\int _{0}^{1}||L'(\vartheta ;\varpi )||^{2} d\vartheta =\sum _{j=1}^{10}b_{j}(\varpi )\hat{h}_{j},\quad (\lambda , \alpha ) \in [-1,1], ~ \beta =0\}. \end{aligned}$$

  (4.21)

  The steps described in “Construction of GHT-Bézier developable surfaces by using I-GWO algorithm” are required to solve this optimization model.

• 2. Optimization Model II

  In this optimization model, the energy value of interpolation curve is measured to determine the smoothness of the curve. Smoother curve will be obtained when the energy value is minimum, and the function for energy is given in Eq. (4.22),

  $$\begin{aligned} En(\varpi )=\int _{0}^{1}||L''(\vartheta ;\varpi )||^{2} d\vartheta ,\quad (\lambda , \alpha ) \in [-1,1], ~ \beta =0. \end{aligned}$$

  (4.22)

  In 3D projective space, the mathematical form of the interpolation curve is given as,

  $$\begin{aligned} ||L''(\vartheta ;\varpi )||^{2}=\left[ \sum _{j=0}^{3}w_{j}\digamma ''_{j,r}(\vartheta )\right] ^{2}+[\sum _{j=0}^{3}x_{j}\digamma ''_{j,r}(\vartheta )]^{2}+\left[ \sum _{j=0}^{3}y_{j}\digamma ''_{j,r}(\vartheta )\right] ^{2}. \end{aligned}$$

  (4.23)

  The above Eq. (4.23) is simplified in Eq. (4.24) as follows,

  $$\begin{aligned} ||L''(\vartheta ;\varpi )||^{2}=\sum _{j=1}^{10}v_{j}(\vartheta ;\varpi )\hat{h}_{j}, \end{aligned}$$

  (4.24)

  where the values of $v_{j}$ are same as defined in “Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm” and the values of $\hat{h}_{j}$ are given in “GHT-Bézier interpolation curve developable surfaces by using I-GWO algorithm”. After some simplifications, the optimization model II gives the minimum values of fitness function with optimal shape control parameters expressed as in Eq. (4.25).

  $$\begin{aligned} min~\{En(\varpi )=\int _{0}^{1}||L''(\vartheta ;\varpi )||^{2} d\vartheta =\sum _{j=1}^{10} g_{j}(\varpi )\hat{h}_{j},\quad (\lambda , \alpha ) \in [-1,1], ~ \beta =0\}. \end{aligned}$$

  (4.25)

  These optimal shape control parameters generate the geodesic interpolation GHT-Bézier developable surfaces with higher developability degree. The steps described in “Construction of GHT-Bézier developable surfaces by using I-GWO algorithm” are used to generate the developable surface with higher developability degree.

• 3. Optimization Model III

  In this model, the interpolation curve with minimum curvature variation energy (CVEn) value is determined, and its mathematical representation is given in Eq. (4.26) as,

  $$\begin{aligned} CVEn(\varpi )=\int _{0}^{1}||L'''(\vartheta ;\varpi )||^{2} d\vartheta ,\quad (\lambda , \alpha ) \in [-1,1], ~ \beta =0. \end{aligned}$$

  (4.26)

  The mathematical form of interpolation curve in 3D projective space is given in Eq. (4.27) as,

  $$\begin{aligned} ||L'''(\vartheta ;\varpi )||^{2}=\left[ \sum _{j=0}^{3}w_{j}\digamma '''_{j,r}(\vartheta )\right] ^{2}+\left[ \sum _{j=0}^{3}x_{j}\digamma '''_{j,r}(\vartheta )\right] ^{2}+ \left[ \sum _{j=0}^{3}y_{j}\digamma '''_{j,r}(\vartheta )\right] ^{2}. \end{aligned}$$

  (4.27)

  The above equation can be simplified in Eq. (4.28) as follows,

  $$\begin{aligned} ||L'''(\vartheta ;\varpi )||^{2}=\sum _{j=1}^{10}t_{j}(\vartheta ;\varpi )\hat{h}_{j} \end{aligned}$$

  (4.28)

  where the values of $t_{j}$ are given in “Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm” and the values of $\hat{h}_{j}$ are defined in this “GHT-Bézier interpolation curve developable surfaces by using I-GWO algorithm” (Optimization model I). After solving this optimization model III, the minimum value of the fitness function given in Eq. (4.29) is obtained for the optimal shape control parameters by applying the I-GWO algorithm.

  $$\begin{aligned} min~\{CVEn(\varpi )=||L'''(\vartheta ;\varpi )||^{2}=\sum _{j=1}^{10}f_{j}(\varpi )\hat{h}_{j}\}. \end{aligned}$$

  (4.29)

  The steps are described in “Construction of GHT-Bézier developable surfaces by using I-GWO algorithm” to get the required result.

Construction of GHT-Bézier developable surfaces by using I-GWO algorithm

In this section, the procedure is described to solve the above-defined optimization models by using the I-GWO algorithm. The detailed steps are given as follows:

Results and discussion

In this section, some numerical examples are given to show the efficiency of the I-GWO algorithm. Three shape optimization models are solved to obtain the optimal shape control parameters which generate the developable surfaces with a higher developability degree.

Example 6.1

In this example, the GHT-Bézier enveloping developable surfaces are constructed with different shape parameters. I-GWO algorithm is performed by using optimization models (“Shape optimization of the GHT-Bézier developable surface based on improved-Grey Wolf optimization algorithm”), which generates the optimal shape parameters and gives the higher developability degree of GHT-Bézier enveloping developable surfaces. Consider the specified pattern of control planes given in Eq. (6.1),

$$\begin{aligned} {\left\{ \begin{array}{ll} \ell _{1}=(5 \sqrt{2}, -5 \sqrt{2}, 5, 125),\quad \ell _{2} = (-5 \sqrt{2}, -5 \sqrt{2}, 5, 125),\\ \ell _{3} = (-5 \sqrt{2}, 5 \sqrt{2}, 5, 125), \quad \ell _{4} = (5 \sqrt{2}, 5 \sqrt{2}, 5, 125), \end{array}\right. } \end{aligned}$$

(6.1)

and three wolf candidates are arbitrarily chosen with small values of fitness functions with each wolf has three different values of $\lambda ,$ $\alpha ,$ and $\beta .$ The three optimization models are solved one by one iteratively using I-GWO algorithm until minimum values of the fitness functions are obtained. The corresponding shape parameters are the optimal shape parameters for that optimization model and used to determine the developability degree, the results for each optimization model are tabulated in Table 1. From table value, it can concluded that the higher developability degree is achieved by optimization model III which is CVEn with developability degree 0.96700.

Table 1 The result of optimization models for GHT-Bézier enveloping developable surfaces with developability degree values.

Figure 5

The optimized GHT-Bézier enveloping developable surfaces based on model I, II and III with I-GWO.

The resultant values in Table 1, for three optimization models are obtained after 10th iteration and the I-GWO algorithm is shown to be more efficient because it used fewer iterations with multi-objective functions. The optimized developable surfaces and the iteration scheme of the dual curve for each model are shown in Fig. 5a–f respectively.

Example 6.2

The spine curve of GHT-Bézier developable surfaces is optimized by using the I-GWO algorithm in this example. For the proposed surface, the control planes are given in Eq. (6.2) as,

$$\begin{aligned} {\left\{ \begin{array}{ll} \ell _{1}=(\frac{13}{2}, \frac{13}{2}, \frac{13\sqrt{2}}{2},169 ),\quad \ell _{2} = (\frac{-15}{2}, \frac{15}{2}, \frac{15\sqrt{2}}{2},225),\\ \ell _{3} = (-10,-10,10\sqrt{2},400), \quad \ell _{4} = (\frac{25}{2}, \frac{-25}{2}, \frac{25\sqrt{2}}{2},625). \end{array}\right. } \end{aligned}$$

(6.2)

The spine curve GHT-Bézier developable surface is constructed with different values of shape parameters. The values of shape parameters, values of the fitness function, and developability degree for each optimization models are given in Table 2. The iteration scheme of the dual curve and optimized spine curve of GHT-Bézier developable surfaces are shown in Fig. 6a–f. The higher developability degree is achieved by optimization model III based on Table values.

Figure 6

The optimized spine curve GHT-Bézier developable surfaces based on model I, II and III with I-GWO.

Table 2 The result of optimization models for GHT-Bézier spine developable surfaces with developability degree values.

Example 6.3

In this example, the Cylinder GHT-Bézier developable surfaces are constructed by using various shape parameters. Consider the control points given in the following Eq. (6.3):

$$\begin{aligned} {\left\{ \begin{array}{ll} \ell _{0,0}=(1.5,0,0 ),\quad \ell _{0,1} = (1.5,1.8,0),\\ \ell _{1,0} = (1,0,1), \quad \ell _{1,1} = (1,1.8,1),\\ \ell _{2,0}=(2,0,2),\quad \ell _{2,1} = (2,1.8,2),\\ \ell _{3,0} = (3,0,1), \quad \ell _{3,1} = (3,1.8,1),\\ \ell _{4,0} = (2.5,0,0), \quad \ell _{4,1} = (2.5,1.8,0).\\ \end{array}\right. } \end{aligned}$$

(6.3)

The Improved Grey Wolf Optimization (I-GWO) algorithm is used to iteratively solve the optimization models along with the control points for the cylindrical GHT-Bézier developable surfaces shown in Fig. 7. The optimization models generate the optimal shape parameters to determine the developability degree, and to construct the cylinder GHT-Bézier developable surfaces. The corresponding values of each optimization model are summarized in Table 3. According to the table values, the higher developability degree is obtained by using Optimization Model I, achieving a developability degree of 0.9562.

Figure 7

The optimized cylinder GHT-Bézier developable surfaces based on model I, II and III with I-GWO.

Table 3 The result of optimization models for cylinder GHT-Bézier developable surfaces with developability degree values.

Example 6.4

In this example, the geodesic interpolation curve on GHT-Bézier developable surfaces defined in Eq. (3.10) is optimized with three shape optimization models (as defined in “GHT-Bézier interpolation curve developable surfaces by using I-GWO algorithm”). The control points for the interpolation curve in 3D projective space are given in Eq. (6.4),

$$\begin{aligned} {\left\{ \begin{array}{ll} \ell _{1}=(0,0,0 ),\quad \ell _{2} = (1,0,2),\\ \ell _{3} = (2,0,2), \quad \ell _{4} = (3,0,0), \end{array}\right. } \end{aligned}$$

(6.4)

with the expression given in Eq. (3.14) is used. The geodesic interpolation curve GHT-Bézier surface with different shape parameters is constructed. The optimal shape control parameters, and corresponding values of fitness function and developability degree are given in Table 4. Figure 8a–f shows the iterative scheme for each optimization models and the optimized geodesic interpolation curve on GHT-Bézier developable surfaces, respectively. Optimization model III achieved the higher developability degree with 0.9998.

Figure 8

The optimized geodesic interpolation curve GHT-Bézier developable surfaces based on model I, II and III with I-GWO.

Table 4 The result of optimization models for geodesic interpolation GHT-Bézier developable surfaces with developability degree values.

Example 6.5

In this example, a cone is optimized with geodesic interpolation GHT-Bézier curve on it. The geodesic interpolation of GHT-Bézier curve on the cone is constructed by using Eq. (3.15) with the following set of control points given in Eq. (6.5),

$$\begin{aligned} {\left\{ \begin{array}{ll} \ell _{1}=(0,0,0 ),\quad \ell _{2} = (1,0.5,0),\\ \ell _{3} = (2,0.5,0), \quad \ell _{4} = (3,0,0). \end{array}\right. } \end{aligned}$$

(6.5)

The values of fitness functions and developability degree with optimal shape control parameters are given in Table 5. The optimized geodesic interpolation GHT-Bézier curve on the cone, and the iteration scheme of optimization models with the I-GWO algorithm are shown in Fig. 9a–f. It is concluded that the higher developability degree is obtained by solving optimization model III.

Figure 9

The optimized geodesic interpolation GHT-Bézier curve on cone based on model I, II and III with I-GWO.

Table 5 The result of optimization models for GHT-Bézier geodesic curve on cone with developability degree values.

In the optimization method using the GWO algorithm, the solution space is quite large, leading to slower convergence. However, with the introduction of the DLH search strategy in the I-GWO algorithm, the solution space is significantly reduced, allowing the algorithm to quickly identify the optimal or near-optimal solution. As a result, convergence is consistently achieved around the 10th iteration. When re-running the algorithm with varied initial conditions, the optimal solution is still obtained at the 10th iteration, which serves as the stopping criteria of the proposed method.

Comparative analysis of I-GWO with numerous optimization algorithms

The performance of the proposed Improved Grey Wolf Optimizer (I-GWO) is evaluated against six well-known metaheuristic algorithms: BAT, PSO, MLO, ANN-MFO, GWO, and ALO. The comparison is based on the developability degree obtained for five types of developable surface constructions given in Table 6, 7, 8, 9 and 10. The control points for the four developable surfaces (Enveloping Developable surface, Spine Developable surface, Cylinder GHT-Bézier developable surface, Geodesic Interpolation Developable surface, Developable surface as cone, respectively) are given as follows:

$$\begin{aligned} & {\left\{ \begin{array}{ll} \ell _{1}=(3 \sqrt{2}, -3 \sqrt{2}, 3, 39),\quad \ell _{2} = (-3 \sqrt{2}, -3 \sqrt{2}, 3, 39),\\ \ell _{3} = (-3 \sqrt{2}, 3 \sqrt{2}, 3, 39), \quad \ell _{4} = (3 \sqrt{2}, 3 \sqrt{2}, 3, 39), \end{array}\right. }\\ & {\left\{ \begin{array}{ll} \ell _{1}=(\frac{-13}{2}, \frac{-13}{2}, \frac{13\sqrt{2}}{2},169 ),\quad \ell _{2} = (\frac{-15}{2}, \frac{-15}{2}, \frac{15\sqrt{2}}{2},225),\\ \ell _{3} = (8,8,8\sqrt{2},256), \quad \ell _{4} = (\frac{25}{2}, \frac{25}{2}, \frac{25\sqrt{2}}{2},625), \end{array}\right. }\\ & {\left\{ \begin{array}{ll} \ell _{0,0}=(1.5,0,0 ),\quad \ell _{0,1} = (1.5,1.8,0),\\ \ell _{1,0} = (1,0,1), \quad \ell _{1,1} = (1,1.8,1),\\ \ell _{2,0}=(2,0,2),\quad \ell _{2,1} = (2,1.8,2),\\ \ell _{3,0} = (3,0,1), \quad \ell _{3,1} = (3,1.8,1),\\ \ell _{4,0} = (2.5,0,0), \quad \ell _{4,1} = (2.5,1.8,0),\\ \end{array}\right. }\\ & {\left\{ \begin{array}{ll} \ell _{1}=(0.9,1,3.3 ),\quad \ell _{2} = (1,2.9,1),\\ \ell _{3} = (2,6,1), \quad \ell _{4} = (3.7,1,0). \end{array}\right. } ~~~~~~~~~~~ {\left\{ \begin{array}{ll} \ell _{1}=(4,1,0 ),\quad \ell _{2} = (1,6.5,1),\\ \ell _{3} = (2,0.5,9.3), \quad \ell _{4} = (3,1,8.8). \end{array}\right. } \end{aligned}$$

A higher developability degree generally implies better optimization performance for this application. The graphical comparison shown in Fig. 10 clearly illustrates I-GWO’s edge over other algorithms in terms of higher developability degree and stable convergence behavior. This indicates a more effective exploration and exploitation balance in the search space for developable surface construction.

Table 6 Comparison result of enveloping developable surfaces.

Table 7 Comparison result of spine developable surfaces.

Table 8 Comparison result of cylinder GHT-Bézier developable surfaces.

Table 9 Comparison result for geodesic interpolation curve developable surfaces.

Table 10 Comparison result for geodesic on cone.

Figure 10

Comparison between I-GWO and other optimization algorithms.

Friedman test-based statistical comparison of optimization algorithms for surface developability

To evaluate the performance of the proposed I-GWO algorithm on large-scale problems, five different developable surfaces were considered: S1 (Enveloping), S2 (Spine), S3 (Cylinder), S4 (Geodesic Interpolation), and S5 (Cone). The developability degree was used as the performance metric.

The Friedman test is applied under the same dimensional settings across these surfaces to statistically compare the performance of all algorithms. Figure 11 illustrates the performance comparison of algorithms across all five surfaces, further confirming that I-GWO achieves the highest developability degree among all algorithms tested. As shown in Table 11, I-GWO consistently outperform than other algorithms, demonstrating its superior ability to estimate optimal solutions for large-scale shape optimization problems.

Similarly, the Wilcoxon test is used to compare I-GWO to other algorithms on the based of developability degree of the surfaces. This test performs pairwise comparison for all algorithms and demonstrate the superiority of I-GWO algorithm as shown in the Fig. 12.

Figure 11

Comparison of optimization algorithms across developability degree using Freidman Test.

Table 11 Performance comparison of algorithms across developability degree of surfaces based on Friedman test.

Figure 12

Algorithm comparison on different developable surfaces based in Wilcoxon test.

Wider applicability of I-GWO algorithm

The Improved Grey Wolf Optimization (I-GWO) algorithm has wider applicability compared to other metaheuristic optimization algorithms due to several unique features that enhance its versatility across different problem domains. I-GWO introduces improvements to the standard Grey Wolf Optimization (GWO) by enhancing the balance between global exploration (searching new areas of the solution space) and local exploitation (refining existing solutions). Many meta-heuristic algorithms, such as Particle Swarm Optimization (PSO) or Genetic Algorithms (GA), may struggle to strike this balance effectively, often leading to premature convergence. I-GWO’s ability to maintain this balance makes it suitable for both simple and complex optimization problems.

• 1. Parameter Adaptability: I-GWO offers better control over algorithm parameters, allowing for adaptive adjustments during the optimization process. This reduces the sensitivity to initial parameter settings, which is a common drawback in other meta-heuristics like Ant Colony Optimization (ACO) or GA, where improper parameter tuning can drastically affect performance. The dynamic adjustment in I-GWO enhances its robustness across various problem scales.

• 2. Improved Convergence Speed: Compared to traditional GWO and other metaheuristics like Simulated Annealing (SA) or Differential Evolution (DE), I-GWO shows high convergence rates. By improving the hunting mechanism and hierarchy in GWO, I-GWO is able to achieve faster convergence.

• 3. Handling Multimodal and Complex Problems: I-GWO algorithm contain improved search mechanism which helps it explore more thoroughly and escape local optima more effectively than algorithms like GA or PSO. This advantage makes I-GWO particularly useful in areas like engineering designing.

• 4. Broad Domain Flexibility: The general framework of I-GWO allows it to be applied to a wide range of optimization problems across different fields, including engineering design, machine learning (for hyper parameter optimization and feature selection), energy system optimization, biomedical applications (like medical image analysis and diagnostics), and robotics (for path planning and control). Many other algorithms tend to be more specialized or less adaptable across these domains.

The current I-GWO differs from previous versions by introducing dynamic convergence factor, parameter adaptability, broad domain flexibilty and an improved position update mechanism. Unlike earlier models with fixed or linear parameters, this approach adapts based on iteration progress and solution quality, enhancing convergence speed and accuracy. These modifications make the algorithm more effective for complex shape optimization problems, as reflected in the improved developability results.

Limitations of I-GWO algorithm

The Improved Grey Wolf Optimization (IGWO) algorithm, while offering broader applicability, also has some limitations when compared to other metaheuristic algorithms. I-GWO algorithm, similar to PSO or Ant Colony Optimization (ACO), may struggle with high-dimensional problems. As dimensions increases it results with low convergence speed, and finding optimal solutions becomes more difficult.

Application design for product modeling based on I-GWO

Developability is an important intrinsic property of a surface which required variety of applications in product design. Previous studies provided valuable foundational understanding of surface developability through global and local optimization techniques. Building upon these studies, the proposed research introduces an Improved Grey Wolf Optimizer (I-GWO) based framework to achieve a higher degree of developability with fewer iterations. Unlike previous methods that focused solely on deformation minimization or flattenability improvement, this methodology is extended by constructing complex, multi-strip GHT-Bézier developable surfaces optimized through I-GWO. This enhancement is demonstrated by designing several practical product shapes by using multiple connected developable strips. Each surface is constructed through the optimal choice of shape parameters using the I-GWO algorithm.

In this section, by using the formulation of the ruled surface given in Eq. (3.5), various complicated multi-strip developable surfaces are constructed. According to current industrial trends, the automotive industry increasingly relies on developable surfaces for designing various products like car bodies, ship hulls and shoe upper etc, where the higher degree of developability ensures better manufacturability, minimal material waste, and simplified sheet metal forming. The I-GWO algorithm with few iterations generates the optimal shape parameters which are used to construct the aforementioned designing products with higher developability degree. Figures 13 and 14 illustrate the construction process and corresponding iteration schemes, emphasizing the practical applicability and effectiveness of the proposed method in modern product design. In Fig. 13a the construction of single strip is given while in Fig. 13b the complete design of vase in 3D profile is shown which is obtained by joining various strips of developable surfaces, while each strip has higher devlopability degree and is designed with optimal shape parameters, and in Fig. 13c the iteration scheme of I-GWO is given for the optimized shape.

In Fig. 14a,b, the shape design of car body is given which is obtained by joining multi-strip developable surfaces, where each strip is designed by the optimal choice of shape parameters using I-GWO algorithm. The body panels are typically formed from flat metal sheets, making developable surfaces ideal due to their ability to be unfolded without stretching. Similar to the above shape, the single strip of car body profile is shown in Fig. 14a, while complete shape of car body connected with multi-strip developable surfaces along with iteration scheme of I-GWO algorithm is given in Fig. 14b,c.

Figure 13

(a) Single strip Vase Profile, (b) complete design of multi-strip vase profile, (c) iteration scheme of I-GWO algorithm for vase profile.

Figure 14

(a) Single strip car body profile. (b) Design of multi-strip car body profile, (c) iteration scheme of I-GWO algorithm for car body profile.

Concluding remarks

In this study, the shape optimization of GHT-Bézier developable surfaces using the Improved Grey Wolf Optimization (I-GWO) algorithm has been described. Using the searching strategy and hunting mechanism of gray wolves, this metaheuristic approach iteratively optimizes the shape control parameters across three objective models: arc length (AL), minimum energy (En), and curvature variation energy (CVEn). These models are then solved using the I-GWO algorithm. The optimal values of the shape parameters are based on the minimum values of the fitness function which is obtained by solving optimization models. Finally, the GHT-Bézier developable surfaces are constructed by using optimized shape control parameters and these surfaces possess higher developability degree. Several examples validate the effectiveness of the proposed method. A comparative analysis involving seven other optimization algorithms across four types of developable surfaces demonstrates that I-GWO consistently outperforms the alternatives. Finally, the practical applications in product modeling based on the I-GWO optimized surfaces are also illustrated, highlighting the real-world relevance of the proposed technique.

For future work, the I-GWO algorithm or other meta-heuristics techniques incorporating with machine learning methods, could yield even more efficient solutions. Additionally, expanding the scope of this technique to more complex surface designs, real-time applications, and industrial problems will be valuable.

All the Figs. 5a–c, 6a–c, 7a–c, 8a–c, 9a–c, 13b, 14a,b are obtained by using the MATLAB and Mathematica coding. The author of the manuscript has drawn all these images. The email has also been sent to srep@nature.com which confirms that the author of the manuscript has drawn these images. While Figs. 1a–c and 2 are taken from the literature review and Wikipedia which are properly cited in the revised manuscript.