Seasonal quantile forecasting of solar photovoltaic power using Q-CNN-GRU

Abstract

Accurately predicting solar power is essential for ensuring electric grid reliability and integrating renewable energy sources. This paper presents a novel approach to probabilistic solar power forecasting by combining Convolutional Neural Networks (CNN) with Gated Recurrent Units (GRU) into a hybrid Quantile-CNN-GRU model. The proposed model generates intra-day probabilistic quantile forecasts and is rigorously evaluated using datasets from geographically and climatically diverse regions and hemispheres: the Netherlands (temperate maritime climate), Alice Springs (arid desert climate), and Hebei (humid subtropical climate). These datasets cover varied temporal horizons (1-hour, 6-hour, 12-hour, and 24-hour predictions) and seasonal conditions (summer, fall, spring, and winter), highlighting the model’s adaptability to different scenarios. The performance of the proposed Quantile-CNN-GRU model is benchmarked against state-of-the-art deep learning models, including standalone quantile-based architectures such as Quantile-GRU and Quantile-Long Short Term Memory (LSTM). A comprehensive evaluation framework is applied, employing probabilistic tools like the Continuous Ranked Probability Score (CRPS) for assessing forecast reliability, sharpness, and reliability diagrams with consistency bars to evaluate the calibration of the predictions. Results demonstrate that the proposed Quantile-CNN-GRU model consistently outperforms its counterparts in terms of CRPS, across varying forecast horizons and seasonal conditions. To further enhance performance, a multivariate case study incorporating exogenous inputs, specifically Numerical Weather Prediction (NWP) data, is conducted. Through sensitivity analysis, the influence of these additional inputs on forecast horizons and seasonal variability is systematically explored. The study reveals that integrating NWP data significantly improves the model’s predictive skill, particularly for longer forecast horizons and during transitional seasons like spring and fall, when solar variability is higher.

Introduction

The United Nations reports that climate change is largely driven by our heavy dependence on fossil fuels, which are responsible for more than 75% of global greenhouse gas emissions¹. The need for a global shift toward sustainable and environmentally friendly energy sources has never been more urgent. This goal is reflected in the Paris Agreement, an international accord aimed at limiting the global average temperature increase to below 2°C². Among renewable energy options, solar energy stands out for its many benefits. It is the most abundant, fastest-growing, and cheapest energy source available on Earth, accessible in most countries with varying potential levels, though its full potential remains largely untapped globally³. However, solar energy faces a significant challenge: its intermittency. Solar power generation fluctuates due to factors like the time of day, weather conditions, seasonal changes, and geographic location, complicating traditional methods of managing daily grid operations⁴. Grid operators must adapt their day-ahead, hour-ahead, and real-time procedures to accommodate these variations in solar power generation⁵. Despite its intermittent nature, solar energy’s generation patterns are not random⁶. The ability to predict solar resources with reasonable accuracy plays a critical role in integrating solar energy into the grid. Day-ahead and hour-ahead forecasts can be highly accurate, making it easier to manage the integration of solar power plants into electrical grids. Accurate solar forecasting, especially when considering prediction intervals, is essential. It helps minimize the risks associated with grid operations and optimizes energy storage, ensuring a balance between energy supply and demand⁷.

Solar forecasting is a diverse field that includes a wide range of models, each with different applications, operations, and structures. These models are generally grouped into three categories: machine learning models, physical models, and statistical models⁸. In recent years, deep learning—a subset of machine learning—has gained traction as a promising approach in forecasting research. Several deep learning algorithms, such as convolutional neural networks (CNN), gated recurrent units (GRU), long-short-term memory (LSTM)⁹and Recurrent Neural Networks (RNN), have been employed in numerous studies to predict solar irradiance or photovoltaic (PV) power output. Hybrid models, which hybridize two or more methods to generate the forecast, have gained popularity due to their superior ability to forecast solar irradiation more accurately than standalone models¹⁰. However, these models focus mainly on predicting the mean or average value of the hourly generation of PV energy at a future moment¹¹. While deterministic forecasting models offer some utility, they are inherently limited in their ability to quantify the uncertainties intrinsic to the predicted value. In fact, numerous researchers, including¹²have underscored the limitations of deterministic forecasts. They argue that a comprehensive understanding of the variability and unpredictability inherent in Solar Surface Radiation (SSR) predictions is paramount. This understanding can furnish precise risk assessments for future SSR values, thereby facilitating informed decision-making. Deterministic forecasts, which fail to distinguish between noise and actual data, may not provide reliable insights, particularly if we operate under the assumption of uniformly distributed measurements. In contrast, the prediction of the probability distribution of future values can shed light on situations characterized by noise or unpredictability. Consequently, a non-precise understanding of forecast uncertainties can contribute to a reduction in the standby capacity and costs associated with flexible traditional power generators, also known as spinning reserves, and the energy storage necessary for grid balance¹³. In contrast, probabilistic forecasting models (PFMs) are capable of quantifying such uncertainties¹⁴. These models are gaining momentum as they provide future predictions along with their associated probabilities¹⁵, thereby enabling the quantification of the risk associated with decisions based on these predictions. Despite its potential, probabilistic forecasting has been the subject of relatively few studies, indicating a promising area for future research¹⁶. For instance, a study by Sharma et al.⁷ presents a comparison between a long short-term memory neural network and other simpler approaches for one-day-ahead probabilistic forecasts for a solar power system. Other studies explore various methods applied to probabilistic forecasting in the solar power area. For instance, Fan Lin et al.⁶ propose a new method for intra-day probabilistic solar power forecasting. The authors use fat-tailed distributions to model solar power output and a DeepAR model to map predictors into parameters of the fat-tailed distribution. They also introduce a novel loss function for efficient model training. The proposed model has shown high effectiveness and reliability in providing intra-day probabilistic solar power forecasting. More recently, Xiong et al.¹⁷. proposed a deep probabilistic solar power forecasting framework that combines Transformer networks with Gaussian process approximation, demonstrating superior performance in probabilistic forecasting tasks with 22.6–39.7% improvement in CRPS compared to conventional methods.

Most papers focus on other types of probabilistic methods. For instance, in¹⁸the Monte Carlo Dropout method is used to represent model uncertainty in deep learning. By randomly dropping various units during forecasting, different results are generated, providing a measure of uncertainty. This method can be particularly useful when wanting to capture the inherent variability and uncertainty in solar power generation. However, solar energy is very volatile and can experience extreme events; therefore, there is a need for quantile forecasting. A quantile forecast provides an estimate of the probability that a random variable will be below a certain value. This can be particularly useful when interested in the tails of a distribution, such as extreme events, which are important in solar forecasting to manage the risks associated with over- or under-production of solar power¹⁹. Currently, there is a lack of a structured method to incorporate these forecasts into operational processes and planning schedules. Nevertheless, the significance of these forecasts in developing power systems that are more economical, steady, and dependable is beginning to be acknowledged by operators, with a multitude of research initiatives currently underway²⁰. Furthermore, the literature is replete with a vast number of related studies, which can facilitate the use of probabilistic forecasts²¹.

This paper presents a probabilistic Q-CNN-GRU architecture for quantile forecasting of solar power across three distinct locations: Hebei, China, Bill, Netherlands, and Alice Springs, Australia. The forecasts are made for intraday and day a head (1 h, 6 h, 12 h, 24 h) across four different seasons. Furthermore, a case study was conducted in Hebei province, china for multivariate forecasting. Key contributions of this study include:

• The introduction of a probabilistic deep learning method, Q-CNN-GRU, which integrates GRU and CNN to generate 99 quantile outputs across multiple stations for four seasons.

• The model is rigorously trained and tested on data from three distinct geographical locations with different climatic types, offering a robust evaluation of its performance.

• The proposed model is benchmarked against renowned state-of-the-art models such as Q-LSTM and Q-GRU.

• A comprehensive evaluation is conducted across four seasons and multiple steps (1 h, 6 h, 12 h, 24 h) providing an in-depth understanding of the model’s performance under various conditions. Additionally, a multivariate forecast was tested on the Hebei stations, demonstrating that multivariate forecasting, with the correct inputs, is superior to univariate ones.

• The Continuous Ranked Probability Score (CRPS) and Reliability Diagram with consistency bars are employed for evaluating the model’s performance, ensuring a rigorous assessment of its forecasting capabilities. The CRPS is normalized by the plant rate power (nominal power), which allows comparison of results between different sites.

• The present study adheres closely to the ROPES guidelines formulated by Yang²².

• This work addressees the limited research on the impact of seasonal variations in probabilistic quantile solar power forecasting.

This methodology harnesses the capabilities of quantile deep learning architecture, thereby facilitating the generation of high-precision probabilistic forecasts. Furthermore, it acknowledges the significance of multivariate forecasting, emphasizing the necessity of selecting appropriate input parameters for optimal results. This approach not only enhances the accuracy of predictions but also contributes to the advancement of forecasting methodologies in the field. It underscores the potential of deep learning and multivariate analysis in transforming the landscape of probabilistic forecasting. The organization of this paper is as follows: Sect. 2 provides a comprehensive description of the dataset. Section 3 outlines the preprocessing steps undertaken in the study. The methodology employed is introduced in Sect. 4, while Sect. 5 presents evaluation using the Continuous Ranked Probability Score (CRPS) and reliability diagram with consistency bar as the probabilistic evaluation metric. Section 6 discusses the experimental results and their implications. A study on multivariate forecasting is analyzed in Sect. 7. Finally, Sect. 8 draws conclusions from the study.

Dataset

Three publicly available datasets were used to evaluate the effectiveness of our model. The first dataset originates from residential solar photovoltaic (PV) systems in the province of Utrecht, Netherlands, specifically station ID003 from a total of 175 stations²³ .This dataset provides minute-level power readings from January 2014 to December 2017, with precise geographical coordinates mapped on a 150 m × 150 m grid. An illustrative figure can be found in reference²⁴.The second dataset is sourced from the Desert Knowledge Australia Solar Center (DKASC) in Alice Springs, Australia²⁵. It includes data from the Trina solar assembly, which employs monocrystalline silicon solar panels with dual-axis trackers. This assembly features the Trina TSM-175DC01 panel (model 91-site-1 A) installed in 2009 with a 10.5 kW array, recording power data every 5 min, from August 14, 2013, to December 31, 2024. An illustrative figure can be found in reference²⁶ .The third data set, the PVOD dataset²⁷contains 15-minute resolution power data from 10 PV stations in Hebei Province, China. For this study, Station00, Station01, and Station02 were used, the PVOD data set integrates numerical weather prediction (NWP) data derived from the Weather Research and Forecasting (WRF) model, driven by European Center for Medium-Range Weather Forecasts (ECMWF) ERA5 data. The WRF model provides predictions for 28 to 54 h of horizon with a grid resolution of 4 km and a temporal resolution of 15 min. An illustrative figure can be found in reference²⁷.

Preprocessing

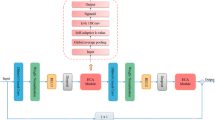
The data preprocessing pipeline follows a systematic seven-step approach to transform raw solar power datasets into a format suitable for deep learning models. As illustrated in Fig. 1, the workflow progresses from time series format conversion through resampling, zenith angle filtering, missing value handling, data splitting, standardization, and sliding window preparation. This strategy was applied to three geographically diverse datasets from the Netherlands, Australia, and China, ensuring data quality and temporal consistency while preparing supervised learning pairs through a 48-hour lookback window for robust intra-day forecasting.

Fig. 1

Comprehensive data preprocessing pipeline for solar power forecasting including time series conversion, filtering, and supervised learning preparation.

Methodology

The gated recurrent unit (GRU)

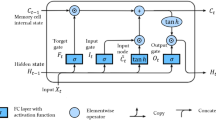
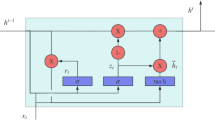
The Gated Recurrent Unit (GRU)²⁸ is a type of recurrent neural network that uses gating mechanisms to regulate the flow of information between cells in the network. These gates play a key role in managing dependencies within sequence data and help address challenges like the vanishing gradient problem. The GRU operates with two main gates: the update gate and the reset gate, along with a current memory content. Together, they decide how much past information should be retained and passed forward, and how much should be discarded.

Update gate

The update gate, denoted as z_t, decides the extent of past information to be passed to the future. It is computed using the equation.

$$\:{z}_{t}=\:\sigma\:\left({W}_{z}\cdot\:\left[{h}_{\left\{t-1\right\}},\:{x}_{t}\right]\right)$$

(1)

where:

• W_z is the weight matrix for the update gate,

• h_t−1 is the hidden state at the previous time step,

• x_t is the input at the current time step,

• σ is the sigmoid function.

Reset gate

The reset gate, denoted as r_t, determines the amount of past information to forget. It is computed as.

$$\:{r}_{t}=\:\sigma\:\left({W}_{r}\cdot\:\left[{h}_{\left\{t-1\right\}},\:{x}_{t}\right]\right)$$

(2)

where W_r is the weight matrix for the reset gate.

Current memory content

The current memory content, denoted as ht, uses the reset gate to store relevant information from the past. It is computed as.

$$\:{\stackrel{\sim}{h}}_{t}=tanh\:\left(W\:.\:\left[{r}_{t}*\:{h}_{t-1},\:{x}_{t}\right]\right)$$

(3)

where:

• W is the weight matrix, and.

• ∗ denotes element-wise multiplication.

Final memory

The final memory at the current time step is a combination of the past memory content, controlled by the update gate, and the current memory content. It is computed as.

$$\:{h}_{t}=\:\left(1\:\--\:{z}_{t}\right)*\:{h}_{t-1}+\:{z}_{t}*\:{\stackrel{\sim}{h}}_{t}$$

(4)

In these equations, h_t is the hidden state at time t, x_t is the input at time t, and W are the weight parameters the model learns. The sigmoid function σ outputs a value between 0 and 1, which assists the update and reset gates in deciding the amount of information to retain or discard. The GRU’s architecture allows it to capture both short-term and long-term dependencies in sequence data, making it a powerful tool for tasks such as time series forecasting, natural language processing, and more.

Convolutional neural networks (CNNs)

CNN is a feed-forward network composed of three different layers, each of which has its functioning²⁹. The convolutional layer works on finding local relationships in the input data, like in our case, the spatial patterns from power and its related input data historical power, while the pooling layer reduces the dimensions of a target variable, and the fully connected layer works on predicting the target variable³⁰. Very few studies reported using CNN in solar forecasting despite being good at extracting hidden features in a given dataset³⁰. CNN is first used for two-dimensional (2D) problems like image and video processing, however, recently one-dimensional (1D) version of it has been used in time series forecasting³¹. The structure of the 1D CNN network is shown in Fig. 2.

Quantile regression

Quantile regression is a robust technique, especially when the focus is on modeling conditional quantile functions rather than just the mean, as is common in ordinary least squares regression. It offers a more comprehensive analysis by capturing different aspects of central tendency and dispersion, making it highly effective in the presence of outliers in response data³². In the context of probabilistic forecasting, where the direct formulation of probabilistic training samples from historical data is a challenge, quantile regression (QR) provides a powerful solution. By predicting multiple quantiles (e.g., 10th, 50th, 90th percentiles) instead of a single value, QR allows for the construction of the probability distribution without requiring explicit probabilistic data during training. The quantile loss function, defined as:

$$\:{L}_{q\left(\widehat{{y}_{q}},\:y\right)}=max\:\left.\left(\:q\:\cdot\:\left(y\:-\:\widehat{{y}_{q}}\right),\:\left(q\:-\:1\right)\cdot\:\left(\widehat{{y}_{q}}-\:y\right)\right.\right)$$

(5)

Fig. 2

Convolutional neural network (CNN) architecture showcasing the sequence of layers, including the input layer, convolutional layers with filters, max pooling layers for dimensionality reduction, fully connected layers, and the output layer, designed for spatial feature extraction in solar power forecasting applications.

ensures that each quantile prediction yˆ_q corresponds to a specific quantile level q ∈ [0, 1], such as q = 0.5 for the median or q = 0.9 for the 90th percentile. This asymmetric penalization of over- and under-estimations allows the model to effectively learn the conditional quantiles, providing a more nuanced and accurate forecast. In a deep learning model, such as the.

CNN-GRU architecture, the final output layer is designed to predict multiple quantiles for each time step. This multi-quantile forecast is represented by:

$$\:\widehat{{y}_{q}}=\:{f}_{\theta\:\left({X}_{t}\right)},\:q\:\in\:\{0.1,\:0.5,\:0.9\}$$

(6)

where $\:{f}_{\theta\:}$ is the CNN-GRU model with parameters θ, and the predicted quantile levels provide confidence intervals for the forecasted values. By applying the quantile loss function during training, the model is capable of predicting a range of outcomes that reflect different levels of uncertainty, significantly enhancing the accuracy and reliability of probabilistic forecasts³³.

Q-CNN-GRU architecture

Combining Convolutional Neural Networks (CNN) with Gated Recurrent Units (GRU) creates a powerful architecture for solar forecasting, effectively capturing both spatial and temporal dependencies in the data. CNNs are particularly effective at processing spatial data, identifying patterns and relationships across different locations, such as multiple photovoltaic (PV) installations or points on a solar irradiance map. This is achieved through their convolutional layers, which apply filters to the input data to produce feature maps³³. These feature maps enable the network to automatically and adaptively learn spatial hierarchies of features, thus recognizing spatial dependencies in the data. In contrast, GRUs are designed to handle temporal data, excelling at capturing long-term dependencies in sequential datasets, which is common in time series forecasting³⁴. GRUs utilize an update gate and a reset gate to regulate the flow of information, ensuring the network efficiently manages time-based dependencies and temporal variations in the data³⁵ The model is trained using quantile regression, which is implemented with a custom loss function for each quantile. This enables the model to predict a range of possible future outcomes (quantiles) rather than a single point estimate. The model forecasts 99 quantiles, ranging from 0.01 to 0.99, providing a fuller picture of potential outcomes and their associated probabilities. This approach is particularly useful for decision-making under uncertainty, as it offers a more comprehensive view of possible scenarios, allowing for better-informed decisions.

To prevent overfitting during training, the model leverages an early stopping callback. After training, the model outputs quantile-based predictions. These predictions are then evaluated using the Continuous Ranked Probability Score (CRPS), a metric that compares the predicted quantiles with the true values. Importantly, the CRPS scores are normalized by the nominal power (plant rate power). This normalization ensures that the forecast performance is consistent across sites, allowing for a meaningful comparison of forecast performance, especially when evaluating sites with differing nominal power capacities. By normalizing the CRPS, we ensure that the forecast performance is not skewed by differences in plant size. The approach has been shown to improve forecast accuracy while maintaining computational efficiency, making it an ideal tool for intra-day decision-making in PV power output forecasting.

Model fine-tuning

The proposed Conv1D-GRU architecture was carefully fine-tuned to balance model complexity, generalization capability, and computational efficiency. The network processes input sequences shaped (batch_size, 48, 1), corresponding to 48 consecutive hourly observations of normalized solar power output. This temporal window effectively captures both diurnal cycles and short-term meteorological fluctuations. The feature extraction module consists of two sequential 1D convolutional layers, each comprising 22 filters with a kernel size of 4, ReLU activation, and ‘same’ padding. These layers output a consistent temporal shape of (batch_size, 48, 22), enabling the preservation of local temporal features. A MaxPooling1D layer with a pool size of 1 follows, maintaining the sequence length while offering structural adaptability. Temporal dependencies are modeled using a GRU layer with 31 hidden units, reducing the representation to (batch_size, 31). GRUs were selected over LSTMs due to their lower computational overhead and similar performance in modeling long-term dependencies. To enhance generalization, dropout regularization with a rate of 10% is applied to the GRU input connections during training. The probabilistic forecasting module comprises 99 parallel Dense layers, each producing a single output corresponding to quantile levels τ ∈ {0.01, 0.02, …, 0.99}, with linear activation functions to support direct quantile regression. Model training is performed using the Adam optimizer with default parameters (learning rate = 0.001, β₁ = 0.9, β₂ = 0.999) and a mini-batch size of 32. The loss function is the quantile (pinball) loss, applied individually to each quantile output. Training is limited to a maximum of 30 epochs, with early stopping (patience = 10) based on validation loss monitoring. This approach halts training when no improvement is observed over ten consecutive epochs and restores the best-performing model weights. Overfitting is mitigated through a combination of architectural and procedural strategies. In addition to dropout and early stopping, the total parameter count is intentionally kept moderate (approximately 8,847 parameters), comprising 198 from the Conv1D layers, 2,046 from the GRU layer, and 6,534 from the 99 Dense output heads. Temporal order is preserved during training, thus maintaining the inherent sequential structure of solar power time series data. These strategies collectively contribute to robust generalization and reliable probabilistic forecasting performance.

Tools for performance evaluation

In this section, we present two primary tools used to evaluate the performance of the proposed Q-CNN-GRU model: the Continuous Ranked Probability Score (CRPS) and the Reliability Diagram with consistency bars.

Continuous ranked probability score (CRPS)

The Continuous Ranked Probability Score (CRPS) is a widely-used metric for assessing the accuracy of probabilistic forecasts by comparing the predicted cumulative distribution function (CDF) to the observed data³⁶. CRPS is particularly valuable in quantile-based forecasting, as it evaluates the difference between the predicted CDF and the step-function CDF of the actual observations³⁷. The formula for CRPS is given by:

$$\:CRPS=\frac{1}{N}{\sum\:}_{i=1}^{N}{\int\:}_{-\infty\:}^{\infty\:}{\left[{\widehat{P}}_{i}^{\text{f}\text{c}\text{a}\text{s}\text{t}}\left(x\right)-{P}_{i}^{{x}_{0}}\left(x\right)\right]}^{2}dx\:$$

(7)

where $\:{\widehat{P}}_{i}^{\text{f}\text{c}\text{a}\text{s}\text{t}}\left(x\right)$ represents the predicted CDF, and $\:{P}_{i}^{{x}_{0}}\left(x\right)$is a step function that jumps from 0 to 1 at the point where the forecasted variable equals the observed value$\:\:{x}_{0}$. In practice, when only a discrete set of quantiles (e.g., 5th, 10th, 50th, 90th, and 95th percentiles) is available, we interpolate between these quantiles to approximate the continuous CDF. This piecewise linear interpolation allows for an accurate CRPS computation by capturing the behavior between quantiles, even in the absence of a continuous probabilistic distribution. CRPS rewards models that tightly concentrate the predicted probability around the actual observations, yielding lower CRPS values for better accuracy. Conversely, models that exhibit bias or fail to sharpen their predictions are penalized with higher CRPS values. By applying this criterion, we ensure that our model’s performance reflects its ability to provide reliable uncertainty estimates. CRPS can address both reliability and resolution, decomposing into three components: reliability, resolution, and uncertainty.

Reliability diagram with consistency bars

The Reliability Diagram is a graphical verification tool used to evaluate the reliability of probabilistic forecasts. It compares the forecasted probabilities of an event to the observed frequencies, providing insight into the calibration of the forecasting model. A perfectly reliable forecast aligns observed proportions with forecast probabilities, resulting in points that lie on the diagonal line of the reliability diagram. To address practical challenges such as limited data and serial correlation in observations, reliability diagrams are supplemented with consistency bars. These bars, as suggested by Brocker and Smith (2007)³⁸account for data limitations and serial dependencies, providing a statistical range within which observed proportions should fall for the forecast to be considered reliable. If observed proportions lie within these consistency bars, the hypothesis that the forecast is reliable cannot be rejected³⁶. The reliability diagram, complemented by consistency bars, offers a robust visual diagnostic tool to assess the calibration of probabilistic forecasts. When combined with CRPS, these tools provide a comprehensive evaluation framework, encompassing both forecast accuracy and reliability under uncertainty.

Results and discussion

The efficacy of the proposed probabilistic model for photovoltaic (PV) power forecasting was evaluated using the Continuous Ranked Probability Score (CRPS) and the reliability diagrams. This evaluation was conducted using historical PV power data from three distinct locations: Hebei Province, China; The Bilt, Netherlands; and Alice Springs, Australia. The model was tested across varying seasons and time horizons (1-hour, 3-hour, 12-hour, and 24-hour forecasts) and compared against state-of-the-art deep learning models, specifically Q-GRU and Q-LSTM. To support the performance analysis, we incorporated ERA5³⁹ reanalysis data to examine how seasonal weather variability and cloud cover influence forecast reliability across the three study sites.

CRPS evaluation

The Continuous Ranked Probability Score (CRPS), normalized to the capacity of each station, facilitates comparisons across different locations. As a negatively oriented metric, lower CRPS values indicate a higher forecast accuracy. The presented results Tables 1 and 2, and Table 3. demonstrate that the Q-CNN-GRU model consistently outperforms alternative models across all locations and forecasting horizons. Moreover, aligning with established findings that the accuracy of the forecast decreases as the forecasting horizon increases due to the accumulation of errors. Among the locations studied, Alice Springs exhibits the lowest CRPS values across all seasons and horizons, reflecting its stable climatic conditions characterized by consistent sunshine and predominantly clear skies. The best performance is achieved in summer for 1-hour ahead forecasts (CRPS: 0.0327), followed by spring, fall, and winter. The highest CRPS is observed in winter for 24-hour ahead forecasts (CRPS: 0.112). A similar seasonal pattern is evident for Hebie, China, where the temperate climate ensures that spring and summer results are closely aligned, while winter shows the weakest performance. In contrast, the Netherlands presents an intriguing case where forecasts in winter outperform those in summer (e.g., CRPS: 0.0386 for 1-hour ahead in winter versus 0.0842 in summer). This seemingly counterintuitive result is consistent with the findings of⁴⁰which attributed the improved winter precision to the predictability of overcast days. In contrast, summer forecasts are less accurate due to the higher variability in solar irradiance, a factor also highlighted in²⁴. Furthermore, transitional seasons, such as spring, exhibit increased variability, leading to reduced forecast accuracy for longer horizons (e.g., CRPS: 0.1487 for 24-hour ahead forecasts in spring, which is the worst of all). These findings show the importance of considering regional climatic conditions when evaluating photovoltaic forecasting models. Regions with consistent solar irradiance, such as Alice Springs, achieve superior performance because of reduced variability, while areas like northern Europe, where cloud cover and seasonal changes dominate, require more robust modeling approaches to account for variability and enhance forecast reliability.

Table 1 CRPS values for the three models (Q-CNNGRU, Q-LSTM, Q-GRU) across all four seasons (summer, winter, fall, spring) and forecasting horizons (1 h, 6 h, 12 h, 24 h) for Alice springs, Australia.

Table 2 CRPS values for the three models (Q-CNNGRU, Q-LSTM, Q-GRU) across all four seasons (summer, winter, fall, spring) and forecasting horizons (1 h, 6 h, 12 h, 24 h) for bill, the Netherlands.

Comparative study for CRPS values in solar forecasting

Our findings demonstrate notable advancements in solar power forecasting, particularly with the Q-CNN-GRU model. For instance, in Alice Springs, the model achieves a CRPS of 0.0327 for a 1-hour forecast, which is significantly lower than the AnEn model’s CRPS of 0.15 for similar timeframes in Italy as depicted in Table 4. Although the accuracy of the models depends on the location of the plant and the year under consideration, the Q-CNN-GRU model highlights its precision over other models, such as Bayesian Model Averaging (BMA), SHADECast, and SolarSTEPS, which generally focus on percentage improvements rather than absolute CRPS values. Additionally, the Q-CNN-GRU model shows robust performance over longer horizons, with a CRPS of 0.0883 for a 24-hour forecast in Alice Springs. Regional variations are also observed, with slightly higher CRPS values in Hebei, China, reflecting challenges commonly found in the literature. Overall, our model provides highly accurate forecasts that are comparable to other advanced models, particularly for short-term horizons, while demonstrating adaptability across diverse geographical contexts.

Reliability diagram

The reliability diagrams depicted in Figs. 3 and 4, and Fig. 5 offer valuable insights into the model’s probabilistic performance, complementing the results from the Continuous Ranked Probability Score (CRPS). The Observed Probability.

Table 3 CRPS values for the three models (Q-CNNGRU, Q-LSTM, Q-GRU) across all four seasons (summer, winter, fall, spring) and forecasting horizons (1 h, 6 h, 12 h, 24 h) for hebei, China.

Table 4 CRPS values from the literature for solar forecasting across regions, lead times, and models.

(y-axis) reflects the actual likelihood of events occurring within the predicted quantile, while the Nominal Probability (x-axis) represents the predicted confidence level. The Perfect Reliability Line (dashed black line) marks the ideal calibration, where the predictions perfectly match the observations, and the Observed Probability Curve (blue line) illustrates the alignment of the model’s predictions with the observed outcomes. The 90% Consistency Bars (shaded pink region) indicate the acceptable range of prediction uncertainty. In the Netherlands (Spring & Summer), the blue curve deviates significantly from the perfect reliability line, indicating poor calibration, which corresponds to higher CRPS values due to increased variability, likely caused by fluctuating weather conditions. In Fall & Winter, the reliability improves, with winter showing the best reliability, potentially due to reduced weather variability. When comparing this to Alice Springs (arid climate) and Hebei, China (monsoon-influenced continental climate), both regions demonstrate better performance during spring and summer, when variability is lower. However, reliability drops in winter, particularly in Alice Springs, though it remains superior to that in the Netherlands. These observations highlight that forecast reliability improves in stable weather conditions with reduced variability, as seen in the fall and winter for the Netherlands, and in summer for Alice Springs and Hebei. The higher variability during spring and summer in the Netherlands poses a challenge to the forecast model’s reliability, suggesting the need for the inclusion of additional weather variables. Ongoing work with the Hebei dataset focuses on improving reliability through feature augmentation, which could provide valuable insights for improving the model in other regions, such as the Netherlands. This analysis underscores the importance of seasonal variability in forecast reliability and demonstrates the potential for model improvement through feature augmentation to enhance calibration.

Fig. 3

Reliability diagrams related to one-hour PV power forecasts across different seasons in the Alice Springs, Australia: (a) Spring, (b) Summer, (c) Winter, (d) autumn. Consistency bars for a 90% confidence level around the ideal line are individually computed for each nominal proportion.

Fig. 4

Reliability diagrams related to one-hour PV power forecasts across different seasons in Bill, the Netherlands: (a) Spring, (b) Summer, (c) Winter, (d)autumn. Consistency bars for a 90% confidence level around the ideal line are individually computed for each nominal proportion.

Fig. 5

Reliability diagrams related to one-hour PV power forecasts across different seasons in Hebei, china: (a) Spring, (b) autumn, (c) Winter, (d) Summer. Consistency bars for a 90% confidence level around the ideal line are individually computed for each nominal proportion.

Meteorological analysis and site-specific weather variability

To explain the reliability degradation patterns observed in Figs. 3 and 4, and 5, we conducted a comprehensive meteorological analysis using ERA5³⁹ reanalysis data examining seasonal weather variability across our three study sites. The analysis reveals distinct climate-driven patterns that directly correlate with solar forecasting challenges.

Table 5 Seasonal mean cloud fraction, annual standard deviation, and coefficient of variation for each study site.

Fig. 6

Seasonal sky condition distributions by site: (a) Utrecht, Netherlands, (b) Hebei Province, China, (c) Alice Springs, Australia. Stacked bars represent the percentage of clear, few clouds, scattered, broken, and overcast conditions observed across seasons.

Fig. 7

Forecast difficulty heatmap by site and season, color intensity indicates qualitative difficulty levels: low, medium, high, and very high, derived from seasonal cloud cover variability and sky condition diversity.

As shown in Table 5, Utrecht, Netherlands exhibits a maritime temperate climate with consistently high total cloud cover ranging from 64.1% in spring to 74.2% in winter, and the lowest annual variability (σ = 0.042). This indicates stable atmospheric conditions, particularly in winter, which are favorable for reliable solar forecasting, while transitional periods like spring introduce moderate uncertainty. Alice Springs, Australia presents an arid continental regime with strong seasonal contrasts—summer cloud cover is lowest (16.6%), supporting optimal forecast conditions, while increased winter cloudiness (35.2%) reflects greater atmospheric instability and reduced predictability. Hebei Province, China shows the highest seasonal cloud cover variability (σ = 0.134), indicative of a monsoon-influenced regime. Winter offers the clearest conditions (25.4%), but summer brings a sharp increase to 56.6%, suggesting a significant rise in forecast difficulty during the monsoon season. Sky condition distributions Fig. 6 and the forecast difficulty heatmap Fig. 7 confirm that reliability is governed more by atmospheric stability than by absolute cloud cover. Both persistently clear and overcast conditions enable accurate forecasting, while transitional periods marked by mixed sky conditions consistently impair performance. These findings strenghten the need for climate-aware forecasting systems that dynamically adapt prediction strategies based on site-specific and seasonal atmospheric patterns, rather than relying solely on historical averages.

Multivariate forecast

A multivariate forecast case study was conducted on a dataset from China, where exogenous variables were used to improve the performance of the model. A sensitivity analysis was performed, as described in the following, to select the most relevant variables for the multivariate forecasting task.

Sensitivity analysis

In this experiment, sensitivity analysis was applied to the PV Power Output Dataset (PVOD), which includes 14 features derived from Numerical Weather Prediction (NWP) data and local measurements, along with timestamps. The dataset, originating from Hebei province, China, captures the temporal and spatial variability of solar power generation. Sensitivity analysis assessed the impact of each input feature, such as temperature, humidity, irradiance, and wind speed, on the forecasted solar power output. By calculating the correlation coefficients between each feature and the power output, we identified the variables with the most significant influence on the model’s predictions. Although advanced feature selection methodologies utilizing machine learning techniques for predictor weighting and optimization have been demonstrated to enhance forecasting performance, as evidenced by Alaoui et al.⁴⁶ who employed random forest and XGBoost algorithms for systematic variable selection in meteorological applications, our correlation-based sensitivity analysis provides a robust and interpretable foundation for identifying key predictors in solar power forecasting.Features with higher correlation were prioritized in the forecasting model, improving its accuracy and efficiency. This process allows us to identify the most important drivers of solar power generation, ensuring that the model is focused on the most relevant factors, while minimizing the impact of less influential features. Ultimately, sensitivity analysis will guide the development of a more robust and precise forecasting model for solar power. The analysis of the bar chart in Fig. 8 and the correlation heatmap in Fig. 9 highlights that solar irradiance variables, including lmd_totalirrad, nwp_globalirrad, and nwp_directirrad, exhibit the strongest positive correlations with power generation, with correlation coefficients reaching as high as 1.0, 0.93, and 0.92, respectively. These findings confirm that solar irradiance is the primary driver of power output in photovoltaic systems. Temperature variables, such as nwp_temperature and lmd_temperature (both 0.43), have a moderate positive impact, reflecting their secondary role in influencing power production. Wind speed (nwp_windspeed: 0.55, lmd_windspeed: 0.38) shows a weaker but noticeable positive correlation, suggesting a limited contribution to power generation. On the other hand, variables like nwp_humidity (-0.38) and pressure variables (nwp_pressure: -0.16, lmd_pressure: -0.18) have minimal or negative correlations, indicating their inverse or negligible effects on power output. Wind direction has no significant correlation with power production. Therefore, in our multivariate case, we chose the solar irradiance variables as exogenous input parameters for the model.

Evaluation for multivariate forecasting

The results in Table 6, Fig. 10, and Fig. 11 clearly demonstrate that the multivariate Q-CNN-GRU model, which incorporates additional solar irradiance variables alongside historical solar power data (NWP and LMD irradiance variables), consistently outperforms the univariate model that relies solely on historical solar power data. This conclusion is supported by both the CRPS values and reliability diagrams. The reliability diagrams highlight the improved calibration of the multivariate forecasts, with the observed probability curve (blue line) closely aligning with the perfect reliability line or within consistency bars. This improved calibration indicates that the multivariate model effectively captures the underlying variability and uncertainty in solar power forecasting. Furthermore, the CRPS values reinforce these findings, as the multivariate model exhibits significantly lower scores across all forecasting horizons (1 h, 6 h, 12 h, 24 h) and seasons. An additional bar chart illustrates the percentage improvement in CRPS values when transitioning from the univariate to the multivariate model. Significant improvements are observed, particularly for the 1-hour horizon, where summer (> 20%) and winter (~ 18%) show the largest gains. This shows the importance of including solar irradiance variables, as they enable the multivariate model to better capture seasonal and short-term variability that the univariate model could not. Although the improvements are less pronounced for longer horizons, the multivariate approach consistently outperforms the univariate model across all seasons and horizons. This demonstrates the value of integrating external weather variables, which enhance forecast accuracy, especially during highly variable conditions such as fall and winter in case of Hebei, china. These results highlight the potential of feature augmentation, specifically the incorporation of solar irradiance variables, in improving both the reliability and accuracy of solar power forecasts. Such advancements are particularly critical for addressing challenges in regions with high variability in weather conditions.

Fig. 8

Ranking of 13 input parameters derived from numerical weather prediction (NWP) data and local measurements, based on the value of correlation coefficient (R).

Fig. 9

Correlation Heatmap for 14 features derived from numerical weather prediction (NWP) data and local measurements, along with timestamps.

Table 6 CRPS values in multivariate case for the three models (Q-CNN-GRU, Q-LSTM, Q-GRU) across all four seasons (summer, winter, fall, spring) and forecasting horizons (1 h, 6 h, 12 h, 24 h) for hebei, China.

Fig. 10

Reliability diagrams related to one-hour multivariate PV power forecasts across different seasons in Hebei, china: (a) winter, (b) Summer, (c) autumn, (d) Spring. Consistency bars for a 90% confidence level around the ideal line are individually computed for each nominal proportion.

Fig. 11

Bar chart showing the improvement in CRPS values from univariate to multivariate case, across all four seasons (summer, winter, fall, spring) and forecasting horizons (1 h, 6 h, 12 h, 24 h) for Q-CNN-GRU model for Hebei, china.

Conclusion

In this paper, we evaluate the effectiveness of a hybrid deep learning model that combines a Convolutional Neural Network (CNN) and a Gated Recurrent Unit (GRU) to generate intra-day probabilistic quantile predictions. The model’s performance is analyzed using datasets from three geographically distinct locations: the Netherlands, Australia, and China. Predictions are made for various time horizons, including 1-hour, 6-hour, 12-hour, and 24-hour intervals, across all four seasons.

The proposed model is benchmarked against state-of-the-art deep learning models, including the standalone Quantile Gated Recurrent Unit (Q-GRU) and Quantile Long Short-Term Memory (Q-LSTM). The evaluation employs metrics such as the Continuous Ranked Probability Score (CRPS) and reliability diagrams with consistency bars to assess both the sharpness and reliability of the probabilistic predictions.

Empirical results demonstrate that the proposed model consistently outperforms the alternatives, achieving the lowest CRPS across all time horizons and seasons. This shows the model’s exceptional capability to produce accurate and reliable probabilistic predictions under varying temporal and seasonal conditions. Furthermore, a case study conducted in a multivariate setting, with input variables selected based on sensitivity analysis, revealed significant performance improvements compared to the univariate approach.

By leveraging the strengths of ensemble deep learning architectures, this methodology represents a significant advancement in energy yield prediction for photovoltaic (PV) power plants. The results highlight its potential to transform solar power forecasting, contributing to more efficient and sustainable energy production strategies.