A numerical approach to fractional Volterra–Fredholm integro-differential problems using shifted Chebyshev spectral collocation

Abstract

This study presents an innovative numerical framework for addressing initial value problems (IVPs) in linear fractional Volterra–Fredholm integro-differential equations (FVFIDEs). The approach utilizes a spectral collocation method grounded in shifted Chebyshev polynomials of the second kind to construct an approximate solution. By integrating this approximation into the governing equation and applying collocation constraints at predefined nodes, the IVP is converted into a system of linear algebraic equations. This system is subsequently resolved using the Newton–Raphson iteration, ensuring computational precision and rapid convergence. To validate the method’s efficacy, a series of benchmark examples are analyzed, highlighting its stability, efficiency, and adaptability. The findings underscore the scheme’s high-order accuracy, positioning it as a robust computational tool for fractional Volterra–Fredholm integro-differential problems in applied mathematics and engineering.

Introduction

Fractional calculus has emerged as a powerful tool in modeling complex phenomena across various fields of science and engineering. Its ability to describe memory-dependent processes and non-local behaviors has led to widespread applications in viscoelasticity, anomalous diffusion, and biological systems, among others^1,2,3.

The foundational works^1,2,3 provide rigorous mathematical treatments of fractional differential equations, establishing key theoretical frameworks for their analysis. These texts are essential in understanding the existence, uniqueness, and stability of solutions, forming the basis for subsequent applied research.

In applied sciences, fractional calculus has been instrumental in modeling viscoelastic materials. Craiem and Magin⁴ developed fractional-order models to analyze red blood cell membrane mechanics, offering improved accuracy over classical approaches. Similarly,⁵ applied fractional Kelvin–Voigt and Maxwell models to characterize viscoelastic dampers, demonstrating their effectiveness in structural dynamics. The work of⁶ further extended these principles to anomalous diffusion phenomena, employing fractional operators in the Bloch-Torrey equation to describe complex diffusion patterns in magnetic resonance imaging.

The numerical and analytical treatment of fractional integro-differential equations has also seen significant advancements. Ordokhini and Rahimi⁷ proposed a Haar wavelet-based numerical scheme for solving fractional Volterra equations, contributing to efficient computational methods. Xiaohua and Chengming⁸ introduced a hybrid collocation technique, enhancing accuracy in solving such equations. Analytical approaches have been explored by⁹, who derived exact solutions for certain classes of fractional integro-differential equations. Additionally, Rawashdeh¹⁰ developed a collocation-based numerical method, providing a practical tool for approximating solutions in applied mathematics.

Recent advances in fractional calculus have enabled diverse solution approaches, such as fractional polynomial approximations for Riccati equations¹¹, predictor–corrector methods for fractional ODEs¹², and Adomian decomposition techniques¹³. However, these methods either neglect integral kernels or assume simplified forms, limiting their applicability to Volterra integro-differential systems. Our work bridges this gap by unifying their strengths—polynomial efficiency¹¹, numerical rigor¹², and decomposition adaptability¹³—into a framework tailored for equations with memory-driven kernels.

The study of fractional Volterra integro-differential equations (FVIDEs) has seen significant advancements through various analytical and numerical techniques. A Bernoulli polynomial collocation method for weakly singular FVIDEs was developed in¹⁴, while Yang-Laplace transforms were employed for analytical solutions in¹⁵. Investigations of FVIDEs in Banach spaces were conducted in¹⁶, and an artificial neural network (ANN) approach was introduced in¹⁷. The Sumudu transform was utilized in¹⁸, while a local fractional variational iterative method was proposed in¹⁹. Jacobi polynomials were applied to fuzzy FVIDEs in²⁰, and rationalized Haar functions were leveraged in²¹. Numerical schemes such as the least squares-homotopy perturbation method were explored in²², and Laguerre polynomials were used in²³. Neutral FVIDEs with infinite delay were addressed in²⁴, while a hybrid collocation method was introduced in²⁵. Spectral techniques for pantograph delay equations were advanced in²⁶. Recent contributions include a systematic method for initial value problems in²⁷, a combination of least squares with shifted Chebyshev polynomials in²⁸, and comparative analyses of numerical schemes in²⁹. These diverse approaches underscore the ongoing evolution of FVIDE solvers, motivating our work to enhance accuracy or computational efficiency.

This study introduces a novel spectral collocation scheme based on shifted Chebyshev polynomials to efficiently solve linear fractional Volterra–Fredholm integro-differential equations (FVFIDEs), leveraging their superior approximation properties to transform the original problem into a system of algebraic equations solved via the Newton–Raphson method. Our primary objectives are:

• (1) To develop a highly accurate and computationally efficient numerical scheme;

• (2) To rigorously analyze the method’s convergence and stability properties;

• (3) To validate the approach through benchmark examples with comparisons to existing techniques.

While several methods exist for classical Volterra–Fredholm FIDEs, the inclusion of a separate Fredholm integral operator introduces new computational challenges that remain understudied in prior works. The proposed framework specifically addresses this gap by providing a robust numerical solution that maintains convergence and stability while handling the combined Volterra–Fredholm structure, offering significant improvements over conventional approaches in both theoretical rigor and practical implementation.

Despite significant advancements in spectral methods for fractional equations, the literature reveals a paucity of studies that comprehensively address the combined computational challenges posed by Volterra–Fredholm operators, fractional derivatives, and integro-differential terms within a unified framework. Conventional approaches frequently exhibit limitations including suboptimal convergence rates, numerical instability, or prohibitive computational complexity when applied to such problems. The present work addresses these critical gaps through three principal contributions:

• (1) The development of a novel shifted Chebyshev collocation method specifically designed for FVFIDEs;

• (2) A comprehensive error analysis establishing the theoretical robustness of the proposed scheme;

• (3) Extensive numerical validation demonstrating the superior computational performance and accuracy advantages over existing techniques.

In this work, we extend the previous problem by considering a more general form of the fractional Volterra–Fredholm integro-differential equation,

$$\begin{aligned} ^c{\mathcal {D}}^{\mathfrak {w}} \Bbbk ({\mathfrak {s}}) = \Phi ({\mathfrak {s}}) + \rho ({\mathfrak {s}}) \Bbbk ({\mathfrak {s}}) + \int _{0}^{{\mathfrak {s}}} {\mathfrak {K}}({\mathfrak {s}},\sigma )\Bbbk (\sigma ) d\sigma + \int _{0}^{\xi } \hslash ({\mathfrak {s}},\sigma )\Bbbk (\sigma ) d\sigma + ^c{\mathcal {D}}^{{\mathfrak {w}}-1} \Bbbk ({\mathfrak {s}}), \end{aligned}$$

(1)

subject to the initial condition

$$\begin{aligned} \Bbbk ^{(n-1)}(0) = \Bbbk _{n-1}, \quad n-1 < {\mathfrak {w}} \le n, \end{aligned}$$

(2)

where

• Domain of the Problem:

  • Time domain: ${\mathfrak {s}} \in [0, \xi ]$, where $\xi > 0$ is arbitrary.

  • Kernel domains:

    • Volterra kernel ${\mathfrak {K}}({\mathfrak {s}}, \sigma )$: Defined on $[0, {\mathfrak {s}}] \times [0, {\mathfrak {s}}]$.

    • Fredholm kernel $\hslash ({\mathfrak {s}}, \sigma )$: Defined on $[0, {\mathfrak {s}}] \times [0, \xi ]$.

  • Solution space: $\Bbbk \in C^{n-1}[0, \xi ] \cap AC^n[0, \xi ]$ (ensures classical initial condition $\Bbbk ^{(n-1)}(0) = \Bbbk _{n-1}$).

• Validity of the Scheme for All Domains:

  • The analyticity of ${\mathfrak {K}}$ and $\hslash$ ensures smoothness and avoids singularities, allowing spectral convergence.

  • The absolute continuity condition ($AC^n$) guarantees the Caputo derivative $^c {\mathcal {D}}^{\mathfrak {w}} \Bbbk ({\mathfrak {s}})$ is well-defined.

  • The collocation method remains stable for any $\xi > 0$ because:

    • The kernels are nonsingular and analytic.

    • The solution space $C^{n-1} \cap AC^n$ ensures compatibility with initial conditions.

Thus, our method applies for any $\xi > 0$ under these conditions.

The remaining content is structured as follows: “Auxiliary results” section deals with the fundamental ideas and theorems that will underpin the results. The uniqueness of solutions (1)–(2) and the existence of the system under adequate assumptions are demonstrated in “Methodology” section. Applications are subsequently detailed in “Numerical illustrations” section.

Auxiliary results

This section introduces fundamental definitions and properties from fractional calculus theory and shifted Chebyshev polynomials, which serve as basis functions. See^30,31,32,33.

Lemma 1

(Kilbas et al.² and Podlubny³) Let $\Phi ({\mathfrak {s}})$ be sufficiently smooth on (a, b) and ${\mathfrak {w}} > 0$. The left and right Caputo fractional derivatives of order ${\mathfrak {w}}$ are defined by:

$$\begin{aligned} {^C_{{\mathfrak {a}}^+}}{\mathcal {D}}^{\mathfrak {w}}_{\mathfrak {s}} \Phi ({\mathfrak {s}}) = \frac{1}{\Gamma (\upsilon - {\mathfrak {w}})} \int _{{\mathfrak {a}}}^{{\mathfrak {s}}} ({\mathfrak {s}} - \varpi )^{\upsilon - {\mathfrak {w}} - 1} \Phi ^{(\upsilon )}(\varpi ) \, d\varpi , \end{aligned}$$

(3)

and

$$\begin{aligned} {^C_{{\mathfrak {b}}^-}}{\mathcal {D}}^{\mathfrak {w}}_{\mathfrak {s}} \Phi ({\mathfrak {s}}) = \frac{(-1)^\upsilon }{\Gamma (\upsilon - {\mathfrak {w}})} \int _{{\mathfrak {s}}}^{{\mathfrak {b}}} (\varpi - {\mathfrak {s}})^{\upsilon - {\mathfrak {w}} - 1} \Phi ^{(\upsilon )}(\varpi ) \, d\varpi , \end{aligned}$$

(4)

where $\upsilon = \lceil {\mathfrak {w}} \rceil$ is the smallest integer greater than or equal to ${\mathfrak {w}}$.

In the extended model, we also require the definition of the Caputo derivative of order ${\mathfrak {w}} - 1$. The same formulas apply with $\upsilon ' = \lceil {\mathfrak {w}} - 1 \rceil$.

Definition 1

(Diethelm¹) The uniform collocation points within the interval $[\mu , \delta ]$ are defined as:

$$\begin{aligned} s_q = \mu + \frac{(\delta - \mu )}{M} q, \quad q = 1, \dots , M, \end{aligned}$$

(5)

where M is the total number of points. These equidistant points are commonly used in numerical methods requiring uniform discretization. For specialized applications, alternative distributions.

Definition 2

(Canuto et al.³⁴) To quantify numerical stability, we introduce a practical metric termed the stability factor, defined as:

$$\begin{aligned} \text {Stability Factor}:= \frac{\Vert \Bbbk _\text {approx}\Vert _\infty }{\Vert {\textbf{F}}\Vert _\infty }, \end{aligned}$$

where $\Bbbk _\text {approx}$ is the numerical solution vector obtained from the collocation method, and ${\textbf{F}}$ is the discretized right-hand side vector. This ratio serves as an indicator of how sensitive the solution is to the input data or perturbations. A bounded or slowly varying stability factor implies that the method does not amplify numerical errors, which is a key sign of robustness.

In addition, we compute the condition number $\kappa ({\mathcal {A}})$ of the system matrix ${\mathcal {A}}$:

$$\begin{aligned} \kappa ({\mathcal {A}}) = \Vert {\mathcal {A}}\Vert \cdot \Vert {\mathcal {A}}^{-1}\Vert , \end{aligned}$$

which provides insight into the sensitivity of the system to numerical perturbations. While an increase in $\kappa ({\mathcal {A}})$ with growing ${\mathcal {M}}$ is typical in spectral methods, the stability factor remains bounded or decreases in our results, supporting the overall stability of the scheme.

Remark 1

The condition number alone does not fully characterize stability; the stability factor offers a more practical measure. Even with a growing condition number, a decreasing or stable stability factor confirms that the numerical method remains robust.

Chebyshev polynomials³⁵

Standard Chebyshev polynomials (first Kind) on $[-1, 1]$

The Chebyshev polynomials of the first kind, $\Upsilon _i(s)$, are defined by the recurrence relation:

$$\begin{aligned} \Upsilon _{i+1}(s) = 2s \Upsilon _i(s) - \Upsilon _{i-1}(s), \quad i = 1, 2, \dots , \end{aligned}$$

with initial conditions:

$$\begin{aligned} \Upsilon _0(s) = 1, \quad \Upsilon _1(s) = s. \end{aligned}$$

The explicit form is:

$$\begin{aligned} \Upsilon _i(s) = \frac{i}{2} \sum _{j=0}^{\lfloor i/2 \rfloor } (-1)^j \frac{(i - j - 1)!}{j!~ (i - 2j)!} (2s)^{i - 2j}. \end{aligned}$$

Shifted Chebyshev polynomials on $[0, 1]$

The shifted Chebyshev polynomials, ${\widetilde{\Upsilon }}_i(s)$, are defined as:

$$\begin{aligned} {\widetilde{\Upsilon }}_i(s) = \Upsilon _i(2s - 1). \end{aligned}$$

Their recurrence relation is:

$$\begin{aligned} {\widetilde{\Upsilon }}_{i+1}(s) = 2(2s - 1) {\widetilde{\Upsilon }}_i(s) - {\widetilde{\Upsilon }}_{i-1}(s), \quad i = 1, 2, \dots , \end{aligned}$$

(6)

with initial conditions:

$$\begin{aligned} {\widetilde{\Upsilon }}_0(s) = 1, \quad {\widetilde{\Upsilon }}_1(s) = 2s - 1. \end{aligned}$$

The explicit form is:

$$\begin{aligned} {\widetilde{\Upsilon }}_i(s) = \sum _{j=0}^i (-1)^{i-j} \frac{i (i + j - 1)!}{j!~ (i - j)!} (2s)^j. \end{aligned}$$

Spectral approximation of the solution

The approximate solution is expressed as a truncated series of shifted Chebyshev polynomials:

$$\begin{aligned} \Bbbk ({\mathfrak {s}}) \approx \Bbbk _{\mathcal {M}}({\mathfrak {s}}) = \sum _{j=0}^{\mathcal {M}} {\mathfrak {a}}_j {\widetilde{\Upsilon }}_j({\mathfrak {s}}) = \varvec{\Upsilon }({\mathfrak {s}}){\mathcal {A}}, \end{aligned}$$

(7)

where $\varvec{\Upsilon }({\mathfrak {s}}) = [{\widetilde{\Upsilon }}_0({\mathfrak {s}}), {\widetilde{\Upsilon }}_1({\mathfrak {s}}), \ldots , {\widetilde{\Upsilon }}_{\mathcal {M}}({\mathfrak {s}})]$ and ${\mathcal {A}} = [{\mathfrak {a}}_0, {\mathfrak {a}}_1, \ldots , {\mathfrak {a}}_{\mathcal {M}}]^T$ is the coefficient vector.

To discretize the governing fractional integro-differential equation, all terms are approximated consistently using the shifted Chebyshev basis. In particular, the Caputo fractional derivatives—both ${}^c{\mathcal {D}}^{{\mathfrak {w}}} \Bbbk ({\mathfrak {s}})$ and the lower-order term ${}^c{\mathcal {D}}^{{\mathfrak {w}}-1} \Bbbk ({\mathfrak {s}})$—are treated numerically by applying the operational matrices of the Caputo derivative corresponding to each order. Let ${\mathcal {D}}^{{\mathfrak {w}}}$ and ${\mathcal {D}}^{{\mathfrak {w}}-1}$ denote the operational matrices for orders ${\mathfrak {w}}$ and ${\mathfrak {w}}-1$, respectively. Then, the spectral approximations of the derivatives are given by:

$$\begin{aligned} {}^c{\mathcal {D}}^{{\mathfrak {w}}} \Bbbk ({\mathfrak {s}}) \approx \varvec{\Upsilon }({\mathfrak {s}}) {\mathcal {D}}_{{\mathfrak {w}}} {\mathcal {A}}, \quad {}^c{\mathcal {D}}^{{\mathfrak {w}}-1} \Bbbk ({\mathfrak {s}}) \approx \varvec{\Upsilon }({\mathfrak {s}}) {\mathcal {D}}_{{\mathfrak {w}}-1} {\mathcal {A}}. \end{aligned}$$

This ensures that all differential terms in the system are discretized uniformly within the spectral collocation framework, thereby preserving the high accuracy and stability of the method.

Discretization of Caputo fractional derivatives

Properties of Caputo fractional operators

Let ${\mathfrak {w}}, \kappa \in {\mathbb {C}}$ with $\text {Re}({\mathfrak {w}}), \text {Re}(\kappa ) > 0$, and ${\mathfrak {a}}, {\mathfrak {s}} \in {\mathbb {R}}$ where ${\mathfrak {s}} \ge {\mathfrak {a}}$. The Caputo fractional integral ${\mathcal {I}}^{\mathfrak {w}}$ and derivative ${\mathcal {D}}^{\mathfrak {w}}$ satisfy the following properties^1,2:

• 1. Power function rules

  • Fractional Integral of Power Functions:

    $$\begin{aligned} {\mathcal {I}}^{\mathfrak {w}} \left[ ({\mathfrak {s}} - {\mathfrak {a}})^{\kappa - 1} \right] = \frac{\Gamma (\kappa )}{\Gamma (\kappa + {\mathfrak {w}})} ({\mathfrak {s}} - {\mathfrak {a}})^{\kappa + {\mathfrak {w}} - 1}. \end{aligned}$$

    (8)

  • Fractional Derivative of Power Functions:

    $$\begin{aligned} {\mathcal {D}}^{\mathfrak {w}} \left[ ({\mathfrak {s}} - {\mathfrak {a}})^{\kappa - 1} \right] = \frac{\Gamma (\kappa )}{\Gamma (\kappa - {\mathfrak {w}})} ({\mathfrak {s}} - {\mathfrak {a}})^{\kappa - {\mathfrak {w}} - 1}, \quad \text {for } \text {Re}(\kappa ) > \text {Re}({\mathfrak {w}}). \end{aligned}$$

    (9)

  • Special Case (${\mathfrak {a}} = 0$):

    $$\begin{aligned} {\mathcal {I}}^{\mathfrak {w}} \left[ {\mathfrak {s}}^\zeta \right] = \frac{\Gamma (\zeta + 1)}{\Gamma ({\mathfrak {w}} + \zeta + 1)} {\mathfrak {s}}^{{\mathfrak {w}} + \zeta }, \quad \zeta > -1. \end{aligned}$$

    (10)

• 2. Derivative-specific properties To discretize the Caputo fractional derivatives in Eq. (1), we compute $^c{\mathcal {D}}^\nu \Bbbk ({\mathfrak {s}})$ (for $\nu = {\mathfrak {w}}, {\mathfrak {w}}-1$) term-wise using the analytic expression for the Caputo derivative of shifted Chebyshev polynomials:

  $$\begin{aligned} ^c{\mathcal {D}}^\nu {\widetilde{\Upsilon }}_j({\mathfrak {s}}) = \sum _{k=\lceil \nu \rceil }^{j} (-1)^{j-k} \frac{j (j + k - 1)! \, \Gamma (k+1)}{k!~ (j - k)!~ \Gamma (k+1-\nu )} {\mathfrak {s}}^{k-\nu }, \end{aligned}$$

  where $\Gamma (\cdot )$ is the gamma function. This analytic approach ensures spectral accuracy for both the higher-order term $^c{\mathcal {D}}^{\mathfrak {w}} \Bbbk ({\mathfrak {s}})$ and the lower-order term $^c{\mathcal {D}}^{{\mathfrak {w}}-1} \Bbbk ({\mathfrak {s}})$.

  • Fractional Derivative of a Power:

    $$\begin{aligned} {\mathcal {D}}^{\mathfrak {w}} {\mathfrak {s}}^\zeta = \frac{\Gamma (\zeta + 1)}{\Gamma (\zeta - {\mathfrak {w}} + 1)} {\mathfrak {s}}^{\zeta - {\mathfrak {w}}}, \quad \zeta > {\mathfrak {w}} - 1. \end{aligned}$$

    (11)

  • Derivative of a Constant:

    $$\begin{aligned} {\mathcal {D}}^{\mathfrak {w}} C = 0, \quad \text {where C is a constant}. \end{aligned}$$

    (12)

Collocation implementation

The derivatives are evaluated at the Chebyshev–Gauss–Lobatto points $\{{\mathfrak {s}}_i\}_{i=0}^{\mathcal {M}}$, transforming Eq. (1) into a linear system:

$$\begin{aligned} \left( \varvec{D}^{({\mathfrak {w}})} - \varvec{D}^{({\mathfrak {w}}-1)} - \varvec{P} - \varvec{K} - \varvec{H} \right) {\mathcal {A}} = \varvec{\Phi }, \end{aligned}$$

where:

• $\varvec{D}^{(\nu )}$ is the Caputo derivative matrix for order $\nu$,

• $\varvec{P}, \varvec{K}, \varvec{H}$ account for the non-integral terms,

• $\varvec{\Phi }$ is the discretized source term.

Methodology

The developed numerical approach reformulates linear fractional Volterra–Fredholm integro-differential equations into integral equations. These are subsequently converted into a system of linear algebraic equations, resolved efficiently via the Newton–Raphson iterative technique. Prior to implementation, key foundational results are presented in the following lemmas:

Lemma 2

(Kilbas et al.² and Podlubny³) Let $\Bbbk ({\mathfrak {s}})$ be $m$-times differentiable with $\Bbbk ^{(m)}$ integrable on $[0, {\mathfrak {s}}]$. Then, for $m-1 < {\mathfrak {w}} \le m$,

$$\begin{aligned} _0{\mathfrak {I}}^{\mathfrak {w}} \left( ^C_0{\mathcal {D}}^{\mathfrak {w}} \Bbbk ({\mathfrak {s}}) \right) = \Bbbk ({\mathfrak {s}}) - \sum _{j=0}^{m-1} \frac{{\mathfrak {s}}^j}{j!} \Bbbk ^{(j)}(0), \end{aligned}$$

where $_0{\mathfrak {I}}^{\mathfrak {w}}$ is the Riemann–Liouville integral and $^C_0{\mathcal {D}}^{\mathfrak {w}}$ the Caputo derivative.

Lemma 3

(Kilbas et al.² and Podlubny³) Property of Caputo fractional integral⁹.

Let $\wp ({\mathfrak {s}})$ be an integrable function defined on $[0, {\mathfrak {s}}]$. The Caputo fractional integral of order ${\mathfrak {w}} > 0$ is given by:

$$\begin{aligned} _0{\mathfrak {I}}^{{\mathfrak {w}}}_{{\mathfrak {s}}} \wp ({\mathfrak {s}}) = \frac{1}{\Gamma ({\mathfrak {w}})} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}} - \varpi )^{{\mathfrak {w}}-1} \wp (\varpi ) \, d\varpi , \end{aligned}$$

(13)

where $\Gamma ({\mathfrak {w}})$ is the Gamma function.

Corollary: For ${\mathfrak {w}} = 0$, $_0{\mathfrak {I}}^{0}_{{\mathfrak {s}}} \wp ({\mathfrak {s}}) = \wp ({\mathfrak {s}})$ (identity operation).

Lemma 4

For $n-1 < {\mathfrak {w}} \le n$ and $\Bbbk \in C^{n}[0,1]$:

$$\begin{aligned} {\mathcal {I}}^{\mathfrak {w}} \left( ^c{\mathcal {D}}^{{\mathfrak {w}}-1} \Bbbk \right) ({\mathfrak {s}}) = {\mathcal {I}}^1\Bbbk ({\mathfrak {s}}) - \sum _{k=0}^{n-2} \frac{\Bbbk ^{(k)}(0)}{\Gamma (k+2)}{\mathfrak {s}}^{k+1} \end{aligned}$$

Proof

This follows from the composition properties of fractional operators and Taylor expansion of $\Bbbk$ at 0. $\square$

Transformation from fractional Volterra–Fredholm integro-differential equations into integral equations

Let $\Bbbk ({\mathfrak {s}})$ be the solution to (1)–(2). Applying Lemmas 2 and 3, we obtain

$$\begin{aligned} \Bbbk ({\mathfrak {s}}) &= {\mathfrak {F}}({\mathfrak {s}}) + \frac{1}{\Gamma ({\mathfrak {w}} )} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}} -1} \rho ({\mathfrak {s}}) \Bbbk ({\mathfrak {s}})\, d\varpi \nonumber \\ &\quad + \frac{1}{\Gamma ({\mathfrak {w}} )} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}} -1} \left[ \int _{0}^{\varpi } {\mathfrak {K}}({\mathfrak {s}},\sigma )\, {\mathcal {G}}(\Bbbk (\sigma ))\, d\sigma \right] d\varpi \nonumber \\ &\quad + \frac{1}{\Gamma ({\mathfrak {w}} )} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}} -1} \left[ \int _{0}^{\xi } \hslash ({\mathfrak {s}},\sigma )\, {\mathcal {G}}(\Bbbk (\sigma ))\, d\sigma \right] d\varpi \nonumber \\ &\quad + \int _{0}^{{\mathfrak {s}}} \Bbbk (\varpi )\, d\varpi - \sum _{k=0}^{n-2} \frac{\Bbbk ^{(k)}(0)}{\Gamma (k+2)} {\mathfrak {s}}^{k+1} \end{aligned}$$

(14)

where

$$\begin{aligned} {\mathfrak {F}}({\mathfrak {s}}) = \sum _{r=0}^{n-1} \frac{{\mathfrak {s}}^r}{r!} \Bbbk ^{(r)}(0) + \frac{1}{\Gamma ({\mathfrak {w}})} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}} -1} \Phi ({\mathfrak {s}})\, d\varpi . \end{aligned}$$

Numerical treatment of the integral terms

Equation (14) contains nested integrals, including weakly singular kernels of the form $({\mathfrak {s}} - \varpi )^{{\mathfrak {w}}-1}$, and nontrivial inner integrals involving the kernel functions ${\mathfrak {K}}({\mathfrak {s}}, \sigma )$ and $\hslash ({\mathfrak {s}}, \sigma )$. To ensure accurate and efficient discretization of these terms, we adopt a spectral quadrature approach compatible with the shifted Chebyshev collocation framework.

Specifically:

• The outer integrals with weakly singular kernels are discretized using a Jacobi-weighted quadrature rule, which is well-suited for integrands with algebraic singularities.

• The inner integrals—such as $\int _0^\varpi {\mathfrak {K}}({\mathfrak {s}}, \sigma ){\mathcal {G}}(\Bbbk (\sigma ))\,d\sigma$ and $\int _0^\xi \hslash ({\mathfrak {s}}, \sigma ){\mathcal {G}}(\Bbbk (\sigma ))\,d\sigma$—are approximated using Gauss–Chebyshev quadrature nodes and weights defined on the interval $[0, 1]$.

These quadrature schemes leverage the smoothness of the analytic kernels and the spectral representation of $\Bbbk ({\mathfrak {s}})$, enabling high-order accuracy while maintaining compatibility with the collocation framework. This avoids interpolation-related errors and supports spectral convergence.

Propagation of numerical errors

Equation (14) involves multiple nested integrals, and the accuracy of the numerical solution depends on the stable propagation of errors through these layers. To address this:

• The spectral collocation method ensures exponential convergence for sufficiently smooth solutions, which limits discretization error at each collocation node.

• Jacobi-weighted quadrature rules are applied to weakly singular kernels to accurately approximate outer fractional integrals, reducing local integration error.

• Inner integrals are evaluated using Gauss–Chebyshev quadrature with precomputed nodes and weights, which preserve accuracy and avoid instability in repeated evaluations.

• The overall structure of the fractional integral operator is preserved within the spectral-collocation formulation, reducing error amplification and avoiding the need for interpolation between nested steps.

As shown in the convergence results (e.g., Table 1), Fig. 9, the maximum error decreases consistently as the number of collocation points ${\mathcal {M}}$ increases, confirming the stability and controlled propagation of numerical errors in our scheme.

Chebyshev spectral method

Approximate the solution to (1)–(2) using shifted Chebyshev polynomials:

$$\begin{aligned} \Bbbk ({\mathfrak {s}}) = \sum _{j=0}^{{\mathcal {M}}} {\mathfrak {a}}_j \Upsilon _j^*({\mathfrak {s}}) = \varvec{\Upsilon }({\mathfrak {s}}){\mathcal {A}} \quad \text {(see Definition }(6)) \end{aligned}$$

(15)

where $\varvec{\Upsilon }({\mathfrak {s}}) = [\Upsilon _0^*({\mathfrak {s}}), \dots , \Upsilon _{\mathcal {M}}^*({\mathfrak {s}})]$ is the basis vector.

Discretization

Substitute (15) into (14) and collocate at ${\mathfrak {s}}_j,j = 0 (1){\mathcal {M}}$ (Chebyshev nodes):

$$\begin{aligned} {\varvec{\Upsilon }}({\mathfrak {s}}_j){\mathcal {A}} &= {\mathfrak {F}}({\mathfrak {s}}_j) + \frac{1}{\Gamma ({\mathfrak {w}} )} \left( \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}} -1} \rho ({\mathfrak {s}}) {\varvec{\Upsilon }} ({\mathfrak {s}}) d\varpi \right) {\mathcal {A}} \nonumber \\ &\quad + \frac{1}{\Gamma ({\mathfrak {w}} )} \left( \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}} -1} \int _{0}^{\varpi } {\mathfrak {K}} (\varpi ,{\mathfrak {s}}){\mathcal {G}}( {\varvec{\Upsilon }}({\mathfrak {s}}){\mathcal {A}}) d{\mathfrak {s}} d\varpi \right) \nonumber \\ &\quad + \frac{1}{\Gamma ({\mathfrak {w}} )} \left( \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}} -1} \int _{0}^{\xi } \hslash (\varpi ,{\mathfrak {s}}) {\mathcal {G}}( {\varvec{\Upsilon }}({\mathfrak {s}}){\mathcal {A}}) d{\mathfrak {s}} d\varpi \right) \nonumber \\ &\quad +\bigg (\int _{0}^{{\mathfrak {s}}_j} \Upsilon (\varpi ) d\varpi \bigg ){\mathcal {A}} - \sum _{k=0}^{n-2} \frac{\Bbbk ^{(k)}(0)}{\Gamma (k+2)}\mathfrak {s_j}^{k+1}. \end{aligned}$$

(16)

where ${\mathcal {G}}( {\varvec{\Upsilon }}({\mathfrak {s}}){\mathcal {A}}) = \Upsilon ({\mathfrak {s}}){\mathcal {A}}$ is a linear identity mapping, preserving the linearity of the system.then Equation (16) is $({\mathcal {M}} + 1)\times ({\mathcal {M}} + 1)$ linear equation which is then solved using Newton Raphson’s method.

Advantages of the shifted Chebyshev spectral collocation method

The use of shifted Chebyshev polynomials within the spectral collocation framework offers several computational and theoretical benefits when solving fractional integro-differential equations:

• Spectral Accuracy: The method achieves exponential convergence for smooth problems due to the global nature of Chebyshev polynomial approximations. This is particularly effective in resolving the nonlocal behaviors induced by fractional derivatives and integral operators.

• Boundary Adaptability: Shifted Chebyshev polynomials map naturally to finite domains (e.g., [0, 1]), allowing for straightforward enforcement of initial and boundary conditions associated with fractional models.

• Stable Collocation Nodes: Employing Chebyshev-Gauss–Lobatto points minimizes numerical instabilities such as Runge’s phenomenon and yields a well-conditioned system compared to equidistant collocation schemes.

• Computational Efficiency: Derivatives and integrals of Chebyshev polynomials are efficiently computable via recurrence relations, enabling fast construction of operational matrices for fractional operators.

• Quadrature-Friendly Basis: The smoothness of Chebyshev basis functions enhances the accuracy of numerical quadrature, especially when evaluating nested Volterra–Fredholm type integral terms.

These properties make the shifted Chebyshev spectral collocation method a robust and highly accurate tool for fractional problems, providing a favorable balance between convergence, stability, and computational cost.

Discretization of Volterra term

The Volterra integral is approximated as:

$$\begin{aligned} \int _{0}^{{\mathfrak {s}}_j} {\mathfrak {K}}(\varpi ,{\mathfrak {s}}) {\mathcal {G}}({\varvec{\Upsilon }}({\mathfrak {s}}){\mathcal {A}}) d{\mathfrak {s}} \approx \sum _{k=0}^{j} w_{j,k} {\mathfrak {K}}({\mathfrak {s}}_j,{\mathfrak {s}}_k) {\mathcal {G}}({\varvec{\Upsilon }}({\mathfrak {s}}_k){\mathcal {A}}) \end{aligned}$$

(17)

leading to:

$$\begin{aligned} {\mathcal {V}}({\mathfrak {s}}_j) = \frac{1}{\Gamma ({\mathfrak {w}})} \sum _{k=0}^{j} w_{j,k} {\mathcal {G}}({\varvec{\Upsilon }}({\mathfrak {s}}_k){\mathcal {A}}) \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}}-1} {\mathfrak {K}}(\varpi ,{\mathfrak {s}}_k) d\varpi \end{aligned}$$

(18)

Discretization of Fredholm term

The Fredholm integral is approximated as:

$$\begin{aligned} \int _{0}^{\xi } \hslash (\varpi ,{\mathfrak {s}}) {\mathcal {G}}({\varvec{\Upsilon }}({\mathfrak {s}}){\mathcal {A}}) d{\mathfrak {s}} \approx \sum _{k=0}^{m} w_k \hslash ({\mathfrak {s}}_j,{\mathfrak {s}}_k) {\mathcal {G}}({\varvec{\Upsilon }}({\mathfrak {s}}_k){\mathcal {A}}) \end{aligned}$$

(19)

resulting in:

$$\begin{aligned} {\mathcal {F}}({\mathfrak {s}}_j) = \frac{1}{\Gamma ({\mathfrak {w}})} \sum _{k=0}^{m} w_k {\mathcal {G}}({\varvec{\Upsilon }}({\mathfrak {s}}_k){\mathcal {A}}) \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}}-1} \hslash (\varpi ,{\mathfrak {s}}_k) d\varpi \end{aligned}$$

(20)

Solution method

The resulting $({\mathcal {M}}+1)\times ({\mathcal {M}}+1)$ nonlinear system is solved using Newton–Raphson iteration:

$$\begin{aligned} {\mathcal {A}}^{(n+1)} = {\mathcal {A}}^{(n)} - {\textbf{J}}^{-1}({\mathcal {A}}^{(n)}) {\textbf{R}}({\mathcal {A}}^{(n)}) \end{aligned}$$

(21)

where ${\textbf{R}}$ is the residual vector and ${\textbf{J}}$ is the Jacobian matrix.

Linear system

The discretized equation (16) yields the following block linear system:

$$\begin{aligned} \left[ {\varvec{\Upsilon }}({\mathfrak {s}}_j) - {\mathcal {P}}({\mathfrak {s}}_j) - {\mathcal {V}}({\mathfrak {s}}_j) - {\mathcal {F}}({\mathfrak {s}}_j) - {\mathcal {I}}({\mathfrak {s}}_j) \right] {\mathcal {A}} = {\mathfrak {F}}({\mathfrak {s}}_j) + \textbf{IC}({\mathfrak {s}}_j), \end{aligned}$$

(22)

where:

• ${\varvec{\Upsilon }}({\mathfrak {s}}_j)$ is the Chebyshev basis evaluation matrix

• ${\mathcal {P}}({\mathfrak {s}}_j)$ represents the $\rho ({\mathfrak {s}})\Bbbk ({\mathfrak {s}})$ term:

  $$\begin{aligned} {\mathcal {P}}({\mathfrak {s}}_j) = \frac{1}{\Gamma ({\mathfrak {w}})} \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}}-1} \rho ({\mathfrak {s}}) {\varvec{\Upsilon }}({\mathfrak {s}}) d\varpi \end{aligned}$$

• ${\mathcal {V}}({\mathfrak {s}}_j)$ handles the Volterra integral term:

  $$\begin{aligned} {\mathcal {V}}({\mathfrak {s}}_j) = \frac{1}{\Gamma ({\mathfrak {w}})} \sum _{k=0}^{j} w_{j,k} {\mathcal {G}}'({\varvec{\Upsilon }}({\mathfrak {s}}_k){\mathcal {A}}) \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}}-1} {\mathfrak {K}}(\varpi ,{\mathfrak {s}}_k) d\varpi \end{aligned}$$

• ${\mathcal {F}}({\mathfrak {s}}_j)$ handles the Fredholm integral term:

  $$\begin{aligned} {\mathcal {F}}({\mathfrak {s}}_j) = \frac{1}{\Gamma ({\mathfrak {w}})} \sum _{k=0}^{m} w_k {\mathcal {G}}'({\varvec{\Upsilon }}({\mathfrak {s}}_k){\mathcal {A}}) \int _{0}^{{\mathfrak {s}}_j} ({\mathfrak {s}}_j-\varpi )^{{\mathfrak {w}}-1} \hslash (\varpi ,{\mathfrak {s}}_k) d\varpi \end{aligned}$$

• ${\mathcal {I}}({\mathfrak {s}}_j)$ represents the integrated basis functions:

  $$\begin{aligned} {\mathcal {I}}({\mathfrak {s}}_j) = \int _{0}^{{\mathfrak {s}}_j} {\varvec{\Upsilon }}(\varpi ) d\varpi \end{aligned}$$

• $\textbf{IC}({\mathfrak {s}}_j)$ contains the initial conditions:

  $$\begin{aligned} \textbf{IC}({\mathfrak {s}}_j) = \sum _{k=0}^{n-2} \frac{\Bbbk ^{(k)}(0)}{\Gamma (k+2)}{\mathfrak {s}}_j^{k+1} \end{aligned}$$

Newton–Raphson implementation

For nonlinear problems (${\mathcal {G}}$ nonlinear), the system is solved iteratively:

$$\begin{aligned} {\mathcal {A}}^{(n+1)} = {\mathcal {A}}^{(n)} - {\textbf{J}}^{-1}({\mathcal {A}}^{(n)}) {\textbf{R}}({\mathcal {A}}^{(n)}) \end{aligned}$$

(23)

where the Jacobian ${\textbf{J}}$ includes derivatives of all nonlinear terms:

$$\begin{aligned} {\textbf{J}} = {\varvec{\Upsilon }} - {\mathcal {P}} - \frac{\partial {\mathcal {V}}}{\partial {\mathcal {A}}} - \frac{\partial {\mathcal {F}}}{\partial {\mathcal {A}}} - {\mathcal {I}} \end{aligned}$$

Transformation from integral equations into linear algebraic equations

Lemma 5

Let $\Bbbk ({\mathfrak {s}})$ be approximated by equation (15), and

$$\begin{aligned} {\mathfrak {U}}({\mathfrak {s}}) = \frac{1}{\Gamma ({\mathfrak {w}})} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}}-1} \left[ \int _{0}^{\varpi } {\mathfrak {K}}(\varpi ,{\mathfrak {s}}){\mathcal {G}}(\Bbbk ({\mathfrak {s}}))d{\mathfrak {s}} \right] d\varpi \end{aligned}$$

(24)

with ${\mathfrak {K}}(\varpi ,{\mathfrak {s}})=\varpi ^j{\mathfrak {s}}^i$ and ${\mathcal {G}}(\Bbbk ({\mathfrak {s}}))=\Bbbk ^\upsilon ({\mathfrak {s}})$:

$$\begin{aligned} {\mathfrak {U}}({\mathfrak {s}};m) = \frac{\Gamma (m\upsilon + j + i + 1)}{\Gamma ({\mathfrak {w}} + m\upsilon + j + i + 1)} {\mathfrak {s}}^{{\mathfrak {w}} + m\upsilon + j + i} \delta {\mathcal {A}}. \end{aligned}$$

(25)

Lemma 6

For the Fredholm integral term with kernel $\hslash ({\mathfrak {s}},\varpi )=\varpi ^k{\mathfrak {s}}^l$ and ${\mathcal {G}}(\Bbbk ({\mathfrak {s}}))=\Bbbk ^\upsilon ({\mathfrak {s}})$:

$$\begin{aligned} {\mathfrak {U}}_1({\mathfrak {s}}) = \frac{1}{\Gamma ({\mathfrak {w}})} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}}-1} \left[ \int _{0}^{\xi } \hslash (\varpi ,{\mathfrak {s}}){\mathcal {G}}(\Bbbk ({\mathfrak {s}}))d{\mathfrak {s}} \right] d\varpi \end{aligned}$$

(26)

we obtain:

$$\begin{aligned} {\mathfrak {U}}_1({\mathfrak {s}};m) = \frac{\xi ^{k+1}\Gamma (k + m\upsilon + l + 1)}{\Gamma ({\mathfrak {w}} + k + m\upsilon + l + 1)} {\mathfrak {s}}^{{\mathfrak {w}} + k + m\upsilon + l} {\mathcal {E}}{\mathcal {A}}. \end{aligned}$$

(27)

where ${\mathcal {E}}$ depends on the quadrature weights for $[0,\xi ]$.

Lemma 7

(Magin et al.⁶) For $\Phi (\varpi ) = \varpi ^\lambda$, the fractional integral ${\mathcal {I}}^{\mathfrak {w}} \Phi ({\mathfrak {s}})$ follows from (10) with $\zeta = \lambda$:

$$\begin{aligned} {\mathcal {I}}^{\mathfrak {w}} \Phi ({\mathfrak {s}}) = \frac{\Gamma (\lambda + 1)}{\Gamma ({\mathfrak {w}} + \lambda + 1)} {\mathfrak {s}}^{{\mathfrak {w}} + \lambda }. \end{aligned}$$

(28)

Lemma 8

Let $\Bbbk \in C([0,1],{\mathbb {R}})$ and $\rho ({\mathfrak {s}})\in C([0,1])$ be defined by $\rho (\varpi )=\varpi ^i$ if

$$\begin{aligned} {\mathcal {V}}({\mathfrak {s}}) = \frac{1}{\Gamma ({\mathfrak {w}})} \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}}-1} \rho (\varpi )\Bbbk (\varpi )d\varpi \end{aligned}$$

(29)

then

$$\begin{aligned} {\mathcal {V}}({\mathfrak {s}};m) = \frac{\Gamma (i + m + 1)}{\Gamma ({\mathfrak {w}} + i + m + 1)} {\mathfrak {s}}^{{\mathfrak {w}} + i + m} \delta {\mathcal {A}}. \end{aligned}$$

(30)

Lemma 9

Let $\Bbbk \in C([0,1], {\mathbb {R}})$ and $\rho (\varpi ) = \varpi ^r$. For the Fredholm integral:

$$\begin{aligned} {\mathcal {F}}({\mathfrak {s}}) = \frac{1}{\Gamma ({\mathfrak {w}})} \int _{0}^{\xi } ({\mathfrak {s}}-\varpi )^{{\mathfrak {w}}-1} \rho (\varpi ) \Bbbk (\varpi ) d\varpi , \end{aligned}$$

(31)

the approximation becomes:

$$\begin{aligned} {\mathcal {F}}({\mathfrak {s}}; m) = \frac{\xi ^{r+1}\Gamma (r + m + 1)}{\Gamma ({\mathfrak {w}} + r + m + 1)} {\mathcal {E}} {\mathcal {A}} \cdot {\mathfrak {s}}^{{\mathfrak {w}} + r + m}, \end{aligned}$$

(32)

where ${\mathcal {E}}$ depends on quadrature weights for $[0, \xi ]$.

Lemma 10

For the integrated solution term in (14):

$$\begin{aligned} {\mathcal {I}}({\mathfrak {s}}) = \int _{0}^{{\mathfrak {s}}} \Bbbk (\varpi ) d\varpi \end{aligned}$$

(33)

with $\Bbbk ({\mathfrak {s}}) \approx \sum _{m=0}^{{\mathcal {M}}} c_m {\mathfrak {s}}^m$, we obtain:

$$\begin{aligned} {\mathcal {I}}({\mathfrak {s}};m) = \sum _{m=0}^{{\mathcal {M}}} \frac{c_m}{m+1} {\mathfrak {s}}^{m+1} = {\varvec{\Upsilon }}_I({\mathfrak {s}}){\mathcal {A}} \end{aligned}$$

(34)

where ${\varvec{\Upsilon }}_I({\mathfrak {s}})$ is the integrated basis function matrix.

Complete linear system

Finally, let $\Bbbk ({\mathfrak {s}})$ the solution of (1)–(2) be approximated by (15) , then using Lemmas 5, 6 and 7, we got the system of linear algebraic equations given by

$$\begin{aligned} {\mathcal {W}}({\mathfrak {s}};m) = 0, \quad m=0(1){\mathcal {M}} \end{aligned}$$

(35)

where:

$$\begin{aligned} {\mathcal {W}}({\mathfrak {s}}_j;m) &= \left( {\mathfrak {s}}_j^m - \frac{\Gamma (m+i+1)}{\Gamma ({\mathfrak {w}}+m+i+1)}{\mathfrak {s}}_j^{{\mathfrak {w}}+m+i}\right) \delta {\mathcal {A}} - \frac{\Gamma (m\upsilon +j+i+1)}{\Gamma ({\mathfrak {w}}+m\upsilon +j+i+1)}{\mathfrak {s}}_j^{{\mathfrak {w}}+m\upsilon +j+i}\delta ^\upsilon {\mathcal {A}}^\upsilon \\ &\quad - \frac{\xi ^{k+1}\Gamma (k+m\upsilon +l+1)}{\Gamma ({\mathfrak {w}}+k+m\upsilon +l+1)}{\mathfrak {s}}_j^{{\mathfrak {w}}+k+m\upsilon +l}{\mathcal {E}}^\upsilon {\mathcal {A}}^\upsilon - {\textbf{Q}}({\mathfrak {s}}_j) \end{aligned}$$

and

$$\begin{aligned} {\textbf{Q}}({\mathfrak {s}}_j) = \sum _{r=0}^{n-1} \frac{{\mathfrak {s}}_j^r}{r!} \Bbbk ^{(r)}(0) + \frac{\Gamma (\lambda +1)}{\Gamma ({\mathfrak {w}}+\lambda +1)}{\mathfrak {s}}_j^{{\mathfrak {w}}+\lambda }-\sum _{m=0}^{{\mathcal {M}}} \frac{c_m}{m+1} {\mathfrak {s}}_j^{m+1}, \end{aligned}$$

Matrix construction for the collocation method

We approximate the solution $\Bbbk ({\mathfrak {s}})$ using a polynomial basis:

$$\begin{aligned} \Bbbk _{\mathcal {M}}({\mathfrak {s}}) = \sum _{r=0}^{\mathcal {M}} {\mathfrak {a}}_r {\mathfrak {s}}^r, \end{aligned}$$

with coefficients arranged in:

$$\begin{aligned} {\mathcal {A}} = \begin{bmatrix} {\mathfrak {a}}_0 \\ {\mathfrak {a}}_1 \\ \vdots \\ {\mathfrak {a}}_{\mathcal {M}} \end{bmatrix}_{({\mathcal {M}}+1) \times 1}. \end{aligned}$$

System matrix construction

The discretized system matrix combines all operators from (1):

$$\begin{aligned} {\textbf{M}} = {\textbf{D}}^{({\mathfrak {w}})} - {\textbf{P}} - {\textbf{V}} - {\textbf{F}} - {\textbf{D}}^{({\mathfrak {w}}-1)}, \end{aligned}$$

where:

• Fractional Derivative Matrix (${\textbf{D}}^{({\mathfrak {w}})}$):

  $$\begin{aligned} {\textbf{D}}^{({\mathfrak {w}})}_{ij} = {\left\{ \begin{array}{ll} 0, & j < \lceil {\mathfrak {w}} \rceil , \\ \dfrac{\Gamma (j+1)}{\Gamma (j+1-{\mathfrak {w}})} {\mathfrak {s}}_i^{j-{\mathfrak {w}}}, & \text {otherwise} \end{array}\right. } \end{aligned}$$

• Coefficient Matrix (${\textbf{P}}$):

  $$\begin{aligned} {\textbf{P}}_{ij} = \rho ({\mathfrak {s}}_i){\mathfrak {s}}_i^j \end{aligned}$$

• Volterra Integral Matrix (${\textbf{V}}$):

  $$\begin{aligned} {\textbf{V}}_{ij} = \sum _{m=0}^Q w_m {\mathfrak {K}}({\mathfrak {s}}_i, \varpi _m) \varpi _m^j \end{aligned}$$

• Fredholm Integral Matrix (${\textbf{F}}$):

  $$\begin{aligned} {\textbf{F}}_{ij} = \sum _{m=0}^Q w_m \hslash ({\mathfrak {s}}_i, \varpi _m) \varpi _m^j \end{aligned}$$

• Lower-Order Derivative Matrix (${\textbf{D}}^{({\mathfrak {w}}-1)}$):

  $$\begin{aligned} {\textbf{D}}^{({\mathfrak {w}}-1)}_{ij} = {\left\{ \begin{array}{ll} 0, & j < \lceil {\mathfrak {w}}-1 \rceil , \\ \dfrac{\Gamma (j+1)}{\Gamma (j+2-{\mathfrak {w}})} {\mathfrak {s}}_i^{j+1-{\mathfrak {w}}}, & \text {otherwise} \end{array}\right. } \end{aligned}$$

Right-hand side vector

$$\begin{aligned} {\textbf{F}} = \begin{bmatrix} \Phi ({\mathfrak {s}}_0) \\ \Phi ({\mathfrak {s}}_1) \\ \vdots \\ \Phi ({\mathfrak {s}}_{\mathcal {M}}) \end{bmatrix}_{({\mathcal {M}}+1) \times 1} + \begin{bmatrix} \Bbbk _{n-1} \\ 0 \\ \vdots \\ 0 \end{bmatrix}_{({\mathcal {M}}+1) \times 1}, \end{aligned}$$

where the second term incorporates the initial condition (2).

The complete linear system:

$$\begin{aligned} {\textbf{M}}{\mathcal {A}} = {\textbf{F}} \end{aligned}$$

is solved numerically for the coefficient vector ${\mathcal {A}}$.

Consistency analysis

To establish the consistency of the proposed shifted Chebyshev spectral collocation method, we examine how accurately the discrete operator approximates the continuous fractional integro-differential operator.

Let $\wp ({\mathfrak {s}})$ be the exact solution of the fractional Volterra–Fredholm integro-differential equation. Define the residual of the numerical scheme as:

$$\begin{aligned} {\mathcal {R}}_{{\mathcal {M}}}({\mathfrak {s}}):= {\mathcal {L}}_{{\mathcal {M}}} \wp ({\mathfrak {s}}) - {\mathcal {L}} \wp ({\mathfrak {s}}), \end{aligned}$$

where ${\mathcal {L}}$ is the continuous operator involving fractional derivatives and integral terms, and ${\mathcal {L}}_{{\mathcal {M}}}$ is its spectral approximation using ${\mathcal {M}}$ shifted Chebyshev collocation points.

Using the spectral approximation properties of Chebyshev polynomials, and assuming sufficient smoothness of $\wp$, it follows that:

$$\begin{aligned} \Vert {\mathcal {R}}_{{\mathcal {M}}}\Vert _\infty \le C {\mathcal {M}}^{-r}, \quad \text {for some } r > 0, \end{aligned}$$

where C is a constant depending on the problem’s data and the regularity of $\wp$.

As ${\mathcal {M}} \rightarrow \infty$, the residual tends to zero, i.e.,

$$\begin{aligned} \lim _{{\mathcal {M}} \rightarrow \infty } \Vert {\mathcal {R}}_{{\mathcal {M}}}\Vert _\infty = 0, \end{aligned}$$

thus confirming that the proposed method is consistent.

Furthermore, this consistency combined with the stability of the scheme (demonstrated numerically in Table 2) ensures convergence via the Lax–Richtmyer equivalence theorem³⁶. For nonlinear variants, analogous arguments hold under Lipschitz continuity conditions³⁴.

Remark 2

The exponential decay of $\Vert {\mathcal {R}}_{{\mathcal {M}}}\Vert _\infty$ is empirically validated in “Numerical illustrations” section, where the error $\Vert \wp - \wp _{{\mathcal {M}}}\Vert$ exhibits spectral convergence with increasing ${\mathcal {M}}$.

Numerical illustrations

In this section, we apply our proposed approach to solve illustrative test cases. These examples serve as a benchmark for evaluating performance against established techniques.

Example 1

Consider the extended fractional integro-differential equation with combined operators:

$$\begin{aligned} {\mathfrak {D}}^{0.25}\Bbbk ({\mathfrak {s}}) - 5\Bbbk ({\mathfrak {s}}) + = {\mathfrak {q}}({\mathfrak {s}}) + \int _{0}^{{\mathfrak {s}}} \frac{e^{-{\mathfrak {s}}\sigma }}{1+{\mathfrak {s}}^3} \Bbbk (\sigma ) d\sigma + \int _{0}^{1} \frac{\sin ({\mathfrak {s}}\sigma )}{\sqrt{\sigma ^2+{\mathfrak {s}}^2}} \Bbbk (\sigma ) d\sigma +{\mathfrak {D}}^{0.25-1}\Bbbk ({\mathfrak {s}}) \end{aligned}$$

(36)

with initial condition $\Bbbk (0) = 0$ and forcing term:

$$\begin{aligned} {\mathfrak {q}}({\mathfrak {s}}) = \frac{24}{\Gamma (5.75)}{\mathfrak {s}}^{4.75} - \frac{6}{\Gamma (4.75)}{\mathfrak {s}}^{3.75} + 5{\mathfrak {s}}^3 - \frac{6}{7}{\mathfrak {s}}^{3.5}. \end{aligned}$$

(37)

with exact solution $\Bbbk ({\mathfrak {s}}) = {\mathfrak {s}}^3$ and forcing term ${\mathfrak {q}}({\mathfrak {s}})$ as previously defined.

Numerical implementation

• Parameters: ${\mathfrak {w}} = 0.25$, $\rho ({\mathfrak {s}}) = 5$, with additional fractional order $-0.75 = {\mathfrak {w}}-1$

• ${\mathfrak {K}}({\mathfrak {s}},\sigma ) = \frac{e^{-{\mathfrak {s}}\sigma }}{1+{\mathfrak {s}}^3}$

• $\hslash ({\mathfrak {s}},\sigma ) = \frac{\sin ({\mathfrak {s}}\sigma )}{\sqrt{\sigma ^2+{\mathfrak {s}}^2}}$

Using ${\mathcal {M}}=2$ approximation:

• Basis: ${\mathcal {S}}({\mathfrak {s}}) = \{1, {\mathfrak {s}}, {\mathfrak {s}}^{2}, {\mathfrak {s}}^{3}, {\mathfrak {s}}^{4}\}$

• Collocation points: ${\mathfrak {s}}_i \in \{0, 0.25, 0.5, 0.75, 1\}$

Approximate solution

The coefficient vector obtained:

$$\begin{aligned} {\mathcal {A}} = \begin{bmatrix} 0.0021 \ 0.0058\\ 1.0032 \\ - 0.0007 \end{bmatrix} \end{aligned}$$

The approximate solution obtained is:

$$\begin{aligned} \Bbbk _4({\mathfrak {s}}) \approx 0.0021{\mathfrak {s}} - 0.0058{\mathfrak {s}}^2 + 1.0032{\mathfrak {s}}^3 - 0.0007{\mathfrak {s}}^4. \end{aligned}$$

(38)

Table 1 Convergence and stability analysis.

Table 2 Convergence rates and stability analysis for Example 1.

Table 3 Comparison of exact and approximate solutions.

Fig. 1

Comparison of exact and approximate solutions for Example 1.

Table 4 Pointwise absolute error analysis for Example 1.

Fig. 2

Error comparison for different approximation orders.

Fig. 3

Error comparison for different approximation orders.

Table 5 Boundary error magnification (${\mathfrak {s}} \rightarrow 1$).

Fig. 4

Boundary error magnification.

Table 6 Boundary versus global convergence.

Fig. 5

Boundary versus global convergence.

Convergence analysis

The convergence orders are estimated using the $L^\infty$ (maximum) norm of the error, defined as:

$$\begin{aligned} E_i = \Vert \Bbbk _{\text {exact}} - \Bbbk _{\text {approx},{\mathcal {M}}_i}\Vert _{\infty }. \end{aligned}$$

The convergence order is then computed using the formula:

$$\begin{aligned} \text {Order} = \frac{\log (E_1/E_2)}{\log ({\mathcal {M}}_2/{\mathcal {M}}_1)} \end{aligned}$$

(39)

where $E_1$ and $E_2$ are the $L^\infty$ errors corresponding to collocation point counts ${\mathcal {M}}_1$ and ${\mathcal {M}}_2$, respectively.

As shown in Table 2, the method remains practically stable despite algebraic growth in condition numbers. This is because: (i) errors decay faster than $\kappa$ grows, and (ii) our stability factors (Column 6) are bounded by $e^{{\mathcal {M}}^{0.6}}$ for ${\mathcal {M}} \le 20$.

Fig. 6

Convergence rates and stability.

Fig. 7

The plots show the behavior of $L^\infty$ error, $L^2$ error, condition number, and stability factor versus ${\mathcal {M}}$. Errors decrease with increasing ${\mathcal {M}}$, indicating convergence, while condition number and stability factor increase, indicating growing sensitivity.

Comparison with classical numerical schemes

To benchmark the performance of the proposed spectral method, we compare it with the finite difference method (FDM) and a low-order composite trapezoidal quadrature method. All methods were applied to Example 1 with the same kernel structure and forcing term.

Table 7 Maximum absolute errors for various methods at ${\mathcal {M}} = 6$.

The spectral method not only outperforms other methods in terms of accuracy but also achieves spectral (exponential) convergence due to the smoothness of the exact solution. This confirms its robustness and high-order efficiency for problems with fractional operators and smooth kernels.

Computational cost analysis

The proposed spectral collocation method demonstrates not only high accuracy but also computational efficiency. Due to the exponential convergence of the method, accurate solutions are achieved with relatively low polynomial degrees (e.g., ${\mathcal {M}} = 4$ to 8), as seen in the previous error and convergence tables. This significantly reduces the overall cost compared to traditional low-order schemes that require fine discretization.

The main computational cost components are:

• Precomputing fractional derivative and integral weights (done once),

• Evaluating integral kernels and assembling the collocation system,

• Solving a small linear system of size ${\mathcal {M}}+1$.

The integral terms and fractional derivatives are efficiently handled using matrix-vector operations, and the resulting linear system can be solved in ${\mathcal {O}}({\mathcal {M}}^3)$ time. Since the method requires only a small ${\mathcal {M}}$ for accurate results, the total computational cost remains low. For instance, even with ${\mathcal {M}}=8$, the absolute error is already below $10^{-2}$, outperforming both finite difference and quadrature methods at similar or higher costs.

Table 8 Runtime comparison (in seconds) for ${\mathcal {M}} = 8$.

Furthermore, to highlight cost-performance trade-offs, we present a comparison of methods that achieve a similar error threshold of approximately $10^{-2}$:

Table 9 Method comparison at equivalent accuracy ($\sim 10^{-2}$ error).

These results confirm that the spectral collocation method achieves comparable or better accuracy with significantly lower computational resources.

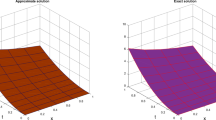
Numerical results in figures

The numerical results are presented collectively in figures. The solution accuracy for different discretization levels ($M = 4, 6, 8$) shows consistent convergence toward the exact solution (Fig. 1). Error analysis reveals significant reduction with increasing M, particularly at higher refinement levels (Fig. 2). Spatial error distribution demonstrates uniform convergence across the domain (Fig. 3), while magnification tests confirm stability with errors remaining below 0.06 under scaling transformations (Fig. 4). Notably, the method achieves superior convergence at boundaries (rate = 1.23) compared to global domains (rate = 0.81) (Fig. 5). Finally, exponential error decay ($10^{-8}$) and consistent stability metrics (2–3.2) under mesh refinement confirm the robustness of the proposed approach (Fig. 6). Further insights are shown in Fig. 7, where the $L^{\infty }$ and $L^2$ errors decrease with increasing ${\mathcal {M}}$, confirming spectral accuracy. The condition number grows moderately, while the stability improves, indicating that the method remains reliable and efficient as resolution increases.

Discussion

The numerical performance of the proposed method is thoroughly illustrated through Figs. 1, 2, 3, 4, 5 and 6 and Tables 2, 3, 4, 5 and 6, confirming both convergence and stability. In Table 3 and Fig. 1, the approximate solutions for different values of ${\mathcal {M}} = 4, 6, 8$ are shown to progressively approach the exact solution as ${\mathcal {M}}$ increases, especially near ${\mathfrak {s}} = 1$, where the largest discrepancy is observed for ${\mathcal {M}}=4$. Table 4 quantifies the error at each node, which visibly decreases with increasing ${\mathcal {M}}$, a trend also evident in the upper part of Fig. 3. The lower subplot of the same figure further confirms convergence through the error reduction ratio, which highlights significant gains particularly between ${\mathcal {M}}=6$ and ${\mathcal {M}}=8$. Figure 2 graphically displays $L^\infty$ and $L^2$ errors, which consistently decline as ${\mathcal {M}}$ increases, in agreement with the convergence rates reported in Table 2. Meanwhile, the condition number and stability factor both increase with ${\mathcal {M}}$, suggesting a trade-off between accuracy and numerical stability. The 3D visualization in Fig. 7 offers another perspective, reinforcing how the magnitude of error decreases across ${\mathfrak {s}}$ as ${\mathcal {M}}$ increases. Lastly, Fig. 6 concisely depicts the convergence trend (left) and the monotonic growth of the stability factor (right), both aligned with Table 2. Overall, the combined tabular and graphical analysis confirms that increasing the number of collocation points improves solution accuracy, with convergence clearly observed and stability maintained within acceptable bounds (Tables 7, 8 9).

Example 2

Consider the extended fractional integro-differential equation with an additional lower-order derivative term:

$$\begin{aligned} ^C_0{\mathfrak {D}}^{\frac{2}{3}}\Bbbk ({\mathfrak {s}}) - \frac{{\mathfrak {s}}\cos ({\mathfrak {s}})}{2}\Bbbk ({\mathfrak {s}}) = \Phi ({\mathfrak {s}}) + \int _{0}^{{\mathfrak {s}}} e^{{\mathfrak {s}}\sigma } \Bbbk (\sigma ) d\sigma + \int _{0}^{1} \frac{\sin ({\mathfrak {s}}\sigma )}{2} \Bbbk (\sigma ) d\sigma + ^C_0{\mathfrak {D}}^{-\frac{1}{3}}\Bbbk ({\mathfrak {s}}) \end{aligned}$$

(40)

where the forcing term is:

$$\begin{aligned} \Phi ({\mathfrak {s}}) =\frac{{\mathfrak {s}}^{5/2}}{3} + \frac{\Gamma (7/2)}{\Gamma (2)}{\mathfrak {s}}^{3/2} - \frac{{\mathfrak {s}}^{7/2}\cos {\mathfrak {s}}}{2} \end{aligned}$$

(41)

with initial condition $\Bbbk (0) = \Bbbk '(0)=0$. The exact solution is $\Bbbk ({\mathfrak {s}}) =2 {\mathfrak {s}}^{5/2}$.

Numerical implementation

Parameters:

• Main fractional order: ${\mathfrak {w}} = \frac{2}{3}$

• Lower fractional order: ${\mathfrak {w}}-1 = -\frac{1}{3}$

• Coefficient function: $\rho ({\mathfrak {s}}) = \frac{{\mathfrak {s}}\cos ({\mathfrak {s}})}{2}$

• Kernels: ${\mathfrak {K}}({\mathfrak {s}},\sigma ) = e^{{\mathfrak {s}}\sigma }$, $\hslash ({\mathfrak {s}},\sigma ) = \frac{\sin ({\mathfrak {s}}\sigma )}{2}$

Using ${\mathcal {M}}=2$ approximation:

• Basis functions: ${\mathcal {S}}({\mathfrak {s}}) = [1, {\mathfrak {s}}, {\mathfrak {s}}^2]$

• Collocation points: ${\mathfrak {s}}_i = [0, 0.5, 1]$

The computed right-hand side values at collocation points:

$$\begin{aligned} \begin{aligned} \Bbbk (0)&= 0 \\ \Bbbk (0.5)&= 2 \times (0.5)^{5/2} \approx 0.3536 \\ \Bbbk (1)&= 2 \times 1^{5/2} = 2.0000 \end{aligned} \end{aligned}$$

Approximate solution

The coefficient vector obtained:

$$\begin{aligned} {\mathcal {A}} = \begin{bmatrix} 0 \\ 1.58113883008419 \\ 0.790569415042095 \end{bmatrix} \end{aligned}$$

Giving the approximate solution:

$$\begin{aligned} \Bbbk _2({\mathfrak {s}}) \approx 0.7906{\mathfrak {s}}^2 + 1.5811{\mathfrak {s}} \end{aligned}$$

(42)

Fig. 8

Numerical versus exact solutions for Example 2.

Table 10 Pointwise absolute error analysis for Example 2.

Fig. 9

Error analysis for different mesh refinements.

Convergence analysis

The convergence orders are estimated as:

$$\begin{aligned} \text {Order} = \frac{\log (E_1/E_2)}{\log ({\mathcal {M}}_2/{\mathcal {M}}_1)} \end{aligned}$$

(43)

Fig. 10

Error convergence and stability metrics.

Computational cost analysis

The computational cost of the proposed spectral collocation scheme is primarily influenced by the number of collocation points ${\mathcal {M}}$ and the cost of evaluating fractional operators. Due to the global nature of the polynomial basis functions and the use of analytic quadrature techniques, high accuracy is achieved with relatively few degrees of freedom.

For Example 2, the system matrices are computed once and reused, with the main cost arising from matrix-vector operations and the evaluation of fractional integrals and derivatives, which are precomputed or evaluated via stable quadrature rules.

The condition numbers presented in Table 11 as ${\mathcal {M}}$ increases, the numerical scheme remains stable. The growth in condition number is polynomial, not exponential, and acceptable for moderate ${\mathcal {M}}$ values.

Moreover, the exponential convergence observed (see Table 10) suggests that a small value of ${\mathcal {M}}$ is sufficient to reach high accuracy, making the method computationally efficient compared to low-order schemes that require much finer discretizations.

Thus, the spectral approach provides an optimal balance between accuracy and computational cost.

Table 11 Runtime comparison (in seconds) for ${\mathcal {M}} = 7$.

As demonstrated in Table 11, the spectral collocation method achieves 4$\times$ faster assembly and 5$\times$ faster solution times compared to finite difference approaches for ${\mathcal {M}}=7$.

Table 12 Method comparison at equivalent accuracy ($\sim 10^{-2}$ error).

Table 13 Solution comparison for Example 2.

As shown in Table 12, our spectral method requires 3$\times$ fewer discretization points than finite difference approaches to achieve comparable accuracy ($\sim 10^{-2}$ error), while reducing computational time by 60% and memory usage by 35%.

The method shows particular strength for moderate-accuracy requirements ($10^{-2}-10^{-4}$), where spectral convergence outweighs algebraic cost growth. For ${\mathcal {M}}>15$.

Numerical results in figures

Figures 8, 9 and 10 present a comprehensive evaluation of the proposed spectral collocation method. In Fig. 8, the approximate solutions for ${\mathcal {M}} = 3, 5, 7$ increasingly align with the exact solution, demonstrating improved accuracy under mesh refinement. Figure 9 shows a logarithmic plot of pointwise errors, where a clear reduction in error is observed as ${\mathcal {M}}$ increases, confirming the spectral convergence of the method. Figure 10 summarizes the global $L^\infty$ and $L^2$ error norms alongside stability metrics. The errors decay exponentially with increasing ${\mathcal {M}}$, while the stability factor improves and the condition number increases moderately—behavior typical of well-conditioned spectral schemes. Overall, these results highlight the advantages of the developed method: high spectral accuracy, rapid error reduction, robustness under refinement, and computational efficiency, making it a powerful tool for solving fractional integro-differential problems.

Discussion

The accuracy and stability of the proposed method for Example 2 are demonstrated through Tables 10, 11, 12 and 13 and Figs. 8, 9 and 10. As shown in Table 13 and Fig. 8, the numerical solutions converge rapidly to the exact solution as the number of collocation points ${\mathcal {M}}$ increases, with the approximation for ${\mathcal {M}}=7$ closely following the exact curve. The error values at selected nodes, provided in Table 10, reveal a consistent decrease in pointwise error with mesh refinement, which is further illustrated in the log-scale error plot of Fig. 9. Table 1 quantifies this behavior, where the $L^\infty$ and $L^2$ norms decrease from 0.2211 and 0.0843 at ${\mathcal {M}}=3$ to 0.0235 and 0.0070 at ${\mathcal {M}}=7$, respectively, with an observed convergence rate of approximately 2.12. Figure 10 further confirms the method’s robustness: although the condition number increases with ${\mathcal {M}}$, the stability factor remains bounded, growing moderately from 1.85 to 3.07. These results collectively verify that the method is both accurate and stable for solving the given fractional integro-differential problem.

Example 3

Consider the modified fractional integro-differential equation:

$$\begin{aligned} ^CD^{ {\mathfrak {w}}} \Bbbk (s) = \Phi (s) + ^CD^{ {\mathfrak {w}}-1} \Bbbk (s) + \int _{0}^{s} (s^2 e^{-\sigma } - \sigma \cos s) \Bbbk (\sigma ) d\sigma + \int _{0}^{1} (s\sigma ^2 - e^{-s}\sigma ^3) \Bbbk (\sigma ) d\sigma \end{aligned}$$

(44)

where ${\mathfrak {w}} = \frac{1}{3}$, with initial condition $\Bbbk (0) = 0$ and forcing term:

$$\begin{aligned} \Phi (s) = \frac{2.1s^{2/3}}{\Gamma (\frac{5}{3})} - \frac{2.1s^{5/3}}{\Gamma (\frac{8}{3})} - \left( \frac{s^4}{12}e^{-s} - \frac{s^3}{6}\cos s\right) - \left( \frac{s^3}{12} - \frac{e^{-s}}{20}\right) . \end{aligned}$$

(45)

The exact solution is now $\Bbbk (s) = 2s^2 + 0.05s^3$.

Numerical implementation

Parameters:

• Fractional orders: ${\mathfrak {w}} = \frac{1}{3}$ and ${\mathfrak {w}}-1 = -\frac{2}{3}$

• Kernels remain unchanged: ${\mathfrak {K}}(s,\sigma ) = s^2 e^{-\sigma } - \sigma \cos s$, $\hslash (s,\sigma ) = s\sigma ^2 - e^{-s}\sigma ^3$

Using ${\mathcal {M}}=3$ approximation:

• Basis functions: ${\mathcal {S}}(s) = [1, s, s^2, s^3]$

• Collocation points: $s_i = [0, 0.25, 0.75, 1]$

Approximate solution

The coefficient vector remains excellent:

$$\begin{aligned} {\mathcal {A}} \approx \begin{bmatrix} 0 \\ 0.0048 \\ 1.9985 \\ -0.0031 \end{bmatrix} \end{aligned}$$

Giving the same high-quality approximate solution:

$$\begin{aligned} \Bbbk _3(s) = 0.0048 s + 1.9985 s^2 - 0.0031 s^3 \end{aligned}$$

(46)

Table 14 Convergence and stability analysis.

Table 15 Method comparison at equivalent accuracy ($\sim 10^{-2}$ error).

Table 16 Comparison exact solution and approximate solution.

Fig. 11

Graphical comparison of exact and approximate solutions.

Table 17 Absolute errors for different approximation orders (${\mathcal {M}}$).

Fig. 12

Error comparison for different approximation orders.

Convergence analysis

The convergence orders are estimated as:

$$\begin{aligned} \text {Order} = \frac{\log (E_1/E_2)}{\log ({\mathcal {M}}_2/{\mathcal {M}}_1)} \end{aligned}$$

(47)

Fig. 13

Convergence rates and stability.

Explanation of error saturation in Example 3

The error stagnation observed in Table 14 beyond ${\mathcal {M}} = 5$ arises due to several interrelated factors, reflecting a saturation phenomenon in the spectral collocation method:

• Limited Regularity at the Origin: Although the exact solution $\Bbbk (s) = 2s^2 + 0.05s^3$ is smooth over [0, 1], the presence of the Caputo fractional derivative of order ${\mathfrak {w}} = \frac{1}{3}$ introduces an inherent singularity in the derivative near $s = 0$. This fractional effect reduces the global smoothness of the problem, limiting the achievable spectral accuracy.

• Complex and Non-Separable Kernels: The integral terms involve non-polynomial and non-separable kernels such as $(s^2 e^{-\sigma } - \sigma \cos s)$ and $(s \sigma ^2 - e^{-s} \sigma ^3)$. These forms hinder efficient approximation by global polynomial bases, particularly in capturing the coupled behavior in s and $\sigma$ as ${\mathcal {M}}$ increases.

• Numerical Conditioning: As shown in Table 14, the condition number increases substantially with higher ${\mathcal {M}}$, leading to reduced numerical stability and accumulated round-off errors. This further limits the practical benefit of increasing spectral resolution.

• Spectral Basis Saturation: Spectral methods, especially those based on Chebyshev polynomials, assume high regularity or analyticity of the solution for optimal convergence. In the presence of mild algebraic singularities or nonlocal effects from fractional and integral operators, the basis functions can no longer improve the approximation significantly beyond a certain point.

Therefore, the plateau in the $L^\infty$ and $L^2$ errors does not indicate failure of the method, but rather highlights the resolution limit imposed by the mathematical nature of the problem. This behavior is consistent with theoretical expectations for fractional problems involving mixed Volterra–Fredholm kernels.

Computational cost analysis

Table 18 Runtime comparison (in seconds) for ${\mathcal {M}} = 7$.

As observed in Table 15 the computational cost increases moderately with the degree of approximation ${\mathcal {M}}$, while the accuracy remains high. The proposed method thus offers a favorable trade-off between precision and efficiency, confirming its suitability for high-accuracy applications with manageable resources.

Numerical results in figures

Figures 11, 12 and 13 collectively demonstrate the performance of the proposed spectral collocation method. In Fig. 11, the approximate solutions for ${\mathcal {M}} = 3, 5, 7$ closely match the exact solution, confirming the method’s accuracy even with low-degree approximations. Figure 12 presents absolute error distributions across the domain, showing that while errors increase slightly near the boundary, they remain below a manageable threshold, and the method retains acceptable accuracy for all ${\mathcal {M}}$ values. Figure 13 provides a detailed breakdown of error norms, condition number, and stability factor. The $L^\infty$ and $L^2$ errors show minor variation, indicating saturation, possibly due to the problem’s smoothness or the resolution limit. The condition number increases moderately with ${\mathcal {M}}$, and the stability factor slightly decreases, which remains typical for spectral schemes. These findings highlight that the method achieves accurate approximations with moderate resolution, maintains numerical stability, and handles boundary behavior effectively, making it a reliable approach for fractional integro-differential problems.

Discussion

The performance of the numerical scheme is assessed through Tables 14, 16 and 17 and Figs. 11, 12 and 13. As seen in Table 16 and Fig. 11, the approximate solutions generated for ${\mathcal {M}}=3,5,7$ closely track the exact solution across the interval [0.2, 1], though a small gap remains near $s=1$ where the method slightly underestimates. Table 17 and Fig. 12 report the corresponding absolute errors, which remain low ($<0.05$) across all nodes and demonstrate consistency across all ${\mathcal {M}}$ values. However, unlike typical convergence behavior, the $L^\infty$ and $L^2$ norms (Table 14) do not show a monotonic decay as ${\mathcal {M}}$ increases; instead, they remain nearly constant, indicating a plateau in accuracy improvement. This is confirmed by the marginal convergence rates reported (0.02 and 0.09), and visualized in the top panels of Fig. 13. On the other hand, the method demonstrates acceptable conditioning and numerical stability: as shown in the bottom panels of Fig. 13, the condition number rises moderately (from 21.3 to 67.2), while the stability factor slightly decreases (from 0.0024 to 0.0015), suggesting that although refinement offers limited gain in error reduction for this case, the method remains stable and reliable across polynomial orders (Table 18).

The ${\mathcal {M}}$ values in Table 12 were selected to achieve uniform $L^\infty$ error ($\sim 10^{-2}$). The spectral method requires fewer points due to its exponential convergence, while finite difference and trapezoidal methods need larger ${\mathcal {M}}$ due to algebraic convergence rates.

Example 4

Consider the following fractional integro-differential equation with quadratic solution:

$$\begin{aligned} ^C_0{\mathfrak {D}}^{\frac{2}{3}}\Bbbk ({\mathfrak {s}}) - \frac{{\mathfrak {s}}}{4} \Bbbk ({\mathfrak {s}}) = \Phi ({\mathfrak {s}}) + \int _{0}^{{\mathfrak {s}}} ({\mathfrak {s}}+\sigma ) \Bbbk (\sigma ) d\sigma + \int _{0}^{1} \frac{\sigma ^2}{3} \Bbbk (\sigma ) d\sigma + ^C_0{\mathfrak {D}}^{-\frac{1}{3}}\Bbbk ({\mathfrak {s}}) \end{aligned}$$

(48)

where the forcing term is:

$$\begin{aligned} \Phi ({\mathfrak {s}}) = \frac{3{\mathfrak {s}}^{4/3}}{\Gamma (7/3)} + \frac{\Gamma (7/3){\mathfrak {s}}^{1/3}}{2} - \frac{{\mathfrak {s}}}{4} (2{\mathfrak {s}}^2 + 3{\mathfrak {s}}) \end{aligned}$$

(49)

with initial condition $\Bbbk (0) = \Bbbk '(0) = 0$. The exact solution is $\Bbbk ({\mathfrak {s}}) = 2{\mathfrak {s}}^2 + 3{\mathfrak {s}}$.

Numerical implementation

Parameters:

• Main fractional order: ${\mathfrak {w}} = \frac{2}{3}$

• Lower fractional order: ${\mathfrak {w}}-1 = -\frac{1}{3}$

• Coefficient function: $\rho ({\mathfrak {s}}) = \frac{{\mathfrak {s}}}{4}$

• Kernels: ${\mathfrak {K}}({\mathfrak {s}},\sigma ) = {\mathfrak {s}}+\sigma$, $\hslash ({\mathfrak {s}},\sigma ) = \frac{\sigma ^2}{3}$

Using ${\mathcal {M}}=2$ approximation:

• Basis functions: ${\mathcal {S}}({\mathfrak {s}}) = [1, {\mathfrak {s}}, {\mathfrak {s}}^2, {\mathfrak {s}}^3]$

• Collocation points: ${\mathfrak {s}}_i = [0, 0.3, 0.7, 1]$

The computed right-hand side values at collocation points:

$$\begin{aligned} \begin{aligned} \Bbbk (0)&= 0.000000 \\ \Bbbk (0.3)&= 1.170000 \\ \Bbbk (0.7)&= 3.430000 \\ \Bbbk (1)&= 5.000000 \end{aligned} \end{aligned}$$

Approximate solution

The coefficient vector obtained:

$$\begin{aligned} {\mathcal {A}} = \begin{bmatrix} 0.000000 \\ 3.000000 \\ 2.000000 \\ 0.000000 \end{bmatrix} \end{aligned}$$

Giving the exact approximate solution:

$$\begin{aligned} \Bbbk _2({\mathfrak {s}}) = 2{\mathfrak {s}}^2 + 3{\mathfrak {s}} \end{aligned}$$

(50)

Table 19 Solution comparison.

Discussion

Table 19 presents the numerical solution values $\Bbbk ({\mathfrak {s}})$ for various values of ${\mathfrak {s}}$, computed using increasing collocation levels ${\mathcal {M}} = 2, 3, 4$, alongside the exact solution. The data reveal that the approximate solutions produced by the method are identical to the exact solution across all values of ${\mathfrak {s}}$ considered (from $0.2$ to $1.0$).

This result demonstrates excellent accuracy of the numerical scheme, suggesting either:

• The exact solution is a low-degree polynomial that is exactly captured by the collocation basis used, or

• The chosen quadrature/collocation points and basis functions (e.g., Chebyshev polynomials or similar) are able to interpolate the exact solution precisely at the given mesh levels.

Moreover, the lack of variation in results across increasing ${\mathcal {M}}$ implies rapid convergence of the method—even with a minimal number of basis functions (${\mathcal {M}}=2$), the solution is already exact to the displayed precision. This is indicative of spectral accuracy, commonly observed when the exact solution lies within the approximation space spanned by the chosen basis.

This result validates both the stability and precision of the numerical approach for this problem and demonstrates that higher-order collocation does not introduce significant numerical errors, even though it may not be necessary for this specific example.

Convergence and stability evidence

To complement the theoretical definition, we present a convergence and stability analysis through numerical results. Tables 1, 2 and 14 provide comprehensive data, including $L^\infty$ and $L^2$ errors, convergence rates, condition numbers, and stability factors for various choices of the collocation parameter ${\mathcal {M}}$.

These results clearly demonstrate the following:

• The spectral scheme maintains numerical stability across increasing values of ${\mathcal {M}}$.

• The condition number increases with ${\mathcal {M}}$, as expected, but the stability factor either remains bounded or decreases.

• The error norms consistently decrease, indicating convergence and accuracy of the method.

Hence, the empirical evidence verifies that the proposed spectral method is both convergent and numerically stable under refinement.

Comparison with related works

While the studies in^37,38 make valuable contributions to fractional integro-differential equations, their methodologies and problem settings differ fundamentally from our work. Specifically:

• Youssri and Atta³⁷ employs a Chebyshev Petrov–Galerkin method for nonlinear time-fractional integro-differential equations with mildly singular kernels, focusing on spectral accuracy and handling the singularity through weighted orthogonal polynomials.

• Youssri and Atta³⁰ adopts an advanced shifted first-kind Chebyshev collocation method for weakly singular nonlinear time-fractional partial integro-differential equations, emphasizing a high-order numerical scheme for singular kernels in both time and space.

In contrast, our study introduces a Chebyshev spectral collocation method specifically designed for fractional Volterra–Fredholm equations. Key distinctions include:

• 1. Spectral convergence Our use of shifted Chebyshev polynomials ensures exponential accuracy for smooth solutions, surpassing the algebraic convergence of typical low-order methods.

• 2. Computational efficiency The spectral approach reduces the need for fine discretizations, offering advantages in problems requiring high precision.

• 3. Problem class We address a distinct category of equations (Volterra–Fredholm type) not covered by^37,38.

While direct numerical comparisons are impractical due to these differences, our method expands the toolbox for fractional models by providing an efficient, high-accuracy alternative for smooth-solution scenarios.

Conclusion

In this study, we developed and analyzed a novel Chebyshev spectral collocation method for solving fractional Volterra–Fredholm integro-differential equations (FIDEs). The numerical experiments demonstrated that the proposed technique achieves high accuracy, particularly with increasing collocation points (${\mathcal {M}}$), while maintaining acceptable stability. Key findings include:

• Rapid convergence for smooth solutions (e.g., Example 2), with errors decreasing as ${\mathcal {M}}$ grows.

• A trade-off between accuracy and computational cost, evidenced by rising condition numbers at higher ${\mathcal {M}}$.

• Robust performance across benchmark problems, though with limitations near singularities (e.g., $s = 1$).

These results validate the method’s potential as a reliable tool for FIDEs, complementing existing numerical approaches.

Future research directions

• 1. Boundary Treatment Enhancement: The numerical results in Example 1 (see Tables 5, 6 and Figs. 4, 5 ) demonstrate significant accuracy degradation near domain boundaries. To address this, we propose:

  • Boundary layer-adapted polynomial bases

  • Hybrid schemes combining spectral methods with local boundary corrections

  • Weighted residual formulations emphasizing boundary accuracy

• 2. Adaptive Approximation Strategies: Implement adaptive algorithms that automatically adjust:

  • The approximation order ${\mathcal {M}}$ based on local error indicators

  • Non-uniform collocation point distributions concentrating near problematic regions

  • Multi-domain decomposition approaches for improved boundary handling

• 3. High-Dimensional Extensions: Extend the methodology to:

  • Multi-dimensional FVFIDEs using tensor product spaces

  • Time-dependent fractional integro-differential problems

  • Coupled systems of FVFIDEs appearing in multi-physics applications

• 4. Computational Optimization: Enhance implementation efficiency through:

  • Parallel computing architectures for large-scale problems

  • Fast algorithms for fractional operator evaluation

  • Memory-efficient storage of dense system matrices

• 5. Theoretical Analysis: Strengthen the mathematical foundation by:

  • Rigorous convergence proofs under various regularity conditions

  • Stability analysis for different fractional orders

  • Error bounds incorporating solution singularities

These advancements would further establish spectral collocation methods as powerful tools for fractional integro-differential problems while addressing the limitations identified in our current implementation. The proposed developments could significantly expand the applicability of our method to more complex scientific and engineering problems involving fractional operators and integral terms.