Development of a deep learning model for survival prediction in heart failure: competing risk and frailty model

Abstract

This study presents a novel deep learning (DL) framework, the Deep Neural Frailty Competing Risks (DNFCR) model, which simultaneously integrates frailty and competing risks (CR) for mortality prediction in heart failure (HF). While existing models like Neural Frailty Models (NFM) address frailty and DeepHit handles CR, DNFCR is the first DL approach to combine both components, offering improved handling of censored data in healthcare applications. We evaluated DNFCR against established models (DeepSurv, CoxPH) using real-world HF data, assessing its ability to capture unobserved heterogeneity through proportional (DNFCR_PF) and non-proportional (DNFCR_NF) frailty structures. In this retrospective cohort study, we analyzed 435 HF patients (enrolled March–September 2018; 5-year follow-up until July 2023) with 57 demographic/clinical features, categorized by cause-specific mortality. The models’ performance was evaluated using the C-index, IBS, and INBLL. Our results in mortality from heart failure demonstrated marginal but consistent improvements in predictive accuracy when incorporating frailty (C-index: ~0.66). Differences in predicting other-cause mortality were minimal across the models. DNFCR-PF also performed better regarding the IBS (0.17 ± 0.01) and INBLL (0.02 ± 0.53). However, the clinical relevance of the cause-specific mortality requires further validation in both outcome categories. Comparative analysis revealed that DNFCR and traditional models achieved comparable accuracy in survival prediction, highlighting that DL’s superiority is context-dependent and influenced by data and unmeasured confounders. Strengths include DNFCR’s potential for personalized risk stratification and adaptability to other diseases with CR. The DNFCR model showed DL potential in HF survival prediction but requires clinical validation compared to traditional approaches.

Introduction

Competing risk analysis (CR) is a vital area of medical research and healthcare that aims to predict the timing of specific events¹. A prime example is cardiovascular disease, a leading cause of death worldwide. Among cardiovascular diseases, heart failure (HF) is associated with high morbidity and mortality. HF is the third leading cause of cardiovascular death in developed countries² and significantly contributes to morbidity and hospital admissions³.

Accurately predicting the survival of HF patients is essential for guiding clinical decision-making, personalizing treatment plans, and, ultimately, improving patient outcomes⁴. Advanced analytical techniques are needed to achieve this goal, as traditional survival models often fail to fully capture the complexity of CR and its impact on patient survival⁵.

In many medical studies, CR arises when multiple causes of death may influence the occurrence of a specific event, such as death from a particular cause⁵. Traditional survival analysis methods, such as the Kaplan-Meier method, log-rank tests, and Cox models, assume noninformative censoring, where secondary causes of death are treated as censored data^6,7. However, this assumption may lead to biased estimates due to the correlation between event occurrence and censoring times⁸. Additionally, classical survival models assume a linear relationship between independent and dependent variables⁹, which may not capture the complexity of CR. This highlights the need for specialized, advanced analytical techniques that account for nonindependence and nonlinear relationships to provide more accurate and reliable inferences in such analyses^7,8.

This research presents a novel approach that explicitly incorporates frailty¹⁰ to account for potential correlations in CR. Frailty refers to unobserved covariates at the individual or cluster level that impact the occurrence of an event, and it also enables the modeling of nonlinear relationships within a deep learning (DL) framework^10,11.

The preliminary analysis of our data revealed complex relationships among various variables, including BMI, LVEF, SPO2, temperature, heart rate, DBP, and SBP. These variables exhibited a diverse range of relationships, such as compound, power, S-shaped, growth, exponential, logistic, cubic, and quadratic patterns, all of which explained a portion of the variance in the dependent variable. Given the limitations of classical models in handling such complexity, we opted for DL methods, which offer higher accuracy and better predictive capabilities by identifying novel patterns overlooked in previous analyses. CR and frailty challenge DL models by introducing bias when correlated event types are treated as independent CR and unmeasured features create frailty. Ignoring these factors inflates prediction variance, as Wu et al. (2023) demonstrated in neural frailty networks¹⁰. These factors can substantially affect model performance and accuracy. A systematic review by Monterrubio-Gómez et al. (2022)¹² examined DL based methods¹³for time-to-event analysis, highlighting two key advantages: (i) DL models can automatically learn complex, nonlinear interactions and temporal patterns that traditional manual feature engineering might overlook (Feature Importance). (ii) Unique characteristics include the ability to process high-dimensional data, handle missing data through embedding layers, and model time-varying effects without relying on proportional hazards assumptions. These features make DL models valuable for survival analysis in complex clinical settings¹².

Despite this progress, current DL models (e.g., DeepHit) handle CR but assume frailty is negligible, while frailty models (e.g., NFM) often ignore CR. This dual oversight limits real-world applicability, as HF patients exhibit both phenomena. Frailty increases vulnerability to both HF progression and competing infections². Methodologically, frailty induces dependence between competing events (e.g., HF patients may die sooner from “any” cause, linking HF and non-HF mortality risks). Ignoring this inflates HF mortality estimates⁸. This underscores the need for broader model generalization to accommodate a wider range of survival analysis scenarios.

Our DNFCR model integrates a gamma frailty component to address unobserved heterogeneity and incorporates competing risk analysis to consider multiple potential causes of mortality. We aim to compare the performance of this model against that of established methods, such as DeepSurvCR¹⁴, to comprehensively evaluate its effectiveness in real-world scenarios and its ability to improve survival predictions.

This article is structured as follows: First, we review the literature on CR, deep learning, and frailty models. Next, we outline the methodology used in this study, detailing how frailty concepts are integrated into deep neural networks for CR analysis. Finally, we describe our experimental setup and compare the performance of our model with that of DeepSurvCR.

Literature review

Recent years have seen significant advancements in DL for survival analysis, particularly in addressing CR and unobserved heterogeneity. However, critical gaps remain in how existing models integrate these complexities, often leading to biased or oversimplified predictions.

Limitations of current DL approaches

Lee et al. (2018) introduced DeepHit, a nonparametric model for survival time distribution that outperformed traditional methods but fails to account for unobserved heterogeneity (frailty) and assumes independent CR, limiting its clinical applicability¹⁵. Rietschel et al. (2018) improved feature selection for medical data but did not address how irrelevant features might interact with latent patient-specific frailty¹⁶. While DeepCompete (Huang & Liu, 2020) enhanced CR handling, it relies on proportional hazard assumptions, often violated in real-world data¹⁷. Similarly, Nagpal et al.’s (2020) Deep Survival Machines advanced parametric estimation but ignores frailty, risking biased predictions in heterogeneous populations¹⁸.

Gaps in frailty integration

Recent frailty models, such as those by Tran et al. (2020) and Mendel et al. (2022), incorporated random effects into neural networks but require prespecified frailty distributions (e.g., Gamma or Gaussian), which may not capture true underlying heterogeneity^11,19.

The DNN-FM (Lee et al., 2023) and NFM (Wu et al., 2023) made strides by integrating multiplicative frailty for censored data, yet NFM’s reliance on parametric frailty limits flexibility, and neither model fully resolves the interplay between frailty and CR^10,20.

Our proposed DNFCR model advances prior work by:

• 1. Nonparametric Frailty Learning: Unlike NFM or DNN-FM, DNFCR learns frailty distributions directly from data, eliminating the need for restrictive parametric assumptions.

• 2. Joint Modeling of Frailty and CR: While DeepHit and DeepCompete treat CR as independent processes, DNFCR explicitly models their dependence on latent frailty, reducing bias in risk estimation.

• 3. Dynamic Covariate-Frailty Interactions: Building on Hong et al.’s (2022) contrastive learning, DNFCR captures time-varying relationships between covariates, frailty, and CR, a feature overlooked by earlier frailty models.

By unifying these innovations, DNFCR offers a more flexible and interpretable framework for survival analysis, particularly in complex clinical scenarios like HF, where unobserved heterogeneity and CR are pervasive.

Materials and methods

Study population

We retrospectively analyzed data from 529 consecutive patients with acute heart failure with reduced ejection fraction (HFrEF; LVEF ≤ 40%) who were admitted to Rajaie Cardiovascular Medical Center (RCMCH) between March and August 2018 and received standard guideline-directed medical therapy. The study inclusion criteria required: (i) confirmed HFrEF diagnosis, (ii) index hospitalization during the study period, (iii) receipt of appropriate HF treatment, and (iv) at least one documented follow-up within six months’ post-discharge.

Exclusion criteria

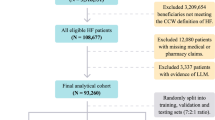
We excluded 94 patients (17.8%) for either having > 20% missing clinical data (n = 63) or not receiving HF-specific treatment (n = 31). The final analytical cohort thus comprised 435 patients with complete treatment and follow-up data.

The enrollment flowchart (Fig. 1) details 529 screened → 94 excluded (31 untreated, 63 incomplete data) → 435 analyzed. Untreated patients were excluded as their outcomes (often palliative-care-associated) would distort treated-HFrEF trajectories, consistent with ESC-HF-LT registry standards.

Fig. 1

Study enrollment flowchart.

We followed them from 2018 to July 2023 (5 years). This dataset consists of 57 characteristics (demographic and clinical). We categorized patients by cause of death into two groups: those who died from HF and those who died from other causes.

Ethics approval

This study was approved by the ethics committee of the School of Medical Sciences, Tarbiat Modares University, under the approval ID IR.MODARES.REC.1402.012. The participants’ privacy was preserved. All participants completed an informed consent form. International agreements approved all the processes (World Medical Association, Declaration of Helsinki, Ethical Principles for Medical Research Involving Human Subjects).

Statistical analysis

Raw data was organized into a database for analysis. Continuous variables are reported as means ± standard deviations, and categorical variables are shown as frequencies and percentages. Statistical analysis was performed using Python, with the DNFCR and DeepSurvCR models implemented in PyTorch. Due to the lack of standard training/testing splits in the survival dataset, we used a 5-fold cross-validation method, allocating one fold for testing and 20% for validation⁸.

We employed three key metrics to evaluate model performance:

• (i) The concordance probability (C-index) $\:(\mathcal{C}=\mathbb{P}\left[\widehat{S}\left({T}_{i}\mid\:{Z}_{i}\right)<\widehat{S}\left({T}_{j}\mid\:{Z}_{j}\right)\mid\:{T}_{i}<{T}_{j},{\delta\:}_{i}=1\right])$; measures how accurately the model ranks patient survival times, where 0.5 indicates random prediction and 0.7–0.8 represents clinically useful discrimination. Discrimination (c-index) indicates the model’s ability to separate patients with different outcomes.

• (ii) The Integrated Brier Score (IBS) $\:\begin{array}{c}{(\mathcal{S}}_{\text{I}\text{B}\text{S}}\left(\widehat{S}\right(t\mid\:x),(z,d\left)\right)=\frac{1}{{t}_{2}-{t}_{1}}{\int\:}_{{t}_{1}}^{{t}_{2}}\:{\mathcal{S}}_{\text{Brier\:}}^{t}\left(\widehat{S}\right(t\mid\:x),(z,d\left)\right)dt)\\\:\end{array}$quantifies prediction error through mean squared differences (0=perfect, 0.25=random), with our score of 0.17 demonstrating 32% improvement over chance. Calibration (Brier score) reflects how well predicted probabilities match observed outcomes.

• (iii) The Integrated Negative Binomial Log-Likelihood (INBLL) assesses prediction confidence while accounting for censored data, where values approaching zero (like our 0.02) reflect greater reliability. Together, these metrics provide complementary insights - the C-index evaluates ranking accuracy, IBS measures overall error magnitude, and INBLL gauges uncertainty, enabling a comprehensive assessment of clinical utility²¹

  $$\begin{aligned}NBLL& =-\frac{1}{N}\sum\:_{i=1}^{N}\:\left[\frac{\text{l}\text{o}\text{g}\left(1-\widehat{S}\left(t\mid\:{x}_{i}\right)\right)I\left({T}_{i}\le\:t,{e}_{i}=1\right)}{\widehat{G}\left({T}_{i}\right)}+\frac{\text{l}\text{o}\text{g}\widehat{S}\left(t\mid\:{x}_{i}\right)I\left({T}_{i}>t\right)}{\widehat{G}\left(t\right)}\right] \\ INBLL & =\frac{1}{{l}_{2}-{l}_{1}}{\int\:}_{{l}_{1}}^{{t}_{2}}\:NBLL\left(t\right)dt.\end{aligned}$$

Survival analysis with competing risks

Survival analysis aims to estimate the time to an event (e.g., HF-related death), frequently dealing with censoring. In this study, we consider the problem of CR survival prediction when more than one event is possible and when each patient experiences only one of those events. This is a common scenario in HF prognosis, where a patient can die either of HF or other complications (e.g., cancer).

Given the training dataset $\:D=\left\{{T}^{\left(j\right)},\:{e}^{\left(j\right)},\:{{c}^{\left(j\right)},\:x}^{\left(j\right)}\right\},\:j=1,\dots\:,N$, where $\:{T}^{\left(j\right)}$ is the time to event for patient j,$\:\:{e}^{\left(j\right)}$ is the event indicator, $\:{c}^{\left(j\right)}$ is the censoring and $\:{x}^{\left(j\right)}$ are the patient features, we want to learn to predict the probability that an event occurs before some time$\:\:T,\:P({T}^{\left(j\right)}\le\:t,\:{e}^{\left(j\right)}=e|{x}^{\left(j\right)})$, known as the cause-specific for events. Classical analysis methods can address CR via special-cause Cox models, but implementing these methods requires an independence assumption²². When independence among CR is not confirmed, their relationship can be described via frailty as “unobserved dispersion” in the model.

This study introduces the DNFCR method, a novel DL approach for estimating time-to-event in CR in the presence of frailty.

Deep neural frailty competing risk (DNFCR) framework

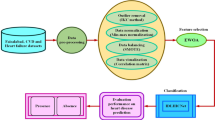
DNFCR employs two distinct deep neural network architectures to model CR in survival analysis (Fig. 2). The key idea is to utilize the censored observations appropriately in the likelihood function to obtain consistent parameter estimates despite incomplete information about event times. The incorporation of frailty into the deep neural network model allows the DNFCR structure to account for individual-specific characteristics and changes influenced by unobserved factors that may impact event risk.

Fig. 2

Model structure for analyzing competing risks with deep neural networks and frailty components. DeepsurvCR: Deep neural survival competing risk; DNFCR: Deep neural networks frailty competing risks.

Unobservable factors varying among individuals can lead to intraindividual correlation.

For the frailty variable u, we utilize the gamma density function:

$$\:{G}_{\theta\:}\left(x\right)=\frac{1}{\theta\:}\text{log}\left(1+\theta\:x\right),\theta\:\ge\:0$$

(1)

We begin by integrating the conditional survival function with frailty to derive the observed likelihood function for the competing risk:

$$\:\begin{array}{c}S\left(t \left| \right. X\right)={\mathbb{E}}_{{u}_{i}\sim\:{f}_{\theta\:}}\left[{e}^{-{u}_{i}{\int\:}_{0}^{t}\:{e}^{h\left(s,X\right)}ds}\right]\\\:=:{e}^{-{G}_{\theta\:}\left({\int\:}_{0}^{t}\:{e}^{h\left(s,X\right)}ds\right)}\end{array}\:\:$$

(2)

The frailty transform $\:{G}_{\theta\:}\left(x\right)=-\text{l}\text{o}\text{g}\left({\mathbb{E}}_{{u}_{i}\sim\:{f}_{\theta\:}}\left[{e}^{-{u}_{i}\text{x}}\right]\right)$ is defined as the ($\:-\text{l}\text{o}\text{g}$) of the Laplace transform of the frailty distribution for each cause. Consequently, the conditional cumulative hazard function is given by $\:{\:\text{H}\left(t\right|X)=G}_{\theta\:}\left({\int\:}_{0}^{t}\:{e}^{h\left(s,X\right)}ds\right)$.

For the PF model, we utilize two multilayer perceptrons (MLPs), denoted as $\:{h}^{\Lambda}={h}^{\Lambda}(t;{W}^{h},{b}^{h})$ and $\:\widehat{m}=\widehat{m}(X;{W}^{m},{b}^{m})$), to approximate the functions h and m, parameterized by $\:{(W}^{h},{b}^{h})$ and $\:({W}^{m},{b}^{m})$, respectively. Here, W represents a collection of weight matrices across all layers of the MLPs, whereas b represents a set of bias vectors across all layers. Considering the standard results regarding the likelihood of censored data as presented in Eq. (2), the learning of parameters under the PF framework can be expressed as follows²³:

$$\:\begin{array}{c}L\left({\text{W}}^{h},{\text{b}}^{h},{\text{W}}^{m},{\text{b}}^{m},\theta\:\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:=\frac{1}{n}\left[\begin{array}{c}\sum\:_{i\in\:\left[n\right]}\:{\delta\:}_{i}\text{log}{g}_{\theta\:}\left({e}^{\widehat{m}\left({X}_{i}\right)}{\int\:}_{0}^{{T}_{i}}\:{e}^{\widehat{h}\left(s\right)}ds\right)+{\delta\:}_{i}\widehat{h}\left({T}_{i}\right)+{\delta\:}_{i}\widehat{m}\left({X}_{i}\right)\\\:-{G}_{\theta\:}\left({e}^{\widehat{m}\left({X}_{i}\right)}{\int\:}_{0}^{{T}_{i}}\:{e}^{\widehat{h}\left(s\right)}ds\right)\end{array}\right]\end{array}$$

(3)

in which$\:{g}_{\theta\:}\left(x\right)=\frac{\partial\:}{\partial\:x}{G}_{\theta\:}\left(x\right).$.

The estimated conditional cumulative risk and survival functions are represented by Eq. (4).

$$\:\begin{array}{c}{\widehat{\text{H}}}_{\text{P}\text{F}}(t\mid\:X)={G}_{{\widehat{\theta\:}}_{n}}\left({\int\:}_{0}^{t}\:{e}^{{\widehat{h}}_{n}\left(s\right)+{\widehat{m}}_{n}\left(X\right)}ds\right),\\\:{\widehat{S}}_{\text{P}\text{F}}(t\mid\:X)={e}^{-{\widehat{\text{H}}}_{\mathbf{P}\mathbf{F}}(t\mid\:X)},\end{array}$$

(4)

For the NF model:

$$\:\begin{array}{c}L\left({\text{W}}^{v},{\text{b}}^{v},\theta\:\right)\\\:=\frac{1}{n}\left[\begin{array}{c}\sum\:_{i\in\:\left[n\right]}\:{\delta\:}_{i}\text{log}{g}_{\theta\:}\left({\int\:}_{0}^{{T}_{i}}\:{e}^{\widehat{v}\left(s,{X}_{i},\:\:{\text{W}}^{v},{\text{b}}^{v}\right)}ds\right)+{\delta\:}_{i}\widehat{v}\left({T}_{i},{X}_{i},\:{\text{W}}^{v},{\text{b}}^{v}\right)\\\:-{G}_{\theta\:}\left({\int\:}_{0}^{{T}_{i}}\:{e}^{\widehat{v}\left(s,{X}_{i},\:\:{\text{W}}^{v},{\text{b}}^{v}\right)}ds\right)\end{array}\right]\:\:\:\end{array}$$

(5)

The estimated conditional cumulative risk and survival functions are represented by Eq. (6).

$$\:\begin{array}{c}{\widehat{\text{H}}}_{\text{N}\text{F}}(t\mid\:X)={G}_{{\widehat{\theta\:}}_{n}}\left({\int\:}_{0}^{t}\:{e}^{{\widehat{v}}_{n}\left(s,X\right)}ds\right),\:\\\:{\widehat{S}}_{\text{N}\text{F}}(t\mid\:X)={e}^{-{\widehat{\text{H}}}_{\mathbf{N}\mathbf{F}}(t\mid\:X)},\end{array}$$

(6)

Results

This study analyzed the mortality of 435 HF patients over five years, focusing on deaths from HF versus other causes. In total, 43.96% of all patients died from HF, 26.64% died from other causes, and 29.4% survived. The median survival time was 43.40 months (Table 1).

Table 1 Distribution of causes of death after heart failure.

The one-year survival rate for patients who died from HF was 80.66% (95% CI: 0.76–0.84), decreasing to 68.3% (95% CI: 0.63–0.72) at three years and 59.52% (95% CI: 0.54–0.64) at five years. For those who died from other causes, the survival rates were 91.78% (95% CI: 0.88–0.94) at one year, 79.08% (95% CI: 0.74–0.83) at three years, and 70.29% (95% CI: 0.64–0.75) at five years.

Figure 3 presents the impact of the cause of death on survival in HF patients. The analysis showed that HF itself is a major contributor to mortality in this study population, leading to a reduced probability of survival compared to deaths from other causes.

Fig. 3

Kaplan-Meier survival analysis for heart failure patients, stratified by cause of death.

The mean age of all patients was 56.57 ± 18.11 years, ranging from 14 to 95. Among those who died from HF, the average age was 59.26 ± 1.40 years, with the highest mortality in the 56–65 age group. Of these, 63.1% were male, 89.4% were Freelancers, and 87.5% held an Undergraduate degree. Additionally, 93.1% resided in urban areas, and 89.4% were married.

In contrast, patients who died from other causes had a mean age of 62.04 ± 1.71 years, with the peak mortality rate in the 66–75 age group. Of these, 52.6% were male, 81.4% were Freelance, and 82.5% held an Undergraduate. Furthermore, 89.7% lived in Urban, and 89.7% were married (Tables 2 and 3 provide additional details on other features).

Table 2 Distribution of symptoms and disease characteristics in patients diagnosed with heart failure by cause of death.

Table 3 Distribution of clinical characteristics in patients diagnosed with heart failure by cause of death.

To identify the optimal learning rate for the deepsurv and DNFCR models, we conducted experiments using a range of learning rates [0.1, 0.01, 0.001, 0.0001, 0.00001, 0.003, 0.006, 0.008, 0.01, 0.02, 0.03, 0.05, 0.07], and we evaluated performance based on the IBS, INBLL, and c-index criterion. This process involved creating and deploying a new deepsurv model for each learning rate, utilizing a negative log-likelihood loss function and the Adam optimizer in 200 epochs, during which learning rate and weight decay were monitored. We systematically compared model performance across these learning rates and determined the optimal rate. Ultimately, results were categorized into two groups: mortality due to HF and mortality from other causes (Table 4).

Table 4 Table of best hyperparameter Values.

Figure 4 depicts the structure of a 55-layer deep neural network, specifically developed for the Deepsurv and DNFCR models.

Fig. 4

The flowchart of DeepsurvCR and DNFCR on heart failure data.

Statistical comparisons

Survival analysis revealed that the traditional CoxPH model achieved C-indices of 0.61 for HF mortality and 0.58 for other causes mortality. Then, we assessed the performance of DNFCR_PF and DNFCR_NF relative to their nonfrailty counterpart, DeepSurvCR. The results presented in Table 5 showed that the DNFCR_PF model achieved the highest c-index value of 0.66 ± 0.04 compared to other models for mortality from HF. Additionally, the DNFCR_PF model showed superior performance in both INBLL and IBS metrics. In predicting death from other causes, the DeepsurvCR model performs better regarding the C-index, while the DNFCR models exhibit similar performance in IBS.

Table 5 DNFCR models in comparison with the non-frailty deepsurvcr model.

Pairwise DeLong tests confirmed that all three advanced models (DNFCR-PF, DNFCR-NF, and DeepSurvCR) demonstrated statistically superior discriminative ability compared to the traditional CoxPH model. The DNFCR-PF model showed particular strength in predicting HF mortality, with its enhanced precision evidenced by superior IBS and INBLL relative to other models. While between-model differences for mortality from other causes predictions were non-significant (p > 0.05) (Table 6; Fig. 5).

Table 6 Performance comparison of DNFCR models versus deepsurvcr and coxph models.

Fig. 5

Comparative performance of survival prediction models in heart failure patients: ΔC-index analysis with 95% confidence intervals.

Clinical validation through calibration analysis

The calibration plots (Fig. 6, Panel A) demonstrate that the DNFCR model achieves high accuracy in predicting mortality from HF at 1- and 3-year time horizons (showing close alignment with the ideal line), while exhibiting minor deviations in 5-year predictions, likely attributable to reduced sample size in long-term follow-ups. For non-HF mortality, while 1-year and 5-year predictions showed systematic underestimation, the mid-range (3-year) predictions maintained clinically acceptable accuracy (± 5% from ideal) (Fig. 6, Panel B).

Fig. 6

Calibration for mortality from heart failure (A) and mortality from other causes (B) at 1-, 3-, and 5-year intervals.

Discussion

This study aimed to investigate the accuracy of a DL model with a frailty approach to HF data. The DNFCR method introduces a novel approach for modeling mortality in CR, utilizing two different neural structures.

Although existing models like NFM incorporate frailty and DeepHit addresses CR, the DNFCR framework represents the first DL approach to simultaneously integrate both components. Overall, the DNFCR framework provides a method to handle censored data while accounting for frailty and CR. Although its predictive accuracy is moderate (C-index ~ 0.66), it could become a valuable tool for healthcare applications where censorship frequently occurs.

Our findings showed marginal improvements when incorporating frailty. This reflects that incorporating frailty into DL models for predicting outcomes in patients with HF can improve model accuracy. Frailties are utilized in time-to-event modeling to account for unobserved heterogeneity among individuals who can impact event occurrence. In time-to-event analysis, frailty models extend traditional survival models such as the Cox model by introducing random effects, known as frailties. These frailties capture individual-specific characteristics that affect the event of interest but are not directly observed. By incorporating frailties, time event models can better address the variability in event times that the measured covariates cannot explain.

This study compared several survival models: The CoxPH, the DeepSurveCR model, the DNFCR model with proportional frailty (DNFCR_PF), and the DNFCR model with nonproportional frailty (DNFCR_NF). Despite the small sample size, the DeepSurve and DNFCR models showed comparable accuracy in predicting survival time. This preliminary comparison highlights methodological differences but does not conclusively establish superiority for clinical use.

These models capture complex, nonlinear relationships between input variables and survival outcomes¹⁴. In line with our results, in the study by Ruofan Wu et al., the authors examined the results of their real-world survival data. They used five survival datasets plus one nonsurvival dataset to evaluate NFM models. These include four small datasets, including METABRIC, RotGBSG, FLCHAIN, and SUPPORT, and a large dataset called KKBOX. The results show that the NFM model outperforms 12 other reference models and provides significant improvements, especially on the METABRIC, SUPPORT, and MIMIC-III datasets. Thus, NFM, as a robust and practical framework for survival prediction, has demonstrated better results in evaluation criteria such as IBS and INBLL than other models¹⁰.

Another study proposed combining DL techniques with feature enhancement methods to assess cardiovascular disease risk in patients, achieving a prediction accuracy of 90%²⁴.

While the DNFCR model demonstrates innovation in integrating frailty with CR, its discriminative power (C-index: 0.66) remains moderate compared to the ideal threshold of 0.75 for clinical decision-making. This performance is consistent with existing DL models in similar clinical contexts, such as DeepSurv (C-index: 0.65) and NFM (C-index: 0.62–0.69)^10,25. The modest discrimination may reflect both the inherent noise in real-world clinical data (e.g., unmeasured confounders) and the complexity of modeling correlated CR. Although larger datasets could improve precision, particularly for rare events.

Overall, these studies indicate that DL models, with their ability to model intricate relationships and employ advanced structures such as neural networks, can achieve superior performance in survival data analysis compared with traditional models.

On the other hand, some studies indicate that no definitive and consistent results demonstrate the absolute superiority of DL models over classical models²⁶. While DL has garnered attention for its ability to model complex and nonlinear relationships, particularly in survival time prediction, its performance is not always significantly better than that of traditional models. Certain comparisons indicated that classical models can perform satisfactorily and, in some cases, even surpass DL models²⁷.

Some studies suggest that DL models may need more data for training and fine-tuning and may not consistently outperform traditional models when data are scarce²⁸. DNFCR and the CoxPH model are essential for analyzing CR, yet they differ fundamentally in structure and application. Additionally, a model’s suitability depends on the data’s specific characteristics and research requirements, so one cannot universally assert that DL models are superior to traditional models^26,27.

While the DNFCR-PF model’s C-index of 0.66 represents moderate discriminative ability, its clinical value emerges from three key innovations: (1) simultaneous handling of CR, avoiding overestimation of HF-specific mortality prevalent in traditional models; (2) incorporation of frailty as a proxy for unmeasured patient heterogeneity, mirroring clinical assessment practices; and (3) superior calibration (IBS 0.17 ± 0.01) enabling reliable absolute risk estimation. In practice, this model could stratify patients into actionable risk tiers, identifying those with > 50% 1-year mortality risk who may benefit from advanced therapies while flagging low-risk patients for de-escalation. The modest C-index reflects the inherent complexity of HF prognostication, where competing comorbidities and treatment responses create irreducible uncertainty. Future integration of dynamic biomarkers and larger datasets may enhance performance, but the current framework already provides clinically meaningful distinctions that traditional Cox models cannot achieve.

Strengths

The DNFCR model, while initially developed for HF patients, has the potential to be applied to other patient groups, such as those with different types of heart failure or even other complex diseases, provided that the relevant data from these populations are appropriately adjusted. However, its performance may vary depending on the specific characteristics of the new dataset, such as sample size, data quality, and the presence of CR. The model’s ability to account for frailty and unobserved heterogeneity enhances survival predictions, offering more personalized and accurate estimates. While the model’s current performance is limited, future iterations with improved accuracy could potentially help identify high-risk patients, facilitating timely interventions that may reduce mortality. By incorporating frailty, the model better reflects individual patient characteristics, allowing for more targeted treatment strategies and improved resource allocation. Additionally, the model could be adapted for use in other clinical settings, improving outcomes in diseases where CR is a factor. Overall, the DNFCR model represents a theoretical approach that may, after substantial refinement and validation, contribute to clinical decision-making and improve the quality of care across diverse patient populations.

This study highlights the potential of DL models, particularly those incorporating frailty, for improving the prediction of patient outcomes in complex diseases such as HF. While these models demonstrate superior performance in capturing complex relationships between variables and survival outcomes, their practical application requires careful consideration. While DL models can significantly enhance predictive accuracy, they may necessitate large datasets and computational resources. Additionally, traditional models such as the Cox model may still be suitable for specific scenarios, especially when data are limited. Therefore, the optimal choice of model should be based on a careful assessment of the particular clinical context and the trade-off between model complexity and predictive accuracy.

Limitations

Given the stringent inclusion and exclusion criteria, our study cohort represents a specific subset of HF patients, which may limit the generalizability of our findings to broader HF populations typically examined in traditional studies.

On the other hand, analyzing CR with frailty via a DL approach in real-world settings involves several challenges that necessitate further research and advanced methods. The DNFCR model represents a preliminary step toward addressing unobserved heterogeneity in survival analysis, but its clinical applicability requires further validation. The DNFCR framework often requires extensive, accurate datasets that are frequently hard to obtain in practice. Additionally, the black box nature of neural networks complicates result interpretation and understanding of prediction mechanisms, posing significant limitations in applications where interpretability is crucial. Small sample size, internal validation, and lack of external benchmarks preclude definitive claims about clinical impact.

Understanding the strengths and limitations of each model is crucial for informed decision-making regarding adoption and implementation in practice.

Future Directions: Larger datasets, external validation in multi-center, and integration with established clinical risk scores are needed to justify real-world use.

Conclusion

This study introduces a novel approach to survival prediction in HF patients by developing a DNFCR model. The DNFCR model demonstrates a technical innovation and a proof-of-concept for integrating frailty into competing risk analysis, because it can account for unobserved heterogeneity and analyze CR, but requires further validation before clinical application. Given the similarity in performance, choosing the best model may depend on different factors, such as model complexity, training time, and computational cost. Ultimately, this research emphasizes the importance of integrating DL with frailty models and competing risk analysis to improve predictions and facilitate more precise therapeutic decisions, highlighting methodological challenges that warrant further research.